Bad data identification method considering the on-load tap changer model

With the connection and integration of renewable energy, the on-load tap-changer (OLTC) has become an important device for regulating voltage in distribution networks. However, due to non-smooth and non-linear characteristics of OLTC, traditional bad data identification and state estimation methods for transmission network are limited when applied to the distribution network. Therefore, the nonlinearity and droop control constraints of the OLTC model are considered in this paper. At the same time, the quadratic penalty function is introduced to realize the fast normalization of the tap position. It proposes a two-stage bad data identification method based on mixed-integer linear programming. In the first stage, suspicious measurements are identified using projection statistics and maximum normalized residual methods for preprocessing the measurement data. In the second stage, a linearization approach utilizing hyhrid data-physical driven is applied to handle nonlinear constraints, leading to the development of a bad data identification model based on mixed-integer linear programming. Finally, the proposed methodology is validated using a modified IEEE-33 node test feeder example, demonstrating the accuracy and efficiency of bad data identification.

1 Introduction

In the context of distribution network state estimation, the integrity of the estimation process can be compromised by the presence of erroneous data. Such data may arise from a variety of sources, including heterogeneous measurement instruments, sensor failures, and communication disruptions. These inaccuracies have the potential to severely impact the reliability and accuracy of the state estimation outcomes (Chen et al., 2021). The same time, With the continuous integration of renewable energy sources, OLTC is increasingly being utilized in power grid applications every year. It plays an important role in ensuring the safe and reliable operation of distribution networks and grid dispatching (Ju and Huang, 2023).The relevant parameters of the on-load tap-changer device exhibit nonlinearity and discreteness in mathematical models, and traditional continuous variable processing methods may reduce the accuracy of state estimation.

Traditional methods for bad data identification primarily encompass residual search methods (Handschin et al., 1975; Lin and Abur, 2018; Zhao and Mill, 2018), zero residual methods (Zhuang and Balasubramanian, 1987), and estimation-based methods (Huang and Lin, 2004). These approaches are susceptible to errors such as misjudgment and missed detection. Contemporary techniques for bad data detection and identification predominantly include optimization-based and intelligent algorithm-based approaches. Among these, optimization-based methods have demonstrated a significant capacity for accurate identification of erroneous measurement data. A literature (Irving, 2008) proposes a robust state estimation model based on mixed integer nonlinear programming (MINLP). This method has high accuracy in identifying bad data, but lacks precision in estimation. Additionally, the model is nonconvex, nonlinear, and introduces a large number of 0/1 integer variables, making it difficult to solve. When the scale of the system increases, the solution efficiency de-creases. The Schweppe-type generalized M-estimator with Huber psi-function (SHGM) is currently a method with good robustness (Mili et al., 1996). Introduces coefficients that reflect the lever-age properties, which can suppress the weight of bad data in leverage points and weaken the effect of bad data residuals in the objective function. However, it cannot completely filter out the impact of bad data. Existing methods need further improvement in terms of computational efficiency, accuracy, and ability to handle bad data.

For state estimation problems involving discrete variables, modelling and solving based on MINLP methods may have low convergence and computational efficiency. In order to avoid solving MINLP problems, in traditional state estimation, OLTC tap positions are usually treated as continuous variables (Shiroi and Hosseinie, 2008), which may lead to biases in the estimated results due to mismatch with the actual operating characteristics of OLTC. The literature (Korres et al., 2004; Teixeira et al., 1992; Handschin and Kliokys, 1995) presents, in addition to the traditional treatment of continuous variables, using rounding or sensitivity analysis to round the tap positions to integers. These integer values are then taken as known parameters and used in the state estimation problem to solve state variables such as voltage magnitude and phase angle. The literature (Maalouf et al., 2013) develops a mixed integer quadratic programming model with discrete variables, which can effectively address the tap position rounding issue with high accuracy, although the approach is more complex. Furthermore, the literature (Nanchian et al., 2017) applies a hybrid particle swarm optimization method to solve MINLP problems that involve discrete tap positions, but the algorithm has a long computation time and low efficiency.

To address the challenges of nonlinearity and low efficiency in bad data identification for OLTC discrete variables, this paper introduces a two-stage bad data identification method utilizing a positive curvature quadratic penalty function to facilitate rapid adjustment of OLTC tap positions. This method enhances solution efficiency while maintaining the accuracy of identification. The main contributions are as follows:

1) In order to improve the accuracy of bad data identification, an optimization-based method for bad data identification is proposed in this paper. This method can accurately and effectively identify the presence of bad data in the measurement data, demonstrating a good identification accuracy.

2) To cope with the issue of low efficiency in solving traditional MINLP models due to a large number of discrete and nonlinear constraints, this paper presents a two-stage bad data identification model based on mixed integer linear programming (MILP). In the first stage, all measurements are distinguished using projection statistics and maximum normalized residual methods, generating a reduced set of suspicious measurements. In the second stage, a linearization model based on hyhrid data-physical driven is proposed to linearize nonlinear constraints, leading to a MILP-based bad data identification method that significantly improves the accuracy and efficiency of bad data identification.

The organizational structure of this paper is as follows: Section 2 introduces the method of identifying leverage points and suspicious measurement bad data based on projection statistics and maximum normalized residual method, and obtains the reduction of suspicious measurement set; Section 3 introduces the traditional MINLP bad data identification model, and proposes a hyhrid data-physical driven linearization model considering OLTC constraints, and constructs a bad data identification model based on MILP; Section 4 illustrates the experimental at IEEE-33 node test feeder; Section 5 provides the conclusion.

2 Stage 1: reduction of suspicious measurement set

In this paper, the reduced suspicious measurement set mainly consists of two parts. The first part involves the identification of leverage points through the use of projection statistics, while the second part involves the identification of suspicious measurements in non-leverage points using the maximum normalized residual method. The detailed explanation of the two algorithm processes is provided below.

2.1 Identification of leveraged measurements using projection statistics

This subsection describes the mathematical model for identifying leverage points based on projection statistics. Firstly, the connotation of leverage points and their impact on state estimation are introduced. Currently, there are two types of definitions for leverage points. As shown in Figure 1, the first type is based on regression model analysis, while the second type is based on the analysis of diagonal elements of the hat matrix. The difference between the two methods is as follows: The first type constructs a factor space composed of the measurement Jacobian matrix and the measurement vector, obtaining the distribution of row vectors in each group of measurement Jacobian matrix and the measurement vector in the factor space, and identifies outliers as leverage points; the second type is based on residual sensitivity analysis, namely, determining whether the measurement residual increases significantly when there is a large measurement error in the system, and identifying measurements where the measurement error cannot be positively fed back to the measurement residual as leverage points.

Figure 1

Figure 1. Dy11 on-load tap changer equivalent model.

The first method based on regression model analysis is introduced as follows. The first-order Taylor expansion is performed at the initial value point $x_0$ and the approximate expression of the measurement error is obtained as follows:

$\Delta z_i=H_i\Delta x+e_i(1)$

Where, $\Delta z_i$ is the error between the true measurement value and the measurement vector; $H_i$ represents the ith row element of the Jacobian matrix $H$; $\Delta x$ represents the error between the current estimated value of the state variable and the initial value.

The above Equation 1 is called the regression analysis model in statistics. $\Delta z_i$ is the output of the regression analysis model, $\Delta x$ are the regression variables, and $H$ is the coefficient matrix of the regression analysis. $\left(\Delta z_i,H_i\right)$ represents a point in the factor space and also indicates the relationship between the measurement vector and the true value, as well as the state variables. The regression factor is defined as, in the $m\times n$ dimensional Jacobi matrix, there is a total of m $H_i$,and the elements of each $H_i$ correspond to an n-dimensional space coordinate, then they are all located in this n-dimensional space. These coordinates are called the corresponding measured factors, and the n-dimensional space is the factor space of the regression analysis.

Due to the system network parameters, measurement errors, and other reasons, abnormal values may appear in the above factor space, that is, the data is quite different from other data, and it is shown as outliers in the two-dimensional space. When outliers appear in the Y-space ' of the factor space, that is, in the ordinate axis ' $\Delta z_i$ ' direction, they are bad data in the conventional sense of state estimation. When the outliers only appear in the ' X-space ' of the factor space, that is, in the ' $h_i$ ' direction of the abscissa axis, the corresponding measurement is leverage measurement; when the outliers occur in ' X-space ' and ' Y-space ' at the same time, the corresponding measurement is the leverage measurement bad data. In the state estimation of power system, the leverage measurement is determined by the network topology, line parameters, measurement position and the meter error of the measurement instrument. Once the system network parameters are determined, whether the leverage measurement will become the inherent attribute of a certain measurement will not change with the change of the state variables and measurement values of the system.

To identify outliers in the “X-space,” that is, to identify anomalies in the row vectors of the Jacobian matrix compared to other row vectors, this can be achieved by calculating distance measures between the individual row vectors. The Mahalanobis distance and other similar distance measures based on this can be used to calculate the distances between the row vectors. The criterion of such methods is to compare the distance between the row vectors with a set threshold. Measurements greater than this threshold are considered leverage measurements. The threshold setting criterion is to designate measurements that are far from most other measurements as leverage measurements. However, in cases where there are multiple leverage measurements in a system, problems may arise due to mutual masking between the leverage measurements, causing this type of method to potentially struggle to accurately identify systems with multiple leverage measurements.

The second method based on residual sensitivity analysis is introduced as follows. The estimation of the measurement error based on the least square method is defined as $\Delta \widehat{z}$, and the matrix expression is as follows.

$\left\{\begin{array}{l}\Delta \widehat{z}=H{\left(H^T{R}^{-1}H\right)}^{-1}{H}^T{R}^{-1}\Delta z\\ W=H{\left(H^T{R}^{-1}H\right)}^{-1}{H}^T{R}^{-1}\end{array}\right.(2)$

Where, $W$ is defined as a hat matrix.

When Equations 1, 2, the measurement residual is defined as the difference between the measured value and the estimated measurement vector, which can be equivalent to the error between the estimated measurement error value $\Delta \widehat{z}$ and the measurement error value.

$r=\Delta z-\Delta \widehat{z}=\left(I-W\right)\Delta z=S\Delta z(3)$

In the equation, $I$ is the identity matrix with diagonal elements equal to 1 and off-diagonal elements equal to 0; $S$ defines the residual sensitivity matrix, with its matrix expression shown as shown in Equation 4:

$S=I-H{\left(H^T{R}^{-1}H\right)}^{-1}{H}^T{R}^{-1}(4)$

The hat matrix $W$ has the property of idempotence, where the matrix elements satisfy as shown in Equation 5:

$W_{ii}=W_{ii}^2+{\displaystyle \sum _{i\ne j}}{W}_{ij}^2(5)$

From the above equation, Based on Equation 3, we know that when the diagonal elements of are close to 0. If the measurement error is large and the diagonal elements of the multiplication of the sensitivity matrix remains very small, indicating that the measurement error cannot be reflected in the residual of the measurement, then define this type of measurement as a leverage measurement. Furthermore, the leverage measurement can also be determined by comparing with its expected value to assess its relative magnitude.

The expected value is calculated as shown in Equation 6:

$\overline{W}=E\left[K_{ii}\right]=\frac{1}{m}{\displaystyle \sum _{i=1}^m}{K}_{ii}=\frac{2n-1}{m}(6)$

If $W_{ii}\gg \overline{W}$,it is determined that the measurement corresponding to the diagonal element is determined to be a leverage measurement. On the basis of empirical experience, it is generally considered that when $W_{ii}\ge 2\overline{W}$, the measurement is a leverage measurement.

To avoid the difficult identification of leverage measurements that may arise from the two aforementioned methods, this paper adopts a method based on projection statistical values for the identification of leverage measurement. This method circumvents the calculation problem of the covariance matrix and directly utilizes the projections of the row vectors of the Jacobian matrix onto the relevant subspace to identify leverage measurements. First, calculate the projection statistical values for all measurements, with the calculation formula as follows:

$P{S}_i=\underset{k}{\max }\frac{\left|H_i{H}_k^T\right|}{S_k}(7)$

Where $P{S}_i$ represents the statistical projection value for measurement $i$, $H_i$ represents the $i$-th element of the Jacobian matrix $H$; $H_k^T$ represents the transpose of the $k$-th element of the Jacobian matrix $H$; $S_k$ represents the covariance of $H_i$ and $H_k^T$.

The calculation formula for $S_k$ is given by the following equation:

$S_k=1.1926\underset{i}{lomed}\underset{j\ne i}{lomed}\left|H_i{H}_k^T+H_j{H}_k^T\right|(8)$

Where, $\text{lomed}$ is defined as $\left[\left(m+1\right)/2\right]$, $\left[x\right]$ represents the value of the integer part of n. For example,: $m=6$, $\left[\left(m+1\right)/2\right]=3$.

After calculating the projection statistical values corresponding to each measurement based on Equations 7, 8, compare them numerically with the projection statistical cutoff values. Under a Gaussian distribution, the projection statistics typically follow a Chi-square distribution, satisfying Equation 9:

$b_i={\chi }_{v,0.975}^2(9)$

Where, $b_i$ is the calculated cutoff value.

When comparing the calculated projection statistical values with the cut off values, you can determine whether the measurement is a leverage measurement based on the comparison results.

$D_i=\left(P{S}_i\cdot /b_i\right)>1(10)$

If the calculated projection statistical value D for measurement $i$ satisfies Equation 10, then measurement $i$ is determined to be a leverage measurement. The calculation of projection statistical values only involves simple algebraic operations and does not require matrix inversion. Therefore, even in cases where the Jacobian matrix is very sparse, accurate identification of leverage measurements can be achieved in a system with multiple leverage measurements.

2.2 Identification of suspicious bad data using maximum normalized residual method

As the calculation of residuals is approximate to the error values, it may not be able to detect bad data. By using standardized residuals, a more accurate method for identifying bad data can be obtained. The normalized residual value for measurement i can be obtained by dividing the residual value by the corresponding diagonal element in the residual covariance matrix.

$r_i^N=\frac{\left|r_i\right|}{\sqrt{{\mathrm{\Omega }}_{ii}}}=\frac{\left|r_i\right|}{\sqrt{R_{ii}{S}_{ii}}}(11)$

In Equation 11: $r_i^N$ represents the normalized residual value; $R$ represents the measurement error covariance matrix; $S$ represents the sensitivity matrix; $\mathrm{\Omega }$ represents the residual covariance matrix; $r$ represents the residual value.

${\mathrm{\Omega }}_{ii}=R_{ii}-h_i\cdot T_{i}1\le i\le m(12)$

In Equation 12: $\mathrm{\Omega }$ is the residual covariance matrix, $T=G^{-1}{H}^T$, $G$ is the gain matrix, The calculation formula of $G$ is $G=\left(H^T{R}^{-1}H\right)$ , $R_{ii}={\sigma }_i^2$ represent the measurement variance matrix of the error $i$.

When solving the weighted least squares state estimation, the residual value can be calculated. The calculation formula is as shown in Equation 13:

$r=z-h\left(x\right)(13)$

For non-leverage measurement, the normalized residual vector $r^N$ obeys the standard normal distribution, As Equation 14:

$r_i^N\sim N\left(0,1\right)(14)$

Therefore, the maximum element in $r^N$ is compared with the statistical threshold to determine the existence of suspicious measurement bad data. The threshold can be selected according to the required detection sensitivity level.

3 Stage 2: bad data identification based on mixed integer linear programming

In order to improve the solving efficiency of the traditional MINLP model, the hybrid data-physical-driven linearization model is first applied to linearize the non-linear constraints in the state estimation of on-load tap changer in transformers. Subsequently, an MILP-based bad data identification model is constructed. The following provides a detailed description of the linearization process and the construction of the optimization model.

3.1 Bad data identification based on MINLP

The traditional MINLP-based bad data identification model is represented as follows:

$\min {\displaystyle \sum _{i=1}^m}{b}_i(15)$

$s.t.c\left(x\right)=0(16)$

$h_i\left(x\right)-z_i^{\mathrm{m}}\ge -3{\sigma }_i-\mathrm{M}{b}_i(17)$

$h_i\left(x\right)-z_i^{\mathrm{m}}\le 3{\sigma }_i+\mathrm{M}{b}_i(18)$

In Equations 15–18: $c\left(x\right)$ represents equality constraints, including balanced node phase angle constraints, injection equality constraints, and load tap transformer droop control constraints., and $h_i\left(x\right)$ represents nonlinear measurement equations, including node voltage amplitude measurement equations, branch current amplitude square measurement equations, branch active power measurement equations, and branch reactive power measurement equations. $z_i^{\mathrm{m}}$ represents measurement values, M is a large positive number, taken as 10,000 in this paper. $b_i$ is a binary variable. When $b_i$ equals 0, it indicates that measurement $i$ is not bad data, and the corresponding measurement equation inequality constraint is effective. When $b_i$ equals 1, it can be determined that the measurement corresponding to $i$ is bad data, and the corresponding measurement equation inequality constraint is invalid.

The bad data identification method based on mixed integer can overcome the problem that the residual method is difficult to identify the bad data of the multi-leverage measurement system, and has high identification accuracy. However, due to the serious non-convex nonlinearity of the model, the requirement for the solver is high, and the computational efficiency of the model solution is low.

3.2 The hybrid data-physical-driven measurement equation linearization model

3.2.1 OLTC model considering non-smooth control characteristics

OLTC includes two parts, “transformer” and “tap changer.” Unlike traditional transformers, an OLTC sets the tap position as an unknown variable during modelling. By controlling the amplitude of the secondary side voltage to meet a certain dead band range, the OLTC adjusts the tap position to maintain the voltage level at the load center within a certain error range, thereby enhancing the power quality for the user. This paper proposes a droop control model for the OLTC, where the amplitude of the secondary side voltage and the tap turns ratio of the OLTC align with the droop control curve.

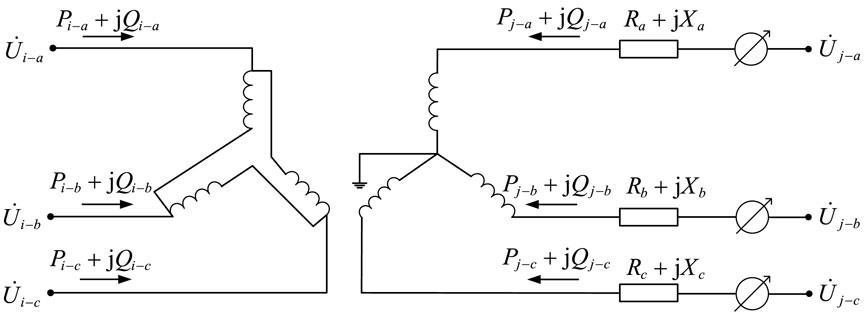
Define the column name of the nodal association matrix to represent the node $i-a$, $i-b$, $i-c$, $j-a$, $j-b$, $j-c$,the line name corresponds to the branch connected to $i-a$,the branch connected to $j-a$,the branch connected to $i-b$,the branch connected to $j-b$,the branch connected to $i-c$,the branch connected to $j-c$,where $i$、 $j$ represent node; $a$、 $b$、 $c$ represented by three phases of each node. The nodal correlation matrix is as shown in Equation 19:

$\begin{array}{l}node\\ C=branch\left[\begin{array}{cccccc}1& -1& & & & \\ & & & 1& & \\ & 1& -1& & & \\ & & & & 1& \\ -1& & 1& & & \\ & & & & & 1\end{array}\right]\end{array}(19)$

Where represents the association between a branch and a node, with its direction flowing out of the node; and represents the association between a branch and a node, with its direction flowing into the node.

Taking phase A as an example, according to the law of energy conservation on the primary and secondary sides of the transformer, the voltage and current on the winding satisfy the following relationship:

$\left\{\begin{array}{l}\frac{{\dot{I}}_{i-a}}{{\dot{I}}_{j-a}}=-\frac{1}{t_a}\\ \frac{{\dot{U}}_{i-a}}{{\dot{U}}_{j-a}-{\dot{I}}_{j-a}/y_a}=t_a\end{array}\right.(20)$

Here, ${\dot{I}}_{i-a}$ and ${\dot{I}}_{j-a}$ represent the branch currents flowing through the branches connected by $i-a$ and $j-a$, respectively. $y_a=1/\left(R_a+\mathrm{j}{X}_a\right)$ represents the equivalent internal impedance of phase A of the transformer, $t_a$ represents the turns ratio of phase A.

The relationship between branch current and node voltage is expressed as shown in Equation 21:

$\left\{\begin{array}{c}\begin{array}{c}{\dot{I}}_{i-a}=-\frac{1}{t_a}{\dot{I}}_{j-a}\\ =-\frac{1}{t_a}\left({\dot{U}}_{j-a}-\frac{{\dot{U}}_{i-a}}{t_a}\right)y_a\\ =\frac{y_a}{t_a^2}{\dot{U}}_{i-a}-\frac{y_a}{t_a}{\dot{U}}_{j-a}\end{array}\\ \begin{array}{c}{\dot{I}}_{j-a}=\left({\dot{U}}_{j-a}-\frac{{\dot{U}}_{i-a}}{t_a}\right)y_a\\ =-\frac{y_a}{t_a}{\dot{U}}_{i-a}+y_a{\dot{U}}_{j-a}\end{array}\end{array}\right.(21)$

Equation 20 is expressed as a matrix as shown in Equation 22:

$\left[\begin{array}{l}{\dot{I}}_{i-a}\\ {\dot{I}}_{j-a}\end{array}\right]=\left[\begin{array}{cc}\frac{y_a}{t_a^2}& -\frac{y_a}{t_a}\\ -\frac{y_a}{t_a}& y_a\end{array}\right]\left[\begin{array}{l}{\dot{U}}_{i-a}\\ {\dot{U}}_{j-a}\end{array}\right](22)$

Similarly, the relationship between the branch current and node voltage for phases B and C is derived, and the relationship between the three-phase branch current and voltage is ultimately obtained as follows:

$\left\{\begin{array}{l}\dot{I}=Y_{\mathit{pr}}\dot{U}\\ Y_{\mathit{pr}}=\left[\begin{array}{cccccc}\frac{y_a}{t_a^2}& -\frac{y_a}{t_a}& & & & \\ -\frac{y_a}{t_a}& y_a& & & & \\ & & \frac{y_b}{t_b^2}& -\frac{y_b}{t_b}& & \\ & & -\frac{y_b}{t_b}& y_b& & \\ & & & & \frac{y_c}{t_c^2}& -\frac{y_c}{t_c}\\ & & & & -\frac{y_c}{t_c}& y_c\end{array}\right]\end{array}\right.(23)$

In Equation 23: $\dot{I}={\left[\begin{array}{cccccc}{\dot{I}}_{i-a}& {\dot{I}}_{j-a}& {\dot{I}}_{i-b}& {\dot{I}}_{j-b}& {\dot{I}}_{i-c}& {\dot{I}}_{j-c}\end{array}\right]}^T$ represents the branch current matrix of the OLTC, $\dot{U}={\left[\begin{array}{cccccc}{\dot{U}}_{i-a}& {\dot{U}}_{j-a}& {\dot{U}}_{i-b}& {\dot{U}}_{j-b}& {\dot{U}}_{i-c}& {\dot{U}}_{j-c}\end{array}\right]}^T$ represents the node voltage matrix of the OLTC; $Y_{\mathit{pr}}$ is defined as the original admittance matrix; $t_b$, $t_c$ respectively represent the B and C phase transformation turns ratios.

By combining the original admittance matrix with the node-branch incidence matrix, the node admittance matrix is obtained from the following equation:

$Y_{bus}=C^T{Y}_{\mathit{pr}}C$

The branch power connected to each node is calculated using the node injection power expression as shown in Equations 24 and 25:

$P_{i-\phi }^{\text{Reg}}=U_{i-\phi }{\displaystyle \sum _{\beta =\mathrm{A},\mathrm{B},\mathrm{C}}}\left[U_{j-\beta }\left(G_{ij-\phi \beta }^{\text{Reg}}\cos {\theta }_{ij-\phi \beta }+B_{ij-\phi \beta }^{\text{Reg}}\sin {\theta }_{ij-\phi \beta }\right)\right](24)$

$Q_{i-\phi }^{\text{Reg}}=U_{i-\phi }{\displaystyle \sum _{j=\mathrm{A},\mathrm{B},\mathrm{C}}}{U}_{j-\beta }\left(-B_{ij-\phi \beta }^{\text{Reg}}\cos {\theta }_{ij-\phi \beta }+G_{ij-\phi \beta }^{\text{Reg}}\sin {\theta }_{ij-\phi \beta }\right)(25)$

$G_{ij-\phi \beta }^{\text{Reg}}$ and $B_{ij-\phi \beta }^{\text{Reg}}$ represent the real and imaginary parts of the corresponding elements in the node admittance matrix $Y_{bus}$ of the on-load tap changer, $G_{ij-\phi \beta }^{\text{Reg}}$ represents the mutual conductance between node $i-\phi$ and node $j-\beta$, $B_{ij-\phi \beta }^{\text{Reg}}$ represents the mutual susceptance between node $i-\phi$ and node $j-\beta$; The row name and column name of $Y_{bus}$ are expressed as: node $i-a$, $i-b$, $i-c$, $j-a$, $j-b$, $j-c$.

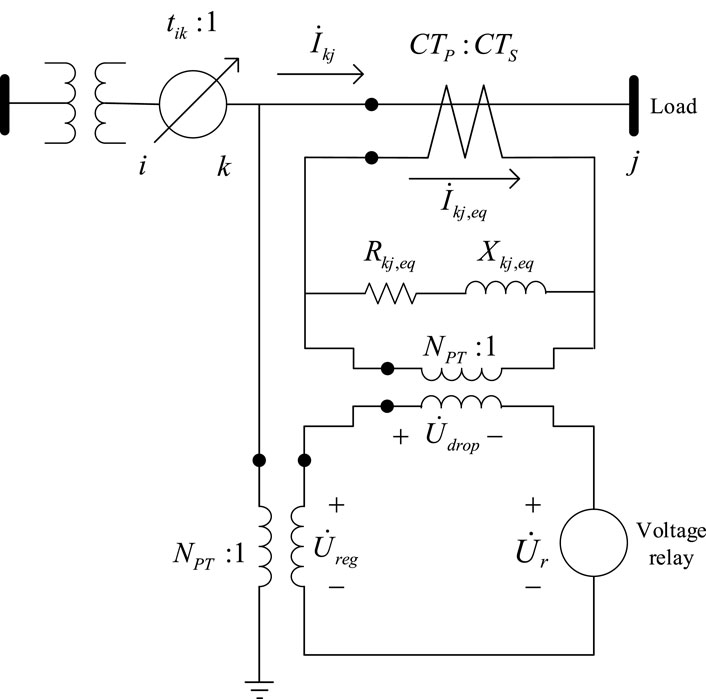
The following describes the modelling of the regulator part in Figure 2.

Figure 2

Figure 2. Detailed schematic diagram of OLTC voltage regulator part.

The tap position of OLTC are regulated through a control circuit. When voltage control, direct control cannot be carried out on the high-voltage circuit. Therefore, voltage and current transformers are used to construct a simulated circuit - the control circuit. The control circuit is a proportional model of the actual line. For example, if the actual line transformer has a secondary side rated at 2.4 kV, the control circuit operates at a voltage level of 120 V. By monitoring the voltage of the control circuit, the voltage at the load center of the actual line can be determined. If the voltage is below the normal level, indicating that the voltage at the loading center is below the position of the normal level, the tap changer is adjusted to raise the voltage at the loading center. For three-phase supply voltages below 10 kV, the allowable deviation is 7% of the rated voltage. For single-phase supply voltages of 220 V, the allowable deviation is +7% and −10% of the rated voltage. $R_{kj,eq}$ and $X_{kj,eq}$ are the proportional impedances of the actual line in the control circuit and are typically known quantities.

For the control circuit, the current rating of the primary winding of the current transformer is set as $C{T}_P$, and the current rating of the secondary winding is set as $C{T}_S$ (usually taken as 5). The voltage transformer turns ratio is set as $N_{PT}$. First, according to Ohm’s law, the equivalent impedance of the three-phase line is calculated as shown in Equation 26:

$R_{line}+\mathrm{j}{X}_{line}=\frac{{\dot{U}}_k-{\dot{U}}_j}{{\dot{I}}_{kj}}(26)$

It should be noted that the equivalent impedance of the three-phase line is not the actual line impedance; it is the turns ratio of the actual measured voltage on the secondary side to the load center voltage difference to the load side current under the rated turns ratio.

The equivalent impedance of the line compensator is calculated from the equivalent impedance of the three-phase line as $R_{kj,eq}$、 $X_{kj,eq}$ using the formula as shown in Equation 27:

$R_{eq,kj}+\mathrm{j}{X}_{eq,kj}=\left(R_{line}+\mathrm{j}{X}_{line}\right)·\frac{C{T}_P}{N_{PT}·C{T}_S}(27)$

The current in the compensator branch is obtained from the actual line current ${\dot{I}}_{kj}$ and the current transformer ${\dot{I}}_{kj,eq}$.

${\dot{I}}_{kj,eq}={\dot{I}}_{kj}·\frac{C{T}_S}{C{T}_P}(28)$

In Equation 28: ${\dot{I}}_{kj}={\left[\begin{array}{ccc}{\dot{I}}_{kj-a}& {\dot{I}}_{kj-b}& {\dot{I}}_{kj-c}\end{array}\right]}^T$ represents the three-phase current in the line.

The voltage difference ${\dot{U}}_{drop}$ of the compensator branch is obtained as shown in Equation 29:

${\dot{U}}_{drop}=\left(R_{kj,eq}+\mathrm{j}{X}_{kj,eq}\right)·{\dot{I}}_{kj,eq}(29)$

Finally, the control voltage of the compensator branch is as shown in Equation 30:

${\dot{U}}_r=\frac{{\dot{U}}_3}{N_{PT}}-{\dot{U}}_{drop}(30)$

Applying the droop control to the control voltage and tap changer turns ratio, taking phase A as an example, the principle of droop control for the OLTC is introduced. Define $\Delta t_a$, $\Delta t_b$, $\Delta t_c$ as the adjustment amounts of the tap changer turns ratio for phases A, B, and C relative to their respective initial turns ratios, and add to the objective function as shown in Equation 31:

$\min \left(\Delta t_a^2+\Delta t_b^2+\Delta t_c^2\right)(31)$

The physical meaning of the above equation is that when the control voltage is within the dead zone, the OLTC tap position remains unchanged.

The $\Delta t_a-U_{r-a}$ droop control function of the variation in the variable turns ratio variation and the control voltage is shown in Equation 31:

$\Delta t_a=\left\{\begin{array}{l}\Delta t_{\max }-\Delta t_0{U}_{\min }\le U_{r-a}<U_l\\ k_{dr1}\left(U_{r-a}-U_{dbl}\right)U_l\le U_{r-a}\le U_{dbl}\\ 0U_{dbl}<U_{r-a}<U_{dbh}\\ k_{dr2}\left(U_{r-a}-U_{dbh}\right)U_{dbh}\le U_{r-a}\le U_h\\ t_{\min }-\Delta t_0{U}_h<U_{r-a}\le U_{\max }\end{array}\right.(32)$

The relationship between $\Delta t_a$ and the control voltage $U_{r-a}$ satisfies the following curve in Figure 3:

Figure 3

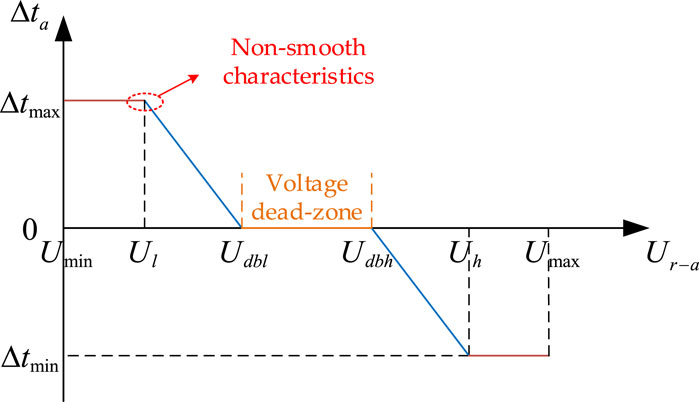
Figure 3. Voltage regulation control curve showing the variation of the turns ratio with control voltage droop.

Where, $\Delta t_{\max }$ and $\Delta t_{\min }$ respectively represent the upper and lower limits of the variation in turns ratio $\Delta t$; $\Delta t_0$ represents the change in tap position corresponding to the initial turns ratio; $U_{dbh}$ and $U_{dbl}$ respectively represent the upper and lower bounds of the voltage dead zone; $U_h$ and $U_l$ respectively represent the upper and lower bounds of the voltage droop control curve; $U_{\max }$ and $U_{\min }$ respectively represent the upper and lower bounds of the bus voltage magnitude; $k_{dr1}$ and $k_{dr2}$ respectively represent the droop control coefficients, and $k_{dr1}<0$, $k_{dr2}<0$ . When the voltage $U_{r-a}$ is within the dead zone range, the OLTC does not actuate, and the variation in turns ratio is 0.

The relationship between the droop control coefficient and the variation in the turns ratio and the voltage is as shown in Equation 33:

$\left\{\begin{array}{l}{k}_{dr1}=\frac{\Delta t_{\max }}{U_l-U_{dbl}}\\ k_{dr2}=\frac{-\Delta t_{\min }}{U_{dbh}-U_h}\end{array}\right.(33)$

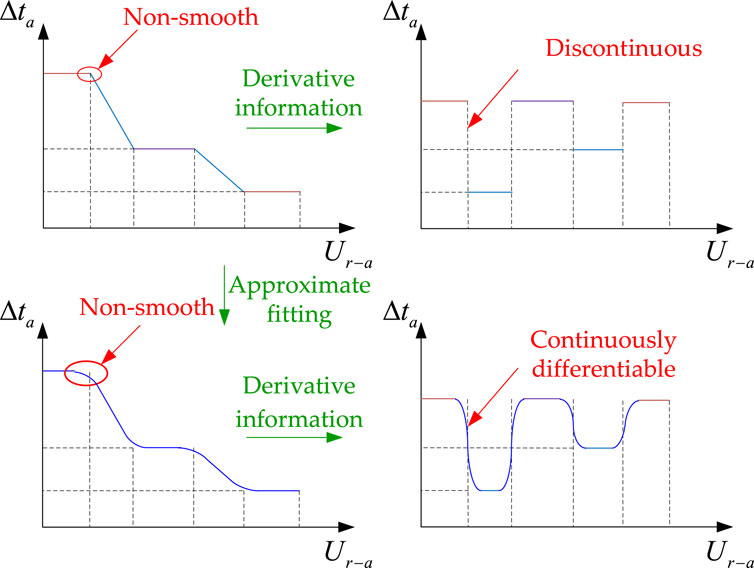
From Figure 3, it can be seen that the characteristic curve represents a piecewise function. When the system operates near the turning point, the derivative is discontinuous, the algorithm search direction is uncertain, and it is difficult to smoothly switch operating curves, so the piecewise droop control function has strong non-smooth characteristics and is difficult to solve. Usually, mixed integer nonlinear programming is used to describe piecewise function control characteristics, but this method has low computational efficiency. In this paper, a fitting function is used to approximate the piecewise function, and the fitted droop control function is shown in Equation 34:

$\begin{array}{l}\Delta t_a=\Delta t_{\max }+\frac{k_{dr1}}{\alpha }\left[\ln \left(1+e^{\alpha \left(U_{r-a}-U_l\right)}\right)-\ln \left(1+e^{\alpha \left(U_{r-a}-U_{dbl}\right)}\right)\right]\\ +\frac{k_{dr2}}{\alpha }\left[\ln \left(1+e^{\alpha \left(U_{r-a}-U_{dbh}\right)}\right)-\ln \left(1+e^{\alpha \left(U_{r-a}-U_h\right)}\right)\right]\end{array}(34)$

Where, $\alpha$ is the fitting coefficient, set $\alpha =500$ in this paper.

Approximately fitting the piecewise droop control function can transform it into a smooth function that is continuously differentiable, as shown in Figure 4. The smoothing function can avoid sudden changes in derivative order during algorithm iteration calculations, thus improving the convergence of the algorithm.

Figure 4

Figure 4. Derivative comparison diagram before and after fitting.

The variation of the ratio of the voltage regulator and the tap variable satisfies the relationship is shown in Equation 34:

$\Delta t_a=x_{d-a}·\Delta d(35)$

In the equation, $x_{d-a}$ is the phase A tap-changer variable; $\Delta d$ is the turns ratio change corresponding to a 1-tap adjustment, which is typically taken as $\Delta d=0.00625\mathrm{p}.\mathrm{u}.$ in distribution networks.

In this paper, the discrete tap-changer variable is first treated as a continuous variable for state estimation calculations to obtain a continuous optimal solution for state estimation. Subsequently, a positive curvature quadratic penalty function is introduced in the objective function, and the state estimation is continued using the continuous optimal solution as the initial value to obtain an integer solution for the tap-changer setting.

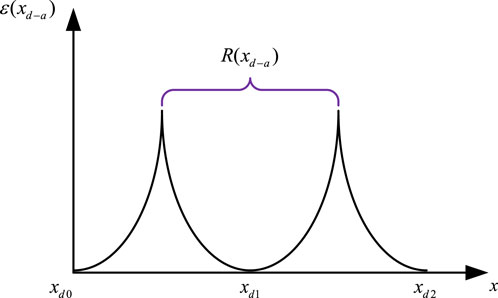
Taking phase A as an example, the positive curvature quadratic penalty function is shown in Figure 5. $x_{d0}$、 $x_{d1}$、 $x_{d2}$ are any three continuous discrete component values. Define the neighborhood $R\left(x_{d-a}\right)$ as shown in Equation 36:

$R\left(x_{d-a}\right)=\left\{x_{d-a}|x_{d1}-\frac{1}{2}\Delta d\le x_{d-a}\le x_{d1}+\frac{1}{2}\Delta d\right\}(36)$

Figure 5

Figure 5. Quadratic penalty function model.

Where, $x_{d1}$ is the neighborhood center, which is the closest discrete grading value determined according to the continuous optimal solution.

In the optimization process, when the value of $x_{d-a}$ is in the neighborhood of the above definition, the penalty function $\epsilon \left(x_{d-a}\right)$ is introduced:

$\epsilon \left(x_{d-a}\right)=\frac{1}{2}{\mu }_d{\left(x_{d-a}-x_{d1}\right)}^2(37)$

In the equation, ${\mu }_d$ is the penalty factor, a known quantity; the penalty function will force $x_{d-a}$ within the neighborhood to approach the neighborhood center. From Equation 37, we can obtain the first and second derivatives of the quadratic penalty function within the neighborhood.

$\left\{\begin{array}{l}\frac{\partial \epsilon \left(x_{d-a}\right)}{\partial x_d}={\mu }_d\left(x_{d-a}-x_{d1}\right)\\ \frac{{\partial }^2\epsilon \left(x_{d-a}\right)}{\partial {x_d}^2}={\mu }_d\end{array}\right.(38)$

From Equation 38, it can be observed that for the Newton method, the introduction of a penalty function in the objective function will result in the incremental inclusion of the first and second derivative terms in the Jacobian matrix and the Hessian matrix during the optimization iteration. Through this procedure, not only can rapid convergence of OLTC tap positions be achieved, but also the positive definiteness of the iteration matrix can be strengthened, thereby improving algorithm convergence. From a perspective in the field of power systems, this approach enables efficient adjustment of OLTC tap positions and enhances algorithm convergence by modifying derivative terms in iterative matrices.

3.2.2 Hybrid data-physical-driven linearization

Nonlinear constraints in the model of OLTC mainly fall into two categories: the first category is branch power constraints; the second category is droop control nonlinear constraints. Due to the introduction of the unknown variable $t$ of the voltage regulator in the branch power constraint and the logarithmic function in the droop control nonlinear constraints, the aforementioned physical linearization methods are no longer applicable. In this paper, it is proposed to utilize a first-order Taylor expansion for physical linearization, followed by using Partial Least Squares Regression (PLSR) to calculate compensation errors, resulting in the development of a hybrid data-physical-driven Linearization model.

Firstly, introduce the principle of linearization of power constraints. For ease of description, define the relationship between the branch power of the transformer and the variables as shown in Equation 39:

$\left\{\begin{array}{l}{P}_{i-\phi }^{\text{Reg}}=f_{i-\phi }^P\left(X^{\text{Reg}}\right)\\ Q_{i-\phi }^{\text{Reg}}=f_{i-\phi }^Q\left(X^{\text{Reg}}\right)\\ X^{\text{Reg}}={\left[\begin{array}{ccccc}{\theta }_{i-\text{ABC}}& U_{i-\text{ABC}}& {\theta }_{j-\text{ABC}}& U_{j-\text{ABC}}& t_{\text{ABC}}\end{array}\right]}^T\end{array}\right.(39)$

Where $X^{\text{Reg}}$ represents the variables of the on-load tap-changing transformer, composed of the phase angle and voltage magnitude of the primary and secondary sides, and the three-phase turns ratio; $f_{i-\phi }^P$ and $f_{i-\phi }^Q$ respectively represent the functional relationships between the active and reactive power of phase $\phi$ branch and the variables of the on-load tap-changing transformer.

The first-order Taylor expansion is performed at the initial point $X^{\text{Reg},0}$ of the variable, as shown in Equation 40:

$\left\{\begin{array}{l}{f}_{i-\phi }^P\left(X^{\text{Reg}}\right)\approx f_{i-\phi }^P\left(X^{\text{Reg},0}\right)+f_{i-\phi }^{P^{\prime }}\left(X^{\text{Reg},0}\right)·\left(X^{\text{Reg}}-X^{\text{Reg},0}\right)+\Delta P_{i-\phi }^{\text{Reg}}\\ f_{i-\phi }^Q\left(X^{\text{Reg}}\right)\approx f_{i-\phi }^Q\left(X^{\text{Reg},0}\right)+f_{i-\phi }^{Q^{\prime }}\left(X^{\text{Reg},0}\right)·\left(X^{\text{Reg}}-X^{\text{Reg},0}\right)+\Delta Q_{i-\phi }^{\text{Reg}}\end{array}\right.(40)$

In the equations, $f_{i-\phi }^{P^{\prime }}$ and $f_{i-\phi }^{Q^{\prime }}$ represent the partial derivatives of the active and reactive power functions of the phase $\phi$ branch with respect to each variable in $X^{\text{Reg}}$; $\Delta P_{i-\phi }^{\text{Reg}}$ and $\Delta Q_{i-\phi }^{\text{Reg}}$ respectively represent the compensating errors of the active and reactive power of the phase $\phi$ branch, and the compensating errors are also calculated using the PLSR method.

Next, the linearization principle of the droop control function of the OLTC is introduced. Similar to the linearization principle of branch power, the functional relationship between the turns ratio change and the control voltage is defined in Equation 41:

$\Delta t=f^{\Delta t}\left(U_r\right)(41)$

Where, $f^{\Delta t}$ represents the functional relationship between the variable ratio variation and the secondary side control voltage.

The first-order Taylor series expansion is performed at the initial value point $U_{r,0}$ of the variable, as shown in Equation 42:

$f^{\Delta t}\left(U_r\right)\approx f^{\Delta t}\left(U_{r,0}\right)+f^{\Delta t^{\prime }}\left(U_{r,0}\right)·\left(U_r-U_{r,0}\right)+\Delta t_r(42)$

In the formula, $f^{\Delta t^{\prime }}$ represents the derivative of the variable turns ratio variation function to the variable $U_r$ ; $\Delta t_r$ represents the compensation error of the variable turns ratio variation.

Then, the PLSR algorithm is used for data-driven error compensation, the specific principle and mathematical expressions are as follows:

The compensation error $\Delta y$ of active power is defined in Equation 43:

$\left\{\begin{array}{l}\Delta y=\xi y^{\prime }+\eta \\ \Delta y={\left[\begin{array}{cc}\Delta P_{PV-\phi }^m& \Delta Q_{PV-\phi }^m\end{array}\right]}^T\\ y^{\prime }={\left[\begin{array}{cc}{P}_{load}^{PV-\phi }& Q_{load}^{PV-\phi }\end{array}\right]}^T\end{array}\right.(43)$

Among them, $\xi$ is the coefficient matrix and $\eta$ is the constant matrix, which are obtained by PLSR fitting is the independent variable matrix of load composition; $P_{load}^{PV-\phi }$ and $Q_{load}^{PV-\phi }$ represent the vectors composed of active and reactive loads of the grid-connected node $\phi$ phase of the system.

The independent variable set and the dependent variable set can be obtained from the results of the power flow calculation. After obtaining the set of independent variables R and the dependent variable set Z, it is standardized.

$\left\{\begin{array}{c}{R}^{*}=\left(R-\overline{R}\right)S_R^{-1}\\ Z^{*}=\left(Z-\overline{Z}\right)S_Z^{-1}\end{array}\right.(44)$

In Equation 44: $R^{*}$, $Z^{*}$ represent the standardized independent variables and dependent variable sets; $\overline{R}$ and $S_R$ respectively represent the mean and standard deviation of the independent variable set R.

For the standardized independent variable and dependent variable sets, the least squares regression analysis method is used to calculate the fitting coefficients, with the knowledge in the field of power systems:

$C=\text{PLS}\left(R^{*},Z^{*}\right)(45)$

$\eta =\overline{Z}-\frac{\overline{R}}{S_R}C\odot S_Z(46)$

In Equations 45 and 46: C represents the regression coefficient matrix obtained by PLSR. ξ and η represent the coefficient matrix and the constant matrix in the linear regression equation, respectively. Thus, the compensation error $\Delta y$ can be obtained. Finally, the correction equation of the measurement is shown in Equation 47:

$\begin{array}{l}{f}_{PV-\phi }^{m-p}\left(X_{PV}\right)\approx f_{PV-\phi }^{m-p}\left(X_{PV}^0\right)+\nabla f_{PV-\phi }^{m-p}\left(X_{PV}^0\right)\times \left(X_{PV}-X_{PV}^0\right)+\Delta P_{PV-\phi }^m\\ f_{PV-\phi }^{m-Q}\left(X_{PV}\right)\approx f_{PV-\phi }^{m-Q}\left(X_{PV}^0\right)+f_{PV-\phi }^{m-Q}\left(X_{PV}^0\right)\times \left(X_{PV}-X_{PV}^0\right)+\Delta Q_{PV-\phi }^m\end{array}(47)$

3.3 Bad data identification model based on MILP

For the suspicious measurement set, the MILP bad data identification model is constructed based on the hyhrid data-physical driven linearization method as shown in Equations 48–51:

$\min {\displaystyle \sum _{i=1}^m}{b}_i(48)$

$s.t.c^L\left(x\right)=0(49)$

$h_i^L\left(x\right)-z_i^{\mathrm{m}}\ge -3{\sigma }_i-\mathrm{M}{b}_i(50)$

$h_i^L\left(x\right)-z_i^{\mathrm{m}}\le 3{\sigma }_i+\mathrm{M}{b}_i(51)$

Where, $c^L\left(x\right)$ represents the linearized equality constraint, and $h_i^L\left(x\right)$ represents the linearized measurement equation of the line.

When $z_i$ is a normal measurement, that is, it does not belong to the suspicious measurement set, Formulas 50, 51 in the model should be rewritten as shown in Equations 52 and 53:

$h_i^L\left(x\right)-z_i^{\mathrm{m}}\ge -3{\sigma }_i(52)$

$h_i^L\left(x\right)-z_i^{\mathrm{m}}\le 3{\sigma }_i(53)$

The MILP bad data identification method is not affected by the leverage point, and can quickly and accurately identify the bad data in the leverage measurement.

4 Case study

Due to the need for further improvement in the accuracy and computational efficiency of the current bad data identification method in distribution networks, this paper proposes a bad data identification method based on MILP model to simultaneously address the issues of model accuracy and computational efficiency. In this chapter, a typical low-voltage 42-node distribution network case study is used to validate the effectiveness of the proposed bad data identification model. The relevant case studies are conducted on the MATLAB software platform, utilizing an Intel(R) Core(TM) i5-10210U CPU 1.60 GHz processor. The simulation calculations are carried out using per unit values, with a base voltage of 13.8 kV and a base power of 100 kVA for the case study system. The state estimation calculations are initialized in a flat start manner, with measurement values subject to Gaussian distribution errors with mean of 0 and variance of σ² added to the true values. The standard deviations for voltage measurements, branch power measurements, and node injection power measurements are set as ${\sigma }_i=0.004$, ${\sigma }_{\text{Bran}}=0.008$, and ${\sigma }_{\text{Node}}=0.01$.

For ease of analysis, this paper selects two mathematical indicators, the Root Mean Square Error (RMSE) and the Maximum Absolute Error (MAE). In this paper, RMSE represents the square root of the ratio of the sum of the squares of errors between the estimated values and the true values to the data dimension; MAE is generally used to measure the range of absolute errors, i.e., the maximum absolute error between the estimated values and the true values. The mathematical expressions for these two indicators are as follows:

$\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _i^n}{\left(x_i-{\widehat{x}}_i\right)}^2}(54)$

$\text{MAE}=\max \left\{\left|x_i-{\widehat{x}}_i\right|\right\}i=1,2,3\dots (55)$

In the equation, ${\widehat{x}}_i$ represents the true value of the state variable $x_i$.

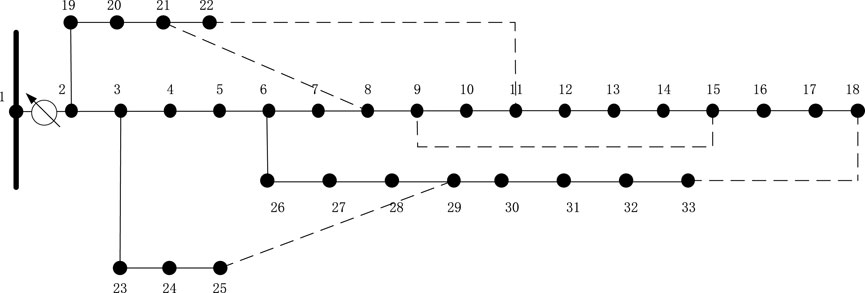
To verify the model, the modified IEEE-33 node test feeder is used to test the linearization and bad data identification model proposed in this paper.

The schematic diagram of the modified IEEE-33 node test feeder is shown in Figure 6. The feeder consists of 33 nodes and 32 branches. The power flow results of the system are used as the normal measurements for the entire system, including 402 measurements, including 6 voltage magnitude measurements, 198 branch power measurements, and 198 node injection power measurements.

Figure 6

Figure 6. A modified IEEE-33 node test feeder.

4.1 Linearization accuracy comparison

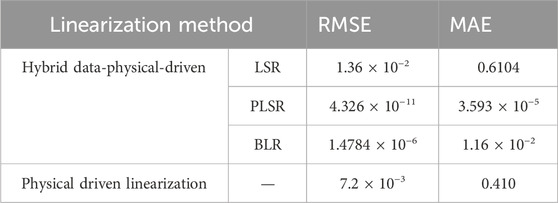
Firstly, test the hybrid data-physical-driven linearization model proposed in this paper. Based on the IEEE 33-node parameters, training and test datasets can be generated from the AC power flow model. The case study sets training and testing data as simulated data randomly generated within the range of 95%–105% of the actual load after removing outliers, with a total of 100 sets of training samples. The measurement linearization accuracy obtained from three hybrid data-physical-driven methods, namely, Taylor expansion linearization, PLSR regression, Least squares regression (LSR) (Shao et al., 2023), and Bayesian linear regression (BLR) (Liu et al., 2019), are compared. To facilitate analysis, the difference between the linearized power flow results and the true values is represented by two mathematical indicators, RMSE and MAE, as shown in Equations 54, 55 respectively. The comparison results in Table 1.

Table 1

Table 1. Comparison of the accuracy between linearization methods.

As shown in Table 1, the hybrid data-physical-driven Linearization method proposed in this paper has a higher advantage in terms of linearization accuracy. Compared to physical-driven linearization, This method can improve the accuracy by 10⁸ of magnitude. Additionally, compared to data-driven error compensation methods such as LSR and BLR, the PLSR method used in this paper has the highest accuracy and is closer to the results of nonlinear constraints.

4.2 OLTC tap position analysis

The OLTC tap position is verified by introducing a positive curvature quadratic penalty function into the tap position alignment model proposed in this paper. The tap position is treated as a continuous variable for state estimation calculations, obtaining a continuous optimal state estimate. The positive curvature quadratic penalty function is introduced into the objective function, using the continuous optimal solution as the initial value to continue the state estimation and obtain an integer solution for the tap position. Two different tap position processing models for on-load tap changing are set up to verify the effectiveness of the proposed model.

Model 1:. Traditional direct treatment of the tap position as a continuous variable.

Model 2:. Tap position rounding method based on positive curvature quadratic penalty function for OLTC.

The accuracy of voltage magnitude estimation for the two models is shown in Table 2.

The results indicate that for the OLTC model, the method of rounding tap positions with a positive curvature quadratic penalty function can lead to state estimation results with higher accuracy.

Table 2

Table 2. Voltage magnitude estimation results under different OLTC tap position handling methods.

4.3 Analysis of bad data identification results

4.3.1 Comparative analysis of traditional statistical methods for bad data identification

According to the two-stage bad data identification model proposed in this paper, 10 bad data are set as shown in Table 3. At the same time, the false alarm rate is set to $P_e=0.0025$. By querying the standard normal distribution table, the normal range of normalized residuals can be obtained, and the detection threshold $\tau$ is set to 3 and the threshold D for the projection statistics is set to 1.

Table 3

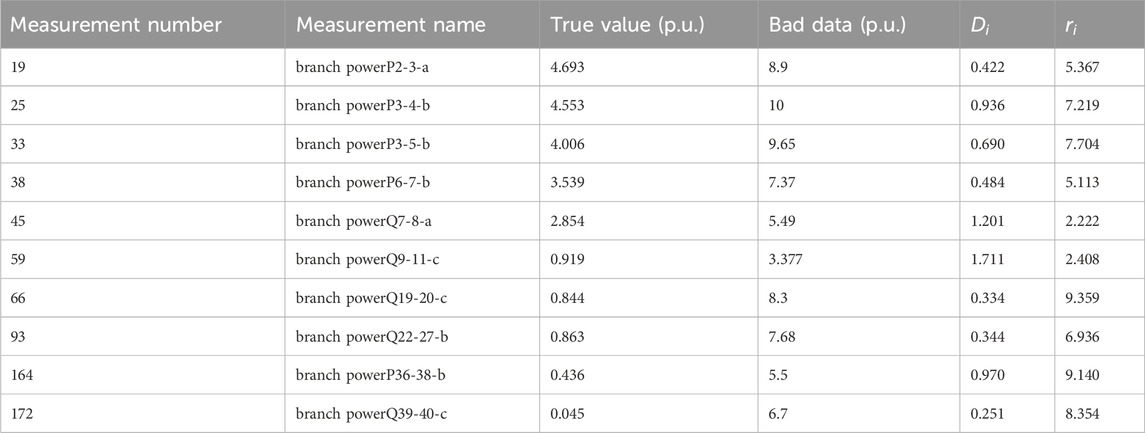
Table 3. Detail information of the bad data and the corresponding projection statistics and normalized residual values.

According to Table 4, among the 10 bad data, the projection statistical method effectively identified only 8 pcs bad data, while all other measurements with projection statistics values greater than 1 resulted in false alarms. Similarly, the maximum normalized residual method also failed to accurately identify the bad data. Therefore, both traditional statistical methods for bad data identification have certain limitations.

Table 4

Table 4. Comparison of results of different identification methods.

4.3.2 Comparative analysis of single-stage and two-stage bad data identification methods

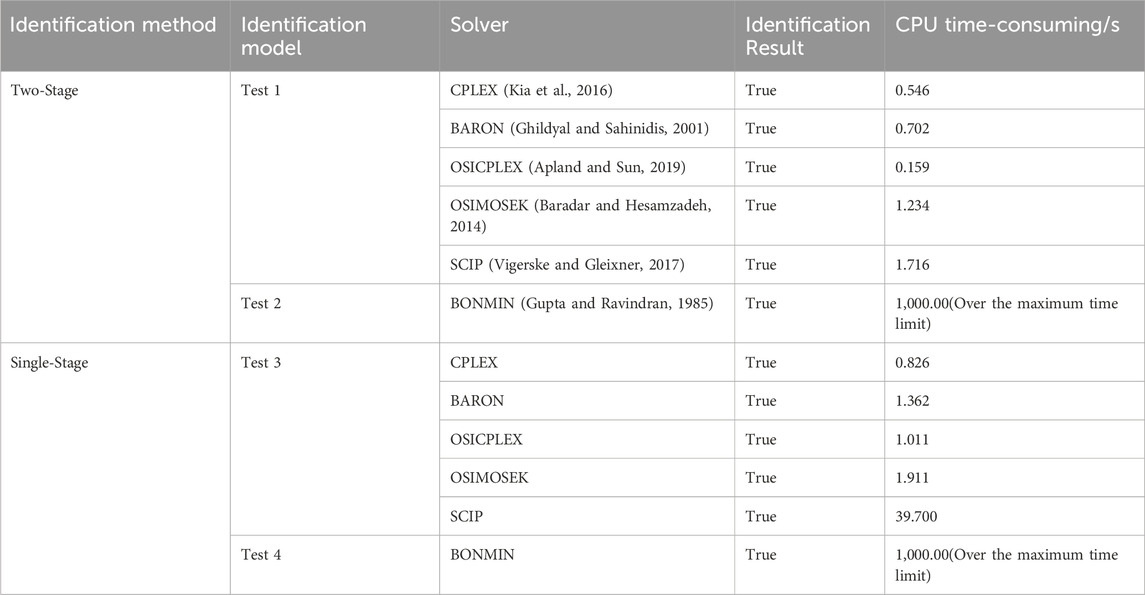
Due to the potential for misjudgments and missed detections by traditional statistical methods when multiple measurement bad data points are present in the system, these methods may not accurately identify measurement bad data. In contrast, the MILP bad data identification model used in the second stage can accurately identify all measurement bad data in the set identified by traditional methods when misjudgments or missed detections occur in the first stage. Therefore, in the first stage of this paper, all 265 lever measurements in the system were placed into a suspicious measurement set. The maximum normalized residual method was then used to identify the remaining 137 measurements, thereby validating the accuracy of the proposed bad data identification model and its efficiency compared to the single-stage model. Four sets of tests were conducted to compare the bad data identification method proposed in this paper with the traditional MINLP-based bad data identification method:

Test 1: Compression of the suspicious measurement set using the MILP-based two-stage bad data identification method proposed in this paper;

Test 2: Compression of the suspicious measurement set using the traditional MINLP-based two-stage bad data identification method;

Test 3: No compression of the suspicious measurement set, directly using the MILP-based single-stage bad data identification method;

Test 4: No compression of the suspicious measurement set, using the traditional MINLP-based single-stage bad data identification method.

Models were built for both methods in the GAMS optimization software, different solvers were called for calculation, and the results were compared and analyzed.

According to Table 5, for the modified IEEE-33 node test feeder case chosen in this paper, the two-stage model reduces the number of 0/1 integer variables and improves identification accuracy. However, for traditional MINLP-based bad data identification models, feasible solutions could not be obtained with most solvers, with correct results only achievable using the BONMIN solver. In contrast, the MILP-based bad data identification model achieved accurate identification results with most solvers. In terms of identification efficiency, even with the two-stage model, the MINLP identification model’s solving time reached the computational limit of 1,000 s, and the solver exited abnormally, indicating limited applicability. For the MILP-based bad data identification method, using the two-stage model, the SCIP solver improved solving efficiency by approximately 23 times, and the CPLEX solver achieved the highest efficiency, requiring only 0.546 s.

Table 5

Table 5. Comparison of test results of different bad data identification methods.

5 Conclusion

To cope with the issue that existing traditional identification methods do not consider the nonlinear and discrete characteristics of on-load tap changers, making it difficult to achieve accurate and efficient identification of bad data., This paper proposes a MILP-based two stage bad data identification method. Detailed control characteristics of on-load tap changers are modelled, and a positive curvature quadratic penalty function is introduced to achieve fast tap normalization. In the first stage, leveraging projection statistics and maximum normalization residue methods effectively identifies leverage points and suspicious bad data, reduces the set of suspicious measurements. In the second stage, by linearizing nonlinear constraints and solving bad data identification model based on the MILP, the efficiency of the solution is greatly enhanced. The proposed model can achieve efficient and accurate identification of bad data, while ensuring optimal solutions by introducing penalty functions into the objective function for effective tap normalization.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author contributions

SH: Conceptualization, Funding acquisition, Methodology, Writing–original draft. CR: Formal Analysis, Investigation, Writing–original draft. MZ: Project administration, Resources, Writing–review and editing. LC: Software, Supervision, Writing–review and editing. YM: Validation, Visualization, Writing–review and editing. TZ: Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by State Grid Hebei Electric Power Co., Ltd. science and technology projects, grant number kj2023-076.

Conflict of interest

Authors SH, CR, and LC were employed by Economic and Technology Research Institute of State Grid Hebei Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from State Grid Hebei Electric Power Co.,Ltd. The funder had the following involvement in the study: the study design, collection, analysis, interpretation of data, and the writing of this article.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Apland, J., and Sun, B. (2019). A Multi-Period, multiple objective, mixed integer programming, GAMS model for transit system planning

Google Scholar

Baradar, M., and Hesamzadeh, M. R. (2014). A stochastic SOCP optimal power flow with wind power uncertainty. 1–5. doi:10.1109/PESGM.2014.6939790

CrossRef Full Text | Google Scholar

Chen, Y. (2021). Power system state estimation. Beijing, China: Science Press.

Google Scholar

Ghildyal, V., and Sahinidis, N. V. (2001). “Solving global optimization problems with baron,” in From Local to Global Optimization. Nonconvex Optimization and Its Applications. Editors A. Migdalas, P. M. Pardalos, and P. Värbrand (Boston, MA: Springer. doi:10.1007/978-1-4757-5284-7_10

CrossRef Full Text | Google Scholar

Gupta, O. K., and Ravindran, A. (1985). Branch and bound experiments in convex nonlinear integer programming. Manage. Sci. 31 (12), 1533–1546. doi:10.1287/mnsc.31.12.1533

CrossRef Full Text | Google Scholar

Handschin, E., and Kliokys, E. (1995). Transformer tap position estimation and bad data detection using dynamic signal modelling. IEEE T. Power Syst. 10 (2), 810–817. doi:10.1109/59.387921

CrossRef Full Text | Google Scholar

Handschin, E., Schweppe, F. C., Kohlas, J., and Fiechter, A. (1975). Bad data analysis for power system state estimation. IEEE Trans. Power Apparatus Syst. 94 (2), 329–337. doi:10.1109/T-PAS.1975.31858

CrossRef Full Text | Google Scholar

Huang, S. J., and Lin, J. M. (2004). Enhancement of anomalous data mining in power system predicting-aided state estimation. IEEE T. Power Syst. 19 (1), 610–619. doi:10.1109/TPWRS.2003.818726

CrossRef Full Text | Google Scholar

Irving, M. R. (2008). Robust state estimation using mixed integer programming. IEEE T. Power Syst. 23 (3), 1519–1520. doi:10.1109/TPWRS.2008.926721

CrossRef Full Text | Google Scholar

Ju, Y., and Huang, Y. (2023). State estimation for an AC/DC hybrid power system adapted to non-smooth characteristics. Power Syst. Prot. Control 51, 141–150. doi:10.19783/j.cnki.pspc.220368

CrossRef Full Text | Google Scholar

Kia, R., Shahnazari-Shahrezaei, P., and Zabihi, S. (2016). Solving a multi-objective mathematical model for a multi-skilled project scheduling problem by CPLEX solver. IEEE, 1220–1224. doi:10.1109/IEEM.2016.7798072

CrossRef Full Text | Google Scholar

Korres, G. N., Katsikas, P. J., and Contaxis, G. C. (2004). Transformer tap setting observability in state estimation. IEEE T. Power Syst. 19 (2), 699–706. doi:10.1109/TPWRS.2003.821629

CrossRef Full Text | Google Scholar

Lin, Y., and Abur, A. (2018). A highly efficient bad data identification approach for very large scale power systems. IEEE T. Power Syst. 33 (6), 5979–5989. doi:10.1109/TPWRS.2018.2826980

CrossRef Full Text | Google Scholar

Liu, Y., Zhang, N., Wang, Y., Yang, J., and Kang, C. (2019). Data-Driven power flow linearization: a regression approach. IEEE T. Smart Grid 10 (3), 2569–2580. doi:10.1109/TSG.2018.2805169

CrossRef Full Text | Google Scholar

Maalouf, H., Jabr, R. A., and Awad, M. (2013). Mixed-integer quadratic programming based rounding technique for power system state estimation with discrete and continuous variables. Electr. Pow. Compo. Sys. 41 (5), 555–567. doi:10.1080/15325008.2012.755233

CrossRef Full Text | Google Scholar

Mili, L., Cheniae, M. G., Vichare, N. S., and Rousseeuw, P. J. (1996). Robust state estimation based on projection statistics [of power systems]. IEEE T. Power Syst. 11, 1118–1127. doi:10.1109/59.496203

CrossRef Full Text | Google Scholar

Nanchian, S., Majumdar, A., and Pal, B. (2017). Three-Phase state estimation using hybrid particle swarm optimization. IEEE T. Smart Grid. 8 (3), 1035–1045. doi:10.1109/TSG.2015.2428172

CrossRef Full Text | Google Scholar

Shao, Z., Zhai, Q., and Guan, X. (2023). Physical-Model-Aided Data-Driven linear power flow model: an approach to address missing training data. IEEE T. Power Syst. 38 (3), 2970–2973. doi:10.1109/TPWRS.2023.3256120

CrossRef Full Text | Google Scholar

Shiroi, M., and Hosseinie, S. H. (2008). “Observability and estimation of transformer tap setting with minimal PMU placement,” in IEEE power and energy society general meeting - conversion and delivery of electrical energy in the 21st century. Paper presented at the 2008. doi:10.1109/PES.2008.4596382

CrossRef Full Text | Google Scholar

Teixeira, P. A., Brammer, S. R., Rutz, W. L., Merritt, W. C., and Salmonsen, J. L. (1992). State estimation of voltage and phase-shift transformer tap settings. IEEE T. Power Syst. 7 (3), 1386–1393. doi:10.1109/59.207358

CrossRef Full Text | Google Scholar

Vigerske, S., and Gleixner, A. (2017). SCIP: global optimization of mixed-integer nonlinear programs in a branch-and-cut framework. Optim. Methods Softw. 33 (3), 563–593. doi:10.1080/10556788.2017.1335312

CrossRef Full Text | Google Scholar

Zhao, J., and Mili, L. (2018). Vulnerability of the largest normalized residual statistical test to leverage points. IEEE T. Power Syst. 33 (4), 4643–4646. doi:10.1109/TPWRS.2018.2831453

CrossRef Full Text | Google Scholar

Zhuang, F., and Balasubramanian, R. (1987). Bad data processing in power system state estimation by direct data deletion and hypothesis tests. IEEE Power Eng. Rev. PER-7 (5), 40. doi:10.1109/MPER.1987.5527244

CrossRef Full Text | Google Scholar