Dynamic state awareness for distribution network based on robust adaptive cubature kalman filter

With the rapid development of the economy and society, the demand for power quality is constantly increasing. As a crucial part of grid situational awareness, distribution network state estimation plays a vital role in providing critical data support for other advanced applications, which is significant for ensuring the safe and reliable operation of the distribution network. Therefore, this paper proposes a dynamic state awareness method for distribution networks based on the robust adaptive cubature Kalman filter (RACKF). The proposed solution, grounded on the core computational concept of the cubature Kalman filter (CKF), constructs a robust noise statistical estimator (NSE) composed of a biased NSE and an unbiased NSE to adapt to the unknown and time-varying process noise parameters in the dynamic state estimation process. The proposed solution can ensure that the calculated process noise parameters always meet the constraints and guarantee the robustness of the algorithm. In addition, an estimation strategy for the fusion of multi-time scale measurement data is developed according to the RACKF-based dynamic state estimation features in order to realize system state corrections and updates. The results of simulation experiments and comparisons with traditional CKF methods demonstrate the accuracy and superiority of the proposed solution.

1 Introduction

In recent years, with the rapid development of clean energy technology, more and more distributed power generation sources such as photovoltaics and wind power have been integrated into the distribution grid due to their non-polluting characteristics (Ma et al., 2021). However, with the increasing integration of distributed generation sources and the continued growth of controllable loads, distribution networks are facing severe challenges in terms of reduced power supply reliability and deteriorating power quality (Ma et al., 2022). Therefore, the power grids are driven to the evolution towards smart grids characterized by efficiency, flexibility, intelligence, sustainability, etc (Khalid, 2024). And, the current trend lies in endowing distribution networks with stronger active regulation capabilities through the implementation of flexible and effective coordinated control technologies and management measures. In this regard, distribution network state estimation as a crucial component of the situational awareness for distribution systems plays an indispensable role in optimizing the operation of distribution networks, achieving rapid fault recovery, and ensuring the reliable performance of relay protection (Ashok et al., 2017)- (Wang et al., 2022).

The state estimation methods of power systems can be mainly divided into two types. One is the static state estimation method, which is mainly based on the Weighted Least Square (WLS). This method only utilizes the measurement data of the current measurement snapshot to estimate the current operating state of the system. With the development of phasor measurement technology, distribution phasor measurement units (DPMU) are gradually being deployed in distribution networks to further enhance the measurement level of the distribution network (Zhang et al., 2020). The DPMU serves as a complement to supervisory control and data acquisition (SCADA) measurements, providing data support for functions such as state estimation (Lin et al., 2018)- (von Meier et al., 2017). Therefore, related applications (e.g., event detection) based on DPMU data have grown significantly in recent years (Liu et al., 2020). For instance, a review of state estimation using hybrid DPMU and SCADA data is developed in (Cheng et al., 2024). However, the differences in measurement accuracy between DPMU and SCADA are more likely to result in low efficiency or even non-convergence in the solution of WLS-based static state estimation.

Compared with static state estimation methods, dynamic state estimation not only utilizes measurement information at the current time slot but also employs state prediction values obtained from the previous time slot, which can satisfy the requirements for dynamic state tracking in power systems (Zhao et al., 2019)- (Shih and Huang, 2002). Moreover, the dynamic state estimation computation process does not require iterative calculations and thus does not suffer from the numerical problem of non-convergence. To accommodate the nonlinearity of power systems, current dynamic state estimation methods for power systems have primarily evolved into methods such as extended Kalman filter (EKF), unscented Kalman filter (UKF) and cubature Kalman filter (CKF) under the basic Kalman filter framework. Among them, EKF linearizes the nonlinear equations of the system by performing a Taylor series expansion and discarding terms above the second order, which can lead to truncation errors and reduce estimation accuracy. For example, a robust iterative EKF based on the maximum likelihood method was proposed in (Zhao et al., 2017) to achieve dynamic state estimation in the presence of gross measurement errors. A multi-step adaptive interpolation method was proposed in (Akhlaghi et al., 2018) that measures the nonlinearity of the measurement equations and state equations to mitigate the negative impact on estimation accuracy, thereby improving the performance of dynamic state estimation. UKF utilizes the unscented transformation to approximately obtain the statistical characteristics of the state variables after nonlinear transformation, thus ensuring that the accuracy reaches at least second-order. For instance (Wang et al., 2012), and (Zhao, 2017) employed UKF to achieve dynamic state estimation for power systems. However, the UKF has many parameters to select during the unscented transformation (e.g., proportional correction factor, etc.), which puts a burden on the UKF to maintain a better performance. Although UKF and EKF have been integrated in (Kong et al., 2022) to achieve state estimation based on interacting multiple models, they do not change the inherent shortcomings of EKF and UKF. In addition, the fusion estimation of multi-time scale measurement data is not realized in the dynamic state estimation methods described previously. Therefore, there is a need to establish an estimation strategy for the fusion of multi-time scale measurement data applicable to dynamic state estimation.

Compared to the EKF and UKF, the CKF is presently seen as a superior alternative due to its higher level of accuracy, stability, and scalability for higher-dimensional issues (Panda et al., 2009). The CKF algorithm generates a set of equally weighted cubature points based on the spherical-radial rule to approximate the nonlinearization, enabling high-order nonlinear filtering without the need to select any parameters. This can effectively overcome the shortcomings of UKF, such as difficulty in parameter selection, poor flexibility, and low estimation accuracy for high-order systems (Arasaratnam and Haykin, 2009). However, Kalman-type filters (including CKF) can only demonstrate superior performance when accurate process and measurement noise parameters are accurately known (Zhao, 2018). The constant fluctuations in power load can lead to sudden changes in the state of the distribution network, resulting in continuous variations in the statistical parameters of process noise. In addition, there are also certain modeling errors in the construction of state equations for power systems, which can also lead to inaccuracies in the process noise parameters. Therefore, the statistical parameters of process noise are time-varying and difficult to accurately obtain, which makes it challenging to guarantee the performance of traditional state estimation methods based on Kalman-type filters. To address this issue, previous works have established noise statistic estimators (NSE) to estimate noise parameters. For example, the Sage-Husa NSE was used in (Zhang, 2009) to estimate the time-varying noise covariance matrix. However, the NSE in the aforementioned studies may lead to violations of constraints in the estimated noise parameters, thereby reducing the robustness of the state estimation algorithm. Moreover, there is still a lack of robust NSE that is effectively applicable to CKF.

To address the aforementioned challenges faced in distribution network state estimation, this paper derives a robust NSE to establish the robust adaptive cubature Kalman filter (RACKF), and further proposes a dynamic state estimation method based on RACKF with the corresponding estimation strategy for the fusion of multi-time scale measurement data. The proposed solution not only inherits the advantage of CKF in achieving efficient filtering without the need for parameter selection but also guarantees the adaptability and robustness of CKF. The main technical contributions made in this paper can be summarized as follows.

(1) A robust NSE consisting of a biased NSE and an unbiased NSE is constructed based on the core computational concept of CKF and provides a rigorous proof of the semi-positive definiteness of the estimated parameters, which can adaptively estimate process noise parameters during the state estimation to cope with the fluctuations in noise parameters caused by modeling errors and state changes. Furthermore, the NSE can ensure that the calculated process noise parameters always satisfy the constraints, significantly enhancing the robustness of the algorithm.

(2) An estimation strategy for the fusion of multi-time scale measurement data is developed according to the RACKF-based dynamic state estimation features, which can realize system state corrections and updates utilizing abundant DPMU measurements.

(3) Simulation experiments on the IEEE 33-bus system and comparisons with the traditional CKF method demonstrate the accuracy and superiority of the proposed method in dynamic state estimation of distribution networks.

The remainder of this paper is structured as follows. Section 2 introduces the problem formulation. Section 3 elaborates on the principles of CKF and RACKF. Section 4 develops the estimation strategy for the fusion of multi-time scale measurement data and summarizes the specific implementation steps of the proposed solution. The performance of the proposed solution is verified through simulation in Section 5. This paper is concluded in Section 6.

2 Problem formulation

The goal of state estimation is to capture the real-time operational state of the distribution network based on the hybrid SCADA and DPMU measurement data. In general, the real-time operational state of the distribution network is characterized by a set of state variables, including the voltage magnitudes of each bus and the voltage phase angles of all buses except the reference bus, as shown in Equation 1.

$x_k={\left[V_m,{\delta }_m\right]}^{\mathrm{T}}(1)$

where $V_m$ and ${\delta }_m$ are voltage magnitude and phase angle of $m$-th bus, respectively.

The focus of this paper is on dynamic state estimation, so it is necessary to establish the state equations of the distribution network. The state equation of the distribution network can be constructed as Equation 2 based on the two-parameter exponential smoothing method.

$\left\{\begin{array}{l}{x}_{k\left.+1\right|k}=S_k+b_k\\ S_k=\alpha x_k+\left(1-\alpha \right)x_{k|k-1}\\ b_k=\beta \left(S_k-S_{k-1}\right)+\left(1-\beta \right)b_{k-1}\end{array}\right.(2)$

where $S_k$ and $b_k$ are horizontal and vertical components, respectively; $\alpha$ and $\beta$ are smoothing parameters, and they characterize trust in recent historical data and forward historical data, respectively; The subscripts $k$ and $k-1$ indicate time slots.

As stated previously, the measurement of the distribution network consists of a hybrid measurement of DPMU and SCADA. Therefore, the measurement vector of the distribution network can be expressed as Equation 3.

$z_k={\left[V_m{P}_m{Q}_m{P}_{mt}{Q}_{mt}{\delta }_m\right]}^{\mathrm{T}}(3)$

where $V_m$ and ${\delta }_m$ are voltage magnitude and phase angle measurements of $m$-th bus, respectively; $P_m$ and $Q_m$ are inject active and reactive power measurements of $m$-th bus, respectively; $P_{mt}$ and $Q_{mt}$ are active and reactive flow measurements of branch $m-t$, respectively. In the distribution network, only some buses are equipped with DPMU and hence phase angle measurements in Equation 3 are only available for a subset of buses.

Corresponding to the various measurement types in the measurement vector and considering that the conductance branch to the ground can be neglected for distribution lines, the distribution network measurement equations also need to be constructed for dynamic state estimation, as shown in Equation 4.

$\left\{\begin{array}{l}{V}_m=V_m\\ P_m=V_m{\displaystyle \sum _t}{V}_t\left(G_{mt}\cos {\delta }_{mt}+B_{mt}\sin {\delta }_{mt}\right)\\ Q_m=V_m{\displaystyle \sum _t}{V}_t\left(G_{mt}\sin {\delta }_{mt}-B_{mt}\cos {\delta }_{mt}\right)\\ P_{mt}=V_m^2{g}_{mt}-V_m{V}_t{g}_{mt}\cos {\delta }_{mt}-V_m{V}_t{b}_{mt}\sin {\delta }_{mt}\\ Q_{mt}=-V_m^2{b}_{mt}-V_m{V}_t{g}_{mt}\sin {\delta }_{mt}+V_m{V}_t{b}_{mt}\cos {\delta }_{mt}\\ {\delta }_m={\delta }_m\end{array}\right.(4)$

where $G_{mt}$ and $B_{mt}$ are the real and imaginary parts of the position element of the $m\text{th}$ row and the $t\text{th}$ column of the node admittance matrix, respectively; ${\delta }_{mt}={\delta }_m-{\delta }_t$; $g_{mt}$ and $b_{mt}$ are the conductance and susceptance of the corresponding branch, respectively.

At this point, the state-space model required for dynamic state estimation of distribution networks can be modeled as (2) and (4). In the compact form, the state-space model of the distribution network can be represented as Equation 5.

$\left\{\begin{array}{l}{x}_{k+1}=f\left(x_k\right)+w_k\\ z_{k+1}=h\left(x_{k+1}\right)+v_{k+1}\end{array}\right.(5)$

where $x_k$ and $z_{k+1}$ are the $n$-dimensional state vector and $h$-dimensional measurement vector of the system, respectively; $w_k$ and $v_{k+1}$ represent the process noise and measurement noise vectors, respectively, and they satisfy $w_k\sim N\left(0,Q_k\right)$ and $v_{k+1}\sim N\left(0,R_{k+1}\right)$; $Q_k$ and $R_{k+1}$ denote the covariance matrices of process noise and measurement noise, respectively.

From the construction of the distribution network state equations Equation 2, it is essentially a prediction model, so there will be some modeling errors. Also, the noise is time-varying due to the constant change of the system state, so it is necessary to adapt to the unknown and time-varying noise parameters in the dynamic state estimation process. For this reason, this paper derives a robust NSE consisting of a biased NSE and an unbiased NSE based on the core computational concept of CKF and thus RACKF is constructed to guarantee the performance of state estimation. The detailed principle of RACKF including the robust NSE is described in Section 3.

Although measurement accuracy and redundancy have improved with increased DPMU deployment. However, it also creates challenges for the fusion of multi-time scale measurement data from DPMU and SCADA. Therefore, an estimation strategy for the fusion of multi-time scale measurement data is developed in this paper according to the RACKF-based dynamic state estimation features, as detailed in Section 4.

3 Robust adaptive cubature kalman filter

3.1 Fundamentals of CKF algorithm

The CKF algorithm generates a set of equally weighted cubature points based on the spherical-radial rule to approximate nonlinearities, enabling high-order nonlinear filtering without the need to select any parameters. The computational process of the CKF algorithm comprises two main stages: prediction and filtering. In the prediction stage, the CKF algorithm utilizes the state estimate results and covariance information from the previous time slot, in conjunction with the state equation, to predict the state at a future time slot. During the filtering stage, the algorithm corrects the prediction results using actual observation data, thereby obtaining the state estimate results and covariance for the current time slot. The entire computational process of the CKF is detailed as follows.

Stage 1: Prediction. During the prediction process, a set of equally weighted cubature points should first be generated around the state estimation results from the previous time slot based on the spherical-radial rule, where the number of cubature points is twice the dimension of the state vector (i.e., $2n$). The generation method for the cubature point set and weights is presented in Equations 6, 7.

$X_k^i=\sqrt{P_k}{\xi }_i+{\widehat{x}}_k,i=1,2,\cdots ,2n(6)$

$W_i=\frac{1}{2n},i=1,2,\cdots ,2n(7)$

where $X_k^i$ denotes the $i$-th cubature point constructed from the state estimation result at time slot $k$; ${\widehat{x}}_k$ is the state estimation result at time slot $k$; $\sqrt{P_k}$ represents the Cholesky decomposition of $P_k$ and $P_k$ is the covariance matrix of estimation error at time slot $k$; ${\xi }_i$ is the $i$-th column of matrix $\mathbf{\xi }$ and $\mathbf{\xi }$ is shown in Equation 8; $W_i$ represents the weight of the $i$-th cubature point.

$\mathbf{\xi }=\sqrt{n}\left[\begin{array}{cccccccc}1& 0& \cdots & 0& -1& 0& \cdots & 0\\ 0& 1& \cdots & 0& 0& -1& \cdots & 0\\ ⋮& ⋮& \cdots & ⋮& ⋮& ⋮& \cdots & ⋮\\ 0& 0& \cdots & 1& 0& 0& \cdots & -1\end{array}\right](8)$

By substituting all cubature points into the state equation of the distribution network to propagate them, the predicted values of all cubature points can be obtained, as shown in Equation 9.

$x_{k\left.+1\right|k}^i=f\left(X_k^i\right)(9)$

where $x_{k\left.+1\right|k}^i$ is the cubature point after propagation through the state equation. Accordingly, the predicted value of state and the prediction error covariance matrix can be calculated based on Equations 10, 11, respectively.

${\widehat{x}}_{k\left.+1\right|k}={\displaystyle \sum _{i=1}^{2n}}{W}_i{x}_{k\left.+1\right|k}^i(10)$

$P_{k\left.+1\right|k}={\displaystyle \sum _{i=1}^{2n}}{W}_i{x}_{k\left.+1\right|k}^i{\left(x_{k\left.+1\right|k}^i\right)}^{\mathrm{T}}-{\widehat{x}}_{k\left.+1\right|k}{\left({\widehat{x}}_{k\left.+1\right|k}\right)}^{\mathrm{T}}+Q_k(11)$

Stage 2: Filtering. Based on the predicted values of the state, a new set of cubature points $X_{k\left.+1\right|k}^i$ can be generated according to Equation 12, and then these points are substituted into the measurement equation to obtain the measurement predictions of the cubature point set $z_{k\left.+1\right|k}^i$, as shown in Equation 13.

$X_{k\left.+1\right|k}^i=\sqrt{P_{k\left.+1\right|k}}{\xi }_i+{\widehat{x}}_{k\left.+1\right|k},i=1,2,\cdots ,2n(12)$

$z_{k\left.+1\right|k}^i=h\left(X_{k\left.+1\right|k}^i\right)(13)$

By performing weighted summation on the cubature point set of all measurement predictions, the final measurement prediction can be obtained, as shown in Equation 14. Subsequently, the measurement prediction error covariance matrix and the cross-covariance matrix between the state prediction and the measurement prediction can be calculated based on Equations 15, 16, respectively.

${\widehat{z}}_{k\left.+1\right|k}={\displaystyle \sum _{i=1}^{2n}}{W}_i{z}_{k\left.+1\right|k}^i(14)$

$P_{zz,k\left.+1\right|k}={\displaystyle \sum _{i=1}^{2n}}{W}_i{z}_{k\left.+1\right|k}^i{\left(z_{k\left.+1\right|k}^i\right)}^{\mathrm{T}}-{\widehat{z}}_{k\left.+1\right|k}{\left({\widehat{z}}_{k\left.+1\right|k}\right)}^{\mathrm{T}}+R_{k+1}(15)$

$P_{xz,k\left.+1\right|k}={\displaystyle \sum _{i=1}^{2n}}{W}_i{x}_{k\left.+1\right|k}^i{\left(z_{k\left.+1\right|k}^i\right)}^{\mathrm{T}}-{\widehat{x}}_{k\left.+1\right|k}{\left({\widehat{z}}_{k\left.+1\right|k}\right)}^{\mathrm{T}}(16)$

where ${\widehat{z}}_{k\left.+1\right|k}$ represents the measurement prediction obtained through propagation, while $P_{zz,k\left.+1\right|k}$ and $P_{xz,k\left.+1\right|k}$ represent the measurement prediction error covariance matrix and the cross-covariance matrix, respectively.

Finally, the Kalman gain can be calculated to update the state vector and covariance matrix, as shown in Equations 17–19.

$K_{k+1}=P_{xz,k\left.+1\right|k}{P}_{zz,k\left.+1\right|k}^{-1}(17)$

${\widehat{x}}_{k+1}={\widehat{x}}_{k\left.+1\right|k}+K_{k+1}\left(z_{k+1}-{\widehat{z}}_{k\left.+1\right|k}\right)(18)$

$P_{k+1}=P_{k\left.+1\right|k}-K_{k+1}{P}_{zz,k\left.+1\right|k}{K}_{k+1}^{\mathrm{T}}(19)$

where $K_{k+1}$ denotes the Kalman gain at $k+1$ time slot.

After obtaining the estimated state vector and the estimation error variance matrix at the time slot $k+1$, one can return to the prediction step for the state estimation at the next time slot.

3.2 Noise statistics estimator

During the state estimation process, if the process noise variance matrix $Q_k$ is inaccurate, it can severely impact the estimation performance of the CKF algorithm, making it difficult to accurately estimate the system state. Therefore, it is necessary to estimate the process noise variance matrix $Q_k$ in real time during dynamic state estimation to ensure the performance of state estimation. Based on the computational rule of CKF, the CKF-based Sage-Husa NSE can be developed as Equations 20–22. Therefore, an unbiased NSE that considers adaptive forgetting can be constructed.

$d_{k+1}=\frac{1-b}{1-b^{k+1}}(20)$

${\epsilon }_{k+1}=z_{k+1}-{\widehat{z}}_{k\left.+1\right|k}(21)$

$\begin{array}{l}\hfill Q_{k+1}=\left(1-d_{k+1}\right)Q_k+d_{k+1}\left[K_{k+1}{\epsilon }_{k+1}{\epsilon }_{k+1}^{\mathrm{T}}{K}_{k+1}^{\mathrm{T}}+\right.\\ \hfill \left.P_k-{\displaystyle \sum _{i=1}^{2n}}{W}_i{x}_{k\left.+1\right|k}^i{\left(x_{k\left.+1\right|k}^i\right)}^{\mathrm{T}}-{\widehat{x}}_{k\left.+1\right|k}{\left({\widehat{x}}_{k\left.+1\right|k}\right)}^{\mathrm{T}}\right]\end{array}(22)$

where $d_{k+1}$ is forgetting coefficient at time slot $k+1$; $b$ is forgetting factor; ${\epsilon }_{k+1}$ denotes the residual difference between the system measure and the measure prediction at time slot $k+1$.

According to the definition of covariance matrix, it must be a semi-positive definite matrix. Assuming that matrices $A$ and $B$ are both semi-positive definite matrices, it is not guaranteed that $A-B$ is still semi-positive definite by the properties of semi-positive definite matrices. Therefore, the subtraction operation in Equation 22 may lead to $Q_{k+1}$ losing its semi-positive definiteness, which can cause the algorithm to become ill-conditioned during computation and unable to continue running. Therefore, in order to ensure the robustness of the algorithm (i.e., The computation is not made to terminate because the estimated noise statistics parameter violates semi-positive definiteness.) while retaining most of the covariance correction terms in the unbiased NSE to ensure high estimation accuracy, a well-performing biased NSE must be established to estimate the process noise variance matrix. Regarding this, a biased NSE is derived from an unbiased NSE shown in Equation 23 (Caceres et al., 2009).

$Q_{k+1}=\left(1-d_{k+1}\right)Q_k+d_{k+1}\left[\text{diag}{\left({\widehat{x}}_{k+1}-{\widehat{x}}_{k\left.+1\right|k}\right)}^2-\left(P_{k+1}-P_{k\left.+1\right|k}+Q_k\right)\right](23)$

where $\text{diag}\left(·\right)$ denotes a diagonal matrix constructed with diagonal elements of matrix $\left(·\right)$.

Rearranging Equation 19, and substituting it into Equation 23, Equation 24 can be obtained.

$Q_{k+1}=\left(1-d_{k+1}\right)Q_k+d_{k+1}\left[\text{diag}{\left({\widehat{x}}_{k+1}-{\widehat{x}}_{k\left.+1\right|k}\right)}^2+K_k{P}_{zz,k\left.+1\right|k}{K}_k^{\mathrm{T}}-Q_k\right](24)$

According to (18) and (21), and discarding $-Q_k$, the biased NSE (25) can be finally derived from Equation 23.

$Q_{k+1}=\left(1-d_{k+1}\right)Q_k+d_{k+1}\left[\text{diag}\left(K_{k+1}{\epsilon }_{k+1}{\epsilon }_{k+1}^{\mathrm{T}}{K}_{k+1}^{\mathrm{T}}\right)+K_{k+1}{P}_{zz,k\left.+1\right|k}{K}_{k+1}^{\mathrm{T}}\right](25)$

Proof: Since both the initial $Q_k$ and $\left[\text{diag}\left(K_{k+1}{\epsilon }_{k+1}{\epsilon }_{k+1}^{\mathrm{T}}{K}_{k+1}^{\mathrm{T}}\right)\right.$$\left.+K_{k+1}{P}_{zz,k\left.+1\right|k}{K}_{k+1}^{\mathrm{T}}\right]$ are semi-positive definite, the $Q_{k+1}$ calculated from Equation 25 can also be guaranteed to be semi-positive definite. That is, the robustness of the RACKF algorithm is strong, and the estimated $Q_{k+1}$ will not violate the semi-positive definiteness, thus making the algorithm ill-conditioned.

By combining (25) with (22), a fault-tolerant NSE can be constructed. Specifically, when $Q_{k+1}$ computed from the unbiased NSE (22) is not positive semi-definite, $Q_{k+1}$ can be recalculated based on the biased NSE (25) to ensure the robustness of the algorithm on the basis of retaining a large amount of correction information.

4 RACKF-based dynamic state estimation for distribution networks

4.1 Estimation strategy for the fusion of multi-time scale measurement data

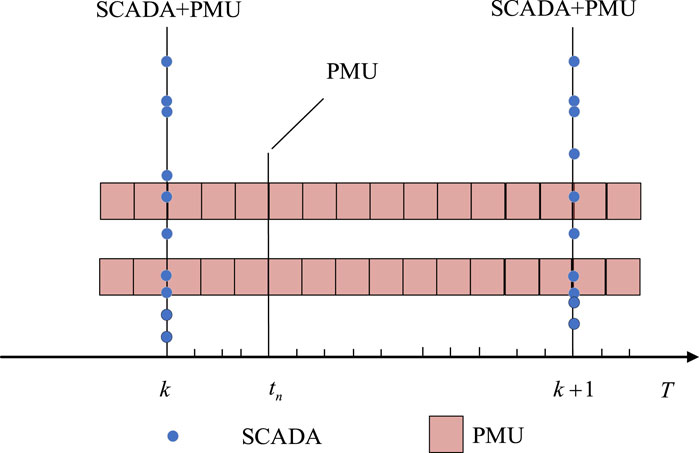
As stated previously, the current sources of measurement data in distribution networks are mainly SCADA and DPMU. As shown in Figure 1, a complete frame of data can be obtained together with the DPMU measurements at the time slot of SCADA sampling. Then, dynamic state estimation can be performed according to the state-space model described in Section 2. However, there will be DPMU measurement between two complete frames of DPMU and SCADA data due to the higher sampling frequency of DPMU. In this regard, a fusion estimation strategy is proposed in this paper for multi-timescale measurement data applicable to dynamic state estimation features. At time slots $k$ and $k+1$, the complete measurement data is obtained and a complete prediction and filtering step is performed for state estimation using the RACKF. Only DPMU measurement data can be obtained at the time slot $t_n$. Therefore, the state prediction step is not carried out considering that the DPMU sampling interval is small. Instead, only the filtering step is performed using the estimated state and error covariance matrix at the time slot $k$ in order to correct and update the system state using DPMU data.

Figure 1

Figure 1. Diagram of measurement frequency for PMU and SCADA.

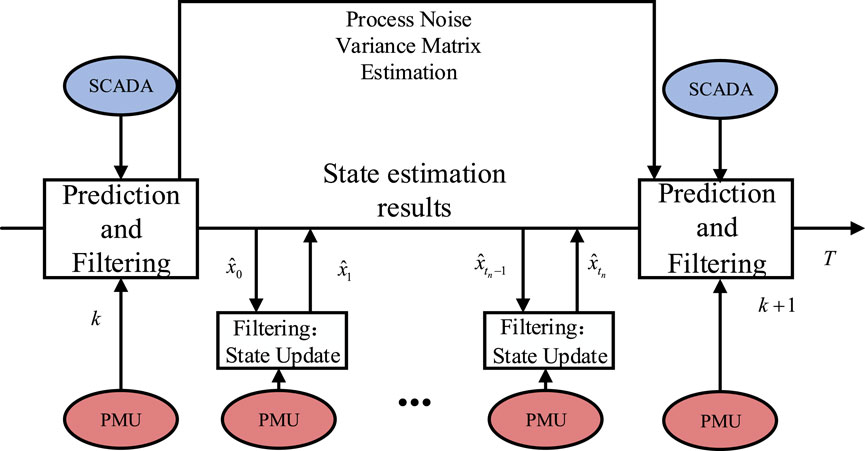
A concrete implementation of data fusion estimation based on RACKF dynamic state estimation is detailed in Figure 2. More specifically, the complete prediction and filtering session is achieved by using the measurement data of SCADA and DPMU at the time slot $k$ to achieve state estimation and to estimate the statistical parameter of the process noise $Q_{k+1}$ for use in the next complete state estimation process. At time slot $k+1$, the state estimation results obtained at time slot $k$, $Q_{k+1}$, and the hybrid DPMU and SCADA measurement data are used for the prediction and filtering session to complete the state estimation. When the DPMU measurements are obtained between time slots $k$ and $k+1$, the results of the most recent state estimation are used as a starting point, and only the filtering session of the RACKF is performed to correct and update the system state. As shown in Figure 2, the most recent state estimation result is ${\widehat{x}}_{t_n-1}$ when computing ${\widehat{x}}_{t_n}$. The filtering Process is performed using ${\widehat{x}}_{t_n}$. It is worth noting that in the calculation of the RACKF filtering step, the predicted state values ${\widehat{x}}_{k\left.+1\right|k}$ and prediction error covariance matrix $P_{k\left.+1\right|k}$ to be used in Equation 12 for generating cubature points are replaced with ${\widehat{x}}_{t_n-1}$ and $P_k$, respectively, and similarly, ${\widehat{x}}_{k\left.+1\right|k}$ used in Equation 18 is replaced with ${\widehat{x}}_{t_n-1}$.

Figure 2

Figure 2. RACKF-based estimation of PMU and SCADA data fusion.

4.2 RACKF-based dynamic state estimation process for distribution networks

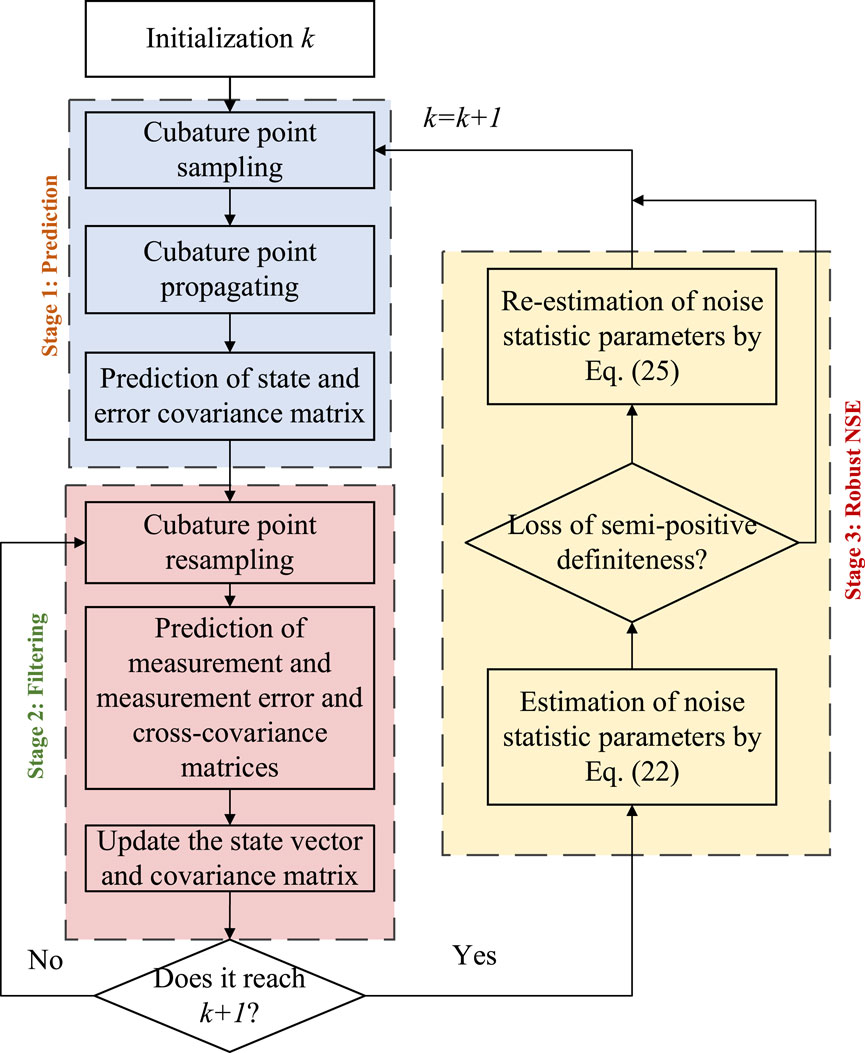
The specific implementation steps of the proposed dynamic state estimation based on RACKF and fusing multi-time scale measurement data are summarized in Figure 3. First, initialize the state values ${\widehat{x}}_0$ and the estimation error covariance matrix $P_0$ and set $k=1$. After that, the prediction step is carried out. Specifically, cubature point sampling is performed according to Equation 6–8. State prediction and prediction covariance matrix calculations were performed according to the state equations Equation 2 and Equations 9–11. This is followed by the computation of the filtering step. The cubature points are sampled again according to Equation 12. Then the measurement predictions and covariance matrices are calculated based on measurement equations Equation 4 and Equations 13–16. Finally, the Kalman gain is calculated according to Equation 17 and the state and estimation error covariance matrix is updated according to Equations 18, 19. If the time slot $k+1$ has not yet been reached at this point and only DPMU measurements have been received, only state corrections are performed as described in Section 4.1. After reaching the time slot $k+1$, the estimation of the statistical parameters of the process noise is performed according to Equations 20–22 and Equation 25. The updated process noise parameters are utilized to go back to the prediction step for the calculation of the state estimation for the next time when the complete hybrid of measurement data is received, and $k=k+1$.

Figure 3

Figure 3. Flowchart of RACKF-based dynamic state estimation for distribution networks.

5 Case studies

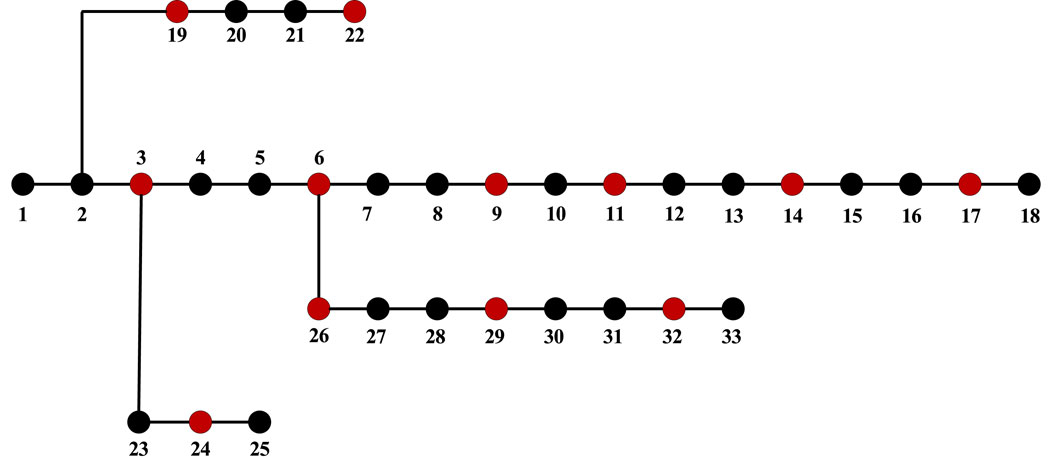
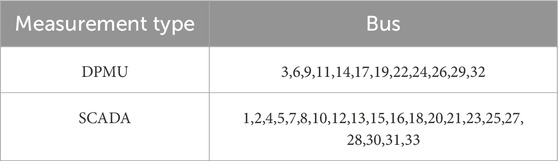
In this section, the IEEE 33-bus system is used for simulation experiments, and a comparison is made with the traditional CKF algorithm to validate the effectiveness of the solution proposed in this paper. The topology of the IEEE 33-bus system is shown in Figure 4. All parameters of the IEEE 33-bus system can be found in (Baran and Wu, 1989). The measurement configuration is shown in Table 1 and denoted as red and black dots in Figure 4 for DPMU and SCADA measurements, respectively. To have more realistic case studies in this work, the IEEE 33-bus system is constructed in MATPOWER for power flow computation and Gaussian noise is added to obtain the measurement data (Asprou and Kyriakides, 2017)- (Zimmerman et al., 2011). The standard deviation of the measurement error in the SCADA system is 0.02 with a mean value of 0. The standard deviation of the DPMU voltage magnitude measurement error is 0.005 with a mean value of 0, and the standard deviation of the DPMU phase angle measurement error is 0.002 with a mean value of 0. Furthermore, the forgetting factor $b$ is set to 0.96 and the smoothing parameters $\alpha$ and $\beta$ are set to 0.8 and 0.5 in the simulations. $Q_0$ is set to ${10}^{-6}\mathrm{{\rm I}}$ (Wang et al., 2022). Then, the state estimation performance of the proposed method is tested in the following subsections.

Figure 4

Figure 4. Topology and measurement configuration of the IEEE 33-bus system.

Table 1

Table 1. The measurement configuration of the IEEE 33-bus system.

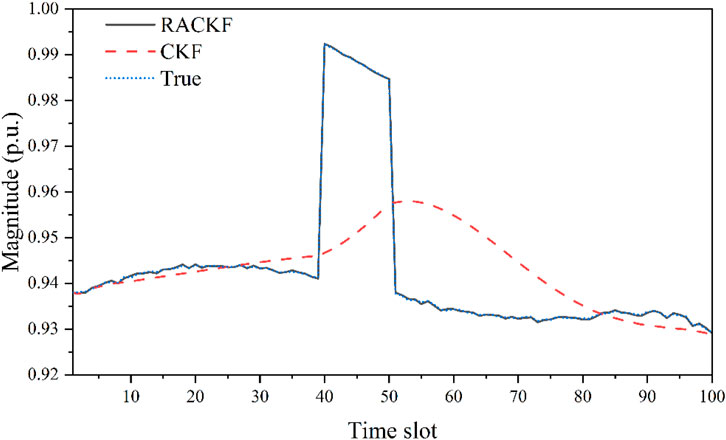
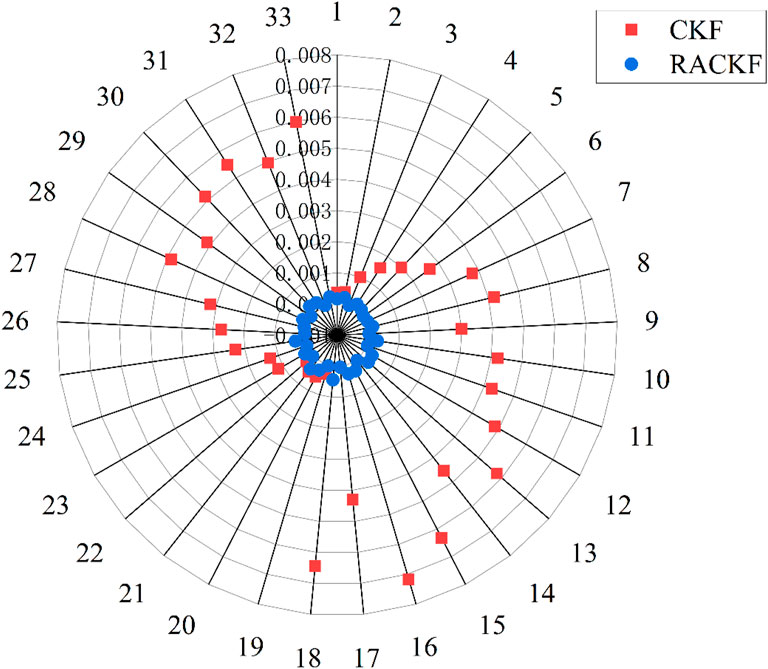
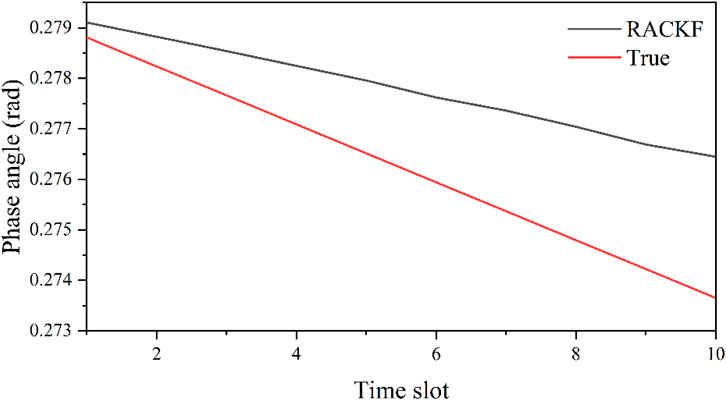
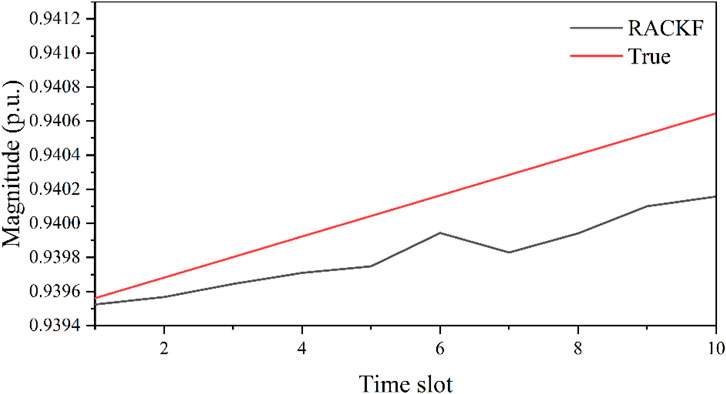
In this simulation, a sudden load drop is set at the 40-th time slot and the load level remains until the 50-th time slot, after which it returns to the original load level. During the dynamic state estimation, it is found that the process noise covariance matrix calculated by the unbiased NSE loses semi-positive definiteness 99 times out of 100 time slots, suggesting that the creation of the proposed robust NSE for dynamic state estimation is effective and necessary. Then, the state estimation results of bus 31 were randomly selected for analysis. The curves of voltage phase angle and magnitude varying with time are presented in Figures 5, 6, respectively. As can be seen, both for voltage magnitude and phase angle, during the steady-state operation phase of the system from time slots one to 39, CKF and RACKF are able to achieve good estimation performance, with the state estimation results being close to the true values. However, the estimation results of RACKF are more accurate than CKF because the NSE involved is adaptive to the modeling error. When the load at the 40th time slot experiences severe fluctuations and suddenly drops, the CKF algorithm lacks the necessary noise adaptive ability as its process noise variance matrix always equals the initial value. This indicates that the estimation accuracy of the CKF algorithm entirely depends on the initially set noise statistical parameters, which often deviate significantly from the actual situation. Consequently, the mismatch of the process noise variance matrix prevents the CKF algorithm from effectively tracking the state changes, leading to filter divergence and a significant increase in the error of its state estimation results, thus failing to meet the actual needs. Even when the system load level recovers to its original state at the 51st time slot, the CKF algorithm still exhibits a significant discrepancy between its noise statistical parameter values and the true values due to the inaccurate state estimation results from previous time slots. This results in the inability of the state estimation to converge accurately at each subsequent time slot, and the existence of persistent large errors. Consequently, the accuracy of the CKF algorithm fails to meet the requirements.

Figure 5

Figure 5. Estimated voltage phase angle results of bus 31.

Figure 6

Figure 6. Estimated voltage magnitude results of bus 31.

In contrast, the NSE in the RACKF algorithm is capable of accurately estimating both the magnitude and phase angle process noise parameters online simultaneously. After completing the state estimation at each time slot, it updates the process noise variance matrix and uses the estimated $Q_{k+1}$ for the state estimation at the next time slot. This mechanism enables the RACKF algorithm to adaptively respond to changes in the system state, thereby accurately tracking the system state and ensuring the highest state estimation accuracy.

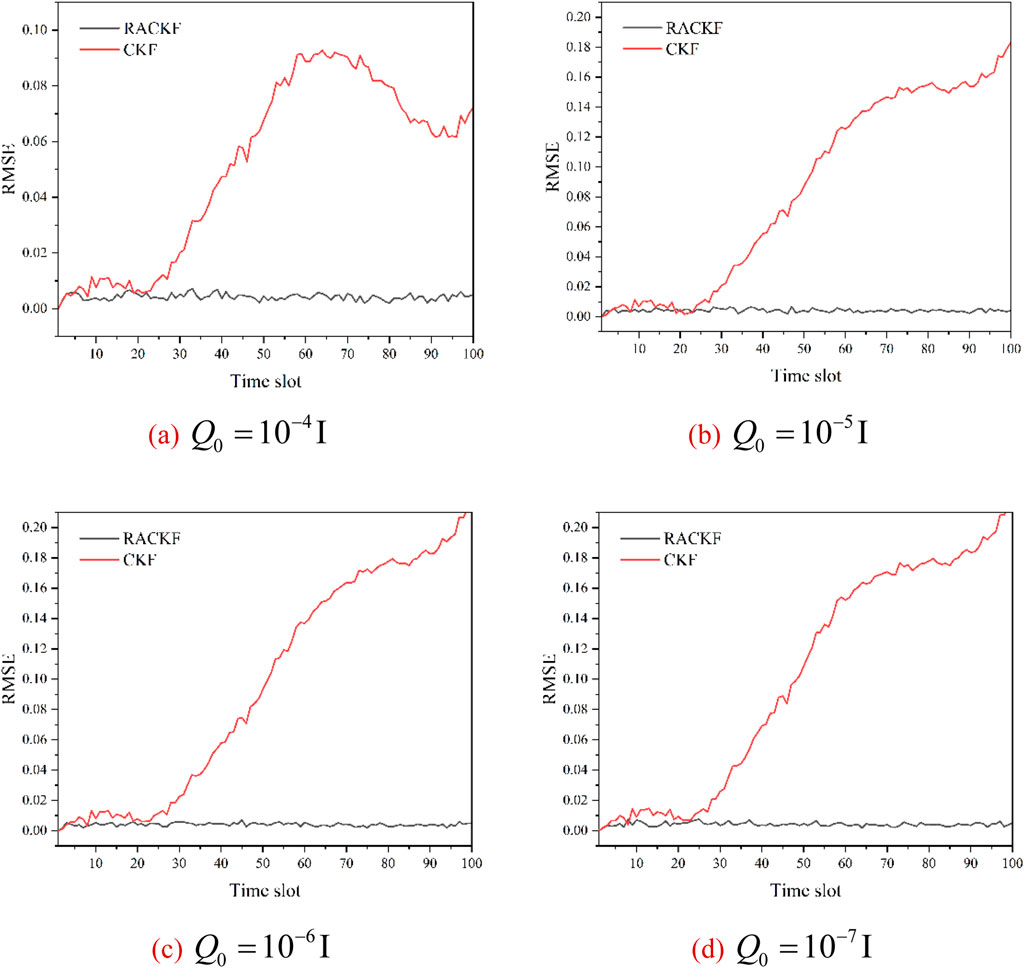
In practical applications, there may exist significant deviations in the initial settings of process noise parameters, leading to inconsistencies with the actual situation. In such cases, even if the system maintains stable operation, it may still result in inaccurate state estimation results. To comprehensively evaluate the performance of the proposed method under different initial process noise parameters, the initial process noise parameters $Q_0$ are set to ${10}^{-4}\mathrm{{\rm I}}$, ${10}^{-5}\mathrm{{\rm I}}$, ${10}^{-6}\mathrm{{\rm I}}$ , and ${10}^{-7}\mathrm{{\rm I}}$, respectively. During the entire simulation, the load level is maintained stable without significant changes. After the simulation, the root mean square error (RMSE) of the relative error for each algorithm under different initial process noise parameters is compared in Figure 7. RMSE of the relative error can be calculated according to (26) (Panda et al., 2023).

$RMSE=\sqrt{\frac{1}{N}{{\displaystyle \sum _{i=1}^n}\left(\frac{x_i-{\widehat{x}}_i}{x_i}\right)}^2}(26)$

where $x_i$ and ${\widehat{x}}_i$ are the true and estimated values of $i$-th state variables; $N$ is the total number of sate variables.

Figure 7

Figure 7. RMSE of CKF and RACKF for different $Q_0$.

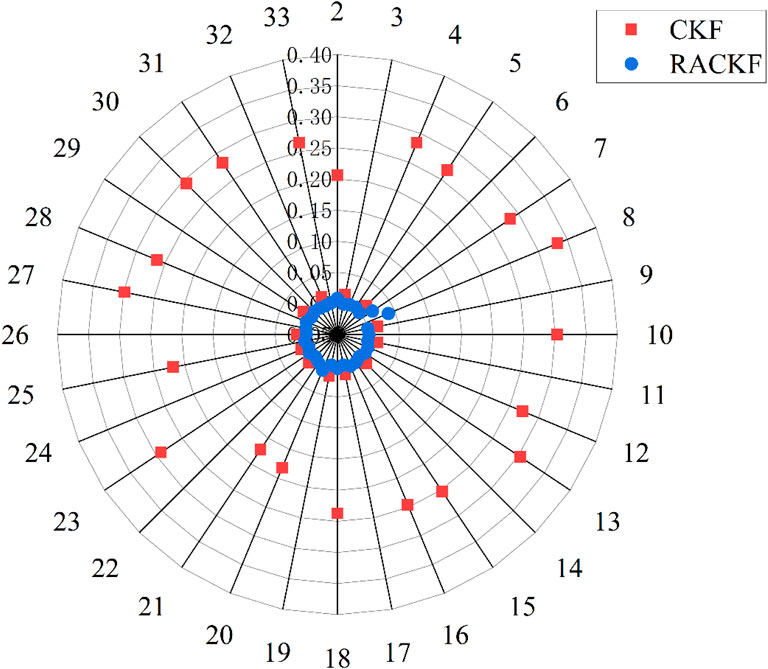
From the comparison of the results in Figure 7, it can be observed that regardless of the accuracy of the initial process noise statistical parameter $Q_0$, the RACKF algorithm is able to achieve accurate estimation of the process noise statistical parameters during the state estimation, thereby adapting to the real process noise. Consequently, the RMSE of the relative error in its state estimation results rapidly converges to a lower level. In contrast, the state estimation accuracy of the CKF algorithm entirely depends on the initially set process noise parameters. When the initial process noise parameters are not accurately set, the state estimation error of the CKF algorithm gradually accumulates over time, resulting in a generally upward trend in the RMSE of the relative error. This demonstrates that the RACKF algorithm exhibits greater robustness and adaptability when dealing with different initial noise parameter scenarios.

Taking the case of $Q_0={10}^{-6}\mathrm{{\rm I}}$ as an example, the average relative errors of the state estimation results for 33 buses at 100 time slots obtained using RACKF and CKF are compared, as shown in Figures 8, 9, respectively. From the figures, it can be visualized again that the estimation performance of RACKF is significantly higher than that of CKF, both for phase angle and magnitude, which again reflects the superiority of the method proposed in this paper.

Figure 8

Figure 8. Comparison of relative errors in phase angle estimation results.

Figure 9

Figure 9. Comparison of relative errors of magnitude estimation results.

In addition, it is assumed that there are 10 DPMU data samples between the two SCADA samples to validate the estimation strategies for the fusion of multi-time scale measurement data proposed in this paper. After simulation, bus 32 is arbitrarily selected to compare the state update results with the true state, as shown in Figures 10, 11. It can be seen that the deviation between the estimated and true values of magnitude and phase angle shows an overall upward trend because the DPMU measurements are used to update the system state without a prediction step and are only corrected on the basis of the estimated results of the previous time slot. The deviation rises until the complete state estimation process is performed at the time slot of arrival of the complete data, then the next time slot of update starts from the new state and the error goes back to the initial level. Due to the high sampling frequency of the DPMU, the state of the system does not change much between two DPMU sampling intervals, so even if the error rises to the time slot of maximum it is still considered to be accepted.

Figure 10

Figure 10. Voltage phase angle update results of bus 32.

Figure 11

Figure 11. Voltage magnitude update results of bus 32.

6 Conclusion

To achieve accurate state awareness for the distribution network, a dynamic state estimation method incorporating multiple time scale measurement data is proposed in this paper. In the proposed solution, a robust NSE consisting of a biased NSE and an unbiased NSE is constructed based on the core computational concept of CKF and hence RACKF is developed. Through the robust NES, the time-varying process noise parameters can be adapted during the dynamic state estimation, while the robustness of the RACKF is guaranteed. In addition, an estimation strategy for the fusion of multi-time scale measurement data is developed according to the RACKF-based dynamic state estimation features. It effectively achieves distribution network state updates using abundant DPMU measurements.

The superior performance of the proposed method is verified through a series of simulations in the IEEE 33-bus system and compared with the conventional CKF algorithm and the key findings are summarized as follows: the process noise variance matrix obtained from the proposed robust NSE can strictly maintain the semi-positive definiteness. The solution proposed in this paper is not only superior to the conventional CKF algorithm in state estimation accuracy when the system is running steady, but also can still accurately adapt to the process noise parameters and realize the tracking of the real state of the system when the load sharply fluctuates. In addition, the RMSE of the state estimation results of the proposed method in this paper is smaller than that of the traditional CKF algorithm, regardless of the initial process noise parameter settings.

The development of information technology has led to an increasing level of intelligence and automation in the current distribution network. However, the ensuing drawback is that the distribution network is vulnerable to cyber-attacks. Therefore, further research efforts can be made in the future on dynamic state estimation of distribution networks under cyber-attacks.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

RD: Conceptualization, Writing–original draft. YW: Methodology, Writing–original draft. DL: Writing–original draft. LW: Writing–review and editing. XT: Conceptualization, Writing–original draft. JW: Validation, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This paper was supported by the science and technology project of Zhejiang Dayou Group Co., Ltd. Under grant DY2023-11.

Conflict of interest

Authors RD and XT were employed by State Grid Hangzhou Xiaoshan Power Supply Company.

Authors YW, DL, LW, and JW were employed by Zhejiang Zhongxin Power Engineering Construction Co., Ltd.

The authors declare that this study received funding from Zhejiang Dayou Group Co., Ltd. The funder had the following involvement in the study: the construction of RACKF and estimation strategy.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akhlaghi, S., Zhou, N., and Huang, Z. (2018). A multi-step adaptive interpolation approach to mitigating the impact of nonlinearity on dynamic state estimation. IEEE Trans. SMART GRID 9 (4), 3102–3111. doi:10.1109/tsg.2016.2627339

CrossRef Full Text | Google Scholar

Arasaratnam, I., and Haykin, S. (2009). Cubature kalman filters. IEEE Trans. AUTOMATIC CONTROL 54 (6), 1254–1269. doi:10.1109/TAC.2009.2019800

CrossRef Full Text | Google Scholar

Ashok, A., Govindarasu, M., and Wang, J. (2017). Cyber-physical attack-resilient wide-area monitoring, protection, and control for the power grid. Proc. IEEE 105 (7), 1389–1407. doi:10.1109/jproc.2017.2686394

CrossRef Full Text | Google Scholar

Asprou, M., and Kyriakides, E. (2017). Identification and estimation of erroneous transmission line parameters using PMU measurements. IEEE Trans. POWER Deliv. 32 (6), 1–2519. doi:10.1109/tpwrd.2017.2648881

CrossRef Full Text | Google Scholar

Baran, M. E., and Wu, F. F. (1989). Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 4 (2), 1401–1407. doi:10.1109/61.25627

CrossRef Full Text | Google Scholar

Caceres, M. A., Sottile, F., and Spirito, M. A.Ieee (2009). “Adaptive location tracking by kalman filter in wireless sensor networks,” in Proceedings paper 2009 IEEE international conference on wireless and mobile computing, 2009.

CrossRef Full Text | Google Scholar

Cheng, G., Lin, Y., Ali, A., Gomez-Exposito, A., and Wu, W. (2024). A survey of power system state estimation using multiple data sources: PMUs, SCADA, AMI, and beyond. IEEE Trans. smart grid 15 (1), 1129–1151. doi:10.1109/tsg.2023.3286401

CrossRef Full Text | Google Scholar

Khalid, M. (2024). Smart grids and renewable energy systems: perspectives and grid integration challenges. Energy strategy Rev. 51, 101299. doi:10.1016/j.esr.2024.101299

CrossRef Full Text | Google Scholar

Kong, X., Zhang, X., Zhang, X., Wang, C., Chiang, H.-D., and Peng, Li (2022). Adaptive dynamic state estimation of distribution network based on interacting multiple model. IEEE Trans. Sustain. energy 13 (2), 643–652. doi:10.1109/tste.2021.3118030

CrossRef Full Text | Google Scholar

Lin, Z., Wen, F., Ding, Yi, Xue, Y., Liu, S., Zhao, Y., et al. (2018). WAMS-based coherency detection for situational awareness in power systems with renewables. IEEE Trans. Power Syst. 33 (5), 5410–5426. doi:10.1109/tpwrs.2018.2820066

CrossRef Full Text | Google Scholar

Liu, Y., Wu, L., and Jie, Li (2020). D-PMU based applications for emerging active distribution systems: a review. Electr. Power Syst. Res. 179, 106063. doi:10.1016/j.epsr.2019.106063

CrossRef Full Text | Google Scholar

Ma, D., Hu, X., Zhang, H., Sun, Q., and Xie, X. (2021). A hierarchical event detection method based on spectral theory of multidimensional matrix for power system. IEEE Trans. Syst. MAN Cybernetics-systems 51 (4), 2173–2186. doi:10.1109/tsmc.2019.2931316

CrossRef Full Text | Google Scholar

Ma, D., Liu, M., Zhang, H., Wang, R., and Xie, X. (2022). Accurate power sharing and voltage regulation for AC microgrids: an event-triggered coordinated control approach. IEEE Trans. Cybern. 52 (12), 13001–13011. doi:10.1109/tcyb.2021.3095959

PubMed Abstract | CrossRef Full Text | Google Scholar

Panda, A., Mahapatra, S., Achu, G. K. R., and Panda, R. C. (2009). Lowering carbon emissions from a zinc oxide rotary kiln using event-scheduling observer-based economic model predictive controller. Chem. Eng. Reasearch Des. 207, 420–438. doi:10.1109/TAC.2009.2019800

CrossRef Full Text | Google Scholar

Panda, A., Princes Sindhuja, P., Vijayan, V., and Panda, R. C. (2023). Operational control for the evolution of enthalpy in an SBR carrying out nitration of 4-chlorobenzotrifluoride and the thermal runway. Chem. Eng. Reasearch Des. 197, 774–799. doi:10.1016/j.cherd.2023.08.008

CrossRef Full Text | Google Scholar

Shih, K. R., and Huang, S. J. (2002). Application of a robust algorithm for dynamic state estimation of a power system. IEEE Trans. Power Syst. 17 (1), 141–147. doi:10.1109/59.982205

CrossRef Full Text | Google Scholar

von Meier, A., Stewart, E., McEachern, A., Andersen, M., and Mehrmanesh, L. (2017). Precision micro-synchrophasors for distribution systems: a summary of applications. IEEE Trans. Smart grid 8 (6), 2926–2936. doi:10.1109/tsg.2017.2720543

CrossRef Full Text | Google Scholar

Wang, S., Gao, W., and Meliopoulos, A. P. S. (2012). An alternative method for power system dynamic state estimation based on unscented transform. IEEE Trans. Power Syst. 27 (2), 942–950. doi:10.1109/tpwrs.2011.2175255

CrossRef Full Text | Google Scholar

Wang, Y., Xia, M., Yang, Q., Song, Y., Chen, Q., and Chen, Y. (2022). Augmented state estimation of line parameters in active power distribution systems with phasor measurement units. IEEE Trans. Power Deliv. 37 (5), 3835–3845. doi:10.1109/tpwrd.2021.3138165

CrossRef Full Text | Google Scholar

Zhang, J., Wang, Yi, Yang, W., and Zhang, N. (2020). Topology identification and line parameter estimation for non-PMU distribution network: a numerical method. IEEE Trans. Smart grid 11 (5), 4440–4453. doi:10.1109/tsg.2020.2979368

CrossRef Full Text | Google Scholar

Zhang, S. (2009). “An adaptive unscented kalman filter for dead reckoning systems,” in Paper presented at the 2009 international conference on information engineering and computer science.

CrossRef Full Text | Google Scholar

Zhao, J. (2017). Power system dynamic state estimation considering measurement correlations. Trans. Energy Convers. 32 (4), 1630–1632. doi:10.1109/tec.2017.2742405

CrossRef Full Text | Google Scholar

Zhao, J. (2018). Dynamic state estimation with model uncertainties using H_∞ extended kalman filter. IEEE Trans. Power Syst. 33 (1), 1099–1100. doi:10.1109/tpwrs.2017.2688131

CrossRef Full Text | Google Scholar

Zhao, J., Gomez-Exposito, A., Netto, M., Mili, L., Ali, A., Terzija, V., et al. (2019). Power system dynamic state estimation: motivations, definitions, methodologies, and future work. IEEE Trans. Power Syst. 34 (4), 3188–3198. doi:10.1109/tpwrs.2019.2894769

CrossRef Full Text | Google Scholar

Zhao, J., Netto, M., and Mili, L. (2017). A robust iterated extended kalman filter for power system dynamic state estimation. IEEE Trans. Power Syst. 32 (4), 3205–3216. doi:10.1109/tpwrs.2016.2628344

CrossRef Full Text | Google Scholar

Zimmerman, R. D., Murillo-Sánchez, C. E., and Thomas, R. J. (2011). MATPOWER: steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 26 (1), 12–19. doi:10.1109/tpwrs.2010.2051168

CrossRef Full Text | Google Scholar