Thermodynamic analysis of a cascade organic Rankine cycle power generation system driven by hybrid geothermal energy and liquefied natural gas

The combination of renewable energy and liquefied natural gas (LNG) cold energy can effectively improve energy utilization efficiency and achieve the goal of energy conservation and emission reduction, which is one of the important directions of future development. This work proposed a cascade organic Rankine cycle (ORC) driven by a geothermal heat source and an LNG heat sink. Seven organic fluids are chosen as candidates to form different working fluid pairs. The effects of the main design parameters on system performance are carried out through the thermodynamic analysis. Then, the optimal design conditions and fluid selection schemes are searched based on the single-objective optimization results. Finally, the exergy destruction study is conducted under the optimal design conditions and working fluid pair. Results showed that the cascade ORC system using the working fluid pair of R601/R290 had the highest exergy efficiency, which could reach 20.02%. At the same time, under the optimal design conditions, the secondary cycle condenser and LNG direct expansion brought high exergy destruction, which was respectively 29.3% and 25.8%, and followed by the two turbines in the cascade ORC system, which were 16.1%, 11.2% and 7.7%.

1 Introduction

With the rapid economic development in recent years, energy and environmental problems have become increasingly prominent. Vigorously developing renewable energy and improving the efficiency of energy and resource utilization can effectively alleviate the above problems (Liu et al., 2024; Wang et al., 2024a; Wang et al., 2022; Wang et al., 2024b). Considering much medium- or low-grade heat exists in different kinds of renewable energies, like solar energy (Xiao et al., 2022), geothermal energy (Wang et al., 2023), biomass energy (Sun et al., 2022), etc., power generation is a suitable utilization way to harness the heat. Especially for the geothermal energy, it has the advantages of stable operation, abundant reserves, and non-pollution. Thus, the development of an efficient, and economical technology to explore the application potential of geothermal energy is of great significance.

Until now, many power generation technologies, like the heat engine (Tian et al., 2021), Kalina cycle (Sohrabi et al., 2023), trilateral flash cycle (Lai et al., 2021; Iqbal et al., 2020), etc., are potential selections. Among them, the organic Rankine cycle (ORC) technology with the advantages of simple structure, easy maintenance, low cost, and wide range of installed capacity (Li et al., 2021), has attracted increasing attention in the last decade. In the geothermal field, Li et al. (2024) carried out an experimental study to discuss the dynamic performance of ORC devices with the geothermal heat source temperature decrease. Results showed that the installed capacity and power output were proportional to the geothermal mass flow rate while the enhanced geothermal system’s life cycle was inversely proportional to it. Bahrami and Rosen (2024) proposed a novel geothermal-driven zero-emission system for cooling, power, and hydrogen production, which was composed of ORC, half-effect absorption chiller, and PEM electrolysis. Through exergoeconomic analysis and multi-objective optimization, it was found that the proposed system could reach 48% of the exergy efficiency and a hydrogen production rate of 1.1 kg/h at the optimal design conditions. Assareh et al. (2024) explored the application of ORC for building energy management with cooling heating power hydrogen liquefaction generation. Reyes-Antonio et al. (2024) studied the multi-objective design of the ORC system for low-enthalpy applications based on end-user demand variations. At the same time, the effects of the coupling mechanism with energy storage systems were analyzed under the off-grid operating conditions. Wang et al. (2023) studied the multi-mode and exergoeconomic analysis of a CCHP system, composed of ORC, vapor compression heat pump, and vapor compression refrigeration cycle, applied in the geothermal field. The proposed system performances under seven different operation modes were investigated and compared based on the different design conditions.

Except for paying attention to the above application on the heat source side, the use of cryogenic exergy of liquefied natural gas (LNG) can also effectively improve energy utilization efficiency. LNG with features of nontoxicity, cleanliness, and inexpensive has drawn much attention, and the relevant data speculate that the demand quantity of LNG will reach 500 million tons by 2030 (Li et al., 2016). Generally, the LNG storage tank is normally at low temperature (about 111.51 K) and 0.1 MPa conditions (Rao et al., 2013), and the corresponding capacity may be larger than 10,000 m³. The volume would be reduced by 625 times than natural gas (NG) which makes LNG easier to transport by sea and road, and safer and more economical than pipeline transportation. When the LNG is heated to ambient temperature, there will be more than 800 kJ/kg cryogenic exergy released (Li et al., 2016) which has great application potential. Mosaffa and Farshi (2021) conducted a thermodynamic feasibility analysis of an innovative salinity gradient solar ponds-based ORC and LNG cold energy. Results showed that the proposed system using R245ca/R236ea (0.6/0.4) had the best thermal performance among all selected fluids. Fang et al. (2023) carried out exergoeconomic, exergoenvironmental investigation and multi-objective optimization of a novel CCHP system for LNG cold energy recovery. They compared the PSO algorithm with NSGA-II and results showed that the proposed system had exergy efficiency, product unit cost, and product unit environmental impact of 70.20%, 21.50 $/GJ, and 57.91 mPts/GJ, respectively. Zheng et al. (2022) studied thermoeconomic performance, working fluid selection, and cost projection of a precooler-integrated dual-stage combined cycle system driven by LNG cold energy. Results found that there was a mismatch between thermodynamic and economic optimal design points, and the economic optimal design points were at a lower pumped pressure.

Combining geothermal energy with LNG would be a desirable application prospect. Mardan Dezfouli et al. (2023) studied a hybrid power generation system of geothermal ORC and LNG. Two separate cycles consisting of CO₂ and C₅H₁₂, which were fed by geothermal water and LNG, were proposed and analyzed in the aspects of energy, exergy, and exergoeconomics. Results showed that the proposed cycle had a net output power of 271.6 kW, an exergy destruction rate of 1,532 kW, and f_k of 16.5%, respectively, after optimization. This combination could further enhance geothermal resource exploitation efficiency in terms of energy and economics. Emadi and Mahmoudimehr (2019) carried out a modeling and thermo-economic optimization of a novel multi-generation system driven by a geothermal heat source and LNG heat sink. The proposed system realized great improvements in cooling, power generation, and hydrogen production capacities. Results showed that the system designed with an exergy efficiency of 24.92%, a total cost rate of 423.5 ($/hr), and a hydrogen production capacity of 276.1 (kg/hr) was obtained as the optimal solution. Besides, single-stage is used to realize the power generation in most cases. Considering the large temperature difference (>200 K) between the heat source and heat sink, and the high volume ratio of organic fluid which makes the turbine complicated and expensive, the cascade ORC is proposed with higher efficiency (Xue et al., 2015).

In the current study, most researchers pay more attention to system structure innovation and optimization of design conditions (Habibi et al., 2018; Rejeb et al., 2022; Mehrpooya et al., 2017). Actually, for a cascade ORC system driven by a geothermal heat source and LNG heat sink, the system performances are dramatically affected by the choice of working fluids. However, the impact of different fluid combinations on system performance needs further investigation. In this paper, the pairwise combination of different working fluids is applied to the cascaded ORC system, and after preliminary trial calculations, seven working fluids with better performance, namely R290, R600, R600a, R601, R601a, R125, and R116, are selected and combined into working fluid pairs, and the system performance is analyzed by numerical simulation. The main contributions of this paper are as follows:

(1) A cascade ORC system driven by geothermal heat source and LNG heat sink is proposed and studied.

(2) Simulations are conducted to investigate the effect of different parameters on the performance of the system, and the optimal fluid selection schemes are obtained.

The structural framework of this paper is as follows: the system descriptions containing system structure, assumptions, and fluid choice are introduced in Section 2. The detailed mathematical models are illustrated in Section 3. Section 4 is the model validation. The parametric analysis the fluid selection results, and the main conclusions are put in Section 5 and Section 6, respectively.

2 System descriptions

2.1 System structure

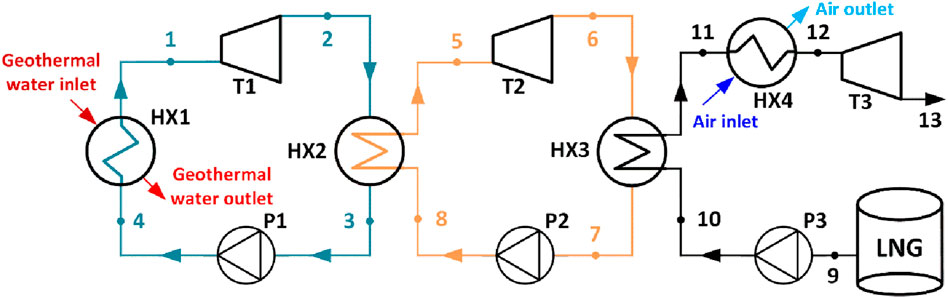
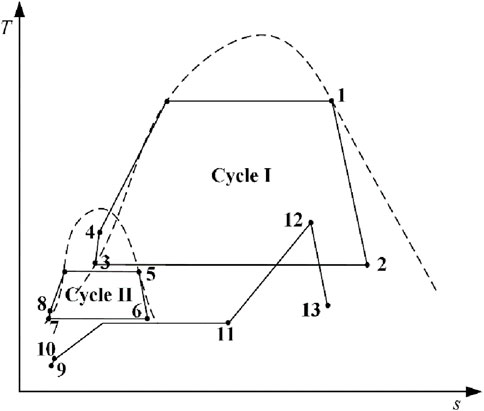
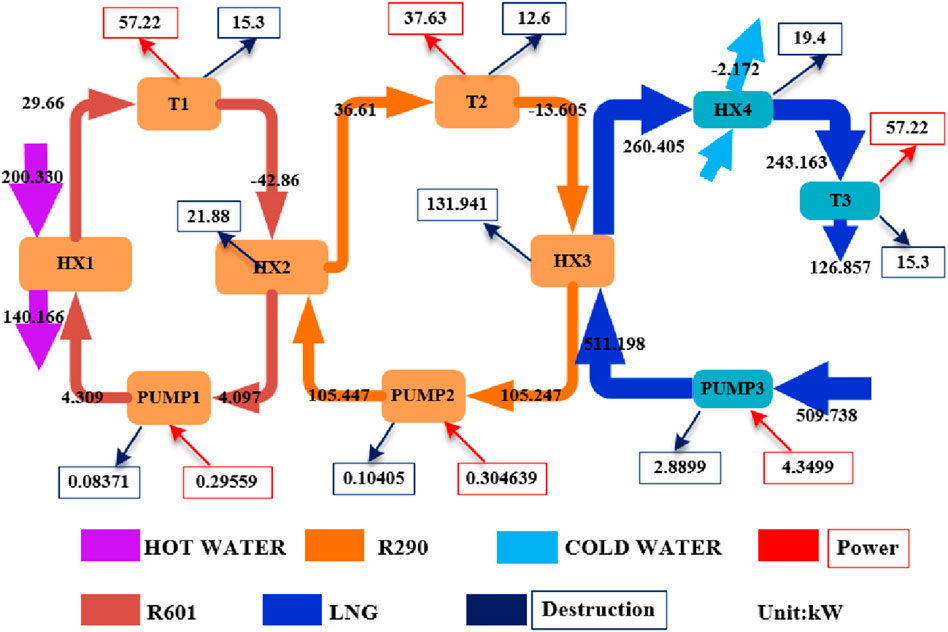
The schematic diagram of the cascade ORC system driven by geothermal energy and LNG is shown in Figure 1. In the leftmost cycle, the heat in geothermal water is transmitted to the organic fluid in the heat exchanger 1 (HX1). The organic fluid at a high-pressure vapor state (at State 1) enters into turbine 1 (T1) generating mechanical work. After that, the expanded organic fluid (at State 2) is cooled by another stream of organic fluid in the heat exchanger 2 (HX2). The saturated liquid state organic fluid (at State 3) is pressurized by pump 1 (P1) and flows into HX1 again (at State 4) to absorb heat from geothermal water. The process of the middle cycle is similar to that of the leftmost cycle. In the middle cycle, another high-pressure organic fluid (at State 8) flows into the HX2 being heated into a vapor state (at State 5). Subsequently, the vapor fluid enters turbine 2 (T2) generating mechanical work. Then, the expanded organic fluid (at State 6) is cooled by LNG in the heat exchanger 3 (HX3). The saturated liquid state organic fluid (at State 7) is pressurized by pump 2 (P2) and (at State 8) flows into HX2 again. In the rightmost cycle, the LNG (at State 9) is withdrawn from the storage tank and pumped into HX3. Then LNG (at State 10) is gasified to saturated NG, which is still cryogenic (at State 11). The heat exchanger 4 (HX4) is added to superheat the gas to reach approximately 10 K lower than the ambient temperature (at State 12). Thus, more electricity can be generated when superheated NG enters into the turbine 3 (T3). Finally, the expanded NG is available to the user for direct use or post-processing use. The exhaust stream can be further conveyed to the city gas transmission and distribution network, and the cooled air at the outlet of HX4 can be utilized as well, which is beyond the scope of this paper. The corresponding T-s diagram of the proposed system is shown in Figure 2.

Figure 1

Figure 1. Schematic diagram of the cascade ORC system driven by geothermal energy and LNG.

Figure 2

Figure 2. T-s diagram of the cascade ORC system driven by geothermal energy and LNG.

2.2 System assumptions

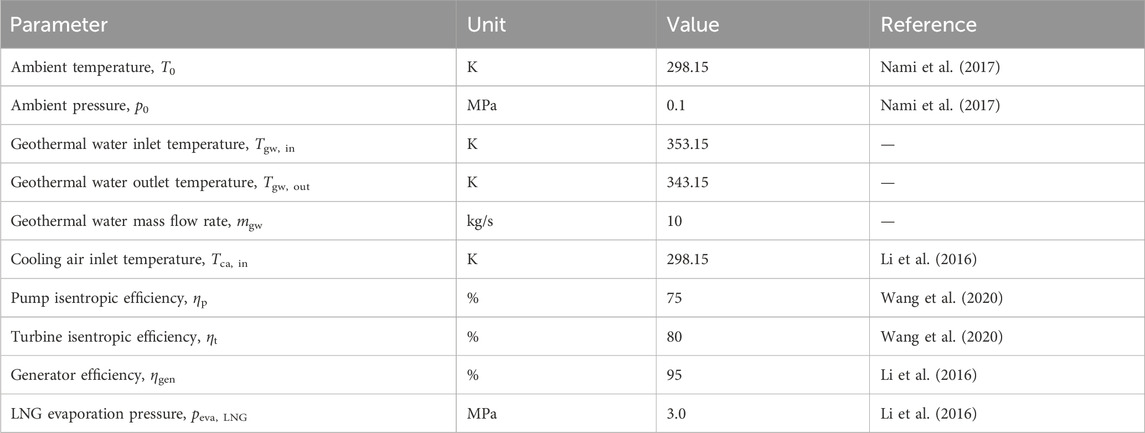
The relative input parameters and calculation conditions are given in Table 1. Some reasonable assumptions for system simulation are as follows:

• Dry and isentropic fluids are in a saturated vapor state while wet fluid is in a superheated vapor state at the inlets of T1 and T2, respectively;

• Working fluids are in a saturated liquid state at the state points 3, 7, and 11, respectively;

• Heat losses and pressure drops in pipes are ignored;

• LNG is composed of methane, ethane, propane, isobutane, butane, isopentane, pentane, and nitrogen, and the corresponding mass fractions are 0.9133, 0.0536, 0.0214, 0.0047, 0.0046, 0.0001, 0.0001, and 0.0022 (Bao et al., 2017);

• The liquid in the LNG storage tank is saturated at ambient pressure, and the evaporation pressure is 3 MPa;

• The outlet pressure of T3 is assumed to be 0.4 MPa.

Table 1

Table 1. Input parameters and calculation conditions.

2.3 Fluid selection principle

Working fluid selection in ORC systems is an all-important work during the system simulation processes, because the system performance, investment costs, and equipment sizing are influenced by the thermophysical properties of organic fluids. Considering that the application background of this paper is in LNG and geothermal fields, the critical temperature of the working fluid should be higher than the maximum operating temperature. At the same time, the triple-point temperature of the working fluid should be maintained below the minimum operating temperature. Besides, the condensing pressure should be above 5 kPa as it is technically difficult to maintain a vacuum below this value in the condenser. Referring to related works (Li et al., 2016), the following working fluids are selected as candidates for research in this paper, and the thermophysical properties of the selected fluids are shown in Table 2.

Table 2

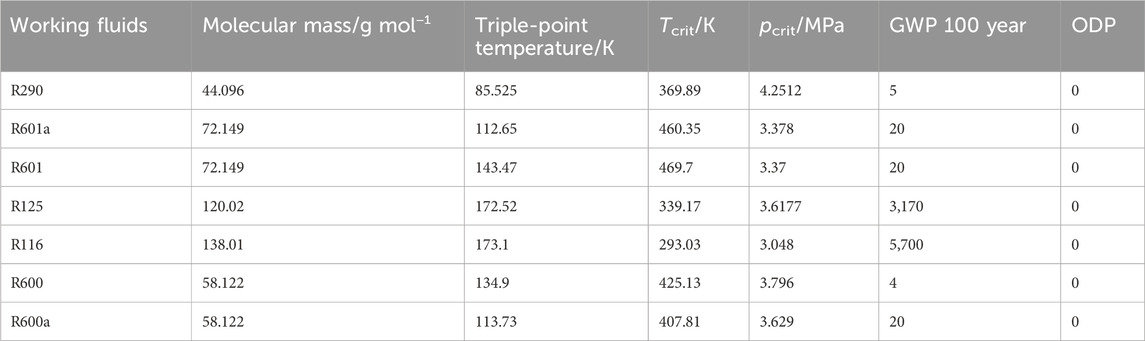
Table 2. Thermo-physical properties of the different working fluids (Tian et al., 2020).

3 Mathematical models

In the entire system, the universal energy balance equation can be defined as (Equation 1):

$\mathrm{\Sigma }{m}_{\text{in}}{h}_{\text{in}}+Q=\mathrm{\Sigma }{m}_{\text{out}}{h}_{\text{out}}+W(1)$

where h represents the specific enthalpy; m represents the mass flow rate; W is the power output, and Q represents the heat absorption amount.

More precisely, the heat transfer in HX1, HX2, HX3, and HX4 are expressed (Equations 2–5):

$Q_{\text{HX}1}=m_{\text{gw}}\left(h_{\text{gw},\text{in}}-h_{\text{gw},\text{out}}\right)=m_{\text{wf}1}\left(h_1-h_4\right)(2)$

$Q_{\text{HX}2}=m_{\text{wf}1}\left(h_2-h_3\right)=m_{\text{wf}2}\left(h_5-h_8\right)(3)$

$Q_{\text{HX}3}=m_{\text{wf}2}\left(h_6-h_7\right)=m_{\text{LNG}}\left(h_{11}-h_{10}\right)(4)$

$Q_{\text{HX}4}=m_{\text{LNG}}\left(h_{12}-h_{11}\right)=m_{\text{ca}}\left(h_{\text{ca},\text{out}}-h_{\text{ca},\text{in}}\right)(5)$

The power consumption of each pump can be expressed as (Equations 6–8):

$W_{\mathrm{P}1}=m_{\text{wf}1}\left(h_4-h_3\right)=m_{\text{wf}1}\left(h_{4\mathrm{s}}-h_3\right)/{\eta }_{\mathrm{p}}(6)$

$W_{\mathrm{P}2}=m_{\text{wf}2}\left(h_8-h_7\right)=m_{\text{wf}2}\left(h_{8\mathrm{s}}-h_7\right)/{\eta }_{\mathrm{p}}(7)$

$W_{\mathrm{P}3}=m_{\text{LNG}}\left(h_{10}-h_9\right)=m_{\text{LNG}}\left(h_{10}-h_9\right)/{\eta }_{\mathrm{p}}(8)$

The power output of each turbine can be expressed as (Equations 9–11):

$W_{\mathrm{T}1}=m_{\text{wf}1}\left(h_1-h_2\right)=m_{\text{wf}1}\left(h_1-h_{2\mathrm{s}}\right){\eta }_{\mathrm{t}}(9)$

$W_{\mathrm{T}2}=m_{\text{wf}2}\left(h_5-h_6\right)=m_{\text{wf}2}\left(h_5-h_{6\mathrm{s}}\right){\eta }_{\mathrm{t}}(10)$

$W_{\mathrm{T}3}=m_{\text{LNG}}\left(h_{12}-h_{13}\right)=m_{\text{LNG}}\left(h_{12}-h_{13\mathrm{s}}\right){\eta }_{\mathrm{t}}(11)$

The net power output of the system (W_net) can be defined as (Equation 12):

$W_{\text{net}}=\left(W_{\mathrm{T}1}+W_{\mathrm{T}2}+W_{\mathrm{T}3}-W_{\mathrm{P}1}-W_{\mathrm{P}2}-W_{\mathrm{P}3}\right){\eta }_{\text{gen}}(12)$

The thermal efficiency of the system (η_th) is expressed as (Equation 13):

${\eta }_{\text{th}}=W_{\text{net}}/Q_{\text{in}}=W_{\text{net}}/\left[m_{\text{gw}}\left(h_{\text{gw},\text{in}}-h_{\text{gw},\text{out}}\right)\right](13)$

The cold energy efficiency of the system (η_C) can be defined as (Equation 14):

${\eta }_{\mathrm{C}}=W_{\text{net}}/E_{\text{LNG}}=W_{\text{net}}/\left[\left(h_9-T_0{s}_9\right)-\left(h_{13}-T_0{s}_{13}\right)\right](14)$

The exergy efficiency of the system (η_ex) is expressed as (Equation 15):

${\eta }_{\text{ex}}=W_{\text{net}}/\left(E_{\text{gw}}+E_{\text{LNG}}\right)(15)$

The exergy destruction of each heat transfer can be expressed as (Equations 16–19):

${\dot{E}}_{\mathrm{d},\text{HX}1}={\dot{E}}_{\text{gw},\text{in}}+{\dot{E}}_4-{\dot{E}}_{\text{gw},\text{out}}-{\dot{E}}_1(16)$

${\dot{E}}_{\mathrm{d},\text{HX}2}={\dot{E}}_2+{\dot{E}}_8-{\dot{E}}_3-{\dot{E}}_5(17)$

${\dot{E}}_{\mathrm{d},\text{HX}3}={\dot{E}}_6+{\dot{E}}_{10}-{\dot{E}}_7-{\dot{E}}_{11}(18)$

${\dot{E}}_{\mathrm{d},\text{HX}4}={\dot{E}}_{\text{ca},\text{in}}+{\dot{E}}_{11}-{\dot{E}}_{\text{ca},\text{out}}-{\dot{E}}_{12}(19)$

The exergy destruction of each turbine can be expressed as (Equations 20–22):

${\dot{E}}_{\mathrm{d},\text{turpine}1}={\dot{E}}_1-{\dot{E}}_2-{\dot{W}}_{\mathrm{T}1}(20)$

${\dot{E}}_{\mathrm{d},\text{turpine}2}={\dot{E}}_5-{\dot{E}}_6-{\dot{W}}_{\mathrm{T}2}(21)$

${\dot{E}}_{\mathrm{d},\text{turpine}3}={\dot{E}}_{12}-{\dot{E}}_{13}-{\dot{W}}_{\mathrm{T}3}(22)$

The exergy destruction of each turbine can be expressed as (Equations 23–25):

${\dot{E}}_{\mathrm{d},\text{pump}1}={\dot{E}}_3-{\dot{E}}_4+{\dot{W}}_{\mathrm{p}1}(23)$

${\dot{E}}_{\mathrm{d},\text{pump}2}={\dot{E}}_7-{\dot{E}}_8+{\dot{W}}_{\mathrm{p}2}(24)$

${\dot{E}}_{\mathrm{d},\text{pump}3}={\dot{E}}_3-{\dot{E}}_{10}+{\dot{W}}_{\mathrm{p}3}(25)$

4 Model validation

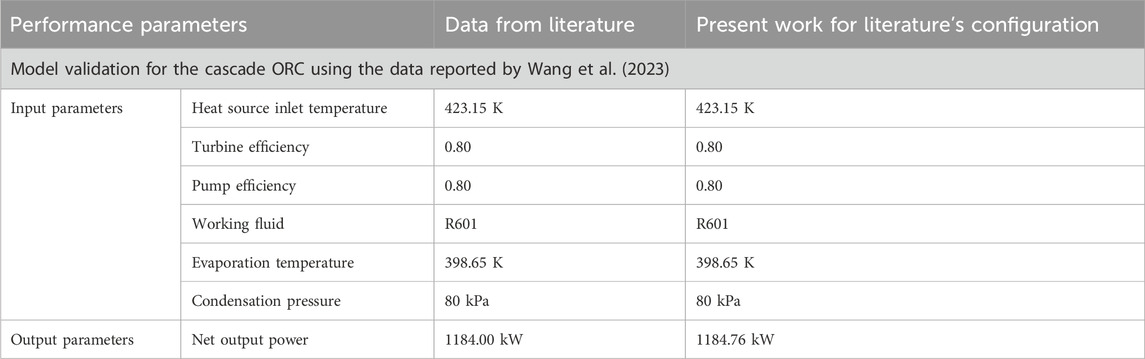
The data reported in the literature are selected to validate the model of the proposed cascade ORC system. The model is validated to be performed separately for the ORC subsystem. Referring to Table 3, the comparison results show the current model and the data obtained from the literature.

Table 3

Table 3. Model validation for the proposed cascaded ORC system.

5 Results and discussions

The following describes and discusses the simulation results based on the aforementioned model. Firstly, the impact of key parameters on system performance is analyzed. Subsequently, research is conducted on the matching of working fluids for the two-stage low-temperature ORC system. The best-performing working fluid in terms of exergy efficiency is selected for single-objective optimization of the system, aiming to find its optimal operating conditions. Finally, exergy destruction analysis is conducted on the system’s optimal operating conditions.

5.1 Parametric study

Before proceeding with a system optimization analysis, it is critical to investigate the impact of critical parameters on system performance. Therefore, this section focuses on how to perform parametric analysis to understand these influencing factors. Table 4 lists the state parameters (temperature, pressure, and mass flow) at each point of the cascade ORC system under the design conditions.

Table 4

Table 4. The parameter values for each state point of the cascade ORC system.

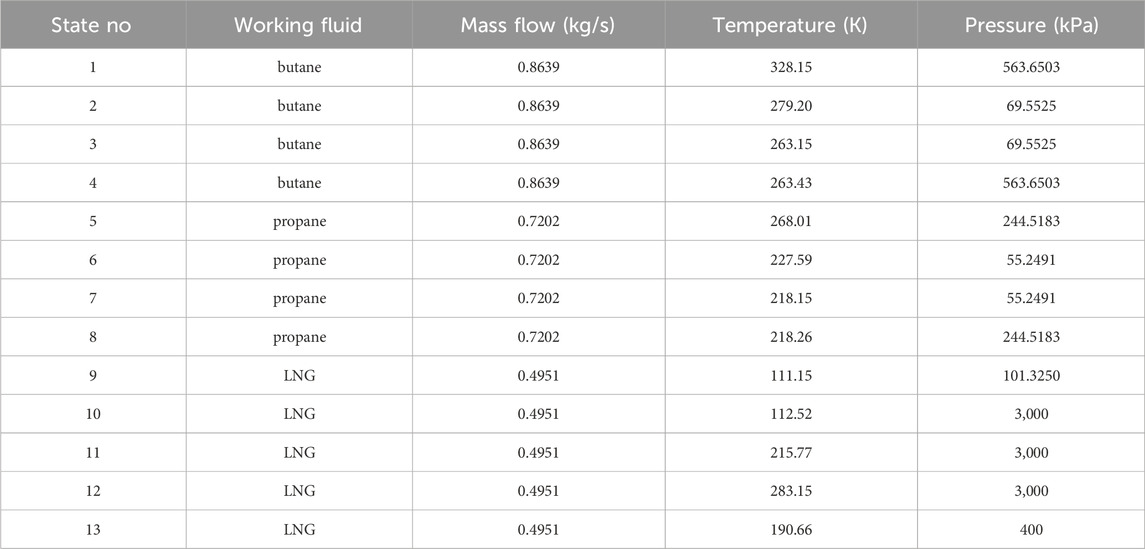
Figure 3 illustrates the effect of the evaporation temperature (T_eva1) of the primary ORC cycle system on the system parameters and performance. When T_eva increases from 317.15 to 328.15 K, η_e monotonically increases from 19.55% to 20.08%. The reason is that as T_eva1 increases, the ΔT_eva1 in the evaporator gradually decreases from 29.08 to 18.55 K, as shown in Figure 3B. Therefore, under the condition of a constant heat source, the average temperature difference between hot and cold fluids in the evaporator decreases, and η_e gradually increases. At the same time, when T_eva1 increases from 317.15 to 328.15 K, W_net increases monotonically from 163.21 to 167.63 kW. This is mainly because the W_t1 increases with the evaporation temperature, and as the T_eva1 increases the inlet pressure of the compressor and reduces its power consumption, the W_t1 rises from 58.69 to 65.15 kW. The increase in power generation further improves the thermodynamic and economic performance of the system. In addition, the efficiency of cold energy utilization has also been slightly improved.

Figure 3

Figure 3. Effects of T_eva1 on system performances and parameters.

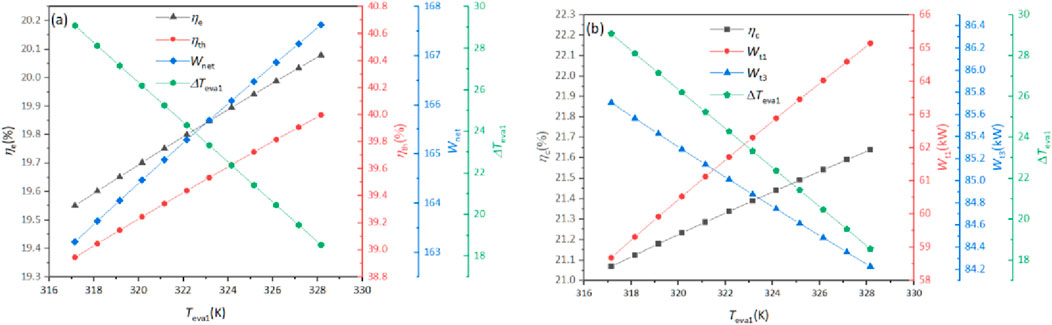
Figure 4 illustrates the effect of the condensing temperature (T_con1) of the primary ORC cycle system on the system parameters and performance. When T_con1 increases from 253.15 to 263.15 K, η_e monotony decreases from 19.60% to 18.89%. The reason for this can be seen in the Carnot cycle: when the endothermic temperature is constant, the increase in the exothermic temperature reduces the efficiency of the Carnot cycle. In addition, as the condensation temperature of the system increases, the W_net of the system decreases from 163.64 to 157.72 kW, mainly due to the decrease in the outlet temperature of turbine 1, which reduces W_t1 from 59.31 to 50.96 kW, as shown in Figure 4B.

Figure 4

Figure 4. Effects of T_con1 on system performances and parameters.

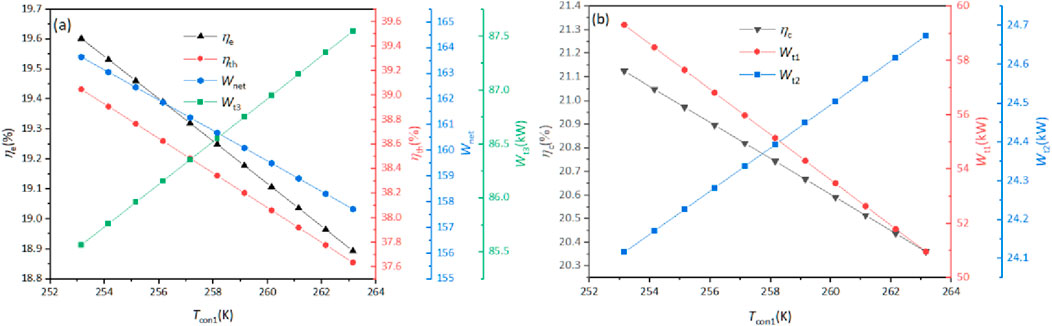
Figure 5 illustrates the effect of the evaporation temperature (T_eva2) of the secondary ORC cycle system on system parameters and performance. When T_eva2 increases from 233.15 to 243.15 K, η_e monotonically increases from 18.60% to 19.60%. This is because, as T_eva2 increases, the ΔT_eva2 in the evaporator of the secondary ORC recirculating system gradually decreases. Therefore, under the condition of a constant heat source, the average temperature difference between hot and cold fluids in the evaporator decreases, and η_e gradually increases. At the same time, when T_eva2 increases from 233.15 to 243.15 K, W_net increases monotonically from 155.24 to 163.64 kW. This is mainly because W_t2 increases with increasing evaporation temperature, and as T_eva2 increases the inlet pressure of the compressor and reduces its power consumption, W_t2 rises from 12.97 to 24.12 kW.

Figure 5

Figure 5. Effects of T_eva2 on system performances and parameters.

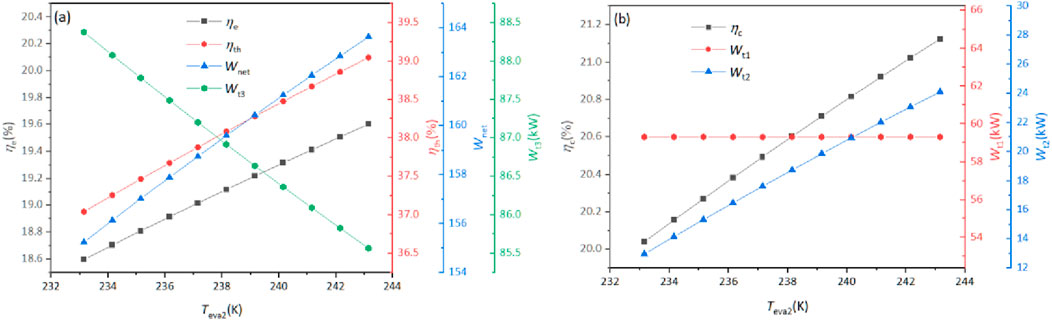
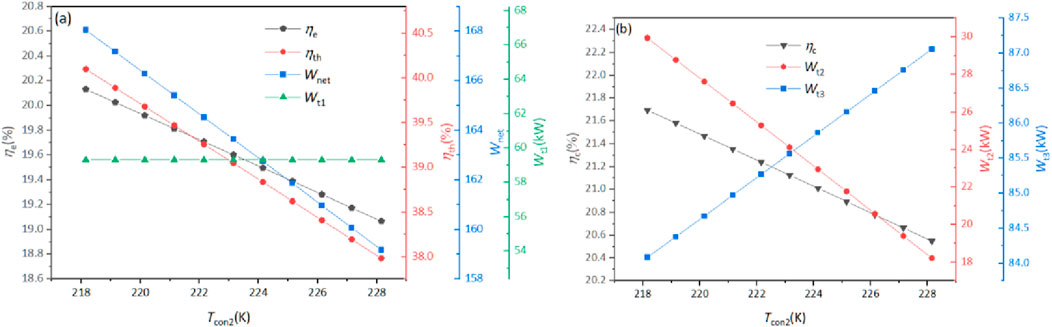
Figure 6 illustrates the effect of the condensation temperature (T_con2) of the secondary ORC cycle system on system parameters and performance. When T_con2 increases from 218.15 to 228.15 K, η_e monotonicity decreases from 20.13% to 19.07%. The reason for this can also be seen in the Carnot cycle: when the endothermic temperature is constant, the increase in the exothermic temperature reduces the efficiency of the Carnot cycle. In addition, as the condensation temperature of the system increases, the W_net of the system decreases from 168.05 to 159.18 kW, mainly due to the decrease in the outlet temperature of turbine 2, which reduces W_t2 from 29.95 to 18.21 kW, as shown in Figure 6B.

Figure 6

Figure 6. Effects of T_con2 on system performances and parameters.

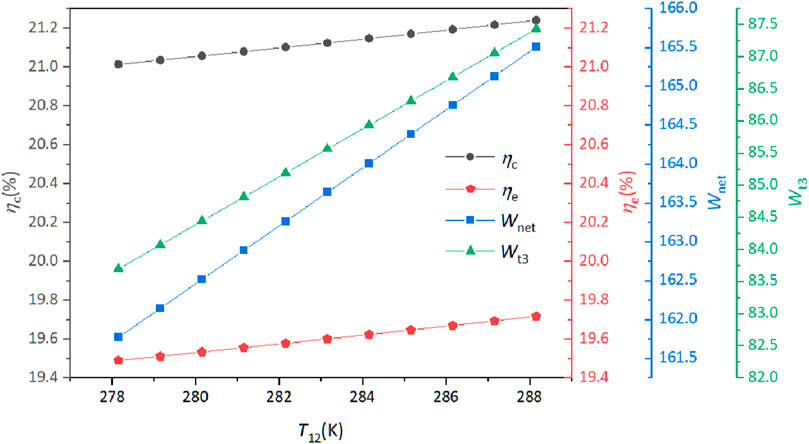
Figure 7 illustrates the effect of the inlet pressure of the LNG turbine (Turbine 3) on the performance of the system, as the T₁₂ increases from 278.15 to 288.15 K, the system’s W_net increases from 161.77 to 165.51 kW, and the increase is almost entirely due to the work done by Turbine 3, which is obvious. In addition, we can see that with the increase of T₁₂, both η_e and η_c of the system increase slightly.

Figure 7

Figure 7. Effects of T₁₂ on system performances and parameters.

5.2 Optimization results and working fluid selection

According to the literature survey and preliminary screening, six working fluid pairs are selected, and the working fluids of the primary and secondary ORC cycles are R600/R290, R601a/R290, R601/R600, R601/R290, R600a/R290, and the two-stage ORC working fluids both are R290. In order to find the optimal working fluid pair and the optimal operating condition of the cascade ORC system, we take the thermal efficiency of the system as a single objective function for single-objective optimization, and take the T_eva1, T_con1, ΔT_eva1, T_con2, T₁₂, and P_LNG six variables as decision variables. The range of the decision variables is as follows, T_eva1 (318.15–328.15 K), T_con1 (253.15–263.15 K), ΔT_eva1 (10–20 K), T_con2 (218.15–228.15 K), T₁₂ (273.15–283.15 K), P_LNG (2,000–3,000 kPa) (Li et al., 2016). The parameters of single-objective optimization are set as follows, the termination tolerance of the function value is 10⁻⁴, the maximum number of iterations is 10³, the termination tolerance about the current point x is 10⁻⁵⁰, and the maximum number of function calculations is 10⁸.

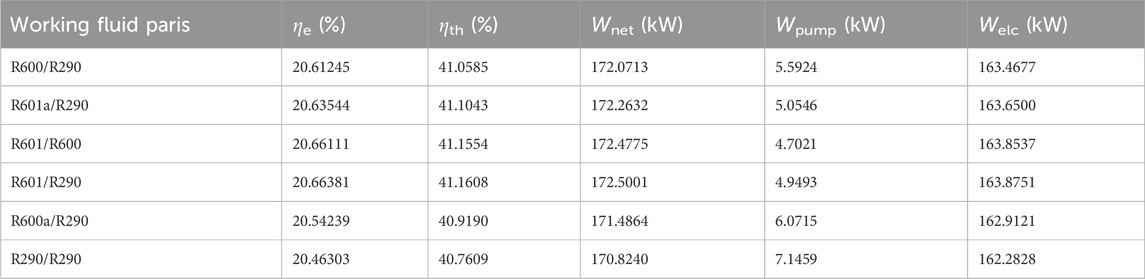
Single-objective optimization of the single-objective function with exergy efficiency is performed, and the results of single-objective optimization are shown in Table 5. We can see that working fluid pairs R601/R600 and R601/R290 have better performance, and R601/R290 has a slightly better performance. So we choose this working fluid pair R601/R290 for the subsequent exergy destruction analysis, and the optimal working conditions are selected, the evaporation temperatures of the cascade ORC system are 328.15 and 253.15 K, the condensing temperatures of the cascade ORC system are 263.15 and 218.15 K, the inlet temperature of turbine 3 is 283.15 K, and the outlet pressure of the LNG pump is 3,000 kPa.

Table 5

Table 5. Results of single-objective optimization analysis for different working fluid pairs.

5.3 Exergy destruction analysis

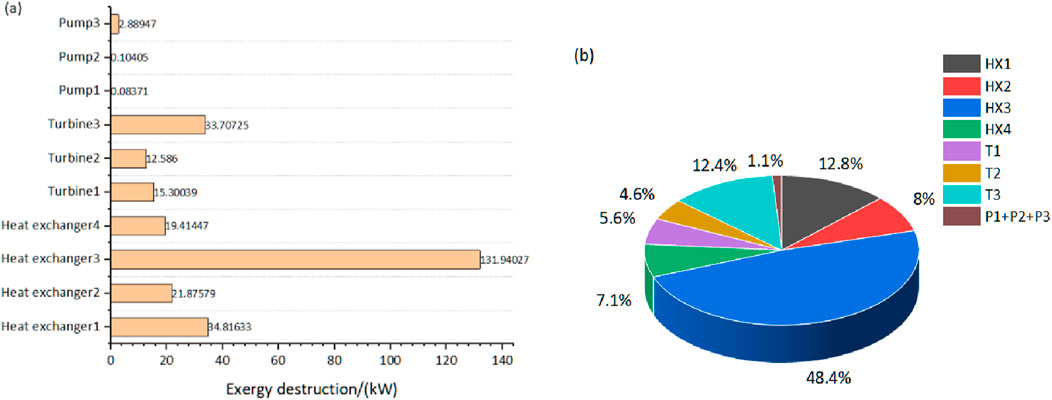
According to the results of single-objective optimization, we select the working fluid pair R601/R290, the optimal operating condition of the system, and then carry out the exergy destruction analysis of the system to explore the areas where the system can be improved. The Sankey diagram of exergy flows under the design parameters is displayed in Figure 8. And the Figure 9 shows the exergy destruction and proportions of each component of the system. As can be seen from Figure 9, the components with the highest exergy destruction is the condenser of the secondary ORC cycle, accounting for 48.4%. In addition, the second, third, fourth, and fifth major exergy destruction are the primary ORC cycle evaporator, turbine 3, the condenser of the primary ORC cycle and heat exchanger 4, respectively, and the proportion of exergy destruction are 12.8%, 12.4%, 8% and 7.1%, respectively. The main cause of exergy destruction in condensers and evaporators is the significant temperature difference that occurs during the heat transfer of the working fluid. Irreversibility brings about the exergy destruction of compressors and expanders, and improving the isentropic efficiency of components can reduce exergy destruction. Other components of the system, such as pumps, have relatively low exergy destruction and relatively little room for optimization of exergy destruction.

Figure 8

Figure 8. Sankey diagram of exergy flows.

Figure 9

Figure 9. Exergy destruction analysis of components of the system.

6 Conclusion

In this paper, a cascade ORC system driven by a geothermal heat source and an LNG heat sink is proposed and studied. The design parameters of the system performance are studied through numerical analysis, and different fluid options are selected and compared. Finally, the heat loss analysis is carried out under the optimal operating conditions. From the results of the study, the following conclusions can be drawn:

(1) The cascade ORC system driven by a geothermal heat source and LNG heat sink proposed in this paper, different fluid selection schemes have a great influence on the system performance, and the R601/R290 fluid selection scheme has the highest system exergy efficiency, which can reach 20.02%.

(2) Under the optimal operating conditions of this system, the condenser of the secondary ORC cycle brings the highest exergy destruction of 48.4%.

(3) The VR of each turbine in a cascade ORC is much smaller compared to a single-stage ORC, making the design and manufacture of the turbine much easier. As a result, the technical difficulties and high costs associated with multi-stage expansion can be avoided.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ZP: Writing–original draft. YF: Writing–review and editing. HC: Resources, Visualization, Writing–review and editing. YS: Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (grant number 52106199), the Natural Science Foundation of Hebei Province (grant number E2023502067), the Science Research Project of Hebei Education Department (grant number BJK2024065), and the Fundamental Research Funds for the Central Universities (grant number 2023MS122).

Conflict of interest

Author ZP was employed by Zhanjiang Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Assareh, E., Agarwal, N., Baji, H. S., Taghipoor, A., and Lee, M. (2024). A newly application of Organic Rankine Cycle for building energy management with cooling heating power hydrogen liquefaction generation- South Korea. Energy Nexus 13, 100281. doi:10.1016/j.nexus.2024.100281

CrossRef Full Text | Google Scholar

Bahrami, H.-R., and Rosen, M. A. (2024). Exergoeconomic evaluation and multi-objective optimization of a novel geothermal-driven zero-emission system for cooling, electricity, and hydrogen production: capable of working with low-temperature resources. Geotherm. Energy 12 (1), 12. doi:10.1186/s40517-024-00293-7

CrossRef Full Text | Google Scholar

Bao, J., Lin, Y., Zhang, R., Zhang, N., and He, G. (2017). Strengthening power generation efficiency utilizing liquefied natural gas cold energy by a novel two-stage condensation Rankine cycle (TCRC) system. Energy Convers. Manag. 143, 312–325. doi:10.1016/j.enconman.2017.04.018

CrossRef Full Text | Google Scholar

Emadi, M. A., and Mahmoudimehr, J. (2019). Modeling and thermo-economic optimization of a new multi-generation system with geothermal heat source and LNG heat sink. Energy Convers. Manag. 189, 153–166. doi:10.1016/j.enconman.2019.03.086

CrossRef Full Text | Google Scholar

Fang, Z., Pan, Z., Ma, G., Yu, J., Shang, L., and Zhang, Z. (2023). Exergoeconomic, exergoenvironmental analysis and multi-objective optimization of a novel combined cooling, heating and power system for liquefied natural gas cold energy recovery. Energy 269, 126752. doi:10.1016/j.energy.2023.126752

CrossRef Full Text | Google Scholar

Habibi, H., Zoghi, M., Chitsaz, A., Javaherdeh, K., and Ayazpour, M. (2018). Thermo-economic analysis and optimization of combined PERC - ORC - LNG power system for diesel engine waste heat recovery. Energy Convers. Manag. 173, 613–625. doi:10.1016/j.enconman.2018.08.005

CrossRef Full Text | Google Scholar

Iqbal, M. A., Rana, S., Ahmadi, M., Date, A., and Akbarzadeh, A. (2020). Experimental study on the prospect of low-temperature heat to power generation using Trilateral Flash Cycle (TFC). Appl. Therm. Eng. 172, 115139. doi:10.1016/j.applthermaleng.2020.115139

CrossRef Full Text | Google Scholar

Lai, K.-Y., Lee, Y.-T., Lai, T.-H., and Liu, Y.-H. (2021). Using a partially evaporating cycle to improve the volume ratio problem of the trilateral flash cycle for low-grade heat recovery. Entropy 23 (5), 515. doi:10.3390/e23050515

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Yang, Z., Hu, S., and Duan, Y. (2021). Influences of fluid corrosivity and heat exchanger materials on design and thermo-economic performance of organic Rankine cycle systems. Energy 228, 120589. doi:10.1016/j.energy.2021.120589

CrossRef Full Text | Google Scholar

Li, P., Li, J., Pei, G., Munir, A., and Ji, J. (2016). A cascade organic Rankine cycle power generation system using hybrid solar energy and liquefied natural gas. Sol. Energy 127, 136–146. doi:10.1016/j.solener.2016.01.029

CrossRef Full Text | Google Scholar

Li, T., Wang, Z., Gao, X., Qiao, Y., Zhang, Y., and Jin, F. (2024). Dynamic power generation performance of enhanced geothermal system during life cycle in gonghe basin, China. Appl. Therm. Eng. 248, 123216. doi:10.1016/j.applthermaleng.2024.123216

CrossRef Full Text | Google Scholar

Liu, Z., Li, M., Virguez, E., and Xie, X. (2024). Low-carbon transition pathways of power systems for Guangdong-Hongkong-Macau Region in China. Energy and Environ. Sci. 17, 307–322. doi:10.1039/d3ee02181e

CrossRef Full Text | Google Scholar

Mardan Dezfouli, A. H., Niroozadeh, N., and Jahangiri, A. (2023). Energy, exergy, and exergoeconomic analysis and multi-objective optimization of a novel geothermal driven power generation system of combined transcritical CO2 and C5H12 ORCs coupled with LNG stream injection. Energy 262, 125316. doi:10.1016/j.energy.2022.125316

CrossRef Full Text | Google Scholar

Mehrpooya, M., Ashouri, M., and Mohammadi, A. (2017). Thermoeconomic analysis and optimization of a regenerative two-stage organic Rankine cycle coupled with liquefied natural gas and solar energy. Energy 126, 899–914. doi:10.1016/j.energy.2017.03.064

CrossRef Full Text | Google Scholar

Mosaffa, A. H., and Farshi, L. G. (2021). Thermodynamic feasibility evaluation of an innovative salinity gradient solar ponds-based ORC using a zeotropic mixture as working fluid and LNG cold energy. Appl. Therm. Eng. 186, 116488. doi:10.1016/j.applthermaleng.2020.116488

CrossRef Full Text | Google Scholar

Nami, H., Mahmoudi, S., and Nemati, A. (2017). Exergy, economic and environmental impact assessment and optimization of a novel cogeneration system including a gas turbine, a supercritical CO2 and an organic Rankine cycle (GT-HRSG/SCO2). Appl. Therm. Eng. 110, 1315–1330. doi:10.1016/j.applthermaleng.2016.08.197

CrossRef Full Text | Google Scholar

Rao, W.-J., Zhao, L.-J., Liu, C., and Zhang, M.-G. (2013). A combined cycle utilizing LNG and low-temperature solar energy. Appl. Therm. Eng. 60 (1-2), 51–60. doi:10.1016/j.applthermaleng.2013.06.043

CrossRef Full Text | Google Scholar

Rejeb, O., Alirahmi, S. M., Assareh, E., El Haj Assad, M., Jemni, A., Bettayeb, M., et al. (2022). Innovative integrated solar powered polygeneration system for green Hydrogen, Oxygen, electricity and heat production. Energy Convers. Manag. 269, 116073. doi:10.1016/j.enconman.2022.116073

CrossRef Full Text | Google Scholar

Reyes-Antonio, C. A., Iglesias-Silva, G. A., Rubio-Maya, C., and Fuentes-Cortés, L. F. (2024). Multi-objective design of off-grid low-enthalpy geothermal generation systems considering partial-load operations. Energy 294, 130872. doi:10.1016/j.energy.2024.130872

CrossRef Full Text | Google Scholar

Sohrabi, A., Asgari, N., Imran, M., and Wakil Shahzad, M. (2023). Comparative energy, exergy, economic, and environmental (4E) analysis and optimization of two high-temperature Kalina cycles integrated with thermoelectric generators for waste heat recovery from a diesel engine. Energy Convers. Manag. 291, 117320. doi:10.1016/j.enconman.2023.117320

CrossRef Full Text | Google Scholar

Sun, Z., Wang, S., and Aziz, M. (2022). Highly integrated system for ammonia and electricity production from biomass employing direct chemical looping: exergy and exergoeconomic analyses. Energy Convers. Manag. 251, 115013. doi:10.1016/j.enconman.2021.115013

CrossRef Full Text | Google Scholar

Tian, H., Liu, P., and Shu, G. (2021). Challenges and opportunities of Rankine cycle for waste heat recovery from internal combustion engine. Prog. Energy Combust. Sci. 84, 100906. doi:10.1016/j.pecs.2021.100906

CrossRef Full Text | Google Scholar

Tian, Z., Yue, Y., Gu, B., Gao, W., and Zhang, Y. (2020). Thermo-economic analysis and optimization of a combined Organic Rankine Cycle (ORC) system with LNG cold energy and waste heat recovery of dual-fuel marine engine. Int. J. Energy Res. 44 (13), 9974–9994. doi:10.1002/er.5529

CrossRef Full Text | Google Scholar

Wang, S., Li, K., Yu, W., Liu, C., and Guan, Z. (2024b). Effects of non-condensable gas on thermodynamic performance of transcritical organic Rankine cycle. Energy 292, 130513. doi:10.1016/j.energy.2024.130513

CrossRef Full Text | Google Scholar

Wang, S., Liu, C., Li, Q., Liu, L., Huo, E., and Zhang, C. (2020). Selection principle of working fluid for organic Rankine cycle based on environmental benefits and economic performance. Appl. Therm. Eng. 178, 115598. doi:10.1016/j.applthermaleng.2020.115598

CrossRef Full Text | Google Scholar

Wang, S., Liu, C., Tang, J., Xiao, T., Huo, E., and Guan, Z. (2023). Multi-mode and exergoeconomic analysis of a novel combined cooling, heating, and power system applied in the geothermal field. Energy Convers. Manag. 276, 116565. doi:10.1016/j.enconman.2022.116565

CrossRef Full Text | Google Scholar

Wang, S., Liu, C., Zhang, S., Li, Q., and Huo, E. (2022). Multi-objective optimization and fluid selection of organic Rankine cycle (ORC) system based on economic-environmental-sustainable analysis. Energy Convers. Manag. 254, 115238. doi:10.1016/j.enconman.2022.115238

CrossRef Full Text | Google Scholar

Wang, S., Tang, J., Liu, C., Li, Q., Sun, Z., and Huo, E. (2024a). Techno-economic-environmental analysis and fluid selection of transcritical organic Rankine cycle with zeotropic mixtures. J. Clean. Prod. 436, 140690. doi:10.1016/j.jclepro.2024.140690

CrossRef Full Text | Google Scholar

Xiao, T., Liu, C., Wang, X., Wang, S., Xu, X., Li, Q., et al. (2022). Life cycle assessment of the solar thermal power plant integrated with air-cooled supercritical CO2 Brayton cycle. Renew. Energy 182, 119–133. doi:10.1016/j.renene.2021.10.001

CrossRef Full Text | Google Scholar

Xue, X., Guo, C., Du, X., Yang, L., and Yang, Y. (2015). Thermodynamic analysis and optimization of a two-stage organic Rankine cycle for liquefied natural gas cryogenic exergy recovery. Energy 83, 778–787. doi:10.1016/j.energy.2015.02.088

CrossRef Full Text | Google Scholar

Zheng, S., Li, C., and Zeng, Z. (2022). Thermo-economic analysis, working fluids selection, and cost projection of a precooler-integrated dual-stage combined cycle (PIDSCC) system utilizing cold exergy of liquefied natural gas. Energy 238, 121851. doi:10.1016/j.energy.2021.121851

CrossRef Full Text | Google Scholar

Nomenclature

A area of heat exchanger (m²)

E exergy rate (kW)

H enthalpy (kJ/kg)

I exergy loss (kW)

m mass flow rate (kg s⁻¹)

p pressure (kPa)

Q heat transfer rate (kW)

s entropy (kJ kg⁻¹ K⁻¹)

T temperature (K)

W power (kW)

X decision variables

y objective function

Abbreviations

CCHP combined cooling, heating and power

GWP global warming potential

HX heat exchanger

ODP ozone depletion potential

ORC organic Rankine cycle

LNG liquefied natural gas

NG natural gas

Subscripts/superscripts

ca cooling air

crit critical

gen generator

gw geothermal water

in inlet

p pump

out outlet

t turbine

wf working fluid

0 ambient state point

1, 2, 3, 4 state point