Research on single-phase grounding detection method in small-current grounding systems based on image recognition

In small-current grounding systems, the fault current during a single-phase grounding fault is small, and the transient process is complex, leading to challenges in line selection accuracy and reliability. This paper proposes a single-phase grounding line selection method based on transfer learning using the ResNet-50 model. Zero-sequence voltage and current waveforms at the fault moment are preprocessed and combined to generate training data for the model. Simulation results using PSCAD demonstrate that the proposed method achieves 99.77% validation accuracy, even under noisy conditions. These results confirm the method’s feasibility and reliability in identifying grounding faults in various conditions.

1 Introduction

The small-current grounding systems include high-resistance grounding, arc suppression coil grounding, and ungrounded systems. When a single-phase grounding fault occurs, a complete circuit cannot be formed, resulting in a very small fault current; thus, the system can continue operating for 1–2 h. However, this can cause damage to the insulation performance of the equipment. Therefore, the “Technical Guidelines for Distribution Networks” stipulate that after a single-phase grounding fault occurs, the relevant line switch should trip after a delay to quickly eliminate the fault and isolate the fault area (State Grid Corporation of China, 2017). Nevertheless, due to the inconspicuous nature of fault signals, the success rate of single-phase grounding detection using traditional small-current grounding methods remains low, and the detection of single-phase grounding faults in small-current grounding systems has not yet been effectively resolved (Sapountzoglou et al., 2019). Therefore, a new fault line selection method needs to be proposed to improve the accuracy of fault line selection.

Current line selection methods for single-phase grounding faults in small-current systems can be mainly divided into three categories: methods based on fault steady-state quantities, transient quantities, and modern signal processing technologies (Gururajapathy et al., 2017; Li et al., 2011). The following sections will discuss these three types of methods in detail.

1.1 Steady-state algorithms for fault line selection in low-current grounding

1.1.1 Zero-sequence current amplitude and phase comparison method

The zero-sequence current amplitude and phase comparison method identifies the faulted line by comparing the magnitude and phase differences of the zero-sequence currents in various lines. A commonly used approach is the group amplitude-phase comparison method, which selects several lines with relatively large zero-sequence current magnitudes for comparison, analyzing the relative differences in their phases and magnitudes. When a single-phase ground fault occurs, the zero-sequence current magnitude of the faulted line is typically larger, and its phase differs significantly from that of other non-faulted lines. This amplitude-phase comparison method can effectively identify the faulted line. However, its effectiveness diminishes in systems grounded through arc suppression coils, as the resonant characteristics of the arc suppression coil can interfere with the magnitude and phase of the zero-sequence current, reducing the accuracy of fault location.

1.1.2 Fifth harmonic method (Gao and Lin, 2018)

In harmonic disturbances, the fifth harmonic amplitude in the faulted line is generally the highest, and its phase is often opposite to that of the normal lines. By comparing the magnitude and phase differences of the fifth harmonics between the faulted and normal lines, the faulted line can be more accurately identified. However, due to the low proportion of the fifth harmonic in the faulted zero-sequence current (less than 10%), its accuracy in practical applications is not very high.

1.1.3 Zero-sequence admittance method (Chai et al., 2020; Li et al., 2023; Zhang et al., 2024)

Zero-sequence admittance is defined as the ratio of zero-sequence current to zero-sequence voltage. Under normal operating conditions, zero-sequence admittance is typically located in the first quadrant of the complex admittance plane. However, when a fault occurs, zero-sequence admittance may shift to the second or third quadrant of the complex admittance plane. Although the faulted line can be identified by analyzing changes in zero-sequence admittance before and after the fault, this method heavily relies on accurately determining the zero-sequence admittance under normal conditions. This dependency significantly limits the applicability of the zero-sequence admittance method.

1.2 Transient algorithms for fault line selection in low-current grounding

1.2.1 Transient energy method (Wei et al., 2022; Xie et al., 2020)

The transient energy method identifies the faulted line by analyzing the transient energy changes in the lines at the moment of fault occurrence. When a single-phase ground fault occurs, the transient energy of the faulted line is usually significantly higher than the sum of the other lines. Specifically, this method uses high-frequency sampled zero-sequence current data from Distributed Phasor Measurement Units (D-PMU) to calculate the transient energy of each line. By comparing the transient energy of different lines, the faulted line can be accurately located. However, this method requires high-precision synchronous measurement equipment and high-frequency data collection, leading to higher system deployment costs, which limits its practical application.

1.2.2 First half-wave method (Gong, 2022; Peng et al., 2012)

The first half-wave method identifies the faulted line by analyzing the polarity and magnitude of the first half-wave of transient zero-sequence current during a single-phase ground fault. When the fault occurs at the peak of the phase voltage, the transient zero-sequence current magnitude of the faulted line is usually large, and its polarity is opposite to that of the non-faulted lines, allowing accurate identification of the faulted line. However, due to the short duration of the first half-wave, this method may be limited under low voltage or in the presence of interference.

1.2.3 Hilbert-Huang transform (HHT) method (Anand and Affijulla, 2020; Song et al., 2021)

The HHT method identifies the faulted line by performing Empirical Mode Decomposition (EMD) on the zero-sequence current signal at the moment of fault occurrence, extracting instantaneous frequency and energy characteristics. This method is effective in handling nonlinear and non-stationary signals, making it particularly suitable for complex fault analysis. However, due to its high computational complexity and sensitivity to noise, it may require optimization when combined with other methods in practical applications.

1.2.4 Waveform image similarity method (He et al., 2021; He et al., 2022)

The waveform image similarity method identifies the faulted line by analyzing the waveform of the transient zero-sequence current during a fault, decomposing it into several non-power frequency components, and extracting waveform coefficients of characteristic frequency bands. By calculating the similarity between the waveform coefficients of different lines, the faulted line can be identified. This method demonstrates high accuracy in handling complex faults, especially in environments with multiple interferences. However, due to its high computational complexity, practical applications may require balancing the demand for computational resources.

1.3 Fault line selection algorithms based on modern signal processing techniques

1.3.1 Fault line selection based on wavelet transform (Ahmed et al., 2023; Gao et al., 2021)

Wavelet analysis, characterized by good localization in both time and frequency domains and multi-resolution properties, is particularly suitable for analyzing singular signals, allowing examination of both time-domain and frequency-domain characteristics in different frequency ranges. Fault line selection based on wavelet transform analyzes grounding fault signals using wavelet transform, extracting amplitude and phase information from the fault zero-sequence current waveform. Generally, wavelet analysis is used for analyzing grounding fault transient signals, and fault line selection is made based on relationships such as opposite phase and maximum amplitude during the transient process. The sensitivity of wavelet analysis to singularities is both an advantage and a disadvantage, as the selection results are easily affected by interference signals.

1.3.2 Fault line selection based on artificial intelligence

Neural networks and fuzzy theory are relatively mature technologies within the field of artificial intelligence. Neural networks (Gao et al., 2021; Song et al., 2020; Tong et al., 2021; Wang et al., 2024; Zhang et al., 2022) can make judgments based on the mapping between electrical quantities and faults, while fuzzy logic (Jiao et al., 2020; Shang et al., 2020; Guan et al., 2020; Zhang et al., 2023) uses some conventional criteria based on input signals to obtain fault line selection results, deriving membership functions based on fuzzy theory, and finally integrating the fault line selection result information to obtain the final fault line selection outcome. The advantage of neural networks lies in their powerful learning and generalization capabilities, making them suitable for analyzing complex nonlinear relationships, especially in the context of multivariable fault signals. However, the training process of neural networks requires extensive data support, and the training results are sensitive to initial conditions. Fuzzy logic excels in handling uncertainty and fuzziness, enabling reasonable decision-making under incomplete information. However, its performance depends on the design of rules and the definition of membership functions, requiring fine-tuning in complex scenarios to achieve optimal results.

This paper proposes a transfer learning approach using the ResNet-50 model, which does not require selecting feature quantities. By training with the superimposed waveforms of zero-sequence voltage and zero-sequence current at the moment of the fault, the model can accurately select the fault line under different initial fault angles, grounding transition resistances, and fault distances, providing a new idea for fault line selection in distribution networks.

2 Transient singal characteristic analysis

2.1 Transient equivalent circuit

When a single-phase grounding fault occurs at the neutral point of an arc suppression coil grounding system, the transient capacitive current, transient inductive current, and transient grounding current at the fault point can be analyzed using the equivalent circuit shown in Figure 1.

Figure 1

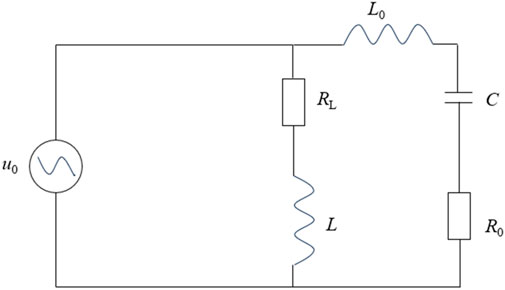
Figure 1. Transient equivalent circuit for single-phase grounding faults in resonant grounding systems.

As shown in Figure 1, the transient equivalent circuit describes the dynamics of single-phase grounding faults in resonant grounding systems. The transient response of the system can be analyzed by considering the interaction of capacitive and inductive components. The oscillatory behavior at the fault point is primarily driven by the energy exchange between the inductance $L_0$ and the capacitance $C$, while the damping effect is determined by the resistive components.

2.2 Transient capacitor current

Due to the high natural frequency of the transient capacitive current and the fact that the inductance of the arc suppression coil $L$ is much greater than $L_0$, the effects of $R_L$ and $L$ shown in Figure 1 can be neglected. Therefore, by using the series circuit composed of $L_0$, $R_0$ and $C$, and applying the zero-sequence sinusoidal voltage $u_0$ across it, the transient response of the capacitive current $i_C$ can be effectively determined as shown in Equation 1.

$R_0{i}_c+L_0\frac{d{i}_c}{dt}+\frac{1}{C}{\int }_0^1{i}_{c}dt=U_m\sin \left(\omega t+\phi \right)(1)$

where $U_m$ is the amplitude of the phase voltage; $\phi$ is the initial phase angle of the fault.

Therefore, the transient capacitive current $i_C$ includes the transient free oscillation component $i_{C_{os}}$ and the steady-state power frequency component $i_{C_{st}}$.

At the initial time, the initial condition satisfies the following conditions as described in Equation 2:

$\left\{\begin{array}{l}{I}_{C_{os}}+I_{C_{st}}=0\\ I_{C_m}=U_m\omega C\end{array}\right.(2)$

By performing Laplace transform operations, the relevant mathematical expressions can be obtained:

$i_C=i_{C_{os}}+i_{C_{st}}=I_{C_m}\left[\left(\frac{{\omega }_f}{\omega }\sin \left(\phi \right)\sin \left({\phi }_{f}t\right)-\cos \left(\phi \right)\cos \left({\phi }_{f}t\right)\right)e^{-\delta t}+\cos \left(\omega t+\phi \right)\right](3)$

In Equation 3, $i_C$ represents the total transient capacitive current, which is a combination of the transient free oscillation component $i_{C_{os}}$ and the steady-state power frequency component $i_{C_{st}}$. Here, $I_{C_m}$ is the amplitude of the steady-state current component, $\omega$ is the angular frequency of the system, and ${\omega }_f$ is the natural angular frequency of the system. The phase angles $\phi$ and ${\phi }_f$ correspond to the steady-state and transient components, respectively, while $\delta$ is the damping coefficient, which affects the rate at which the transient oscillations decay.

In power systems, the time constant ${\tau }_C$ is considered a constant, and its value has a significant impact on the system’s dynamic response. The magnitude of ${\tau }_C$ directly determines the damping rate of the system’s free oscillations: when ${\tau }_C$ is large, the system’s free oscillations decay more slowly; conversely, when ${\tau }_C$ is small, the decay rate of the free oscillations increases. Additionally, the free oscillation component $i_{C_{os}}$ in the power system is influenced by $\sin \phi$ and $\cos \phi$ and can be generated under ground faults at any phase angle $\phi$. Specifically, when the phase angle $\phi$ equals zero, the value of the free oscillation is minimal; when the phase angle $\phi$ equals $\pi /2$, that is, under a ground fault at the voltage peak, the value of the free oscillation is maximal, occurring at a quarter of the free oscillation period $T_f$. In this case, the amplitude of $i_{C_{os}}$ is at its maximum and is proportional to the ratio of the system’s ${\omega }_f$ to $\omega$. The larger this ratio, the higher the maximum amplitude ${\gamma }_{C_{\max }}$ of the free oscillation component.

When a single-phase ground fault occurs and the voltage of the faulted phase drops to 0, no additional transient capacitive current free oscillation component is generated. Under this condition the voltage difference across the capacitor is 0, preventing a rapid change in the charge within the capacitor and resulting in minimal transient capacitive current. In this case, the amplitude of the transient free oscillation current reaches its minimum value when the time is equal to half of the free oscillation period $T_f$. This minimum amplitude can be described by the following Equation 4:

$i_{C_{os\min }}=I_{Cm}\frac{{\omega }_f}{\omega }{e}^{T_f/2T_C}(4)$

Alternatively, it can be calculated using the ratio:

${\gamma }_{C_{\min }}=\frac{{\omega }_f}{\omega }{e}^{T_f/2T_C}(5)$

Equation 5 indicate that, when the phase angle $\phi$ is zero, the transient capacitive current has a free oscillation component equal in amplitude to the power frequency capacitive current.

Analyzing the free oscillation current is crucial because it is directly related to the stability and safety of the system. The calculation of the natural angular frequency ${\omega }_f$ is a core part of this analysis, and the derivation process is shown in Equation 6:

$\left\{\begin{array}{l}{\omega }_f=\sqrt{{\omega }_0^2-{\delta }^2}\\ {\omega }_0=\sqrt{\frac{1}{L_{0}C}}\\ T_0=2\pi \sqrt{L_{0}C}\end{array}\right.(6)$

The attenuation ratio of the current amplitude, ${\gamma }_C$, reflects the degree of current amplitude attenuation after a time period of $T_0/2$ and can be calculated using the following Equation 7:

${\gamma }_C=e^{\frac{R_0{T}_0}{4L_0}}(7)$

This ratio is generally used to assess the damping characteristics of the power grid. Experimental observations have found that the damping ratio in overhead line networks typically ranges between 1.5 and 2.0, indicating significant current attenuation after half a cycle.

Experimental results indicate that the dynamic response of cable lines is influenced by their physical characteristics. The free oscillation frequency of cable lines is relatively high, typically ranging from 1,500 to 3,000 Hz. This characteristic results in a shorter response time during transients, allowing cable lines to reach a steady state more quickly. In contrast, the free oscillation frequency of overhead lines usually ranges from 300 to 1,500 Hz.

2.3 Transient inductor current

When analyzing the transient process of an arc suppression coil, the first consideration is the expression of the magnetic flux in the core. During the transient process, the magnetic flux in the core remains the same as it is in the unsaturated state. Therefore, the known expression for the magnetic flux under static conditions can be directly used to determine the magnetic flux in the core during the transient process, which in turn allows for the calculation of the neutral point current through the arc suppression coil. As shown in Figure 1, according to Kirchhoff’s second law, we can derive the following expression for the magnetic flux, as described in Equation 8:

$U_m\sin \left(\omega t+\phi \right)=R_L{i}_L+N\frac{d{\varphi }_L}{dt}(8)$

where $N$ is the number of turns in the arc suppression coil in the system; ${\varphi }_L$ is the magnetic flux passing through the iron core of the arc suppression coil.

The relationship between the current through the arc suppression coil and the magnetic flux linkage can be expressed as shown in Equation 9:

$L{I}_L=N{\varphi }_L(9)$

Since the magnetic flux through the core of the arc suppression coil is zero. Substituting $I_L$ into Equation 8, the magnetic flux ${\varphi }_L$ can be obtained as:

$\left\{\begin{array}{l}{\varphi }_L={\varphi }_{st}\frac{\omega L}{Z}\left\{\cos \left(\phi +\epsilon \right)e^{-\frac{t}{{\tau }_L}}-\cos \left(\omega t+\phi +\xi \right)\right\}\\ {\varphi }_{st}=\frac{U_m}{N\omega }\\ \xi =\arctan \left(\frac{R_L}{\left(\omega L\right)}\right)\\ Z=\sqrt{R_L^2+{\left(\omega L\right)}^2}\end{array}\right.(10)$

where ${\varphi }_{st}$ is the steady-state magnetic flux; $\xi$ is the phase angle of the compensating current; $Z$ is the impedance of the arc suppression coil; ${\tau }_L$ is the time constant of the inductive circuit.

Since $R_L\ll \omega L$, the impedance of the arc suppression coil can be approximated as $Z\approx \omega L$, and the phase angle of the compensation current, denoted by $\xi$, can be considered to be zero. Equation 10 can be simplified to Equation 11:

$\left\{\begin{array}{l}{I}_L=I_{Lm}\left\{\cos \phi e^{-\frac{t}{{\tau }_L}}-\cos \left(\omega t+\phi \right)\right\}\\ I_{Lm}=U_m/\omega L\end{array}\right.(11)$

where $I_{Lm}$ is the amplitude of the inductive current.

2.4 Transient grounding current

In a low-current grounding system, the transient process at a single-phase ground fault point is mainly composed of transient capacitive current and transient inductive current. The values are described in Equation 12:

$i_D=i_C+i_L=\left(I_{Cm}-I_{Lm}\right)\cos \left(\omega t+\phi \right)+I_{Cm}\left(\frac{{\omega }_f}{\omega }\sin \phi \sin \left({\omega }_{f}t\right)-\cos \phi \cos \left({\omega }_{f}t\right)\right)e^{-\frac{t}{{\tau }_C}}+I_{Lm}\cos \phi e^{-\frac{t}{{\tau }_L}}(12)$

In the equation: the first term is the steady-state component of the ground fault current, and the remaining two terms are the transient components of the ground fault current.

In power systems, the amplitude of transient capacitive current is typically much larger than that of transient inductive current, and it decays more rapidly as well. Whether the neutral point of the power grid is ungrounded or grounded through an arc suppression coil, the amplitude and frequency of the transient grounding current are primarily influenced by the transient capacitive current, with its amplitude also being dependent on the initial phase angle.

Based on the above analysis, the transient frequency during a single-phase grounding fault in a low-current grounding system typically ranges from 300 to 1,500 Hz (Abdel-Fattah and Lehtonen, 2010). This frequency determines the duration of the initial half-wave and provides essential guidance for selecting the data window length for the ResNet-50 model.

3 Line selection process for low current grounding based on ResNet-50

3.1 Image preprocessing

To superimpose the zero-sequence voltage and zero-sequence current on a single image, it is necessary to normalize the sampled values of the zero-sequence voltage and zero-sequence current, as shown in the following Equation 13:

$\left\{\begin{array}{l}{u}_0^{nor}\left(t\right)=\frac{u_0\left(t\right)}{\max \left(\left|u_0\left(t\right)\right|\right)},t\in \left[t_0,t_0+1ms\right]\\ i_{0k}^{nor}\left(t\right)=\frac{i_{0k}\left(t\right)}{\max \left(\left|i_{0k}\left(t\right)\right|\right)},t\in \left[t_0,t_0+1ms\right]\end{array}\right.(13)$

where $u_0$ is the sampled value of the bus zero-sequence voltage for the first half-wave, and $i_{0k}$ is the sampled value of the zero-sequence current for the kth feeder. $u_0^{nor}$ and $i_{0k}^{nor}$ are the normalized zero-sequence voltage and the normalized zero-sequence current of the kth feeder, respectively. $t_0$ is the fault occurrence time.

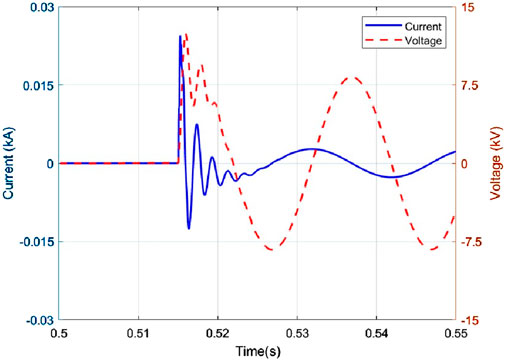
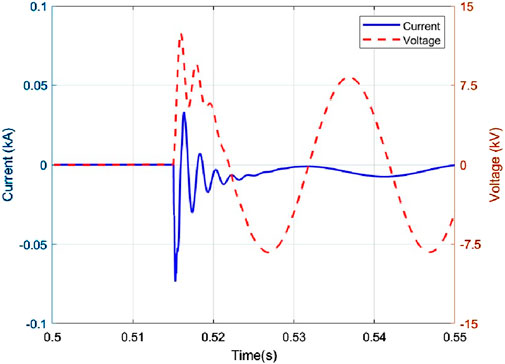
As shown in Figure 2, the waveforms of a single-phase ground fault under normal line conditions are presented. During the first half wave after the fault occurs, the zero-sequence current and zero-sequence voltage maintain the same phase relationship. Figure 3 shows the waveforms of a single-phase ground fault in a faulty line. In this scenario, during the first half wave after the fault occurs, the zero-sequence current and voltage are in opposite phases. This difference can be used to distinguish normal lines from faulty lines.

Figure 2

Figure 2. Voltage-current waveforms during a normal line single-phase grounding fault.

Figure 3

Figure 3. Voltage-current waveforms for a faulted line during a single-phase grounding fault.

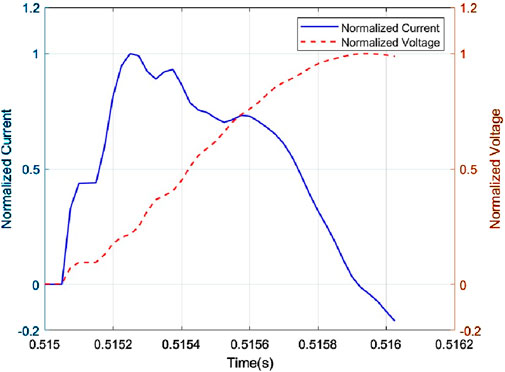
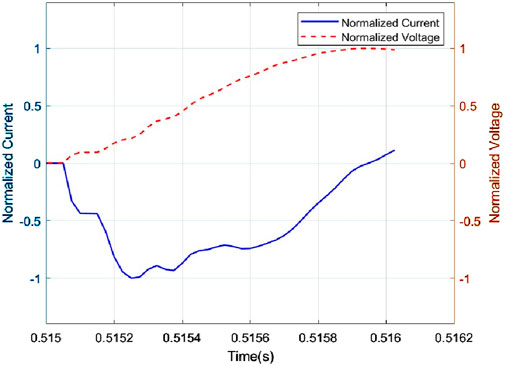
Figures 4, 5 show the preprocessed waveforms for the normal line and the faulty line, respectively. These figures highlight the transient process and normalize the voltage and current waveforms to make the features more apparent. This helps the ResNet-50 model in fault line selection.

Figure 4

Figure 4. Preprocessed waveform for a normal line during a single-phase grounding fault.

Figure 5

Figure 5. Preprocessed waveform for a faulted line during a single-phase grounding fault.

3.2 ResNet-50 convolutional neural network model

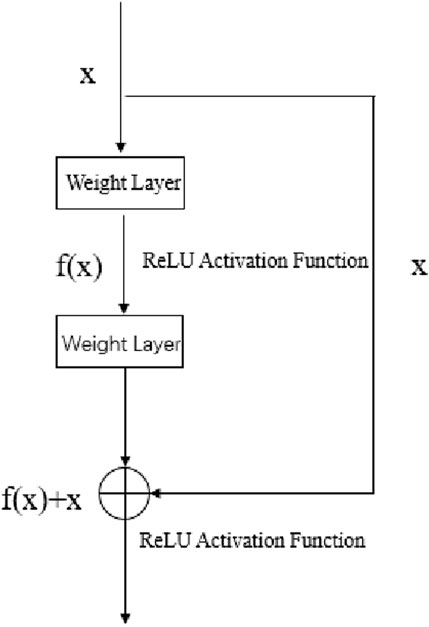
ResNet-50 is a type of deep convolutional neural network. It was proposed by Kaiming He et al. (He et al., 2016), where the concept of residual learning was first introduced. This effectively alleviates the problems of gradient vanishing and gradient explosion, significantly improving the algorithm’s reliability. Specifically, the residual module includes two or more convolutional layers, as well as a skip connection that directly adds the input to the output, as shown in Figure 6. The residual block, illustrated in Figure 6, consists of a series of weight layers followed by Rectified Linear Unit (ReLU) activation functions. The input x is passed through these layers to produce f(x), which is then added to the original input x to form the output f(x)+x. This skip connection helps in preserving the gradient flow during backpropagation, thereby mitigating the issues of vanishing and exploding gradients.

Figure 6

Figure 6. Residual block structure in a deep residual network.

The loss function used for training the ResNet-50 model is the Cross-Entropy Loss, which is well-suited for classification tasks. This function measures the difference between the predicted class probabilities and the true class labels, guiding the optimization process to minimize the prediction error.

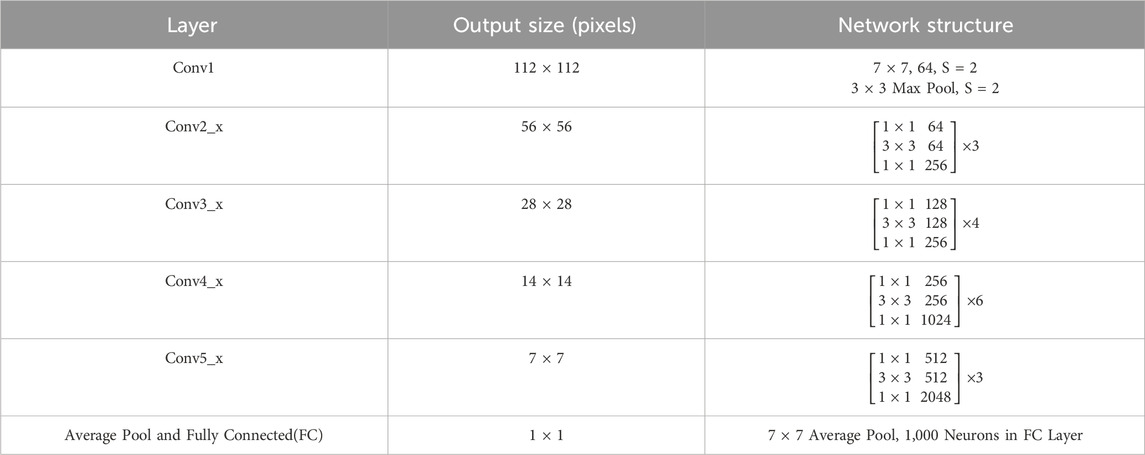
This model includes an input module, 4 residual modules, and an output module. In this paper, the number of neurons in the final fully connected layer is changed to 2 to adapt it for single-phase ground fault line selection. The network structure is shown in Table 1.

Table 1

Table 1. ResNet-50 network architecture.

3.3 Fault recognition algorithm process

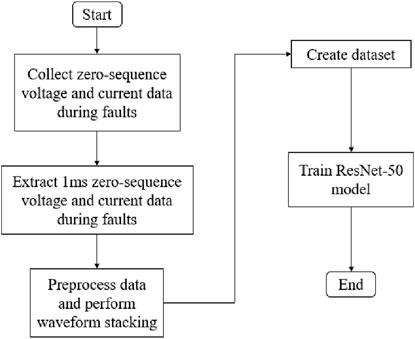
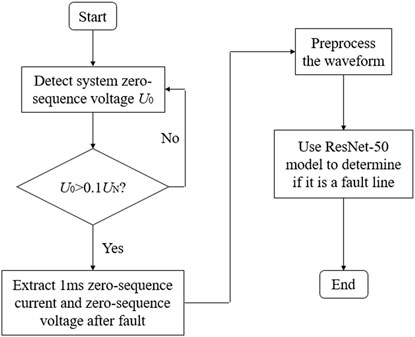
Applying ResNet-50 to small current grounding fault line selection, the fault identification algorithm flowchart is shown in Figures 7, 8. The specific process is as follows.

(1) Collect zero-sequence voltage and zero-sequence current data at the time of the fault, intercept the data within 1 m of the fault occurrence, preprocess it, and superimpose the waveforms to form a dataset.

(2) Build the ResNet-50 model, input the dataset obtained above to train the network, and train the model.

(3) The system continuously detects the bus zero-sequence voltage $U_0$ based on real-time collected voltage and current data. When $U_0>0.1U_N$, the line selection device is activated, and the zero-sequence voltage and zero-sequence current of the output line are recorded.

(4) Intercept the zero-sequence voltage and zero-sequence current within 1 m of the fault occurrence, preprocess the zero-sequence voltage and zero-sequence current, and superimpose the processed zero-sequence voltage and zero-sequence current.

(5) Use the trained ResNet-50 model to make line selection judgments based on the superimposed waveform.

Figure 7

Figure 7. ResNet-50 training process for single-phase grounding fault detection.

Figure 8

Figure 8. Application process of ResNet-50 for fault line selection.

4 Simulation analysis

4.1 Construction of simulation model

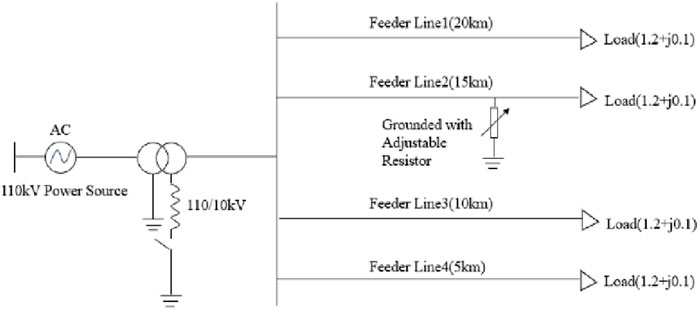
To verify the accuracy of the proposed method, the PSCAD tool was used to simulate the system, and a 110/10 kV simulation grid was constructed. The small current grounding system established in this study is shown in Figure 9. The model and parameters are as follows: the power source is an infinite power source, the transformer capacity is 1,000 MVA, the transformation ratio is 110/10 kV, and there are four outgoing lines connected to the substation bus. The lengths of the feeders are as follows: 20 km (Line 1), 15 km (Line 2), 10 km (Line 3), and 5 km (Line 4). The line parameters are unit positive-sequence impedance $Z_1=\left(0.17+j0.38\right)\mathrm{\Omega }/\text{km}$, unit zero-sequence impedance $Z_0=\left(0.23+j1.72\right)\mathrm{\Omega }/\text{km}$, and the end of each line is equipped with a transformer and load.

Figure 9

Figure 9. Simulated model of a small current grounding system.

By selecting different fault initial phase angles, grounding transition resistances, fault point distances, and arc suppression coil compensation degrees, different conditions of single-phase grounding faults are simulated. The types and values of the varying parameters are shown in Table 2, in which both full compensation and over-compensation scenarios are included to ensure a comprehensive evaluation of the ResNet-50 model under various conditions.

Table 2

Table 2. Parameter distribution.

4.2 Verification of line selection results in a noise free environment

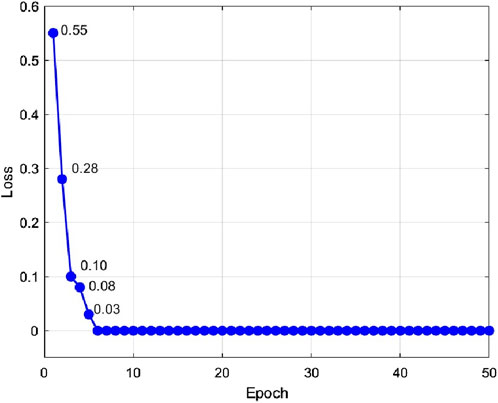
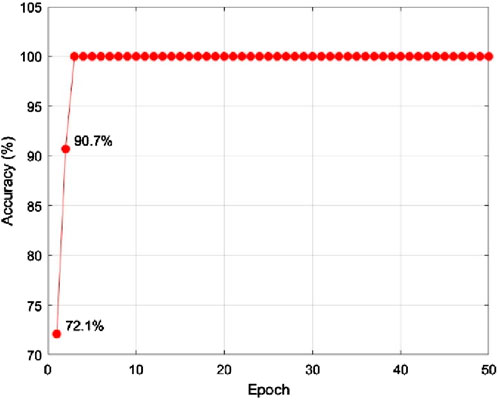
In a noise-free environment, by setting different compensation methods, single-phase grounding fault simulations are performed for different positions on lines L1 to L4, with various initial fault phases and different grounding resistances. As shown in Table 2, the dataset consists of 1,536 samples, with 80% used for training, 10% for validation, and 10% for testing. This division ensures that the ResNet-50 model is trained, validated, and tested on separate data subsets to accurately assess its performance. These simulated waveforms are input into the ResNet-50 model for training, with a batch size of 32 and 50 iterations. Ten percent of the dataset is randomly selected as the validation set for verification, and the validation accuracy reaches 100%.

The ResNet-50 model training results are shown in Figures 10, 11. Figure 10 illustrates the algorithm loss, which gradually converges, indicating effective model training. Figure 11 displays the validation accuracy, which stabilizes at 100%, indicating that the model has high accuracy in a noise-free environment. These results demonstrate that the ResNet-50 model can accurately identify and classify single-phase grounding faults under ideal conditions.

Figure 10

Figure 10. Changes in algorithm loss during model training.

Figure 11

Figure 11. Model validation accuracy in a noise-free environment.

4.3 Verification of line selection results under simulated noise environment

Noise refers to irregular information that is unrelated to the original signal. The ratio of the original signal to the noise is called the signal-to-noise ratio (SNR). To verify the noise resistance capability of the proposed method, 30 Decibel (dB) Gaussian white noise was added to the fault zero-sequence current and voltage, and tests were conducted. The test results are as follows.

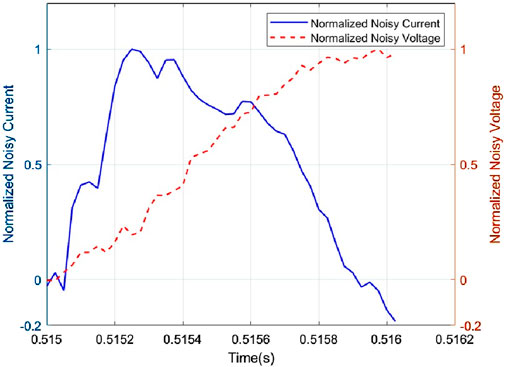
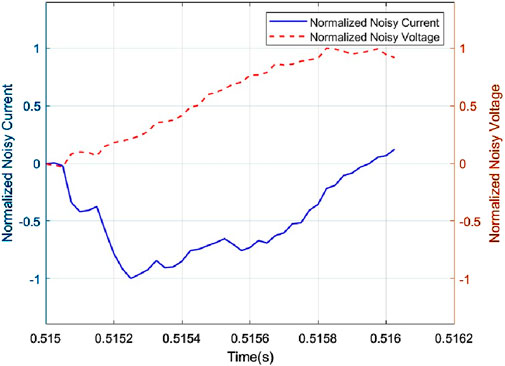
Figures 12, 13 show the waveforms under normal and fault line noise environments. Despite the presence of significant noise, Figure 12 shows that in a normal line noise environment, the zero-sequence current and zero-sequence voltage maintain the same phase relationship. Figure 13 illustrates that in a fault line noise environment, the zero-sequence current and voltage are in opposite phases. These results indicate that even when the data is corrupted by noise, the distinct characteristics of the normal and fault conditions remain evident.

Figure 12

Figure 12. Waveform under normal line noise environment.

Figure 13

Figure 13. Waveform under normal fault noise environment.

The verification results show that the waveform validation accuracy in a noisy environment is still 99.77%, indicating that even in a 30 dB noise environment, the algorithm can still efficiently perform single-phase grounding fault line selection. This high validation accuracy demonstrates the model’s robustness and its ability to effectively filter out noise while retaining the essential features needed for accurate fault detection.

4.4 Verification of selection results in real environments

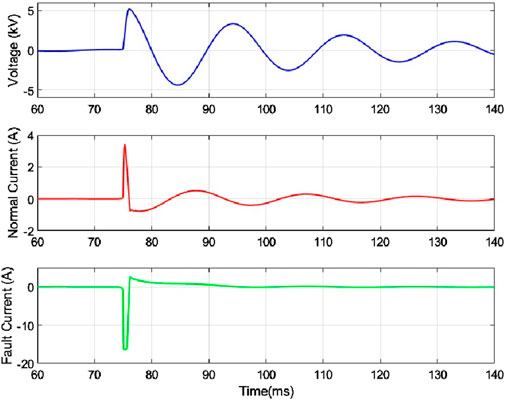
To verify the effectiveness of the proposed method in a real-world environment, waveform data recorded on-site in Xi’an, Shaanxi, were used. These data were collected using advanced recording equipment provided by NARI Relays, a subsidiary of the State Grid Corporation of China. The waveform data accurately represent the voltage and current conditions during single-phase grounding faults in an actual distribution network. A total of 25 on-site waveforms were input into the trained ResNet-50 model for verification. The verification results demonstrate that the line selection accuracy for all test waveforms is 100%.

Figure 14 shows some of the on-site recorded waveforms, including voltage, normal current, and fault current. The figure clearly illustrates the fault occurrence time and its impact on the system: the single-phase grounding fault occurred at approximately 75 milliseconds, causing a significant disturbance in the voltage waveform within the first millisecond. Both the normal current and fault current waveforms exhibit pronounced spikes, with opposite phases, immediately following the fault occurrence. The verification results confirm the reliability and adaptability of the proposed method under various fault conditions, providing strong support for fault detection in actual distribution networks.

Figure 14

Figure 14. On-site recorded waveforms during a single-phase grounding fault.

5 Conclusion

This study introduces a novel and highly effective approach to single-phase grounding fault line selection in low-current systems, utilizing the ResNet-50 model. Through extensive simulations and on-site waveform data validation, the proposed method has demonstrated remarkable adaptability and accuracy across a wide range of fault conditions. The ResNet-50 model, leveraging transfer learning and automated feature extraction, successfully eliminates the need for manual intervention. This significantly improves detection efficiency and ensures highly accurate results. Notably, the model maintains an impressive validation accuracy of 99.77%, even in the presence of significant noise (up to 30 dB), highlighting its robustness and reliability in real-world environments.

The use of advanced image recognition techniques in this method greatly simplifies fault detection processes. It minimizes the need for complex hardware and requires only minimal input data from a single line, which in turn enhances operational efficiency. This streamlined approach not only reduces the complexity of detection equipment but also lowers associated costs, making it highly practical for wide-scale deployment.

Data availability statement

The datasets presented in this article are not readily available because The dataset contains sensitive personal information and is subject to GDPR regulations. Access to the dataset requires approval from the Institutional Review Board (IRB) of [Your Institution]. The dataset is available only to registered users of the [specific database/repository] and can be used only for non-commercial research purposes. Users must cite the original publication when using the dataset. Data sharing is subject to a data use agreement that must be signed by the requesting party. The dataset has been anonymized to protect participants’ identities, and re-identification is prohibited. Requests to access the datasets should be directed to Xukun XU, Mzk3MTM5Nzk5QHFxLmNvbQ==.

Author contributions

GW: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. XX: Data curation, Formal Analysis, Investigation, Resources, Supervision, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Author GW was employed by China National Offshore Oil Corporation Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdel-Fattah, M. F., and Lehtonen, M. (2010). “Transient-based protection as a solution for earth-fault detection in unearthed and compensated neutral medium voltage distribution networks,” in Proc. 2010 electric power quality and supply reliability conf (Espoo, Finland: Aalto Univ.), 221–228. doi:10.1109/PQ.2010.5549993

CrossRef Full Text | Google Scholar

Ahmed, N., Hashmani, A. A., Khokhar, S., Tunio, M. A., and Faheem, M. (2023). Fault detection through discrete wavelet transform in overhead power transmission lines. Energy Sci. Eng. 11 (11), 4181–4197. doi:10.1002/ese3.1573

CrossRef Full Text | Google Scholar

Anand, A., and Affijulla, S. (2020). Hilbert-Huang transform based fault identification and classification technique for AC power transmission line protection. Int. Trans. Electr. Energy Syst. 30 (10), e12558. doi:10.1002/2050-7038.12558

CrossRef Full Text | Google Scholar

Chai, Y., Chen, X., and Zhang, K. (2020). “Research on ground fault line selection method based on zero sequence admittance,” in 2020 IEEE international conference on information technology, big data and artificial intelligence (ICIBA), 1, 14–17. doi:10.1109/ICIBA50161.2020.9277013

CrossRef Full Text | Google Scholar

Gao, J., Guo, M., and Chen, D. (2021). Fault line detection using waveform fusion and one-dimensional convolutional neural network in resonant grounding distribution systems. CSEE J. Power Energy Syst. 7 (2), 250–260. doi:10.17775/CSEEJPES.2020.02560

CrossRef Full Text | Google Scholar

Gao, J., Wang, X., Wang, X., Yang, A., Yuan, H., and Wei, X. (2021). A high-impedance fault detection method for distribution systems based on empirical wavelet transform and differential faulty energy. IEEE Trans. Smart Grid 13 (2), 900–912. doi:10.1109/TSG.2021.3129315

CrossRef Full Text | Google Scholar

Gao, S., and Lin, Z. (2018). “Study on section location of medium voltage distribution network based on fifth harmonic current fault component,” in 2018 IEEE 3rd advanced information technology, electronic and automation control conference (IAEAC), 1326–1331. doi:10.1109/IAEAC.2018.8577724

CrossRef Full Text | Google Scholar

Gong, J. (2022). Wavelet packet coefficient of transient first half wave line selection method for single-phase grounding fault. In IOP conf. Ser, earth environ. Sci., IOP conference series: earth and environmental science, 983(1): 012012. Bristol, England: IOP Publishing. doi:10.1088/1755-1315/983/1/012012

CrossRef Full Text | Google Scholar

Guan, H., Yang, B., Wang, H., Wu, D., Zhao, B., Liu, J., et al. (2020). Multiple faults diagnosis of distribution network lines based on convolution neural network with fuzzy optimization. IAENG Int. J. Comput. Sci. 47 (3), 289–298.

Google Scholar

Gururajapathy, S. S., Mokhlis, H., and Illias, H. A. (2017). Fault location and detection techniques in power distribution systems with distributed generation: a review. Renew. Sust. ENERG Rev. 74, 949–958. doi:10.1016/j.rser.2017.03.021

CrossRef Full Text | Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR). Las Vegas, NV, USA, 770–778. doi:10.1109/CVPR.2016.90

CrossRef Full Text | Google Scholar

He, Y., Wei, K., Zhang, J., and Liu, J. (2021). “A new method for single-phase grounding fault line selection based on waveform similarity,” in 2021 IEEE 4th international electrical and energy conference (CIEEC), 1–6. doi:10.1109/CIEEC50170.2021.9510521

CrossRef Full Text | Google Scholar

He, Y., Zhang, X., Wu, W., Zhang, J., Bai, W., Guo, A., et al. (2022). Faulty line selection method based on comprehensive dynamic time warping distance in a flexible grounding system. ENERGIES 15 (2), 471. doi:10.3390/en15020471

CrossRef Full Text | Google Scholar

Jiao, S., Zhang, Q., Wang, Q., and Wen, S. (2020). “A new method for single-phase Grounding Fault line selection based on fuzzy fusion,” in 2020 39th Chinese control conference (CCC), 3071–3076. doi:10.23919/CCC50068.2020.9189002

CrossRef Full Text | Google Scholar

Li, L., Gao, H., Cong, W., and Yuan, T. (2023). Location method of single line-to-ground faults in low-resistance grounded distribution networks based on ratio of zero-sequence admittance. Int. J. Electr. Power Energy Syst. 146, 108777. doi:10.1016/j.ijepes.2022.108777

CrossRef Full Text | Google Scholar

Li, Y., Gao, H., Du, Q., Qi, X., Pang, Q., and Zhu, G. (2011). “A review of single-phase-to-ground fault location methods in distribution networks,” in 2011 4th international conference on electric utility deregulation and restructuring and power technologies (DRPT) (China: Weihai), 938–943. doi:10.1109/DRPT.2011.5994028

CrossRef Full Text | Google Scholar

Peng, F., Zhou, Y. S., Liu, Y. F., Yuan, A. H., and Zhu, L. (2012). Line selection analysis of ground fault in distribution network based on chief half-wave and remnant current. Adv. Mater. Res. 482, 2197–2203. doi:10.4028/www.scientific.net/AMR.482-484.2197

CrossRef Full Text | Google Scholar

Sapountzoglou, N., Raison, B., and Silva, N. (2019). “A fault localization method for single-phase to ground faults in LV smart distribution grids,” in Proc. ELECTRIMACS 2019. Salerno, Italy, May 21-23, 2019.

Google Scholar

Shang, D., Zhao, H., Wang, L., and Ji, X. (2020). Research of fault line selection algorithm based on fuzzy theory for distribution network. CSEE J. Power Energy Syst. 6 (2), 250–260. doi:10.1049/icp.2020.0120

CrossRef Full Text | Google Scholar

Song, J., Li, Y., and Zhang, Y. (2021). Faulty line detection method based on improved Hilbert-Huang transform for resonant grounding systems. Int. Trans. Electr. Energy Syst. 31 (3), 1–15. doi:10.1002/2050-7038.12760

CrossRef Full Text | Google Scholar

Song, Y., Huang, H., and Chen, Y. (2020). The method of BP algorithm for genetic simulated annealing algorithm in fault line selection. J. Phys. Conf. Ser. 1650 (3), 032187. doi:10.1088/1742-6596/1650/3/032187

CrossRef Full Text | Google Scholar

State Grid Corporation of China (2017). Technical guidelines for distribution network. Q/GDW10370—2016 [S]. Beijing, China: China Electric Power Press. (in Chinese).

Google Scholar

Tong, H., Qiu, R. C., Zhang, D., Yang, H., Ding, Q., and Shi, X. (2021). Detection and classification of transmission line transient faults based on graph convolutional neural network. CSEE J. Power Energy Syst. 7 (3), 456–471. doi:10.17775/CSEEJPES.2020.04970

CrossRef Full Text | Google Scholar

Wang, H., Shi, Y., and Guo, W. (2024). Fault line selection method for power distribution network based on graph transformation and ResNet50 model. Information 15 (7), 375. doi:10.3390/info15070375

CrossRef Full Text | Google Scholar

Wei, X., Wang, X., Gao, J., Yang, D., Wei, K., and Guo, L. (2022). Faulty feeder detection for single-phase-to-ground fault in distribution networks based on transient energy and cosine similarity. IEEE Trans. Power Deliv. 37 (5), 3968–3979. doi:10.1109/TPWRD.2022.3142186

CrossRef Full Text | Google Scholar

Xie, W., Wang, X., Fang, C., Zhang, H., Shi, F., Xing, X., et al. (2020). Field experiment using transient energy method to locate a single-phase to ground fault. Glob. Energy Interconnect. 3 (6), 585–594. doi:10.1016/j.gloei.2021.01.002

CrossRef Full Text | Google Scholar

Zhang, J., Zhou, Y., Ding, J., Gao, X., Wang, D., and Ma, T. (2023). “A method for fault line selection of small current grounding system based on MEEMD and FCM,” in 2023 international conference on power system technology (PowerCon), 1–6. doi:10.1109/PowerCon58120.2023.10331204

CrossRef Full Text | Google Scholar

Zhang, L., Liu, H., Su, G., Zhang, S., and You, X. (2024). Line selection of single-phase fault grounding system based on the deviation criterion of composite zero-sequence admittance. J. Phys. Conf. Ser. 2785 (1), 012113. doi:10.1088/1742-6596/2785/1/012113

CrossRef Full Text | Google Scholar

Zhang, Q., Ma, W., Li, G., Ding, J., and Xie, M. (2022). Fault diagnosis of power grid based on variational mode decomposition and convolutional neural network. Electr. Power Syst. Res. 208, 107871. doi:10.1016/j.epsr.2022.107871

CrossRef Full Text | Google Scholar