Extracting metal oxide redox thermodynamics from TGA measurements requires moving beyond the linearized van ‘t Hoff approach

Thermodynamic modeling of metal oxide reduction is crucial for optimizing chemical processes and materials in systems dependent on off-stoichiometric reduction/re-oxidation cycling. Two prevalent methods for extracting reduction thermodynamics from thermogravimetric data are linearized van ‘t Hoff (VH) analysis and the compound energy formalism (CEF). This work evaluates the accuracy of these methods by constructing invertible ground truth thermodynamic models, generating hypothetical thermogravimetric data, and determining the reduction thermodynamic using both VH and CEF methods. Our findings reveal that the VH method produces absolute errors 3–5 times higher than the CEF in kJ/mol O or J/mol O K for enthalpy and entropy of reduction, respectively. In contrast, the CrossFit CEF (CF-CEF) method yields errors often less than 10 kJ/mol O or J/mol O K. Moreover, the CF-CEF method provides models based on mole fraction, temperature, and extent of reduction, while a typical VH analysis provides thermodynamics of only the specific compositions measured. Although simple to implement, the VH method suffers from significant, non-systematic errors due to entropy/enthalpy compensation and defect modeling. Consequently, we recommend the more complex but robust, CF-CEF method for extracting redox thermodynamics from thermogravimetric measurements.

Introduction

Many chemical processes exploit the flexible cationic oxidation states of metal oxides ($\left.{\mathrm{M}}_{\mathrm{x}}{\mathrm{O}}_{\mathrm{z}}\right)$ to drive desired chemical reactions. These reactions occur through the facile formation and annihilation of O-vacancies during off-stoichiometric reduction/re-oxidation (redox) reactions (Equations 1, 2 respectively). This mechanism is fundamental in various applications including gas reforming (Guo et al., 2023; Ahmad et al., 2021; LeValley et al., 2014), gas separation and pumping (Bulfin et al., 2019; Krzystowczyk et al., 2021; Cai et al., 2022; Gu et al., 2018; Xu et al., 2020; Bulfin et al., 2017; Vieten et al., 2016; Bush et al., 2021; De Souza, 2015), thermochemical energy storage (Mane et al., 2023; Wexler et al., 2023; Hashimoto et al., 2023; Bayon et al., 2021a; Sai Gautam et al., 2020a; Park et al., 2023; van de Krol et al., 2008; Mastronardo et al., 2020; Chen et al., 2021; Babiniec et al., 2015; Jin et al., 2021; Abraham et al., 2016; Tahir et al., 2023), thermochemical water and carbon dioxide splitting (Singh et al., 2015; Brendelberger et al., 2019; Bork et al., 2019; Zhu et al., 2002; Muhich et al., 2018; Tran et al., 2024; Arifin et al., 2020), nuclear energy production and safety (Moore et al., 2013; Sundman et al., 2011), and numerous catalytic processes (Liu et al., 2021; Fuks et al., 2013; Barry et al., 1992; Kolodiazhnyi et al., 2016; Rousseau et al., 2020; Teh et al., 2021; Young et al., 2023). By leveraging the redox properties of metal oxides, these processes achieve efficient and effective chemical transformations.

${\mathrm{M}}_{\mathrm{x}}{\mathrm{O}}_{\mathrm{z}-\mathrm{\delta }1}\to {\mathrm{M}}_{\mathrm{x}}{\mathrm{O}}_{\mathrm{z}-\mathrm{\delta }2}+\frac{\left(\mathrm{\delta }1-\mathrm{\delta }2\right)}{2}{\mathrm{O}}_2(1)$

${\mathrm{M}}_{\mathrm{x}}{\mathrm{O}}_{\mathrm{z}-\mathrm{\delta }2}+\frac{\left(\mathrm{\delta }1-\mathrm{\delta }2\right)}{2}{\mathrm{O}}_2\to {\mathrm{M}}_{\mathrm{x}}{\mathrm{O}}_{\mathrm{z}-\mathrm{\delta }1}(2)$

The selection and optimization of redox active metal oxides, $\left({\mathrm{M}}_{\mathrm{x}}{\mathrm{O}}_{\mathrm{z}}\right)$, in chemical processes rely heavily on well-characterized redox thermodynamic data (Mastronardo et al., 2020; Zhang et al., 2023; Qian et al., 2021; Yoo et al., 2017). This characterization is typically achieved through thermogravimetric analysis (TGA), which involves measuring the mass loss of the material as a function of temperature and O₂ pressure (Hoes et al., 2017; Takacs et al., 2016; Panlener et al., 1975; Bayon et al., 2021b; Krug et al., 1976). From this data, the enthalpy and entropy of reduction can be extracted.

The solid state oxygen chemical potential, ${\mu }_O^{\text{solid}}$, and thus the reduction free energy, is inferred from the gas phase oxygen chemical potential, ${\mu }_O^{\text{gas}}$, and the equilibrium condition, as shown in Equation 3 (Hoes et al., 2017; Takacs et al., 2016; Panlener et al., 1975; Bayon et al., 2021b; Krug et al., 1976). In this context, $\mathbf{x}$ represents the mole fraction vector of various cations in the ${\mathrm{M}}_{\mathbf{x}}{\mathrm{O}}_{\mathrm{z}}$ composition, where δ denotes the extent of oxygen off-stoichiometry; T is the temperature, and pO₂ is the O₂ partial pressure.

$\frac{1}{2}{G}_{{\mathrm{O}}_2}\left(T,p{O}_2\right)={\mu }_O^{\text{gas}}\left(T,p{O}_2\right)\stackrel{eq.}{\iff }{\mu }_O^{\text{solid}}\left(T,\delta ,\mathbf{x}\right)=-\frac{\partial G\left(T,\delta ,\mathbf{x}\right)}{\partial \delta }(3)$

Although the route to converting measured data points into thermodynamic quantities is well defined in principle, i.e., Equation 3, the method for reliably extracting the δ, T, pO₂, and mole fraction, x, (TpOX) relationship into thermodynamic quantities remains unclear. While the chemical potential alone dictates the spontaneity of the reaction, the extraction of enthalpy and entropy of reduction from the chemical potential provides crucial information necessary for processes design. Particularly, the enthalpy of reduction is required for managing heat flows and determining if a material carries sufficient energy to drive a desired oxidation reaction. Therefore, accurate extraction of these thermodynamic properties is the key to elucidating controlling properties for the off stoichiometric reactions (i.e., composition, temperature, pressure, etc.). We note that although calorimetry can measure enthalpies of reaction, doing so with solids is complex and would require extensive experimentation to build a compositional or non-stoichiometric dependent model (Yoo et al., 2017).

Currently, one of the most widely used techniques for extracting reduction thermodynamics from experimental data is linearized van ‘t Hoff (VH) analysis (Hashimoto et al., 2023; Yoo et al., 2017; Bayon et al., 2021b; Van’t Hoff and Hoff, 1884). This approach relates the equilibrium constant of redox at a constant δ, $K_{\mathrm{\delta }}\left(T\right)$, to changes in temperature (T) as shown in Equation 4.

$\mathit{ln}\left(K_{\mathrm{\delta }}\right)=\mathit{ln}{\left(\frac{P_{O2}}{P^o}\right)}^{\frac{1}{2}}=-\frac{{\frac{\partial H}{\partial \delta }}_{red}}{RT}+\frac{{\frac{\partial S}{\partial \delta }}_{red}}{R}(4)$

The slope and intercept of a VH plot correlate 1/T and ln (pO2) to the enthalpy $\left({\frac{\partial H}{\partial \delta }}_{red}\right)$ and entropy $\left({\frac{\partial S}{\partial \delta }}_{red}\right)$ of reduction, respectively. To achieve this correlation, data must be determined for constant δ across various T and pO₂ values. Nonlinearized VH approaches are more rigorous and usually lead to a more accurate results, but often require higher fidelity data outside of TGA results or extremely fine TpOX meshes (Yoo et al., 2017). Such TpOX meshes are experimentally expensive and therefore often prohibitive. For detailed studies on the limitations of VH analysis please see these excellent reviews (Chaires, 1997; Zhukov and Karlsson, 2007; Liu and Sturtevant, 1997).

Deploying the VH method presents four main challenges:

1) Delineating entropy and enthalpy from only free energy information.

2) Assuring thermodynamic quantities are temperature independent.

3) Collecting sufficient δ data to mitigate errors associated with constant δ interpolations.

4) Characterizing each composition X independently.

Since only the chemical potential of the oxygen is known and experimental error introduces ambiguity in line fitting, determining the slope and intercept of the VH plot can lead to compensation or trade-off, between entropy and enthalpy terms of the free energy (Yoo et al., 2017). This issue is exacerbated when the experimental temperature range is small, increasing the error in the extrapolated intercept (Hoes et al., 2017). The most commonly adopted approach to VH analysis of TGA redox materials assumes that ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ are temperature independent. While this assumption may hold over small temperature ranges (tens of K), metal oxide reduction experiments and thermochemical cycling typically occur over temperature ranges of hundreds of K, where temperature dependence can be significant.

The collection of constant δ data is challenging as the off-stoichiometry is unknown a priori; therefore, generally one approximates either by interpolation or by fitting a defect model to predict the points. Arriving at T and pO₂ operating points with constant δ is unreliable using interpolation given the high non-linearity of reaction equilibria. Furthermore, correctly and confidently implementing a defect model is also challenging, arising because one can construct defect models in multiple ways (Zhang et al., 2023; Qian et al., 2021; Bergeson-Keller et al., 2022) and depend on making assumptions that may or may not reflect the thermodynamic and reactions occurring. Often, defect models also assume no temperature dependence, which may be the faster/easier estimation of thermodynamics, but, unbeknownst to the analyzer, may deviate vastly from the true thermodynamic trends (Chaires, 1997). These underlying assumptions and interpolated fits of T and pO₂ required to construct the defect model exacerbate the errors inherent within the linearized VH method, i.e., an assumed temperature independence of ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$. Repeating this construction for multiple values of δ determines ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ as a function of δ and compounds the error even further. The error resulting from these interpolations could be minimized via extensive data collection through extremely fine TpOX meshes. Extrapolation should be avoided, requiring even further data collation to report reduction thermodynamics across wide temperature ranges (100s of K).

Finally, each composition must be characterized individually (i.e., each $\mathbf{x}$ in ${\mathrm{M}}_{\mathbf{x}}{\mathrm{O}}_{\mathrm{z}}$), because the thermodynamics of one compound does not inform those of similar compositions. Despite these known deficiencies, the VH method remains the leading reduction thermodynamic analysis method for ${\mathrm{M}}_{\mathrm{x}}{\mathrm{O}}_{\mathrm{z}}$ material characterization due to its ease of implementation.

The Compound Energy Formalism (CEF) (Hillert and Staffansson, 1970) overcomes many of the VH method limitations in characterizing the reduction thermodynamics of a family of ${\mathrm{M}}_{\mathrm{x}}{\mathrm{O}}_{\mathrm{z}}$ materials, by fitting a more nuanced and temperature dependent free energy form. While the CEF also correlates the system Gibbs free energy through the oxygen chemical potential of the gas phase and the solid phase, as Equation 3 shows, it represents the Gibbs free energy as a combination of solid solutions on a set of sub-lattices. The free energy is described via the summation of three terms (Equation 5): 1) a linear combination of the Gibbs free energies of the so-called endmember compounds representing the composition of the solid solution, 2) a configurational entropy term, and 3) an excess term that accounts for interactions on and between the sub-lattices.

$G^{\text{soln}}=G^{\text{endmembers}}-T\ast S_{\text{config}}+G^{\text{excess}}(5)$

The sub-lattices represent the unique sites in the crystal lattice, each with fractional occupancy by different elements, oxidation states, and/or vacancies. Equations 6–9 show how to calculate these terms.

$G^{\text{endmembers}}={\displaystyle \sum _i^N}\prod {\gamma }_M^z{G}_i^{\text{endmember}}(6)$

$S_{\text{config}}=-R{\displaystyle \sum _z}{n}_z{\displaystyle \sum _X}{\gamma }_M^z\ast \mathit{ln}\left({\gamma }_M^z\right)(7)$

$G^{\text{excess}}={\displaystyle \sum _h}{\gamma }_1^h{\gamma }_2^h{\displaystyle \sum _{k\ne h}}{\displaystyle \sum _{M=1}^2}{\gamma }_M^k{\displaystyle \sum _{l\ne h\ne k}}{\displaystyle \sum _{M=1}^2}{\gamma }_M^l{\mathcal{L}}_{h:k:l}(8)$

${\mathcal{L}}_{h:k:l}={\displaystyle \sum _{\nu =0}^1}{\left({\gamma }_1^h-{\gamma }_2^h\right)}^{\nu }{L}_{h:k:l}^{\nu }(9)$

where $\gamma$ is the site fraction of a species on a sublattice site, $N$ is the total number of endmember terms, $n$ is the total number of sites, z is a particular sub-lattice, and M counts over the components that can occupy a site on sublattice z. The excess term of Equation 5, is the most complex. A three sublattice model with two possible components per sublattice is used as an example in Equations 8, 9, where $h$, $k$, and $l$ are the sublattices. The $L_{h:k:l}^{\nu }$ terms in $G^{\text{excess}}$ are described by a Redlich-Kister (RK) expansion Redlich and Kister (1948) of the $\mathrm{\gamma }$ site fraction terms up to order m, shown here (as is typical) with an upper limit of ν = 1. Depending on the construction of the site fraction terms, the CEF method makes no assumptions about the material aside from being a continuous function; meaning if there is a step change in the thermodynamics due to a phase change the CEF will model “through” the step change and two models may be necessary depending on the magnitude of the step change. The construction of the CEF allows for all possible controlling factors to be considered (i.e., interactions with O vacancies, cation vacancies, and reducing species) if the site interaction terms are allowed to account for those factors. For a more complete description of CEF construction, we refer the readers to Refs (Bayon et al., 2021a; Hillert and Staffansson, 1970; Wilson et al., 2023; Sai Gautam et al., 2020b; Wilson and Muhich, 2024).

The key drawback to the CEF model approach in fitting thermochemical data is the large number of degrees of freedom (DOF) inherent in the construction of the CEF model. Linear, or near linear, dependencies in the excess term parameters and enthalpy and entropy can arise from the large parameter space. The former makes it challenging to find a global minimum when fitting, while the latter can result in compensation, or tradeoffs, between enthalpy and entropy, which equate to the same free energy. These challenges have prevented the widespread use of the CEF for thermochemical fitting. To solve these problems, we recently developed the CrossFit CEF(CF-CEF) method (Wilson et al., 2023), which reformulates the CEF fitting procedure to circumvent the challenges of linear dependence between some excess terms and delineate entropic and enthalpic contributions to the free energy. The CF-CEF optimizes the CEF model parameters using both computational (ab initio methods) and experimental (TGA) data. The experimental data informs the model via Equation 3, while we incorporate the computational data via the non-derivative free energy relationship $G\left(T=0,\delta ,\mathbf{x}\right)\approx H\left(T=0,\delta ,\mathbf{x}\right)$. We fit the shared parameters between $\frac{\partial G\left(T,\delta ,\mathbf{x}\right)}{\partial \delta }$ and $G\left(T=0\right)$ using a combined objective function resulting in one model informed by both data sets.

As outlined above, the advantages and disadvantages of the VH and CEF methods, i.e., simplicity but potential ambiguity in accuracy versus complexity but robustness of fit, are well known. However, to the best of our knowledge, no one has reported a quantification of the relative (in-)accuracy of these methods. Therefore, this work compares the accuracy of the linear VH analysis and CF-CEF method using a perfectly invertible, thermodynamic data set based on an Einstein solid model of heat capacity (Rogers, 2005), selected reduction enthalpies, and randomly generated sub-lattice interaction terms. Thus, the ground truth reduction thermodynamics are known exactly providing a means for error analysis between the two methods. In this work, we only examine hypothetical data sets because directly measured experimental data enthalpies and entropy, as opposed to extracted quantities, are not widely available. Three sets of hypothetical perovskite materials $\left({\mathrm{A}}_{\mathrm{x}}{\mathrm{A}}_{1-\mathrm{x}}^{\prime }{\mathrm{B}}_{\mathrm{y}}{\mathrm{B}}_{1-\mathrm{y}}^{\prime }{\mathrm{O}}_{3-\mathrm{\delta }}\right)$ are compiled: 1) a material with high reduction enthalpies capable of splitting water via solar thermochemical water splitting with compositional change in x; 2) a thermochemical energy storage material Hashimoto et al. (2023) with moderate reduction enthalpies with compositional change in y; and 3) a complex high and low reduction energy material that varies in both x and y (Wexler et al., 2023). The range in hypothetical thermodynamic and compositional data tests the flexibility of each of the methods. The complexity of the ground truth materials is kept simple (no phase changes or cation vacancy formation) so that one need not determine if those factors are contributing to the error in the models. Validation of these methods via experimental means is already well studied (in the case of VH) or the subject of current studies (Wilson et al., 2023; Wilson and Muhich, 2024) (in the case of CF-CEF) and is outside the scope of this work. Overall, this work shows that the VH method has errors as high as 105 kJ/mol O and 70 J/mol O K for ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ respectively for some material compositions. Conversely, the maximum error in the CF-CEF method is 3 times smaller across all compositions studied in both ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ , having maximum error of 36 kJ/mol O and 21 J/mol O K respectively. These findings suggest that the metal oxide redox community should transition to thermodynamic characterization by the CEF to ensure accuracy.

Methods

This section first briefly describes the VH analysis and CF-CEF fitting methods. Then, we explain the construction of the hypothetical ground truth thermodynamic data generated using the heat capacity modeled as an Einstein solid for subsequent fitting by both the VH and CF-CEF approaches. Finaly, we explain how we constructed realistic but hypothetical ground truth thermodynamics data sets. The comparison between methods presented here focuses on the quinary metal oxide perovskite material ($\left.{\mathrm{A}}_{\mathrm{x}}{\mathrm{A}}_{1-\mathrm{x}}^{\prime }{\mathrm{B}}_{\mathrm{y}}{\mathrm{B}}_{1-\mathrm{y}}^{\prime }{\mathrm{O}}_{3-\mathrm{\delta }}\right)$. We use the variables x and y to develop unique hypothetical materials representing different application spaces, further described below.

Van ‘t Hoff method construction and implementation

We define a defect model that assumes redox activity occurs only on the B-site of the perovskite as shown in Equation 10. Using Kröger–Vink notation (Kröger and Vink, 1956), we describe the defect reaction charge transfer in Equation 11. We write the equilibrium constant at a constant T ($K_T$) by utilizing the free energy relationship with O2 chemical potential, as indicated in Equation 3, and apply Kröger–Vink notation for the perovskite redox reaction in Equation 12. Finally, we express $K_T$ in terms of δ in Equation 13 for use in a VH analysis.

${\text{ABO}}_3\to {\text{ABO}}_{3-\mathrm{\delta }}+\frac{\delta }{2}{\mathrm{O}}_2(10)$

$2B_B^{\times }+O_O^{\times }\to 2B_B^{\prime }+V_O^{..}(11)$

$K_T=\frac{\left[V_O\right]{\left[B_B^{\prime }\right]}^2}{\left[O_O^{\times }\right]{\left[B_B^{\times }\right]}^2}{p}_{O2}^{\frac{1}{2}}(12)$

$K_T=\frac{\left(1-\frac{\delta }{3}\right){\left(1-2\delta \right)}^2}{\frac{\delta }{3}{\left(2\delta \right)}^2}{p}_{O2}^{\frac{1}{2}}(13)$

The defect model allows the determination of constant δ values across many T and pO₂ points, Figure 1 (right). For each δ of interest, one must solve for ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ utilizing Equation 4. One generally fits K_T using the data pairs of δ and pO₂ at a each temperature, and then extracts its temperature dependence from linear fits, as shown in Figure 1 (left). The slope of the line in Figure 1 (left) is ${\frac{\partial H}{\partial \delta }}_{red}$ and the intersect is ${\frac{\partial S}{\partial \delta }}_{red}$. One completes the ln (K_δ) fit for every constant δ value and repeats the process for each mol fraction x in the ${\mathrm{M}}_{\mathbf{x}}{\mathrm{O}}_{\mathrm{z}-\mathrm{\delta }}$ material.

Figure 1

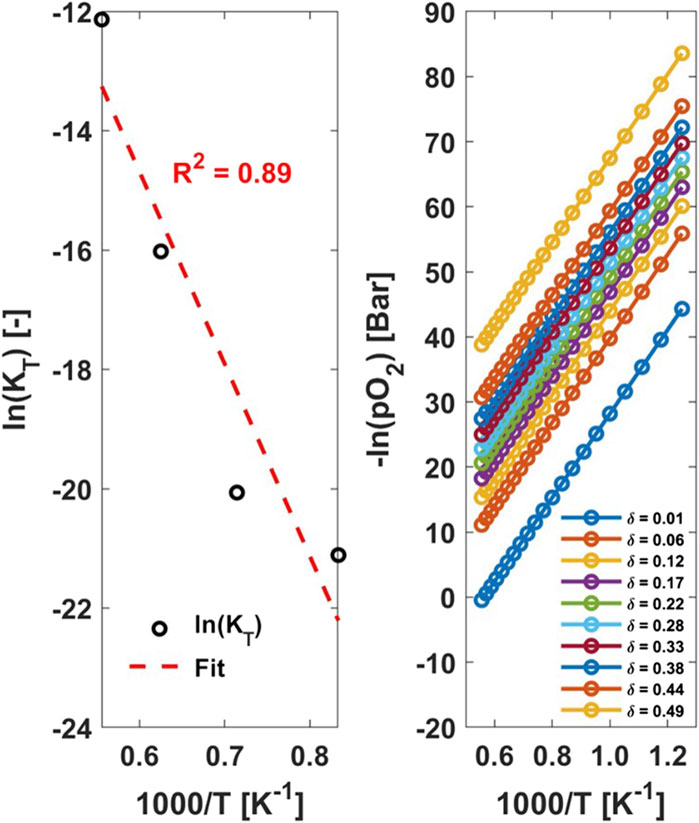
Figure 1. (left) ln ($K_T$) versus 1,000/T plot from which one can derive thermodynamic properties. (right) -ln (pO₂) versus 100/T for constant delta curves enables the interpolation/extrapolation of the delta dependence of enthalpy and entropy of reduction.

CrossFit CEF construction and implementation

The CEF construction depends on which sublattice the substitutions sit, i.e., A or B, and will vary in the generic ${\mathrm{A}}_{\mathrm{x}}{\mathrm{A}}_{1-\mathrm{x}}^{\prime }{\mathrm{B}}_{\mathrm{y}}{\mathrm{B}}_{1-\mathrm{y}}^{\prime }{\mathrm{O}}_{3-\mathrm{\delta }}$. Based on the specific construction, Equations 5–9 change to generate the overall solution model. A purpose built MATLAB code, based on the CF-CEF implementation (Wilson et al., 2023), constructs the CEF model for any ${\mathrm{A}}_{\mathrm{x}}{\mathrm{A}}_{1-\mathrm{x}}^{\prime }{\mathrm{B}}_{\mathrm{y}}{\mathrm{B}}_{1-\mathrm{y}}^{\prime }{\mathrm{O}}_{3-\mathrm{\delta }}$ composition with reduction on the B site. The partial interaction free energies used to describe $G_i^{endmember}$ in Equation 5 and the $L_{h:k:l}^{\nu }$ in $G^{\text{excess}}$, each term generically referred to as $g_j$, are described via a constant heat capacity expansion derived in Equations 14–17, where $H_o$ and $S_o$ are used as fitting parameters to estimate the first integral in Equations 15, 16.

$C_p=A(14)$

$∆H={\displaystyle \underset{0}{\overset{T^o}{\int }}}{C}_{p}dT+{\displaystyle \underset{T^o}{\overset{T}{\int }}}{C}_{p}dT=H^o+AT-A{T}^o(15)$

$∆S={\displaystyle \underset{0}{\overset{T^o}{\int }}}\frac{C_p}{T}dT+{\displaystyle \underset{T^o}{\overset{T}{\int }}}\frac{C_p}{T}dT=S^o+Aln\left(\frac{T}{T^o}\right)(16)$

$∆{\mathit{g}}_{\mathit{j}}={\mathit{H}}_{\mathit{j}}^{\mathrm{o}}+\left({\mathit{A}}_{\mathit{j}}-{\mathit{S}}_{\mathit{j}}^{\mathrm{o}}\right)\mathit{T}-\mathit{A}{\mathit{T}}^{\mathit{o}}-{\mathit{A}}_{\mathit{j}}\mathit{T}\mathit{l}\mathit{n}\left(\frac{\mathit{T}}{{\mathit{T}}^{\mathit{o}}}\right)(17)$

Note that due to the definite integration of $C_p$ from a reference temperature $T^o$ to $T$, $H_o$ and $S_o$ provide a thermal correction from the hypothetical DFT data at T = 0 K to the temperature data found in the hypothetical experimental data set. Equation 17 represents the best, most physical, first order expansion. For further development and fundamental analysis of the CEF model see Ref. (Hillert and Staffansson, 1970; Wilson et al., 2023; Hillert, 1996; Hillert, 2001; Spencer, 2008; Ji et al., 2022; Cacciamani, 2016).

While the consideration of a constant heat capacity may seem overly simplistic, we find that this expansion describes the enthalpy and entropy of these ${\mathrm{M}}_{\mathrm{x}}{\mathrm{O}}_{\mathrm{z}}$ materials well, as the heat capacity is relatively constant within the temperature range of interest. Supplementary Figure SI-1 illustrates the accuracy of the enthalpy and entropy from the integrations of $C_p=A$ as compared to $C_p^{\text{Ein}}$ and $C_p^{\text{Emp}}$.

Constructing the CEF state function with a definite integral provides a more physical fit, especially with respect to temperature trends, and aids in preventing tradeoff between H and S. However, it causes an inherent error in the fit to the DFT data since $G^{\text{soln}}\left(T=0\right)=H^o\approx E_{DFT}$ because $H^o$ carries some temperature information. This issue is of minimal concern because the CF-CEF method uses DFT information solely to localize the free energy space, i.e., delineate H and S contributions. The $∆g_j$ in $G_i^{\text{endmember}}$ and $G^{\text{excess}}$ contain the parameters of the model to be optimized via the use of a sum of residual squared errors (RSS) objective function relating $\frac{\partial G\left(T,\delta ,\mathbf{x}\right)}{\partial \delta }$ and $G\left(T=0\right)$ as constructed in previous work (Wilson et al., 2023) and shown in Equation 18. We weight the error in the objective function such that the model cannot move too far away from the DFT localization but favors the deviation from experimental data to correct for temperature trends and curvature ($\left.{\omega }_1=0.1,{\omega }_2=0.9\right)$.

$Error={\omega }_1{\displaystyle \sum _{DFTdata}}{\left(G^{\text{soln}}\left(T=0\right)-E_{\text{DFT}}\right)}^2+{\omega }_2{\displaystyle \sum _{\mathit{exp}data}}{\left(-\frac{\partial G^{\text{soln}}}{\partial \delta }-{\mu }_{\exp }\right)}^2(18)$

Ground truth model construction, data generation using einstein solid, and error determination

In this section we discuss the construction of an invertible data set by selecting end member reduction energies, imposing a temperature dependence and randomly selecting excess terms. We generate “data points” from the ground truth model with random noise added. We generate a temperature dependent heat capacity ($C_p^{\text{Ein}}$) using the Einstein solid model Rogers (2005) as shown in Equation 19. ${\theta }_T$ is varied for each hypothetical material, as Figure 2 (top) shows. We use N = 5 (for ABO₃) or N = 4.5 (for ABO_2.5) to construct the endmember heat capacity. To both simplify and extract specific $C_p$ parameters, we performed a fit of an empirical heat capacity ($C_p^{\text{Emp}}$), Equation 20, to ($C_p^{\text{Ein}}$) as shown in Figure 2 (bottom), thus, deriving the ground truth parameters utilized in the reduction thermodynamic model in the form of a CEF model. The fit of the empirical model to the Einstein heat capacity ($\left.C_p^{\text{Ein}}\right)$ results in a maximum difference in heat capacities of <1 J/mol in the temperature range of interest (>300 K), Supplementary Figure S1 found in the SI. Using the empirical fit enables a direct comparison of the underlying heat capacity and the extracted models. Given that the difference between $C_p^{\text{Ein}}$ and ${\mathrm{C}}_{\mathrm{p}}^{\text{Emp}}$ is essentially 0 and this enables direct comparison, we choose to model the heat capacities with the empirical fit, ${\mathrm{C}}_{\mathrm{p}}^{\text{Emp}}$.

$C_p^{\text{Ein}}=3N{k}_b{\left(\frac{{\theta }_T}{T}\right)}^2\frac{\mathit{exp}\left(\frac{{\theta }_T}{T}\right)}{{\left(\mathit{exp}\left(\frac{{\theta }_T}{T}\right)-1\right)}^2}(19)$

${\mathrm{C}}_{\mathrm{p}}^{\text{Emp}}=A+BT+C{T}^2+D{T}^3+\frac{E}{T^2}(20)$

Figure 2

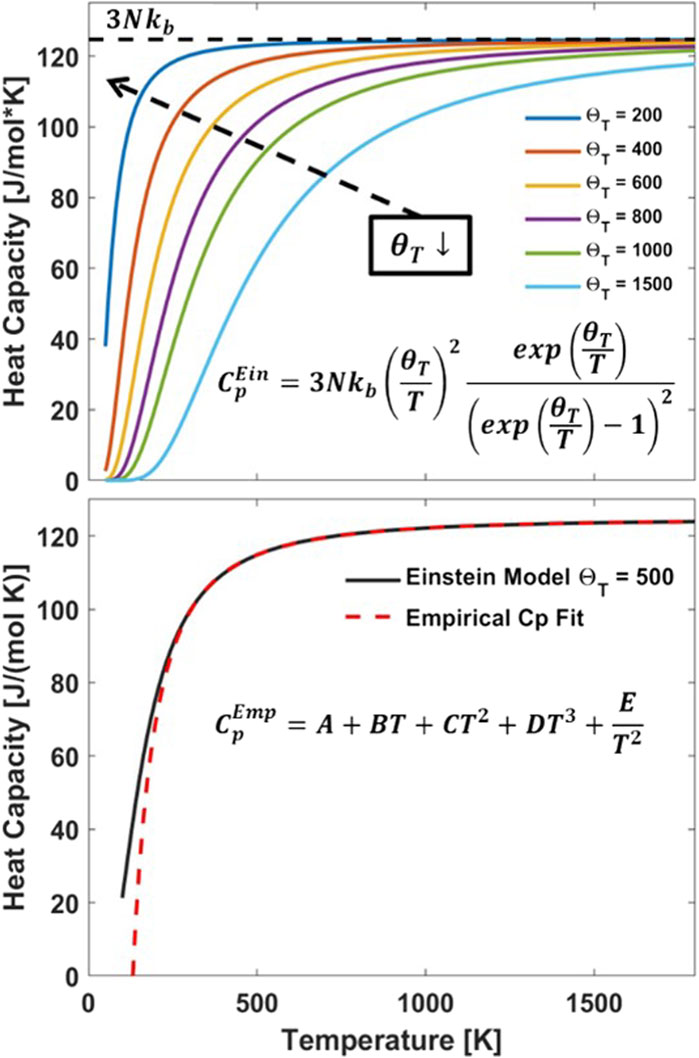
Figure 2. (top) Einstein heat capacity ($\left.C_p^{\text{Ein}}\right)$ dependence on T and ${\theta }_T$. Higher ${\theta }_T$ means $C_p^{\text{Ein}}$ reaches theoretical maximum (3Nk_b) faster. (bottom) empirical heat capacity $\left(C_p^{\text{Emp}}\right)$ fit to $C_p^{\text{Ein}}$ at ${\theta }_T$ = 500.

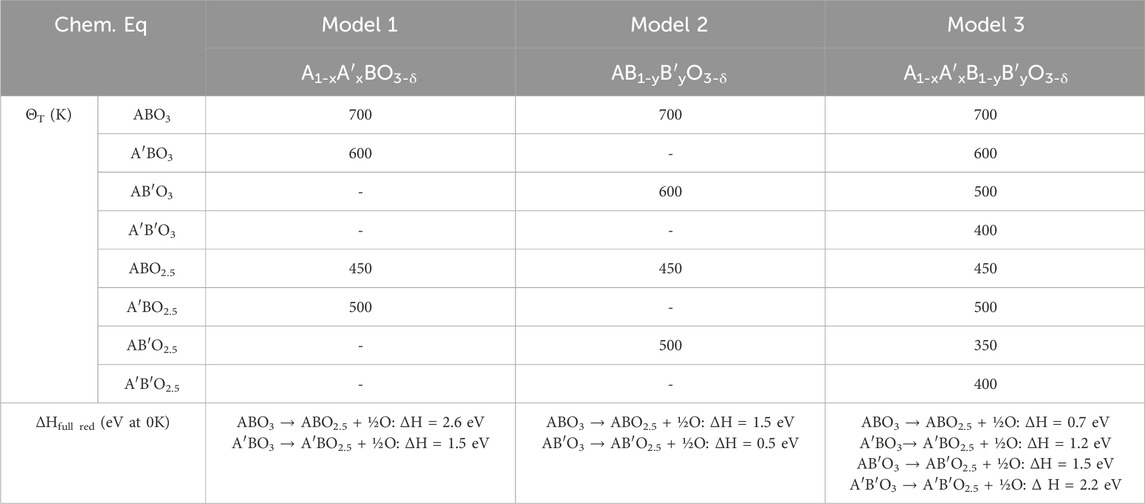
We generated three different ground truth models based on three different materials with varying thermodynamic trends. The materials vary in three ways: 1) the substitutions on the A and B lattice, 2) the reduction energy values for the ternaries (ABO₃ →ABO_2.5), and 3) the temperature dependence (via ${\theta }_T$ as described below) for each ABO₃ or ABO_2.5 composition. Table 1 shows the selected values for reduction energy and ${\theta }_T$. We adjust the Einstein temperature values for each material to mimic different heat capacities for materials with different compositions and reduction extents. To impart non-linearities in δ, we adopt interaction terms between sublattices along the lines of the CEF as it is a more extensive model and enables direct invertibility. Without the use of these interaction terms, one would need to model $C_p^{\text{Ein}}$ for every mol fraction and δ value in the desired data set size.

Table 1

Table 1. Ground truth $C_p^{\text{Ein}}$ $\left({\theta }_T\right.$) and reduction energy settings for generated models.

We construct the first model material, Model 1, with reduction enthalpies in a range (1.5–2.2 eV) that enables thermochemical water or CO₂ splitting (WS/CDS) with compositional variation on the A sublattice only. We selected the reduction energy values for the unsubstituted and fully substituted material such that the material becomes easier to reduce as x increases from zero to one. The second, Model 2, represents a thermochemical energy storage (TCES) material with lower reduction energies (0.5–1.5 eV) than Model 1. The Model 2 material has substitutions on the B sublattice such that the reduction energy decreases as y increases from zero to one. The final material, Model 3, is a quinary material with compositional variation on both the A and B sublattices. This material’s reduction energies increase from 0.7 to 2.2 eV as x and/or y increases from zero to one.

We randomly select three L terms to include in the model as the controlling excess terms. The SI contains the full list of possible L terms. We include three excess terms as previously done in our earlier work (Wilson et al., 2023; Wilson and Muhich, 2024), which fit real data but showed overfitting characteristics when using more than three excess terms. We did not investigate selecting more or fewer controlling terms, as doing so would only complicate or simplify the model’s curvature without altering the VH/CEF comparison. Selecting fewer or more excess terms to represent the ground truth model would simply create a different material altogether. Further investigation into the CEF functional form and its intricacies is left to future work. A normal distribution with a mean of zero and a standard deviation of 1 × 10⁻³ kJ/mol defines the parameters. Randomly selecting excess terms can result in some constructed models being wildly unphysical. Although we could have fit these hypothetical materials, inaccuracies would obscure whether the method is flawed or the thermodynamic trends are unreasonable. Therefore, we constructed 50 random perturbations and randomly selected models from the physically reasonable constructions. The chosen models met expected physical criteria: 1) ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ are positive from δ = 0–0.5; 2) ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ temperature dependence at any δ value is <0.1 kJ/K; 3) $\frac{{\partial }^2{H}_{red}}{\partial {\delta }^2}\left(0\le \delta \le 0.5\right)$ crosses zero at most once (i.e., the ${\frac{\partial H}{\partial \delta }}_{red}$ curve does not oscillate).

We added random noise in the δ dataset generated from the model thermodynamics to simulate experimental error. The random deviations were based on a normal distribution with a mean of zero and a standard deviation set to a desired noise value. For the work here, we consider two noise (standard deviation) values: 1 × 10⁻³ and 2 × 10⁻³.

To quantify the accuracy of VH and CF-CEF methods, we first determine the average and standard deviation of ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ across the temperature range of the ground truth data. Next, we calculate the absolute error relative to the average ground truth ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ value at each constant δ value considered using the VH method. Then we average the errors across all δ values to determine the average absolute ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ errors for each composition x. Although the CF-CEF method includes temperature dependence, for consistency, we compare only the averages of the ground truth thermodynamics to the average CF-CEF predicted thermodynamics across the temperature range of the data. While we report the error for the CF-CEF at the same mole fractions as VH, it is important to note that the CF-CEF method produces results for all compositions, T, and δ values.

Results and discussion

For each hypothetical material, the CF-CEF method outperforms the VH analysis, having error values of tens of kJ/mol or J/Kmol for enthalpy and entropy, respectively. The VH method was inconsistent in either over or underestimating both ${\frac{\partial H}{\partial \delta }}_{red}$ and $\frac{\partial S}{{\delta }_{red}}$ across most compositions tested, having absolute errors on the order of multiple tens of kJ/mol or J/Kmol, respectively. This section first discusses the base case Model 1, the water splitting material. It then examines the effect of the underlying thermodynamics through the other two test cases. The TCES material case, Model 2, is an example of where VH should perform well, being that it has smaller compositional and off-stoichiometric dependency. Lastly, we investigate a complex material varying in x and y with curvature in the reduction enthalpy. Then we consider the effect of varying the noise and quantity of the hypothetical experimental data.

Dependence of underlying thermodynamics on the effectiveness of VH and CEF

Base case model 1

Model 1 compares the CF-CEF and VH model performance of a hypothetical WS/CDS material varying in composition on the A sublattice only (${\mathrm{A}}_{1-\mathrm{x}}{\mathrm{A}}_{\mathrm{x}}^{\prime }{\text{BO}}_{3-\mathrm{\delta }}$). Figure 3 shows the ground truth thermodynamic trends with solid lines across the mole fractions x equal zero to one in 0.2 increments. The excess L terms, randomly selected for this model, are L8, L68, and L74; L8 accounts for an interaction on the A sublattice while L68 and L74 account for interactions on the oxygen sublattice. TpOX data from the ground truth thermodynamics of this model was generated from six evenly spaced points: T = [800, 1,000, 1,200, 1,400, 1,600, 1800] K, x = [0, 0.2, 0.4, 0.6, 0.8, 1.0], and pO₂ = [1 × 10⁻¹⁰, 7.32 × 10⁻⁹, 5.36 × 10⁻⁷, 3.92 × 10⁻⁵, 2.87 × 10⁻³, 0.21] Bar. We note that the pO₂ points are evenly distributed in logspace. The unique TpOX combinations resulted in 107 total data points after removing TpOX points that resulted in δ < 0.005 or δ > 0.495 as it is difficult to accurately measure δ < 0.005, and materials are likely to decompose at δ > 0.495. Additionally, we duplicated the data by, and separately added in noise with a standard deviation of 1 × 10⁻³ to simulate multiple samplings of experimental data collection.

Figure 3

Figure 3. Generated water (or CO₂) splitting material, Model 1, ground truth thermodynamic trend (solid), and model fits to the ground truth data with standard deviation noise of 1 × 10^-3 added to δ to simulate experimental error, CF-CEF (dashed), VH (circles).

We individually extracted the ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ of the WS/CDS hypothetical material using the VH method at each mol fraction x in the generated data set. Figure 3 (black dashed lines) and Figure 4 (left) show the predicted thermodynamic trends. The VH method estimates ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ at all δ values having an average absolute error across δ of 38 ± 28 kJ/mol O and 20 ± 16 J/mol O K $,$ respectively. Table 2 displays the complete, unaveraged error analysis for every mole fraction x. Overall, the VH method performs poorly with a large absolute average error, comparatively, for both ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ and large deviations in that error. These large errors would likely lead to mis-categorizing materials as good (or bad) performers for the WS/CDS application. Thus, in this case, VH is not a reliable or consistent measure for the reduction of thermodynamic determination.

Figure 4

Figure 4. (Left) Enthalpy (top) and Entropy (bottom) of reduction thermodynamics prediction by VH analysis for Model 1. (Right) Enthalpy (top) and Entropy (bottom) of reduction thermodynamics prediction by CF-CEF method for Model 1.

Table 2

Table 2. Model 1 error in CF-CEF and VH analysis.

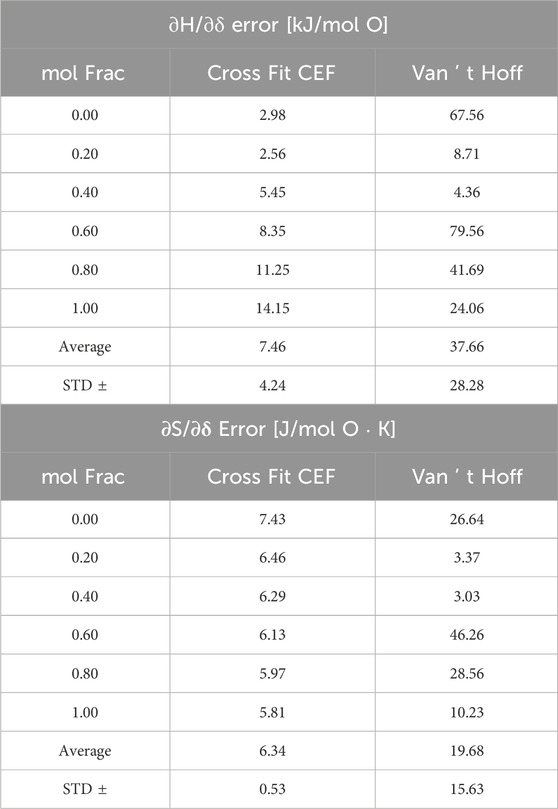
The CF-CEF method predicts the thermodynamics of Model 1 much more accurately than the VH method with an error of only 7 ± 4 kJ/mol O and 6 ± 0.5 J/mol O K for ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$, respectively. Table 2 shows the complete error analysis for the CF-CEF predictions for compositions used in the VH analysis. Furthermore, the CF-CEF produces a model as a function of x, T, and δ as compared to VH trends that are only a function of δ. Therefore, the CF-CEF yields a more complete thermodynamic picture of the hypothetical WS/CDS material as Figure 4 (right) shows.

Using the CF-CEF method, we can make a direct comparison between the optimized and ground truth constructed model parameters. The excess terms found in CF-CEF method are L8, L22, and L68. The linear combination of the CF-CEF excess terms is different by one term, predicting L22 instead of the ground truth term L74. However, the linear combination of the ground truth excess terms as compared to the optimized CF-CEF excess terms has a max difference of ∼20 kJ/mol at T = 1200K. We find that the temperature dependence difference in excess terms $\left(\frac{\partial \left(\partial G^{excess}\right)}{\partial \delta \partial T}\right)$ is negligible (<1 kJ/mol). Figure 5(top) shows similar curvature in the linear combination of excess terms. while Figure 5 (bottom) shows the absolute difference in excess free energy at T = 1200K. As discussed in previous work (Wilson et al., 2023), the excess free energy primarily influences the curvature of the total free energy surface and generally contributes ≤10% to the total. We hypothesize that this difference arises because the CF-CEF method fits the endmember terms separately from the excess terms leading to some curvature dependence across x and δ being captured by the endmember fit parameters. To test this hypothesis, we held the endmember parameters constant at the ground truth values and optimized only the excess terms. In this case, the CrossFit method yielded the exact same excess terms as the ground truth model.

Figure 5

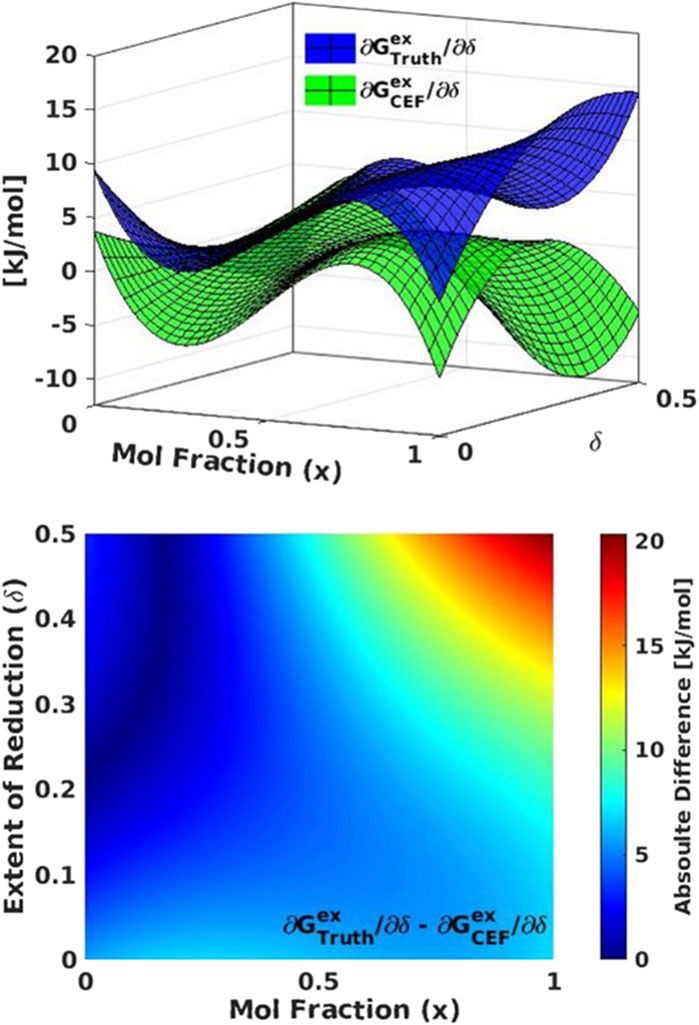
Figure 5. Model 1 comparison of (top) excess free energy (Gex) for the ground truth (blue) compared to the CF-CEF derived excess free energy (green). (bottom) The absolute difference between Gex for the ground truth and CF-CEF models.

Effectiveness of the methods on model two data

To ensure that the better performance of the CEF over the VH method was not coincidental, we generated and analyzed additional data sets. Model 2 compares the CF-CEF and VH model performance of a hypothetical TCES material varying in composition on the B sublattice only (${\text{AB}}_{1-\mathrm{y}}{\mathrm{B}}_{\mathrm{y}}^{\prime }{\mathrm{O}}_{3-\mathrm{\delta }}$). This TCES material is meant to be one that easily reduces (reduction eV≤1.5 eV). Thus, an experimentalist would be able to measure δ values at more easily accessible T and pO₂ points (T values <1000 K and pO₂ > 1 × 10⁻²) than that for WS/CDS. Therefore, we construct this material to maximize the likelihood that the VH analysis could accurately extract the thermodynamics, even with a simplistic defect model.

Figure 6 shows the ground truth thermodynamic trends as solid lines across the mole fractions x = 0, 0.2, 0.4, 0.6, 0.8, 1.0. The randomly selected excess L terms are L35, L43, and L51. We generated TpOX data from six evenly spaced points in each: T = [400, 560, 720, 880, 1,040, 1,200] K; x = [0, 0.2, 0.4, 0.6, 0.8, 1.0]; and pO₂ = [1 × 10⁻², 1.84 × 10⁻², 3.38 × 10⁻², 6.21 × 10⁻², 0.11, 0.21] Bar, again evenly distributed in log space. Following the same process as Model 1, we generated 266 data points (133 unique TpOX points with replicated random noise) with 0.005 < δ < 0.495.

Figure 6

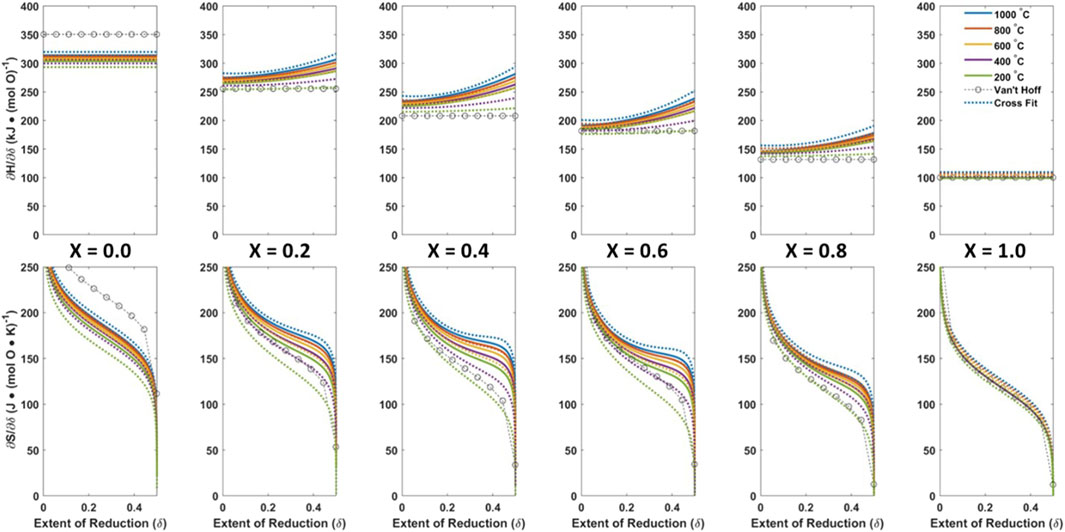
Figure 6. Generated TCES splitting material, Model 2, ground truth thermodynamic trend (solid), and model fits to the ground truth data with standard deviation noise of 1 × 10^-3 added to δ to simulate experimental error, CF-CEF (dashed), VH (circles).

Table 3 shows the errors in the VH and CF-CEF methods. VH extracted thermodynamics display average errors of 24 ± 13 kJ/mol O and 20 ± 12 J/mol O K ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$, respectively, which are lower than the error found for materials from Model 1. The lower error was expected because it provided a greater number of data points. Although this error is lower, the expected variation in the error is approximately 60% of the error itself, again indicating the non-systematic nature of the error.

Table 3

Table 3. Model 2 errors in CF-CEF and VH analysis.

Even with a material designed for easy thermodynamic extraction by VH analysis, the CF-CEF method outperforms it in predicting ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$. The CF-CEF produced model achieved an error of only 6 ± 2 kJ/mol O and 9 ± 5 J/mol O K ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$, respectively. Thus, the CEF had one-third to one-sixth the error of the VH method on the same data. The CrossFit method converged to L33, L35, and L49 as the three-contributing excess terms. One of the three ground truth excess terms, L35, match. Again, as with the Model 1 case, we compare the linear combinations of excess terms between the ground truth and the CF-CEF terms. Figure 7 illustrates similar trends between models and a maximum difference in excess free energy of <3 kJ/mol at T = 800K. We can attribute this small mismatch to the optimization of the endmember parameters as discussed with Model 1. Again, we verified the attribution to the decoupled optimization scheme when holding the endmember parameters constant at the ground truth value and the CrossFit method converges to the same excess terms. Despite errors in capturing the excess terms, the thermodynamic data extracted by the CEF fits very well.

Figure 7

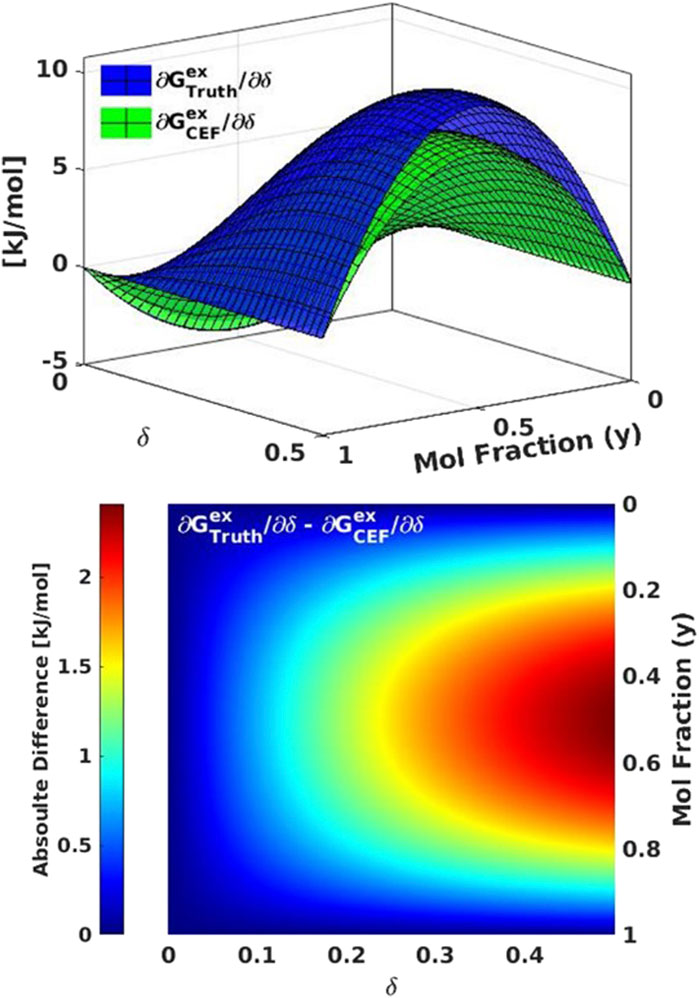
Figure 7. Model 2 comparisons of (top) excess free energy (Gex) for the ground truth (blue) to the CF-CEF derived excess free energy (green). (bottom) The absolute difference between Gex for the ground truth and CF-CEF models.

Effectiveness of the methods on model 3 data

Model 3 compares the CF-CEF and VH model performance of a complex hypothetical quinary material that varies in composition on the A and B sublattices ($\left.{\mathrm{A}}_{1-\mathrm{x}}{\mathrm{A}}_{\mathrm{x}}^{\prime }{\mathrm{B}}_{1-\mathrm{y}}{\mathrm{B}}_{\mathrm{y}}^{\prime }{\mathrm{O}}_{3-\mathrm{\delta }}\right)$. The thermodynamic trends of this material are complex and change significantly with variations in x and y. The SI shows all ground truth thermodynamic trends as solid lines across the mol fractions x = 0, 0.2, 0.4, 0.6, 0.8, 1.0 and y = 0, 0.2, 0.4, 0.6, 0.8, 1.0, resulting in 36 compositions. Figure 8 shows the best and worst fits, for simplicity, derived from the VH method compared to CF-CEF. The excess L terms, randomly selected, are L27, L42, and L74. We generated the TpOX points from the thermodynamics of this model with six evenly spaced variables: T = [800, 1,000, 1,200, 1,400, 1,600, 1800] K, x and y = [0, 0.2, 0.4, 0.6, 0.8, 1.0], and pO₂ = [1 × 10⁻¹⁰, 7.32 × 10⁻⁹, 5.36 × 10⁻⁷, 3.92 × 10⁻⁵, 2.87 × 10⁻³, 0.21] Bar. The result is a total of 1,582 data points (791 unique TpOX points, with two sets of random noise added) following the same process as Model 1.

Figure 8

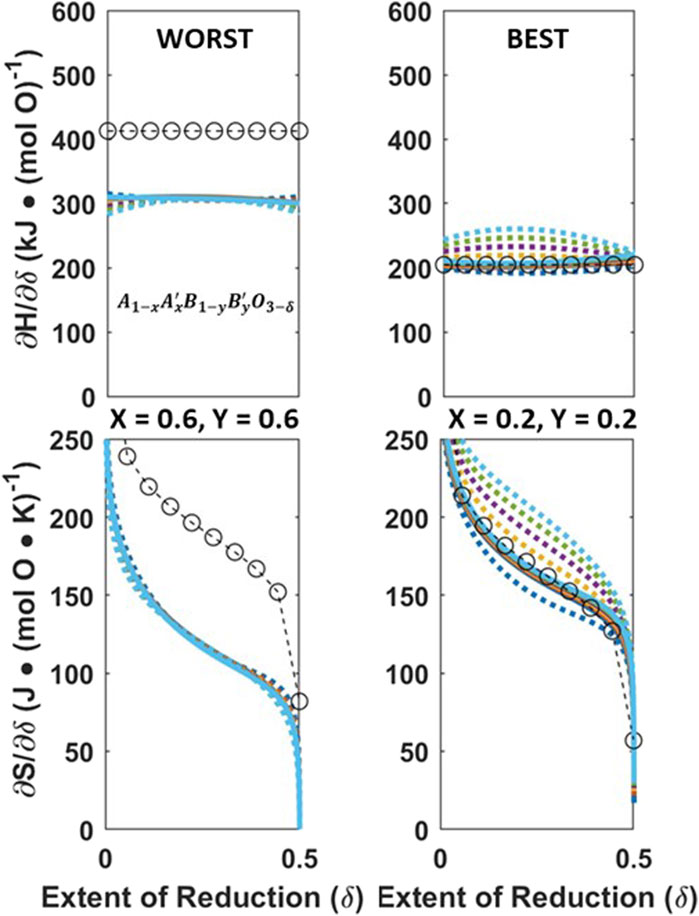
Figure 8. Worst (left) and best (right) VH fit (circles) to Model 3, $A_{1-x}{A}_x^{\prime }{B}_{1-y}{B}_y^{\prime }{O}_{3-\delta }$, ground truth (solid) compared to CF-CEF fits (dashed).

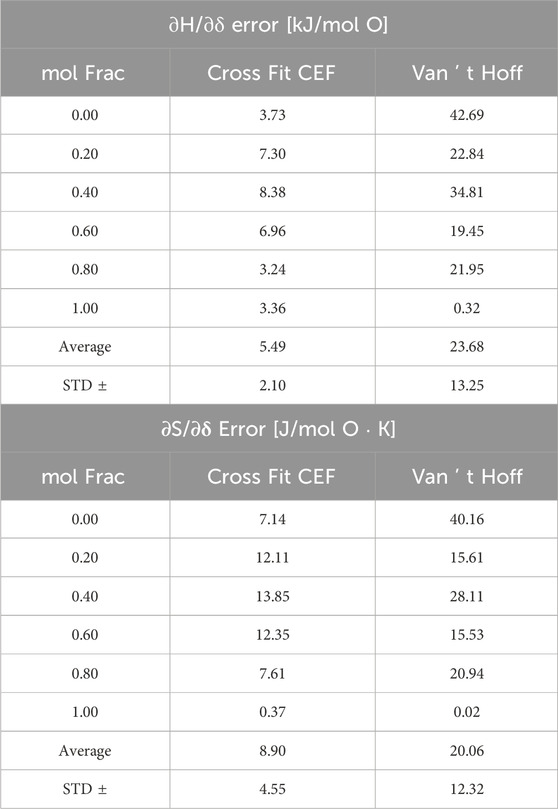
The error for VH across all 36 compositions can be found in the SI, Tabel SI-1, and achieved an average accuracy of 40 ± 28 kJ/mol O and 29 ± 22 J/mol O K ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ respectively across all compositions. With this material family, VH analysis varied in accuracy extensively with some compositions having errors as high as 105 kJ/mol O and 70 J/mol O K for ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ respectively. At best, the VH analysis achieved an error of 3 kJ/mol O and 4 J/mol O K, ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ respectively. Again, the variability in accuracy is a major challenge as it suggests large uncertainty as to the accuracy of any extracted data set.

The CF-CEF method achieved an average error of 17 ± 10 kJ/mol O and 9 ± 5 J/mol O K ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ respectively for Model 3. The CrossFit method converged to L27, L42, and L76 as the three contributing excess terms. Two of the three ground truth excess terms, L27 and L42 match those of the true ground state model and the linear combinations of excess terms had a max difference in free energy of ∼30 kJ/mol. The dimensionality of the excess free energy prevents visualization of the free energy surface (a function of x, y and δ), nonetheless, SI Supplementary Figures S1-8 shows a 3-D volume plot of the difference between the ground truth and CF-CEF excess free energy. The CF-CEF method performs consistently across all compositions with Model 3 having a maximum absolute error of 36 kJ/mol O and 21 J/mol O K for ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red},$ respectiviely, which significantly outperforms the VH approach. Thus, as material complexity increases, VH gets substantially worse, but the CEF retains accuracy.

Noise sensitivity

We next examine the sensitivity of both the CF-CEF and VH models to noise in the data by doubling the normally distributed random valuations used in creating the data. Here, we use only the base case Model 1 for the invertible data set. We regenerated data at the same TpOX points as done with Model 1 but with a normal distribution of noise double that used for Model 1. The error in the CF-CEF method is effectively unchanged by additional noise in the data with a difference of <1 kJ/mol O and J/mol O K, ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ respectively from the lower noise dataset fit. Conversely, the VH model absolute error increases by 8 kJ/mol O on average in ${\frac{\partial H}{\partial \delta }}_{red}$ to 45 kJ/mol and by 10 J/mol O K to 29 J/K mol O in ${\frac{\partial S}{\partial \delta }}_{red}$. Table 4 lists the new error values at every mol fraction for the increased noise in the data. Thus, small increases in noise have a larger effect on VH than the CEF method.

Table 4

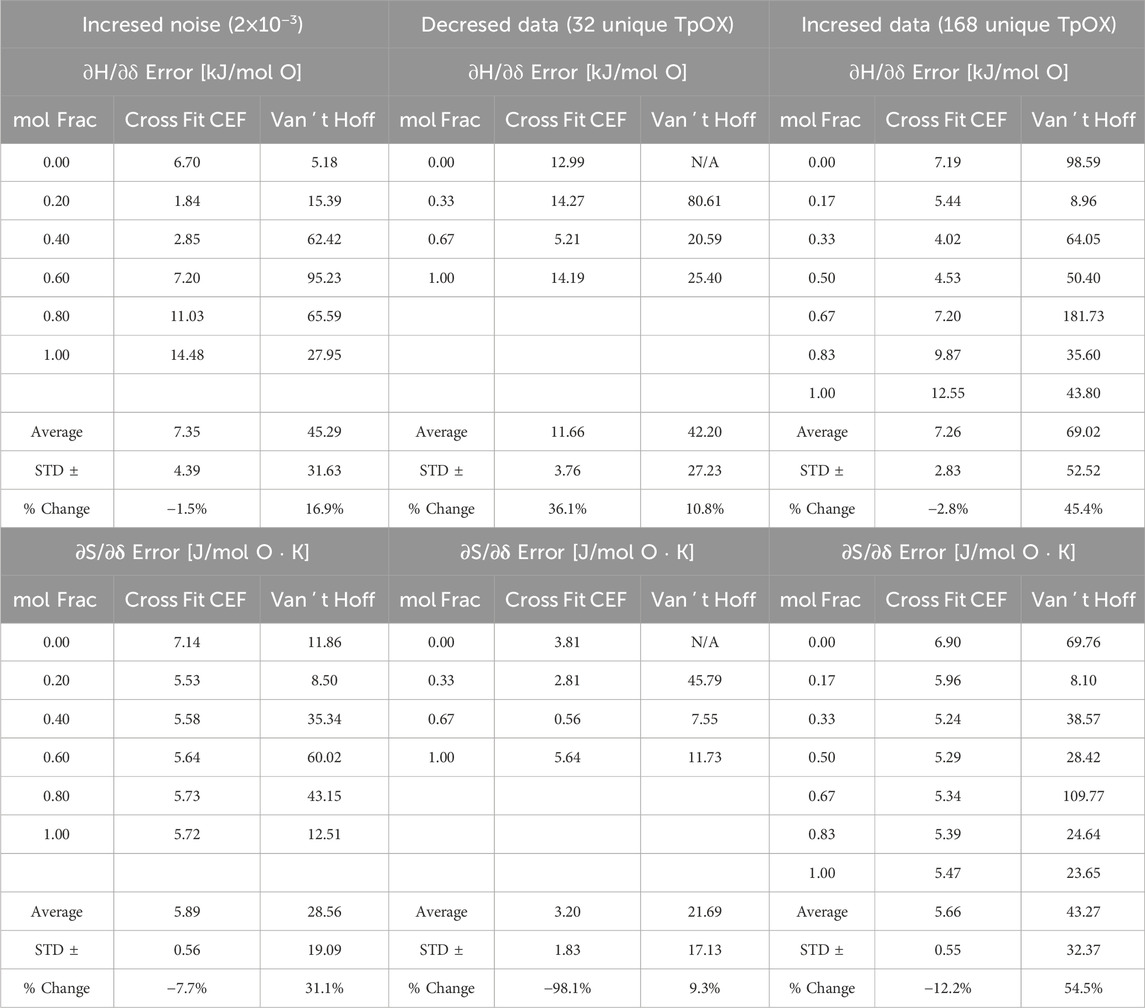
Table 4. Model 1 error in CF-CEF and VH analysis. (left) Nosie in data doubled, (middle) decrease in data available, (right) increase in data available. Percent change is relative to the average errors reported in Table 2.

Data amount sensitivity

The sensitivity of CEF and VH methods to the number of available data points is examined by altering the number of evenly spaced TpOX points on a mesh grid from six to either four or seven: T = [800, 1,133, 1,467, 1800] K, x = [0, 0.33, 0.67, 1.0], and pO₂ = [1 × 10⁻¹⁰, 1.28 × 10⁻⁷, 1.64 × 10⁻⁴, 0.21] or T = [800, 967, 1,133, 1,300 1,467, 1,633, 1800] K, x = [0, 0.17, 0.33, 0.50, 0.67, 0.83, 1.0], and pO₂ = [1 × 10⁻¹⁰, 3.58 × 10⁻⁹, 1.28 × 10⁻⁷, 4.58 × 10⁻⁶, 1.64 × 10⁻⁴, 5.90 × 10⁻³, 0.21] respectively. After applying the off-stoichiometry restrictions of 0.005 < δ < 0.495, the mesh grid of four TpOX resulted in 32 unique points and the mesh grid of seven points resulted in 168 unique points, ∼30% or ∼168% percent de/increase, respectively, in TpOX points from the original dataset. Again, we duplicated the data with the noise standard devotion equal to 1 × 10⁻³ as previously discussed for Model 1. Table 4 lists the new error values at every mol fraction for the changes in mesh grids of the data generated.

As expected, with less data available the error in ${\frac{\partial H}{\partial \delta }}_{red}$ increased in both models by +4 kJ/mol O CF-CEF and VH analysis. The ${\frac{\partial S}{\partial \delta }}_{red}$ predicted by the CF-CEF method had a smaller error decreasing by 3.1 J/mol O K while VH analysis error increased in ${\frac{\partial S}{\partial \delta }}_{red}$ by 2 J/mol O K. While the CF-CEF method shows a consistent increase in the error across all mol fractions with less available data, VH analysis shows an inconsistent response with varying the maximum and minimum errors achieved at various compositions and number of data points as compared to the base case Model 1.

Again, as expected, in the case with more data available, the error in ${\frac{\partial H}{\partial \delta }}_{red}$ decreased in the CF-CEF, being −2 kJ/mol O, but increased by +31 kJ/mol O CF-CEF for van ‘t Hoff analysis respectively (7.26 and 69 kJ/mol O average error, respectively) almost doubling. The ${\frac{\partial S}{\partial \delta }}_{red}$ followed the same trend decreasing for CF-CEF and increasing for VH: −0.7 J/mol O K and +23 J/mol O K for the CF-CEF and VH analysis respectfully (5.66 and 43 kJ/mol O average error, respectively). In the CF-CEF method, the model is relatively unaffected, showing little change in average error across all x values while VH shows a notable fluctuation in the average error and standard deviation of error indicating markable sensitivity to the quantity of data specifically the unexpected trend of becoming worse on average with more data. In all, the CF-CEF method outperforms VH analysis and shows a more robust response to dataset sizes and noise. This finding is significant because it illustrates the unreliable nature of VH analysis and exemplifies the need to shift the practice of the metal oxide thermodynamics field towards a more robust thermodynamic modelling technique, such as the CF-CEF.

Statistical analysis of VH and CF-CEF methods on model 1

In this section we perform a statistical analysis of the VH and CF-CEF methods again utilizing Model 1 as the base case. First, we will discuss the linear models associated with VH analysis and their effects on the prediction of thermodynamic properties and replication of data. This will be followed by an analysis on the robust nature of the CF-CEF by analyzing 20 additional ground truth models. The additional ground truth models are constructed in the same fashion as was done with the Model 1 case albeit a different random selection of controlling excess terms therefore creating 20 unique models with different thermodynamic trends and properties.

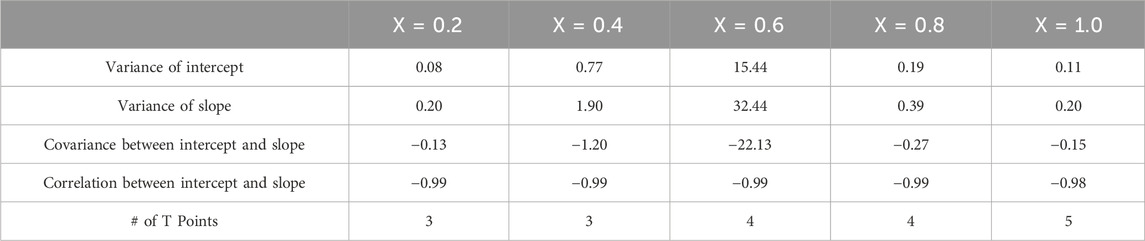
Table 5 shows the statistical values of intercept variance, slope variance, slope/intercept covariance, correlation, and number of points for each fit $K_T$ for Equation 13. Note x = 0 is not present in Table 5 as there were only 2 T data points at that mol fraction leading to a perfect linear fit. The covariance of the linear models is of interest as non-zero values indicate dependence between the slope and intercept. For example, if the data has a specific range and mean, changes in the estimate of the slope is compensated by adjustments in the intercept to maintain the overall fit of the regression line (i.e., the tradeoff between the predicted enthalpy and entropy of reduction). This compensation is apparent in the fit of $K_T$ at x = 0.6 in Model 1. Of note, however, is how well the defect model fits the δ data but still has large errors in enthalpy and entropy of reduction, shown in Figure 9. Conversely, the linear fit of $K_T$ at x = 1.0 is almost perfect, leading to good predictions of enthalpy and entropy of reduction, but poor recreation of the δ data. This inconsistency and trade-off is the achilleas heal of VH analysis which the CF-CEF method mitigates.

Table 5

Table 5. Statistical analysis of K_T fits for VH at mol fractions x = [0.2,0.4,0.6,0.8,1.0].

Figure 9

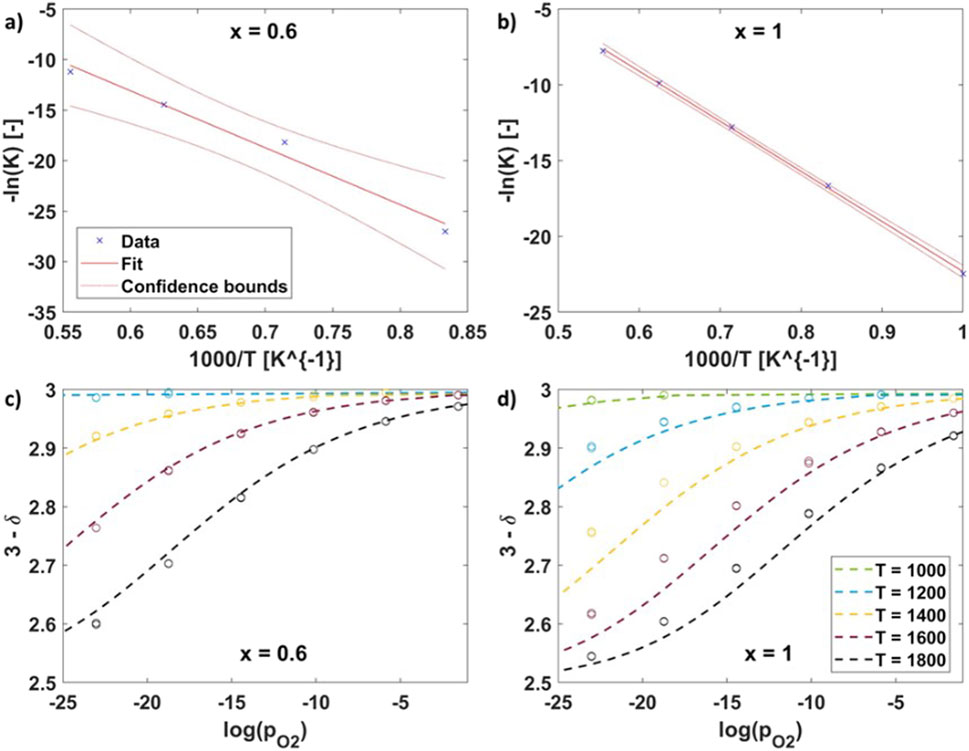
Figure 9. (A, B) linear regression of defect model to find K_T for x = 0.6 and x = 1.0 respectively) and (C, D) defect models (dashed lines) based on extracted K_T for x = 0.6 and x = 1.0 respectively.

The CF-CEF method was evaluated on 20 additional variations of Model 1. The enthalpy and entropy of reduction error is evaluated across an extremely fine mesh of 125,000 TpOX points derived from the same T, P, and X bounds of Model 1. The cumulative distribution function (CDF) of each model is plotted in Figure 10. The CDF is a fundamental concept in probability and statistics that applies to any type of distribution, whether unimodal, bimodal, or multimodal. The CDF indicates probabilities F(X) of finding value X at or below F(X). We apply the CDF to the mean absolute error (MAE) of enthalpy and entropy of reduction as well as the precited δ value at all 125,000 TpOX points. We show that the MAE across 125,000 data points for each of the 20 CF-CEF has an error ranging 3.35–10.95 kJ/mol O and 2.52–8.97 J/mol O K of enthalpy and entropy of reduction respectively. Furthermore, 90% of the MAE is ≤20 kJ/mol O for reduction enthalpy and ≤17 J/mol O K for reduction entropy. The long tails of the CDF exist due to some outlier points of the model predicting incorrect values at the large delta extremes of the ground truth model (i.e., δ > 0.48). The outliers represent <1% of the total 125,000 data points. Similarly, the CDF of the CF-CEF error in predicting δ for each of these models is very low where over 99.99% of the predicted δ values is <1 × 10⁻², as shown in Figure 10C inlay. Note these errors are near the imposed noise level of 1 × 10^-3 indicating that the CF-CEF method has a superior ability in predicting reduction thermodynamics and delta values accurately.

Figure 10

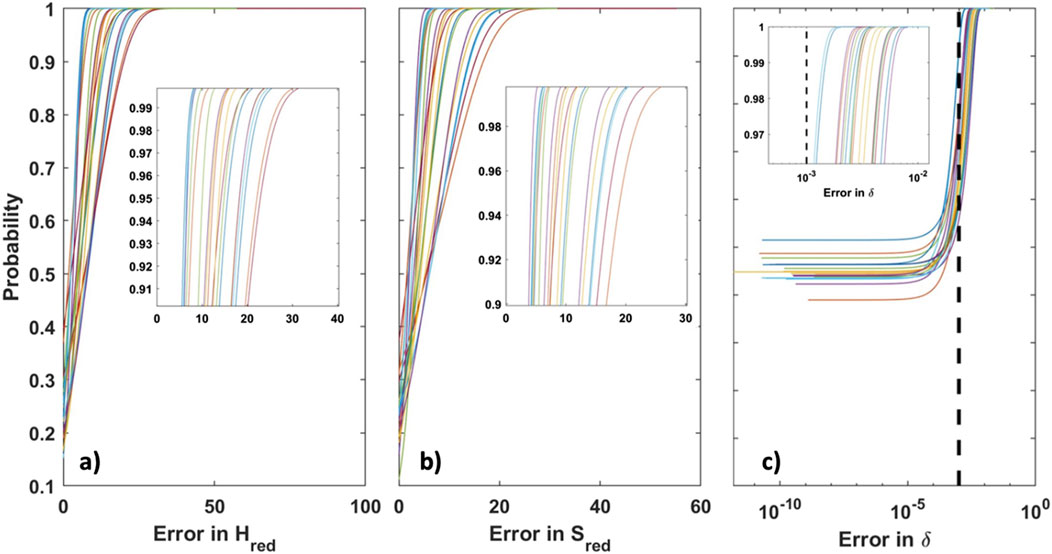
Figure 10. (A) CDF of MAE of enthalpy of reduction (Hred) for 20 models. (B) CDF of MAE of entropy of reduction (Sred) for 20 models. (C) CDF of MAE of predicted δ for 20 models plotted on a log scale. Blacked dash line represents the imposed noise in δ. Inlays are included for each plot for ease of visualization of probability values 0.9–1.0.

Conclusion

Overall, this work demonstrates that the linearized VH approach is insufficient for reliably extracting thermodynamic information from TGA data. In contrast, the CF-CEF method proves to be highly accurate, offering a comprehensive thermodynamic picture (i.e., ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ as a function of mole fraction, T and δ). In all cases tested, the CF-CEF method outperforms VH analysis, with errors of at most, tens of kJ/mol O or J/mol O K for ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$ respectively. Conversely, the VH method exhibits errors 2–5 times higher than that of CF-CEF. We find that VH analysis performs better on lower enthalpy materials often where there is more TpOX data. The CF-CEF method consistently performs well across varying levels of thermodynamic complexity, whereas the VH method is only effective for the simplest material. Additionally, the CF-CEF method shows minimal sensitivity to dataset size or noise with average variations of less than 5 kJ or J in ${\frac{\partial H}{\partial \delta }}_{red}$ and ${\frac{\partial S}{\partial \delta }}_{red}$, respectively. Although larger datasets with multiple temperature points temperature points should improve VH fits, they still underfund and widely vary as compared to the CF-CEF method. Furthermore, the CF-CEF method provides a model that accounts for composition, T, and δ. Overall, this work quantifies the errors associated with VH analysis and highlights the robustness of the CF-CEF methodology. Moving forward, researchers should use the more robust CEF method for thermodynamic extraction. To this end, the development of a generic, open-source, and user-friendly interface for the CF-CEF would greatly benefit the field by enabling simple and reliable thermodynamic data extraction.

Associated content

Contains Cp model comparisons. A list of Redlich-Kister expansion of $\mathcal{L}$ terms. A table of errors for Model 3 and Model 3 thermodynamic plots versus van ‘T Hoff analysis for the same dataset.

Data availability statement

The datasets presented in this study can be found in online repositories in online repositories found on GitHub on the MuhichLab repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author contributions

SW: Conceptualization, Data curation, Formal Analysis, Investigation, Writing–original draft. PS: Formal Analysis, Writing–original draft. ES: Writing–review and editing. CM: Writing–review and editing, Supervision.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Department of Energy Computational Science Graduate Fellowship under Award Number DE-SC0022158. This work is also supported by the U.S. Department of Energy’s Energy Efficiency & Renewable Energy office under Award Number DE-EEDE-EE0010732. This material is partially based upon work supported by the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, specifically the Hydrogen and Fuel Cell Technologies Office through the HydroGEN Advanced Water Splitting Materials Consortium as well grant DE-EE0010733.

Acknowledgments

All fitting calculations were conducted in MATLAB^© 2021a. The authors gratefully acknowledge Research Computing at Arizona State University (Jennewein et al., 2023) for providing HPC resources that have contributed to the research results reported within this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1470010/full#supplementary-material

Refernces

Abraham, A., Schoenitz, M., and Dreizin, E. L. (2016). Energy storage materials with oxide-encapsulated inclusions of low melting metal. Acta Mater. 107, 254–260. doi:10.1016/j.actamat.2016.01.074

CrossRef Full Text | Google Scholar

Ahmad, Y. H., Mohamed, A. T., Kumar, A., and Al-Qaradawi, S. Y. (2021). Solution combustion synthesis of Ni/La2O3 for dry reforming of methane: tuning the basicity via alkali and alkaline earth metal oxide promoters. RSC Adv. 11, 33734–33743. doi:10.1039/D1RA05511A

PubMed Abstract | CrossRef Full Text | Google Scholar

Arifin, D., Ambrosini, A., Wilson, S. A., Mandal, B., Muhich, C. L., and Weimer, A. W. (2020). Investigation of Zr, Gd/Zr, and Pr/Zr – doped ceria for the redox splitting of water. Int. J. Hydrogen Energy 45, 160–174. doi:10.1016/j.ijhydene.2019.10.177

CrossRef Full Text | Google Scholar

Babiniec, S. M., Coker, E. N., Miller, J. E., and Ambrosini, A. (2015). Investigation of La Sr1−Co M1−O3− (M = Mn, Fe) perovskite materials as thermochemical energy storage media. Sol. Energy 118, 451–459. doi:10.1016/j.solener.2015.05.040

CrossRef Full Text | Google Scholar

Barry, T. I., Dinsdale, A. T., Gisby, J. A., Hallstedt, B., Hillert, M., Jansson, B., et al. (1992). The compound energy model for ionic solutions with applications to solid oxides. J. Phase Equilibria 13, 459–475. doi:10.1007/BF02665760

CrossRef Full Text | Google Scholar

Bayon, A., Hashimoto, J., and Muhich, C. (2021a). Advances in chemical engineering. Editor W. Lipiński (Academic Press), 58, 55–90.

CrossRef Full Text | Google Scholar

Bayon, A., Hashimoto, J., and Muhich, C. (2021b). “Fundamentals of solar thermochemical gas splitting materials,” in Advances in chemical engineering, 58. Elsevier, 55–90. doi:10.1016/bs.ache.2021.10.006

CrossRef Full Text | Google Scholar

Bergeson-Keller, A. M., Sanders, M. D., and O’Hayre, R. P. (2022). Reduction thermodynamics of Sr_xCe_xMnO₃ and Ce_xSr_xMnO₄ perovskites for solar thermochemical hydrogen production. Energy Technol. 10, 2100515. doi:10.1002/ente.202100515

CrossRef Full Text | Google Scholar

Bork, A. H., Povoden-Karadeniz, E., Carrillo, A. J., and Rupp, J. L. M. (2019). Thermodynamic assessment of the solar-to-fuel performance of La0.6Sr0.4Mn1-yCryO3-δ perovskite solid solution series. Acta Mater. 178, 163–172. doi:10.1016/j.actamat.2019.07.022

CrossRef Full Text | Google Scholar

Brendelberger, S., Vieten, J., Roeb, M., and Sattler, C. (2019). Thermochemical oxygen pumping for improved hydrogen production in solar redox cycles. Int. J. Hydrogen Energy 44, 9802–9810. doi:10.1016/j.ijhydene.2018.12.135

CrossRef Full Text | Google Scholar

Bulfin, B., Lapp, J., Richter, S., Gubàn, D., Vieten, J., Brendelberger, S., et al. (2019). Air separation and selective oxygen pumping via temperature and pressure swing oxygen adsorption using a redox cycle of SrFeO3 perovskite. Chem. Eng. Sci. 203, 68–75. doi:10.1016/j.ces.2019.03.057

CrossRef Full Text | Google Scholar

Bulfin, B., Vieten, J., Starr, D. E., Azarpira, A., Zachäus, C., Hävecker, M., et al. (2017). Redox chemistry of CaMnO 3 and Ca 0.8 Sr 0.2 MnO 3 oxygen storage perovskites. J. Mater. Chem. A 5, 7912–7919. doi:10.1039/c7ta00822h

CrossRef Full Text | Google Scholar

Bush, H. E., Nguyen, N. P., Farr, T., Loutzenhiser, P. G., and Ambrosini, A. (2021). Air separation via a two-step solar thermochemical cycle based on (Ba,La)xSr1-xFeO3-δ: thermodynamic analysis. Solid State Ionics 368, 115692. doi:10.1016/j.ssi.2021.115692

CrossRef Full Text | Google Scholar

Cacciamani, G. (2016) An introduction to the calphad method and the compound energy formalism (CEF). Tecnologia em Metalurgia, Materiais e Mineração 13 (1), 16–24.

CrossRef Full Text | Google Scholar

Cai, R., Dou, J., Krzystowczyk, E., Richard, A., and Li, F. (2022). Chemical looping air separation with Sr0.8Ca0.2Fe0.9Co0.1O3-δ perovskite sorbent: packed bed modeling, verification, and optimization. Chem. Eng. J. 429, 132370. doi:10.1016/j.cej.2021.132370

CrossRef Full Text | Google Scholar

Chaires, J. B. (1997). Possible origin of differences between van't Hoff and calorimetric enthalpy estimates. Biophys. Chem. 64, 15–23. doi:10.1016/S0301-4622(96)02205-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Kubota, M., Yamashita, S., and Kita, H. (2021). Investigation of Sr-based perovskites for redox-type thermochemical energy storage media at medium-high temperature. J. Energy Storage 38, 102501. doi:10.1016/j.est.2021.102501

CrossRef Full Text | Google Scholar

De Souza, R. A. (2015). Oxygen diffusion in SrTiO3 and related perovskite oxides. Adv. Funct. Mater. 25, 6326–6342. doi:10.1002/adfm.201500827

CrossRef Full Text | Google Scholar

Fuks, D., Mastrikov, Y., Kotomin, E., and Maier, J. (2013). Ab initio thermodynamic study of (Ba, Sr)(Co, Fe) O 3 perovskite solid solutions for fuel cell applications. J. Mater. Chem. A 1, 14320–14328. doi:10.1039/c3ta12874a

CrossRef Full Text | Google Scholar

Gu, X.-K., Samira, S., and Nikolla, E. (2018). Oxygen sponges for electrocatalysis: oxygen reduction/evolution on nonstoichiometric, mixed metal oxides. Chem. Mater. 30, 2860–2872. doi:10.1021/acs.chemmater.8b00694

CrossRef Full Text | Google Scholar

Guo, Q., Geng, J., Pan, J., Zou, L., Tian, Y., Chi, B., et al. (2023). Brief review of hydrocarbon-reforming catalysts map for hydrogen production. Energy Rev. 2, 100037. doi:10.1016/j.enrev.2023.100037

CrossRef Full Text | Google Scholar

Hashimoto, J., Bayon, A., Tamburro, O., and Muhich, C. L. (2023). Thermodynamic and structural effects of Fe doping in magnesium manganese oxides for thermochemical energy storage. Energy and Fuels 37, 4692–4700. doi:10.1021/acs.energyfuels.2c04266

CrossRef Full Text | Google Scholar

Hillert, M. (1996). Some properties of the compound energy model. Calphad 20, 333–341. doi:10.1016/S0364-5916(96)00035-1

CrossRef Full Text | Google Scholar

Hillert, M. (2001). The compound energy formalism. J. Alloys Compd. 320, 161–176. doi:10.1016/S0925-8388(00)01481-X

CrossRef Full Text | Google Scholar

Hillert, M., and Staffansson, L. (1970). The regular solution model for stoichiometric phases and ionic melts. Acta Chem. Scand. 24, 3618–3626. doi:10.3891/acta.chem.scand.24-3618

CrossRef Full Text | Google Scholar

Hoes, M., Muhich, C. L., Jacot, R., Patzke, G. R., and Steinfeld, A. (2017). Thermodynamics of paired charge-compensating doped ceria with superior redox performance for solar thermochemical splitting of H2O and CO2. J. Mater. Chem. A 5, 19476–19484. doi:10.1039/C7TA05824A

CrossRef Full Text | Google Scholar

Jennewein, D. M., Lee, J., Kurtz, C., Dizon, W., Shaeffer, I., Chapman, A., et al. (2023). in The Sol Supercomputer at Arizona State University (NY, USA: Association for Computing Machinery).

Google Scholar

Ji, Y., Abernathy, H. W., and Chen, L.-Q. (2022). Thermodynamic models of multicomponent nonstoichiometric solution phases using internal process order parameters. Acta Mater. 223, 117462. doi:10.1016/j.actamat.2021.117462

CrossRef Full Text | Google Scholar

Jin, F., Xu, C., Yu, H., Xia, X., Ye, F., Li, X., et al. (2021). CaCo0.05Mn0.95O3−δ: a promising perovskite solid solution for solar thermochemical energy storage. ACS Appl. Mater. and Interfaces 13, 3856–3866. doi:10.1021/acsami.0c18207

CrossRef Full Text | Google Scholar

Kolodiazhnyi, T., Sakurai, H., Belik, A., and Gornostaeva, O. (2016). Unusual lattice evolution and magnetochemistry of Nb doped CeO2. Acta Mater. 113, 116–123. doi:10.1016/j.actamat.2016.04.052

CrossRef Full Text | Google Scholar

Kröger, F. A., and Vink, H. J. (1956). “Frederick seitz and david turnbull,” in Solid state physics, 3. Academic Press, 307–435.

Google Scholar

Krug, R. R., Hunter, W. G., and Grieger, R. A. (1976). Enthalpy-entropy compensation. 1. Some fundamental statistical problems associated with the analysis of van't Hoff and Arrhenius data. J. Phys. Chem. 80, 2335–2341. doi:10.1021/j100562a006

CrossRef Full Text | Google Scholar

Krzystowczyk, E., Haribal, V., Dou, J., and Li, F. (2021). Chemical looping air separation using a perovskite-based oxygen sorbent: system design and process analysis. ACS Sustain. Chem. and Eng. 9, 12185–12195. doi:10.1021/acssuschemeng.1c03612

CrossRef Full Text | Google Scholar

LeValley, T. L., Richard, A. R., and Fan, M. (2014). The progress in water gas shift and steam reforming hydrogen production technologies – a review. Int. J. Hydrogen Energy 39, 16983–17000. doi:10.1016/j.ijhydene.2014.08.041

CrossRef Full Text | Google Scholar

Liu, D., Dou, Y., Xia, T., Li, Q., Sun, L., Huo, L., et al. (2021). B-site La, Ce, and Pr-doped Ba0.5Sr0.5Co0.7Fe0.3O3-δ perovskite cathodes for intermediate-temperature solid oxide fuel cells: effectively promoted oxygen reduction activity and operating stability. J. Power Sources 494, 229778. doi:10.1016/j.jpowsour.2021.229778

CrossRef Full Text | Google Scholar

Liu, Y., and Sturtevant, J. M. (1997). Significant discrepancies between van't Hoff and calorimetric enthalpies. III. Biophys. Chem. 64, 121–126. doi:10.1016/S0301-4622(96)02229-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Mane, R., Kim, H., Han, K., Kim, H., Lee, S. S., Roh, H. S., et al. (2023). Important factors of the A-site deficient Mn perovskites design affecting the CO oxidation activity. Catal. Today 114347, 114347. doi:10.1016/j.cattod.2023.114347

CrossRef Full Text | Google Scholar

Mastronardo, E., Qian, X., Coronado, J. M., and Haile, S. M. (2020). The favourable thermodynamic properties of Fe-doped CaMnO3 for thermochemical heat storage. J. Mater. Chem. A 8, 8503–8517. doi:10.1039/D0TA02031A

CrossRef Full Text | Google Scholar

Moore, E., Guéneau, C., and Crocombette, J.-P. (2013). Diffusion model of the non-stoichiometric uranium dioxide. J. Solid State Chem. 203, 145–153. doi:10.1016/j.jssc.2013.04.006

CrossRef Full Text | Google Scholar

Muhich, C., Hoes, M., and Steinfeld, A. (2018). Mimicking tetravalent dopant behavior using paired charge compensating dopants to improve the redox performance of ceria for thermochemically splitting H2O and CO2. Acta Mater. 144, 728–737. doi:10.1016/j.actamat.2017.11.022

CrossRef Full Text | Google Scholar

Panlener, R. J., Blumenthal, R. N., and Garnier, J. E. (1975). A THERMODYNAMIC STUDY OF NONSTOICHIOMETRIC CERIUM DIOXIDE. J. Phys. Chem. Solids 36, 1213–1222. doi:10.1016/0022-3697(75)90192-4

CrossRef Full Text | Google Scholar

Park, J., Xu, B., Pan, J., Zhang, D., Lany, S., Liu, X., et al. (2023). Accurate prediction of oxygen vacancy concentration with disordered A-site cations in high-entropy perovskite oxides. npj Comput. Mater. 9, 29. doi:10.1038/s41524-023-00981-1

CrossRef Full Text | Google Scholar

Qian, X., He, J., Mastronardo, E., Baldassarri, B., Yuan, W., Wolverton, C., et al. (2021). Outstanding properties and performance of CaTi0.5Mn0.5O3–δ for solar-driven thermochemical hydrogen production. Matter 4, 688–708. doi:10.1016/j.matt.2020.11.016

CrossRef Full Text | Google Scholar

Redlich, O., and Kister, A. T. (1948). Algebraic representation of thermodynamic properties and the classification of solutions. Industrial and Eng. Chem. 40, 345–348. doi:10.1021/ie50458a036

CrossRef Full Text | Google Scholar

Rogers, D. (2005). Einstein's other theory: the Planck-Bose-Einstein theory of heat capacity. Princeton University Press.

Google Scholar

Rousseau, R., Glezakou, V.-A., and Selloni, A. (2020). Theoretical insights into the surface physics and chemistry of redox-active oxides. Nat. Rev. Mater. 5, 460–475. doi:10.1038/s41578-020-0198-9

CrossRef Full Text | Google Scholar

Sai Gautam, G., Stechel, E. B., and Carter, E. A. (2020a). Exploring Ca–Ce–M–O (M = 3d transition metal) oxide perovskites for solar thermochemical applications. Chem. Mater. 32, 9964–9982. doi:10.1021/acs.chemmater.0c02912

CrossRef Full Text | Google Scholar

Sai Gautam, G., Stechel, E. B., and Carter, E. A. (2020b). A first-principles-based sub-lattice formalism for predicting off-stoichiometry in materials for solar thermochemical applications: the example of ceria. Adv. Theory Simulations 3, 2000112. doi:10.1002/adts.202000112

CrossRef Full Text | Google Scholar

Singh, A. K., AuYeung, N. J., Randhir, K., Mishra, R., Allen, K. M., Petrasch, J., et al. (2015). Thermal reduction of iron oxide under reduced pressure and implications on thermal conversion efficiency for solar thermochemical fuel production. Industrial and Eng. Chem. Res. 54, 6793–6803. doi:10.1021/ie504402x

CrossRef Full Text | Google Scholar

Spencer, P. (2008). A brief history of CALPHAD. Calphad 32, 1–8. doi:10.1016/j.calphad.2007.10.001

CrossRef Full Text | Google Scholar

Sundman, B., Guéneau, C., and Dupin, N. (2011). Modeling multiple defects in ionic phases like UO2± using the compound energy formalism. Acta Mater. 59, 6039–6047. doi:10.1016/j.actamat.2011.06.012

CrossRef Full Text | Google Scholar

Tahir, F., Saeed, M. A., and Ali, U. (2023). Biomass energy perspective in Pakistan based on chemical looping gasification for hydrogen production and power generation. Int. J. Hydrogen Energy 48, 18211–18232. doi:10.1016/j.ijhydene.2023.01.247

CrossRef Full Text | Google Scholar

Takacs, M., Hoes, M., Caduff, M., Cooper, T., Scheffe, J., and Steinfeld, A. (2016). Oxygen nonstoichiometry, defect equilibria, and thermodynamic characterization of LaMnO3 perovskites with Ca/Sr A-site and Al B-site doping. Acta Mater. 103, 700–710. doi:10.1016/j.actamat.2015.10.026

CrossRef Full Text | Google Scholar

Teh, L. P., Setiabudi, H., Timmiati, S., Aziz, M., Annuar, N., and Ruslan, N. (2021). Recent progress in ceria-based catalysts for the dry reforming of methane: a review. Chem. Eng. Sci. 242, 116606. doi:10.1016/j.ces.2021.116606

CrossRef Full Text | Google Scholar

Tran, J. T., Warren, K. J., Wilson, S. A., Muhich, C. L., Musgrave, C. B., and Weimer, A. W. (2024). An updated review and perspective on efficient hydrogen generation via solar thermal water splitting. WIREs Energy Environ. 13, e528. doi:10.1002/wene.528

CrossRef Full Text | Google Scholar

van de Krol, R., Liang, Y., and Schoonman, J. (2008). Solar hydrogen production with nanostructured metal oxides. J. Mater. Chem. 18, 2311–2320. doi:10.1039/B718969A

CrossRef Full Text | Google Scholar

Van't Hoff, J. H., and Hoff, J. H. (1884). Etudes de dynamique chimique. F. Muller and Company.

Google Scholar

Vieten, J., Bulfin, B., Call, F., Lange, M., Schmücker, M., Francke, A., et al. (2016). Perovskite oxides for application in thermochemical air separation and oxygen storage. J. Mater. Chem. A 4, 13652–13659. doi:10.1039/c6ta04867f

CrossRef Full Text | Google Scholar

Wexler, R. B., Sai Gautam, G., Bell, R. T., Shulda, S., Strange, N. A., Trindell, J. A., et al. (2023). Multiple and nonlocal cation redox in Ca–Ce–Ti–Mn oxide perovskites for solar thermochemical applications. Energy and Environ. Sci. 16, 2550–2560. doi:10.1039/D3EE00234A

CrossRef Full Text | Google Scholar

Wilson, S. A., and Muhich, C. L. (2024). A Bayesian method for selecting data points for thermodynamic modeling of off-stoichiometric metal oxides. J. Mater. Chem. A, 13328–13337. doi:10.1039/D3TA06627D

CrossRef Full Text | Google Scholar

Wilson, S. A., Stechel, E. B., and Muhich, C. L. (2023). Overcoming significant challenges in extracting off-stoichiometric thermodynamics using the compound energy formalism through complementary use of experimental and first principles data: a case study of Ba1-xSrxFeO3-δ. Solid State Ionics 390, 116115. doi:10.1016/j.ssi.2022.116115

CrossRef Full Text | Google Scholar

Xu, M., Ermanoski, I., Stechel, E. B., and Deng, S. (2020). Oxygen pumping characteristics of YBaCo4O7+δ for solar thermochemical cycles. Chem. Eng. J. 389, 124026. doi:10.1016/j.cej.2020.124026

CrossRef Full Text | Google Scholar

Yoo, J., Yoo, C.-Y., Yu, J.-H., and Jacobson, A. J. (2017). Determination of oxygen nonstoichiometry in SrFeO3−δ by solid-state Coulometric titration. J. Am. Ceram. Soc. 100, 2690–2699. doi:10.1111/jace.14755

CrossRef Full Text | Google Scholar

Young, S. D., Chen, J., Sun, W., Goldsmith, B. R., and Pilania, G. (2023). Thermodynamic stability and anion ordering of perovskite oxynitrides. Chem. Mater. 35, 5975–5987. doi:10.1021/acs.chemmater.3c00943

CrossRef Full Text | Google Scholar

Zhang, D., De Santiago, H. A., Xu, B., Liu, C., Trindell, J. A., Li, W., et al. (2023). Compositionally complex perovskite oxides for solar thermochemical water splitting. Chem. Mater. 35, 1901–1915. doi:10.1021/acs.chemmater.2c03054

CrossRef Full Text | Google Scholar

Zhu, J.-Y., Park, T., Isola, P., and Efros, A. A. (2002). in Proceedings of the IEEE international conference on computer vision, 2223–2232.

Google Scholar

Zhukov, A., and Karlsson, R. (2007). Statistical aspects of van't Hoff analysis: a simulation study. J. Mol. Recognit. Interdiscip. J. 20, 379–385. doi:10.1002/jmr.845

PubMed Abstract | CrossRef Full Text | Google Scholar