- 1Guoneng Qinghai Yellow River MaerDang Hydropower Development Co., Ltd., Qinghai, China
- 2Beijing SP Zhishen Control Technology Co., Ltd., Beijing, China
- 3School of Automation Engineering, Northeast Electric Power University, Jilin, China
With the promotion and development of clean energy, it is challenging to ensure the optimization of control performance in frequency control of the hydropower-photovoltaic hybrid microgrid system caused by the output power fluctuation of photovoltaic power generation. In this study, an optimal load frequency controller (LFC) for a hydropower-photovoltaic hybrid microgrid system was designed to improve the dynamic response when the load and photovoltaic output power are perturbed based on the off-policy integral reinforcement learning algorithm. First, a mechanism model of the hydropower-photovoltaic hybrid microgrid system was established. Next, the LFC problem was transformed into a zero-sum game control problem based on the characteristics of the power system. Subsequently, three neural networks were employed to approximate the Nash equilibrium solution of the zero-sum game with historical input and output data when the system dynamics are completely unknown. Finally, simulation experiments were conducted to verify the effectiveness and optimality of the proposed method. The introduction of this method provides a new perspective for frequency control for the hydropower-photovoltaic hybrid microgrid system.
1 Introduction
With the development of the national economy and society, the contradiction between increasing energy demand and energy shortages has become increasingly obvious (Gilani et al., 2020; Patnaik et al., 2020; Zhang and Kong, 2022). Traditional thermal power generation causes problems such as the consumption of nonrenewable energy and excessive carbon emissions (Ahmad et al., 2018; Cowie et al., 2020; Olabi and Abdelkareem, 2022). Hydropower and solar energy have attracted the attention of researchers owing to their renewable and environment-friendly nature (Gielen et al., 2019; Zepter et al., 2019).
However, photovoltaic (PV) power generation is intermittent, leading to unstable output power and microgrid frequency oscillations (Thirunavukkarasu and Sawle, 2021; Chen et al., 2022; Wu and Yang, 2023). To ensure the frequency stability of a microgrid, it is necessary to supplement controllable power sources, such as hydroelectric units or energy storage devices, to fill the power deficit, which can effectively maintain the microgrid frequency stability (Coban et al., 2022). The power quality of PV power systems can be improved by utilizing a control algorithm for controllable power sources, which is applied to obtain an optimal load frequency controller (LFC) system (Papaefthymiou et al., 2010; Ma et al., 2014; Dhundhara and Verma, 2020). Some researchers focus on the suppression of local load fluctuations and their interactions with the distribution system (Khalid et al., 2022). Additionally, the role of ancillary services and the integration of renewable energy should also be addressed upon introduction to minimize fluctuations and cover intermittency (Khalid et al., 2022; Rehman et al., 2024; Osman et al., 2022).
Owing to their simple structure and ease of implementation, proportional-integral-derivative (PID) control methods are widely used in microgrid LFC (Mohamed et al., 2020; Nisha and Jamuna, 2022). Ray et al. (2011) utilized a PI controller to regulate the frequency of a microgrid and achieve the required frequency ratings. Guha et al. (2021) designed a fractional-order PID method to solve the frequency stabilization problem of microgrid systems with uncertain parameters. Huang et al. (2021) used fuzzy reasoning in PID to improve the control performance of a hydraulic turbine regulation system.
Many practical power systems can only be partially modeled, and models of unknown parts are unavailable (Ganguly et al., 2018; Li et al., 2023; Wu and Yang, 2023). Dynamic characteristics of droop-controlled inverters are evaluated by a reduce-order small-signal transfer function model, which is designed on the basis of the Jordan continued-fraction expansion to provide a preprocessing method for real-time power system simulation (Wang et al., 2020). Therefore, owing to the insensitivity to the dynamics of the unmodeled parts of the controlled object, adaptive control methods have been proposed by continuously identifying system parameters to achieve the ideal control effect. Adaptive control methods can be used to resolve problems arising from parameter variations in the LFC of a power system. Zeng et al. (2015) designed a port-controlled Hamiltonian system that decomposed nonlinear control into stabilizing control with a given equilibrium point and proposed L-2 adaptive control for application to a hydroelectric generator unit. Fang et al. (2011) effectively improved the dynamic performance of the hydraulic turbine regulation process using an improved particle swarm optimization algorithm, which was applied to the optimal design of the parameters of a hydraulic turbine regulation system to achieve an optimal positive setting of the parameters. Tran et al. (2021) used a combination of second-order sliding film control and a state estimator for frequency regulation to reduce the number of overtones. Although these methods can achieve better control performance, they have not been widely popularized in practical power systems owing to their complexity and difficulty.
The adaptive dynamic programming (ADP) algorithm is an emerging intelligent control algorithm that solves the problem of dimensional disasters caused by the traditional dynamic programming (DP) method (Werbos, 1992; Vamvoudakis and Lewis, 2010; Lewis et al., 2012; Bellman and Dreyfus, 2015) and is suitable for systems with a high degree of nonlinearity. Shuai et al. (2020) used a hybrid ADP algorithm to achieve optimal operation of gas and electric systems. Xue et al. (2022) used ADP for the real-time scheduling of battery heat storage tank integrated heat and power systems, providing optimal economic operation strategies. The off-policy integral reinforcement learning (IRL) algorithm is proposed based on the theory of the ADP algorithm, which can explore system information with historical input and output data, thereby overcoming the difficulty of traditional ADP relays on neural network weights in the training process to find the continuous excitation function. Chai et al. (2017) used the game theory to solve multi-objective trajectory optimization problems for aerial vehicles. Song et al. (2019) proposed an off-policy IRL algorithm to solve an optimal control problem with partially known system dynamics. Based on the ADP algorithm, this paper proposes an integral reinforcement learning method that requires only the historical input-output data of the system, allowing for optimal solutions even when the system dynamics are completely unknown.
To the best of our knowledge, in the hydropower-photovoltaic hybrid microgrid system, the challenges of considering system disturbances and employing model-free methods for frequency control are quite evident. Traditional frequency control methods typically rely on a mathematical model of the system and assume that disturbances are known or predictable. However, in real microgrid systems, disturbances such as load variations and fluctuations in renewable energy output are often unpredictable, and obtaining an accurate model of the system can be difficult or complex. The existing reinforcement learning methods for frequency control in the hydropower-photovoltaic hybrid microgrid systems have not simultaneously addressed disturbances in the system and utilized the model-free approaches, which motivates our study. The focus of this paper is on how to abstract a hybrid power generation system with disturbances as a zero-sum game problem and solve it using the proposed model-free method. This approach provides a theoretical foundation and basis for the grid integration of a series of photovoltaic combined power generation systems. The main contributions of this article are as follows:
1. A hydropower-photovoltaic hybrid microgrid system model was constructed on the basis of the mechanistic modeling of the hydraulic turbine and photovoltaic power generation, meanwhile treating the photovoltaic power generation perturbed as the disturbance term.
2. Based on the power generation characteristics, the secondary frequency modulation control signal was used as the control vector, and the input system load frequency and solar energy power were used as the perturbation vectors of the hydropower-photovoltaic microgrid power system, which transforms the LFC problem into a zero-sum optimal control problem. By solving the Nash equilibrium of the zero-sum game, the optimal control rate and the maximum disturbance that the system can withstand can be obtained, thereby controlling the load frequency of the hydropower-photovoltaic hybrid microgrid system.
3. An off-policy IRL algorithm was adopted to resolve the zero-sum optimal control problem in which three networks were employed to approximate the Nash equilibrium point of the zero-sum game to obtain the optimal LFC of the hybrid system. The proposed method overcomes the limitation of existing solution methods that require precise system model information.
2 Problem statement
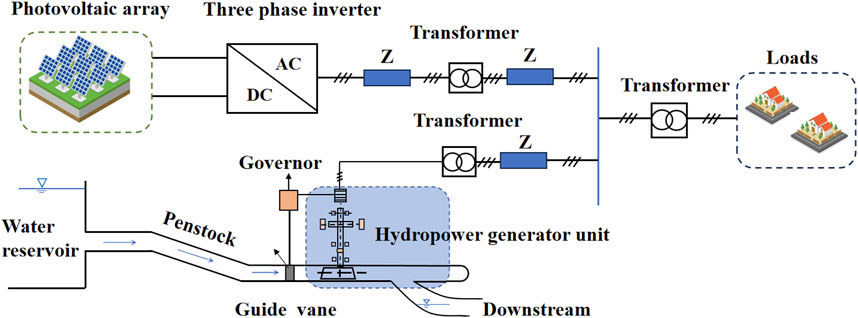
The hydropower-photovoltaic microgrid power system effectively exploits the inherent frequency regulation advantages of hydropower units while integrating solar energy generation resources within the same regional grid. This hybrid system aims to enhance the overall frequency quality of the microgrid by balancing both renewable energy inputs and electrical load demand. However, such integration significantly increases the operational requirements for the Load Frequency Control (LFC) controller. In this study, Figure 1 outlines the core structure of the system: a power busbar connects hydropower units (HP), photovoltaic generation units (PV), and electrical loads. Specifically, the PV units are connected to the alternating current (AC) microgrid through direct current (DC) to alternating current (AC) conversion using DC/AC inverters.
The frequency stability of this isolated microgrid relies heavily on maintaining an active power balance within the network. Variations in electrical load and the intermittent, fluctuating output from photovoltaic sources can disturb this balance, leading to changes in system frequency. A central feature of the hydropower-photovoltaic microgrid system is the hydro-turbine generator, which is responsible for providing rotational reserves that help regulate frequency by adjusting the mechanical input to the turbine. This response compensates for any mismatch between generation and demand, ensuring system stability.
The hydropower units play a critical role in Load Frequency Control (LFC) tasks. The primary function of the LFC system is to regulate water flow into the turbines of the hydropower generators. It achieves this by dynamically adjusting the active power output of the hydropower units in real-time, depending on the load and intermittent power output from the solar resources. This real-time control is vital for compensating fluctuations in both solar power production and load changes, stabilizing the generator speed, and ultimately controlling the frequency of the microgrid.
To improve the effectiveness of the system and minimize control costs, an advanced optimal load frequency controller was designed, utilizing an off-policy Inverse Reinforcement Learning (IRL) algorithm. This controller ensures the stability of the grid-connected voltage in the hydropower-photovoltaic microgrid by optimizing the dynamic allocation of power resources. In essence, it manages the trade-offs between ensuring grid frequency stability and maintaining operational cost efficiency, leading to a robust, reliable, and sustainable microgrid power system.
3 Materials and methods
3.1 Establishment of the hydro turbine group model
The hydro turbine group consisted of hydro turbines, governors, and generators. A turbine group model was established for each part.
The equations of moment and flow of the hydro turbine are expressed as Equation 1:
where
When
where
The hydro turbine governor can be simplified as a first-order inertial link by ignoring the nonlinear factors, as Equation 3:
where
Equation 2 is substituted into Equation 4 after the Laplace transformation. The differential equation is obtained by the Laplace transformation of Equation 2, and Equation 4 is substituted into the differential equation to obtain the hydro turbine differential equation as follows:
The second-order model of the generator includes the rotor rotation motion equation and the equation that characterizes the relationship between the power angle and speed, as follows:
where
By combining Equations 4–6, the following mathematical model of the hydro-turbine group can be obtained:
3.2 Establishment of the photovoltaic model
PV panels convert solar energy into electrical energy based on PV effects. The main body of the frequency control in this study was the hydropower unit. Therefore, in this subsection, a first-order model with time constant
where
3.3 Establishment of the hydropower-photovoltaic microgrid power system model
The transient changes in the voltage and power angle of the system can be ignored in the frequency control analysis. Therefore, in the analysis process of LFC,
By combining Equations 7, 8, the hydro-photovoltaic microgrid power system can be derived as Equation 9:
Here,
where the system state variable
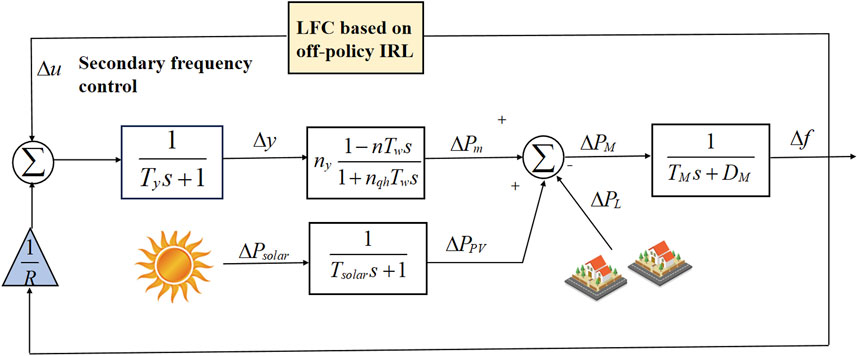
Thus far, the load frequency control problem of the hydropower-photovoltaic microgrid power system has been transformed into a zero-sum game optimal control problem, wherein the input of the governor was taken as the control variable and the load frequency and solar power were taken as the disturbance variables.
4 Results of the optimal controller based on off-policy IRL algorithm
The hydropower-photovoltaic microgrid power system model was established using Equation 10, where
where in the utility function can be described as Equation 12:
where the coefficient matrices
The purpose of the zero-sum game is to solve for an optimal control that satisfies Equation 13.
The zero-sum game selects to minimize the player set
When there is a unique set of solutions that satisfy the following Nash equilibrium condition Equation 15:
the cost function of every player can be written as Equation 16:
Using the Leibniz formula and differentiating Equation 6, the Bellman equation of the zero-sum game can be obtained as follows:
where
The optimal control policy
The Hamilton-Jacobi-Bellman equation can be obtained by substituting Equations 20, 21 into Equation 17 as follows:
The following equations were used to update the control and disturbance policies as Equations 23, 24:
where the superscript
The Equation 11 can be transformed as Equation 25:
The Equation 22 can be rewritten as follows:
By deriving Equation 23, we get
From Equations 26, 27, the system dynamic matrices A, B, and F are replaced. Equation 27 overcomes the difficulty of obtaining the dynamic information of the system in practical applications.
According to Equation 28, the residual can be written as follows:
Substituting Equations 28–30 into Equation 31 yields
In order to simplify Equation 32, the following parameters are defined as Equations 33–39:
Then, Equation 32 can be written as Equation 40:
The Equations 41–43 are then generated to obtain the optimal solutions:
Finally, Equation 32 can be written as follows:
In order to solve weight
upon substituting Equation 45 is substituted in Equations 44, 46 is obtained as follows:
Various numerical integrals in domain D were acquired to calculate
in which,
where
Upon substituting Equations 48, 49 in Equation 47, the following equation is obtained:
The zero-sum problem can be solved using Algorithm 1 as follows:
Algorithm 1.Off-policy IRL method to solve the optimal control problem.
Step 1: Start with the signals
Step 2: The values of cost function, control, and disturbance are set initial admissible weight vectors as
Step 3: Calculate the
Step 4: Let k = k + 1, return to step 3, and go on.
Step 5: Until
It is worth mentioning that the input and output data of the hydropower-photovoltaic microgrid power system are necessary to solve the zero-sum problem when the system dynamics are completely unknown.
5 Discussion
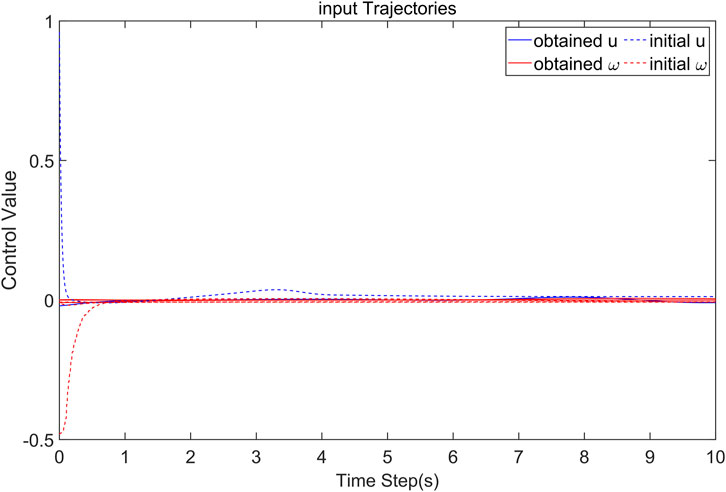
The hydropower-photovoltaic microgrid power system model was established, the proposed Algorithm 1 was utilized to solve the LFC control, and the simulation was realized in the MATLAB platform. Simulation results verified that the microgrid can maintain frequency stability despite local load and PV disturbances. The control and disturbance curves eventually approach to 0, as shown in Figure 3. The Figure 3 illustrates the behavior of two variables over a period of 10 time steps, designated on the x-axis. The y-axis represents the Control Value ranging from −0.5 to 1.0. The graph features two sets of trajectories for the control u and ω, each represented by both initial estimated values and adjusted values obtained using the Algorithm 1. The dashed and solid lines indicate the approximation curves under initial admissive control and Algorithm 1, respectively. It can be seen that the convergence speed of Algorithm 1 is better than that of the initial admissible control method. The frequency finally stabilized. For variable ω, it starts from a lower value and similarly converge towards zero. Overall, the obtained trajectories using Algorithm 1 exhibit a more rapid convergence towards 0 for both u and ω compared to their respective initial trajectories. Demonstrating the enhanced performance of Algorithm 1 over the initial admissible control method.
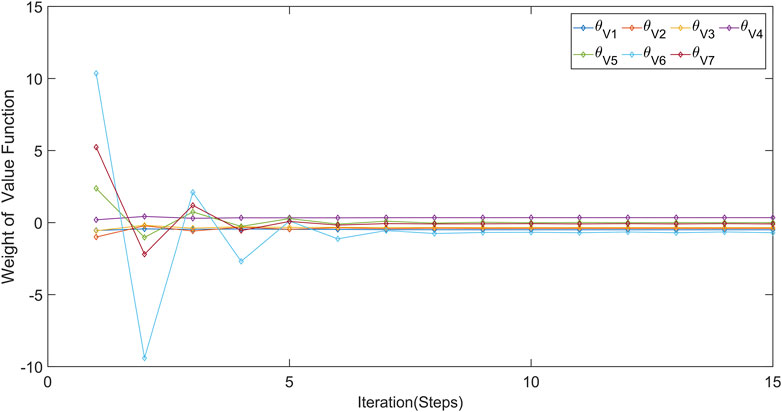
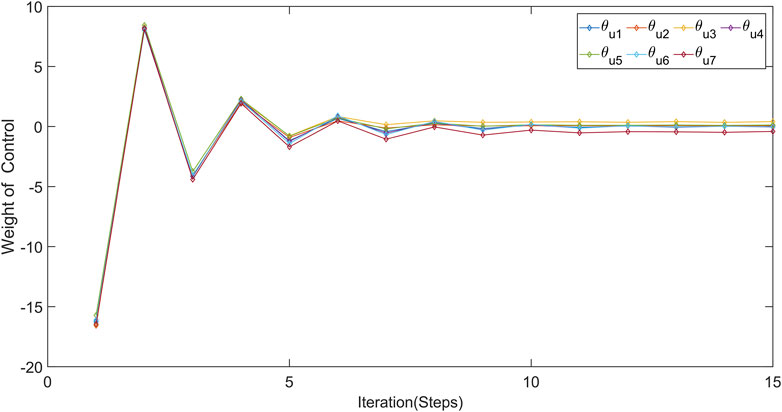
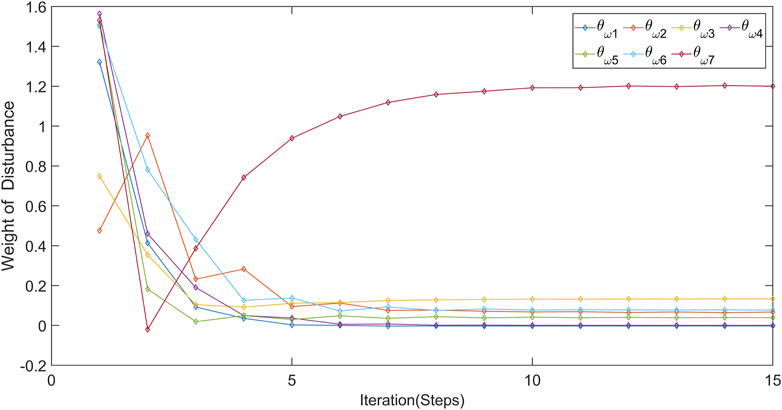
The weight convergence curves of the three networks are shown in Figures 4–6. These three figures illustrates the convergence of weights for every seven different networks
Compared to traditional Dynamic Programming methods, the proposed method effectively overcomes the “curse of dimensionality,” significantly reducing the computational burden when solving high-dimensional matrices. In contrast to previous reinforcement learning approaches for controlling the optimal frequency of hydropower-photovoltaic microgrid power systems, this method incorporates the consideration of disturbance factors, providing a robust theoretical basis for the grid integration of hybrid power generation systems.
The desired voltage and current is 50 hz sinusoidal waves, such that the systemis dynamic with high frequency. Yet the IRL method depends a process to collect the control and states data from the system under a quasi-optimal control, which may lead to the power oscillation and need more time to turn the system from the transient state to steady state. Therefore, the limitation of this method is that it is currently only applicable to offline systems.
6 Conclusion
This paper focused on the hydropower-photovoltaic hybrid microgrid system and designed an optimal LFC using the IRL algorithm. First, the mechanism models of the hydro turbine generator and the photovoltaic generator were established, respectively. Second, a state-space model of the hydropower-photovoltaic hybrid microgrid system was developed, and based on the power generation characteristics, it was transformed in solving a zero-sum game problem. Third, the IRL algorithm was employed to approximate the Nash equilibrium point of the zero-sum game problem using three neural networks. Finally, the simulation experiments were conducted to verify the effectiveness of the proposed method.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
EW: Conceptualization, Writing–original draft, Writing–review and editing. LY: Methodology, Writing–review and editing. FZ: Writing–review and editing. XL: Writing–review and editing. JL: Writing–original draft. LS: Writing–original draft. MZ: Writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by a grant for the project “Research and engineering demonstration of a safe, autonomous, and controllable intelligent control system for 10 million kilowatts of clean energy” (CSIEKJ220700539).
Conflict of interest
Authors EW and LY were employed by Guoneng Qinghai Yellow River MaerDang Hydropower Development Co., Ltd. Authors FZ, XL, and JL were employed by Beijing SP Zhishen Control Technology Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbreviations
LFC, load frequency controller; PV, photovoltaic; PID, proportional-integral-derivative; ADP, adaptive dynamic programming; IRL, integral reinforcement learning.
References
Ahmad, S., Ahmad, A., and Yaqub, R. (2018). Optimized energy consumption and demand side management in smart grid. Smart Grid as a Solut. Renew. Effic. Energy, 1–25. doi:10.4018/978-1-5225-0072-8.ch001
Bellman, R. E., and Dreyfus, S. E. (2015). Applied dynamic programming. Princeton, New Jersey: Princeton University Press.
Chai, R., Savvaris, A., Tsourdos, A., and Chai, S. (2017). Multi-objective trajectory optimization of space manoeuvre vehicle using adaptive differential evolution and modified game theory. Acta Astronaut. 136, 273–280. doi:10.1016/j.actaastro.2017.02.023
Chen, Z., Chen, J., Fu, K., and Xue, L. (2022). Power coordination control strategy of microgrid based on photovoltaic generation. MATEC Web Conf. 355, 03065. doi:10.1051/matecconf/202235503065
Coban, H. H., Rehman, A., and Mousa, M. (2022). Load frequency control of microgrid system by battery and pumped-hydro energy storage. Water 14, 1818. doi:10.3390/w14111818
Cowie, P., Townsend, L., and Salemink, K. (2020). Smart rural futures: will rural areas be left behind in the 4th Industrial Revolution?. J. Rural. Stud. 79, 169–176. doi:10.1016/j.jrurstud.2020.08.042
Dhundhara, S., and Verma, Y. P. (2020). Application of micro pump hydro energy storage for reliable operation of microgrid system. IET Renew. Power Gener. 14, 1368–1378. doi:10.1049/iet-rpg.2019.0822
Fang, H., Chen, L., and Shen, Z. (2011). Application of an improved PSO algorithm to optimal tuning of PID gains for water turbine governor. Energy Convers. Manag. 52, 1763–1770. doi:10.1016/j.enconman.2010.11.005
Ganguly, S., Shiva, C. K., and Mukherjee, V. (2018). Frequency stabilization of isolated and grid connected hybrid power system models. J. Energy Storage. 19, 145–159. doi:10.1016/j.est.2018.07.014
Gielen, D., Boshell, F., Saygin, D., Bazilian, M. D., Wagner, N., and Gorini, R. (2019). The role of renewable energy in the global energy transformation. Energy Strategy Rev. 24, 38–50. doi:10.1016/j.esr.2019.01.006
Gilani, M. A., Kazemi, A., and Ghasemi, M. (2020). Distribution system resilience enhancement by microgrid formation considering distributed energy resources. Energy 191, 116442. doi:10.1016/j.energy.2019.116442
Guha, D., Roy, P. K., and Banerjee, S. (2021). Equilibrium optimizer-tuned cascade fractional-order 3DOF−PID controller in load frequency control of power system having renewable energy resource integrated. Int. Trans. Electr. Energy Syst. 31, e12702. doi:10.1002/2050-7038.12702
Huang, Z., Liu, X., Fu, H., and Du, Z. (2021). A novel parameter optimisation method of hydraulic turbine regulating system based on fuzzy differential evolution algorithm and fuzzy PID controller. Int. J. Bio Inspired Comput. 18, 153–164. doi:10.1504/IJBIC.2021.119203
Khalid, H. M., Muyeen, S. M., and Kamwa, I. (2022). An improved decentralized finite-time approach for excitation control of multi-area power systems. Sustain. Energy, Grids Netw. 31, 100692. doi:10.1016/j.segan.2022.100692
Lewis, F. L., Vrabie, D., and Syrmos, V. L. (2012). Optimal control. Hoboken, New Jersey: John Wiley & Sons.
Li, J., Guo, W., and Liu, Y. (2023). Nonlinear state feedback-synergetic control for low frequency oscillation suppression in grid-connected pumped storage-wind power interconnection system. J. Energy Storage. 73, 109281. doi:10.1016/j.est.2023.109281
Ma, T., Yang, H., Lu, L., and Peng, J. (2014). Technical feasibility study on a standalone hybrid solar-wind system with pumped hydro storage for a remote island in Hong Kong. Renew. Energy. 69, 7–15. doi:10.1016/j.renene.2014.03.028
Mohamed, R., Helaimi, M., Taleb, R., Gabbar, H. A., and Othman, A. M. (2020). Frequency control of microgrid system based renewable generation using fractional PID controller. IJEECS 19, 745–755. doi:10.11591/ijeecs.v19.i2.pp745-755
Nisha, G., and Jamuna, K. (2022). Frequency stabilization of stand-alone microgrid with tuned PID controller. ECS Trans. 107, 773–782. doi:10.1149/10701.0773ecst
Olabi, A. G., and Abdelkareem, M. A. (2022). Renewable energy and climate change. Renew. Sustain. Energy Rev. 158, 112111. doi:10.1016/j.rser.2022.112111
Osman, N., Khalid, H. M., Tha’er, O. S., Abuashour, M. I., and Muyeen, S. M. (2022). A PV powered DC shunt motor: study of dynamic analysis using maximum power Point-Based fuzzy logic controller. Energy Convers. Manag. X 15, 100253. doi:10.1016/j.ecmx.2022.100253
Papaefthymiou, S. V., Karamanou, E. G., Papathanassiou, S. A., and Papadopoulos, M. P. (2010). A wind-hydro-pumped storage station leading to high RES penetration in the autonomous island system of Ikaria. IEEE Trans. Sustain. Energy. 1, 163–172. doi:10.1109/TSTE.2010.2059053
Patnaik, B., Mishra, M., Bansal, R. C., and Jena, R. K. (2020). AC microgrid protection–A review: current and future prospective. Appl. Energy. 271, 115210. doi:10.1016/j.apenergy.2020.115210
Ray, P. K., Mohanty, S. R., and Kishor, N. (2011). Proportional–integral controller based small-signal analysis of hybrid distributed generation systems. Energy Convers. Manag. 52, 1943–1954. doi:10.1016/j.enconman.2010.11.011
Rehman, A. U., Ullah, Z., Qazi, H. S., Hasanien, H. M., and Khalid, H. M. (2024). Reinforcement learning-driven proximal policy optimization-based voltage control for PV and WT integrated power system. Renew. Energy 227, 120590. doi:10.1016/j.renene.2024.120590
Shuai, H., Ai, X., Fang, J., Ding, T., Chen, Z., and Wen, J. (2020). Real-time optimization of the integrated gas and power systems using hybrid approximate dynamic programming. Int. J. Electr. Power Energy Syst. 118, 105776. doi:10.1016/j.ijepes.2019.105776
Song, R., Wei, Q., and Li, Q. (2019). Off-policy integral reinforcement learning method for multi-player non-zero-sum games. Adapt. Dyn. Program. Single Multiple Control., 227–249. doi:10.1007/978-981-13-1712-5_12
Thirunavukkarasu, M., and Sawle, Y. (2021). Smart microgrid integration and optimization. Act. Electr. Distrib. Netw. Smart Approach, 201–235. doi:10.1002/9781119599593.ch11
Tran, A. T., Minh, B. L. N., Huynh, V. V., Tran, P. T., Amaefule, E. N., Phan, V. D., et al. (2021). Load frequency regulator in interconnected power system using second-order sliding mode control combined with state estimator. Energies 14, 863. doi:10.3390/en14040863
Vamvoudakis, K. G., and Lewis, F. L. (2010). Online actor–critic algorithm to solve the continuous-time infinite horizon optimal control problem. Automatica 46, 878–888. doi:10.1016/j.automatica.2010.02.018
Wang, R., Sun, Q., Pinjia, Z., Yonghao, G., Dehao, Q., and Peng, W. (2020). Reduced-order transfer function model of the droop-controlled inverter via Jordan continued-fraction expansion. IEEE Trans. Energy 35, 1585–1595. doi:10.1109/TEC.2020.2980033
Werbos, P. (1992). Approximate dynamic programming for real-Time control and neural modeling. Handb. Intelligent Control.
Wu, J., and Yang, F. (2023). A dual-driven predictive control for photovoltaic-diesel microgrid secondary frequency regulation. Appl. Energy. 334, 120652. doi:10.1016/j.apenergy.2023.120652
Xue, X., Ai, X., Fang, J., Yao, W., and Wen, J. (2022). Real-time schedule of integrated heat and power system: a multi-dimensional stochastic approximate dynamic programming approach. Int. J. Electr. Power Energy Syst. 134, 107427. doi:10.1016/j.ijepes.2021.107427
Zeng, Y., Zhang, L. X., Guo, Y. K., and Qian, J. (2015). Hamiltonian stabilization additional L 2 adaptive control and its application to hydro turbine generating sets. Int. J. Control Autom. Syst. 13, 867–876. doi:10.1007/s12555-013-0460-7
Zepter, J. M., Lüth, A., Crespo del Granado, P. C., and Egging, R. (2019). Prosumer integration in wholesale electricity markets: synergies of peer-to-peer trade and residential storage. Energy Build. 184, 163–176. doi:10.1016/j.enbuild.2018.12.003
Keywords: hydropower-photovoltaic hybrid microgrid system, load frequency controller, off policy integral reinforce learning algorithm, data-based optimal control, neural networks
Citation: Wang E, Yuan L, Zeng F, Liu X, Liu J, Sun L and Zhuang M (2024) Load frequency optimal control of the hydropower-photovoltaic hybrid microgrid system based on the off-policy integral reinforcement learning algorithm. Front. Energy Res. 12:1464722. doi: 10.3389/fenrg.2024.1464722
Received: 15 July 2024; Accepted: 26 September 2024;
Published: 10 October 2024.
Edited by:
Wenping Zhang, Tianjin University, ChinaReviewed by:
Linfei Yin, Guangxi University, ChinaHaris M. Khalid, University of Dubai, United Arab Emirates
Qiuye Sun, Northeastern University, China
Copyright © 2024 Wang, Yuan, Zeng, Liu, Liu, Sun and Zhuang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lingfang Sun, c3VubGZAbmVlcHUuZWR1LmNu
 Enzhong Wang1
Enzhong Wang1 Min Zhuang
Min Zhuang