Towards a more secure reconstruction-based anomaly detection model for power transformer differential protection

Introduction: Cyberattacks against Power Transformer Differential Protection (PTDP) have the potential to cause significant disruption and widespread blackouts in power infrastructure. Recent literature has demonstrated how reconstruction-based anomaly detection models can play a critical role in enhancing the security of PTDP against such attacks. However, these models themselves are vulnerable to cyber threats. Adversarial sample generation is an example of a threat against reconstruction-based anomaly detection models.

Methods: To address this threat, we propose an approach for adversarial training of such models appropriate for PTDPs. We then review and compare the effect of adversarial training on the performance of four different model architectures. To demonstrate the efficacy of our proposed approach for improved security and performance in PTDP scenarios, the IEEE PSRC D6 benchmark test system is tested in an OPAL-RT environment.

Results: Simulation results show the effectiveness of the proposed method for improved detection of cyberattacks.

1 Introduction

The growing integration of communication protocols in smart power grids has increased the grid’s exposure to cyber threats yielding an observable rise in the rate and sophistication of cyberattack attempts against these infrastructures (Glenn et al., 2016). The Ukrainian power grid and Colonial Pipeline attacks are prominent examples of such cyberattacks (Case, 2016; Hobbs, 2021) demonstrating their potential for widespread blackout, economic loss, and even loss of life (Case, 2016; Hobbs, 2021; Slowik, 2018; National Academies of Sciences, 2017). To enhance the cybersecurity of power system substations, machine learning-based anomaly detection models can play a vital role as suggested in the recent literature (Jahromi et al., 2021; Khaw et al., 2020; Jahromi et al., 2020; Khaw et al., 2019; Guato Burgos et al., 2024; Narang and Bag, 2024; Akagic and Džafić, 2024). However, as the use of machine learning models increases, it has become apparent that the associated model itself can become a target for attackers.

For example, deep neural networks have achieved high performance for a variety of classification problems including anomaly detection. This largely stems from optimizing the weights of an associated multi-layer network of nonlinear artificial neurons (Goodfellow et al., 2016; Rezaee et al., 2024) using a back propagation algorithm. As it is often difficult to interpret the results of such an optimization, the associated network model may exhibit counter-intuitive properties. One such example involves expecting a well-performing deep neural network to be robust to small perturbations of the input. However, it has been shown that small perturbations may result in unexpected outputs from a model (Szegedy et al., 2013; Ferrara, 2024). These perturbed inputs are termed adversarial samples that exist, in part, because of model linearity in high-dimensional spaces. In fact, some deep neural network architectures including Long Short-Term Memory (LSTM) are designed to behave linearly, which makes them easier to optimize but leaves them vulnerable to linear input perturbations (Goodfellow et al., 2014). Hence, attackers can leverage such model characteristics to mislead power grid decision-making processes. Thus, machine learning models have their own vulnerabilities with the risk of exploitation more significant in integral cyber-physical environments such as smart power grids. In general, attacks against machine learning models fall into two categories: attacks during training and attacks at test/inference. Training time attacks include, but are not limited to, data poisoning (Koh and Liang, 2017; Yang et al., 2023; Cinà et al., 2023) and backdoor attacks (Chen et al., 2017; Wu et al., 2023), which both target model integrity. Training time attacks can also target confidentiality in specific scenarios such as federated learning (McMahan et al., 2017; Wen et al., 2023; Ji et al., 2024). In contrast, adversarial sample generation, model extraction, and membership inference are examples of inference time attacks (Goodfellow et al., 2014; Tramèr et al., 2016; Shokri et al., 2017; Liu et al., 2023; Zhang et al., 2024).

Power transformers represent integral components of power system substations linking critical points between different grid voltage levels. Power Transformer Differential Protection (PTDP) has been used as a main protection mechanism in power transformers (Horowitz and Phadke, 2014). A cyberattack on the PTDP can force a false tripping of the differential protection relays, possibly disconnecting system loads. In this work, we address cyberattacks that occur in inference time. We focus on adversarial sample generation, which demonstrates the most potential in PTDP settings, where the attacker’s goal is to craft input feature perturbations to craft samples that cause false prediction by anomaly detection models (Szegedy et al., 2013; Kurakin et al., 2016a); the perturbed inputs for a given model that produce incorrect results are known as adversarial samples. Ironically, these adversarial samples can also be leveraged to improve machine learning model security using an approach called adversarial training (Goodfellow et al., 2014). Here, the machine learning model is preemptively trained on the adversarial samples, so that the model has forewarning of such attacks. In classification tasks, this involves finding adversarial examples, adding them with the correct label to the training set, and retraining the model to achieve greater robustness and security to such attacks. Previous work on adversarial training is applicable to supervised learning contexts (Madry et al., 2017; Sanchez-Matilla et al., 2020; Wang et al., 2019; Fu et al., 2023). However, adversarial sample generation is also a significant threat to unsupervised settings such as reconstruction-based anomaly detection. Specifically, in reconstruction-based anomaly detection, the models operate in a self-supervised manner, meaning they do not utilize labeled data. Instead of having samples from every class, these models are trained solely on benign samples. Consequently, it is challenging to integrate adversarial samples during training due to the absence of malicious samples in dataset. Our approach addresses this gap by proposing seed selection methods and reformulating adversarial training methods. This is crucial for enhancing the robustness of reconstruction-based anomaly detection models, especially in critical applications like power grid monitoring, where maintaining performance against adversarial attacks is essential.

To tackle the aforementioned challenge, the main contributions of this work are summarized as:

$•$ The timely problem of cyberattacks on PTDP is studied. For the first time, the effect of False Data Injection (FDI) and Time Synchronization (TS) attacks are formulated mathematically.

$•$ We propose a new method for adversarial training of reconstruction-based anomaly detection models applicable to PTDPs. Given such models are self-supervised, the proposed method aims to force the model to reconstruct adversarial samples poorly without the use of training labels. We compare the effect of adversarial training on the performance of four different reconstruction-based anomaly detection models: the linear autoencoder, fully connected autoencoder, 1D convolutional network and LSTM.

$•$ We study the ability of our adversarial training approach to generalize adversarial samples generated by three methods: Projected Gradient Descent (PGD), DeepFool and Jacobian-Based Saliency Map Attack (JSMA) to study the ability of our approach to address a variety of cyberattacks.

While the proposed adversarial training method is formulated for reconstruction-based anomaly detection for PTDP, we assert that the method is general and can be applied to a wide variety of other smart grid monitoring, control and protection applications.

The remainder of the paper is organized as follows. Section 2 discusses reconstruction-based models in the context of cybersecurity applications. Section 3 studies cyber-physical attacks of PTDP. Section 4 presents possible attacks against reconstruction-based anomaly detection models. In Section 5, we propose a novel adversarial training method to enhance the security of reconstruction-based models. Section 6 details the test system used for data generation as well as the empirical results. Finally, the paper concludes in Section 7.

2 Reconstruction-based anomaly detection

Reconstruction-based anomaly detection models are machine learning models that aim to differentiate malicious behaviour in a system by assessing its deviation from a model of “normal” behaviour. In our scenario, the attacker launches cyberattacks as described in Sections III-A and III-B to trigger a transformer’s protective relay when no actual system fault exists. Such an attach has the potential to disrupt the system leading to cascading failure and possible blackout. Anomaly detection in this context, then, detects the legitimacy of the data sequence, used by a corresponding protective relay for decision-making, when the relay is activated.

Unlike classification models, reconstruction-based anomaly detection models are trained only on benign data. The benign data, in this formulation, consists of legitimate power system fault data sequences that have been previously captured by measurement devices. The training process of an autoencoder involves finding parameters of a corresponding encoder/decoder model shown in Figure 1 such that the encoder transforms the input into a latent space of reduced dimensionality and the decoder generates a reconstructed output which is an accurate estimate of the input data sequence. Specifically, the resulting autoencoder model would be able to reconstruct inputs with a reconstruction error given by Equation 1:

$MS{E}_i=\Vert X_i-M\left(X_i\right){\Vert }_2^2,(1)$

where $X_i$ is the input data sequence, $M(X_i)$ is the result of successively encoding and decoding $X_i$, $\Vert \cdot {\Vert }_2$ is the $L_2$ norm and $MS{E}_i$ is the mean squared error of $X_i$ and $M(X_i)$.

Figure 1

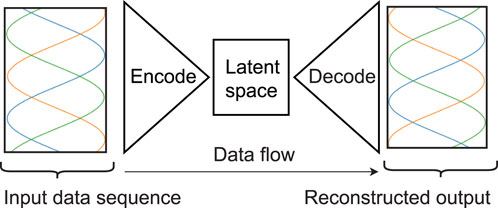
Figure 1. Autoencoder structure. In anomaly detection, the autoencoder is trained on benign data such that the reconstructed output is very similar in a mean squared error sense to the input data sequence.

Since the model is trained only on benign data, we expect to observe larger reconstruction errors when the input is not from the distribution of benign electrical faults. Hence, we can identify, with high probability, malicious/anomalous behaviour by setting a threshold $ϵ$ for the reconstruction error as in Equation 2:

$MS{E}_i>ϵ\to \text{anomalous\hspace{0.17em}data\hspace{0.17em}sequence.}(2)$

Different autoencoder architectures can be used to implement reconstruction-based anomaly detection. We consider four popular model types, including linear autoencoder, fully connected autoencoder, 1-dimensional convolutional neural networks (CNN) and Long Short Term Memory (LSTM) as suggested in Jahromi et al. (2021), and compare the effects of different adversarial training approaches on them in this paper.

3 Cyber attack scenarios against PTDP

We begin framing our motivation for anomaly detection by developing attack models for PTDPs. Specifically, we focus on the design of False Data Injection (FDI) and Time Synchronization (TS) cyberattacks. To the best of the authors’ knowledge, this is the first time such attacks on PTDPs have been formulated in the literature. The following notation is used: $\mathit{X}=\mathit{X}|\angle {\theta }_X$ represents a vector of magnitude of $|\mathit{X}|$ or $X$ and a phase angle of ${\theta }_X$.

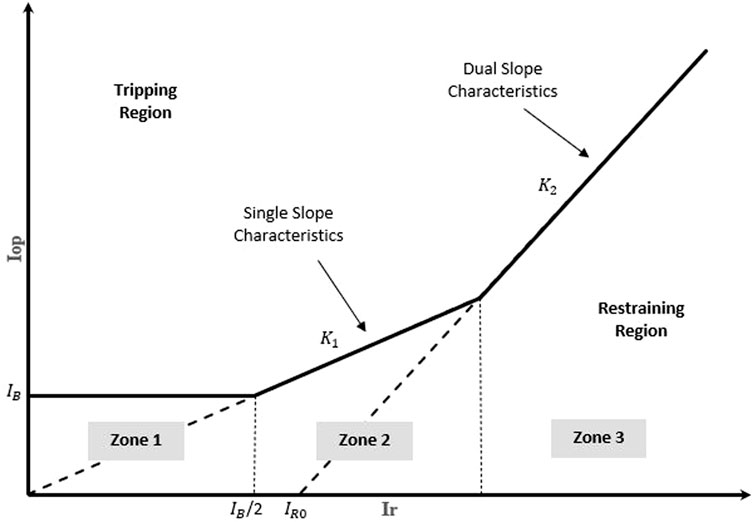
Differential protection in power systems protects a specified zone or piece of equipment (such as a transformer) by comparing the phase angles and magnitudes of the same electrical quantities (e.g., current) taken at specific locations and operates when an internal fault is likely to have occurred within an associated zone based on the observed electrical quantities. A relay that senses and operates on the phase difference between the current entering into the power transformer, ${\mathit{I}}_{\mathbf{1}}=|{\mathit{I}}_{\mathbf{1}}|\angle {\theta }_1$, and the current leaving the power transformer, ${\mathit{I}}_{\mathbf{2}}=|{\mathit{I}}_{\mathbf{2}}|\angle {\theta }_2$, is called a power transformer current differential relay. Figure 2 shows the restraining characteristics between the operating current, $I_{op}$ and the restraining current $I_r$ of a power transformer differential relay as defined in Equations 3, 4:

$|{\mathit{I}}_{\mathit{o}\mathit{p}}|=\left.‖{\mathit{I}}_{\mathbf{1}}|\angle {\theta }_1+|{\mathit{I}}_{\mathbf{2}}|\angle {\theta }_2\right|(3)$

$|{\mathit{I}}_{\mathit{r}}|=|{\mathit{I}}_{\mathbf{1}}|+|{\mathit{I}}_{\mathbf{2}}|.(4)$

Figure 2

Figure 2. Restraining characteristics of transformer differential protection.

The relay picks up when the operating point moves from the restraining region to the tripping region in Figure 2; i.e., $|{\mathit{I}}_{\mathit{o}\mathit{p}}|>|{\mathit{I}}_{\mathit{p}\mathit{u}}|$ where the pick-up current ${\mathit{I}}_{\mathit{p}\mathit{u}}$ is defined in Equation 5:

${\mathit{I}}_{\mathit{p}\mathit{u}}=\left\{\begin{array}{cc}{I}_B\hfill & \text{in\hspace{0.17em}Zone\hspace{0.17em}}1\hfill \\ k_1{\mathit{I}}_{\mathit{r}}\hfill & \text{in\hspace{0.17em}Zone\hspace{0.17em}}2\hfill \\ k_2\left({\mathit{I}}_{\mathit{r}}-I_{R0}\right)\hfill & \text{in\hspace{0.17em}Zone\hspace{0.17em}}3\hfill \end{array}\right.,(5)$

and $I_B$, $k_1$, $k_2$ and $I_{R0}$ are the settings of the relay. Zone 1 to Zone 3 define the characteristics of the relay. $I_B$ is usually set between 0.3 and 0.5 pu and accommodates CT remanence and accuracy errors. Slope $k_1$ considers the differences between ${\mathit{I}}_{\mathbf{1}}$ and ${\mathit{I}}_{\mathbf{2}}$ due to steady-state and proportional errors such as power transformer tap-changer, CT errors, excitation current and relay errors. Therefore, $k_1$ should be set above normal steady state and proportional errors (Laboratories, 2022). Slope $k_2$ accommodates transient errors caused by CT saturation.

3.1 False data injection attacks on PTDP

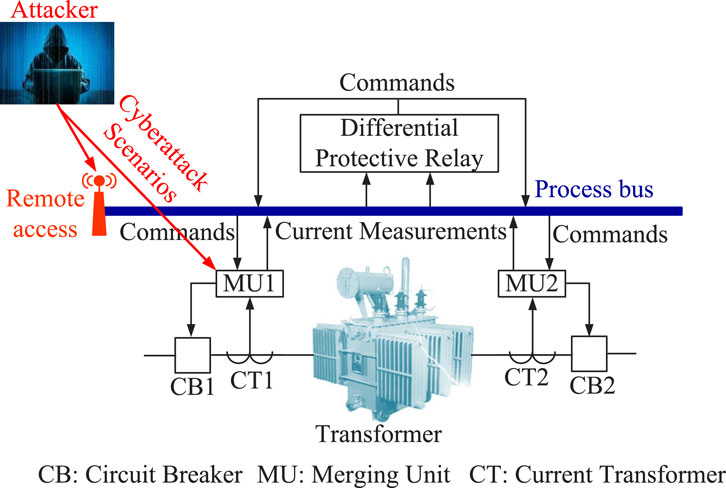
In this threat model, we assume that a cyberattacker has remote access to the corresponding substation automation system of the PTDP through a malicious device which is connected to the process bus or merging unit; see Figure 3. The attacker is either assumed to have recruited a substation employee who has authority to access communication devices to install the malicious device or to have infiltrated an appropriate component of the supply chain to insert it. Recent literature points to the feasibility of such attacks. With access to the process bus or data through the malicious device, the attacker can disrupt the flow of information packets to the relay IEDs and forward falsified packet payloads (intended to coerce false tripping) to the IEDs using a combination of man-in-the-middle and FDI attacks.

Figure 3

Figure 3. PTDP threat model.

Specifically, we consider FDI attacks that yield a malicious change in the current measurements to instigate tripping. It is shown in the literature (Taha et al., 2016; Lee and Kundur, 2014) that an FDI attack can affect both the magnitude and angle of the measurements and/or system states. Therefore, we assume that the attacker injects an attack signal $\mathrm{\Delta }{\mathit{I}}_{\mathbf{1}}=|\mathrm{\Delta }{\mathit{I}}_{\mathbf{1}}|\angle \mathrm{\Delta }{\theta }_1$ into the current value of the first transformer side such that $|{\mathit{I}}_{\mathbf{1}}|\angle {\theta }_1$ becomes $(|{\mathit{I}}_{\mathbf{1}}|+|\mathrm{\Delta }{\mathit{I}}_{\mathbf{1}}|)\angle ({\theta }_1+\mathrm{\Delta }{\theta }_1)$ after cyberattack. Substituting in $(3)$ and $(4)$, the operating and restraining currents after attack, $|{\mathit{I}}_{\mathit{o}\mathit{p}}^{\mathit{a}}|$ and $|{\mathit{I}}_{\mathit{r}}^{\mathit{a}}|$ can be calculated as shown in Equations 6, 7:

$|{\mathit{I}}_{\mathit{o}\mathit{p}}^{\mathit{a}}|=\left|\left(|{\mathit{I}}_{\mathbf{1}}|+|\mathrm{\Delta }{\mathit{I}}_{\mathbf{1}}|\right)\angle \left({\theta }_1+\mathrm{\Delta }{\theta }_1\right)+|{\mathit{I}}_{\mathbf{2}}|\angle {\theta }_2\right|(6)$

$a|{\mathit{I}}_{\mathit{r}}^{\mathit{a}}|=|{\mathit{I}}_{\mathit{r}}|+|\mathrm{\Delta }{\mathit{I}}_{\mathbf{1}}|.(7)$

The value of $|{\mathit{I}}_{\mathit{o}\mathit{p}}|$ is ideally zero during normal (no-fault) operation, and hence $|{\mathit{I}}_{\mathbf{1}}|\angle {\theta }_1=-|{\mathit{I}}_{\mathbf{2}}|\angle {\theta }_2$. Substituting into (6) to calculate the operating current due to the attack results in Equation 8:

$|{\mathit{I}}_{\mathit{o}\mathit{p}}^{\mathit{a}}|=\left|\left(|{\mathit{I}}_{\mathbf{1}}|+|\mathrm{\Delta }{\mathit{I}}_{\mathbf{1}}|\right)\angle \left({\theta }_1+\mathrm{\Delta }{\theta }_1\right)-|{\mathit{I}}_{\mathbf{1}}|\angle {\theta }_1\right|.(8)$

Therefore, for the relay to pick up during an attack, the current difference has to be greater than ${\mathit{I}}_{\mathit{p}\mathit{u}}^{\mathit{a}}$; that is,

$\left|\left(|{\mathit{I}}_{\mathbf{1}}|+|\mathrm{\Delta }{\mathit{I}}_{\mathbf{1}}|\right)\angle \left({\theta }_1+\mathrm{\Delta }{\theta }_1\right)-|{\mathit{I}}_{\mathbf{1}}|\angle {\theta }_1\right|>{\mathit{I}}_{\mathit{p}\mathit{u}}^{\mathit{a}},(9)$

where ${\mathit{I}}_{\mathit{p}\mathit{u}}^{\mathit{a}}=f({\mathit{I}}_{\mathit{r}}+\mathrm{\Delta }{\mathit{I}}_{\mathbf{1}})$ is the post-attack pick-up current.

In order to cause tripping during the attack, the attacker must adjust the value of the attack signal, $|\mathrm{\Delta }{\mathit{I}}_{\mathbf{1}}|\angle \mathrm{\Delta }{\theta }_1$, to satisfy Equation 9.

This can be achieved through a few sub-scenarios, each one of them resulting in different measurement patterns. Hence, we leverage these sub-scenarios to diversify our attack datasets. This can be mathematically formulated to represent different sub-scenarios as follows.

3.1.1 Manipulating current magnitude

In this scenario, we assume that the attacker injects malicious data only on the magnitude of the current ${\mathit{I}}_{\mathbf{1}}$; hence, $\mathrm{\Delta }{\theta }_1=0$. Substituting into (9), the value of $|\mathrm{\Delta }{\mathit{I}}_{\mathbf{1}}|$ should satisfy:

$|\mathrm{\Delta }{\mathit{I}}_{\mathbf{1}}|>\left\{\begin{array}{cc}{I}_B\hfill & \text{in\hspace{0.17em}Zone\hspace{0.17em}}1\hfill \\ \frac{k_1{\mathit{I}}_{\mathit{r}}}{1-k_1}\hfill & \text{in\hspace{0.17em}Zone\hspace{0.17em}}2\hfill \\ \frac{k_2\left({\mathit{I}}_{\mathit{r}}-I_{R0}\right)}{1-k_2}\hfill & \text{in\hspace{0.17em}Zone\hspace{0.17em}}3\hfill \end{array}\right..(10)$

3.1.2 Manipulating current phase angle

In this scenario, we assume that the attacker manipulates the phase angle of the current ${\mathit{I}}_{\mathbf{1}}$. In this case, the value of ${\mathit{I}}_{\mathbf{1}}$ after the attack is $|{\mathit{I}}_{\mathbf{1}}|\angle ({\theta }_1+\mathrm{\Delta }{\theta }_1)$ and the magnitude of ${\mathit{I}}_{\mathit{r}}$ is preserved. Substituting into Equation 9 gives:

$\left.‖{||\mathit{I}}_{\mathbf{1}}|\angle \left({\theta }_1+\mathrm{\Delta }{\theta }_1\right)-|{\mathit{I}}_{\mathbf{1}}|\angle {\theta }_1|\right|>{\mathit{I}}_{\mathit{p}\mathit{u}}^{\mathit{a}}.(11)$

To satisfy Equation 11, $\mathrm{\Delta }{\theta }_1$ should be selected within the following interval for tripping:

$\mathrm{\Delta }{\theta }_1\in \left[2\arcsin \frac{|{\mathit{I}}_{\mathit{p}\mathit{u}}|}{2|{\mathit{I}}_{\mathbf{1}}|},2\pi -2\arcsin \frac{|{\mathit{I}}_{\mathit{p}\mathit{u}}|}{2|{\mathit{I}}_{\mathbf{1}}|}\right].(12)$

3.1.3 Replay attack

Here, the attacker injects current magnitude data from a previously captured fault in the system. This way, the injected data is consistent with a snapshot of a benign fault. Therefore, the attacker aims to have a better chance of bypassing the protective systems. In this scenario, the values should satisfy the criteria mentioned in Equation 10.

3.2 Time synchronization attacks

TS attacks are also a kind of man-in-the-middle attacks. However, in contrast to FDI attacks, TS attacks target the timing information in a smart grid, by incorporating the delay of time synchronization pulses being sent from one node to another in the communication network. in timing errors or cause the loss of synchronization, TS attacks cause catastrophic failures of the PTDP due to the timing error and/or the loss of communication caused by the attack (Han and Crossley, 2019). For PTDP, TS attacks can be represented as a change in the phase angle of current measurements ${\theta }_1$ (Zhang et al., 2013). Given that $\mathrm{\Delta }{\theta }_1$ should be selected as in Equation 12 to initiate false tripping, the attacker can correspondingly change the time reference by $\mathrm{\Delta }t$ for an appropriate $\mathrm{\Delta }{\theta }_1$ as Equation 13:

$\mathrm{\Delta }t=\frac{\mathrm{\Delta }{\theta }_1}{2\pi f},(13)$

where $f$ is the power frequency of the system.

Applying the reconstruction-based anomaly detection models of Section 2 shows promising results in detecting the aforementioned attacks in a variety of scenarios (Jahromi et al., 2021; Khaw et al., 2020). However, as discussed, the models themselves can be a target of the cyberattack. In the subsequent two sections, we will address the following key points:

$•$ Adversarial Sample Generation Methods: An overview of methods used to generate adversarial samples targeting our anomaly detection models, designed to protect PTDP.

$•$ Seed Generation in Absence of Malicious Data: We propose how to generate seeds when there are no malicious data point available in the dataset.

$•$ Expected Output for Generated Seeds: We propose the expected output for the seeds generated from previous step.

$•$ Reformulation of adversarial training in order to be applicable to reconstruction-based anomaly detection models, utilizing the dataset generated in the preceding steps.

4 Attacks against anomaly detection model

We consider reconstruction-based anomaly detection models that are trained on benign data using the four architectures discussed in Section 2. In adversarial sample generation, the attacker’s goal is to craft samples that the model will misclassify. In our problem context, the attacker aims to devise samples that are detected as faults by the differential relay while not being detected as anomalous by the anomaly detection model. We consider three well known adversarial sample generation approaches, and propose novel modifications, where appropriate, for our reconstruction-based anomaly detection methods.

4.1 Adversarial sample generation methods

In our proposed modified methods, adversarial sample generation exploits vulnerabilities in anomaly detection models, making it a potent method to compromise PTDP. By subtly altering input data, attackers can evade detection mechanisms, posing a significant challenge to system integrity. This approach offers a accessible means of attack, emphasizing the need for robust defense mechanisms to counter evolving threats.

4.1.1 Projected gradient descent (PGD) attack

Fast Gradient Sign Method (FGSM) is a method of generating adversarial examples. Starting from an input that the model correctly classifies, a small perturbation is calculated as shown in Equation 14:

$\eta =\sigma .sgn\left({\nabla }_{X}L\left(\mathrm{\Theta },X,y\right)\right),(14)$

where $X$ is the original input sample, $y$ is the target/label, $\mathrm{\Theta }$ are model parameters, $L$ is the loss function, ${\nabla }_{X}L$ represents the gradient of $L$ with respect to $X$, and scalar $\sigma$ determines the magnitude of the perturbations. Then, the perturbation $\eta$ is added to $X$ to obtain an adversarial sample as follows: $X^{*}=X+\eta$.

This method is successful for a variety of models (Goodfellow et al., 2014). However, the success rate of FGSM is not always optimal, and selecting $\sigma$ can be challenging compared to its iterative version, the Projected Gradient Descent (PGD) (Kurakin et al., 2016b; Kurakin et al., 2016a). In PGD, FGSM is applied iteratively in small step sizes starting with the original input sample (also known as the seed) $X_0$:

$X_{i+1}=X_i+\sigma .sgn\left({\nabla }_{X_i}L\left(\mathrm{\Theta },X_i,y\right)\right),(15)$

where $X_{i+1}$ is the adversarial sample at step $i+1$, $X_i$ is the adversarial sample at step $i$. Hence, adversarial sample generation is typically discussed in relation to supervised classification models, which is not compatible with anomaly detection where no label $y$ exists.

To address this limitation, our approach adapts PGD to unsupervised contexts by replacing the traditional loss function in Equation 15 with Equation 16:

$L\left(\mathrm{\Theta },X_i\right)=MSE\left(X_i-M\left(X_i\right)\right),(16)$

where $M(X_i)$ is the reconstructed output for input $X_i$. For each step in adversarial sample generation, we thus have Equation 17:

$X_{i+1}=X_i+\sigma .sgn\left({\nabla }_{X_i}MSE\left(X_i-M\left(X_i\right)\right)\right).(17)$

Compared to Equation 16, $M(X_i)$ changes after each step, and it is the current reconstruction of $X_i$. Using Equation 18, at each step, we achieve a new sample $X_{i+1}$ that is reconstructed by $M$ with a lower reconstruction error. Hence, we move toward lower reconstruction error by repeating this step. However, as this is not a convex problem, it is not guaranteed to converge to adversarial samples and pass the decision boundary for every chosen seed.

4.1.2 DeepFool attack

DeepFool is another iterative approach focused on more efficient adversarial sample generation (Moosavi-Dezfooli et al., 2016). Here, a linear classifier is first assumed for formulation:

$f\left(X\right)=W^{T}X+b,(18)$

whereby the corresponding decision boundary is given by Equation 19:

$F=X:W^{T}X+b=0.(19)$

The main idea behind DeepFool is to project the initial input sample (or seed) $X_0$ onto and slightly across the decision boundary. In the first step, the perturbation needed for the projection is calculated as shown in Equation 20:

$d=-\frac{f\left(X_0\right)}{\Vert W{\Vert }_2^2}W.(20)$

Then, the attack sample is calculated as in Equation 21:

$X^{*}=X_0+\left(1+ϵ\right)d,ϵ\ll 1,(21)$

where $ϵ$ is a very small positive number [$ϵ=0.02$ is used (Moosavi-Dezfooli et al., 2016)] to help push an attack sample $X^{*}$ over the decision boundary by a small amount.

This attack can be generalized to nonlinear classifiers by applying the approach iteratively. Starting with an initial input seed sample, $X_0$, at each iteration $i$, $f$ is linearized around $X_i$, and the perturbation $d_i$ is calculated as in Equation 22:

$d_i=-\frac{f\left(X_i\right)}{\Vert \nabla f\left(X_i\right){\Vert }_2^2}\nabla f\left(X_i\right).(22)$

The next iteration of the attack sample is computed as in Equation 23:

$X_{i+1}=X_i+d_i,(23)$

with the iterations continuing until the generated attack sample crosses the decision boundary.

4.1.3 Jacobian-Based Saliency Map Attack (JSMA)

This method is based on the saliency map of the input (Moosavi-Dezfooli et al., 2016). Large absolute values refer to features that considerably impact the outcome. At each iteration, the Jacobian matrix is first calculated as give in Equation 24:

$J_f\left(X\right)={\left[\frac{\delta f_j\left(X\right)}{\delta x_i}\right]}_{i=1\dots M,j=1\dots N},(24)$

where $X$ is the input vector (or seed), $f_j$ is the output of the network at index $j$, $x_i$ is the input at index $i$, $M$ is the size of input and $N$ is the total number of outputs. Then, a saliency map is created using Equation 25:

$S\left(X,c\right)=\left\{\begin{array}{c}0\text{\hspace{0.17em}if\hspace{0.17em}}{J}_{ij}\left(X\right)<0\text{\hspace{0.17em}or\hspace{0.17em}}{\mathrm{\Sigma }}_{j\ne c}{J}_{ij}\left(X\right)>0\hfill \\ J_{ij}\left(X\right)|{\mathrm{\Sigma }}_{j\ne c}{J}_{ij}\left(X\right)|\text{\hspace{0.17em}otherwise}\hfill \end{array}\right.,(25)$

where $i$ is the input index, $j$ is the output index, $J_{ij}$ is the partial derivative of $f_j(X)$ with respect to $x_i$ and $c$ is a given output index. For a scalar output problem, this simplifies to Equation 26:

$S_i\left(X\right)=\left\{\begin{array}{c}0\text{\hspace{0.17em}if\hspace{0.17em}}{J}_i\left(X\right)<0\hfill \\ J_i\left(X\right)\text{\hspace{0.17em}otherwise}\hfill \end{array}\right.,(26)$

where $J_i$ is the partial derivative of $f(X)$ with respect to $x_i$ and $S_i$ is the value of the saliency map for input index $i$. Then, at each step, we select the feature that has the maximum value in saliency map as shown in Equation 27:

$maxIndex=\arg {\max }_{i}S\left(X\right),(27)$

and then modify the attack sample as in Equation 28:

$X_{i+1,maxIndex}=X_{i,maxIndex}+\theta ,(28)$

where $\theta$ is a problem-specific perturbation amount. Same as the previous methods, we apply this approach until the attack sample passes the decision boundary.

4.2 Seed selection in anomaly detection problems

Selecting the initial samples, also known as seeds, from which to generate adversarial samples is an essential step in the aforementioned approaches. As shown in Figure 4, choosing seeds in classification problems is straightforward because samples from each class exist in the training set. In a reconstruction-based anomaly detection model, the model is trained only on benign data. Moreover, the attacker aims to devise samples that are detected as faults by the differential relay while not being detected as anomalous by the anomaly detection model. Hence, the seeds must come from the set of anomalous data unavailable during training.

Figure 4

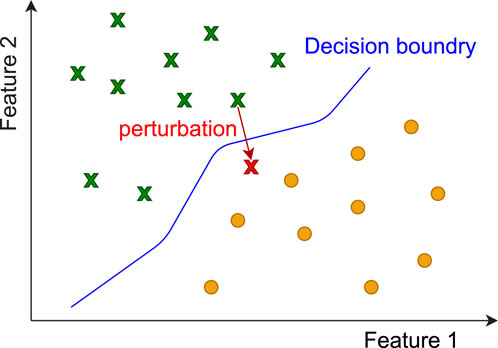
Figure 4. Adversarial sample generation in classification problems. Yellow circles and green cross signs each represent samples from one class. The red cross represents an adversarial sample generated using one of the samples from the green class as the seed.

To address this challenge, we devise an approach to generate seeds randomly. Given the non-discriminate way in which anomalies are detected, we consider any data sequence that is reconstructed “poorly” by the model as a potential seed; the idea is clarified in Figure 5. We assert that because the model is not trained on random data sequences, it is not capable of reconstructing them with low error. Moreover, random data sequences can give us randomly spread data points in the feature space. Hence, using them as seeds gives us the potential to generate a rich set of adversarial samples. Thus, in this work, we consider random data sequence seeds. Algorithm 1 details the process of generating adversarial examples. As we discuss in the next section, adversarial samples can be utilized to enhance the model’s robustness. It is worth noting that, unlike image processing, where the human eye limits the perturbations allowed by the attacker, in our setting, there are no limitations on the set of perturbations that an attacker can make in order to achieve adversarial samples. Even in the field of image processing, the set of perturbations that an attacker is willing to make is an open problem. If we know those sets of perturbations, then we know the actual decision boundary, which is not the case. Therefore, it is important to monitor the performance of the models after adversarial training on the set of data that has not been perturbed to prevent overfitting.

Figure 5

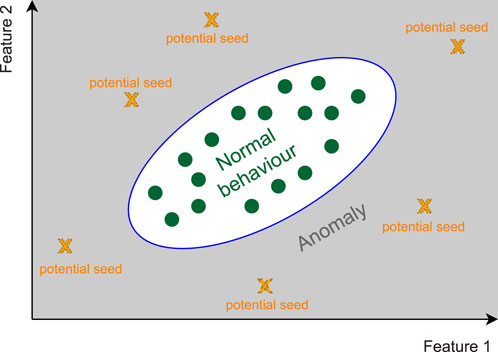
Figure 5. Adversarial sample generation in reconstruction based anomaly detection problems. The grey area represents the space from which samples will be detected as anomalies.

Algorithm 1.Adversarial sample generation.

seed: Randomly generated data sequence

1 $ad{v}_x\leftarrow seed$

2 for iteration $\leftarrow$ 0 to maxIterations do

3  $grad\leftarrow {\nabla }_{ad{v}_x}MSE(ad{v}_x-M(ad{v}_x))$

4 $perturbation\leftarrow \sigma \ast sgn(grad)$

5 $ad{v}_x\leftarrow ad{v}_x+perturbation$

6 $reconstructionError\leftarrow MSE(ad{v}_x,M(ad{v}_x))$

7 if $reconstructionError<threshold$ then

8   return $ad{v}_x$

9  end

10 end

5 Adversarial training for reconstruction-based anomaly detection model

Adversarial training is an effective defense technique that can be used to enhance the robustness and security of machine learning models against adversarial sample generation (Madry et al., 2017). In this approach, we first find a set of adversarial samples. Then, we retrain the model using those samples with the correct classification (of the original seed). In supervised learning, this process is straightforward because there is a simple label for each seed.

The distinction with unsupervised anomaly detection is that training is only conducted on benign data. Hence, we cannot append adversarial samples (which are correctly classified as anomalous) to our training set. This requires that we reformulate adversarial training in the context of reconstruction based models and introduce a new methodology.

5.1 Adversarial training for classification problems

Adversarial training, for standard classification, can be formulated as a saddle point problem shown in Equation 29 (Madry et al., 2017):

$mi{n}_{\begin{array}{c}\theta \end{array}}{\mathbf{E}}_{\left(x,y\right)\sim D}\left(ma{x}_{\delta }L\left(\theta ,x+\delta ,y\right)\right),(29)$

where $\delta$ is the perturbation added to the seed $x$ of label $y$ and ${\mathbf{E}}_{(x,y)\sim D}$ denotes population risk. The inner maximization problem aims to find the adversarial sample that maximizes the loss, while the outer optimization endeavours to train a model that minimizes the loss for the generated attack samples. However, since $y$ (which is the label corresponding to $x$) does not apply to unsupervised contexts, we must reformulate the problem for reconstruction-based anomaly detection.

5.2 Adversarial training for reconstruction-based anomaly detection models

First, in our setting, the attacker’s goal is to add perturbations to a sample initially detected as an anomaly by the model to craft a new sample with low reconstruction error. Therefore, we propose to change the inner optimization problem to Equation 30:

$\rho \left(\theta \right)={\mathbf{E}}_{\left(x\right)\sim D}\left(mi{n}_{\delta }L\left(\theta ,x+\delta ,M\left(x+\delta \right)\right)\right),(30)$

where $y$ is replaced by $M(x+\delta )$ to reflect the task of the inner optimization to find a new sample $x+\delta$ that is closest to its reconstruction $M(x+\delta )$. This new formulation reflects the self-supervised nature of the problem.

Unlike Equation 29, we start with an anomalous seed that corresponds to high reconstruction error, thus to move toward the non-anomalous sample’s distribution, we must make changes to the seed to generate new seeds with lower reconstruction error. This implies the inner optimization problem must change to a minimization. Moreover, in order to make the model unable to reconstruct adversarial samples with low reconstruction error, we must maximize the risk for adversarial samples population.

Our proposed changes results in a new formulation, in which, an anomalous input seed that is effectively perturbed would be detected as normal with low reconstruction error requiring a minimization of the associated loss with respect to $\delta$.

Moreover, adversarial training should aim to maximize reconstruction error for adversarial samples to flag them as being truly anomalous as given by:

$ma{x}_{\begin{array}{c}\theta \end{array}}\rho \left(\theta \right)=ma{x}_{\begin{array}{c}\theta \end{array}}{\mathbf{E}}_{\left(x\right)\sim D}\left(mi{n}_{\delta }L\left(\theta ,x+\delta ,M\left(x+\delta \right)\right)\right).(31)$

We remind the reader that for the first time we consider adversarial training for reconstruction-based models, for which the training data consists of solely benign data and the model’s input and expected output are the same. Thus, to achieve the goals of adversarial training as described by Equation 31, we propose to employ adversarial samples in training (although they are anomalous) to help with security, but instead restrict the expected output to deviate significantly from the adversarial sample input as follows:

$X^{\prime }=argma{x}_{x^{\prime }}MSD\left(x-x^{\prime }\right),(32)$

where $X^{\prime }$ is the expected output used for training with the adversarial sample input $x$ and MSD is the Mean Squared Distance. By employing Equation 32 that maximized reconstruction error to create an adversarial training set, we expect the model will adapt to appropriately address adversarial samples and flag such attacks. Figure 6 shows an example of an adversarial input $X$ and the corresponding expected output $X^{\prime }$ that will be used in adversarial training; note that data is scaled in the range $[-\mathrm{1,1}]$ in each time step.

Figure 6

Figure 6. Adversarial input $X$ (dashed green line) and expected output $X^{\prime }$ (solid blue line) example.

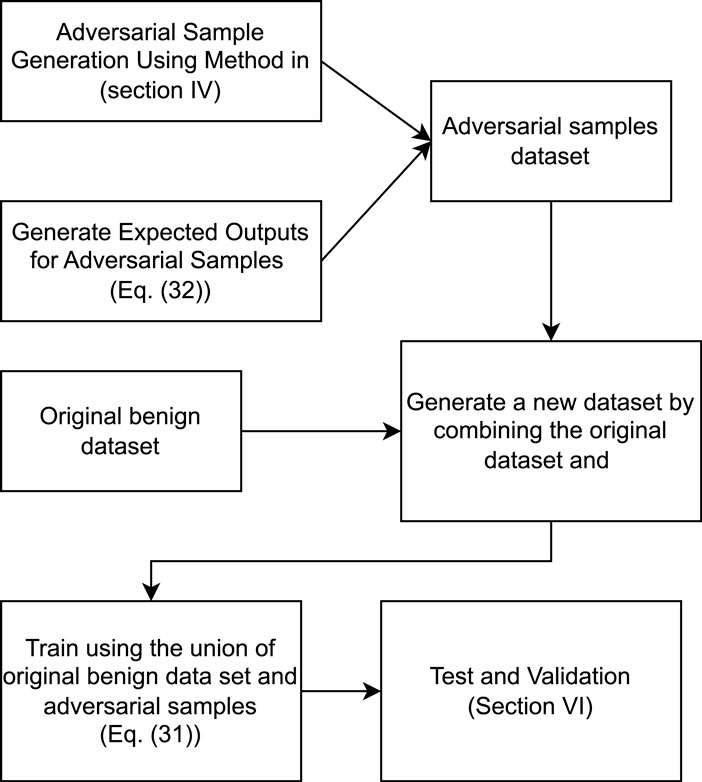
Table 1 highlights the differences between adversarial training for classification vs. reconstruction-based anomaly detection models. Figure 7, summarizes the adversarial training steps described above in a flowchart.

Table 1

Table 1. Key differences between adversarial training for classification vs. reconstruction-based models.

Figure 7

Figure 7. Adversarial training steps flowchart.

6 Testing and validation

6.1 Test system and data generation

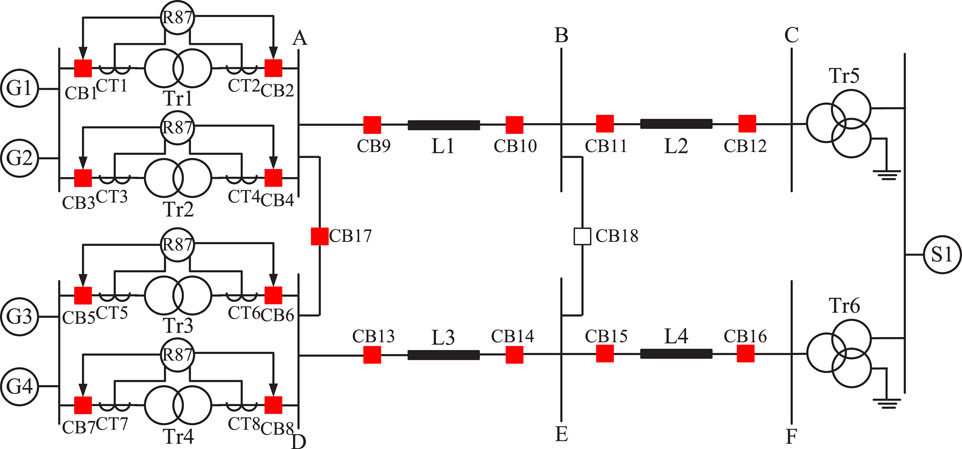
The IEEE power system relaying committee (PSRC) D6 benchmark test system is simulated via OPAL-RT HYPERSIM to generate the data sets in our studies (Gras et al., 2017). The test system consists of two parallel transmission lines that connect a power plant consisting of four 250 MVA generator units to a 230 kV transmission network. Differential protective relays are used to protect the power plant transformers as shown in Figure 8. The settings of the differential protection relays are adjusted as per the SEL-587 relay parameters mentioned in (Laboratories, 2022).

Figure 8

Figure 8. The IEEE PSRC D6 benchmark test system.

Simulations are run for different generation levels of generator units ranging from 350 MW to 360 MW (inclusive) with a step size of 2 MW. This results in $6^4=1296$ different generation level simulation cases for all possible permutations of generation levels. Each simulation is performed for 1.5 s whereby a fault is triggered at a randomly selected time between $t=1$ s and $t=1.02$ s; this interval is selected because it encompasses one frequency cycle (which has a period of 0.0167 s) of a 60 Hz power system to ensure that the fault happens at different points of the current waveform to create a diversely rich data set. Specifically, each generation level case is run 16 times varying the fault start time. Moreover, three different fault types, one-phase-to-ground, two-phase-to-ground, and three-phase-to-ground, are considered for each fault start time. This results in 62,208 different data sequence sets captured during the simulations. As typical, $80\%$ of the data sets are used for training while the remaining $20\%$ are split in half for validation and test data sets. It should be noted that measurements are sampled at the rate of 4,800 packets/sec to be consistent with IEC 61850-9-2 standard for Sampled Value (SV) packet specifications (Brunner et al., 2004).

Input to the anomaly detection model is selected to be a window size of 10 m, which is equivalent to 48 samples of current and angle measurements (for the given sampling rate of 4,800 packets/sec). At each time step, there are 6 current measurements captured from the two current transformers (CTs) on each side of the transformer and 3 phase angle measurements, which amounts to a total of 9 measurements. A 10 m window $W$ is extracted as in Equation 33:

$W=\left[S_{f-23},\dots ,S_f,\dots ,S_{f+24}\right],(33)$

where $S_i$ is the measurement vector at the $i$th time step and $f$ is the middle timestep in the extracted window chosen as below:

$f=\left(t_f\right)+d,d\sim u\left\{-\mathrm{10,10}\right\},(34)$

where $t_f$ is the fault starting timestep and $d$ is an integer uniformly selected from the set $[-\mathrm{10,10}]$.

6.2 Optimizing the architecture of the ML-based anomaly detection systems

An important parameter for machine learning-based anomaly detection systems is the input data length. Because a sliding window of 10 m, (48 samples, each consisting of 9 measurements) is fed as input, the corresponding length of the input (and output, which mirrors the input for reconstruction-based techniques) is $9\times 48=432$. The random search method is adopted for hyperparameter tuning and the Adam optimizer is used for all the models with the learning rate set to 0.001. As such, the hyperparameters of the four reconstruction-based anomaly detection architectures were selected as follows.

1) Linear autoencoder: This model consists of input/output layers of size 432 each and a code layer of size 30. The linear activation function is used for all the neurons.

2) Fully connected autoencoder: This model consists of an input/output size of 432, a hidden layer of size 196, code layer of size 40 in both the encoder and decoder parts.

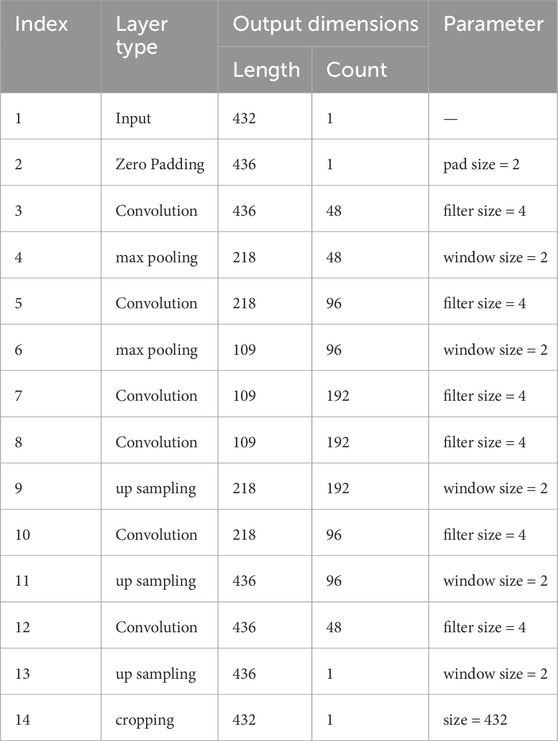
3) 1D convolutional autoencoder: The number of filters, structure of convolution, max-pooling and upsampling layers, and the associated hyperparameters are detailed in Table 2.

4) LSTM: A many-to-many unidirectional LSTM network with one LSTM layer consisting of 20 LSTM units is employed. The input of the model is a data sequence of 48 time steps with a vector of 9 measurements in each time step.

Table 2

Table 2. 1D convolutional network structure.

6.3 Simulation results

The following case studies are considered for the testing of the proposed method. Precision and recall metrics, which are better suited for imbalanced datasets, are used to evaluate the performance of anomaly detection systems.

6.3.1 Model performance before adversarial training

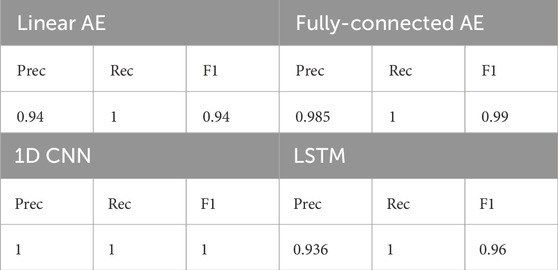
In order to evaluate the performance of the models described in Section 6, an attack dataset is created by generating 250 attack samples from each category as described in Section 3, which amounts to 1,000 attack samples in total. Table 3 shows the performance of the models before adversarial training.

Table 3

Table 3. Performance of the anomaly detection systems before adversarial training.

For each model, a threshold is selected to maximize the recall and then maximize the precision when the recall is fixed. Although the linear autoencoder is a powerful baseline technique, we observe that, in our problem, it has the weakest performance due to insufficient learning capacity compared to the other architectures. In contrast, the CNN demonstrates the best performance, even above LSTM which is designed for sequence prediction. However, this is not unexpected (Bai et al., 2018; Zhang et al., 2015) and we observe that the shift-invariance properly of CNNs helps to achieve the superior performance, in part, because of the random shifts added to the dataset as outlined in Equation 34.

6.3.2 Models performance after adversarial training

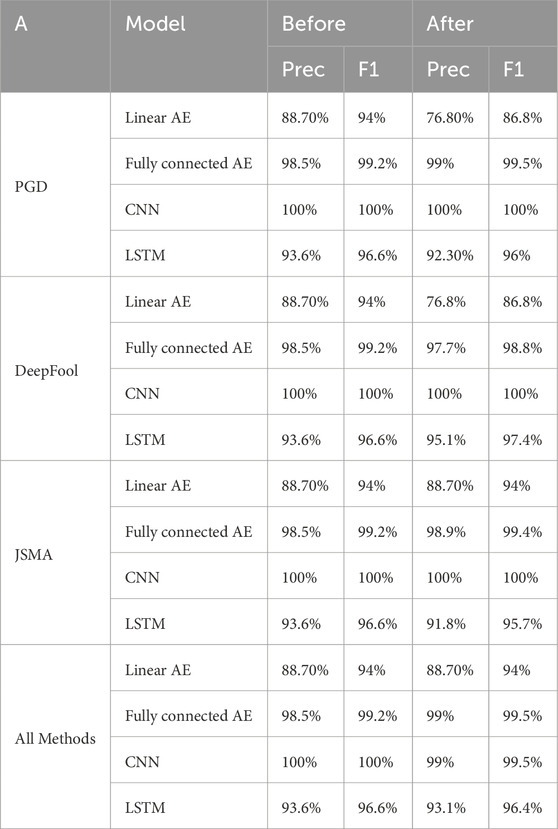
We generated 500 adversarial samples using Algorithm 1 and divided the adversarial data set into non-overlapping training and test sets of 250 samples each. All four models were able to learn the adversarial samples; this was tested using the adversarial sample generalization set for which all four models were able to identify 100 percent of the samples as anomalies. However, as discussed in Kurakin et al. (2016b), adversarial training may have the effect of decreasing model performance if the model is not sufficiently powerful. As such, we also evaluated the performance of the models on the benign samples after adversarial training and results are shown in Table 4. Note that all recall values are 100% and A denotes the adversarial sample generation method.

Table 4

Table 4. Performance of The Anomaly Detection Systems before and after adversarial training.

As observed in the table, there is a dramatic drop in the performance of the linear autoencoder in the case of PGD and DeepFool and a slight decrease in LSTM model performance in case of PGD, JSMA and all methods combined. In contrast, the 1D CNN maintained its stellar performance in case of PGD, DeepFool and JSMA, and the fully connected autoencoder’s performance slightly increased after adversarial training except for the DeepFool case. We argue that the slight increase in the performance after adversarial training can be attributed to the fact that adversarial training can act as a regularizer (Kurakin et al., 2016b).

6.3.3 Generalization of adversarial training

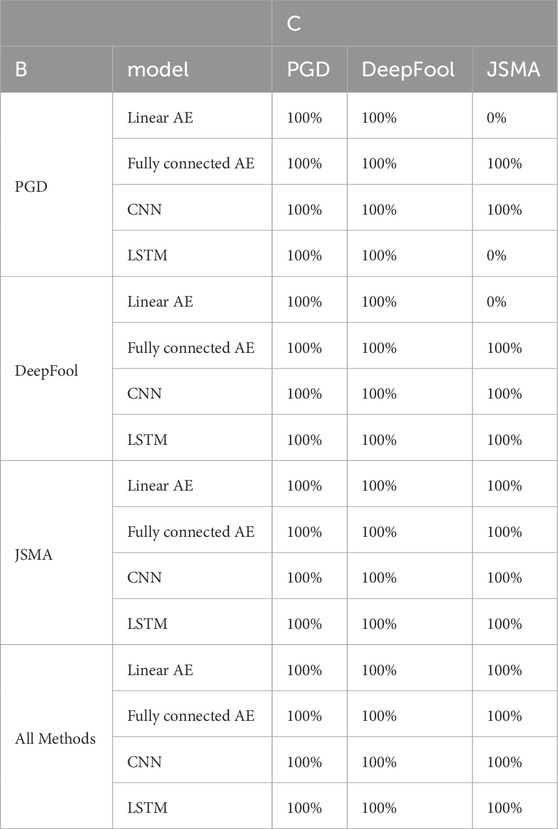
We study the ability of our adversarial training approach to generalize against other attacks. This case study helps to pick the best adversarial sample generation method for adversarial training. To be more specific, we investigated the generalization effect of adversarial training against adversarial test sets not used in the adversarial training process. These test sets are generated using the methods discussed in IV and results are shown in Table 5 where B denotes the method used to generate adversarial samples for adversarial training and C denotes the method used to generate adversarial samples for the generalization set. The results show the generalization of the adversarial training against the same method used in the adversarial training and other methods not used in the training process. Notably, 0% of adversarial sample sets are detected with models before adversarial training. Adversarial training generalizes to unseen samples generated by the same method detecting 100% of the test set. Moreover, using PGD and JSMA samples, the new model is also robust against DeepFool-generated samples. However, using PGD for linear autoencoder and LSTM models does not generalize for JSMA samples, and similar results are observed when DeepFool is used for adversarial training of linear autoencoder. JSMA outperforms the others in our problem by generalizing to the other two methods for all four models. JSMA emphasis on changing the most effective features to craft adversarial samples can be a reason to achieve attack samples distribution that the other methods are unable to achieve. Hence, generalization achieved through adversarial training using them can result in a more inclusive decision border.

Table 5

Table 5. Generalization performance of the adversarial training.

7 Conclusion

In this paper, we demonstrate, for the first time, how false data injection and time synchronization attacks can be designed specifically to target power transformer differential protection. To address this, reconstruction-based anomaly detection models are investigated to enhance cybersecurity of smart grids. However, these models themselves are shown to be vulnerable to cyberattack and we assert in this paper that security of such models can be addressed, in part, through adversarial training. Hence, we propose the first approach for adversarial training of reconstruction-based anomaly detection models and apply that to the problem of power transformer differential protection.

To generate adversarial samples, we leverage three different approaches: PGD, DeepFool, and JSMA. The performance of the models on non-adversarial datasets are studied before and after adversarial training. Moreover, we study the abilities of the models to generalize to unseen adversarial samples generated by other adversarial sample generation methods. Results demonstrate that JSMA exhibits the best generalization over all the models and adversarial samples generated using PGD and DeepFool. Moreover, after adversarial training, the CNN can maintain its performance over non-adversarial samples by 100% precision and recall. According to the results, employing the proposed method for adversarial training with the CNN model architecture combined with JSMA adversarial sample generation results in a more secure anomaly detection model compared to the other approaches. Future work will expand upon our approach to adversarial sample generation and will address other attacks against anomaly detection models for smart grid cybersecurity. Also, this research could be expanded by exploring other adversarial defenses including robust feature learning. Moreover, Using the results of this research, including the high performance of JSMA in adversarial sample generation, can give us hints in order to engineer the features. Another research direction is to investigate the possibility of feature engineering in order to propose features that can be used in shallow or simpler machine learning models in order to detect anomalies. Also, this approach can be expanded to other types of power system protection mechanisms beyond PTDP.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

MJ: Conceptualization, Formal Analysis, Investigation, Methodology, Project administration, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. MoK: Conceptualization, Formal Analysis, Investigation, Methodology, Writing–review and editing, Writing–original draft. MaK: Funding acquisition, Resources, Validation, Writing–review and editing, Writing–original draft. DK: Funding acquisition, Project administration, Resources, Supervision, Validation, Writing–review and editing, Writing–original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akagic, A., and Džafić, I. (2024). Enhancing smart grid resilience with deep learning anomaly detection prior to state estimation. Eng. Appl. Artif. Intell. 127, 107368. doi:10.1016/j.engappai.2023.107368

CrossRef Full Text | Google Scholar

Bai, S., Kolter, J. Z., and Koltun, V. (2018). An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv Prepr. arXiv:1803.01271. doi:10.48550/arXiv.1803.01271

CrossRef Full Text | Google Scholar

Brunner, C., Lang, G., Leconte, F., and Steinhauser, F. (2004). Implementation guideline for digital interface to instrument transformers using iec 61850–9–2. Tech. Rep.

Google Scholar

Case, D. U. (2016). Analysis of the cyber attack on the Ukrainian power grid. Electr. Inf. Shar. Analysis Cent. (E-ISAC) 388.

Google Scholar

Chen, X., Liu, C., Li, B., Lu, K., and Song, D. (2017). Targeted backdoor attacks on deep learning systems using data poisoning. arXiv Prepr. arXiv:1712.05526. doi:10.48550/arXiv.1712.05526

CrossRef Full Text | Google Scholar

Cinà, A. E., Grosse, K., Demontis, A., Vascon, S., Zellinger, W., Moser, B. A., et al. (2023). Wild patterns reloaded: a survey of machine learning security against training data poisoning. ACM Comput. Surv. 55 (13s), 1–39. doi:10.1145/3585385

CrossRef Full Text | Google Scholar

Ferrara, E. (2024). The butterfly effect in artificial intelligence systems: implications for ai bias and fairness. Mach. Learn. Appl. 15, 100525. doi:10.1016/j.mlwa.2024.100525

CrossRef Full Text | Google Scholar

Fu, X., Peng, Y., Liu, Y., Lin, Y., Gui, G., Gacanin, H., et al. (2023). Semi-supervised specific emitter identification method using metric-adversarial training. IEEE Internet Things J. 10, 10778–10789. doi:10.1109/jiot.2023.3240242

CrossRef Full Text | Google Scholar

Glenn, C., Sterbentz, D., and Wright, A. (2016). Cyber threat and vulnerability analysis of the us electric sector. Idaho Falls, ID (United States): Idaho National Lab.INL.

Google Scholar

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep learning. MIT press.

Google Scholar

Goodfellow, I. J., Shlens, J., and Szegedy, C. (2014). Explaining and harnessing adversarial examples. arXiv preprint arXiv:1412.6572.

Google Scholar

Gras, H., Mahseredjian, J., Rutovic, E., Karaagac, U., Haddadi, A., Saad, O., et al. (2017). A new hierarchical approach for modeling protection systems in emt-type software in Intern. Conf. Power syst. Transients.

Google Scholar

Guato Burgos, M. F., Morato, J., and Vizcaino Imacaña, F. P. (2024). A review of smart grid anomaly detection approaches pertaining to artificial intelligence. Appl. Sci. 14 (3), 1194. doi:10.3390/app14031194

CrossRef Full Text | Google Scholar

Han, M., and Crossley, P. (2019). Vulnerability of ieee 1588 under time synchronization attacks in 2019 IEEE power and energy society general meeting (PESGM) (IEEE), 1–5.

CrossRef Full Text | Google Scholar

Hobbs, A. (2021). The colonial pipeline hack: exposing vulnerabilities in us cybersecurity.

Google Scholar

Horowitz, S. H., and Phadke, A. G. (2014). Power system relaying. John Wiley and Sons.

Google Scholar

Jahromi, M. Z., Jahromi, A. A., Kundur, D., Sanner, S., and Kassouf, M. (2021). Data analytics for cybersecurity enhancement of transformer protection. ACM Sigenergy Energy Inf. Rev. 1 (1), 12–19. doi:10.1145/3508467.3508469

CrossRef Full Text | Google Scholar

Jahromi, M. Z., Jahromi, A. A., Sanner, S., Kundur, D., and Kassouf, M. (2020). Cybersecurity enhancement of transformer differential protection using machine learning in 2020 IEEE power and energy society general meeting (PESGM) (IEEE), 1–5.

CrossRef Full Text | Google Scholar

Ji, S., Tan, Y., Saravirta, T., Yang, Z., Liu, Y., Vasankari, L., et al. (2024). Emerging trends in federated learning: from model fusion to federated x learning. Int. J. Mach. Learn. Cybern. 15, 3769–3790. doi:10.1007/s13042-024-02119-1

CrossRef Full Text | Google Scholar

Khaw, Y. M., Jahromi, A. A., Arani, M. F., Sanner, S., Kundur, D., and Kassouf, M. (2020). A deep learning-based cyberattack detection system for transmission protective relays. IEEE Trans. Smart Grid 12 (3), 2554–2565. doi:10.1109/TSG.2020.3040361

CrossRef Full Text | Google Scholar

Khaw, Y. M., Jahromi, A. A., Fm, A. M., Kundur, D., Sanner, S., and Kassouf, M. (2019). Preventing false tripping cyberattacks against distance relays: a deep learning approach in 2019 IEEE international conference on communications, control, and computing technologies for smart grids (SmartGridComm) (IEEE), 1–6.

Google Scholar

Koh, P. W., and Liang, P. (2017). Understanding black-box predictions via influence functions in International conference on machine learning (Sydney, Australia: PMLR), 1885–1894.

Google Scholar

Kurakin, A., Goodfellow, I., and Bengio, S. (2016b). Adversarial machine learning at scale. arXiv Prepr. arXiv:1611.01236. doi:10.48550/arXiv.1611.01236

CrossRef Full Text | Google Scholar

Kurakin, A., Goodfellow, I., Bengio, S., et al. (2022a). Adversarial examples in the physical world.

Google Scholar

Laboratories, S. E. (2022). Sel-587 current differential relay. SEL-578 Data Sheet.

Google Scholar

Lee, D., and Kundur, D. (2014). Cyber attack detection in pm measurements via the expectation-maximization algorithm in 2014 IEEE global conference on signal and information processing (GlobalSIP) (IEEE), 223–227.

CrossRef Full Text | Google Scholar

Liu, G., Tian, Z., Chen, J., Wang, C., and Liu, J. (2023). Tear: exploring temporal evolution of adversarial robustness for membership inference attacks against federated learning. IEEE Trans. Inf. Forensics Secur. 18, 4996–5010. doi:10.1109/tifs.2023.3303718

CrossRef Full Text | Google Scholar

Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and Vladu, A. (2017). Towards deep learning models resistant to adversarial attacks arXiv preprint arXiv:1706.06083.

Google Scholar

McMahan, B., Moore, E., Ramage, D., Hampson, S., and y Arcas, B. A. (2017). Communication-efficient learning of deep networks from decentralized data in Artificial intelligence and statistics (Fort Lauderdale, FL: PMLR), 1273–1282.

Google Scholar

Moosavi-Dezfooli, S.-M., Fawzi, A., and Frossard, P. (2016). Deepfool: a simple and accurate method to fool deep neural networks in Proceedings of the IEEE conference on computer vision and pattern recognition, 2574–2582.

Google Scholar

Narang, J. K., and Bag, B. (2024). Deep learning-based integrated attack detection framework to protect distance relays against cyberattacks. Electr. Power Syst. Res. 231, 110346. doi:10.1016/j.epsr.2024.110346

CrossRef Full Text | Google Scholar

National Academies of Sciences (2017). Engineering, and Medicine and others, Enhancing the resilience of the nation’s electricity system. National Academies Press.

Google Scholar

Rezaee, K., Rezakhani, S. M., Khosravi, M. R., and Moghimi, M. K. (2024). A survey on deep learning-based real-time crowd anomaly detection for secure distributed video surveillance. Personal Ubiquitous Comput. 28 (1), 135–151. doi:10.1007/s00779-021-01586-5

CrossRef Full Text | Google Scholar

Sanchez-Matilla, R., Li, C. Y., Shamsabadi, A. S., Mazzon, R., and Cavallaro, A. (2020). Exploiting vulnerabilities of deep neural networks for privacy protection. IEEE Trans. Multimedia 22 (7), 1862–1873. doi:10.1109/tmm.2020.2987694

CrossRef Full Text | Google Scholar

Shokri, R., Stronati, M., Song, C., and Shmatikov, V. (2017). Membership inference attacks against machine learning models in 2017 IEEE symposium on security and privacy (SP) (IEEE), 3–18.

CrossRef Full Text | Google Scholar

Slowik, J. (2018). Anatomy of an attack: detecting and defeating crashoverride. Montreal, QC: VB2018, October.

Google Scholar

Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I., et al. (2013). Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199.

Google Scholar

Taha, A. F., Qi, J., Wang, J., and Panchal, J. H. (2016). Risk mitigation for dynamic state estimation against cyber attacks and unknown inputs. IEEE Trans. Smart Grid 9 (2), 886–899. doi:10.1109/tsg.2016.2570546

CrossRef Full Text | Google Scholar

Tramèr, F., Zhang, F., Juels, A., Reiter, M. K., and Ristenpart, T. (2016). Stealing machine learning models via prediction apis in 25th {USENIX} security symposium ({USENIX} security 16), 601–618.

Google Scholar

Wang, X., Li, J., Kuang, X., Tan, Y.-a., and Li, J. (2019). The security of machine learning in an adversarial setting: a survey. J. Parallel Distributed Comput. 130, 12–23. doi:10.1016/j.jpdc.2019.03.003

CrossRef Full Text | Google Scholar

Wen, J., Zhang, Z., Lan, Y., Cui, Z., Cai, J., and Zhang, W. (2023). A survey on federated learning: challenges and applications. Int. J. Mach. Learn. Cybern. 14 (2), 513–535. doi:10.1007/s13042-022-01647-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., Han, X., Qiu, H., and Zhang, T. (2023). Computation and data efficient backdoor attacks in Proceedings of the IEEE/CVF international conference on computer vision, 4805–4814.

Google Scholar

Yang, Z., He, X., Li, Z., Backes, M., Humbert, M., Berrang, P., et al. (2023). Data poisoning attacks against multimodal encoders in International conference on machine learning (Honolulu, HI: PMLR), 39299–39313.

Google Scholar

Zhang, M., Yu, N., Wen, R., Backes, M., and Zhang, Y. (2024). Generated distributions are all you need for membership inference attacks against generative models in Proceedings of the IEEE/CVF winter conference on applications of computer vision, 4839–4849.

Google Scholar

Zhang, X., Zhao, J., and LeCun, Y. (2015). Character-level convolutional networks for text classification. Adv. neural Inf. Process. Syst. 28. doi:10.48550/arXiv.1509.01626

CrossRef Full Text | Google Scholar

Zhang, Z., Gong, S., Dimitrovski, A. D., and Li, H. (2013). Time synchronization attack in smart grid: impact and analysis. IEEE Trans. Smart Grid 4 (1), 87–98. doi:10.1109/tsg.2012.2227342

CrossRef Full Text | Google Scholar