Fault probability identification method for distribution networks based on mov-MF distribution

To address the fault identification challenge in distribution networks, a method leveraging a mixture of the von Mises–Fisher (mov-MF) distribution model for fault probability identification is proposed. Initially, the synchronous phasor measuring unit is employed to gather the post-fault steady-state voltage phase quantities, and then, the voltage phase angle values are combined to form a three-dimensional feature quantity. Subsequently, the mov-MF distribution model is initialized through the spherical K-means algorithm and the minimum message length algorithm. This model is further refined via the expectation–maximization algorithm to iteratively optimize distribution parameters. The test set data are input into the mov-MF distribution model, which has been constructed using typical fault data, to discern fault types. Finally, the efficacy of the proposed method is validated through simulation verification conducted on the IEEE 33-node distribution system. The analysis of the examples demonstrates the accuracy of the mov-MF distribution model-based fault identification method in identifying single-phase ground, two-phase ground, two-phase interphase, and three-phase short-circuit faults.

1 Introduction

The requirements for ensuring power supply quality and reliability of modern distribution networks as the terminal facing users are gradually increasing (Sheng et al., 2023). Currently, the main grounding methods for distribution networks in China are either ungrounded neutral points or grounding through arc suppression coils. Due to the complex structure of distribution networks, various types of faults are likely to occur in practical operation. Single-phase grounding short circuit is the most common type of short circuit fault. If the short circuit is caused by the contact between the line and tree branches or the ground, the transient resistance of this short circuit is high, resulting in a weak fault electrical quantity that is difficult to detect, thereby affecting the normal operation of the distribution network. When faults occur in distribution networks, the primary task is to identify the faults. Therefore, efficient and reliable methods for fault identification in distribution networks are of great significance for the safe operation of distribution networks (Peng et al., 2023).

Zhu et al. (2020) utilized current, voltage, and power data at the maximum power point in the time domain as feature quantities, combined with Pearson’s coefficient similarity and relative Euclidean distance deviation for fault-type differentiation. Jiang et al. (2021) used dynamic time warping (DTW) similarity and electrical volume data sequence similarity, and the combination of both inputs into a classifier significantly outperformed single features. Zhang et al. (2022a) proposed a waveform similarity-based identification method to construct two reconstructed currents by comparing the one-dimensional time-domain sampled values of the currents at the two ends of a transmission line and used the Kendall’s tau coefficient (KTC) waveform similarity algorithm to achieve reliable fault identification. Zhang et al. (2022b) proposed a sparse representation method based on one-dimensional time-domain current signals to construct a fault feature dictionary and calculate the feature residuals to determine the fault category. Liu et al. (2020) built a support vector machine model for high-resistance grounding fault identification using time-domain current-voltage magnitude and frequency as features. Ghaemi et al. (2022) used an integrated learning approach combined with multiple classifiers to accurately identify the fault type and location using one-dimensional time-domain voltage and current measurements, which maintains high classification accuracy even in the presence of measurement errors.

In contrast to the previous paper, which proposes to judge the fault type by constructing the signal similarity or deviation value as a one-dimensional feature quantity, another class of methods automatically proposes multi-dimensional feature quantities and makes the fault-type judgment through intelligent algorithms. Yang and Yu (2022) used a discrete wavelet transform to decompose three-phase voltage and zero-sequence sequences and constructed multidimensional time–frequency matrices to input into the ResNet network, which improved the effect of fault-type identification in distribution networks. Xingquan et al. (2022) converted the time-domain three-phase voltage and current data during faults into a multidimensional time–frequency spectral gray scale map, combined with SVM and a deep convolutional neural network, to improve the accuracy of high-resistance fault classification. Biswas et al. (2023) used variational mode decomposition (VMD) to quickly extract different frequency components of the fault current signal, which is input into the CNN for fault-type identification in the frequency domain to shorten the detection time and ensure the accuracy. Azizi and Seker (2022) processed the current time-domain signal through the Hilbert–Huang transform, formed the multidimensional feature quantity of the frequency-domain signal combination under different frequencies, and used BrownBoost algorithm to classify the data space, which improved the accuracy of fault-type classification. Feng et al. (2022) used the linear discriminant analysis (LDA) algorithm to incorporate the frequency-domain optimal fault features, which constitute two-dimensional and three-dimensional feature quantities, into the Bayesian classification model based on the kernel distribution to achieve fault location identification, in which the three-dimensional feature quantities are better than the two-dimensional feature quantities.

The fault identification methods mentioned in the literature can be broadly categorized into two types:

1. Extraction of time-domain electrical quantities: In this category, time-domain electrical quantities such as voltage and current amplitudes are extracted as one-dimensional features to represent fault types. Fault identification is achieved through methods such as constructing similarity or deviation values and comparing them against thresholds.

2. Time-frequency transformation methods: This category involves transforming the collected time-domain signals into multidimensional time–frequency matrices or forming grayscale images using time–frequency transformation methods. Intelligent algorithms are then employed to automatically extract multidimensional feature sets for fault type identification, resulting in improved accuracy compared to the first category. However, establishing time–frequency matrices or forming grayscale images requires complex preprocessing of time-domain signals, leading to longer computation times. Compared to one-dimensional features, multidimensional feature sets contain richer fault information and exhibit better classification performance. It is worth noting that the signals processed in the literature mostly consist of phasor magnitudes, overlooking the fault information contained in phase angles.

Wang et al. (2021a) utilized an improved VMD combined with fuzzy c-means (FCM) to achieve classification and identification of rolling bearing fault types through FCM clustering. Qi et al. (2021) utilized the von Mises–Fisher (v-MF) distribution combined with the standard Euclidean distance to analyze the similarity between different samples for sample selection. Initialization of different groups requires pre-setting a lower limit for the grouping values but does not implement merging of similar groups. Chen et al. (2015) proposed the combination of the expectation–maximization (EM) algorithm and the v-MF algorithm. By selecting the positioning data on crystal positions to form a v-MF distribution and using cosine similarity as the clustering basis, crystal-type identification is carried out. However, the consideration for the number of groups in mixed distributions is not addressed. Garcia-Fernandez et al. (2019) utilizes the v-MF distribution to construct Gaussian filters for target direction measurement. Angle information is used to form two-dimensional and three-dimensional vectors for tracking target directions, but the establishment of distributions for multiple targets is not implemented. Data clustering is a fundamental step in data analysis. The application of von Mises–Fisher (v-MF) distribution-based clustering methods has shown good utility in sample selection (Qi et al., 2021), crystal-type identification (Chen et al., 2015), direction measurement tracking (Garcia-Fernandez et al., 2019), and other areas.

1.1 Contributions

The main contributions of this paper are summarized below.

• In this paper, we propose a probabilistic fault identification method based on the mixed von Mises–Fisher (v-MF) distribution. The mov-MF distribution of sample data is established, and fault probability is calculated by integrating the data to be measured into the established mov-MF distribution. Fault-type identification is then achieved based on the resulting probability magnitude. The biggest innovation of the mov-MF-based probabilistic fault identification method for distribution networks proposed in this paper is the fault-type identification by establishing the clustering distribution of 3D vector data on the spherical space. In power systems, there are a large number of 3D vectors, so the method is suitable for power system data analysis. Compared with the two types of fault identification methods introduced in the previous paper, the method proposed in this paper can make the accuracy of fault identification higher by using 3D vectors; the use of 3D eigenvectors in the time domain to establish the mov-MF distribution without complex data preprocessing makes the algorithm more concise, ensures accuracy, and at the same time, improves the computational efficiency.

• To establish the mixed von Mises–Fisher (v-MF) distribution of sample data more accurately, we employ the spherical K-means algorithm and minimum message length (MML) for parameter initialization. Subsequently, these parameters are iteratively optimized using the expectation–maximization (EM) algorithm to refine the accuracy of the mov-MF distribution parameters. We validate this approach through simulations conducted on an IEEE 33-node distribution system, where various fault conditions are set. The test results are compared with those reported in Xingquan et al. (2022) and Azizi and Seker (2022). Our findings demonstrate that the proposed method achieves accurate fault-type identification. Moreover, the acquisition of feature vectors is simplified, and the accuracy is comparable to that of the comparison method. Importantly, our method exhibits robust performance across different fault conditions, highlighting its broad applicability.

1.2 Paper organization

The remainder of the paper is structured as follows: Section 2 provides an introduction to the fundamental theory of von Mises–Fisher (v-MF) distribution and the expectation–maximization (EM) algorithm. Section 3 outlines the initialization method for parameters of the mov-MF distribution, along with the algorithm for fault-type identification based on the mov-MF distribution. Section 4 verifies the effectiveness and applicability of the proposed method through simulation examples.

2 The von Mises–Fisher basic theory

The von Mises–Fisher distribution is the probability distribution of directional statistics for spherical surface data. A d-dimensional unit random vector x (i.e., $x\in {\mathbb{R}}^d$ and $‖x‖=1$) is said to have the d-variate von Mises–Fisher (v-MF) distribution if its probability density function is given by

$f\left(x|\mu ,\kappa \right)=c_d\left(\kappa \right)e^{\left(\kappa {\mu }^{T}x\right)},(1)$

In the Eq. 1, where $‖\mu ‖=1$, $\kappa \ge 0,d\ge 2$. The normalizing constant $C_d\left(\kappa \right)$ is given by

$c_d\left(\kappa \right)={\left(\kappa \right)}^{d/2-1}/{\left(2\pi \right)}^{d/2}{I}_{d/2-1}\left(\kappa \right),(2)$

where $I_d\left(\kappa \right)$ represents the first kind-modified Bessel function.

The probability density $f\left(x|\mu ,\kappa \right)$ function is determined by the mean direction $\mu$ and concentration parameter $\kappa$. The mean direction $\mu$ represents the central direction of clustering of this type of data on the spherical surface, indicating the direction of clustering. The concentration parameter $\kappa$ represents the concentration of data in this direction. A higher value indicates a higher degree of clustering of data in this direction. The specific comparison chart is shown in Figure 1

Figure 1

Figure 1. Clustering effects of different concentration parameters.

2.1 Maximum likelihood estimation

For a given dataset $\chi$, we want to find the maximum likelihood estimates of the parameters: mean direction $\mu$ and concentration parameter $\kappa$ of its probability density function $f\left(\chi |\mu ,\kappa \right)$. Assuming these data are independently and identically distributed, the logarithm of the likelihood for $\chi$ can be expressed as

$\ln P\left(\chi |\mu ,\kappa \right)=n\ln c_d\left(\kappa \right)+\kappa {\mu }^{T}r.(3)$

To obtain the maximum likelihood estimates of mean direction $\mu$ and concentration parameter $\kappa$, we introduce Lagrange multipliers and derive the maximum likelihood estimation from Equation 3, resulting following Eqs 4, 5:

$\widehat{\mu }=\frac{r}{‖r‖}=\frac{{\sum }_{i=1}^n{x}_i}{‖{\sum }_{i=1}^n{x}_i‖},(4)$

$\frac{I_{d/2}\left(\widehat{\kappa }\right)}{I_{d/2-1}\left(\widehat{\kappa }\right)}=\overline{r}=\frac{‖{\sum }_{i=1}^n{x}_i‖}{n}.(5)$

Due to the implicit equation involving the ratio of Bessel functions in the calculation process of the above expression, it is impossible to obtain an exact analytical solution directly. Therefore, we must use numerical asymptotic approximation methods to obtain an approximate solution for the concentration parameter $\widehat{\kappa }$, expressed using Eq. 6. We select the best performing approximate solution method proposed in Zhe et al. (2019):

$\widehat{\kappa }=\frac{\overline{r}d-{\overline{r}}^3}{1-{\overline{r}}^2}.(6)$

2.2 Parameter estimation of mov-MF distribution based on the EM algorithm

The process of using v-MF distributions for fault-type identification requires a hybrid model containing multiple v-MF distributions. We now consider a mix of $k$ v-MF (mov-MF) distributions that serves as a generative model for directional data. Let ${\left\{f_h\left(x|\mu ,\kappa \right)\right\}}_{h=1}^k$ denote the hth v-MF distribution, then a mixture of these k v-MF distributions given by Eq. 7:

$f\left(x|{\left\{{\mu }_h,{\kappa }_h,{\pi }_h\right\}}_{h=1}^k\right)={\sum }_{h=1}^k{\pi }_h{f}_h\left(x|{\mu }_h,{\kappa }_h\right),(7)$

where ${\pi }_h$ denotes the weights of the different types of components and the sum is 1. We randomly select the hth v-MF distribution with weights ${\pi }_h$ and sample a point from that distribution $f_h\left(x|{\mu }_h,{\kappa }_h\right)$. Let $\chi =\left\{x_1,\cdots ,x_n\right\}$ be the dataset of n independently sampled points that follow Eq. 7. Let $Z=\left\{z_1,\cdots ,z_n\right\}$ be the corresponding set of hidden random variables that indicate the particular v-MF distribution from which the points are sampled. In particular, $z_i=h$ if $x_i$ is sampled from $f_h\left(x|{\mu }_h,{\kappa }_h\right)$. Assuming that the values in the set $Z$ are known, the log-likelihood of the observed data is given by

$\ln P\left(\chi ,Z|\mu ,\kappa \right)={\displaystyle \sum _i^n}\ln \left({\pi }_{zi}{f}_{zi}\left(x_i|{\mu }_{zi},{\kappa }_{zi}\right)\right).(8)$

Equation 8 is actually a random variable dependent on Z, which follows a distribution. This random variable is referred to as the complete data log-likelihood. Given a particular value of $\left(\chi ,\mu ,\kappa \right)$, the conditional probability expectation of $Z|\left(\chi ,\mu ,\kappa \right)$ is calculated, and this estimation forms the E-step in an EM framework.

Using an EM approach for maximizing the expectation of Eq. 8), we can summarize the steps for estimating the mov-MF parameters based on the EM algorithm.

Algorithm 1.EM algorithm.

Input: set X of data points

Output: a mov-MF distribution; initialize all ${\pi }_h,{\mu }_h,{\kappa }_h,h=1,...,k$

Repeat

{The E-step of EM}

for $i=1$ to $n$ do

 for $h=1$ to $k$ do

  $f_h\left(x_i|{\mu }_h,{\kappa }_h\right)\leftarrow c_d\left({\kappa }_h\right)e^{\left({\kappa }_h{{\mu }_h}^T{x}_i\right)}$

 end for

 for $h=1$ to $k$ do

  $p\left(h|x_i,\mu ,\kappa \right)\leftarrow \frac{{\pi }_h{f}_h\left(x_i|{\mu }_h,{\kappa }_h\right)}{{\sum }_{l=1}^k{\pi }_l{f}_l\left(x_i|{\mu }_l,{\kappa }_l\right)}$

 end for

end for

{The M-step pf EM}

for $h=1$ to $k$ do

  ${\pi }_h=\frac{1}{n}{\displaystyle \sum _{i=1}^n}p\left(h|x_i,\mu ,\kappa \right)$

  $r_h={\displaystyle \sum _{i=1}^n}{x}_{i}p\left(h|x_i,\mu ,\kappa \right)$

  ${\widehat{\mu }}_h=\frac{r_h}{‖r_h‖}$

  $\widehat{\kappa }=\frac{{\overline{r}}_{h}d-{{\overline{r}}_h}^3}{1-{{\overline{r}}_h}^2}$

end for

until convergence

On termination, the algorithm gives the parameters ${\pi }_h,{\mu }_h,{\kappa }_h$ of the k v-MF distributions that model the dataset $\chi$, as well as the soft-clustering, i.e., the posterior probabilities $p\left(h|x_i,\mu ,\kappa \right)$, for all $h$ and $i$.

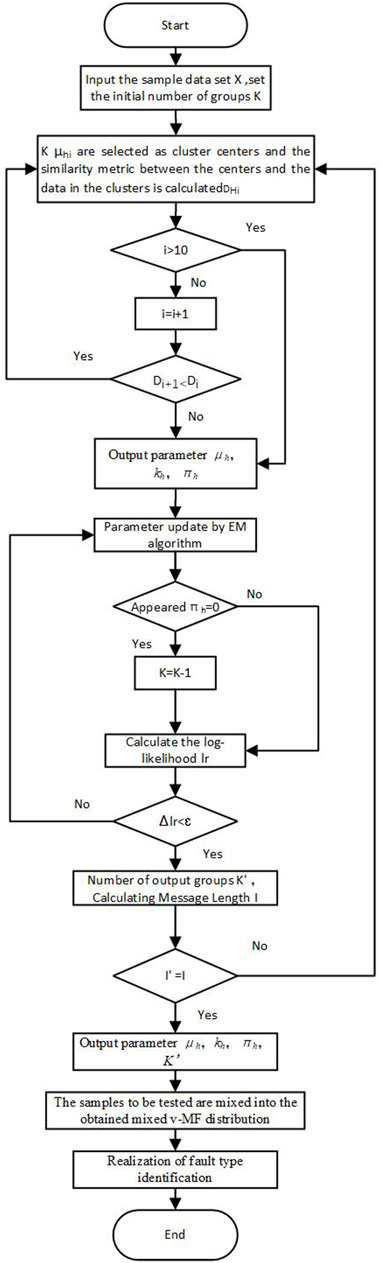
3 Steps for designing the fault identification model based on mov-MF distribution

3.1 Data preprocessing and dataset construction

The fault signals of the distribution network are acquired and combined to form a three-dimensional vector $\mathrm{\Psi }\left({\phi }_1,{\phi }_2,{\phi }_3\right)$, which is converted into directional data by L2 normalization. The dataset consists of voltage phasors measured by the PMU under different fault conditions. After a fault occurs, the positive–negative–zero-sequence voltage phasors of different types of faults vary widely, and the main difference exists between the phase angles. The L2 normalized data are distributed on the unit sphere, and the different types of fault vectors are combined to form a dataset in the form of a matrix.

3.2 Calculation of the parameters of the mov-MF distribution

As the EM algorithm is needed to establish the mov-MF distribution, there is an important problem that in the case of the known distribution $\chi$, we need to solve the distribution of the average direction $\mu$ and concentration parameters $\kappa$. From Section 2.2, we need to use the log-likelihood function as the objective function to estimate the unknown parameters $\mu$ and $\kappa$, and the log-likelihood function is non-convex; there are some small local maxima and local minima, so avoiding such problems is essential to improve the performance of the EM algorithm. Therefore, avoiding such problems is crucial to improve the performance of the EM algorithm. The EM algorithm is more sensitive to the initial value, and the clustering result fluctuates greatly with the change in the initial value, so it is chosen to determine the reasonable starting state of the EM by the preliminary clustering of the data.

3.2.1 mov-MF model parameter initialization

The mov-MF parameters are computed by initializing the spherical K-means algorithm, updating the parameters by the EM algorithm, and determining whether the optimality is reached based on the cosine similarity $D$.

Initialization is performed using the spherical K-means algorithm (Mashal and Hosseini, 2015), where the $n\times d$ data matrix is first divided into K clusters, K generally needs to be set in advance, and K data points are selected as the initial cluster centers. Before the algorithm, it is assumed that in the case of a mov-MF distribution, all classified clusters are equal a priori, i.e., for each distribution ${\pi }_h=\frac{1}{k},h=1,\cdots ,k$, while it is further assumed that all classified clusters have equal concentration parameters, which are generally set to ${\kappa }_h=100$. For the case of mov-MF distribution, some distant data points are selected as initialization parameters ${\mu }_h$ for different clusters.

In order to realize the classification of different data points, the distance metric between different points on the unit hypersphere is defined, which can be mainly categorized into Euclidean distance, Manhattan distance, cosine distance, and correlation distance, etc., depending on the clustering requirements. Jianyuan et al. (2023) explained the rationality of using cosine similarity as a distance metric for clustering. Therefore, we choose to calculate the cosine similarity $S$ as the clustering metric.

$S={x_i}^T{\mu }_h.(9)$

Thus, the cluster label to which each data point belongs is determined based on the similarity of the data point to the initial cluster center.

$X_h\leftarrow X_h\cup \left\{x_i\right\},h=\underset{h^{\prime }}{\mathrm{argmax}{x_i}^T{\mu }_{h^{\prime }}}.(10)$

From this, we obtain the center of each cluster ${\mu }_h$, initialize again to select a set of cluster centers ${\mu }_h$, and compare the distance between the data points in the cluster and the center point $D$, $D=1-S$. If the distance $D$ of the current clustering result is smaller than that of the previous generation, then update the clustering result until the distance $D$ does not change anymore to get the optimal clustering result of the K clusters at this time and compute the average direction ${\mu }_h$, concentration parameter ${\kappa }_h$, and mixing distribution weight ${\pi }_h$ of each cluster at this time, which is used as the initial parameter of the mov-MF model. In order to improve the accuracy of the initial parameters, multiple initializations are usually performed, and the group with the smallest distance $D$ is chosen as the initialization parameter.

3.2.2 mov-MF model group score determination

On the basis of step a), the group score of the sample data is determined by the MML algorithm, and according to the log-likelihood $l_r$ and the minimum message length $I\left(\pi \right)$ to determine whether the optimal group score is reached or not and through many iterations of the EM algorithm, the mov-MF distribution of the typical sample data is obtained.

When the mov-MF model group scores are determined, then the EM algorithm is used to estimate the mixture distribution parameters, i.e., the mixture distribution weights and the parameters for each subgroup. Thus, we need to determine the optimal number of subgroups for the mixture distribution and the corresponding distribution parameters.

Therefore, the minimum message length (MML) algorithm is used for group score $K$ determination. First, we need to encode the parameters using MML and calculate the message length corresponding to different parameters. The log-likelihood ratio of the mov-MF distribution for a set of fractions is given by Eq. 11:

$\left(\chi \left|\mathrm{\Phi }\right.\right)={\displaystyle \sum _{i=1}^n}\ln {\displaystyle \sum _{h=1}^K}{\pi }_h{f}_h\left(x_i;{\mathrm{\Theta }}_h\right),(11)$

where ${\pi }_h$ and $f_h\left(x_i;{\mathrm{\Theta }}_h\right),{\mathrm{\Theta }}_h=\left({\mu }_h,{\kappa }_h\right)$ are the weights and probability densities of the hth group component, respectively, under the assumption that the initial number of group scores, $K$, is determined; $K$ is a number of groupings for the current hypothesis; and the maximum likelihood is estimated to be ${\mathrm{\Phi }}_{ML}=\underset{\mathrm{\Phi }}{\mathrm{argmax}}\left(\chi \left|\mathrm{\Phi }\right.\right)$, using the EM algorithm for the estimation of the above mixing parameters.

For step E, rewriting the formulas for calculating the conditional expectation probability of the joint distribution, expressed by Eqs 12, 13:

$r_{hi}=\frac{{\pi }_{h}f\left(x_i;{\mathrm{\Theta }}_h\right)}{{\sum }_{h=1}^K{\pi }_{h}f\left(x_i;{\mathrm{\Theta }}_h\right)},\forall 1\le i\le N,1\le h\le K,(12)$

$n_h={\displaystyle \sum _i^N}{r}_{hi}.(13)$

For the M-step, assuming an estimate ${\mathrm{\Phi }}^{\left(t\right)}$ for the tth iteration, the local parameters and the maximum log-likelihood estimates used to compute the next one, and the weights of the hth component are updated as ${\pi }_h^{\left(t+1\right)}=\frac{n_h^{\left(t\right)}}{N}$.

Based on the expression proposed in Kasarapu and Allison (2015) for encoding the component weights, the message length expression for the hybrid weights ${\pi }_h$ is redefined on this basis by combining the log-likelihood $l_r\leftarrow E\left({\sum }_{h=1}^k{\pi }_h{f}_h\left(x|{\mu }_h,{\kappa }_h\right)\right)$ obtained from the E-step:

$I\left(\pi \right)=-l_r+N{\displaystyle \sum _{h=1}^K}\ln {\pi }_h+\ln N\cdot \left(K-1\right)!(14)$

According to the initialization parameters obtained by the spherical K-means algorithm, the log-likelihood $l_r$ and the message length of the hybrid weight $I\left(\pi \right)$ in the initial state. The message length of the hybrid weight expressed by Eq. 14. Execute the E-step to calculate the initial log-likelihood was executed using the initialization parameters ${\mu }_h$, ${\kappa }_h$, and ${\pi }_h$, and then the M-step was executed to calculate the parameters at the time of maximization of the expectation; after completing the calculation of the corresponding parameters for each subgroup, the log-likelihood and the message length were updated at this time. If a subgroup of a subgroup is set to 0, the subgroup is removed from the model, and the number of subgroups is reduced. At the end of each E-step and M-step, the log-likelihood is compared with the previous generation by calculating the log-likelihood and judging whether convergence occurs based on the threshold value $\Delta l_r$. calculated from Eq. 15.

$\Delta l_r=\frac{l_r^{\left(t+1\right)}-l_r^t}{{l_r}^t}<\epsilon ,\epsilon ={10}^{-12}.(15)$

Meanwhile, after each iteration of the E–M step to the number of confirmed groups, the new message length $I^{\prime }\left(\pi \right)$ is recalculated, checking whether the current message length is no longer changing and thus determining whether the optimal result is reached.

It is likely that there are two or even more similar groupings in the initialization phase, and when there are such groupings with very close average directions, group merging is required. Using the mean direction ${\mu }_h$ of each group, the similarity between different groups is calculated, the similarity is used to determine if they are similar groups, these groups are merged, and the parameters ${\mu }_h$, ${\kappa }_h$, and ${\pi }_h$ and the number of groups $K$ are updated.

3.3 Fault-type identification

After establishing a mov-MF distribution based on the sample data, the samples to be tested are mixed into the constructed sample mov-MF distribution, and the probabilities of the samples to be tested attributed to different types of faults are calculated. The fault label is then determined according to the size of the probability, thus realizing fault-type identification.

Labeling of fault types $h=1,2,\dots ,k$, weights ${\pi }_h$ are the weights corresponding to different fault types in the mov-MF model obtained from the sample data; $r_{hi}$ is the probability of the fault types of the data to be measured, and according to the size of the probability, the vector of the data to be measured is assigned to the grouping of the fault types with the largest probability to realize the fault-type identification.

$h=\arg \underset{h\in \left\{1\dots k\right\},i\in \left\{1\dots N\right\}}{\max }{r}_{hi}.(16)$

Algorithm 2.Fault identification algorithm.

Step 1: Input sample dataset $\chi$, set the initial number of groups $K$, and set the initial ${\kappa }_h=100$, ${\pi }_h=\frac{1}{K}$.

Step 2: Select K ${\mu }_{hi}$ as cluster centers, calculate the similarity index $D_{hi}$ between the selected cluster centers and the data in the clusters, and if it is smaller than the previous generation result, then re-select the cluster centers and repeat step 2 until $D_{hi}$ is larger than the previous generation result.

Step 3: After the initial cluster centers ${\mu }_h$ are selected, the obtained initialization parameters and dataset $\chi$ are used to estimate and update the parameters by the EM algorithm (Algorithm 1).

Step 4: After obtaining the mov-MF distribution of the $K$ subgroups, determine whether to keep the subgroups by judging whether ${\pi }_h$ is zero or not.

Step 5: Calculate the log-likelihood $\Delta l_r$ and determine whether convergence has been reached; if not, return to step 3.

Step 6: Calculate the message length of the mixed weights $I\left(\pi \right)$ and determine whether the message length is no longer changing, otherwise return to step 2.

Step 7: Output ${\mu }_h$, ${\kappa }_h$, ${\pi }_h$, and $K$ and, get the mixture v-MF distribution of sample dataset $\chi$ for. Mix the samples to be tested into this distribution, and realize the fault-type identification by Eq. 16.

The step-by-step flowchart is shown in Figure 2:

Figure 2

Figure 2. Flowchart of fault identification based on the mov-MF algorithm.

4 Example analysis

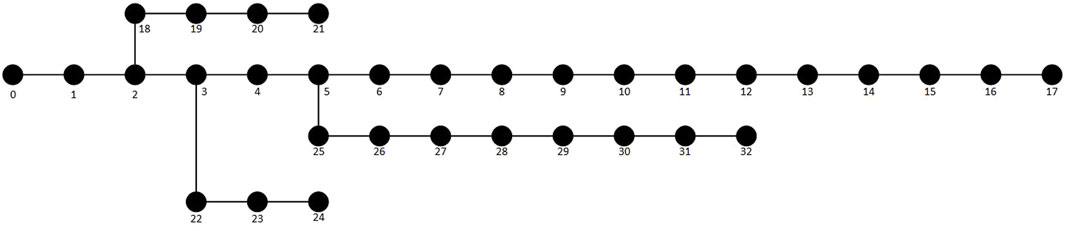
In order to verify the effectiveness of the fault identification method based on the mov-MF model proposed in this paper, simulation experiments are carried out in MATLAB/Simulink on the IEEE33 node 10-kV distribution system, as shown in Figure 3, to obtain the fault sample data.

Figure 3

Figure 3. 10-kV IEEE33 node distribution network model.

4.1 Sample data

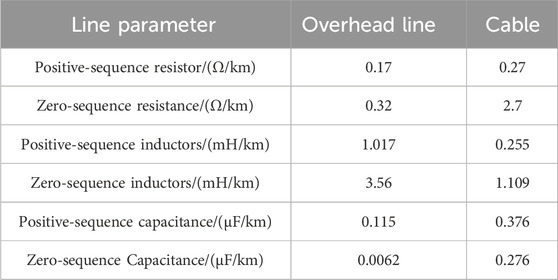
Fault points are set between nodes 8–9, 13–14, 18–19, and 23–24, respectively, where nodes 20–21, 11–17, 22–24, and 29–32 are connected by overhead lines, and the rest of the lines are connected by cables, and the parameters of each sequence of the overhead lines and cables are shown in Table 1, line model parameters (Wang et al., 2021b). The system is a 10-kV distribution network. It is set up with transformer grounding methods that are neutral ungrounded and neutral grounded via arcing coil(0.8697H). Only one of the above fault parameters is changed in each simulation, and the duration of each type of fault is 0.1 s. The synchronized phase data are collected using a PMU, and a measuring device is installed at each node, with an update interval of 10 m and a sampling frequency of 6.4 kHz. A total of 560 sets of fault samples are generated, of which 420 sets comprise the training set and 140 sets comprise the test set. The fault conditions are neutral ungrounded; neutral grounded via arcing coil; transition resistance 0Ω, 1Ω, 10Ω, and 1000Ω and has access to distributed power; and the abovementioned seven conditions are grouped into four fault points for single-phase grounded short-circuit faults (AG,BG,CG), two-phase grounded short-circuit faults (ABG,BCG,ACG), three-phase short-circuit faults, and two-phase interphase short-circuit faults (AB,BC,AC); 80 fault samples are generated for each group, and 33 data points are obtained for each set of data, and the mov-MFs are established, respectively, under different conditions.

Table 1

Table 1. Line model parameter.

Based on the principle in Section 3.1, the vector dataset suitable for building the mov-MF model is constructed. In the mov-MF model, the main judgment basis for fault-type identification is the average direction $\mu$ of the grouped clusters, so the phase angle values of the positive–negative-sequence and zero-sequence voltage phasors at the moment of 0.05 s after the fault are selected to be combined into the three-dimensional feature vectors $\mathrm{\Psi }\left({\phi }_{u_1},{\phi }_{u_2},{\phi }_{u_0}\right)$.

The feature vectors extracted from the typical sample fault dataset are used as initial vectors for L2 normalization to obtain the normalized ${\mathrm{\Psi }}^{\prime }\left({\phi }_{u_1},{\phi }_{u_2},{\phi }_{u_0}\right)$. The 3D feature vectors of each data point for each fault type obtained after normalization are combined to form a 330 × 3 initial vector matrix ${\mathrm{\Psi }}^{\prime }={\left[\begin{array}{ccccc}{{\mathrm{\Psi }}^{\prime }}_1& {{\mathrm{\Psi }}^{\prime }}_2& \cdots & {{\mathrm{\Psi }}^{\prime }}_{329}& {{\mathrm{\Psi }}^{\prime }}_{330}\end{array}\right]}^T$, and the corresponding mov-MF distribution is modeled on the basis of this dataset.

4.2 Type identification under different fault conditions

After establishing the mov-MF distribution model based on the historical sample fault dataset, the simulation is then carried out according to different fault conditions, and the test dataset of a particular fault is mixed into the history set of the mov-MF model for different conditions completed in Section 4.1 based on the historical samples for identification in each test.

4.2.1 Different transformer grounding methods

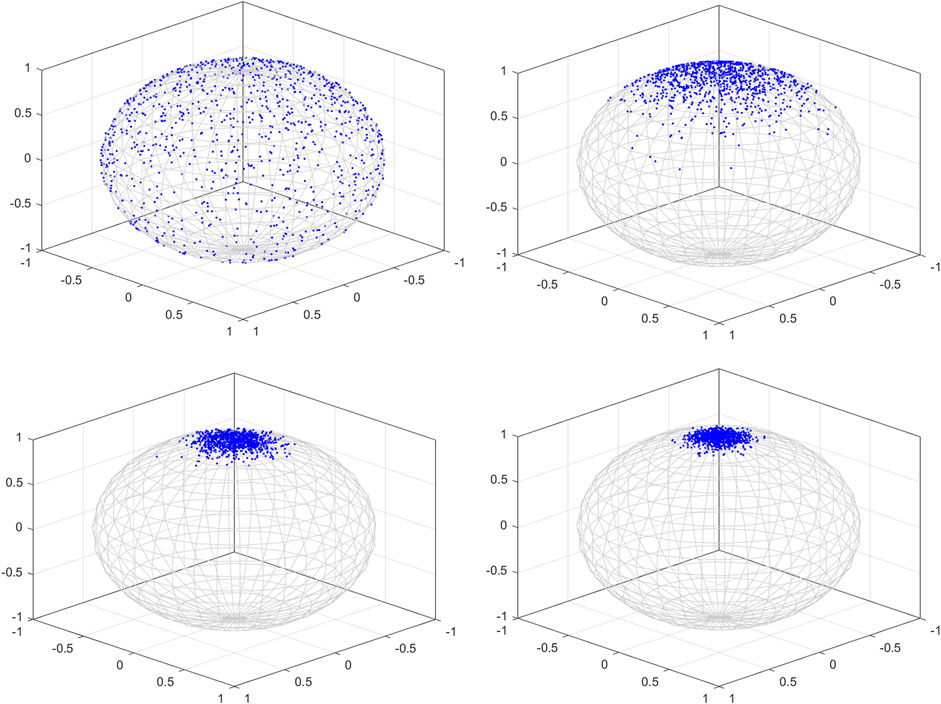
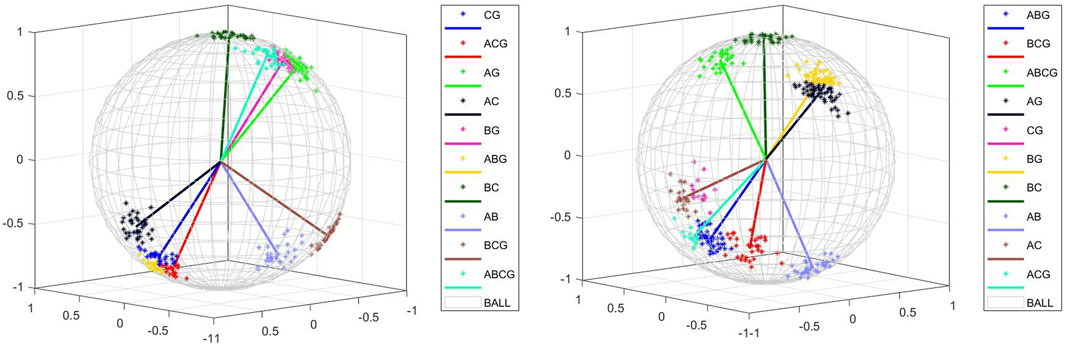
The purpose of changing the transformer grounding method is to verify the applicability of the fault identification method proposed in this paper under this condition. The simulation model is a 10-kV distribution network model, so two small current grounding methods are set. The compensation method of the arc-canceling coil is set to be over-compensation, and the simulation is carried out. Fault-type identification is carried out by establishing the mov-MF model, and the mov-MF model established according to the positive-, negative, and zero-sequence phases is shown in Figure 4.

Figure 4

Figure 4. Neutral ungrounded mov-MF distribution of neutral grounded through arc suppression coil.

The small current grounding method does not have much effect on the positive-, negative-, and zero-sequence voltage phase angles, and the obtained mov-MF distributions are similar. Eighty sets of test datasets are mixed into the obtained mov-MF distributions for different neutral grounding methods, and the labeling results are used to determine whether the classification is correct or not. The typical data mean direction matrix when the neutral point is not grounded is:

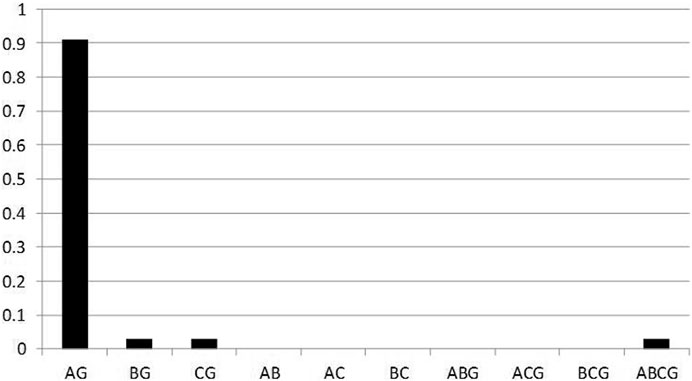
According to the average direction of typical faults, the cosine similarity was calculated between the test data set and the average direction of a certain type of fault, the probability of belonging to that type of fault was also calculated according to the number of data point labels, and the type of fault with the highest probability was selected to judge that it belongs to that type of fault. The A-phase short-circuit grounding fault was taken as an example under the condition of neutral ungrounded, and the fault probability $r_{hi}$ was calculated, as shown in Figure 5.

Figure 5

Figure 5. Fault-type probability diagram (AG, neutral ungrounded).

The overall accuracy results for the 40 test sets are shown in Table 2.

Table 2

Table 2. Fault identification accuracy under different grounding modes.

Transformer neutral point through the arcing coil grounding will limit the fault phase current. The method proposed in this paper does not have much impact, so the 10-kV distribution network applicable to the small current grounding method is applicable to this method.

4.2.2 Fault transition resistance impact analysis

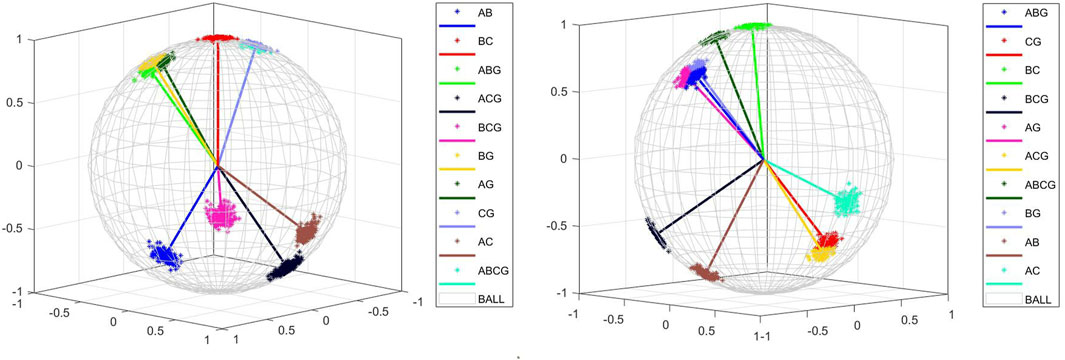
Changing the transition resistance when the fault occurs, the transition resistors with sizes of 0Ω, 1Ω, 10Ω, and 1000Ω are selected, and simulation experiments are carried out by changing the fault type and the initial phase angle of the fault at different fault locations. The mov-MF model is established for fault type identification, and the mov-MF model is also established according to the positive and negative zero sequence phases as shown in Figure 6.

Figure 6

Figure 6. mov-MF distribution of different transition resistors (0Ω and 1000Ω).

Varying the transition resistance size, the mov-MF distributions are different due to the fact that 0Ω, 1Ω, and 10Ω all differ from 1000Ω, but the expected results can still be achieved for type differentiation under each condition. The 160 sets of test datasets are mixed into the obtained mov-MF distributions for different neutral grounding methods, and the labeling results are used to determine whether the classification is correct or not. The typical data mean direction matrix for a transition resistance of 0Ω is:

The A-phase short-circuit ground fault under the condition of 0Ω transition resistance is taken as an example, and the fault probability $r_{hi}$ is calculated as shown in Figure 7:

Figure 7

Figure 7. Fault-type probability diagram (AG, 0Ω).

The judgment process is the same as shown in section IV.B.a), and the results of 80 sets of test data are shown in Table 3.

Table 3

Table 3. Fault identification accuracy under different transition resistors.

When a single-phase high-resistance grounded short-circuit occurs, the transition resistance will have a certain effect on the fault phase voltage amplitude, and for positive-, negative-, and zero-sequence phase angles, the transition resistance does not have much effect, so the fault-type identification accuracy is not affected under the condition of different fault transition resistances, and it still maintains a high accuracy rate.

4.2.3 Impact analysis of connecting to distributed power sources

DG is connected at nodes 17, 21, 24, and 32, and DG is a 1.5 kW/230 V PV power supply. The transformer grounding method is selected as neutral ungrounded, and the transition resistance is 0 Ω. Simulation experiments are carried out by changing the fault types at different locations. Fault type identification is carried out by establishing a mov-MF model, and the mov-MF model established according to the positive and negative zero sequence phasors is shown in Figure 8.

Figure 8

Figure 8. mov-MF distribution after connecting to DG.

After accessing the distributed power supply, the impact on the vectors we use to build the mov-MF distribution will not be significant, so the obtained mov-MF distribution is similar to the previous distribution and still differentiates between different types of faults based on the feature vectors. The 10 sets of test datasets are mixed into the obtained mov-MF distribution, and the labeling results are used to judge whether the classification is correct or not. The typical data mean direction matrix after accessing the DG is:

$\left[\begin{array}{c}{\mu }_1\\ ⋮\\ {\mu }_{10}\end{array}\right]=\left[\begin{array}{ccc}-0.631218228528535& -0.542200651398354& -0.554600758741366\\ -0.479847261990186& -0.0858554318574786& 0.873141139782731\\ -0.122723196711859& -0.710487151061130& 0.692926421177503\\ -0.00614141822594962& 0.669614264944898& -0.742683660224511\\ -0.0804373299381854& -0.0702110133474672& 0.994283787234378\\ 0.0282440012654692& -0.630164345667798& 0.775947919542022\\ -0.182608156880069& 0.738532954956005& -0.649017207387305\\ -0.0319915375253993& -0.592815736939139& -0.804702456541588\\ 0.00827657042339661& 0.922151265513940& -0.386740923478581\\ -0.00258341173453716& -0.762914549679774& 0.646494173114281\end{array}.\right]$

Take the example of a short-circuit ground fault in phase A after connecting to the DG, and calculate the fault probability $r_{hi}$ as shown in Figure 9:

Figure 9

Figure 9. Fault-type probability graph (AG, DG).

The judgment process is the same as shown in section IV.B.a, and the results of 20 sets of test data are shown in Table 4.

Table 4

Table 4. Fault identification accuracy after connecting to DG.

After accessing the distributed power supply, the fault current and voltage amplitude will slightly increase when a fault occurs compared with when it is not connected. For positive-, negative-, and zero-sequence voltage phase angles, access to distributed power supply has little effect on it; as a feature vector can still establish a clearly classified hybrid v MF distribution, the accuracy of fault-type identification is not affected, and the accuracy rate is still high.

4.2.4 Comparative analysis of different algorithms

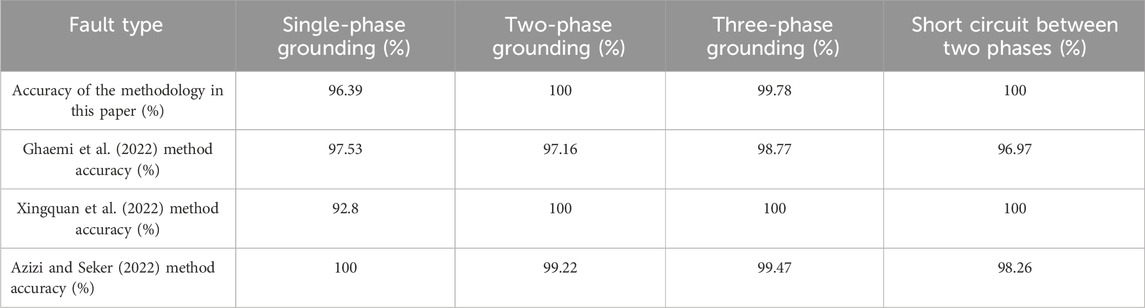
The algorithm proposed in this paper is compared with the existing algorithms, and in Table 4, with the ensemble algorithm of multilayer classifiers (Ghaemi et al., 2022), the CNN–SVM algorithm (Xingquan et al., 2022), and the BrownBoost–HHT algorithm (Azizi and Seker, 2022), and compared with the algorithms that make use of the one-dimensional feature quantities, there is an improvement in the fault identification rate for two-phase short circuits, two-phase inter-phase, and three-phase short circuits; compared with the fault identification methods that make use of intelligent algorithms, the mov MF distribution of the three-dimensional feature quantity established by the algorithm proposed in this paper is simpler in the model, and the algorithm is clearer. The acquisition of the feature quantity is simpler, and the accuracy of fault-type identification is comparable to the algorithm.

The comprehensive analysis of Table 5 shows that the accuracy of fault-type identification using the method based on the mov-MF distribution is slightly lower than other types of faults when single-phase ground faults and three-phase grounding faults occur. When establishing the mov-MF distribution, a dataset consisting of phase angle values of positive-, negative-, and zero-sequence voltages is chosen, and the mov-MF distribution is able to extract the average direction of the same type of fault vectors as a feature value based on the vector data, so we carry out the fault-type identification based on this characteristic.

Table 5

Table 5. Classification accuracy of different fault types.

4.2.5 Simulation test time

The methodology in this paper needs to be applied with consideration of the required hardware base and the time-consuming identification work. As an example, the running time of the MATLAB fault classification program is analyzed to test the time taken to identify different types of faults under ungrounded neutral conditions, and the proposed methodology is applied to identify a single fault. The test hardware is a conventional mainstream PC with AMD Ryzen-5,000 processor and 16 GB RAM, and the time required to build the mov-MF distribution under these conditions is approximately 15 s. When a fault occurs, the probabilistic identification method of distribution network based on hybrid v-MF can achieve classification judgment within 1 s, which is a rapid response, and has engineering application significance and practical value.

5 Conclusion

This paper introduces a novel method for fault-type identification in distribution networks utilizing a mixed von Mises–Fisher (v-MF) distribution. The method involves constructing three-dimensional feature quantities derived from the positive, negative-, and zero-sequence voltage phase angles observed at the time of the fault. Subsequently, the mov-MF distribution is generated to classify the fault type based on the integration of current data with historical distributions. Consequently, the following conclusions can be drawn:

In this paper, we propose a method for fault-type identification utilizing 3D direction vectors to construct a mixed von Mises–Fisher (v-MF) distribution. By leveraging the positive–negative–zero-sequence voltage phasors associated with various fault types, we establish the mov-MF distribution using sample data from diverse fault scenarios. The probability that the faults under test belong to different fault types is estimated by discerning the discrepancy between the mean directions of distinct fault types. Consequently, our method achieves fault-type identification with high accuracy.

The method proposed in this paper remains unaffected by changes in neutral grounding mode, fault transition resistance, and variations in fault locations. It exhibits robust applicability under diverse working conditions.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author contributions

JL: writing–review and editing and writing–original draft. ZS: writing–review and editing and writing–original draft. BL: writing–review and editing and supervision.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Azizi, R., and Seker, S. (2022). Microgrid Fault detection and classification based on the boosting ensemble method with the hilbert-huang transform. IEEE Trans. Power Deliv. 37 (3), 2289–2300. doi:10.1109/tpwrd.2021.3109023

CrossRef Full Text | Google Scholar

Biswas, S., Nayak, P. K., Panigrahi, B. K., and Pradhan, G. (2023). An intelligent fault detection and classification technique based on variational mode decomposition-CNN for transmission lines installed with UPFC and wind farm. Electr. Power Syst. Res. 223, 109526. doi:10.1016/j.epsr.2023.109526

CrossRef Full Text | Google Scholar

Chen, Y.-H., Wei, D., Newstadt, G., DeGraef, M., Simmons, J., and Hero, A. (2015). “Statistical estimation and clustering of group-invariant orientation parameters,” in 2015 18th International Conference on Information Fusion (Fusion), Washington, DC, USA, 06-09 July 2015.

Google Scholar

Feng, X. U. X., Chenjie, X. U., Zhang, Y., Zhao, Y., and Wang, S. (2022). Fault location of active distribution network based on traveling wave feature classification. J. Chongqing Univ. 45 (11), 59–68. doi:10.11835/j.issn.1000-582X.2021.219

CrossRef Full Text | Google Scholar

Garcia-Fernandez, A. F., Tronarp, F., and Sarkka, S. (2019). Gaussian Target Tracking With Direction-of-Arrival von Mises–Fisher Measurements. IEEE Trans. Signal Process. 67 (11), 2960–2972. doi:10.1109/tsp.2019.2911258

CrossRef Full Text | Google Scholar

Ghaemi, A., Safari, A., Afsharirad, H., and Shayeghi, H. (2022). Accuracy enhance of fault classification and location in a smart distribution network based on stacked ensemble learning. Electr. Power Syst. Res. 205, 107766. doi:10.1016/j.epsr.2021.107766

CrossRef Full Text | Google Scholar

Jiang, X., Stephen, B., and McArthur, S. (2021). Automated distribution network fault cause identification with advanced similarity metrics. IEEE Trans. Power Deliv. 36 (2), 785–793. doi:10.1109/tpwrd.2020.2993144

CrossRef Full Text | Google Scholar

Jianyuan, WANG, Zhang, Y., and Cheng, L. I. U. (2023). Fault line selection method of distribution network based on the fusion of parameter optimized variational modal decomposition and improved K clustering criterion. South. Power Syst. Technol. 17 (7), 135–145. doi:10.13648/j.cnki.issn1674-0629.2023.07.015

CrossRef Full Text | Google Scholar

Kasarapu, P., and Allison, L. (2015). Minimum message length estimation of mixtures of multivariate Gaussian and von Mises-Fisher distributions. Mach. Learn. 100, 333–378. doi:10.1007/s10994-015-5493-0

CrossRef Full Text | Google Scholar

Liu, H., Ran, J., Yang, Q., Wang, K., and He, L. (2020). “High impedence ground fault identification method in medium voltage networks based on experiments,” in The 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Online Conference, 02-03 July 2020.

Google Scholar

Mashal, M., and Hosseini, R. (2015). “K-means plus plus for Mixtures of von Mises-Fisher Distributions,” in 2015 7th Conference on Information and Knowledge Technology (IKT).

Google Scholar

Peng, N., Zhang, P., Liang, R., Zhang, Z., Liu, X., Wang, H., et al. (2023). Fault section identification of the power cables in urban distribution networks by amplitude differences between the zero-sequence currents and those flowing in cable sheaths and armors. IEEE Trans. Smart Grid 14 (4), 2593–2606. doi:10.1109/tsg.2022.3222209

CrossRef Full Text | Google Scholar

Qi, L., Liu, H., Xiong, Q., and Chen, Z. (2021). Just-in-time-learning based prediction model of BOF endpoint carbon content and temperature via vMF mixture model and weighted extreme learning machine. Comput. Chem. Eng. 154, 107488. doi:10.1016/j.compchemeng.2021.107488

CrossRef Full Text | Google Scholar

Sheng, Y., Wang, B., Yu, H., Li, L., Liu, Y., and Zhang, L. (2023). An overview of Fault Identification techniques in power distribution networks: methods and models. IET Conf. Proc. 2023 (15), 192–198. doi:10.1049/icp.2023.2141

CrossRef Full Text | Google Scholar

Wang, H., Wu, F., and Zhang, L. (2021a). Fault diagnosis of rolling bearings based on improved empirical mode decomposition and Fuzzy C-means algorithm. Trait. Du. Signal 38 (2), 395–400. doi:10.18280/ts.380217

CrossRef Full Text | Google Scholar

Wang, X., Zhang, X., Zhao, Q., Xu, J., and Zhang, Y. (2021b). Fault section location in distribution system based on transient zero-mode current. Smart Power 49 (3), 103–110.

Google Scholar

Xingquan, J. I., Chen, J., Zhang, Y., Qi, L. I. U., Gong, Z., and Xu, B. (2022). Fault classification in distribution network based on CNN-SVM. Smart Power 50 (1), 94–100.

Google Scholar

Yang, L., and Yu, L. (2022). Grounding fault identification and line selection of distribution network based on improved two-branch ResNet. Electr. Meas. Instrum. 59 (10), 100–107. doi:10.1109/JIOT.2021.3131171

CrossRef Full Text | Google Scholar

Zhang, G. X., Tong, X. Y., Hong, Q., and Booth, C. D. (2022a). Waveform similarity-based robust pilot protection for transmission lines. IEEE Trans. Power Deliv. 37 (3), 1856–1865. doi:10.1109/tpwrd.2021.3099348

CrossRef Full Text | Google Scholar

Zhang, Y., guo, H. A. O. Z., Lin, Z., Yang, S., Liu, Z., and Xiaojun, Y. U. (2022b). Transmission line fault classification method based on deep dictionary learning. Electr. Power Autom. Equip. 42 (11). doi:10.16081/j.epae.202204031

CrossRef Full Text | Google Scholar

Zhe, X., Chen, S., and Yan, H. (2019). Directional statistics-based deep metric learning for image classification and retrieval. Pattern Recognit. 93, 113–123. doi:10.1016/j.patcog.2019.04.005

CrossRef Full Text | Google Scholar

Zhu, H. L., Shi, Y., Wang, H. Z., and Lu, L. X. (2020). New feature extraction method for photovoltaic array Output time series and its application in fault diagnosis. IEEE J.10 (4), 1133–1141. doi:10.1109/jphotov.2020.2981833

CrossRef Full Text | Google Scholar