
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res., 09 May 2024
Sec. Process and Energy Systems Engineering
Volume 12 - 2024 | https://doi.org/10.3389/fenrg.2024.1301700
This research presents a novel methodology for tackling the combined thermal-wind economic load dispatch (ELD) issue in contemporary power system. The proposed approach involves hybridizing active-set algorithm (ASA), interior point algorithm (IPA) and sequential quadratic programming (SQP) into grey wolf optimization (GWO) algorithm, while effectively incorporating the intricacies associated with renewable energy sources (RES). A more accurate model is made possible by hybridization for complex systems with memory and hereditary characteristics. The GWO is used as a tool for global search while ASA, IPA and SQP methods are used for rapid local optimization mechanism. The performance evaluation of the design heuristics is carried out on 37 thermal and 3 wind power generating units and outcomes endorse the effectiveness of the proposed scheme over state-of-the-art counterparts. The worthy performance is further validated on statistical assessments in case of thermal-wind integrated ELD problem in terms of measure of central tendency and variation on cost and complexity indices.
There has been observed a drastic increasing demand of electrical energy due to recent developments in domestic, commercial and industrial infrastructures over the past few decades. In this regard, public utility electric supply companies are forced to operate power grid nearly at full load capacities. Under such heavily stressed conditions there will be substantial generational, operational and maintenance costs. Furthermore, there will be an increased power losses, stability and power breakdown matters. In today’s modern power system optimal ELD has been given considerable importance owing to the increased electrical energy generation cost and depletion of fossil fuels used in thermal power generating units. The basic aim of ELD problem is to optimally allocate the active power generation output from thermal power generating units while taking care of the operational constraints associated with power system. By reducing the generation cost and increasing system’s reliability through optimal active power allocation, the overall energy capabilities of electrical energy generation increase. The research community has greater interest to approach the conventional ELD problem realistically due to numerous practical scenarios associated with power system. The input-output fuel cost generation curve is basically non-differentiable, non-convex and non-linear owing to the multilevel steam generating valves associated with modern steam operated thermal power generating units commonly known as VPLE. The systematic opening of these steam valves generates ripples in fuel-cost characteristics curve and can be modelled by imposing absolute sine term in main quadratic function of ELD problem (Kaboli and Alqallaf, 2019). There has been observed a greater emission of toxic gases such as carbon-mono-oxide (CO), Sulphur oxide (SO) and nitrogen oxide (NOx) as a result of electrical power generation from fossil fuels operated thermal power generating units. Due to these hazardous environmental concerns, mathematical formulations have been developed to reduce generation cost and emission levels of above-mentioned toxic gases simultaneously (Yu et al., 2018). The addition of alternate energy resources such as wind and solar energies have rectified the concerns of higher generation cost and emission levels of toxic gases to a greater extent. The integration of renewable energy resources into thermal power plants has led to modifications of conventional quadratic fuel cost characteristic equation by adding Beta and Weibull distribution functions that addresses the stochastically varying behavior of solar and wind power availability respectively (Jiang et al., 2015a; Jadoun et al., 2018). There are some physical limitations associated with some of the generating unit shaft’s bearings due to amplified vibrations occurring in some regions of shaft’s rotational axis. These prohibited operating zones (POZs) are encountered by introducing disjoint sub regions in input-output fuel cost characteristics function making it non-convex and non-linear optimization problem (Jeddi and Vahidinasab, 2014). The physical phenomenon associated with dynamic ELD problem is encountered by using ramp rate handling strategy during different hours of the day by including upper and lower ramp limits for thermal power generating units (Sattar et al., 2020). Conventional based numerical techniques are not able to solve constrained optimization problems owing to the stiff situations introduced as a result of considering practical constraints in conventional ELD problem. These techniques are unable to produce global optimum outcomes and are often trapped in local optimum regions. In this regard various nature inspired global optimum techniques have been developed over the years to address global optimum stagnation. Particle swarm optimization (PSO) is metaheuristic nature inspired global technique adopted to find optimal results of ELD integrated with stochastic wind (SW) forming hybrid energy generating units (Eberhart and Kennedy, 1995; Jeyakumar et al., 2006; Jiang et al., 2015b; Pandit et al., 2015). Genetic algorithm (GA) is exploited to deal with ELD integrated with physical constraints where numerical techniques failed to give global optimum outcomes (Chopra and Kaur, 2012). More stable and précised results were recorded using hybrid genetic algorithm (HGA) by appropriate scheduling of active power generation outputs (Balamurugan et al., 2014). Combined economic emission multi-objective load dispatch problem is implemented using differential evolution (DE) based strategy (Balamurugan et al., 2014). IEEE 03, 06 and 13 thermal generating based ELD problem is implemented using Improved tabu search algorithm (ITSA) in (Senthil and Manikandan, 2010). Evolutionary programming (EP) strategy has been found an effective mechanism to counter non-linear and stiff scenarios of ELD problems in (Sinha et al., 2003). Six units-based hybrid energy generating units are exploited using modified version of ant colony optimization (ACO) in (Gopalakrishnan and Krishnan, 2013). Recently developed hybrid imperialistic competitive sequential quadratic programming (HIC-SQP) has been applied to optimize the stochastic behavior in terms of direct cost, overestimated cost and underestimated cost of wind power availability integrated with thermal power generating units in order to reduce generation cost as well as emission of toxic gases simultaneously (Morshed and Asgharpour, 2014). Additionally, recently developed meta-heuristics-based searching algorithms have been applied in power and energy sectors reported in (Abbassi et al., 2019; El-Fergany et al., 2019; Mohseni et al., 2019; Zhang et al., 2020a; Fathy, 2020; Yang et al., 2020).
Development of biological inspired meta heuristic strategy of GWO developed by Mirjalili (Mirjalili et al., 2014; Faris et al., 2018) is fascinating methodology to be applied to stiff scenarios of practical ELD problem. Numerous preponderant problems of optimization are addressed using GWO (Alzubi et al., 2019; Salgotra et al., 2019; Zhang et al., 2020b) that includes feature selection (Chantar et al., 2020), vehicular adhoc networks (Fahad et al., 2018), power system stabilizer design (Shakarami and Davoudkhani, 2016), hydro-power prediction (Dehghani et al., 2019) and energy management (Jiang, 2021; Yang et al., 2022).
In proposed research, the global optimum capabilities through biological inspired meta-heuristics paradigm of GWO algorithm integrated with SQP, ASA and IPA are effectively applied on hybrid energy generating units of thermal and wind power. According to recent survey, the metaheuristic strategy of GWO has not been applied so far on SW problems of ELD. The salient features of proposed research can be categorized as.
• To optimally allocate the active power generation output from thermal generating units and wind power units to reduce the overall fuel generation cost and wind power generation cost.
• Comparative studies of GWO heuristics hybridized with SQP, ASA and IPA outcomes with up-to-date solvers for validating and verifying the strength of proposed hybridized schemes.
The paper is laid out as follows.
The paper is organized with mathematical formulation for ELD problem with VPLE and integrated SW in Section 2 followed by methodologies of GWO algorithm and applications for ELD and SW in Sections 3, 4 respectively.
This study involves system model of 40 thermal power generating units containing VPLE and 37 thermal power generating units with an integration of renewable energy in the form of 3 wind power producing plants.
The main objective/fitness function reflecting input output characteristics between active power generation in MW and fuel generation cost in $/hr. Can be modelled using quadratic fuel cost function as expressed in Eq. 1 (Kaboli and Alqallaf, 2019).
C1 is total fuel cost generation in $/hr. whereas tg is total number of thermal power generating units. Generation coefficients reflecting the social, economic and other related terms are being shown by coefficients “A”, “B” and “C” for mth thermal power generating unit in quadratic fuel cost formulation.
For flexible power generation operation, each thermal unit is equipped with a series of steam operated valves that allows controlled injection of steam on turbines as per load demand (Kaboli and Alqallaf, 2019). This physical phenomenon can bemodelled with an introduction of absolute and sine terms in quadratic fuel cost function making it non smooth function due to ripples involved with VPLE as shown in Eq. 2.
Where Em and Fm are generation coefficients involved with VPLE.
The significant advantage of integrating SW power in thermal power generating units is reflected by economic and environmentally friendly electrical power generation. In power generation system comprising of both thermal and wind power generating units, there have been developed various models for characterizing the scheduling of real power generation and operational generation cost. Due to inherent random speed of wind power, power generation operator is uncertain regarding its availability. He may overestimate wind power availability where actual power is less than that of power predicted and extra power is purchased to fulfill the load requirements. Sometimes due to underestimation of wind power availability some extra power is available and compensation is provided to wind power supplier’s cost for not utilizing the complete wind power available. Total generation cost of wind power can be modelled as shown in Eq. 3 (Morshed and Asgharpour, 2014).
C3 is total wind power generation cost and wg is total number of wind power generation units. CW. P (DIR, n), CW. P (OE, n) and CW. P (UE, n) are terms associated with direct cost, over-estimated cost and under-estimated cost associated with wind power generating units. Output wind power generation is directly proportional to CW. P (DIR, n) and can be expressed mathematically for nth wind power generation unit as expressed in Eq. 4.
In Eq. 4 qn is coefficient expressing direct electrical energy cost from nth wind power generating unit in $/MWh whereas W. Pn is real electrical output power in MW from nth wind power generating unit. CW. P (OE, n) is unbalanced over-estimated cost as a result of overestimation of wind power availability, so some extra real power in MW is purchased due to electrical power shortage from wind power generating units and can be expressed mathematically as shown in Eq. 5.
Crw, n is cost coefficient for overestimation in $/MWh for nth wind power generating unit whereas X (VOE, n) is expected value of wind power overestimation for nth wind power generating unit and can be expressed mathematically in Eq. 6.
VIN, VOUT and Vr are cut-in, cut-out and rated speed of wind in meters per second whereas V1 = VIN+(Vr-V IN) *W. P1/W. Pr being intermediary parameter. Cn and Kn are coefficients of Weibull distribution reflecting scale and shape factor for nth wind power generating unit. W. Pn and W. Pr are generated and rated electrical power in MW for nth wind power generating unit. Moreover, the incomplete gamma function having two parameters and can be mathematically expressed in Eq. 7 as follow (Liu and Xu, 2010a).
While a standard gamma function involves a single parameter expressed as shown in Eq. 8.
CW. P (UE, n) is the penalty cost imposed as a result of underestimating the availability of wind power where the actual active power available out of wind power generating units is more than that of predicted active power. Compensation in this regard is provided to wind power supplier’s cost as expressed in Eq. 9.
Cew,n is cost coefficient for underestimation in $/MWh for nth wind power generating unit, Y (VUE,n) is expected value of wind power underestimation for nth wind power generating unit and can be expressed in Eq. 10.
The overall objective function can be modelled by combining quadratic fuel cost function involving V.P.L.E (C2) and wind power generation availability cost function (C3) as total generation cost (TGC) in $/hr as shown in Eqs 11, 12.
The most important constraint to be handled properly while optimizing total generation cost is that the total active power generation output from different thermal and wind power generating units should be equal to total load demand as expressed in Eq. 13.
Active power generation output from each thermal and wind power generating unit should be less than or equal to its maximum generation limit and should be greater than or equal to its minimum generation limit such that.
In Eq. 14 “Pm, min” and “Pm, max” are active power generation limits for mth thermal power generating unit while “W. Pr, n” is rated active power generation for nth wind power unit in Eq. 15.
Global search-based technique dependent on GWO algorithm hybrid with local search-based techniques of SQP, ASA and IPA adopted for rapid local convergence is applied to solve constrained optimization problem of power generating system. For evaluating the efficiency and performance of designed hybridized scheme two case studies consisting 40 thermal generating units and 3 wind power generating units are considered. Figure 1 shows proposed work methodology.
GWO algorithm is newly developed population based meta heuristic algorithm proposed by Mirjalili (Mirjalili et al., 2014). GWO algorithm gets its inspiration from social hierarchy of grey wolves (Canes lupus) which belongs to Canidae family. They usually are known as apex predators meaning they are among top of ranking in food chain. Usually, they live in a pack consisting of 5–12 members on an average. It has been observed that grey wolves usually adopt very strict socially dominating hierarchy. The leaders in a pack are alphas. They are responsible for making decisions regarding sleeping, time to wake, and hunting, etc. Decisions made by alphas are strictly implemented throughout the pack. However, some democratic system is also implemented regarding some issues in which alpha follows the decisions of other wolves in a pack. All other wolves acknowledge the dominancy of alphas in a pack by holding their tails down. Alpha wolves in a pack may not be considered as a strongest wolf in a pack but the best one in managing the daily basis affairs of the pack. Alphas are responsible for maintaining strength and discipline in a pack.
The subordinate wolves in a pack are betas. They are second in line after alphas, playing role of advisors to alphas and help alphas in decision making. Betas may be either male or female and are responsible for implementing decisions made by alphas to other wolves in downstream and gives regular feedback regarding decision’s implementation to alphas. Betas are considered as fittest candidates to replace alphas in case if alphas die or get too old. Third in line after alphas and betas are delta wolves. Delta follows the command and instructions laid down by alphas and betas. Caretakers, hunters, scouts, elders and sentinels belong to this category. Caretakers take care of weak and wounded wolves whereas scouts keep an eagle eye on all boundaries and generate an alert in case of any danger. Sentinels make sure the safety of entire pack. Fourth in line and bottom of hierarchy comes omega wolves. Omegas has to follow all commands and instructions by all dominating wolves. They usually receive food and all other incentives in last. Among all social activities, hunting is the most important and interesting activity of grey wolves. Keeping in mind the hunting behavior of grey wolves, GWO algorithm is implemented in which initial population of grey wolves is generated and these wolves move in multi-dimensional search space in search of prey. The position vectors of these search agents i-e grey wolves are considered to be the problem’s variables whereas the distance between search agent and its prey is considered to be the fitness value of required objective function. In GWO algorithm each search agent moves in hyper dimensional place and updates its position with respect to its prey over the course of its iterations. The remaining search agents down the hierarchy update their positions with reference to the best individual search agents obtained. The main aim of GWO algorithm is to find the shortest possible path between search agents and prey. Hunting process mainly follows to track, chase and approach prey. Once approach the prey, encircle and start harassment the prey till it gets stationary and finally attacking the prey. GWO mimics the hunting mechanism by mathematical model for searching, approaching, encircling and attacking the prey.
In designing the mathematical model for GWO algorithm, the fittest candidates for required solutions are considered as alphas. The second and third best candidates in terms of required solutions considered are betas and deltas respectively. All three candidates guide and assist the hunting mechanism of GWO algorithm. The lowest candidate considered is omega and is compelled to follow alphas, betas and deltas. While exploring the search space, the search agents diverge from one another and readjust their position vectors in hyper dimensional search space while searching for the prey. Coefficient vector Av provides different random generated values that compel search agents to diverge from the position of prey. While vector Cv provides random generated weights. Exploration of search space by vectors Av and Cv make sure the global optimum solutions by GWO algorithm and are mathematically expressed as shown in Eqs 16, 17.
Component P1 of coefficient vector Av linearly decreases from 2 to 0 during successive iteration whereas C1 and C2 being random vectors in the range of 0–1.
Once the prey is approached by search agents during exploration, they start encircling the prey. The best search agents in terms of positions are alphas, betas and gammas while rest of search agents in a pack update their positions with respect to the positions of best search agents obtained so far. The following Eqs 18, 19 has been proposed tomimic the encircling behavior of search agents round the prey.
Ds is linear distance between search agent and prey and indicates the fitness value of each search agent during the course of iteration. Lesser the distance between search agent and the prey more is the fitness value and vice versa. Xprey and Xwolf are position vectors for prey and search agents respectively.
The search agents have the potential to track the location of prey and once approached it encircle the prey. Alphas for the instant are best search agents and leads the hunting process while rest of search agents in a pack update their positions with respect to alphas. Due to diverged search space, we are not sure about optimum location of prey, we therefore consider the positions of alphas, betas and gammas as best solutions and rest of search agents update their positions accordingly. Following formulas regarding the subject matter has been proposed as mentioned in Eqs 20–27.
Hunting mechanism led by search agents is compiled by attacking the prey when it comes in stationary position. In exploitation phase the value of component P1 of coefficient vector Av is linearly decreased from 2 to 0 over the course of iteration. The decrease in P1 is hence set responsible and set fluctuation range for Av. This decrement makes sure that next position for search agent can be anywhere between the position of search agent and position of prey for random values of Av in the range −1 to 1. Exploration takes place for values of Av >1 and search agents diverge from its prey whereas exploitation takes place for values of Av <1 and search agents are forced to converge towards the prey and attack them.
Summary of GWO algorithm is presented below.
• Set initial population of search agents i-e wolves. Population size is set by the number of wolves. Each wolf is considered as a candidate solution to the given problem and problem variables are defined by the position vector of each search agent in one dimensional, two dimensional and higher dimensional search space.
• For each search agent in initial generated population, set position vectors by assigning lower and upper bounds and also set maximum number of iterations as stopping criteria.
• The fitness value of each search agent is evaluated by passing each agent from objective function and its fitness value is evaluated based on the distance between search agent and prey. The best fitness of each search agent is categorized in order of alpha, beta and gamma.
• Each search agent updates its position over the course of successive iteration.
• GWO algorithm is terminated once pre-defined tolerance or maximum number of iterations are reached.
Algorithm 1.GWO Algorithm.
• Set initial population of search agents.
• Set position vector of each search agents by setting
• Evaluate the fitness level of each search agent by passing through desired objective function.
•
•
•
• while (n<iterations)
• for each search agent update the position using equation (26)
• end for loop
• Update position vector of each search agent by updating values for
• Evaluate fitness value of all search agents
• Update
• n=n+1
• end while loop
Step 1:. Initializing population of grey wolves.
Random initial population of search agents, i.e., grey wolves consisting of alpha, beta and gamma wolves is generated. Each search agent of initial population provides feasible solutions to constrained optimization problem of ELD. The position vector of each search agent represents active power generation in KW or MW within its upper and lower bound of each power generating unit. The position of each search agent is set by the initialization of sets of controlled variables in terms of active power generation. Initial population of grey wolves in terms of active power generation of each power generating unit for ELD problem containing SW is presented below.
Where “m” and “n” are total numbers of thermal power generating units and wind power generating units respectively whereas “z” represents population size of grey wolves.
Step 2:. Evaluating fitness level of grey wolves.
After the generation of initial population of grey wolves, the fitness level of each set of search agents is evaluated based on its fitness value by passing them through required objective functions in Eq 2 and Eq. 3. The fitness value of each search agent reflects how far is its position from prey in terms of generation cost in $/hr.
Step 3:. Sorting in terms of its fitness levels.
The fitness value of each search agent reflecting total generation cost in $/hr. is sorted and is placed in order such that alpha wolves having the best fitness value while second and third best fitness values are for beta and gamma wolves respectively.
Step 4:. Position updating mechanism.
During the course of iteration in GWO algorithm, each search agent is motivated to update its current position with respect to prey based upon searching, prey encircling followed by hunting and attacking. In this regard different positions adopted by each search agent represents the possible controlled variables of real power output in MW for each power generating unit to reduce total generation cost in dollars per hour.
Step 5:. Checking inequality constraint violation.
If the position of any search agent violates its limits, bring back to its limits. These limits reflect the minimum and maximum power generation limits for each power generating unit.
Step 6:. Stopping criteria.
If there is no comprehensive change of fitness. or predefined number of iterations have reached, the execution of GWO algorithm is stopped else return to Step 2.
In order to show the effectiveness of nature-inspired computational paradigm via grey wolf optimization (GWO) algorithm, two case studies dependents upon ELD-VPLE and ELD-VPLE-SW have been proposed. For rapid local convergence the optimized results of GWO algorithm have been hybridized with local search-based techniques of SQP, ASA, and IPA.
This case study consists of 40 thermal power generating units whose fuel cost coefficients have been taken from (Morshed and Asgharpour, 2014) and power demand considered is 10,500 MW. The physical phenomenon reflecting the realistic behavior of power system dynamics has been included by considering VPLE. In case study 1 GWO is applied through variants that ranges from 500 search agents’ number to 5000. The randomness of the optimized simulation results of GWO algorithm cannot be ignored owing to its stochastically varying behavior. In this regard 100 independent trials for each variant of GWO algorithm with 1,000 iterations have been applied to closely monitor the probability of deviations in optimized results. The best fuel cost value in $/hr. for each variant of GWO algorithm among 100 independent trials along with its execution time is tabulated in Table 1. Among all ten variants of GWO algorithm, comparatively GWO-8 showed better convergence for minimum fuel cost of 121979.8310 $/hr. with execution time of 578.98 s. The learning curve for the best variant recorded is shown in Figure 2, while the values for deciding variables in terms of active power generations output in MW for GWO-8 variant is shown in Supplementary Appendix Table SA1 table A1 of appendix.
Algorithm2.Local Search Algorithms (SQP, ASA and IPA).
Inputs: The best individual search agents sorted by GWO Algorithm for 40 generating units for ELD-VPLE and ELD-SW. Mathematically can be represented as follows:
Output: The best individual search agents sorted by GWO for 40 generating units are further refined by local search techniques.
Initialization: Parameters, assignments and constraints of local search (SQP, ASA and IPA) techniques are initialized.
Termination: Stopping criteria for all local search techniques are set as follows:
• Max Function Evaluations=300000;
• Max Iterations=1000;
• Tolerance Function=1e-12;
• Tolerance X=1e-10;
• Algorithms
o 'interior-point',
o 'active-set',
o 'SQP';
•Finite Difference Type='central';
• Tolerance Con=1e-12;
While (Stopping criteria satisfied) do
Cost Calculation: Calculate fuel cost for ELD-WV function usingequation 2and total cost of integrated stochastic wind for ELD-VPLE-SW usingequation 12
Stoppage: Exit from the main loop if all stopping criteria are met else continue.
End:
Furthermore, the statistical results for execution time in seconds and fuel generation cost among 100 independent trials for each variant are placed in Table 2. The 100 independent trials for best variant of GWO and histogram are shown in Figure 3. The mean value of fuel cost goes on decreasing while computational complexity goes on increasing with each successive set of increased search agent’s number. Moreover, the standard deviation reflects dynamics of search space increases by increasing search agent’s number.
The optimized results of each variant of GWO were given to local based search techniques of SQP, ASA and IPA for further refinement. Table 3 consists of the best simulation results among 100 independent trials for each hybridized scheme of GWO algorithm in terms of computational execution, function counts (FC), iterations and fuel generation cost. The stopping criteria for each local based search techniques are presented in Algorithm 2. Among hybridized variants of GWO algorithm with IPA, the prime optimized outcomes with regard to fuel generation cost of 121426.8340 $/hr. were recorded for GWO-IPA-7 while in case of SQP and ASA the prime optimized outcomes with regard to fuel generation cost of 121448.6012 $/hr. and 121498.2729 $/hr. were recorded for GWO-SQP-10 and GWO-ASA-8 respectively. The hybridized scheme of GWO algorithm with IPA gave minimum fuel cost of 121426.8340 $/hr. compared to SQP and ASA algorithms. The values for deciding variables i-e active power generation outputs in MW in case of GWO-IPA-7 variant are shown in Supplementary Appendix Table SA2.
In case of ELD problem with VPLE, outcomes were collate with benchmark solvers that includes GA-ASA-1 to GA-ASA-9 (Jamal and MenKhanRaja, 2019), EP-SQP (Attaviriyanupap et al., 2002), NPSO-RLS (Selvakumar and Thanushkodi, 2007a), EP-SQP (Chiang, 2007a), PSO-LRS (Kuo, 2008), NPSO (Kuo, 2008), NPSO-LRS (Kuo, 2008), CBPSO-RVM (Selvakumar and Thanushkodi, 2007b), ACO (Pereira-Neto et al., 2005a), SOH-PSO (Vlachogiannis and Lee, 2009), GA-PS-SQP (Chiang, 2007b), QPSO (Lu et al., 2010), BBO (Liu and Xu, 2010b), SA-PSO (Panigrahi et al., 2008), IGAMU (Hosseinnezhad and Babaei, 2013), ESO (Pereira-Neto et al., 2005b), MHSA (Arul et al., 2013), MFO-8 (Khan et al., 2021), MFO-IPA-7 (Khan et al., 2021), MFO-SQP-6 (Khan et al., 2021) and MFO-ASA-2 (Khan et al., 2021) in Table 4. Among reported results the best results were found for BBO (Liu and Xu, 2010b) while the proposed GWO-IPA-7 performed even better in terms of fuel cost giving value of 121426.8340 $/hr. compared to that of BBO of 121426.953 $/hr.
The statistical results for all hybridized schemes of GWO algorithm based on 100 independent trials in terms of mean and standard deviations for execution time, iterations, FC and fuel cost are tabulated in Table 5. In case of GWO-IPA-7 the values of mean and standard deviations for execution time, iterations, FC and fuel cost recorded are 1.44 ± 0.44, 136 ± 40, 11300 ± 3316 and 121878.6558 ± 292.2390 respectively Simulation results in terms of fuel cost values for best recorded hybridized variants of GWO algorithm i-e., GWO-IPA-7, GWO-SQP-10 and GWO-ASA-8 for 100 independent trials are shown in Figure 4. Furthermore, the statistical performance indices among best variants in case of hybridized GWO algorithm with local search algorithm of IPA was aided with histogram, boxplot and cumulative density function (CDF) based analysis presented in Figure 5. Histogram based analysis shows that majority of independent runs have occurred around the mean value of Gaussian fit while the mean values tabulated in Table 5 are reflected by the median lines of boxplot. Whereas 70–75 percent results were found accurate as it is well obvious from boxplot analysis.
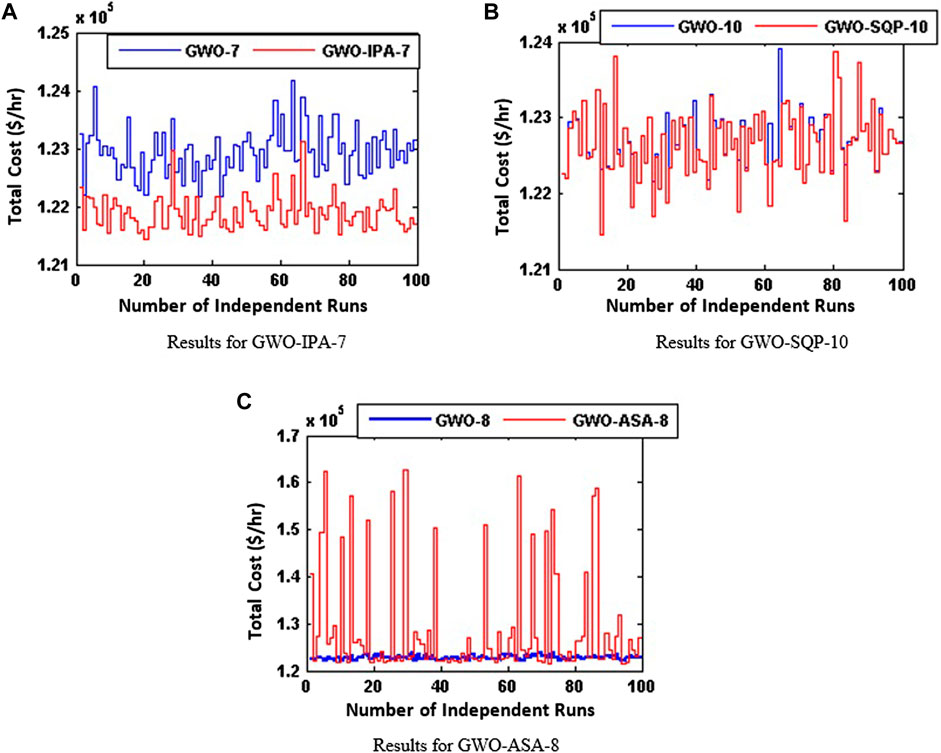
Figure 4. Comparison of 100 independent trials among hybridized variants of GWO algorithm for case study 1.
A modified case study of ELD-VPLE of 40 generators is considered by taking 37 thermal power generating units of case study 1 and last three units of wind power generating units are considered for case study 2. ELD-VPLE containing SW is incorporated by using system model formulation of Eq. 3. Total generation cost is incorporated using Equation (11). Units’ data for thermal and wind power generating units have been taken from (Morshed and Asgharpour, 2014). Hundred independent trials for each variant of GWO algorithm with 1,000 iterations have been applied. The best total cost value in $/hr. along with its fuel cost value, wind power cost and execution time for each variant of GWO algorithm among 100 independent trials is tabulated in Table 6.
Comparatively the pre-eminent simulation outcomes of total cost of 133910.1427 $/hr. were recorded in case of GWO-6 with fuel cost and wind power costs of 117293.6596 and 16613.5577 respectively. The learning curve for GWO-6 is shown in Figure 6, while the values for deciding variables in terms of active power generations output in MW for GWO-6 variant is shown in Supplementary Appendix Table SA3. The 100 independent trials and histogram for best variant of GWO, i.e., GWO-6 are shown in Figure 7. The analysis is further based on statistical results for execution time and fuel cost in terms of mean and standard deviations among 100 independent trials for each variant and are placed in Table 7. The mean value of total cost goes on decreasing while computational complexity goes on increasing with each successive set of increased search agent’s number. Moreover, the standard deviation reflects dynamics of search space increases by increasing search agent’s number.
Furthermore SQP, ASA and IPA were incorporated with each variant of GWO algorithm i-e. GWO-1 to GWO-8 for refinement of global optimum outcomes of GWO. The best optimized results for each hybridized variant of GWO algorithm among 100 independent trials is presented in Table 8. Algorithm 2 presents stopping criteria for SQP, ASA and IPA. Among hybridized scheme methodology of GWO-IPA-8 gave better convergence result with total cost of 133387.9413 $/hr. having fuel cost of 116778.50040 $/hr. and wind power cost of 16609.44323 $/hr. The 100 independent trials data for each scheme of hybridized GWO variants were analyzed in terms of statistical performance indices. The total cost for all hybridized schemes of GWO variants against 100 independent trials are shown in Figure 8, while Table 9 shows the numerical outcomes of statistical performance indices in terms of mean and standard deviations for time, iterations, function count and total cost. The findings for computational time, iterations, function counts and fuel generation cost through mean and standard deviation operators are 8.62 ± 7.12, 138 ± 39, 11468 ± 3188 and 133876.62 ± 312.8869, respectively for GWO-IPA-8. In case of GWO-SQP-5, the values for time, iterations, function count and fuel cost are 0.93 ± 1.54, 22 ± 46, 2038 ± 3791 and 134960.52 ± 614.5898, respectively. Total generation cost based on 100 independent trials in case of each hybridized variant of GWO algorithm was analyzed for statistical observations aided with histogram, boxplot and CDF based studies. These statistical based observation plots are presented in Figure 9. The occurrence of most of independent trials data is around the mean value of Gaussian fit in histogram based analysis. Table 9 reflects the occurrence of median values closest to the mean values of median lines for boxplots excluding outliers. Reasonable accuracy for 100 independent trials with probability occurrence of more than 0.8 is investigated using CDF plots. The results of the proposed variant of GWO hybrid with SQP, IPA and ASA to solve the ELD problem with VPLE involving SW impact were compared with the state-of-the-art reported solvers including HIC-SQP (Morshed and Asgharpour, 2014), MFO-9 (Khan et al., 2021), MFO-SQP-10 (Khan et al., 2021), MFO-ASA-10 (Khan et al., 2021), MFO-IPA-9 (Khan et al., 2021), PWTED1 (Azizipanah-Abarghooee et al., 2012), DWTED1 (Azizipanah-Abarghooee et al., 2012) and are listed Table 10. Among the reported results, the best was found for MFO-IPA-9 with total cost 133809.3271$/hr. having fuel cost of 117199.8838$/hr. and wind power cost of 16609.44328$/hr. Among the proposed variants of GWO algorithm, GWO-6 outperformed by optimizing total generation cost to 133910.1427 $/hr. with fuel cost of 117293.6596 $/hr. and wind power cost of 16613.5577 $/hr. Among hybridized schemes of each variant of GWO algorithm with local search-based algorithms, GWO-IPA-8 performed better in terms of total generation cost of 133387.9413 $/hr. having fuel cost of 116778.50040 $/hr. and wind power cost of 16609.44323 $/hr. The second-best results among hybridized schemes were found for GWO-ASA-8 with total generation cost of 133401.5454 $/hr. having fuel cost of 116792.10294 $/hr. and wind power cost of 16609.44323$/hr. followed by GWO-SQP-5 with total generation cost of 133476.2280 $/hr.
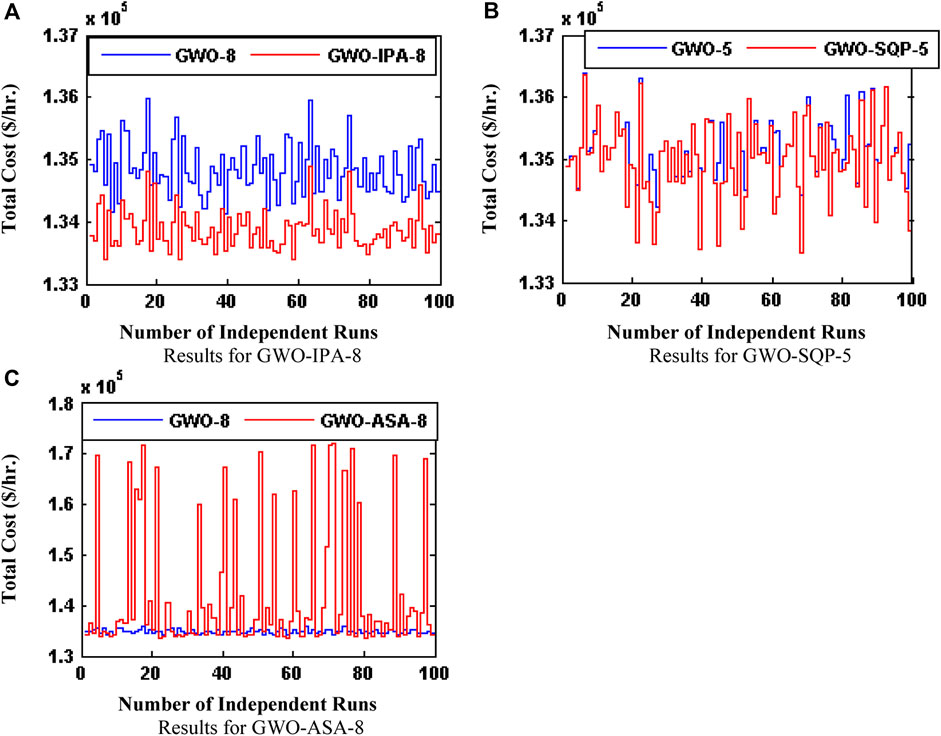
Figure 8. Comparison of 100 independent trials among hybridized variants of GWO algorithm for case study 2.
This work makes a significant contribution to the field of power system optimization by using the hybrid GWO method to solve the challenging ELD problem. Our study’s methodology has demonstrated a significant decrease in fuel generating costs and an improvement in the operational efficiency of the power system. The hybrid GWO algorithm has resulted in notable improvements in performance. However, it is critical to identify potential roadblocks and avenues for more research. Concluding remarks are listed as follows.
• Total generation cost of hybrid energy generating units in terms of fuel generation cost and stochastically varying wind power cost is efficiently optimized by exploring and exploiting the searching capabilities of GWO algorithm.
• The effectiveness of proposed GWO algorithm is tested based on different variants. Each set of GWO variant is depending upon the population size of search agents. For further refinement the global outcomes of GWO algorithm are used as starting points for local search-based algorithms of SQP, ASA, and IPA.
• Two case studies involving 40 thermal generators and 3 wind power generators have been considered to show the effectiveness of proposed GWO algorithm.
• For case study 1, GWO-8 variant gave better result for fuel generation cost of 121979.8310 $/hr., while GWO-IPA-7 showed better results of 121426.8340 $/hr.
• For case study 2, GWO-6 variant showed better optimized results for total generation cost of 133910.1427$/hr. with fuel generation cost of 117293.6596 $/hr. and wind power cost of 16613.5577 $/hr. while total generation cost of 133387.9413$/hr. with total generation cost of 116778.50040 $/hr. and wind power cost of 16609.44323 $/hr. were recorded for GWO-IPA-8.
• The performance of proposed case studies was performed based upon 100 independent trials data through statistical, histogram, boxplot and cdf based analysis.
The approach adopted in the present research work may be utilized in the significant areas pertaining to electric power system (Cui et al., 2020; He et al., 2020; Zhou et al., 2020) including integrated hydro-thermal-wind systems (Wang et al., 2019).
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
AW: Conceptualization, Formal Analysis, Methodology, Supervision, Writing–review and editing, Resources. BK: Conceptualization, Formal Analysis, Supervision, Writing–original draft, Writing–review and editing, Resources. TK: Funding acquisition, Software, Writing–original draft, Data curation, Project administration. K-CK: Funding acquisition, Project administration, Supervision, Investigation, Writing–original draft. SR: Funding acquisition, Project administration, Supervision, Conceptualization, Writing–review and editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research is supported by the National Research Foundation of Korea under grant No. NRF-2021R111A3053429.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1301700/full#supplementary-material
Abbassi, R., Abbassi, A., Heidari, A. A., and Mirjalili, S. (2019). An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 179, 362–372. doi:10.1016/j.enconman.2018.10.069
Alzubi, Q. M., Anbar, M., Alqattan, Z. N. M., Al-Betar, M. A., and Rosni, A. (2019). Intrusion detection system based on a modified binary grey wolf optimisation. Neural Comput. Appl. 32, 6125–6137. doi:10.1007/s00521-019-04103-1
Arul, R., Ravi, G., and Velusami, S. (2013). Chaotic self-adaptive differential harmony search algorithm based dynamic economic dispatch. Int. J. Electr. Power and Energy Syst. 50, 85–96. doi:10.1016/j.ijepes.2013.02.017
Attaviriyanupap, P., Kita, H., Tanaka, E., and Hasegawa, J. (2002). A hybrid EP and SQP for dynamic economic dispatch with nonsmooth fuel cost function. IEEE Trans. Power Syst. 17 (2), 411–416. doi:10.1109/tpwrs.2002.1007911
Azizipanah-Abarghooee, R., Niknam, T., Roosta, A., Malekpour, A. R., and Zare, M. (2012). Probabilistic multiobjective wind-thermal economic emission dispatch based on point estimated method. Energy 37 (1), 322–335. doi:10.1016/j.energy.2011.11.023
Balamurugan, K., Muralisachithnndam, R., and Krishnan, S. R. (2014). Differential evolution based solution for combined economic and emission power dispatch with valve loading effect. Int. J. Electr. Eng. Inf. 6 (1), 74–92. doi:10.15676/ijeei.2014.6.1.6
Chantar, H., Mafarja, M., Alsawalqah, H., Heidari, A. A., Aljarah, I., and Faris, H. (2020). Feature selection using binary grey wolf optimizer with elite-based crossover for Arabic text classification. Neural Comput. Appl. 32 (16), 12201–12220. doi:10.1007/s00521-019-04368-6
Chiang, C. L. (2007a). Genetic-based algorithm for power economic load dispatch. IET generation, Transm. distribution 1 (2), 261–269. doi:10.1049/iet-gtd:20060130
Chiang, C. L. (2007b). Genetic-based algorithm for power economic load dispatch. IET generation, Transm. distribution 1 (2), 261–269. doi:10.1049/iet-gtd:20060130
Chopra, L., and Kaur, R. (2012). Economic load dispatch using simple and refined genetic algorithm. Int. J. Adv. Eng. Technol. 5 (1), 584–590.
Cui, H., Xia, W., Yang, S., and Wang, X. (2020). Real-time emergency demand response strategy for optimal load dispatch of heat and power micro-grids. Int. J. Electr. Power and Energy Syst. 121, 106127. doi:10.1016/j.ijepes.2020.106127
Dehghani, M., Riahi-Madvar, H., Hooshyaripor, F., Mosavi, A., Shamshirband, S., Zavadskas, E. K., et al. (2019). Prediction of hydropower generation using grey wolf optimization adaptive neuro-fuzzy inference system. Energies 12 (2), 289. doi:10.3390/en12020289
Eberhart, R., and Kennedy, J. (1995). “A new optimizer using particle swarm theory,” in MHS'95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, October, 1995, 39–43.
El-Fergany, A. A., Hasanien, H. M., and Agwa, A. M. (2019). Semi-empirical PEM fuel cells model using whale optimization algorithm. Energy Convers. Manag. 201, 112197. doi:10.1016/j.enconman.2019.112197
Fahad, M., Aadil, F., Khan, S., Shah, P. A., Muhammad, K., Lloret, J., et al. (2018). Grey wolf optimization based clustering algorithm for vehicular ad-hoc networks. Comput. Electr. Eng. 70, 853–870. doi:10.1016/j.compeleceng.2018.01.002
Faris, H., Aljarah, I., Al-Betar, M. A., and Mirjalili, S. (2018). Grey wolf optimizer: a review of recent variants and applications. Neural Comput. Appl. 30 (2), 413–435. doi:10.1007/s00521-017-3272-5
Fathy, A. (2020). Butterfly optimization algorithm based methodology for enhancing the shaded photovoltaic array extracted power via reconfiguration process. Energy Convers. Manag. 220, 113115. doi:10.1016/j.enconman.2020.113115
Gopalakrishnan, R., and Krishnan, A. (2013). An efficient technique to solve combined economic and emission dispatch problem using modified Ant colony optimization. Sadhana 38 (4), 545–556. doi:10.1007/s12046-013-0153-1
He, L., Lu, Z., Geng, L., Zhang, J., Li, X., and Guo, X. (2020). Environmental economic dispatch of integrated regional energy system considering integrated demand response. Int. J. Electr. Power and Energy Syst. 116, 105525. doi:10.1016/j.ijepes.2019.105525
Hosseinnezhad, V., and Babaei, E. (2013). Economic load dispatch using θ-PSO. Int. J. Electr. power and energy Syst. 49, 160–169. doi:10.1016/j.ijepes.2013.01.002
Jadoun, V. K., Pandey, V. C., Gupta, N., Niazi, K. R., and Swarnkar, A. (2018). Integration of renewable energy sources in dynamic economic load dispatch problem using an improved fireworks algorithm. IET Renew. Power Gener. 12 (9), 1004–1011. doi:10.1049/iet-rpg.2017.0744
Jamal, R., Men, B., Khan, N., and Raja, M. (2019). Hybrid bio-inspired computational heuristic paradigm for integrated load dispatch problems in volving stochastic wind. Energies 12 (13), 2568. doi:10.3390/en12132568
Jeddi, B., and Vahidinasab, V. (2014). A modified harmony search method for environmental/economic load dispatch of real-world power systems. Energy Convers. Manag. 78, 661–675. doi:10.1016/j.enconman.2013.11.027
Jeyakumar, D. N., Jayabarathi, T., and Raghunathan, T. (2006). Particle swarm optimization for various types of economic dispatch problems. Int. J. Electr. Power and Energy Syst. 28 (1), 36–42. doi:10.1016/j.ijepes.2005.09.004
Jiang, S., Ji, Z., and Wang, Y. (2015a). A novel gravitational acceleration enhanced particle swarm optimization algorithm for wind–thermal economic emission dispatch problem considering wind power availability. Int. J. Electr. Power and Energy Syst. 73, 1035–1050. doi:10.1016/j.ijepes.2015.06.014
Jiang, S., Ji, Z., and Wang, Y. (2015b). A novel gravitational acceleration enhanced particle swarm optimization algorithm for wind–thermal economic emission dispatch problem considering wind power availability. Int. J. Electr. Power and Energy Syst. 73, 1035–1050. doi:10.1016/j.ijepes.2015.06.014
Jiang, Z. (2021). Installation of offshore wind turbines: a technical review. Renew. Sustain. Energy Rev. 139, 110576. doi:10.1016/j.rser.2020.110576
Kaboli, S. H. A., and Alqallaf, A. K. (2019). Solving non-convex economic load dispatch problem via artificial cooperative search algorithm. Expert Syst. Appl. 128, 14–27. doi:10.1016/j.eswa.2019.02.002
Khan, B. S., Raja, M. A. Z., Qamar, A., and Chaudhary, N. I. (2021). Design of moth flame optimization heuristics for integrated power plant system containing stochastic wind. Appl. Soft Comput. 104, 107193. doi:10.1016/j.asoc.2021.107193
Kuo, C. C. (2008). A novel coding scheme for practical economic dispatch by modified particle swarm approach. IEEE Trans. Power Syst. 23 (4), 1825–1835. doi:10.1109/tpwrs.2008.2002297
Liu, X., and Xu, W. (2010a). Minimum emission dispatch constrained by stochastic wind power availability and cost. IEEE Trans. Power Syst. 25 (3), 1705–1713. doi:10.1109/tpwrs.2010.2042085
Liu, X., and Xu, W. (2010b). Minimum emission dispatch constrained by stochastic wind power availability and cost. IEEE Trans. Power Syst. 25 (3), 1705–1713. doi:10.1109/tpwrs.2010.2042085
Lu, H., Sriyanyong, P., Song, Y. H., and Dillon, T. (2010). Experimental study of a new hybrid PSO with mutation for economic dispatch with non-smooth cost function. Int. J. Electr. Power and Energy Syst. 32 (9), 921–935. doi:10.1016/j.ijepes.2010.03.001
Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007
Mohseni, S., Brent, A. C., and Burmester, D. (2019). A demand response-centred approach to the long-term equipment capacity planning of grid-independent micro-grids optimized by the moth-flame optimization algorithm. Energy Convers. Manag. 200, 112105. doi:10.1016/j.enconman.2019.112105
Morshed, M. J., and Asgharpour, A. (2014). Hybrid imperialist competitive-sequential quadratic programming (HIC-SQP) algorithm for solving economic load dispatch with incorporating stochastic wind power: a comparative study on heuristic optimization techniques. Energy Convers. Manag. 84, 30–40. doi:10.1016/j.enconman.2014.04.006
Pandit, M., Chaudhary, V., Dubey, H. M., and Panigrahi, B. K. (2015). Multi-period wind integrated optimal dispatch using series PSO-DE with time-varying Gaussian membership function based fuzzy selection. Int. J. Electr. Power and Energy Syst. 73, 259–272. doi:10.1016/j.ijepes.2015.05.017
Panigrahi, B. K., Pandi, V. R., and Das, S. (2008). Adaptive particle swarm optimization approach for static and dynamic economic load dispatch. Energy Convers. Manag. 49 (6), 1407–1415. doi:10.1016/j.enconman.2007.12.023
Pereira-Neto, A., Unsihuay, C., and Saavedra, O. R. (2005a). Efficient evolutionary strategy optimisation procedure to solve the nonconvex economic dispatch problem with generator constraints. IEE Proceedings-Generation, Transm. Distribution 152 (5), 653–660. doi:10.1049/ip-gtd:20045287
Pereira-Neto, A., Unsihuay, C., and Saavedra, O. R. (2005b). Efficient evolutionary strategy optimisation procedure to solve the nonconvex economic dispatch problem with generator constraints. IEE Proceedings-Generation, Transm. Distribution 152 (5), 653–660. doi:10.1049/ip-gtd:20045287
Salgotra, R., Singh, U., and Sharma, S. (2019). On the improvement in grey wolf optimization. Neural Comput. Appl. 32, 3709–3748. doi:10.1007/s00521-019-04456-7
Santra, D., Sarker, K., Mukherjee, A., and Mondal, S. (2019). Combined economic emission and load dispatch using hybrid metaheuristics. Int. J. Hybrid Intell. 1 (2-3), 211–238. doi:10.1504/ijhi.2019.10025164
Sattar, M. K., Ahmad, A., Fayyaz, S., Ul Haq, S. S., and Saddique, M. S. (2020). Ramp rate handling strategies in dynamic economic load dispatch (DELD) problem using grey wolf optimizer (GWO). J. Chin. Inst. Eng. 43 (2), 200–213. doi:10.1080/02533839.2019.1694446
Selvakumar, A. I., and Thanushkodi, K. (2007a). A new particle swarm optimization solution to nonconvex economic dispatch problems. IEEE Trans. power Syst. 22 (1), 42–51. doi:10.1109/tpwrs.2006.889132
Selvakumar, A. I., and Thanushkodi, K. (2007b). A new particle swarm optimization solution to nonconvex economic dispatch problems. IEEE Trans. power Syst. 22 (1), 42–51. doi:10.1109/tpwrs.2006.889132
Senthil, K., and Manikandan, K. (2010). Economic thermal power dispatch with emission constraint and valve point effect loading using improved tabu search algorithm. Int. J. Comput. Appl. 3 (9), 6–11. doi:10.5120/770-1080
Shakarami, M. R., and Davoudkhani, I. F. (2016). Wide-area power system stabilizer design based on grey wolf optimization algorithm considering the time delay. Electr. Power Syst. Res. 133, 149–159. doi:10.1016/j.epsr.2015.12.019
Sinha, N., Chakrabarti, R., and Chattopadhyay, P. K. (2003). Evolutionary programming techniques for economic load dispatch. IEEE Trans. Evol. Comput. 7 (1), 83–94. doi:10.1109/tevc.2002.806788
Vlachogiannis, J. G., and Lee, K. Y. (2009). Economic load dispatch—a comparative study on heuristic optimization techniques with an improved coordinated aggregation-based PSO. IEEE Trans. Power Syst. 24 (2), 991–1001. doi:10.1109/tpwrs.2009.2016524
Wang, Y., Zhao, M., Chang, J., Wang, X., and Tian, Y. (2019). Study on the combined operation of a hydro-thermal-wind hybrid power system based on hydro-wind power compensating principles. Energy Convers. Manag. 194, 94–111. doi:10.1016/j.enconman.2019.04.040
Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive overview of meta-heuristic algorithm applications on PV cell parameter identification. Energy Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595
Yang, Y., Bremner, S., Menictas, C., and Kay, M. (2022). Modelling and optimal energy management for battery energy storage systems in renewable energy systems: a review. Renew. Sustain. Energy Rev. 167, 112671. doi:10.1016/j.rser.2022.112671
Yu, X., Yu, X., Lu, Y., and Sheng, J. (2018). Economic and emission dispatch using ensemble multi-objective differential evolution algorithm. Sustainability 10 (2), 418. doi:10.3390/su10020418
Zhang, H., Heidari, A. A., Wang, M., Zhang, L., Chen, H., and Li, C. (2020a). Orthogonal Nelder-Mead moth flame method for parameters identification of photovoltaic modules. Energy Convers. Manag. 211, 112764. doi:10.1016/j.enconman.2020.112764
Zhang, Y., Jin, Z., and Chen, Y. (2020b). Hybridizing grey wolf optimization with neural network algorithm for global numerical optimization problems. Neural Comput. Appl. 32 (14), 10451–10470. doi:10.1007/s00521-019-04580-4
Keywords: grey wolf optimization, interior point algorithm, active set algorithm, sequential quadratic programming, economic load dispatch problem, stochastic wind
Citation: Wadood A, Khan BS, Khurshaid T, Kim K-C and Rhee SB (2024) Chaos-infused wind power integration in the grey wolf optimal paradigm for combine thermal-wind power plant systems. Front. Energy Res. 12:1301700. doi: 10.3389/fenrg.2024.1301700
Received: 25 September 2023; Accepted: 20 March 2024;
Published: 09 May 2024.
Edited by:
Fazal Akbar, University of Edinburgh, United KingdomReviewed by:
Kamran Zeb, National University of Sciences and Technology (NUST), PakistanCopyright © 2024 Wadood, Khan, Khurshaid, Kim and Rhee. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Abdul Wadood, d2Fkb29kQGFpcnVuaXZlcnNpdHkucGs=; Ki-Chai Kim, a2NraW1AeW51LmFjLmty
†These authors have contributed equally to this work
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.