Nonparametric probabilistic forecasting based stochastic optimal scheduling of integrated electricity and gas systems

The volatility and sporadic availability of renewable energy create significant challenges to the optimal scheduling of integrated electricity and gas systems (IEGS). This paper develops a nonparametric probabilistic forecasting based stochastic scheduling approach of IEGS. The quantile at a series of quantile levels can be generated by direct quantile regression method. Given the set of predicted quantiles, a set of representative scenarios for wind power uncertainty can be obtained by using Monte Carlo simulation method and scenario reduction approach. Based on the implicit finite difference scheme, the original partial differential equations of the gas network are discretized to establish an algebraic model, which provide possibility for efficient solution. Then, the nonconvexity caused by the momentum equation is eliminated by the second-order core relaxation. Finally, the stochastic optimal scheduling model is reformulated as a second-order core programming problem. Numerical simulations are performed to showcase the superiority of the established stochastic optimal scheduling model.

1 Introduction

With the rapid development of natural gas power generation and power-to-gas technology, the power system has established a strong coupling relationship with the gas system (Chen et al., 2021a). Coordinated optimization of integrated electricity and gas systems (IEGS) is of great significance for improving energy efficiency. Besides, natural gas-fired units (NGUs) have the advantage of convenient regulation, which provides a new way to deal with the volatility and intermittency of renewable energy (Shao et al., 2017).

Recently, both academia and industry have been studying the coordinated optimization of IEGS. A dynamic optimal power and gas flow model is developed (Fang et al., 2018) to account for the cushion effects of gas dynamics. By considering the reserve scheduling and renewable uncertainties, a scheduling model of IEGS is formulated (Liu et al., 2019), which focus on enhancing the economic and security of IEGS. A unit commitment model of hybrid power and gas system is proposed (Chen et al., 2019), of which convex envelopes are applied to relax the nonlinear momentum equation. A non-isothermal optimal power and gas flow model is presented (Chen et al., 2021b) to reveal the effects of gas thermodynamics on the power system operation. A model for optimal power and gas flow that takes into account security constraints is developed in (Correa-Posada and Sánchez-Martın, 2014), where linear sensitivity factors are used to conduct a quick calculation of N-1 contingency of gas pipeline. A model considering operation constraints for unit commitment is put forward in (Liu et al., 2009), of which the benders decomposition method is employed to separately solve the optimization problems of hybrid power and gas systems.

Clean energy, particularly wind power, has made rapid progress with the transformation of the global energy landscape. However, the random changes in wind speed result in strong fluctuations in wind power generation, seriously threatening the stable operation of IEGS. Reference (Alabdulwahab et al., 2017) presents a stochastic dispatch method for hybrid power and gas system that considers the uncertainty of renewable energy and component contingency. A robust dispatch model of IEGS is developed in (Yang et al., 2018), of which a standard gas network method is proposed to consider gas dynamics. A stochastic optimal scheduling approach for IEGS is established in (Zhang and Shahidehpour, 2016) considering hourly electricity demand response. The studies mentioned above all make the assumption that the forecast error of wind power generation conforms to a specific distribution.

However, the stochastic dispatch model of IEGS mainly adopted the point prediction results or the wind power historical data to obtain wind power probability distribution, making it difficult to accurately quantify the time-varying non-stationary wind power prediction uncertainty. Nonparametric probabilistic forecasting can accurately quantify the wind power uncertainty and does not depend on a assumptions regarding the distribution of errors in wind power forecasts, which outperforms parametric probabilistic forecasting with respect to reliability and accuracy (Wan et al., 2014; Wan et al., 2020).

To this end, this paper establishes a stochastic optimal scheduling approach for IEGS, which integrates the advantages of nonparametric probabilistic forecasting to address the randomness of wind power. The method of direct quantile regression (DQR) is applied to generate the quantile at a series of quantile levels. A combination of Monte Carlo simulation and scenario reduction approach is employed to provide a set of representative scenarios by using the predictive quantile. Every representative scenario represents a conglomerate of numerous analogous scenarios. Then, the original partial differential equations of the natural network model are discretized by the implicit finite difference scheme to establish an algebraic model of the natural gas network. The proposed implicit finite difference scheme has second-order accuracy in both space and time, which provides an accurate approximation of the partial differential equations. The second-order core relaxation eliminates the nonconvexity of the momentum equation, allowing the stochastic optimal scheduling problem to be formulated as a second-order core programming (SOCP) model. This model can be efficiently solved by well-established optimization software. Case studies based on a test system validate the superiority of the developed stochastic scheduling method.

The remainder is organized as follows. The model of IEGS is proposed in Section 2. In Section 3, the formulation of the stochastic scheduling model is presented. The simulation results are shown in Section 4. The paper concludes in Section 5.

2 Model of IEGS

2.1 Natural gas network model

The flow of natural gas in pipelines is determined by both the momentum equation and the continuity equation. The momentum equation is a description of Newton’s second law (Antenucci and Sansavini, 2018), given as

$\frac{\partial \left(\rho v^2\right)}{\partial x}+\frac{\partial \left(\rho v\right)}{\partial t}+\frac{\partial p}{\partial x}+\frac{\epsilon v^2}{2d}\rho +g\rho \sin \theta =0(1)$

where v, ρ and p represent the velocity, density, and pressure of the gas, respectively; $\epsilon$ and d represent the friction factor and the diameter of the pipeline, respectively.

The continuity equation indicates that the natural gas travels continuously along the pipeline (Clegg and Mancarella, 2015), shown as

$\frac{\partial \rho }{\partial t}+\frac{\partial f}{S\partial x}=0(2)$

where f indicates the mass flow rate of pipeline, S represents the pipeline area.

The state equation expresses the connection between density and pressure, given as

$p=\rho c^2(3)$

where c is the speed of sound, which is determined by

$c^2=ZRT(4)$

where Z is the compressibility factor; R refers to the gas constant; T indicates the gas temperature.

Based on the steady-state condition, the state variables do not change with time. Thus, the partial differential terms with respect to time equal to 0 and the momentum Eq. 1 as well as the continuity Eq. 2 become (Correa-Posada and Sanchez-Martin, 2015)

$\frac{\partial \left(\rho v\right)}{\partial t}+\frac{\partial p}{\partial x}+\frac{\epsilon v^2}{2d}\rho =0(5)$

$\frac{\partial \rho }{\partial t}+\frac{\partial f}{S\partial x}=0(6)$

However, solving Eqs 5, 6 efficiently is challenging due to the form of partial differential. Therefore, the implicit finite difference scheme is introduced to transform the partial differential equations to algebraic equations. The difference scheme is proposed in (Kiuchi, 1994), shown as

$\frac{\partial G}{\partial x}=\frac{G_{i+1}^{t+1}-G_i^{t+1}}{\Delta x}+O\left(\Delta x^2\right)(7)$

where G represents the state variables (pressure p and mass flow rate f); $\Delta t$ and $\Delta x$ denote the temporal and spatial resolution, respectively.

The individual term G is approximated by

$G=\frac{G_{i+1}^{t+1}+G_i^{t+1}}{2}+O\left(\Delta x^2\right)(8)$

By substituting Eqs 7, 8 into Eqs 5, 6, the algebraic equations of the natural gas network are formulated as

$f_i=f_j=f_p(9)$

$f_p^2-\frac{2S^{2}d}{\epsilon lTRZ}\cdot \left(p_i^2-p_j^2\right)=0(10)$

The flow rate of gas within the pipeline should meet the specified capacity limits.

$f_p^{\min }\le f_{p,t}\le f_p^{\max }(11)$

where $f_p^{\min }$ and $f_p^{\max }$ determine the range of mass flow rate for pipeline p.

The nodal pressure is constrained by

$p_i^{\min }\le p_{i,t}\le p_i^{\max }(12)$

where $p_i^{\min }$ and $p_i^{\max }$ determine the range of pressure of node i.

The output of gas supplier is limited by

$f_i^{\mathrm{s},\min }\le f_{i,t}^{\mathrm{s}}\le f_i^{\mathrm{s},\max }(13)$

where $f_{i,t}^{\mathrm{s}}$ is the output of gas supplier i; $f_i^{\mathrm{s},\min }$ and $f_i^{\mathrm{s},\max }$ determine the range of the output for gas supplier i.

Moreover, the gas demand and the gas consumption of NGUs are satisfied by the gas supplier, given as (Zhang et al., 2018)

${\displaystyle \sum _t}{\displaystyle \sum _i}{f}_{i,t}^{\mathrm{s}}={\displaystyle \sum _t}\left({\displaystyle \sum _j}{f}_{j,t}^{\text{de}}+{\displaystyle \sum _j}{f}_{k,t}^{\mathrm{G}}+{\displaystyle \sum _p}{f}_{p,t}^{\text{con}}\right)(14)$

where $f_{j,t}^{\text{de}}$ indicates the gas demand of node j; $f_{k,t}^{\mathrm{G}}$ indicates the gas consumption for natural gas-fired unit k.

The operational pressure of NGUs has restrictions, shown as

$p_i^{\mathrm{G},\min }\le p_{i,t}^{\mathrm{G}}\le p_i^{\mathrm{G},\max }(15)$

where $p_{i,t}^{\mathrm{G}}$ is the pressure of NGU i at time t; $p_i^{\mathrm{G},\min }$ and $p_i^{\mathrm{G},\max }$ determine the range of pressure for NGU i.

The proposed natural gas network model contains nonconvex quadratic constraint (10), which poses challenges to solving the model. Thus, second-order cone relaxation is employed to convexify the quadratic constraint (10), given as

$f_p^2\le \frac{2S^{2}d}{\epsilon lTRZ}\cdot \left(p_i^2-p_j^2\right)(16)$

Eq. 20 can be transformed into standard SOC form:

${‖\begin{array}{c}{f}_p\\ \frac{2S^{2}d}{\epsilon lTRZ}\cdot p_j\end{array}‖}_2\le \frac{2S^{2}d}{\epsilon lTRZ}\cdot p_i(17)$

The application of the second-order cone relaxation technique transforms the proposed natural gas network model into a convex form, allowing for efficient solutions.

In a natural gas system, a gas compressor is assigned to compensate for pressure caused by friction loss in the pipeline (Abbaspour et al., 2005), depicted as

$H{P}_p^{\text{com}}={\chi }_p{f}_p^{\text{com}}\left[{\left(\frac{p_i}{p_j}\right)}^{{\nu }_n}-1\right](18)$

$GHV\cdot f_p^{\text{co}}={\gamma }_{p}H{P}_p^{\text{com}}(19)$

$k_p^{\min }\le \frac{p_i}{p_j}\le k_p^{\max }(20)$

$f_p^{\text{com},\min }\le f_p^{\text{com}}\le f_p^{\text{com},\max }(21)$

where $H{P}_p^{\text{com}}$ is the horsepower of compressor cross pipeline p at time t; ${\chi }_p$ and ${\nu }_n$ denote the horsepower constants of compressor p; $GHV$ indicates the gross heating value of natural gas; ${\gamma }_p$ refers to the energy conversion coefficient of compressor p; $k_p^{\min }$ and $k_p^{\max }$ determine the range of compression ratio of compressor p, respectively; $f_p^{\text{com},\min }$ and $f_p^{\text{com},\max }$ determine the range of mass flow rate of compressor p, respectively.

2.2 Power system model

The DC power flow model is adopted in this paper to consider the scheduling of active power, expressed as

$P_{k,t}=B_k\left({\phi }_{i,t}-{\phi }_{j,t}\right)(22)$

where $P_{k,t}$ indicates the active power flow of the transmission line k at time t; $B_k$ indicates the susceptance of transmission line k; ${\phi }_{i,t}$ and ${\phi }_{j,t}$ denote the voltage angle of bus i and j, respectively.

In the power system, the power requirements are satisfied by coal-fired generators (CGs) and NGUs, given as

${\displaystyle \sum _t}\left({\displaystyle \sum _i}{P}_{i,t}^{\mathrm{C}}+{\displaystyle \sum _j}{P}_{j,t}^{\mathrm{G}}\right)={\displaystyle \sum _t}{\displaystyle \sum _q}{P}_{q,t}^{\text{de}}(23)$

where $P_{i,t}^{\mathrm{C}}$ indicates the active power output of CG i; $P_{j,t}^{\mathrm{G}}$ indicates the active power output of NGU j; $P_{q,t}^{\text{de}}$ is the power demand of bus q at time t.

The output of CG should satisfy the capacity limit, shown as

$P_i^{\mathrm{C},\min }\le P_{i,t}^{\mathrm{C}}\le P_i^{\mathrm{C},\max }(24)$

where $P_i^{\mathrm{C},\min }$ and $P_i^{\mathrm{C},\max }$ determine the range of active power output of CG i.

The power output of NGU should also meet the capacity limit, given as

$P_i^{\mathrm{G},\min }\le P_{i,t}^{\mathrm{G}}\le P_i^{\mathrm{G},\max }(25)$

where $P_i^{\mathrm{G},\min }$ and $P_i^{\mathrm{G},\max }$ determine the range of active power output of NGU i.

The transmission line imposes constraints on the flow of active power.

$P_k^{\min }\le P_{k,t}\le P_k^{\max }(26)$

where $P_k^{\min }$ and $P_k^{\max }$ determine the range of active power flow through transmission line k.

Voltage phase angle is limited by

${\phi }_i^{\min }\le {\phi }_{i,t}\le {\phi }_i^{\max }(27)$

where ${\phi }_i^{\min }$ and ${\phi }_i^{\max }$ determine the range of voltage phase angle of bus i.

3 Nonparametric probabilistic forecasting based stochastic scheduling of IEGS

3.1 Objective function

The stochastic optimization algorithm takes into account the probability distribution of uncertain parameters and typically utilizes the probability density function to depict their variations (Qadrdan et al., 2014). Afterwards, various scenarios can be generated at random through techniques such as Monte Carlo simulation.

The primary goal of the stochastic scheduling model is to minimize the anticipated overall operational cost of IEGS, expressed as

$\min {\displaystyle \sum _z}\left[{\varphi }_z\times {\displaystyle \sum _{t=1}}\left({\displaystyle \sum _{i=1}}{a}_{i,t}{P}_{i,t,z}^{\mathrm{C}}+{\displaystyle \sum _{j=1}}{b}_{j,t}{f}_{j,t,z}^{\mathrm{s}}\right.\right](28)$

where ${\varphi }_z$ is the occurrence probability of wind power scenario z; $a_{i,t}$ and $b_{j,t}$ indicate the cost factors of CG i and gas supplier j, respectively.

3.2 Nonparametric probabilistic forecasting method

The volatility and sporadic availability of renewable energy create significant challenges to the optimal scheduling of IEGS. The utilization of probabilistic forecasting for wind power can offer critical insights for scheduling of power system in the presence of a substantial amount of wind power.

Typically, probabilistic forecasting methods encompass both parametric and nonparametric approaches. Parametric probabilistic forecasting relies on assumptions regarding the distribution of errors in wind power forecasts. Nonparametric probabilistic forecasting, however, can accurately measure the uncertainty of wind power and is not reliant on a specific probability distribution of forecasting errors, resulting in better reliability and accuracy.

In this paper, the DQR method is utilized to quantify the uncertainty of wind power. The quantile $q_t^{\omega }$ can be defined by

$\mathrm{Pr}\left(x_t\le q_t^{\omega }\right)=\omega (29)$

$q_t^{\omega }=Y_t^{-1}\left(\omega \right)(30)$

where Pr () denotes the probability operator; $Y_t$ denotes the cumulative distribution function of wind power; $x_t$ indicates the random variable of wind pwoer; $\omega$ indicates quantile level of the quantile.

Based on the obtained quantile $q_t^{\omega }$, a set of predicted quantiles for wind power can be obtained through the nonparametric probability prediction method of DQR, expressed as

${\widehat{Y}}_{t+k|t}=\left\{{\widehat{q}}_{t+k|t}^{{\omega }_i}|0\le {\omega }_1<{\omega }_2<\cdots <{\omega }_n\le 1\right\}(31)$

where ${\widehat{q}}_{t+k|t}^{{\omega }_i}$ is the approximation of real quantile $q_{t+k|t}^{\omega }$; ${\widehat{Y}}_{t+k|t}$ indicates the predicted quantile with proportions within the range of 0–1, $y_t$ indicates the probability density function; $Y_t$ indicates the cumulative distribution function.

The DQR method based on the extreme learning machine can transform the probabilistic forecasting into a linear programming model that can be efficiently solved. By introducing the DQR method, the predictive quantile series with proportions can be easily obtained. Given a set of predicted quantiles, the scenarios of wind power output can be obtained by Monte Carlo Simulation. Nevertheless, the straightforward implementation of a significant number of uncertainty scenarios would significantly prolong the computation time. Therefore, the scenario reduction method (Jiang et al., 2020) is applied to reduce the number of scenarios. As an effective tool for the scenario reduction, SCENRED provided by the General Algebraic Modelling System (Zhang et al., 2016) is applied in this paper.

Moreover, for deterministic method that do not consider the probabilistic information involved in wind power uncertainty, spinning reserve should be deployed to address the wind power uncertainty, given as

$S{R}_t={\displaystyle \sum _k}\left(P_k^{\mathrm{C},\max }-P_{k,t}^{\mathrm{C}}\right)\ge S{R}^{\min }(32)$

where $S{R}_t$ denotes the reserve that can be scheduled; $S{R}^{\min }$ indicates the minimum reserve of the IEGS.

3.3 Model summary

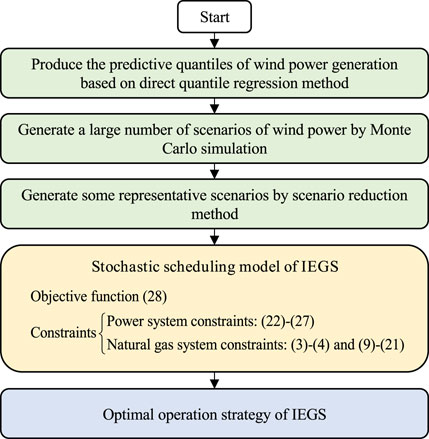
Figure 1 displays the flowchart of the stochastic scheduling model for IEGS. First, a set of predicted quantiles can be obtained by the DQR method. Afterwards, numerous wind power scenarios are created using the Monte Carlo simulation. The scenario reduction method clusters the generated scenarios into several representative scenarios. The nonconvex constraints of gas network are relaxed based on the SOC relaxation. In conclusion, the stochastic scheduling model of IEGS can be expressed as a SOCP model that can be efficiently solved.

FIGURE 1

FIGURE 1. The flowchart of the stochastic scheduling model.

4 Case study

4.1 System configuration

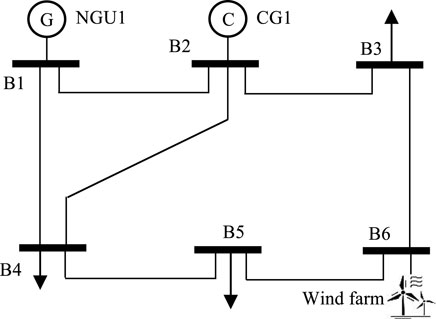
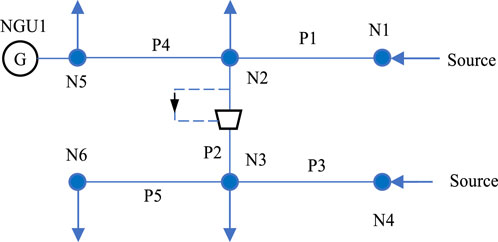
The topology of the test system is given in Figures 2, 3. The testing system is made up of a gas system with 6 nodes and a power system with 6 buses. The power demands of the test system are satisfied by 1 wind farm, 1 NGU and 1 CG. The wind farm is situated on bus 6, while the NGU is positioned on bus 1 in the power system and node 5 in the natural gas system. The CG is installed at bus 2. All simulations are performed on CPLEX-MATLAB solver on a PC with Inter Core i7 3.60GHz and 32GB RAM. To demonstrate the effectiveness of the proposed stochastic scheduling model for IEGS, two cases are considered.

FIGURE 2

FIGURE 2. Topology of the 6-bus power system.

FIGURE 3

FIGURE 3. Topology of the 6-node natural gas system.

Case 1: Optimal scheduling of IEGS without stochastic condition.

Case 2: Nonparametric probabilistic forecasting based stochastic optimal scheduling of IEGS.

Case 1 is a deterministic scenario in which spinning reserve is necessary to mitigate the uncertainty of the wind power. In Case 2, the consideration of wind power uncertainty includes the incorporation of probabilistic information.

4.2 Simulation results

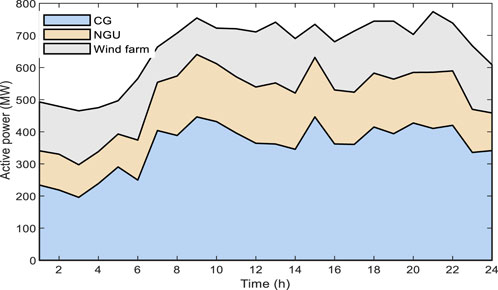
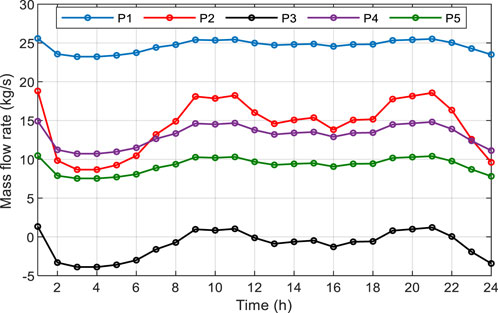
Case 1: The method of single-point wind forecasting can be used to obtain wind power generation. The scheduling results for Case 1 are presented in Figure 4. It can be observed that the power demands are satisfied by the CG, NGU, and wind power generation. The CG and NGU adjust their output to ensure that the wind power can be fully consumed. The natural gas system and the power system are coupled by the NGUs. Hence, the power generation of NGUs has an impact on the equilibrium of the natural gas system. Figure 5 displays the rate of mass flow within pipeline for Case 1. It can be seen that the incoming gas equals to the outgoing gas at each node.

FIGURE 4

FIGURE 4. The scheduling results of Case 1.

FIGURE 5

FIGURE 5. Mass flow rate of each pipeline in Case 1.

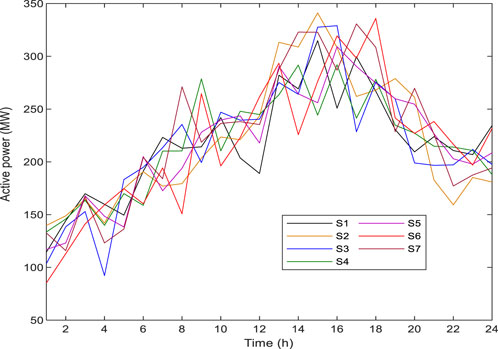
Case 2: The security and economy of IEGS face significant challenges due to the volatility and sporadic availability of renewable energy. The probabilistic information involved in wind power generation is considered in Case 2 to address the uncertainty of renewable energy. Based on the set of predicted quantiles, 3,000 wind power generation scenarios are obtained by Monte Carlo simulation. To reduce computational burden, 3,000 scenarios are reduced to a total of 7 representatives by the scenario reduction method. Seven scenarios are capable of approximating original model.

The obtained 7 representative scenarios of wind power generation are given in Figure 6. The power output of wind farms differs in every scenario. Table 1 lists the probability and total costs of IEGS in different scenario. It can be seen that the total costs of IEGS in scenarios are different from each other. This is due to the fact that every representative scenario is comprised of a combination of comparable scenarios. By utilizing the nonparametric probability forecasting method, the secure operation of power system with high penetration of wind power can be can guaranteed.

FIGURE 6

FIGURE 6. Representative scenarios of wind power generation in Case 2.

TABLE 1

TABLE 1. Comparison of results for different scenarios in Case 3.

The comparison of results for different cases is depicted in Table 2. Due to the different output of wind farm, it can be seen that the operation costs in scenario S2, S3, and S5 are higher than the expected total operation cost. Moreover, it can be easily observed that the expected total operation cost for 7 representative scenarios is $739,172, which is almost 1% lower that of Case 1, validating the significance of stochastic method in cost reduction. Given the probability information of wind power uncertainty, the operation strategy of IEGS has better economy and security.

TABLE 2

TABLE 2. Comparison of results for different cases.

4.3 Larger test system

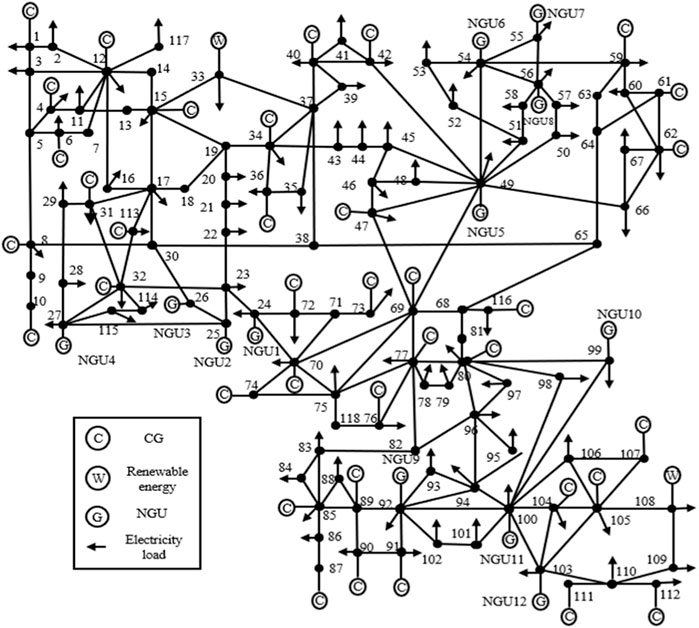
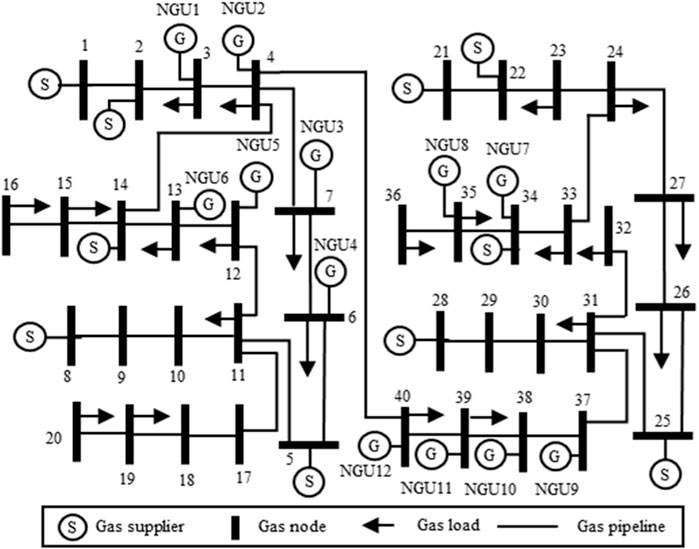
A larger system composed of a gas system with 40 nodes and a power system with 118 buses is given in Figures 7, 8. Detailed topology data can be found in (Chen et al., 2021b). The Monte Carlo simulation method generates 5,000 stochastic scenarios. The scenario reduction method reduces all stochastic scenarios to 7 representative scenarios.

FIGURE 7

FIGURE 7. IEEE 118-bus test system.

FIGURE 8

FIGURE 8. 40-node natural gas test system.

The probably and total costs of the 7 scenarios are presented in Table 3. The total operation cost is seen to differ across different scenarios. The operation costs in scenario S1, S4, S5 and S6 are higher than the expected total operation cost because the wind power fluctuations in these scenarios are stronger than other scenarios.

TABLE 3

TABLE 3. Comparison of results for different cases.

The total operation cost in various scenarios is provided in Table 4. The expected total operation cost in Case 2 is $4,935,092, which is 0.94% lower than that of Case 1. By considering the stochastic condition, the IEGS can operate more economically.

TABLE 4

TABLE 4. Comparison of results for different cases.

5 Conclusion

To address the volatility and sporadic availability of wind power, this paper presents a nonparametric probabilistic forecasting based stochastic optimal scheduling approach for IEGS. The DQR method is used to generate predictive quantile series for wind power. Given a set of predicted quantiles, a combination of Monte Carlo simulation and scenario reduction approach is employed to provide a set of representative scenarios. The original partial differential equations of the natural network model are discretized by the implicit finite difference scheme to establish an algebraic model of the gas network. The nonconvexity of the momentum equation is eliminated by the second-order core relaxationF, and the proposed stochastic optimal scheduling problem is cast into a SOCP model. The simulation results validate that the proposed stochastic scheduling model outperforms the deterministic model, achieving a nearly 1% reduction in total operation cost. The proposed stochastic scheduling model offers even greater benefits in large systems, opening up a new path towards secure and cost-effective operation of a significant percentage of renewable energy power systems.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary material.

Author contributions

JC: Methodology, Writing–original draft. DC: Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Science and Technology Project of State Grid Fujian Electric Power Company Limited (52130423000J).

Conflict of interest

JC and DC were employed by State Grid Fujian Electric Power Research Institute.

The authors declare that this study received funding from State Grid Fujian Electric Power Company Limited. The funder had the following involvement in the study: data collection and analysis.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbaspour, M., Chapman, K., and Krishnaswami, P. (2005). Nonisothermal compressor station optimization. J. Energy Resour. Technol. 127, 131–141. doi:10.1115/1.1871248

CrossRef Full Text | Google Scholar

Alabdulwahab, A., Abusorrah, A., Zhang, X., and Shahidehpour, M. (2017). Stochastic security-constrained scheduling of coordinated electricity and natural gas infrastructures. IEEE Syst. J. 11 (3), 1674–1683. doi:10.1109/jsyst.2015.2423498

CrossRef Full Text | Google Scholar

Antenucci, A., and Sansavini, G. (2018). Gas-constrained secure reserve allocation with large renewable penetration. IEEE Trans. Sustain. Energy 9 (2), 685–694. doi:10.1109/tste.2017.2756091

CrossRef Full Text | Google Scholar

Chen, D., Wan, C., Song, Y., Guo, C., and Shahidehpour, M. (2021b). Non-isothermal optimal power and gas flow. IEEE Trans. Power Syst. 36 (6), 5453–5464. doi:10.1109/tpwrs.2021.3084941

CrossRef Full Text | Google Scholar

Chen, D., Wan, C., Song, Y., Liu, H., and Wang, F. (2021a). N-1 security-constrained coordinated scheduling of integrated electricity and natural gas system considering gas dynamics and wind power uncertainty. IET Renew. Power Gener. 15 (7), 1408–1421. doi:10.1049/rpg2.12087

CrossRef Full Text | Google Scholar

Chen, S., Conejo, A., Sioshansi, R., and Wei, Z. (2019). Unit commitment with an enhanced natural gas-flow Model. IEEE Trans. Power Syst. 34 (5), 3729–3738. doi:10.1109/tpwrs.2019.2908895

CrossRef Full Text | Google Scholar

Clegg, S., and Mancarella, P. (2015). Integrated modeling and assessment of the operational impact of power-to-gas (P2G) on electrical and gas transmission networks. IEEE Trans. Sustain. Energy 6 (4), 1234–1244. doi:10.1109/tste.2015.2424885

CrossRef Full Text | Google Scholar

Correa-Posada, C., and Sánchez-Martın, P. (2014). Security-constrained optimal power and natural-gas flow. IEEE Trans. Power Syst. 29 (4), 1780–1787. doi:10.1109/tpwrs.2014.2299714

CrossRef Full Text | Google Scholar

Correa-Posada, C., and Sanchez-Martin, P. (2015). Integrated power and natural gas model for energy adequacy in short-term operation. IEEE Trans. Power Syst. 30 (6), 3347–3355. doi:10.1109/tpwrs.2014.2372013

CrossRef Full Text | Google Scholar

Fang, J., Zeng, Q., Ai, X., Chen, Z., and Wen, J. (2018). Dynamic optimal energy flow in the integrated natural gas and electrical power systems. IEEE Trans. Sustain. Energy 9 (1), 188–198. doi:10.1109/tste.2017.2717600

CrossRef Full Text | Google Scholar

Jiang, Y., Wan, C., Chen, C., Shahidehpour, M., and Song, Y. (2020). A hybrid stochastic-interval operation strategy for multi-energy microgrids. IEEE Trans. Smart Grid 11 (1), 440–456. doi:10.1109/tsg.2019.2923984

CrossRef Full Text | Google Scholar

Kiuchi, T. (1994). An implicit method for transient gas flows in pipe networks. Int. J. Heat Fluid Flow 15, 378–383. doi:10.1016/0142-727x(94)90051-5

CrossRef Full Text | Google Scholar

Liu, C., Shahidehpour, M., Fu, Y., and Li, Z. (2009). Security-constrained unit commitment with natural gas transmission constraints. IEEE Trans. Power Syst. 24 (3), 1523–1536. doi:10.1109/tpwrs.2009.2023262

CrossRef Full Text | Google Scholar

Liu, F., Bie, Z., and Wang, X. (2019). Day-ahead dispatch of integrated electricity and natural gas system considering reserve scheduling and renewable uncertainties. IEEE Trans. Sustain. Energy 10 (2), 646–658. doi:10.1109/tste.2018.2843121

CrossRef Full Text | Google Scholar

Qadrdan, M., Wu, J., Jenkins, N., and Ekanayake, J. (2014). Operating strategies for a GB integrated gas and electricity network considering the uncertainty in wind power forecasts. IEEE Trans. Sustain. Energy 5 (1), 128–138. doi:10.1109/tste.2013.2274818

CrossRef Full Text | Google Scholar

Shao, C., Wang, X., Shahidehpour, M., Wang, X., and Wang, B. (2017). An MILP-based optimal power flow in multicarrier energy systems. IEEE Trans. Sustain. Energy 8 (1), 239–248. doi:10.1109/tste.2016.2595486

CrossRef Full Text | Google Scholar

Wan, C., Xu, Z., Pinson, P., Dong, Z., and Wong, K. (2014). Probabilistic forecasting of wind power generation using extreme learning machine. IEEE Trans. Power Syst. 29 (3), 1033–1044. doi:10.1109/tpwrs.2013.2287871

CrossRef Full Text | Google Scholar

Wan, C., Zhao, C., and Song, Y. (2020). Chance constrained extreme learning machine for nonparametric prediction intervals of wind power generation. IEEE Trans. Power Syst. 35 (5), 3869–3884. doi:10.1109/tpwrs.2020.2986282

CrossRef Full Text | Google Scholar

Yang, J., Zhang, N., Kang, C., and Xia, Q. (2018). Effect of natural gas flow dynamics in robust generation scheduling under wind uncertainty. IEEE Trans. Power Syst. 33 (2), 2087–2097. doi:10.1109/tpwrs.2017.2733222

CrossRef Full Text | Google Scholar

Zhang, X., Shahidehpour, M., Alabdulwahab, A., and Abusorrah, A. (2016). Hourly electricity demand response in the stochastic day-ahead scheduling of coordinated electricity and natural gas networks. IEEE Trans. Power Syst. 31 (1), 592–601. doi:10.1109/tpwrs.2015.2390632

CrossRef Full Text | Google Scholar

Zhang, X., Shahidehpour, M., Alabdulwahab, A., and Abusorrah, A. (2016). Hourly electricity demand response in the stochastic day-ahead scheduling of coordinated electricity and natural gas networks. IEEE Trans. Power Syst. 31 (1), 592–601. doi:10.1109/tpwrs.2015.2390632

CrossRef Full Text | Google Scholar

Zhang, Y., Hu, Y., Ma, J., and Bie, Z. H. (2018). A mixed-integer linear programming approach to security-constrained co-optimization expansion planning of natural gas and electricity transmission systems. IEEE Trans. Power Syst. 33 (6), 6368–6378. doi:10.1109/tpwrs.2018.2832192

CrossRef Full Text | Google Scholar