Optimal real-time tuning of autonomous distributed power systems using modern techniques

This work considers using a novel heuristic population-based evolutionary algorithm [viz., the moth flame optimization (MFO) algorithm] to regulate the conventional controller installed in an autonomous power system (APS). The moth flame optimization algorithm intends to produce the optimal magnitudes of the proportional-integral-derivative plus second derivative (PIDD²) controller parameters along with its first- and second-order low-pass filter constraints (installed in the investigated autonomous power system). The present task includes a comparison of the voltage response profiles of the investigated system obtained by the proposed moth flame optimization-based proportional-integral-derivative plus second derivative controller and those obtained by other algorithms (conveyed in current state-of-the-art literature) based on a proportional-integral controller. A fast-acting Sugeno fuzzy logic (SFL) technique is used to achieve the dynamic online results of the investigated autonomous power system model for online, off-nominal operational circumstances. Under step perturbations, the time-domain transient investigation in reference to voltage and/or mandate of load for the proposed autonomous power system model is inspected. Additionally, the robustness of the proposed moth flame optimization-based proportional-integral-derivative plus second derivative controller is investigated to test its behavior. An investigation has been provided by varying the model components of the studied autonomous power system model. It may be reported, as per the results obtained from the simulation, that the proposed moth flame optimization-based proportional-integral-derivative plus second derivative controller is an effective control strategy for the autonomous power system. The current research effort indicates that the proposed moth flame optimization algorithm, along with Sugeno fuzzy logic, may be useful for the actual time process of an autonomous power system.

1 Introduction

Power sector deregulation, increased environmental concern, and sustainable development/supply security make the power system extremely decentralized; as a result, it is largely responsible for the shift from large central generation to scalable distributed generation (DG). DG generates electricity in smaller quantities closer to end users (Huda and Zivanovic, 2017), which remarkably boosts energy efficiency, reduces carbon emissions, improves grid resilience, and curbs the requirement for new transmission investments. However, in order to effectively use DG technology, the various generators have to be synchronized and fine-tuned to sustainably serve the growing digital and automated infrastructures, and excess energy in low load-demand conditions must be fed to the grid efficiently. Thus, fine-tuning various distributed generators for the system to efficiently carry out these functions introduces a new set of problems to the power system, necessitating the development of new techniques to keep up with the trail of these challenges. As a result, the focus of this work is primarily to model and optimize an optimal automatic voltage regulator (AVR) controller for the autonomous distributed power model.

Regardless of the load condition, the AVR loop guarantees that the voltage profile remains within acceptable limits by constantly tracking the generator terminal voltage and correcting the generator exciter voltage accordingly. Thus, for effective AVR performance, a controller is often incorporated in the loop, and as a result, different controllers such as proportional integral PI (Hussain et al., 2017), (Eke et al., 2021), proportional integral derivative PID and its variants (Lahcene et al., 2017; Sambariya and Gupta, 2017; Blondin et al., 2018; Mosaad et al., 2018; Ali et al., 2020; Bhullar et al., 2020; Veinovi, 2022), integral double derivative with filter IDDF (Rajbongshi and Saikia, 2017), and many others (Moschos and Parisses, 2022), (Sikander et al., 2018) have been investigated over the years for AVR control. However, optimal controller parameter tuning is achieved by employing various techniques such as metaheuristic optimization techniques, artificial intelligence techniques, or a combination of the two to maximize the benefits of each distinct approach.

Metaheuristic optimization techniques are collections of coherent and effective intelligent techniques used to solve complex, high-order, non-linear engineering problems even with time delays; their efficacy and consistency can be seen in almost all power systems disciplines such as operation, control, scheduling, and energy management (Ma et al., 2016; Ayalew et al., 2019; Bukar and Tan, 2019; Ghalambaz et al., 2021; Rodrigues et al., 2021), although of significant importance AVR control is well highlighted in (Hussain et al., 2017), (Sambariya and Gupta, 2017), (Lahcene et al., 2017), (Mosaad et al., 2018), (Moschos and Parisses, 2022), (Banerjee et al., 2012; Gözde et al., 2017; Bourouba et al., 2019; Mosaad et al., 2019; Jumani et al., 2021; Micev et al., 2021), a brief and comprehensive study, particularly on the new metaheuristic technique used on AVR, can be seen in (Kouba and Boudour, 2019) and (Oladipo et al., 2020). However, despite being a promising technique for solving engineering problems, the metaheuristic optimization technique often suffers from inefficiency due to difficult parameter tuning and non-assurance of convergence because its performance is highly dependent on fine parameter tuning (Madic et al., 2013). As a result, few parameters or parameter-free techniques, as seen in Mosaad et al. (2018), Bhullar et al. (2020), Eke et al. (2021), are required for greater performance.

Artificial intelligence techniques, on the other hand, execute tasks that typically require human intelligence, and their ability to operate in real time is of particular interest. In generally, when AI techniques are used to tune controller parameters or to optimize a process, consistently good results are obtained, as seen in Elsisi (2019); but their operation requires complex analysis with a long convergence time (Mosaad et al., 2018).

However, a good balance, particularly between exploration and exploitation, is achieved by hybridization; thus, superior performance is guaranteed when these techniques are combined, as seen in (Al Gizi et al., 2015a; Al Gizi et al., 2015b; Al Gizi, 2019; Ali and Khaniki, 2020; Mokeddem and Mirjalili, 2020; Ozgenc et al., 2020). Hence, this work is focused on modeling and optimizing an autonomous distributed power system using a high-performance proportional-integral-derivative-second order derivative (PIDD²) controller improved using the Moth flame optimization (MFO) technique (Mirjalili, 2015) and/or in conjunction with real-time Sugeno fuzzy logic (SFL). MFO was suggested and well deliberated in Mirjalili (2015), and has been used since then in different fields (Shehab et al., 2020), including power systems, as seen in Mohanty (2019), Chatterjee et al. (2020), Chatterjee and Mohammed (2022). Moreover, MFO variants were well studied in literature; the authors of (Nadimi-Shahraki et al., 2021a) propose a migration-based moth-flame optimization (M-MFO) technique that is projected to avoid risk of local optima entrapment. The primary focus of M-MFOs is on taming the location of unlucky moths by traveling them stochastically in the initial iterations using an arbitrary migration (RM) operator, sustaining the result modification by distinctly storing new skilled results in a controlling archive, and finally manipulating around the locations protected in the controlling archive using a guided migration (GM) operator. Further, an improved moth-flame optimization (I-MFO) algorithm is proposed by the authors of (Nadimi-Shahraki et al., 2021b) to deal with established MFO problems by positioning stuck moths in local optima by defining memory for each moth. The stuck moths have a tendency to eliminate the local optima by using the enhanced wandering around search (AWAS) strategy. Also, (Nadimi-Shahraki et al., 2022) postulated an operational hybridization of the whale optimization algorithm (WOA) and an improved moth-flame optimization algorithm (MFO) named WMFO to resolve the OPF problem. The WOA and the improved MFO work together in the WMFO to effectively determine capable zones and offer high-quality results.

It should be noted that the introduction of SFL to carry parameter specifications in real-time makes the techniques presented here behave as if they are parameter-free, allowing for easy achievement of good balance. Consequently, the main objectives of this work are:

a) To tune the offline parameters of the PIDD² controller using the MFO technique for the APS being considered.

b) To explore the utility and applicability of SFL-based controller tuning in online real-time situations.

c) To compare the voltage profile response obtained from the proposed technique with that acquired by other studied techniques.

d) To investigate the model’s performance for a wide range of important system parameters and disturbances for practical implementation.

2 Methodology

2.1 Power system modeling

A standard distributed energy generator (DEG) consisting of an AVR, speed governor, and controller is depicted in Figure 1; the upper half of the blocks are the mechanical model of the speed governor with an integrator of gain $K_{ii}$ and droop $R$, while the lower half of the blocks are the electrical model of the AVR system of the studied DEG system with a PIDD² controller. The integral controller eliminates the studied system’s steady-state frequency error, which is modeled by the transfer function given in Eq. 1.

$G_{Integral}=\frac{K_{ii}}{s}(1)$

FIGURE 1

FIGURE 1. Block diagram of the investigated APS’s transfer function.

The generator inertia (H), damping constant (D), and governor controller variables are the key features influencing frequency aberration. On a diesel engine, the inertia constant (H) can be documented as the ratio of energy deposited in revolving components of the diesel generator to the rated apparent power, whereas the actuator is normally implemented to refer to the fuel system’s actuator, which controls the volume of diesel fuel inserted into the engine. The transfer function of Eqs 2–4 models the DEG, valve actuator, inertia, and load of the power system under consideration, where ${\tau }_D$ and ${\tau }_V$ are respectively the time constant of the diesel generator system and valve actuator system while $H$ and $D$ are respectively the inertia and damping constants of the DEG under consideration (Banerjee et al., 2012).

$G_{\mathit{DEG}}=\frac{1}{1+s{\tau }_D}(2)$

$G_{VA}=\frac{1}{1+s{\tau }_V}(3)$

$G_{IL}=\frac{1}{2Hs+D}(4)$

The AVR system comprises four major parts: a generator, an exciter, an amplifier, and a sensor. The sensor detects the voltage at the synchronous generator’s terminal indefinitely. The signal is rectified and smoothed and then directed to the comparator for comparison with a pre-set signal. The comparator’s voltage error is then amplified through the amplifier and directed to the exciter to regulate the windings of an alternator field. Furthermore, the transfer function of an amplifier, exciter, and generator is modeled by a gain and a time constant, as shown in Eqs 5–7, where $K_A$ and ${\tau }_A$, $K_E$ and ${\tau }_E$ and $K_G$ and ${\tau }_G$, respectively, denote the gain and the time constant of the amplifier, modern exciter, and generator systems (Banerjee et al., 2012).

$G_{Amplifier}\left(s\right)=\frac{K_A}{1+s{\tau }_A}(5)$

$G_{Exciter}\left(s\right)=\frac{K_E}{1+s{\tau }_E}(6)$

$G_{Generator}\left(s\right)=\frac{K_G}{1+s{\tau }_G}(7)$

2.2 Controller modeling

Unlike the conventional PID controller, which has three main components for improving system performance, the PIDD² controller employed here has an additional component called second-order derivative gain $\left(K_{D_2}\right)$ for better performance. As a result, the four parameters, namely, $K_P$, $K_I$, $K_D$ and a second-order derivative gain $\left(K_{D_2}\right)$, must be carefully modeled according to the transfer function expressed by Eq. 8.

$G_{PID{D}^2}=K_P+\frac{K_I}{s}+s{K}_D+s^2{K}_{D_2}(8)$

However, two low-pass filters have been employed in the controller design for smoother and better response; these are the first-order low-pass filter for first-order derivatives and a second-order low-pass filter for second-order derivatives in their corresponding tracks, as shown in Eqs 9, 10. Thus, the overall transfer function of the employed PIDD² controller can be represented by Eq. 11 where $N$ and $N_D$ are the filter coefficients and $T$ and $T_D$ are the time constants.

$G_{First\_Filter}\left(s\right)=\frac{s}{s\left(\frac{1}{N}\right)T+1}(9)$

$G_{Second\_Filter}\left(s\right)=\frac{s^2}{s^2{\left(\frac{1}{N_D}\right)}^2{T}_D^2+2s\left(\frac{1}{N_D}\right)T_D+1}(10)$

$G_{PID{D}^2}\left(s\right)=K_P+\frac{K_I}{s}+s{K}_D\left(\frac{1}{s\left(1/N\right)T+1}\right)+s^2{K}_{D_2}\left(\frac{1}{s^2{\left(\frac{1}{N_D}\right)}^2{T}_D^2+2s\left(\frac{1}{N_D}\right)T_D+1}\right)(11)$

The suitability of the proposed technique is assessed by a flexible time domain performance index known as the “figure of merit” (FOD), represented in Eq. 12; it is implemented using the system’s essential dynamic attributes based on desired specifications and constraints. Consequently, the main target of this optimization task is to minimize FOD, which is directly dependent on the system’s transient response parameters. It should be noted that the $\beta$ magnitude in Eq. 12 is set to 1.0. Therefore, based on Eq. 12, the design constraints are the controller parameter limits, which are characterized by Eq. 13 as the set of minimum and maximum specified design variables.

$FOD=\left(1-e^{-\beta }\right)\left(M_P+E_{SS}\right)+e^{-\beta }\left(T_S-T_R\right)(12)$

$\left.\begin{array}{l}{K}_P^{\min }\le K_P\le K_P^{\max }\\ K_I^{\min }\le K_I\le K_I^{\max }\\ K_D^{\min }\le K_D\le K_D^{\max }\\ K_{D_2}^{\min }\le K_{D_2}\le K_{D_2}^{\max }\\ N^{\min }\le N\le N^{\max }\\ T^{\min }\le T\le T^{\max }\\ N_D^{\min }\le N_D\le N_D^{\max }\\ T_D^{\min }\le T_D\le T_D^{\max }\end{array}\right\}(13)$

2.3 SFL for online tuning of the PIDD² controller

Fuzzy control deviates from conventional control theories to a greater extent because it attempts to model logical reasoning with a vague statement rather than the usual true or false. Sugeno fuzzy logic (SFL) is an efficient fuzzy control technique for a system with fast-changing dynamics like AVR; it can modify the controller’s parameters with precision even online and in a real-time environment. Real-time operations guarantee that balance is achieved between load and generation at all times by making the best use of asynchronous data and control to accommodate changing conditions and delays in communication; fuzzy control is extensively discussed in (Mohagheghi and Harley, 2004). Figure 2 shows the structure of a fuzzy logic-based PIDD² controller, the implementation of which necessitates two inputs to yield a control signal $\left(u\right)$: incremental change in error $\left(\Delta e\right)$, and derivative of the incremental change in error, $\left(\Delta \dot{e}\right)$.

FIGURE 2

FIGURE 2. Fuzzy-based PIDD² controller.

The incremental change in error shown in Eq. 14 is the difference between the change in reference voltage and the change in terminal voltage, whereas the derivative of incremental change in error shown in Eq. 15 is the rate of change of incremental change in error, where $\Delta e_i$ and $\Delta e_{i-1}$ are the incremental change in error at the time $i$ and $\left(i-1\right)$, respectively, while $t$ is the sample time in seconds.

$\Delta e=\left(\Delta V_{ref}-\Delta V_s\right)(14)$

$\Delta \dot{e}=\frac{\Delta e_i-\Delta e_{i-1}}{t}(15)$

These two inputs ($\left(\Delta e\right)$; $\left(\Delta \dot{e}\right)$) are split into seven fuzzy classes: positive large (PL), positive medium (PM), positive small (PS), zero (ZR), negative small (NS), negative medium (NM), and negative large (NL). The membership functions of this fuzzy control, which show the degree of membership of the real variable in the corresponding fuzzy variable, are displayed in Figure 3 for the input $\left(\Delta e\right)$ and $\left(\Delta \dot{e}\right)$ for the output $\left(u\right)$. The membership function is made up of two trapezoidal memberships and five triangular membership components, making up seven MFs with two inputs and one output, as depicted in Figure 4 and the corresponding control values specified in Table 1. Therefore, as indicated in Table 1, the output MF is determined by two input MFs in each cell of the control rule. Hence the control rules are realized as follows: if input 1 and input 2 are both true, then output 1 is true. Figure 4 depicts the surface plot profile of the control signal with the deviation of the incremental change in error and the derivative of the incremental change in the error signal.

FIGURE 3

FIGURE 3. Membership functions of the MFO-SFL-based PIDD² controller (A) input $\left(\Delta e\mathrm{o}\mathrm{r}\Delta \dot{e}\right)$ and (B) output $\left(u\right)$.

TABLE 1

TABLE 1. Control rules of the MFO-SFL-based PIDD² controller.

FIGURE 4

FIGURE 4. Signal surface plot with$\left(\Delta e\right)$ and $\left(\Delta \dot{e}\right)$.

3 MFO overview

Moth Flame Optimization (MFO) is inspired by moth night navigation features; fundamentally, MFO mimics the unwanted behavior of moths while navigating in the presence of artificial light and performs its optimization. MFO was proposed and extensively discussed in (Mirjalili, 2015), and it has since been used in a variety of fields (Shehab et al., 2020), including power systems, as seen in (Mohanty, 2019; Chatterjee et al., 2020; Chatterjee and Mohammed, 2022). It is a population-based algorithm that employs two important components: moths and flames. Therefore, it is randomly initiated in space by establishing candidate solutions (moths), then computing their fitness levels and aligning with the flames, which is the best position moths can reach. Afterward, exploitation and exploration are adaptively ensured by a progressive and systematic reduction in the number of flames; thus, for a moth to attain a greater position, it must update its position over and over again according to the position of the flame until convergence is achieved, at which point the process is terminated. The relevant equations required for executing the algorithm are established in (Mirjalili, 2015; Shehab et al., 2020; Chatterjee and Mohammed, 2022), and the general formulation for implementing the MFO algorithm as used in APS is specified in Algorithm 1, (Chatterjee and Mohammed, 2022).

3.1 MFO algorithm

The MFO algorithm assumes that the moths are the candidate result and that their location in space is the variable quantity of the problem. As a result, the moths can fold away in 1-d, 2-d, 3-d, or hyper-dimensional space by changing their location vectors. Because this is a population-based algorithm, the set of moths is described in a matrix that is well-defined in Eq. 16 (Mirjalili, 2015)

$M=\left[\begin{array}{l}{m}_{\mathrm{1,1}}{m}_{\mathrm{1,2}}........m_{1,d}\\ m_{\mathrm{2,1}}{m}_{\mathrm{2,2}}........m_{2,d}\\ .....\\ .....\\ .....\\ m_{n,1}{m}_{n,2}........m_{n,d}\end{array}\right](16)$

Where $n$ is the moth numeral data, and $d$ is the variable numerical data (dimension).

It is assumed that there is an array of the corresponding fitness magnitudes for all moths, as stated in Eq. 17 (Mirjalili, 2015).

$OM={\left[O{M}_{1}O{M}_2..O{M}_n\right]}^T(17)$

It should be noted that the fitness magnitude for each moth will be the return magnitude of the fitness (objective) function. The fitness function sends the location vector (1st row in the matrix $M$, for example,) of an individual moth, which then conveys the fitness function’s output with the corresponding moth as its fitness magnitude ($O{M}_1$ in the matrix $OM$ well-defined in Eq. 17, for instance).

The MFO algorithm has an additional critical component known as flames, for which, similar to the moth matrix, an additional matrix is used as shown in Eq. 18 (Mirjalili, 2015).

$F=\left[\begin{array}{l}{F}_{\mathrm{1,1}}{F}_{\mathrm{1,2}}...F_{1,d}\\ F_{\mathrm{2,1}}{F}_{\mathrm{2,2}}...F_{2,d}\\ ....\\ ....\\ ....\\ F_{n,1}{F}_{n,2}...F_{n,d}\end{array}\right](18)$

It is clear from Eq. 18 that the size of $M$ and $F$ are identical. It is also intended for the flames to have an array for capturing the equivalent fitness magnitudes, as shown in Eq. 19 (Mirjalili, 2015).

$OF={\left[O{F}_{1}O{F}_2..O{F}_n\right]}^T(19)$

Individually, the moths and flames (both of which are results) differ because their magnitudes change in each iteration. Moths are actual searching agents that travel from place to place in the search space, with flames being the best location attained so far.

The MFO algorithm is a three-tuple that estimates the global desirable solution for the optimization issues and is expressed in Eq. 20 (Mirjalili, 2015).

$MFO=\left(I,P,T\right)(20)$

In Eq. 20, $I$ is a function that explains the fitness magnitudes of an arbitrary population of moths. The analytical model of this function is provided in Eq. 21 (Mirjalili, 2015).

$I:\varphi \to \left\{M,OM\right\}(21)$

The function $P$ in Eq. 21 is the main function that transfers the moths in the search space. This function, ultimately, yields a modernized form of the matrix $M$ after receiving it, as shown in Eq. 22 (Mirjalili, 2015).

$P:M\to M(22)$

If the conclusion condition is fulfilled, then the function $T$ in Eq. 20 yields true; otherwise, it yields false, as given in Eq. 23 (Mirjalili, 2015).

$T:M\to \left\{true,false\right\}(23)$

The overall form of the MFO algorithm is defined in Algorithm 1:.

Algorithm 1:. Overall form of the MFO algorithm (Mirjalili, 2015).

M=I();

while T(M) is equal to fasle

   M=P(M);

end

The function $I$ must compute the objective function magnitudes after producing preliminary results. In this function, the use of any arbitrary distribution is permitted. The technique shown in Algorithm 2 is employed by default.

Algorithm 2:. Computation of the objective function (Mirjalili, 2015).

for i=1: n

  for j=1: d

 M (i,j)=(ub(i)-Ib(i))*rand()+1b(i);

  end

end

OM=Fitness Function(M)

In Algorithm 2, there are two additional arrays named $ub$ and $lb$ which outline the upper and lower constraints of the variable quantities, respectively, as shown in Eqs 24, 25 (Mirjalili, 2015).

$ub=\left[u{b}_1,u{b}_2,u{b}_3,....,u{b}_{n-1},u{b}_n\right](24)$

where $u{b}_i$ represents the upper constraint of the $i^{th}$ variable.

$lb=\left[l{b}_1,l{b}_2,l{b}_3,....,l{b}_{n-1},l{b}_n\right](25)$

where $l{b}_i$ represents the lower constraint of the $i^{th}$ variable.

The location of individual moths is improved with respect to a flame implementation Eq. 26 (Mirjalili, 2015).

$M_i=S\left(M_i,F_j\right)(26)$

where $M_i$ specifies the $i^{th}$ moth, $F_j$ specifies the $j^{th}$ flame, and $S$ specifies the spiral function.

A logarithmic spiral, as used in the MFO algorithm in (Mirjalili, 2015), is presented in Eq. 27.

$S\left(M_i,F_j\right)=D_i.e^{bt}.\cos \left(2\pi t\right)+F_j(27)$

where $D_i$ is the gap of the $i^{th}$ moth for the $j^{th}$ flame, $b$ is a constant for maintaining the shape of the logarithmic spiral, and $t$ is an arbitrary number in the range [-1, 1].

The variable quantity $D$ can be designed as per Eq. 28 (Mirjalili, 2015).

$D_i=\left|F_j-M_i\right|(28)$

where $M_i$ specifies $i^{th}$ moth, $F_j$ specifies $j^{th}$ flame.

The spiral traveling technique of moths is described in Eq. 27. According to the equation, the succeeding location of a moth is described with respect to flame. The spiral technique instructs the moths to inform flames about their locations, making it the main portion of the proposed methodology. The spiral equation allows a moth to hover around a flame. As a result, the search space can be guaranteed for its exploration and exploitation.

The chances of discovering better outcomes can be ensured by taking the best results so far as flames. Hence, the current best results attained are stowed in the matrix $F$. Then the moths must modify their locations in relation to the matrix F throughout the optimization process. It is contrived that $t$ is an arbitrary number $\left[r,1\right]$ in order to emphasize additional exploitation, where $r$ is linearly weakened from −1 to −2 throughout the iteration sequence. In this procedure, the moths become more adept at exploiting their respective flames more effortlessly, according to the number of iterations.

Similar flames aid the moths in varying their locations. The first moth constantly modifies its location with respect to the best flame, while the last moth modifies its position with respect to the worst flame. In the search space, with respect to $n$ dissimilar positions, the location-modifying procedure of moths may damage the exploitation of the best result. An adaptive technique is employed to achieve the desired number of flames.

The equation in Eq. 29 can be implemented in this context (Mirjalili, 2015):

$flamenumber=round\left(N-l*\frac{N-1}{T}\right)(29)$

where $l$ signifies the current number of iterations, $N$ specifies the maximum number of flames, and $T$ is the maximum number of iterations. Exploitation and exploration of the search space are well-adjusted by the decrease in the number of flames. The stages of the $P$ function are illustrated in Algorithm 3. The execution of the $P$ function continues in order to moves the moth in search space until true magnitude of $T$ function is reached. Then the finest moth is returned as the finest optimized approached magnitude at the end of $P$-function.

Algorithm 3:. Overall stages of function $P$ (Mirjalili, 2015).

Update flame number using (29)

OM=Fitness Function (M)

If iteration==1

  F=sort (M);

  OF=sort (OM);

else

  F=sort(M_t-1,M_t);

  OF=sort(M_t-1,M_t);

end

for i=1:n

 for j=1:d

   Update r and t

   Calculate D using (28) with respect to the corresponding moth

   Update M(i,j) using (26) and (27) with respect to the corresponding moth

 end

end

4 Results and discussion

An autonomous fuel cell distributed power system depicted in Figure 1, with system parameters presented in Appendix A (Banerjee et al., 2012), is considered here for AVR systematic investigation, along with an exceptional proportional-integral-derivative-second order derivative (PIDD²) controller; the controller was tuned both offline and online by MFO and SFL-MFO techniques under varying generator gain and time constants. Also evaluated is system performance (specifically voltage response) under various disturbances and uncertainties. As a result, the important findings of this research are discussed below, with the results of particular interest highlighted in the respective tables. All simulations were carried out in MATLAB/SIMULINK (version 7.10) on a 2.77 GHz, Intel Core™ i7 computer, with the maximum number of iterations and population size set to 100 and 50 for each algorithm.

4.1 Comparison of transient response characteristics

In this section, the transient characteristics of the system are investigated and compared under two conditions: distinct gain and time constant of the generator ($K_G$; ${\tau }_G$) and distinct form of step disturbances ($\Delta V_{ref}$; $\Delta P_d$).

4.2 First condition: Distinct ${\mathrm{K}}_{\mathrm{G}}$ and ${\mathrm{\tau }}_{\mathrm{G}}$

In the first case, the transient characteristics of the system with varying gain and generator time constant values for the various techniques considered (proposed and studied) are examined and then compared for the same set of $K_G$; ${\tau }_G$. The results highlighted in Table 2 show the optimized gain and transient parameters obtained by each technique, with an emphasis on the MFO-based PIDD² technique (outlined in bold text). The table shows that the MFO-based PIDD² controller offers the best values for settling time ($T_S$), rise time ($T_R$), and peak overshoot ($M_P$), resulting in a lower value of FOD being constantly incurred by the proposed MFO technique. This performance is evident from the better voltage response profile obtained by the proposed technique in Figure 5 in comparison to other controllers for the different sets of $K_G$ and ${\tau }_G$.

TABLE 2

TABLE 2. MFO-optimized controller gains and transient response parameters with varying $K_G$ and ${\tau }_G$.

FIGURE 5

FIGURE 5. Comparison of transient characteristics for (A) $K_G=0.7$; ${\tau }_G=1.2$ s, (B) $K_G=0.8$ and ${\tau }_G=1.2$ s, (C) $K_G=0.9$; ${\tau }_G=1.0$ s and (D) $K_G=1.0$ and ${\tau }_G=1.6$ s.

4.3 Second condition: Distinct $\Delta {\mathrm{V}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ and $\Delta {\mathrm{P}}_{\mathrm{d}}$

In this condition, the transient characteristics of the system for the different techniques considered (proposed and studied) are examined and compared for the distinct values of reference voltage and load perturbation $\Delta V_{ref}$ and $\Delta P_d$. Therefore, either zero, negative or positive forms of $\Delta V_{ref}$ and $\Delta P_d$ are applied simultaneously to the system for the apparent value of $K_G=1.0$ and ${\tau }_G=1.0s$. The results, shown in Figure 6, demonstrate how effectively the disturbances are handled by the system, as the system itself was able to adjust, withstand, and fine-tune all the deviations separately and concurrently. Furthermore, Figure 6 clearly illustrates the excellent performance of the proposed technique in suppressing oscillations and recovering faster than the other methodologies studied in this work for the same sets of disturbances. To some extent, these have certainly validated the flexibility of the proposed technique.

FIGURE 6

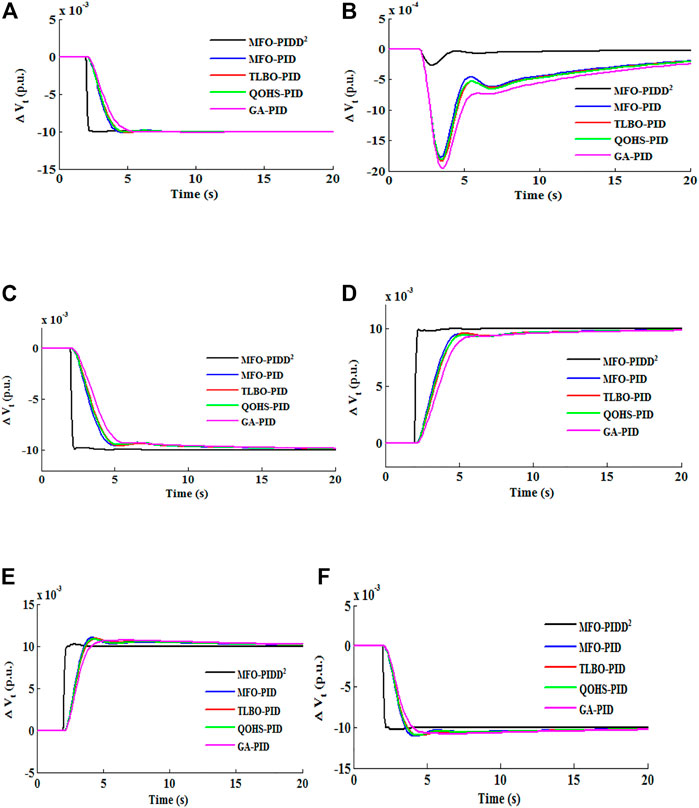
FIGURE 6. Comparison of transient characteristics for distinct disturbances at $K_G=1.0$ and ${\tau }_G=1.0$ s. (A) $\Delta V_{ref}=-0.01,\Delta P_d=0.00$, (B) $\Delta V_{ref}=0.00,\Delta P_d=-0.01$, (C) $\Delta V_{ref}=-0.01,\Delta P_d=0.01$, (D) $\Delta V_{ref}=0.01,\Delta P_d=-0.01$, (E) $\Delta V_{ref}=0.01,\Delta P_d=0.01$, and (F) $\Delta V_{ref}=-0.01,\Delta P_d=-0.01$.

4.4 Convergence

The comparative convergence profile, which was established by plotting the minimum FOD value against the number of iterations (as shown in Figure 7), demonstrates the high performance of the proposed technique; indeed, it converges faster and offers a lower FOD value as compared to the other techniques considered in this work.

FIGURE 7

FIGURE 7. Comparison of convergence profiles for the studied APS with $K_G=1.0$ and ${\tau }_G=1.0$ s.

4.5 Robustness analysis

Due to parametric uncertainties, models are an imperfect representation of reality. Consequently, a controller that is perfectly tuned to a model may reduce system performance or stability. To avoid this problem, the MFO-based PIDD² technique edge is checked using robustness analysis by systematically subjecting the model to broad variations of some essential parameters, such as ${\tau }_{A,}{\tau }_{E,}{\tau }_G\mathrm{a}\mathrm{n}\mathrm{d}{\tau }_S$ in the range of ±50% and the step of ±25%. However, as highlighted in Figure 8 and supported by the transient characteristics presented in Table 3, a ±50% deviation from the nominal specification of the model did not result in the system exceeding requirements or failing to meet intent; this undoubtedly indicates the technique’s robustness to stochasticity.

FIGURE 8

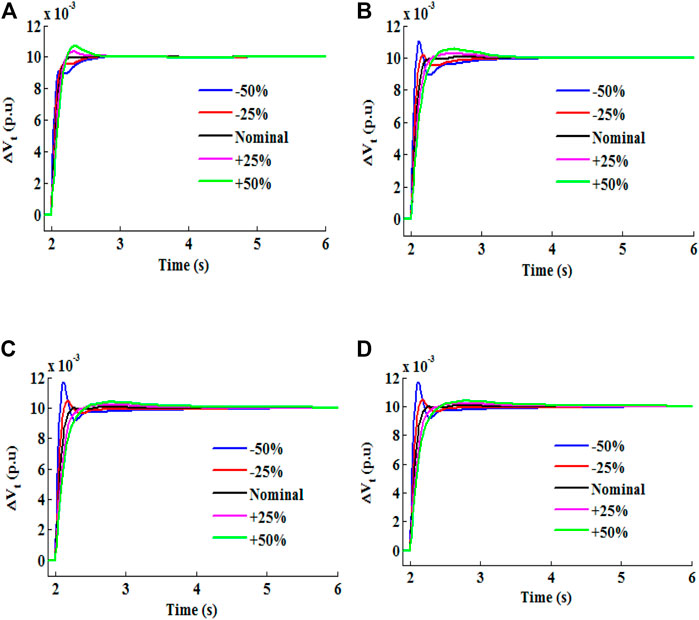
FIGURE 8. Voltage response profile of the MFO-optimized and PIDD²-controlled APS with variations in- (A) ${\tau }_A$, (B) ${\tau }_E$, (C) ${\tau }_G$ and (D) ${\tau }_S$.

TABLE 3

TABLE 3. Robustness examination for MFO-based PIDD² technique.

4.6 SFL real-time response

Having obtained outstanding results with the MFO-based PIDD² technique offline, SFL control is introduced into the system for parameter specification online and in real-time, yielding the online optimum controller gains, transient characteristics, and FOD values at a different set of $K_G$ and ${\tau }_G$ for the different technique (proposed and studied) as shown in Table 4. The optimum controller gains in real-time operation for distinct values of $K_G$; ${\tau }_G$ are determined via the fuzzy rule and the Sugeno inference system. However, for each set of $K_G$; ${\tau }_G$, the proposed techniques outlined in the bold text offer the minimum value of settling time ($T_S$), rise time ($T_R$), and peak overshoot ($M_P$), implying that the proposed technique always incurs a lower FOD value, even online after load perturbation. This outstanding performance can be precisely grasped graphically by comparing the typical voltage response profile obtained by the proposed technique to the different techniques studied (as seen in Figure 9).

TABLE 4

TABLE 4. SFL-based controller gains, Transient characteristics, and FOD values.

FIGURE 9

FIGURE 9. Typical comparative voltage response profiles of the online SFL technique.

5 Conclusion

This work used an autonomous distributed power model to conduct a comprehensive investigation. First, the model was investigated offline using the MFO-PIDD² technique, which gave an excellent transient response that died out and settled faster than other techniques considered. Furthermore, the comparative convergence and robustness analyses clearly demonstrated the high performance and flexibility of the technique. Also, the study was expanded to operate in online mode by synchronizing real-time SFL with the MFO-PIDD², which gave improved control that outperformed other online techniques used in this study. Lastly, the techniques presented here demonstrate improved resilience with better control and coordination than previous techniques offered in the recent literature on the model; thus, the technique can be used as an effective instrument for enhancing systems with identical or similar specifications.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This paper is based upon work supported by Science, Technology and Innovation Funding Authority (STDF) under grant number (43180).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al Gizi, A. J. H. (2019). A particle swarm optimization, fuzzy PID controller with generator automatic voltage regulator. Soft Comput. 23, 8839–8853. doi:10.1007/s00500-018-3483-4

CrossRef Full Text | Google Scholar

Al Gizi, A. J. H., Mustafa, M. W., Al zaidi, K. M. A., and Al-zaidi, M. K. J. (2015). Electrical power and energy systems integrated PLC-fuzzy PID simulink implemented AVR system. Int. J. Electr. Power Energy Syst. 69, 313–326. doi:10.1016/j.ijepes.2015.01.009

CrossRef Full Text | Google Scholar

Al Gizi, A. J. H., Mustafa, M. W., Al-geelani, N. A., and Alsaedi, M. A. (2015). Sugeno fuzzy PID tuning, by genetic-neutral for AVR in electrical power generation. Appl. Soft Comput. J. 28, 226–236. doi:10.1016/j.asoc.2014.10.046

CrossRef Full Text | Google Scholar

Ali, M., and Khaniki, L. (2020). Feedback error learning controller based on RMSprop and salp swarm algorithm for automatic voltage regulator system,” in 10th International Conference on Computer and Knowledge Engineering (ICCKE), 425–430. 2020 October.

Google Scholar

Ali, Z. M., Hasanien, H. M., Abdel, S. H. E., Micev, M., and Martin, C. (2020). Optimal design of automatic voltage regulation controller using hybrid simulated annealing – manta ray foraging optimization algorithm. Ain Shams Eng. J. 12, 641–657. doi:10.1016/j.asej.2020.07.010

CrossRef Full Text | Google Scholar

Ayalew, F., Hussen, S., and Pasam, G. K. (2019). Optimization techniques in power system: Review. Int. J. Eng. Appl. Sci. Technol. 3, 8–16.

Google Scholar

Banerjee, A., Mukherjee, V., and Ghoshal, S. P. (2012). Seeker optimization algorithm for load-tracking performance of an autonomous power system. Int. J. Electr. Power Energy Syst. 43, 1162–1170. doi:10.1016/j.ijepes.2012.06.066

CrossRef Full Text | Google Scholar

Bhullar, A. K., Kaur, R., Sondhi, S., Bhullar, A. K., Kaur, R., and Sondhi, S. (2020). Optimization of fractional order controllers for AVR system using distance and levy-flight based crow search algorithm. IETE J. Res., 1–18.

CrossRef Full Text | Google Scholar

Blondin, M. J., Sanchis, J., Sicard, P., and Herrero, J. M. (2018). New optimal controller tuning method for an AVR system using a simplified Ant Colony Optimization with a new constrained Nelder-Mead algorithm. Appl. Soft Comput. J. 62, 216–229. doi:10.1016/j.asoc.2017.10.007

CrossRef Full Text | Google Scholar

Bourouba, B., Ladaci, S., and Schulte, H. (2019). Optimal design of fractional order PIλDμ controller for an AVR system using Ant Lion Optimizer. IFAC Pap. 52, 200–205. doi:10.1016/j.ifacol.2019.11.304

CrossRef Full Text | Google Scholar

Bukar, A. L., and Tan, C. W. (2019). A review on stand-alone photovoltaic-wind energy system with fuel cell: System optimization and energy management strategy. J. Clean. Prod. 221, 73–88. doi:10.1016/j.jclepro.2019.02.228

CrossRef Full Text | Google Scholar

Chatterjee, S., and Mohammed, A. N. (2022). “Performance evaluation of novel moth flame optimization (MFO) technique for AGC of hydro system,” in IOT with smart systems. Smart innovation, systems and technologies, springer nature Singapore, 251, 377–392.

CrossRef Full Text | Google Scholar

Chatterjee, S., Shiva, C. K., and Mukherjee, V. (2020). “Automatic generation control of multi-area hydro power system using moth flame optimization technique,” in 3rd International Conference on Recent Developments in Control, Automation and Power Engineering (RDCAPE), 395–403.

Google Scholar

Eke, I., Saka, M., Gozde, H., Arya, Y., and Taplamacioglu, M. C. (2021). Heuristic optimization based dynamic weighted state feedback approach for 2DOF PI-controller in automatic voltage regulator. Eng. Sci. Technol, Int. J. 24, 899–910. doi:10.1016/j.jestch.2020.12.023

CrossRef Full Text | Google Scholar

Elsisi, M. (2019). Design of neural network predictive controller based on imperialist competitive algorithm for automatic voltage regulator. Neural comput. Appl. 31, 5017–5027. doi:10.1007/s00521-018-03995-9

CrossRef Full Text | Google Scholar

Ghalambaz, M., Jalilzadeh, R., and Hossein, A. (2021). Building energy optimization using grey wolf optimizer (GWO). Case Stud. Therm. Eng. 27, 101250. doi:10.1016/j.csite.2021.101250

CrossRef Full Text | Google Scholar

Gözde, H., Taplamacioglu, M. C., and Ari, M. (2017). “Simulation study for global neighborhood algorithm based optimal automatic voltage regulator (AVR) system,” in 5th International Istanbul Smart Grid and Cities Congress and Fair (ICSG), 46–50.

Google Scholar

Huda, A. S. N., and Zivanovic, R. (2017). Large-scale integration of distributed generation into distribution networks: Study objectives, review of models and computational tools. Renew. Sustain. Energy Rev. 76, 974–988. doi:10.1016/j.rser.2017.03.069

CrossRef Full Text | Google Scholar

Hussain, I., Das, D. C., and Sinha, N. (2017). Reactive power performance analysis of dish – stirling solar thermal – diesel hybrid energy system. IET Renew. Power Gener. 11, 750–762. doi:10.1049/iet-rpg.2016.0579

CrossRef Full Text | Google Scholar

Jumani, A., Khan, I., Hamadneh, N. N., and Khan, A. (2021). Optimal design of fractional order PID controller based automatic voltage regulator system using gradient-based optimization algorithm. J. King Saud. Univ. - Eng. Sci. Article in Press. doi:10.1016/j.jksues.2021.07.009

CrossRef Full Text | Google Scholar

Kouba, N. E. L. Y., and Boudour, M. (2019). A brief review and comparative study of nature-inspired optimization algorithms applied to power system control. Cham: Springer.

Google Scholar

Lahcene, R., Abdeldjalil, S., and Aissa, K. (2017). “Optimal tuning of fractional order PID controller for AVR system using simulated annealing optimization algorithm,” in IEEE 2017 5th International Conference on Electrical Engineering - Boumerdes (ICEE-B), 1–6.

CrossRef Full Text | Google Scholar

Ma, K., Yao, T., Yang, J., and Guan, X. (2016). Residential power scheduling for demand response in smart grid. Int. J. Electr. Power Energy Syst. 78, 320–325. doi:10.1016/j.ijepes.2015.11.099

CrossRef Full Text | Google Scholar

Madic, M., Markovic, D., and Radovanovic, M. (2013). Comparison of meta-heuristic algorithms for solving machining optimization problems. Facta Univ. Mech. Eng. 11, 29–44.

Google Scholar

Micev, M., Calasan, M., and Oliva, D. (2021). Design and robustness analysis of an Automatic Voltage Regulator system controller by using Equilibrium Optimizer algorithm. Comput. Electr. Eng. 89, 106930. doi:10.1016/j.compeleceng.2020.106930

CrossRef Full Text | Google Scholar

Mirjalili, S. (2015). Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-Based Syst. 89, 228–249. doi:10.1016/j.knosys.2015.07.006

CrossRef Full Text | Google Scholar

Mohagheghi, S., and Harley, R. G. (2004). “Modified takagi-sugeno fuzzy logic based controllers for a static compensator in a multimachine power system,” in IEEE Industry Applications Conference, 2637–2642.

Google Scholar

Mohanty, B. (2019). Performance analysis of moth flame optimization algorithm for AGC system. Int. J. Model. Simul. 39, 73–87. doi:10.1080/02286203.2018.1476799

CrossRef Full Text | Google Scholar

Mokeddem, D., and Mirjalili, S. (2020). Improved Whale Optimization Algorithm applied to design PID plus second-order derivative controller for automatic voltage regulator system. J. Chin. Inst. Eng. 43, 541–552. doi:10.1080/02533839.2020.1771205

CrossRef Full Text | Google Scholar

Mosaad, A. M., Attia, M. A., and Abdelaziz, A. Y. (2018). Comparative performance analysis of AVR controllers using modern optimization techniques. Electr. Power Components Syst. 46, 2117–2130. doi:10.1080/15325008.2018.1532471

CrossRef Full Text | Google Scholar

Mosaad, A. M., Attia, M. A., and Abdelaziz, A. Y. (2019). Whale optimization algorithm to tune PID and PIDA controllers on AVR system. Ain Shams Eng. J. 10, 755–767. doi:10.1016/j.asej.2019.07.004

CrossRef Full Text | Google Scholar

Moschos, I., and Parisses, C. (2022). A novel optimal PI^λDND²N² controller using coyote optimization algorithm for an AVR system. Eng. Sci. Technol. Int. J. 26, 100991. doi:10.1016/j.jestch.2021.04.010

CrossRef Full Text | Google Scholar

Nadimi-Shahraki, M. H., Fatahi, A., Zamani, H., Mirjalili, S., Abualigah, L., and Abd Elaziz, M. (2021). Migration-based moth flame optimization algorithm. Processes 9, 2276. doi:10.3390/pr9122276

CrossRef Full Text | Google Scholar

Nadimi-Shahraki, M. H., Fatahi, A., Zamani, H., Mirjalili, S., and Abualigah, L. (2021). An improved moth-flame optimization algorithm with adaptation mechanism to solve numerical and mechanical engineering problems. Entropy 23, 1637. doi:10.3390/e23121637

PubMed Abstract | CrossRef Full Text | Google Scholar

Nadimi-Shahraki, M. H., Fatahi, A., Zamani, H., Mirjalili, S., and Oliva, D. (2022). Hybridizing of whale and moth-flame optimization algorithms to solve diverse scalesof optimal power flow problem. Electronics 11, 831.

CrossRef Full Text | Google Scholar

Oladipo, S., Sun, Y., and Wang, Z. (2020). “Optimization of PID and FOPID controllers with new generation metaheuristic algorithms for controlling AVR system: Concise Survey,” in Proc: 2020 12th International Conference on Computational Intelligence and Communication Networks (CICN), 280–286. 25-26 September.

CrossRef Full Text | Google Scholar

Ozgenc, B., Ayas, M. S., and Altas, I. H. (2020). “A hybrid optimization approach to design optimally tuned PID controller for an AVR system,” in International congress on human computer interaction, optimization and robotic application (HORA), 1–5.

CrossRef Full Text | Google Scholar

Rajbongshi, R., and Saikia, L. C. (2017). Combined control of voltage and frequency of multi-area multisource system incorporating solar thermal power plant using LSA optimised classical controllers. IET Gener. Transm. Distrib. Res. 11, 2489–2498. doi:10.1049/iet-gtd.2016.1154

CrossRef Full Text | Google Scholar

Rodrigues, F., Molina, Y., Silva, C., and Naupari, Z. (2021). Simultaneous tuning of the AVR and PSS parameters using particle swarm optimization with oscillating exponential decay. Int. J. Electr. Power Energy Syst. 133, 107215. doi:10.1016/j.ijepes.2021.107215

CrossRef Full Text | Google Scholar

Sambariya, D. K., and Gupta, T. (2017). “Optimal design of PID controller for an AVR system using monarch butterfly optimization,” in IEEE, International Conference on Information, Communication, Instrumentation and Control, 1–6.

CrossRef Full Text | Google Scholar

Shehab, M., Abualigah, L., Al, H., Hamzeh, H., Mohammad, A., and Khasawneh, A. M. (2020). Moth – flame optimization algorithm: Variants and applications. Neural comput. Appl. 32, 9859–9884. doi:10.1007/s00521-019-04570-6

CrossRef Full Text | Google Scholar

Sikander, A., Thakur, P., Bansal, R. C., and Rajasekar, S. (2018). A novel technique to design cuckoo search based FOPID controller for AVR in power systems. Comput. Electr. Eng. 70, 261–274. doi:10.1016/j.compeleceng.2017.07.005

CrossRef Full Text | Google Scholar

Veinovi, S. (2022). Optimized four-parameter PID controller for AVR systems with respect to robustness. Int. J. Electr. Power Energy Syst. 135 (2022), 107529.

CrossRef Full Text | Google Scholar

Glossary

The following abbreviations are used in this document:

$\mathit{D}$ DEG damping constant

${\mathit{E}}_{\mathit{S}\mathit{S}}$ Steady-state error, p. u.

$\mathit{H}$ DEG inertia constant

${\mathit{K}}_{\mathit{A}}$ Constant gain of the amplifier

${\mathit{K}}_{\mathit{D}}$ Derivative gain of the controller

${\mathit{K}}_{{\mathit{D}}_{\mathbf{2}}}$ Second-order derivative gain of the controller

${\mathit{K}}_{\mathit{E}}$ Constant gain of the exciter

${\mathit{K}}_{\mathit{G}}$ Constant gain of the generator

${\mathit{K}}_{\mathit{i}\mathit{i}}$ Constant gain of the integral speed governor controller

${\mathit{K}}_{\mathit{I}}$ Integral controller gain

${\mathit{K}}_{\mathit{P}}$ Proportional controller gain

${\mathit{K}}_{\mathit{S}}$ Constant sensor gain

${\mathit{M}}_{\mathit{P}}$ Maximum overshoot, p. u.

$\mathit{N}$ Filter co-efficient of the PIDD² controller filter

${\mathit{N}}_{\mathit{D}}$ Second-order filter co-efficient of the PIDD² controller’s filter

$\mathit{R}$ Constant droop of the speed governor

$\mathit{t}$ Sample time, s

$\mathit{T}$ Time constant of the PIDD² controller filter, s

${\mathit{T}}_{\mathit{D}}$ PIDD² controller time constant, s

${\mathit{T}}_{\mathit{R}}$ Rise time, s

${\mathit{T}}_{\mathit{S}}$ Settling time, s

$\mathit{\beta }$ Constant parameter of the figure of demerit

$\Delta \mathit{e}$ Incremental change in terminal voltage error, p. u.

$\Delta {\mathit{e}}_{\mathit{i}}$ Incremental change in terminal voltage error at time $i$, p. u.

$\Delta {\mathit{e}}_{\mathit{i}-\mathbf{1}}$ Incremental change in terminal voltage error at time $\left(i-1\right)$, p. u.

$\Delta \dot{\mathit{e}}$ Derivative of incremental change in error in terminal voltage, p. u.

$\Delta {\mathit{V}}_{\mathit{e}}\left(\mathit{s}\right)$ Error voltage, p. u.

$\Delta {\mathit{V}}_{\mathit{r}\mathit{e}\mathit{f}}\left(\mathit{s}\right)$ Incremental change in reference voltage, p. u.

$\Delta {\mathit{V}}_{\mathit{s}}\left(\mathit{s}\right)$ Feedback voltage, p. u.

$\Delta {\mathit{V}}_{\mathit{t}}\left(\mathit{s}\right)$ Incremental change in terminal voltage, p. u.

${\mathit{\tau }}_{\mathit{A}}$ Amplifier time constant, s

${\mathit{\tau }}_{\mathit{D}}$ DEG time constant, s

${\mathit{\tau }}_{\mathit{E}}$ Exciter time constant, s

${\mathit{\tau }}_{\mathit{G}}$ Generator time constant, s

${\mathit{\tau }}_{\mathit{S}}$ Sensor time constant, s

${\mathit{\tau }}_{\mathit{V}}$ Time constant of the valve actuator, s.

Appendix A

$K_A$ = 10.0, ${\tau }_A$ = 0.1 s, $K_E$ = 1.0, ${\tau }_E$ = 0.4 s, $K_S$ = 1.0, ${\tau }_S$ = 0.05 s, ${\tau }_D$ = 2.31 s, ${\tau }_V$ = 0.82 s, $K_1$ = 1 $K_2$ = 0.2, $K_3$ = 1.5, $H$ = 0.1, $D$ = 2.22, $R$ = 0.074 and $K_{ii}$ = 0.1000. The values of $K_G$ and ${\tau }_G$ are load dependent.