- College of Electrical Engineering, Shanghai University of Electric Power, Shanghai, China
With wind power integrated into the power system on a large scale, the system has become vulnerable to the frequency stability issue. The battery energy storage system (BESS) is considered the key solution to improving the system frequency regulation performance due to its fast response ability. Furthermore, the construction of wind-storage combined frequency regulation systems has been developed for many years, in which the optimal capacity configuration of the wind-storage system is getting more attention. However, the secondary frequency drop (SFD) caused by wind turbines (WTs) participating in primary frequency regulation (PFR) is neglected in most existing capacity configurations, which is worthy of further study. In this paper, the optimal capacity of the wind-storage combined frequency regulation system is studied from the perspective of SFD. The time-domain expressions of two-stage system frequency response considering SFD are derived based on the wind-storage combined frequency regulation model. Next, considering the technical and economic characteristics of wind-storage combined frequency regulation, an optimization model of the energy storage capacity configuration is established with the objective of minimizing the sum of the maximum frequency deviations in two stages and the energy storage cost. The optimization model is solved by the multi-objective salp swarm algorithm (MSSA) to obtain the setting value of wind-storage combined frequency regulation parameters and the optimal energy storage capacity. The effectiveness of the proposed method is verified in MATLAB. The simulation results show that the proposed model can effectively improve the frequency regulation effect of the system and ensure the optimal capacity configuration with better economy.
1 Introduction
Wind power is the fastest developing and most competitive power generation technology in renewable energy generation with its outstanding advantages of low costs and mature technology (Amir et al., 2022). However, because wind turbines (WTs) are connected to the grid through power electronic converters, they have little or no inertial response, reducing the overall inertia of the power system. Therefore, the increasing wind power penetration will threaten the frequency stability of the power system (Li et al., 2021; Zaheeruddin et al., 2021; Guo and Wu, 2022; Kheshti et al., 2022; Zhang et al., 2022). Rapid development of the energy storage system has provided a new solution for frequency regulation with its flexible charge–discharge ability and fast dynamic response (Zhang et al., 2020; Akram et al., 2021; Meng et al., 2021; Subroto et al., 2021; Guan, 2022). Moreover, the construction of the wind-storage combined frequency regulation system can effectively ensure the secure and stable operation of the system (Rahimi et al., 2021; Dantas et al., 2022; Xiong et al., 2022).
In recent years, the optimal configuration of energy storage capacity in the wind-storage combined system has received significant attention (Sandelic et al., 2018; Cao et al., 2019; Liu et al., 2020; Salman et al., 2020) because it will directly influence the security and economy of system operation (Wang et al., 2018; Wang et al., 2019; Shin and Hur, 2020). Excessive energy storage capacity will increase the investment and maintenance costs, whereas insufficient energy storage capacity cannot meet the demand of concentrated and large loads, making it hard to improve the power quality and the overall operation effect of the system in essence (Masaud et al., 2017; Chen et al., 2021; Wan et al., 2021).
The methods implemented for the energy storage capacity configuration in the wind-storage system mainly consider the two objectives of economy and reliability comprehensively to realize capacity optimization, in that both the economic and technical characteristics are of great significance in the wind-storage combined system. In fact, most studies on the optimal configuration of energy storage capacity in wind-storage systems mainly consider the costs or benefits of wind-storage combined frequency regulation as the objective constrained by frequency security (Peng et al., 2019; Bera et al., 2021). In Peng et al. (2019), based on the proposed fuzzy-based coordinated control and sizing strategy, an optimization model for minimizing the operation and frequency regulation costs of the wind-storage combined system is presented to determine the energy storage capacity. Meanwhile, in Bera et al. (2021), a novel planning strategy for optimally sizing an energy storage system is proposed to minimize the operational costs of the system and meet the frequency stability constraint. However, few research studies have considered secondary frequency drop (SFD) caused by wind turbines participating in frequency regulation. To eliminate SFD, the control method of the battery energy storage system (BESS) should be changed to add the extra active power output. Thus, the existing optimal configurations without considering SFD can easily contribute to the inaccuracy of the energy storage capacity, which will affect the overall system frequency regulation performance.
Since the SFD is an important factor indicating the effect of system frequency regulation, several wind-storage coordinated frequency regulation control strategies to reduce SFD were proposed, as in Wu et al. (2017), Rahimi et al. (2021), and Ma and Li (2022). In Wu et al. (2017), the BESS’s fast and accurate active power control is fully used to resolve the SFD issue in wind rotor speed recovery. In Rahimi et al. (2021), the coordination of WTs and energy storage can improve the frequency stability of a low inertia microgrid, thus improving the second frequency nadir due to the inertia response of WTs. In Ma and Li (2022), a wind-storage combined virtual inertial control system based on quantization and regulation decoupling of active power increments is proposed to solve problems such as SFD by using the BESS to compensate for the power shortages of WTs. However, in these literature studies, the capacity configuration and the SFD issue have not been taken into account at the same time.
Motivated by the issues mentioned previously, we focus the scope of this paper on the optimal capacity configuration of the wind-storage combined frequency regulation system considering SFD. With the inspiration of the technical and economic characteristics of wind-storage combined frequency regulation, we aimed to effectively solve the problem of the energy storage capacity allocated without considering SFD (Peng et al., 2019; Salman et al., 2020; Bera et al., 2021), which has significant potential to improve both the effect of frequency regulation and the economy of the BESS participating in primary frequency regulation (PFR).
The contributions of this paper are as follows:
• Derive the time-domain expressions of the two-stage system frequency response with SFD under the establishment of the wind-storage combined frequency regulation model.
• Establish an optimal capacity configuration model constrained by the charge–discharge power and the state of charge (SOC) of the BESS with the minimum sum of the maximum frequency deviations in two stages and the minimum energy storage cost as the optimization objectives based on the life cycle cost (LCC) theory.
• The comparison of capacity configuration between considering and not considering SFD is presented to show the effectiveness of the proposed method.
• Different wind power penetration levels are considered and simulated to affirm the suitability of the proposed model for a power system with a high wind power penetration level.
The rest of this paper is organized as follows: Section 2 deduces time-domain expressions of the two-stage system frequency response considering SFD based on the model of the wind-storage combined system participating in PFR. Section 3 describes the objective functions and constraints of the optimal capacity configuration model of the wind-storage system. Section 4 presents the optimization results to analyze and prove the effectiveness of the proposed method. The last section concludes the paper.
2 Model of the wind-storage system participating in PFR
2.1 Establishment of the wind-storage combined frequency regulation model
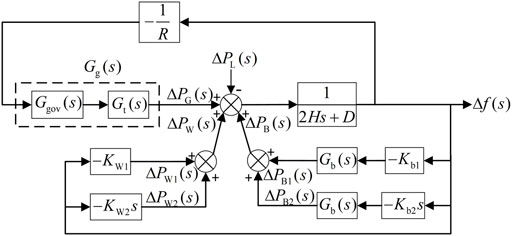
The model of the wind-storage system participating in PFR of a power grid is shown in Figure 1. Wind turbines adopt integrated inertia control, and the BESS adopts virtual integrated inertia control to respond to system frequency change in a timely manner and provide active power support.
In Figure 1, ΔPL(s) is the variation of load power; ΔPG(s), ΔPW(s), and ΔPB(s) are the power output variation of traditional units, WTs, and BESS, respectively; ΔPW1(s) and ΔPW2(s) are the power output variation of WTs with droop control and inertia control, respectively; ΔPB1(s) and ΔPB2(s) are the power output variation of the BESS with virtual droop control and virtual inertia control, respectively; Δf(s) is the frequency deviation of the power grid; R is the adjustment coefficient of traditional units; Kw1 and Kw2 are the droop control and inertia control coefficients of WTs, respectively; Kb1 and Kb2 are the virtual droop coefficient and the virtual inertia coefficient of the BESS, respectively; Gg(s) and Gb(s) are the transfer functions of traditional units and BESSs, respectively; H is the inertia time constant of the power grid; D is the damping factor of the system.
The model of thermal power units Gg(s) consists of the governor model and the steam turbine model (Singh et al., 2021b; Singh and Zaheeruddin, 2021), as shown in Equation 1:
where Ggov(s) is the transfer function of the governor and Gt(s) is the transfer function of a non-reheated steam turbine.
The specific expressions of Ggov(s) and Gt(s) are as follows:
where Tg is the time constant of the governor and Tt is the time constant of the steam turbine.
The BESS model Gb(s) is equivalent to a first-order inertia model (Singh et al., 2021a; Li C. P. et al., 2022), which can be expressed as follows:
where Tb is the response time constant of the BESS.
The dynamic grid frequency model of the wind-storage system is given in Figure 1
where
2.2 Analysis of WTs participating in PFR
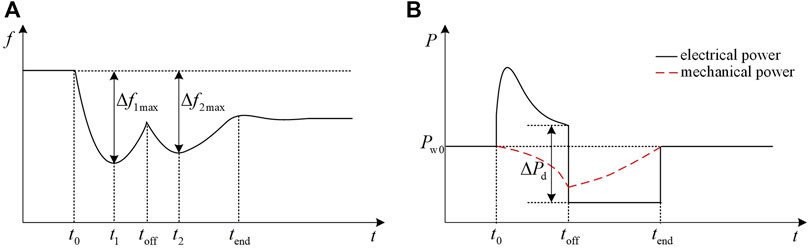
Wind turbines are expected to operate normally under maximum power point tracking (MPPT) conditions. The system frequency response and power output curves of WTs participating in PFR of the power grid are shown in Figures 2A, B respectively. In Figure 2, t0 is the time when power disturbance occurs; toff is the time of WTs exiting frequency regulation; tend is the time when the operation mode of wind turbines changes to the MPPT mode; Pw0 is the initial power output of wind turbines; ΔPd is the variation of electrical power when WTs exit frequency regulation. Figure 2 shows that the process of WTs participating in PFR can be divided into two stages, i.e., stages I and II.
Stage I: A load increase of ΔPL as the power disturbance at t0 causes the system frequency to drop; then, WTs increase the electrical power output by releasing rotor kinetic energy to participate in PFR. As rotor speed decreases, the mechanical power input of WTs reduces.
Stage II: WTs exit frequency regulation to recover rotor speed at toff. The sudden drop in electrical power causes the power imbalance in the system to change abruptly, leading to SFD. The electrical power Pw remains constant while being less than the mechanical power Pm during rotor speed recovery. When the rotor absorbs active power and returns to its initial speed, the WTs switch to the MPPT mode.
2.3 Method of energy storage capacity configuration
BESS configuration for PFR can effectively compensate for the power deficit caused by wind turbines exiting frequency regulation. Since the capacity of the BESS directly affects the security and economy of system operation, it is imperative to allocate energy storage capacity reasonably to improve the effect of frequency regulation and reduce the economic cost.
Considering the power convert system (PCS) efficiency and charge–discharge efficiency of the BESS in the frequency regulation period of Tf, the rated power Prated of the BESS can be expressed as in Eq. 7:
where t0 is the initial time of frequency regulation; Tf is the time period of frequency regulation; η1 and η2 are the efficiencies of the DC–DC and DC–AC converters of the PCS, respectively; ηch and ηdis are charging and discharging efficiencies of the BESS, respectively; ΔPB(t) is the power instruction of the BESS at time t (it is assumed that when the BESS is in the charging mode, its power is positive, and it is negative in the discharging mode).
The SOC of the BESS and its constraint are given by Eqs 8, 9, respectively (Khalid et al., 2015a; Khalid et al., 2015b).
where SOC0 and SOC(t) are the SOC of the BESS at the initial time and t, respectively; SOCmax and SOCmin are the upper and lower limits of SOC, respectively; Δt is the time interval of power instruction; and Erated is the rated capacity of the BESS.
Considering the PCS efficiency and charge–discharge efficiency of the BESS in the frequency regulation period of Tf, the rated capacity Erated of the BESS can be expressed as follows:
2.4 Wind-storage combined frequency regulation model considering SFD
2.4.1 PFR model of stage I
The frequency response model of wind-storage combined frequency regulation can be deduced according to Figure 1. When load disturbance occurs, the frequency response model of stage I is expressed as follows:
where Ggen(s), Gb1(s), and Gw(s) are transfer functions of thermal power units, BESSs, and WTs, respectively.
The specific expressions of Ggen(s), Gb1(s), and Gw(s) are
where Kb11 and Kb12 are, respectively, the virtual droop coefficient and the virtual inertia coefficient of the BESS at stage I.
Equation 11 can be simplified as
where mi and nj are the coefficients of the s-domain function, as shown in Supplementary Material.
Following the partial fraction expansion and the inverse Laplace transform given in Eq. 15, the time-domain expression of the system frequency response of stage I can be obtained as follows:
where Ai, p, q, ζ, ω, and φ are the coefficients of the time-domain expression, as shown in Supplementary Material.
Based on Eq. 16, the maximum frequency deviation Δf1max of stage I can be expressed as follows:
where t1 is the time at which the frequency nadir of stage I occurs. The derivation process is shown in Supplementary Material.
2.4.2 PFR model of stage II
At toff, when stage I ends, WT exiting frequency regulation leads to SFD. The BESS and thermal power units participate in PFR together at stage II to compensate for the power deficit observed due to the rotor speed recovery of wind turbines.
When wind turbines exit frequency regulation, the frequency response model of stage II can be expressed as follows:
where Gb2(s) is the transfer function of the BESS and ΔPoff(s) is the power deficit at the time when WTs exit frequency regulation.
The specific expressions of Gb2(s) and ΔPoff(s) are
where Kb21 and Kb22 are, respectively, the virtual droop coefficient and virtual inertia coefficient of the BESS at stage II; PL0 is the initial load power; PG (toff), PB(toff), and PW(toff) are, respectively, the power output of thermal power units, BESSs, and WTs at the time when wind turbines exit frequency regulation; kopt is the coefficient of the MPPT curve of wind turbines; ω0 is the initial value of wind rotor speed; and HW is the equivalent time constant of wind turbines.
Referring to the derivation process of stage I, the time-domain expression of system frequency response of stage II Δf2(t), the maximum frequency deviation Δf2max as well as the time at which the maximum appears t2 can be obtained.
3 Capacity optimization of the wind-storage system
3.1 Objective functions
Wind-storage combined frequency regulation can improve the effect of frequency regulation, but the economic cost should be taken into account. The wind-storage system participates in PFR from the perspective of SFD. Therefore, the sum of the maximum frequency deviations in two stages and the energy storage cost are considered objective functions so as to ensure frequency stability and improve the economy of BESSs participating in frequency regulation. The objective functions are expressed as follows:
where Δf12max is the sum of the maximum frequency deviations in two stages; CLCC is the energy storage cost; Cinv is the initial investment and replacement cost; Cbop is the balance of plant cost; Com is the operation and maintenance cost; Cscr is the scrap disposal cost; and Cres is the recovery residual value.
3.1.1 The sum of the maximum frequency deviations in two stages
The objective function is to minimize the sum of the maximum frequency deviations in two stages: the absolute value of the maximum frequency deviation of stage I Δf1max and that of stage II Δf2max. Since the maximum frequency deviations of stages I and II have been discussed in Sections 3.1 and 3.2, respectively, they will not be described here.
3.1.2 Energy storage cost
Based on the LCC theory considering the sum of all direct or indirect costs in the processes of investment, purchase, operation, maintenance, and recovery in the whole life cycle of the system (Swierczynski et al., 2015; Torkashvand et al., 2020), the economic model of the BESS is established for minimizing the energy storage cost, which includes the following five aspects.
3.1.2.1 Initial investment and replacement cost
The initial investment cost refers to the fixed capital of a one-time investment for the purchase of main equipment in the initial stage of energy storage project construction, which consists of the power cost and energy cost determined by the rated power Prated and the rated capacity Erated of the BESS, respectively. The replacement cost usually involves the replacement of energy storage elements, and the combination of these two costs can be described as follows:
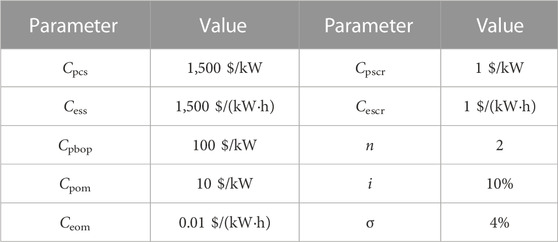
where Cpcs is the per unit cost of power of the PCS; Cess is the per unit cost of energy; i is the interest rate; T is the lifetime; and n is the number of times energy storage must be replaced.
3.1.2.2 Balance of plant cost
The balance of plant cost refers to the purchase fund for auxiliary equipment of the energy storage system such as cables, network facilities, and control servers, that is:
where Cpbop and Cebop are the per unit balance of plant cost corresponding to the power and capacity of BESSs, respectively.
3.1.2.3 Operation and maintenance cost
The operation and maintenance cost refers to the capital dynamically invested to ensure normal operation of energy storage during its lifetime, which usually includes the fixed part determined by the PCS and the variable part determined by the charging and discharging quantities of the energy storage system, namely,
where Cpom is the per unit operation and maintenance cost of the power; Ceom is the per unit operation and maintenance cost of the electric quantity; W(t) is the annual charging and discharging quantity of the energy storage system.
3.1.2.4 Scrap disposal cost
The scrap disposal cost refers to the cost generated by the harmless disposal and recycling after the scrapping of battery energy storage equipment in the lifetime, namely,
where Cpscr is the per unit scrap disposal cost of power and Cescr is the per unit scrap disposal cost of capacity.
3.1.2.5 Recovery residual value
The recovery residual value refers to the recoverable residual value (negative cost) of the fixed assets of the energy storage system at the end of its lifetime, namely,
where σ is the rate of the recovery residual value, generally 3%–5%.
3.2 Constraints
3.2.1 Charge–discharge power constraint of the BESS
The BESS charge–discharge power is limited to its rated power (Khalid and Peng, 2020; Khalid et al., 2022). This constraint is formulated as follows:
where Pe(t) is the charge–discharge power of the BESS at time t.
3.2.2 SOC constraint of the BESS
In order to avoid the influence of excessive charge and discharge on the lifetime of the BESS, the SOC constraint is shown in Eq. 9.
3.3 Optimization method
The salp swarm algorithm (SSA) is a novel heuristic intelligent algorithm inspired by the swarming behavior of salps (salp chain) (Mirjalili et al., 2017). It has been applied to solve problems such as multi-objective optimization, with the advantages of simple structure, few parameters, and easy realization. The SSA algorithm divides the population into two groups: leader and followers. The leader is the salp at the front of the chain, guiding the swarm, which is followed by the rest of the salps, namely, the followers.
In the SSA, the optimization target is taken as the food source called F; thus, the position of the leader can be expressed by Eq. 29.
where x1j is the position of the first salp (leader) in the jth dimension; Fj is the position of the food source in the jth dimension; ubj and lbj are the upper and lower bounds of the jth dimension, respectively; c1 is the most important parameter balancing exploration and exploitation; c2 and c3 are random numbers ranging from 0 to 1.
The specific expression of c1 is as follows:
where l is the current iteration and L is the maximum number of iterations.
The position of the followers can be expressed by Eq. 31.
where xij is the position of ith follower salp in the jth dimension.
In the optimization process of the multi-objective salp swarm algorithm (MSSA), the Pareto optimal set will be updated continuously and put in the repository having a limited size. Suppose the desired number of non-dominated solutions is M, the basic steps of the MSSA are as follows:
1) Design a repository to store non-dominated solutions obtained from the algorithm.
2) If a salp in the new population dominates one or several solutions in the repository, add the salp to the repository and remove the dominated solutions from it. If a salp is in a non-dominated relationship with all repository residents, add it to the repository. If a salp is dominated by at least one of the repository residents, discard it straight away.
3) Assign the non-dominated solution i a rank ranki based on the density of its neighboring solutions. The higher the rank, the more neighboring solutions it has, implying that the solutions around it are denser. When the number of non-dominated solutions in the repository is more than M, discard the solutions with higher ranks to ensure the number of solutions in the repository remains M and make the distribution of the Pareto optimal set as wide and uniform as possible.
4) Since the individuals in the repository are all non-dominated solutions, there is no absolute optimal individual. The food source chased by the leader of the next generation can be determined by ranking the solutions and using a roulette wheel selection.
Algorithm 1. Pseudo-code of the proposed method.Input: Kw1, Kw2, Kb11, Kb12, Kb21, Kb22, and toff
Output: ∆f12max and CLCC
1 for t = 1: toff do
2 Obtain the value of ∆f1 by Eq. 16
3 end for
4 for t = toff: 40 do
5 Obtain the value of ∆f2 by an equation similar to that of (16)
6 end for
7 ∆f12max← ∆f1max+∆f2max;
8 CLCC ←Cinv + Cbop + Com + Cscr -Cres;
9 Initialize the salp population xi (i = 1, 2, ., n) considering ub and lb;
10 while end criterion is not met do
11 Calculate the fitness of each search agent (salp);
12 Determine the non-dominated salps;
13 Update the repository considering the obtained non-dominated salps;
14 if the repository becomes full, then
15 Call the repository maintenance procedure to remove one repository resident;
16 Add the non-dominated salp to the repository;
17 end if
18 Choose a source of food from repository: F=SelectFood (repository);
19 Update c1 by Eq. 30;
20 for each salp xi do
21 if (i = = 1) then
22 Update the position of the leading salp by Eq. 29;
23 else
24 Update the position of the follower salp by Eq. 31;
25 end if
26 end for
27 Amend the salps based on the upper and lower bounds of variables;
28 end while
29 return repository
The proposed method can be transformed into a pseudo-code, as shown in Algorithm 1. The variables of input and output are defined at the top of the table. A for loop is applied for obtaining the values of Δf1 and Δf2, followed by the calculation of output variables Δf12max and CLCC, and the while loop for the MSSA optimizing the proposed model. These loops are shown in lines 1–3, 4–6, 7–8, and 9–29, respectively.
4 Case study
4.1 Simulation system
In order to verify the feasibility and effectiveness of the proposed model and method, the simulation system including thermal power units, WTs, load, and BESSs is taken as an example to study the optimal capacity configuration of the wind-storage system considering SFD. The rated capacity of thermal power units is 600 MW; the wind power system is made up of 100 WTs, each having a rated capacity of 2 MW; and the load capacity is 300 MW. The adjustment coefficient of thermal power units is 4%, the governor time constant is 0.2 s, and the steam turbine time constant is 0.3 s, the grid inertia time constant is 4 s, and the damping factor of the system is 2, the equivalent time constant of WTs is 10.38 s, the response time constant of the BESS is 0.1 s, the SOC ranges from 0.1 to 0.9 with an initial value of 0.5 (Tan et al., 2020; Li S. J. et al., 2022), and the PCS efficiency and charge–discharge efficiency of the BESS are both 90%. The lifetime of the BESS is 14 years. The population size and the maximum iteration of the MSSA are both 100.
4.2 Optimization parameters
The economic parameters of the BESS are shown in Table 1.
4.3 Optimization results
Assuming that the load increases from 300 MW to 320 MW at 1 s, the system frequency decreases. WTs, thermal power units, and BESSs participate in PFR, and SFD is considered only if the BESS reduces it. In order to study the optimal capacity configuration of the wind-storage combined frequency regulation system under different wind power penetration levels, two simulation scenarios with different wind power penetration levels are set: in scenario 1, the wind power penetration is 11%, with the power output of thermal power units and WTs being 267 and 33 MW, respectively. In scenario 2, the wind power penetration is 33%, with the power output of thermal power units and WTs being 201 and 99 MW, respectively.
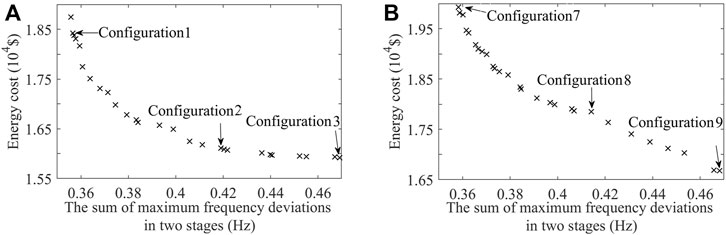
According to the optimization model and the method proposed in this paper, the optimal capacity configuration of the wind-storage combined frequency regulation system under two different wind power penetration levels is simulated and analyzed. The Pareto results for the energy storage cost and the sum of the maximum frequency deviations in two stages are shown in Figures 3, 4. The comparison of the two figures shows that 1) the energy storage cost and the sum of the maximum frequency deviations in two stages are two contradictory goals, that is, the required energy storage capacity and cost will decrease as the sum of the maximum frequency deviations in two stages increases. 2) In the case of the same wind power penetration level, the Pareto results considering SFD are inclined to the lower left of the coordinate system when compared with those without considering SFD. The aforementioned phenomena indicate that the reasonable energy storage capacity configuration and considering SFD can improve the economy of energy storage participating in frequency regulation to a certain extent.
4.3.1 Simulation of scenario 1
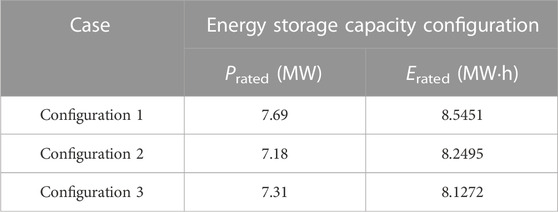
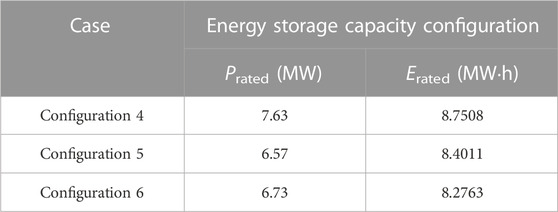
In the Pareto results of scenario 1, three sets of configurations with the close sum of the maximum frequency deviations in two stages as shown in Figures 3A, 4A are chosen for analysis, among which the sum of the maximum frequency deviations in two stages of configurations 1, 2, and 3 considering SFD is 0.357, 0.413, and 0.467 Hz and that of configurations 4, 5, and 6 without considering SFD is 0.359, 0.416, and 0.464 Hz, respectively. The corresponding optimization results are shown in Tables 2, 3, and the energy storage capacity configurations are shown in Tables 4, 5.
It can be seen from the optimization results that the active power output of the wind-storage system is low when its frequency regulation control parameters are small, leading to a large frequency deviation of the system. To reduce the system frequency deviation, the frequency regulation control parameters of the wind-storage system should be increased; thus, the energy storage cost increases with increase in energy storage capacity. The comparison of the energy storage costs of chosen configurations shows that the energy storage cost without considering SFD is about 3.43% higher on average than that considering SFD when the sums of the maximum frequency deviations in two stages are close in such circumstances.
Figure 5A shows the system frequency curves of configurations 1, 2, 4, and 5 in scenario 1. As can be seen from Figure 5A, the frequency nadir can be improved by increasing the frequency regulation control parameters of the wind-storage system, thus improving the frequency regulation effect of the system.
4.3.2 Simulation of scenario 2
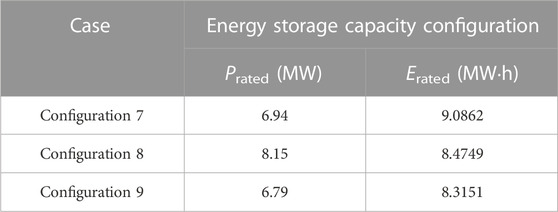
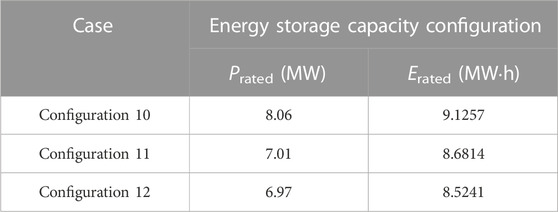
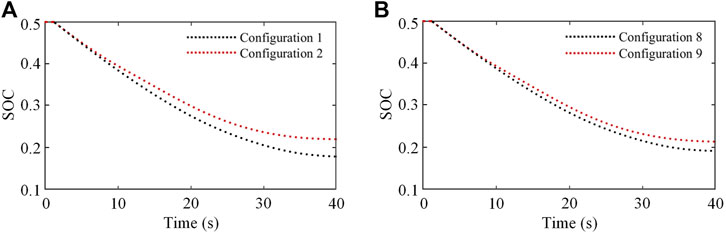
Similar to scenario 1, in the Pareto results of scenario 2, three sets of configurations with the close sum of the maximum frequency deviations in two stages as shown in Figures 3B, 4B are chosen for analysis, among which the sum of the maximum frequency deviations in two stages of configurations 7, 8, and 9 considering SFD is 0.355, 0.418, and 0.468 Hz and that of configurations 10, 11, and 12 without considering SFD is 0.357, 0.415, and 0.465 Hz, respectively. The corresponding optimization results are shown in Tables 6, 7, and the energy storage capacity configurations are shown in Tables 8, 9. Figure 5B shows the system frequency curves of configurations 8, 9, 11, and 12 in Scenario 2. Figure 6 shows that the optimal capacity configuration of energy storage considering SFD is reasonable as its SOC value changes within the upper and lower limits.
The comparison of the energy storage costs of chosen configurations shows that the energy storage cost without considering SFD is about 5.40% higher on average than that considering SFD when the sums of the maximum frequency deviations in two stages are close in two such circumstances. Thus, according to the two scenarios, the energy storage cost without considering SFD is about 4.42% higher on average than that considering SFD. In addition, it can be seen from the optimization results under two different wind power penetration levels that the frequency drop is more severe in the higher wind power penetration level. In order to ensure the frequency regulation effect of the high wind power penetration level is basically the same as that of the low wind power penetration level, the energy storage cost will increase as the energy storage frequency regulation control parameters increase.
In conclusion, both SFD and wind power penetration levels will influence the optimal capacity configuration of the wind-storage combined frequency regulation system, in which the energy storage cost considering SFD is lower than that without considering SFD, and the sum of the maximum frequency deviations in two stages is smaller. Hence, it is beneficial to improve the economy of energy storage participating in frequency regulation and the system frequency regulation effect with SFD considered. When the sums of the maximum frequency deviations in two stages considering SFD are close to those without considering SFD, the comparison of energy storage costs in two such circumstances shows that the average growth rate of energy storage costs increases as the wind power penetration increases. It can be seen that the optimization effect considering SFD is more obvious with the high wind power penetration level.
5 Conclusion
In this paper, the time-domain expressions of two-stage system frequency response of wind-storage combined frequency regulation systems are derived by considering SFD. Under the constraints of charge–discharge power and the SOC of the BESS, an optimization model for minimizing the sum of the maximum frequency deviations in two stages and the energy storage cost is established. The MSSA is used to solve the optimization model and obtain the setting value of the frequency regulation control parameters of the wind-storage combined system and the optimal capacity configuration of energy storage. Based on the analysis of the optimization results, the following conclusions can be summarized:
1) The comparison of the optimization results of capacity configuration in different scenarios shows that the capacity configuration considering SFD can reduce the sum of the maximum frequency deviations in two stages and the energy storage cost than without considering SFD, thus improving the frequency regulation effect and the economy of the system.
2) The energy storage cost and the sum of the maximum frequency deviations in two stages are two contradictory objectives in the optimal capacity configuration of the wind-storage combined frequency regulation system. This is because the active power output of the wind-storage system is low when the frequency regulation control parameters are small, leading to the large frequency deviation of the system. The control parameters should be increased so as to reduce the frequency deviation, which results in an increase in the energy storage cost with more energy storage capacity required.
3) The optimization effect considering SFD is more obvious as the wind power penetration level increases, which is important and useful for the power system with high wind power integration.
The proposed model improves the PFR capability of the wind-storage system and the economy of energy storage participating in frequency regulation. As a result, the proposed method is expected to be a good choice for the optimal capacity configuration of wind-storage combined frequency regulation in the power system.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research was supported by the National Natural Science Foundation of China (51977128) and the Shanghai Science and Technology Project (20142202600).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1037587/full#supplementary-material
References
Akram, U., Mithulananthan, N., Raza, M. Q., Shah, R., and Milano, F. (2021). RoCoF restrictive planning framework and wind speed forecast informed operation strategy of energy storage system. IEEE Trans. Power Syst. 36 (1), 224–234. doi:10.1109/TPWRS.2020.3001997
Amir, M., Prajapati, A. K., and Refaat, S. S. S. (2022). Dynamic performance evaluation of grid-connected hybrid renewable energy-based power generation for stability and power quality enhancement in smart grid. Front. Energy Res. 10, 16. doi:10.3389/fenrg.2022.861282
Bera, A., Chalamala, B., Byrne, R. H., and Mitra, J. (2021). “Optimal planning of energy storage in wind integrated systems considering frequency stability,” in 2021 IEEE Power and Energy Society General Meeting, Washington, DC, USA, 26-29 July 2021, 1–5. doi:10.1109/PESGM46819.2021.9638110
Cao, M. J., Xu, Q. S., Nazaripouya, H., Chu, C. C., Pota, H. R., and Gadh, R. (2019). Engineering energy storage sizing method considering the energy conversion loss on facilitating wind power integration. IET Gener. Transm. Distrib. 13 (9), 1693–1699. doi:10.1049/iet-gtd.2018.6358
Chen, H., Shi, J., Liu, R., Huang, L., Jia, Y., and Wu, H. (2021). “Optimal planning of primary frequency regulation capacity of wind-storage combined systems,” in 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22-24 October 2021, 2178–2183. doi:10.1109/EI252483.2021.9713134
Dantas, N. K. L., Souza, A. C. M., Vasconcelos, A. S. M., Junior, W. D. S., Rissi, G., Dall'Orto, C., et al. (2022). Impact analysis of a battery energy storage system connected in parallel to a wind farm. Energies 15 (13), 4586. doi:10.3390/en15134586
Guan, M. (2022). Scheduled power control and autonomous energy control of grid-connected energy storage system (ESS) with virtual synchronous generator and primary frequency regulation capabilities. IEEE Trans. Power Syst. 37 (2), 942–954. doi:10.1109/TPWRS.2021.3105940
Guo, Z., and Wu, W. (2022). Data-driven model predictive control method for wind farms to provide frequency support. IEEE Trans. Energy Convers. 37 (2), 1304–1313. doi:10.1109/TEC.2021.3125369
Khalid, H. M., Ahmed, Q., and Peng, J. C. H. (2015a). Health monitoring of li-ion battery systems: A median expectation diagnosis approach (MEDA). IEEE Trans. Transp. Electrif. 1 (1), 94–105. doi:10.1109/tte.2015.2426431
Khalid, H. M., Ahmed, Q., Peng, J. C. H., and Rizzoni, G. (2015b). Current-split estimation in li-ion battery pack: An enhanced weighted recursive filter method. IEEE Trans. Transp. Electrif. 1 (4), 402–412. doi:10.1109/tte.2015.2492557
Khalid, H. M., Flitti, F., Muyeen, S. M., Elmoursi, M. S., Sweidan, T. O., and Yu, X. H. (2022). Parameter estimation of vehicle batteries in V2G systems: An exogenous function-based approach. IEEE Trans. Ind. Electron. 69 (9), 9535–9546. doi:10.1109/tie.2021.3112980
Khalid, H. M., and Peng, J. C. H. (2020). Bidirectional charging in V2G systems: An in-cell variation analysis of vehicle batteries. IEEE Syst. J. 14 (3), 3665–3675. doi:10.1109/jsyst.2019.2958967
Kheshti, M., Lin, S., Zhao, X., Ding, L., Yin, M., and Terzija, V. (2022). Gaussian distribution-based inertial control of wind turbine generators for fast frequency response in low inertia systems. IEEE Trans. Sustain. Energ. 13 (3), 1641–1653. doi:10.1109/TSTE.2022.3168778
Li, C. P., Li, J., Li, J. H., Zhang, X. C., and Hou, T. (2022). Optimization strategy of secondary frequency modulation based on dynamic loss model of the energy storage unit. J. Energy Storage 51, 104425. doi:10.1016/j.est.2022.104425
Li, H., Qiao, Y., Lu, Z., Zhang, B., and Teng, F. (2021). Frequency-constrained stochastic planning towards a high renewable target considering frequency response support from wind power. IEEE Trans. Power Syst. 36 (5), 4632–4644. doi:10.1109/TPWRS.2021.3066991
Li, S. J., Xu, Q. S., Xia, Y. X., and Hua, K. (2022). Comprehensive setting and optimization of Dead-Band for BESS participate in power grid primary frequency regulation. Int. J. Electr. Power Energy Syst. 141, 108195. doi:10.1016/j.ijepes.2022.108195
Liu, Y., Wu, X. G., Du, J. Y., Song, Z. Y., and Wu, G. L. (2020). Optimal sizing of a wind-energy storage system considering battery life. Renew. Energy 147, 2470–2483. doi:10.1016/j.renene.2019.09.123
Ma, D. Z., and Li, W. Y. (2022). Wind-storage combined virtual inertial control based on quantization and regulation decoupling of active power increments. Energies 15 (14), 5184. doi:10.3390/en15145184
Masaud, T. M., Oyebanjo, O., and Sen, P. K. (2017). Sizing of large-scale battery storage for off-grid wind power plant considering a flexible wind supply-demand balance. IET Renew. Power Gener. 11 (13), 1625–1632. doi:10.1049/iet-rpg.2016.0839
Meng, G., Chang, Q., Sun, Y., Rao, Y., Zhang, F., Wu, Y., et al. (2021). Energy storage auxiliary frequency modulation control strategy considering ACE and SOC of energy storage. IEEE Access 9, 26271–26277. doi:10.1109/ACCESS.2021.3058146
Mirjalili, S., Gandomi, A. H., Mirjalili, S. Z., Saremi, S., Faris, H., and Mirjalili, S. M. (2017). Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 114, 163–191. doi:10.1016/j.advengsoft.2017.07.002
Peng, B., Zhang, F., Liang, J., Ding, L., and Wu, Q. W. (2019). An optimal control and sizing strategy for a coordinated WTG-ES system to provide frequency support. Int. J. Electr. Power Energ. Syst. 113, 251–263. doi:10.1016/j.ijepes.2019.05.052
Rahimi, T., Ding, L., Kheshti, M., Faraji, R., Guerrero, J. M., and Tinajero, G. D. A. (2021). Inertia response coordination strategy of wind generators and hybrid energy storage and operation cost-based multi-objective optimizing of frequency control parameters. IEEE Access 9, 74684–74702. doi:10.1109/ACCESS.2021.3081676
Salman, U. T., Al-Ismail, F. S., and Khalid, M. (2020). Optimal sizing of battery energy storage for grid-connected and isolated wind-penetrated microgrid. IEEE Access 8, 91129–91138. doi:10.1109/ACCESS.2020.2992654
Sandelic, M., Stroe, D. I., and Iov, F. (2018). Battery storage-based frequency containment reserves in large wind penetrated scenarios: A practical approach to sizing. Energies 11 (11), 3065. doi:10.3390/en11113065
Shin, H., and Hur, J. (2020). Optimal energy storage sizing with battery augmentation for renewable-plus-storage power plants. IEEE Access 8, 187730–187743. doi:10.1109/ACCESS.2020.3031197
Singh, K., Amir, M., Ahmad, F., and Khan, M. A. (2021a). An integral tilt derivative control strategy for frequency control in multimicrogrid system. IEEE Syst. J. 15 (1), 1477–1488. doi:10.1109/jsyst.2020.2991634
Singh, K., Amir, M., Ahmad, F., and Refaat, S. S. (2021b). Enhancement of frequency control for stand-alone multi-microgrids. IEEE Access 9, 79128–79142. doi:10.1109/access.2021.3083960
Singh, K., and Zaheeruddin, (2021). Enhancement of frequency regulation in tidal turbine power plant using virtual inertia from capacitive energy storage system. J. Energy Storage 35, 102332. doi:10.1016/j.est.2021.102332
Subroto, R. K., Lian, K. L., Chu, C. C., and Liao, C. J. (2021). A fast frequency control based on model predictive control taking into account of optimal allocation of power from the energy storage system. IEEE Trans. Power Deliv. 36 (4), 2467–2478. doi:10.1109/TPWRD.2021.3078217
Swierczynski, M., Stroe, D. I., Stan, A. I., and Teodorescu, R. (2015). Lifetime and economic analyses of lithium-ion batteries for balancing wind power forecast error. Int. J. Energ. Res. 39 (6), 760–770. doi:10.1002/er.3278
Tan, Z. X., Li, X. R., He, L., Li, Y., and Huang, J. Y. (2020). Primary frequency control with BESS considering adaptive SoC recovery. Int. J. Electr. Power Energy Syst. 117, 105588. doi:10.1016/j.ijepes.2019.105588
Torkashvand, M., Khodadadi, A., Sanjareh, M. B., and Nazary, M. H. (2020). A life cycle-cost analysis of li-ion and lead-acid besss and their actively hybridized ESSs with supercapacitors for islanded microgrid applications. IEEE Access 8, 153215–153225. doi:10.1109/access.2020.3017458
Wan, C., Qian, W. T., Zhao, C. F., Song, Y. H., and Yang, G. Y. (2021). Probabilistic forecasting based sizing and control of hybrid energy storage for wind power smoothing. IEEE Trans. Sustain. Energ. 12 (4), 1841–1852. doi:10.1109/tste.2021.3068043
Wang, C. F., Teng, Q. J., Liu, X. Y., Zhang, F., He, S. Y., Liang, Z. T., et al. (2019). Optimal sizing of energy storage considering the spatial-temporal correlation of wind power forecast errors. IET Renew. Power Gener. 13 (4), 530–538. doi:10.1049/iet-rpg.2018.5438
Wang, H., Wang, T. X., Xie, X. H., Ling, Z. X., Gao, G. L., and Dong, X. (2018). Optimal capacity configuration of a hybrid energy storage system for an isolated microgrid using quantum-behaved particle swarm optimization. Energies 11 (2), 454. doi:10.3390/en11020454
Wu, Z. P., Gao, D. W., Zhang, H. G., Yan, S. J., and Wang, X. (2017). Coordinated control strategy of battery energy storage system and PMSG-WTG to enhance system frequency regulation capability. IEEE Trans. Sustain. Energ. 8 (3), 1330–1343. doi:10.1109/tste.2017.2679716
Xiong, L., Yang, S., Huang, S., He, D., Li, P., Khan, M. W., et al. (2022). Optimal allocation of energy storage system in DFIG wind farms for frequency support considering wake effect. IEEE Trans. Power Syst. 37 (3), 2097–2112. doi:10.1109/TPWRS.2021.3111017
Zaheeruddin, , Singh, K., and Amir, M. (2021). Intelligent fuzzy TIDF-II controller for load frequency control in hybrid energy system. IETE Tech. Rev. 17, 1355–1371. doi:10.1080/02564602.2021.1994476
Zhang, S. Q., Liu, H. Y., Wang, F., Yan, T., and Wang, K. F. (2020). Secondary frequency control strategy for BESS considering their degree of participation. Energy Rep. 6, 594–602. doi:10.1016/j.egyr.2020.11.183
Zhang, Z., Zhou, M., Wu, Z., Liu, S., Guo, Z., and Li, G. (2022). A frequency security constrained scheduling approach considering wind farm providing frequency support and reserve. IEEE Trans. Sustain. Energ. 13 (2), 1086–1100. doi:10.1109/TSTE.2022.3150965
Nomenclature
BESS Battery energy storage system
SFD Secondary frequency drop
WT Wind turbine
PFR Primary frequency regulation
LCC Life cycle cost
SOC State of charge
MPPT Maximum power point tracking
PCS Power convert system
SSA Salp swarm algorithm
MSSA Multi-objective salp swarm algorithm
ΔPL Variation of load power
ΔPG Power output variation of traditional units
ΔPW Power output variation of WTs
ΔPB Power output variation of the BESS
Δf Frequency deviation of the power grid
R Adjustment coefficient of traditional units
Kw1 Droop control coefficient of WTs
Kw2 Inertia control coefficient of WTs
Kb1 Virtual droop coefficient of the BESS
Kb2 Virtual inertia coefficient of the BESS
H Inertia time constant of the power grid
D Damping factor of the system
Gg Model of thermal power units
Ggov Transfer function of the governor
Gt Transfer function of the non-reheated steam turbine
Tg Time constant of the governor
Tt Time constant of the steam turbine
Gb BESS model
Tb Response time constant of the BESS
toff The time of WTs exiting frequency regulation
t0 Initial time of frequency regulation
Tf Time period of frequency regulation
η1 Efficiency of the DC–DC converter of the PCS
η2 Efficiency of the DC–AC converter of the PCS
ηch Charging efficiency of the BESS
ηdis Discharging efficiency of the BESS
SOC0 SOC of the BESS at the initial time
SOCmax Upper limit of the SOC
SOCmin Lower limit of the SOC
Prated Rated power of the BESS
Erated Rated capacity of the BESS
Ggen Transfer function of thermal power units
Gw Transfer function of WTs
Δf12max Sum of the maximum frequency deviations in two stages
CLCC Energy storage cost
Cinv Initial investment and replacement cost
Cbop Balance of plant cost
Com Operation and maintenance cost
Cscr Scrap disposal cost
Cres Recovery residual value.
Keywords: wind-storage system, primary frequency regulation, secondary frequency drop, capacity configuration, multi-objective salp swarm algorithm
Citation: Li D, Wan R, Xu B, Yao Y, Dong N and Zhang X (2023) Optimal capacity configuration of the wind-storage combined frequency regulation system considering secondary frequency drop. Front. Energy Res. 11:1037587. doi: 10.3389/fenrg.2023.1037587
Received: 06 September 2022; Accepted: 17 February 2023;
Published: 10 March 2023.
Edited by:
S. M. Muyeen, Qatar University, QatarReviewed by:
Mohammad Amir, Jamia Millia Islamia, IndiaHaris M. Khalid, Higher Colleges of Technology, United Arab Emirates
Copyright © 2023 Li, Wan, Xu, Yao, Dong and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bo Xu, eHVib0BzaGllcC5lZHUuY24=
 Dongdong Li
Dongdong Li