Power allocation method of battery energy storage system considering state balance in smoothing photovoltaic power fluctuations

Aiming at the imbalances of SOC (state of charge, SOC) and SOH (state of health, SOH) for battery energy storage system (BESS) in smoothing photovoltaic power fluctuations, a power allocation method of BESS is proposed. Firstly, the hierarchical structure of the power allocation method is given, including acquisition of the grid-connected photovoltaic power reference and double-layer power allocation strategy for BESS. Secondly, a swing door trend algorithm optimized by the improved Aquila optimizer is devised and used to deal with the raw photovoltaic power to obtain the grid-connected signal. Next, the dynamic grouping principle considering the SOC and SOH of battery units is devised, and the double-layer power allocation method of BESS is designed in terms of the dynamic grouping results of battery units. Finally, the proposed power allocation method is simulated through actual data, and the results compared with other methods show that it can smooth photovoltaic power fluctuations more effectively, and the SOC and SOH can be balanced more quickly and accurately, which verifies its effectiveness.

1 Introduction

Photovoltaic power generation has the characteristics of no pollution, no noise, and renewability, and it has attracted more and more attention around the world (Sharadga et al., 2020). The fluctuations of photovoltaic power caused by the random variations of solar radiation and ambient temperature will bring a significant challenge to the reliable and stable operation of the power system (De la Parra et al., 2015) (Dong et al., 2020). At the same time, it is not conducive to the increase in renewable energy consumption (Jaszczur et al., 2021) (Jaszczur and Hassan, 2020). The battery energy storage system (BESS) has a fast and flexible capability in power regulation. Configuring a BESS for a photovoltaic power station can suppress the fluctuations of grid-connected photovoltaic power effectively. It can also increase the grid-connected capacity of photovoltaic energy and reduce the operating pressure of the power system (Rana et al., 2022) (Khezri et al., 2020).

To reduce the fluctuations of grid-connected photovoltaic power, it is first necessary to obtain the grid-connected photovoltaic power reference in terms of the grid-connected standard on the photovoltaic power. The current research is carried out mainly based on various filtering algorithms and other algorithms. The moving average algorithm and the double moving average algorithm are used in (Jiang and Hong, 2012) and (Prasad et al., 2022), respectively. The low-pass filtering algorithm considering the state of charge (SOC) of the energy storage system is designed in (Huixiang et al., 2020) and (Syed et al., 2020). However, the low-pass filtering algorithm has a delay problem that is difficult to overcome. Another difficulty directly affecting the inhibition of the power fluctuations is the selection of the time constant in the low-pass filter. A fixed-order empirical mode decomposition is devised in Liu et al., 2022, but it does not fully consider the volatility of the photovoltaic power, and the large fluctuations exist sometimes. An optical storage model is proposed to suppress the power fluctuations and corresponding control methods is devised to solve the intermittent output of new energy for grid connection. In the model, the constraints of charging and discharging the energy storage module fail to take the battery units SOC into account, which is not conducive to protecting the energy storage device (Abdalla et al., 2021) (Othman et al., 2020). Therefore, the above studies based on various filtering algorithms only have a relatively limited effect on suppressing the fluctuations of photovoltaic power. More importantly, the imbalances of SOC and state of health (SOH) among battery units have not yet been considered, which weakens the schedulable potential and is unable to reduce the life loss of BESS in power regulation.

Aiming at the problem of the SOC imbalance of battery units when BESS smoothing the fluctuations of photovoltaic power, most of the existing studies are to achieve the SOC balance by changing the power regulated by the battery units (Ali et al., 2021) (Morstyn et al., 2014). An energy management scheme considering the SOC balance is proposed in Ali et al., 2021 based on a multi-agent system, where each energy storage unit is used as a controllable agent, and the active power reference of each energy storage unit is adjusted in proportion to the level of the SOC to reduce the SOC imbalance. A distributed cooperative control method is designed in Morstyn et al., 2014. It changes the charging and discharging behaviors of multiple battery units to ensure that the SOC among all battery units tends to be consistent. Although the above solutions have made outstanding contributions to the balance of the SOC among battery units, there is still a problem of the low balance in SOC.

Additionally, achieving the balance of SOH among battery units can prolong the lifetime of BESS. A life cycle model for the battery unit is established in Weng et al., 2013. It is optimized by a public dataset, and a balancing system is constructed based on the model. The power allocation scheme redistributing the output current into each battery unit according to their SOH state is designed in Goh et al., 2022 to achieve the balance in SOH. A SOH-awareness balancing scheme is devised in Azimi et al., 2022 by reducing the load current of the battery units with lower SOH. A prediction model and SOH balancing scheme are created in Shili et al., 2016 to compensate for the aging difference of the battery units by generating the voltage dispersion and balancing the aging speed of each battery unit. Finally, the maximization of the lifetime through balancing the SOH is achieved. Although the composite control system of the combined power generation system proposed in the literature can adjust the output of the energy storage system according to the demand, the strategy is limited to the degree of mitigation of photovoltaic fluctuations, and the battery units SOH is not considered (Shen et al., 2020) (Parlikar et al., 2021). The optimization strategy of the optical storage model proposed in the literature is based on the charge and discharge protection of the energy storage module, but it does not consider the number of charge and discharge times and costs of the energy storage module, and it does not improve the system’s consumption of photovoltaic resources (Kroposki et al., 2020) (Victoria et al., 2021). A simplified SOH balancing topology is proposed in Farahani, 2021 to achieve the balance of the SOH in the battery units within a battery group. However, the SOH balancing scheme as mentioned earlier can only achieve the SOH balance among the battery units inside a single battery group. It cannot achieve SOH balance of all battery units for the whole BESS.

Based on the analysis above, few studies have considered reducing the life loss through the simultaneous improvement of the consistencies of SOC and SOH among battery units in smoothing the fluctuations of photovoltaic power with BESS. The main contributions of the research can be summarized as follows:

1) For the relatively weak performance of the current research to reduce the fluctuations of the photovoltaic power, a Swing Door Trending (SDT) algorithm optimized by the improved Aquila Optimizer (IAO) algorithm is proposed, which is called the IAO-SDT algorithm. The IAO-SDT algorithm is used to extract the characteristic data points of the photovoltaic power to obtain the grid-connected power reference of the photovoltaic power station.

2) Aiming at the low consistencies of SOC and SOH among all battery units during operation, a dynamic grouping method that considers SOC and SOH in all battery units simultaneously is proposed. The dynamic grouping time is determined by the standard deviation of the SOC among the battery units. Whether the SOH of each battery unit deviating from the predetermined range is used to divide the battery group. If the SOH of one or more battery units deviates from the predetermined range, the battery units are divided into three groups: The priority charging group, the priority discharge group, and the outlier group. Otherwise, they are divided into two groups: The priority charging group and the priority discharging group.

3) Based on the dynamic grouping results of battery units, the double-layer power allocation method of BESS is designed. The action sequence of the battery groups depends on the positive and negative values of the power regulation reference of BESS. Then, the power regulation reference undertaken by each battery group is distributed from the power regulation reference of BESS, where the power allocation in upper-layer from BESS to the battery groups is achieved; then, the power regulation reference of the battery groups is allocated to the battery units inside the battery groups in terms of the principle of maximum charge/discharge power or the principle of SOC balance, and the power allocation in the lower-layer from the battery groups to the battery units is conducted.

The operating data of a photovoltaic power station is used to verify the proposed method. The simulated results show that the proposed method, compared with other approaches, minimizes the fluctuation rate of the grid-connected photovoltaic power, and further improves the balances of SOC and SOH among battery units.

The organizational structure of the rest of this study: Section 2 introduces the hierarchical structure and the implementation process of the proposed method; Section 3 presents the IAO-SDT algorithm to obtain the grid-connected photovoltaic power reference; Section 4 devises a double-layer power allocation strategy based on the dynamic grouping technology; Section 5 conducts the simulation verification; Section 6 summarizes the main conclusion.

2 Hierarchical structure and implementation process

Figure 1 gives the hierarchical structure and the implementation process of this study. It shows that this study includes the two main contents:

1) Acquisition of the grid-connected photovoltaic power reference: The IAO algorithm is presented to speed up the convergence speed and enhance the optimization accuracy, and it is used to optimize the compression offset of the SDT algorithm; the IAO-SDT algorithm is applied to extract the characteristic data points from the raw photovoltaic power; the grid-connected photovoltaic power reference is obtained by connecting these feature data and it is also used to be compared with the raw photovoltaic power to get the power regulation reference of BESS.

2) Double-layer power allocation strategy for BESS: The dynamic grouping time is determined by the standard deviation of the SOC among the battery units, and the SOH of each battery unit deviating from the predetermined range is used to divide the battery group; the action sequence of the battery group is determined by the power regulation reference of BESS, and then double-layer power allocation from BESS to battery units is realized; eventually, every battery unit responds to its power regulation reference, and the whole process of the power regulation of BESS assisting the photovoltaic station is completed.

FIGURE 1

FIGURE 1. Hierarchical structure and implementation process of this study.

3 Acquisition of grid-connected photovoltaic power reference based on IAO-SDT algorithm

3.1 Principle and deficiency of SDT algorithm

The SDT algorithm proposed by Bristol in 1990 (Bristol, 1990) has been effectively applied in the wind power ramp events and the SCADA system data compression due to its high compression ratio, fast execution speed, and controllable error (Cui et al., 2015) (Mah et al., 1995). SDT is a linear segmented algorithm, simple in calculation, small in compression and reconstruction, small in storage space and fast in operation, so it is widely used in industrial engineering practice. When processing the field data, the use of SDT algorithm can significantly decrease the demand for storage space and reduce the possibility of congestion in the network. Meanwhile, it can measure the value of some points and improve the performance of the control system. The implementation steps of the SDT algorithm are as follows:

Step 1: Initialization.

$\{\begin{array}{l}{\mathit{k}}_{1\mathit{d}}=\frac{{\mathit{x}}_1-\left({\mathit{x}}_0+\mathit{E}\right)}{{\mathit{t}}_1-{\mathit{t}}_0}\\ {\mathit{k}}_{2\mathit{d}}=\frac{{\mathit{x}}_1-\left({\mathit{x}}_0-\mathit{E}\right)}{{\mathit{t}}_1-{\mathit{t}}_0}\end{array}(1)$

where $t_0$ and $x_0$ are the initial moment and the corresponding data value, respectively; $t_1$and $x_1$are the first moment and the corresponding data value, respectively; $k_{1d}$and $k_{2d}$ are the initial values of the upper and lower pivot gate slopes, respectively; E is the compression offset.

Step 2: Calculation of the slope.

$\{\begin{array}{l}{\mathit{k}}_1=\frac{{\mathit{x}}_{\mathit{i}}-\left({\mathit{x}}_{\mathit{k}}+\mathit{E}\right)}{{\mathit{t}}_{\mathit{j}}-{\mathit{t}}_{\mathit{k}}}\\ {\mathit{k}}_2=\frac{{\mathit{x}}_{\mathit{j}}-\left({\mathit{x}}_{\mathit{k}}-\mathit{E}\right)}{{\mathit{t}}_{\mathit{j}}-{\mathit{t}}_{\mathit{k}}}\\ {\mathit{k}}_{\mathit{j}}=\frac{{\mathit{x}}_{\mathit{j}}-{\mathit{x}}_{\mathit{k}}}{{\mathit{t}}_{\mathit{j}}-{\mathit{t}}_{\mathit{k}}}\end{array}(2)$

where $t_j$and $x_j$ are the jth moment and the corresponding data value, respectively; $t_k$ and $x_k$ are the kth moment and the corresponding data value, respectively.

Step 3: Updating the slope.

$\{\begin{array}{l}{\mathit{k}}_{1\mathit{d}}=\mathbf{max}\left\{{\mathit{k}}_1,{\mathit{k}}_{1\mathit{d}}\right\}\\ {\mathit{k}}_{2\mathit{d}}=\mathbf{max}\left\{{\mathit{k}}_2,{\mathit{k}}_{2\mathit{d}}\right\}\end{array}(3)$

Step 4: Extraction of feature data.

${\mathit{k}}_{1\mathit{d}}\ge {\mathit{k}}_{2\mathit{d}}(4)$

If Eq. 4 is satisfied, the data value at the last moment is recorded as the feature data, and it returns to step 2; otherwise, it returns to Step 3.

In this study, the raw grid-connected photovoltaic power data at 5 min intervals over one-day-ahead 24 h is selected. The SDT algorithm is used to extract the feature data, and the grid-connected photovoltaic power reference curve is obtained by connecting the extracted feature data. It is worth noting that the compression offset E in the SDT algorithm directly affects the extraction result of the feature data. If selecting a larger E, fewer feature data will be extracted. Therefore, a suitable E is so essential that the IAO is used to find the optimal value E.

3.2 Improved aquila optimizer

The Aquila Optimizer (AO) was proposed in 2021 (Abualigah et al., 2021), and it is inspired by the behavior of the eagles in capturing prey in nature. The optimization process of the AO is represented by four methods: the search space selected by the high soaring of vertical diving, the exploration within the diverging search space by the profile flight of the short glide attack, the exploitation of the convergent search space by the low flight of the slow descent attack, and finally diving on foot and catching the prey. The specific steps are as follows:

Step 1: Selection of a search space.

${\mathit{X}}_1(\mathit{n}+1)={\mathit{X}}_{\mathbf{best}}\left(\mathit{n}\right)\times \left(1-\frac{\mathit{n}}{{\mathit{N}}_{\mathbf{max}}}\right)+({\mathit{X}}_{\mathbf{M}}\left(\mathit{n}\right)-{\mathit{X}}_{\mathbf{best}}\left(\mathit{n}\right)\times \mathit{r}\mathit{a}\mathit{n}\mathit{d})(5)$

${\mathit{X}}_{\mathbf{M}}\left(\mathit{n}\right)=\frac{1}{\mathit{N}}{\sum }_{\mathit{i}=1}^{\mathbf{N}}{\mathit{X}}_{\mathit{i}\mathit{l}}\left(\mathit{n}\right),\forall \mathit{j}=\mathrm{1,2},\dots ,\mathit{D}(6)$

where n is the number of iterations; ${\mathit{X}}_1\left(n+1\right)$ is the solution of the next iteration of $n$, generated by the first search method; ${\mathit{X}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}\left(n\right)$ is the optimal solution at the nth iteration; $n$ and $N_{\max }$ are the current iteration and the maximum number of iterations, respectively; N is the number of Aquila individuals; ${\mathit{X}}_{\mathrm{M}}\left(n\right)$ is the average value of the current solutions of all Aquila individuals at the nth iteration; rand is a random value between 0 and 1; D is the search variable dimension.

Step 2: Global search.

${\mathit{X}}_2\left(\mathit{n}+1\right)={\mathit{X}}_{\mathbf{best}}\left(\mathit{n}\right)\times \mathbf{L}\mathbf{e}\mathbf{v}\mathbf{y}\left(\mathit{D}\right)+{\mathit{X}}_{\mathbf{R}}\left(\mathit{n}\right)+\left(\mathit{y}-\mathit{x}\right)\times \mathit{r}\mathit{a}\mathit{n}\mathit{d}(7)$

where ${\mathit{X}}_2\left(n+1\right)$ is the solution of ${\mathit{X}}_2$ for the next iteration of $n$, generated by the second search method; ${\mathit{X}}_{\mathrm{R}}\left(n\right)$ is to take the current solution in any Aquila individual in the $n$th iteration; $Levy\left(D\right)$ is the $Levy$ flight distribution function, and the calculation equation is as follows:

$\{\begin{array}{l}Levy\left(D\right)=s\times \frac{\mathit{u}\times \mathit{\sigma }}{{\left|\mathit{v}\right|}^{1/\mathit{\beta }}}{\mathit{X}}_{\mathbf{R}}\left(\mathit{n}\right)+\left(\mathit{y}-\mathit{x}\right)\times \mathit{r}\mathit{a}\mathit{n}\mathit{d}\\ \sigma =\frac{\mathit{\Gamma }\left(1+\mathit{\beta }\right)\times \mathbf{sin}\left(\mathit{\pi }\mathit{\beta }/2\right)}{\mathit{\Gamma }\left[\left(1+\mathit{\beta }\right)/2\right]\times \mathbf{\beta }\times 2^{\left(\mathit{\beta }-1\right)/2}}\end{array}(8)$

where the parameter s is selected as 0.01; u and v are random numbers between 0 and 1, and the parameter $\beta$ is 1.5; y₁ and y₂ are used to represent the spiral shape in the search, and the calculation is as follows:

${\mathit{y}}_1=\mathit{r}\times \mathbf{cos}\left(\mathit{\theta }\right)(9)$

${\mathit{y}}_2=\mathit{r}\times \mathbf{sin}\left(\mathit{\theta }\right)(10)$

where r and $\theta$ are calculated as follows:

$\mathit{r}={\mathit{r}}_1+\mathit{U}\times {\mathit{D}}_1(11)$

$\mathit{\theta }=-\mathit{\omega }\times {\mathit{D}}_1+{\mathit{\theta }}_1(12)$

${\mathit{\theta }}_1=\frac{3\mathit{\pi }}{2}(13)$

where r₁ is a random value between 1 and 20; U is 0.00565; D₁ is an integer between 1 and the dimension D of the search variable, and ω is 0.005.

Step 3: Local mining.

${\mathit{X}}_3\left(\mathit{n}+1\right)=\left({\mathit{X}}_{\mathbf{best}}\left(\mathit{n}\right)-{\mathit{X}}_{\mathbf{M}}\left(\mathit{n}\right)\right)\times {\mathit{\delta }}_1-\mathit{r}\mathit{a}\mathit{n}\mathit{d}+\left(\left(\mathit{U}\mathit{B}-\mathit{L}\mathit{B}\right)\times \mathit{r}\mathit{a}\mathit{n}\mathit{d}+\mathit{L}\mathit{B}\right)\times {\mathit{\delta }}_2(14)$

where ${\mathit{X}}_3\left(n+1\right)$ is the solution of the next iteration of $n$, generated by the third method; ${\delta }_1$ and ${\delta }_2$ are both 0.1; LB is the lower limit of the variables, and UB is the upper limit of the variables.

Step 4: Reduction of the search area.

${\mathit{X}}_4(\mathit{n}+1)=\mathit{Q}\mathit{F}\times {\mathit{X}}_{\mathbf{best}}\left(\mathit{n}\right)-({\mathit{G}}_1\times \mathit{X}\left(\mathit{n}\right)\times \mathit{r}\mathit{a}\mathit{n}\mathit{d})-{\mathit{G}}_2\times \mathbf{L}\mathbf{e}\mathbf{v}\mathbf{y}\left(\mathit{D}\right)+\mathit{r}\mathit{a}\mathit{n}\mathit{d}\times {\mathit{G}}_1(15)$

$\mathit{Q}\mathit{F}\left(\mathit{n}\right)={\mathit{n}}^{\frac{2\times \mathit{r}\mathit{a}\mathit{n}\mathit{d}-1}{\left(1-{\mathit{N}}_{\mathit{max}}\right)}}(16)$

where ${\mathit{X}}_4\left(n+1\right)$ is the solution for the next iteration of $n$, generated by the fourth search method; $QF$ is the quality function to balance the search strategy; $G_1$ is the various movement of the eagle tracking the prey during hunting, and $X\left(n\right)$ is the current solution at the nth iteration. To speed up the optimization speed, the modified step size is shown below:

${\mathit{G}}_1=2\times \mathit{r}\mathit{a}\mathit{n}\mathit{d}–1(17)$

$\mathit{\mu }={\mathit{a}}_1+{\mathit{a}}_2\times \mathit{ln}\left[{\mathit{a}}_3-{\mathit{a}}_4\times \mathit{n}+\sqrt{{\mathit{a}}_5+{\left({\mathit{a}}_3-{\mathit{a}}_4\times \mathit{n}\right)}^2}\right](18)$

where $a_1$, $a_2$, $a_3$, $a_4$ and $a_5$ are the step size parameters, and their values are selected as 1.1, 0.2, 30, 1.5, and 1, respectively.

Compared with existing optimization algorithms such as Whale Optimization Algorithm (WOA), Sine Cosine Algorithm (SCA), Slime Mould Algorithm (SMA), the AO optimizer has faster optimization speed and higher convergence accuracy under the same conditions (Abualigah et al., 2021). Specifically, in the first and second steps of the AO optimization algorithm, the larger search range makes it possible to lock the optimal solution in a shorter time, and the third and fourth steps make the AO optimizer obtain higher optimization accuracy than other optimization algorithms in a shorter time.

3.3 Acquisition of grid-connected photovoltaic power reference

Firstly, the compression ratio $Y_a$, the sum of the errors $C_{az}$, the power fluctuation rate $V_a$, and the power reference $P_{\mathrm{r}·\mathrm{b}}$ tracked by BESS are defined as follows:

${\mathit{Y}}_{\mathit{a}}=\frac{{\mathit{N}}_1}{{\mathit{N}}_2}(19)$

${\mathit{C}}_{\mathit{a}\mathit{z}}=\frac{1}{{\mathit{N}}_2}{\sum }_{\mathit{t}=1}^{{\mathit{N}}_2}\left|{\mathit{P}}_{\mathbf{b}}\left(\mathit{t}\right)-{\mathit{P}}_{\mathbf{y}}\left(\mathit{t}\right)\right|(20)$

${\mathit{V}}_{\mathit{a}}=\frac{1}{{\mathit{T}}_1}{\sum }_0^{{\mathbf{T}}_1}\left\{\mathbf{m}\mathbf{a}{\mathbf{x}}_{{\mathit{t}}_{\mathit{i}}\le \mathit{t}\le {\mathit{t}}_{\mathit{i}}+10\mathbf{min}}\left\{{\mathit{P}}_{\mathbf{b}}\left(\mathit{t}\right)\right\}-\mathbf{m}\mathbf{i}{\mathbf{n}}_{{\mathit{t}}_{\mathit{i}}\le \mathit{t}\le {\mathit{t}}_{\mathit{i}}+10\mathbf{min}}\left\{{\mathit{P}}_{\mathbf{b}}\left(\mathit{t}\right)\right\}\right\}/{\mathit{P}}_{\mathbf{v}\mathbf{N}}(21)$

${\mathit{P}}_{\mathbf{r}·\mathbf{b}}\left(\mathit{t}\right)={\mathit{P}}_{\mathbf{y}}\left(\mathit{t}\right)-{\mathit{P}}_{\mathbf{g}}\left(\mathit{t}\right)(22)$

where N₁ is the number of extracted feature data points; N₂ is the number of raw photovoltaic power data points; $P_{\mathrm{g}}\left(t\right)$, $P_{\mathrm{y}}\left(t\right)$, and $P_{\mathrm{r}·\mathrm{b}}\left(t\right)$ are the reference of grid-connected photovoltaic power, the original power value, and the power reference of BESS at the time t, respectively; $t_i$ is the ith time interval (10min for each interval), and T₁ is the scheduling period. $Y_a$ reflects the ability of the SDT algorithm to compress the data; $C_{az}$ characterizes the demand for the capacity of BESS, and $V_a$ expresses the power fluctuation rate of the photovoltaic power.

Then, combined with the requirement of evaluating the fluctuations in Zilong Yang et al., 2019, the grid-connected power at every 10min interval should not exceed 1/3. The fitness function to solve the optimal compression offset of the SDT algorithm optimized by the IAO algorithm is designed in Eq. 23, and the constraint conditions are shown in Eq. 24:

$\mathbf{min}\mathit{f}={\mathit{\alpha }}_1·{\mathit{Y}}_{\mathit{a}}+{\mathit{\alpha }}_2·{\mathit{C}}_{\mathit{a}\mathit{z}}+{\mathit{\alpha }}_3·{\mathit{V}}_{\mathit{a}}(23)$

$\left\{\mathbf{m}\mathbf{a}{\mathbf{x}}_{{\mathit{t}}_{\mathit{i}}\le \mathit{t}\le {\mathit{t}}_{\mathit{i}}+10\mathbf{min}}\left\{{\mathit{P}}_{\mathit{g}}\left(\mathit{t}\right)\right\}-\mathbf{m}\mathbf{i}{\mathbf{n}}_{{\mathit{t}}_{\mathit{i}}\le \mathit{t}\le {\mathit{t}}_{\mathit{i}}+10\mathbf{min}}\left\{{\mathit{P}}_{\mathit{g}}\left(\mathit{t}\right)\right\}\right\}\le \left(1/3\right){\mathit{P}}_{\mathit{v}\mathit{N}}(24)$

where ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ are the weights; $P_{vN}$ is the installed capacity of the photovoltaic power station. In this study, the values of ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ determined by the repeated experiments takes 110, 600, and 80, respectively. The output of the fitness function $P_g$ is the grid-connected photovoltaic power reference.

To verify the superiority of the SDT algorithm optimized by the IAO algorithm, the raw photovoltaic power is dealt with by the proposed algorithm. The result is shown in Figure 2. It shows that the maximum deviation between the raw power and grid-connected power optimized by the SDT algorithm is 0.1474 MW and meets the requirements of the fluctuations in Lixing L V et al., 2021, which means that the maximum charge/discharge power of BESS is 0.1474 MW every time. It reduces the need of the capacity for the BESS. The compression ratio $Y_a$ of the SDT algorithm is 10%, because there are many zero-power data in the raw photovoltaic power curve. The power fluctuation rate $V_a$ of the raw photovoltaic power data is 0.61%, but the power fluctuation rate $V_a$ of the grid-connected power reference is 0.14%. It indicates that the IAO-SDT algorithm has a significant effect on reducing the fluctuations.

FIGURE 2

FIGURE 2. Extracted grid-connected power signals based on IAO-SDT algorithm.

The optimization process of the IAO algorithm and the AO algorithm to search for the optimal solution is compared and shown in Figure 3. It indicates that the IAO algorithm takes less time than the AO algorithm to find a better optimal result. Moreover, the comparative indexes between these the proposed IAO-SDT algorithm and the AO-SDT algorithm are shown in Table 1. It displays that the SDT algorithm optimized by the IAO algorithm outputs a lower fluctuation rate and reduces the requirement of the capacity of BESS as well. Ultimately, the IAO-SDT algorithm has a good optimization performance.

FIGURE 3

FIGURE 3. Comparison of optimization process between IAO algorithm and AO algorithm.

TABLE 1

TABLE 1. Result comparison between IAO-SDT algorithm and AO-SDT algorithm.

4 Dual-layer power allocation strategy based on dynamic grouping for BESS

4.1 Dynamic grouping technique

For BESS, when responding to the power signal, the power signal is usually divided equally or distributed under a certain proportion to the battery units. The coordination allocation of battery units is not adequately considered (Lixing et al., 2021). Furthermore, the current methods require every battery unit in the battery group to participate in the response. So the dynamic grouping approach of the BESS is designed to solve this problem.

When charging the BESS, the battery units with lower SOC should be charged first. Contrarily, battery units with higher SOC should discharge first. Consequently, the SOC of each battery unit tends to be gradually consistent, and the charge/discharge power and the left available capacity of the BESS could both be maintained in good condition for the next cycle. The dynamic grouping approach is designed as follows.

1) Determination of grouping time

After running for some time, the SOC of the battery unit may change, so the grouping of the BESS will be adjusted after some fixed time as usual. To improve the SOC consistency among the battery units, the battery units in the battery groups are dynamically updated in this study when the SOC standard deviation ${\delta }_1$ of one or more battery units is greater than the threshold value ${\gamma }_1$ as shown in Eq. 25. ${\gamma }_1$ could be flexibly set to satisfy the various working conditions.

${\mathit{\delta }}_1>{\mathit{\gamma }}_1(25)$

2) Determination of grouping principle

Moreover, when dividing the BESS into the battery groups, the dynamic grouping principle adopted by the current research is designed only according to the SOC of battery units. But the SOH of some battery unis may be gradually reduced to its lifetime limitation, such as 80%, and these battery units will have to be out of service (Chen et al., 2020). Hence, the grouping of the BESS in the study considers the SOC and the SOH concurrently.

At the time of dynamic grouping, the SOH of the battery units is first judged as whether deviating from the predetermined range shown in Eq. 26. If the SOH of one or more battery units deviates from the predetermined range, the battery units are divided into three battery groups: the priority charging group, the priority discharge group, and the outlier group. These battery units whose SOH deviates from the predetermined range belong to the outlier group. The remaining battery units are ordered by the SOC from low to high. The battery units with lower SOC are given to the priority charging group, and the battery units with higher SOC are assigned to the priority discharging group. The number of battery units assigned to the priority charging group and the priority discharge group is the same. If the SOH in any battery unit does not diverge from the predetermined range, all battery units are divided into two battery groups: the priority charging group and the priority discharge group. The method of how to assign the battery units into the two battery groups is the same as above.

${\mathit{\mu }}_{\mathit{t}}-{\mathit{\gamma }}_2{\mathit{\delta }}_{2,\mathit{t}}\le {\mathit{S}\mathit{O}\mathit{H}}_{\mathit{n},\mathit{t}}\le {\mathit{\mu }}_{\mathit{t}}+{\mathit{\gamma }}_2{\mathit{\delta }}_{2,\mathit{t}}(26)$

where ${\mu }_t$ is the average value of the SOH at the time $t$; ${\delta }_{2,t}$ is the standard deviation of the SOH at the time $t$; ${\gamma }_2$ is the weight coefficient. With a larger ${\gamma }_2$, the SOH consistency among the battery units will be worsen, and the SOC consistency among the battery units will be better. Therefore, ${\gamma }_2$ could be appropriately determined under different working conditions.

3) Calculation of SOH

Currently, the calculation of the SOH can use the estimation methods based on the capacity degradation or the internal resistance increase (Guha and Patra, 2017). Since the capacity change of the battery unit is easier to be measured during operation (Meng et al., 2020), the calculation accuracy with the method based on the capacity degradation is higher than the latter, and it is used in the study to calculate the SOH of the battery unit as follows (Li et al., 2017):

$\mathit{S}\mathit{O}\mathit{H}=\frac{{\mathit{C}}_{\mathit{m}\mathbf{M}}}{{\mathit{C}}_{\mathbf{N}}}\times 100\%(27)$

where $C_{\mathrm{N}}$ is the nominal capacity of the battery unit, and$C_{m\mathrm{M}}$ is the discharging capacity measured at the $m$th measurement.

The estimation methods based on capacity degradation and internal resistance increase are the most used in SOH estimation. The residual capacity method is the SOH estimation method used in the research, and it is also a widely used SOH estimation method for battery units. In practice, the aging process of batteries is quite complex, related to various factors such as ambient temperature, discharge rate, and depth of discharge (DOD). The literature (Ma et al., 2020) gives a specific method for estimating SOH in practical engineering. The calculation of SOH is as follows:

$\mathbf{S}\mathbf{O}{\mathbf{H}}_{\mathit{i},\mathit{t}}=\frac{\Delta \mathbf{S}\mathbf{O}{\mathbf{C}}_{\mathbf{a}\mathbf{l}\mathbf{l}\_\mathbf{min}}}{\Delta \mathbf{S}\mathbf{O}{\mathbf{C}}_{\mathit{i},\mathit{t}}}(28)$

where ${\Delta \mathrm{S}\mathrm{O}\mathrm{C}}_{all\_\mathit{min}}$ is the minimum value among all average SOC variation rates during relative SOH estimation progress, and ${\Delta \mathrm{S}\mathrm{O}\mathrm{C}}_{i,t}$ is the SOC change rate of the ith battery cell at the time t.

4) Calculation of SOC and its constraints

SOC represents the remaining capacity of the battery units. Accurate estimation of the SOC is of great importance in describing the state of the battery units (Jiang et al., 2021). Numerous methods could be used to estimate of the SOC of the battery units, such as the open-circuit voltage method, ampere-hour integral method, neural network, and Kalman filter (Yu and Gao, 2013). Since the ampere-hour integral method is simple in principle and easy to calculate, it is used to estimate the SOC of the battery units in the study:

${\mathit{S}\mathit{O}\mathit{C}}_{\mathit{n},\mathit{t}}={\mathit{S}\mathit{O}\mathit{C}}_{\mathit{n},\mathit{t}-1}+\frac{\int {\mathit{P}}_{\mathbf{b}\mathit{n},\mathit{t}}\mathit{d}\mathit{t}}{{\mathit{C}}_{\mathit{n}}}(29)$

where $SO{C}_{n,t}$ is the SOC of the $n$th battery unit at the time $t$; $P_{\mathrm{b}n,t}$ is the charge/discharge power of the $n$th battery unit at the time $t$, and it is positive when charging and negative when discharging; $C_n$ is the maximum energy storage capacity of the $n$th battery unit.

4.2 Double-layer power allocation strategy

When the BESS responds to the power reference, the existing methods generally ignore the state difference of each battery unit, which leads to overcharge and over-discharge of some battery units and affects the lifetime of the battery units. In addition, the frequent and irregular response of the BESS may also reduce the sustainable regulation ability in the next period. To minimize the loss of lifetime and maintain the reasonable sustainably schedulable potential for the BESS, this study designs a double-layer power allocation strategy for BESS in response to its power reference. The sustainably schedulable potential means that the SOC of the battery units in each battery group should be kept within an optimal range to ensure that the charge/discharge power of the BESS reaches the maximum in the next schedulable cycle (Yu et al., 2011).

4.2.1 Battery group action sequence determination and upper-layer power allocation

1) For the power allocation without the outlier group

When the SOH of all battery units stays within the predetermined range, the battery units are divided into the priority charging group, and the priority discharge group. The operating state of the BESS is judged by the power regulation reference $P_{\mathrm{r}·\mathrm{b}}$, and the action sequence of the battery group could also be determined. The power regulation reference $P_{\mathrm{r}·\mathrm{b}}$ is distributed into the battery groups according to the maximum charge/discharge power of the battery group and the action sequence.

1) Power allocation in charge

If $P_{\mathrm{r}·\mathrm{b}}>0$, the BESS needs to be charged, and the action sequence of the two battery groups is from the priority charging group to the priority discharging group. The maximum charging powers of the priority charging group and the priority discharging group are written as $P_{\mathrm{g}\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}$ and $P_{\mathrm{g}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}}$, respectively.

When $P_{\mathrm{r}·\mathrm{b}}\le P_{\mathrm{g}\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}$, only the priority charging group is responsible for regulating the power reference. Then, the secondary distribution of the power reference in the battery units inside the priority charging group is realized according to the principle of SOC balance, and the priority discharging group do not need to run, where the principle of SOC balance will be introduced in Section 4.2.2.

When $P_{\mathrm{r}·\mathrm{b}}>P_{\mathrm{g}\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}$, the priority charging group works with the maximum charge power, and the priority discharging group undertaking the left power adopts the principle of SOC balance for power distribution in the battery units within the group.

2) Power allocation in discharge

If $P_{\mathrm{r}·\mathrm{b}}<0$, the BESS needs to be discharged, and the action sequence of the two battery groups is from the priority discharging group to the priority charging group.

When $P_{\mathrm{r}·\mathrm{b}}\ge -P_{\mathrm{g}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}}$, only the priority discharging group undertakes the power regulation reference of BESS, and the power distribution of the battery units inside the discharging group is conducted by the principle of SOC balance. The priority charging group does not need to run.

When $P_{\mathrm{r}·\mathrm{b}}<-P_{\mathrm{g}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}}$, the priority discharging group works with the maximum discharge power, and the priority charging group adopts the principle of SOC balance to complete the remaining power distribution in the battery units within the group.

2) For the power allocation with the outlier group

When the SOH of one or more battery units deviates from the predetermined range, the battery units are divided into the priority charging group, the priority discharge group, and the outlier group. The operating state of the BESS is also judged by the power regulation reference $P_{\mathrm{r}·\mathrm{b}}$, and the action sequence of the battery group can be determined. The power regulation reference $P_{\mathrm{r}·\mathrm{b}}$ is distributed into the battery groups according to the maximum charge/discharge power of the battery group and the action sequence.

1) Power allocation in charge

If $P_{\mathrm{r}·\mathrm{b}}>0$, the BESS needs to be charged, and the action sequence of the three battery groups is arranged as follows: the priority charging group, the priority discharging group, and the outlier group. The maximum charging powers of the priority charging group and the priority discharging group are also written as $P_{\mathrm{g}\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}$ and $P_{\mathrm{g}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}}$, respectively.

When $P_{\mathrm{r}·\mathrm{b}}\le P_{\mathrm{g}\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}$, only the priority charging group undertakes the power regulation reference of the BESS, and the secondary power distribution into the battery units inside it according to the principle of SOC balance; the remaining two battery groups do not operate.

When $P_{\mathrm{r}·\mathrm{b}}\le P_{\mathrm{g}\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}+P_{\mathrm{g}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}}$, the priority charging group works with the maximum charge power, and the priority discharging group adopts the principle of SOC balance for power distribution within the group; the outlier group does not operate.

When $P_{\mathrm{r}·\mathrm{b}}>P_{\mathrm{g}\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}+P_{\mathrm{g}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}}$, the priority charging group and the priority discharging group both work with its maximum charge power, and the outlier group adopts the principle of SOC balance for left power distribution within its group.

2) Power allocation in discharge

If $P_{\mathrm{r}·\mathrm{b}}<0$, the BESS needs to be discharged, and the action sequence of the three battery groups is arranged as follows: The priority discharging group, the priority charging group, and the outlier group.

When $P_{\mathrm{r}·\mathrm{b}}\ge -P_{\mathrm{g}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}}$, only the priority discharging group undertakes the power regulation reference of the BESS, and the power distribution inside its battery units according to the principle of SOC balance; the remaining battery groups do not operate.

When $P_{\mathrm{r}·\mathrm{b}}\ge -\left(P_{\mathrm{g}\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}+P_{\mathrm{g}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}}\right)$, the priority discharging group works with the maximum discharge power, and the priority charging group adopts the principle of SOC balance to complete the left power distribution within the group; the outlier group does not operate.

When $P_{\mathrm{r}·\mathrm{b}}<-\left(P_{\mathrm{g}\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}+P_{\mathrm{g}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}}\right)$, the priority charging group and the priority discharging group both work with their maximum discharge powers, and the outlier group adopts the principle of SOC balance to complete the left power distribution within the group.

The power distribution principles that the battery groups should adopt under different conditions are summarized in Table 2 and Figure 4, respectively.

TABLE 2

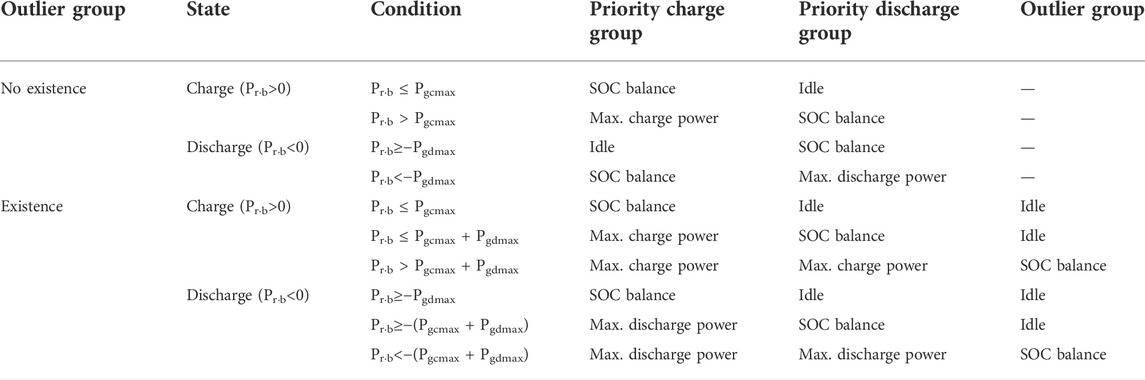
TABLE 2. Power distribution principle for battery units in each battery group with different states.

FIGURE 4

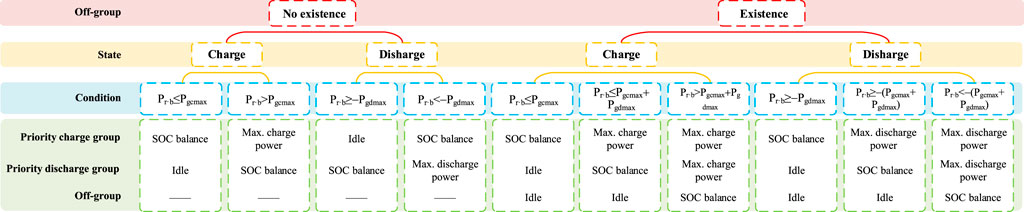
FIGURE 4. Power distribution principle for battery units in each battery group with different states.

4.2.2 Lower-layer power allocation

The lower-layer power allocation from the battery group to the battery units inside it is completed by both the power allocation results in the upper-layer and the power distribution principle adopted by each battery group.

1) Principle of maximum charge/discharge power

The maximum charge/discharge power allocation means that the battery unit participates in the power regulation with its full charge/discharge power under reasonable constraints.

2) Principle of SOC balance

Since the SOC of the battery units in a battery group may differs greatly from each other during operation, it is anticipated that the battery units with lower SOC will be charged firstly. The battery units with higher SOC will be discharged firstly to realize the relative balance of the SOC among the battery units. For this reason, the arctan function is used to describe the charge/discharge process of the battery unit to characterize its charge/discharge capacity (Vicidomini et al., 2017). In this study, the charge function f_ch and discharge function f_dis are set as follows:

${\mathit{f}}_{\mathbf{c}\mathbf{h}}\left({\mathit{S}\mathit{O}\mathit{C}}_{\mathit{n},\mathit{t}}\right)=0.5-0.33·\mathbf{arctan}\left(2·\left({\mathit{S}\mathit{O}\mathit{C}}_{\mathit{n},\mathit{t}}-0.5\right)\right)(30)$

${\mathit{f}}_{\mathbf{d}\mathbf{i}\mathbf{s}}\left({\mathit{S}\mathit{O}\mathit{C}}_{\mathit{n},\mathit{t}}\right)=0.5+0.33·\mathbf{arctan}\left(2·\left({\mathit{S}\mathit{O}\mathit{C}}_{\mathit{n},\mathit{t}}-0.5\right)\right)(31)$

When the battery group needs to be charged, the power allocation approach of SOC balance is depicted as follows:

$\frac{{\mathit{P}}_{\mathbf{r}·\mathbf{b}\mathit{i},\mathit{t}}}{{\mathit{f}}_{\mathbf{c}\mathbf{h}}\left({\mathit{S}\mathit{O}\mathit{C}}_{\mathit{i},\mathit{t}-1}\right)}=\frac{{\mathit{P}}_{\mathbf{r}·\mathbf{b}\mathit{j},\mathit{t}}}{{\mathit{f}}_{\mathbf{c}\mathbf{h}}\left({\mathit{S}\mathit{O}\mathit{C}}_{\mathit{j},\mathit{t}-1}\right)}\forall \mathit{i},\mathit{j}\in \mathit{N}(32)$

where $P_{\mathrm{r}·\mathrm{b}i,t}$ and $P_{\mathrm{r}·\mathrm{b}j,t}$ is the power reference assigned into the ith battery unit and the jth battery unit at the time $t$, respectively.

When the battery group requires to be discharged, the power allocation approach of SOC balance is written as follows:

$\frac{{\mathit{P}}_{\mathbf{r}·\mathbf{b}\mathit{i},\mathit{t}}}{{\mathit{f}}_{\mathbf{d}\mathbf{i}\mathbf{s}}\left({\mathit{S}\mathit{O}\mathit{C}}_{\mathit{i},\mathit{t}-1}\right)}=\frac{{\mathit{P}}_{\mathbf{r}·\mathbf{b}\mathit{j},\mathit{t}}}{{\mathit{f}}_{\mathbf{d}\mathbf{i}\mathbf{s}}\left({\mathit{S}\mathit{O}\mathit{C}}_{\mathit{j},\mathit{t}-1}\right)}\forall \mathit{i},\mathit{j}\in {\mathit{N}}^{*}(33)$

4.2.3 Battery unit responding to power reference

After the power regulation reference is assigned to the battery units, they should respond to the power reference separately under some constraints.

1) Maximum charge/discharge power limitation

When the battery unit participates in the power regulation, the high-rate charge/discharge method is generally not used, so the power allocated to the battery units must meet the following constraints:

${\mathit{P}}_{\mathit{b}\mathit{n},\mathit{t}}=\{\begin{array}{l}{\mathit{P}}_{\mathbf{b}\mathbf{m}\mathbf{a}\mathbf{x}\mathit{n}},{\mathit{P}}_{\mathbf{r}·\mathit{b}\mathit{n}}>{\mathit{P}}_{\mathbf{b}\mathbf{m}\mathbf{a}\mathbf{x}\mathit{n}}\\ {\mathit{P}}_{\mathbf{r}·\mathit{b}\mathit{n}},{\mathit{P}}_{\mathbf{b}\mathbf{m}\mathbf{i}\mathbf{n}\mathit{n}}\le {\mathit{P}}_{\mathbf{r}·\mathit{b}\mathit{n}}\le {\mathit{P}}_{\mathbf{b}\mathbf{m}\mathbf{a}\mathbf{x}\mathit{n}}\\ {\mathit{P}}_{\mathbf{b}\mathbf{m}\mathbf{i}\mathbf{n}\mathit{n}},{\mathit{P}}_{\mathbf{r}·\mathit{b}\mathit{n}}<{\mathit{P}}_{\mathbf{b}\mathbf{m}\mathbf{i}\mathbf{n}\mathit{n}}\end{array}(34)$

where $P_{\mathrm{r}·\mathrm{b}n}$ is the power allocated to the lower-layer of the $n$th battery unit; $P_{\mathrm{b}\mathrm{m}\mathrm{a}\mathrm{x}n}$ and $P_{\mathrm{b}\mathrm{m}\mathrm{i}\mathrm{n}n}$ are the maximum charging power and the maximum discharging power of the $n$th battery unit, respectively.

2) SOC limitation

During the operation of the battery units, it is necessary to avoid overcharge and over-discharge. The SOC is used to characterize the capacity limit of the BESS (Christensen and Newman, 2003), and the corresponding constraint is:

${\mathit{S}\mathit{O}\mathit{C}}_{\mathbf{min}\mathit{i}}\le {\mathit{S}\mathit{O}\mathit{C}}_{\mathit{i},\mathit{t}}\le {\mathit{S}\mathit{O}\mathit{C}}_{\mathbf{max}\mathit{i}}(35)$

where $SO{C}_{\max i}$ and $SO{C}_{\min i}$ are the upper limit and lower limit of the SOC for the $i$th battery unit, respectively.

3) Charge/discharge states limitation

The simultaneous charge state and discharge state are impossible for a battery unit and should be avoided, so the constraint is:

${\mathit{u}}_{\mathit{i},\mathit{t}}^{\mathrm{charge}}+{\mathit{u}}_{\mathit{i},\mathit{t}}^{\mathrm{discharge}}\le 1(36)$

where $u_{i,t}^{charge}$ and $u_{i,t}^{discharge}$ are the charge flag and the discharge flag of the $i$th battery unit at the time $t$, respectively. For charging, $u_{i,t}^{charge}$ is selected as 1 and $u_{i,t}^{discharge}$ is selected as 0. For discharging, $u_{i,t}^{discharge}$ is chosen as 1 and $u_{i,t}^{charge}$ is selected as 0. For other states they are also chosen as 0.

5 Simulation verification and analysis

5.1 Simulated data

The simulation verification is carried out in an actual 6.6 MW photovoltaic power station at high-speed railway station in China. The scale of the BESS equipped for the photovoltaic power station is 1.2MW/1.8 MWh. Ten battery units is included in the BESS, and the initial SOC is given as: 0.4, 0.42, 0.46, 0.47, 0.48, 0.5, 0.52, 0.54, 0.57, and 0.6. The initial SOH is given as: 1, 0.99999, 0.99998, 0.99996, 0.9995, 0.99985, 0.99983, 0.99982, 0.99981, and 0.99980. The initial SOH standard deviation is 8.3327e-05. The maximum charge/discharge power of every battery unit is 0.12 MW.

5.2 Results and analysis of dynamic grouping

To reflect the superiority of the power allocation method proposed in this research, it is compared with the other three approaches, which are called approach-I, approach-II, and approach-III. Approach-I adopts the dynamic grouping algorithm, but the power reference is equally shared within the group. Approach-II does not use the grouping algorithm, and the power reference is equally shared in the battery units. The power reference of BESS under Approach-III is responded to by the battery unit one by one. Approach-IV comes from the reference (Wang et al., 2021). Approach-V comes from the reference (Li et al., 2018).

The ratio of the tracking power reference is calculated as Eq. 37:

$\mathit{\beta }=\frac{{\mathit{N}}_3}{{\mathit{N}}_2}(37)$

where $N_3$ is the number of data points that can track the power reference, and $\beta$ is the proportion of the power reference that can be well followed.

Table 3 shows the comparative result of the ratio $\beta$ under different approaches. It indicates that $\beta$ is the highest in the proposed method. Therefore, the performance of tracking the power reference under the proposed method is also the best.

TABLE 3

TABLE 3. Comparison of various power allocation approaches.

The power allocation result in the ten battery units is shown in Figure 5. It displays that the allocated power references in all the battery units do not exceed their maximum charge/discharge powers, and the effect of the power allocation is satisfactory.

FIGURE 5

FIGURE 5. Power allocation result for battery units.

5.3 Results and analysis of battery units to track power references

To verify that the proposed power allocation method can improve the consistencies of the SOC and SOH effectively, the average value and standard deviation of SOC and SOH are calculated at the end of the regulation for the battery units, and the results are shown in Table 4. It can be seen from the comparison that compared with other control strategies, the standard deviation of SOC and SOH in the proposed method is the smallest, and the average value of SOC and SOH in the proposed method is at a low level as well. The results show that the power allocation method improves the uniformity of SOC and SOH significantly, thereby avoiding premature withdrawal of the battery units and improving the sustainable scheduling capability of BESS.

TABLE 4

TABLE 4. Comparison of SOC and SOH regulated by various approaches.

The tracking performance of the battery units and the BESS is shown in Figures 6A,B, respectively. Figure 6A indicates that the battery units respond to their assigned power reference smoothly, and Figure 6B the BESS can basically track the power reference. For these points without being fully tracked, the reason is that the power reference in these points exceeds the charge/discharge power limit of the BESS, and only about 1% of the data cannot be tracked. since the SOC of all battery units shown in Figure 7A does not exceed the limit, and the regulation performance is also acceptable. Figure 7B also manifests that the proposed method can further improve the consistency of the SOH among the battery units, and the standard deviation of the SOH among the battery units is only 6.8817e-05.

FIGURE 6

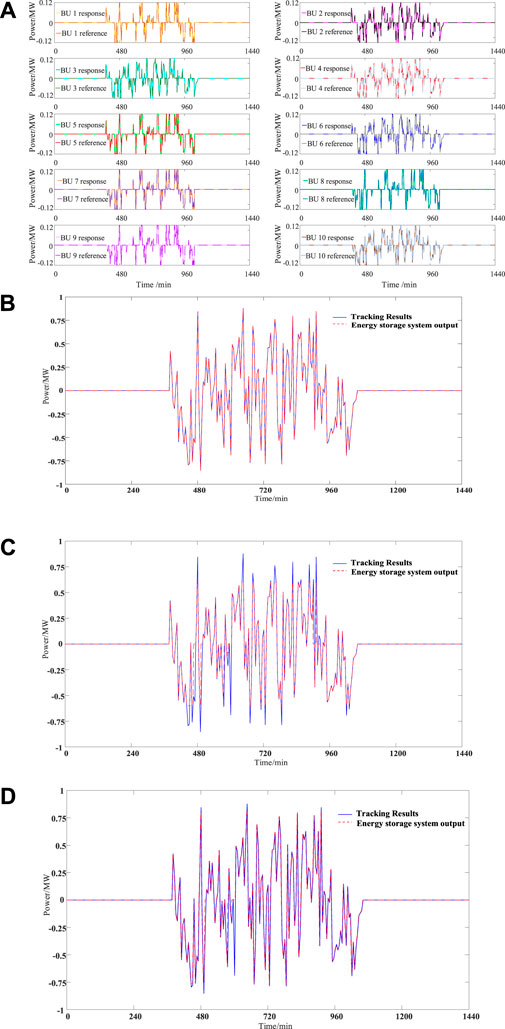
FIGURE 6. (A) Tracking results of the power references by the battery units. (B) Tracking result of the power reference by BESS for proposed approach. (C) Tracking result of the power reference by BESS for approach-IV. (D) Tracking result of the power reference by BESS for approach-V.

FIGURE 7

FIGURE 7. (A) Variation of SOC for battery units. (B) Variation of SOH for battery units.

As shown in the above simulation diagrams, the approaches IV and V both have tracking errors when tracking the same photovoltaic grid-connected power signal, but the proposed method can achieve the high-precision tracking in the whole process. So the regulation performance of the proposed mthod is more acceptable.

5.4 Result of grid-connected photovoltaic power

The raw grid-connected power and actual grid-connected power regulated by the BESS are compared and shown in Figure 8. It manifests that the output of the photovoltaic station aided the BESS is able to track the grid-connected power reference well. Hence, the validity of the proposed power allocation method is testified.

FIGURE 8

FIGURE 8. Raw and actual grid-connected powers for photovoltaic power station.

6 Conclusion

Aiming at the low consistencies of SOC and SOH in smoothing the fluctuations of the photovoltaic power through the BESS, a power allocation method considering the state balance of the battery units is presented for the BESS. The research conclusions can be summarized as follows:

1) An approach based on the SDT algorithm optimized by IAO algorithm is designed to acquire the grid-connected photovoltaic power reference. The original AO algorithm is improved to speed up its convergence speed and enhance the optimization accuracy. The IAO-SDT algorithm finds the optimal compression offset of the SDT algorithm more quickly, and the optimization accuracy is higher. The result of the raw photovoltaic power data processed by the IAO-SDT algorithm shows that the grid-connected photovoltaic power reference is effectively extracted, and its fluctuation rate is reduced to satisfy the grid-connected standard better.

2) The dynamic grouping algorithm of the battery units is devised. The dynamic grouping time is determined by the standard deviation of the SOC of the battery units. The dynamic grouping principle is designed according to their SOH and SOC. The grouping status of the battery units is dynamically updated at the dynamic grouping time. Compared with the existing fixed grouping scheme, the consistency of SOC and SOH is guaranteed to a greater extent with the designed dynamic grouping method.

3) A double-layer power allocation strategy for the battery units is proposed. The power regulation reference that each battery group should undertake is determined, and its internal power allocation method is designed to complete the upper-layer power distribution. The lower-layer power distribution of the battery units is also intended to ensure that the power regulation reference allocated by the battery units does not exceed its maximum charge/discharge power. The simulation results show that the proposed double-layer power allocation strategy can help the BESS track the power reference effectively, and ensure that the SOC and SOH of the battery units are both gradually balanced to be consistent.

In the future, the proposed power allocation method can be further improved by considering the benefit of the photovoltaic station.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

JZ contributed to conception and design of the study. LH organized the database. PPT performed the statistical analysis. JZ wrote the first draft of the manuscript. XBC wrote sections of the manuscript. XY made substantial contributions to the conception or design of the updated work, and interpreted data for the updated work. XHD made substantial contributions to the conception or design of the updated work, interpreted data for the updated work, and revised it for important intellectual content. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

State Grid Science and Technology Project “Multi energy collaborative optimization and intelligent management and control technology of high proportion clean energy high-speed railway stations”. Item code: 5204XQ21N001.

Conflict of interest

Authors LH, XY, and XC were employed by the company State Grid Hebei Electric Power Co., Ltd. Xiongan New District Power Supply Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdalla, A. N., Nazir, M. S., Tao, H., Cao, S., Ji, R., Jiang, M., et al. (2021). Integration of energy storage system and renewable energy sources based on artificial intelligence: An overview. J. Energy Storage 40, 102811. doi:10.1016/j.est.2021.102811

CrossRef Full Text | Google Scholar

Abualigah, L., Yousri, D., Abd Elaziz, M., Ewees, A. A., Al-qaness, M. A., and Gandomi, A. H. (2021). Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Industrial Eng. 157, 107250. doi:10.1016/j.cie.2021.107250

CrossRef Full Text | Google Scholar

Ali, Z., Putrus, G., Marzband, M., Bagheri Tookanlou, M., Saleem, K., Ray, P. K., et al. (2021). Heuristic multi-agent control for energy management of microgrids with distributed energy sources[C]//2021 56th international universities power engineering conference (UPEC). IEEE, 1–6. doi:10.1109/upec50034.2021.9548152

CrossRef Full Text | Google Scholar

Azimi, V., Allam, A., and Onori, S. (2022). Extending life of lithium-ion battery packs by taming heterogeneities via an optimal control-based active balancing strategy[J]. arXiv preprint arXiv:2203.04226.

Google Scholar

Bristol, E. H. (1990). Swing door trending: Adaptive trend recording. ISA Natl. Conf. Proc., 749–753.

Google Scholar

Chen, X., Tang, J., Li, W., and Xie, L. (2020). Operational reliability and economy evaluation of reusing retired batteries in composite power systems. Int. J. Energy Res. 44 (5), 3657–3673. doi:10.1002/er.5147

CrossRef Full Text | Google Scholar

Christensen, J., and Newman, J. (2003). Effect of anode film resistance on the charge/discharge capacity of a lithium-ion battery. J. Electrochem. Soc. 150 (11), A1416. doi:10.1149/1.1612501

CrossRef Full Text | Google Scholar

Cui, M., Zhang, J., Florita, A. R., Hodge, B. M., Ke, D., Sun, Y., et al. (2015). An optimized swinging door algorithm for wind power ramp event detection[C]//2015. IEEE Power & Energy Soc. General Meet., 1–5. doi:10.1109/pesgm.2015.7286272

CrossRef Full Text | Google Scholar

De la Parra, I., Marcos, J., García, M., and Marroyo, L. (2015). Control strategies to use the minimum energy storage requirement for PV power ramp-rate control. Sol. Energy 111, 332–343. doi:10.1016/j.solener.2014.10.038

CrossRef Full Text | Google Scholar

Dong, J., Olama, M. M., Kuruganti, T., Melin, A. M., Djouadi, S. M., Zhang, Y., et al. (2020). Novel stochastic methods to predict short-term solar radiation and photovoltaic power. Renew. Energy 145, 333–346. doi:10.1016/j.renene.2019.05.073

CrossRef Full Text | Google Scholar

Farahani, G. (2021). DC–DC Series‐resonant converter with multi-stage current-driven for balance charger of series‐connected lithium‐ion batteries. IET Power Electron. 14 (5), 992–1007. doi:10.1049/pel2.12081

CrossRef Full Text | Google Scholar

Goh, H. H., Lan, Z., Zhang, D., Dai, W., Kurniawan, T. A., and Goh, K. C. (2022). Estimation of the state of health (SOH) of batteries using discrete curvature feature extraction. J. Energy Storage 50, 104646. doi:10.1016/j.est.2022.104646

CrossRef Full Text | Google Scholar

Guha, A., and Patra, A. (2017). State of health estimation of lithium-ion batteries using capacity fade and internal resistance growth models. IEEE Trans. Transp. Electrific. 4 (1), 135–146. doi:10.1109/tte.2017.2776558

CrossRef Full Text | Google Scholar

Huixiang, L., Caixue, C., and Zhigang, X. (2020). A wavelet packet-dual fuzzy control method for hybrid energy storage to suppress wind power fluctuations[J]. Appl. Energy 279, 115776.

Google Scholar

Jaszczur, M., Hassan, Q., Abdulateef, A. M., and Abdulateef, J. (2021). Assessing the temporal load resolution effect on the photovoltaic energy flows and self-consumption. Renew. Energy 169, 1077–1090. doi:10.1016/j.renene.2021.01.076

CrossRef Full Text | Google Scholar

Jaszczur, M., and Hassan, Q. (2020). An optimisation and sizing of photovoltaic system with supercapacitor for improving self-consumption. Appl. Energy 279, 115776. doi:10.1016/j.apenergy.2020.115776

CrossRef Full Text | Google Scholar

Jiang, C., Wang, S., Wu, B., Fernandez, C., Xiong, X., and Coffie-Ken, J. (2021). A state-of-charge estimation method of the power lithium-ion battery in complex conditions based on adaptive square root extended Kalman filter. Energy 219, 119603. doi:10.1016/j.energy.2020.119603

CrossRef Full Text | Google Scholar

Jiang, Q., and Hong, H. (2012). Wavelet-based capacity configuration and coordinated control of hybrid energy storage system for smoothing out wind power fluctuations. IEEE Trans. Power Syst. 28 (2), 1363–1372. doi:10.1109/tpwrs.2012.2212252

CrossRef Full Text | Google Scholar

Khezri, R., Mahmoudi, A., and Haque, M. H. (2020). Optimal capacity of solar PV and battery storage for Australian grid-connected households. IEEE Trans. Ind. Appl. 56 (5), 5319–5329. doi:10.1109/tia.2020.2998668

CrossRef Full Text | Google Scholar

Kroposki, B., Bernstein, A., King, J., Vaidhynathan, D., Zhou, X., Chang, C. Y., et al. (2020). Autonomous energy grids: Controlling the future grid with large amounts of distributed energy resources. IEEE Power Energy Mag. 18 (6), 37–46. doi:10.1109/mpe.2020.3014540

CrossRef Full Text | Google Scholar

Li, N., Gao, F., Hao, T., Ma, Z., and Zhang, C. (2017). SOH balancing control method for the MMC battery energy storage system. IEEE Trans. Ind. Electron. 65 (8), 6581–6591. doi:10.1109/tie.2017.2733462

CrossRef Full Text | Google Scholar

Li, Y., Li, X., Jia, X., Ma, R., and Hui, D. (2018). Monitoring and control for hundreds megawatt scale battery energy storage station based on multi-agent: Methodology and system design[C]//2018 IEEE international conference of safety produce informatization (IICSPI). IEEE, 765–769. doi:10.1109/iicspi.2018.8690406

CrossRef Full Text | Google Scholar

Liu, D., Chen, H., Tang, Y., Liu, C., Cao, M., Gong, C., et al. (2022). Slope micrometeorological analysis and prediction based on an ARIMA model and data-fitting system. Sensors 22 (3), 1214. doi:10.3390/s22031214

PubMed Abstract | CrossRef Full Text | Google Scholar

Lixing, L. V., Shaohua, C., and Xiaobai, Z. (2021). Control strategy for secondary frequency regulation of power system considering SOC consensus of large-scale battery energy storage[J]. Therm. power Gener. 50 (7), 108–117.

Google Scholar

Ma, Z., Gao, F., Gu, X., Li, N., Wu, Q., Wang, X., et al. (2020). Multilayer SOH equalization scheme for MMC battery energy storage system. IEEE Trans. Power Electron. 35 (12), 13514–13527. doi:10.1109/tpel.2020.2991879

CrossRef Full Text | Google Scholar

Mah, R. S. H., Tamhane, A. C., Tung, S. H., and Patel, A. (1995). Process trending with piecewise linear smoothing. Comput. Chem. Eng. 19 (2), 129–137. doi:10.1016/0098-1354(94)e0042-l

CrossRef Full Text | Google Scholar

Meng, J., Cai, L., Stroe, D. I., Ma, J., Luo, G., and Teodorescu, R. (2020). An optimized ensemble learning framework for lithium-ion Battery State of Health estimation in energy storage system. Energy 206, 118140. doi:10.1016/j.energy.2020.118140

CrossRef Full Text | Google Scholar

Morstyn, T., Hredzak, B., and Agelidis, V. G. (2014). Distributed cooperative control of microgrid storage. IEEE Trans. Power Syst. 30 (5), 2780–2789. doi:10.1109/tpwrs.2014.2363874

CrossRef Full Text | Google Scholar

Othman, M. H., Mokhlis, H., Mubin, M., Talpur, S., Ab Aziz, N. F., Dradi, M., et al. (2020). Progress in control and coordination of energy storage system-based VSG: A review. IET Renew. Power Gener. 14 (2), 177–187. doi:10.1049/iet-rpg.2019.0274

CrossRef Full Text | Google Scholar

Parlikar, A., Truong, C. N., Jossen, A., and Hesse, H. (2021). The carbon footprint of island grids with lithium-ion battery systems: An analysis based on levelized emissions of energy supply. Renew. Sustain. Energy Rev. 149, 111353. doi:10.1016/j.rser.2021.111353

CrossRef Full Text | Google Scholar

Prasad, E. N., Dash, P. K., and Sahani, M. (2022). Diagnosing utility grid disturbances in photovoltaic integrated DC microgrid using adaptive multiscale morphology with DFA analysis. Sustain. Energy, Grids Netw. 29, 100574. doi:10.1016/j.segan.2021.100574

CrossRef Full Text | Google Scholar

Rana, M. M., Uddin, M., Sarkar, M. R., Shafiullah, G., Mo, H., and Atef, M. (2022). A review on hybrid photovoltaic – battery energy storage system: Current status, challenges, and future directions. J. Energy Storage 51, 104597. doi:10.1016/j.est.2022.104597

CrossRef Full Text | Google Scholar

Sharadga, H., Hajimirza, S., and Balog, R. S. (2020). Time series forecasting of solar power generation for large-scale photovoltaic plants. Renew. Energy 150, 797–807. doi:10.1016/j.renene.2019.12.131

CrossRef Full Text | Google Scholar

Shen, L., Cheng, Q., Cheng, Y., Wei, L., and Wang, Y. (2020). Hierarchical control of DC micro-grid for photovoltaic EV charging station based on flywheel and battery energy storage system. Electr. power Syst. Res. 179, 106079. doi:10.1016/j.epsr.2019.106079

CrossRef Full Text | Google Scholar

Shili, S., Hijazi, A., Sari, A., Lin-Shi, X., and Venet, P. (2016). Balancing circuit new control for supercapacitor storage system lifetime maximization. IEEE Trans. Power Electron. 32 (6), 4939–4948. doi:10.1109/tpel.2016.2602393

CrossRef Full Text | Google Scholar

Syed, M. A., Abdalla, A. A., Al-Hamdi, A., and Muhammad, K. (2020). Double moving average methodology for smoothing of solar power fluctuations with battery energy storage[C]//2020 International Conference on Smart Grids and Energy Systems (SGES). IEEE, 291–296.

Google Scholar

Vicidomini, G., Petrone, G., Monmasson, E., and Spagnuolo, G. (2017). FPGA based implementation of a sliding-mode observer for battery state of charge estimation[C]//2017 IEEE 26th International Symposium on Industrial Electronics (ISIE). IEEE, 1268–1273. doi:10.1109/isie.2017.8001427

CrossRef Full Text | Google Scholar

Victoria, M., Haegel, N., Peters, I. M., Sinton, R., Jager-Waldau, A., del Canizo, C., et al. (2021). Solar photovoltaics is ready to power a sustainable future. Joule 5 (5), 1041–1056. doi:10.1016/j.joule.2021.03.005

CrossRef Full Text | Google Scholar

Wang, W., Han, X., Wu, Y., Li, H., Li, X., Wang, S., et al. (2021). Energy management of battery energy storage station considering system operation efficiency[C]//2021 International Conference on Power System Technology (POWERCON). IEEE, 1100–1104. doi:10.1109/powercon53785.2021.9697503

CrossRef Full Text | Google Scholar

Weng, C., Cui, Y., Sun, J., and Peng, H. (2013). On-board state of health monitoring of lithium-ion batteries using incremental capacity analysis with support vector regression. J. Power Sources 235, 36–44. doi:10.1016/j.jpowsour.2013.02.012

CrossRef Full Text | Google Scholar

Yang, Zilong, Song, Zhenhao, pan, Jing, Chen, Zhuo, and Wang, Yibo (2019). Multi-mode coordinated control strategy of distributed PV and energy storage system[J]. Proc. CSEE 39 (08), 2213–2220+4. doi:10.13334/j.0258-8013.pcsee.182342

CrossRef Full Text | Google Scholar

Yu, D. X., and Gao, Y. X. (2013). SOC estimation of Lithium-ion battery based on Kalman filter algorithm[C]//Applied Mechanics and Materials. Trans. Tech. Publ. Ltd. 347, 1852–1855. doi:10.4028/www.scientific.net/amm.347-350.1852

CrossRef Full Text | Google Scholar

Yu, Z., Zinger, D., and Bose, A. (2011). An innovative optimal power allocation strategy for fuel cell, battery and supercapacitor hybrid electric vehicle. J. Power Sources 196 (4), 2351–2359. doi:10.1016/j.jpowsour.2010.09.057

CrossRef Full Text | Google Scholar