A Multi-Scale Time Method for the State of Charge and Parameter Estimation of Lithium-Ion Batteries Using MIUKF-EKF

Accurate state estimation is essential for the safe and reliable operation of lithium-ion batteries. However, the accuracy of the battery state estimation depends on the accuracy of the battery parameters. Because the state of charge (SOC) cannot be directly measured, estimation methods based on the Kalman filter are widely used. However, it is difficult to estimate SOC online and get high accuracy results. This article proposes a method for parameter identification and SOC estimation for lithium-ion batteries. Because the lithium-ion battery has slow-varying parameters (such as internal resistance, and polarization resistance), and the SOC has fast-varying characteristics, so a multi-scale multi-innovation unscented Kalman filter and extended Kalman filter (MIUKF-EKF) are used to perform online measurement of battery parameters and SOC estimation in this method. The battery parameters are estimated with a macro-scale, and the SOC is estimated with a micro-scale. This method can improve the estimation accuracy of the SOC in real-time. Results of experiments indicate that the algorithm has higher accuracy in online parameter identification and SOC estimation than in the dual extended Kalman filter (DEKF) algorithm.

1 Introduction

With the increasing demand for energy in the human society, the increasing environmental problem was introduced by the large consumption of fossil energy. New energy power generation sources such as wind power and photoelectricity attract more and more attention (Xu et al., 2021). However, due to the randomness and intermittence of new energy, it is difficult to be absorbed by the grid and results in huge waste. Energy storage power stations can solve the grid absorbance problem of wind power and photoelectricity. Energy storage using batteries is the most mature and reliable energy storage technology at this stage. However, the biggest obstacle of the battery application in grid energy storage is the safety of the battery. When the battery or battery pack is used under overcharge, short circuit, and other insecure conditions, the life of the battery will be reduced, and even unsafe behaviors such as combustion and explosion will occur (Binelo et al., 2019). Accurate SOC estimation can increase the battery’s cruising range and prolong its service life. Therefore, the SOC estimation technique plays an important role in the battery performance and prolongs the service life.

Scholars have conducted a lot of research on SOC estimation algorithms. There are mainly three kinds of SOC estimation algorithms:

1) Direct estimation methods, including the conventional ampere hour method (APM) (Leng et al., 2014) and open circuit voltage (OCV) method (Xing et al., 2014). The direct estimation methods are simple in theory and easy to implement, but the APM relies heavily on accurate initial SOC values. If the current measure has an error, the error of the APM method will gradually increase over time, and this method does not have the ability to correct it. The OCV methods require a long rest time to obtain an accurate OCV. An OCV-SOC curve to online estimate the SOC of a battery in real-time was established by a look-up table (Xiong et al., 2018).

2) Data-driven estimation methods, including the neural network method (He et al., 2014; Hannan et al., 2018), fuzzy logic method (Singh et al., 2006; Zheng et al., 2019), and support vector machine (SVM) (Patil et al., 2015; Sheng and Xiao, 2015). A deep feedforward neural network (DNN) for SOC estimation was proposed (Chemali et al., 2018). A novel joint support vector machine known as the cubature Kalman filter (SVM-CKF) method is proposed (Song et al., 2021). The SVM is used to train the output data of the CKF algorithm to obtain the model. At the same time, the output data of the model are used to compensate the original SOC for accurate SOC estimation. These methods utilize a large amount of experimental data to find the hidden nonlinear relationship between external characteristic parameters and SOC changes.

3) Model-based estimation methods. This kind of estimation methods are based on battery characteristic models and equivalent circuit models. After the battery model is established, model-based SOC estimation methods can be divided into the adaptive filter-based method and observer method. The adaptive filter-based methods include the extended Kalman filter (EKF) method (Yan et al., 2017; Guo et al., 2018) and the unscented Kalman filter (UKF) method (Qin et al., 2019; Yu et al., 2019). Observer methods have the sliding mode observer method (Sandoval-Chileno et al., 2020; Sakile and Sinha, 2022) and the Luenberger observer method (Ceraolo et al., 2020). An enhanced closed loop estimator is proposed based on EKF, considering the complete model of OCV with hysteresis (Perez et al., 2015). Xu et al. (2014) described the influence of different frequencies on electrochemical impedance spectroscopy (EIS) and estimated the SOC using the fractional Kalman filter (FKF) based on the electrochemical model. Combining the UKF algorithm with the particle filter (PF) algorithm, a comprehensive estimation method of UKF-PF was proposed to estimate the SOC of the battery (Nguyen et al., 2020). Compared with the single UKF algorithm, the experiment showed that the estimation accuracy and reliability were all improved.

In the model-based estimation methods, the accuracy of battery model parameters determines the estimation performance, so the parameter identification of batteries has been paid more and more attention. There are two kinds of methods for battery model parameter identification: offline identification (Lin et al., 2020) and online identification (Xu et al., 2014; Wei et al., 2017). A common feature of the aforementioned SOC estimation methods is that the model parameters are identified with offline data. In practical applications, the battery model parameters will change, which means that these parameters need to be updated in real-time to ensure the accuracy of the battery model. Therefore, online identification methods are proposed based on the collection of battery working real-time data. To capture real-time parameter changes, a recursive least square (RLS) method was proposed with multiple adaptive forgetting factors (Duong et al., 2015). The study improved the accuracy of estimation of SOC through the online update of parameters. A forgetting factor recursive least square (FFRLS) algorithm is used to identify and update the battery model parameters online to address the parameter mismatch issue caused by battery ageing and temperature fluctuation (Xin et al., 2021). An online parameter identification method using DEKF to estimate the battery SOC and capacity concurrently was proposed with a one-time scale (Plett, 2004a; Plett, 2004b; Plett, 2004c; Plett, 2006). However, the battery model parameters change slowly while the SOC changes quickly. Due to data saturation and computational complexity, using a uniform time scale is easy to cause large errors. Therefore, a one-time scale is not the best option to identify the parameters and estimate SOC. To address these issues, an online co-estimation method of battery model parameters and SOC is proposed based on the dual Kalman filter algorithm with a multi-time scale (Rui et al., 2014). This EKF algorithm only uses the error data at the current time in each SOC estimation process. If the process has an error, it is easy to cause poor estimation accuracy.

This article proposed a multi-scale multi-innovation unscented Kalman filter and an extended Kalman filter (MIUKF-EKF) to perform online measurement of battery parameters and SOC estimation. The EKF is used to identify battery parameters with a macro time scale, and then, the MIUKF is used to estimate the SOC with a micro time scale. Afterward, the SOC and the identified parameters are used to update the system state. The effectiveness of the proposed algorithm has been verified through experiments under the dynamic test. The results showed that the proposed MIUKF-EKF algorithm has higher accuracy than the DEKF algorithm in SOC estimation.

2 Battery System Description

2.1 Battery Model

The type of battery model and the accuracy of parameter identification of the battery model can affect the performance of battery SOC estimation. There are various battery equivalent circuit models (ECMs). The widely employed ECMs include the Rint model, the Thevenin model, the partnership for a new generation of vehicle (PNGV) model, and the general nonlinear (GNL) model. In this study, we used the second-order Thevenin model to describe the battery dynamics relationships, as shown in Figure 1.

FIGURE 1

FIGURE 1. Second-order RC battery model.

The model parameters in Figure 1 are described as follows. In the circuit, $U_{OC}$ represents the OCV, and there is a nonlinear relationship with SOC. $U_t$ represents the terminal voltage. $I$ represents the load current, and positive current means discharge state. $R_0$ is the ohmic internal resistance. $R_1$ and $C_1$ are the electrochemical polarization resistance and capacitance. $R_2$ and $C_2$ are the concentration differences of polarization resistance and capacitance. $U_1$ and $U_2$ are the electrochemical polarization voltage and the concentration difference polarization voltage. The RC network is used to simulate the dynamic characteristics of the generation and elimination in the polarization phenomenon. This study replaces the battery OCV with $f\left(SOC\right)$. The mathematical expression of the established model is as follows:

$\{\begin{array}{c}{\dot{U}}_1=\frac{I}{C_1}-\frac{U_1}{R_1{C}_1},\\ {\dot{U}}_2=\frac{I}{C_2}-\frac{U_2}{R_2{C}_2},\\ U_t=U_{\text{oc}}-U_1-U_2-I{R}_0=f\left(SOC\right)-U_1-U_2-I{R}_0.\end{array}(1)$

SOC is defined as the ratio of the remaining capacity to the rated capacity, which can be expressed as follows:

$\text{SOC}={\text{SOC}}_0-\frac{1}{Q_N}{\displaystyle \int \eta Idt},(2)$

where $SO{C}_0$ indicates the initial SOC value, $Q_N$ is the rated capacity, and $\eta$ represents the Coulombic efficiency, which is equal to 1 in this article.

According to the second-order Thevenin model, the state space equation of the system can be obtained by taking the SOC and the two capacitor voltages as the state variables. The state equation is obtained as follows:

$\{\begin{array}{c}\begin{array}{c}{\dot{U}}_1=\frac{I}{C_1}-\frac{U_1}{R_1{C}_1},\\ {\dot{U}}_2=\frac{I}{C_2}-\frac{U_2}{R_2{C}_2},\end{array}\\ \mathrm{SOC}=\mathrm{S}\mathrm{O}{\text{C}}_0-\frac{1}{Q_N}{\displaystyle \int \eta I_{t}dt.}\end{array}(3)$

Taking load current as the input and terminal voltage as observation variable, the observation equation is as follows:

$U_t=f\left(SOC\right)-U_1-U_2-I{R}_0.(4)$

2.2 Multi-Time Scale Discretizing Model

To facilitate the algorithm design based on the battery model, it is necessary to discrete the battery model for establishing the transfer relationship between each state at this time and the next time. Since the battery model parameters change slowly while SOC changes rapidly, we adopt the multi-time scale method to describe SOC changes with the micro-time scale and parameter changes with the macro time scale. The discrete nonlinear system can be expressed as follows:

$\begin{array}{c}{\mathbf{X}}_{k,l+1}=\mathbf{F}\left({\mathbf{X}}_{k,l},{\theta }_k,{\mathbf{u}}_{k,l}\right)+w_{k,l},{\theta }_{k+1}={\theta }_k+b_k,\\ {\mathbf{Y}}_{k,l}=\mathbf{G}\left({\mathbf{X}}_{k,l},{\theta }_k,{\mathbf{u}}_{k,l}\right)+v_{k,l}\end{array}(5)$

where ${\mathbf{X}}_{k,l+1}$ represents the system state vector at the time $t_{k,l}$, and $t_{k,l}=t_{k,0}+l\times T$, $t_{k,0}=t_{k-1,L}(l=\mathrm{1,2,3,4},\mathrm{...},L)$; $k$ and $l$ represent the time index for the micro time scale and macro time scale; $T$ is the sampling time between the two adjacent measurement points; $L$ is the time scale separation level. $k$ and $l$ represent the time index for the micro-time scale and macro-time scale; ${\mathbf{u}}_{k,l}$ is the system input vector at time $t_{k,l}$; ${\mathbf{Y}}_{k,l}$ represents the system measurement vector at time $t_{k,l}$; $w_{k,l}$ and $v_{k,l}$ represent the process noise vector for state and the measurement noise vector, and their covariance vectors are $Q_{k,l}$ and $R_{k,l}$; ${\theta }_k$ is the parameter vector; $b_k$ is the process noise vector for the model parameter, and the covariance vector is $Q_k^{\theta }$.

The model parameters are slowly time-varying. We assume that the battery is a time-invariant system, and the load current is constant at each sampling interval. Then, we get the analytic solution:

$\{\begin{array}{c}{U}_1\left(\left(k+1\right)T\right)=\exp \left(-\frac{T}{R_1{C}_1}\right)U_1\left(kT\right)+{\displaystyle \underset{0}{\overset{T}{\int }}\exp \left(-\frac{t}{R_1{C}_1}\right)dt\cdot \frac{I\left(kT\right)}{C_1},}\\ U_2\left(\left(k+1\right)T\right)=\exp \left(-\frac{T}{R_2{C}_2}\right)U_2\left(kT\right)+{\displaystyle \underset{0}{\overset{T}{\int }}\exp \left(-\frac{t}{R_2{C}_2}\right)dt\cdot \frac{I\left(kT\right)}{C_2}.}\end{array}(6)$

Eq. 2 can be discretized as follows:

${\text{SOC}}_{k,l}={\text{SOC}}_{k,l-1}-\frac{\eta T}{Q_N}{I}_{k,l-1}.(7)$

We can get the electrochemical polarization voltage $U_1$, the concentration difference polarization voltage $U_2 and$ SOC with the system in Eq. 8 with the multi-time scale.

$\left[\begin{array}{c}{U}_{k,l}^1\\ U_{k,l}^2\\ SO{C}_{k,l}\end{array}\right]=\left[\begin{array}{ccc}\text{exp}\left(-\frac{T}{C_1{R}_1}\right)& 0& 0\\ 0& \text{exp}\left(-\frac{T}{C_2{R}_2}\right)& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{U}_{k,l-1}^1\\ U_{k,l-1}^2\end{array}\\ SO{C}_{k,l-1}\end{array}\right]+\left[\begin{array}{c}\left(1-\text{exp}\left(-\frac{T}{C_1{R}_1}\right)\right)R_1\\ \left(1-\text{exp}\left(-\frac{T}{C_2{R}_2}\right)\right)R_2\\ -\frac{\eta T}{Q_N}\end{array}\right]I_{k,l-1}.(8)$

The discretization state transition and measurement with the multi-time scale can be obtained.

${\mathbf{X}}_{k,l+1}=\mathbf{F}\left({\mathbf{X}}_{k,l},\theta ,{\mathbf{u}}_{k,l_k}\right)=\left[\begin{array}{ccc}\text{exp}\left(-\frac{T}{C_1{R}_1}\right)& 0& 0\\ 0& \text{exp}\left(-\frac{T}{C_2{R}_2}\right)& 0\\ 0& 0& 1\end{array}\right]{\mathbf{X}}_{k,l}+\left[\begin{array}{c}\left(1-\text{exp}\left(-\frac{T}{C_1{R}_1}\right)\right)R_1\\ \left(1-\text{exp}\left(-\frac{T}{C_2{R}_2}\right)\right)R_2\\ -\frac{\eta T}{Q_N}\end{array}\right]{\mathbf{u}}_{k,l},(9)$

${\mathbf{Y}}_{k,l}=\mathbf{G}\left({\mathbf{X}}_{k,l},{\theta }_k,{\mathbf{u}}_{k,l}\right)=f\left(SO{C}_{k,l}\right)-U_{k,l}^1-U_{k,l}^2-R_0{\mathbf{u}}_{k,l},(10)$

where ${\mathbf{X}}_{\mathit{k},l}={\left[\begin{array}{ccc}{\mathit{U}}_{\mathit{k},l}^1& {\mathit{U}}_{\mathit{k},l}^2& \mathit{SO}{\mathit{C}}_{\mathit{k},l}\end{array}\right]}^{\mathit{T}}$, ${\mathbf{u}}_{\mathit{k},\mathit{l}}={\mathit{I}}_{\mathit{k},\mathit{l}}$, and ${\mathbf{Y}}_{\mathit{k},l}={\mathit{U}}_{\mathit{k},l}^t$, ${\mathit{U}}_{k,l}^t$ represent the system state vector at the time ${\mathit{t}}_{k,l}$.

3 Battery Model Parameters and SOC Estimation Algorithm

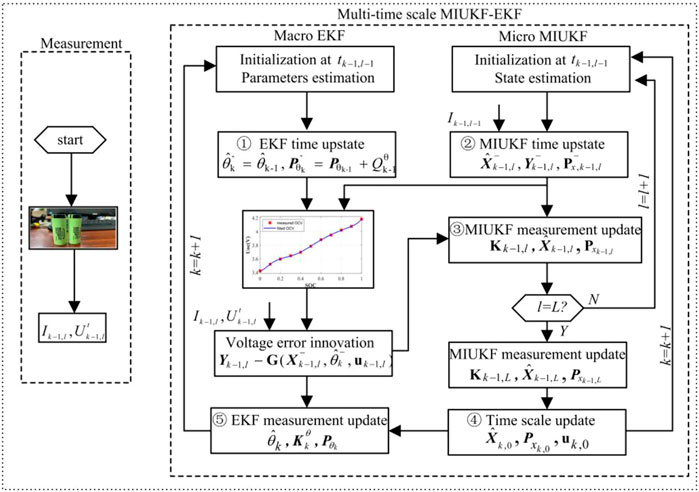
In practical applications, battery model parameters are not constant values. If SOC is estimated by constant battery parameters, the accuracy of SOC will be affected. The joint estimation of battery state and parameters can effectively solve the problem of time-varying battery model parameters. Considering that the battery parameters changes are slower than the system state, it is not an optimal method to use the same calculated time scale for battery parameter and state estimation. Therefore, the multi-time scale method, which uses the macro-scale to calculate the battery parameters and micro-scale to calculate the battery state, will lower the computation time. The multi-time scale SOC estimation method adopts the multi-innovation unscented Kalman filter (MIUKF)–extended Kalman filter (EKF) structure, and the battery state estimator and parameter estimator are designed, respectively. The flowchart of the MIUKF-EKF algorithm is shown in Figure 2.

FIGURE 2

FIGURE 2. Flowchart of the MIUKF-EKF algorithm.

The MIUKF-EKF algorithm uses two filters that run simultaneously. The MIUKF estimates battery SOC with a micro-time scale, and the EKF estimates battery parameters with a macro-time scale. At each macro calculation time step $k$, the EKF executes a time update step, a state prediction step, and a measurement upstate step. At each micro calculation time step $l$, the MIUKF executes the time update state step and the measurement update step. Comparing the micro time scale $l$ with the time scale separation level $L$, when $l=L$, the EKF enters the next cycle in the time step $k+1$. $j$ is the length of the multi-innovation. The equations for the state and parameter estimation are shown in Table 1.Here, ${\widehat{\mathit{\theta }}}_0$, $P_{{\mathit{\theta }}_0}$, $x_{\mathrm{0,0}}$, and $P_{x_{\mathrm{0,0}}}$ are the initialization values of the algorithm. ${\widehat{\mathit{x}}}_{\mathrm{0,0}},{\widehat{\mathit{\theta }}}_0$ are the initial values of the battery state and parameters. ${\mathit{P}}_{x_{\mathrm{0,0}}}$and ${\mathit{P}}_{{\mathit{\theta }}_0}$ represent the initial system state and parameter covariance vectors for the state filter and the parameter filter, respectively. After the aforementioned five steps, the estimations of the battery parameter and SOC are completed. The estimations will then be the initial estimator state of the proposed algorithm for the next estimation.

TABLE 1

TABLE 1. Algorithm of the multi scale MIUKF-EKF.

In the time update equations for the MIUKF, ${\widehat{\mathit{X}}}_{\mathit{k}-1,l}^{\mathit{i}},{\mathit{Y}}_{\mathit{k}-1,\mathit{l}}^{\mathit{i}}$ are the sigma point set constructed by the unscented transformation (UT) method. A finite number of Sigma points is obtained by the method of the symmetric sampling strategy so that the probability distribution characteristics of these sampling points are approximate to the probability density distribution of known variables. When the state variables are three-dimensional columns, they can construct seven Sigma points totally. $W_i$ is the weighting coefficient of the sigma point set. Sigma points and weighting coefficients can be obtained from the following equations:

$\{\begin{array}{c}{\widehat{\mathit{X}}}_{k-1,l}^0={\widehat{\mathit{X}}}_{k-1,l},\\ {\widehat{\mathit{X}}}_{k-1,l}^i={\widehat{\mathit{X}}}_{k-1,l}+{\left(\sqrt{(n+\kappa ){\mathbf{P}}_{x,k-1,l}^{-}}\right)}_i,i=1,\mathrm{...},n,\\ {\widehat{\mathit{X}}}_{k-1,l}^i={\widehat{\mathit{X}}}_{k-1,l}-{\left(\sqrt{(n+\kappa ){\mathbf{P}}_{x,k-1,l}^{-}}\right)}_{i-n},i=n+1,\mathrm{...},2n,\end{array}(11)$

$\{\begin{array}{c}{W}_0^{\left(m\right)}=\frac{\kappa }{n+\kappa },\\ W_0^{\left(c\right)}=\frac{\kappa }{n+\kappa }+\left(1-{\alpha }^2+\beta \right),\\ W_i^{\left(m\right)}=W_i^{\left(c\right)}=\frac{\kappa }{2\left(n+\kappa \right)},i=\mathrm{1,2},\mathrm{...},2n,\end{array}(12)$

where $n$ is the dimension of the state variable, $\kappa$ is the scale parameter, which can adjust the distance between Sigma point and the mean value, $\alpha$ is the state control of sampling point distribution and usually set to $1e^{-4}\le \alpha \le 1$ , and $\beta$ is the state distributed parameter. $\beta =2$ is the optimal value in Gaussian distribution.

MIUKF uses multi-innovation to modify the state variables and improves the estimation accuracy of UKF by reusing the old information. In the measurement update equations for the MIUKF, ${\mathit{e}}_k$ is the error innovation at time $k,$ $\text{ where }{\mathit{e}}_{\mathit{k}}={\mathit{Y}}_{\mathit{k}}-\mathit{G}\left({\mathit{X}}_{\mathit{k}},{\mathit{\theta }}_{\mathit{k}},{\mathbf{u}}_{\mathit{k}}\right)$. The UKF algorithm only uses the error data at the current time in each SOC estimation process. If the error of the observation value is large or the values of the process covariance and the observation covariance are inconsistent with the noise model of the system, it is easy to cause the slow convergence speed of the algorithm and poor estimation accuracy. In order to make full use of the information of historical data, the single innovation in the current moment is expanded to a multi-innovation vector containing the current and previous instantaneous innovations.

In the measurement update equations for the EKF, ${\mathbf{C}}_k^{\mathbf{\theta }}$ is not only the function of the system state $\mathit{X}$ but also the function of the system parameter $\theta$. So it needs to use the total derivative for calculation. The following equation can be obtained as follows:

${\mathbf{C}}_k^{\theta }={\frac{d\mathbf{G}\left({\widehat{\mathit{X}}}_{k,0},\text{θ},{\mathbf{u}}_k\right)}{d\text{θ}}|}_{\theta ={\widehat{\theta }}_k^{-}}=\frac{\partial \mathbf{G}\left({\widehat{\mathit{X}}}_{k,0},{\widehat{\mathit{\theta }}}_k^{-},{\mathbf{u}}_k\right)}{\partial {\widehat{\theta }}_k^{-}}+\frac{\partial \mathbf{G}\left({\widehat{\mathit{X}}}_{k,0},{\widehat{\theta }}_k^{-},{\mathbf{u}}_k\right)}{\partial {\widehat{\mathit{X}}}_{k,0}}\times \frac{d{\widehat{\mathit{X}}}_{k,0}}{d{\widehat{\mathit{\theta }}}_k^{-}},(13)$

$\frac{d{\widehat{\mathit{X}}}_{k,0}}{d{\widehat{\mathit{\theta }}}_k^{-}}=\frac{d\mathbf{F}\left({\widehat{\mathit{X}}}_{k-1,L-1},{\widehat{\theta }}_k^{-},{\mathbf{u}}_{k-1,L-1}\right)}{d{\widehat{\mathit{\theta }}}_k^{-}}=\left(\frac{\partial \mathbf{F}\left({\widehat{\mathit{X}}}_{k-1,L-1},{\widehat{\mathit{\theta }}}_k^{-},{\mathbf{u}}_{k-1,L-1}\right)}{\partial {\widehat{\mathit{\theta }}}_k^{-}}+\frac{\partial \mathbf{F}\left({\widehat{\mathit{X}}}_{k-1,L-1},{\widehat{\mathit{\theta }}}_k^{-},{\mathbf{u}}_{k-1,L-1}\right)}{\partial {\widehat{\mathit{X}}}_{k-1,L-1}}\frac{d{\widehat{\mathit{X}}}_{k-1,L-1}}{d{\widehat{\mathit{\theta }}}_k^{-}}\right),(14)$

$\frac{\mathit{d}{\widehat{\mathit{X}}}_{k-1,L-1}}{d{\widehat{\mathit{\theta }}}_{\mathit{k}}^{-}}=\frac{d}{d{\widehat{\mathit{\theta }}}_{\mathit{k}}^{-}}\left({\widehat{\mathit{X}}}_{k-1,L-1}^{-}+{\mathbf{K}}_{k-1,L-1}\left({\mathit{Y}}_{k-1,L-1}\right)\mathrm{-}\mathbf{G}\left({\widehat{\mathit{X}}}_{\mathit{k}\mathrm{-}1,\mathit{L}\mathrm{-}1}^{\mathrm{-}},{\widehat{\mathit{\theta }}}_{\mathit{k}}^{\mathrm{-}},{\mathbf{u}}_{\mathit{k}-1,\mathit{L}-1}\right)\right).(15)$

The implementation structure of the multi-scale MIUKF-EKF algorithm is shown in Figure 3.

FIGURE 3

FIGURE 3. Implementation structure of the multi-time scale MIUKF-EKF algorithm.

4 Simulation and Experimental Results

The battery test platform uses a testing system (NEWARE CT-4008T) to charge and discharge the battery. The testing system can support eight channels for experiment at the same time, and the measurement accuracy of the current and voltage can be up to ±0.05% of full scale. In the experiment, the battery used for this test is a lithium battery with the specifications listed in Table 2. In this article, all the experiments are conducted at an ambient temperature of 25°C, and the date is recorded at an interval of 1 s.

TABLE 2

TABLE 2. Specification of the tested lithium battery.

4.1 OCV-SOC Relationship

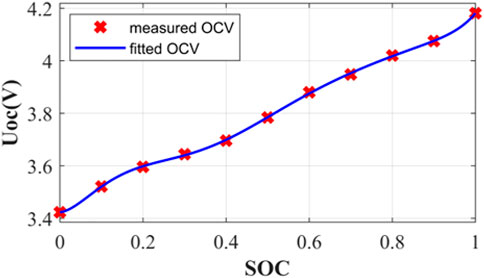
The OCV of the lithium battery indicates the electrochemical reaction inside the battery without load, and the voltage of the battery should reach an equilibrium state. It is assumed that the open circuit voltage is numerically equal to the terminal voltage of the battery after the battery to be open circuit for a long time. Because the OCV of the battery cannot be measured directly, it is necessary to determine the terminal voltage of the battery under a specific SOC by the open circuit voltage of the battery. The functional relationship between OCV and SOC is nonlinear. The battery is fully charged under nominal conditions to preset the SOC to 100%. After 4 h depolarization, the OCV corresponding to 100% SOC is measured. Then, the cell is discharged for an SOC decrement of 10% with 1.5 A current. After 4 h, the OCV is measured. This discharge cycle is repeated 11 times, and the terminal voltage at the end of each discharge cycle is recorded. The relationship between OCV and SOC can be obtained, and the identified results are shown in Figure 4.

FIGURE 4

FIGURE 4. Relationship curve of OCV versus SOC.

MATLAB tool is used for 8-order fitting of measurement data. The expression of the OCV-SOC relationship curve can be obtained by polynomial fitting:

$f\left(SOC\right)=aSO{C}^8+bSO{C}^7+cSO{C}^6+dSO{C}^5+eSO{C}^4+fSO{C}^3+gSO{C}^2+hSOC+i.$

The polynomial coefficient results for a–i are shown in Table 3.

TABLE 3

TABLE 3. Polynomial coefficient results.

4.2 Battery Test

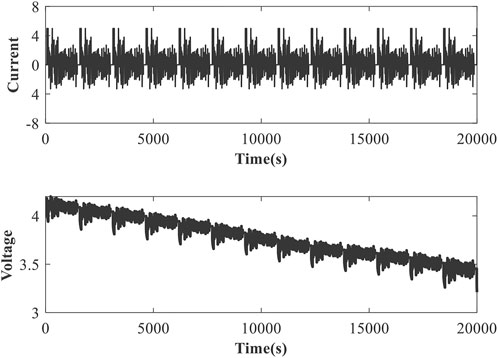
The battery test can charge or discharge the battery according to the set working conditions. In order to verify the effectiveness of the proposed algorithm in a complex dynamic situation, the dynamic operating condition test is used. For the dynamic operating condition test, the total time is 20,000 s. The load current and measurement terminal voltage are shown in Figure 5.

FIGURE 5

FIGURE 5. Current and measurement terminal voltage.

4.3 Battery Model Parameter Identification

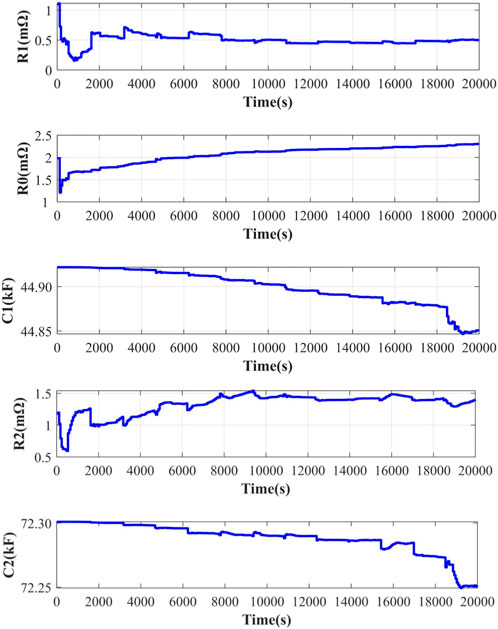
The parameters of the second-order Thevenin model need to be identified. The estimated values of the battery model parameters by the MIUKF-EKF algorithm are presented in Figure 6.

FIGURE 6

FIGURE 6. Results of parameter identification using MIUKF-EKF.

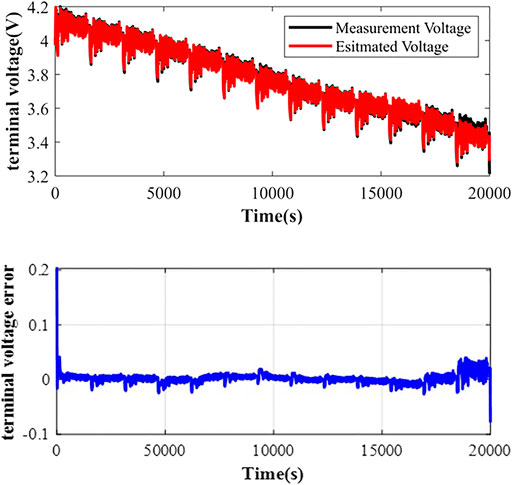
Furthermore, the accuracy of MIUKF-EKF for online identification of battery parameters is verified by comparing the measurement terminal voltage with estimated terminal voltage. The results are shown in Figure 7. It can be obtained that the maximum absolute error is 0.02 V after removing the first large error caused by the incorrect initial SOC value. The mean absolute error was 0.0050 V, and the relative mean absolute error was 0.05%. It is clearly seen that the estimated terminal voltage agrees well with the measured voltage. This illustrates the effectiveness of the battery parameter identification method by the proposed MIUKF-EKF.

FIGURE 7

FIGURE 7. Experimental terminal voltage results.

4.4 SOC Estimation Results and Analysis

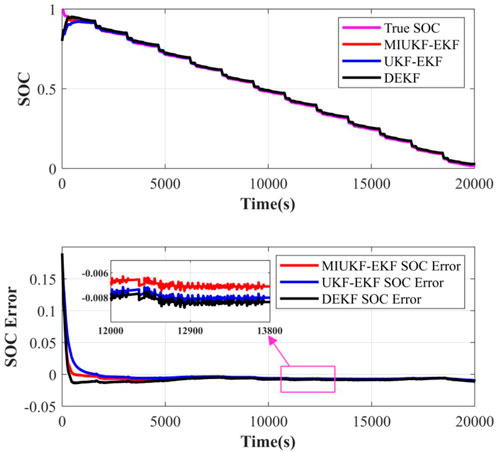
With the accurate model parameters, the SOC estimation results based on the MIUKF-EKF algorithm are compared with the DEKF algorithm and UKF-EKF algorithm under the dynamic operating condition test. In this article, the true SOC is obtained by the APM method for comparison purposes. The SOC estimation results using the MIUKF-EKF, UKF-EKF, and DEKF algorithms are shown in Figure 8.

FIGURE 8

FIGURE 8. SOC estimates and corresponding errors.

It can be seen that MIUKF-EKF has a more accurate SOC estimation than UKF-EKF and DEKF. The SOC estimation error of MIUKF-EKF is bounded within -0.8% for most of the time, but DEKF goes outside of this interval. In addition, the three algorithms are also compared in computational efficiency. To minimize the influence of randomness, the three methods are carried out five times, and then, an average is taken for comparison. The simulations were run in MATLAB R2020b on a PC with an Intel(R) Core(TM) i5-8250U CPU @ 1.60 GHz processor and 12.0-GB RAM. The average calculation time of MIUKF-EKF, UKF-EKF, and DEKF algorithms are 0.472, 0.522, and 0.552 s. It can be observed that the multi-time scale MIUKF-EKF algorithm consumes less computation time. Therefore, we can conclude that the proposed multi-time scale MIUKF-EKF not only improves the accuracy and performance of SOC estimation but also alleviates the computing time.

5 Conclusion

As the lithium-ion battery has slow-varying parameters and the SOC is varying fast, a multi-time scale MIUKF-EKF algorithm to estimate the SOC of the lithium battery is proposed. The multi-time scale MIUKF-EKF algorithm estimates the SOC of the lithium battery on the micro-scale and estimates battery parameters on the macro-scale. The effectiveness and superiority of the proposed algorithm have been verified by comparing with the UKF-EKF and DEKF algorithms through experiments under the dynamic operating condition test. The results showed that the proposed MIUKF-EKF algorithm outperforms other methods in terms of SOC estimation accuracy and improves the computational efficiency.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

SJ and YS performed the algorithm, experiments, and result analysis. ZC contributed to the conception and design of the work. WL performed algorithm programming. All authors read and contributed to manuscript writing and revision.

Conflict of Interest

SJ and YS were employed by the company PowerChina HuaDong Engineering Corporation Limited.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Binelo, M. D. F. B., Sausen, A. T. Z. R., Sausen, P. S., and Binelo, M. O. (2019). Mathematical Modeling and Parameter Estimation of Battery Lifetime Using a Combined Electrical Model and a Genetic Algorithm. Tend. Mat. Apl. Comput. 20 (1), 149. doi:10.5540/tema.2019.020.01.149

CrossRef Full Text | Google Scholar

Ceraolo, M., Lutzemberger, G., Poli, D., and Scarpelli, C. (2020). Luenberger-Based State-Of-Charge Evaluation and Experimental Validation with Lithium Cells. J. Energy Storage 30, 101534. doi:10.1016/j.est.2020.101534

CrossRef Full Text | Google Scholar

Chemali, E., Kollmeyer, P. J., Preindl, M., and Emadi, A. (2018). State-of-Charge Estimation of Li-Ion Batteries Using Deep Neural Networks: A Machine Learning Approach. J. Power Sources 400, 242–255. doi:10.1016/j.jpowsour.2018.06.104

CrossRef Full Text | Google Scholar

Duong, V.-H., Bastawrous, H. A., Lim, K., See, K. W., Zhang, P., and Dou, S. X. (2015). Online State of Charge and Model Parameters Estimation of the LiFePO4 Battery in Electric Vehicles Using Multiple Adaptive Forgetting Factors Recursive Least-Squares. J. Power Sources 296, 215–224. doi:10.1016/j.jpowsour.2015.07.041

CrossRef Full Text | Google Scholar

Guo, L., Li, J., and Fu, Z. (2018). “Lithium-Ion Battery SOC Estimation and Hardware-In-The-Loop Simulation Based on EKF,” in 10th International Conference on Applied Energy (ICAE), Hong Kong, China, Aug. 22-25, 2599–2604.

Google Scholar

Hannan, M. A., Lipu, M. S. H., Hussain, A., Saad, M. H., and Ayob, A. (2018). Neural Network Approach for Estimating State of Charge of Lithium-Ion Battery Using Backtracking Search Algorithm. IEEE Access 6, 10069–10079. doi:10.1109/access.2018.2797976

CrossRef Full Text | Google Scholar

He, W., Williard, N., Chen, C., and Pecht, M. (2014). State of Charge Estimation for Li-Ion Batteries Using Neural Network Modeling and Unscented Kalman Filter-Based Error Cancellation. Int. J. Electr. Power & Energy Syst. 62, 783–791. doi:10.1016/j.ijepes.2014.04.059

CrossRef Full Text | Google Scholar

Leng, F., Tan, C. M., Yazami, R., and Le, M. D. (2014). A Practical Framework of Electrical Based Online State-Of-Charge Estimation of Lithium Ion Batteries. J. Power Sources 255, 423–430. doi:10.1016/j.jpowsour.2014.01.020

CrossRef Full Text | Google Scholar

Lin, H. E., Minkang, H. U., Wei, Y. J., Liu, B. J., and Shi, Q. (2020). State of Charge Estimation by Finite Difference Extended Kalman Filter with HPPC Parameters Identification. Sci. China Technol. Sci. 63 (3), 12. doi:10.1007/s11431-019-1467-9

CrossRef Full Text | Google Scholar

Patil, M. A., Tagade, P., Hariharan, K. S., Kolake, S. M., Song, T., Yeo, T., et al. (2015). A Novel Multistage Support Vector Machine Based Approach for Li Ion Battery Remaining Useful Life Estimation. Appl. Energy 159, 285–297. doi:10.1016/j.apenergy.2015.08.119

CrossRef Full Text | Google Scholar

Plett, G. L. (2004a). Extended Kalman Filtering for Battery Management Systems of LiPB-Based HEV Battery Packs. J. Power Sources 134 (2), 252–261. doi:10.1016/j.jpowsour.2004.02.031

CrossRef Full Text | Google Scholar

Plett, G. L. (2004b). Extended Kalman Filtering for Battery Management Systems of LiPB-Based HEV Battery Packs. J. Power Sources 134 (2), 262–276. doi:10.1016/j.jpowsour.2004.02.032

CrossRef Full Text | Google Scholar

Plett, G. L. (2004c). Extended Kalman Filtering for Battery Management Systems of LiPB-Based HEV Battery Packs. J. Power Sources 134 (2), 277–292. doi:10.1016/j.jpowsour.2004.02.033

CrossRef Full Text | Google Scholar

Plett, G. L. (2006). Sigma-Point Kalman Filtering for Battery Management Systems of LiPB-Based HEV Battery Packs. J. Power Sources 161 (2), 1356–1368. doi:10.1016/j.jpowsour.2006.06.003

CrossRef Full Text | Google Scholar

Qin, X., Gao, M., He, Z., and Liu, Y.Ieee (2019). “State of Charge Estimation for Lithium-Ion Batteries Based on NARX Neural Network and UKF,” in 17th IEEE International Conference on Industrial Informatics, Helsinki, Finland, 22-25 July 2019 (INDIN), 1706–1711.

CrossRef Full Text | Google Scholar

Rui, Xiong, Fengchun, Sun, Hongwen, He, and Zheng, Chen (2014). A Data-Driven Multi-Scale Extended Kalman Filtering Based Parameter and State Estimation Approach of Lithium-Ion Polymer Battery in Electric Vehicles. Appl. energy 113, 463–476. doi:10.1016/j.apenergy.2013.07.061

CrossRef Full Text | Google Scholar

Sakile, R., and Sinha, U. K. (2022). Lithium‐Ion Battery State of Charge Estimation Using a New Extended Nonlinear State Observer. Advcd Theory Sims 5 (3), 2100552. doi:10.1002/adts.202100552

CrossRef Full Text | Google Scholar

Sandoval-Chileño, M. A., Castañeda, L. A., Luviano-Juárez, A., Gutiérrez-Frías, O., and Vazquez-Arenas, J. (2020). Robust State of Charge Estimation for Li-Ion Batteries Based on Extended State Observers. J. Energy Storage 31, 101718. doi:10.1016/j.est.2020.101718

CrossRef Full Text | Google Scholar

Sheng, H., and Xiao, J. (2015). Electric Vehicle State of Charge Estimation: Nonlinear Correlation and Fuzzy Support Vector Machine. J. Power Sources 281, 131–137. doi:10.1016/j.jpowsour.2015.01.145

CrossRef Full Text | Google Scholar

Singh, P., Vinjamuri, R., Wang, X., and Reisner, D. (2006). Design and Implementation of a Fuzzy Logic-Based State-Of-Charge Meter for Li-Ion Batteries Used in Portable Defibrillators. J. Power Sources 162 (2), 829–836. doi:10.1016/j.jpowsour.2005.04.039

CrossRef Full Text | Google Scholar

Song, Q., Wang, S., Xu, W., Shao, Y., and Fernandez, C. (2021). A Novel Joint Support Vector Machine - Cubature Kalman Filtering Method for Adaptive State of Charge Prediction of Lithium-Ion Batteries. Int. J. Electrochem. Sci. 16 (8), 210823. doi:10.20964/2021.08.26

CrossRef Full Text | Google Scholar

Wei, J., Dong, G., and Chen, Z. (2017). On-Board Adaptive Model for State of Charge Estimation of Lithium-Ion Batteries Based on Kalman Filter with Proportional Integral-Based Error Adjustment. J. Power Sources 365, 308–319. doi:10.1016/j.jpowsour.2017.08.101

CrossRef Full Text | Google Scholar

Xin, L. A., Yh, A., Hg, A., Xh, B., Xf, B., Hd, C., et al. (2021). Remaining Discharge Energy Estimation for Lithium-Ion Batteries Based on Future Load Prediction Considering Temperature and Ageing Effects. Energy 238, 121754. doi:10.1016/j.energy.2021.121754

CrossRef Full Text | Google Scholar

Xing, Y., He, W., Pecht, M., and Tsui, K. L. (2014). State of Charge Estimation of Lithium-Ion Batteries Using the Open-Circuit Voltage at Various Ambient Temperatures. Appl. Energy 113, 106–115. doi:10.1016/j.apenergy.2013.07.008

CrossRef Full Text | Google Scholar

Xiong, R., Cao, J., Yu, Q., He, H., and Sun, F. (2018). Critical Review on the Battery State of Charge Estimation Methods for Electric Vehicles. Ieee Access 6, 1832–1843. doi:10.1109/access.2017.2780258

CrossRef Full Text | Google Scholar

Xu, J., Cao, B., Chen, Z., and Zou, Z. (2014). An Online State of Charge Estimation Method with Reduced Prior Battery Testing Information. Int. J. Electr. Power & Energy Syst. 63, 178–184. doi:10.1016/j.ijepes.2014.06.017

CrossRef Full Text | Google Scholar

Xu, W., Wang, S., Jiang, C., Fernandez, C., Yu, C., Fan, Y., et al. (2021). A Novel Adaptive Dual Extended Kalman Filtering Algorithm for the Li‐ion Battery State of Charge and State of Health Co‐Estimation. Int. J. Energy Res. 45 (10), 14592–14602. doi:10.1002/er.6719

CrossRef Full Text | Google Scholar

Yan, W., Niu, G., Tang, S., and Zhang, B.Ieee (2017). “State-of-Charge Estimation of Lithium-Ion Batteries by Lebesgue Sampling-Based EKF Method,” in 43rd Annual Conference of the IEEE-Industrial-Electronics-Society, Beijing,China, 29 Oct-01 Nov (IECON), 3233–3238.

CrossRef Full Text | Google Scholar

Yu, C.-X., Xie, Y.-M., Sang, Z.-Y., Yang, S.-Y., and Huang, R. (2019). State-Of-Charge Estimation for Lithium-Ion Battery Using Improved DUKF Based on State-Parameter Separation. Energies 12 (21), 4036. doi:10.3390/en12214036

CrossRef Full Text | Google Scholar

Zheng, W., Xia, B., Wang, W., Lai, Y., Wang, M., and Wang, H. (2019). State of Charge Estimation for Power Lithium-Ion Battery Using a Fuzzy Logic Sliding Mode Observer. Energies 12 (13), 2491. doi:10.3390/en12132491

CrossRef Full Text | Google Scholar