- College of Information Science and Engineering, Northeastern University, Shenyang, China
Ensuring the control of power systems is crucial for their safe operation. This paper analyses the robust controllability of complex power systems from the structural sighta structural point of view. Stressing the dominant role of generators in the control of power systems, we propose three kinds of controllable networks by generator nodes. Additionally, the satisfied conditions and the relevant proof of zero forcing set in the controllable networks by generator nodes and extra nodes are given. Besides, tThe satisfied conditions and the relevant proofs of the largest set of removable edges that have no -effect on the strong structural controllability in three kinds of controllable networks by generator nodes are also proposed. Finally, the robustness of strong structural controllability of IEEE 39 bus system and IEEE 14 bus system have been analyzed. The zero-forcing set and the largest set of removable edges of IEEE 39 bus system and IEEE 14 bus system are provided.
1 Introduction
With the development of economy and society, the scale of power systems grows rapidlyZhang et al. (2019), ensuring the safe and stable power transmission has thus become a hot research issue Kiaei et al. (2021). There is a growing demand for power systems with high robustness, that is, they can withstand large disturbances, such as transmission line damage, accidental loss of large generators, or heavy load loss Mahmud et al. (2017). Many researches on the control of power systems at the device level have been proposed, such as braking resistor Rubaai et al. (2005), fast valving of turbines Hassan et al. (1999), utilizing reactor and capacitor units Taylor and Leuven (1996), flexible ac transmission system devices Haque (2004), power system stabilizers Chung et al. (2002), and energy storage systems Kiaei et al. (2021). In addition, as the power system as is a special complex network, complex network theory is also an important tool to study its controllability Chu and lu (2017). The controllability analysis of power systems has the question that capturing the time-dependent interactions between the components, which is difficult. Fortunately, the controllability study is based on the complex network theory regardless of the coupling strength between the components.
In complex networks, structural controllability (weak structural controllability) and strong structural controllability are two basic directions of network controllability analysis. The week structural controllability was first proposed by Lin (1974), that means almost all networks of the identical topology have the same controllability. Nevertheless, the dependencies between system parameters in actual networks leads to networks being uncontrollable, although it is weekly structurally controllable. Thus, the notion of strong structural controllability was proposed by Mayeda and Yamada (1979). The network is strong structurally controllable if alladmissible numerical realizations of its coupling matrix and control input matrix are controllable. Bowden et al. (2012) extended the strong structural controllability to multiple entry systems. Whereafter, the strong structural controllability were further investigated by constrained matchings Chapman and Mesbahi (2013) and cycle families Jarczyk et al. (2011).
Group (2008) was first proposed the concept of zero-forcing set (ZFS) to investigate the minimum rank problem for symmetric patterned matrices, which is connected with a particular coloring of nodes in a graph. Then, zero forcing set was extended to directed graphs by Barioli et al. (2009). Furthermore, Monshizadeh et al. (2014) has shown the correspondence between zero-forcing sets and the strong structural controllability by the view of a network-centric point. Subsequently, ZFS was widely used in the analysis of strong structural controllability of undirected networks Mousavi and Mesbahi (2018), networks with missing connection information, Jia et al. (2021) and other networks.
When complex network theory is applied to a power system, the accuracy of analysis will be affected by oversimplification of the influence of electrical characteristics Hines et al. (2010), but too much consideration of electrical characteristics will greatly increase the computational complexity. Therefore, the reasonable combination of structural characteristics and electrical characteristics is still an unsolved problem. Li et al. (2015) investigated the weak structural controllability of power systems. The minimum input theorem was used to find the drive node set that makes the network weakly structurally controllable in an unweighted directed model. However, the absent of electrical characteristics makes the research results deviate from the actual situation. Yang et al. (2020) established a directed network model that can reflect the intrinsic direction of the power system for weak structural controllability analysis. The edge weighs were considered in the search method of maximum weak controllable scope. Nevertheless, this work didn’t did not consider the different functions of different nodes in control. In particular, the special status of generator nodes is was ignored. In the modern power industry, the control of generators can realize active power control and frequency response, voltage/reactive power control, and ride-through for both voltage and frequency Hatziargyriou et al. (2021). Thus, generator nodes play a dominant role in the control of power systems.
Based on the above research gaps, the main contributions of this paper are as follows:
1. Considering the dominant role of generators in the control of power systems, precisely controllable networks by generator nodes, redundantly controllable networks by generator nodes, and controllable networks by generator nodes, and extra nodes are defined.
2. The satisfied conditions and the relevant proof of zero-forcing set in the controllable networks by generator nodes and extra nodes are given.
3. The satisfied conditions and the relevant proofs of the largest set of removable edges in three kinds of controllable networks by generator nodes are given.
The remains of this paper are organized as follows: Section 2 introduces the network modeling method of power systems. Section 3 analyzses the strong structural controllability of power systems. Section 4 analyzses the robustness of controllable networks by generator nodes. Section 5 concludes the paper with discussions.
2 Network Modelling of Power Systems
In this paper, the power system is abstracted as a digraph. Network modeling is the critical prerequisite of structural controllability analysis. The accuracy of structural controllability analysis is closely related to the described natures of power systems in a network model. We assume that the construction structure of power systems and the configuration of generators and loads are known correctly.
2.1 Basic Model Topology Principles
The dynamic characteristics of power systems are so tanglesome entangled that a generic dynamical equation that describes them all is out of the question. Prosperously, the controllability of nonlinear system and its linearized dynamics is are often structurally similar. The power system is described as a digraph D (V, E) with nodes and edges, V = {v1, … , vN} is the node set, and the E = {(vi, vj), vi, vj ∈ V} is the edge set, N is the scale of networks. According to Ohm’s law, a power system with scale N can be writed written as linear equations, as follows:
where Zij is the impedance of transmission lines. If there is a transmission line from node vi to node vj, then Zij = Zji ≠ 0 or else Zij = Zji = 0. Ui is the voltage of bus, and Ii is the injection current of bus.
The basic topology of the network model is constructed based on the transmission line architecture of power systems. Topology principles in this paper are described as follows.
• The buses of power plants, substations, and loads are abstracted to nodes. The node set is classified into generator node set VG, transmission node set VT, and load node set VL.
• The high voltage transmission lines are abstracted as edges, only the lines whose voltage above 110 KV are considered.
• Parallel transmission lines on the same tower and neglecting shunt capacitor lines are merged to prevent multiple edges in the basic topology model and generate a simple topology model.
• The influences of the relay protection devices and the stability control devices in power systems are not under consideration.
2.2 Definition of Edge Direction
The direction of power flowing was defined as the direction of edges in the network model in some literatures Liu et al. (2018); Dey et al. (2016). However, the direction of power flowing is time-variant, which and only describes the direction of edges in power systems at a certain time. The network model proposed in this paper wants to have an edge direction which can express the intrinsic properties of power systems. Therefore, the author’s previous definition of edge direction in a network model of a power system Yang et al. (2020) is used again in this paper, where the direction of an edge is determined by its electrical betweenness.
In graph theory, the betweenness of edges is an important global geometric quantity that reflects the influence of edges in the whole network Freeman (1978). Betweenness of an edge is defined as the portion of the number of shortest paths between all nodes pairs that pass through the edges divided by the number of shortest paths between all node pairs. However, the power is transmitted in complex power systems in accordance with electrical characteristics. The power from node vi to node vj flows through every edges in complex power systems. Thus, betweenness in graph theory is unfit for evaluating edges in power systems.
Electrical betweenness of edges is an evaluation index Wang et al. (2011) that, which is related to the network structure and the configuration of generators and loads.
If there is a unit current supplied from the generator node vi to the load node vj (Ii = 1, Ij = −1), the voltage of node vk can be writed as
The electrical betweenness of edge (vm, vn) is the sum of the currents flowing through the edge for all node pairs of generator and load that have unit current transmitted in complex power systems. Then, the electrical betweenness of edge (vm, vn) is depicted as follows.
Wi is the capacity of generator node vi, and Wj is the maximal demand of load node vj. Imn(i, j) is the generated current in the edge (vm, vn) when an unit current is supplied from the generator node vi to the load node vj.
Assuming that the admittance of edge (vm, vn) is ymn, Imn(i, j) can be obtained
where ymn is admittance.
The electrical betweenness matrix of edges is isomorphic with the impedance matrix, which is an antisymmetric matrix with Be (m, n) = −Be (m,n)T. The electrical betweenness matrix is rewrited as:
The edge direction in the network model: If Be (m, n) > 0, there is an edge from node vm to node vn in the network model.
3 Strong Structural Controllabity of Power Systems
3.1 Weak Structural Controllability and Strong Structural Controllabity
Consider the linear-time-invariant system:
where
A system is controllable if it can be moves from its initial state x0 to any desired final state within a limited time. Due to many models of physical and technical systems are being structured, dynamics of nonlinear-time-invariant system is often linear-time-invariant.
Then, let
Based on the network model of power systems in section 2, the structure pattern of a power system coupling matrix can be experessed as:
The system
The system
Theorem 1 Trentelman et al. (2012): A class of systems defined by the structure matrices
Graph theory is also the main direction of analyzing strong structural controllability. Concepts mentioned in this paper are introduced in the following passage, strong structurally controllable is reduced to controllable.
Out-neighbor: If (vm, vn) ∈ E, then node vn is the out-neighbor of node vm. In Figure 1A, v4 is the out-neighbor of v2.
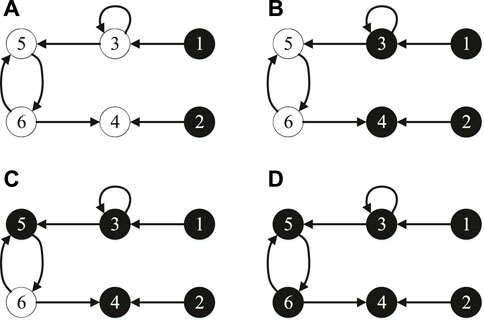
FIGURE 1. A forcing process based on color change rule in a digraph with six nodes and seven edges. (A) A graph with drive node set VD = {v1, v2}; (B) v1 force v3 to be black and v2 force v4 to be black; (C) v3 force v5 to be black; (D) v5 force v6 to be black.
Color change rule: There are white nodes and black nodes in a directed graph D (V, E). If a black node vm ∈ V has only out-neighbor vn ∈ V, it forces vn to be black. In Figures 1A,B, v1 force v3 to be black and v2 force v4 to be black.
Forcing process: The color change process that repeaterepeats the color change rule until no more color changes is called a forcing process. Figures 1A–D is a forcing process. In the first step, v1 forces v3 to be black and v2 forces v4 to be black. In the second step, v3 forces v5 to be black. In the final step, v5 forces v6 to be black.
Drive node set: let VD ⊂ V is the set of initially black nodes in V, then VD is drive node set. In Figure 1A, drive node set is VD = {v1, v2}.
Controllable node set: The set of final black nodes after the forcing process is called the controllable node set VC(VD) of drive node set VD. In Figure 1, controllable node set of VD = {v1, v2} is VC(VD) = {v1, v2, v3, v4, v5, v6}.
Zero forcing set (ZFS): If VC(VD) = V, then VD is a zero-forcing set (ZFS). In Figure 1, drive node set VD = {v1, v2} is a zero-forcing set.
Theorem 2 Monshizadeh et al. (2014): A network system with dynamics 6) is strong structural controllable if and only if VD ⊂ V is a zero-forcing set of the structure described digraph D (V, E) of system 6).
3.2 Drive Node set in Power Systems
3.2.1 Controllable Networks by Generator Nodes
The energy flow along the transmission line of a power system changes in real time. The system coupling matrixs of power systems have innumerable numerical implementations with the same zero-nonzero pattern. Therefore, the power system with the driver nodes’ configuration that realizes the weak structure control of the system is possible uncontrollable at a time. Power system is the most important social infrastructure network. It is very important to keep it under control for the safe and stable operation of power systems. Thus, the configuration of drive nodes with strong structural controllability is more in line with the control requirements of a power system.
Power systems areis a complex network with special physical characteristics. As shown in the previous network modeling, different nodes have different properties. Therefore, the strong structural controllability analysis of power systems should fully consider the differences between nodes.
In the modern power industry, synchronous generators are widely used in wind power generation, hydroelectric power generation, diesel power generation, and nuclear power generation. Synchronous generators play a dominant role in power systems. Synchronous generators convert part of the mechanical energy into sinusoidal AC electrical energy, while the other part is stored as kinetic energy in the huge rotating mass of the rotor. When the power system is disturbed, the rotor absorbs or releases energy to maintain the internal energy balance of the system. With the development of the power system, it has progressively become more dependent on fast response power electronic devices. The converter interfaces generation technologies can provide numerous services, such as active power control and frequency response, voltage/reactive power control, and ride-through for both voltage and frequency. In a nutshell, the generator node must be a drive node in the digraph of power systems. Then, we have VG ⊂ VD in the strong structural control of power systems.
Due to the special status of generator nodes in power system control, there are three different situations of strong structural controllability of a power network, which are defined as follows.
Definition 1 (precisely controllable networks by generator nodes) A structure described digraph of power systems is a precisely controllable network by generator nodes if the following conditions hold:
• The generator node set in the power system happens to be a zero-forcing set (VC(VG) = V).
• All proper subsets of generator nodes are not zero-forcing sets (VC(VD)⫋V for all VD⫋VG).
As despicted in Figure 2A digraph of power system with the generator node set VG = {v4, v5}. Let VD = VG, then Vc(VD) = V. Furthermore, if VD = {v4}, VC(VD) = {v3, v4}⫋V, and if VD = {v5}, VC(VD) = {v2, v5}⫋V. Thus, the power system in Figure 2A is the a precisely controllable networks by generator nodes.
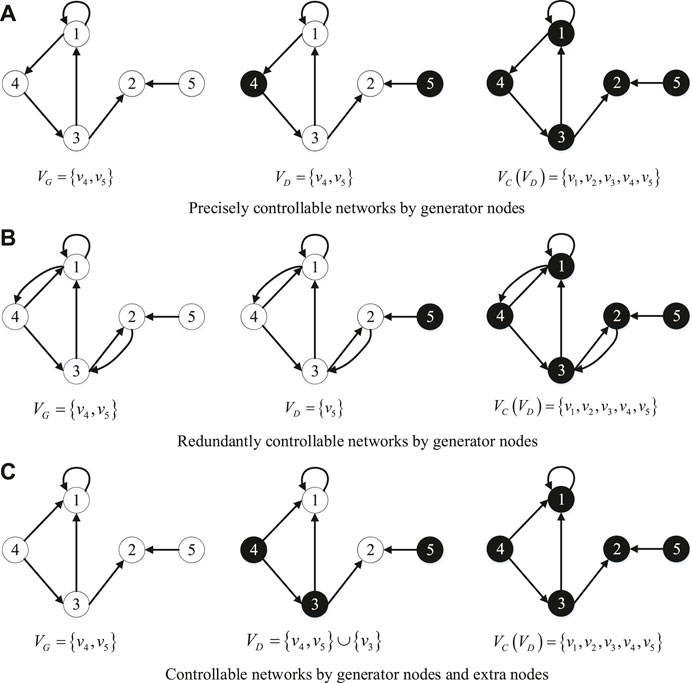
FIGURE 2. Three kind of controllable networks by generator nodes. (A) Precisely controllable networks by generator nodes; (B) Redundantly controllable networks by generator nodes; (C) Controllable networks by generator nodes and extra nodes.
Definition 2 (redundantly controllable networks by generator nodes) A structure described digraph of power systems is a redundantly controllable network by generator nodes if there is at least one zero-forcing set is in the proper subset of the generator node set in the power system (∃ZFS⫋VG).
As despicted in Figures 2A,B digraph of power system with the generator node set VG = {v4, v5}. Let VD = {v5}, then VC(VD) = V. Thus, the power system in Figure 2B is the redundantly controllable networks by generator nodes.
Definition 3 (controllable networks by generator nodes and extra nodes) A structure described digraph of power systems is a controllable networks by generator nodes and extra nodes if the controllable node set of generator node set is the proper subset of node set (VC(VG)⫋V).
The extra nodes belong to the transmission node set VT or the load node set VL. In actual power systems, the substation realizes system control through load station transfer and load cutting strategies. Load nodes achieve system control through demand response.
As despicted in Figures 2A,C digraph of power system with the generator node set VG = {v4, v5}. Let VD = VG, then VC(VD) = {v1, v2, v4, v5}⫋V. Furthermore, when VD = VG ∪ {v4}, VC(VD) = {v1, v2, v3, v4, v5} = V. Thus, the power system in Figure 2C is the controllable networks by generator nodes and extra nodes.
3.2.2 Zero-Forcing Set of Controllable Networks by Generator Nodes and Extra Nodes
In this section, we focus on the zero-forcing set of controllable networks by generator nodes and extra nodes. Because this kind of networks cannot achieve strong structural controllability through generator nodes alone, we will investigate the conditions satisfied to satisfy of extra nodes in their zero-forcing set.
Then, we will introduce some of the concepts used in the follows.
A path is a special kind of graph consists consisting of disjoint edges and nodes.
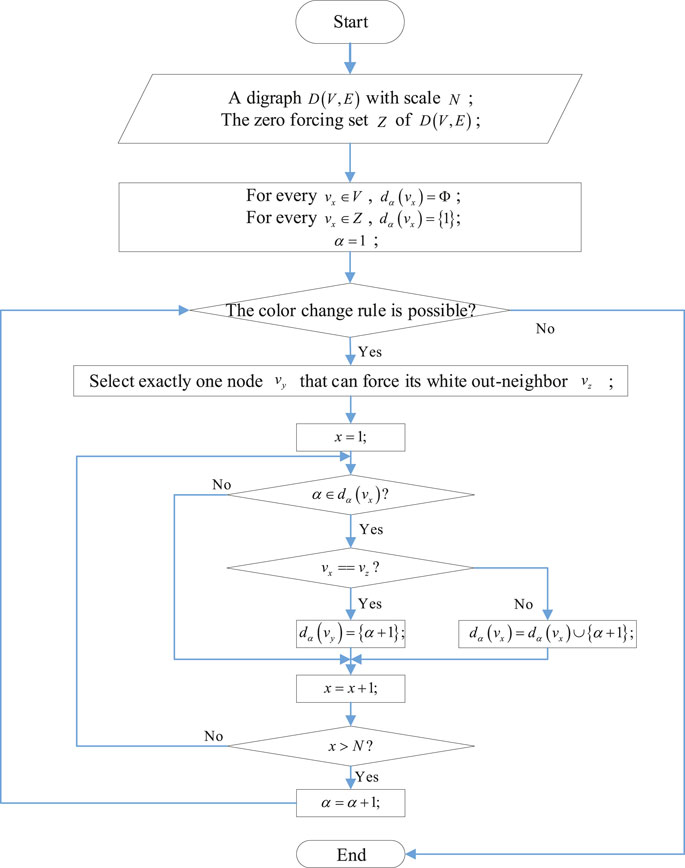
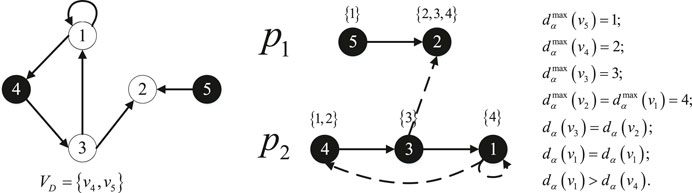
Distribution of integers on a path: let p = (Vp, Ep) is be a directed path with scale Np. Let α ≥ Np is be an integer. Let Dp denotes the distribution of integers from 1 to α among Np nodes of p in a way, and every node is endowed at least one number. Besides, for i = 1, … , α − 1, two integers i and i + 1 are either assigned to one node, or i is given to a node and i + 1 is given to its out-neighbor. Thus, every node v ∈ Vp is given a set of successive integers, denoted by dα(v). For every 1 ≤ β ≤ α, let vα(β, p) is be the node v ∈ Vp and β ∈ dα(v). Let vα(1, p) be the start node of p. Furthermore, let
For two path p1 and p2 with integer distribution
For a distinct directed path set p = {p1, … , pm}, where
An efficient set of distribution
The distribution algorithm that gives every node a successive set of integers of a digraph with a zero-forcing set is depicted in Figure 3. As shown in Figure 4, a digraph D (V, E) is forced by drive nodes VD = {v4, v5}. After the forcing process, the distribution of integers on two paths
Definition 4 (precisely controllable subnetworks by generator nodes Dg (Vg, Eg)) In controllable networks by generator nodes and extra nodes DV, E, let generator nodes be black nodes and other nodes be white. After the forcing process, the final black nodes are denoted in Vg. The edge set Eg is defined, such that Eg = {(vm, vn) (vm, vn) ∈ E and vm, vn ∈ Vg}. Then, the precisely controllable subnetworks by generator nodes is consist of node set Vg and edge set Eg, and VG is a ZFS of Dg.
Theorem 3: The precisely controllable subnetworks by generator nodes Dg (Vg, Eg) is consist of a set of paths
Proof: VG with |VG| = NG is a zero-forcing set of Dg.
As described in the distribution algorithm, the nodes in VG are given {1} in Step 1. Then, exactly one node in Dg is forced to be black in other eachstep. Let vm be the last black node of pi in step j − 1, then j − 1 ∈ dα(vm). If in step j, vm can force vm+1 to be black, then dα(vm+1) = {j}. Otherwise, dα(vm) = dα(vm) ∪ {j}, and vm is still the last black node of pi. Thus, for x = 1, … , α − 1, we have only one node v ∈ Vg such that
Suppose that the edges
If two nodes u and v belong to different path pi and pj, respectively. u is not the end node of pi, because
If two nodes, u and v, belong to a path pi, as mentioned above, v is a white put-neighbor of u in Step
Based on Theorem 3, we can make the inference of the zero-forcing set Z of controllable networks by generator nodes and extra nodes, as shown in Lemma 1.
Lemma 1: The zero-forcing set Z of controllable networks by generator nodes and extra nodes D (V, E) (|V| = N) is consists of two parts, Z = VG ∪ VEN. We have the precisely controllable subnetworks by generator nodes Dg (Vg, Eg). All nodes in set V − Vg can form a set of paths
Remark 1: According to Theorem 3, we can infer that for every digraph with a zero-forcing set, all nodes in the digraph can consist of a forcing path set with the start nodes in the zero-forcing set, and the forcing path set has an efficient distribution. Moreover, except for the forcing path set, any edge (u, v) in the digraph satisfies dα(u) ≥ dα(v). The controllable networks by generator nodes and extra nodes is a digraph with the zero-forcing set VG ∪ VEN. Thus, all nodes in the digraph can consist of a forcing path set with the start nodes in VG ∪ VEN, and all the other edges (u, v) in the network satisfies dα(u) ≥ dα(v).
4 Robustness of Controllable Networks by Generator Nodes
Transmission lines in a power system can be damaged and disconnected from the system due to factors such as natural disasters or a perceived deliberate attack. Damage to a transmission line causes edges to be removed from its network model. The structural change of a network model also leads to the change of strong structural controllability of networks. Therefore, this paper analyzes the robustness of three kinds of controllable networks by generator nodes.
Definition 5 (The largest set of removable edges) The largest set of removable edges Er is the subset of E in the controllable networks by generator nodes D (V, E) with zero-forcing set Z. Remove If any subsets of Er are removed, the strong structural controllability of D (V, E) from Z remains. We define NR = |Er| as the robustness evaluation parameters of strong structural controllability.
Theorem 4: The largest set of removable edges Er of precisely controllable networks D (V, E) by generator nodes is
Proof: According to the color change rule and Theorem 2, the subnetwork
Based on Theorem 4, we can get the largest set of removable edges Er of controllable networks D (V, E) by generator nodes and extra nodes, as shown in Lemma 2.
Lemma 2: The largest set of removable edges Er of controllable networks D (V, E) by generator nodes and extra nodes is
Remark 2: According to Theorem 4, we can infer that for a digraph in which drive node set is a zero-forcing set, the largest set of removable edges contains all edge in the digraph except the edges in the forcing paths that the start nodes belong to its zero-forcing set. The controllable network by generator nodes and extra nodes is a digraph in which the drive node set and the zero-forcing set are both VG ∪ VEN. Thus, the largest set of removable edges of the network contains all edges in the digraph except the edges in the forcing paths that the start nodes belong to VG ∪ VEN.
Theorem 5: There exists a zero-forcing set Z⫋VG of redundantly controllable networks D (V, E) by generator nodes. The largest set of removable edges Er of redundantly controllable networks D (V, E) by generator nodes is
Proof: According to the color change rule and Theorem 2, the subnetwork
5 Instance Analysis
5.1 Instance of Controllable Network by Generator Nodes and Extra Nodes
In this subsection, IEEE 39 bus system is selected to analysis analyze the strong structural controllability and the robustness of strong structural controllability in this paper. There are 39 buses, 10 generator nodes, and 46 edges in the system. The wiring diagram and the network model of IEEE 39 bus system are depicted in Figures 5A,B, respectively, where the red nodes are generator nodes.

FIGURE 5. (A) Wiring diagram of IEEE 39 bus system; (B) Network model of IEEE 39 bus system. The red nodes are generator nodes.
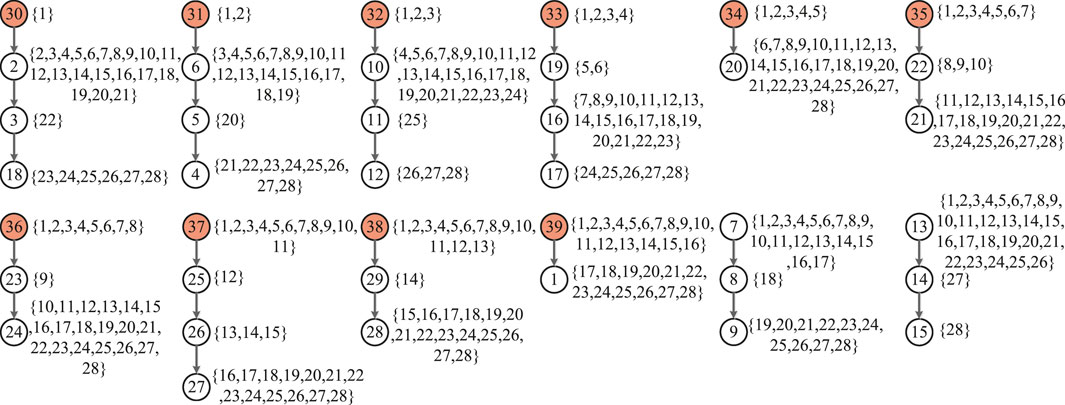
According to the above definition, the IEEE 39 bus system is the a controllable network s by generator nodes and extra nodes. A zero-forcing set of the system is Z = VG ∪ VEN = {v30, v31, v32, v33, v34, v35, v36, v37, v38, v39} ∪ {v7, v13}. The forcing paths are depicted in Figure 6, where solid lines are edges in path sand dotted lines are other edges in the system. The integer’s distribution on these forcing paths are given in Figure 7, which is an efficient set of distribution. α = 1–12 + 39 = 28. For every 1 ≤ j < 28, there are is exactly one node in this path set such that
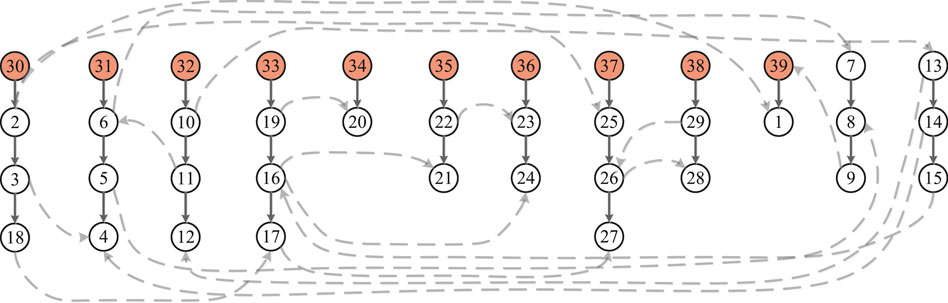
FIGURE 6. The forcing paths in the IEEE 39 bus system. Solid lines are edges in paths and dotted lines are other edges in the system.
5.2 Instance of Redundantly Controllable Networks by Generator Nodes
In this subsection, IEEE 14 bus system is selected to analysis analyze the strong structural controllability and the robustness of strong structural controllability in this paper. There are 14 buses, five generator nodes, and 20 edges in the system. The wiring diagram and the network model of IEEE 14 bus system are depicted in Figures 8A,B, respectively, where the red nodes are generator nodes.
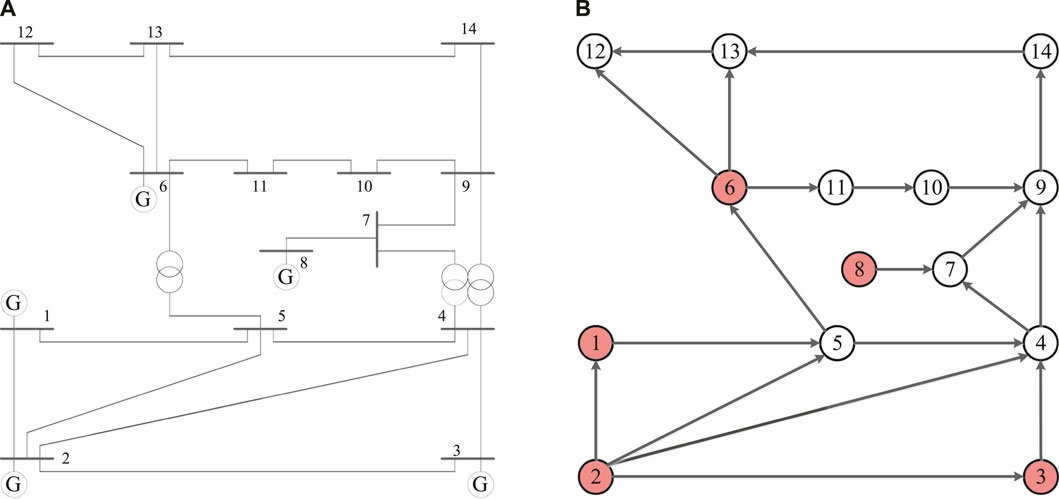
FIGURE 8. (A) Wiring diagram of IEEE 14 bus system; (B) Network model of IEEE 14 bus system. The red nodes are generator nodes.
According to the above definition, the IEEE 14 bus system is the a redundantly controllable networks by generator nodes. A zero-forcing set of the system is Z ⊂ VG = {v1, v2, v6, v8}. The forcing paths are depicted in Figure 9A. The integer’s distribution on the forcing paths of four drive nodes are given in Figure 9B, which is an efficient set of distribution. α1 = 1–4 + 14 = 11. For every 1 ≤ j < 11, there are is exactly one node in this path set such that
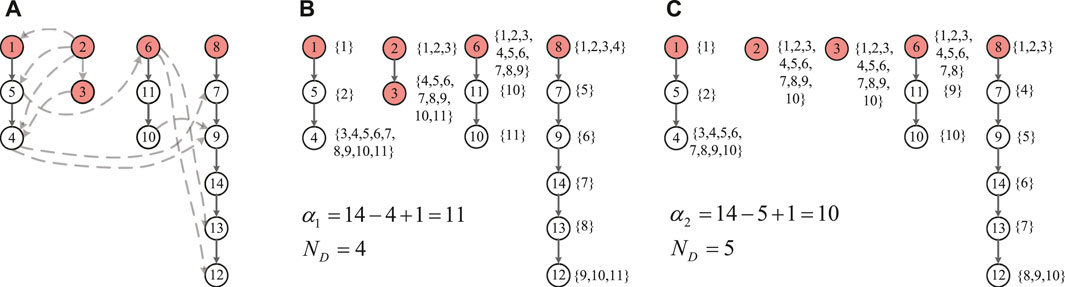
FIGURE 9. (A) The forcing paths of four drive nodes in the IEEE 14 bus system. (B) The integer’s distribution on the forcing paths of four drive nodes in the IEEE 14 bus system. (C)The integer’s distribution on the forcing paths of five drive nodes in the IEEE 14 bus system.
According to the Theorem 5, the largest set of removable edges Er of IEEE 14 bus system is
6 Conclusion
This paper analyses analyzes the robust strong structural controllability of complex power systems. Considering the dominant role of generators in the control of power systems, we define three kinds of controllable networks by generator nodes, precisely controllable networks by generator nodes, redundantly controllable networks by generator nodes, and controllable networks by generator nodes and extra nodes. Additionally, the satisfied conditions of zero-forcing set in the controllable networks by generator nodes and extra nodes are given in Theorem 3 and Lemma 1, and the relevant proof is also given. Besides, the robustness of strong structural controllability in three kinds of controllable networks by generator nodes are analyzed. We give the satisfied conditions and the relevant proofs of the largest set of removable edges in three kinds of controllable networks by generator nodes. Finally, the robust strong structural controllability of the IEEE 39 bus system is investigated. We have found that the IEEE 39 bus system is the a controllable networks by generator nodes and extra nodes, and the scale of the largest set of removable edges is 19.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
YS and DY contributed to the theorem derivation and proof. YS wrote the first draft of the manuscript. XG and JQ contributed to manuscript revision, read, and approved the submitted version.
Funding
This work was supported by the National Natural Science Foundation of China (U1908217), the Liaoning Revitalization Talents Program (XLYC1902055), National Key Research and Development Project (2018YFB1700500), and the Fundamental Research Funds for the Central Universities (N180415004).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Barioli, F., Fallat, S., Hall, H., Hershkowitz, D., Hogben, L., Van der Holst, H., et al. (2009). On the Minimum Rank of Not Necessarily Symmetric Matrices: a Preliminary Study. Electronic. J. Linear. Algebra. 18, 126–145. doi:10.13001/1081-3810.1300
Bowden, C., Holderbaum, W., and Becerra, V. M. (2012). Strong Structural Controllability and the Multilink Inverted Pendulum. IEEE Trans. Autom. Contr. 57, 2891–2896. doi:10.1109/TAC.2012.2191180
Chapman, A., and Mesbahi, M. (2013). On Strong Structural Controllability of Networked Systems: a Constrained Matching Approach.” in Proc. American Control Conf (IEEE), 6126. doi:10.1109/acc.2013.6580798
Ching-Tai Lin, C. T. (1974). Structural Controllability. IEEE Trans. Autom. Contr. 19, 201–208. doi:10.1109/tac.1974.1100557
Chu, C.-C., and Iu, H. H.-C. (2017). Complex Networks Theory for Modern Smart Grid Applications: A Survey. IEEE J. Emerg. Sel. Top. Circuits Syst. 7, 177–191. doi:10.1109/JETCAS.2017.2692243
Chung, C. Y., Wang, K. W., Tse, C. T., and Niu, R. (2002). Power-system Stabilizer (Pss) Design by Probabilistic Sensitivity Indexes (Psis). IEEE Trans. Power Syst. 17, 688–693. doi:10.1109/TPWRS.2002.800914
Dey, P., Mehra, R., Kazi, F., Wagh, S., and Singh, N. M. (2016). Impact of Topology on the Propagation of Cascading Failure in Power Grid. IEEE Trans. Smart Grid 7, 1970–1978. doi:10.1109/TSG.2016.2558465
Freeman, L. C. (1978). Centrality in Social Networks Conceptual Clarification. Soc. Netw. 1, 215–239. doi:10.1016/0378-8733(78)90021-7
Group, A. M. R. G. W. (2008). Zero Forcing Sets and the Minimum Rank of Graphs. Linear Algebra its Appl. 428, 1628–1648. doi:10.1016/j.laa.2007.10.009
Haque, M. H. (2004). Improvement of First Swing Stability Limit by Utilizing Full Benefit of Shunt Facts Devices. IEEE Trans. Power Syst. 19, 1894–1902. doi:10.1109/TPWRS.2004.836243
Hassan, F. F., Balasubramanian, R., and Bhatti, T. S. (1999). New Fast Valving Scheme Using Parallel Valves for Transient Stability Improvement. IEE Proc. Gener. Transm. Distrib. 146, 330–336. doi:10.1049/ip-gtd:19990176
Hatziargyriou, N., Milanovic, J., Rahmann, C., Ajjarapu, V., Canizares, C., Erlich, I., et al. (2021). Definition and Classification of Power System Stability - Revisited & Extended. IEEE Trans. Power Syst. 36, 3271–3281. doi:10.1109/TPWRS.2020.3041774
Hines, P., Cotilla-Sanchez, E., and Blumsack, S. (2010). Do topological Models Provide Good Information about Electricity Infrastructure Vulnerability? Chaos 20, 033122. doi:10.1063/1.3489887
Jarczyk, J. C., Svaricek, F., and Alt, B. (2011). “Strong Structural Controllability of Linear Systems Revisited,” in Proc. 50th IEEE Conf. on Decision and Control and Eur. Control Conf (IEEE), 1213. doi:10.1109/cdc.2011.6160392
Jia, J., van Waarde, H. J., Trentelman, H. L., and Camlibel, M. K. (2021). A Unifying Framework for Strong Structural Controllability. IEEE Trans. Autom. Contr. 66, 391–398. doi:10.1109/TAC.2020.2981425
Kiaei, I., Rostami, M., and Lotfifard, S. (2021). Robust Decentralized Control of Synchronous Generators for Improving Transient Stability of Multimachine Power Grids. IEEE Syst. J. 15, 3470–3479. doi:10.1109/JSYST.2020.3025028
Li, Y.-S., Ma, D.-Z., Zhang, H.-G., and Sun, Q.-Y. (2015). Critical Nodes Identification of Power Systems Based on Controllability of Complex Networks. Appl. Sci. 5, 622–636. doi:10.3390/app5030622
Liu, B., Li, Z., Chen, X., Huang, Y., and Liu, X. (2018). Recognition and Vulnerability Analysis of Key Nodes in Power Grid Based on Complex Network Centrality. IEEE Trans. Circuits Syst. II 65, 346–350. doi:10.1109/TCSII.2017.2705482
Mahmud, M. A., Hossain, M. J., Pota, H. R., and Oo, A. M. T. (2017). Robust Partial Feedback Linearizing Excitation Controller Design for Multimachine Power Systems. IEEE Trans. Power Syst. 32, 3–16. doi:10.1109/TPWRS.2016.2555379
Mayeda, H., and Yamada, T. (1979). Strong Structural Controllability. SIAM J. Control Optim. 17, 123–138. doi:10.1137/0317010
Monshizadeh, N., Zhang, S., and Camlibel, M. K. (2014). Zero Forcing Sets and Controllability of Dynamical Systems Defined on Graphs. IEEE Trans. Autom. Contr. 59, 2562–2567. doi:10.1109/TAC.2014.2308619
Mousavi, S. S., Haeri, M., and Mesbahi, M. (2018). On the Structural and Strong Structural Controllability of Undirected Networks. IEEE Trans. Autom. Contr. 63, 2234–2241. doi:10.1109/TAC.2017.2762620
Rubaai, A., Ofoli, A. R., Cobbinah, D., and Kankam, M. D. (2005). Two-layer Supervisory Controller-Based Thyristor-Controlled Braking Resistor for Transient Stability Crisis. IEEE Trans. Ind. Appl. 41, 1539–1547. doi:10.1109/TIA.2005.857465
Taylor, C. W., and Van Leuven, A. L. (1996). Caps: Improving Power System Stability Using the Time-Overvoltage Capability of Large Shunt Capacitor Banks. IEEE Trans. Power Deliv. 11, 783–792. doi:10.1109/61.489335
Trentelman, H., Stoorvogel, A., and Hautus, M. (2012). Control Theory for Linear Systems. Berlin, Germany: Springer.
Wang, K., Zhang, B.-h., Zhang, Z., Yin, X.-g., and Wang, B. (2011). An Electrical Betweenness Approach for Vulnerability Assessment of Power Grids Considering the Capacity of Generators and Load. Phys. A Stat. Mech. its Appl. 390, 4692–4701. doi:10.1016/j.physa.2011.07.031
Yang, D.-S., Sun, Y.-H., Zhou, B.-W., Gao, X.-T., and Zhang, H.-G. (2020). Critical Nodes Identification of Complex Power Systems Based on Electric Cactus Structure. IEEE Syst. J. 14, 4477–4488. doi:10.1109/JSYST.2020.2967403
Keywords: strong structural controllability, robustness, power system, generator control, network modeling
Citation: Sun Y, Yang D, Gao X and Qin J (2022) Robust Strong Structural Controllability of Complex Power Systems. Front. Energy Res. 10:913893. doi: 10.3389/fenrg.2022.913893
Received: 06 April 2022; Accepted: 20 April 2022;
Published: 13 June 2022.
Edited by:
Wei Hu, Zhejiang University, ChinaReviewed by:
Nannan Rong, Tianjin Polytechnic University, ChinaXiao Feng, University of Southampton, United Kingdom
Copyright © 2022 Sun, Yang, Gao and Qin . This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dongsheng Yang, eWFuZ2RvbmdzaGVuZ0BtYWlsLm5ldS5lZHUuY24=
 Yunhe Sun
Yunhe Sun Dongsheng Yang
Dongsheng Yang Xiaoting Gao
Xiaoting Gao Jia Qin
Jia Qin