Distributed Economic Dispatch Based on Finite-Time Double-Consensus Algorithm of Integrated Energy System

To reduce the operating cost and enhance the energy utilization efficiency of the integrated energy system (IES), an economic dispatch algorithm is proposed based on finite-time double-consensus. First, an economic dispatch model of IES under two modes of operation, islanded and grid-connected, is constructed considering energy transmission losses. After that, the optimal improved incremental cost and power output allocation of the IES can be found out in finite time. The proposed algorithm contains two finite-time consistency protocols simultaneously that can solve the optimal values of the incremental cost of electricity and heat of integrated energy system, solving the strong coupling problem of multi-energy systems. The proposed algorithm not only has a faster convergence rate but also enables switching freely between the two operation modes. In addition, a distributed method for quickly discovering the total system power mismatch is proposed in the process of algorithm solving. The finite-time convergence of the proposed algorithm is demonstrated. Finally, the IES simulation based on the IEEE 30-node power system and the Bali 32-node thermal system is established. The analysis of the simulation results shows that the algorithm proposed in this paper is effective.

1 Introduction

At present, the world is facing increasing pressure to save energy and protect the environment, and how to reduce environmental pollution based on ensuring a continuous supply of energy is a problem that countries have to consider (Yang and Su, 2021). Integrated energy system (IES) is a significant way to consume various types of distributed renewable energy, which is important for promoting the consumption of various types of renewable energy and establishing a new type of green and low-carbon power system (Li et al., 2021). IES is a deep integration of multiple energy sources and information technology that can promote the sustainable development of energy. With the increasing demand for IES to replace conventional energy systems in recent years, the research on various key technologies and theories about IES, such as dynamic modeling (Shen et al., 2020), multi-energy flow calculation (Yao et al., 2021), optimal cooperative operation (Qin et al., 2020), energy management (Li et al., 2020) and economic dispatch problem (EDP) (Lu et al., 2021; Liu et al., 2019), is receiving widely concerned.

The EDP has always been a hot issue in power and energy system research, and this is no exception in IES. Economic dispatch (ED) is a dispatching method to achieve the lowest cost through rational utilization of energy and equipment while satisfying safety and energy quality. The EDP can be equated to the planning problem of finding the minimum value of the cost function while satisfying the capacity constraint of each unit and the system power balance constraint. Traditional centralized control algorithms have also been applied to solve EDPs, such as model predictive control (Yu et al., 2019; Huang et al., 2021) and deep reinforcement learning (Lin et al., 2020). The advantage of centralized is reflected in the ease of unified management of resources within the system. Still, there are drawbacks such as high communication requirements, high computational load, and vulnerability to attacks (Xu et al., 2015). To overcome the shortcomings of centralized algorithms, distributed algorithms and multi-agent technology have gradually received widespread attention. Compared with centralized algorithms, distributed algorithms require fewer communication resources and have higher robustness and information security. Several distributed algorithms have been proposed to solve the EDP, such as the alternating direction multiplier method (Chen and Yang, 2018), diffusion algorithm (Chen and Sayed, 2012) and consensus algorithm (Binetti et al., 2014; Yang et al., 2017).

The consensus algorithm is used to achieve the economic optimum of the whole system by iteratively converging the incremental cost of each capacity unit to the consistency. Still, a centralized controller is required in the initially designed algorithm to calculate the total power deviation to ensure the power balance (Pu et al., 2017). Due to the stochastic nature of wind generation, its modeling should be different from conventional units. The uncertainty of the wind turbine output is considered in (Guo et al., 2016), and the power balance is achieved based on projected gradient that gets rid of the centralized control center. Saddle point dynamics is introduced in the iterative process of the consensus algorithm to search for an economically optimal solution in (Bai et al., 2019), which achieves fully distributed. Considering that communication delays always exist in real systems, the time-varying delay is considered in (Huang et al., 2019). The algorithm can still converge under certain communication delay conditions. In modeling the EDP, the cost function of equipment output is usually designed as a convex quadratic function to ensure the speed and convergence of the algorithm. To make the algorithm perform well even when the cost function is a general convex function, a method based on secant approximation is proposed to achieve efficient convergence (Zhong et al., 2021). (Chen et al., 2017; Zaery et al., 2020) use finite-time consensus for solving the EDP so that the algorithm converges in a determined finite time. In addition, issues such as network loss compensation (Sun et al., 2021) and information security encryption (Yan et al., 2021) have been considered.

However, most of the ED algorithms in the above literature are only proposed for power systems. For IESs, there is less literature on solving the EDP by consensus algorithms, and how to deal with the coupling relationship among multiple energy sources is one of the focuses of problem. A double-consensus algorithm is proposed in (Sun et al., 2019) to construct two consistency protocols in parallel to solve the strong coupling between electric and heat and achieve the economic optimum of the whole system. Based on (Sun et al., 2019), a distributed robust algorithm capable of resisting network attacks is proposed (Huang et al., 2022). The event-triggered mechanism is also applied to the economic dispatch problem to reduce the communication between agents (Li et al., 2019).

In summary, finite-time consensus allows the states of the agents to converge quickly to consistency in finite time. Event-triggered consensus (Chen et al., 2022) is to set the trigger function and trigger conditions. The communication between the agents is generated only when trigger conditions are met, which has the advantage of reducing the requirement for communication. The traditional consensus (Hong et al., 2022) haven’t the advantages of both. To the authors’ knowledge, the finite-time the consensus algorithm to solve the EDP of IES has not been discussed in depth. Based on the results obtained in the previous study, an ED strategy of IES is proposed based on the finite-time double-consensus algorithm in this paper, which can achieve economic optimality in both modes of system operation in islanded and grid-connected. The main contributions are as follows.

1) The ED strategy for IES is proposed based on the finite-time double-consensus algorithm, which solves the strong coupling problem among different energies by simultaneously executing two consistency protocols to achieve economic optimization. The proposed algorithm can achieve fast convergence in a finite time while allowing free and smooth switching between two modes of operation, that is, grid-connected and islanded. A distributed method to discover the total system power mismatch within finite step iterations is proposed to achieve power supply and demand balance during the algorithm execution.

2) The EDP model for IES considering transmission losses of electric and thermal energy is constructed, which has two modes of operation. The electric and thermal output coupling of combined heat and power units (CHPs) is considered in the model. And their operable domains are considered as output constraints.

3) The Lyapunov function for improved incremental cost deviation is constructed and the finite-time convergence of the proposed algorithm is demonstrated by theoretical analysis.

The rest of the paper is organized as follows: Preliminaries introduces some basic knowledge of graph theory used in this paper. Problem Formulation introduces the modeling of IES and the optimal solution of the EDP. Finite-Time Double-Consensus Algorithm proposes the finite-time double-consensus algorithm to solve the EDP. Case Studies demonstrates the effectiveness of the algorithm through data analysis of the constructed system. Conclusion summarizes the conclusions and provides an outlook.

2 Preliminaries

2.1 Graph Theory

For any IES containing $n$ agents, its communication network topology graph is generally represented by an undirected graph $G=\left(V,E\right)$, where $V=\left\{\mathrm{1,2},\dots ,n\right\}$ denotes the set of agents and $E\subseteq V\times V$ denotes the set of edges between agents. The elements $\left(i,j\right)$ denote that agent $i$ and $j$ are interconnected and can communicate and receive information from each other. If there is a communication line between agent $i$ and $j$, then agent $j$ is a neighbor of $i$. The set consisting of all neighbors of agent $i$ is denoted as $\left\{j\in V|\left(i,j\right)\in E\right\}$. The adjacency matrix $A=\left[a_{ij}\right]$ can represent the connectivity of $G$. For an undirected graph, if there is a communication path between $i$ and $j$, then $a_{ij}=a_{ji}=1$; otherwise $a_{ij}=a_{ji}=0$. The diagonal element $a_{ii}=0$ is defined. Let $D_i={\displaystyle \sum _{j\in N_i}{a}_{ij}}$, then the diagonal matrix $D=diag\left(D_i\right)$ is the degree matrix of $G$. Define the Laplacian matrix of a graph $G$ as $L=D-A$. An undirected graph $G$ is connected if there exists at least one path between any two agents. For a connected graph $G$, its Laplacian matrix $L$ has only one zero eigenvalue, and the rest of the eigenvalues are greater than 0. A sequential ordering of all its eigenvalues can be expressed as $0={\lambda }_1\left(L\right)< {\lambda }_2\left(L\right)<\dots <{\lambda }_n\left(L\right)$.

3 Problem Formulation

3.1 Integrated Energy System Modeling

Assume an IES with $N$ agents, where the agents include power generating units (PGUs), heat generating units (HGUs) and CHPs. The IES is connected to the distribution network, and the system receives exchange power from the distribution network when operating in grid-connected mode. The operating cost of each unit can be approximated as a convex quadratic function of its output. The cost functions for different types of units can be expressed as follows:

$\begin{array}{c}{C}_P={\displaystyle \sum _{i\in N_P}{C}_{P_i}\left(P_{G_i}\right)}={\displaystyle \sum _{i\in N_P}{\alpha }_{P_i}}+{\beta }_{P_i}{P}_{G_i}+{\gamma }_{P_i}{P}_{G_i}^2\end{array}(1)$

$\begin{array}{c}{C}_C={\displaystyle \sum _{i\in N_C}{C}_{C_i}\left(P_{C_i},Q_{C_i}\right)}={\displaystyle \sum _{i\in N_C}{\alpha }_{C_i}}+{\beta }_{C_i}{P}_{C_i}+{\gamma }_{C_i}{P}_{C_i}^2+{\zeta }_{C_i}{Q}_{C_i}+{\eta }_{C_i}{Q}_{C_i}^2+{\theta }_{C_i}{P}_{C_i}{Q}_{C_i}\end{array}(2)$

$\begin{array}{c}{C}_H={\displaystyle \sum _{i\in N_H}{C}_{H_i}\left(Q_{H_i}\right)}={\displaystyle \sum _{i\in N_H}{\alpha }_{H_i}}+{\beta }_{H_i}{Q}_{H_i}+{\gamma }_{H_i}{Q}_{H_i}^2\end{array}(3)$

where $C_P$, $C_C$, and $C_H$ denote the total operating costs of PGUs, CHPs, and HGUs, respectively; $N_P$, $N_C$, and $N_H$ denote the set of PGUs, CHPs, and HGUs; $C_{P_i}$, $C_{C_i}$, and $C_{H_i}$ denote the operating costs of the $i$ th PGU, CHP, and HGU. $P_{G_i}$ and $P_{C_i}$ denote the power output of the $i$ th PGU and CHP. $Q_{C_i}$ and $Q_{H_i}$ denote the heat output of the $i$ th CHP and HGU. ${\alpha }_{P_i}$, ${\beta }_{P_i}$, ${\gamma }_{P_i}$, ${\alpha }_{C_i}$, ${\beta }_{C_i}$, ${\gamma }_{C_i}$, ${\zeta }_{C_i}$, ${\eta }_{C_i}$, ${\theta }_{C_i}$, ${\alpha }_{H_i}$, ${\beta }_{H_i}$, and ${\gamma }_{H_i}$ are the operating cost coefficients of the $i$ th PGU, CHP, and HGU, respectively.

At the same time, each unit of the IES has to satisfy some equality constraints and inequality constraints. The equality constraints are electrical and thermal power balance constraints:

$\begin{array}{c}{\displaystyle \sum _{i\in N_P}{P}_{G_i}}+{\displaystyle \sum _{i\in N_C}{P}_{C_i}}+P_M-P_L-P_{loss}=0\end{array}(4)$

$\begin{array}{c}{\displaystyle \sum _{i\in N_H}{Q}_{H_i}}+{\displaystyle \sum _{i\in N_C}{Q}_{C_i}}-Q_L-Q_{loss}=0\end{array}(5)$

where $P_L$ and $Q_L$ denote the total power and thermal load demand, and $P_M$ is the power obtained from the distribution network under the grid-connected mode of system operation. When the system is in islanded mode, $P_M=0$. $P_{loss}$ and $Q_{loss}$ denote the total transmission loss of electric and thermal power generated by the transmission line and heating pipeline, respectively. They are approximated as functions of the output power, $P_{loss}={\displaystyle \sum _{i\in N_P}{B}_{P_i}{P}_{G_i}}+{\displaystyle \sum _{i\in N_C}{B}_{C_i}{P}_{C_i}}$, $Q_{loss}={\displaystyle \sum _{i\in N_H}{B}_{H_i}{Q}_{H_i}}+{\displaystyle \sum _{i\in N_C}{B}_{C_i}{Q}_{C_i}}$, $B_{P_i}$, $B_{C_i}$, and $B_{H_i}$ are loss coefficients.

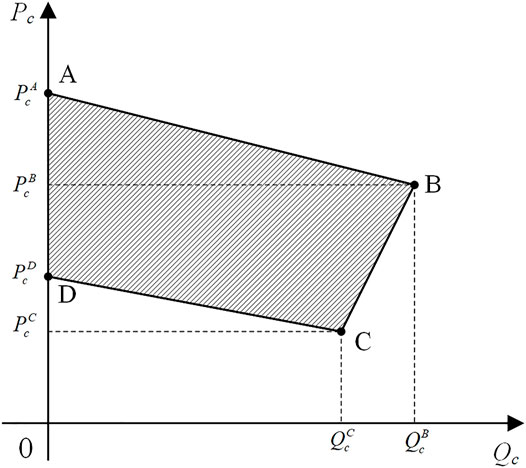
The inequality constraints, that is, the power output limits of PGUs and HGUs and the operable domain constraint of CHPs:

$\begin{array}{c}{\underset{¯}{P}}_{G_i}\le P_{G_i}\le {\overline{P}}_{G_i}\end{array}(6)$

$\begin{array}{c}{\underset{¯}{Q}}_{H_i}\le Q_{H_i}\le {\overline{Q}}_{H_i}\end{array}(7)$

The lower and upper limits of the electrical output of the $i$ th PGU are ${\underset{¯}{P}}_{G_i}$ and ${\overline{P}}_{G_i}$, and the lower and upper limits of the thermal output of the $i$ th HGU are ${\underset{¯}{Q}}_{H_i}$ and ${\overline{Q}}_{H_i}$, respectively. For CHP, its electric and thermal output is bounded by its operable domain, as shown in Figure 1. The boundary of this operable region is specified in the form of a linear inequality (Soroudi, 2017):

$\begin{array}{c}{P}_{C_i}-P_{C_i}^A-\left(\frac{P_{C_i}^B-P_{C_i}^A}{Q_{C_i}^B-Q_{C_i}^A}\right)\times Q_{C_i}\le 0\end{array}(8)$

$\begin{array}{c}{P}_{C_i}-P_{C_i}^B-\left(\frac{P_{C_i}^C-P_{C_i}^B}{Q_{C_i}^C-Q_{C_i}^B}\right)\times \left(Q_{C_i}-Q_{C_i}^B\right)\ge 0\end{array}(9)$

$\begin{array}{c}{P}_{C_i}-P_{C_i}^C-\left(\frac{P_{C_i}^D-P_{C_i}^C}{Q_{C_i}^D-Q_{C_i}^C}\right)\times \left(Q_{C_i}-Q_{C_i}^C\right)\ge 0\end{array}(10)$

$\begin{array}{c}{P}_{C_i}^C\le P_{C_i}\le P_{C_i}^A\end{array}(11)$

$\begin{array}{c}0\le Q_{C_i}\le Q_{C_i}^B\end{array}(12)$

where $P_{C_i}^A$, $P_{C_i}^B$, $P_{C_i}^C$, $P_{C_i}^D$, $Q_{C_i}^A$, $Q_{C_i}^B$, $Q_{C_i}^C$, and $Q_{C_i}^D$ are the coordinates of the four vertices $A$, $B$, $C$, and $D$ of the operable domain of the $i$ th CHP on the $P_C$ axis and the $Q_C$ axis as shown in Figure 1.

FIGURE 1

FIGURE 1. Operable domain of CHP.

3.2 Economic Dispatch Problem

The EDP of the IES is to distribute the output power of each unit reasonably on the basis of ensuring power balance to minimize the operating cost. The objective function of the EDP is defined as follows:

$\begin{array}{c}\min C=C_P+C_C+C_H+{\mu }_0{P}_M\end{array}(13)$

where $C$ is the operating cost of the whole IES and ${\mu }_0$ is the electricity price of the distribution network.

The equality constraints and inequality constraints are specified in Eqs. 6–12 also need to be satisfied in solving the objective function. When only the equality constraints are considered, the following Lagrangian function can be constructed:

$\begin{array}{c}L=C+{\mu }_P\left(P_L+P_{loss}-{\displaystyle \sum _{i\in N_P}{P}_{G_i}}-{\displaystyle \sum _{i\in N_C}{P}_{C_i}}-P_M\right)+{\mu }_H\left(Q_L+Q_{loss}-{\displaystyle \sum _{i\in N_H}{Q}_{H_i}}-{\displaystyle \sum _{i\in N_C}{Q}_{C_i}}\right)\end{array}(14)$

where $\mathrm{ℒ}$ is the Lagrangian function and ${\mu }_P$, ${\mu }_H$ are the Lagrangian multipliers corresponding to the electrical and thermal power, respectively. The optimal solution of the system can be obtained by finding the partial derivatives from the Karush-Kuhn-Tucker (KKT) condition as

$\begin{array}{c}\frac{\partial \mathrm{ℒ}}{\partial P_{G_i}}=2{\gamma }_{P_i}{P}_{G_i}+{\beta }_{P_i}+{\mu }_P\left(B_{P_i}-1\right)=0\end{array}(15)$

$\begin{array}{c}\frac{\partial \mathrm{ℒ}}{\partial P_{C_i}}=2{\gamma }_{C_i}{P}_{C_i}+{\beta }_{C_i}+{\theta }_{C_i}{Q}_{C_i}+{\mu }_P\left(B_{C{P}_i}-1\right)=0\end{array}(16)$

$\begin{array}{c}\frac{\partial \mathrm{ℒ}}{\partial Q_{C_i}}=2{\eta }_{C_i}{Q}_{C_i}+{\zeta }_{C_i}+{\theta }_{C_i}{P}_{C_i}+{\mu }_H\left(B_{C{H}_i}-1\right)=0\end{array}(17)$

$\begin{array}{c}\frac{\partial \mathrm{ℒ}}{\partial Q_{H_i}}=2{\gamma }_{H_i}{Q}_{H_i}+{\beta }_{H_i}+{\mu }_H\left(B_{H_i}-1\right)=0\end{array}(18)$

$\begin{array}{c}\frac{\partial \mathrm{ℒ}}{\partial P_M}={\mu }_0-{\mu }_P=0\end{array}(19)$

$\begin{array}{c}\frac{\partial \mathrm{ℒ}}{\partial {\mu }_P}=P_L+P_{loss}-{\displaystyle \sum _{i\in N_P}{P}_{G_i}}-{\displaystyle \sum _{i\in N_C}{P}_{C_i}}-P_M=0\end{array}(20)$

$\begin{array}{c}\frac{\partial \mathrm{ℒ}}{\partial {\mu }_H}=Q_L+Q_{loss}-{\displaystyle \sum _{i\in N_H}{Q}_{H_i}}-{\displaystyle \sum _{i\in N_C}{Q}_{C_i}}=0\end{array}(21)$

The improved incremental cost of each unit is defined as

$\begin{array}{c}{\mu }_{P_i}^P=\frac{\partial C_{P_i}}{\partial P_{G_i}}\cdot \frac{1}{\left(1-\frac{\partial P_{loss}}{\partial P_{G_i}}\right)}\end{array}(22)$

$\begin{array}{c}{\mu }_{P_i}^C=\frac{\partial C_{C_i}}{\partial P_{C_i}}\cdot \frac{1}{\left(1-\frac{\partial P_{loss}}{\partial P_{C_i}}\right)}\end{array}(23)$

$\begin{array}{c}{\mu }_{H_i}^C=\frac{\partial C_{C_i}}{\partial Q_{C_i}}\cdot \frac{1}{\left(1-\frac{\partial Q_{loss}}{\partial Q_{C_i}}\right)}\end{array}(24)$

$\begin{array}{c}{\mu }_{H_i}^H=\frac{\partial C_{H_i}}{\partial Q_{H_i}}\cdot \frac{1}{\left(1-\frac{\partial Q_{loss}}{\partial Q_{H_i}}\right)}\end{array}(25)$

From Eqs. 15–21, according to the equal micro-incremental rate criterion, when the cost consumed per unit of active power generated by each unit is the same, that is, when the improved incremental cost ${\mu }_P$ or ${\mu }_H$ of each unit reaches the consistent values ${\mu }_P^{\ast }$ and ${\mu }_H^{\ast }$, the overall operating cost of IES takes a minimal value. It achieves the goal of economically optimal dispatch of the system. If the system is operated in grid-connected mode, according to Eq. 19, the improved incremental cost ${\mu }_P$ of the system should converge to the electricity price ${\mu }_0$, then we have

$\begin{array}{c}\{\begin{array}{c}{\mu }_{P_1}^P={\mu }_{P_2}^P=\dots ={\mu }_{P_i}^P={\mu }_{P_1}^C=\dots ={\mu }_{P_i}^C={\mu }_P^{\ast },islandedmode\\ {\mu }_{P_1}^P={\mu }_{P_2}^P=\dots ={\mu }_{P_i}^P={\mu }_{P_1}^C=\dots ={\mu }_{P_i}^C={\mu }_0, grid-connectedmode\end{array}\end{array}(26)$

$\begin{array}{c}{\mu }_{H_1}^H={\mu }_{H_2}^H=\dots ={\mu }_{H_i}^H={\mu }_{H_1}^C=\dots ={\mu }_{H_i}^C={\mu }_H^{\ast }\end{array}(27)$

If the inequality constraint of the objective function is considered, the maximum output power can only reach its upper limit and the minimum can only reach its lower limit. In the case of satisfying this condition, the results of Eqs. 15–18 can be transformed, and the optimal solution of the improved incremental cost also needs to satisfy the following relation:

$\begin{array}{c}\{\begin{array}{c}\frac{2{\gamma }_{P_i}{P}_{G_i}+{\beta }_{P_i}}{1-B_{P_i}}>{\mu }_P^{\ast },P_{G_i}={\underset{¯}{P}}_{G_i}\\ \frac{2{\gamma }_{P_i}{P}_{G_i}+{\beta }_{P_i}}{1-B_{P_i}}={\mu }_P^{\ast },{\underset{¯}{P}}_{G_i}<P_{G_i}<{\overline{P}}_{G_i}\\ \frac{2{\gamma }_{P_i}{P}_{G_i}+{\beta }_{P_i}}{1-B_{P_i}}<{\mu }_P^{\ast },P_{G_i}={\overline{P}}_{G_i}\end{array}\end{array}(28)$

$\begin{array}{c}\{\begin{array}{c}\frac{2{\gamma }_{C_i}{P}_{C_i}+{\beta }_{C_i}+{\theta }_{C_i}{Q}_{C_i}}{1-B_{C{P}_i}}>{\mu }_P^{\ast },P_{C_i}={\underset{¯}{P}}_{C_i}\\ \frac{2{\gamma }_{C_i}{P}_{C_i}+{\beta }_{C_i}+{\theta }_{C_i}{Q}_{C_i}}{1-B_{C{P}_i}}={\mu }_P^{\ast },{\underset{¯}{P}}_{C_i}<P_{C_i}<{\overline{P}}_{C_i}\\ \frac{2{\gamma }_{C_i}{P}_{C_i}+{\beta }_{C_i}+{\theta }_{C_i}{Q}_{C_i}}{1-B_{C{P}_i}}<{\mu }_P^{\ast },P_{C_i}={\overline{P}}_{C_i}\end{array}\end{array}(29)$

$\begin{array}{c}\{\begin{array}{c}\frac{2{\eta }_{C_i}{Q}_{C_i}+{\zeta }_{C_i}+{\theta }_{C_i}{P}_{C_i}}{1-B_{C{H}_i}}>{\mu }_H^{\ast },Q_{C_i}={\underset{¯}{Q}}_{C_i}\\ \frac{2{\eta }_{C_i}{Q}_{C_i}+{\zeta }_{C_i}+{\theta }_{C_i}{P}_{C_i}}{1-B_{C{H}_i}}={\mu }_H^{\ast },{\underset{¯}{Q}}_{C_i}<Q_{C_i}<{\overline{Q}}_{C_i}\\ \frac{2{\eta }_{C_i}{Q}_{C_i}+{\zeta }_{C_i}+{\theta }_{C_i}{P}_{C_i}}{1-B_{C{H}_i}}<{\mu }_H^{\ast },Q_{C_i}={\overline{Q}}_{C_i}\end{array}\end{array}(30)$

$\begin{array}{c}\{\begin{array}{c}\frac{2{\gamma }_{H_i}{Q}_{H_i}+{\beta }_{H_i}}{1-B_{H_i}}>{\mu }_H^{\ast },Q_{H_i}={\underset{¯}{Q}}_{H_i}\\ \frac{2{\gamma }_{H_i}{Q}_{H_i}+{\beta }_{H_i}}{1-B_{H_i}}={\mu }_H^{\ast },{\underset{¯}{Q}}_{H_i}\le Q_{H_i}\le {\overline{Q}}_{H_i}\\ \frac{2{\gamma }_{H_i}{Q}_{H_i}+{\beta }_{H_i}}{1-B_{H_i}}<{\mu }_H^{\ast },Q_{H_i}={\overline{Q}}_{H_i}\end{array}\end{array}(31)$

Based on the equal micro-incremental rate criterion, the optimal incremental cost of IES can be determined iteratively. A traditional centralized control strategy can achieve this control goal by collecting information from all agents in the system integrated through a control center to calculate the optimal solution to the EDP. However, distributed generators are becoming more and more widely put into use, and centralized control is challenging to meet the demand. How to solve ${\mu }_P^{\ast }$ and ${\mu }_H^{\ast }$ and achieve the optimal power distribution of IES by distributed methods is what will be discussed in the next section of this paper.

4 Finite-Time Double-Consensus Algorithm

To overcome the disadvantages of centralized control, distributed ED algorithms based on incremental cost consistency have been proposed. Each agent only needs to obtain the parameters and states of local and neighbors. There are two main structures of consensus algorithms for solving the EDP. 1) The algorithm proposed by (Pu et al., 2017) requires a central controller to collect the output power information of all agents to obtain the total output power and calculate the total power mismatch to pass to the leader for feedback regulation. It cannot guarantee the power balance if the central controller fails. 2) The algorithm proposed by (Chen and Li, 2021) estimates the power mismatch value of the local agents by each agent in the process of iteration. Finally, the power mismatch estimation value of each agent converges to 0, and the system reaches power balance. This method removes the centralized control center but slows down the algorithm’s convergence, which is not conducive to the EDP that requires high convergence speed.

Based on the above algorithms, a distributed ED strategy for IES based on the finite-time double-consensus algorithm is proposed in this paper. The proposed algorithm uses a distributed approach to obtain the total power mismatch and make the improved incremental cost converge to the consistency in finite time, which not only effectively accelerates the convergence speed but also solves the problem of electrical and thermal coupling. At the same time, free switching between two operation modes is also allowed.

4.1 Total Power Mismatch Discovery

Note that the output power information of each unit is available only to the local node and its neighbors. Determining the total power mismatch of the system in a distributed manner is the first problem to be dealt with. Define the net output power of each unit as

$\begin{array}{c}{P}_{G_i}^S=P_{G_i}-B_{P_i}{P}_{G_i}=\left(1-B_{P_i}\right)P_{G_i}\end{array}(32)$

$\begin{array}{c}{P}_{C_i}^S=P_{C_i}-B_{C{P}_i}{P}_{C_i}=\left(1-B_{C{P}_i}\right)P_{C_i}\end{array}(33)$

$\begin{array}{c}{Q}_{C_i}^S=Q_{C_i}-B_{C{H}_i}{Q}_{G_i}=\left(1-B_{C{H}_i}\right)Q_{C_i}\end{array}(34)$

$\begin{array}{c}{Q}_{H_i}^S=Q_{H_i}-B_{H_i}{Q}_{H_i}=\left(1-B_{H_i}\right)Q_{H_i}\end{array}(35)$

where $P_{G_i}^S$, $P_{C_i}^S$, $Q_{C_i}^S$, and $Q_{H_i}^S$ denote the net output power of the $i$ th PGU, CHP, and HGU, respectively, which can be calculated directly at the local agent and sent to neighbors. The Laplacian matrices defining the communication topologies of the power and thermal networks are $\widehat{L}$ and $\tilde{L}$, and the adjacency matrices are $\widehat{A}=\left[{\widehat{a}}_{ij}\right]$ and $\tilde{A}=\left[{\tilde{a}}_{ij}\right]$, respectively. To ensure that the iterations converge in a finite number of steps, the weight factor update formula for agent $i$ can be chosen as (Kibangou, 2012)

$\begin{array}{c}{w}_{ij}\left(k\right)=\{\begin{array}{c}\frac{1}{{\lambda }_{k+1}\left(L\right)},j\mathit{ϵ}{N}_i\\ 1-\frac{D_i}{{\lambda }_{k+1}\left(L\right)},j=i,k=\mathrm{1,2},\cdots ,m\\ 0,otherwise\end{array}\end{array}(36)$

where ${\lambda }_{k+1}\left(L\right)$ represents the eigenvalue of the Laplacian matrix $L$, which is mentioned at the end of Section 2.1. From Eq. 36, the weight factor matrices of the power and thermal networks are obtained as $\widehat{W}\left(k\right)=\left[{\widehat{w}}_{ij}\left(k\right)\right]$ and $\tilde{W}\left(k\right)=\left[{\tilde{w}}_{ij}\left(k\right)\right]$, and then the total power output discovery algorithm is designed as follows:

$\begin{array}{c}{P}_t^S\left(k+1\right)=\widehat{W}\left(k\right)P_t^S\left(k\right)\end{array}(37)$

$\begin{array}{c}{Q}_t^S\left(k+1\right)=\tilde{W}\left(k\right)Q_t^S\left(k\right)\end{array}(38)$

where, $P_t^S={\left[P_{G_{i,t}}^S,P_{C_{i,t}}^S\right]}^T$ represents the vector of net electric output, and $Q_t^S={\left[Q_{H_{i,t}}^S,Q_{C_{i,t}}^S\right]}^T$ represents the vector of net thermal output. After iteration, the state of each agent will converge to the average of the initial state of each agent. Assuming that the numbers of agents of both electric and heat network are known as $n_P$ and $n_Q$, the algorithm converges after $n_P-1$ and $n_Q-1$ iterations. The total net electric and thermal output of the system is

$\begin{array}{c}{P}_{total}\left(t\right)=n_P{P}_t^S\left(n_P\right)\end{array}(39)$

$\begin{array}{c}{Q}_{total}\left(t\right)=n_Q{Q}_t^S\left(n_Q\right)\end{array}(40)$

where $P^S\left(n_P\right)$ and $Q^S\left(n_Q\right)$ are the convergence values of the algorithm after $n_P-1$ and $n_Q-1$ iterations. The total power mismatch can be expressed as

$\begin{array}{c}\mathrm{\Delta }P\left(t\right)=P_L-P_{total}\left(t\right)\end{array}(41)$

$\begin{array}{c}\mathrm{\Delta }Q\left(t\right)=Q_L-Q_{total}\left(t\right)\end{array}(42)$

This power mismatch will be used as a feedback quantity when solving for the optimal improved incremental cost ${\mu }_P^{\ast }$ and ${\mu }_H^{\ast }$ to achieve power balance.

4.2 Optimal Incremental Cost and Output Solution

The agent connected to the distribution network is selected as the leader of the power network to communicate with the distribution network to receive electric price information and connection status information. The finite-time double-consensus algorithm for solving the improved incremental cost is designed as follows:

$\begin{array}{c}{\dot{\mu }}_P={\alpha }_P\left[{\displaystyle \sum _{j\mathit{ϵ}{N}_i}{\widehat{a}}_{ij}sig{\left({\mu }_{P_j}\left(t\right)-{\mu }_{P_i}\left(t\right)\right)}^m}+b{\widehat{g}}_{i}sig{\left({\mu }_0-{\mu }_{P_i}\left(t\right)\right)}^m+c\cdot {\epsilon }_P\cdot \mathrm{\Delta }P\left(t\right)\right]\end{array}(43)$

$\begin{array}{c}{\dot{\mu }}_H={\alpha }_H\left[{\displaystyle \sum _{j\mathit{ϵ}{N}_i}{\tilde{a}}_{ij}sig{\left({\mu }_{H_j}\left(t\right)-{\mu }_{H_i}\left(t\right)\right)}^m}+{\epsilon }_H\cdot \mathrm{\Delta }Q\left(t\right)\right]\end{array}(44)$

where ${\alpha }_P$ and ${\alpha }_H$ are control gains, $sig{\left(x\right)}^m=sgn\left(x\right)\cdot {\left|x\right|}^m$, $0<m<1$, if agent $i$ is connected to the leader, then ${\widehat{g}}_i=1$; otherwise ${\widehat{g}}_i=0$. $b=1,c=0$ means the system is in grid-connected mode, when operating in islanded mode then $b=0,c=1$. This signal change can be transferred from the distribution network to the leader. ${\epsilon }_P$ and ${\epsilon }_H$ are power regulation coefficients.

Lemma 1 (Wang and Xiao, 2010): Let ${\vartheta }_1,{\vartheta }_2,\cdots ,{\vartheta }_n\ge 0$ and $0<d\le 1$, then we have

$\begin{array}{c}{\displaystyle \sum _{i=1}^n{\vartheta }_i^d}\ge {\left({\displaystyle \sum }_{i=1}^n{\vartheta }_i\right)}^d\end{array}(45)$

Lemma 2 (Zhang et al., 2012): Let $G=diag\left(g_i\right)$, for an undirected connected graph with Laplacian matrix with the following properties:

1)$x$ is a column vector composed of state variables of each agent with $x^T\left(L+G\right)x=\frac{1}{2}{\displaystyle \sum _{i,j=1}^n{a}_{ij}{\left(x_j-x_i\right)}^2}+{\displaystyle \sum _{i=1}^n{g}_i{\left(x_i\right)}^2}$.

2)$x^T\left(L+G\right)x\ge {\lambda }_2{x}^{T}x$, where ${\lambda }_2$ is the second smallest eigenvalue of the matrix $\left(L+G\right)$ and ${\lambda }_2>0$.

Lemma 3 (Wang and Xiao, 2010): If there exists a continuous positive definite function $V\left(x\right)$ of the system, if it satisfies the existence of positive numbers $c>0$ with $\alpha \in \left(\mathrm{0,1}\right)$ and an open neighborhood $\mathit{V}\subseteq \mathcal{D}$ containing the origin, such that

$\begin{array}{c}\dot{V}\left(x\right)+cV{\left(x\right)}^{\alpha }\le 0\end{array}(46)$

then the origin is the finite-time stable equilibrium point of the system. $V\left(x\right)$ reaches 0 in finite time as follows:

$\begin{array}{c}T\left(x\right)\le \frac{V{\left(x\right)}^{1-\alpha }}{c\left(1-\alpha \right)}\end{array}(47)$

Theorem 1: For an undirected connected graph $G$, the algorithms in Eqs. 43, 44 can converge in finite steps.

Proof: Taking Eq. 43 as an example, define the amount of deviation of the improved incremental cost as ${\delta }_{Pi}\left(t\right)= {\mu }_{P_i}\left(t\right)-{\mu }_0$ such that the deviation vector ${\mathit{\delta }}_{\mathit{P}}\left(t\right)=\left[{\delta }_{P1}\left(t\right),{\delta }_{P2}\left(t\right),\cdots ,{\delta }_{Pn}\left(t\right)\right]$, and since ${\mu }_0$ is time-invariant, ${\dot{\delta }}_{Pi}\left(t\right)={\dot{\mu }}_{Pi}\left(t\right)$. The following Lyapunov function is chosen as

$\begin{array}{c}V\left(t\right)=\frac{1}{2}{\displaystyle \sum _{i=1}^n{\delta }_{Pi}^2\left(t\right)}\end{array}(48)$

Taking the differential of $V\left(t\right)$, then there is

$\begin{array}{l}\dot{V}\left(t\right)={\displaystyle \sum _{i=1}^n{\delta }_{Pi}{\dot{\delta }}_{Pi}}\\ ={\displaystyle \sum _{i=1}^n{\delta }_{Pi}}{\displaystyle \sum _{j=1}^n{\widehat{a}}_{ij}sig{\left({\delta }_{Pj}-{\delta }_{Pi}\right)}^m}-{\widehat{g}}_{i}sig{\left({\delta }_{Pi}\right)}^m\\ =-\frac{1}{2}\left[{\displaystyle \sum _{i,j=1}^n{\widehat{a}}_{ij}\left({\delta }_{Pj}-{\delta }_{Pi}\right)sig{\left({\delta }_{Pj}-{\delta }_{Pi}\right)}^m}+{\displaystyle \sum _{i=1}^{n}2{\widehat{g}}_i{\delta }_{Pi}sig{\left({\delta }_{Pi}\right)}^m}\right]\\ \begin{array}{c}=-\frac{1}{2}\left[{\displaystyle \sum _{i,j=1}^n{\left({\widehat{a}}_{ij}^{\frac{2}{1+m}}sig{\left({\delta }_{Pj}-{\delta }_{Pi}\right)}^2\right)}^{\frac{1+m}{2}}}+{\displaystyle \sum _{i=1}^n{\left(2{\widehat{g}}_i^{\frac{2}{1+m}}sig{\left({\delta }_{Pi}\right)}^2\right)}^{\frac{1+m}{2}}}\right]\end{array}\end{array}(49)$

According to Lemma 1, it follows that

$\begin{array}{c}\dot{V}\left(t\right)\le -\frac{1}{2}{\left[{\displaystyle \sum _{i,j=1}^n\left({\widehat{a}}_{ij}^{\frac{2}{1+m}}sig{\left({\delta }_{Pj}-{\delta }_{Pi}\right)}^2\right)}+{\displaystyle \sum _{i=1}^n\left(2{\widehat{g}}_i^{\frac{2}{1+m}}sig{\left({\delta }_{Pi}\right)}^2\right)}\right]}^{\frac{1+m}{2}}\end{array}(50)$

Let $a_{ij}={\widehat{a}}_{ij}^{\frac{2}{1+m}}$ and $g_i={\widehat{g}}_i^{\frac{2}{1+m}}$, which is obtained from Lemma 2

$\begin{array}{c}\dot{V}\left(t\right)\le -\frac{1}{2}{\left[2{\lambda }_2{\mathit{\delta }}_{\mathit{P}}^{\mathit{T}}{\mathit{\delta }}_{\mathit{P}}\right]}^{\frac{1+m}{2}}\\ \begin{array}{c}\le -\frac{1}{2}{\left[4{\lambda }_{2}V\left(t\right)\right]}^{\frac{1+m}{2}}\end{array}\end{array}(51)$

Let $c^{\prime }=\frac{1}{2}{\left(4{\lambda }_2\right)}^{\frac{1+m}{2}}$, we can get $\dot{V}+c^{\prime }{V}^{\frac{1+m}{2}}\le 0$. Then according to Lemma 3, the error of the improved incremental cost can converge to 0 in finite time $T\le \frac{2V^{\frac{1-m}{2}}\left(0\right)}{c^{\prime }\left(1-m\right)}$.

Finally, the output power is solved according to the improved incremental cost. When considering the system inequality constraints shown in Eqs. 6–12, the output power of each unit can be expressed as

$P_{G_i}\left(t\right)=\{\begin{array}{cc}{\underset{¯}{P}}_{G_i },& \frac{\left(1-B_{P_i}\right){\mu }_{P_i}-{\beta }_{P_i}}{2{\gamma }_{P_i}}<{\underset{¯}{P}}_{G_i }\\ \frac{\left(1-B_{P_i}\right){\mu }_{P_i}-{\beta }_{P_i}}{2{\gamma }_{P_i}},& {\underset{¯}{P}}_{G_i }<\frac{\left(1-B_{P_i}\right){\mu }_{P_i}-{\beta }_{P_i}}{2{\gamma }_{P_i}}<{\overline{P}}_{G_i}\\ {\overline{P}}_{G_i},& \frac{\left(1-B_{P_i}\right){\mu }_{P_i}-{\beta }_{P_i}}{2{\gamma }_{P_i}}>{\overline{P}}_{G_i}\end{array}(52)$

$\begin{array}{c}{P}_{C_i}\left(t\right)=\{\begin{array}{cc}{\underset{¯}{P}}_{C_i },& \frac{\left(1-B_{C{P}_i}\right){\mu }_{P_i}-{\beta }_{C_i}-{\theta }_{C_i}{Q}_{C_i}}{2{\gamma }_{C_i}}<{\underset{¯}{P}}_{G_i }\\ \frac{\left(1-B_{C{P}_i}\right){\mu }_{P_i}-{\beta }_{C_i}-{\theta }_{C_i}{Q}_{C_i}}{2{\gamma }_{C_i}},& {\underset{¯}{P}}_{G_i }<\frac{\left(1-B_{C{P}_i}\right){\mu }_{P_i}-{\beta }_{C_i}-{\theta }_{C_i}{Q}_{C_i}}{2{\gamma }_{C_i}}<{\overline{P}}_{G_i}\\ {\overline{P}}_{C_i},& \frac{\left(1-B_{C{P}_i}\right){\mu }_{P_i}-{\beta }_{C_i}-{\theta }_{C_i}{Q}_{C_i}}{2{\gamma }_{C_i}}>{\overline{P}}_{G_i}\end{array}\end{array}(53)$

$Q_{C_i}\left(t\right)=\{\begin{array}{cc}{\underset{¯}{Q}}_{C_i },& \frac{\left(1-B_{C{H}_i}\right){\mu }_{H_i}-{\zeta }_{C_i}-{\theta }_{C_i}{P}_{C_i}}{2{\eta }_{C_i}}<{\underset{¯}{Q}}_{C_i }\\ \frac{\left(1-B_{C{H}_i}\right){\mu }_{H_i}-{\zeta }_{C_i}-{\theta }_{C_i}{P}_{C_i}}{2{\eta }_{C_i}},& {\underset{¯}{Q}}_{C_i }<\frac{\left(1-B_{C{H}_i}\right){\mu }_{H_i}-{\zeta }_{C_i}-{\theta }_{C_i}{P}_{C_i}}{2{\eta }_{C_i}}<{\overline{Q}}_{C_i}\\ {\overline{Q}}_{C_i},& \frac{\left(1-B_{C{H}_i}\right){\mu }_{H_i}-{\zeta }_{C_i}-{\theta }_{C_i}{P}_{C_i}}{2{\eta }_{C_i}}>{\overline{Q}}_{C_i}\end{array}(54)$

$Q_{H_i}\left(t\right)=\{\begin{array}{cc}{\underset{¯}{Q}}_{H_i },& \frac{\left(1-B_{H_i}\right){\mu }_{H_i}-{\beta }_{H_i}}{2{\gamma }_{H_i}}<{\underset{¯}{Q}}_{H_i }\\ \frac{\left(1-B_{H_i}\right){\mu }_{H_i}-{\beta }_{H_i}}{2{\gamma }_{H_i}},& {\underset{¯}{Q}}_{H_i }<\frac{\left(1-B_{H_i}\right){\mu }_{H_i}-{\beta }_{H_i}}{2{\gamma }_{H_i}}<{\overline{Q}}_{H_i}\\ {\overline{Q}}_{H_i},& \frac{\left(1-B_{H_i}\right){\mu }_{H_i}-{\beta }_{H_i}}{2{\gamma }_{H_i}}>{\overline{Q}}_{H_i}\end{array}(55)$

The output power of each unit can be determined based on the improved incremental cost. If the output power exceeds the limit, it is optimized to the limit of the output power. If the system works in grid-connected mode, $P\left(t\right)$ does not need to be involved as a feedback quantity in solving ${\mu }_P^{\ast }$, and the power mismatch is compensated by the exchange power of the distribution network.

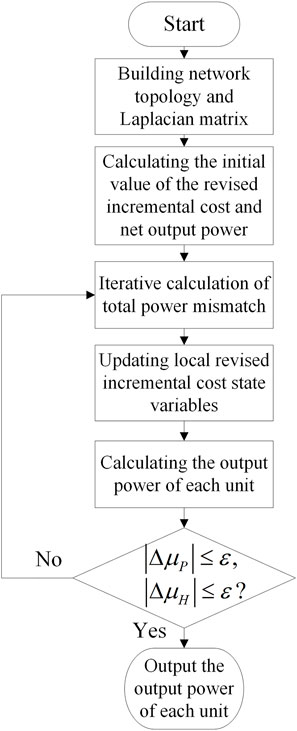
According to the above-proposed algorithm, the steps for solving the EDP of the IES are shown in Figure 2, and the corresponding steps are described as follows:

Step 1 Each agent updates the information of itself and neighbors through the communication network, constructs the topology of the IES, and sets the Laplacian matrix of the topology diagram of the electric and heat network.

Step 2 Calculating the initial values of the improved incremental cost and net output power according to Eqs. 22–25, Eqs. 32–35, and determining the initial state variables of each agent.

Step 3 Calculating the total power mismatch value based on the power output of each agent. Updating improved incremental cost state variables according to the power mismatch.

Step 4 Calculating the output power of each unit based on the improved incremental cost. The power exchanged with the distribution network needs to be calculated if operating in grid-connected mode, but not if in islanded mode.

Step 5 Calculating the electric and thermal improved incremental cost errors, and if the errors satisfy the convergence accuracy $\epsilon$, output the optimal solution for each unit’s output; if not, repeat Step 3.

FIGURE 2

FIGURE 2. The ED solution process of IES.

5 Case Studies

5.1 Simulation Setup

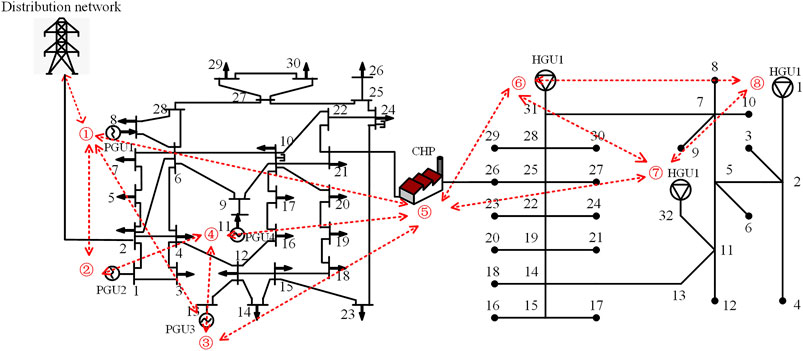
To test the effectiveness of the proposed algorithm, a 30–32 nodes IES is built for simulation and analysis. The IES is improved by coupling the IEEE 30-node electric system with the Bali 32-node thermal system (Liu et al., 2016), and its communication topology is shown in Figure 3.

FIGURE 3

FIGURE 3. The schematic of 30–32 nodes IES.

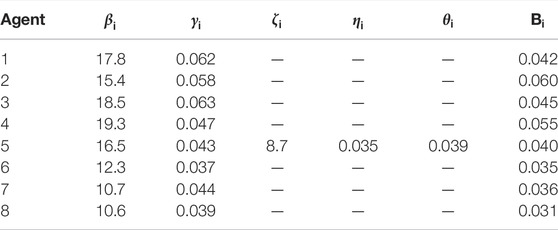
Agents one to four represent PGUs, agent 5 represents CHP, and agents six to eight represent HGUs. The dashed lines in the figure represent the communication lines among each agent. The communication line exists between agent 1 and the distribution network, which can receive the electricity price sent by the distribution network. The parameters of each distributed unit in the system are set as shown in Table 1. The upper and lower output limits of each PGU and HGU are 80 kW and 200 kW. The coordinates of the four vertices of the operational domain of the CHP are (0, 220), (180, 170), (165, 70), and (0, 85). The communication interval among agents is 0.05 s. The model is programmed and solved using the MATLAB 2021a simulation platform.

TABLE 1

TABLE 1. Cost factor parameters for each unit.

5.2 Effectiveness Analysis

5.2.1 Analysis of Effectiveness in Islanded Operation Mode

This subsection will verify the effectiveness of the algorithm in islanded operation mode. The system is set in islanded operation mode, and the total electrical power demand $P_L$ and the total thermal power demand $Q_L$ are set to 500kW and 550 kW in the initial state. The initial values of each unit output are $P_{G_1}=75kW$, $P_{G_2}=95kW$, $P_{G_3}=115kW$, $P_{G_4}=128kW$, $P_{C_i}=87kW$, $Q_{H_1}=155kW$, $Q_{H_2}=170kW$, $Q_{H_3}=95kW$, $Q_{C_1}=130kW$. First, we verify the effectiveness and convergence speed of algorithms in Eqs. 43, 44. As shown in Figure 4, the electric and thermal outputs converge to their initial state averages of $\overline{P}=100kW$ and $\overline{Q}=137.5kW$ after several steps of iteration. This demonstrates that the algorithm can accurately estimate the total electric and thermal outputs of the whole system in a distributed manner.

FIGURE 4

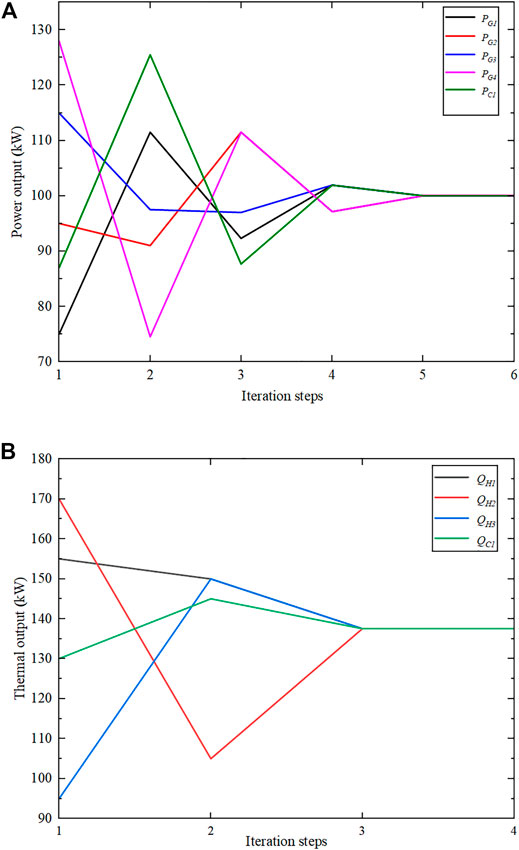
FIGURE 4. Total output power iterative process. (A) Electrical power output. (B) Thermal power output.

After that, the effectiveness of the proposed finite-time double-consensus algorithm is verified. The operation results are shown in Figure 5. Figure 5A shows the iterative process of improved incremental cost. Figure 5B and Figure 5C show the corresponding output and power mismatch of each unit, respectively. As can be obtained from the figures, the power and thermal improved incremental cost converge to the optimal values of 31.0 cent/kWh and 22.91 cent/kWh at $t=1.2s$, and the output of each unit is $P_{G_1}=100.19kW$, $P_{G_2}=126.02kW$, $P_{G_3}=92.29kW$, $P_{G_4}=112.53kW$, $P_{C_1}=94.85kW$, $Q_{H_1}=137.42kW$, $Q_{H_2}=134.24kW$, $Q_{H_3}=153.49kW$, $Q_{C_1}=145.02kW$. The power mismatch of the system is 0. At $t=2s$, $P_L$ and $Q_L$ change to 600kW and 480kW. After recalculation, the power and heat improved incremental costs converge to the new optimal values. At $t=4s$ $P_L$ and $Q_L$ change to 520kW and 620kW, the algorithm can converge to the new optimal value again. When the load demand changes and the algorithm is activated for regulation, the power mismatch of the system fluctuates briefly and finally converges to 0. The system achieves power balance and economic optimum.

FIGURE 5

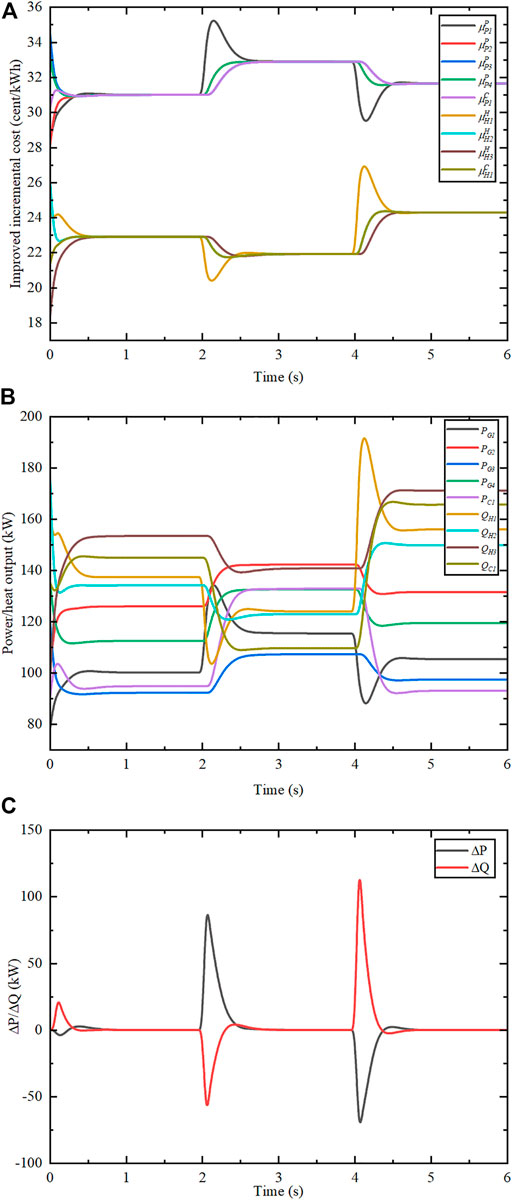
FIGURE 5. Algorithm results in islanded operation mode. (A) Improved incremental cost. (B) Power output of each unit. (C) Electrical and thermal power mismatch.

5.2.2 Analysis of Effectiveness in Grid-Connected Operation Mode

The system is set in grid-connected operation mode. The distribution network electricity price ${\mu }_0$ is set to 36 cent/kWh, and the total electric power demand $P_L$ and total thermal power demand $Q_L$ are 760kW and 530kW. The algorithm operation results are shown in Figure 6. According to the findings in Section 3.2, when the IES is operated in grid-connected mode, its power improved incremental cost should converge to the distribution network electricity price. The output of each unit is shown in Figure 6B as $P_{G_1}=140.43kW$, $P_{G_2}=169.05kW$, $P_{G_3}=131.89kW$, $P_{G_4}=165.61kW$, $P_{C_1}=169.08kW$, $Q_{H_1}=142.72kW$, $Q_{H_2}=139.71kW$, $Q_{H_3}=158.55kW$, $Q_{C_1}=109.28kW$, in addition to the electric power from the distribution network $P_M=21.78kW$. At $t=4s$, $P_L$ and $Q_L$ change to 790kW and 590kW, while ${\mu }_P$ remains constant at the convergence value of 36 cent/kWh, and the output of the PGUs remains unchanged. The variation of the electric power obtained from the distribution network is $P_M=60.53kW$. When the algorithm starts, the thermal power deviation fluctuates and gradually converges to 0, but the electric power mismatch is always 0. This is because the electric power mismatch is always compensated by the distribution network in the grid-connected mode.

FIGURE 6

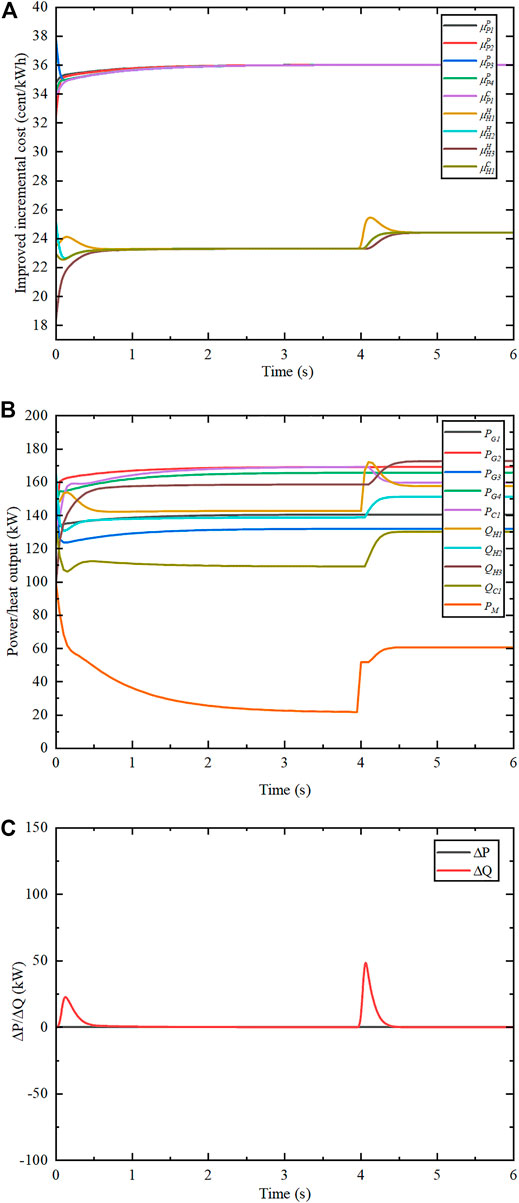
FIGURE 6. Algorithm results in grid-connected operation mode. (A) Improved incremental cost. (B) Power output of each unit. (C) Electrical and thermal power mismatch.

5.2.3 Operational State Switching Verification

This subsection will focus on testing whether the proposed algorithm can perform free switching between the two operation modes to cope with sudden distribution network faults and reconnection after fault repair. At the initial moment, the system is set in islanded mode with total electrical power demand $P_L$ and total thermal power demand $Q_L$ of 780 and 530 kW. The algorithm results are shown in Figure 7. The system operates in islanded mode, so the power exchanged with the distribution network is 0.

FIGURE 7

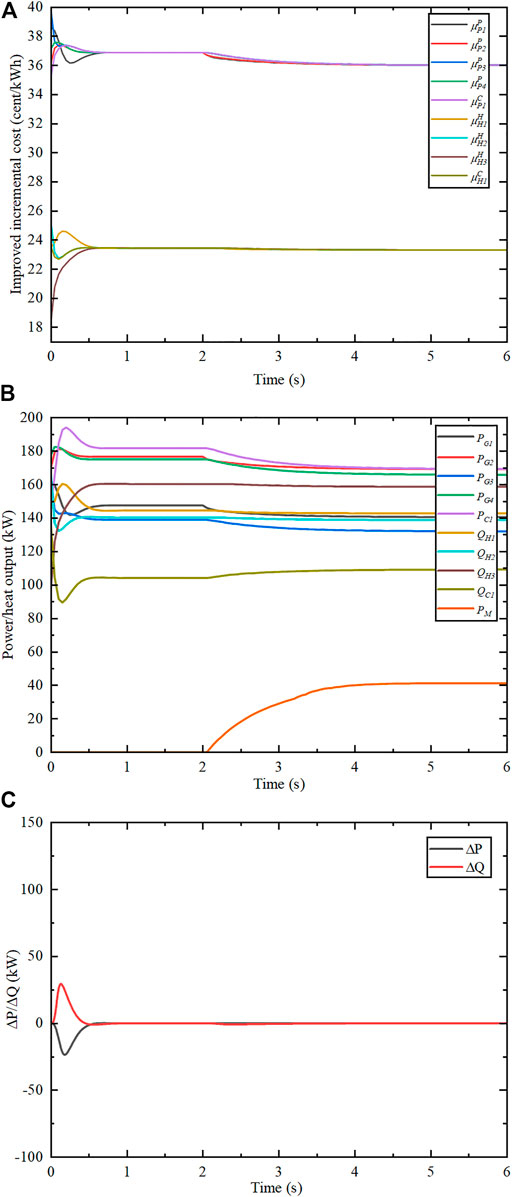
FIGURE 7. Algorithm results when operation mode switching. (A) Improved incremental cost. (B) Power output of each unit. (C) Electrical and thermal power mismatch.

At $t=2s$, the distribution network is reconnected, and the system switches to grid-connected mode to continue operation. ${\mu }_P$ is regulated and finally converges to 36 cent/kWh, and the electrical output is updated to $P_{G_1}=140.51kW$, $P_{G_2}=169.15kW$, $P_{G_3}=132.02kW$, $P_{G_4}=165.77kW$, and $P_{C_1}=169.30kW$, while the power to be obtained from the distribution network $P_M=41.11kW$. Since the total electrical and thermal power demand of the system is the same as before, the value of ${\mu }_H$ and the heat output of each unit remain essentially unchanged. As can be obtained in Figure 7C, the deviation of the electric power caused by the change of the improved incremental cost is compensated on the power provided by the distribution network when the operation mode is switched. The deviation of the thermal power only shows small fluctuations and recovers quickly. This proves that the algorithm is still effective when the operation state of the system is switched and does not cause large fluctuations of the power deviation. The proposed algorithm has a “plug-and-play” feature.

5.2.4 Comparison Analysis With Other Algorithms

Finally, the algorithm proposed in this paper is compared with those in other existing papers in the same simulation scenario. Table 2 shows the comparative analysis with the three algorithms in three existing papers. All three papers also solve the EDP by the incremental cost iterative method. The advantages of the algorithm proposed in this paper is shown in Table 2. In addition, Figure 8 shows the convergence speed of this paper compared with the algorithm proposed in (Chen and Li, 2021) in solving the EDP of the same system. With the same parameters and initial values of each agent, the proposed algorithm converges at about $t=1s$, while the algorithm in (Chen and Li, 2021) takes about $t=3s$ to converge. The algorithm proposed in this paper tends to have a faster convergence rate than the algorithm in (Chen and Li, 2021).

TABLE 2

TABLE 2. Comparison of algorithms proposed in related literature.

FIGURE 8

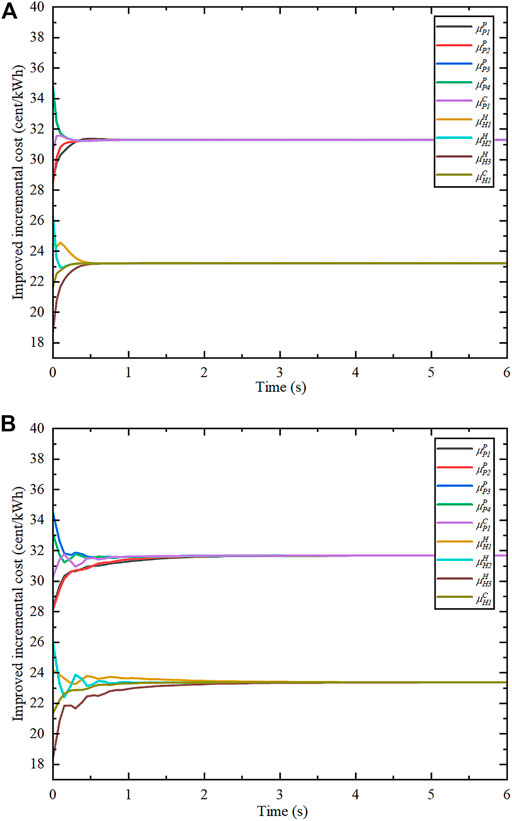
FIGURE 8. Comparison of the convergence speed of the two algorithms. (A) The algorithm proposed in this paper. (B) The algorithm proposed in (Chen and Li, 2021).

6 Conclusion

In this article, a distributed algorithm is proposed for solving the EDP of IES, which can obtain the optimal solution in a finite time and can switch smoothly between two operation modes. Firstly, the ED model is developed for IES under two operation modes considering transmission losses. Then, a finite-time double-consensus algorithm is proposed to solve the coupling problem among multiple energies and achieve the economic optimum of the system in finite time. Finally, a simulation study is conducted for the case. Several experiments indicate that the proposed algorithm is effective in two operation modes and has the advantage of fast convergence. The research is essential to enhance economic efficiency and improve the energy utilization of IES.

In the upcoming research work, based on the results obtained from the above studies, the energy types of IES, such as gas and cold, can be further expanded. In addition, communication delay and cyber-attacks need to be considered when designing control strategies to enhance their robustness.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

Both JY and JD contributed to designing the study, performing the research, analyzing the data, and writing the paper.

Funding

This work was supported in part by National Key R&D Program of China under Grant 2018YFA0702200 and in part by National Natural Science Foundation of China under Grant 61773099.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, L., Ye, M., Sun, C., and Hu, G. (2019). Distributed Economic Dispatch Control via Saddle Point Dynamics and Consensus Algorithms. IEEE Trans. Contr. Syst. Technol. 27 (2), 898–905. doi:10.1109/TCST.2017.2776222

CrossRef Full Text | Google Scholar

Binetti, G., Davoudi, A., Lewis, F. L., Naso, D., and Turchiano, B. (2014). Distributed Consensus-Based Economic Dispatch with Transmission Losses. IEEE Trans. Power Syst. 29 (4), 1711–1720. doi:10.1109/TPWRS.2014.229-943610.1109/tpwrs.2014.2299436

CrossRef Full Text | Google Scholar

Chen, G., Ren, J., and Feng, E. N. (2017). Distributed Finite-Time Economic Dispatch of a Network of Energy Resources. IEEE Trans. Smart Grid 8 (2), 822–832. doi:10.1109/TSG.2016.2516017

CrossRef Full Text | Google Scholar

Chen, G., and Yang, Q. (2018). An ADMM-Based Distributed Algorithm for Economic Dispatch in Islanded Microgrids. IEEE Trans. Ind. Inf. 14 (9), 3892–3903. doi:10.1109/TII.2017.2785366

CrossRef Full Text | Google Scholar

Chen, J., and Sayed, A. H. (2012). Diffusion Adaptation Strategies for Distributed Optimization and Learning over Networks. IEEE Trans. Signal Process. 60 (8), 4289–4305. doi:10.1109/TSP.2012.2198470

CrossRef Full Text | Google Scholar

Chen, W., and Li, T. (2021). Distributed Economic Dispatch for Energy Internet Based on Multiagent Consensus Control. IEEE Trans. Autom. Contr. 66 (1), 137–152. doi:10.1109/TAC.2020.2979749

CrossRef Full Text | Google Scholar

Chen, Y., Li, C., Qi, D., Li, Z., Wang, Z., and Zhang, J. (2022). Distributed Event-Triggered Secondary Control for Islanded Microgrids with Proper Trigger Condition Checking Period. IEEE Trans. Smart Grid 13 (2), 837–848. doi:10.1109/TSG.2021.3115180

CrossRef Full Text | Google Scholar

Guo, F., Wen, C., Mao, J., and Song, Y.-D. (2016). Distributed Economic Dispatch for Smart Grids with Random Wind Power. IEEE Trans. Smart Grid 7 (3), 1572–1583. doi:10.1109/TSG.2015.2434831

CrossRef Full Text | Google Scholar

Hong, J., Hui, H., Zhang, H., Dai, N., and Song, Y. (2022). Distributed Control of Large-Scale Inverter Air Conditioners for Providing Operating Reserve Based on Consensus with Nonlinear Protocol. IEEE Internet Things J., 1. doi:10.1109/JIOT.2022.3151817

CrossRef Full Text | Google Scholar

Huang, B., Li, Y., Zhan, F., Sun, Q., and Zhang, H. (2022). A Distributed Robust Economic Dispatch Strategy for Integrated Energy System Considering Cyber-Attacks. IEEE Trans. Ind. Inf. 18 (2), 880–890. doi:10.1109/TII.2021.3077509

CrossRef Full Text | Google Scholar

Huang, B., Liu, L., Zhang, H., Li, Y., and Sun, Q. (2019). Distributed Optimal Economic Dispatch for Microgrids Considering Communication Delays. IEEE Trans. Syst. Man. Cybern. Syst. 49 (8), 1634–1642. doi:10.1109/TSMC.2019.2900722

CrossRef Full Text | Google Scholar

Huang, X., Yang, B., Yu, F., Pan, J., Xu, Q., and Xu, W. (2021). Optimal Dispatch of Multi-Energy Integrated Micro-energy Grid: A Model Predictive Control Method. Front. Energy Res. 9, 766012. doi:10.3389/fenrg.2021.766012

CrossRef Full Text | Google Scholar

Kibangou, A. Y. (2012). “Graph Laplacian Based Matrix Design for Finite-Time Distributed Average Consensus,” in Proceedings of the American Control Conference (ACC), Montreal, QC, Canada, 27-29 June 2012, 1901–1906. doi:10.1109/ACC.2012.6315398

CrossRef Full Text | Google Scholar

Li, P., Zhang, F., Ma, X., Yao, S., Zhong, Z., Yang, P., et al. (2021). Multi-Time Scale Economic Optimization Dispatch of the Park Integrated Energy System. Front. Energy Res. 9, 743619. doi:10.3389/fenrg.2021.743619

CrossRef Full Text | Google Scholar

Li, Y., Gao, D. W., Gao, W., Zhang, H., and Zhou, J. (2020). Double-Mode Energy Management for Multi-Energy System via Distributed Dynamic Event-Triggered Newton-Raphson Algorithm. IEEE Trans. Smart Grid 11 (6), 5339–5356. doi:10.1109/TSG.2020.3005179

CrossRef Full Text | Google Scholar

Li, Y., Zhang, H., Liang, X., and Huang, B. (2019). Event-Triggered-Based Distributed Cooperative Energy Management for Multienergy Systems. IEEE Trans. Ind. Inf. 15 (4), 2008–2022. doi:10.1109/TII.2018.2862436

CrossRef Full Text | Google Scholar

Lin, L., Guan, X., Peng, Y., Wang, N., Maharjan, S., and Ohtsuki, T. (2020). Deep Reinforcement Learning for Economic Dispatch of Virtual Power Plant in Internet of Energy. IEEE Internet Things J. 7 (7), 6288–6301. doi:10.1109/JIOT.2020.2966232

CrossRef Full Text | Google Scholar

Liu, F., Bie, Z., and Wang, X. (2019). Day-Ahead Dispatch of Integrated Electricity and Natural Gas System Considering Reserve Scheduling and Renewable Uncertainties. IEEE Trans. Sustain. Energy 10 (2), 646–658. doi:10.1109/TSTE.2018.2843121

CrossRef Full Text | Google Scholar

Liu, X., Wu, J., Jenkins, N., and Bagdanavicius, A. (2016). Combined Analysis of Electricity and Heat Networks. Appl. Energy 162, 1238–1250. doi:10.1016/j.apenergy.2015.01.102

CrossRef Full Text | Google Scholar

Lu, S., Gu, W., Meng, K., and Dong, Z. (2021). Economic Dispatch of Integrated Energy Systems with Robust Thermal Comfort Management. IEEE Trans. Sustain. Energy 12 (1), 222–233. doi:10.1109/TSTE.2020.2989793

CrossRef Full Text | Google Scholar

Pu, T., Liu, W., Chen, N., Wang, X., and Dong, L. (2017). Distributed Optimal Dispatching of Active Distribution Network Based on Consensus Algorithm. Proc. CSEE 37 (6), 1579–1590. doi:10.13334/j.0258-8013.pcsee.160937

CrossRef Full Text | Google Scholar

Qin, Y., Wu, L., Zheng, J., Li, M., Jing, Z., Wu, Q. H., et al. (2020). Optimal Operation of Integrated Energy Systems Subject to the Coupled Demand Constraints of Electricity and Natural Gas. Csee Jpes 6 (2), 444–457. doi:10.17775/CSEEJPES.2018.00640

CrossRef Full Text | Google Scholar

Shen, F., Ju, P., Shahidehpour, M., Li, Z., Wang, C., and Shi, X. (2020). Singular Perturbation for the Dynamic Modeling of Integrated Energy Systems. IEEE Trans. Power Syst. 35 (3), 1718–1728. doi:10.1109/TPWRS.2019.2-95367210.1109/tpwrs.2019.2953672

CrossRef Full Text | Google Scholar

Soroudi, A. (2017). Power System Optimization Modeling in GAMS. Cham: Springer.

Google Scholar

Sun, Q., Fan, R., Li, Y., Huang, B., and Ma, D. (2019). A Distributed Double-Consensus Algorithm for Residential We-Energy. IEEE Trans. Ind. Inf. 15 (8), 4830–4842. doi:10.1109/TII.2019.2921431

CrossRef Full Text | Google Scholar

Sun, Y., Wu, X., Wang, J., Hou, D., and Wang, S. (2021). Power Compensation of Network Losses in a Microgrid with BESS by Distributed Consensus Algorithm. IEEE Trans. Syst. Man. Cybern. Syst. 51 (4), 2091–2100. doi:10.1109/TSMC.2020.2968605

CrossRef Full Text | Google Scholar

Wang, L., and Xiao, F. (2010). Finite-Time Consensus Problems for Networks of Dynamic Agents. IEEE Trans. Autom. Contr. 55 (4), 950–955. doi:10.1109/TAC.2010.2041610

CrossRef Full Text | Google Scholar

Xu, Y., Zhang, W., and Liu, W. (2015). Distributed Dynamic Programming-Based Approach for Economic Dispatch in Smart Grids. IEEE Trans. Ind. Inf. 11 (1), 166–175. doi:10.1109/TII.2014.2378691

CrossRef Full Text | Google Scholar

Yan, Y., Chen, Z., Varadharajan, V., Hossain, M. J., and Town, G. E. (2021). Distributed Consensus-Based Economic Dispatch in Power Grids Using the Paillier Cryptosystem. IEEE Trans. Smart Grid 12 (4), 3493–3502. doi:10.1109/TSG.2021.3063712

CrossRef Full Text | Google Scholar

Yang, J., and Su, C. (2021). Robust Optimization of Microgrid Based on Renewable Distributed Power Generation and Load Demand Uncertainty. Energy 223, 120043. doi:10.1016/j.energy.2021.120043

CrossRef Full Text | Google Scholar

Yang, Z., Xiang, J., and Li, Y. (2017). Distributed Consensus Based Supply-Demand Balance Algorithm for Economic Dispatch Problem in a Smart Grid with Switching Graph. IEEE Trans. Ind. Electron. 64 (2), 1600–1610. doi:10.1109/TIE.2016.2615037

CrossRef Full Text | Google Scholar

Yao, S., Gu, W., Lu, S., Zhou, S., Wu, Z., Pan, G., et al. (2021). Dynamic Optimal Energy Flow in the Heat and Electricity Integrated Energy System. IEEE Trans. Sustain. Energy 12 (1), 179–190. doi:10.1109/TSTE.2020.298-868210.1109/tste.2020.2988682

CrossRef Full Text | Google Scholar

Yu, J., Li, Z., Guo, Y., and Sun, H. (2019). Decentralized Chance-Constrained Economic Dispatch for Integrated Transmission-District Energy Systems. IEEE Trans. Smart Grid 10 (6), 6724–6734. doi:10.1109/TSG.2019.2910757

CrossRef Full Text | Google Scholar

Zaery, M., Wang, P., Huang, R., Wang, W., and Xu, D. (2020). Distributed Economic Dispatch for Islanded DC Microgrids Based on Finite-Time Consensus Protocol. IEEE Access 8, 192457–192468. doi:10.1109/access.2020.3032641

CrossRef Full Text | Google Scholar

Zhang, H., Lewis, F. L., and Qu, Z. (2012). Lyapunov, Adaptive, and Optimal Design Techniques for Cooperative Systems on Directed Communication Graphs. IEEE Trans. Ind. Electron. 59 (7), 3026–3041. doi:10.1109/TIE.2011.2160140

CrossRef Full Text | Google Scholar

Zhong, H., Yan, X., and Tan, Z. (2021). Real-Time Distributed Economic Dispatch Adapted to General Convex Cost Functions: A Secant Approximation-Based Method. IEEE Trans. Smart Grid 12 (3), 2089–2101. doi:10.1109/TSG.2020.3049054

CrossRef Full Text | Google Scholar