Experimental and numerical investigations into molten-pool sloshing motion for severe accident analysis of sodium-cooled fast reactors: A review

Safety issues are particularly crucial for sodium-cooled fast reactors (SFRs). Data obtained from SFR safety analyses over recent years have shown that a specific type of sloshing motion probably occurs in the molten pool during core disruptive accidents (CDAs) of SFRs due to local neutronic power excursion or pressure developments, thereby significantly influencing recriticality. Recognizing the importance of improving the evaluation of CDAs of SFRs, extensive knowledge about this phenomenon has been garnered through experimental studies of their thermal-hydraulic mechanism and characteristics. Based on these studies, simulations using various numerical approaches, such as SIMMER code, the finite volume particle method, and the smoothed particle hydrodynamic method, have attempted to reproduce the sloshing motion under various experimental conditions to verify their reasonability and applicability, thereby promoting the development of SFR safety analysis. To provide useful references for future SFR safety analyses and assessments, we have systematically reviewed and summarized these experimental and numerical investigations into the thermal-hydraulic aspect of molten-pool sloshing motion. In addition, to enhance deeper and more comprehensive research into sloshing motion, we have also discussed future prospects. Knowledge gained from experimental and numerical investigations into molten-pool sloshing motion is valuable not only for improving and verifying SFR safety analysis codes but also for providing reference data for studies of sloshing motion in other fields of engineering.

1 Introduction

Sodium-cooled fast reactor (SFRs) are considered to be predominant among Generation IV nuclear reactor systems due to their outstanding breeder characteristics and the considerable experience accrued in their construction and operation (Raj et al., 2015). Nevertheless, for the nuclear power industry, safety is always an important issue for its developments, and SFRs are no exception. Therefore, to accelerate SFR developments and applications, analysis of their safety is crucial, particularly for severe accidents such as core disruptive accidents (CDAs) (Tentner et al., 2010; Ohshima and Kubo, 2016). In the initiation phase of CDA, due to the specific core design of SFRs, the nonenergetic initial power transient could be generally brought by the negative reactivity effect as a result of fuel dispersion with pin disruption, which would be superior to the positive reactivity effects such as void reactivity (Maschek et al., 1992a; Suzuki et al., 2014). In such nonenergetic case, the accident scenario may proceed from the initiating phase to a transition phase (Maschek et al., 1992a; Suzuki et al., 2014; Suzuki et al., 2015). In this phase, due to the melting of the reactor core, a large molten pool at the whole-core scale can be formed, with an adequate molten fuel spatial configuration to exceed prompt criticality (see Figure 1). Within the molten pool, a complex system with multiphase flows is believed to form, including molten fuel, molten structure, refrozen fuel, liquid coolant, fission gas, fuel vapor, solid fuel pellets, and other materials (Liu et al., 2006, 2007; Tentner et al., 2010). Results calculated using SIMMER-II code (a Euler-based code for fast-reactor safety analysis) revealed that in the large molten pool, a specific flow pattern might exist that could trigger the central compacting fluid motions (Bohl, 1979; Maschek et al., 1982; Kondo et al., 1985; Theofanous and Bell, 1986). As shown in Figure 1, during the extension of the molten pool, portions of liquid coolant may be entrapped in the pool, thereby leading to a local fuel–coolant interaction (FCI), which could cause bubble expansion and pressure development, disturbing the stability of the pool by pushing the liquid fuel away from the central core region toward the peripheral regions, then impelling it back to the center through gravity (Maschek et al., 1992a; Yamano et al., 2009; Zhang et al., 2018; Cheng et al., 2019d). Therefore, taking into consideration the sensitivity of SFRs to dimensional variations or core-material relocations, such bubble expansion and subsequent centralized, inward sloshing motion could potentially promote recriticality and lead to an energetic power excursion due to fuel compactions in the molten pool (Theofanous and Bell, 1986; Maschek et al., 1992a; Yamano et al., 2009; Tatewaki et al., 2015). This could lead to the accident progressing to the core expansion phase, thereby threatening the structural stability of the reactor vessel. It should be noted that although the sloshing motion is also of great importance and has attracted great attention in fields other than nuclear energy (e.g., the steel industry, volcanology, Earth sciences, and fluidized beds) (Sakai et al., 1984; Bi, 2007; Hatayama, 2008; Namiki et al., 2016; Thaker et al., 2020), this review will concentrate on investigations into molten-pool sloshing motion in relation to CDAs of SFRs due to its special pattern and mechanism compared with those seen in other science and engineering fields.

FIGURE 1

FIGURE 1. Molten pool formation and sloshing motion.

In recent decades, it has become clear that an understanding of molten-pool sloshing motion is very important for the improved evaluation of SFR severe accident scenarios, particularly regarding energetic recriticality. A series of experimental investigations was carried out at Karlsruhe Institute of Technology (KIT), Kyushu University, and Sun Yat-Sen University (SYSU) that considered various conditions, such as dam-break, fluid-step, and gas-injection conditions (Maschek et al., 1992a; Maschek et al., 1992b; Morita et al., 2014; Cheng et al., 2018c; Cheng et al., 2018d; Cheng et al., 2019a; Cheng et al., 2019b; Cheng et al., 2019c; Cheng et al., 2020; Xu et al., 2022). Basic mechanisms (e.g., peripheral pushing of molten fuel and gravitation-induced inward centralized sloshing) and important sloshing characteristics (e.g., the maximal inward and outward sloshing liquid heights) were phenomenologically observed via dam-break and fluid-step experiments (Maschek et al., 1992a; Maschek et al., 1992b), in which the outward and inward sloshing motions were both triggered by gravity. However, it should be pointed out that in an actual scenario of a CDA in an SFR, as the molten pool forms and enlarges (e.g., as a result of the failure of control rod guide tubes), and due to the possibility for a portion of the liquid sodium coolant to be entrapped in it, outward sloshing motion could be initiated by rapid vapor generation and pressure buildup around the central pool region through local FCI (Cheng et al., 2014; Cheng et al., 2015; Zhang et al., 2018). Therefore, it is reasonable to assume that the use of the gas-injection method for simulating vapor expansion can achieve more realistic conditions for the molten-pool sloshing motion triggered by local FCI. Furthermore, the vaporization of fuel or structural materials in cases of large power depositions may also contribute to the sloshing motion. In a preliminary study of molten-pool sloshing motion while taking into consideration thermal-hydraulic or neutronic disturbances, Morita et al. (2014) carried out gas-injection experiments to investigate the overlaying (i.e., mitigating or augmenting) effects of various modes of hydraulic disturbance. Furthermore, aimed at a deeper and more comprehensive understanding of the sloshing motion initiated by local FCI, a series of experimental investigations using the gas-injection method without hydraulic disturbances in pure liquid pools was conducted by Cheng et al. (2018c), to investigate the flow-regime patterns of sloshing motion in more detail. While observing that it is possible to find the co-existence of molten structural materials and fuel under actual accident conditions, Cheng et al. (2020) performed further experimental investigations into sloshing motion in pools with liquid stratification. In addition to experiments in liquid pools without solid phases and considering the fact that, in an actual reactor accident, solid phase materials may be present in the pool as a result of incomplete melting of structural materials and fuel pellets (Liu et al., 2006, 2007), experiments in liquid pools with solid phases (such as solid particles and solid obstacles with rod-shaped structures) have also been performed under dam-break and gas-injection conditions to accumulate valuable knowledge concerning the effects of solid phases on sloshing characteristics (Maschek et al., 1992a; Maschek et al., 1992b; Cheng et al., 2018d; Cheng et al., 2019a; Cheng et al., 2019b; Cheng et al., 2019c; Xu et al., 2022). These previous experimental investigations into sloshing motion are summarized in Figure 2.

FIGURE 2

FIGURE 2. Previous experiments and numerical investigations regarding sloshing motion.

In recent decades, however, to better reproduce sloshing motions and thereby improve the assessment of the evolution of severe SFR accidents, in addition to experimental investigations, numerical simulations and validations of molten-pool sloshing motion have been developed and greatly progressed by employing various computational fluid dynamics (CFD) codes and methods. Based on the dam-break and fluid-step experiments performed by Maschek et al. (1992a, 1992b), SIMMER-II, AFDM, and IVA3 codes were used by Munz and Maschek (1992) and Maschek et al. (1992a) to create a preliminary simulation of sloshing motion. Then, to improve the reliability and accuracy of SFR safety analysis, Pigny (2010) and Yamano et al. (2012) employed SIMMER-IV code to perform numerical simulations at the Commissariat à l’Energie Atomique et aux Energies Alternatives (CEA) and the Japan Atomic Energy Agency (JAEA), respectively. It was verified that experimental sloshing characteristics (such as compaction velocities) can be rationally reproduced by SIMMER-IV for both dam-break and fluid-step cases. The applicability of particle methods for simulating sloshing motion was also validated in accordance with dam-break experiments. For instance, the simulation rationality of the finite volume particle (FVP) method was demonstrated by Guo et al. (2010, 2012) at Kyushu University through simulations for dam-break sloshing with/without solid particles. Vorobyev et al. (2010, 2011) and Vorobyev (2012) at KIT, Buruchenko and Crespo (2014) at South Ural State University (SUSU) and University of Vigo (UVigo), and Jo et al. (2019, 2021) at Seoul National University (SNU) confirmed the reliability of simulation results obtained using the smoothed particle hydrodynamic (SPH) method. Furthermore, Morita et al. (2014) carried out SIMMER-III numerical simulations related to gas-injection experiments with hydraulic disturbances. These numerical investigations into sloshing motion are also summarized in Figure 2, where a brief introduction of each simulation code/method is provided.

Understanding and knowledge obtained from experiments and numerical simulations about the mechanisms and characteristics of molten-pool sloshing motion are of great importance for improving the safety evaluations of SFRs (e.g., improvement and verification of SFR safety analysis codes with proper neutronic models) and providing reference data for investigations into sloshing motion in other fields of engineering. Considering these aspects, we aimed to carry out a comprehensive systematic review and discussion of previous experiments and numerical simulations of molten-pool sloshing motion in cases of CDAs in SFRs. In Section 2, the experimental and numerical investigations for dam-break and fluid-step sloshing are introduced, while investigations involving gas-injection conditions are discussed and summarized in Section 3. In Section 4, conclusions are described, and some future prospects are discussed to provide a valuable reference and guidance for encouraging deeper and more comprehensive investigations on this topic in the future.

2 Dam-break and fluid-step sloshing motions

2.1 Dam-break and fluid-step sloshing motions in pure liquid pools

2.1.1 Description of experiments

To provide experimental evidence for the numerical analysis of sloshing motion, Maschek et al. (1992a, 1992b) conducted several dam-break and fluid-step sloshing experiments. Figures 3A–C show the main experimental devices, which included two Plexiglas containers of cylindrical shape. For the dam-break and fluid-step experiments, the inner container was filled with water and rapidly pulled up to release this water so that the subsequent sloshing motion could be initiated through the gravitation. From symmetrical dam-break experiments, it was observed that the liquid would first slosh out toward the peripheral area of the outer container and then slosh inward to pile up in the central region, finally resulting in a central liquid peak (see Figure 4A). It was confirmed that, due to gravity, an inner container of larger diameter (D_in) or higher initial water height (H_in), which resulted in greater inertia of the liquid, increased the sloshing intensity, as characterized by the maximal water heights of peripheral outward and centralized inward sloshing motion (Maschek et al., 1992b). However, if the sloshing system was asymmetric, not only did the inward sloshing motion become chaotic with no centralized sloshing peak observed but the maximal peripheral sloshing heights were also observably different between the left and right sides due to the different lengths of the propagating liquid waves (see Figure 4B). This difference in peripheral sloshing heights increased when an asymmetric system with greater off-centeredness (R_off) was employed.

FIGURE 3

FIGURE 3. Main devices used for dam-break and fluid-step experiments under different conditions (containers that are open at the top). (A) Symmetrical dam-break condition. (B) Asymmetrical dam-break condition. (C) Fluid-step condition. (D) Dam-break condition with symmetrically distributed rod-shaped obstacles. (E) Dam-break condition with asymmetrically distributed rod-shaped obstacles. (F) Dam-break condition with ring-shaped obstacles. (G) Dam-break condition with a particle ring. (H) Dam-break condition with a central particle bed.

FIGURE 4

FIGURE 4. Typical dam-break and fluid-step sloshing motion (Maschek et al., 1992b; Yamano et al., 2012; Jo et al., 2021). (A) Symmetric dam-break sloshing motion (D_in = 11 cm, H_in = 20 cm). (B) Asymmetric dam-break sloshing motion (D_in = 11 cm, H_in = 20 cm, off-centeredness = 8.25 cm). (C) Fluid-step sloshing motion (D_in = 11 cm, H_out = 5 cm, H_in = 20 cm).

In addition to dam-break experiments, fluid-step experiments were performed to more comprehensively clarify the sloshing characteristics, by introducing additional liquid of various heights within the outer container (H_out) (see Figure 3C) and coloring the inner water to visually distinguish it from the outer water. As shown in Figure 4C, experimental results showed that the inner colored water pushed the clear, outer water to the peripheries of the outer container after being discharged, before being compressed by the inward sloshing clear water to form a water hump. This would then collapse due to gravity, resulting in a second, outward sloshing motion in the deeper region, subsequently leading to a second inward sloshing motion that extruded a centralized sloshing peak. It was found that a higher H_out can lead to more repeats of sloshing as a result of less energy being dissipated in the deeper water region (Maschek et al., 1992b). Furthermore, a similar effect of a liquid’s inertia on the enhancement of sloshing intensity was observed in experiments conducted under fluid-step conditions.

Briefly, based on the dam-break and fluid-step sloshing experiments using pure liquid pools, it was concluded that the symmetricity and the overall inertia of the liquid in a sloshing system noticeably affects the characteristics of the sloshing motion.

2.1.2 Numerical simulations

To reproduce the symmetric dam-break and fluid-step sloshing motions, three CFD codes, SIMMER-II (Smith, 1978; Bohl and Luck, 1990), AFDM (advanced fluid-dynamics model) (Bohl et al., 1990), and IVA3 (Kolev, 1993), were examined first (Munz and Maschek, 1992). However, although the basic sloshing process could be rationally reproduced, relatively inaccurate results were obtained, especially for the methods with a first-order differencing scheme (i.e., SIMMER-II and IVA3). With developments in computing science and technology, in recent years a SIMMER-IV code with a higher-order differencing scheme (Yamano et al., 2003a), the FVP method (Zhang et al., 2007), and the SPH method (Gingold and Monaghan, 1977) were used to simulate dam-break sloshing and obtain more accurate simulation results (Guo et al., 2010, 2012; Vorobyev et al., 2010; 2011; Vorobyev, 2012; Yamano et al., 2012; Buruchenko and Crespo, 2014; Jo et al., 2019, Jo et al., 2021). The SIMMER-IV code was also used in an attempt to simulate fluid-step sloshing motion (Pigny, 2010). Tables 1 and 2 summarize the results of simulated sloshing characteristics using different numerical methods for dam-break and fluid-step cases, respectively.

TABLE 1

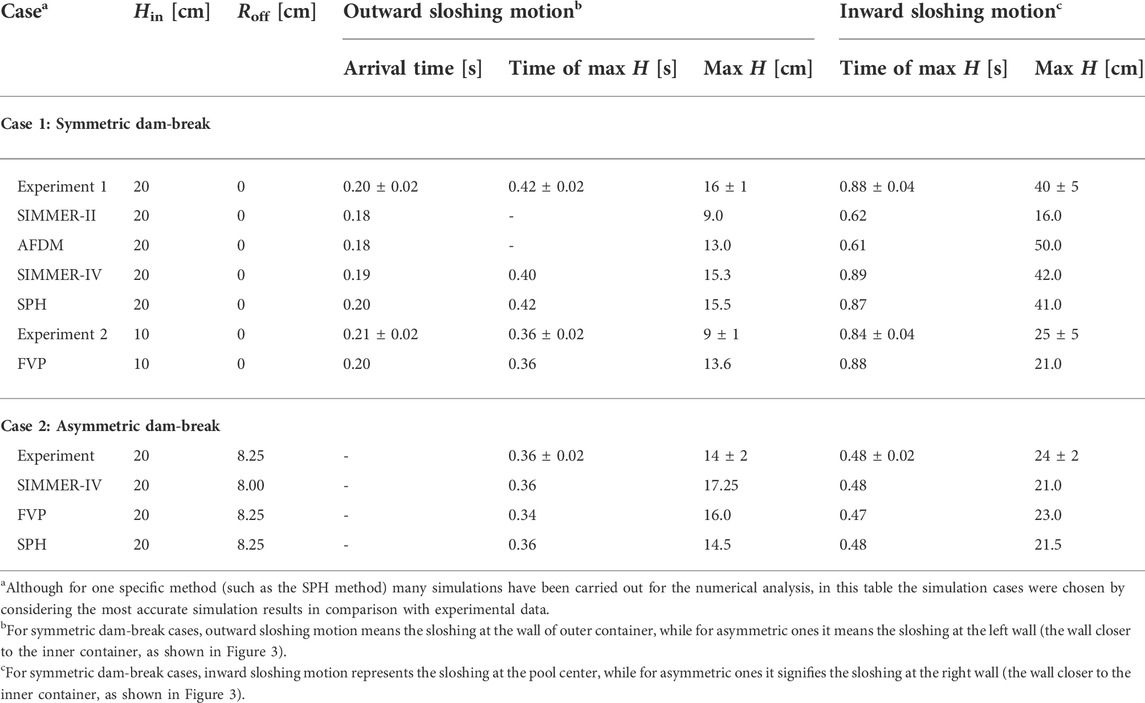
TABLE 1. Comparison of sloshing characteristics for experiments and numerical simulations under dam-break conditions with water at room temperature (D_in = 11 cm) (Maschek et al., 1992a; Maschek et al., 1992b; Munz and Maschek, 1992; Guo et al., 2012; Yamano et al., 2012; Buruchenko and Crespo, 2014; Jo et al., 2021).

TABLE 2

TABLE 2. Comparison of sloshing characteristics for experiments and numerical simulations under fluid-step conditions (D_in = 11 cm, H_in = 20 cm, H_out = 5 cm) (Maschek et al., 1992a; Maschek et al., 1992b; Pigny, 2010).

Simulation snapshots for the SIMMER-IV and SPH methods under dam-break conditions are shown in Figure 4A. It can be seen from these figures that the sloshing motion could be rationally reproduced by the simulations. The simulation results shown in Tables 1 and 2 further validate the simulation accuracy of SIMMER-IV, SPH, and FVP. According to simulations performed by Yamano et al. (2012) using the SIMMER-IV code, it was found that the sloshing characteristics could be better simulated by using 3D R-θ-Z geometry (see the data in Table 1), while the centralized maximal height of sloshing and its time were both overestimated in 2D R-θ-Z simulations due to the larger momentum of inward sloshing liquid resulting from the lack of circumferential energy dissipation. On the other hand, compared with simulations with X-Y-Z geometry, the R-θ-Z simulations can effectively avoid the non-smooth curved boundary of liquid when sloshing outward (Yamano et al., 2012), thereby providing more reliable results for maximal sloshing heights. Nevertheless, irrespective of the simulation geometry, SIMMER-IV can generally provide reliable simulation results regarding the times of maximum heights, which represent that the compaction velocities determine significantly the ramp rates in CDA of SFR.

For simulations using particle methods (i.e., SPH and FVP methods), more information about the flow shape and fragmentation of the liquid was obtained (see Figure 4A). In addition, it was confirmed that simulations with a higher resolution showed greater agreement with experimental results; this is because lower resolution would generally lead to a lower particle number density for inward sloshing motion, causing a diminished bulk flow of liquid piling up motion, thereby underestimating the centralized sloshing height (Guo et al., 2010, 2012; Vorobyev, 2012; Buruchenko and Crespo, 2014; Jo et al., 2019; Jo et al., 2021). Furthermore, by referring to Richardson’s extrapolation and the grid convergence index (GCI) (Roache, 1972, Roache, 1998), it was found that as the resolution increased (i.e., a larger particle number (N_p) was applied in calculations), the maximal centralized sloshing height tended to increase and converge to a maximal value close to the experimental data when the particle number became infinite, indicating the necessity of sufficient resolution for accurately reproducing sloshing motion (Jo et al., 2021). The FVP simulations conducted by Guo et al. (2010, 2012)showed that the choice of cut-off radius, which is a defined length characterizing the range of influence of each particle in a simulation, seemed to only have a slight impact on the simulation results. Additionally, it was determined that simulations that considered air particles (i.e., two-phase simulations) showed the best agreement with experiments due to the prevention of local numerical errors from particle deficiency in the free surface area, especially for the centralized sloshing peak (Jo et al., 2021). Through two-phase SPH simulations, it was found that gas might be entrapped in the water during the centralized sloshing motion, revealing the possibility of pressure buildup resulting from vapor trapped during the sloshing motion. Overall, more accurate simulation results were obtained using the SPH method.

2.2 Dam-break and fluid-step sloshing motions with solid obstacles

2.2.1 Description of experiments

To study the influence of the presence of solid obstacles (due to the possible incomplete melting of structural materials) on the sloshing motion, two types of obstacles, namely, rod- and ring-shaped obstacles, were employed. In the case of rod-shaped obstacles, as shown in Figures 3D,E, symmetrical (12 rods) and asymmetrical (half-symmetrical, 6 rods) distributions of rods around the inner column were considered, with varying distances from the centers of the rods to the center of the container, while the diameter of the rods was geometrically scaled down based on their blockage ratio (Maschek et al., 1992a; Maschek et al., 1992b). Figure 5B shows the sloshing motions seen in some typical cases with rod-shaped obstacles. It was found that the rod-shaped obstacles had no significant impact on the outward sloshing characteristics, but greatly dampened the inward sloshing (see Figures 4A, 5B, and compare the data with those of experiment 1 shown in Table 1 and experiments 1 and 2 shown in Table 3). This is because rod-shaped structures may impact on the inward centralized sloshing intensity to augment the inherent unsteadiness of the converging liquid waves moving inward. Such a dampening impact on inward sloshing intensity was restrained to some degree when a longer R_c (i.e., greater distance between the rods and the center) or asymmetrical distribution of rods was employed. For fluid-step cases, the effect of rod-shaped obstacles restricting inward sloshing motion seemed to be less evident. This is because in general, based on fluid-dynamics theory (Stoker, 1957), in such an oscillating sloshing system, most of the damping is relevant to the surface waves, and the kinetic energy is mostly stored in these wave packages. Therefore, compared with the dam-break cases, there was less energy dissipation in such oscillating sloshing systems with interactions between surface waves and deepwater waves (Maschek et al., 1992b).

FIGURE 5

FIGURE 5. Typical dam-break and fluid-step sloshing motion with solid obstacles/particles (Maschek et al., 1992b; Guo et al., 2012; Vorobyev, 2012). (A) Dam-break experiment with ring-shaped obstacles (D_in = 11 cm, H_in = 20 cm, H_ring = 3 cm). (B) Dam-break experiment and simulation with symmetrically distributed rod-shaped obstacles (R_c = 9.9 cm, D_in = 11 cm, H_in = 20 cm) (for the simulation case, rods are hidden in the snapshots to allow better visualization). (C) Particle-ring dam-break experiment and simulation (H_pb = 1 cm, D_in = 11 cm, H_in = 20 cm). (D) Central-particle dam-break experiment and simulation (H_pb = 7 cm, D_in = 11 cm, H_in = 23 cm).

TABLE 3

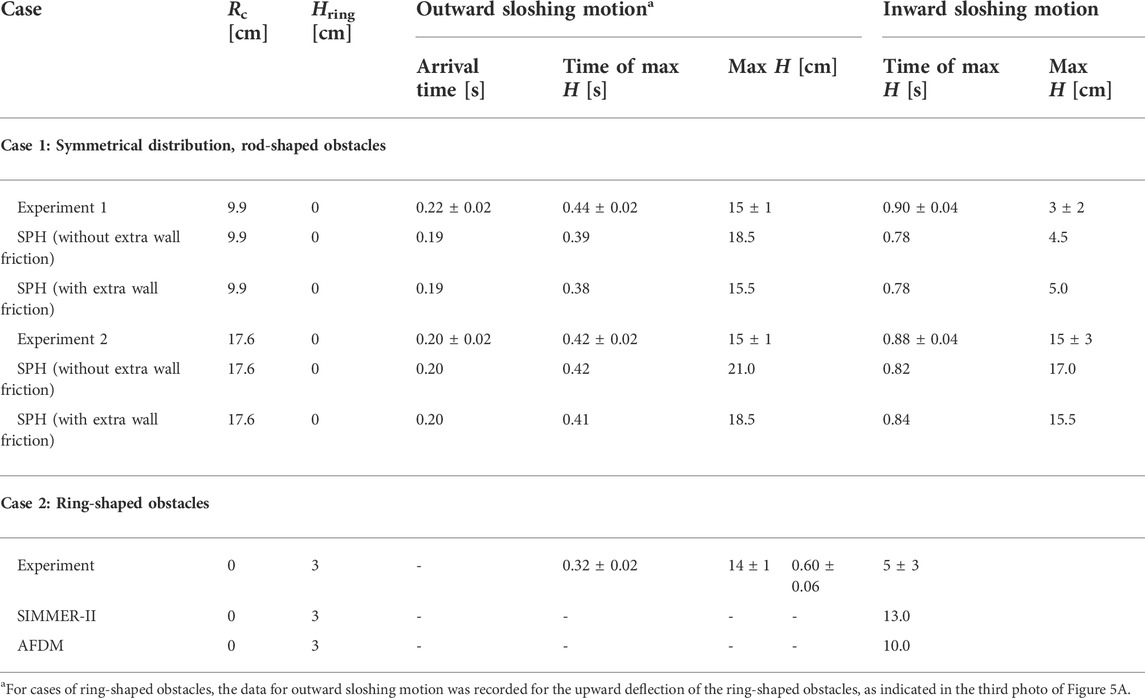
TABLE 3. Comparison of sloshing characteristics for dam-break experiments and numerical simulations with solid obstacles (D_in = 11 cm, H_in = 20 cm) (Maschek et al., 1992a; Maschek et al., 1992b; Munz and Maschek, 1992; Vorobyev et al., 2011; Vorobyev, 2012).

For the experiments using ring-shaped obstacles, as shown in Figures 3A,G, Plexiglas rings of a specific height (H_ring = 2 or 3 cm) were placed at the bottom of the pool between the outer container and the inner liquid column. As can be seen from the dam-break sloshing motion with ring-shaped obstacles that is shown in Figure 5A, due to deflection by the ring-shaped obstacles, a bowl-type liquid structure formed first during the outward sloshing motion, and the intensity of the outward sloshing at the peripheral area of the outer container and the inward sloshing at the pool center was observably diminished. Similarly, the diminishing effect of ring-shaped obstacles on sloshing intensity could also be seen in fluid-step experiments. In summary, the dampening influence of solid obstacles on the intensity of pool sloshing motion was confirmed, suggesting it might be difficult to achieve an intensive, centralized sloshing motion in cases where solid obstacles were present in a molten pool under accident conditions.

2.2.2 Numerical simulations

To simulate sloshing motions in the presence of solid obstacles, the SIMMER-II, AFDM, and SPH methods were employed. As shown in Figure 5B, the dam-break sloshing motion with symmetrically distributed rod-shaped obstacles was rationally reproduced by the SPH method, and the dampening effect of these obstacles could be well described by SPH simulations (Vorobyev et al., 2010; Vorobyev et al., 2011; Vorobyev, 2012; Buruchenko and Crespo, 2014; Jo et al., 2019; Jo et al., 2021). In particular, Vorobyev et al. (2011) found that the effect of wall friction caused by rod-shaped obstacles, which is related to momentum dissipation, played an essential role in the sloshing motions. Generally, as shown in Table 3, underestimating the wall friction would lead to an overestimate of sloshing intensity. On the other hand, Munz and Maschek (1992) determined that SIMMER-II and AFDM can provide reasonable phenomenological simulations of dam-break sloshing motions with ring-shaped obstacles. Nevertheless, an obvious overestimate of sloshing intensity (e.g., maximal sloshing height) was observed (see Table 3), which may have been due to the 2D simulation conditions, although the dampening impact of ring-shaped obstacles on the centralized sloshing intensity could be effectively reproduced through comparison with the simulation results for dam-break sloshing motions in pure liquid pools.

2.3 Dam-break sloshing motions with one-sized cylindrical solid particles

2.3.1 Description of experiments

To investigate the influence of solid particles dispersed in the liquid pool, Maschek et al. (1992a, 1992b) carried out several dam-break experiments using cylindrical acrylic particles (ρ_p = 1130 kg/m³) of height and diameter 3 and 2.5 mm, respectively, to form particle beds with a porosity of 40% (see Figure 3H). In the experiments, two types of initial particle location conditions (namely, particle-ring and central particle conditions) were applied. For the particle-ring experiments, a particle bed with a height (H_pb) of 1 or 2 cm was initially located in a ring, of which the inner diameter was 29 cm and the outer diameter was the same as D_out. As for the central particle experiments, a particle bed with a height of 7 or 22 cm was located on the bottom of the inner container. Figures 5C,D show the typical dam-break-sloshing motions under particle-ring and central particle conditions, respectively. According to Figure 5C, it can be observed that in case of particle-ring conditions, the released liquid would first push the particles outward and then slosh inward together with the particles to form an asymmetric multiphase centralized peak, which involved gas, liquid, and solid particles, thereby destroying the coherent sloshing motion and weakening the intensity of inward sloshing. Similarly, asymmetric multiphase centralized sloshing motion occurred in the central-particle experiments using a particle bed with a low height (7 cm), so that the inward sloshing intensity was diminished (see Figure 5D). However, it was found that if the particles dominated the pool (e.g., if the inner column was composed of water and a particle bed of the same height), the multiphase flow would slosh outward but no inward sloshing motion could be observed (Maschek et al., 1992b), indicating the complete dampening of centralized sloshing motion. Hence, based on these findings, it can be concluded that greater particulate domination plays a crucial role in diminishing the intensity of sloshing.

2.3.2 Numerical simulations

Regarding the simulations for dam-break sloshing motions involving solid particles, SIMMER-IV (for particle-ring cases) and FVP (for both particle-ring and central particle cases) were applied (Guo et al., 2012; Yamano et al., 2012). For the Eulerian-based SIMMER-IV code, the solid particles were represented by the volume fraction with a porosity of 40%, and their size was specified so that the same volume-equivalent diameter could be ensured in accordance with that of the particles used in the experiments. However, for this reason, the differences in the maximum sloshing height between solid particles and liquid were not identified. From the SIMMER-IV simulations, the necessity for implementing the particle viscosity model and the momentum diffusion term in the momentum conservation equation (utilized to model the increase in fluid viscosity following the increment of particle volume fraction) was validated, so that the effect of solid particles on sloshing motions can be better reproduced (Yamano et al., 2012). As shown in Table 4, it was found that if the momentum diffusion term and the particle viscosity model were not involved in the calculations, the centralized sloshing intensity would be significantly overestimated due to the larger compaction of the multiphase sloshing mixture. On the other hand, although the sloshing motion could be qualitatively reproduced in the FVP simulations (see Figures 5C,D), it should be highlighted that, as shown in Table 4, the sloshing intensity was overestimated by FVP, which was probably due to the lack of models for the interaction of solid particles (Guo et al., 2012). In short, the lack of consideration of multiphase interactions, which may induce momentum and energy dissipation, seems to lead to the overestimation of sloshing intensity. Therefore, to better reproduce the experimental sloshing motion and achieve more accurate calculations under actual reactor conditions, multiphase interactions should be modeled more appropriately.

TABLE 4

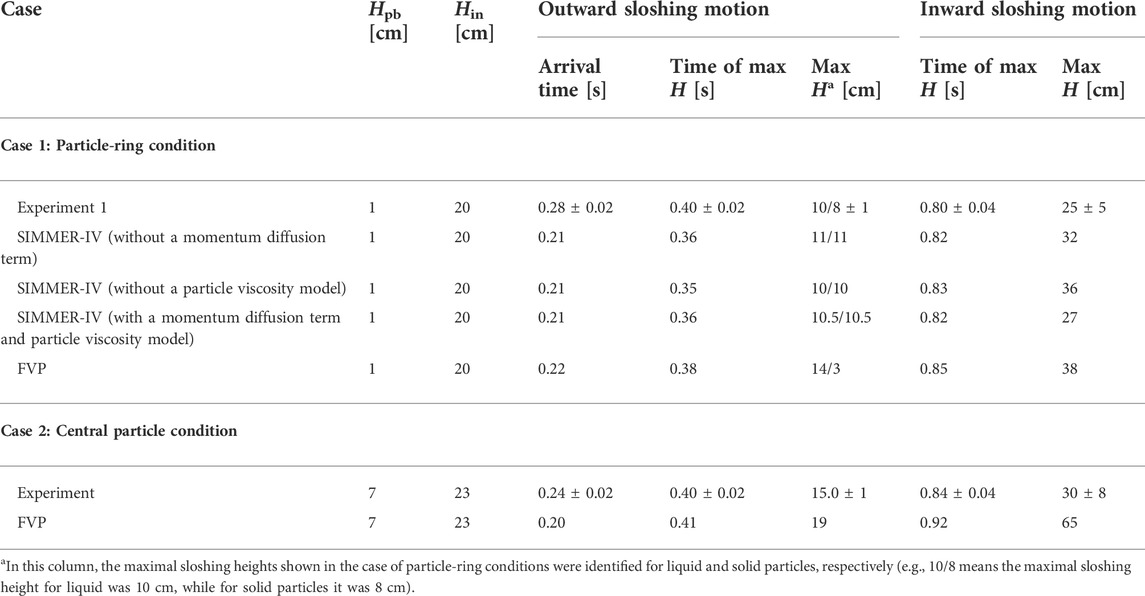
TABLE 4. Comparison of sloshing characteristics for dam-break experiments and numerical simulations with solid particles (D_in = 11 cm) (Maschek et al., 1992b; Guo et al., 2012; Yamano et al., 2012).

3 Sloshing motion under gas-injection conditions

3.1 Gas-injection sloshing motion with hydraulic disturbances in pure liquid pools

3.1.1 Description of experiments

Aimed at preliminarily studying the effect of thermal-hydraulic or neutronic disturbances on sloshing motions, Morita et al. (2014) conducted several experiments that involved introducing hydraulic disturbances by injecting nitrogen gas into a 2D water pool. Figure 6A shows the experimental devices. Before each experiment, the water level and the nitrogen gas pressure and flow rate were initially set at 400 mm, 56 kPa, and 230 L/min, respectively. In the experiments, gas was injected into the pool within 0.2 s through a square nozzle with a side length of 10 cm located at the bottom of the tank. This was performed 10 times with a fixed period (T) of 0.86 s. Then, additional gas at a similar flow rate and pressure (230 L/min and 56 kPa, respectively) was injected at different times (0.25 T or 0.75 T) after the 10 periodic injections, to induce hydraulic disturbances in the liquid pool.

FIGURE 6

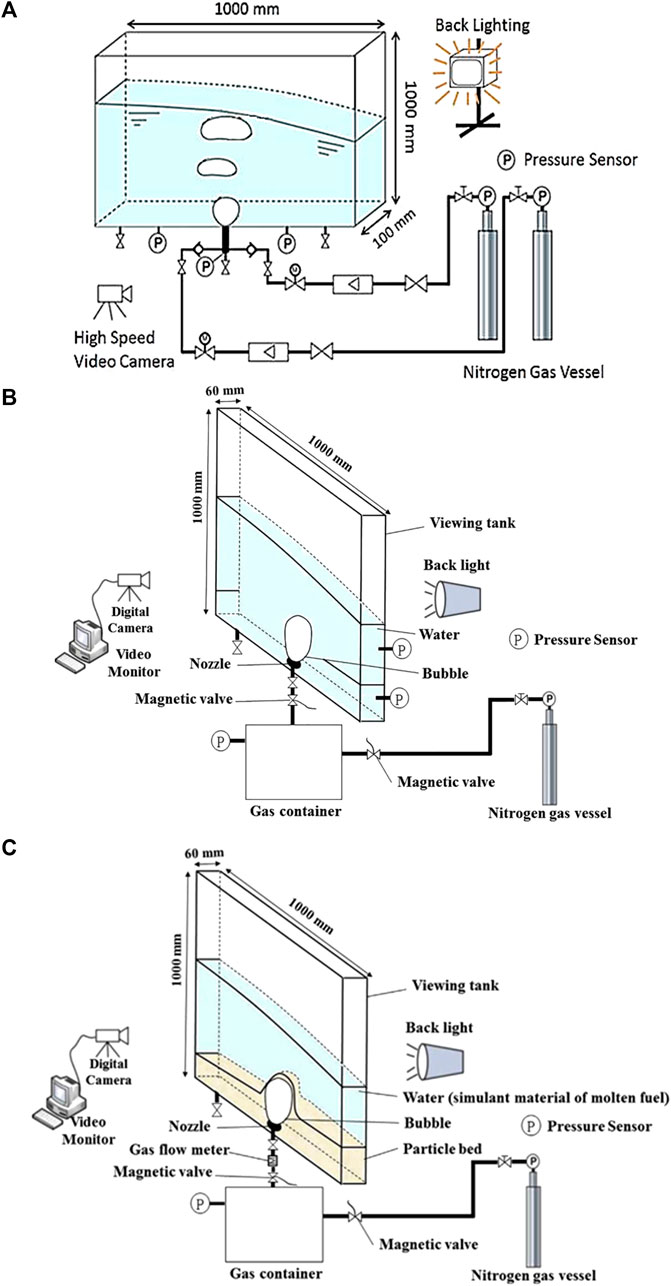
FIGURE 6. Experimental system for gas-injection experiments in liquid pools (Morita et al., 2014; Cheng et al., 2018c; Cheng et al., 2019b). (A) Pure liquid pool with hydraulic disturbances. (B) Pure liquid pool without hydraulic disturbances. (C) Liquid pool without hydraulic disturbances and with a solid particle bed.

Figures 7A–C compare the central and peripheral water-level variations in cases under different types of disturbance in the experiments. It can be seen that the sloshing motion without disturbances (see Figure 7A) is relatively stationary, while observable variations in the water level can be seen after external disturbances were introduced (see Figures 7B,C). In more detail, it can be seen that the disturbance in Type 1 (see Figure 7B) would strengthen (augment) the sloshing motion but in Type 2 (Figure 7C) the sloshing intensity was weakened (mitigated). This was because in Type 1, the gas was injected at the moment when liquid sloshed out toward the wall, then the reflected inward sloshing liquid moved to the central area and joined with the upward gas, which subsequently detached from the liquid and enhanced (augmented) the outward sloshing motion to the peripheral areas (Morita et al., 2014). For Type 2, on the other hand, after being injected the gas reached the liquid surface at the moment when the outward sloshing motion occurred. As a result, the subsequent inward sloshing liquid wave interacted with the wave resulting from the gas detaching from the liquid, leading to a dampened (mitigated) sloshing motion. According to these typical cases of sloshing motion with hydraulic disturbances, the overlaying (namely augmenting or mitigating) effect resulting from interactions between local liquid flows was identified.

FIGURE 7

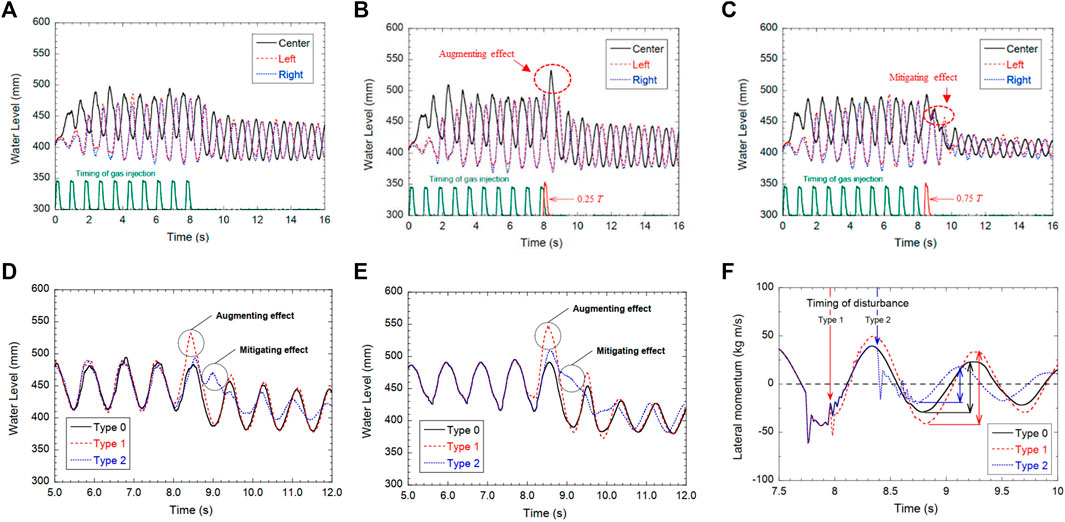
FIGURE 7. Water-level variations indifferent areas of the pool for gas-injection conditions with hydraulic disturbances (Morita et al., 2014). (A) Type 0 experiments: no disturbance. (B) Type 1 experiments: disturbance at 0.25 T (7.955 s). (C) Type 2 experiments: disturbance at 0.75 T (8.385 s). (D) Central water-level variations in experiments. (E) Central water-level variations in simulations. (F) Lateral momentum variations in simulations (a negative lateral momentum means an overall outward sloshing motion of liquid, while a positive one means an overall centralized inward sloshing motion of liquid).

To sum up, although the thermal-hydraulic or neutronic disturbances resulting from local expansion in the molten pool could not be comprehensively represented through the introduced external disturbances triggered by injected gas in the experiments (e.g., the reactivity insertion resulted from the fuel compaction caused by the sloshing motion), it was confirmed that the timing of any external disturbances that were introduced would determine the (mitigating or augmenting) effects on the sloshing intensity.

3.1.2 Numerical simulations

Aiming to provide a deeper understanding of the effect of external disturbances, Morita et al. (2014) applied SIMMER-III codes to perform further analyses. The reliability of SIMMER-III for simulating sloshing motion initiated by injected gas with hydraulic disturbances was validated through comparisons with experimental water-level variations for different types of disturbance. The augmenting and mitigating effects were reasonably simulated as observed in the experiments (see Figures 7D,E). To more comprehensively investigate the characteristics of the entire sloshing system, the lateral liquid momentum was focused on, which was equal to the sum of the products of liquid velocity and liquid mass of all mesh cells (Morita et al., 2014). As shown in Figure 7F, there was generally good agreement between water-level and lateral momentum variations. In addition, Figure 7F shows that the introduction of external disturbances could augment the outward sloshing motion but mitigate the inward sloshing motion. This may indicate that the occurrence of augmented or mitigated sloshing motion following the introduction of an external disturbance could depend on the type of sloshing motion (i.e., outward or inward) at the timing of the disturbance, although further investigations are required to clarify this (e.g., Fourier analysis of signals collected from experiments along with an evaluation of the impulse of a single bubble to obtain fundamental quantities of the oscillator for such a quasi “forced oscillating system”). In addition, further studies that consider neutronic feedback are necessary to rationally evaluate the energetic potential of the molten pool and elucidate the sloshing motions in response to neutronic or thermal-hydraulic disturbances.

3.2 Gas-injection sloshing motion without hydraulic disturbances in liquid pools

Focusing on the sloshing motions induced by local FCI, extensive experiments without hydraulic disturbances were conducted by Cheng et al. (2018c, 2020), who injected nitrogen gas into narrow 2D liquid pools (including pure and stratified liquid pools) to obtain better visualization (see Figure 6B). To simulate the co-existence of molten fuel and molten stainless steel, the stratified liquid was composed of transparent oil and colored water, which possessed comparable density and viscosity ratios to those expected to be crucial parameters affecting sloshing characteristics (Fauske and Koyama, 2002; Cheng et al., 2020). Various parameters, such as the pressure of injected gas (P, 1.5–4.5 bar), the duration of gas injection (ΔT, 0.06–0.1 s), nozzle size (D_n, 10–50 mm), and initial liquid (water or cleaning oil) depth (H_w or H_o, 10–60 cm), were investigated in experiments to comprehensively study the parametric effect on the sloshing motion. Typically, the gas-injection durations were set with consideration of the durations of vapor expansion triggered by local FCIs, according to past investigations of FCIs (Cheng et al., 2014; Cheng et al., 2015; Zhang et al., 2018; Cheng et al., 2019d).

The transient sloshing motions under gas-injection conditions without disturbances are shown in Figure 8. From Figures 8A,B, it can be seen that the shape of the injected gas bubble initially had a concave lower surface following its detachment from the pool bottom, indicating a relatively higher (lower) pressure inside the bubble in comparison with the liquid static pressure at its upper (lower) surface. As the gas bubble rose up, probably due to this difference in pressure, two symmetric vortices with an upward trailing flow, as well as the continuous enlargement and geometrical elongation of the bubble, were observed. When the bubble arrived at the liquid surface, it tended to break up immediately, possibly as a result of the huge difference in pressure between the static water pressure at its base and the atmospheric pressure. Due to this rapid bubble bursting, the two symmetric vortices accelerated and moved to the peripheral areas, simultaneously impelling the central liquid out toward the peripheral areas. After that, the liquid was pushed back to the center of the pool under the gravitational effect and formed a centralized sloshing peak.

FIGURE 8

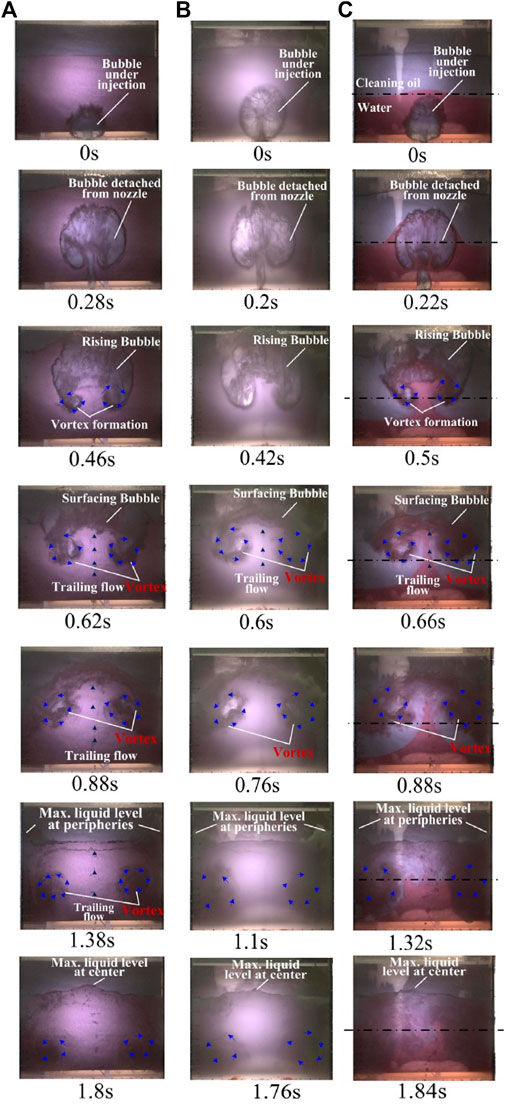
FIGURE 8. Typical sloshing motions in gas-injection experiments without disturbances (ΔT = 0.1 s, p = 4 bar) (Cheng et al., 2020). (A) Pure water pool (H_w = 60 cm, H_o = 0 cm). (B) Pure cleaning oil pool (H_w = 0 cm, H_o = 60 cm). (C) Stratified liquid pool (H_w = 30 cm, H_o = 30 cm).

The sloshing flow-regime characteristics described above were found to be common for various experimental cases, but a comparatively larger bubble was observed in cases of lower liquid density (see Figures 8A,B). Nevertheless, compared with the cases with pure liquid pools, in the cases of pools with stratified liquid it was seen that during the process of the bubble rising upwards, much water was entrained upward by the two vortices along with the upward trailing flow and subsequently diluted the upper cleaning oil region (see Figure 8C). Although a centralized water peak emerged due to the entraining effect of the bubble (see the photo at 0.88 s in Figure 8C), recognizing the thinned colored region near the peak, it should be pointed out that the compaction of water in such situations was very limited. This is because compared with the initial depth of water, the vertical location of water peak was not obviously elevated, and was even lower than the initial water depth for some specific cases (Cheng et al., 2020). It was also verified that, in addition to the injected gas pressure, the ratio of the depth of the different liquids (H_w/H_o) played a prominent role in the abovementioned water entrainments (Cheng et al., 2020). For instance, in cases of a lower depth ratio (i.e., more oil and less water), the water region could remain more static under the influence of the weakened entrainment effect resulting from the greater distances from the water region to the upper surface of the liquid (Cheng et al., 2020). For cases with a greater water depth and a lower oil depth, although the entrainment effect caused by the generated vortices was strengthened, a large majority of the water was diluted and redistributed. Therefore, the above analysis reveals that if liquid stratification occurs under real accidental conditions in a reactor (i.e., a layer of molten structural materials covers the upper surface of molten fuel), regardless of the depth ratio, the fuel compaction may be generally diminished.

For the quantitative analyses of parametric effects, Figure 9A shows the influence of injected gas pressure on the peak height of the liquid level (ΔH_max) in the central and peripheral areas of the pool. From this figure, it can be observed that with increasing gas pressure, the sloshing intensity at the center and peripheral areas increased until a critical pressure was reached (i.e., approximately 3.5, 3, and 4 bar for pure water, pure cleaning oil, and stratified liquid, respectively) and subsequently tended to diminish, indicating a possibly saturated sloshing intensity. This may be understood through the fact that during the inceptive stage of increasing pressure, a more significant influence on the variations in liquid-level height could occur as a result of the much greater lifting force on the rising bubble caused by the higher pressure of injected gas. However, if the injected gas pressure became sufficiently high (such as larger than the critical value), as shown in Figure 9B, the time that the bubble resides in the liquid pool could be noticeably reduced by the much-increased velocity of the rising bubble, resulting in a dampening effect on the sloshing intensity. In Figures 9A,B, a similar tendency in the variation of the residence time of the bubble with gas-injection pressure can be seen. This may be the reason that although the speed of the rising bubble was expected to accelerate with increased injected gas pressure, some transient processes (e.g., bubble bursting as well as deformation and elongation) are likely to play a more prominent role during the bubble rising process (when the pressure was below the critical value). These transient processes therefore result in a longer residence time (Cheng et al., 2018c). Nevertheless, as the injected gas pressure augmented over the critical value, though such effect on extending the bubble residence time resulted from the transient processes still existed to some degree, the overall bubble rising velocity should become a more dominant factor on the residence time.

FIGURE 9

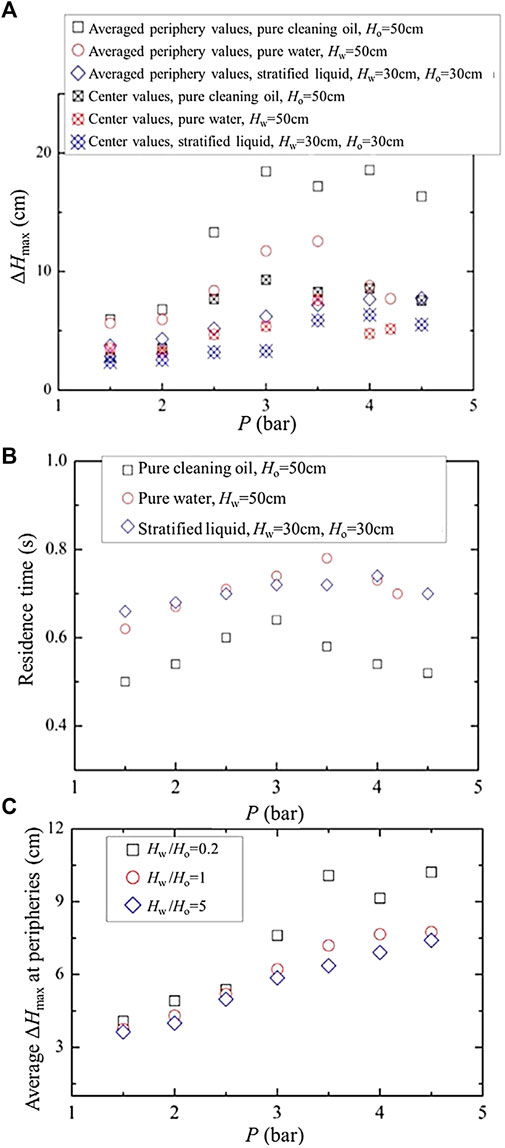
FIGURE 9. Influence of injected gas pressure on sloshing intensity (D_n = 50 mm, ΔT = 0.1 s) (Cheng et al., 2020). (A) Maximal liquid sloshing height. (B) Residence time. (C) Peripheral ΔH_max for stratified liquid (H_pool = 60 cm).

One more important point that can be seen from Figures 9A,B is that for experiments in pure liquid pools, a greater liquid density seemed to diminish the maximal elevation of the liquid level due to the larger resistance force on the rising bubble caused by greater inertia of the liquid. With cases of stratified liquid, as shown in Figure 9C, the sloshing intensity was clearly weakened by employing a greater water–oil depth ratio, which signified more fraction of larger-density water in the pool to restrain the upward movement of rising bubble due to its relatively larger liquid inertial force. Furthermore, due to this larger inertial force of liquid, the critical pressure was found to become relatively larger in cases of larger water–oil ratios (see Figure 9C), revealing that the a much intensive sloshing motion was difficult to attained in this case. It has been demonstrated that the sloshing intensity tended to be strengthened first then diminished afterward with the increasing initial depth of liquid in the pool (H_pool). This may be explained by the fact that a greater depth of liquid could enhance the liquid’s inertia (restricting effect) and prolong the bubble residence time (positive effect) within the liquid pool in such cases (Cheng et al., 2018a). Additionally, it was generally found that smaller nozzle size and longer gas-injection duration could effectively enhance the sloshing motion due to the much more violent hydraulic disturbances to the static liquid pool. However, more analyses are required to quantitatively considering the time-scale couplings and momentum injection rate during the sloshing motion for clarifying the correlations between sloshing intensity and varying parameters.

On balance, owing to the more comprehensive and detailed experiments conducted by Cheng et al. (2018c, 2020), various parametric effects on the sloshing intensity were validated e.g., depth ratio of stratified liquids, injected gas pressure, liquid depth, and gas-injection duration as well as nozzle size. Additionally, a possible way to mitigate fuel compaction in actual reactor accidents was identified, if a layer of molten structural materials exists at the upper area of the molten fuel pool.

3.3 Gas-injection sloshing motion with solid particles

Figure 6C shows the experimental system employed for investigations with solid particles by utilizing gas injection. Considering the probable situations that might occur in a CDA of an SFR, particle beds with different compositions (such as particles of different density, size (d_p, 0.125–8 mm), shape (spherical and non-spherical), components (single size and density, bicomponent mixed-size, bicomponent mixed density), and different initial height (H_pb, 5–30 cm) were used and placed on the bottom of pool, and gas-injection duration (0.06–0.1 s) as well as injected gas pressure (2–4 bar) were also treated as experimental parameters to obtain valuable experimental data for further numerical validation (Cheng et al., 2019a, 2019b, 2019c; Xu et al., 2022).

From the basic experiments with single-sized spherical particles, three stages of development for the sloshing process with solid particles were observed. The first and second experimental snapshots in Figures 10A–E illustrate Stage 1, in which the gas bubble entered at the bottom of a particle bed and rose to the top of the particle bed. In the third and fourth experimental snapshots in Figures 10A–E, Stage 2 is shown, in which the bubble detached from the particle bed with some possibility that particles could be pushed up and subsequently roll down along the edge of the bubble. After that, as displayed in the fifth and sixth experimental snapshots in Figures 10A–E, the bubble moved upward in the upper free liquid area to subsequently induce the outward peripheral and inward centralized sloshing motions. In addition, according to the multiphase interaction mechanism involving liquid, injected gas, and solid particles, three typical flow regimes (Regime I: bubble-impulsion dominant regime; Regime II: transitional regime; and Regime III: bed-inertia dominant regime), as shown in Figure 10, were specified and resulted in three corresponding final particle bed geometries. It should be noted that such characteristics might not emerge for fluidized beds (Didwania and Homsy, 1981; Bai et al., 1999), as under these experimental conditions the particles were far from being fluidized beds (i.e., no fluidization). Based on experimental analyses, as shown in Figure 11, the remarkable parametric effects on the flow-regime transitions and sloshing intensity were investigated and validated. In general, the flow-regime transitions were dictated by two important factors: particle-bed inertia and gas-bubble impulsion.

FIGURE 10

FIGURE 10. Typical sloshing motion under gas-injection conditions with solid particles (spherical glass particles, ΔT = 0.1 s) (Cheng et al., 2019b). (A) Regime I (d_p = 0.125 mm, H_pb = 15 cm, p = 3 bar). (B) Regime II (d_p = 0.5 mm, H_pb = 15 cm, p = 3 bar). (C) Regime II (d_p = 0.5 mm, H_pb = 30 cm, p = 3 bar). (D) Regime II (d_p = 0.5 mm, H_pb = 30 cm, p = 2 bar). (E) Regime III (d_p = 6 mm, H_pb = 15 cm, p = 3 bar).

FIGURE 11

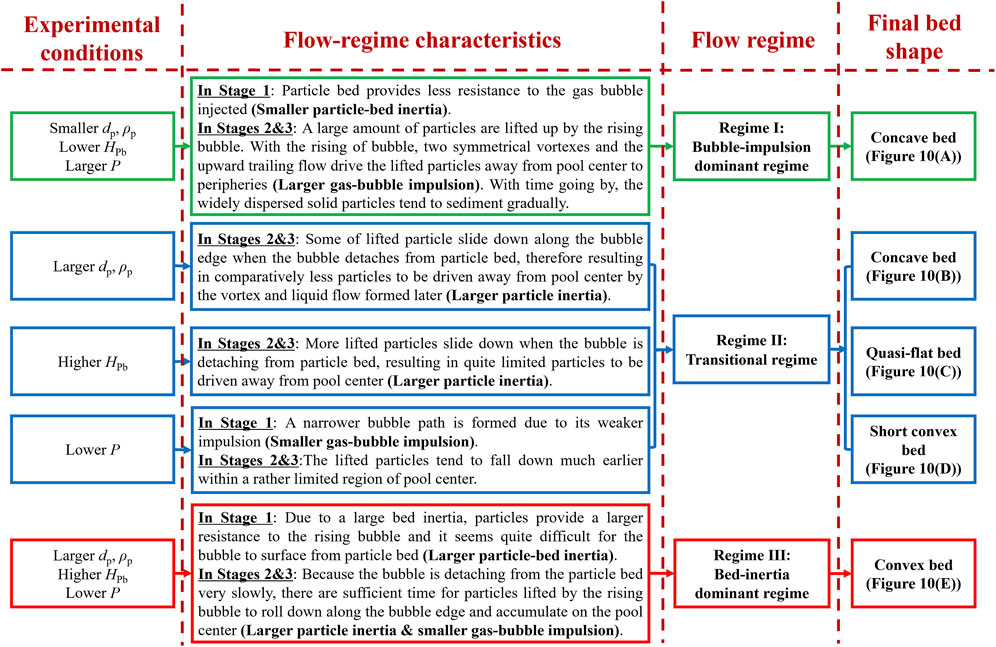
FIGURE 11. Illustrations for different flow-regime characteristics under different experimental conditions.

In the extended experiments with single-sized non-spherical particles, which were conducted considering the fact that various shapes of solid particles may be encountered in an actual CDA, particles of cylindrical, triangular prism, and irregular shapes were taken into account (Cheng et al., 2019c). Based on experimental observations, it was found that as the particle sphericity increased, due to the additional particle–particle friction and collisions resulting from some shape-relevant properties (Cheng et al., 2018b), not only was the overall particle-bed inertia diminished in Stage 1 but also the rolling-down process tended to be prevented in Stage 2, while interactions between the fluid flow and solid particles were enhanced, as a result facilitating regime transitions from a higher number to a lower one.

Recognizing that solid particles may also occur in various sizes in the molten pool of an actual CDA of an SFR, a large number of extended experiments using bicomponent mixed-sized spherical solid particles at the same densities but with different volumetric mixing ratios were conducted by Cheng et al. (2019a) to elucidate the effect of mixed sizes on sloshing motion. From the experiments, although the abovementioned key parametric effects on the flow-regime transitions were in general validated, typically the flow-regime characteristics tended to shift from a higher (e.g., Regime III) to a lower one (e.g., Regime II) if larger weights of smaller particles were employed in the particle mixtures. In addition, compared with the experimental results using single-sized solid particles, an incongruity could be found, especially for experiments employing more smaller particles within the particle mixtures. In the mixed-sized experiments, a quasi-flat bed was not only found in the transitional regime (namely Regime II) but also emerged in Regime II/III and Regime III/II, which signified the flow regimes involving the characteristics of Regime II and Regime III. Particularly, the symbols III/II and II/III were marked for such experimental cases which had more characteristics of Regimes III and II, respectively. The reason for this incongruity may be that although the overall impact of particle-bed inertia was comparatively somewhat larger than that of the gas-bubble impulsion in cases of Regime III/II or II/III, the impulsion of the rising bubble might still exceed the inertia of smaller particles within the particle mixtures. This can cause the separation of particles of different sizes in the particle mixtures, which could lead to flow-regime deviation from a strict Regime II for instance (Cheng et al., 2019a). This may also explain why the in-between flow regimes were mostly emerged when more particles with small size presented in the particle mixtures. Noticing this point, further dimensional analysis may therefore be needed to classify the flow regimes and patterns more elaborately.

Considering the co-existence of other non-melted or refrozen materials (e.g., control rods and structures) in the molten pool during an actual scenario of a CDA in an SFR, further experiments were carried out by Xu et al. (2022) using bicomponent mixed-density particles of identical sizes. In general, they re-confirmed the fundamental effects of experimental parameters (such as particle size, injected gas pressure, and height of the particle bed) on the flow-regime transitions. For the effect of mixed-density particles, it was found that if the particle mixtures were composed of more high-density particles, the flow regimes would transit from a lower one to a higher one due to the relatively larger overall particle-bed inertia. However, compared with the mixed-size cases, the aforementioned in-between flow regimes were not found. This may be due to the smaller particles being more likely to pass through the larger gaps (or void spaces) among larger particles, while for mixed-density cases, due to the identical size of each component, the capability of lighter particles to pass through the gaps between heavier ones was thought to be largely restrained.

In short, based on experiments using gas injection with solid particles, it was demonstrated that through increasing the overall particle-bed inertia by particle-bed-related parameters (e.g., particle density, particle size, and height of the particle bed), not only would the gas-bubble impulsion effect in Stage 1 be to some extent limited within the particle bed but also the rolling-down effect of solid particles along with their sedimentation effect lifted by upward moving injected gas in Stage 2, resulting in the flow regimes shifting from lower to higher ones.

4 Conclusion and future prospects

4.1 Conclusion

Studies into molten-pool sloshing motion are important for the improved evaluation of the transition phase of CDAs in SFRs. Knowledge gained from experimental and numerical investigations into the mechanisms and characteristics of molten-pool sloshing motion are valuable not only for the improvement and verification of SFR safety analysis codes (which can invoke the simulation using actual materials in reactors and coupling with neutronic models) but also to provide reference data for studies of sloshing motion in other fields of engineering. We have systematically reviewed and discussed experimental and numerical studies into sloshing characteristics that have been performed in the past, focusing on thermal-hydraulics aspects under various conditions, including dam-break, fluid-step, and gas-injection conditions. Based on these studies, the important characteristics necessary for evaluating sloshing intensity (e.g., the maximal heights that emerge during peripheral outward and centralized inward sloshing motions) were identified, and the applicability of various simulation approaches (such as SIMMER code, SPH, and FVP methods) were validated through comparisons of both qualitative and quantitative experimental observations.

In the pioneering dam-break and fluid-step sloshing experiments in pure liquid pools, it was found that the sloshing characteristics were significantly affected by the overall liquid inertia and symmetricity of the sloshing system. With the further consideration of the non-melted or refrozen solid materials (e.g., control rods and structural materials) that may be present in a molten pool during an actual CDA in an SFR, dam-break and fluid-step experiments with solid phases (including rod- and ring-shaped obstacles, and solid particles) were conducted, and the dampening effect of the presence of solid phases on sloshing intensity was confirmed. This illustrated the difficulty of obtaining an intensive sloshing motion when sufficient amount of solid phases still existed in the molten pool during the CDA of SFR. As for the numerical simulations, the reasonability and applicability of SIMMER-IV code, SPH, and FVP methods for reproducing a dam-break along with the fluid-step sloshing motions in pure liquid pools (particularly for the compaction velocity) were validated. In general, for Eulerian-based methods (such as SIMMER code), the notable influences of the spatial differencing order and simulation geometries on the numerical accuracy were found. For the particle methods, more accurate results could be attained, with higher resolution, but this also caused an unavoidable reduction in numerical efficiency. In addition, it was revealed that vapor-trapping phenomena might occur during centralized sloshing motion, in accordance with the two-phase SPH simulations. However, from the simulations of dam-break experiments with solid phases, the necessity for modeling the multiphase interactions (particularly for those on solid phases) to obtain adequate simulation rationality and accuracy was demonstrated, whereas the dampening effect of solid phases on sloshing intensity could not observed or were underestimated.

As sloshing motion might be encountered as a result of rapid vapor generation and pressure buildup due to local FCIs within a large-scale molten pool during its formation and enlargement, the gas-injection method was used to study this type of sloshing motion. To study the effect of thermal-hydraulic disturbances on sloshing motions, several experiments using the gas-injection method were carried out with hydraulic disturbances in a pure-water pool. Based on these experiments, the mitigating and augmenting effects on the sloshing intensity were found to depend on the timing of the external disturbances that were introduced, due to the interactions between local liquid flows; these could also be reproduced well through the SIMMER-III calculations. On the other hand, to more deeply and comprehensively elucidate the sloshing mechanism and the characteristics triggered by a local FCI, several experiments were conducted using the gas-injection method without hydraulic disturbances in liquid pools without solid phases, and various parametric effects were taken into account. Based on qualitative and quantitative experimental observations, it was confirmed that a maximal sloshing intensity was likely to emerge a critical pressure of injected gas, whose value is up to the liquid inertia (e.g., liquid density and liquid depth) as well as the depth ratio of stratified liquids, was reached. Moreover, it was revealed that fuel compaction might be diminished in real reactor accidents in cases where the stratification of molten fuel and molten structural materials was present, although the possibility of reactivity insertion due to molten-pool stratification should be noted for the real accidents. In the gas-injection experiments with solid particles, three typical flow regimes, referred to as the bubble-impulsion dominant regime, the transitional regime, and the bed-inertia dominant regime, were identifiable and were dominated by the overall gas-bubble impulsion and particle-bed inertia in different stages during the sloshing process. However, in the cases with mixed-size particles, some in-between flow regimes were found to appear due to the different prominence of larger-size particles and smaller-size particles in the particle bed against the gas-bubble impulsion, indicating a different time scale for momentum dissipation between larger and smaller particles.

4.2 Discussion and future prospects

Although much valuable knowledge and understanding concerning molten-pool sloshing motion have been gained through experiments and numerical simulations with their analyses of thermal-hydraulics mechanisms, in general, the analyses and discussions are lacking in their consideration of momentum dissipation processes (e.g., interfacial dynamics between fluid and particles). The contributors to the dissipation of momentum (e.g., particle size, particle density, particle components, intensity of gas-impulsion, and liquid properties) should be studied. In addition, the behaviors of the fluid and solid mixture may be different with the different time scale of impulsion built-up. Therefore, more elaborate studies into the initiators of sloshing motion (e.g., local FCIs and fuel or steel vapor generation) should be performed to better understand the mechanism and characteristics of molten-pool sloshing. On the other hand, it should be pointed out that compared with the parametric conditions that were considered in the experiments, the actual conditions in reactor accidents are more complicated. Furthermore, as experiments at real scale with real materials are difficult to perform, the verification of safety analysis codes/methods is of great significance if it is based on more elaborate experiments that clarify the mechanism of sloshing motion under the possible conditions that may occur during a CDA. The numerical accuracy for reproducing the sloshing motion (particularly for cases with solid phases) should also be further improved for the improved assessment of severe SFR accidents. In addition, investigations should focus on the sloshing intensity and fuel compaction velocity, which are anticipated to be of great importance to the power deposition and recriticality issues during a CDA of an SFR.

In the future, experimental and numerical studies into the sloshing mechanism and characteristics could include but are not limited to the following aspects.

1) Further gas-injection experiments with external disturbances that consider more complete parametric conditions. Although it has been confirmed that the timing of insertion of external disturbances is a key factor for augmenting or mitigating the sloshing intensity, it remains necessary to conduct additional experiments with a variety of other parameters (such as gas-injection duration period along with pressure, intensity of disturbances, and location of disturbance insertion) to gain a deeper clarification of the effect of external disturbances to study the determining regular for the overlaying (namely augmenting or mitigating) effects and the timing of introducing external disturbances.

2) Further experiments and validations for multicomponent (i.e., more than three components) mixed solid particles (including mixed-sized and mixed-density particles) using gas-injection methods. Although some important sloshing characteristics were captured in past investigations by using mixed-sized and mixed-density spherical particles under gas-injection conditions, it should be noted that only bicomponent particle mixtures were used. Therefore, to obtain more information regarding the sloshing motion under a more realistic particulate situation, further experimental investigations should be performed with multicomponent mixed particles. In addition, considering the incongruities found in the previous bicomponent mixed-sized experiments, elaboration of some dimensional analyses may be necessary to evaluate the flow-regime characteristics and identifications during the sloshing motion with particle bed consisted of multicomponent mixed particles.

3) Further gas-injection experiments in large-scale 3D pools. In earlier experiments that focused on sloshing motions initiated by local FCIs, 2D liquid pools were used to ensure sufficient experimental visualization so that the basic and essential sloshing mechanisms and characteristics could be identified and understood. By referring the previous experimental studies regarding the debris bed self-leveling behavior by using gas-injection method for the CDA analysis of SFR (Cheng et al., 2011; Cheng et al., 2013a; Cheng et al., 2013b), it may be feasible that insights and fundamental understandings obtained through 2D experiments can be validated in large-scale 3D experiments, although some deviations or changes concerning the specific values of parameters (such as the critical gas-injection pressure) may occur due to the dimensional and scale changes (e.g., the length scale of the ratio of liquid pool height to diameter, and the time scale of bubble influence) and wall effects. Thus, to obtain a more comprehensive understanding of the molten-pool sloshing motion initiated by a local FCI, it will be necessary to perform large-scale 3D experiments with proper scale and dimensional analysis for space-, mass-, energy-, and time-scales to assess similarity rules. These large-scale 3D studies may validate the knowledge of the sloshing mechanism and characteristics accumulated from 2D experiments, while any changes in critical values following the dimensional and scale variations should also be investigated.

4) Numerical simulations for sloshing motion under gas-injection conditions without disturbances. In the earlier numerical studies, a variety of numerical approaches was attempted and validated in the dam-break and fluid-step sloshing experiments. However, the applicability of these approaches or other numerical methods, e.g., the moving particle semi-implicit (MPS) method that is applicable in the simulation of multiphase flows with various interfaces between phases (Park et al., 2016; Liu et al., 2021), should be continuously examined to obtain more reliable analysis for the evaluation of the sloshing motion in a CDA of an SFR based on the gas-injection experiments for simulating the sloshing motion triggered by local FCIs, during which the high-velocity gas flow along with large bubble deformation should be considered.

5) Further numerical simulations for sloshing motion with solid phases by appropriate treatment of the multiphase interactions involving the solid phases. In earlier numerical simulations for sloshing motion with solid phases, the need to appropriately estimate the multiphase interactions was demonstrated. Although reasonable simulation results could be obtained by employing some macroscopic models (such as the particle viscosity model) and technical approaches (e.g., adding a momentum diffusion term and wall friction), it should be recognized that the solid phase still played a less prominent role in the sloshing motion in such cases compared with other phases. Thus, the development and use is anticipated of more effective models or methods for reproducing the sloshing motion with a significant amount of solids (e.g., for gas-injection experiments with solid particles). For sloshing motion with solid particles, taking into account the past numerical investigations into particle-related phenomena for the assessment of severe accidents in SFRs (Shamsuzzaman et al., 2014; Tagami and Tobita, 2014; Guo et al., 2017; Tagami et al., 2018; Sheikh et al., 2020), in which solid particles played a major role in the multiphase behaviors, microscopic models for inter-particle collisions and contacts or the discrete element method (DEM) may additionally be considered in the simulations to provide appropriate estimates of particle–particle interactions.

6) Further investigations into the effect of coupling between nuclear power deposition as well as recriticality and pool sloshing motion based on the knowledge obtained from thermal-hydraulics studies. Some investigations have been performed to study the coupling between nuclear power deposition as well as recriticality and pool sloshing motion (e.g., a SIMMER-III simulation to study the power deposition and criticality during sloshing motion by assuming a mass of molten fuel fragment falls into the molten pool (Tatewaki et al., 2015)), and the effect of the power excursion and recriticality on the sloshing intensity were preliminarily studied. However, it should be noted that the knowledge from the studies into the thermal-hydraulic aspect of sloshing motion is of great importance to verify the reasonability and reliability of the simulation studies regarding power deposition and recriticality, which will also influence the sloshing characteristics in an actual CDA. Therefore, in the future, based on thermal-hydraulic experiments, investigations may be performed using the verified SFR safety analysis codes/methods coupled with reliable neutronic models for the further comprehensive evaluation of the transition phase of CDAs in SFRs.

Author contributions

RX performed the research and wrote the manuscript. SC guided the research and reviewed the manuscript.

Funding

The present work was performed with financial support from Guangdong Basic and Applied Basic Research Foundation (No. 2022A1515011582) and Science and Technology Program of Guangdong Province (No. 2021A0505030026) in China.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, D., Issangya, A. S., and Grace, J. R. (1999). Characteristics of gas-fluidized beds in different flow regimes. Ind. Eng. Chem. Res. 38 (3), 803–811. doi:10.1021/ie9803873

CrossRef Full Text | Google Scholar

Bi, H. T. (2007). A critical review of the complex pressure fluctuation phenomenon in gas–solids fluidized beds. Chem. Eng. Sci. 62 (13), 3473–3493. doi:10.1016/j.ces.2006.12.092

CrossRef Full Text | Google Scholar

Bohl, W., and Luck, L. B. (1990). SIMMER-II: A computer program for LMFBR disrupted core analysis. Los Alamos Natl. Lab. Rep. LA-11415-MS, 1–64. doi:10.2172/6851447

CrossRef Full Text | Google Scholar

Bohl, W. (1979). “Some recriticality studies with SIMMER-II,” in Proceedings of the International Meeting on Fast Reactor Technology, Washington, United States, August 19–23, 1979.

Google Scholar

Bohl, W., Wilhelm, D., Parker, F. R., Berthier, J., Goutagny, L., and Ninokata, H. (1990). AFDM: An advanced fluid-dynamics model. Los Alamos Natl. Lab. Rep. LA-11692-MS. doi:10.2172/6664961

CrossRef Full Text | Google Scholar

Buruchenko, S. K., and Crespo, A. J. C. (2014). “Validation DualSPHysics code for liquid sloshing phenomena,” in Proceedings of the 2014 22nd International Conference on Nuclear Engineering, Cambridge, United Kingdom, July 28–30, 2014.

CrossRef Full Text | Google Scholar

Cheng, S., Cui, J., Qian, Y., Gong, P., Zhang, T., Wang, S., et al. (2018a). An experimental investigation on flow-regime characteristics in debris bed formation behavior using gas-injection. Ann. Nucl. Energy 112, 856–868. doi:10.1016/j.anucene.2017.11.028

CrossRef Full Text | Google Scholar

Cheng, S., Gong, P., Wang, S., Cui, J., Qian, Y., Zhang, T., et al. (2018b). Investigation of flow regime in debris bed formation behavior with nonspherical particles. Nucl. Eng. Technol. 50 (1), 43–53. doi:10.1016/j.net.2017.09.003

CrossRef Full Text | Google Scholar

Cheng, S., Jin, W., Qin, Y., Zeng, X., and Wen, J. (2019a). Investigation of flow-regime characteristics in a sloshing pool with mixed-size solid particles. Nucl. Eng. Technol. 52 (5), 925–936. doi:10.1016/j.net.2019.11.006

CrossRef Full Text | Google Scholar

Cheng, S., Li, S., Li, K., Zhang, N., and Zhang, T. (2018c). A two-dimensional experimental investigation on the sloshing behavior in a water pool. Ann. Nucl. energy 114, 66–73. doi:10.1016/j.anucene.2017.12.026

CrossRef Full Text | Google Scholar

Cheng, S., Li, S., Li, K., and Zhang, T. (2019b). An experimental study on pool sloshing behavior with solid particles. Nucl. Eng. Technol. 51 (1), 73–83. doi:10.1016/j.net.2018.09.016

CrossRef Full Text | Google Scholar

Cheng, S., Li, S., Li, K., Zhang, T., Zhang, N., Li, X. a., et al. (2018d). Prediction of flow-regime characteristics in pool sloshing behavior with solid particles. Ann. Nucl. Energy 121, 11–21. doi:10.1016/j.anucene.2018.07.017

CrossRef Full Text | Google Scholar

Cheng, S., Li, X., Liang, F., Li, S., and Li, K. (2019c). Study on sloshing motion in a liquid pool with non-spherical particles. Prog. Nucl. Energy 117, 103086. doi:10.1016/j.pnucene.2019.103086

CrossRef Full Text | Google Scholar

Cheng, S., Matsuba, K., Isozaki, M., Kamiyama, K., Suzuki, T., and Tobita, Y. (2015). A numerical study on local fuel–coolant interactions in a simulated molten fuel pool using the SIMMER-III code. Ann. Nucl. Energy 85, 740–752. doi:10.1016/j.anucene.2015.06.030

CrossRef Full Text | Google Scholar

Cheng, S., Matsuba, K., Isozaki, M., Kamiyama, K., Suzuki, T., and Tobita, Y. (2014). An experimental study on local fuel–coolant interactions by delivering water into a simulated molten fuel pool. Nucl. Eng. Des. 275, 133–141. doi:10.1016/j.nucengdes.2014.05.003

CrossRef Full Text | Google Scholar

Cheng, S., Tanaka, Y., Gondai, Y., Kai, T., Zhang, B., Matsumoto, T., et al. (2011). Experimental studies and empirical models for the transient self-leveling behavior in debris bed. J. Nucl. Sci. Technol. 48 (10), 1327–1336. doi:10.1080/18811248.2011.9711823

CrossRef Full Text | Google Scholar

Cheng, S., Xu, R., Jin, W., Qin, Y., Zeng, X., Li, S., et al. (2020). Experimental study on sloshing characteristics in a pool with stratified liquids. Ann. Nucl. Energy 138, 107184. doi:10.1016/j.anucene.2019.107184

CrossRef Full Text | Google Scholar

Cheng, S., Yamano, H., Suzuki, T., Tobita, Y., Gondai, Y., Nakamura, Y., et al. (2013a). An experimental investigation on self-leveling behavior of debris beds using gas-injection. Exp. Therm. Fluid Sci. 48, 110–121. doi:10.1016/j.expthermflusci.2013.02.014

CrossRef Full Text | Google Scholar

Cheng, S., Yamano, H., Suzuki, T., Tobita, Y., Nakamura, Y., Zhang, B., et al. (2013b). Characteristics of self-leveling behavior of debris beds in a series of experiments. Nucl. Eng. Technol. 45 (3), 323–334. doi:10.5516/NET.02.2012.068

CrossRef Full Text | Google Scholar

Cheng, S., Zhang, T., Meng, C., Zhu, T., Chen, Y., Dong, Y., et al. (2019d). A comparative study on local fuel-coolant interactions in a liquid pool with different interaction modes. Ann. Nucl. Energy 132, 258–270. doi:10.1016/j.anucene.2019.04.048

CrossRef Full Text | Google Scholar

Didwania, A. K., and Homsy, G. M. (1981). Flow regimes and flow transitions in liquid fluidized beds. Int. J. Multiph. Flow 7 (6), 563–580. doi:10.1016/0301-9322(81)90031-8

CrossRef Full Text | Google Scholar

Fauske, H. K., and Koyama, K. (2002). Assessment of fuel coolant interactions (FCIs) in the FBR core disruptive accident (CDA). J. Nucl. Sci. Technol. 39 (6), 608–614. doi:10.1080/18811248.2002.9715241

CrossRef Full Text | Google Scholar

Gingold, R. A., and Monaghan, J. J. (1977). Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Notices R. Astronomical Soc. 181 (3), 375–389. doi:10.1093/mnras/181.3.375

CrossRef Full Text | Google Scholar

Guo, L., Morita, K., and Tobita, Y. (2017). Numerical simulations on self-leveling behaviors with cylindrical debris bed. Nucl. Eng. Des. 315, 61–68. doi:10.1016/j.nucengdes.2017.02.024

CrossRef Full Text | Google Scholar

Guo, L., Zhang, S., Morita, K., and Fukuda, K. (2012). Fundamental validation of the finite volume particle method for 3D sloshing dynamics. Int. J. Numer. Methods Fluids 68 (1), 1–17. doi:10.1002/fld.2490

CrossRef Full Text | Google Scholar

Guo, L., Zhang, S., Morita, K., and Fukuda, K. (2010). “Numerical simulation of 3D liquid sloshing motion with solid particles using finite volume particle method,” in 18th International Conference on Nuclear Engineering, Xi’an, China, May 17–20, 2010, 585–592.

CrossRef Full Text | Google Scholar

Hatayama, K. (2008). Lessons from the 2003 Tokachi-oki, Japan, earthquake for prediction of long-period strong ground motions and sloshing damage to oil storage tanks. J. Seismol. 12 (2), 255–263. doi:10.1007/s10950-007-9066-y

CrossRef Full Text | Google Scholar

Jo, Y., Park, J., and Kim, E. (2019). “Numerical simulation on LMR molten-core sloshing behaviors using smoothed particle hydrodynamics method,” in Proceeding of the Korean Nuclear Society Spring Meeting, Jeju, Korea, May 23–24, 2019.

Google Scholar

Jo, Y., Park, S., Park, J., and Kim, E. S. (2021). Numerical simulation on LMR molten-core centralized sloshing benchmark experiment using multi-phase smoothed particle hydrodynamics. Nucl. Eng. Technol. 53 (3), 752–762. doi:10.1016/j.net.2020.07.039

CrossRef Full Text | Google Scholar

Kolev, N. I. (1993). The code IVA 3 for modelling of transient three-phase flows in complicated 3D geometry/Das Programm IVA3 zur Modellierung transienter Dreiphasen- Strömungen in komplizierten dreidimensionalen Geometrien. Kerntechnik 58 (3), 147–156. doi:10.1515/kern-1993-580305

CrossRef Full Text | Google Scholar

Kondo, S., Furutani, A., and Ishikawa, M. (1985). “SIMMER-II application and validation studies in Japan for energetics accommodation of severe LMFBR accidents,” in Fast Reactor Safety: Proceedings of the International Topical Meeting, Knoxville, United States, April 21–25, 1985.

Google Scholar

Kondo, S., Tobita, Y., Morita, K., and Shirakawa, N. (1992). “SIMMER-III: An advanced computer program for LMFBR severe accident analysis,” in Proceedings of International Confefence on Design and Safety of Advanced Nuclear Power.Plants (ANP'92), Tokyo, Japan, October 25–29, 1992.

Google Scholar

Liu, P., Yasunaka, S., Matsumoto, T., Morita, K., Fukuda, K., and Tobita, Y. (2006). Simulation of the dynamic behavior of the solid particle bed in a liquid pool: Sensitivity of the particle jamming and particle viscosity models. J. Nucl. Sci. Technol. 43 (2), 140–149. doi:10.1080/18811248.2006.9711076

CrossRef Full Text | Google Scholar

Liu, P., Yasunaka, S., Matsumoto, T., Morita, K., Fukuda, K., Yamano, H., et al. (2007). Dynamic behavior of a solid particle bed in a liquid pool: SIMMER-III code verification. Nucl. Eng. Des. 237 (5), 524–535. doi:10.1016/j.nucengdes.2006.08.004

CrossRef Full Text | Google Scholar

Liu, X., Morita, K., and Zhang, S. (2021). Direct numerical simulation of incompressible multiphase flow with vaporization using moving particle semi-implicit method. J. Comput. Phys. 425, 109911. doi:10.1016/j.jcp.2020.109911

CrossRef Full Text | Google Scholar

Maschek, W., Fischer, E., and Asprey, M. (1982). “Transition phase and recriticality analyses for a SNR-type homogeneous core with the SIMMER-II code,” in Proceedings of the LMFBR safety topical meeting, Lyon-Ecully, France, July 19–23, 1982.

Google Scholar

Maschek, W., Munz, C.-D., and Meyer, L. (1992a). Investigations of sloshing fluid motions in pools related to recriticalities in liquid-metal fast breeder reactor core meltdown accidents. Nucl. Technol. 98 (1), 27–43. doi:10.13182/NT92-A34648

CrossRef Full Text | Google Scholar

Maschek, W., Roth, A., Kirstahler, M., and Meyer, L. (1992b). Simulation experiments for centralized liquid sloshing motions. Kernforsch. Karlsr. Rep, 1–51. doi:10.5445/IR/270033132

CrossRef Full Text | Google Scholar

Morita, K., Matsumoto, T., Emura, Y., Abe, T., Tatewaki, I., and Endo, H. (2014). “Investigation on sloshing response of liquid in a 2D pool against hydraulic disturbance,” in The Ninth Korea-Japan Symposium on Nuclear Thermal Hydraulics and Safety (NTHAS-9), Buyeo, Korea, November 16–19, 2014.

Google Scholar

Munz, C.-D., and Maschek, W. (1992). Comparison of results of two-phase fluid dynamics codes and sloshing experiments. Kernforsch. Karlsr. Rep., 1–54. doi:10.5445/IR/270033133

CrossRef Full Text | Google Scholar

Namiki, A., Rivalta, E., Woith, H., and Walter, T. R. (2016). Sloshing of a bubbly magma reservoir as a mechanism of triggered eruptions. J. Volcanol. Geotherm. Res. 320, 156–171. doi:10.1016/j.jvolgeores.2016.03.010

CrossRef Full Text | Google Scholar

Ohshima, H., and Kubo, S. (2016). Handbook of generation IV nuclear reactors. Manchester: Woodhead Publishing.

Google Scholar

Park, S., Park, H. S., Jang, B. I., and Kim, H. J. (2016). 3-D simulation of plunging jet penetration into a denser liquid pool by the RD-MPS method. Nucl. Eng. Des. 299, 154–162. doi:10.1016/j.nucengdes.2015.08.003

CrossRef Full Text | Google Scholar

Pigny, S. L. (2010). Academic validation of multi-phase flow codes. Nucl. Eng. Des. 240 (11), 3819–3829. doi:10.1016/j.nucengdes.2010.08.007

CrossRef Full Text | Google Scholar

Raj, B., Chellapandi, P., and Rao, P. V. (2015). Sodium fast reactors with closed fuel cycle. Boca Raton, United States: CRC Press.

Google Scholar

Roache, P. J. (1972). Computational fluid dynamics. Albuquerque: Hermosa publishers.

Google Scholar

Roache, P. J. (1998). Verification and validation in computational science and engineering. Albuquerque, United States: Hermosa publishers.

Google Scholar

Sakai, F., Nishimura, M., and Ogawa, H. (1984). Sloshing behavior of floating-roof oil storage tanks. Comput. Struct. 19 (1), 183–192. doi:10.1016/0045-7949(84)90217-7

CrossRef Full Text | Google Scholar

Shamsuzzaman, M., Zhang, B., Horie, T., Fuke, F., Matsumoto, T., Morita, K., et al. (2014). Numerical study on sedimentation behavior of solid particles used as simulant fuel debris. J. Nucl. Sci. Technol. 51 (5), 681–699. doi:10.1080/00223131.2014.887481

CrossRef Full Text | Google Scholar

Sheikh, M., Liu, X., Matsumoto, T., Morita, K., Guo, L., Suzuki, T., et al. (2020). Numerical simulation of the solid particle sedimentation and bed formation behaviors using a hybrid method. Energies 13, 5018. doi:10.3390/en13195018

CrossRef Full Text | Google Scholar

Smith, L. L. (1978). SIMMER-II: A computer program for LMFBR disrupted core analysis. Los Alamos Natl. Lab. Rep. LA-7515-M, 1–279.

Google Scholar

Stoker, J. J. (1957). Water waves, the mathematical theory with applications. New York, United States: Interscience Publishers.

Google Scholar

Suzuki, T., Kamiyama, K., Yamano, H., Kubo, S., Tobita, Y., Nakai, R., et al. (2014). A scenario of core disruptive accident for Japan sodium-cooled fast reactor to achieve in-vessel retention. J. Nucl. Sci. Technol. 51 (4), 493–513. doi:10.1080/00223131.2013.877405

CrossRef Full Text | Google Scholar

Suzuki, T., Tobita, Y., Kawada, K., Tagami, H., Sogabe, J., Matsuba, K., et al. (2015). A preliminary evaluation of unprotected loss-of-flow accident for a prototype fast-breeder reactor. Nucl. Eng. Technol. 47 (3), 240–252. doi:10.1016/j.net.2015.03.001

CrossRef Full Text | Google Scholar

Tagami, H., Cheng, S., Tobita, Y., and Morita, K. (2018). Model for particle behavior in debris bed. Nucl. Eng. Des. 328, 95–106. doi:10.1016/j.nucengdes.2017.12.029

CrossRef Full Text | Google Scholar

Tagami, H., and Tobita, Y. (2014). “Numerical simulation for debris bed behavior in sodium cooled fast reactor,” in The 10th International Topical Meeting on Nuclear Thermal-Hydraulics, Operation and Safety (NUTHOS-10), Okinawa, Japan, December 14–18, 2014.

Google Scholar

Tatewaki, I., Morita, K., and Endo, H. (2015). “A study on characteristics of molten pool sloshing in core disruptive accidents of fast reactors,” in 23rd International Conference on Nuclear Engineering: Nuclear Power-Reliable Global Energy (ICONE-23), Chibu, Japan, May 17–21, 2015.

Google Scholar

Tentner, A., Parma, E., Wei, T., and Wigeland, R. (2010). Severe accident approach-final report. Evaluation of design measures for severe accident prevention and consequence mitigation. United States: Argonne National Laboratory.

Google Scholar

Thaker, A. H., Bhujbal, S. V., and Buwa, V. V. (2020). Effects of sloshing gas–liquid interface on dynamics of meandering bubble plumes and mixing in a shallow vessel: PIV and PLIF measurements. Chem. Eng. J. 386, 122036. doi:10.1016/j.cej.2019.122036

CrossRef Full Text | Google Scholar

Theofanous, T., and Bell, C. (1986). An assessment of Clinch River Breeder Reactor core disruptive accident energetics. Nucl. Sci. Eng. 93 (3), 215–228. doi:10.13182/NSE86-A17751

CrossRef Full Text | Google Scholar

Vorobyev, A. (2012). A Smoothed particle hydrodynamics method for the simulation of centralized sloshing experiments. Baden-Württemberg: KIT Scientific Publishing.

Google Scholar

Vorobyev, A., Kriventsev, V., and Maschek, W. (2010). “Analysis of central sloshing experiment using smoothed particle hydrodynamics (SPH) method,” in 18th International Conference on Nuclear Engineering (ICONE18), Xi’an, China, May 17–20, 2010.

CrossRef Full Text | Google Scholar

Vorobyev, A., Kriventsev, V., and Maschek, W. (2011). Simulation of central sloshing experiments with smoothed particle hydrodynamics (SPH) method. Nucl. Eng. Des. 241 (8), 3086–3096. doi:10.1016/j.nucengdes.2011.05.020

CrossRef Full Text | Google Scholar

Xu, R., Cheng, S., Li, S., and Cheng, H. (2022). Knowledge from recent investigations on sloshing motion in a liquid pool with solid particles for severe accident analyses of sodium-cooled fast reactor. Nucl. Eng. Technol. 54 (2), 589–600. doi:10.1016/j.net.2021.08.024

CrossRef Full Text | Google Scholar

Yamano, H., Fujita, S., Tobita, Y., Kamiyama, K., Kondo, S., Morita, K., et al. (2003b). SIMMER-III: A computer program for LMFR core disruptive accident analysis version 3 A model summary and program description. Ibaraki, Japan: Japan Nuclear Cycle Devlopment Institute. JNC-TN--9400-2003-071.

Google Scholar

Yamano, H., Fujita, S., Tobita, Y., Kamiyama, K., Kondo, S., Morita, K., et al. (2003a). SIMMER-IV: A three-dimensional computer program for LMFR core disruptive accident analysis version 2 A model summary and program description. Japan Nuclear Cycle Devlopment Institute. JNC-TN--9400-2003-070.

Google Scholar

Yamano, H., Onoda, Y., Tobita, Y., and Sato, I. (2009). Transient heat transfer characteristics between molten fuel and steel with steel boiling in the CABRI-TPA2 test. Nucl. Technol. 165 (2), 145–165. doi:10.13182/NT09-A4082

CrossRef Full Text | Google Scholar

Yamano, H., Suzuki, T., Tobita, Y., Matsumoto, T., and Morita, K. (2012). “Validation of the SIMMER-IV severe accident computer code on three-dimensional sloshing behavior,” in Proceedings of The 8th Japan-Korea Symposium on Nuclear Thermal Hydraulics and Safety (NTHAS-8), Beppu, Japan, December 9–12, 2012.

Google Scholar

Zhang, S., Morita, K., Fukuda, K., and Shirakawa, N. (2007). A new algorithm for surface tension model in moving particle methods. Int. J. Numer. Methods Fluids 55 (3), 225–240. doi:10.1002/fld.1448

CrossRef Full Text | Google Scholar

Zhang, T., Cheng, S., Zhu, T., Meng, C., and Li, X. a. (2018). A new experimental investigation on local fuel-coolant interaction in a molten pool. Ann. Nucl. Energy 120, 593–603. doi:10.1016/j.anucene.2018.06.031

CrossRef Full Text | Google Scholar

Nomenclature

Symbols

D_in inner diameter of the inner cylinder

D_out inner diameter of the outer cylinder

d_p diameter of solid particles

H_in liquid height in the inner cylinder

H_out liquid height in the outer cylinder

H_pb particle-bed height

H_ring height of ring-shaped obstacle

H_w water depth

H_o depth of cleaning oil

H_pool total depth of liquid in the pool

ΔH_max maximum liquid-level elevation

N_p particle number

P gas-injection pressure

R_c distance of rods from the center of the container

R_off off-centeredness

T gas-injection period

ΔT gas-injection duration

Greek letters

ρ_p density of solid particles