Bald Eagle Search Algorithm for Parameter Identification of Proton Exchange Membrane Fuel Cell

A precise and reliable proton exchange membrane fuel cell (PEMFC) parameter identification performs an essential function in simulation analysis, optimal control, and performance research of actual PEMFC systems. Unfortunately, achieving an accurate, efficient, and stable parameter identification can sometimes be problematic for traditional optimization methods, owing to its strong coupling, inherent nonlinear, and multi-variable characteristics. Therefore, an advanced bald eagle search (BES) algorithm is designed to dependably identify the unknown parameters of the electrochemical PEMFC model in this work. For evaluating and analyzing the overall optimization performance of the BES comprehensively, it is compared with the genetic algorithm (GA) based on MATLAB under three cases. According to the simulation results, the optimum root mean square error (RMSE) achieved by BES is 96.27% less than that achieved by GA in parameter identification, which fully indicates that the precision, accuracy, and stability of the optimization results can be remarkably improved via the application of BES.

1 Introduction

Nowadays, in the context of the ever-increasing energy demand and dwindling fuel reserves (Sun et al., 2020; Liu et al., 2020; Noman et al., 2021), the transformation of traditional fossil energy (Iqbal et al., 2021; Bakeer et al., 2021; Erdiwansyah et al., 2021) and utilization of renewable energy have been brought to global researchers’ attention (Kalyan and Rao, 2021; Liu et al., 2021; Yang et al., 2020a). The exploitation of renewable energy (Zhang et al., 2019; Murty and Kumar, 2020; Zhang et al., 2021) has been proven as a significant measure for energy structure optimization (Huang et al., 2021; Liu et al., 2020; Chen et al., 2018), environmental governance, and ecologic protection (Yao et al., 2015). Meanwhile, proton exchange membrane fuel cell (PEMFC) (Ahmed et al., 2020) is born out as efficient alternative energy, in light of its ability to convert hydrogen (chemical energy) into electricity, with water as the sole by-product.

By virtue of the distinctive superiority of the low operating temperature, high power density, and easy maintenance, PEMFC has obtained a growingly widespread practice in multiple engineering fields, such as distributed generation, portable electronic applications, and transportation fields. For analyzing the characteristics of PEMFC with better accuracy and reliability, a variety of modeling techniques have been presented, such as isothermal one-dimensional mathematical model (Kalyan and Rao, 2021), mechanistic modeling (Liu et al., 2021; Giner et al., 2018), equivalent electrical circuit (Yang et al., 2020a), and steady-state electrochemical model (Zhang et al., 2019). In addition, the steady-state electrochemical model based on the electrochemical reaction mechanism can exceptionally demonstrate the voltage-current (V-I) characteristic under different operating conditions, in which some unknown yet significant parameters are required to estimate accurately and reliably.

Due to the highly nonlinear, multiply variable, and strong coupling characteristics of PEMFC, conventional deterministic optimization methods are restricted to obtaining satisfactory parameter identification results. Over the years, with the rapid advancement of emerging algorithm/soft computing, meta-heuristic algorithms with high adaptability and strong robustness have been universally applied in the field of nonlinear optimization systems. Hence, the parameter identification of PEMFC is achieved via various meta-heuristic algorithms. For instance, the genetic algorithm (GA) was adopted for fitting the Nexa 1.2kW PEMFC real data to obtain an exact identification of PEMFC parameters (Murty and Kumar, 2020). Zhang et al. (2021) applied grey wolf optimization (GWO) to achieve PEMFC parameter identification based on experimental data, which verifies the practicability of the proposed algorithm in simulating the electrical function of commercial PEMFC. Particle swarm optimization (PSO) is utilized to identify the off-line parameters of the Nexa 1.2kW PEMFC system at varying loads (Salim et al., 2015). Meanwhile, other excellent meta-heuristic algorithms were designed to be a useful tool to achieve optimal parameters, that is, artificial bee colony (ABC) (Liu et al., 2020), antlion optimization algorithm (ALO) (Chen et al., 2018), slap swarm optimizer (SSO) (Yao et al., 2015), flower pollination algorithm (FPA) (Ahmed et al., 2020), and improved version of monarch butterfly optimization (IMBO) (Giner-Sanz et al., 2018).

Many meta-heuristic algorithms with terrific effects are adopted to identify unknown parameters of PEMFC despite the complication of certain algorithms’ operation mechanisms and the ideal solutions, which are difficult to obtain with high precision and good stability. What is more, there are still many possibilities to attempt new ones. By simulating the actual operation of the cell in multi-functional environments, this work proposes bald eagle search optimization (BES) (Atlam and Dndar, 2021) to gain the optimum result of parameters in Amphlett’s model (PEMFC model) and tackle the aforementioned defects.

The main objectives and novelties of this study can be summarized as follows:

• A new optimization algorithm using BES is discussed for unknown parameter identification of the PEMFC electrochemical model;

• BES is a simple optimization technique, in which fewer parameters are required to be applied in the calculation process owing to the conciseness of its operation mechanism;

• Compared with GA, BES designed in this work presents a faster practical convergence speed in PEMFC parameters identification;

• Experimental results indicate that BES can efficiently identify parameters with fast convergence speed, high accuracy, and robustness owing to its strong ability to escape from the local optimum of Ballard-Mark-V PEMFC.

The rest of this article is organized as follows: the steady-state electrochemical model of PEMFC and objective function are described in Section 2. Besides, Section 3 thoroughly illustrates the execution mechanism and parameter identification of BES. Section 4 provides the simulation and analysis results in comprehensive cases. Lastly, Section 5 summarizes several conclusions along with future perspectives.

2 Proton Exchange Membrane Fuel Cell Modeling

2.1 Electrochemical Reaction Mechanism of Proton Exchange Membrane Fuel Cell

A typical PEMFC includes two electrodes (cathode and anode) and a proton exchange membrane (PEM), while electrodes are mainly composed of a gas diffusion layer and a platinum-based alloy catalyst layer. Hydrogen is decomposed into hydrogen ions H⁺ and electrons e⁻ through catalytic reaction after passing through the anode catalytic layer. Subsequently, oxygen provided by the cathode catalytic layer integrates with electrons and hydrogen ions to generate water and heat. Figure 1 describes the structure of the reaction mechanism diagram, a single PEMFC, and a PEMFC stack of PEMFC. The electrochemical reaction mechanism in PEMFC is expressed as follows:

FIGURE 1

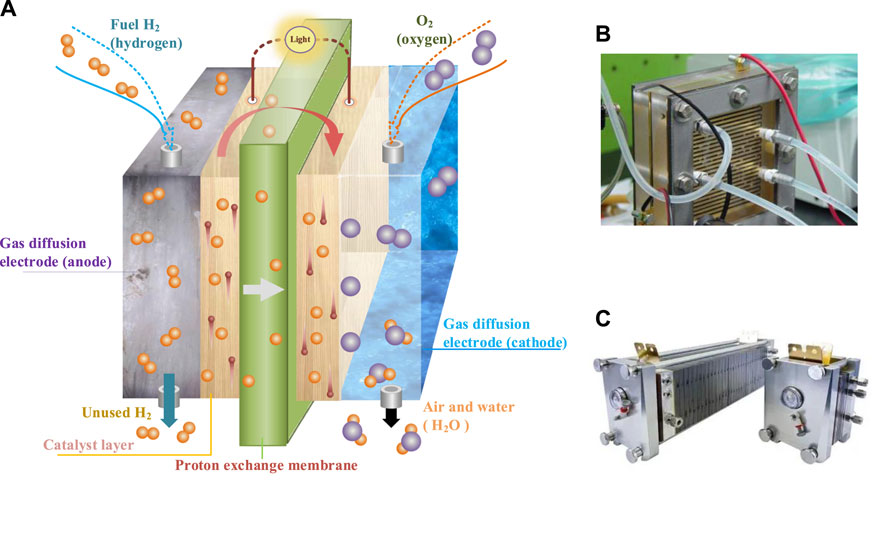
FIGURE 1. Structure of PEMFC. (A) Electrochemical mechanism of PEMFC; (B) single PEMFC, and (C) PEMFC stack.

At anode,

${\text{H}}_2\to 2{\text{H}}^{+}+2{\text{e}}^{-}.(1)$

At cathode,

$2{\text{H}}^{+}+2{\text{e}}^{-}+\frac{1}{2}{\text{O}}_2\to {\text{H}}_2\text{O}.(2)$

Overall chemical reaction,

$2{\text{H}}_2+{\text{O}}_2\to 2{\text{H}}_2\text{O}+\text{heat }+\text{Electricity}.(3)$

2.2 Mathematical Modeling

The net output voltage of the electrochemical model is affected by three kinds of polarization, namely, activation, ohmic, and concentration polarization, while the voltage characteristic function of electrochemical can be written as (Amphlett et al., 1995)

$V_{\text{c}}=E_{\text{nernst}}-V_{\text{act}}-V_{\text{ohmic}}-V_{\text{con}},(4)$

where $E_{\text{nernst}}$ indicates the open-circuit voltage (V); $V_{\text{act}}$ means the activation voltage drop (V); $V_{\text{ohmic}}$ denotes the ohmic voltage drop (V); and $V_{\text{con}}$ represents the concentration voltage drop (V).

In addition, $E_{\text{nernst}}$ calculated from the Nernst equation can be determined by (Ariza et al., 2018)

$E_{\mathrm{nernst}}=\frac{\Delta G}{2F}+\frac{\Delta S}{2F}\left(T_{\text{k}}-T_{\mathrm{ref}}\right)+\frac{RT}{2F}\left[\ln \left(P_{{\text{H}}_2}\right)+\frac{1}{2}\left(P_{{\text{O}}_2}\right)\right],(5)$

where $\Delta G$ is the increment in Gibbs free energy (J/mol); $F$ indicates Faraday’s constant (96,487 C/mol); $\Delta S$ means the increment of entropy (J/mol); R denotes the universal gas constant [8.314 J/(K mol)]; $T_{\text{k}} \text{and }{T}_{\text{ref}}$ represent the operation ambient and reference temperature (K), respectively; $P_{{\text{H}}_2}$ and $P_{{\text{O}}_2}$ stand for the partial pressures of hydrogen and oxygen, respectively (atm), which are formulated as (Ali et al., 2017)

$P_{{\text{H}}_2}=0.5\times R{H}_{\text{a}}\times P_{{\text{H}}_2\text{O}}^{\mathrm{sat}}\times \left[{\left(\frac{R{H}_{\text{a}}\times P_{{\text{H}}_2\text{O}}^{\mathrm{sat}}}{P_{\text{a}}}\times \exp \left(\frac{1.635\left(\frac{i_{\mathrm{cell}}}{A}\right)}{T_{\text{k}}^{1.334}}\right)\right)}^{-1}-1\right],(6)$

$P_{{\text{O}}_2}=R{H}_{\text{c}}\times P_{{\text{H}}_2\text{O}}^{\mathrm{sat}}\times \left[{\left(\frac{R{H}_{\text{a}}\times P_{{\text{H}}_2\text{O}}^{\mathrm{sat}}}{P_{\text{c}}}\times \exp \left(\frac{4.192\left(\frac{i_{\mathrm{cell}}}{A}\right)}{T_{\text{k}}^{1.334}}\right)\right)}^{-1}-1\right],(7)$

where RH_a and RH_c, respectively, denote the relative humidity of vapor at anode and cathode (atm); P_a and P_c are the inlet pressures of anode and cathode (atm), respectively; and $P_{{\text{H}}_2\text{O}}^{\mathrm{sat}}$ represents the saturation pressure of water vapor (atm), which is defined as (Ali et al., 2017)

$T_{\text{c}}=T_{\text{k}}-273.15,(8)$

${\log }_{10}\left(P_{{\text{H}}_2\text{O}}^{\mathrm{sat}}\right)=2.95\times {10}^{-2}\times T_{\text{c}}-9.19\times {10}^{-5}\times T_{\text{c}}^2+1.44\times {10}^{-7}\times T_{\text{c}}^3-2.18.(9)$

Moreover, the activation voltage $V_{\text{act}}$ demonstrates the slowness of the reaction occurring on the electrode surface, which can be given as follows (Ariza et al., 2018):

$V_{\mathrm{act}}={\epsilon }_1+{\epsilon }_2{T}_{\text{k}}+{\epsilon }_3{T}_{\text{k}}\mathrm{l}\mathrm{n}\left(C_{{\text{o}}_2}\right)+{\epsilon }_4{T}_{\text{k}}\mathrm{l}\mathrm{n}\left(i_{\mathrm{cell}}\right),(10)$

where ${\epsilon }_i$ (i = 1,2,3,4) indicates the semi-empirical coefficients and $C_{{\text{o}}_2}$ is the oxygen concentration (mol/ ${\text{cm}}^3$), which is determined by (Ali et al., 2017)

$C_{{\text{O}}_2}=\frac{P_{{\text{O}}_2}}{5.08\times {10}^6\times {\text{e}}^{\left(\frac{-498}{T_{\text{k}}}\right)}}.(11)$

Ohmic voltage drop $V_{\text{ohmic}}$ is mathematically expressed as follows (Ali et al., 2017):

$V_{\mathrm{ohmic}}=i_{\mathrm{cell}}\left(R_{\text{m}}+R_{\text{c}}\right),(12)$

where R_c is the equivalent contact resistance (Ω) and R_m represents the equivalent resistance provided to PEM conduction (Ω), which can be defined by

$R_{\text{m}}={\rho }_{\text{m}}\left(\frac{l}{A}\right),(13)$

where l means the membrane thickness ($\mu \text{m}$), A is the effective electrode area (cm²), and ${\rho }_{\text{m}}$ stands for the specific membrane resistance ($\Omega \Delta$ cm) described by (Amphlett et al., 1995)

${\rho }_{\text{m}}=\frac{181.6\times \left[1+0.03\times \left(\frac{i_{\text{cell}}}{A}\right)+0.062\times {\left(\frac{T_{\text{k}}}{303}\right)}^2{\left(\frac{i_{\text{cell}}}{A}\right)}^{2.5}\right]}{\left[\lambda -0.634-3\times \left(\frac{i_{\text{cell}}}{A}\right)\right]\exp \left[4.18\times \left(\frac{T_{\text{k}}-303}{T_{\text{k}}}\right)\right]},(14)$

where $\lambda$ stands for an empirical parameter.

Furthermore, concentration voltage loss $V_{\text{con}}$ influenced by the concentration can be formulated as (Ariza et al., 2018)

$V_{\text{con}}=-b\text{ln}\left(\text{ln}\frac{J}{A\times J_{\text{max}}}\right),(15)$

where b means the parametric coefficient (V), $J$ is the actual current density, and $J_{\text{max}}$ defines the upper bound current density ($A/c{m}^2$).

On the whole, after referring to the mentioned Eqs 4–15 for PEMFC, there are seven crucial parameters demand to be identified: ${\epsilon }_{1 }$, ${\epsilon }_{2 }$, ${\epsilon }_{3 }$, ${\epsilon }_4$, $b$, $\lambda$, and $R_{\text{c}}$.

2.3 Objective Function

To precisely build a mathematical model of PEMFC based on the aforementioned unknown parameters, it is crucial to utilize an objective function to reliably evaluate parameter identification. In addition, the objection function based on the root mean square error (RMSE) can commendably mirror the deviation between the actual and estimated values.

Consequently, RMSE is accounted as the objective function given by

$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E} \left(x\right)=\sqrt{\frac{1}{N}{\displaystyle \sum }_{i=1}^N{[V_{\mathrm{actual}}\left(i\right)-V_{\mathrm{estimate}}\left(i\right)]}^2},(16)$

where N indicates the total quantity of actual datasets, V_actual is the actual voltage, and V_estimate denotes the estimated voltage.

Additionally, the restraints of crucial parameters can be written as

$\text{s}.\text{t}.\{\begin{array}{c}{\epsilon }_{i,\text{min}}\le {\epsilon }_i\le {\epsilon }_{i,\text{max}}\\ {\lambda }_{\text{min}}\le \lambda \le {\lambda }_{\text{max}}\\ R_{\text{c},\text{min}}\le R_{\text{c}}\le R_{\text{c},\text{max}}\\ b_{\text{min}}\le b\le b_{\text{max}}\end{array} ,\forall i\in \left\{\mathrm{1,2,3,4}\right\}.(17)$

3 Bald Eagle Search Algorithm

3.1 Optimization Mechanism

The BES algorithm (Atlam and Dndar, 2021) is an innovative meta-heuristic algorithm enlightened by biological activities in nature. Individual search strategies can be established through their own mobile or global experience in the group random optimization process to optimize complex problems in the real world. In particular, the self-search and exploration of individuals in the search space are performed by simulating the predation behavior of bald eagles (e.g., prey on salmon living in a specific area). The bald eagles have a specific predation strategy, which can help them consume the least energy while maximizing the probability of predation success.

The bald eagle’s predation strategy has three major aspects: selecting the appropriate search domain, searching in the selected space, and the best chance to swoop on the prey.

In the select stage, the selected search space is related to the last movement of the bald eagle, which can be expressed as

$P_{\text{new},i}=P_{\text{best}}+\alpha \times r(P_{\text{mean}}+P_i),(18)$

where $P_{\text{best}}$ means optimal spatial search position, $\alpha$ is parameters affecting location update, 1.5 ≤ $\alpha$ ≤ 2, $r$ denotes a random number between 0 and 1, $P_{\text{mean}}$ indicates average distribution position of the bald eagle after the previous search.

After determining the search space, the bald eagle will search the space that flies spirally to search for prey and find the best-accelerated dive position. The change of the search position is expressed in polar coordinates as follows (Salim et al., 2015):

$P_{\text{new},i}=P_i+y\left(i\right)\times \left(P_i-P_{i+1}\right)+x\left(i\right)\times (P_i-P_{\text{mean}}),(19)$

$x\left(i\right)=\frac{xr\left(i\right)}{\text{max}\left(\left|xr\right|\right)}, y\left(i\right)=\frac{yr\left(i\right)}{\text{max}\left(\left|yr\right|\right)},(20)$

$xr\left(i\right)=r\left(i\right)\times \sin \left[\theta \left(i\right)\right], yr\left(i\right)=r\left(i\right)\times \cos \left[\theta \left(i\right)\right],(21)$

$\theta \left(i\right)=a\times \pi \times rand, r\left(i\right)=\theta \left(i\right)+R\times rand,(22)$

where $x\left(i\right)$ and $y\left(i\right)$ are values between 0 and 1 for determining the positions of the bald eagle on the corresponding polar axis, respectively; $r\left(i\right)$ and $\theta \left(i\right)$ denote the polar diameter and polar angle of the spiral flight in polar coordinates, respectively; $a$ indicates a parameter that takes a value from 5 to 10; R represents a parameter that controls the search period, between 0.2 and 2; and rand is a random number in [0,1].

In the swooping stage, the bald eagle swoops to the prey at the optimal position, while other bald eagles in the population also move to the best position and dive down to attack the prey. The position updates during the swooping are expressed in polar coordinates as (Oliva et al., 2014)

$P_{\text{new},i}=rand\times P_{\text{best}}+x_1\left(i\right)\times \left(P_i-c_1\times P_{\text{mean}}\right)+y_1\left(i\right)\times (P_i-c_2\times P_{\text{best}}),(23)$

$x_1\left(i\right)=\frac{xr\left(i\right)}{\text{max}\left(\left|xr\right|\right)},y_1\left(i\right)=\frac{yr\left(i\right)}{\text{max}\left(\left|yr\right|\right)},(24)$

$xr\left(i\right)=r\left(i\right)\times \sinh \left[\theta \left(i\right)\right],yr\left(i\right)=r\left(i\right)\times \cos \text{h}\left[\theta \left(i\right)\right],(25)$

$\theta \left(i\right)=a\times \pi \times rand,r\left(i\right)=\theta \left(i\right),(26)$

where $c_1$ and $c_2$, respectively, stand for moving velocities toward the optimal and central positions and are both between 1 and 2.

3.2 Overall Optimization Procedure

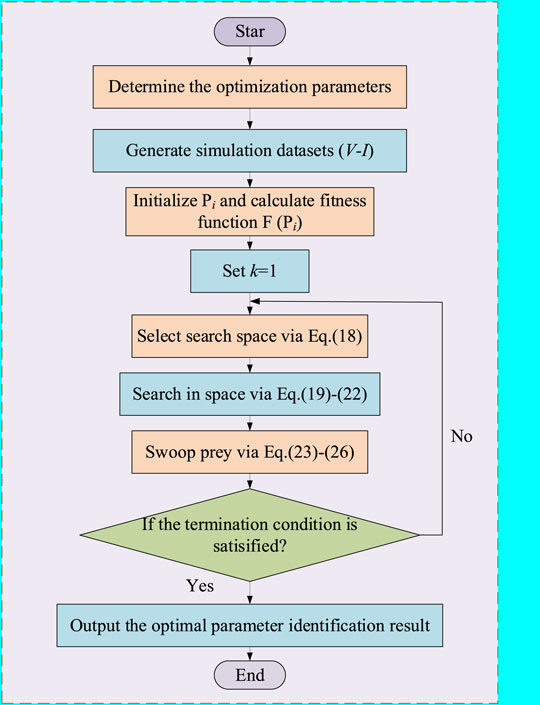
On the basis of the BES algorithm, Figure 2 illustrates the flowchart of PEMFC overall parameter identification. Firstly, it is vital to determine which parameters in the steady-state electrochemical model are identified. After that, the output voltage and current data selected as the actual PEMFC will be regarded as the inputs of BES, while the data are transformed into the objective function according to Eq. 16. Furthermore, BES is employed to identify the parameters in accordance with the built model. Finally, the optimal parameter identification results of PEMFC are output after multiple iterations.

FIGURE 2

FIGURE 2. Overall flowchart of BES-based PEMFC parameter identification.

4 Case Studies

In this section, simulation experiments are performed on PEMFC under three different temperatures and relative humidity of vapor to identify seven crucial parameters (i.e., ${\epsilon }_{1 }$, ${\epsilon }_{2 }$, ${\epsilon }_{3 }$, ${\epsilon }_4$, $b$, $\lambda$, and $R_{\text{c}}$) which are in comparison with those of BES and GA, respectively. Additionally, under two conditions T_k = 333.15K, RH_a = 50%, and RH_c = 50% and T_k = 313.15K, RH_a = 75%, and RH_c = 75%, along with T_k = 353.15K, RH_a = 100%, RH_c = 100%, 25 pairs of V-I data are extracted from Ballard-Mark-V PEMFC, where film thickness is 178 $\mu$m and effective area is 50.6 ${\text{ cm}}^2$. What is more, the boundary conditions of seven unknown parameters are illustrated in Table 1.

TABLE 1

TABLE 1. Range of PEMFC parameters for identification.

For a fair comparison between two meta-heuristic algorithms, each algorithm runs independently 10 times to obtain results, while their maximum iteration number is chosen as k_max = 500, and the population size is set to be identical p_size = 40. The simulations are executed on MATLAB 2019b through a personal computer with IntelR CoreTM i5 CPU at 2.9 GHz and 16 GB of RAM.

4.1 Case 1 (T_k = 333.15K, RH_a = 50%, and RH_c = 50%)

When the experimental condition is set as T_k = 333.15K, RH_a = 75%, and RH_c = 75%, the simulation values of seven unknown parameters are generated by BES and GA algorithms. The satisfactory results of parameter identification and minimum RMSE of the PEMFC model are illustrated in Table 2. Particularly, RMSE acquired by BES is 94.11% lower than those acquired by GA, respectively. Hence, the advisable performance of BES is significantly greater than that of GA, which can be attributed to its consideration of accuracy, reliability, and high efficiency.

TABLE 2

TABLE 2. PEMFC parameter identification results.

What is more, Figure 3A depicts the average RMSE acquired by the two algorithms under 10 independent runs. It is transparent that the accuracy of BES is significantly higher than that of GA, which fully demonstrates BES’s superior performance. Given that the average RMSEs of BES and GA algorithms hardly consist in the same order of magnitude, and the value of GA is about 12 times higher than that of BES, the BES’s effect of the actual data approximation is much better than GA.

FIGURE 3

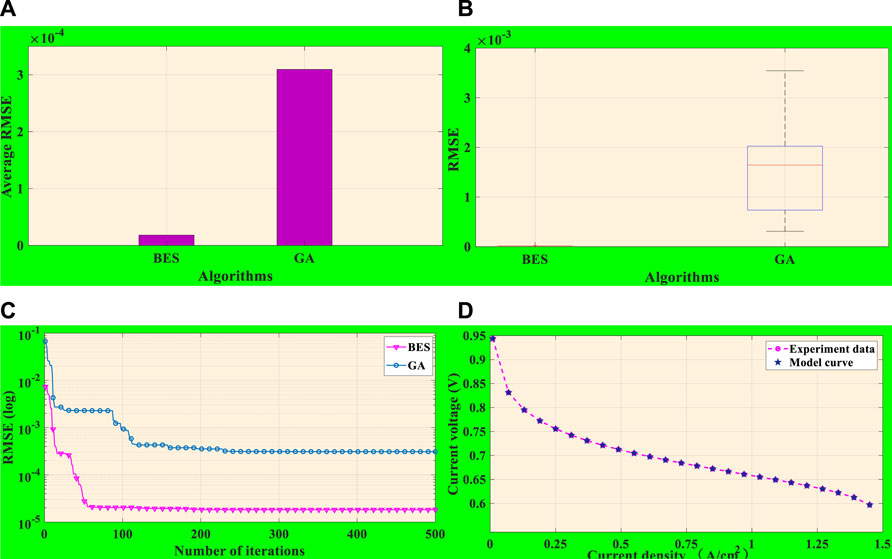
FIGURE 3. Comprehensive analysis of BES and GA under case 1. (A) Average RMSE. (B) Boxplot of RMSE. (C) Convergence curves. (D) Comparison of model datasets by BES with experiment datasets.

Figure 3B shows a boxplot of BES and GA, demonstrating the distribution range and upper/lower bounds of simulation explicitly and comprehensively. It can be seen from the chart that the error fluctuation interval and average RMSE of BES are far less than that of GA. Thus, the BES algorithm has accurate searching ability in PEMFC parameter identification and significant global searching ability.

Meanwhile, convergence graphs of the two algorithms are depicted in Figure 3C, while BES attains a stable optimal solution rapidly in approximately 60 iterations based on a global search.

As a single individual optimization and group cooperation mechanism, BES performs excellent local exploitation and global exploration, by which the accuracy and efficiency of parameter identification can be drastically improved.

Figure 3D describes the output V-I fitting curve on the basis of global optimal parameters identification by BES, upon which one can readily discover that the model curve achieved from BES approximates the experimental data to a great extent. It is undeniable that BES has superb performance in PEMFC parameter identification due to superior optimization ability and effectiveness.

4.2 Case 2 (T_k = 313.15K, RH_a = 75%, and RH_c = 75%)

When the simulation is in the condition of T_k = 313.15K, RH_a = 75%, and RH_c = 75%, the statistical results of seven unknown parameters and RMSE based on BES and GA are shown in Table 3. In particular, RMSE obtained by BES is significantly smaller than GA, while BES is 96.27% smaller than the RMSE of GA. Upon them, it is obvious that BES can considerably improve the accuracy of PEMFC model parameter identification.

TABLE 3

TABLE 3. PEMFC parameter identification results.

Figure 4A presents the average RMSE obtained by BES and GA, illustrating that BES can acquire a lower average RMSE under 10 independent runs. Thus, BES has better accuracy and stability in the unknown parameter identification of PEMFC.

FIGURE 4

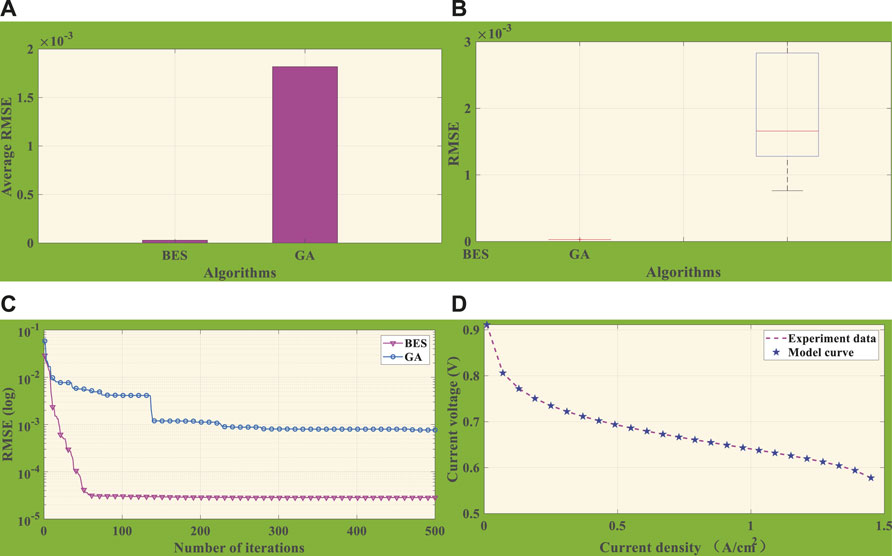
FIGURE 4. Comprehensive analysis of BES and GA under case 2. (A) Average RMSE. (B) Boxplot of RMSE. (C) Convergence curves. (D) Comparison of model datasets by BES with experiment datasets.

In addition, the RMSE boxplot obtained by BES and GA is depicted in Figure 4B, upon which the distribution range and upper/lower bound of BES are lower than those of GA. One can easily observe that the balance between global exploration and local exploitation of BES is better than that of GA.

In the meantime, convergence curves of BES and GA are shown in Figure 4C, where BES has about 55 iterations to achieve convergence, while GA needs 200 iterations to achieve convergence stability. Besides, RMSE after BES convergence is smaller than that of GA, while it can be perceived that BES identifies the unknown parameters of the PEMFC model with more accuracy and efficiency.

Figure 4D demonstrates the output V-I fitting curve obtained by the optimal results of BES, where data via BES are highly fitted with experiment data. The result efficiently reflects that BES has a superior ability for PEMFC parameter identification.

4.2 Case 3 (T_k = 353.15K, RH_a = 50%, and RH_c = 50%)

Table 4 illustrates the best PEMFC electrochemical model parameters and minimum RMSE under the condition of T_k = 353.15K, RH_a = 50%, and RH_c = 50% through BES and GA algorithm. In light of the result, BES represents the optimal performance owing that the minimum RMSE value acquired by BES is 46.13% lower than GA, which can accomplish parameter identification tasks in PEMFC with higher quality and accuracy.

TABLE 4

TABLE 4. PEMFC parameter identification results.

The average RMSE obtained by BES and GA under 10 independent runs is shown in Figure 5A, while the value of the former is about one-quarter of the latter in the case of multiple operations, which is a lot smaller. Hence, BES outperforms GA in parameter identification and shows good stability and global optimization ability.

FIGURE 5

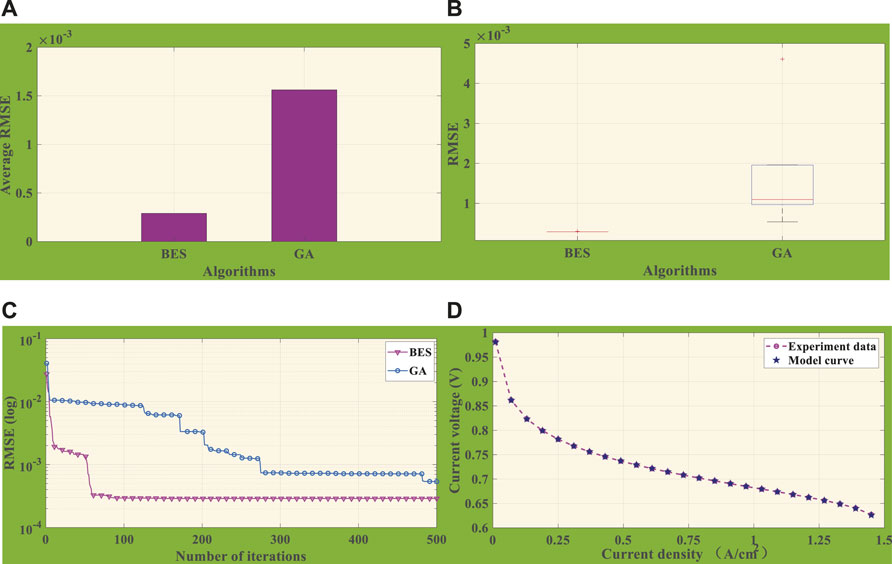
FIGURE 5. Comprehensive analysis of BES and GA under case 3. (A) Average RMSE. (B) Boxplot of RMSE. (C) Convergence curves. (D) Comparison of model datasets by BES with experiment datasets.

As is depicted in Figure 5B, it can be observed from the boxplot of BES and GA that the fluctuation range and average value of RMSE optimized by BES are lower than those of GA with 10 independent runs, which, from the perspective of either its stability or accuracy, effectively confirms the outstanding performance of BES in identifying the accuracy of PEMFC parameters. Moreover, Figure 5C presents the convergence curve of the two algorithms. BES converges at about 90 iterations, while GA does not reach a stable value until 480 iterations. After iterating 270 to 480 times, GA falls into a locally optimal solution and results in low efficiency and reduced accuracy. In general, BES is superior in convergence stability and precision for its exceptional global optimization ability.

In the end, Figure 5D describes convergence graphs of BES algorithms, which indicates that, in the case of parameter identification of BES, the experimental data and model fitting data are highly coincident, while the error is extremely small due to superior accuracy.

5 Conclusion

For the precise and reliable parameter identification of the PEMFC model, a meta-algorithm BES with superior performance is applied in this work, which includes three main contributions/novelties:

• BES is employed to obtain an accurate and credible parameter identification of PEMFC for the first time;

• In line with the simulation results, BES represents significant stability, faster convergence speed, and higher accuracy compared with the GA algorithm under two operation stations;

• Three common case studies (e.g., T_k = 333.15K, RH_a = 50%, and RH_c = 50%; T_k = 313.15K, RH_a = 75%, and RHc = 75%; and T_k = 353.15K, RH_a = 100%, and RH_c = 100%) are emulated, which can validate that BES holds tremendous potential in PEMFC parameter identification, converging to the optimal stable solution rapidly because of the dynamic and proper balance between local exploitation and global exploration. Especially, the errors of BES convergence are significantly reduced by 94.11%, 96.27%, and 46.13%, respectively, in three cases of parameter identification compared with GA.

Future studies will be undertaken as follows:

• BES is proposed as a promising optimization method that remarkably improves the accuracy of the solution in PEMFC parameter identification. It also has the merits of universality and versatility in the meantime, contributing to the realization of parameter identification of more complex models or other FCs;

• In addition, it is worthwhile to perform online identification of PEMFC parameters, while the actual response speed and optimization capability of BES need to be further improved.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.

Author Contributions

BY: conceptualization, writing—reviewing and editing; DL: writing—original draft preparation, investigation; CZ: visualization and contribution to the topic discussion; YH: supervision. JL: performed visualization and validation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors gratefully acknowledge the support of the Opening Foundation of Key Laboratory of Modern Power System Simulation and Control and Renewable Energy Technology, Ministry of Education (Northeast Electric PowerUniversity, MPSS 2022-07).

References

Ahmed, K., Farrok, O., Rahman, M. M., Ali, M. S., Haque, M. M., and Azad, A. K. (2020). Proton Exchange Membrane Hydrogen Fuel Cell as the Grid Connected Power Generator. Energies 13 (24), 6679. doi:10.3390/en13246679

CrossRef Full Text | Google Scholar

Ali, M., El-Hameed, M. A., and Farahat, M. A. (2017). Effective Parameters’ Identification for Polymer Electrolyte Membrane Fuel Cell Models Using Grey Wolf Optimizer. Renew. Energ. 111, 455–462. doi:10.1016/j.renene.2017.04.036

CrossRef Full Text | Google Scholar

Alsattar, H. A., Zaidan, A. A., and Zaidan, B. B. (2020). Novel Meta-Heuristic Bald eagle Search Optimisation Algorithm. Artif. Intelligence Rev. 53, 2237–2264. doi:10.1007/s10462-019-09732-5

CrossRef Full Text | Google Scholar

Amphlett, J. C., Baumert, R. M., Mann, R. F., Peppley, B. A., Rerge, P. R., and Harris, T. J. (1995). Performance Modeling of the Ballard Mark IV Solid Polymer Electrolyte Fuel Cell. J. Electrochem. Soc. 142 (1), 9–15. doi:10.1149/1.2043959

CrossRef Full Text | Google Scholar

Angayarkanni, S. A., Sivakumar, R., and Ramana Rao, Y. V. (2020). Hybrid Grey Wolf: Bald eagle Search Optimized Support Vector Regression for Traffic Flow Forecasting. J. Ambient Intelligence Humanized Comput. 12 (1), 1293–1304. doi:10.1007/s12652-020-02182-w

CrossRef Full Text | Google Scholar

Ariza, H., Correcher, A., Sánchez, C., Pérez-Navarro, Á., and García, E. (2018). Thermal and Electrical Parameter Identification of a Proton Exchange Membrane Fuel Cell Using Genetic Algorithm. Energies 11 (8), 2099. doi:10.3390/en11082099

CrossRef Full Text | Google Scholar

Atlam, Z., and Dndar, G. (2021). A Practical Equivalent Electrical Circuit Model for Proton Exchange Membrane Fuel Cell (PEMFC) Systems. Int. J. Hydrogen Energ. 46, 13230–13239. doi:10.1016/j.ijhydene.2021.01.108

CrossRef Full Text | Google Scholar

Bakeer, A., Salama, H. S., and Vokony, I. (2021). Integration of PV System with SMES Based on Model Predictive Control for Utility Grid Reliability Improvement. Prot. Control. Mod. Power Syst. 6, 14. doi:10.1186/s41601-021-00191-1

CrossRef Full Text | Google Scholar

Bao, S., Ebadi, A., Toughani, M., Dalle, J., and Yldzbas, A. (2020). A New Method for Optimal Parameters Identification of a PEMFC Using an Improved Version of Monarch Butterfly Optimization Algorithm. Int. J. Hydrogen Energ. 45, 17882–17892. doi:10.1016/j.ijhydene.2020.04.256

CrossRef Full Text | Google Scholar

Chen, J., Yao, W., Zhang, C., Ren, Y., and Jiang, L. (2018). Design of Robust MPPT Controller for Grid-Connected PMSG-Based Wind Turbine via Perturbation Observation Based Nonlinear Adaptive Control. Renew. Energ. 101, 34–51. doi:10.1016/j.renene.2018.11.048

CrossRef Full Text | Google Scholar

Erdiwansyah, , Mahidin, , Husin, H., Zaki, M., and Muhibbuddin, (2021). A Critical Review of the Integration of Renewable Energy Sources with Various Technologies. Prot. Control. Mod. Power Syst. 6, 3. doi:10.1186/s41601-021-00181-3

CrossRef Full Text | Google Scholar

Giner-Sanz, J. J., Ortega, E. M., and Herranz, V. P. (2018). Mechanistic Equivalent Circuit Modelling of a Commercial Polymer Electrolyte Membrane Fuel Cell. J. Power Sourc. 379, 328–337. doi:10.1016/j.jpowsour.2018.01.066

CrossRef Full Text | Google Scholar

Huang, S., Wu, Q., Liao, W., Wu, G., Li, X., and Wei, J. (2021). Adaptive Droop-Based Hierarchical Optimal Voltage Control Scheme for Vsc-Hvdc Connected Offshore Wind Farm. IEEE Trans. Ind. Inform. 17 (12), 8165–8176. doi:10.1109/tii.2021.3065375

CrossRef Full Text | Google Scholar

Ijaodola, O. S., El-Hassan, Z., Ogungbemi, E., Khatib, F. N., Wilberforce, T., Thompson, J., et al. (2019). Energy Efficiency Improvements by Investigating the Water Flooding Management on Proton Exchange Membrane Fuel Cell (PEMFC). Energy 179, 246–269. doi:10.1016/j.energy.2019.04.074

CrossRef Full Text | Google Scholar

Iqbal, B., Nasir, A., and Murtaza, A. F. (2021). Stochastic Maximum Power point Tracking of Photovoltaic Energy System under Partial Shading Conditions. Prot. Control. Mod. Power Syst. 6, 30. doi:10.1186/s41601-021-00208-9

CrossRef Full Text | Google Scholar

Isa, Z. M., Nayan, N. M., Arshad, M. H., and Kajaan, N. A. M. (2019). Optimizing PEMFC Model Parameters Using Ant Lion Optimizer and Dragonfly Algorithm: A Comparative Study. Int. J. Electr. Comput. Eng. 9 (6), 5295. doi:10.11591/ijece.v9i6.pp5295-5303

CrossRef Full Text | Google Scholar

Kalyan, C. H. N. S., and Rao, G. S. (2021). Impact of Communication Time Delays on Combined LFC and AVR of a Multi-Area Hybrid System with IPFC-RFBs Coordinated Control Strategy. Prot. Control. Mod. Power Syst. 7, 185. doi:10.1186/s41601-021-00185-z

CrossRef Full Text | Google Scholar

Liu, J., Yao, W., Wen, J., Fang, J., Jiang, L., He, H., et al. (2020). Impact of Power Grid Strength and PLL Parameters on Stability of Grid-Connected DFIG Wind Farm. IEEE Trans. Sustain. Energ. 11 (1), 545–557. doi:10.1109/tste.2019.2897596

CrossRef Full Text | Google Scholar

Liu, S., Zhou, C., and Guo, H. (2021). Operational Optimization of a Building-Level Integrated Energy System Considering Additional Potential Benefits of Energy Storage. Prot. Control. Mod. Power Syst. 4, 184. doi:10.1186/s41601-021-00184-0

CrossRef Full Text | Google Scholar

Murty, V. V. S. N., and Kumar, A. (2020). Multi-objective Energy Management in Microgrids with Hybrid Energy Sources and Battery Energy Storage Systems. Prot. Control. Mod. Power Syst. 5 (1), 1–20. doi:10.1186/s41601-019-0147-z

CrossRef Full Text | Google Scholar

Noman, M., Li, G., and Wang, K. (2021). Electrical Control Strategy for an Ocean Energy Conversion System. Prot. Control. Mod. Power Syst. 6, 12. doi:10.1186/s41601-021-00186-y

CrossRef Full Text | Google Scholar

Oliva, D., Cuevas, E., and Pajares, G. (2014). Parameter Identification of Solar Cells Using Artificial Bee colony Optimization. Energy 72, 93–102. doi:10.1016/j.energy.2014.05.011

CrossRef Full Text | Google Scholar

Priya, K., and Rajasekar, N. (2019). Application of Flower Pollination Algorithm for Enhanced Proton Exchange Membrane Fuel Cell Modeling. Int. J. Hydrogen Energ. 44 (33), 18438–18449. doi:10.1016/j.ijhydene.2019.05.022

CrossRef Full Text | Google Scholar

Salim, R., Nabag, M., Noura, H., and Fardoun, A. (2015). The Parameter Identification of the Nexa 1.2 kW PEMFC’s Model Using Particle Swarm Optimization. Renew. Energ. 82, 26–34. doi:10.1016/j.renene.2014.10.012

CrossRef Full Text | Google Scholar

Sayed, G. I., Soliman, M. M., and Hassanien, A. E. (2021). A Novel Melanoma Prediction Model for Imbalanced Data Using Optimized SqueezeNet by Bald eagle Search Optimization. Comput. Biol. Med. 136, 104712. doi:10.1016/j.compbiomed.2021.104712

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, K., Yao, W., Fang, J., Ai, X., Wen, J., and Cheng, S. (2020). Impedance Modeling and Stability Analysis of Grid-Connected DFIG-Based Wind Farm with a VSC-HVDC. IEEE J. Emerg. Sel. Top. Power Electron. 8 (2), 1375–1390. doi:10.1109/jestpe.2019.2901747

CrossRef Full Text | Google Scholar

Yang, B., Li, D. Y., Zeng, C. Y., Chen, Y. J., Guo, Z. X., Wang, J. B., et al. (2021). Parameter Extraction of PEMFC via Bayesian Regularization Neural Network Based Meta-Heuristic Algorithms. Energy 228, 120592. doi:10.1016/j.energy.2021.120592

CrossRef Full Text | Google Scholar

Yang, B., Wang, J. B., Yu, L., Shu, H. C., Yu, T., Zhang, X. S., et al. (2020). A Critical Survey on Proton Exchange Membrane Fuel Cell Parameter Estimation Using Meta-Heuristic Algorithms. J. Clean. Prod. 265, 121660. doi:10.1016/j.jclepro.2020.121660

CrossRef Full Text | Google Scholar

Yang, B., Wang, J. B., Zhang, X. S., Yu, T., Yao, W., Shu, H. C., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energ. Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yang, B., Zeng, C. Y., Wang, L., Guo, Y., Chen, G. H., Guo, Z. X., et al. (2021). Parameter Identification of Proton Exchange Membrane Fuel Cell via Levenberg-Marquardt Backpropagation Algorithm. Int. J. Hydrogen Energ. 46 (44), 22998–23012. doi:10.1016/j.ijhydene.2021.04.130

CrossRef Full Text | Google Scholar

Yao, W., Jiang, L., Wen, J., Wu, Q., and Cheng, S. (2015). Wide-area Damping Controller for Power System Interarea Oscillations: A Networked Predictive Control Approach. IEEE Trans. Control. Syst. Tech. 23 (1), 27–36. doi:10.1109/tcst.2014.2311852

CrossRef Full Text | Google Scholar

Zhang, H. X., Lu, Z. X., Hu, W., Wang, Y. T., Dong, L., and Zhang, J. T. (2019). Coordinated Optimal Operation of Hydro-Wind-Solar Integrated Systems. Appl. Energ. 242, 883–896. doi:10.1016/j.apenergy.2019.03.064

CrossRef Full Text | Google Scholar

Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Industry Appl. doi:10.1109/TIA.2021.3093841

CrossRef Full Text | Google Scholar

Glossary

ABC artificial bee colony

ALO antlion optimization algorithm

BES bald eagle search

FC fuel cell

FPA flower pollination algorithm

GA genetic algorithm

GWO grey wolf optimization

PEMFC proton exchange membrane fuel cell

PEM proton exchange membrane

SSO slap swarm optimizer

$\mathit{A}$ effective electrode area of the cell, cm²

b parametric coefficient, V

$\mathit{C}{\mathit{O}}_{\mathit{2}}$ Concentration of oxygen, mol/cm³

${\mathit{c}}_1$ moving velocities toward the optimal, between 1 and 2

${\mathit{c}}_2$ moving velocities toward the central positions, between 1 and 2

$E_{nernst}$ open-circuit voltage, V

$\mathit{P}{\mathit{H}}_{\mathit{2}}$ partial pressures of hydrogen, atm

$\mathit{P}{\mathit{O}}_{\mathit{2}}$ partial pressures of oxygen, atm

${\rho }_m$ specific membrane resistance, $\Omega \Delta$ cm

$P_{best}$ optimal spatial search position

$P_{mean}$ average distribution position

$V_c$ PEMFC’s output voltage, V

$V_{act}$ activation voltage drop, V

$V_{ohmic}$ ohmic voltage drop, V

$V_{con}$ concentration voltage drop, V

$J_{\max }$ upper bound current density, A/cm²

$\mathit{J}$ actual current density, A/cm²

l membrane thickness, $\mu \text{m}$

$\mathit{r}$ random number between 0 and 1

R parameter that controls the search period, between 0.2 and 2

${\mathit{R}}_m$ membrane resistance to proton conduction, Ω

$R_c$ contact resistance to electron conduction, Ω

${\epsilon }_1$<b> ${\epsilon }_2$,</b> <b> ${\mathit{\epsilon }}_3$,</b> ${\mathit{\epsilon }}_4$ <b> ${\epsilon }_2$,</b> <b> ${\mathit{\epsilon }}_3$,</b> ${\mathit{\epsilon }}_4$semi-empirical coefficients

$\mathit{\lambda }$ empirical parameter

$\mathit{\alpha }$ moving velocities toward the central positions, between 1 and 2