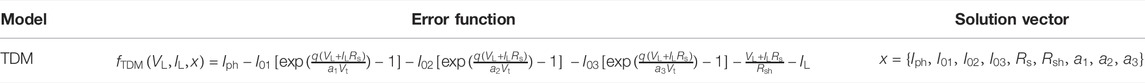Mayfly Optimization Algorithm–Based PV Cell Triple-Diode Model Parameter Identification

The maximum power output and control optimization analysis of photovoltaic (PV) systems are based on accurate and reliable PV cell parameter identification. However, its difficult problems such as high nonlinearity and multimodality have become obstacles to the traditional optimization methods to obtain accurate and efficient results. This study uses a new intelligent optimization algorithm called the mayfly algorithm (MA) to efficiently identify the triple-diode model (TDM) of PV cells and uses the minimum root mean square error (RMSE) as the evaluation index to verify the effectiveness of the algorithm. Moreover, by continuously adjusting the parameters, population number, and iteration times of the MA to better balance the relationship between global development and local optimization, we can obtain more efficient and better optimization results. The research case shows that the MA is superior to other meta-heuristic algorithms in the accuracy and stability of PV cell parameter identification. For example, the minimum standard deviation (SD) of the RMSE obtained by the MA is 1,305 times smaller than another algorithm.

Introduction

In the past few decades, traditional fuel energy has been overused (Yang et al., 2020), which has led to the rise of global temperature and the deterioration of the environment (Wang et al., 2021). At the same time, it has also exacerbated the global energy crisis (Yang et al., 2018a; Wang et al., 2019; Peng et al., 2020). Therefore, in order to change the human energy structure and maintain long-term sustainable development (Yang et al., 2018b; Zhang et al., 2019), an energy revolution is necessary. For sustainable energy development, the development of the technology of solar energy and wind energy has been very mature (Li et al., 2019) and has attracted extensive attention all over the world (Zhang et al., 2020). In particular, solar energy has become the focus of attention in the field of new energy because of its unique advantages (Yang et al., 2016; Sun. et al., 2021).

The PV system has been widely used in solar power generation, which has the advantages of being ubiquitous and inexhaustible, and its characteristics of nearby power supply also avoid the power loss caused by long-distance transmission (Chin et al., 2015). In application, accurate PV modeling based on measured current-voltage (I-V) data is essential for the dynamic behavior analysis of PV systems. So far, three PV models are most widely used, namely, the single-diode model (SDM) (Humada et al., 2016), double-diode model (DDM) (Abbassi et al., 2018), and triple-diode model (TDM) (Khanna et al., 2015). Although the three-diode model has the highest model complexity and computational burden, it is still the most accurate model and has broad research prospects. Therefore, this article studies the parameter identification of PV cells based on the TDM.

Generally, the accurate identification of PV cell parameters is not only very important for the accurate modeling of PV cells but also essential for performance optimization (Youssef et al., 2017), state analysis, and real-time control of PV cells (Chaibi et al., 2019; Yang et al., 2019). However, in practical application, due to various shortcomings and limitations, the result of parameter identification is neither stable nor accurate. These reasons can be classified into two points: I) the parameters provided by the manufacturer can only be applied under standard test conditions (STC), and the data deviation under actual operating conditions will greatly change the output characteristics of PV cells; and II) with the change of service life and weather conditions, the parameters of PV cells are time-varying (Gomes et al., 2017).

The parameter identification of PV cells is highly nonlinear with multimodal obstacles. So far, three kinds of methods have been used to solve this kind of problem, namely, the deterministic technology, analysis method (Chan and Phang, 1987; Saleem and Karmalkar, 2009), and meta-heuristic algorithm. Generally, the analysis method has the characteristics of simple calculation and low accuracy (Wolf and Benda, 2013; Batzelis and Papathanassiou, 2016). Deterministic technology has strict requirements for model characteristics and initial operating conditions (Villalva et al., 2009). This kind of technology is easy to converge prematurely when used in PV cell parameter identification. In comparison, as the promising method used to identify PV cell parameters, a meta-heuristic algorithm has the advantages of easy implementation (Zhang et al., 2021), high robustness, and high efficiency (Mahdavi et al., 2015).

So far, dozens of heuristic algorithms have been applied to the parameter extraction of PV cells, for example, gray wolf optimization (GWO) (Ishaque and Salam, 2011), particle swarm optimization (PSO) (Ye et al., 2009), and genetic algorithm (GA) (Jervase et al., 2001).

A novel MA optimization algorithm is proposed in this study, which is a recently developed heuristic algorithm based on biology. The MA imitates the social behavior of mayflies, especially their mating process, which has the advantages of strong optimization ability and low computational cost.

This study is arranged as follows: PV Cell Modeling and Problem Formulation describes the PV cell modeling and objective function. Multi-Objective Mayfly Algorithm introduces the main optimization principles of the MA. Case Study provides the results of the case study. Finally, Conclusion gives the conclusion.

PV Cell Modeling and Problem Formulation

This section establishes an accurate photovoltaic cell model, which is very important for studying the characteristics of photovoltaic cells. On this basis, the PV system can be better optimized by extracting the output I-V and P-V characteristics of PV cells. Up to now, the three SDM, DDM, and TDM used PV cell models.

Mathematical Modeling

The model of the triple-diode PV cell is summarized in Table 1 to provide a more comprehensive display. As demonstrated in Table 1, I_ph represents the photogenerated current, which is directly proportional to the daylighting area and light intensity of the PV cell; I_d represents the unidirectional current flowing through the PN junction; I_L represents the current output by the PV cell to the external load; R_L represents the external load resistance; R_s represents the equivalent series resistance inside the PV cell; R_sh represents the equivalent bypass resistance inside the PV cell; and I_sh is the current flowing through which, $V_{\text{T}}$ represents the thermal voltage, which is demonstrated as

$V_{\text{T}}=\frac{KT}{q},(1)$

where T denotes cell temperature; K $=1.38\times {10}^{-23}\text{ J}/\text{K}$ denotes the Boltzmann constant; and $q=1.6\times {10}^{-19}\text{ C}$ denotes the electron charge, respectively.

TABLE 1

TABLE 1. Summary on the PV cell triple-diode model.

Objective Function

The purpose is to minimize the error between experimental data and simulation data by finding appropriate parameters. In particular, the root mean square error (RMSE) is selected as the objective function for quantitative evaluation, which is defined as follows:

$\text{RMSE }\left(x\right)=\sqrt{\frac{1}{N}{\displaystyle \sum }_{k=1}^N{\left(f\left(V_{\text{L}},I_{\text{L}},x\right)\right)}^2},(2)$

where $\mathit{ }x$ denotes the solution vector, and $N$ represents the number of experimental data.

Table 2 summarizes the error functions $f(V_{\text{L}},I_{\text{L}},x)$ of the three PV models in detail, and it is necessary to minimize the value of the objective function by optimizing the solution vector x so as to reduce the error between the experimental data and the simulation data.

TABLE 2

TABLE 2. Error functions of the TDM.

Multi-Objective Mayfly Algorithm

Movements of the Male Mayfly

A novel intelligent optimization algorithm was proposed, which simulates the flight and mating process of a mayfly. Moreover, the MA integrates the strength of evolutionary and intelligent optimization algorithms.

In addition to the parameter identification of the TDM, this study attempts to find the solution of the MA with stronger search ability and faster convergence speed. Each male mayfly can be adjusted by the experience of itself and adjacent individuals. $x_i^t$ represents the position of the ith individual at time t in the search space, and the position of the individual can be determined by the speed v at the next time $v_i^{t+1}$, which is described as

$x_i^{t+1}=x_i^t+v_i^{t+1}.(3)$

In general, the speed of male mayflies can be calculated as follows:

$v_{ij}^{t+1}=v_{ij}^t+a_1{\text{e}}^{-\beta r_p^2}\left(pbes{t}_{ij}-x_{ij}^t\right)+a_2{\text{e}}^{-\beta r_g^2}\left(gbes{t}_j-x_{ij}^t\right),(4)$

where $v_{ij}^t$ is the mayfly i in dimension j at time t, and a₁ and a₂ represent the attraction coefficients. p_best and g_best represent the historical optimal position and the optimal position of the mayfly, respectively. The visibility coefficient is β, and r_p and r_g represent the distance between the current position and p_best and the distance between the current position and g_best, respectively. In addition, the calculation method of the distance is described as

$\Vert x-X_i\Vert =\sqrt{{\displaystyle {\sum }_{j=1}^n{\left(x_{ij}-X_{ij}\right)}^2}}.(5)$

The best mayfly individuals in the population must constantly change their speed, which is calculated as follows:

$v_{ij}^{t+1}=v_{ij}^t+d\ast r,(6)$

where the value range of r is (−1,1); moreover, the dance coefficient is d.

Movements of the Female Mayfly

Female mayflies do not congregate but fly to male individuals to reproduce. $y_i^t$ is used to represent the mayfly i at time t, which is expressed as

$y_i^{t+1}=y_i^t+v_i^{t+1}.(7)$

Since the attraction between male and female individuals is random, it can be modeled as a deterministic process. While considering the minimization problem, the calculation process of speed is represented as follows:

$v_{ij}^{t+1}=\{\begin{array}{c}{v}_{ij}^t+a_2{e}^{-\beta r_{\text{mf}}^2}\left(x_{ij}^t-y_{ij}^t\right), if f\left(y_i\right)>f\left(x_i\right)\\ v_{ij}^t+fl\ast r, iff\left(y_i\right)\le f\left(x_i\right)\end{array},(8)$

where r_mf is the distance between the female and male mayfly, and fl represents the random walk coefficient.

Mayfly Mating

An individual is selected from male and female populations to complete mating. The way of selecting parents is the same as that of males attracting females. In particular, the selection can be random or based on their fitness function. Crossover can produce two offspring, and the process is represented as follows:

$\begin{array}{c}\text{o}\text{f}\text{f}\text{s}\text{p}\text{r}\text{i}\text{n}\text{g} 1=L\ast \text{m}\text{a}\text{l}\text{e}+\left(1-L\right)\ast \text{f}\text{e}\text{m}\text{a}\text{l}\text{e} \\ \text{o}\text{f}\text{f}\text{s}\text{p}\text{r}\text{i}\text{n}\text{g} 2=L\ast \text{f}\text{e}\text{m}\text{a}\text{l}\text{e}+\left(1-L\right)\ast \text{m}\text{a}\text{l}\text{e} \end{array},(9)$

where male and female represent male and female parents, respectively, and L denotes a random number.

MA for PV Parameter Identification

Optimization Variables

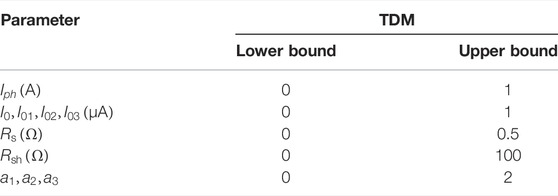
The optimization variables of the TDM of photovoltaic cells are shown in Table 2. In order to make the parameter identification more accurate and effective, various optimization variables are within the upper and lower bounds, which is expressed as

$x_j^{\text{min}}\le x_j\le x_j^{\text{max}}, j=\mathrm{1,2}\dots ,J,(10)$

where x_j is the optimization variable; $x_j^{\text{min}}$ denotes the lower bounds of the jth variable; and $x_j^{\text{max}}$ denotes the upper bounds of the jth variable. In addition, j is the number of variables.

In the process of calculation, mayflies cannot exceed these constraint limits; otherwise, their positions will be reset randomly within the limits, as follows:

$x_j=x_j^{\text{min}}+r_2\left(x_j^{\text{max}}-x_j^{\text{min}}\right),(11)$

where r₂ is a random value between 0 and 1.

Parameter Setting

In PV cell parameter identification, nine parameters should be carefully set, including a₁, a₂, a₃, β, fl, r, d, t_max, and n. The two most important parameters are the population size n and the maximum number of iterations t_max. Generally, the size of t_max and n is directly proportional to the probability of obtaining the optimal solution and inversely proportional to the computational cost. Table 3 shows parameters obtained by the trial and error method.

TABLE 3

TABLE 3. Parameters of the MA for parameter identification of the PV cell.

Application Process

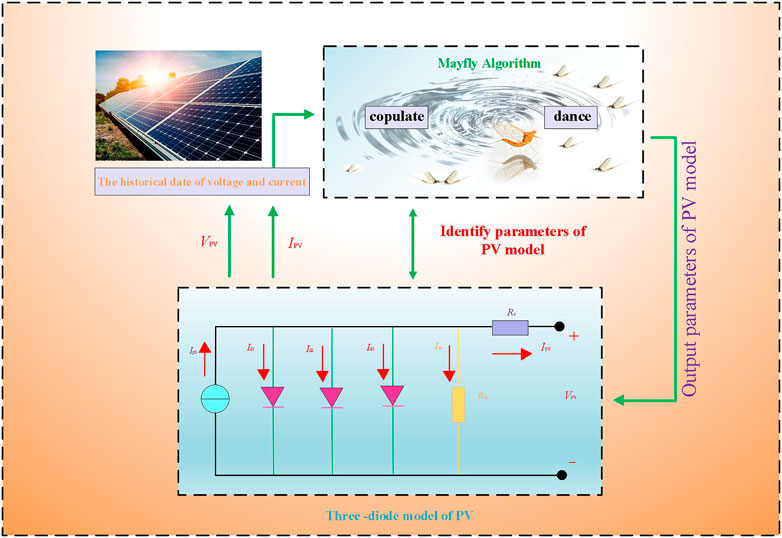
Figure 1 shows the application flow of the MA in parameter identification. The input of the MA is the historical data of the output voltage and current of the PV cell, which can be converted into the objective function through Eq. 2. The MA further executes the optimization program, according to the TDM. Finally, the MA outputs the identification parameters of photovoltaic cells.

FIGURE 1

FIGURE 1. Application process of the MA for parameter identification of the PV cell.

Case Study

In this part, the PV cell TDM is used to extract the parameter based on the MA. To the end, in order to enhance the accuracy of parameter identification, 26 pairs of benchmark current and voltage data sets are used for comparison (Easwarakhanthan et al., 1986). Table 4 denotes the data sets from a 57-mm diameter R.T.C. In addition, the conditions of the French solar cell are G = 1000 W/m² and T = 33°C. This data set is widely used to verify the parameter identification algorithm of PV cells in previous studies (El-Naggar et al., 2012; Gong and Cai, 2013; Oliva et al., 2017; Yu et al., 2017; Chen et al., 2018). Moreover, the benchmark I-V data are only extracted under the conditions of G = 1000 W/m² and T = 33°C, so there is only one fitted I-V curve.

TABLE 4

TABLE 4. I-V data set of the benchmark experiment.

The MA is compared with the PSO algorithm (Oliva et al., 2014). In particular, their maximum number of iterations is designed to be the same, that is, 5,000, and all methods are carried out in 30 independent runs to get a wider range of statistical results. In addition, the population size of the MA is set to 70. The parameter limits of the TDM are shown in Table 5.

TABLE 5

TABLE 5. Parameter bounds of the TDM.

In particular, the best simulation results of both methods are shown in bold. All cases are calculated by MATLAB 2020a through a personal computer, which uses Intel CoreTMi5 CPU with 3.0 GHz and 8 GB memory.

Results and Discussion on the TDM

The results obtained by the two algorithms applied to the TDM are shown in Table 6, as shown in which, the minimum, maximum, average, median, and standard deviation of the RMSE calculated by the MA is the best. Symbols “+,” “−,” and “ = ”indicate that the optimization result of the MA is better than, lower than, or close to its comparison algorithm. For example, the minimum value, median value, and average value of the RMSE obtained by the MA are 0.4, 52.51, and 91.61% lower than the PSO (suboptimal) algorithm, respectively. More importantly, the MA has good accuracy in parameter identification. Therefore, the MA has the most satisfactory performance for the TDM.

TABLE 6

TABLE 6. Statistical results of the RMSE obtained by various algorithms for the TDM.

Table 7 shows the best parameter identification results of the two algorithms for the TDM. Obviously, the MA achieves the best RMSE, followed by the PSO algorithm.

TABLE 7

TABLE 7. Model parameters identified by various algorithms for the TDM.

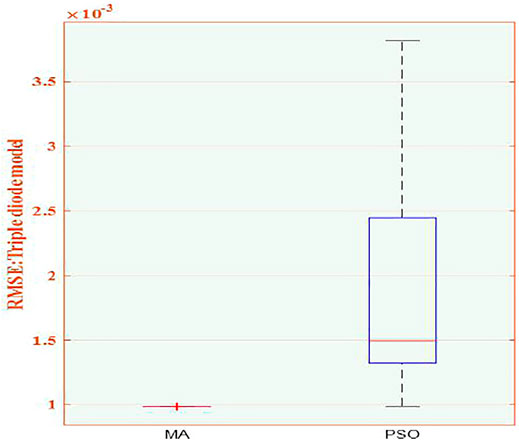
Figure 2 shows the boxplot of MA and PSO algorithms, and Figure 3 shows the output I-V and P-V curves obtained by the MA. It can effectively verify the accuracy of the extracted PV cell parameters. It can be seen that compared with other algorithms, the MA has strong competitiveness in solution accuracy and stability.

FIGURE 2

FIGURE 2. Boxplot of the RMSE obtained by two algorithms for the TDM.

FIGURE 3

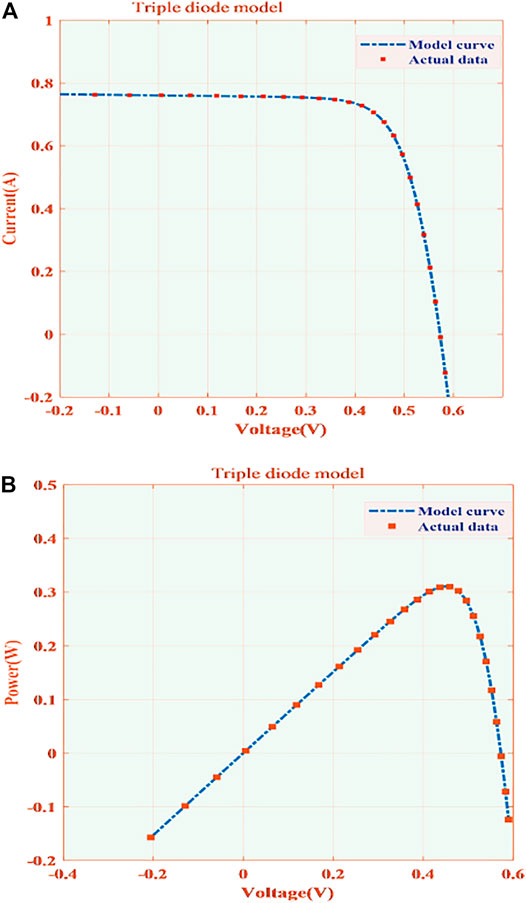
FIGURE 3. Comparison between actual data and the model curve obtained by the MA for the TDM (A) I-V curve and (B) P-V curve.

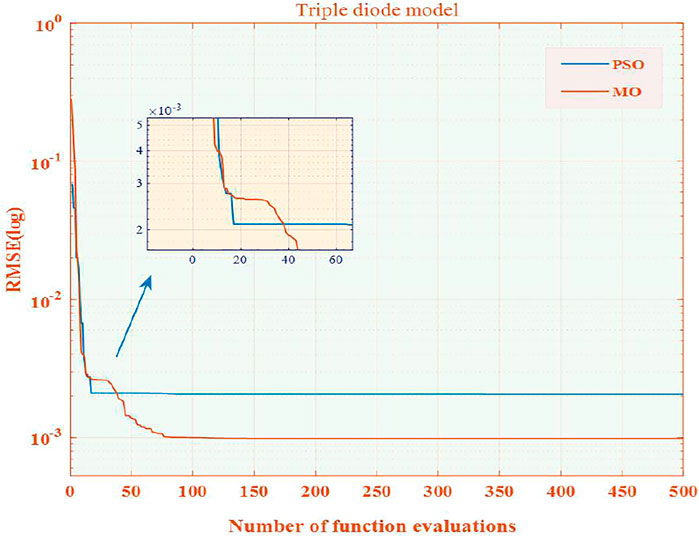
Finally, the convergence diagrams of the two algorithms are given in Figure 4. It is obvious that the MA has strong optimization ability, fast convergence speed, and can well balance local optimization. Compared with the MA, the optimization effect of PSO is not satisfactory.

FIGURE 4

FIGURE 4. Convergence graph of various algorithms for the TDM.

In particular, Figure 4 demonstrates the convergence diagrams of the two algorithms, in which the PSO algorithm is difficult to converge quickly and obtain high-quality optimal solutions. In addition, the MA can easily get a better result through strong search ability and reasonable balance ability.

Statistical Analysis

It is noted that the standard deviation of the RMSE indicates the reliability of parameter extraction. On the TDM, the MA can obviously achieve better performance than the PSO algorithm, thus effectively verifying the excellent reliability of the MA. For example, in the TDM, the standard deviation of the RMSE obtained by the MA is more than 1,305 times smaller than the optimal value of PSO.

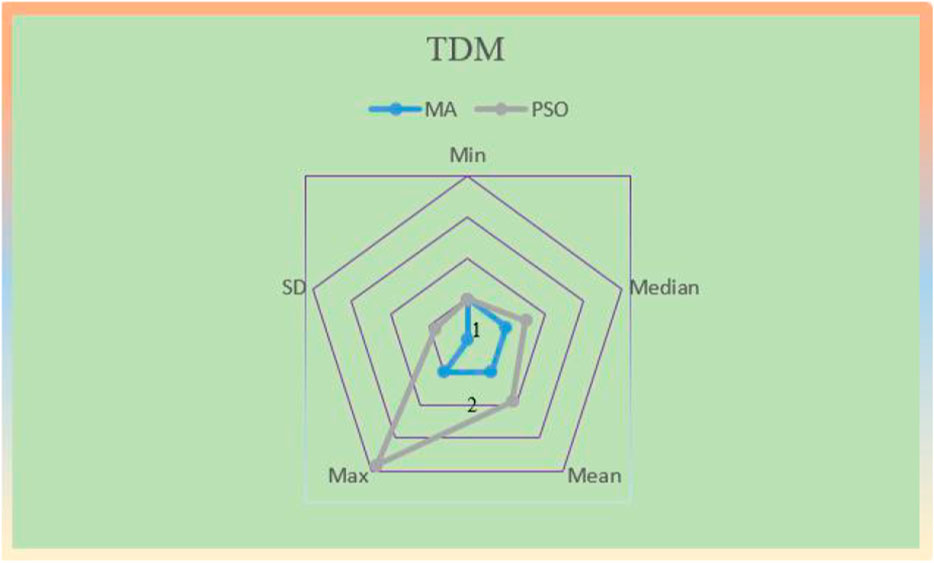
In addition, through 30 independent operations of the TDM, the results of the two methods are shown in Figure 2. Moreover, the superior performance of the MA addition can be shown by the distribution of solutions. The radar charts of the MA and PSO are shown in Figure 5. In particular, the best ranking is two points and then decreases by one point in turn. One can easily identify the comparison of optimization accuracy, convergence stability, and speed between MA and PSO algorithms in PV cell parameter extraction. It can be illustrated by the radar chart that MA’s optimization accuracy is better than that of the PSO algorithm.

FIGURE 5

FIGURE 5. Radar graph of two algorithms for the TDM.

Conclusion

This study adopts a powerful and novel MA to accurately and effectively estimate the parameters of the triple-diode model of PV cells. The algorithm includes the following three contributions/innovations:

• The MA can dynamically balance between local optimization and global optimization to obtain a better solution;

• The MA is applied to the TDM to verify its feasibility and effectiveness;

• Through the case study, it is found that the MA can obtain a higher precision solution than other meta-heuristic algorithms when applied to parameter identification.

The convergence speed and optimization accuracy of the algorithm can be the main directions of future research. Based on the MA, the optimization efficiency can be verified by online parameter estimation of PV cells, which is necessary in practical engineering.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

NC: conceptualization, writing—original draft, and formal analysis; WB: supervision and writing—review and editing; GX: visualization and validation; ZW: data curation and visualization; MW: formal analysis and software; KL: investigation and validation.

Conflict of Interest

NC, WB, GX, ZW, and MW were employed by China Southern Power Grid EHV Transmission Company.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

DDM, double-diode model; DE, differential evolution; G, irradiation, W $/{\text{m}}^2$; GA, genetic algorithm; I-V, current-voltage; MA, mayfly algorithm; MPPT, maximum power point tracking; PSO, particle swarm optimization; PV, photovoltaic; P-V, power-voltage; RMSE, root mean square error; SD, standard deviation; SDM, single-diode model; STC, standard test condition; T, temperature, °C; TDM, triple-diode model.

References

Abbassi, R., Abbassi, A., Jemli, M., and Chebbi, S. (2018). Identification of Unknown Parameters of Solar Cell Models: A Comprehensive Overview of Available Approaches. Renew. Sustain. Energ. Rev. 90, 453–474. doi:10.1016/j.rser.2018.03.011

CrossRef Full Text | Google Scholar

Batzelis, E. I., and Papathanassiou, S. A. (2016). A Method for the Analytical Extraction of the Single-Diode PV Model Parameters. IEEE Trans. Sustain. Energ. 7, 504–512. doi:10.1109/tste.2015.2503435

CrossRef Full Text | Google Scholar

Chaibi, Y., Allouhi, A., Salhi, M., and El-jouni, A. (2019). Annual Performance Analysis of Different Maximum Power point Tracking Techniques Used in PV Systems. Prot. Control. Mod. Power Syst. 4 (4), 171–180. doi:10.1186/s41601-019-0129-1

CrossRef Full Text | Google Scholar

Chan, D. S. H., and Phang, J. C. H. (1987). Analytical Methods for the Extraction of Solar-Cell Single- and Double-Diode Model Parameters from I-V Characteristics. IEEE Trans. Electron. Devices 34 (2), 286–293. doi:10.1109/t-ed.1987.22920

CrossRef Full Text | Google Scholar

Chen, X., Xu, B., Mei, C., Ding, Y., and Li, K. (2018). Teaching-learning-based Artificial Bee colony for Solar Photovoltaic Parameter Estimation. Appl. Energ. 212, 1578–1588. doi:10.1016/j.apenergy.2017.12.115

CrossRef Full Text | Google Scholar

Chin, V. J., Salam, Z., and Ishaque, K. (2015). Cell Modelling and Model Parameters Estimation Techniques for Photovoltaic Simulator Application: A Review. Appl. Energ. 154, 500–519. doi:10.1016/j.apenergy.2015.05.035

CrossRef Full Text | Google Scholar

Easwarakhanthan, T., Bottin, J., Bouhouch, I., and Boutrit, C. (1986). Nonlinear Minimization Algorithm for Determining the Solar Cell Parameters with Microcomputers. Int. J. Solar Energ. 4 (1), 1–12. doi:10.1080/01425918608909835

CrossRef Full Text | Google Scholar

El-Naggar, K. M., AlRashidi, M. R., AlHajri, M. F., and Al-Othman, A. K. (2012). Simulated Annealing Algorithm for Photovoltaic Parameters Identification. Solar Energy 86 (1), 266–274. doi:10.1016/j.solener.2011.09.032

CrossRef Full Text | Google Scholar

Gomes, R. C. M., Vitorino, M. A., de Rossiter Correa, M. B., Fernandes, D. A., and Wang, R. (2017). Shuffled Complex Evolution on Photovoltaic Parameter Extraction: A Comparative Analysis. IEEE Trans. Sustain. Energ. 8 (2), 805–815. doi:10.1109/tste.2016.2620941

CrossRef Full Text | Google Scholar

Gong, W., and Cai, Z. (2013). Parameter Extraction of Solar Cell Models Using Repaired Adaptive Differential Evolution. Solar Energy 94, 209–220. doi:10.1016/j.solener.2013.05.007

CrossRef Full Text | Google Scholar

Humada, A. M., Hojabri, M., Mekhilef, S., and Hamada, H. M. (2016). Solar Cell Parameters Extraction Based on Single and Double-Diode Models: A Review. Renew. Sustain. Energ. Rev. 56, 494–509. doi:10.1016/j.rser.2015.11.051

CrossRef Full Text | Google Scholar

Ishaque, K., and Salam, Z. (2011). An Improved Modeling Method to Determine the Model Parameters of Photovoltaic (PV) Modules Using Differential Evolution (DE). Solar Energy 85 (9), 2349–2359. doi:10.1016/j.solener.2011.06.025

CrossRef Full Text | Google Scholar

Jervase, J. A., Bourdoucen, H., and Al-lawati, A. (2001). Solar Cell Parameter Extraction Using Genetic Algorithms. Meas. Sci. Technol. 12, 1922–1925. doi:10.1088/0957-0233/12/11/322

CrossRef Full Text | Google Scholar

Khanna, V., Das, B. K., Bisht, D., VandanaSingh, P. K., and Singh, P. K. (2015). A Three Diode Model for Industrial Solar Cells and Estimation of Solar Cell Parameters Using PSO Algorithm. Renew. Energ. 78, 105–113. doi:10.1016/j.renene.2014.12.072

CrossRef Full Text | Google Scholar

Li, G. D., Li, G. Y., and Zhou, M. (2019). Model and Application of Renewable Energy Accommodation Capacity Calculation Considering Utilization Level of Interprovincial Tie-Line. Prot. Control. Mod. Power Syst. 4 (4), 1–12. doi:10.1186/s41601-019-0115-7

CrossRef Full Text | Google Scholar

Mahdavi, S., Shiri, M. E., and Rahnamayan, S. (2015). Metaheuristics in Large-Scale Global Continues Optimization: A Survey. Inf. Sci. 295, 407–428. doi:10.1016/j.ins.2014.10.042

CrossRef Full Text | Google Scholar

Oliva, D., Abd El Aziz, M., and Ella Hassanien, A. (2017). Parameter Estimation of Photovoltaic Cells Using an Improved Chaotic Whale Optimization Algorithm. Appl. Energ. 200, 141–154. doi:10.1016/j.apenergy.2017.05.029

CrossRef Full Text | Google Scholar

Oliva, D., Cuevas, E., and Pajares, G. (2014). Parameter Identification of Solar Cells Using Artificial Bee colony Optimization. Energy 72, 93–102. doi:10.1016/j.energy.2014.05.011

CrossRef Full Text | Google Scholar

Peng, X., Yao, W., Yan, C., Wen, J., and Cheng, S. (2020). Two-stage Variable Proportion Coefficient Based Frequency Support of Grid-Connected DFIG-WTs. IEEE Trans. Power Syst. 35 (2), 962–974. doi:10.1109/tpwrs.2019.2943520

CrossRef Full Text | Google Scholar

Saleem, H., and Karmalkar, S. (2009). An Analytical Method to Extract the Physical Parameters of a Solar Cell from Four Points on the Illuminated $J{-}V$ Curve. IEEE Electron. Device Lett. 30, 349–352. doi:10.1109/led.2009.2013882

CrossRef Full Text | Google Scholar

Sun., L., Wang, J., and Tang., L. (2021). A Powerful Bio-Inspired Optimization Algorithm Based PV Cells Diode Models Parameter Estimation. Front. Energ. Res. 9, 147. doi:10.3389/fenrg.2021.675925

CrossRef Full Text | Google Scholar

Villalva, M. G., Gazoli, J. R., and Filho, E. R. (2009). Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 24, 1198–1208. doi:10.1109/tpel.2009.2013862

CrossRef Full Text | Google Scholar

Wang, J., Yang, B., Li, D., Zeng, C., Chen, Y., Guo, Z., et al. (2021). Photovoltaic Cell Parameter Estimation Based on Improved Equilibrium Optimizer Algorithm. Energ. Convers. Manage. 236, 114051. doi:10.1016/j.enconman.2021.114051

CrossRef Full Text | Google Scholar

Wang, L., Wang., Z., Liang, H., and Huang, C. (2019). Parameter Estimation of Photovoltaic Cell Model with Rao-1 Algorithm. Optik - Int. J. Light Electron Opt. 210, 163846. doi:10.1016/j.ijleo.2019.163846

CrossRef Full Text | Google Scholar

Wolf, P., and Benda, V. (2013). Identification of PV Solar Cells and Modules Parameters by Combining Statistical and Analytical Methods. Solar Energy 93, 151–157. doi:10.1016/j.solener.2013.03.018

CrossRef Full Text | Google Scholar

Yang, B., Jiang, L., Wang, L., Yao, W., and Wu, Q. H. (2016). Nonlinear Maximum Power point Tracking Control and Modal Analysis of DFIG Based Wind Turbine. Int. J. Electr. Power Energ. Syst. 74, 429–436. doi:10.1016/j.ijepes.2015.07.036

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on Pv Cell Parameter Identification. Energ. Convers. Manage. 208, 112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Dong, J., and Jiang, L. (2018). Robust Sliding-Mode Control of Wind Energy Conversion Systems for Optimal Power Extraction via Nonlinear Perturbation Observers. Appl. Energ. 210, 711–723. doi:10.1016/j.apenergy.2017.08.027

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Zhang, Y., Chen, J., Sang, Y., et al. (2018). Passivity-based Sliding-Mode Control Design for Optimal Power Extraction of a PMSG Based Variable Speed Wind Turbine. Renew. Energ. 119, 577–589. doi:10.1016/j.renene.2017.12.047

CrossRef Full Text | Google Scholar

Yang, B., Zhong, L., Zhang, X., Shu, H., Yu, T., Li, H., et al. (2019). Novel Bio-Inspired Memetic Salp Swarm Algorithm and Application to MPPT for PV Systems Considering Partial Shading Condition. J. Clean. Prod. 215, 1203–1222. doi:10.1016/j.jclepro.2019.01.150

CrossRef Full Text | Google Scholar

Ye, M., Wang, X., and Xu, Y. (2009). Parameter Extraction of Solar Cells Using Particle Swarm Optimization. J. Appl. Phys. 105 (9), 094502. doi:10.1063/1.3122082

CrossRef Full Text | Google Scholar

Youssef, A., El-Telbany, M., and Zekry, A. (2017). The Role of Artificial Intelligence in Photo-Voltaic Systems Design and Control: a Review. Renew. Sustain. Energ. Rev. 78, 72–79. doi:10.1016/j.rser.2017.04.046

CrossRef Full Text | Google Scholar

Yu, K., Liang, J. J., Qu, B. Y., Chen, X., and Wang, H. (2017). Parameters Identification of Photovoltaic Models Using an Improved JAYA Optimization Algorithm. Energ. Convers. Manage. 150, 742–753. doi:10.1016/j.enconman.2017.08.063

CrossRef Full Text | Google Scholar

Zhang, H., Lu, Z., Hu, W., Wang, Y., Dong, L., and Zhang, J. (2019). Coordinated Optimal Operation of Hydro-Wind-Solar Integrated Systems. Appl. Energ. 242, 883–896. doi:10.1016/j.apenergy.2019.03.064

CrossRef Full Text | Google Scholar

Zhang, X., Tan, T., Zhou, B., Yu, T., Yang, B., and Huang, X. (2021). Adaptive Distributed Auction-Based Algorithm for Optimal Mileage Based AGC Dispatch with High Participation of Renewable Energy. Int. J. Electr. Power Energ. Syst. 124, 106371. doi:10.1016/j.ijepes.2020.106371

CrossRef Full Text | Google Scholar

Zhang, X., Xu, Z., Yu, T., Yang, B., and Wang, H. (2020). Optimal Mileage Based AGC Dispatch of a GenCo. IEEE Trans. Power Syst. 35 (4), 2516–2526. doi:10.1109/tpwrs.2020.2966509

CrossRef Full Text | Google Scholar

Nomenclature

${\mathit{I}}_{\mathit{ph}}$ photocurrent, A

${\mathit{I}}_{\mathbf{d}}$, ${\mathit{I}}_{\mathit{d}\mathbf{1}}$, and ${\mathit{I}}_{\mathbf{d}\mathbf{2}}$, diode’s currents, A

${\mathit{I}}_{\mathbf{0}}$, ${\mathit{I}}_{\mathbf{01}}$, ${\mathit{I}}_{\mathbf{02}}$, and ${\mathit{I}}_{\mathbf{03}}$ diode’s reverse saturation currents, A

${\mathit{R}}_{\mathbf{s}}$ series resistor, Ω

${\mathit{R}}_{\mathbf{sh}}$ shunt resistor, Ω

$\mathit{a}$,${\mathit{a}}_{\mathbf{1}}$,${\mathit{a}}_{\mathbf{2}}$, and${\mathit{a}}_{\mathbf{3}}$ ideality factors of the diode