Energy Optimal Dispatch of the Data Center Microgrid Based on Stochastic Model Predictive Control

Renewable energy outputs such as wind turbines and photovoltaics, as well as data center workloads are both random and uncertain. In order to enhance the stability and economy of the data center in actual operation effectively, a multi-time scale optimal dispatch method for the data center microgrid based on stochastic model predictive control is proposed in this paper. In the day-ahead scheduling stage, the characteristic of the data center that batch workloads are allowed to be served delayed is considered. And the scenario analysis method is applied to describe the uncertainty of loads and renewable energy outputs, based on which an economic optimization scheduling model is established to minimize the system operating cost. The intra-day scheduling utilizes the rolling optimization and feedback correction of model predictive control to correct the deviation of loads and renewable energy outputs and adjust the day-ahead dispatch plan in real time, which ensures the effectiveness of day-ahead plan and the stability of system operating. Through the simulation results of a typical data center microgrid, the effectiveness of the proposed method is verified.

1 Introduction

With the rapid development of big data and cloud computing technology in recent years, the quantity and scale of data centers have been expanding. At the same time, the electricity consumption is also growing tremendously. It is estimated that about 2% of the world’s total electricity consumption is related to data centers, and the power demand of this sector is increasing at an annual rate of 15%–20% (Ebrahimi et al., 2015). The electricity bills that some data centers pay to the electricity market is as high as tens of millions. In order to reduce the electricity consumption costs, more and more data centers choose to connect lower-cost renewable energy generators such as wind turbines (WT) and photovoltaics (PV) to their power supply system (Liu B et al., 2021). Futhermore, data centers belong to the category of first-class loads; hence, power supply cannot be interrupted. It is necessary for data centers to equip with alternative power sources to ensure the sustainable and reliable power supply (Wang et al., 2020). Thus, data center construction areas always integrate energy storage systems (ESS), conventional power generators, and renewable energy generators, which constitute a typical microgrid system (Li and Qi, 2018; Yu et al., 2018). On the other hand, batch workloads in data centers are allowed to be served delayed and migrated and can be flexibly allocated according to the peak–valley difference of the electricity price. With the technology of the energy management and optimal dispatch, the power consumption and operating cost of data centers can be reduced effectively.

Recently, the research on energy management in data centers has been increasing. In the study by Chen et al. (2016a), the data center is considered as a microgrid, where renewable energy outputs and ESS are optimized, but the scheduling of data center workloads was ignored. The classification of data center workloads was studied by Ding et al. (2019), wherein by allocating the batch workloads and utilizing renewable energy, the energy consumption of the data center was reduced effectively. The impact on the main grid caused by data center workload migration is considered in a study by Wang et al. (2016), and the interaction between the main grid and data center is modeled as a two-stage programing problem. In a study by Wen and Liu (2019), an optimal scheduling model of the hybrid wind–solar–hydro power generation system with data center workloads was studied. The demand side and power supply side-joint scheduling was adopted, which improved the economy of the system. In a study by Wang et al. (2017), a day-ahead resource dispatch problem considering conventional generator fuel and carbon emission costs was proposed, and a mixed integer linear programming (MILP) model was formulated to solve it.

Although many progresses have been made in the research on energy management of the data center, most research mainly studied the energy management of the data center operating in a certain scenario. In fact, the renewable energy and data center workloads are quiet random and uncertain. The randomness of renewable outputs and workloads distribution, as well as the change of electricity price, are considered in Ding et al. (2018), and a day-ahead stochastic planning scheme for the data center microgrid (DCMG) was proposed. A stochastic programming based on the MILP model for the data center energy management was proposed in Xu et al. (2019), which can deal with the influence of uncertainty effectively. The aforementioned studies consider the influence of uncertain factors in the data center, but the optimal dispatch was only in the day-ahead stage. In actual operation, real-time variety of workloads and renewable energy outputs will still affect the security and economy of the data center, and the stability of the main grid will be affected at the same time (Liu et al., 2018; Xiong et al., 2020).

Model predictive control (MPC) is an advanced method for process control, which has been widely used in a variety of complex dynamic systems (Camacho and Bordons, 2004). Recently, it also has drawn much attention of the energy management studies. In the study by Chen et al. (2013), a MPC-based appliance scheduling method for a smart home was proposed with the consideration of dynamic prices and appliance usage patterns. In the study by Zhang et al. (2015), a closed-loop scheduling model for microgrid energy management was established based on MPC. Through the closed-loop feedback, model prediction, and iterative update strategy of MPC, the economy of the system was improved. However, the aforementioned scheduling models lack the guidance of day-ahead plans, and the optimization results do not have the global optimality.

The contributions of this article are listed as follows:

(1) Considering the unique characteristics of data center workloads and describing stochastic factors with the scenario analysis method, a multi-time scale optimal dispatch model combining day-ahead and intra-day rolling correction of DCMG was constructed based on stochastic model predictive control (SMPC).

2) The case study of a typical DCMG scenario was conducted to verify the effectiveness and feasibility of the proposed multi-time scale model.

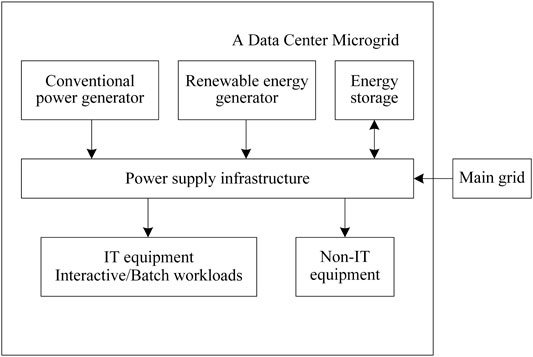
2 The Data Center Microgrid System

The structure of the DCMG is shown in Figure 1. A DCMG usually consists of conventional generators, distributed renewable generators, ESS, and data center loads. In most cases, it needs to purchase electricity power from the main grid. The main difference between the DCMG and general microgrids is the unique power consumption characteristic. The workload of the data center refers to the information and data that need to be processed, which depends on the user’s behavior of using the network, and has greater randomness and uncertainty. The workload also determines the total power consumption of the data center, which is the basis for the flexible adjustment of the data center’s electrical load.

FIGURE 1

FIGURE 1. The structure of a DCMG.

According to the differences in user’s computing requirements, the data center workload can be divided into two categories: the interactive and batch workloads. The interactive workload must be served immediately (usually a few seconds) when the users submit requests for computing services, such as opening a web page, entering passwords, and sending voice messages. The batch workload can be processed more flexibly before the deadline. The service time can be delayed by several hours or even 1 day. The batch job normally includes scientific computing, data backup, image processing, and other data-intensive tasks (Chen et al., 2016b). Therefore, dispatching the batch workload according to the peak-to-valley electricity price can reduce the operating cost of the data center.

The total power consumption of the data center includes the consumption of IT equipments and non-IT equipments (such as refrigeration system, lighting system, etc.). power usage effectiveness (PUE) is an important indicator to measure the energy efficiency of a data center (Jaureguialzo, 2011). It is defined as the ratio of the total power consumption of the data center to the power consumption of IT equipments. The PUE value is always greater than 1, and the lower the PUE value, the more energy-efficient the data center. According to the PUE value and the power consumed by IT equipment, the total power consumption of the data center can be calculated.

3 Energy Optimal Dispatch Model of the DCMG Based on SMPC

3.1 Day-Ahead Optimization Scheduling

3.1.1 The Objective Function

The objective of the day-ahead optimization scheduling is to minimize the total operating cost of the data center. In this article, power demand and renewable energy output forecasts are considered as stochastic parameters owing to their randomness and uncertainty. The scenario analysis method is based on the probability theory; the research object of uncertainty information is described by scenarios, and each scenario constructed corresponds to a certain probability. The key of the method is to fully reflect the uncertainty information with limited scenarios. In this article, it is used to transform the uncertainty of the DCMG into multiple deterministic scenarios. The objective function is shown as follows:

$\min C={\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^T{Pr}_s·F_s^t}}(1)$

$F_s^t={\displaystyle \sum _{i=1}^{N_{\mathrm{DG}}}\left(C_{\mathrm{f}}\left(P_{\mathit{Gi}}^{s,t}\right)+C_{\mathrm{OM}}\left(P_{\mathit{Gi}}^{s,t}\right)+C_{\mathrm{eav}}\left(P_{\mathit{Gi}}^{s,t}\right)\right)}+C_{\mathrm{pp}}\left(P_{\mathrm{Grid}}^{s,t}\right)(2)$

where C indicates the total operating cost of the data center; S indicates the number of total scenarios, which is the combination of the sample sets of each part; Pr_s indicates the probability of the scenario s, which is the product of sample probabilities of each part; T indicates the total time periods of day-ahead optimization scheduling, which is 24 h; F t s indicates the operating cost in the t-th period and the s-th scenario; and N_DG indicates the number of distributed generators. C_f (·), C_OM (·), and C_eav (·) indicate the fuel consumption cost, maintenance cost, and pollution emission cost of distributed generators, respectively; P s,t Gi indicates the output of the ith distributed generator in the t-th period; P s,t Grid indicates the electricity purchase power from the main grid in the t-th period; and C_pp (·) indicates the cost of the purchasing electricity from the main grid.

3.1.2 The Constraint Conditions

Based on the structure of the DCMG shown in Figure 1, the constraints including power consumption of the data center, distributed generators, ESS, and interaction with the main grid need to be considered in the day-ahead dispatch model. In addition, the DCMG system must satisfy the power balance between supply and demand, which is the premise for the data center to realize stable and economic operation.

(1) Data Center Workload Constraint

Suppose that there are M servers with the same structure in the data center, and the loads distribution of each server is equal, limited by the computing power of CPU, there is an upper limit on the workloads that can be processed in each time period that can be calculated as follows:

$L^t\le L_C,\forall t(3)$

where L^t indicates total workloads processed by the CPU in the t-th period, and L_C indicates the upper limit of the workloads processed by the CPU of the data center, and

$L^t=L_{\mathrm{ds}}^t+L_{\mathrm{dt}}^t-{\sigma }_{\mathrm{load}}^t,\forall t(4)$

where L^t_ds and L^t_dt indicate the interactive and batch workloads of the data center in the t-th period, and σ ^t_load indicates the workloads that is being processed in the t-th period.

The process of the flexible scheduling of batch workloads can be expressed as follows (Wang et al., 2017):

$Q_{\mathrm{dt}}^t=Q_{\mathrm{dt}}^{t-1}+L_{\mathrm{dt}}^t-{\sigma }_{\mathrm{load}}^t,\forall t\le (5)$

$Q_{\mathrm{dt}}^T=0(6)$

where Q ^t_dt indicates the batch workloads that have not been processed by the data center until the t-th period.

The power consumed by IT equipments is related to the quantities of workloads processed by the CPU. According to the concept of PUE, the total power consumption of the data center can be calculated. The total power of the data center in the t-th period can be expressed as shown in (Yu et al., 2014):

$P_{\mathrm{Load}}^t=M\left(\delta +\mu L_t\right),\forall t(7)$

$\delta \triangleq P_{\mathrm{idle}}+\left(PUE-1\right)P_{\mathrm{peak}}(8)$

$\mu \triangleq P_{\mathrm{peak}}-P_{\mathrm{idle}}(9)$

where P ^t_Load indicates the total power of the data center in the t-th period; M is the quantity of servers in the data center; δ and μ are the intermediate variables for calculation; P_idle and P_peak respectively indicate the power consumption when the server is in the idle and busy states.

(2) System Power Balance Constraint

${\displaystyle \sum _{i=1}^{N_{\mathrm{DG}}}{P}_{\mathit{Gi}}^{s,t}}+P_{\mathrm{Grid}}^{s,t}=P_{\mathrm{Load}}^{s,t}+P_{\mathrm{ESS}}^{s,t}(10)$

where P s,t ESS indicates the charging and discharging power of ESS in the tth period, the positive value represents ESS charging, and the negative value represents ESS discharging.

(3) Interaction Power with the Main Grid Constraint

$P_{\mathrm{Grid}}^{\min }\le P_{\mathrm{Grid}}^{s,t}\le P_{\mathrm{Grid}}^{\max }(11)$

where Pmin Grid and Pmax Grid respectively indicate the upper and lower limits of the interaction power between the DCMG and the main grid.

(4) Distributed Generators Operating Constrain

$P_{\mathit{Gi}}^{\min }\le P_{\mathit{Gi}}^{s,t}\le P_{\mathit{Gi}}^{\max }(12)$

$\mathrm{\Delta }{P}_{\mathit{Gi}}^{\min }\le P_{\mathit{Gi}}^{s,t}-P_{\mathit{Gi}}^{s,t-1}\le \mathrm{\Delta }{P}_{\mathit{Gi}}^{\max }(13)$

Eq. 12 is the output power constraint of distributed generators, where Pmin Gi and Pmax Gi respectively indicate the maximum and minimum output power of the ith distributed generator. Eq. 13 is the climb power constraint of operating distributed generators, where ΔPmax Gi and ΔPmin Gi respectively indicate the upper and lower limits of the climbing power of the ith distributed generator.

(5) ESS Constraint

The constraints during the operation of ESS mainly include the upper and lower limits of charging and discharging power and the state of charge (SOC) constraint.

$-P_{\mathrm{ESS}}^{\max }\le P_{\mathrm{ESS}}^{s,t}\le P_{\mathrm{ESS}}^{\max }(14)$

where P s,t ESS indicates the maximum of charging and discharging power of ESS.

The SOC of ESS in the t-th period can be expressed by the formulas in following:

$S_{\mathrm{ESS}}^{s,t}=S_{\mathrm{ESS}}^{s,t-1}\left(1-\sigma \right)+\eta \frac{P_{\mathrm{ESS}}^{s,t}\mathrm{\Delta }t}{E_{\mathrm{ESS}}}(15)$

where S s,t ESS indicates the SOC of ESS in the t-th period; σ indicates the self-consumption rate of ESS; η indicates the charging and discharging efficiency of ESS; E_ESS indicates the total capacity of ESS; and Δt indicates the time interval.

The SOC constraint of ESS is expressed as follows:

$S_{\mathrm{ESS}}^{\min }\le S_{\mathrm{ESS}}^{s,t}\le S_{\mathrm{ESS}}^{\max }(16)$

$S_{\mathrm{ESS}}^{s,t=0}=S_{\mathrm{ESS}}^{s,t=T}(17)$

where Smax ESS and Smin ESS respectively indicate the upper and lower limits of the SOC. In addition, the SOC should be consistent at the beginning and the end of the dispatch cycle.

3.2 Intra-Day Rolling Optimization Scheduling

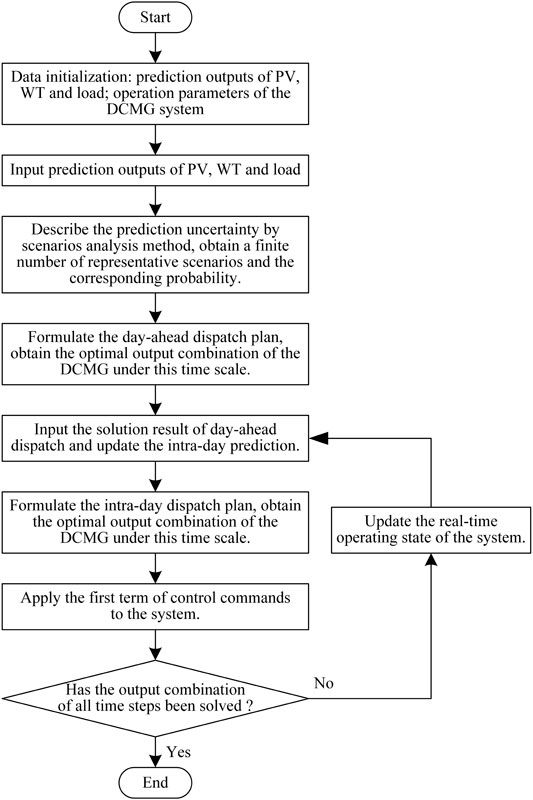
The MPC is a kind of a model-based closed-loop optimization control strategy. The core of MPC is to continuously perform rolling optimization in a finite-time domain based on the mathematical model of the controlled object. The strategy mainly includes the following steps:

(1) At the current time step k and the current state x(k), MPC predicts the future state of the system based on the prediction model. Considering the current and future constraints, obtain the control command sequences at the future time steps k+1, k+2, … , k + M by solving the optimization problem.

(2) Apply the control command of the first time step to the system.

(3) At the time step k+1, update the state x(k+1) and repeat the aforementioned steps.

Taking a typical grid-connected DCMG as an example, it consists of WT, PV, a micro gas turbine (MT), a fuel cell generator (FC), ESS, and data center loads. The state variable at the time step k is

$\mathit{x}\left(k\right)={[P_{\mathrm{MT}}\left(k\right),P_{\mathrm{FC}}\left(k\right),P_{\mathrm{ESS}}\left(k\right),S_{\mathrm{ESS}}\left(k\right),P_{\mathrm{Grid}}\left(k\right)]}^{\mathrm{T}}$

The control variable is

$\mathit{u}\left(k\right)={[\mathrm{\Delta }{P}_{\mathrm{MT}}\left(k\right),\mathrm{\Delta }{P}_{\mathrm{FC}}\left(k\right),\mathrm{\Delta }{P}_{\mathrm{ESS}}\left(k\right)]}^T$

The disturbance variable is

$\mathit{r}\left(k\right)={[\mathrm{\Delta }{P}_{Load}\left(k\right),\mathrm{\Delta }{P}_{WT}\left(k\right),\mathrm{\Delta }{P}_{PV}\left(k\right)]}^T$

The output variable is

$\mathit{y}\left(k\right)={[P_{Grid}\left(k\right),S_{\mathrm{ESS}}\left(k\right)]}^T$

The multi-input and multi-output state space model can be established as follows:

$\begin{array}{c}\mathit{x}(k+\mathrm{\Delta }t)=\left[\begin{array}{c}{P}_{\mathrm{MT}}(k+\mathrm{\Delta }t)\\ P_{\mathrm{FC}}(k+\mathrm{\Delta }t)\\ P_{\mathrm{ESS}}(k+\mathrm{\Delta }t)\\ S_{\mathrm{ESS}}(k+\mathrm{\Delta }t)\\ P_{\mathrm{Grid}}(k+\mathrm{\Delta }t)\end{array}\right]=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& -\eta \frac{\mathrm{\Delta }t}{E_{\mathrm{ESS}}}& 1-\sigma & 0\\ 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{P}_{\mathrm{MT}}\left(k\right)\\ P_{\mathrm{FC}}\left(k\right)\\ P_{\mathrm{ESS}}\left(k\right)\\ S_{\mathrm{ESS}}\left(k\right)\\ P_{\mathrm{Grid}}\left(k\right)\end{array}\right]+\\ \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 0& 0& -\eta \frac{\mathrm{\Delta }t}{E_{\mathrm{ESS}}}\\ -1& -1& -1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{P}_{\mathrm{MT}}\left(k\right)\\ \mathrm{\Delta }{P}_{\mathrm{FC}}\left(k\right)\\ \mathrm{\Delta }{P}_{\mathrm{ESS}}\left(k\right)\end{array}\right]+\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 1& -1& -1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{P}_{\mathrm{Load}}\left(k\right)\\ \mathrm{\Delta }{P}_{\mathrm{WT}}\left(k\right)\\ \mathrm{\Delta }{P}_{\mathrm{PV}}\left(k\right)\end{array}\right]\end{array}(18)$

$\begin{array}{c}\mathit{y}\left(k\right)=\left[\begin{array}{c}{P}_{\mathrm{Grid}}\left(k\right)\\ S_{\mathrm{ESS}}\left(k\right)\end{array}\right]=\left[\begin{array}{ccccc}0& 0& 0& 0& 1\\ 0& 0& 0& 1& 0\end{array}\right]·\\ {\left[\begin{array}{ccccc}{P}_{\mathrm{MT}}\left(k\right)& P_{\mathrm{FC}}\left(k\right)& P_{\mathrm{ESS}}\left(k\right)& S_{\mathrm{ESS}}\left(k\right)& P_{\mathrm{Grid}}\left(k\right)\end{array}\right]}^T\end{array}(19)$

The objective of the intra-day optimization dispatch is to minimize the error between the prediction output value of the output variable and the day-ahead plan value and ensure that the adjustment value of each controllable device in the system is as small as possible. The intra-day rolling optimization dispatch model can be expressed as follows:

$\begin{array}{l}\min J={({\mathit{R}}_{\mathrm{DA}}-{\mathit{Y}}_{\mathrm{f}})}^T{\mathit{W}}_{\mathrm{err}}({\mathit{R}}_{\mathrm{DA}}-{\mathit{Y}}_{\mathrm{f}})+{\mathit{U}}^{\mathrm{T}}{\mathit{Q}}_{\mathrm{u}}\mathit{U}\\ s.t.\{\begin{array}{l}\mathrm{\Delta }{P}_{\mathrm{MT}}^{\min }\le \mathrm{\Delta }{P}_{\mathrm{MT}}^t\le \mathrm{\Delta }{P}_{\mathrm{MT}}^{\max }\\ P_{\mathrm{MT}}^{\min }\le P_{\mathrm{MT}}^t\le P_{\mathrm{MT}}^{\max }\\ \mathrm{\Delta }{P}_{\mathrm{FC}}^{\min }\le \mathrm{\Delta }{P}_{\mathrm{FC}}^t\le \mathrm{\Delta }{P}_{\mathrm{FC}}^{\max }\\ P_{\mathrm{FC}}^{\min }\le P_{\mathrm{FC}}^t\le P_{\mathrm{FC}}^{\max }\\ \mathrm{\Delta }{P}_{\mathrm{ESS}}^{\min }\le \mathrm{\Delta }{P}_{\mathrm{ESS}}^t\le \mathrm{\Delta }{P}_{\mathrm{ESS}}^{\max }\\ P_{\mathrm{ESS}}^{\min }\le P_{\mathrm{ESS}}^t\le P_{\mathrm{ESS}}^{\max }\\ S_{\mathrm{ESS}}^{\min }\le S_{\mathrm{ESS}}^t\le S_{\mathrm{ESS}}^{\max }\end{array}\end{array}(20)$

where R_DA and Y_f respectively indicate the day-ahead plan value and the intra-day prediction output value of the output variable; W_err and Q_u are the weight coefficient matrices.

By solving the above model, the optimal control command sequences of output adjustment for each device in the control time domain was obtained. At the current time step, only the first control command was executed. At the next time step, the aforementioned rolling optimization process is repeated. In addition, the real-time operating state of the system is used for feedback correction during each rolling optimization, which ensures better stability and robustness of the rolling optimization strategy.

3.3 Energy Optimal Dispatch Strategy Based on SMPC

In this article, the energy optimal dispatch of the DCMG was divided into two stages: day-ahead optimization scheduling and intra-day rolling optimization scheduling, constituting a multi-time scale optimal model. The flow chart of the specific optimal model solution process is shown in Figure 2.

FIGURE 2

FIGURE 2. Flow chart of the energy optimal dispatch.

In the aforementioned solving process, the SMPC-based energy optimal dispatch strategy of the DCMG constitutes the MILP problem. Based on MATLAB software, this article uses=d the CPLEX solver and the YALMIP toolbox to solve the aforementioned MILP problem.

4 Case Study

4.1 Setting

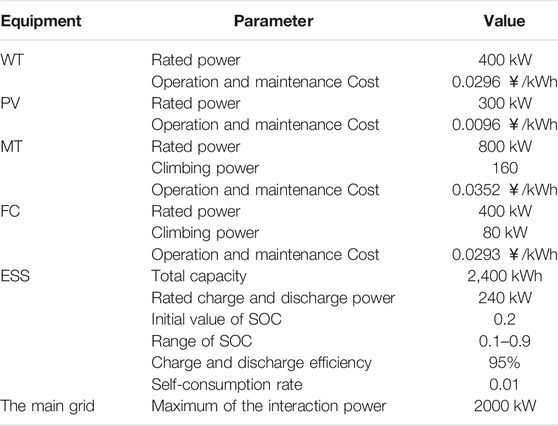
A typical DCMG system was taken as an example. The system structure is consistent with the aforementioned DCMG system. In addition, the data center can purchase electricity from the main grid. The main basic parameters of the system are shown in Table 1. The time-of-use electricity price of the main grid is shown in Table 2 (Xiao et al., 2014).

TABLE 1

TABLE 1. Parameter values of the DCMG system.

TABLE 2

TABLE 2. Electricity price of the main grid parameter values.

Since it is currently difficult to obtain the detailed statistical information of data center workloads, some studies assume that there is a certain proportion relationship between the interactive and batch workloads (Luo et al., 2014; Li and Qi, 2018). In this article, it was set that the ratio of interactive and batch workloads were 4:1. In the actual situation, the ratio depends on the users of the data center. The parameters of the data center are set based on the data in the stdy by Yu et al. (2014). The PUE value is set to 1.2 based on the description of the study by Dou et al. (2017).

4.2 Result Analysis

4.2.1 Day-Ahead Optimization Results

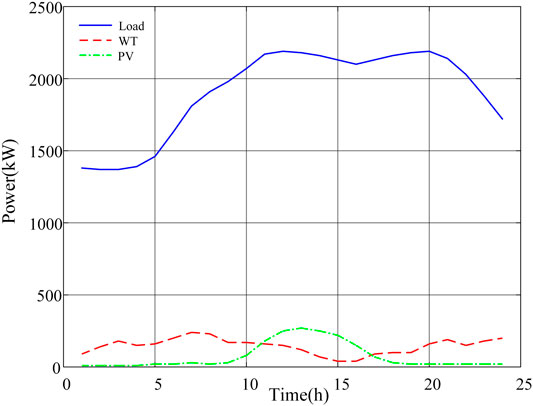
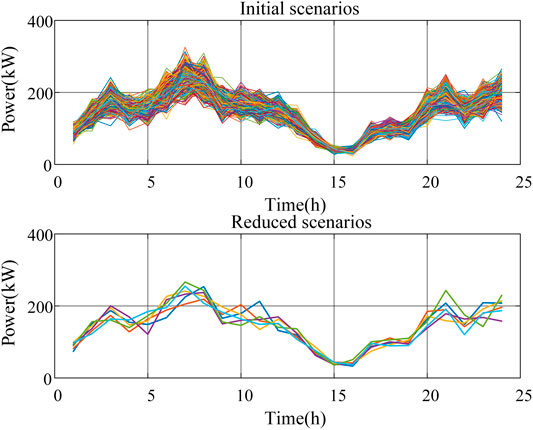
The prediction power curves of WT, PV outputs, and total loads of the data center are shown in Figure 3. Considering that all the prediction errors of them obey the normal distribution, first, a large number of initial power scenarios were generated by Latin hypercube sampling (LHS). Then, based on the similarity of each scenario, the initial scenarios were reduced by employing the backward reduction algorithm (Wang et al., 2015). Finally, a set of loads and renewable energy output scenarios was obtained, as well as corresponding probabilities. Considering that the outputs of WT changes more dramatically (Liu J et al., 2021), the number of WT output scenarios after the reduction was 6, and the number of PV output and load scenarios was 5, with a total of 150 scenarios. Figure 4 shows the results of scenario generation and the reduction of the WT output.

FIGURE 3

FIGURE 3. Prediction power of WT, PV, and load of the data center.

FIGURE 4

FIGURE 4. Scenario generation and reduction results of WT.

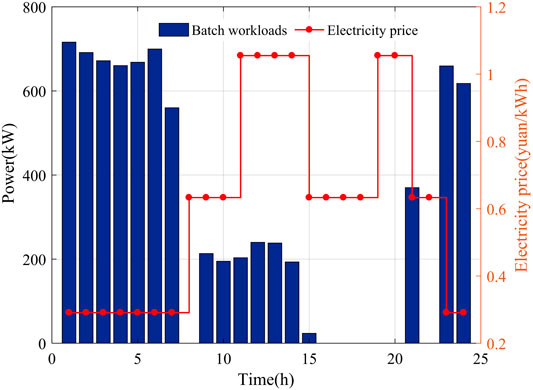
Figure 5 shows the allocation result of the batch workloads of the DCMG system. The interactive workloads in each period need to be served immediately, while the batch workloads allows flexible scheduling. It can be seen that the batch workloads are allocated to the period with the lowest electricity price (23:00-7:00) as far as possible.

FIGURE 5

FIGURE 5. The allocation of data center batch workloads.

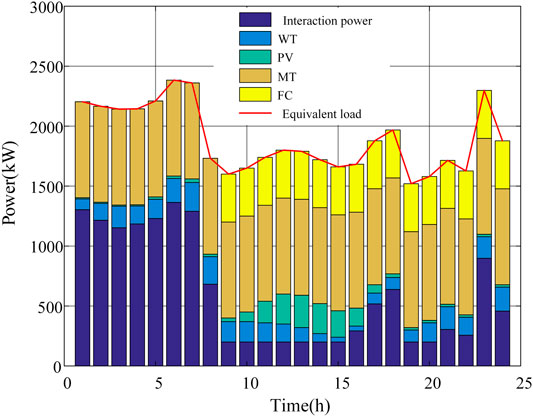
The day-ahead optimization dispatch plan of each device in the DCMG system is shown in Figure 6. For the convenience of analysis, the concept of “equivalent load” in the figure was derived from Eq. 10. The equivalent load is equal to the sum of the load and the charging and discharging power of ESS. It can be seen from Figure 6 that the output of each unit in the DCMG system satisfies the power balance constraint. Because the output power of WT and PV is limited by the installed capacity, it only accounts for a small part of the load demand. When the electricity price is at the peak, MT and FC are the main power supply sources. In the valley period of electricity price, since some batch workloads allocated to these periods are to be served and ESS works in the charging state, the proportion of electricity purchased from the main grid increased obviously.

FIGURE 6

FIGURE 6. Day-ahead Optimization results.

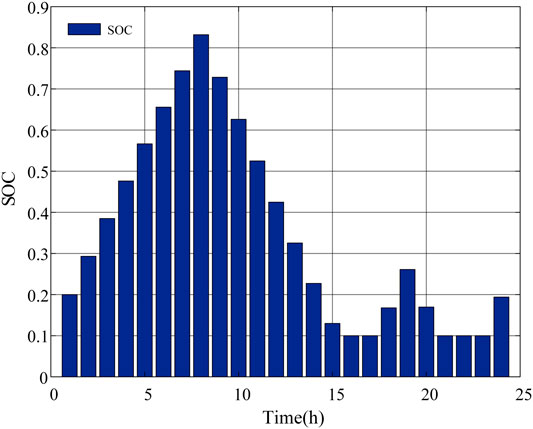
The SOC of ESS is shown in Figure 7. The variation of SOC is maintained within the set range of 0.1–0.9, and SOC satisfies the balance at the beginning and end of the dispatch cycle. It can be seen that ESS is arranged to charge in the valley period and discharge in the peak period, which achieves the “peak-to-valley arbitrage” and improves the economy of system operation.

FIGURE 7

FIGURE 7. SOC of ESS.

4.2.2 Intra-day Rolling Optimization Results

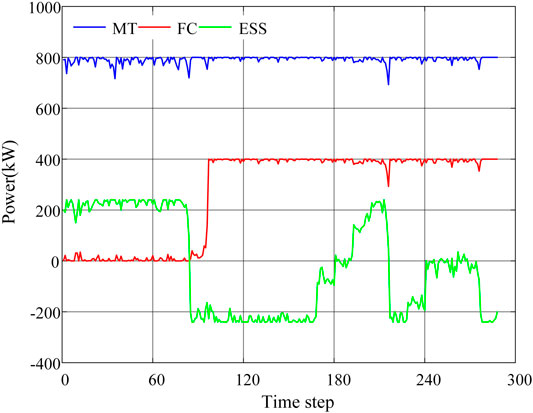
The intra-day rolling optimization period is 1 h, and the time step is 5 min. The number of rolling optimization in 1 day is 288. After the intra-day rolling optimization and adjustment, the actual outputs of MT, FC, and ESS are shown in Figure 8. In order to ensure that the interaction power between the DCMG and the main grid can effectively track the day-ahead plan value, the intra-day optimization scheduling revises the day-ahead outputs of controllable devices to a certain extent.

FIGURE 8

FIGURE 8. Intra-day rolling optimization results.

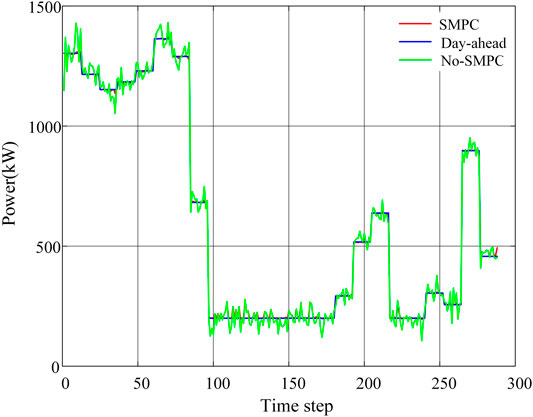
Figure 9 shows the results of the interactive power with the main grid in different cases. In actual operation, if the rolling optimization is not applied, the power fluctuations caused by the prediction error of uncertain factors are all compensated by the main grid. It can be seen from Figure 9 that the interaction power curve without rolling optimization fluctuates sharply near the planned value, resulting in poor stability and security when the DCMG is connected to the main grid. However, the interaction power curve after SMPC-based optimization is basically consistent with the day-ahead planned curve.

FIGURE 9

FIGURE 9. Comparison of interaction power with the main grid.

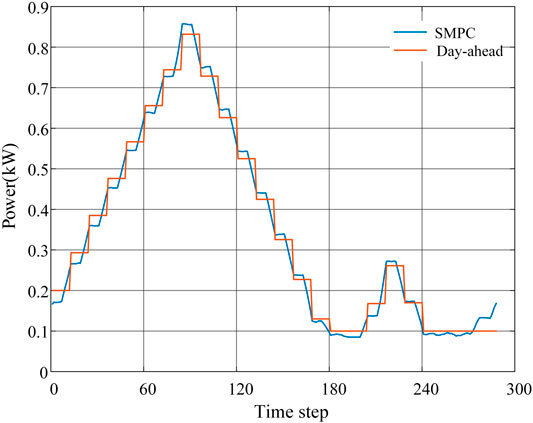
The comparison results of the SOC value between the actual value and the day-ahead plan value are shown in Figure 10. It can be seen that ESS can track the SOC curve of day-ahead plan well during the intra-day actual operation. According to Figures 9, 10, the SMPC-based optimization method proposed in this article can deal with the influence of uncertain factors and ensure the stability and security of the data center in actual operation.

FIGURE 10

FIGURE 10. Comparison of SOC.

Table 3 compares the total operating costs of the DCMG system under different scheduling strategies. It can be seen that the cost of the SMPC-based dispatch decreases more than the no-SMPC dispatch, which shows that the SMPC-based optimal dispatch strategy considering the batch workloads can reduce the operation cost and improve the economy of the DCMG system.

TABLE 3

TABLE 3. Comparison of operating costs.

5 Conclusion

In order to futher improve the operating economy of the data center and reduce the adverse effects casued by the uncertainty of renewable energy outputs and data center workloads, this artilce puts forward a SMPC-based energy optimal dispatch strategy of the DCMG system. The scenario analysis method is used to describe the uncertainty by transforming it into multiple deterministic scenarios. Based on the SMPC method, the DCMG system was optimized from day-ahead and intra-day time scales. In the day-ahead scheduling stage, the optimization dispatch model is established with the objective of preparing the lowest operating cost, which achieves flexible allocation of batch workloads and obtains the optimal output plan for each device. In the intra-day rolling optimization scheduling stage, the actual outputs of controllable devices were adjusted, and the interactive power with the main grid and SOC value of ESS tracked the day-ahead planned value. The results of case analysis show that the rolling optimization and feedback correction mechanism of SMPC can cope with the negative influence of uncertain factors and guarantee the stability and economy of the DCMG system in actual operating.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YZ and JW contributed to conception and design of the study and wrote the original draft. KB contributed to the study methodology and data analysis. QS contributed to data investigation and software analysis. YZ and CZ contributed to supervision and writing-review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) (51807079).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Camacho, E. F., and Bordons, C. (2004). Model Predictive Control. second ed. New York, USA: Springer-Verlag.

Google Scholar

Chen, C., Wang, J., Heo, Y., and Kishore, S. (2013). MPC-based Appliance Scheduling for Residential Building Energy Management Controller. IEEE Trans. Smart Grid 4 (3), 1401–1410. doi:10.1109/TSG.2013.2265239

CrossRef Full Text | Google Scholar

Chen, T., Wang, X., and Giannakis, G. B. (2016b). Cooling-Aware Energy and Workload Management in Data Centers via Stochastic Optimization. IEEE J. Sel. Top. Signal. Process. 10 (2), 402–415. doi:10.1109/JSTSP.2015.2500189

CrossRef Full Text | Google Scholar

Chen, T., Zhang, Y., Wang, X., and Giannakis, G. B. (2016a). Robust Workload and Energy Management for Sustainable Data Centers. IEEE J. Select. Areas Commun. 34 (3), 651–664. doi:10.1109/JSAC.2016.2525618

CrossRef Full Text | Google Scholar

Ding, Z., Cao, Y., Xie, L., Lu, Y., and Wang, P. (2019). Integrated Stochastic Energy Management for Data Center Microgrid Considering Waste Heat Recovery. IEEE Trans. Ind. Applicat. 55 (3), 2198–2207. doi:10.1109/TIA.2018.2890789

CrossRef Full Text | Google Scholar

Ding, Z., Xie, L., Lu, Y., Wang, P., and Xia, S. (2018). Emission-Aware Stochastic Resource Planning Scheme for Data Center Microgrid Considering Batch Workload Scheduling and Risk Management. IEEE Trans. Ind. Applicat. 54 (6), 5599–5608. doi:10.1109/TIA.2018.2851516

CrossRef Full Text | Google Scholar

Dou, H., Qi, Y., Wei, W., and Song, H. (2017). Carbon-Aware Electricity Cost Minimization for Sustainable Data Centers. IEEE Trans. Sustain. Comput. 2 (2), 211–223. doi:10.1109/TSUSC.2017.2711925

CrossRef Full Text | Google Scholar

Ebrahimi, K., Jones, G. F., and Fleischer, A. S. (2015). Thermo-economic Analysis of Steady State Waste Heat Recovery in Data Centers Using Absorption Refrigeration. Appl. Energ. 139, 384–397. doi:10.1016/j.apenergy.2014.10.067

CrossRef Full Text | Google Scholar

Jaureguialzo, E. (2011). “PUE: The Green Grid metric for evaluating the energy efficiency in DC (Data Center). Measurement method using the power demand,” in 2011 IEEE 33rd International Telecommunications Energy Conference (INTELEC), 1–8. doi:10.1109/INTLEC.2011.6099718

CrossRef Full Text | Google Scholar

Li, J., and Qi, W. (2018). Toward Optimal Operation of Internet Data Center Microgrid. IEEE Trans. Smart Grid 9 (2), 971–979. doi:10.1109/TSG.2016.2572402

CrossRef Full Text | Google Scholar

Liu, B., Li, Z., Chen, X., Huang, Y., and Liu, X. (2018). Recognition and Vulnerability Analysis of Key Nodes in Power Grid Based on Complex Network Centrality. IEEE Trans. Circuits Syst. 65 (3), 346–350. doi:10.1109/TCSII.2017.2705482

CrossRef Full Text | Google Scholar

Liu, B., Li, Z., Dong, X., Yu, S. S., Chen, X., Oo, M. T., et al. (2021). Impedance Modeling and Controllers Shaping Effect Analysis of PMSG Wind Turbines. IEEE J. Emerging Selected Top. Power Electron. 9 (2), 1465–1478. doi:10.1109/JESTPE.2020.3014412

CrossRef Full Text | Google Scholar

Liu, J., Miura, Y., Bevrani, H., and Ise, T. (2021). A Unified Modeling Method of Virtual Synchronous Generator for Multi-Operation-Mode Analyses. IEEE J. Emerg. Sel. Top. Power Electron. 9 (2), 2394–2409. doi:10.1109/JESTPE.2020.2970025

CrossRef Full Text | Google Scholar

Luo, J., Rao, L., and Liu, X. (2014). Temporal Load Balancing with Service Delay Guarantees for Data Center Energy Cost Optimization. IEEE Trans. Parallel Distributed Syst. 25 (3), 775–784. doi:10.1109/TPDS.2013.69

CrossRef Full Text | Google Scholar

Wang, H., Huang, J., Lin, X., and Mohsenian-Rad, H. (2016). Proactive Demand Response for Data Centers: A Win-Win Solution. IEEE Trans. Smart Grid 7 (3), 1584–1596. doi:10.1109/TSG.2015.2501808

CrossRef Full Text | Google Scholar

Wang, P., Cao, Y., Ding, Z., Tang, H., Wang, X., and Cheng, M. (2020). Stochastic Programming on Cost Optimization in Geographically Distributed Internet Data Centers. Csee Jpes, 1–14. doi:10.17775/CSEEJPES.2020.02930

CrossRef Full Text | Google Scholar

Wang, P., Xie, L., Lu, Y., and Ding, Z. (2017). “Day-ahead Emission-Aware Resource Planning for Data center Considering Energy Storage and Batch Workloads,” in IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26-28 Nov. 2017 (IEEE), 1–6. doi:10.1109/EI2.2017.8245657

CrossRef Full Text | Google Scholar

Wang, Y., Wu, W., and Zhang, B. (2015). Robust Voltage Control Model for Active Distribution Network Considering Load and Photovoltaic Uncertaintie. Automation Electric Power Syst. 39 (09), 138–144. doi:10.7500/AEPS20141130008

CrossRef Full Text | Google Scholar

Wen, Z., and Liu, J. (2019). An Optimal Scheduling Method for Hybrid Wind-Solar-Hydor Power Generation System with Data Center in Demad Side. Power Syst. Technol. 43 (07), 2449–2460. doi:10.13335/j.1000-3673.pst.2018.1142

CrossRef Full Text | Google Scholar

Xiao, H., Pei, W., Kong, L., Qi, Z., OuYang, H., and Mu, L. (2014). Decision Analysis and Economic Benefit Evaluation of Microgrid Power Output Considering Surplus Photovoltaic Power Selling to Grid. Automation Electric Power Syst. 38 (10), 10–16. doi:10.7500/AEPS20130531009

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Liu, Y., and Zhuo, F. (2020). Modeling and Stability Issues of Voltage-Source Converter Dominated Power Systems: A Review. Csee Jpes. (Early Access), 1–18. doi:10.17775/CSEEJPES.2020.03590

CrossRef Full Text | Google Scholar

Xu, T., Zhang, H., Yang, H., Zhang, M., and Liu, L. (2019). Research on Stochastic Optimization Model of Energy Management for Data Center Microgrids. J. Electric Meas. Instrumentation 33 (08), 101–107. doi:10.13382/j.jemi.B1902158

CrossRef Full Text | Google Scholar

Yu, L., Jiang, T., Cao, Y., and Zhang, Q. (2014). Risk-Constrained Operation for Internet Data Centers in Deregulated Electricity Markets. IEEE Trans. Parallel Distributed Syst. 25 (5), 1306–1316. doi:10.1109/TPDS.2013.2297095

CrossRef Full Text | Google Scholar

Yu, L., Jiang, T., and Zou, Y. (2018). Distributed Real-Time Energy Management in Data Center Microgrids. IEEE Trans. Smart Grid 9 (4), 3748–3762. doi:10.1109/TSG.2016.2640453

CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, T., Liu, Y., and Guo, B. (2015). Optimal Energy Management of a Residential Local Energy Network Based on Model Predictive Control. Proc. CSEE 35 (14), 3656–3666. doi:10.13334/j.0258-8013.pcsee.2015.14.021

CrossRef Full Text | Google Scholar