Production Performance Analysis for Deviated Wells in Carbonate Gas Reservoirs With Multiple Heterogeneous layers

Deviated wells are used to improve the performance of carbonate reservoirs with multiple heterogeneous layers and penetrate the “sweet spot” of each layer, which is full of fractures and vugs. It is difficult to consider in-layer and inter-layer heterogeneities simultaneously, and predict the production performance for these wells accurately. Therefore, a semi-analytical model to analyze the production performance of deviated wells in a multilayer heterogeneous stress-sensitive carbonate gas reservoir is proposed. For each layer, the inner region is a fractured-vuggy porous medium, while the outer region is merely a tight formation with matrix and formation properties, and penetrated inclination angles may be distinct. Pseudo-time/pressure factors are introduced to consider fracture stress sensitivity. Through the application of Laplace transformation, Fourier transform and inverse, Duhamel convolution, and Stehfest numerical inversion, the presented model is solved. The validity of this model is verified through comparison with single-layer composite formation with different porous mediums and vertical well in a multilayer carbonate gas reservoir. Moreover, by matching bottom-hole pressure data collected from a slanted well in the Anyue gas field, the applicability of this model is validated. A synthetic case, which has two composite formations, the first (upper) layer is more permeable than the second (lower) layer, is used to study the variations of inner region radius, fracture/matrix permeability, and inclination angles on production behaviors. The results show the properties of the first layer determine well bottom-hole pressure, whereas the rise of permeability, inner region radius and penetrated angle for the second layer can improve the gas recovery of this layer. In practice, to maintain well bottom-hole pressure with a relatively high level and enhance gas recovery of the tight layer, the inclination angle should be larger than 60° for each layer, and be increased to as large as possible. The findings of this study can help for a better understanding of the production behaviors of deviated wells in multilayer heterogenous reservoirs and could provide some guidance for the design of well trajectory.

1 Introduction

In many carbonate gas reservoirs, there are multiple distinct layers, and there is strong heterogeneity in different directions. Some regions have rich natural fractures, vugs, and are named the “sweet spot,” while other areas are tight and contain only matrix (Jia and Yan, 2014; Ma, et al., 2021; Yan, et al., 2020b). Through the utilization of advanced 3D seismic inversion technology, we can precisely determine the location of the “sweet spot” for each layer. As the distribution of the “sweet spot” is random, to improve the production performance and economic benefits, a deviated well is always used to penetrate the “sweet spot” of different layers. However, the range of the “sweet spot” is limited, which makes the formation exhibit composite properties, and it is difficult to consider this distribution pattern for different layers simultaneously (Jia, et al., 2013; Jia, et al., 2014; Yan, et al., 2020a). Moreover, the gas flow in the slanted wellbore is always complicated, and it is difficult to estimate the production performance. Hence, a reasonable model that can describe the gas flow in a deviated wellbore for multi-layer heterogeneous carbonate gas reservoir is essential. In addition, this model can also be used to differentiate the production contribution for each layer.

For each layer in a multi-layer heterogeneous carbonate gas reservoir, it is an independent composite formation. For vertical wells in a composite reservoir, many mathematical models have been developed and analytical or semi-analytical solutions obtained. Some researchers employ these models to analyze pressure transient behaviors, to estimate production performance, and to acquire the reservoir and technical parameter values, such as the formation radius, reservoir permeability, and skin factor (Olarewaju and Lee, 1987; Prado and Da, 1987; Olarewaju and Lee, 1989; Turki, et al., 1989; Kikani and Jr, 1991; Olarewaju and Lee, 1991; Satman, 1991). In the above mentioned models, under diverse circumstances, the inner area can be a fractured dual-porosity or triple-porosity formation, while the outer area is a tight reservoir. Except for the conventional reservoirs, these models have been widely used in unconventional reservoirs. For unconventional reservoirs, after stimulated reservoir volume (SRV) fracturing with horizontal wells, it is always assumed that the region surrounding the horizontal wellbore is dual porosity or triple-porosity media, while the other regions are tight formations. After reasonable modifications on the previous models, various composite models for describing MFHWs are presented to estimate the pressure and production rate transient behaviors (Zeng, et al., 2015; Zhao, et al., 2014; Wang, et al., 2017). Due to the difficulties of solving these mentioned models, finite element and boundary elements have been employed to obtain numerical solutions (Fan, et al., 2015; Rana and Ertekin, 2012; Wu, et al., 2018). Except for vertical and horizontal wells, recently, Meng, et al. (2018) presented a composite model for deviated wells, where the natural triple-porosity reservoir is in the inner area and the outer area is the tight matrix. However, currently, this proposed model can only be used in a composite formation with a single layer.

In terms of vertical wells in multi-layer reservoirs, many studies have analyzed for pressure and production behaviors, and these studies always assume that the pressure, reservoir and fluids properties, and boundary conditions are different from each other. (Cobb, et al., 1972; Raghavan, et al., 1974; Larsen, 1981; Kuchuk and Wilkinson, 1991; El-Banbi and Wattenbarger, 1996; El-Banbi and Wattenbarger, 1997; Vieira Bela, et al., 2019). For some complex well types, the methods to obtain production behaviors are different from traditional approaches. Through comprehensive reviews, there are primarily three methods that can model gas flowing process, equivalent approximation, numerical, and analytical or semi-analytical approaches. For the equivalent approximation method, the wellbore in the perforated formation is approximately simplified into uniform flux fracture and modified with transient skin factor (Larsen, 1999; Larsen, 2000), which is greatly different from real circumstances. Numerical approaches, for example, the boundary or finite element method, can be utilized to obtain the pressure or production solution for complex wells in a multi-layer reservoir (Jongkittinarukorn and Tiab, 1998; Kuchuk and Habashy, 1996; Kuchuk and Saeedi, 1992), while it is difficult to use and time-consuming. Through the combination of the reflection and transmission principle, and the methods of Laplace transformation, Fourier transformation, and inversion, semi-analytical or analytical solutions can be acquired for these complex-structure wells in multi-layer formation with or without crossflow (Basquet, et al., 1999; Medeiros, et al., 2010; Pan, et al., 2010), whereas the accuracy for these solutions is not satisfied.

Through the above introductions for composite reservoir and multi-layer formation with diverse well structures, studies on composite models mainly apply to vertical and horizontal wells, although Meng et al. (2018) presented the composite model for deviated wells in carbonate gas reservoirs, they assumed that the reservoir has one layer merely. In addition, Meng et al. (2021) proposed a model for analyzing the production performance of slanted wells in multilayer carbonate reservoirs, whereas the interlayer heterogeneity is ignored. For the modeling of multi-layer formation in a complex well structure, the accuracy, efficiency, and applicability for the mentioned three methods should be improved further. Hence, in this article, a semi-analytical model is presented for deviated wells in multilayer heterogeneous carbonate gas reservoirs, where the individual layer is represented with triple-porous media in the inner region and a single porous medium in the outer region. The main novelty of this study lies in the consideration of in-layer and inter-layer heterogeneities simultaneously for stress-sensitive carbonate gas reservoirs with multiple layers. Furthermore, through the combination of some approaches, such as Laplace transform, Stehfest numerical inverse, Fourier transformation and inversion, Duhamel convolution, the pressure and production solutions for deviated wells are obtained.

The structure of this paper first presents physical and mathematical models, and the detailed solution process for this model is given. The validity of this presented model is then verified through a comparison of results with published data and a gas field case. Finally, the influences of prevailing factors, such as radius and natural fractures permeability for the inner region, matrix permeability for the outer region, and the penetrated inclination angle, on the production performance of individual layers are discussed and analyzed.

2 Physical Model and Mathematical Model

2.1 Physical Model

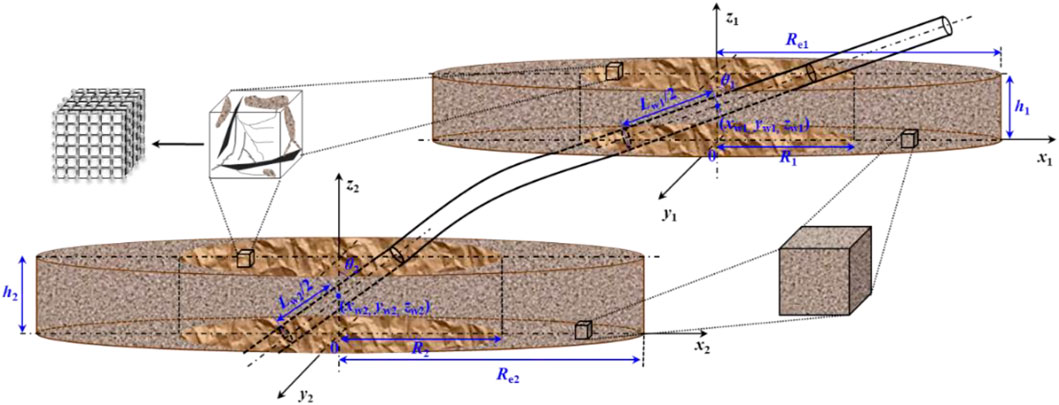
Figure 1 is a schematic diagram of a deviated well with varying inclination angles in a carbonate gas reservoir that has multiple heterogeneous layers. This multilayer reservoir has two layers, and for individual layers, the inner region near the inclined wellbore is a triple porous medium with fractures, vugs, and matrix, and the outer region only has a single medium with matrix. Compared with the second (lower) layer, the first layer has larger permeability and porosity, which is the main layer in this multilayer carbonate gas reservoir.

FIGURE 1

FIGURE 1. Schematic of inclined well in multilayer heterogeneous commingled carbonate reservoir.

For the presented model, it is assumed that the reservoir is composed of n cylindrical and heterogeneous layers, which have closed boundaries in horizontal and vertical directions. The wells produce a constant gas flowing rate and the individual layer is penetrated completely and the flowing rate along the wellbore distributes uniformly. Since the model presented in this paper can be seen as the extension of the model developed by Meng, et al. (2018), assumptions about fluids, rocks, and flowing law for this model can be found in their paper. For any layer, the inclined wellbore is assumed to be located in the inner region. It should be noted that the range of the inner region is small whereas the deviated angle is large, thus the inclined wellbore can also penetrate the inner and outer regions simultaneously, and the above assumptions may not be reasonable. However, in this paper, these circumstances are not explored and could be studied further in the future.

2.2 Stress Sensitivity of Fracture Permeability

In carbonate reservoirs, due to the existence of natural fractures and vugs, many laboratory experiments and pilot tests show that the stress sensitivity is serious for naturally fractured-vuggy formation (Wang, et al., 2016a; Wang, et al., 2016b; Zhao, et al., 2013). Therefore, it is crucial to consider this effect for fracture permeability of the inner region in the developed mathematical model. Meng et al. (2017) assumed that the measured permeability is indeed fracture permeability. Using curve match with data from laboratory experiments, they obtained the relationship between the dimensionless permeability and net confining pressure, as shown in Eq. 1.

$\frac{k}{k_{\text{i}}}={\left(\frac{{\mathit{\sigma }}_{\text{s}}-p}{{\mathit{\sigma }}_{\text{s}}-p_{\text{i}}}\right)}^{-\alpha }(1)$

where α is the exponent to reflect the formation stress sensitivity. According to Meng et al. (2018) it is 0.738 for natural fractured-vuggy formation.

2.3 Mathematical Model

2.3.1 Pressure Solution for Deviated Wells With Unit Rate in Layer j

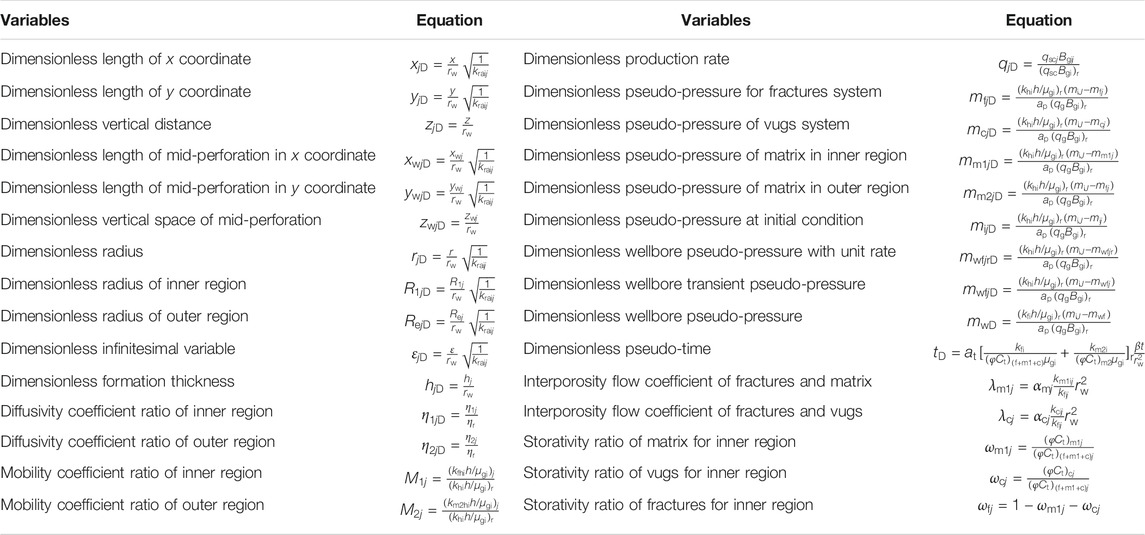
According to the presented mathematical model, the point source solution with the unit rate for layer j in Laplace space can be obtained (see Supplementary Appendix S1), given by Eq. 2. To simplify the form of equations, the relevant dimensionless variables are introduced, and the definitions of these variables are shown in Table 1.

$\begin{array}{l}{\overline{m}}_{\text{f}j\text{rD}}=\frac{m_{\text{i}j\text{D}}}{s}+X\left(r_{j\text{D}},z_{j\text{D}},s\right)\\ =\frac{m_{\text{i}j\text{D}}}{s}+\frac{1}{s{M}_{1j}}\left[\frac{q_{0j}{U}_{0j}-\frac{M_{2j}}{M_{1j}}{T}_{0j}{S}_{0j}}{q_{0j}{W}_{0j}+\frac{M_{2j}}{M_{1j}}{T}_{0j}{V}_{0j}}{I}_0\left(q_{0j}{r}_{j\text{D}}\right)+K_0\left(q_{0j}{r}_{j\text{D}}\right)\right]\\ +\frac{2}{s{M}_{1j}}{\displaystyle \sum _{n=1}^{\infty }\left[\frac{q_{nj}{U}_{nj}-\frac{M_{2j}}{M_{1j}}{T}_{nj}{S}_{nj}}{q_{nj}{W}_{nj}+\frac{M_{2j}}{M_{1j}}{T}_{nj}{V}_{nj}}{I}_0\left(q_{nj}{r}_{j\text{D}}\right)+K_0\left(q_{nj}{r}_{j\text{D}}\right)\right]\cos \left(n\pi \frac{z_{\text{w}j\text{D}}}{h_{j\text{D}}}\right)}\cos \left(n\pi \frac{z_{\text{w}j\text{D}}}{h_{j\text{D}}}\right)\end{array}(2)$

TABLE 1

TABLE 1. Definition of dimensionless variables for layer j.

Since the perforated inclined wellbore in the individual layer is seemed as the line source with uniform flux, based on the superposition principle, and the rotation transform of coordination developed by Ozkan and Raghavan (1991a), Ozkan and Raghavan (1991b), the dimensionless pressure in Laplace space for the deviated well section in layer j could be acquired by integrating on Eq. 2 numerically, and the expression can be written as

$\begin{array}{l}{\overline{m}}_{\text{wf}j\text{rD}}=\frac{m_{\text{i}jD}}{s}+\frac{1}{s{M}_{1j}{L}_{\text{w}j\text{D}}}{\displaystyle {\int }_{-L_{\text{w}j\text{D}}/2}^{L_{\text{w}j\text{D}}/2}\left[\frac{q_{0j}{U}_{0j}-\frac{M_{2j}}{M_{1j}}{T}_{0j}{S}_{0j}}{q_{0j}{W}_{0j}+\frac{M_{2j}}{M_{1j}}{T}_{0j}{V}_{0j}}{I}_0\left(q_{0j}{\tilde{r}}_{j\text{D}}\right)+K_0\left(q_{0j}{\tilde{r}}_{j\text{D}}\right)\right]}d\xi \\ +\frac{2}{s{M}_{1j}{L}_{\text{w}j\text{D}}}{\displaystyle {\int }_{-L_{\text{w}j\text{D}}/2}^{L_{\text{w}j\text{D}}/2}{\displaystyle \sum _{n=1}^{\infty }\left[\frac{q_{nj}{U}_{nj}-\frac{M_{2j}}{M_{1j}}{T}_{nj}{S}_{nj}}{q_{nj}{W}_{nj}+\frac{M_{2j}}{M_{1j}}{T}_{nj}{V}_{nj}}{I}_0\left(q_{nj}{\tilde{r}}_{j\text{D}}\right)+K_0\left(q_{nj}{\tilde{r}}_{j\text{D}}\right)\right]\cos \left(n\pi \frac{{\tilde{z}}_{\text{w}j\text{D}}}{h_{j\text{D}}}\right)}\cos \left(n\pi \frac{z_{\text{w}j\text{D}}}{h_{j\text{D}}}\right)}d\xi \end{array}(3)$

where

$\begin{array}{l}{\tilde{r}}_{j\text{D}}=\sqrt{{\left[x_{j\text{D}}-\left(x_{\text{w}j\text{D}}+\xi \sin \theta {\mathrm{\prime }}_{\mathrm{j}}\right)\right]}^2+{\left(y_{j\text{D}}-y_{\text{w}j\text{D}}\right)}^2},{\tilde{z}}_{\text{w}j\text{D}}=z_{\text{w}j\text{D}}+\xi \text{cos}\theta {\mathrm{\prime }}_{\mathrm{j}}\\ L_{\text{w}j\text{D}}=\frac{L_{\text{w}j}}{r_{\text{w}}}\sqrt{\frac{k_{\text{fi}j}}{k_{\text{fhi}j}}{\sin }^2{\theta }_j+\frac{k_{\text{fi}j}}{k_{\text{fvi}j}}{\cos }^2{\theta }_j},\theta {\mathrm{\prime }}_{\mathrm{j}}=\arctan \left(\tan {\theta }_j\sqrt{\frac{k_{\text{fvi}j}}{k_{\text{fhi}j}}}\right)\end{array}(4)$

L_wjD is the dimensionless length for the deviated well section in layer j and ${\theta }_j^{\text{'}}$ is equivalent inclination angle. If the deviated wellbore is treated as an infinite-conductivity line source, it is more similar to reality. An equivalent point is then chosen to obtain the well bottom-hole flowing pressure (Wang, et al., 2012). The coordination of this point is:

$x_{j\text{D}}=x_{\text{w}j\text{D}}+\frac{0.3L_{\text{w}j}\sin {\theta }_j}{r_{\text{w}}}\sqrt{\frac{k_{\text{fi}j}}{k_{\text{fhi}j}}},y_{j\text{D}}=\sqrt{\frac{k_{\text{fi}j}}{k_{\text{fhi}j}}},z_{j\text{D}}=z_{\text{w}j\text{D}}+\frac{0.3L_{\text{w}j}\cos {\theta }_j}{r_{\text{w}}}\sqrt{\frac{k_{\text{fi}j}}{k_{\text{fvi}j}}}(5)$

2.3.2 Evaluation on Production Performance for Deviated Wells

As the formation pressure and properties are different for diverse layers, the gas production rate for each layer may vary with time. For this situation, it could be handled with the Duhamel theorem (Spath, et al., 1990), and the general formula could be obtained:

$m_{\text{wf}j\text{D}}=m_{\text{i}j\text{D}}+{\displaystyle {\int }_0^{t_{\text{D}}}{q}_{j\text{D}}}\frac{\partial }{\partial \tau }{m}_{\text{wf}j\text{rD}}\left(t_{\text{D}}-\tau \right)d\tau (6)$

According to the principle of Laplace transformation, Eq. 6 can be transformed as:

${\overline{m}}_{\text{wf}j\text{D}}=\frac{m_{\text{i}j\text{D}}}{s}+{\overline{q}}_{j\text{D}}\left(s{\overline{m}}_{\text{wf}j\text{rD}}-m_{\text{i}j\text{D}}\right)(7)$

The bottom-hole flowing pressure for any layer is seen as equally:

${\overline{m}}_{\text{wf}j\text{D}}={\overline{m}}_{\text{wD}}(8)$

After the simple transformation on Eq. 7, the dimensionless production rate in the Laplace domain ${\overline{q}}_{j\text{D}}$ for layer j can be expressed by:

${\overline{q}}_{j\text{D}}=\frac{{\overline{m}}_{\text{wf}j\text{D}}-\frac{m_{\text{i}j\text{D}}}{s}}{s{\overline{m}}_{\text{wf}j\text{rD}}-m_{\text{i}j\text{D}}}=\frac{{\overline{m}}_{\text{wD}}-\frac{m_{\text{i}j\text{D}}}{s}}{s{\overline{m}}_{\text{wf}j\text{rD}}-m_{\text{i}j\text{D}}}(9)$

It can be seen from Eq. 6 that the sum of dimensionless production rate for all layers is equal to one. After the Laplace transformation about dimensionless production rate term, substituting Eq. 9 into Eq. 7, then the dimensionless bottom-hole flowing pressure in Laplace domain could be written as:

${\overline{m}}_{\text{wD}}=\frac{1+{\displaystyle \sum _{j=1}^n\frac{m_{\text{i}j\text{D}}}{s{\overline{m}}_{\text{wf}j\text{rD}}-m_{\text{i}j\text{D}}}}}{{\displaystyle \sum _{j=1}^n\frac{s}{s{\overline{m}}_{\text{wf}j\text{rD}}-m_{\text{i}j\text{D}}}}}(10)$

Substituting the solution of the inclined well section, ${\overline{m}}_{\text{wf}j\text{rD}}$, Eq. 3 into Eq. 10, thus in Laplace space the dimensionless well bottom-hole flowing pressure could be obtained, and ${\overline{q}}_{j\text{D}}$ could also be calculated through the substitution of Eqs 3, 10 into Eq. 9.

The Stehfest numerical inverse presented by Schmittroth (1960) is used in Eqs 9, 10, to acquire the dimensionless pressure and production data in real space. According to the definitions of these two dimensionless variables in Table 1, for layer j, the gas production rate and pseudo well bottom-hole flowing pressure can be obtained. Through the utilization of the method presented by Meng et al. (2018), the gas production rate of individual formation and the well bottom-hole flowing pressure can be calculated at each time step. The detailed solution procedures can also be found in the paper by Meng et al. (2018).

3 Model Validation

3.1 Comparisons With Previous Models

3.1.1 Comparison With Composite Single–Layer Reservoir

Meng et al. (2018) first presented the solution for deviated wells in composite formation with a single layer, which is the basis of the multilayer composite reservoir model in this paper. In their model, the inner region is naturally fractured-vuggy formation, while the outer region is tight formation, and the slanted wellbore is just located in the inner region, which is identical with the assumption in this paper. When formation properties and inclination angle are the same for different layers, then the multilayer reservoir is simplified into the single-layer reservoir theoretically. With the synthetic case constructed by Meng et al. (2018) (the data can be found in their published paper), the well bottom-hole pressure can be calculated. Since Meng et al. (2018) do not give the value of well production rate, hence, in this case, the production rate is set to be 100,000 m³/d. Figure 2 shows the comparison result of calculated well bottom-hole flowing pressure solution between single-layer formation and multilayer reservoir with uniform properties. As shown in Figure 2, there is there is a good match between the single-layer and multilayer reservoir, which verifies the accuracy of the proposed model.

FIGURE 2

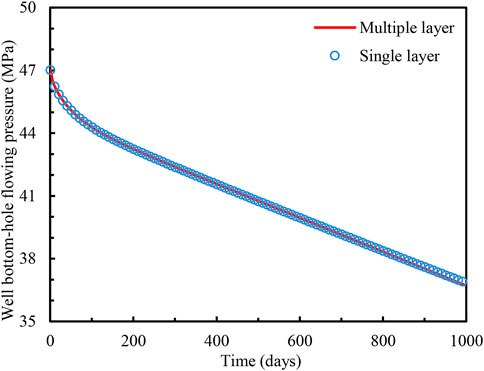
FIGURE 2. Well bottom-hole flowing pressure comparison between the proposed model and composite reservoir with single-layer.

3.1.2 Comparison With Vertical Well in Carbonate Gas Reservoir With Multiple Layers

Guo et al. (2020) present semi-analytical solutions for vertical wells in multi-layer gas reservoirs. For the proposed model in this paper, when the deviated angle is approaching 0°, the properties of the inner and outer regions for the individual layer are identical. The model in this paper is then simplified into the model presented by Guo et al. (2020). The comparisons of bottom-hole pressure and production rate of each layer for these two models are shown in Figure 3. The relevant data to calculate the results can be found in the published paper by Guo et al. (2020), in which the synthetic case in this paper is used. It can be seen from Figure 3 that there is a good match of bottom-hole pressure and production rate of individual layers for these two models, which verifies the validity of the proposed model. In addition, compared with the model presented by Guo et al. (2020), besides the application on the vertical wells in multilayer reservoirs, the proposed model can also be employed in the production behavior evaluation of inclined wells, which indicates that the proposed model in this paper is more general.

FIGURE 3

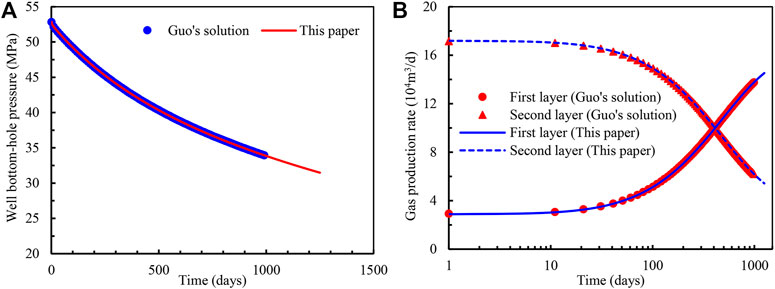
FIGURE 3. Comparisons of (A) well bottom-hole flowing pressure and (B) gas production rate for individual formation between Guo et al. (2020) and the proposed model in this article.

3.2 Match With Field Data

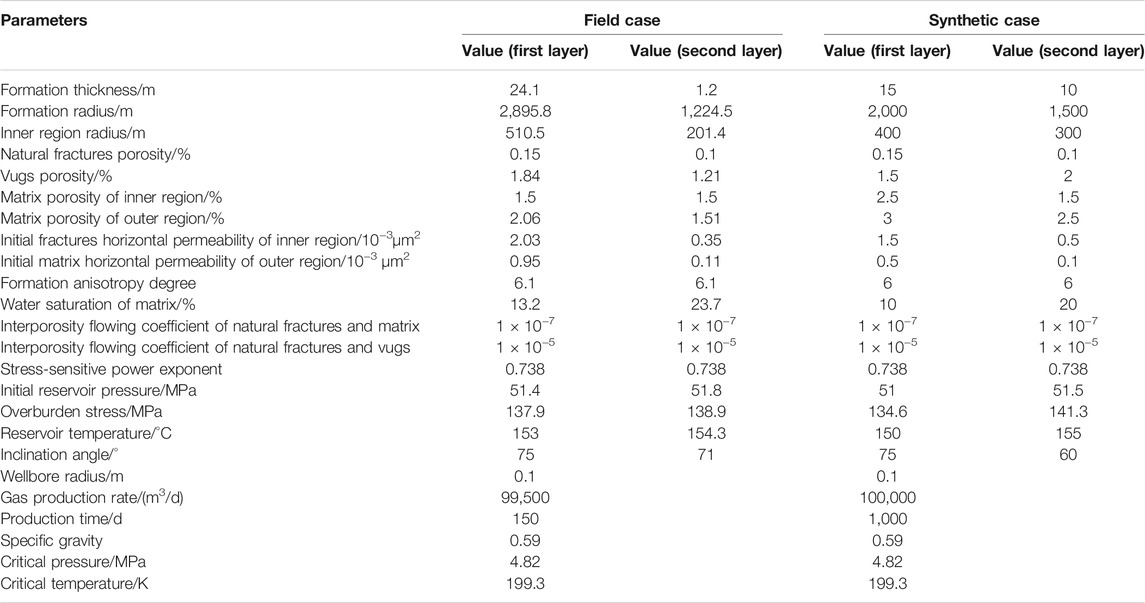
To validate the proposed model further and demonstrate its applicability in practice, a case study was chosen, the Anyue carbonate gas reservoir. In this case, the reservoir has two layers, and both 3D seismic interpretation and drilling data show that the deviated well penetrates the “sweet spot” for each layer, where the region surrounding the wellbore is a fractured-vuggy formation that has lots of natural fractures, and the region far from the well is a tight formation with matrix. In this multilayer reservoir, for each layer, through the method of well logging, the formation thickness, porosity, and water saturation for fractures, vugs and matrix are obtained and through the method of well-testing analysis, the permeability, inter-porosity flowing coefficients, initial pressure and temperature of the reservoir can be acquired. The well trajectory and inclination angle can be obtained from drilling data. The detailed formation and fluid information for this case are given in Table 2. It should be noted that formation anisotropy represents the horizontal-vertical permeability ratio.

TABLE 2

TABLE 2. Reservoir, fluids, and production data applied on the field and synthetic cases.

Since there is a lack of separate layer test information, the well bottom-hole flowing pressure information is acquired to match calculated data with the presented model. Figure 4 shows the comparison of well bottom-hole pressure in Cartesian and semi-log coordination systems. The goal of the introduction of the semi-log scale is the presentation of the initial fitting effect. It can be seen that whether for the Cartesian or semi-log coordination system, the curves fit perfectly between the testing well bottom-hole pressure and this model, which indicates this model could calculate the well bottom-hole flowing pressure precisely, and verifies the practicality of it in examining multilayer heterogeneous carbonate gas reservoirs.

FIGURE 4

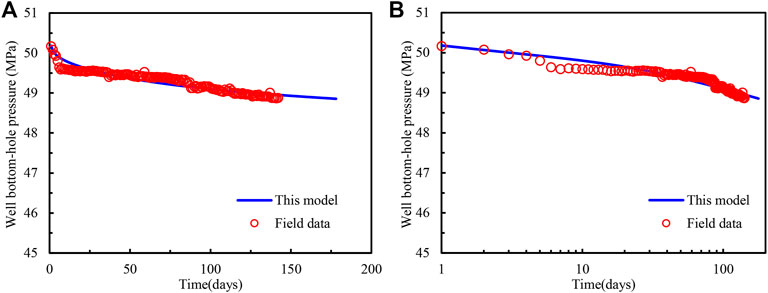
FIGURE 4. Match for well bottom-hole flowing pressure with the presented model in (A) Cartesian and (B) Semi-log coordination systems.

4 Sensitivity Analysis on the Production Performance

According to the information of the field case, a synthetic case, which is shown in Table 2, was constructed to analyze the influences of prevailing factors for multilayer heterogeneous composite reservoirs, such as the radius of the inner region, horizontal permeability of fractures, horizontal permeability of matrix and penetrated inclination angle of the individual layer on production performance, which include the well bottom-hole flowing pressure and gas production rate of individual formation.

4.1 Inner Region Radius

Figures 5, 6 show the influences of inner region radius for first and second formations on the production performance of deviated well and individual layers. It should be noted that in Figures 5B, 6B, the gas production rate for the first layer and second layer are represented with solid and dashed lines, respectively To clearly show the early production distribution, the semi-log scale is used in these figures.

FIGURE 5

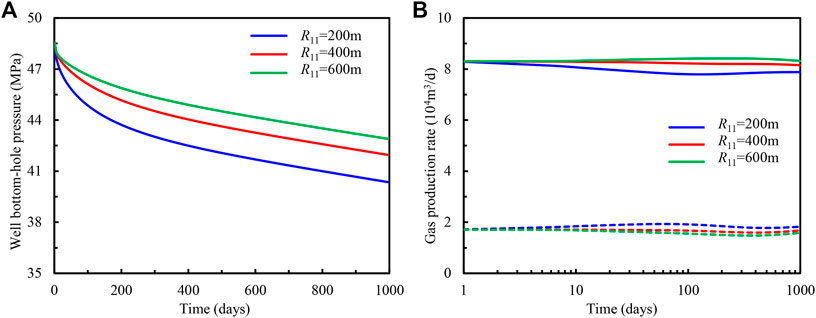
FIGURE 5. Influence of inner region radius for first layer on (A) well bottom-hole flowing pressure and (B) gas production of individual formation.

FIGURE 6

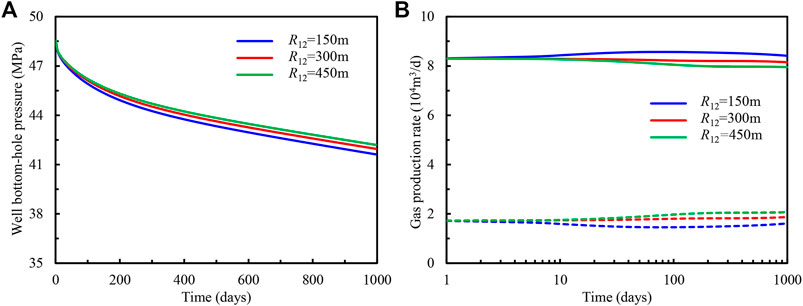
FIGURE 6. Influence of radius for the inner region in the second layer on (A) well bottom-hole flowing pressure and (B) gas production of individual formation.

Through the comparison of Figures 5A, 6A, it is easy to see the variation of radius for the inner region in the first layer has a greater effect on well bottom-hole pressure. The reason for this phenomenon is that the first layer has a larger thickness, porosity, and formation permeability (see Table 2), which is the main layer in this multilayer heterogeneous carbonate gas reservoir. The increase of inner region radius for this layer can greatly improve the level of well bottom-hole pressure. Since the gas production mainly derives from the inner region initially, hence, before the pressure response reaches the interface between the inner region and outer region, the production rate of gas for each layer is identical. As the inner region has larger porosity and permeability, on the condition of constant well production rate, with the increase of range for the inner region, the production rate of gas for any layer increases with the rise of inner region radius for this layer. In addition, the increase of inner region radius will delay the time of reaching this interface, then in Figures 5B, 6B, the time of emerging discrepancy for different cases increases with the inner region radius.

4.2 Horizontal Permeability of Fractures

The influences of horizontal permeability for natural fracture in the inner region on production behaviors are given in Figures 7, 8. As the first layer is the main formation in this multilayer heterogeneous carbonate gas reservoir, the variation law in Figures 7A, 8A is analogous to the curves in Figures 5A, 6A, and the rise of fracture horizontal permeability for the first layer can increase the well bottom-hole pressure significantly, whereas the fracture horizontal permeability of the second layer has little effect on the well bottom-hole pressure. However, since the inner region contributes mostly to the well gas production at the initial stage, and the flowing capacity increases with the fracture horizontal permeability, in contrast with Figures 5B, 6B, in Figures 7B, 8B gas production rate for any layers has a huge initial gap for different scenarios. When the gas production rate from the outer region occupies the larger ratio, the impact of the inner region decreases, and the gaps for different cases reduce continuously. It should be noted that because we assumed that the deviated well produces with a constant rate, while the gas production rate for some formations increases, for other formations it would certainly decline. For example in Figure 7B, with the rise of the horizontal permeability of natural fractures for the first formation, the production rate for this formation increases, while for the second layer, the production rate decreases.

FIGURE 7

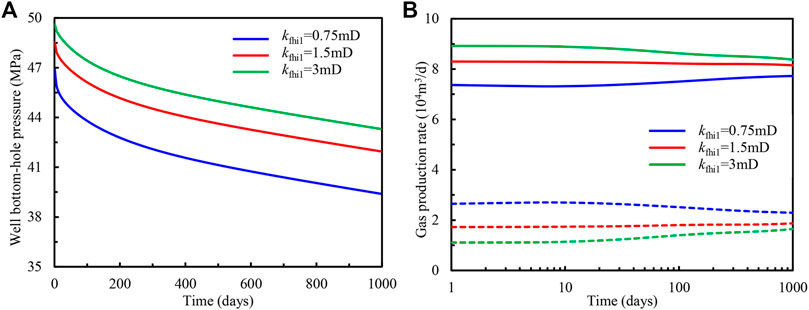
FIGURE 7. Influence of penetrated inclination angle for the first layer on (A) bottom-hole flowing pressure and (B) gas production of individual formation.

FIGURE 8

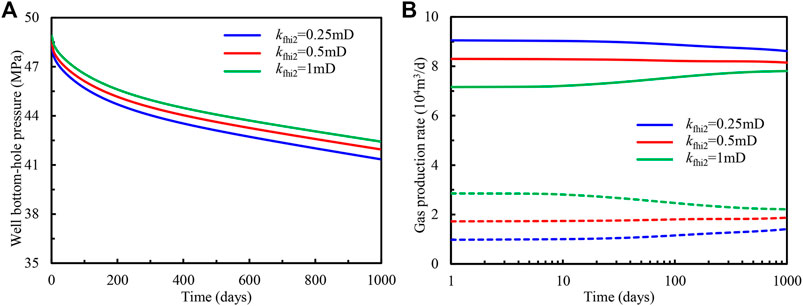
FIGURE 8. Influence of horizontal permeability for natural fracture in the second layer on (A) bottom-hole flowing pressure and (B) gas production of individual formation.

4.3 Horizontal Permeability of Matrix

Since the outer region has a larger area than the inner region, it is important to evaluate the influences of horizontal permeability of matrix on production behaviors, which are given in Figures 9, 10. It can be seen that as the gas supply capacity of the outer region increases with the matrix horizontal permeability, although the well bottom-hole flowing pressure and production rate of gas for different layers are the same for different cases initially, when the time is larger than 30 days, whether for the first or second layers, obviously, these two production index increase with the matrix horizontal permeability of this layer. Compared with Figures 5B, 6B and Figures 7B, 8B, in Figures 9B, 10B, as the radius of the inner region and permeability of natural fractures are equal, hence, there are no discrepancies of well bottom-hole flowing pressure and production rate initially, and the moment of appearing difference are nearly the same for different cases. Furthermore, through the comparison of Figures 7A, 9A, it can be seen that the smaller variation of matrix permeability can cause the huge gaps of bottom-hole pressure, which indicates that the properties of the outer region determine the production behaviors of the deviated well.

FIGURE 9

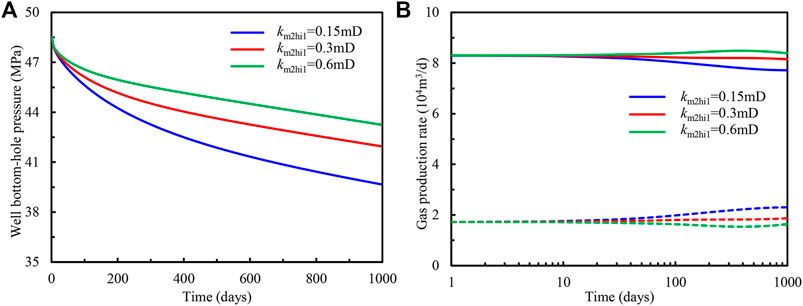
FIGURE 9. Influence of horizontal permeability for matrix in the first layer on (A) bottom-hole flowing pressure and (B) gas production of individual formation.

FIGURE 10

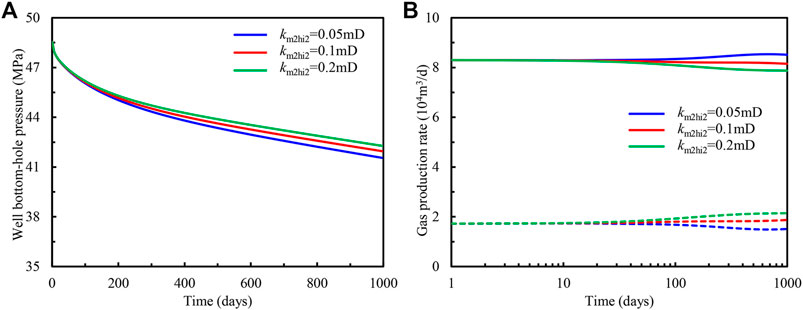
FIGURE 10. Influence of horizontal permeability of matrix in the second layer on (A) bottom-hole flowing pressure and (B) gas production of individual formation.

4.4 Inclination Angle

During the exploitation of the multilayer reservoir with the deviated well, the design of the well trajectory is an important task. It is then crucial to investigate the influence of the inclination angle for each layer on the production performance of individual zone and well bottom-hole flowing pressure (Figures 11, 12). Since the contact area between the slanted wellbore and formation increases with the inclination angle, as shown in Figures 11, 12, the well bottom-hole flowing pressure and gas production rate of the first or second layer increase with the penetrated inclination angle in this layer. As it was assumed that the slanted wellbore is located only in the inner region, the variation of inclination angle influences the production rate distribution at the early stage (Figures 11B, 12B), which is analogous to Figures 7B, 8B. Figure 10 shows the increase of inclination angle for the first layer with larger gas reserve and permeability, the well bottom-hole pressure can be improved largely. Therefore, to keep the well bottom-hole pressure at a high level, the penetrated inclination angle must be greater than a certain value. In addition, as shown in Figure 12, the inclination angle for the second layer has few influences on the well bottom-hole flowing pressure, whereas it can greatly increase the production rate of gas for this layer, which demonstrates the gas recovery of tight formation can be enhanced by enlarging the inclination angle in this layer.

FIGURE 11

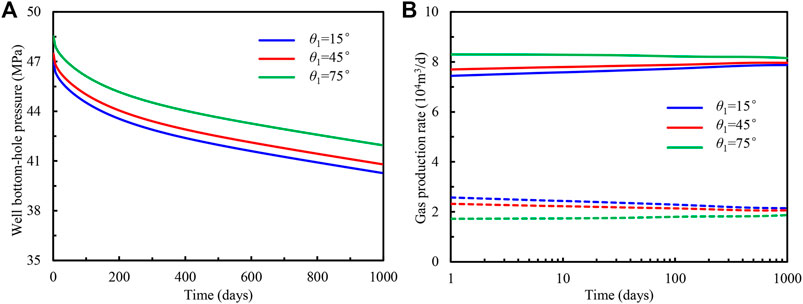
FIGURE 11. Influence of inclination angle in the first layer on (A) well bottom-hole flowing pressure and (B) gas production rate of an individual layer.

FIGURE 12

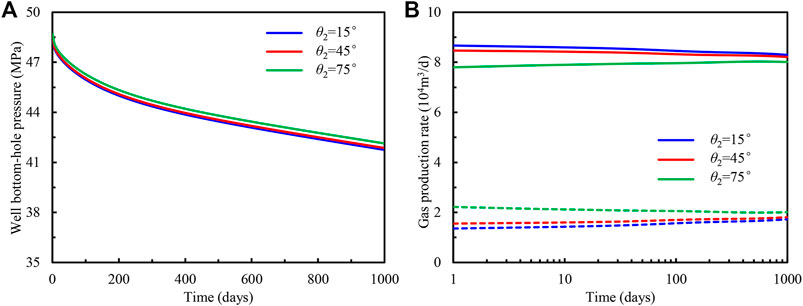
FIGURE 12. Influence of inclination angle in the second layer on (A) bottom-hole flowing pressure and (B) gas production of individual formation.

To determine the critical values of inclination angle for the first and second layers, we plot the curves of the inclination angle for the first layer versus bottom-hole flowing pressure and the inclination angle for the second layer versus cumulative gas production, which is shown in Figure 13.

FIGURE 13

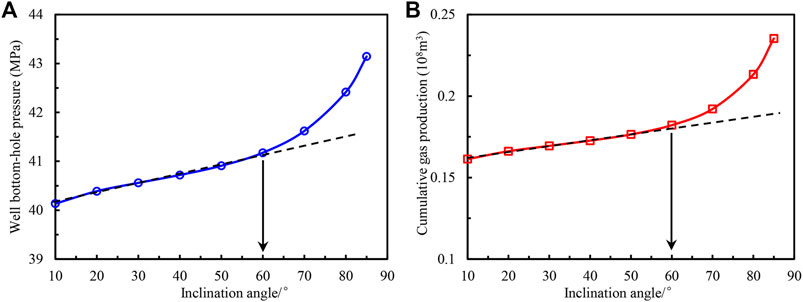
FIGURE 13. (A) bottom-hole flowing pressure and (B) cumulative gas production rate of the second formation for diverse penetrated inclination angles in the first layer and second formation.

Note that the bottom-hole flowing pressure and the cumulative gas production are collected on the 1,000th day. While the inclination angle is smaller than 60°, there is a linear relationship between the inclination angle and bottom-hole flowing pressure or cumulative gas production. When the inclination angle is larger than 60°, the bottom-hole flowing pressure and cumulative gas production increase drastically, whether it is the first layer or the second layer, the critical value of inclination angle for these two layers is 60°. To keep the bottom-hole pressure at a relatively high level and enhance the gas recovery of the tight layer, the penetrated inclination angle should be greater than 60°, and be enlarged as much as possible.

5 Summary and Conclusion

In this paper, a semi-analytical model is proposed to evaluate the production behaviors for slanted wells in commingled carbonate gas reservoirs with multiple heterogeneous layers. Through the comparison with the bottom-hole flowing pressure for a slanted well in a single layer, composite fractured-vuggy carbonate gas reservoir, the validity of this model is verified. Furthermore, a field case in the Anyue carbonate gas reservoir is employed to demonstrate the applicability of this model in practice. Through sensitivity analysis for some prevailing factors, several important conclusions can be drawn:

(1) The rise of radius for the inner region, horizontal permeability of fractures, horizontal permeability of matrix, and inclination angle for some layers can lead to the increase of well bottom-hole flowing pressure and enlarge the production rate of gas for this formation.

(2) The main layer with larger permeability and gas reserve determines the level of well bottom-hole flowing pressure and contributes mostly to the production of deviated wells. The influence of inner region properties, such as fracture horizontal permeability and radius, is limited, and the well production performance mainly depends on the properties of the outer region.

(3) To keep the well bottom-hole pressure at a relatively high level and enhance the gas recovery from the less permeable layer, the penetration inclination angle for the first and second layers should be larger than 60°, and be enlarged as much as possible.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JG and BN proposed original ideas for this paper. HY and CJ contributed to the modeling, programming, result analysis, and discussion. This paper was written by HY and YL. JG and BN provided technical guidance for research work and reviewed the paper.

Funding

This work is supported by the National Science and Technology Major Project (No. 2016ZX05015) and CNPC Science and Technology Major Project (No. 2021DJ1504).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank the reviewers and editors whose critical comments helped prepare this article.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.861780/full#supplementary-material

References

Basquet, R., Caltagirone, J. P., Alabert, F. G., and Batsalle, J. C. (1999). A Semianalytical Approach for Productivity Evaluation of Complex wells in Multilayered Reservoirs. SPE Reserv. Eval. Eng. 2 (6), 506–513. doi:10.2118/59098-pa

CrossRef Full Text | Google Scholar

Cobb, W. M., Ramey, H. J., and Miller, F. G. (1972). Well-Test Analysis for wells Producing Commingled Zones. J. Petrol. Technol. 24 (1), 27–37. doi:10.2118/3014-pa

CrossRef Full Text | Google Scholar

Dranchuk, P. M., Purvis, R. A., and Robinson, D. B. (1973). “Computer Calculation of Natural Gas Compressibility Factors Using the Standing and Katz Correlation,” in Annual Technical Meeting of the Petroleum Society of CIM, 8–12. doi:10.2118/73-112

CrossRef Full Text | Google Scholar

El-Banbi, A. H., and Wattenbarger, R. A. (1996). “Analysis of Commingled Tight Gas Reservoirs,” in SPE Annual Technical Conference and Exhibition, 8–9. doi:10.2118/36736-ms

CrossRef Full Text | Google Scholar

El-Banbi, A. H., and Wattenbarger, R. A. (1997). “Analysis of Commingled Gas Reservoirs with Variable Bottom-Hole Flowing Pressure and Non-Darcy Flow,” in SPE Annual Technical Conference and Exhibition, 5–8. doi:10.2118/38866-ms

CrossRef Full Text | Google Scholar

Fan, D., Yao, J., Hai, S., Hui, Z., and Wei, W. (2015). A Composite Model of Hydraulic Fractured Horizontal Well with Stimulated Reservoir Volume in Tight Oil and Gas Reservoir. J. Nat. Gas Sci. Eng. 24, 115–123. doi:10.1016/j.jngse.2015.03.002

CrossRef Full Text | Google Scholar

Guo, J., Meng, F., Jia, A., Dong, S., Yan, H., Zhang, H., et al. (2020). Production Behavior Evaluation on Multilayer Commingled Stress-Sensitive Carbonate Gas Reservoir. Energy Explor. Exploit. 39 (1), 86–107. doi:10.1177/0144598720964155

CrossRef Full Text | Google Scholar

Hall, K. R., and Yarborough, L. (1973). A New Equation of State for Z-Factor Calculations. Oil Gas J. 71 (7), 82–92.

Google Scholar

Jia, A., Yan, H., Guo, J., He, D., Cheng, L., and Jia, C. (2013). Development Characteristics for Different Types of Carbonate Gas Reservoirs. Acta Petrolei Sinica 34 (5), 914–923.

Google Scholar

Jia, A., Yan, H., Guo, J., He, D., and Wei, T. (2014). Characteristics and Experiences of the Development of Various Giant Gas fields All over the World. Nat. Gas Industry 34 (10), 33–46. doi:10.3787/j.issn.1000-0976.2014.10.005

CrossRef Full Text | Google Scholar

Jia, A., and Yan, H. (2014). Problems and Countermeasures for Various Types of Typical Carbonate Gas Reservoirs Development. Acta Petrolei Sinica 35 (3), 519–527. doi:10.7623/syxb201403014

CrossRef Full Text | Google Scholar

Jongkittinarukorn, K., and Tiab, D. (1998). “Development of the Boundary Element Method for a Horizontal Well in Multilayer Reservoir,” in SPE Rocky Mountain Regional/Low-Permeability Reservoirs Symposium, 5–8. doi:10.2118/39939-ms

CrossRef Full Text | Google Scholar

Kikani, J., and Jr, G. W. W. (1991). Analysis of Pressure-Transient Tests for Composite Naturally Fractured Reservoirs. SPE Form. Val 6 (2), 176–182. doi:10.2118/19786-pa

CrossRef Full Text | Google Scholar

Kuchuk, F. J., and Habashy, T. (1996). Pressure Behavior of Horizontal wells in Multilayer Reservoirs with Crossflow. SPE Form. Val 11 (1), 55–64. doi:10.2118/22731-pa

CrossRef Full Text | Google Scholar

Kuchuk, F. J., and Saeedi, J. (1992). “Inflow Performance of Horizontal wells in Multilayer Reservoirs,” in SPE Annual Technical Conference and Exhibition, 4–7. doi:10.2118/24945-ms

CrossRef Full Text | Google Scholar

Kuchuk, F. J., and Wilkinson, D. J. (1991). Transient Pressure Behavior of Commingled Reservoirs. SPE Form. Val 6 (1), 111–120. doi:10.2118/18125-pa

CrossRef Full Text | Google Scholar

Larsen, L. (1981). “Wells Producing Commingled Zones with Unequal Initial Pressures and Reservoir Properties,” in SPE Annual Technical Conference and Exhibition, 2–5. doi:10.2118/10325-ms

CrossRef Full Text | Google Scholar

Larsen, L. (1999). Determination of Pressure-Transient and Productivity Data for Deviated wells in Layered Reservoirs. SPE Reserv. Eval. Eng. 2 (1), 95–103. doi:10.2118/54701-pa

CrossRef Full Text | Google Scholar

Larsen, L. (2000). Pressure-transient Behavior of Multibranched wells in Layered Reservoirs. SPE Reserv. Eval. Eng. 3 (1), 68–73. doi:10.2118/60911-pa

CrossRef Full Text | Google Scholar

Lee, A. L., Gonzalez, M. H., and Eakin, B. E. (1966). The Viscosity of Natural Gases. J. Petrol. Technol. 18 (8), 997–1000. doi:10.2118/1340-pa

CrossRef Full Text | Google Scholar

Ma, X., Yan, H., Chen, J., He, D., and Xu, W. (2021). Development Patterns and Constraints of Superimposed Karst Reservoirs in Sinian Dengying Formation, Anyue Gas Field, Sichuan Basin. Oil Gas Geology. 42 (6), 1281–1294. doi:10.11743/ogg20210604

CrossRef Full Text | Google Scholar

Medeiros, F., Ozkan, E., and Kazemi, H. (2010). A Semianalytical Approach to Model Pressure Transients in Heterogeneous Reservoirs. SPE Reserv. Eval. Eng. 13 (02), 341–358. doi:10.2118/102834-pa

CrossRef Full Text | Google Scholar

Meng, F., He, D., Yan, H., Zhao, H., Zhang, H., and Li, C. (2021). Production Performance Analysis for Slanted Well in Multilayer Commingled Carbonate Gas Reservoir. J. Pet. Sci. Eng. 204, 108769. doi:10.1016/j.petrol.2021.108769

CrossRef Full Text | Google Scholar

Meng, F., Lei, Q., He, D., Yan, H., Jia, A., Deng, H., et al. (2018). Production Performance Analysis for Deviated wells in Composite Carbonate Gas Reservoirs. J. Nat. Gas Sci. Eng. 56, 333–343. doi:10.1016/j.jngse.2018.06.014

CrossRef Full Text | Google Scholar

Meng, F., Lei, Q., Yan, H., He, D., and Deng, H. (2017). Productivity Assessment for Inclined wells in Gaoshiti-Moxi Carbonate Gas Reservoirs. Spec. Oil Gas Reservoirs 24 (5), 111–115. doi:10.3969/j.issn.1006-6535.2017.05.020

CrossRef Full Text | Google Scholar

Olarewaju, J. S., and Lee, W. J. (1987). “An Analytical Model for Composite Reservoirs Produced at Either Constant Bottomhole Pressure or Constant Rate,” in The 62nd Annual Technical Conference and Exhibition 27-30 September. doi:10.2118/16763-ms

CrossRef Full Text | Google Scholar

Olarewaju, J. S., and Lee, J. W. (1989). A Comprehensive Application of a Composite Reservoir Model to Pressure-Transient Analysis. SPE Reservoir Eng. 4 (3), 325–331. doi:10.2118/16345-pa

CrossRef Full Text | Google Scholar

Olarewaju, J. S., and Lee, W. J. (1991). “Rate Behavior of Composite Dual-Porosity Reservoirs,” in Production Operations Symposium, 7–9. doi:10.2118/21703-ms

CrossRef Full Text | Google Scholar

Ozkan, E., and Raghavan, R. (1991a). New Solutions for Well-Test-Analysis Problems. Part 1- Analytical Considerations. SPE Form. Val 6 (3), 359–368. doi:10.2118/18615-pa

CrossRef Full Text | Google Scholar

Ozkan, E., and Raghavan, R. (1991b). New Solutions for Well-Test-Analysis Problems: Part 2-computational Considerations and Applications. SPE Form. Val 6 (3), 369–378. doi:10.2118/18616-pa

CrossRef Full Text | Google Scholar

Pan, Y., Kamal, M. M., and Kikani, J. (2010). Field Applications of a Semianalytical Model of Multilateral wells in Multilayer Reservoirs. SPE Reserv. Eval. Eng. 13 (6), 861–872. doi:10.2118/121335-pa

CrossRef Full Text | Google Scholar

Prado, L. R., and Da, G. (1987). “An Analytical Solution for Unsteady Liquid Flow in a Reservoir with a Uniformly Fractured Zone Around the Well,” in SPE/DOE Low Permeability Reservoirs Symposium. doi:10.2118/16395-ms

CrossRef Full Text | Google Scholar

Raghavan, R., Topaloglu, H. N., Cobb, W. M., and Ramey, H. J. (1974). Well-test Analysis for wells Producing from Two Commingled Zones of Unequal Thickness. J. Petrol. Technol. 26 (9), 1035–1043. doi:10.2118/4559-pa

CrossRef Full Text | Google Scholar

Rana, S., and Ertekin, T. (2012). “Type Curves for Pressure Transient Analysis of Composite Double-Porosity Gas Reservoirs,” in SPE Western Regional Meeting, 19–23. doi:10.2118/153889-ms

CrossRef Full Text | Google Scholar

Satman, A. (1991). Pressure-transient Analysis of a Composite Naturally Fractured Reservoir. SPE Form. Val 6 (2), 169–175. doi:10.2118/18587-pa

CrossRef Full Text | Google Scholar

Schmittroth, L. A. (1960). Numerical Inversion of Laplace Transforms. Commun. ACM 3 (3), 171–173. doi:10.1145/367149.367172

CrossRef Full Text | Google Scholar

Spath, J. B., Ozkan, E., and Raghavan, R. (1990). “An Efficient Algorithm for Computation of Well Responses in Commingled Reservoirs,” in Annual Technical Meeting, 10–13. doi:10.2118/90-01

CrossRef Full Text | Google Scholar

Turki, L., Demski, J. A., and Grader, A. S. (1989). “Decline Curve Analysis in Composite Reservoirs,” in SPE Eastern Regional Meeting, 24–27. doi:10.2118/spe-19316-ms

CrossRef Full Text | Google Scholar

Vieira Bela, R., Pesco, S., and Barreto, A. (2019). Modeling Falloff Tests in Multilayer Reservoirs. J. Pet. Sci. Eng. 174, 161–168. doi:10.1016/j.petrol.2018.10.101

CrossRef Full Text | Google Scholar

Wang, F., Li, Y., Tang, X., Chen, J., and Gao, W. (2016a). Petrophysical Properties Analysis of a Carbonate Reservoir with Natural Fractures and Vugs Using X-ray Computed Tomography. J. Nat. Gas Sci. Eng. 28, 215–225. doi:10.1016/j.jngse.2015.11.046

CrossRef Full Text | Google Scholar

Wang, Y., Chen, Y., and Li, D. (2016b). “Simulations and Case Studies for Enhancing Production in a Stress-Sensitive Fractured Carbonated Reservoir,” in 50th U.S. Rock Mechanics/Geomechanics Symposium, 26–29.

Google Scholar

Wang, H., Ran, Q., and Liao, X. (2017). Pressure Transient Responses Study on the Hydraulic Volume Fracturing Vertical Well in Stress-Sensitive Tight Hydrocarbon Reservoirs. Int. J. Hydrogen Energ. 42 (29), 18343–18349. doi:10.1016/j.ijhydene.2017.04.143

CrossRef Full Text | Google Scholar

Wang, H., Zhang, L., Guo, J., Liu, Q., and He, X. (2012). An Efficient Algorithm to Compute Transient Pressure Responses of Slanted wells with Arbitrary Inclination in Reservoirs. Pet. Sci. 9 (2), 212–222. doi:10.1007/s12182-012-0201-1

CrossRef Full Text | Google Scholar

Wu, M., Ding, M., Yao, J., Xu, S., Li, L., and Li, X. (2018). Pressure Transient Analysis of Multiple Fractured Horizontal Well in Composite Shale Gas Reservoirs by Boundary Element Method. J. Pet. Sci. Eng. 162, 84–101. doi:10.1016/j.petrol.2017.12.024

CrossRef Full Text | Google Scholar

Yan, H., Deng, H., Wan, Y., Yu, J., Xia, Q., Xu, W., et al. (2020a). The Gas Well Productivity Distribution Characteristics in strong Heterogeneity Carbonate Gas Reservoir in the Fourth Member of Dengying Formation in Moxi Area, Sichuan Basin. Nat. Gas Geosci. 31 (8), 1152–1160. doi:10.11764/j.issn.1672-1926.2020.01.001

CrossRef Full Text | Google Scholar

Yan, H., Peng, X., Xia, Q., Xu, W., Luo, W., Li, X., et al. (2020b). Distribution Features of Ancient Karst Landform in the Fourth Member of the Dengying Formation in the Gaoshiti-Moxi Region and its Guiding Significance for Gas Reservoir Development. Acta Petrolei Sinica 41 (6), 658–670. doi:10.7623/syxb202006002

CrossRef Full Text | Google Scholar

Zeng, H., Fan, D., Yao, J., and Sun, H. (2015). Pressure and Rate Transient Analysis of Composite Shale Gas Reservoirs Considering Multiple Mechanisms. J. Nat. Gas Sci. Eng. 27, 914–925. doi:10.1016/j.jngse.2015.09.039

CrossRef Full Text | Google Scholar

Zhao, L., Chen, Y., Ning, Z., Wu, X., Liu, L., and Chen, X. (2013). Stress Sensitive Experiments for Abnormal Overpressure Carbonate Reservoirs: A Case from the Kenkiyak Fractured-Porous Oil Field in the Littoral Caspian Basin. Pet. Exploration Development 40 (2), 208–215. doi:10.1016/s1876-3804(13)60024-5

CrossRef Full Text | Google Scholar

Zhao, Y.-L., Zhang, L.-H., Luo, J.-X., and Zhang, B.-N. (2014). Performance of Fractured Horizontal Well with Stimulated Reservoir Volume in Unconventional Gas Reservoir. J. Hydrol. 512 (10), 447–456. doi:10.1016/j.jhydrol.2014.03.026

CrossRef Full Text | Google Scholar

Glossary

B_g Gas formation volume factor, m³/sm³

C_g Gas compressibility, MPa⁻¹

C_t Total compressibility, MPa⁻¹

h Formation thickness, m Horizontal direction

k Permeability, 10⁻³ μm²

k_ra Formation anisotropy degree

L_w Slanted well length, m

m Pseudo-pressure, MPa Matrix system

m_wf Wellbore pseudo-pressure, MPa

M Mobility ratio

p Pressure, MPa

p_avg formation average pressure, MPa

p_wf Wellbore pressure, MPa

q_g Gas production rate, m³/d

$\tilde{q}$ Production rate from point source, m³/d

r Radial distance, m Reference condition

r_w Wellbore radius, m

R_e Formation radius, m

s Laplace transform variable

t Time, day

x, y, z Directional coordinates

x_w, y_w, z_w Distance of mid-perforation in x, y and z coordinates, m

α Stress-sensitive power exponent, dimensionless

α_m, α_c Shape factors of matrix and vugs, 1/m²

β Pseudo-time factor

λ Interporosity flow coefficient, dimensionless

ω Storativity ratio, dimensionless

η Hydraulic diffusivity, dimensionless

θ Inclination angle, degree

μ_g Gas viscosity, mPa·s

φ Porosity, fraction

σ_s Overburden pressure, MPa

a_t, a_p Constants, a_t = 86.4, a_p = 1.842 × 10⁻³

ⁱ Initial condition

0 Standard condition

m Pseudo-pressure, MPa Matrix system

f Natural fractures system

c Vugs system

r Radial distance, m Reference condition

w Wellbore

j jth layer

1 Inner region

2 Outer region

h Formation thickness, m Horizontal direction

v Vertical direction

D Dimensionless

^- Laplace domain

^ Fourier domain