Optimal Dispatching Strategy of Active Distribution Network for Promoting Local Consumption of Renewable Energy

Large-scale renewable energy sources (RESs) have been integrated into the active distribution network (ADN). For promoting the local consumption of RESs within ADN, an optimal dispatching strategy was proposed with two-stage hierarchical energy management framework. On the spatial boundary, a two-layer energy management framework was designed with the local optimization layer and the global optimization layer. The local optimization layer was for optimal power flow in the branch feeder with the objective functions of minimizing operation costs and maximizing the consumption of RESs. The global optimization layer was for optimal power flow in the main feeder with the objective functions of minimizing power loss and the voltage deviation of nodes. On the time scale, two-stage optimal dispatching models were established, including the day-ahead optimal models and intra-day optimal models. The day-ahead optimal models identified the operation status of the controllable units, and then the intra-day optimal models were updated with the ultra-short-term forecast results. A risk indicator was introduced to quantify the uncertainty of RES, and a non-dominated sorting genetic algorithm with elite strategy was adopted to solve the multi-objective nonlinear programming problem. An actual project in northern China was used as the testing system. The results of case studies verify that the proposed strategy can effectively realize the maximum local consumption of RESs and support the economic operation of ADN.

Introduction

The high penetration of renewable energy can pose challenges for the operation of a distribution network due to uncertainty and variability. For the future low-carbon society, it is important to design an optimal dispatching strategy of the active distribution network (ADN) to improve the consumption of renewable energy and enhance the economy of the distribution network (Wu et al., 2021).

The research on the dispatching strategy of ADN mainly focused on economical operation. The objective function of the optimal dispatching model was generally set with minimizing power loss (Gildenhuys et al., 2019; Bi et al., 2020; Wu et al., 2021) and the amount of electricity purchased from grid (Wu et al., 2019; Zhang et al., 2020a; Omaji et al., 2020). Some references considered resilience in the objective functions (Wang and Wang, 2015; Zhou et al., 2019). Renewable energy sources (RESs) were often integrated with energy storage systems (ESSs) or controllable distributed generators (CDGs) to form microgrids (MGs). Bi et al. (2020) proposed a learning-based dispatching strategy of MGs with RES and ESS. Ji et al. (2021) proposed a continuous-control, deep reinforcement learning-based online scheduling method for MGs. Dubuisson et al. (2020) proposed a bacterial foraging optimization algorithm for power management in stand-alone MGs. Omaji et al. (2020) established a cooperative game model for MGs. Younesi et al. (2021) proposed bi-level resilience-oriented stochastic scheduling that integrates the economic perspective considering MG resilience function. In Zhang and Yan (2018), an ADN optimal control strategy for energy storage systems and controllable loads was considered and solved by an improved particle swarm algorithm. The above-mentioned literature greatly benefits this paper on objective functions and constraints.

Actually, the difficulty lies in the uncertainty of RESs. At present, most papers established a stochastic programming model to solve the problems of ADNs with RESs. Sampling and clustering were commonly used in some literature so that deterministic scenarios were derived for ease in solving. Ahmadi et al. (2016) proposed a stochastic programming model for distribution companies trading in the electricity market, in which the variability of wind speed was dealt with roulette wheel mechanism. Somma et al. (2017) formulated a stochastic multi-objective linear programming problem for the operation strategies of ADN by using Monte Carlo simulation method to model 24-h scenarios related to solar irradiance. The Monte Carlo simulation in Wang and Wang (2015) was based on the forecasted power and uncertain prediction errors to generate scenarios for distributed generator (DG) outputs. Fang et al. (2017) evaluated the primary frequency response of the power system with important wind power generation, which considered the uncertainty of wind power output. Fan et al. (2021) evaluated the influence of RESs on ADN dynamic performance, in which K-means clustering technique was adopted to select the approximation samples of input variables. Sannigrahi et al. (2019) used K-means algorithm to present a stochastic framework for ADN planning framework. Sampling and clustering algorithms are useful and simple in modeling the uncertainty of RESs. However, multiple scenarios increase the solving times, and it is not convenient for dispatchers to quantitatively evaluate the operation risk caused by the uncertainty of RESs.

There were some studies on the energy management framework of ADNs. Kong et al. (2019) constructed a two-layer distributed optimization model for ADNs and MG with different interests, in which one layer is the active judgment modules and another layer is the active control modules. The active judgment modules included power flow calculation, voltage quality judgment, and supply margining judgment. The active control modules were those controllable units such as CDGs. Li et al. (2018) proposed a three-layer collaborative dispatch system for ADNs, in which the first layer is the distribution network dispatching layer, the second layer is the coordinated control layer, and the third layer is the local control layer. Radhakrishnan and Srinivasan (2016) and Upadhyay and Sharma (2016) constructed a multi-agent system for the distributed energy management system. The son-agent dealt with the uncertainty of RESs, and the parent-agent dealt with the coordination between son-agents. The energy management framework with multiple layers or agents has a clear architecture and reduces the difficulty of solving complex problems. However, the above-mentioned literature needs to consider the coordination relationship between multiple agents or layers and increases the complexity of the controller.

This paper proposed a two-stage hierarchical optimal dispatching model to promote the local consumption of RESs within ADN. The main contributions of this paper are as follows:

(1) A hierarchical energy management framework is proposed for ADN. The global optimization layer of ADN optimizes the load flow in the main feeder for improving the consumption of RESs, and the local optimization layer optimizes the load flow in the branch feeder for the local consumption of RESs. The structure of the dispatching system is simple without the additional coordinated controllers.

(2) The optimal dispatching model is established with two-stage energy management. The day-ahead optimal model identifies the operation status of the controllable units. The intra-day optimal model is updated with ultra-short-term forecast results, and the risk indicator is introduced for quantifying the uncertainty caused by the forecast errors. The optimal dispatching model is easier to be solved.

The rest of this paper is organized as follows: Section 2 presents the hierarchical energy management framework for optimal dispatching of ADN. Section 3 establishes a two-stage hierarchical optimal dispatching model of ADN. Section 4 supports the solving algorithm. Case studies are carried out in Section 5. Finally, Section 6 presents the conclusion of the whole paper.

Problem Formulation

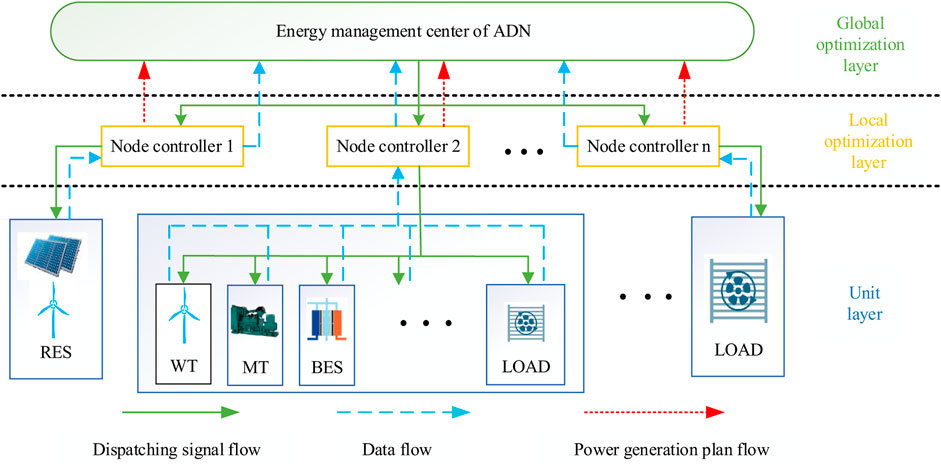
This paper studies an ADN with RESs connected to nodes. As shown in Figure 1, the energy management framework for dispatching ADN is divided into three levels, namely, the global optimization layer, the local optimization layer, and the unit layer.

FIGURE 1

FIGURE 1. Hierarchical energy management architecture of active distribution network.

Bi-direction power flow is permitted in the tie line between grids with ADN. The node in ADN may serve as a load to absorb the power from ADN or as a power source to inject power into ADN. The global optimization layer is for energy management of ADN, which issues the power references to the local optimization layer. The local optimization layer is for the energy management of nodes, which is set as the node controller. Unit layer is for energy management of devices connected with nodes, which is responsible for executing the dispatching instructions from the node controller. In the hierarchical energy management architecture, the corresponding demand of dispatching should be considered. Furthermore, the safe operation of ADN should be satisfied effectively, and renewable energy should be absorbed locally.

The global optimization layer of ADN optimizes the load flow in the main feeder for improving the consumption of RESs. The renewable energy shall be absorbed within ADN as much as possible. If the output of renewable energy is greater than the demand of the load, the curtailed energy can be sold to grid or be stored in energy storage systems. If the output is far less than the demand, the energy will be supplied by grid or regulated by nodes.

The local optimization layer optimizes the load flow in the branch feeder for the local consumption of RESs. It takes the optimized power issued by the energy management center as a constraint, and the regional autonomous control is completed by the unit layer according to the optimization objective of the local optimization layer. The devices in the unit layer are regulated to absorb RESs nearby, which may be CDGs such as hydro, micro-gras turbine (MT), energy storage systems such as battery energy storage (BES), and demand-side response loads (DRLs) such as transferable load (TL) and interruptible (IL).

The information flow in ADN is a loop in which the state information is collected from the unit layer to the local optimization layer and then to the global optimization layer, and the instruction information is released from the energy management center to the node controllers and then to the schedulable units.

At present, the forecast accuracy of renewable energy output is related to the forecast time scale. Generally speaking, the longer the time scale is in the forecast horizon, the worse the forecast accuracy is. In this paper, two-stage hierarchical optimal model will be established for the dispatching strategy of ADN to promote the local consumption of RESs. In the following discussion, day-ahead dispatching plans for the global optimization layer and the local optimization layer will be designed, and then an intra-day optimal dispatching strategy of and will be developed.

Two-Stage Hierarchical Optimal Dispatching Model of Active Distribution Network

Two-stage hierarchical optimal dispatching model is established on the spatial and temporal dimensions. On the spatial boundary, there is a two-layer optimal dispatching model with consideration of promoting the local consumption of RESs, in which the local optimization layer is for the branch feeders (BFs) and the global optimization layer is for the main feeders. On the time scale, there is a two-stage optimal dispatching model with the consideration of reducing the negative influence of the forecast error of RESs, in which the day-ahead optimization is for the states of controllable units and the intra-day optimization is for the updated dispatch strategy.

The forecast error of RESs is collected with the history data. The day-ahead forecast outputs of RESs are given by the short-term forecasting system, which will be used in the day-ahead optimal models. The intra-day forecast outputs in each interval are given by the ultra-short-term forecasting system, which is more accurate than the day-ahead forecast outputs. The dispatching interval of ADN is set as 15 min following the grid dispatching intervals.

Day-Ahead Optimal Model of the Local Optimization Layer

In the local optimization layer, the day-ahead optimal model is for optimal power flow in the branch feeders. The decision variables include the consumption power of RESs connected with the branch feeder, the interactive power of the nodes with the main branch, the outputs and the status of schedulable units connected at the branch feeder, such as the on/off status of CDGs and their generation power, the charge/discharge status of ESSs and their outputs, and the operation status of DRLs and their power.

Objective Functions

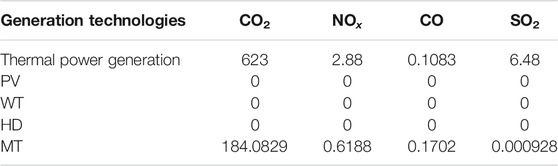
In order to improve the local consumption of RESs as much as possible, Eq. 1 is chosen as the objective function. Meanwhile, the operation cost of the branch feeders should be minimized to manage the economic operation of ADN. Therefore, another objective function is expressed as Eq. 2, which includes the generation costs of CDGs (Eq. 3), operation cost of ESSs (Eq. 4), dispatching costs of schedulable loads (Eq. 5), environment cost (Eq. 6), and purchasing cost of electricity from the node (Eq. 7).

$\max f_1={\displaystyle \sum _{\text{t}}^{\text{T}}\left(P_{\text{PV,}t}+P_{\text{WT,}t}\right)}\mathrm{\Delta }t(1)$

$\min f_2={\displaystyle \sum _t^T\left[C_{\text{CDG,}t}+C_{\text{ESS,}t}+C_{\text{DRL,}t}+C_{\text{e,}t}+C_{\text{PE,}t}\right]}(2)$

$C_{CDG}^t={\displaystyle \sum _{i=1}^{N_{\text{CDG}}}\left\{{\mu }_i^{t}f\left(P_{\text{CDG}i,t}\right)+\left({\mu }_i^t-{\mu }_i^{t-1}\right){\lambda }_{\text{CDG}i}\right\}}(3)$

$C_{\text{ESS,}t}={\displaystyle \sum _{j=1}^M\left(C_{\text{inv}}\frac{{\mu }_j^t{P}_{j,t}^{\text{dis}}-{\mu }_j^t{P}_{j,t}^{\text{ch}}}{2N_{\text{life}}\left(t\right)E_{\text{Br}}}\mathrm{\Delta }t+c_{\text{loss}}\left[\left(1-{\eta }_j^{\text{ch}}\right)P_{j,t}^{\text{ch}}+\left({\eta }_j^{\text{dis}}-1\right)P_{j,t}^{\text{dis}}\right]\mathrm{\Delta }t\right)}(4)$

$C_{\text{DRL,}t}={\displaystyle \sum _{n=1}^{N_{\text{TL}}}{c}_{\text{TL}}{P}_{\text{TL}n,t}\mathrm{\Delta }t+{\displaystyle \sum _{m=1}^{N_{\text{IL}}}{c}_{\text{IL}}{P}_{\text{IL}m,t}\mathrm{\Delta }t}}(5)$

$C_{\text{e,}t}={\displaystyle \sum _{i=1}^{N_{\text{DG}}}{\displaystyle \sum _{s=1}^{N_{\text{S}}}{V}_{\text{e}s}}{Q}_{is,t}{P}_{\text{DG}i,t}}(6)$

$C_{\text{PE,}t}=c_{\text{grid,}t}{P}_{\text{PE},t}(7)$

In Eq. 4 constraints, the cycle life of ESSs was calculated with the charge/discharge depth by the rain flow counting method. For the sake of simple calculation, this paper assumes that all TLs have the same unit scheduling cost and all ILs have the same unit scheduling cost. The environment cost refers to the purification cost of pollutant emissions by CDGs connected with the branch feeder.

Constraints

The power flow balance meets constraint Eq. 8. It should be noted that the outputs of RESs are uncertain, and the power supported by grid is limited by tie-line carrying capacity as shown in Eq. 9.

${\displaystyle \sum _{i=1}^{N_{\text{CDG}}}{P}_{\text{CDG}i,t}}+P_{\text{G},t}+\left(P_{\text{PV},t}+P_{\text{WT},t}\right)+{\displaystyle \sum _{j=1}^M\left({\eta }_{j,t}^{\text{dis}}{P}_{j,t}^{\text{dis}}-{\eta }_{j,t}^{\text{ch}}{P}_{j,t}^{\text{ch}}\right)}=P_{\text{L},t}+P_{\text{TL},t}+P_{\text{IL},t}(8)$

$P_{\text{G},t}\le P_{\text{G},\max }(9)$

Eqs 10–12 are the operation constraints of CDGs, in which Eq. 10 limits the output power, Eq. 11 and Eq. 12 describe the ramp rate, and Eq. 13 guarantees the minimum operating time.

$P_{\text{CDG,}\min }\le P_{\text{CDG}i\text{,}t}\le P_{\text{CDG,m}ax}(10)$

$P_{\text{CDG}i\text{,}t}-P_{\text{CDG}i\text{,}t-1}\le \text{UR}(11)$

$P_{\text{DG}i\text{,}t-1}-P_{\text{DG}i\text{,}t}\le \text{UD}(12)$

$T_{d,\min }\le T_{d,s}\le T_{d,\max }(13)$

The operation constraints of BESs include Eqs 14–19. Eq. 14 limits the state of charge (SoC) of battery, which is to prevent over-charge and over-discharge. Eq. 15 guarantees battery capacity to serve the next dispatching cycle, which is usually set at half of the battery capacity. Eq. 16 and Eq. 17 calculate the real-time SoC, and Eq. 18 and Eq. 19 limit the permitted power in charging and discharging.

$So{C}_{\text{B},\min }<So{C}_{B,t}<So{C}_{B,\max }(14)$

$So{C}_{B,0}=So{C}_{B,T}=0.5(15)$

$So{C}_{B,t}=(1-\delta )So{C}_{B,t-1}+\frac{{\eta }_{\text{ch}}{P}_{\text{ch,}t}\mathrm{\Delta }t}{E_{\text{B}r}}(16)$

$So{C}_{B,t}=(1-\delta )So{C}_{B,t-1}+\frac{P_{\text{dis,}t}\mathrm{\Delta }t}{{\eta }_{\text{dis}}{E}_{\text{Br}}}(17)$

$0<P_{\text{ch,}t}<P_{\text{ch},\max }(18)$

$0<P_{\text{dis,}t}<P_{\text{dis},\max }(19)$

The schedulable loads here include ILs and TLs. Eq. 20 limits the interruptible power of IL, and Eq. 21 limits the interruptible duration of IL. The Eq. 22 and Eq. 23 constrain operation status of IL and TL cannot be changed continuously in adjacent periods. Eq. 24 demands TL to transfer as a whole.

$0\le P_{IL,t}\le P_{\text{IL},\max }(20)$

$T_{\text{IL,min}}\le T_{IL,t}\le T_{\text{IL,max}}(21)$

$\left|{\mu }_{IL,t}-{\mu }_{IL,t-1}\right|={\mu }_{\text{IL}}(22)$

$\left|{\mu }_{DL,t}-{\mu }_{DL,t-1}\right|={\mu }_{\text{DL}}(23)$

$P_{TL,t}=P_{\text{TL}}(24)$

Day-Ahead Optimal Model of the Global Optimization Layer

In the global optimization layer, the day-ahead optimal model is for optimal power flow in the main feeders. The decision variables include the consumption power of RESs connected with the main feeder, the power supported by grid, the power of node injected into the branch feeders, and the outputs and the status of schedulable units connected at the main feeder, such as on/off status of CDGs and their generation power, charge/discharge status of ESSs and their outputs, and operation status of DRLs and their power.

Objective Function

The power flow in the main feeder is optimized to obtain the economic operation of ADN. Eq. 25 is designed as the objective function to promote the local consumption of RESs. The less the power loss is in the main feeder, the more RESs is absorbed locally. Besides this, the key factor restricting the consumption capacity of RESs is the voltage deviation in ADN caused by the fluctuation of RESs. Eq. 26 is designed as the objective function to support the power quality.

$\min f_3={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{ij\in {\Omega }_L}\frac{Z_{ij}\left(P_{ij,t}^2+Q_{ij,t}^2\right)\mathrm{\Delta }t}{V_{j,t}^2}}}(25)$

$\min f_4={\displaystyle \sum _{t=1}^T\left|\frac{V_{i,t}-V_{\text{N}}^i}{V_{\text{N}}^i}\right|}(26)$

Constraints

The power flow constraints are expressed as Eq. 27 and Eq. 28, the power interactive with nodes meets Eq. 29, and the node voltage constraints are expressed as Eq. 30. The other constraints include Eqs. 9–24.

$P_{\text{G},t}-{\displaystyle \sum _{i=1}^N{P}_{i,t}}=V_{i,t}{\displaystyle \sum _{j=1}^N{V}_{j,t}\left(G_{ij}\cos {\delta }_{ij,t}+B_{ij}\sin {\delta }_{ij,t}\right)}(27)$

$Q_{G,t}-{\displaystyle \sum _{i=1}^N{Q}_{i,t}}=V_{i,t}{\displaystyle \sum _{j=1}^N{V}_{j,t}\left(G_{ij}\sin {\delta }_{ij,t}-B_{ij}\cos {\delta }_{ij,t}\right)}(28)$

$P_{i,t}\le P_{i\text{,max}}(29)$

$V_{\min }\le V_{i,t}\le V_{\max }(30)$

Intra-day Updated Optimal Model

It is necessary to update the dispatching strategy designed above because the intra-day forecast outputs of RESs are relatively accurate. Figure 2 shows the intra-day updated dispatching framework. The operation status of units are determined according to the day-ahead optimal model, and the dispatching strategy is updated with intra-day forecast outputs of RESs in every 15-min interval.

FIGURE 2

FIGURE 2. Intra-day updated dispatching framework.

As mentioned above, the operation status of the units are known in the intra-day optimal model, including the on/off status of CDGs, the charge and discharge status of EESs, and the operation status of DRLs. Whether it is the intra-day updated optimal model of the local optimization layer or the intra-day updated optimal model of the global optimization layer, the constraints are the same as that of the day-ahead optimal models. In the following sections, the objective functions will be discussed.

The intra-day optimal model of the local optimization layer is updated with the ultra-short-term forecast outputs of RESs connected with the branch feeder. The decision variables of the intra-day optimal model are the consumption power of RESs, the power of the node injected into the branch feeders, the outputs of CDGs, the outputs of EESs, and the interruptible power of ILs.

For promoting the local consumption of RESs in the branch feeder, Eq. 1 is chosen as the objective function as that of the day-ahead optimal model of the local optimization layer. Besides this, there is another objective function expressed as Eq. 31, which is to minimize the adjustment costs. Adjustment costs refer to the additional operation costs brought about by updating the forecast outputs of RESs.

$\min {f^{\prime }}_2={\displaystyle \sum _t^T\left[\mathrm{\Delta }{C}_{\text{CDG,}t}+\mathrm{\Delta }{C}_{\text{ESS,}t}+\mathrm{\Delta }{C}_{\text{DRL,}t}\right]}(31)$

Since the on/off status of CDGs is determined by the day-ahead scheduling plan, the adjustment cost only considers fuel costs during each dispatching period t. The adjustment cost of CDGs is calculated asEq. 32.

$\mathrm{\Delta }{C}_{\text{CDG,}t}={\displaystyle \sum _{i=1}^{N_{\text{CDG}}}f\left(P_{\text{CDG}i,t}-P{\mathrm{’}}_{\text{CDG}i,t}\right)}(32)$

Similarly, the adjustment cost of ESSs can be expressed as Eqs 33–35. As to the adjustment cost of DRLs, it is expressed as Eq. 36 for ILs while ignoring TLs which keep the optimal operation status of the day-ahead schedule plan.

$\mathrm{\Delta }{C}_{\text{ESS,}t}={\displaystyle \sum _{j=1}^M(C_{\text{life,}t}+C_{\text{loss,}t})}-{\displaystyle \sum _{j=1}^M({C^{\prime }}_{\text{life,}t}+{C^{\prime }}_{\text{loss,}t})}(33)$

${C^{\prime }}_{\text{life,}t}=C_{\text{inv}}\frac{{P^{\prime }}_{j,t}^{\text{dis}}-{P^{\prime }}_{j,t}^{\text{ch}}}{2{N^{\prime }}_{\text{life,}t}{E}_{\text{Br}}}\mathrm{\Delta }t(34)$

${C^{\prime }}_{\text{loss,}t}=c_{\text{loss}}\left[\left(1-{\eta }_j^{\text{ch}}\right){P^{\prime }}_{j,t}^{\text{ch}}+\left({\eta }_j^{\text{dis}}-1\right){P^{\prime }}_{j,t}^{\text{dis}}\right]\mathrm{\Delta }t(35)$

$\mathrm{\Delta }{C}_{\text{DRL,}t}=\left[{\displaystyle \sum _{l=1}^{N_{\text{IL}}}{c}_{\text{IL}}{P}_{\text{IL}l,t}\mathrm{\Delta }t}\right]-\left[{\displaystyle \sum _{l=1}^{N_{\text{IL}}}{c}_{\text{IL}}{P^{\prime }}_{\text{IL}l,t}\mathrm{\Delta }t}\right](36)$

The objective functions of the intra-day optimal model of the global optimization layer is the same as that of the day-ahead optimal model of the global optimization layer.

Solving Algorithm

The day-ahead optimal model is a mixed-integer nonlinear programming problem. There are continuous variables, such as the outputs of CDGs, consumption power of RESs, power supported by grid, power of node injected into the branch feeders, and so on, and there are discrete variables such as the on/off status of CDGs, charge/discharge status of ESSs, operation status of DRLs, and so on. The models can be established as follows:

$\{\min f\left(P,\mu \right),P=\left[P_1,P_2,\cdot \cdot \cdot ,P_n\right],\mu =\left[{\mu }_1,{\mu }_2,\cdot \cdot \cdot {\mu }_m\right]s.t.h\left(P,\mu \right)=0\overline{\text{g}}\le g\left(P,\mu \right)\le \underset{¯}{g}P\in R,\mu \in \left\{\mathrm{0,1}\right\}(37)$

The intra-day optimal model is a nonlinear optimization problem. There are continuous variables, such as outputs of CDGs, consumption power of RESs, charging and discharging power of RESs, and so on. The models can be built up as follows:

$\{\begin{array}{l}\min f\mathrm{’}\left(P\right),\Delta P=\left[P_1,P_2,\cdot \cdot \cdot ,P_n\right]\\ s.t.h\mathrm{’}\left(P\right)=0\\ \overline{P}\le P_j\le \underset{¯}{P},j=1,2,\cdot \cdot \cdot ,D\end{array}(38)$

As mentioned above, the historical data set can be derived to describe the probability distribution of the forecast errors of RESs. Eq. 8 can be transformed as Eq. 39 with the forecast errors.

${\displaystyle \sum _{i=1}^{N_{\text{CDG}}}{P}_{\text{CDG}i,t}}+P_{\text{G},t}+\left({\overline{P}}_{\text{PV},t}+R_{\text{PV},t}\right)+\left({\overline{P}}_{\text{WT},t}+R_{\text{WT},t}\right)+{\displaystyle \sum _{j=1}^M\left({\eta }_{j,t}^{\text{dis}}{P}_{j,t}^{\text{dis}}-{\eta }_{j,t}^{\text{ch}}{P}_{j,t}^{\text{ch}}\right)}=P_{\text{L},t}+P_{\text{TL},t}+P_{\text{IL},t}(39)$

Taking into account the uncertainty of the forecast error, a risk indicator is introduced with a certain confidence level of probability distribution. Under the given confidence level $\alpha$, the risk indicator can be quantified by quantiles, as shown inEq. 40.

$R={\text{CDF}}^{-1}\left(1-\alpha \right)(40)$

The optimal dispatching model established is a multi-objective optimization problem. As it is known, a single-objective optimization problem only has one objective function, which makes it relatively easy to get the global optimal solution. However, when multiple objectives are considered, there are often conflicts between these objectives, so it is difficult to find an appropriate solution. It is common that weight coefficients are set for each sub-objective to convert a multi-objective into a single objective. Although it is simple to obtain the solution, the results are influenced by the weights, and the solution quality is not high enough.

This paper adopts the NSGA-II algorithm to obtain the Pareto optimal solution. The NSGA-II algorithm is a multi-objective intelligent optimization algorithm based on the Pareto optimal solution theory, with the advantages of fast operation and good convergence (Zhang et al., 2020b; Pant et al., 2021). The crowding distance comparison operator is used to quickly obtain the fitness values of different elements. It competes between parent and offspring individuals to produce the next-generation population, which is conducive to maintaining excellent individuals and improving the overall evolution level of the population. The algorithm decomposes the multi-objective optimization problem into multiple single-objective optimization sub-problems and efficiently approaches the whole Pareto frontier by setting the weight vector. When the population size is set to $N$, the initialization weight vector is $\left\{\frac{0}{N-1},\frac{1}{N-1},\cdots ,\frac{N-1}{N-1}\right\}$.

The solution process of algorithm is detailed as Algorithm 1:

Algorithm 1.

Case Study

Overview of the Actual ADN in Northern China

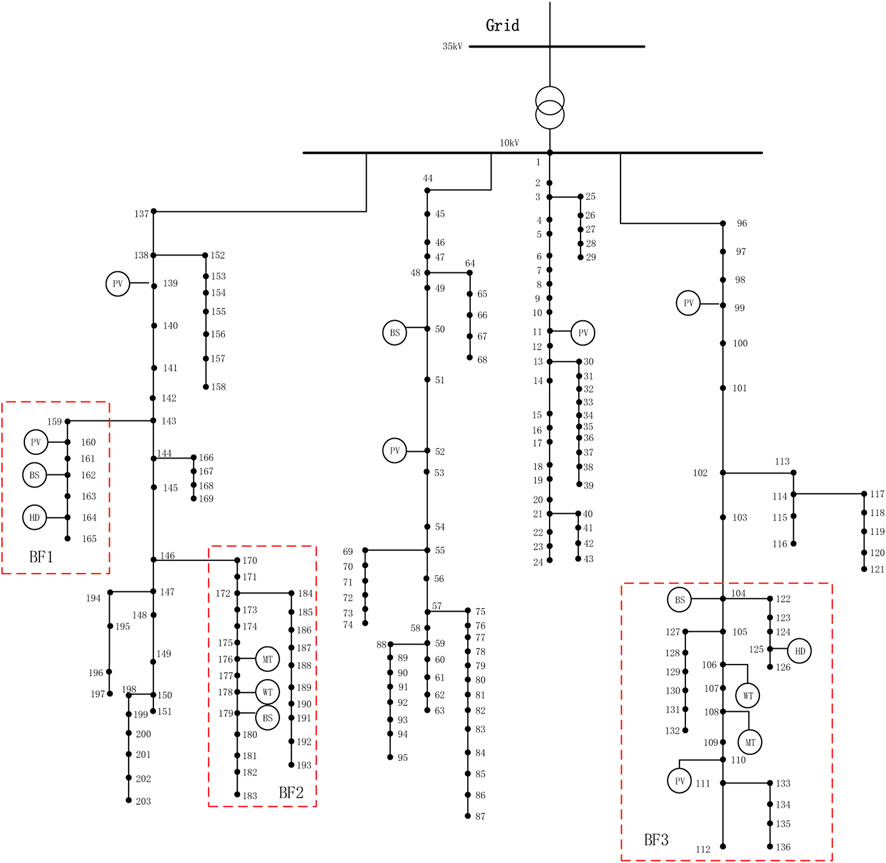
A case study was carried out using an actual distribution network in an area of Yiyang, Henan Province, China, as shown in Figure 3. The ADN contains 203 nodes. The voltage level of the system is 10 kV. The optimization horizon is 24 h, and the dispatch interval is 15 min. Three optimal models can be established with consideration of the combination RESs, CDGs, BESs, and loads. BF1 is connected with node 143, BF2 is connected with node 146, and BF3 is connected with node 103. The installed capacity is 10 MW for each PV, 10 MW for each WT, 2 MW for each BESS, 2 MW for each HD, and 1 MW for each MT.

FIGURE 3

FIGURE 3. A distribution network with three branch feeders.

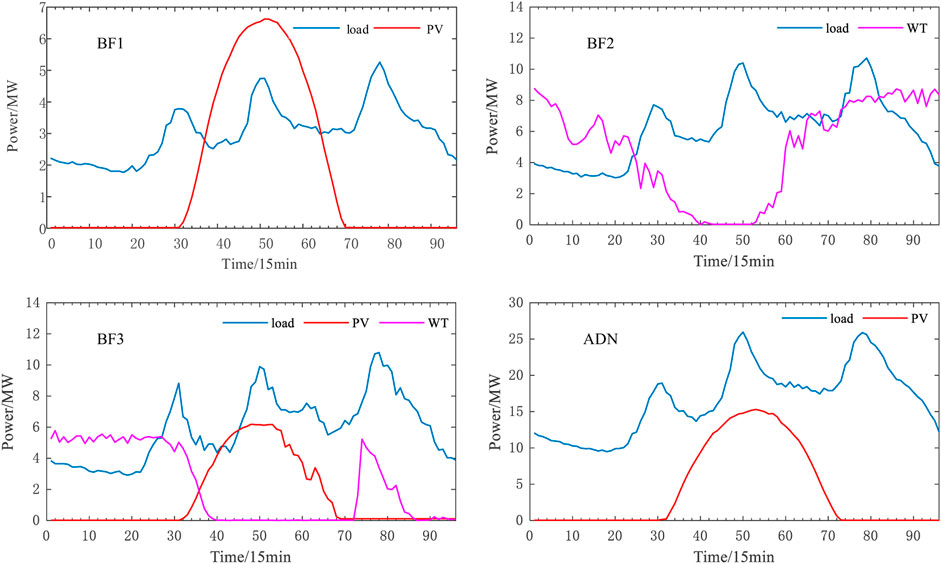
The parameters are displayed in Tables 1–5. Figure 4 shows the forecast curves of the day-ahead load and RESs, and Figure 5 indicates the forecast curves of the ultra-short-term load and RESs.

TABLE 1

TABLE 1. Parameters of micro-gas turbine.

TABLE 2

TABLE 2. Emission parameters of various electricity generation technologies (g/kWh).

TABLE 3

TABLE 3. Processing costs of pollutant emission (yuan/kg).

TABLE 4

TABLE 4. Energy storage system parameters.

TABLE 5

TABLE 5. Price of interactive power between branch feeders and active distribution network.

FIGURE 4

FIGURE 4. Day-ahead load and renewable energy output forecast curve.

FIGURE 5

FIGURE 5. Ultra-short-term load and renewable energy output forecast curve.

Dispatching Strategy of ADN

The non-dominated genetic algorithm (NSGA-II) is used to solve the multi-objective optimization problem. The parameters of the algorithm are set as follows: population size is set to 100, the maximum iterations of genetic operations is 100, selection probability is 0.9, and mutation probability is 0.1. The simulation took 6.174 s with high model convergence.

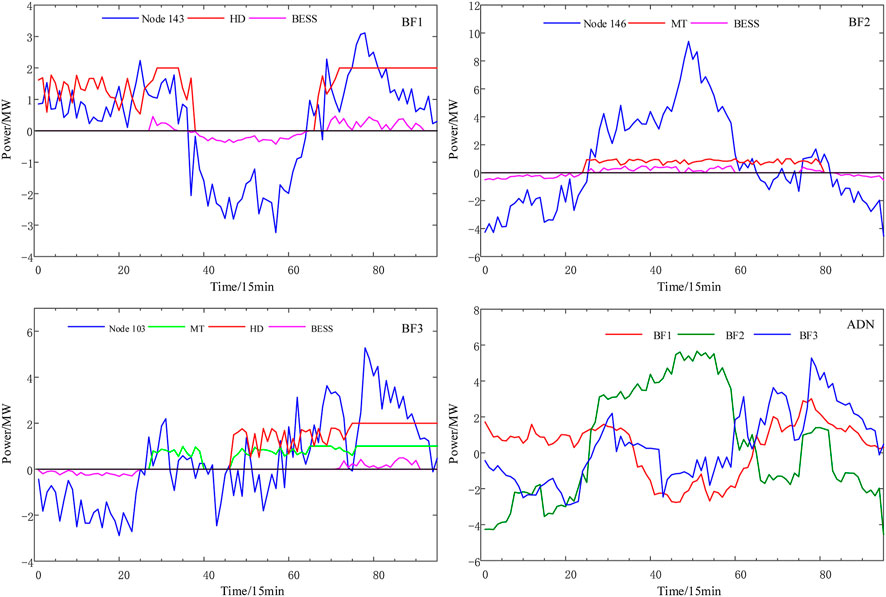
Figure 6 shows the day-ahead optimal results. When the RESs output is larger than the load, the ESS is charging, and when the RESs output is less than the load, the ESS is discharging and DGs begin to work. The fluctuation of RES generation is mainly compensated by the ADN when local DGs and ESSs in BFs cannot compensate it. When the PV output cannot meet the load, ESSs start to discharge at this time. HD is on with high-level output power. The total interactive power fluctuates between 7 and -5 MW.

FIGURE 6

FIGURE 6. Day-ahead optimal results.

Figure 7 presents the dispatching strategy of the intra-day optimal model. The intra-day optimal dispatching strategy modifies the outputs of CDGs and BESs without changing the status set by the day-ahead dispatch plans. There is a certain deviation between the dispatch command of the BFs obtained with optimizing the operation of the ADN and the interactive power curve obtained with optimizing the operation of the BFs. This is due to the different focus of optimal dispatching. In the optimized results, the nodes with BFs are equivalent to the controllable distributed power source, which accepts the dispatching instructions from the energy management center of ADN. Therefore, the local optimization layer executes the dispatching instructions of the globe optimization layer and adjusts the outputs of the controllable units in the branch feeders in time.

FIGURE 7

FIGURE 7. Intra-day optimal results.

According to the power flow calculation, the equivalent voltage amplitude of BF2 is lower than 0.93. Therefore, the intra-day dispatching program of the main feeder needs to be started. The main feeder is optimized with minimizing the node voltage deviation. Then, the node controller accepts the dispatching instructions from the energy management center. Therefore, the outputs of the controllable units connected with branch feeders will be adjusted in time.

Local Consumption of RESs

The local consumption rate of RESs is defined as Eq. 41. It is the proportion consumed by the branch feeder and the maximum output of RESs. The forecast results are used as the maximum outputs of RESs.

$\sigma ={\displaystyle \sum _{t=1}^T\frac{P_{\text{RES}}^{\text{real}}\left(t\right)}{P_{\text{RES}}^{\text{max}}\left(t\right)}\mathrm{\Delta }t}(41)$

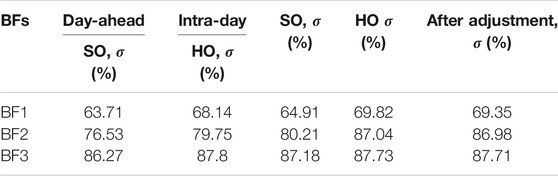
For a convenient illustration, SO is corresponding to the optimal results with single-layer energy management framework, and HO is corresponding to the optimal results with hierarchical energy management framework proposed in this paper. Table 6 presents the local consumption rate on site of BF.

TABLE 6

TABLE 6. Renewable energy consumption rate on site of branch feeder.

As shown in Table 6, the dispatching strategy proposed in this paper can effectively promote the local consumption of RESs. If the node voltage exceeds the operation limit, the global optimization layer optimizes the power curve of the interaction between the nodes and the main feeder with the voltage deviation as the objective. The node controllers will adjust the outputs of the controllable units at the same time with maximizing the local consumption of renewable energy. On the one hand, it can reduce the power loss caused by power transmission. On the other hand, nodes accept the dispatching instructions of ADN center, which is convenient for management without an additional coordinated controller. Upon comparing the results of day-ahead optimization and intra-day optimization, it was shown that the forecast errors of loads and RESs affect the optimal results and verifies the proposed method with two-stage hierarchical optimization.

Table 7 and Table 8 give the day-ahead and intra-day optimal operation cost of BFs, respectively.

TABLE 7

TABLE 7. Day-ahead optimal operation cost of branch feeders.

TABLE 8

TABLE 8. Intra-day optimal operation cost of branch feeders.

By comparing the calculation results SO and HO, it is shown that the energy management strategy proposed in this paper can reduce the operating cost of nodes. At the same time, considering the voltage quality of the main feeder, the operating costs of BFs are increased less than before. The cost of purchasing electricity from the main feeder still occupies a large proportion.

The confidence level of the forecast error of RES affects the operation economy of ADN. The smaller the confidence level is set, the worse the operation economy is shown to be. Table 9 shows a list of the total operation cost of ADN under different confidence levels. It shows that a larger confidence level can help reduce the operation cost of ADN. In engineering projects, the confidence level should be selected reasonably.

TABLE 9

TABLE 9. Total cost in different confidence levels (yuan/day).

Figure 8 shows the total power loss of ADN.

FIGURE 8

FIGURE 8. Total power loss of active distribution network.

As shown in Figure 8, the power loss of ADN is 10.570 MW, and it is reduced by 29.06%, in contrast with the power loss of SO at 14.9 MW. It indicates that the proposed strategy can effectively reduce power loss.

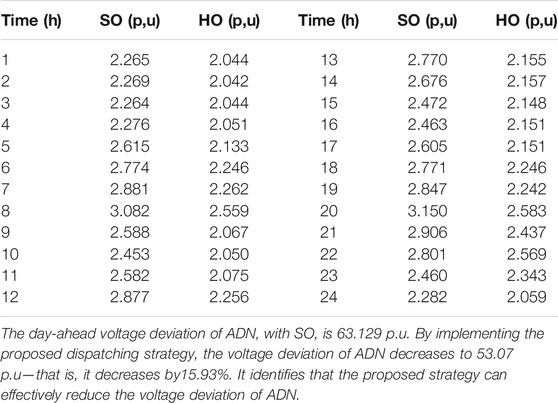
Table 10 presents the voltage deviation of ADN in day-ahead optimization results.

TABLE 10

TABLE 10. Voltage deviation of active distribution network (ADN).

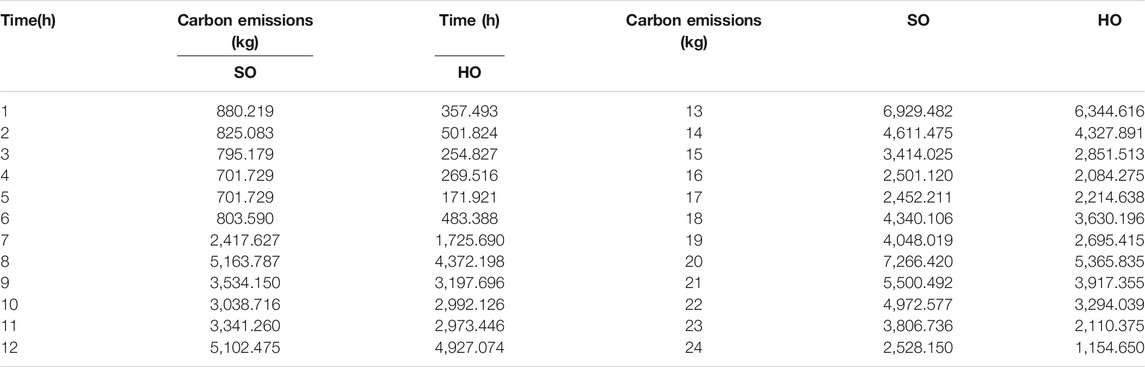
Table 11 imposes the carbon emissions at all scheduled times.

TABLE 11

TABLE 11. Carbon emissions at all scheduled times.

In Table 11, before optimal dispatching, the total carbon emission of all BFs was 79,676.357 kg. Using the energy management strategy proposed in this paper, the total carbon emission of all BFs was 62,217.997 kg, and the carbon emission was reduced to 17,458.36062 kg. That is, the carbon emission is reduced by 21.91%. It shows that the proposed strategy in this paper can effectively reduce carbon emissions. On the one hand, it reduces the amount of fossil fuels, and on the other hand, it reduces the emissions of environmental pollutant gases.

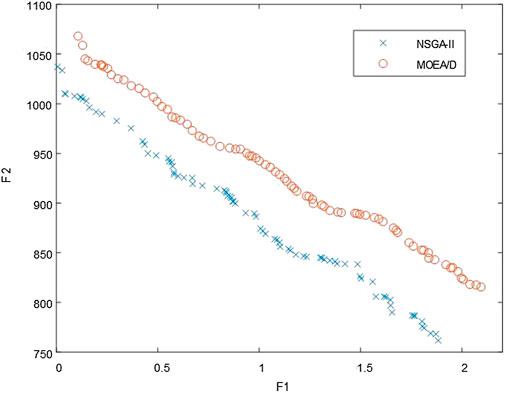
In order to verify the superiority of NSGA-II algorithm, the multi-objective evolutionary algorithm based on decomposition (MOEA/D) (Zhang and Li, 2007) is selected as the comparison algorithm to solve the proposed model. MOEA/D is also commonly used in multi-objective optimization models to avoid local optimization and approach the Pareto frontiers efficiently. The same parameters are set in two algorithms, and the confidence level is 90%. Figure 9 shows the Pareto frontiers with different algorithms.

FIGURE 9

FIGURE 9. Pareto frontiers with different algorithms.

Figure 9 indicates that the result of NSGA-II algorithm is more economical than that of MOEA/D. Besides this, the calculation time used by NSGA-II algorithm is 6.174 s, and the calculation time used by MOEA/D algorithm is 7.351 s. Therefore, the NSGA-II algorithm applied in this paper has an advantage in solving the multi-objective complex optimization model.

In summary, the dispatching strategy proposed in this paper can effectively promote the local consumption of RESs and the economy operation of ADN and reduce carbon emission and power loss while supporting the power quality of nodes.

Conclusion

This paper proposes the optimal dispatching strategy of ADN for promoting the local consumption of RESs. The two-stage hierarchical energy management framework is proposed, in which the structure of the dispatching system is simple and the optimal dispatching model is easier to be solved. The power flow in the main feeder and in the branch feeder is respectively optimized to improve the local consumption of RESs and the economical operation of ADNs. Besides this, the operation risk caused by the uncertainty of RES is quantified, so optimal results are friendly to the operators of ADNs.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

HX: writing-original draft preparation, conception of the study, and methodology; WW: methodology and software; WW: software and data analyses; LT: data analyses and editing. All authors contributed to the article and approved the submitted version.

Conflict of Interest

WW is employed by XJ Group Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

Ahmadi, A., Charwand, M., Siano, P., Nezhad, A. E., Sarno, D., Gitizadeh, M., et al. (2016). A Novel Two-Stage Stochastic Programming Model for Uncertainty Characterization in Short-Term Optimal Strategy for a Distribution Company. Energy. 117, 1–9. doi:10.1016/j.energy.2016.10.067

CrossRef Full Text | Google Scholar

Bi, W., ShuDong, Y. W., and Yang, Q. (2020). “Real-time Energy Management of Microgrid Using Reinforcement Learning,” in 2020 19th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), 38–41. doi:10.1109/dcabes50732.2020.00019

CrossRef Full Text | Google Scholar

Dubuisson, F., Chandra, A., and Rezkallah, M. (2020). A Bacterial Foraging Optimization Technique and Predictive Control Approach for Power Management in a Standalone Microgrid[C]//2020 IEEE Electric Power and Energy Conference (EPEC). Edmonton, AB: IEEE.

Google Scholar

Fan, M., Li, Z., Ding, T., Huang, L., Dong, F., Ren, Z., et al. (2021). Uncertainty Evaluation Algorithm in Power System Dynamic Analysis With Correlated Renewable Energy Sources. IEEE Trans. Power Syst. 36 (6), 5602–5611. doi:10.1109/tpwrs.2021.3075181

CrossRef Full Text | Google Scholar

Fang, W., Liu, H., Chen, F., Zheng, H., Hua, G., and He, W. (2017). DG Planning in Stand-Alone Microgrid Considering Stochastic Characteristic. J. Eng. 2017 (13), 1181–1185. doi:10.1049/joe.2017.0515

CrossRef Full Text | Google Scholar

Gildenhuys, T., Zhang, L., Ye, X., and Xia, X. (2019). Optimization of the Operational Cost and Environmental Impact of a Multi-Microgrid System. Energ. Proced. 158, 3827–3832. doi:10.1016/j.egypro.2019.01.865

CrossRef Full Text | Google Scholar

Ji, Y., Wang, J., Xu, J., and Li, D. (2021). Data-Driven Online Energy Scheduling of a Microgrid Based on Deep Reinforcement Learning. Energies. 14 (8), 2120. doi:10.3390/en14082120

CrossRef Full Text | Google Scholar

Kong, X., Yong, C., and Wang, C. (2019). Optimal Strategy of Active Distribution Network Considering Source–Network–Load. IET Generation, Transm. Distribution. 13 (1), 5586–5596. doi:10.1049/iet-gtd.2018.5781

CrossRef Full Text | Google Scholar

Li, Y., Fan, X., and Cai, Z. (2018). Optimal Active Power Dispatching of Microgrid and Distribution Network Based on Model Predictive Control[J]. Tsinghua Sci. Technology. 23 (3), 11. doi:10.26599/tst.2018.9010083

CrossRef Full Text | Google Scholar

Omaji, S., Javaid, N., and Khalid, A. (2020). Towards Real-Time Energy Management of Multi-Microgrid Using a Deep Convolution Neural Network and Cooperative Game Approach[J]. IEEE Access. 8, 161377–161395. doi:10.1109/ACCESS.2020.3021613

CrossRef Full Text | Google Scholar

Pant, M., Snasel, V., and Verma, S. (2021). A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems[J]. IEEE Access. 9, 57757–57791. doi:10.1109/ACCESS.2021.3070634

CrossRef Full Text | Google Scholar

Radhakrishnan, B. M., and Srinivasan, D. (2016). A Multi-Agent Based Distributed Energy Management Scheme for Smart Grid Applications. Energy. 103, 192–204. doi:10.1016/j.energy.2016.02.117

CrossRef Full Text | Google Scholar

Sannigrahi, S., Ghatak, S. R., and Acharjee, P. (2019). Multi-Scenario Based Bi-level Coordinated Planning of Active Distribution System under Uncertain Environment[J]. IEEE Trans. Industry Appl. 56 (1), 850–863. doi:10.1109/TIA.2019.2951118

CrossRef Full Text | Google Scholar

Somma, M. D., Graditi, G., and Heydarian-Forushani, E. (2017). Stochastic Optimal Scheduling of Distributed Energy Resources with Renewables Considering Economic and Environmental Aspects[J]. Renew. Energ. 116, 272–287. doi:10.1016/j.renene.2017.09.074

CrossRef Full Text | Google Scholar

Upadhyay, S., and Sharma, M. P. (2016). Selection of a Suitable Energy Management Strategy for a Hybrid Energy System in a Remote Rural Area of India. Energy. 94, 352–366. doi:10.1016/j.energy.2015.10.134

CrossRef Full Text | Google Scholar

Wang, Z., and Wang, J. (2015). Self-Healing Resilient Distribution Systems Based on Sectionalization into Microgrids. IEEE Trans. Power Syst. 30 (6), 3139–3149. doi:10.1109/tpwrs.2015.2389753

CrossRef Full Text | Google Scholar

Wu, K., Li, Q., Chen, Z., Lin, J., Yi, Y., and Chen, M. (2021). Distributed Optimization Method with Weighted Gradients for Economic Dispatch Problem of Multi-Microgrid Systems. Energy. 222, 119898. doi:10.1016/j.energy.2021.119898

CrossRef Full Text | Google Scholar

Wu, X., Cao, W., and Wang, D. (2019). A Multi-Objective Optimization Dispatch Method for Microgrid Energy Management Considering the Power Loss of Converters[J]. Energies. 12 (11), 1–19. doi:10.3390/en12112160

CrossRef Full Text | Google Scholar

Younesi, A., Shayeghi, H., Siano, P., and Safari, A. (2021). A Multi-Objective Resilience-Economic Stochastic Scheduling Method for Microgrid. Int. J. Electr. Power Energ. Syst. 131 (1), 106974. doi:10.1016/j.ijepes.2021.106974

CrossRef Full Text | Google Scholar

Zhang, Q., and Li, H. (2007). MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Computat. 11 (6), 712–731. doi:10.1109/tevc.2007.892759

CrossRef Full Text | Google Scholar

Zhang, B., and Yan, N. (2018). “Research on Economic Dispatching Method of Active Distribution Network based on Multi-microgrids[C]//International Conference,” on perconductivity and Electromagnetic Devices, Tianjin, China (Chen Yang, China: Shenyang University of Technology), 1–2.

Zhang, L., Chi, F., and Liu, H. (2020a). “Day-ahead Optimal Dispatch of Active Distribution Network with Micro-energy Grid Considering Demand Response[C]//2020,” in IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China (Chengdu, China: IEEE), 1491–1498.

Google Scholar

Zhang, L., Ge, H., Ma, Y., Xue, J., Li, H., and Pecht, M. (2020b). Multi-Objective Optimization Design of a Notch Filter Based on Improved NSGA-II for Conducted Emissions. IEEE Access. 8, 83213–83223. doi:10.1109/access.2020.2991576

CrossRef Full Text | Google Scholar

Zhou, X., Ai, Q., and Yousif, M. (2019). Two Kinds of Decentralized Robust Economic Dispatch Framework Combined Distribution Network and Multi-Microgrids[J]. Appl. Energ. 253, 113588.1–113588.16. doi:10.1016/j.apenergy.2019.113588

CrossRef Full Text | Google Scholar

Glossary

ADN active distribution network

BESS battery energy storage system

BF branch feeder

CDG controllable distributed generator

DRL demand-side response loads

ESS energy storage system

HD hydro

HO hierarchical optimization

MT micro gas turbine

PV photovoltaics

RESs renewable energy sources

SoC state of charge of battery

SO single-layer optimization

WT wind turbine

TL transferable load

T index of scheduling periods, t = 1, 2, … , $T$

I index of controllable DGs, i = 1,2, … , $N_{DG}$

$j$ index of ESSs, $j$ = 1, 2, … , $M$

N index of transferable load, n = 1, 2, … , $N_{TL}$

M index of interruptible load, m = 1, 2, … , $N_{IL}$

$\alpha$ confidence level

$\sigma$ local consumption rate

Parameters

$P_{\text{G},\text{max}/\text{min}}$ maximum/minimum exchange power between ADN and BF

$P_{G,t}$ purchase and sale of electricity at time t

$P_{\text{CDG}i,t}$ output power of the $\text{i}th$ CDG at time t

$P_{\text{CDG},\text{max}/\text{min}}$ maximum/minimum power of CDG

$P_{L,i}\mathit{、}{Q}_{L,i}$ active and reactive load of ADN at time t

$N_{\text{life}}$ life cycle of ESS at corresponding discharge depth cycle life at charge discharge depth

$P_{\text{TL}n,t}$ dispatching power of the $\text{ n}th$ TL at time t

$P_{\text{IL}m,t}$ dispatching power of the $\text{ m}th$ IL at time t

$P_{j,t}^{\text{ch}/\text{dis}}$ charging/discharging power of $\text{j}th$ ESS at time t

$P_{\text{ch}/\text{dis},\text{max}}$ maximum charge/discharge power of ESS

$P_{\text{line},t}$ transmission power of the ADN

$P_{\text{line},max}$ maximum transmission power of ADN

$P_{\text{RES}}^{\text{max}}\left(t\right)$ the maximal output power of RESs at time t

${\overline{P}}_{\text{PV}/\text{WT},t}$ forecast power of PV/WT at time t in the BF

$P_{\text{PV}/\text{WT},t}$ power of PV/WT at time t in the BF

$P_{Tk,i,t}\mathit{、}{Q}_{Tk,i,t}$ active power and reactive power from $\text{ k}th$ BF at time t

$N_{\text{TL}/\text{IL}}$ number of transferable/interruptible loads

$P_{\text{PCC},i,t}\mathit{、}{Q}_{\text{PCC},i,t}$ active and reactive power from the upper grid

$P_{T,\text{max}/\text{min}}$ maximum and minimum exchange power between ADN and BF

$P_{\text{PCC},\text{max}}$ maximum power injected by the upper grid

$P_{\text{RES}}^{\text{real}}\left(t\right)$ the power of RESs consumed by BFs at time t

$P_{\text{PE},t}$ purchase and sales of electricity at time t

$P_{ij,t}$ active power flowing through the line ij at time t

$Q_{ij,t}$ reactive power flowing through the line ij at time t

$R_{\text{PV}/\text{WT},t}$ forecast error power of PV/WT at time t in the BF

$c_{\text{CDG},\text{t}}$ generation cost of CDGs at time t

$c_{\text{ESS},\text{t}}$ operation cost of ESSs at time t

$C_{\text{inv}}$ the initial investment cost of ESS

$c_{\text{PE},\text{t}}$ electricity purchasing cost at time t

$c_{\text{TL}}$ unit dispatch cost of transferable load

$c_{IL}$ unit dispatch cost of interruptible load

$c_{\text{DRL},\text{t}}$ dispatching cost of schedulable loads at time t

$c_{\text{e},\text{t}}$ environment cost at time t

$c_{\text{grid},\text{t}}$ electricity purchase and sale cost at time t

$c_{\text{loss}}$ unit charge and discharge loss cost of ESS

$N_{\text{life}}$ life cycle of ESS at corresponding discharge depth cycle life at charge discharge depth

${\text{μ}}_j^{\text{ch}/\text{dis}}$ charging/discharging efficiency of $\text{j}th$ ESS

$D_{oD,t}$ dispatch depth of ESS at time t

$E_{\text{Br}}$ rated capacity of BESS

${\eta }_j^{\text{ch}/\text{dis}}$ charge/discharge efficiency of ESS

$So{C}_{\text{B},\text{t}}$ state of charge of BESS at time t

$So{C}_{\text{B},\text{max}/\text{min}}$ maximum and minimum SOC of BESS

$X_{ij}$ reactance of branch $\text{k}$ between node i and j

$G_{ij}\mathit{、}{B}_{ij}$ real and imaginary parts of the admittance matrix between node i and node j

$Z_{ij}$ impedance of line ij

$V_{ij,t}$ end voltage of line ij at time t

$V_{i,t}$ the voltage amplitude of node i at time t

$V_N^i$ the rated voltage of node i

$V_{\text{max}/\text{min}}$ maximum and minimum voltage

$V_{\text{es}}$ environmental value of class s pollutants

${\delta }_{ij,t}$ voltage phase difference between node i and j

$T_{d,s}$ operating time of CDG

$T_{d,\text{min}}$ minimum operating time of CDG

$T_{d,\text{max}}$ maximum operating time of CDG

$\text{UR}$ maximum ramp down rate of CDG

UD maximum ramp up rate of CDG

${\mu }_i^t$ operating status of the $\text{i}th$ CDG at time t

${\lambda }_{\text{CDG}i}$ startup cost of the $\text{i}th$ CDG

$Q_{is,t}$ emission of class s pollutants of the ith CDG at time t

$\mathrm{\Delta }\text{t}$ scheduling interval