- Laboratory of Power and Control Systems (LSPyC), Facultad de Ingeniería, Universidad Nacional de Asunción, Luque, Paraguay
This article presents a model predictive current control of a shunt active power filter based on 7-level cascaded H-bridge converters. By using the spacial vector modulation approach into the model predictive control, a considerable reduction of the computational burden is achieved and makes possible the real-time implementation in a custom experimental setup. Then, the current harmonics on the grid side, caused by non-linear loads connected to the point of common coupling, are compensated. The experimental results confirmed the feasibility and efficacy of the proposed controller.
Introduction
Nowadays, electrical distribution systems present a complex electrical scenario, where different dynamic load devices such as switching power supplies, rectifiers and AC motors are integrated (Habibullin et al., 2014; Mishra et al., 2020). This increasing number of connected devices causes problems such as increased reactive power and the harmonic distortion of the electrical current power grid. Consequently, other issues appear in the distribution grid, for instance, overheating of the conductors, current surges, high current consumption, which leads to resizing connections and possible damage to devices connected to the power grid (Motta and Faúndes, 2016; Das et al., 2020). Consequently, various types of equipment have been proposed to solve these power quality problems, namely.
• Shunt Active Power Filters (SAPF), to mitigate current harmonics (Jia et al., 2020).
• Static Distribution Compensators (DSTATCOM), to mitigate reactive power.
• Dynamic Voltage (DVR) to mitigate voltage unbalance disturbances (Ferreira et al., 2017).
• Unified Power Quality Conditioners (UPQC) to compensate for voltage and current quality problems (Irannezhad et al., 2012; Yang et al., 2021).
Within the SAPF literature, it has been studied extensively, from the different topologies of converters such as those based on Voltage Source Inverters (VSI), Neutral Point Clamped (NPC) and Cascade H-Bridge (CHB) converters (Jin et al., 2020; Po-Ngam, 2014). Depending on the configuration, they can consist of two levels or multilevel. CHB multilevel converters are increasingly seen as a promising solution due to their advantages, such as their high conversion efficiency (Marzo et al., 2021), modular structure (Hekmati et al., 2021), scalability to extend to more levels (Ramos et al., 2020), and higher number of redundant switching states (Comparatore et al., 2017). Note that this system needs a DC-link that can be provided by using a power supply or capacitors. The power supply would increase the costs of the implementation since nine power supplies are required (Wang J. et al., 2020; Wong et al., 2020). For this reason, capacitors with a large capacitance are typically used to emulate a power supply (Qamar et al., 2020). However, the capacitors absorb and deliver energy at the Point of Common Coupling (PCC) point, and between the converters of the same phase, this causes fluctuations in the DC-link voltages and makes variations compared to the reference (Bosch et al., 2017; Tareen and Mekhielf, 2017).
From the control’s point of view, the Proportional-Integral-Derivative (PID) and the Hysteresis control are the most applied techniques for power electronic converters. However, non-linear techniques such as the sliding mode control and the Model-based Predictive Control (MPC) have attracted attention in recent years. MPC has some advantages over the conventional linear current controller, such as important flexibility, including constraints and a suitable dynamic response (Rodas et al., 2021). However, MPC has one of its main disadvantages its high computational burden that makes it difficult to implement in complex systems. Also, MPC has a variable switching frequency that causes more significant stress on the switching devices and introduces non-linearities that propagate in the injected current. To solve MPC’s variable switching behaviour, some modulation techniques such as Pulse-Width Modulator (PWM), Space Vector Modulation (SVM) (Li and Zhao, 2020; Ronanki and Williamson, 2018), and Modulated MPC have been included in the control scheme. Though, most of them are applied to two-level SAPF. On the other hand, for multilevel SAPF based on CHB, the most usual modulator are Phase-Shift PWM (PSPWM) and Level-Shift PWM (LSPWM). PSPWM has some advantages such as easy compression and that it performs a natural balancing of the capacitor voltages (Rao et al., 2020; Ferreira et al., 2017).
In what follows, some recent works carried out regarding the control and modulation techniques used in this work are presented. In (Tarisciotti et al., 2016), an MPC for a SAPF with the fixed switching frequency is proposed and named M2PC. The modulation is included in the MPC structure and then applied to the SAPF based on a two-level VSI to reduce THD currents. A fast multilevel SVPWM method based on the imaginary coordinate with direct control of redundant vectors or zero sequence components is proposed in (Yuan et al., 2020). This latter presents a modification of the SVPWM technique based on the imaginary coordinate system, which is applied to different topologies of multilevel converters. In (Li et al., 2021), a sliding mode SVPWM method for an HTS SAPF is studied. This non-linear controller is combined with the SVPWM technique to be applied to the two-level SAPF. A simplified 3-D NLM-Based SVPWM technique with voltage-balancing capability for three-level NPC cascaded multilevel converter is proposed in (Lin et al., 2019) that presents a modification of the SVPWM modulation technique based on the closest level modulation, applied to the multilevel NPC converter. The previous works show different applications of both the control and the modulation technique, where the proposal of this article is the MPC control technique in combination with the SVPWM modulation technique applied to a SAPF based on cascaded H-bridge converters of 7 levels. Then, in this paper, a method of reducing the switching states using the space voltage vectors consists of obtaining the switching states for the three-level configuration. Once the vectors are selected, they are projected for the 7 levels’ configuration or more. The main advantage of this technique is the reduction of the computational burden by reducing the voltage vectors that allow the possibility of real-time implementation.
The main contribution of this research is the combination of the MPC with the SV-PSPWM technique applied to the 7-level CHB converter. In addition, a PI control is implemented to balance the DC-link voltages in the experimental platform. The proposed control scheme optimizes the prediction with voltage estimates in combination with the input and output signs of each CHB per phase, avoiding using a constant reference. The proposed MPC controller has been implemented in dSPACE-MicroLabBox platform. Also, tests of the control scheme have been carried out on the experimental bench using different operating points.
The article is organized as follows. In the following section, the mathematical model of SAPF applied in a three-phase system based on 7-level CHB SAPF topology is first presented. Subsequently, the current reference generator, the DC-link control, the predictive model, and the PSPWM modulation are presented. In Section 3 the experimentalresults are shown and finally in Section 4 the conclusions of the work are presented.
Fundamental Concepts, Issues, and Problems
Three-phase SAPF Based on Multimodular CHB Converter Model
The right side of Figure 1A shows the general connection scheme of the multimodular SAPF based on 7-level CHB converters to a three-phase distribution power grid at the PCC point. Each CHB module is made up of a DC-link
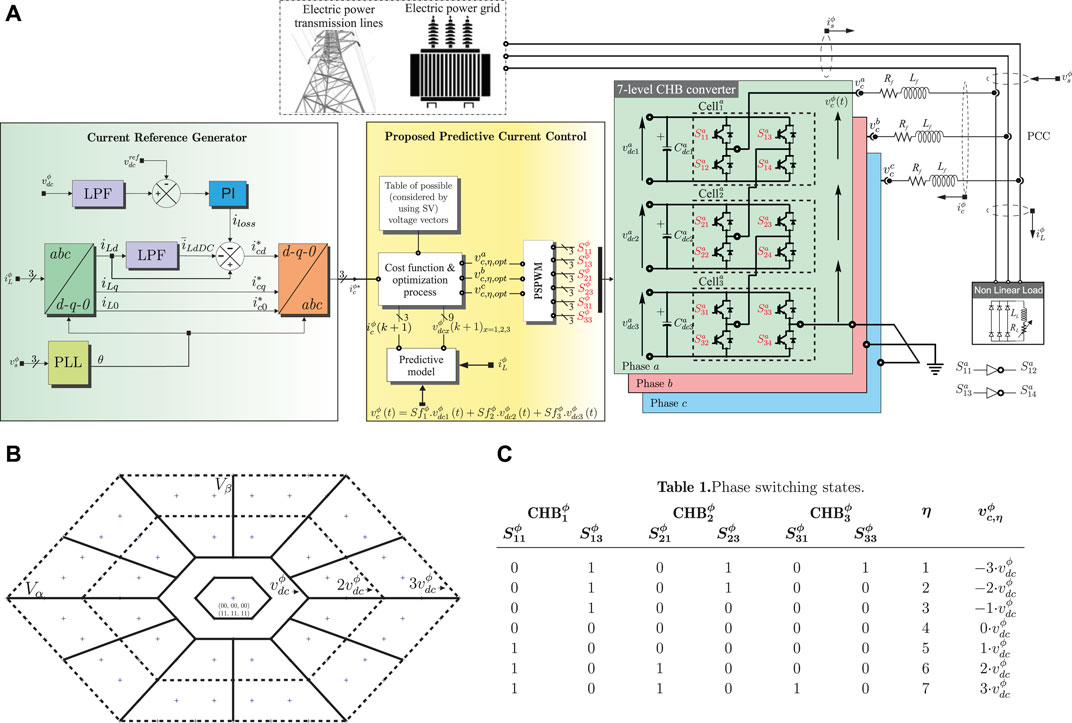
FIGURE 1. (A) Control scheme for the 7-level APF based on H-Bridge converter. (B) 7-level space vector diagram in an α − β coordinate. (C) Phase switching states.
The mathematical model of the SAPF based on 7-level CHB converters is obtained by applying Kirchhoff’s laws from the DC-link in the outgoing direction of the converter to the AC side of the electrical grid. The dynamics of the system is obtained:
where
From this, the control model is obtained, avoiding using a fixed reference voltage. Instead, the measured voltages of each converter with its corresponding sign are used to get the real voltage outputs of the converter.
Current Reference Generation
The calculation of the reference currents
Before the operation of the SAPF, all capacitors need to be charged to the reference voltage
where eϕ(k) represents the error between the reference and the previously filtered measured voltages
Predictive Model
The predictive model can be obtained from Eq. 1 by using a forward-Euler discretization method (Boukezata et al., 2017). Euler’s method is the most basic explicit method for numerical integration of ordinary differential equations and consequently carries a low computational burden, which benefits the experimental implementation (Jia et al., 2020). The SAPF discrete-time model is given by:
where k identifies the actual discrete-time sample, Ts is the sampling time, and
Cost Function and Optimization Process
In MPC technique, a cost function is calculated for different switching state conditions of a system under study to find the most suitable voltage vector. In other words, for all feasible switching state conditions, the cost function is computed, and then, the one that minimizes a pre-defined cost function is selected and applied during the next sampling time to the system. In this paper, the cost function is defined as the error between the prediction and the reference. In the three-phase control scheme, the cost functions are evaluated independently from the following equations:
Next, the optimization algorithm selects the optimal vector
Space Vector Phase-Shift PWM Technique
As mentioned in the previous section, the optimization algorithm evaluates all feasible switching states. SAPF based on 7-level CHB converters, consists of
Once the optimal voltage level has been selected, the PSPWM is carried out, which consists of three triangular carriers
where
Algorithm 1 Optimization algorithm of the proposed modulated MPC current controller.
Experimental Assessment
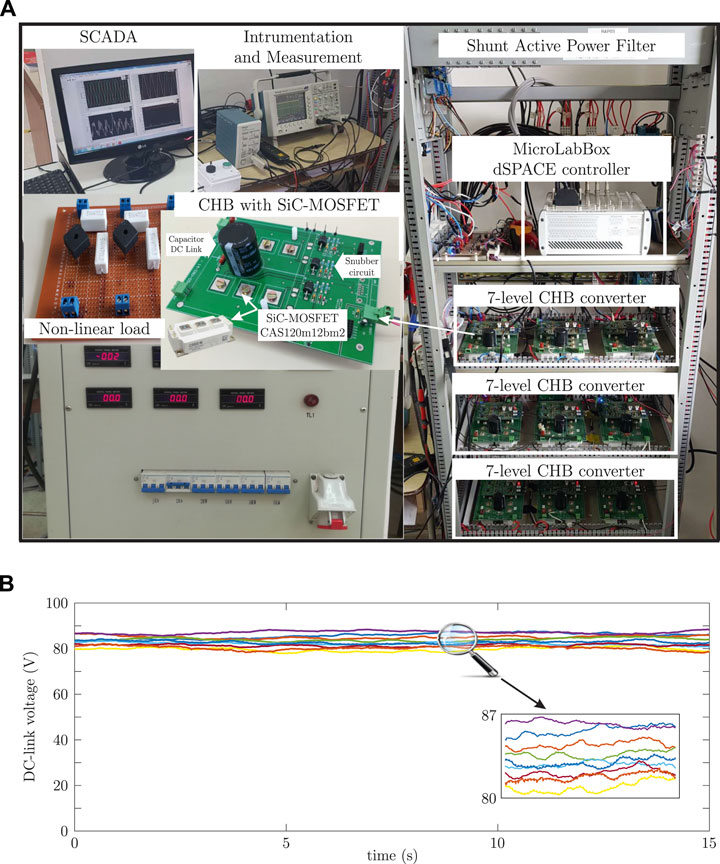
The DSPACE MicroLabBOX was used as controller in an experimental bench of SAPF based on 7-level CHB connected to a balanced power grid with a non-linear load. Each converter uses a SiC-MOSFET switching devices and a DC-link as shown in Figure 2. Then, to verify the performance of the proposed MPC technique, several experimental tests have been carried out using the following parameters:
First, the DC-link voltage regulation is analyzed. The PI control parameters are kp = 0.587 and ki = 0.293 5. So, to verify the PI control that acts on the load and balance of the DC-link voltages, the dynamic response of the voltages
Then, a dynamic analysis of the SAPF is performed. Figures 3A,B show the measured current
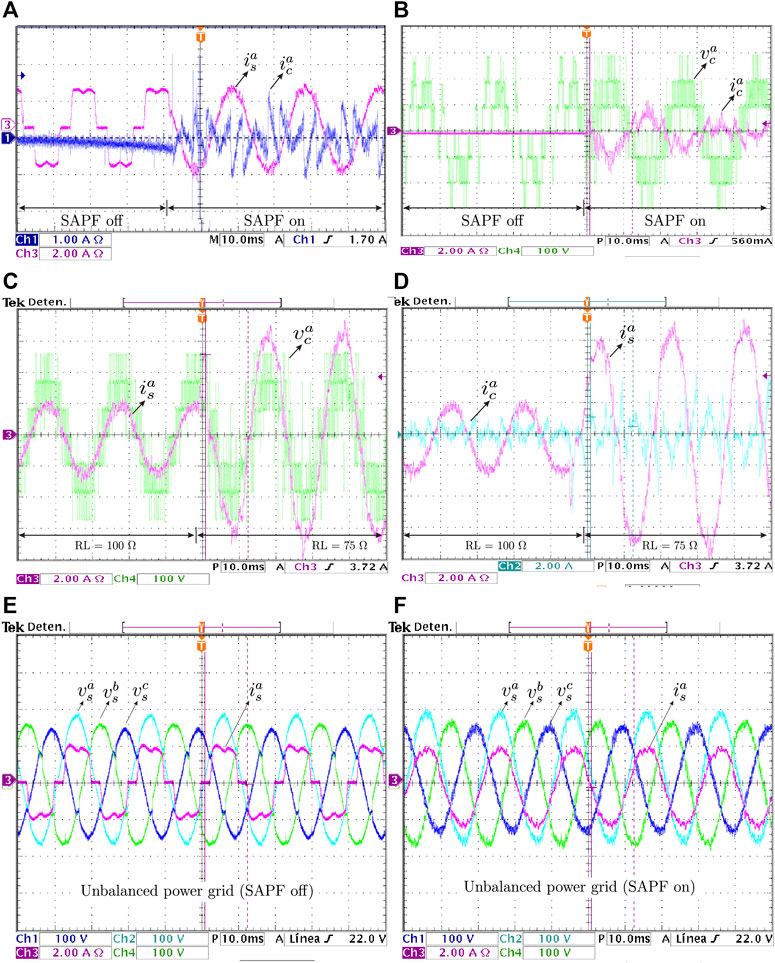
FIGURE 3. Transient behavior of SAPF (A) source current harmonics compensation, (B) voltage and current output of SAPF, (C) current
Last, the analysis of the Total Harmonic Distortion (THD) of the electrical grid current under two non-linear load conditions has been carried out. Figure 4A shows the uncompensated (SAPF off) electrical power grid currents
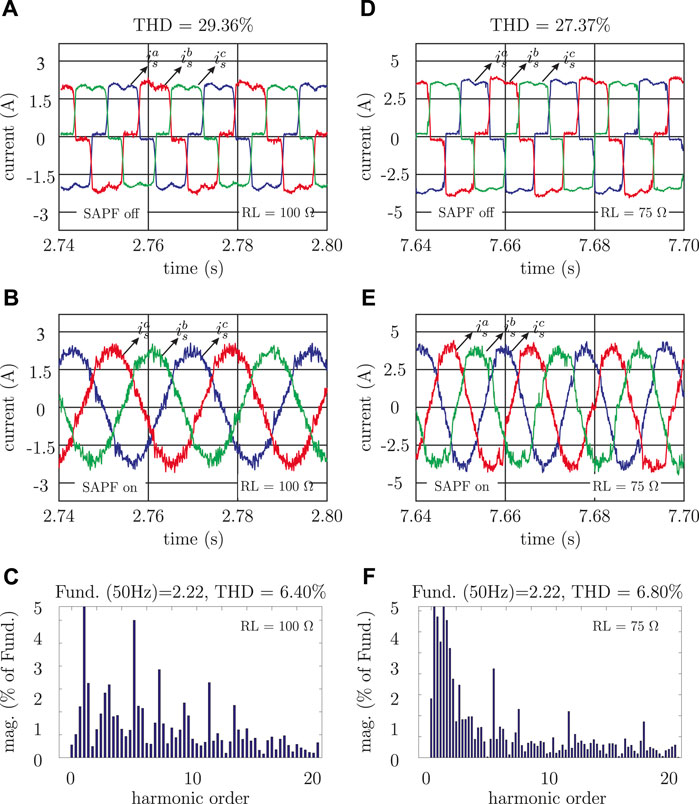
FIGURE 4. Experimental results of source current harmonics compensation at the grid side considering a non-linear load and three operation points. (A) Uncompensated grid current for RL = 100 Ω, (B) Compensated grid current for RL = 100 Ω, (C) THD level of compensated grid current for RL = 100 Ω. (D) Uncompensated grid current for RL = 75 Ω, (E) Compensated grid current for RL = 75 Ω, (F) THD level of compensated grid current for RL = 75 Ω.
Conclusion
This paper presented the real-time implementation of a model predictive current controller equipped with a modulation stage of a SAPF based on 7-level CHB converters, using SiC-MOSFET switching devices. The novel control scheme combines the concepts of model predictive control with the SV-PSPWM technique with the aim to reduce the computational burden. In addition, PI control is added to balance the DC-link voltages of the capacitors. The proposed control scheme has been validated experimentally. It has been shown that the proposed control can reduce 80% of THD caused by non-linear loads. Moreover, the robustness and effectiveness have been demonstrated under different operating points in both, in steady and transient conditions. Future works may include a comparative study of the proposed control schemes against classic control methods.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
AR conceived the idea for this paper. AR, JP and JR were responsible for the primary writing of the manuscript, while LC, MA and RG were responsible for revising the manuscript. All authors contributed to the article and approved the submitted version.
Funding
The Paraguayan Government supported this work through the CONACYT grant POSG16-05 and the PRONII program.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bosch, S., Staiger, J., and Steinhart, H. (2017). Predictive Current Control for an Active Power Filter with LCL-Filter. IEEE Trans. Ind. Electron. 65, 4943–4952.
Boukezata, B., Chaoui, A., Gaubert, J.-P., and Hachemi, M. (2017). “Implementation of Predictive Current Control for Shunt Active Power Filter,” in 2017 6th International Conference on Systems and Control (ICSC), 133–138. doi:10.1109/icosc.2017.7958726
Comparatore, L., Gregor, R., Rodas, J., Pacher, J., Renault, A., and Rivera, M. (2017). “Model Based Predictive Current Control for a Three-phase cascade H-Bridge Multilevel Statcom Operating at Fixed Switching Frequency,” in 2017 IEEE 8th International Symposium on Power Electronics for Distributed Generation Systems (PEDG) (Florianopolis, Brazil: IEEE), 1–6. doi:10.1109/pedg.2017.7972540
Das, S. R., Ray, P. K., Sahoo, A. K., Balasubramanian, K., and Reddy, G. S. (2020). Improvement of Power Quality in a Three-phase System Using an Adaline-Based Multilevel Inverter. Front. Energ. Res. 8, 23. doi:10.3389/fenrg.2020.00023
Ferreira, S. C., Gonzatti, R. B., Pereira, R. R., da Silva, C. H., da Silva, L. B., and Lambert-Torres, G. (2017). Finite Control Set Model Predictive Control for Dynamic Reactive Power Compensation with Hybrid Active Power Filters. IEEE Trans. Ind. Electron. 65, 2608–2617.
Gregor, R., Pacher, J., Espinoza, A., Renault, A., Comparatore, L., and Ayala, M. (2021). Harmonics Compensation by Using a Multi-Modular H-Bridge-Based Multilevel Converter. Energies 14, 4698. doi:10.3390/en14154698
Habibullin, M., Pikalov, V., Mescheryakov, V., and Valtchev, S. (2014). “Active Power Filter with Common Dc Link for Compensation of Harmonic Distortion in Power Grids,” in 2014 16th International Power Electronics and Motion Control Conference and Exposition, 1345–1349. doi:10.1109/EPEPEMC.2014.6980700
He, Y., Liu, Y., Lei, C., and Liu, J. (2020). Equivalent Space Vector Output of Diode Clamped Multilevel Inverters through Modulation Wave Decomposition under Carrier-Based PWM Strategy. IEEE Access 8, 104918–104932. doi:10.1109/access.2020.2999879
Hekmati, P., Brown, I., and Shen, Z. (2021). Open Circuit Switch Fault Detection in Flying Capacitor and Cascaded H-Bridge Multilevel Converters. IEEE Trans. Power Electron. 36, 12332–12341. doi:10.1109/tpel.2021.3078158
Irannezhad, F., Hosseinian, S. H., Abedi, M., and Vahidi, B. (2012). “Using the Instantaneous Power Theory in Order to Control the Current in the Parallel Active Filter to Compensate Reactive Power and Reduction of Harmonics,” in 2012 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), 1–5. doi:10.1109/PEDES.2012.6484390
Jia, G., Chen, M., Tang, S., Zhang, C., and Zhao, B. (2020). A Modular Multilevel Converter with Active Power Filter for Submodule Capacitor Voltage Ripples and Power Losses Reduction. IEEE Trans. Power Electron. 35, 11401–11417. doi:10.1109/tpel.2020.2982440
Jin, Q., Yao, Z., and Guo, M. (2020). “A Control Method of Shunt Active Power Filter for System-wide Harmonic Suppression Based on Complex-Valued Neural Network,” in 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), 1543–1548. doi:10.1109/IPEMC-ECCEAsia48364.2020.9368080
Li, W., Hu, J., Hu, S., Yang, H., Yang, H., and He, X. (2017). Capacitor Voltage Balance Control of Five-Level Modular Composited Converter with Hybrid Space Vector Modulation. IEEE Trans. Power Electron. 33, 5629–5640.
Li, Y., and Zhao, Y. (2020). A Virtual Space Vector Model Predictive Control for a Seven-Level Hybrid Multilevel Converter. IEEE Trans. Power Electron. 36, 3396–3407.
Li, Y., Zhou, Q., Mu, S., Zhang, T., Li, H., and Wang, J. (2021). A Sliding Mode Svpwm Method for a Hts Shunt Active Power Filter. IEEE Trans. Appl. Supercond. 31, 1–2. doi:10.1109/tasc.2021.3117746
Lin, H., Shu, Z., Yao, J., Yan, H., Zhu, L., Luo, D., et al. (2019). A Simplified 3-d Nlm-Based Svpwm Technique with Voltage-Balancing Capability for 3lnpc Cascaded Multilevel Converter. IEEE Trans. Power Electron. 35, 3506–3518.
Marzo, I., Sanchez-Ruiz, A., Barrena, J. A., Abad, G., and Muguruza, I. (2021). Power Balancing in Cascaded H-Bridge and Modular Multilevel Converters under Unbalanced Operation: A Review. IEEE Access. doi:10.1109/access.2021.3103337
Mishra, A. K., Das, S. R., Ray, P. K., Mallick, R. K., Mohanty, A., and Mishra, D. K. (2020). PSO-GWO Optimized Fractional Order PID Based Hybrid Shunt Active Power Filter for Power Quality Improvements. IEEE Access 8, 74497–74512. doi:10.1109/access.2020.2988611
Motta, L., and Faundes, N. (2016). “Active/Passive Harmonic Filters: Applications, Challenges & Trends,” in 2016 17th International Conference on Harmonics and Quality of Power (ICHQP), 657–662. doi:10.1109/ICHQP.2016.7783319
Pandurangan, R., Kaliannan, P., and Shanmugam, P. (2020). Effects of Current Distortion on Dc Link Inductor and Capacitor Lifetime in Variable Frequency Drive Connected to Grid with Active Harmonic Filter. IEEE Trans. Industry Appl. 57, 492–505.
Po-Ngam, S. (2014). “The Simplified Control of Three-phase Four-Leg Shunt Active Power Filter for Harmonics Mitigation, Load Balancing and Reactive Power Compensation,” in 2014 11th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), 1–6. doi:10.1109/ECTICon.2014.6839832
Qamar, M. A., Wang, K., Zheng, Z., Wang, S., and Li, Y. (2020). A Simplified Virtual Vector PWM Algorithm to Balance the Capacitor Voltages of Four-Level Diode-Clamped Converter. IEEE Access 8, 180896–180908. doi:10.1109/access.2020.3028444
Ramos, E. R., Leyva, R., G. Farivar, G., Tafti, H. D., Townsend, C. D., and Pou, J. (2020). Incremental Passivity Control in Multilevel Cascaded H-Bridge Converters. IEEE Trans. Power Electron. 35, 8766–8778. doi:10.1109/tpel.2020.2965164
Rao, B. N., Suresh, Y., Panda, A. K., Naik, B. S., and Jammala, V. (2020). Development of Cascaded Multilevel Inverter Based Active Power Filter with Reduced Transformers. Cpss Tpea 5, 147–157. doi:10.24295/cpsstpea.2020.00013
Ray, S., Gupta, N., and Gupta, R. A. (2017). “Advanced PWM for Balancing DC-link Voltages in Seven-Level Chb Inverter Based Active Filter,” in 2017 Recent Developments in Control, Automation Power Engineering (RDCAPE), 291–296. doi:10.1109/RDCAPE.2017.8358284
Rodas, J., Gonzalez-Prieto, I., Kali, Y., Saad, M., and Doval-Gandoy, J. (2021). Recent Advances in Model Predictive and Sliding Mode Current Control Techniques of Multiphase Induction Machines. Front. Energ. Res. 9, 445. doi:10.3389/fenrg.2021.729034
Ronanki, D., and Williamson, S. S. (2018). A Simplified Space Vector Pulse Width Modulation Implementation in Modular Multilevel Converters for Electric Ship Propulsion Systems. IEEE Trans. Transportation Electrification 5, 335–342.
Sohagh, K. S., Wang, L., Han, X., Qin, W., Zhang, D., and Meng, R. (2020). “Analysis of Id-Iq Strategy for Active Power Filter,” in 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), 722–725. doi:10.1109/iciea48937.2020.9248335
Tareen, W. U. K., and Mekhielf, S. (2017). Three-phase Transformerless Shunt Active Power Filter with Reduced Switch Count for Harmonic Compensation in Grid-Connected Applications. IEEE Trans. Power Electron. 33, 4868–4881.
Tarisciotti, L., Formentini, A., Gaeta, A., Degano, M., Zanchetta, P., Rabbeni, R., et al. (2016). Model Predictive Control for Shunt Active Filters with Fixed Switching Frequency. IEEE Trans. Industry Appl. 53, 296–304.
Wang, C., Zhong, Q.-C., Zhu, N., Chen, S.-Z., and Yang, X. (2020a). Space Vector Modulation in the 45°coordinates α β for Multilevel Converters. IEEE Trans. Power Electron. 36, 6525–6536.
Wang, J., Jin, J., Abu-Siada, A., and Zheng, L. (2020b). “Sliding Mode SVPWM Current Control for Shunt Active Power Filter,” in 2020 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD) (Tianjin, China: IEEE), 1–2. doi:10.1109/asemd49065.2020.9276260
Wong, M.-C., Pang, Y., Xiang, Z., Wang, L., and Lam, C.-S. (2020). Assessment of Active and Hybrid Power Filters under Space Vector Modulation. IEEE Trans. Power Electron. 36, 2947–2963.
Yang, J., Liu, Y., and Yan, R. (2021). A Comparison of Finite Control Set and Continuous Control Set Model Predictive Control Schemes for Model Parameter Mismatch in Three-phase Apf. Front. Energ. Res. 9, 404. doi:10.3389/fenrg.2021.727364
Yuan, X., Gao, Y., and Li, Y. (2020). A Fast Multilevel Svpwm Method Based on the Imaginary Coordinate with Direct Control of Redundant Vectors or Zero Sequence Components. IEEE Open J. Ind. Electron. Soc. 1, 355–366. doi:10.1109/ojies.2020.3044705
Keywords: model predictive control, harmonics compensation, multilevel power converter, shunt active power filter, space vector mudulation
Citation: Renault A, Pacher J, Comparatore L, Ayala M, Rodas J and Gregor R (2022) MPC with Space Vector Phase-Shift PWM (SV-PSPWM) Technique with Harmonic Mitigation Strategy for Shunt Active Power Filters Based on H-Bridge Multilevel Converter. Front. Energy Res. 10:779108. doi: 10.3389/fenrg.2022.779108
Received: 17 September 2021; Accepted: 03 January 2022;
Published: 24 January 2022.
Edited by:
Yuvaraja Teekaraman, Vrije University Brussel, BelgiumReviewed by:
Aravind C. K., Mepco Schlenk Engineering College, IndiaHamed Bizhani, University of Zanjan, Iran
Copyright © 2022 Renault, Pacher, Comparatore, Ayala, Rodas and Gregor. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alfredo Renault, YXJlbmF1bHRAaW5nLnVuYS5weQ==
 Alfredo Renault
Alfredo Renault Julio Pacher
Julio Pacher