An efficient capuchin search algorithm for extracting the parameters of different PV cells/modules

Constructing an equivalent circuit for the photovoltaic (PV) generating unit converging the real operation is a difficult process because of unavailability of some parameters. Many approaches have been conducted in this field; however, they have some problems in computational time and are stuck in local optima. Therefore, this study proposes a simple, robust, and efficient methodology-incorporated capuchin search algorithm (CapSA) to construct the equivalent circuit of the PV generating unit via identifying its parameters. The CapSA is selected as it is simple and requires less computational time in addition to exploration/exploitation balance that avoids local optima. The process is formulated as an optimization problem, which aims at minimizing the root mean square error (RMSE) between measured and simulated currents. A single-diode model (SDM), double-diode model (DDM), and three-diode model (TDM) of different PV cells and panels operating at either constant or variable weather conditions are constructed. A comparison to different programmed metaheuristic approaches is conducted. The best RMSE values obtained by the proposed CapSA are 2.27804E-04, 1.3808E-04, and 1.5182E-04 for SDM, DDM, and TDM of PVW 752 cell, respectively. For the KC200GT panel, the proposed approach achieved the best fitness values of 3.4440E-04, 1.5617E-03, and 6.6008E-03 at 25°C, 50°C, and 75°C, respectively. The obtained results confirmed the superiority and competence of the proposed CapSA in constructing a reliable equivalent circuit for the PV cell/panel.

1 Introduction

Recently, reliance on renewable energy sources (RESs) has gained great attention to preserve the environment from pollution and reduce global warming. Photovoltaic (PV) cells represent the most widespread renewable energy sources in the world. Although the initial cost of their establishment is high, they have very low operating costs as they do not have any mechanical parts. The PV cells are used to convert the solar radiation into direct electrical energy. The PV generating units are widely used in different applications, such as standalone, microgrids, and large grids with other generating units (Ibrahim et al., 2020; Jiao et al., 2020; Ginidi et al., 2021; Sattar et al., 2021). The PV panels consist of many cells that are connected to each other in series and parallel to obtain the current and voltage required, and the performance of the solar cell is affected by the change in temperature and the intensity of solar radiation (Long et al., 2021). The PV solar cell modeling has been carried out through the following steps: selecting the type of equivalent circuit, describing the equations of the selected model, and identifying the optimal parameters of the equivalent circuit. To improve the performance of solar cells, it is necessary to obtain the optimal values ​​of the parameters via analyzing the current–voltage curve and the type of model used (Said et al., 2021). Different models have been constructed for the PV cell, such as a single-diode model (SDM), which requires the definition of five parameters, double-diode model (DDM) with seven parameters to be estimated, and three-diode model (TDM) that involves nine parameters (Wang and Huang, 2018; Premkumar et al., 2021b). The diode reverse saturation current has been considered as the initial parameter employed in calculating the SDM (Şentürk, 2018). Many numerical methods have been conducted to estimate the parameters of the solar cell equivalent circuit, and the Lambert W function has been presented to compute the parameters of the SDM (Ćalasan et al., 2020). Linear least square was used to identify the PV panel parameters using two steps (Reddy and Yammani, 2021). The Newton–Raphson’s maximum likelihood approach has been used to construct the PV cell SDM equivalent circuit via extracting the unknown parameters (Ayang et al., 2019). An iterative approach with two steps has been employed to calculate the SDM parameters using the panel datasheet; the first step was determining the diode ideality factor, and the second step was estimating the model shunt resistance (Stornelli et al., 2019). Many optimization approaches have been applied to extract the parameters of the PV cells/modules, such as drone squadron optimization incorporated with the Newton–Raphson approach, which has been applied with six states of polycrystalline and monocrystalline SDM and DDM; moreover, one state under different operation condition has been investigated (Gnetchejo et al., 2021). A hybrid approach of whale optimization (WO) and particle swarm optimization (PSO) has been presented to solve the problem of evaluating the unknown parameters for both SDM and DDM for the PV panel (Sharma et al., 2021). A stochastic fractal search optimization (SFSO) has been applied to determine the SDM and DDM circuits’ parameters with experimental data of the ESP-160 PPW PV panel (Rezk et al., 2021). An improved grasshopper optimization algorithm (GOA) with lévy flight has been used to obtain the parameters of SDM and DDM for RTC and sharp ND-R250A5 PV panels under different temperatures and solar irradiances (Mokeddem, 2021). Different types of PV modules with SDM, DDM, and TDM circuits have been analyzed at various operating conditions with the aid of an artificial ecosystem optimizer (AEO) (Yousri et al., 2020). A gradient-based optimizer (GBO) (Ismaeel et al., 2021), enhanced GOA by metaphor free with ranking mechanisms (Ahmadianfar et al., 2021), improved GOA with opposition (Premkumar et al., 2021a), and enhanced GBO algorithm by chaotic drifts (Premkumar et al., 2021b) have been applied to identify the parameters of different PV cells/modules under different operating conditions. A turbulent flow of water optimizer (TFWO) has been used to estimate the PV equivalent circuit parameters (Abdelminaam et al., 2021; Said et al., 2021). Moreover, bald eagle search (BES) (Nicaire et al., 2021), improved BES (Ramadan et al., 2021a), hybrid grey wolf and cuckoo search (HGWOCS) (Long et al., 2020a), artificial bee colony (ABC)-based teaching learning (Chen et al., 2018), gorilla troop optimizer (Ginidi et al., 2021), and the whale optimization algorithm-based refraction learning (Long et al., 2020b) have been employed to construct the SDM-based circuit of the PV panel. Furthermore, the JAYA algorithm was enhanced via guided JAYA, chaotic JAYA, and elite opposition JAYA and employed for estimating the parameters of the PV panels (Wang and Huang, 2018; Yu et al., 2019; Premkumar et al., 2021c). The TDM of the PV system has been presented with the Newton–Raphson approach and the LSHADE algorithm under different operation conditions (Bertalero et al., 2021). The problem of estimating optimal parameters of the PV unit equivalent circuit was presented and solved via generalized normal distribution optimization (GNDO) (Zhang et al., 2020), modified jellyfish search optimizer (MJSO) (Abdel-Basset et al., 2021), slime mould algorithm (SMA) (Mostafa et al., 2020), forensic-based investigation algorithm (FBIA) (Shaheen et al., 2021), and chaos game optimization algorithm (CGOA) (Ramadan et al., 2021b). A comprehensive study comprising 28 approaches employed in extracting the PV parameters has been presented in Yang et al. (2020), and a DDM-based circuit of the PV panel has been constructed with the aid of adaptive compass search (ACS) (Zeng et al., 2021). The equivalent circuit of different PV panels has been modeled using an improved equilibrium optimizer based on predictive output data by the back propagation neural network (Wang et al., 2021). An improved GBO with chaotic maps and self-adaptive weighting has been used to estimate the optimal parameters of the PV generating unit (Jiang et al., 2022). A hybrid sine–cosine algorithm (SCA) with differential GBO was introduced to estimate the PV parameters, whereas the differential evolution (DE) and SCA are used to avoid being stuck in local optima and get the global solution (Yu et al., 2022). An approach of hunger games search optimizer (HGSO) with mutation of Cauchy- and Gaussian-based improved Newton–Raphson method has been applied to build and analyze the TDM circuit of the PV panel (Premkumar et al., 2022).

Most reported approaches suffer from some limitations, such as falling in local optima, requiring large consumed time, complicated construction and execution, and requiring many controlling parameters defined by the user, and may cause divergence from the global solution.

These gaps are covered in this work by proposing a novel methodology-incorporated capuchin search algorithm (CapSA) to identify the unknown parameters of the PV cells/panels equivalent circuits. The CapSA is characterized by simplicity, acceptable computation time, and less controlling parameters, and these merits encourage the authors to use the approach to guarantee reliable equivalent circuit that matches to the actual operation. Moreover, a balance between the exploration and exploitation phases of the algorithm enables it to perform well and obtain efficient results.

The main contributions of this work can be summarized as follows:

1) A new approach of CapSA is proposed to extract the optimal parameters of the PV cells/panels equivalent circuits.

2) The proposed CapSA is applied to construct various SDM, DDM, and TDM circuits of the PV system.

3) Comparison to MVO, LAPO, SCA, TSA, EO, and HSA is conducted.

4) The robustness of the proposed CapSA is confirmed through the fetched results.

The article is outlined as follows: Section 2 describes the mathematical model of the PV module, Section 3 introduces the problem formulation, Section 4 clarifies the main principles of CapSA, Section 5 presents the simulation results, and conclusions are given in Section 6.

2 Mathematic model of the photovoltaic module

Three models of PV generating unit are examined: single, double, and three diodes (SDM, DDM, and TDM). These models are widely used to simulate the performance of the solar cell and the panel, and the PV models can be described as follows.

2.1 Single-diode model

In this model, the PV cell is simulated by a current source in parallel with a diode and a shunt resistance, and all are connected in series with a resistance, as shown in Figure 1 (a); the output current of the cell can be described by the following equations (Low and Soon, 2012; Fathy and Rezk, 2017):

$\mathit{I}={\mathit{I}}_{\mathit{g}}-{\mathit{I}}_{\mathit{d}}-{\mathit{I}}_{\mathit{s}\mathit{h}},(1)$

$\mathit{I}={\mathit{I}}_{\mathit{g}}-{\mathit{I}}_{\mathit{d}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+{\mathit{I}\mathit{R}}_{\mathit{s}}\right)}{\mathit{a}\mathit{k}\mathit{T}}-\mathbf{1}\right)\right)-\frac{\left(\mathit{V}+{\mathit{I}\mathit{R}}_{\mathit{s}}\right)}{{\mathit{R}}_{\mathit{s}\mathit{h}}}(2)$

where V, I_g, I_d, R_sh, and R_s are the output voltage, light generated current, diode reverse saturation current, shunt resistance, and series resistance, respectively; a is the ideality factor of the diode; q denotes the electron charge (q = 1.60217646 × 10⁻¹⁹ C); k is the constant of Boltzmann constant (k = 1.3806503 × 10⁻²³ J/K); and T indicates the temperature in Kelvin. The parameters to be identified in this model are a, R_s, R_sh, I_d, and I_g.

FIGURE 1

FIGURE 1. Equivalent circuits of the PV cell. (A) SDM, (B) DDM, and (C) TSM.

2.1.1 Double-diode model

The equivalent circuit of the DDM of the PV cell is shown in Figure 1 (b). In this model, a second diode is used to simulate the effects of recombination, whereas the first one represents the current of diffusion. The output current can be calculated as follows (Askarzadeh and Rezazadeh, 2013; Alam et al., 2015):

$\mathit{I}={\mathit{I}}_{\mathit{g}}-{\mathit{I}}_{\mathit{d}\mathbf{1}}-{\mathit{I}}_{\mathit{d}\mathbf{2}}-{\mathit{I}}_{\mathit{s}\mathit{h}},(3)$

$\mathit{I}={\mathit{I}}_{\mathit{g}}-{\mathit{I}}_{\mathit{d}\mathbf{1}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}\right)}{{\mathit{a}}_{\mathbf{1}}\mathit{k}\mathit{T}}\right)-\mathbf{1}\right)-{\mathit{I}}_{\mathit{d}\mathbf{2}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}\right)}{{\mathit{a}}_{\mathbf{2}}\mathit{k}\mathit{T}}\right)-\mathbf{1}\right)-\frac{\left(\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}\right)}{{\mathit{R}}_{\mathit{s}\mathit{h}}}(4)$

where I_d1 and I_d2 are the diodes’ reverse saturation currents, and a₁ and a₂ are the ideality factors of the diodes. The DDM has seven parameters to be estimated, which are a₁, a₂, R_s, R_sh, I_d1, I_d2, and I_g.

2.1.2 Three-diode model

The equivalent circuit of the TDM is shown in Figure 1 (c). The third diode is used to simulate the leakage current. The output current in such a model can be described as follows (Yousri et al., 2020):

$\mathit{I}={\mathit{I}}_{\mathit{g}}-{\mathit{I}}_{\mathit{d}\mathbf{1}}-{\mathit{I}}_{\mathit{d}\mathbf{2}}-{\mathit{I}}_{\mathit{d}\mathbf{3}}-{\mathit{I}}_{\mathit{s}\mathit{h}},(5)$

$\mathit{I}={\mathit{I}}_{\mathit{g}}-{\mathit{I}}_{\mathit{d}\mathbf{1}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}\right)}{{\mathit{a}}_{\mathbf{1}}\mathit{k}\mathit{T}}\right)-\mathbf{1}\right)-{\mathit{I}}_{\mathit{d}\mathbf{2}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}\right)}{{\mathit{a}}_{\mathbf{2}}\mathit{k}\mathit{T}}\right)-\mathbf{1}\right)-{\mathit{I}}_{\mathit{d}\mathbf{3}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}\right)}{{\mathit{a}}_{\mathbf{3}}\mathit{k}\mathit{T}}\right)-\mathbf{1}\right)-\frac{\left(\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}\right)}{{\mathit{R}}_{\mathit{s}\mathit{h}}},(6)$

where I_d3 and a₃ are the third diode reverse saturation current and its ideality factor. It is noticeable that Eq. 6 contains nine parameters to be identified: a₁, a₂, a₃, R_s, R_sh, I_d1, I_d2, I_d3, and I_g.

3 Problem formulation

Estimating the parameters of the PV equivalent circuit is formulated as an optimization problem, and the considered fitness function to be minimized is root mean square error (RMSE) between the measured and simulated currents. The undefined parameters represent the design variables in the formulated optimization problem. The main target is constructing a reliable circuit with confident I–V curves that converge to the experimental data (Ram et al., 2017; Yu et al., 2018; El-Fergany, 2021). The fitness function can be written as follows:

$\mathit{R}\mathit{M}\mathit{S}{\mathit{E}}_{\mathit{P}\mathit{V}}=\sqrt{\frac{\mathbf{1}}{\mathit{N}}{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\mathit{f}}_{\mathit{P}\mathit{V}}{\left(\mathit{V},\mathit{I},\mathit{x}\right)}^{\mathbf{2}}}=\sqrt{\frac{\mathbf{1}}{\mathit{N}}{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\left({\mathit{I}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}}-{\mathit{I}}_{\mathbf{s}\mathbf{i}\mathbf{m}}\right)}^{\mathbf{2}}},(7)$

where f_PV denotes the function of PV unit, N denotes the nuebr of measured data, I_meas is the measured current, and I_sim indicates the simulated current.

3.1 Fitness function of the single-diode model

The fitness function employed to construct the SDM-based circuit of the PV system can be described as follows:

${\mathit{f}}_{\mathit{S}\mathit{D}\mathit{M}}\left(\mathit{V},\mathit{I},\mathit{x}\right)=\mathit{I}-{\mathit{x}}_{\mathbf{5}}+{\mathit{x}}_{\mathbf{4}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+\mathit{I}{\mathit{x}}_{\mathbf{2}}\right)}{{\mathit{x}}_{\mathbf{1}}\mathit{k}\mathit{T}}-\mathbf{1}\right)\right)+\frac{\left(\mathit{V}+\mathit{I}{\mathit{x}}_{\mathbf{2}}\right)}{{\mathit{x}}_{\mathbf{3}}}(8)$

where x is a vector of design variables (a, R_s, R_sh, I_d, and I_g).

3.2 Fitness function of the double-diode model

In DDM, the considered fitness function is written as follows:

${\mathit{f}}_{\mathit{D}\mathit{D}\mathit{M}}\left(\mathit{V},\mathit{I},\mathit{x}\right)=\mathit{I}-{\mathit{x}}_{\mathbf{7}}+{\mathit{x}}_{\mathbf{5}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+\mathit{I}{\mathit{x}}_{\mathbf{3}}\right)}{{\mathit{x}}_{\mathbf{1}}\mathit{k}\mathit{T}}\right)-\mathbf{1}\right)+{\mathit{x}}_{\mathbf{6}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+{\mathit{I}\mathit{x}}_{\mathbf{3}}\right)}{{\mathit{x}}_{\mathbf{2}}\mathit{k}\mathit{T}}\right)-\mathbf{1}\right)+\frac{\left(\mathit{V}+\mathit{I}{\mathit{x}}_{\mathbf{3}}\right)}{{\mathit{x}}_{\mathbf{4}}},(9)$

where x includes seven parameters: a₁, a₂, R_s, R_sh, I_d1, I_d2, and I_g.

3.3 Fitness function of the three-diode model

In such a model, nine parameters (a₁, a₂, a₃, R_s, R_sh, I_d1, I_d2, I_d3, and I_g) represent the design variables, and they are introduced as x vector; the fitness function considered in such model can be given as follows:

${\mathit{f}}_{\mathit{T}\mathit{D}\mathit{M}}\left(\mathit{V},\mathit{I},\mathit{x}\right)=\mathit{I}-{\mathit{x}}_{\mathbf{9}}+{\mathit{x}}_{\mathbf{6}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+{\mathit{I}\mathit{x}}_{\mathbf{4}}\right)}{{\mathit{x}}_{\mathbf{1}}\mathit{k}\mathit{T}}\right)-\mathbf{1}\right)+{\mathit{x}}_{\mathbf{7}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+\mathit{I}{\mathit{x}}_{\mathbf{4}}\right)}{{\mathit{x}}_{\mathbf{2}}\mathit{k}\mathit{T}}\right)-\mathbf{1}\right)+{\mathit{x}}_{\mathbf{8}}\left(\mathit{exp}\left(\frac{\mathit{q}\left(\mathit{V}+\mathit{I}{\mathit{x}}_{\mathbf{4}}\right)}{{\mathit{x}}_{\mathbf{3}}\mathit{k}\mathit{T}}\right)-\mathbf{1}\right)+\frac{\left(\mathit{V}+{\mathit{I}\mathit{x}}_{\mathbf{4}}\right)}{{\mathit{x}}_{\mathbf{5}}}.(10)$

4 Capuchin search algorithm

The capuchin search algorithm (CapSA) is a novel optimizer that mimics the foraging behavior of the capuchins for searching the food resources over the branches of trees and riverbanks (Braik et al., 2021). During the foraging process, capuchins leap, climb, and swing to search for food. They are social animals that move in the forest as family, where they are live in groups with adult female, male, and small apes. Capuchins’ movements in the forest to find the most abundant food location simulate the global search optimization algorithms. In the foraging, they interact with their leader and with each other by calling, barking, and postures. CapSA can be modeled based on three mechanisms of the motion, as follows.

4.1 Leaping motion

Capuchins move long distances over trees to find and discover food resources; this is similar to the global search mechanism. Here, movement of the capuchins between tress looks like the projectile motion, which can be expressed by the third law of motion, as follows:

${\mathit{x}}_{\mathit{m}}={\mathit{x}}_{\mathbf{0}}+{\mathit{v}}_{\mathbf{0}}\mathit{t}+\frac{\mathbf{1}}{\mathbf{2}}\mathit{a}{\mathit{t}}^{\mathbf{2}},(11)$

where $x_m$, $x_0$, $v_0$, and $t$ are the capuchin new location, initial location, initial speed, and time, respectively. This equation can be modified as follows:

${\mathit{x}}_{\mathit{m}}={\mathit{x}}_{\mathbf{0}}+{\mathit{v}}_{\mathbf{0}}^{\mathbf{2}}\mathbf{sin}\left(\mathbf{2}{\mathit{\theta }}_{\mathbf{0}}\right)/\mathit{g}(12)$

where $g$ denotes the gravitational acceleration and ${\theta }_0$ denotes leaping angle.

4.1.1 Swinging motion

Capuchins wobble on branches of the trees in the foraging process; this action simulates the pendulum motion. This motion mimics the local search phase, and it can be described as follows:

$\mathit{x}=\mathit{L}\mathbf{sin}\mathit{\theta },(13)$

where $L$ is the length of tail and $\theta$ denotes the swing angle of capuchin.

4.1.2 Climbing motion

The capuchins climb to the trees for searching the food resources, and this motion mimics the local searching process in the optimization approach. The climbing motion is described as follows:

${\mathit{x}}_{\mathit{m}}={\mathit{x}}_{\mathbf{0}}+{\mathit{v}}_{\mathbf{0}}\mathit{t}+\mathbf{0.5}\left(\mathit{v}-{\mathit{v}}_{\mathbf{0}}\right){\mathit{t}}^{\mathbf{2}}.(14)$

The initial locations of the capuchins can be calculated as follows:

${\mathit{X}}^{\mathit{i}}={\mathit{X}}^{\mathit{L}\mathit{b}}+\left({\mathit{X}}^{\mathit{U}\mathit{b}}-{\mathit{X}}^{\mathit{L}\mathit{b}}\right)\times \mathit{r}\mathit{a}\mathit{n}\mathit{d},(15)$

where $X^{Lb}$ is the lower limit of the control variable while $X^{Ub}$ is its upper limit and $rand$ is a random number within [0, 1]. The group of the capuchin has two types of the populations: the leader or the alpha and the followers. Both of them search food resource, denoted as $F$. Other capuchins may also join the leader in the foraging behavior and pursue similar locomotion behavior. The leader jumps between the branches to find the source food, and this can be expressed as follows:

${\mathit{X}}^{\mathit{i}}=\mathit{F}+\frac{{\mathit{P}}_{\mathit{b}\mathit{f}}{\left({\mathit{v}}^{\mathit{i}}\right)}^{\mathbf{2}}\mathit{sin}\left(\mathbf{2}{\mathit{\theta }}_{\mathit{j}}\right)}{\mathit{g}},\mathit{i}<\frac{\mathit{n}}{\mathbf{2}};\mathbf{0.1}<\mathit{\epsilon }\le \mathbf{0.2},(16)$

where $P_{bf}$ is the probability of the balance provided by the capuchins tail, $\epsilon$ is a random number, and ${\theta }_j$ deotes the capuchin’s jumbing angle, which is given as follows:

${\theta }_j=\frac{\mathbf{3}}{\mathbf{2}}\mathit{r},(17)$

where $r$ is a random value within [0, 1]. To achieve balance between exploration and exploitation of the CapSA, an operator (τ) represents the life time of the CapSA, and it can cause balance between the global and local searching phases; this operator can be calculated as follows:

$\mathit{\tau }={\mathit{\beta }}_{\mathbf{0}}{\mathit{e}}^{-{\mathit{\beta }}_{\mathbf{1}}{\left(\frac{\mathit{I}\mathit{t}\mathit{e}\mathit{r}}{\mathit{max}\_\mathit{I}\mathit{t}\mathit{e}\mathit{r}}\right)}^{{\mathit{\beta }}_{\mathbf{2}}}},(18)$

where $Iter$ denotes the current iteration while $\mathit{max}\_Iter$ is the maximum number of iterations; ${\beta }_0$, ${\beta }_1$, and ${\beta }_2$ are random numbers with values of 2, 21, and 2, respectively. The velocity of the capuchin can be calculated as follows:

${\mathit{v}}^{\mathit{i}}=\mathit{\rho }{\mathit{X}}^{\mathit{i}}+\mathit{\tau }{\mathit{a}}_{\mathbf{1}}\left({\mathit{X}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}^{\mathit{i}}-{\mathit{X}}^{\mathit{i}}\right){\mathit{r}}_{\mathbf{1}}+\mathit{\tau }{\mathit{a}}_{\mathbf{2}}\left(\mathit{F}-{\mathit{X}}^{\mathit{i}}\right){\mathit{r}}_{\mathbf{2}},(19)$

where $X_{best}^i$ represents the best location of the ith capuchin, $a_1$ and $a_2$ are two positive values that control the effects of $F$ and $X_{best}^i$ on the velocity, $r_1$ and $r_2$ are random numbers in [0, 1], and $\rho$ is an inertia coefficient equal to 0.7. The alpha capuchin can jump on wide areas to find food resources when the food on trees decreases. The leader and the other capuchins’ motions can be represented as follows:

${\mathit{X}}^{\mathit{i}}=\mathit{F}+\frac{{\mathit{P}}_{\mathit{e}\mathit{f}}{\mathit{P}}_{\mathit{b}\mathit{f}}{\left({\mathit{v}}^{\mathit{i}}\right)}^{\mathbf{2}}\mathit{sin}\left(\mathbf{2}\mathit{\theta }\right)}{\mathit{g}},\mathit{i}<\raisebox{1ex}{$\mathit{n}$}\!\left/ \!\raisebox{-1ex}{$\mathbf{2}$}\right.;\mathbf{0.2}<\mathit{\epsilon }\le \mathbf{0.3}(20)$

where $P_{ef}$ is the probability movement of the capuchins on the ground. The motion of the alpha leader on the ground can be expressed as follows:

${\mathit{X}}^{\mathit{i}}={\mathit{X}}^{\mathit{i}}+{\mathit{v}}^{\mathit{i}},\mathit{i}<\raisebox{1ex}{$\mathit{n}$}\!\left/ \!\raisebox{-1ex}{$\mathbf{2}$}\right.;\mathbf{0.3}<\mathit{\epsilon }\le \mathbf{0.5}(21)$

The swinging of the capuchins and alpha leader on the trees branches searching the food in the local region can be expressed as follows:

${\mathit{X}}^{\mathit{i}}=\mathit{F}+\mathit{\tau }{\mathit{P}}_{\mathit{b}\mathit{f}},\mathit{i}<\raisebox{1ex}{$\mathit{n}$}\!\left/ \!\raisebox{-1ex}{$\mathbf{2}$}\right.;\mathbf{0.5}<\mathit{\epsilon }\le \mathbf{0.75}(22)$

Some capuchins and the alpha leader climb the trees and fall several times to find the food as local search, and this can be expressed as follows:

${\mathit{X}}_{\mathit{j}}^{\mathit{i}}={\mathit{F}}_{\mathit{j}}+\mathit{\tau }{\mathit{P}}_{\mathit{b}\mathit{f}}\left({\mathit{v}}_{\mathit{j}}^{\mathit{i}}-{\mathit{v}}_{\mathit{j}-\mathbf{1}}^{\mathit{i}}\right),\mathit{i}<\raisebox{1ex}{$\mathit{n}$}\!\left/ \!\raisebox{-1ex}{$\mathbf{2}$}\right.;\mathbf{0.75}<\mathit{\epsilon }\le \mathbf{1.0}(23)$

Capuchins also move randomly to explore new areas, which is known as the random relocation of the capuchins, and this can be mathematically described as follows:

${\mathit{X}}^{\mathit{i}}=\mathit{\tau }\times \left[{\mathit{X}}^{\mathit{L}\mathit{b}}+\mathit{\epsilon }\times \left({\mathit{X}}^{\mathit{U}\mathit{b}}-{\mathit{X}}^{\mathit{L}\mathit{b}}\right)\right],\mathit{i}<\raisebox{1ex}{$\mathit{n}$}\!\left/ \!\raisebox{-1ex}{$\mathbf{2}$}\right.;\mathit{\epsilon }\le {\mathit{P}}_{\mathit{r}},(24)$

where $P_r$ is a constant equal to 0.1. The behavior of the followers update their locations with respect to their leader according to the following equation.

${\mathit{X}}_{\mathit{j}}^{\mathit{i}}=\frac{\mathbf{1}}{\mathbf{2}}\left({\mathit{X}\mathit{L}}_{\mathit{j}}^{\mathit{i}}+{\mathit{X}}_{\mathit{j}}^{\mathit{i}-\mathbf{1}}\right),\frac{\mathit{n}}{\mathbf{2}}\le \mathit{i}\le \mathit{n},(25)$

where ${XL}_j^i$and $X_j^{i-1}$ are the leader location and the previous location of follower, respectively. The application of the capuchin search algorithm to estimate the optimal parameters of the PV panel equivalent circuit is depicted in Figure 2.

FIGURE 2

FIGURE 2. Flow chart of the proposed CapSA.

5 Simulation and results

In this work, the CapSA approach is used to determine the parameters of different PV models. The parameters are identified for SDM, DDM, and TDM models of R.T.C France, PVM752, PWP-201, STM6-40/36, and STP6-120/36 operated at standard test conditions (STCs). On the other hand, the DDM-based circuit of the KC200GT PV module is constructed and investigated under different temperatures and solar irradiances. The fetched results via the proposed CapSA are compared to MVO, LAPO, SCA, TSA, EO, and HAS. The considered algorithms are executed for 30 independent runs with controlling parameters of 10,000 maximum iteration and a population size of 50 (Pourmousa et al., 2019). The algorithm is executed for 30 independent runs to minimize the effect of random numbers considered in the algorithm. However, the run with the minimum fitness value is selected as the optimal result. The upper and lower bounds (Ub and Lb) of the identified parameters for different PV cells/panels are presented in Table 1. The measured data of I–V for the considered PV cells/panels are shown in Supplementary Table S1, where the number of samples for R.T.C France is 26; PVM752 is 44; whereas the number of patterns for PWP-201, STM6-40/36, and STP6-120/36 are 25, 20, and 24, respectively. Finally, the number of measured patterns for KC200GT is 15 samples.

TABLE 1

TABLE 1. Lower and upper bounds of different PV cells/panels.

5.1 Case 1: Photovoltaic cells

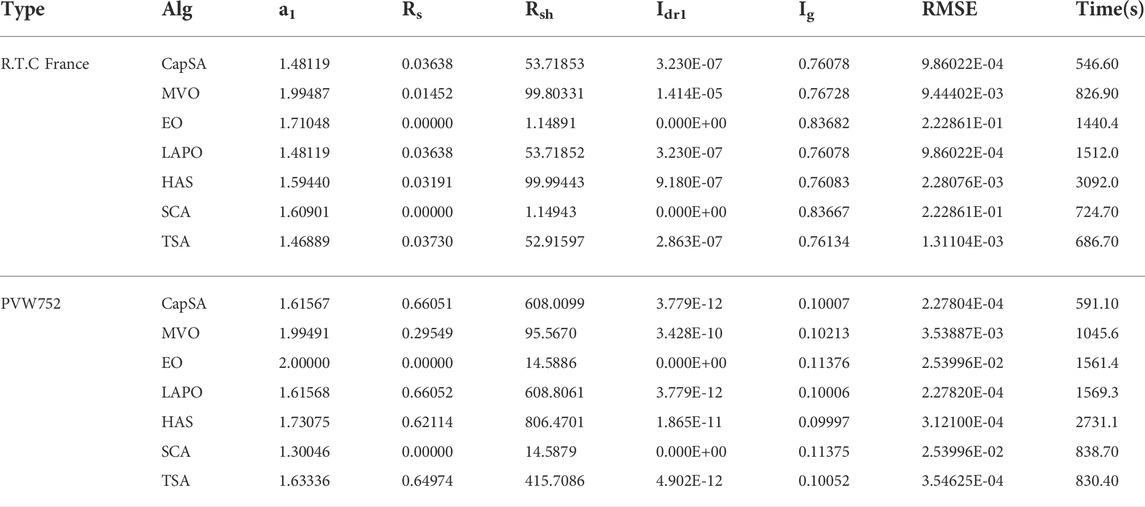
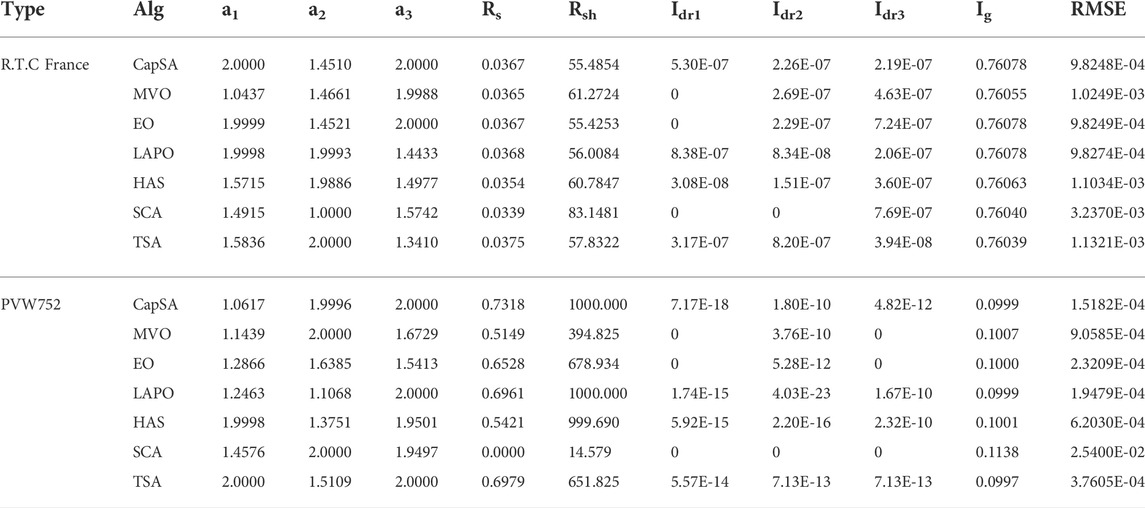
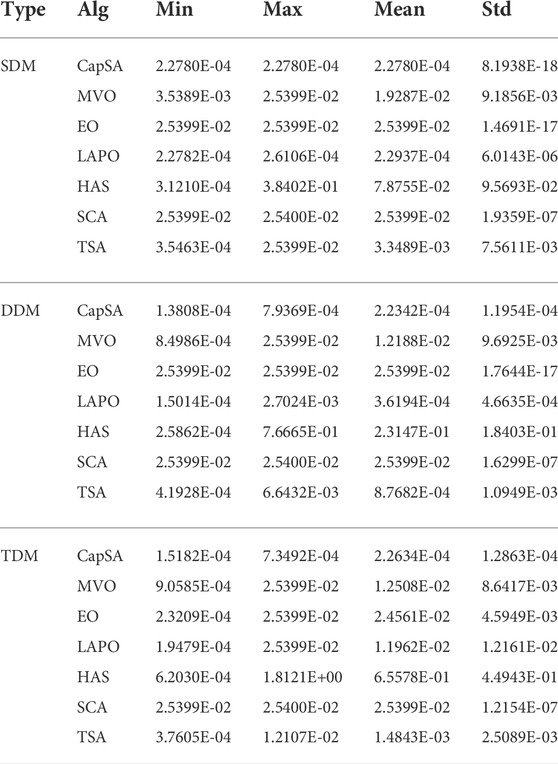
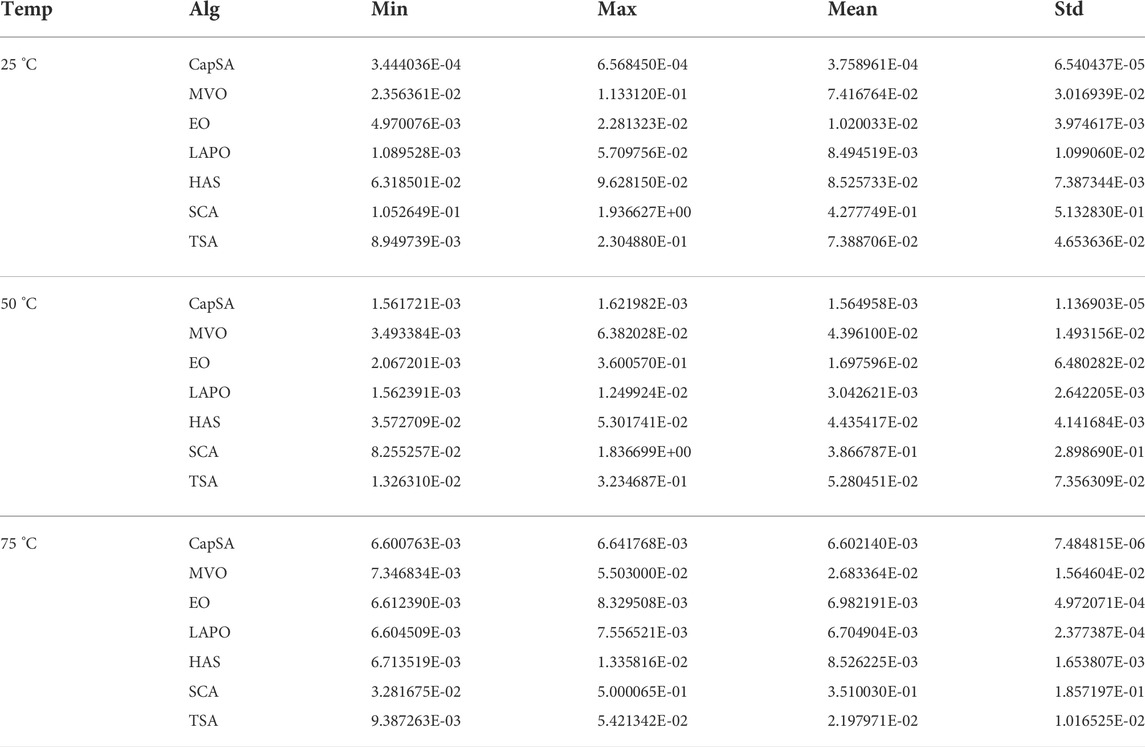
The proposed CapSA is employed to extract the unknown parameters of SDM, DDM, and TDM for the R.T.C France PV cell operated at 33°C and 1000W/m² and the PVM752 GaAs thin film cell at 25°C and 1000W/m². The measured data of I–V and the cell electric characteristics are given in Gao et al. (2018), Rezaee Jordehi (20180, Yu et al. (2018), Yousri et al. (2020), and Lekouaghet et al. (2021). Table 2 illustrates the optimum parameters and the RMSE value of SDM obtained via the proposed CapSA in comparison to other algorithms. The CapSA and LAPO approaches achieved the lowest RMSE value of 9.86022E-04 for the R.T.C France PV cell, whereas the minimum RMSE value of 2.27804E-04 for the PVW752 cell is obtained by a CapSA optimizer. The optimal parameters of DDM obtained via the proposed CapSA and others are tabulated in Table 3, and the R.T.C France minimum RMSE value of 9.8248E-04 is obtained by the proposed CapSA. Regarding to the DDM of PVW752 cell, the proposed CapSA comes in the first rank achieving the least RMSE value of 1.3808E-04, whereas the LAPO comes in the second rank with RMSE of 1.5014E-04. Regarding the computational time given in Table 2, the proposed approach achieved the best consumed time of 546.60 s and 591.10 s during establishing the SDM circuit for R.T.C France and PVW752 PV cells, respectively. TSA came second consuming 686.70 s and 830.0 s for both cells, respectively. On the other hand, the HAS had the longest computational time of 686.70 s and 2731.1 s for the two mentioned cells. Moreover, the proposed CapSA outperformed the others in term of computational time during establishing the DDM-based circuit. Moreover, Table 4 presents the parameters of the TDM-based circuit constructed via CapSA, MVO, LAPO, SCA, TSA, EO, and HAS. The results presented in Table 4 clarified that the lowest RMSE value of 9.8248E-04 is obtained by the proposed CapSA, whereas the worst RMSE value of 3.2370E-03 is obtained via SCA for the R.T.C France PV cell. In case of constructing the TDM for the PVW752 cell, the best obtained RMSE value is 1.5182E-04, which is achieved by the proposed approach. The measured and estimated I–V and P–V curves of SDM, DDM, and TDM for R.T.C France and PVW752 PV cells obtained via the proposed CapSA are given in Figure 3. The convergence curves of the fitness functions obtained via the considered optimizers employed in estimating the SDM parameters of R.T.C France and PVW752 cells are presented in Figure 5. The CapSA achieved the least consumed time to identify the PV parameters during the considered number of runs for SDM and DDM of R.T.C of 546.65s and 605.3 s respectively, while SDM and DDM of PVM752 of 591.15 s and 676.3 s, the HAS approach is the longest one in the term of computational time as it required 3092.0 s. The statistical parameters including the minimum, maximum, mean, and standard deviation (Std) are displayed in Table 5 for the PVW752 cell. Regarding the fetched statistical results for the PVM752 PV cell, the proposed CapSA succeeded in achieving the least standard deviations of 8.1938E-18 in constructing the SDM-based circuit. Moreover, it succeeded in achieving the best minimum fitness values for all studied models. The obtained results reveal that the proposed CapSA is the best approach in estimating the optimal parameters of different models for the R.T.C France and PVW752 cells compared to the others considered approaches.

TABLE 2

TABLE 2. SDM optimal parameters of R.T.C France and PVW752 PV cells.

TABLE 3

TABLE 3. DDM optimal parameters of R.T.C France and PVW752 PV cells.

TABLE 4

TABLE 4. TDM optimal parameters of R.T.C France and PVW752 PV cells.

FIGURE 3

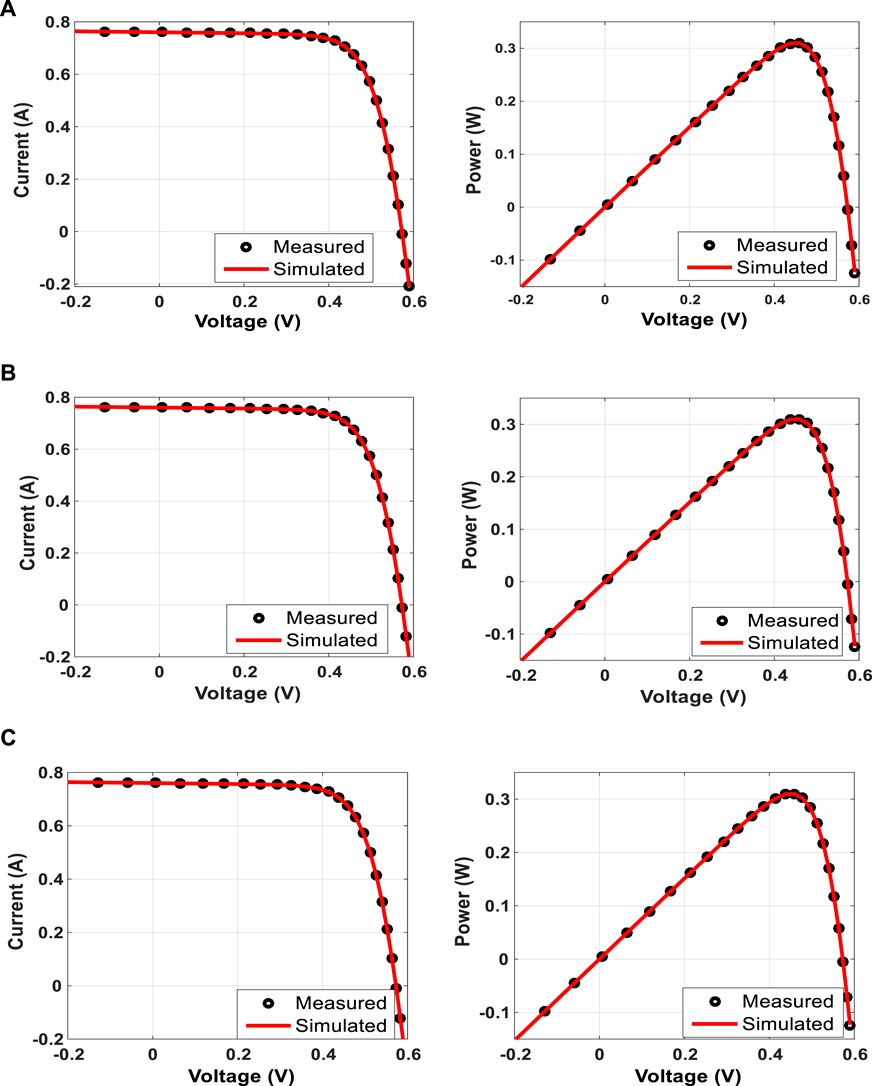
FIGURE 3. Measured and simulated curves obtained via CapSA for the R.T.C France PV cell. (A) SDM, (B) DDM, and (C) TDM.

FIGURE 4

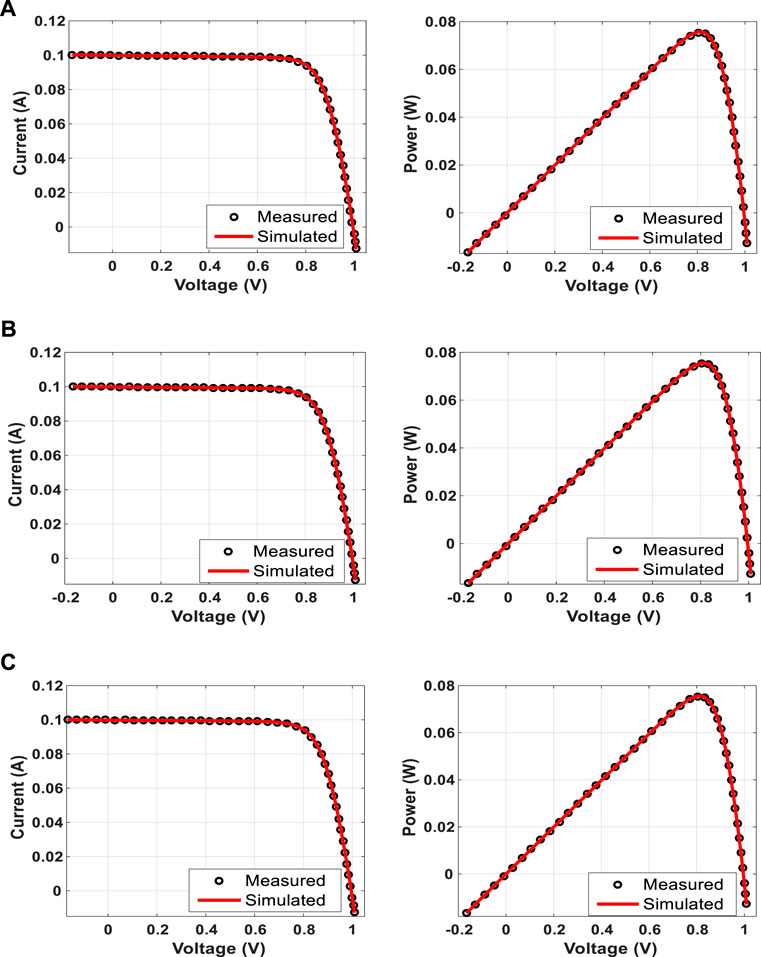
FIGURE 4. Measured and simulated I–V and P–V curves of the PVM752 cell. (A) SDM, (B) DDM, and (C) TDM.

FIGURE 5

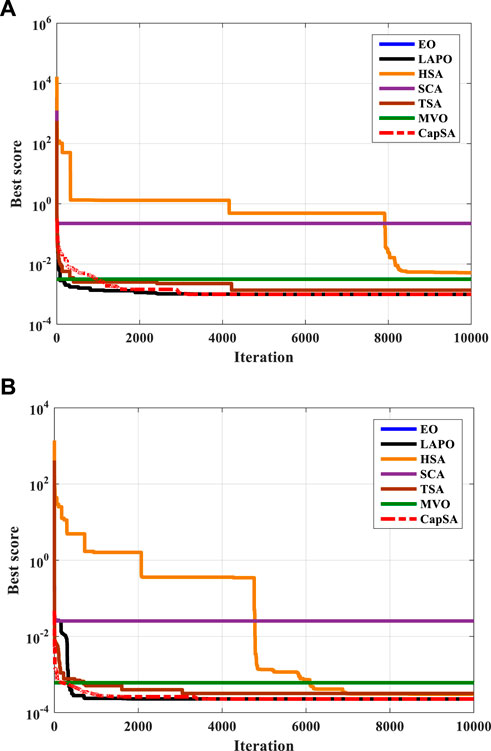
FIGURE 5. Convergence curves of the fitness function obtained via different optimizers. (A) R.T.C France cell and (B) PVW752 cell.

TABLE 5

TABLE 5. Statistical parameters of the approaches applied to PVM752 PV cell.

5.2 Case 2: Photovoltaic panel operation at constant weather conditions

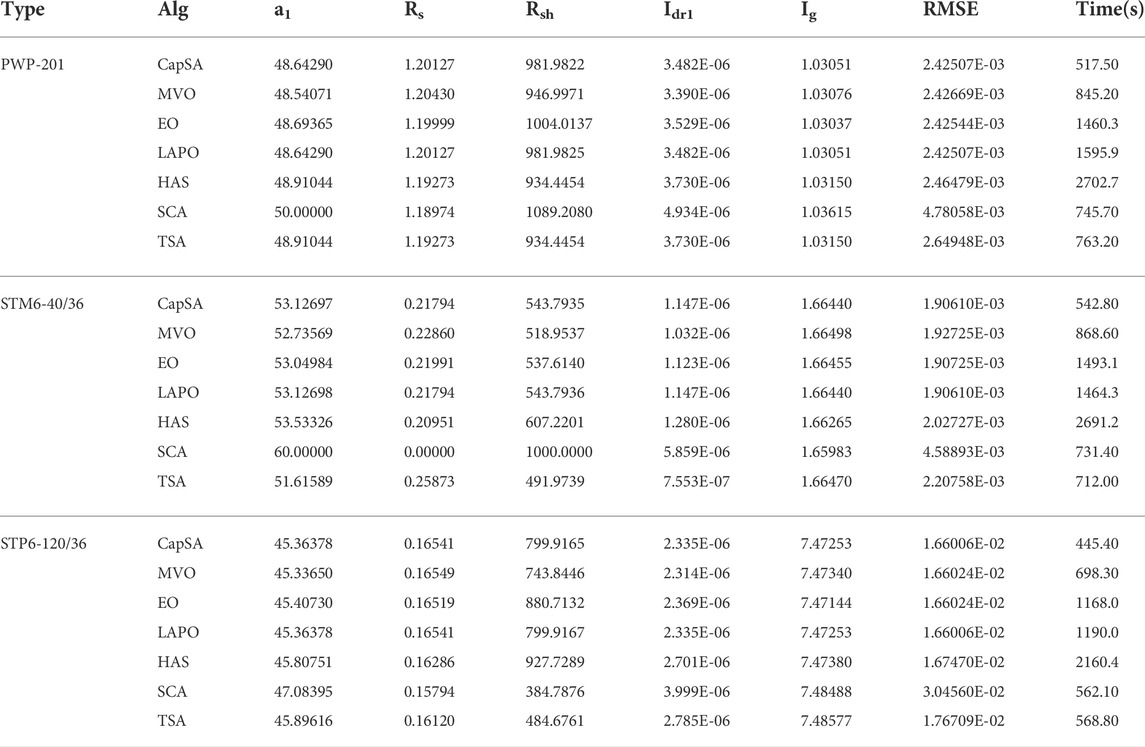
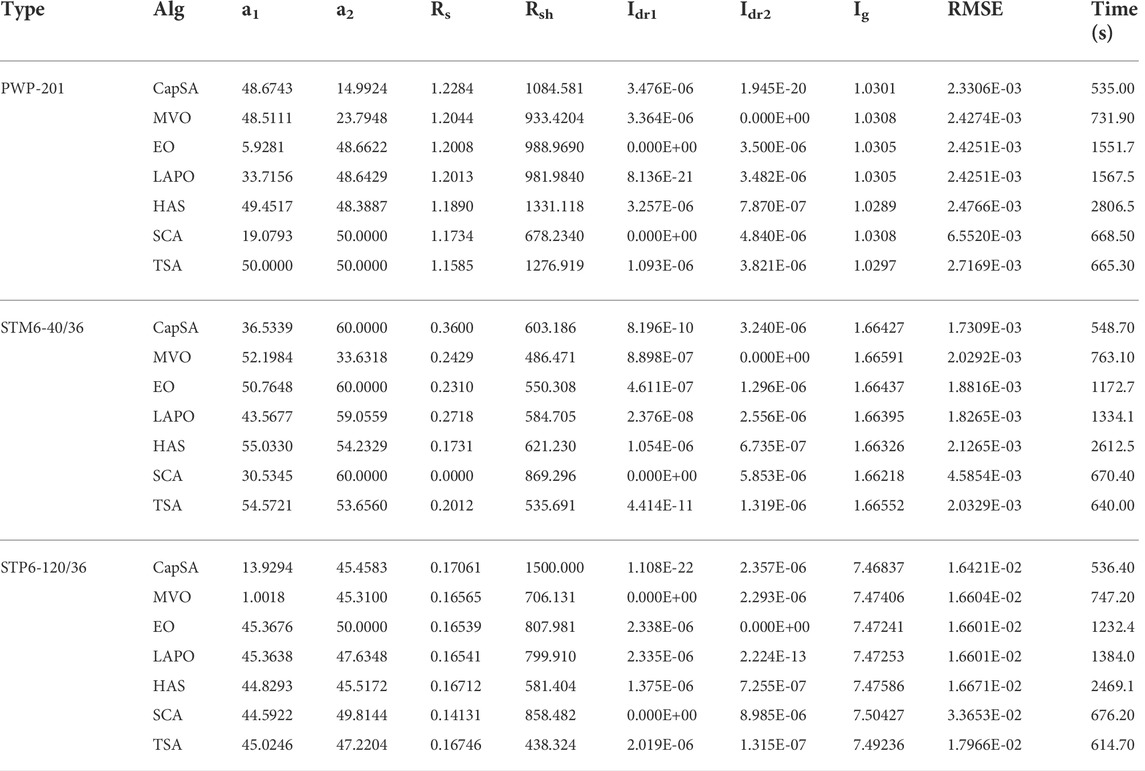
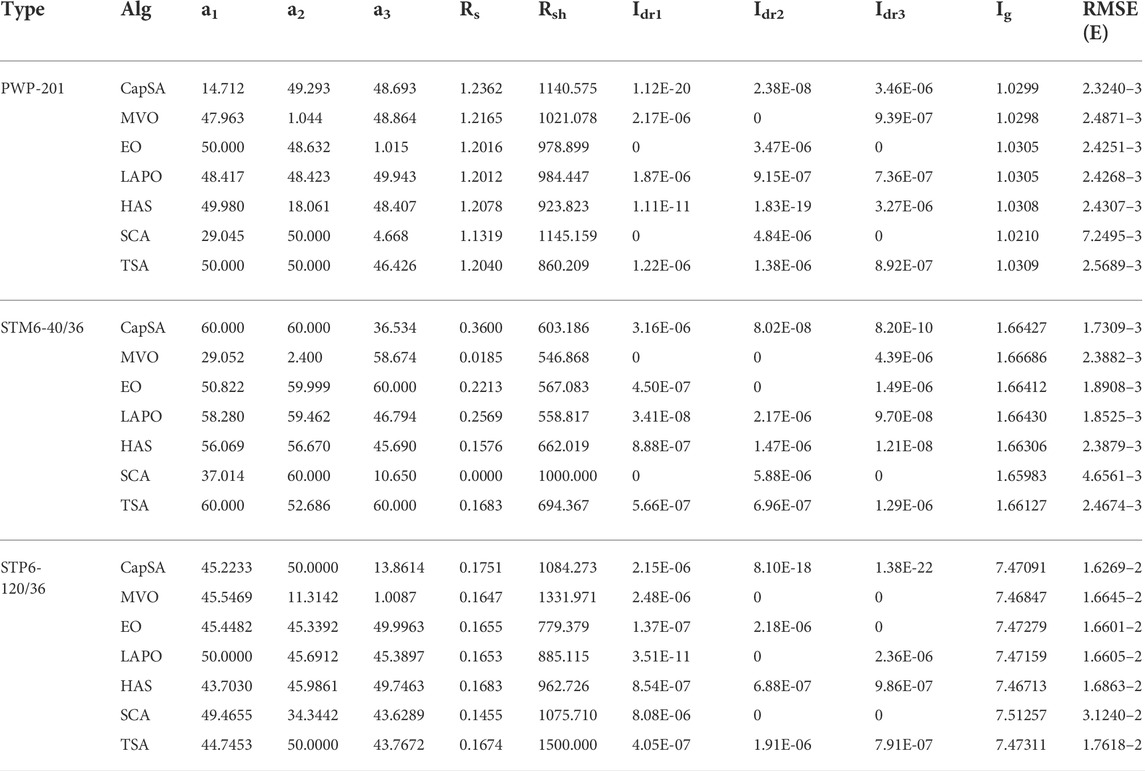
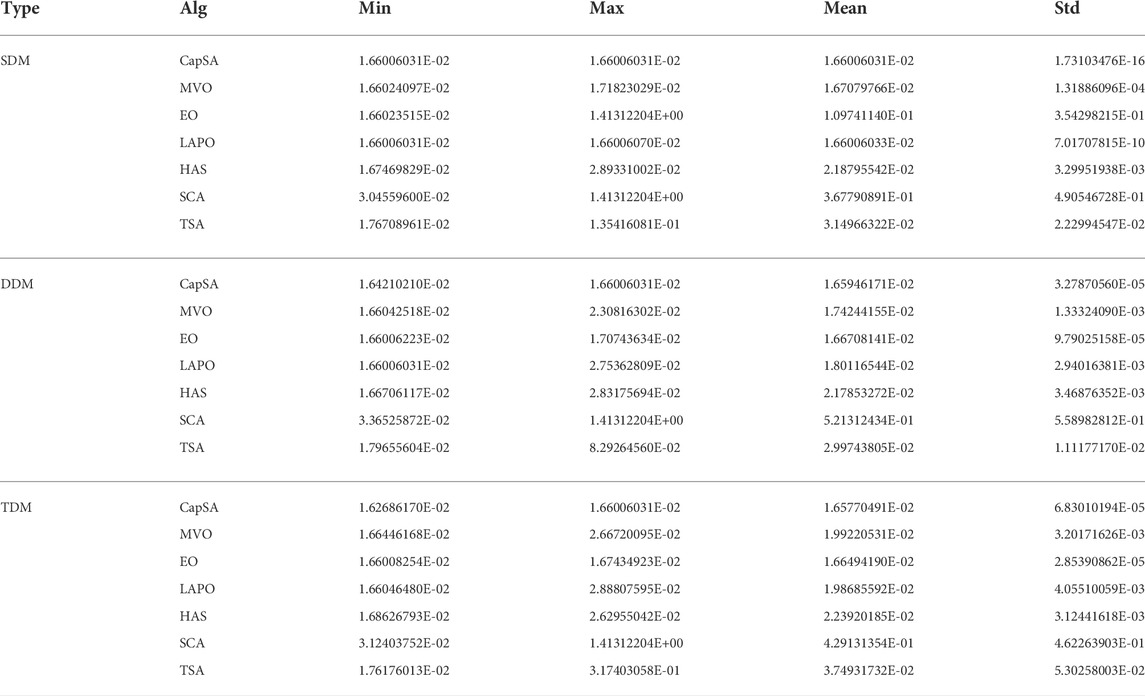
In order to confirm the validity of the proposed CapSA, it is applied to identify the SDM, DDM, and TDM unknown parameters for different PV panels of Photowatt PWP-201, STM6-40/36, and STP6-120/36 PV. The first one is operated at 45°C and 1000W/m², the second one is considered at 51°C and 1000W/m², and the last one is operated at 55°C and 1000W/m². The measured data of I–V for the considered PV panels and electrical characteristics are given in Yu et al. (2019), Long et al. (2020a), Nicaire et al– (2021), and Rezk et al. (2021). The RMSE performance obtained via the considered optimizers during the iterative process for SDM is shown in Figure 6. The fitness value and the estimated parameters of SDM obtained via the proposed CapSA in comparison with MVO, LAPO, SCA, TSA, EO, and HSA are illustrated in Table 6. The minimum obtained RMSE value is 2.42507E-03 by CapSA and LAPO for the PWP-201 PV panel. The STM6-40/36 and STP6-120/36 best RMSE values of 1.90610E-03 and 1.66006E-02 are obtained via CapSA and LAPO, respectively, whereas the worst values are 4.58893E-03 and 3.04560E-02 by SCA. Moreover, Table 7 represents the optimal parameters of DDM; the proposed CapSA achieved the best RMSE values of 2.3306E-03, 1.7309E-03, and 1.6421E-02, whereas the worst RMSE values obtained are 6.5520E-03, 4.5854E-03, and 3.3653E-02 via SCA for PWP-201, STM6-40/36, and STP6-120/36, respectively. Furthermore, the optimal parameters of TDM are presented in Table 8, and the best fitness value is 2.3240E-03 achieved by the proposed CapSA for the PWP-201 panel. In addition, it comes first during analyzing STM6-40/36 and STP6-120/36 panels achieving fitness values of 1.7309E-3 and 1.6269E-2, respectively. On the other hand, the SCA came in the last rank with 7.2495E-3, 4.6561E-3, and 3.1240E-2 for PWP-201, STM6-40/36, and STP6-120/36, respectively. To confirm the efficiency and reliability of the proposed CapSA, Figures 7–9 show the measured and simulated I–V and P–V curves obtained via the proposed approach; the points coincide with each other in the curves, and this confirms the efficiency of the proposed CapSA. The statistical analyses in such case are tabulated in Table 9, where the CapSA for STP6-120/36 achieved the least mean value of 1.6600603E-02 and standard of 1.73103476E-16 for SDM.

FIGURE 6

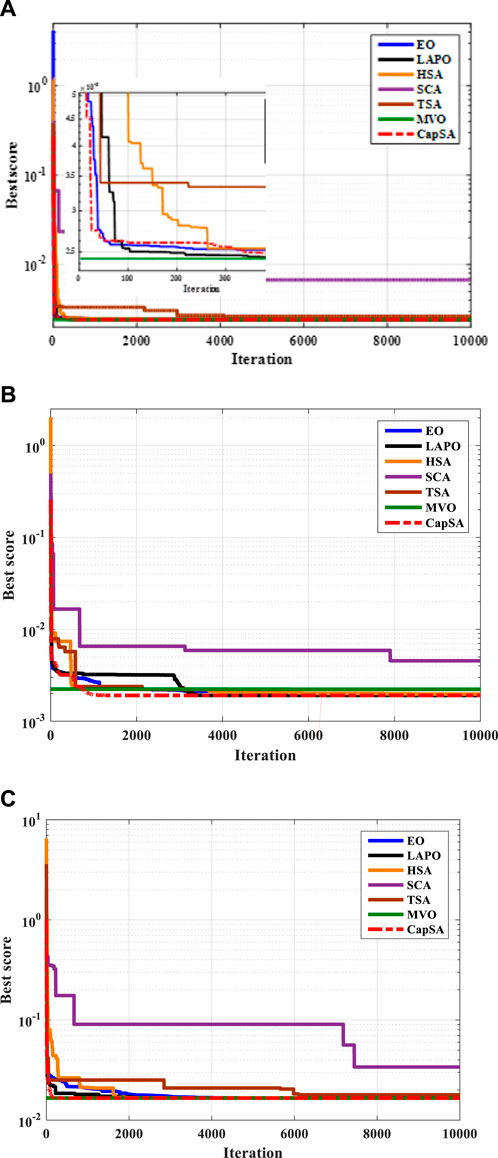
FIGURE 6. Fitness value versus iteration number for (A) PWP-201, (B) STM6-40/36, and (C) STP6-120/36 panels.

TABLE 6

TABLE 6. SDM optimal parameters of PWP-201, STM6-40/36, and STP6-120/36 panels.

TABLE 7

TABLE 7. DDM optimal parameters of PWP-201, STM6-40/36, and STP6-120/36 panels.

TABLE 8

TABLE 8. TDM optimal parameters of PWP-201, STM6-40/36, and STP6-120/36 panels.

FIGURE 7

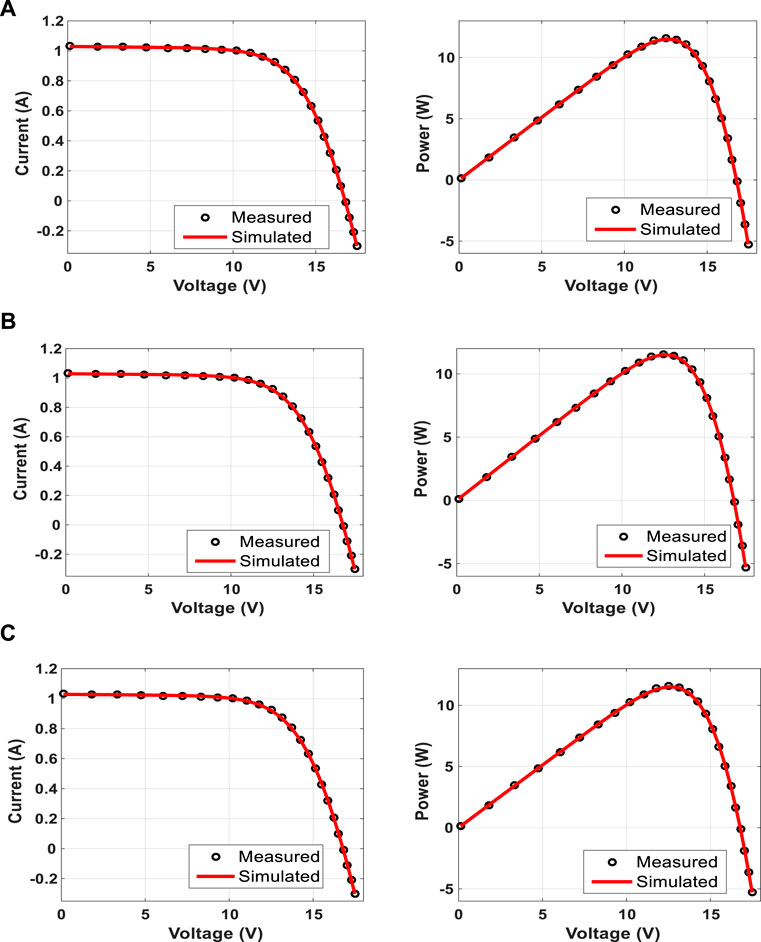
FIGURE 7. Measured and simulated I–V and P–V curves of the PWP-201 PV panel. (A) SDM, (B) DDM, and (C) TDM.

FIGURE 8

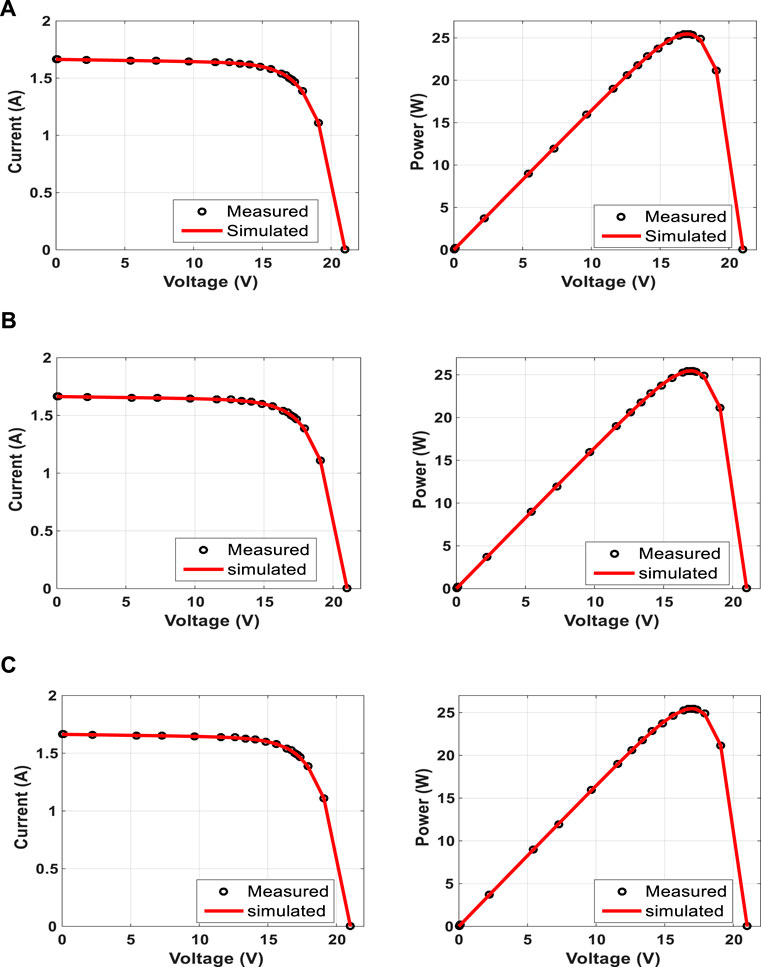
FIGURE 8. Measured and simulated I–V and P–V curves of the STM6-40/36 panel. (A) SDM, (B) DDM, and (C) TDM.

FIGURE 9

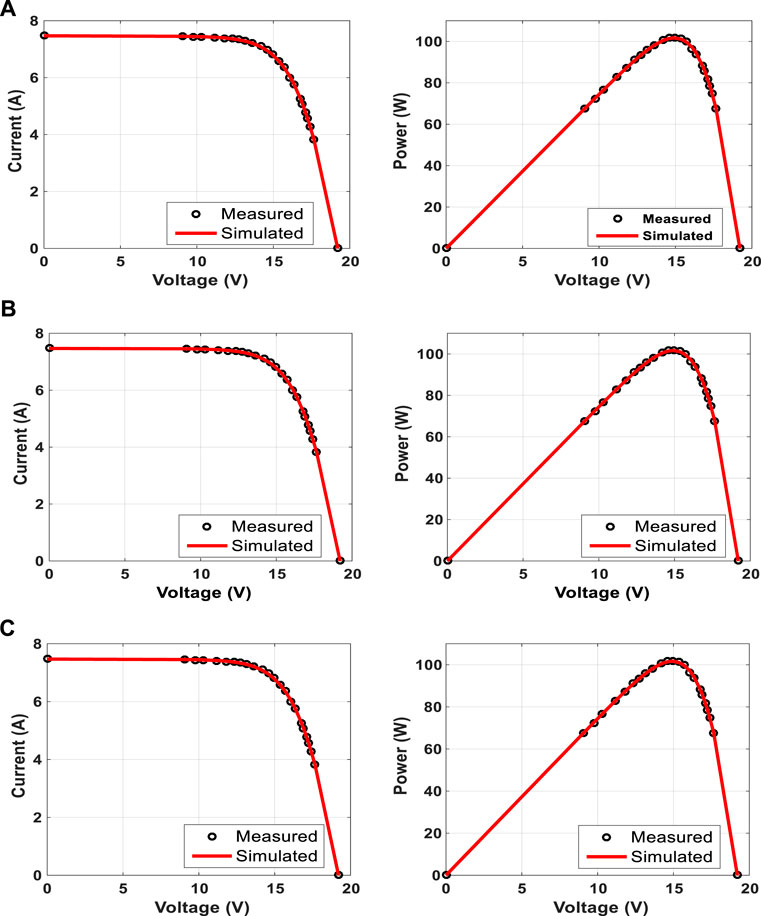
FIGURE 9. Measured and simulated I–V and P–V curves of the STP6-120/36 panel. (A) SDM, (B) DDM, and (C) TDM.

TABLE 9

TABLE 9. Statistical parameters of the approaches applied to the STP6-120/36 panel.

The proposed CapSA achieved great performance by getting estimated curves that are closely matched to the experimental ones; this affirms its competence in such cases.

5.3 Case 3: Photovoltaic panel operation at variable weather conditions

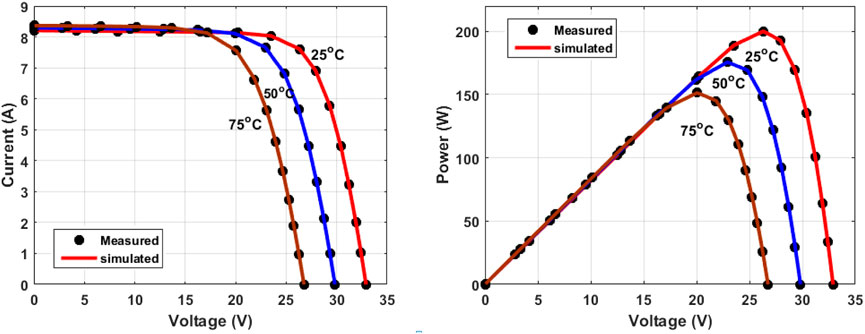
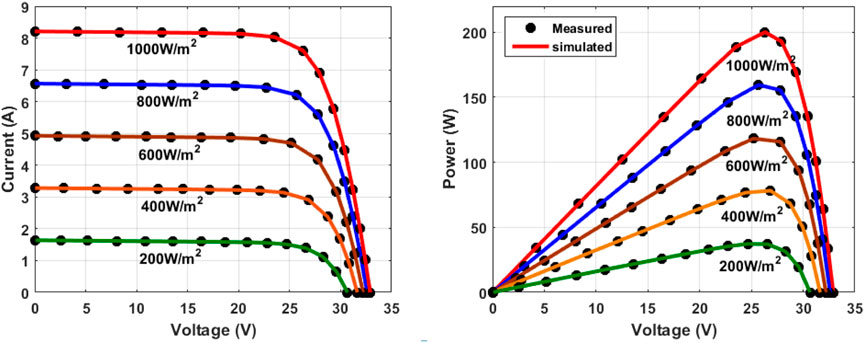
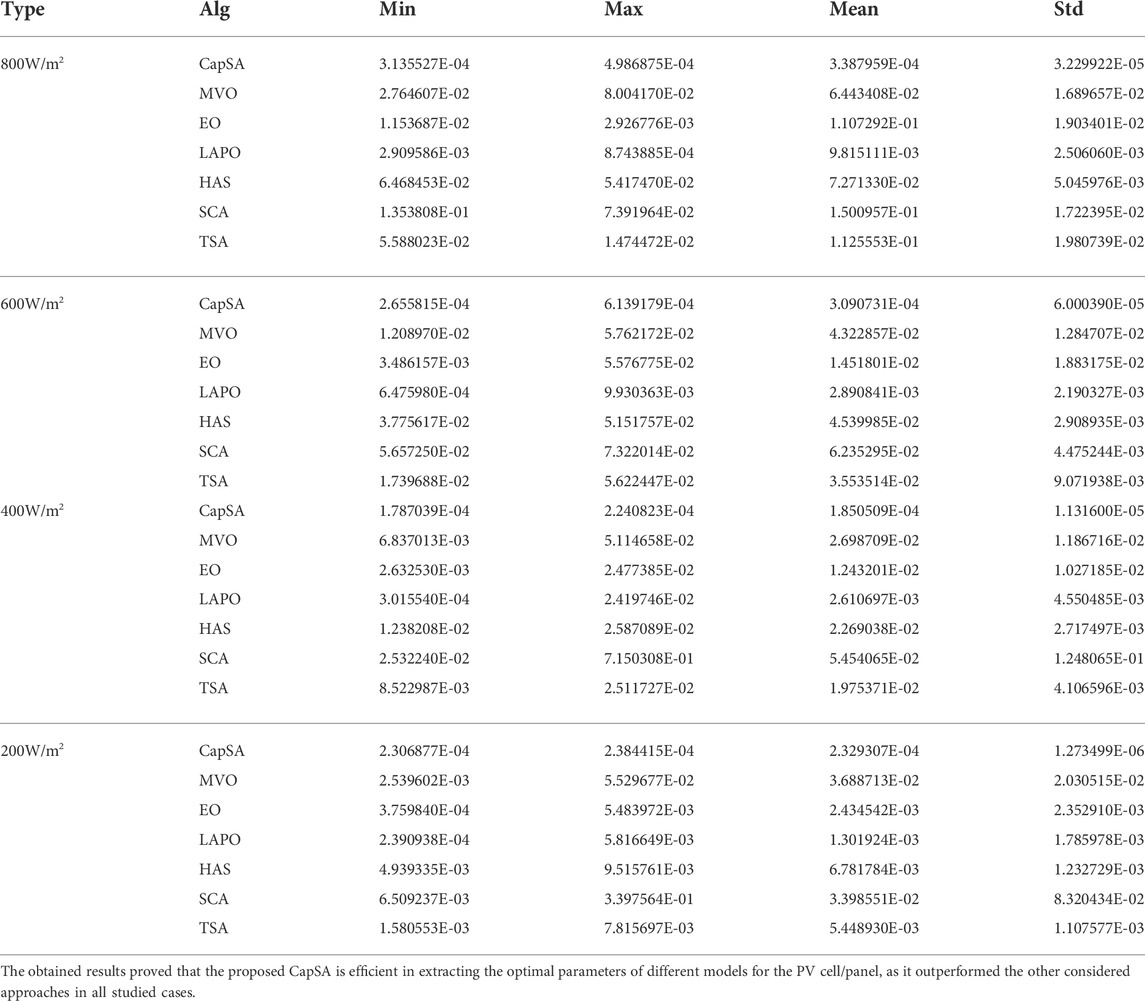
The proposed CapSA is applied to construct the DDM of the KC200GT PV panel operated at different weather conditions. The electrical properties of the panel and the measured data of I–V are presented in Arias García and Pérez Abril (2020). The identified parameters and RMSE values under different temperatures of 25°C, 50°C, and 75°C and irradiance of 1000W/m² are tabulated in Table 10. The proposed CapSA achieved the best RMSE values of 3.4440E-04, 1.5617E-03, and 6.6008E-03 during operation at 25°C, 50°C, and 75°C, respectively. The measured and simulated data of I–V and P–V curves obtained by the proposed CapSA at different temperatures and irradiance of 1000W/m² are presented in Figure 10. Figure 11 illustrates the I–V and P–V curves of the measured and simulated data obtained by the proposed CapSA at 25°C and different irradiances of 1000W/m², 800W/m², 600W/m², 400W/m², and 200W/m². The simulated data are closely matched to the measured points. Additionally, the statistical analysis under different temperatures and irradiances are tabulated in Table 11 and Table 12, respectively.

TABLE 10

TABLE 10. Optimal parameters of DDM for the KC200GT PV panel at different temperatures.

FIGURE 10

FIGURE 10. I–V and P–V curves of KC200GT at different temperatures.

FIGURE 11

FIGURE 11. Measured and simulated I–V and P–V curves of KC200GT at different irradiances.

TABLE 11

TABLE 11. Statistical parameters of the optimizers applied on KC200GT at different temperatures.

TABLE 12

TABLE 12. Statistical parameters of the optimizers applied on KC200GT at different irradiances.

6 Conclusion

This study proposed an efficient approach incorporating the capuchin search algorithm (CapSA) to identify the unknown parameters of SDM-, DDM-, and TDM-based circuits of different PV cells and panels. The considered fitness function is the root mean square error between the measured and simulated currents. R.T.C France, PVM752, PWP-201, STM6-40/36, STP6-120/36, and KC200GT are the cells and panels considered in the analysis. Comparison to a multiverse optimizer (MVO), lighting attachment procedure optimization (LAPO), sine–cosine algorithm (SCA), tunicate swarm algorithm (TSA), equilibrium optimizer (EO), and harmony search algorithm (HSA) is conducted. The proposed approach achieved several features as follow:

1) Regarding the SDM circuit, the proposed CapSA outperformed all considered optimizers achieving the best RMSE values of 9.86022E-04, 2.27804E-04, 2.42507E-03, 1.90610E-03, and 1.66006E-02 with the fastest computational times of 546.6 s, 591.1 s, 517.5 s, 542.8 s, and 445.4 s for the R.T.C France cell, PVW752 cell, PWP-201 panel, STM6-40/36 panel, and STP6-120/36 panel, respectively.

2) For DDM, the proposed CapSA achieved the best fitness values of 9.8248E-04, 1.3808E-04, 2.3306E-03, 1.7309E-03, and 1.6421E-02 with the best computational times of 605.3 s, 676.5 s, 535.0 s, 548.7 s, and 536.4 s for the R.T.C France cell, PVW752 cell, PWP-201 panel, STM6-40/36 panel, and STP6-120/36 panel, respectively.

3) In the case of TDM, the proposed approach achieved RMSE values of 9.8248E-04, 1.5182E-04, 2.3240E-03, 1.7309E-3, and 1.6269E-2 for the R.T.C France cell, PVW752 cell, PWP-201 panel, STM6-40/36 panel, and STP6-120/36 panel, respectively.

4) For the KC200GT panel, the CapSA outperformed the others and achieved the best RMSE values of 3.4440E-04, 1.5617E-03, and 6.6008E-03 at 25°C, 50°C, and 75°C, respectively.

The obtained results confirmed the competence and preference of the proposed CapSA in establishing a reliable equivalent circuit for the PV cell/panel operated at different weather conditions. Establishing a dynamic model of the PV panel is recommended in the future; moreover, enhancing the CapSA approach via hybridization with novel approaches will be considered in future studies.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary materials, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, HA and AF; methodology, ME and MA-D; software, ME and AA; validation, AF, ME, and AA; formal analysis, HA; investigation, HA and ME; resources, MA-D; data curation, AF and MA-D; writing—original draft preparation, HA and ME; writing—review and editing, AF and MA-D; visualization, AF; supervision, AA. All authors have read and agreed to the published version of the manuscript.

Funding

The authors acknowledge the support of King Fahd University of Petroleum and Minerals, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.1028816/full#supplementary-material

References

Abdel-Basset, M., Mohamed, R., Chakrabortty, R. K., Ryan, M. J., and El-Fergany, A. (2021). An improved artificial jellyfish search optimizer for parameter identification of photovoltaic models. Energies 14, 1867. doi:10.3390/en14071867

CrossRef Full Text | Google Scholar

Abdelminaam, D. S., Said, M., and Houssein, E. H. (2021). Turbulent flow of water-based optimization using new objective function for parameter extraction of six photovoltaic models. IEEE Access 9, 35382–35398. doi:10.1109/ACCESS.2021.3061529

CrossRef Full Text | Google Scholar

Ahmadianfar, I., Gong, W., Heidari, A. A., Golilarz, N. A., Samadi-Koucheksaraee, A., and Chen, H. (2021). Gradient-based optimization with ranking mechanisms for parameter identification of photovoltaic systems. Energy Rep. 7, 3979–3997. doi:10.1016/j.egyr.2021.06.064

CrossRef Full Text | Google Scholar

Alam, D. F., Yousri, D. A., and Eteiba, M. B. (2015). Flower Pollination Algorithm based solar PV parameter estimation. Energy Convers. Manag. 101, 410–422. doi:10.1016/j.enconman.2015.05.074

CrossRef Full Text | Google Scholar

Arias García, R. M., and Pérez Abril, I. (2020). Photovoltaic module model determination by using the Tellegen’s theorem. Renew. Energy 152, 409–420. doi:10.1016/j.renene.2020.01.048

CrossRef Full Text | Google Scholar

Askarzadeh, A., and Rezazadeh, A. (2013). Artificial bee swarm optimization algorithm for parameters identification of solar cell models. Appl. Energy 102, 943–949. doi:10.1016/j.apenergy.2012.09.052

CrossRef Full Text | Google Scholar

Ayang, A., Wamkeue, R., Ouhrouche, M., Djongyang, N., Essiane Salomé, N., Pombe, J. K., et al. (2019). Maximum likelihood parameters estimation of single-diode model of photovoltaic generator. Renew. Energy 130, 111–121. doi:10.1016/j.renene.2018.06.039

CrossRef Full Text | Google Scholar

Bertalero, G., Addebito, P., Bancario, C. C., and Cliente, C. A. L. (2021). Parameters extraction of three diode photovoltaic models using boosted LSHADE algorithm and Newton Raphson method. 224 120–136. doi:10.1016/j.energy.2021.120136

CrossRef Full Text | Google Scholar

Braik, M., Sheta, A., and Al-Hiary, H. (2021). A novel meta-heuristic search algorithm for solving optimization problems: Capuchin search algorithm. Neural comput. Appl. 33, 2515–2547. doi:10.1007/s00521-020-05145-6

CrossRef Full Text | Google Scholar

Ćalasan, M., Abdel Aleem, S. H. E., and Zobaa, A. F. (2020). On the root mean square error (RMSE) calculation for parameter estimation of photovoltaic models: A novel exact analytical solution based on Lambert W function. Energy Convers. Manag. 210, 112716. doi:10.1016/j.enconman.2020.112716

CrossRef Full Text | Google Scholar

Chen, X., Xu, B., Mei, C., Ding, Y., and Li, K. (2018). Teaching–learning–based artificial bee colony for solar photovoltaic parameter estimation. Appl. Energy 212, 1578–1588. doi:10.1016/j.apenergy.2017.12.115

CrossRef Full Text | Google Scholar

El-Fergany, A. A. (2021). Parameters identification of PV model using improved slime mould optimizer and Lambert W-function. Energy Rep. 7, 875–887. doi:10.1016/j.egyr.2021.01.093

CrossRef Full Text | Google Scholar

Fathy, A., and Rezk, H. (2017). Parameter estimation of photovoltaic system using imperialist competitive algorithm. Renew. Energy 111, 307–320. doi:10.1016/j.renene.2017.04.014

CrossRef Full Text | Google Scholar

Gao, X., Cui, Y., Hu, J., Xu, G., Wang, Z., Qu, J., et al. (2018). Parameter extraction of solar cell models using improved shuffled complex evolution algorithm. Energy Convers. Manag. 157, 460–479. doi:10.1016/j.enconman.2017.12.033

CrossRef Full Text | Google Scholar

Ginidi, A., Ghoneim, S. M., Elsayed, A., El-Sehiemy, R., Shaheen, A., and El-Fergany, A. (2021). Gorilla troops optimizer for electrically based single and double-diode models of solar photovoltaic systems. Sustainability 13, 9459. doi:10.3390/su13169459

CrossRef Full Text | Google Scholar

Gnetchejo, P. J., Ndjakomo Essiane, S., Dadjé, A., and Ele, P. (2021). A combination of Newton-Raphson method and heuristics algorithms for parameter estimation in photovoltaic modules. Heliyon 7, e06673. doi:10.1016/j.heliyon.2021.e06673

PubMed Abstract | CrossRef Full Text | Google Scholar

Ibrahim, I. A., Hossain, M. J., Duck, B. C., and Nadarajah, M. (2020). An improved wind driven optimization algorithm for parameters identification of a triple-diode photovoltaic cell model. Energy Convers. Manag. 213, 112872. doi:10.1016/j.enconman.2020.112872

CrossRef Full Text | Google Scholar

Ismaeel, A. A. K., Houssein, E. H., Oliva, D., and Said, M. (2021). Gradient-based optimizer for parameter extraction in photovoltaic models. IEEE Access 9, 13403–13416. doi:10.1109/ACCESS.2021.3052153

CrossRef Full Text | Google Scholar

Jiang, Y., Luo, Q., and Zhou, Y. (2022). Improved gradient‐based optimizer for parameters extraction of photovoltaic models. IET Renew. Power Gen. 16, 1602–1622. doi:10.1049/rpg2.12465

CrossRef Full Text | Google Scholar

Jiao, S., Chong, G., Huang, C., Hu, H., Wang, M., Heidari, A. A., et al. (2020). Orthogonally adapted Harris hawks optimization for parameter estimation of photovoltaic models. Energy 203, 117804. doi:10.1016/j.energy.2020.117804

CrossRef Full Text | Google Scholar

Lekouaghet, B., Boukabou, A., and Boubakir, C. (2021). Estimation of the photovoltaic cells/modules parameters using an improved Rao-based chaotic optimization technique. Energy Convers. Manag. 229, 113722. doi:10.1016/j.enconman.2020.113722

CrossRef Full Text | Google Scholar

Long, W., Cai, S., Jiao, J., Xu, M., and Wu, T. (2020a). A new hybrid algorithm based on grey wolf optimizer and cuckoo search for parameter extraction of solar photovoltaic models. Energy Convers. Manag. 203, 112243. doi:10.1016/j.enconman.2019.112243

CrossRef Full Text | Google Scholar

Long, W., Wu, T., Jiao, J., Tang, M., and Xu, M. (2020b). Refraction-learning-based whale optimization algorithm for high-dimensional problems and parameter estimation of PV model. Eng. Appl. Artif. Intell. 89, 103457. doi:10.1016/j.engappai.2019.103457

CrossRef Full Text | Google Scholar

Long, W., Wu, T., Xu, M., Tang, M., and Cai, S. (2021). Parameters identification of photovoltaic models by using an enhanced adaptive butterfly optimization algorithm. Energy 229, 120750. doi:10.1016/j.energy.2021.120750

CrossRef Full Text | Google Scholar

Low, K. S., and Soon, J. J. (2012). Photovoltaic model identification using particle swarm optimization with inverse barrier constraint. IEEE Trans. Power Electron. 27, 3975–3983. doi:10.1109/tpel.2012.2188818

CrossRef Full Text | Google Scholar

Mokeddem, D. (2021). Parameter extraction of solar photovoltaic models using enhanced levy flight based grasshopper optimization algorithm. J. Electr. Eng. Technol. 16, 171–179. doi:10.1007/s42835-020-00589-1

CrossRef Full Text | Google Scholar

Mostafa, M., Rezk, H., Aly, M., and Ahmed, E. M. (2020). A new strategy based on slime mould algorithm to extract the optimal model parameters of solar PV panel. Sustain. Energy Technol. Assessments 42, 100849. doi:10.1016/j.seta.2020.100849

CrossRef Full Text | Google Scholar

Nicaire, N. F., Steve, P. N., Salome, N. E., and Grégroire, A. O. (2021). Parameter estimation of the photovoltaic system using bald eagle search (BES) algorithm. Int. J. Photoenergy 2021, 1–20. doi:10.1155/2021/4343203

CrossRef Full Text | Google Scholar

Pourmousa, N., Ebrahimi, S. M., Malekzadeh, M., and Alizadeh, M. (2019). Parameter estimation of photovoltaic cells using improved Lozi map based chaotic optimization Algorithm. Sol. Energy 180, 180–191. doi:10.1016/j.solener.2019.01.026

CrossRef Full Text | Google Scholar

Premkumar, M., Jangir, P., Elavarasan, R. M., and Sowmya, R. (2021a). Opposition decided gradient-based optimizer with balance analysis and diversity maintenance for parameter identification of solar photovoltaic models. J. Ambient. Intell. Humaniz. Comput. doi:10.1007/s12652-021-03564-4

CrossRef Full Text | Google Scholar

Premkumar, M., Jangir, P., Jebaseelan, S. D. T. S., Elavarasan, R. M., Chen, H., Kumar, C., et al. (2022). Constraint estimation in three-diode solar photovoltaic model using Gaussian and Cauchy mutation-based hunger games search optimizer and enhanced Newton–Raphson method. IET Renew. Power Gen. 16, 1733–1772. doi:10.1049/rpg2.12475

CrossRef Full Text | Google Scholar

Premkumar, M., Jangir, P., Ramakrishnan, C., Nalinipriya, G., Alhelou, H. H., and Kumar, B. S. (2021b). Identification of solar photovoltaic model parameters using an improved gradient-based optimization algorithm with chaotic drifts. IEEE Access 9, 62347–62379. doi:10.1109/ACCESS.2021.3073821

CrossRef Full Text | Google Scholar

Premkumar, M., Jangir, P., Sowmya, R., Elavarasan, R. M., and Kumar, B. S. (2021c). Enhanced chaotic JAYA algorithm for parameter estimation of photovoltaic cell/modules. ISA Trans. 116, 139–166. doi:10.1016/j.isatra.2021.01.045

PubMed Abstract | CrossRef Full Text | Google Scholar

Ram, J. P., Babu, T. S., Dragicevic, T., and Rajasekar, N. (2017). A new hybrid bee pollinator flower pollination algorithm for solar PV parameter estimation. Energy Convers. Manag. 135, 463–476. doi:10.1016/j.enconman.2016.12.082

CrossRef Full Text | Google Scholar

Ramadan, A., Kamel, S., Hassan, M. H., Khurshaid, T., and Rahmann, C. (2021a). An improved bald eagle search algorithm for parameter estimation of different photovoltaic models. Processes 9, 1127. doi:10.3390/pr9071127

CrossRef Full Text | Google Scholar

Ramadan, A., Kamel, S., Hussein, M. M., and Hassan, M. H. (2021b). A new application of chaos game optimization algorithm for parameters extraction of three diode photovoltaic model. IEEE Access 9, 51582–51594. doi:10.1109/ACCESS.2021.3069939

CrossRef Full Text | Google Scholar

Reddy, S. S., and Yammani, C. (2021). A novel two step method to extract the parameters of the single diode model of Photovoltaic module using experimental Power–Voltage data. Opt. (Stuttg). 248, 167977. doi:10.1016/j.ijleo.2021.167977

CrossRef Full Text | Google Scholar

Rezaee Jordehi, A. (2018). Enhanced leader particle swarm optimisation (ELPSO): An efficient algorithm for parameter estimation of photovoltaic (PV) cells and modules. Sol. Energy 159, 78–87. doi:10.1016/j.solener.2017.10.063

CrossRef Full Text | Google Scholar

Rezk, H., Babu, T. S., Al-Dhaifallah, M., and Ziedan, H. A. (2021). A robust parameter estimation approach based on stochastic fractal search optimization algorithm applied to solar PV parameters. Energy Rep. 7, 620–640. doi:10.1016/j.egyr.2021.01.024

CrossRef Full Text | Google Scholar

Said, M., Shaheen, A. M., Ginidi, A. R., El-Sehiemy, R. A., Mahmoud, K., Lehtonen, M., et al. (2021). Estimating parameters of photovoltaic models using accurate turbulent flow of water optimizer. Processes 9, 627. doi:10.3390/pr9040627

CrossRef Full Text | Google Scholar

Sattar, M. A. El, Al Sumaiti, A., Ali, H., and Diab, A. A. Z. (2021). Marine predators algorithm for parameters estimation of photovoltaic modules considering various weather conditions. Neural comput. Appl. 33, 11799–11819. doi:10.1007/s00521-021-05822-0

CrossRef Full Text | Google Scholar

Şentürk, A. (2018). New method for computing single diode model parameters of photovoltaic modules. Renew. Energy 128, 30–36. doi:10.1016/j.renene.2018.05.065

CrossRef Full Text | Google Scholar

Shaheen, A. M., Ginidi, A. R., El-Sehiemy, R. A., and Ghoneim, S. S. M. (2021). A forensic-based investigation algorithm for parameter extraction of solar cell models. IEEE Access 9, 1–20. doi:10.1109/ACCESS.2020.3046536

CrossRef Full Text | Google Scholar

Sharma, A., Sharma, A., Moshe, A., Raj, N., and Pachauri, R. K. (2021). An effective method for parameter estimation of solar PV cell using grey-wolf optimization technique. Int. J. Math. Eng. Manag. Sci. 6, 911–931. doi:10.33889/ijmems.2021.6.3.054

CrossRef Full Text | Google Scholar

Stornelli, V., Muttillo, M., de Rubeis, T., and Nardi, I. (2019). A new simplified five-parameter estimation method for single-diode model of photovoltaic panels. Energies 12, 4271. doi:10.3390/en12224271

CrossRef Full Text | Google Scholar

Wang, J., Yang, B., Li, D., Zeng, C., Chen, Y., Guo, Z., et al. (2021). Photovoltaic cell parameter estimation based on improved equilibrium optimizer algorithm. Energy Convers. Manag. 236, 114051. doi:10.1016/j.enconman.2021.114051

CrossRef Full Text | Google Scholar

Wang, L., and Huang, C. (2018). A novel Elite Opposition-based Jaya algorithm for parameter estimation of photovoltaic cell models. Opt. (Stuttg). 155, 351–356. doi:10.1016/j.ijleo.2017.10.081

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive overview of meta-heuristic algorithm applications on PV cell parameter identification. Energy Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yousri, D., Rezk, H., and Fathy, A. (2020). Identifying the parameters of different configurations of photovoltaic models based on recent artificial ecosystem-based optimization approach. Int. J. Energy Res. 44, 11302–11322. doi:10.1002/er.5747

CrossRef Full Text | Google Scholar

Yu, K., Liang, J. J., Qu, B. Y., Cheng, Z., and Wang, H. (2018). Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Appl. Energy 226, 408–422. doi:10.1016/j.apenergy.2018.06.010

CrossRef Full Text | Google Scholar

Yu, K., Qu, B., Yue, C., Ge, S., Chen, X., and Liang, J. (2019). A performance-guided JAYA algorithm for parameters identification of photovoltaic cell and module. Appl. Energy 237, 241–257. doi:10.1016/j.apenergy.2019.01.008

CrossRef Full Text | Google Scholar

Yu, S., Chen, Z., Heidari, A. A., Zhou, W., Chen, H., and Xiao, L. (2022). Parameter identification of photovoltaic models using a sine cosine differential gradient based optimizer. IET Renew. Power Gen. 16, 1535–1561. doi:10.1049/rpg2.12451

CrossRef Full Text | Google Scholar

Zeng, F., Shu, H., Wang, J., Chen, Y., and Yang, B. (2021). Parameter identification of PV cell via adaptive compass search algorithm. Energy Rep. 7, 275–282. doi:10.1016/j.egyr.2021.01.069

CrossRef Full Text | Google Scholar

Zhang, Y., Jin, Z., and Mirjalili, S. (2020). Generalized normal distribution optimization and its applications in parameter extraction of photovoltaic models. Energy Convers. Manag. 224, 113301. doi:10.1016/j.enconman.2020.113301

CrossRef Full Text | Google Scholar