Dynamics of MHD second-grade nanofluid flow with activation energy across a curved stretching surface

This analysis addresses the influence of activation energy on the MHD flow of second-grade nanoliquid over a convectively heated curved stretched surface. The impact of heat generation/absorption, thermophoresis, and Brownian motion are also incorporated. This current study in addendum reveals the solution narrating the nanofluid flow behaviour of the stretched curve to better the performance of the system. Hence, the mathematical construction of governing partial differential equations (PDEs) is transmitted into nonlinear ODEs by employing appropriate transformations. The attained ODEs are conducted numerically via ND-Solve. It is consequential to report that fluid velocity and temperature fields significantly rise with concurrent enhancing values of the fluid parameter and curvature parameter. Moreover, the concentration field enhances considering the energy activation variable and suppresses with the reaction rate constant while thermophoresis escalates the temperature distribution as the Nusselt number lowers with a stronger internal heat source parameter Q.

Introduction

In recent advancements, nanofluids have obtained immense attention due to their notable thermal transfer and fascinating applications in numerous fields such as computer processes, hybrid power, fuel cell, and other high-energy devices. The fluids are prepared by suspending nanoparticles in base fluids. The size of nanoparticles ≤ 100 nm. The prime idea of nanofluid was coined by Choi and Eastman (1995). Later, Buongiorono (2006) suggested the two main characteristics, namely, Brownian movement and thermophoretic force, to enhance the ability of the ordinary fluid. He found that enhancing the Nusselt number leads to a rise in the nanoparticle volume fraction. Sheikholeslami et al. (2014) discussed the impact of MHD copper nanofluid flow. The theoretical investigation of Al₂O₃ water nano liquid was examined by Malvandi et al. (2015). They discovered that the enforced heat irregularity alters the path of nanoparticle movement and modifies the patterns of the fields. Mahanthesh et al. (2016) reported the squeezing effect of nanofluids which escalates the thermal layer and leads to a depreciation of the rate of heat transport. Ibáñez et al. (2016) explored the MHD nanoliquid flow in a porous channel with a radiation effect. Eid et al. (2017) considered gold nanoparticles in the flow of Sisko nanofluid and revealed that radiation production boosts thermal transport. The Burgers flow of nanofluid with the effect of Cattaneo–Christov was examined by Hayat et al. (2017a). Also, Hayat et al. (2017b) swotted numerically the flow of nanoliquid over a revolving disk in the presence of the slip effect. Zuhra et al. (2018) considered MHD second-grade nanoliquid comprising gyrotactic microorganisms. They concluded that microorganism density leads to increases with momentum slip. The MHD Carreau nanoliquid over a permeable stretching sheet was considered by Khan and Shehzad (2020). Reddy et al. (2019) analyzed the MHD nanoliquid via a stretching sheet. Shah et al. (2021) considered numerical computation of entropy production of nanoliquid due to a porous surface. Khan et al. (2020) thrashed out the consequences of entropy minimization of Casson nanofluid over a rotating cylinder.

The exploration of non-Newtonian fluid has inspired scholars due to its several applications, such as the production of plastic, food processing, and exclusion of tumors. In this current investigation is a subcategory of non-Newtonian fluid termed second-grade fluid. This model takes into consideration the consequences of normal stress in flow conditions, as well as shear thinning and thickening. Tan and Masuoka (2005) described the flow of nanofluid with variable thermal conductivity for the second grade. Rashidi and Majid (2010) analyzed the time-dependent squeezing flow for second-grade fluid. The thermal and species transport analysis of second-grade fluid over a surface with heat flux was deliberated by Das et al. (2016). Jamil et al. (2011) reported the helical flow of second-grade fluid over coaxial cylinders. Turkyilmazoglu (2012) analytically examined the flow of second-grade non-Newtonian fluid with mass transfer over a shrinking sheet. Khan and Pop (2010), Makinde and Aziz (2011), and Hsiao (2010) evaluated the magnetohydrodynamic flow of liquid of second grade with electromagnetic dispersion and non-uniform heat source/sink. Akinbobola and Okoya (2015) swotted second-grade fluid with heat generation. The exact solution of a second-grade fluid via co-axial cylinders was reported by Erdogan and Imrak (2008). Nadeem et al. (2012) explored second-grade fluid over a horizontal cylinder.

Magnetohydrodynamics (MHD) flow has gained the interest of scholars due to its remarkable applications in the industry and engineering. As contained in the structure of the MHD generator, the cooling system is filled with fluids metal, the deposit of energy, pumps, and flow meters. Theoretically, the magnetic fields can persuade a drag identified as Lorentz force in a moving liquid, which depreciates the fluid velocity. Thus, boosting the fluid temperature and concentration. Numerous researchers have analyzed the impact of magnetic parameters, specifically in the boundary layer problem. The impact of magnetic field flow on permeable surfaces with slip conditions was elaborated by Hayat et al. (2011). Makinde et al. (2013) delineated the influence of MHD on nanoliquid with buoyancy effect. The flow of nanoliquid through two-phase models was visualized by Sheikholeslami et al. (2015). Hayat et al. (2016) addressed the influence of second-grade nanofluid. MHD flows over radially shrinking/stretching disks were reported by Soid et al. (2018). Hayat et al. (2015) considered the 3D flow of MHD nanoliquid. Sharif et al. (2019) elucidated MHD nanoliquid via an exponential sheet. Shah et al. (2020) conducted water base nanoparticles consisting of SWCNT and MWCNT over a vertical cone. Shoaib et al. (2020) evaluated numerically MHD hybrid nanoliquid with thermal radiation. They found that thermal transport rate enhances with growing values of magnetic effect and biot number. Recently, Alamri et al. (2019) discussed the second-grade fluid in the presence of Fourier’s heat flux theory.

Activation energy (AE) is the minimal amount of energy needed for a reaction to occur. The activation energy required to transfer energized particles or macromolecules to a location where they would undergo physical transit can be overestimated. The notion of activation energy is commonly useful in thermal engineering. The Bestman (Bestman, 1990) was initially coined with the activation energy of a binary amalgam phenomenon in a porous space. The unsteady natural convective flow was reported by Makinde et al. (2011) with AE. The influences of activation energy on a magnetic nanofluid were investigated by Hamid et al. (2018). Mustafa et al. (2017) and Dhlamini et al. (2022) elaborated on the behaviour of magneto nanoliquid with activation energy. Dawar et al. (2020) conducted a magnetic field flow of nanoliquid with activation energy. Hayat et al. (2022) addressed the effect of AE on the MHD flow of third-grade nanofluid over convective condition. The 3D flow of Casson nanoliquid for the thermal radiative flow with AE was examined by Khan et al. (2019). Hayat et al. (2018) inspected the 3D flow of Darcy–Forchheimer rotating AE. The 3D time-dependent flow of Carreau nanofluid on chemical reaction and AE was explored by Irfan et al. (2019). Other materials that have added value to this work are in the studies by Asogwa et al. (2013); Khan et al. (2017); Ali et al. (2020); Bilal et al. (2021); Jayaprakash et al. (2021); Ali et al. (2022a); Adnan et al. (2022); AdnanAshraf, (2022); AdnanAshraf et al. (2022); AdnanMurtaza et al. (2022); Asogwa et al. (2022); Ali et al. (2022b); Goud et al. (2022); and Weera et al. (2022).

Considering the overview of the abovementioned work, the prime focus of the current analysis is to scrutinize the impact of Arrhenius activation energy on the MHD flow of second-grade nanofluid toward a curved stretched surface. By employing the transformation procedure, PDEs have been transmuted into ODEs, which are then established numerically by ND-Solve using Mathematica. Our obtained physical parameters are prescribed through tables and graphs.

Modeled equation

The second-grade fluid Cauchy stress tensor is given by Mabood and Das (2016).

$\tau =-pI+\mu A_1+{\alpha }_1{A}_2+{\alpha }_2{A}_1^2$

Where$\mu$,$I$,$A_1$, $A_2$,${\alpha }_1$,$and{\alpha }_2$ are the identity tensor, dynamic viscosity, first and second Rivilin Erickson tensor, and material constant.

$A_1=\nabla V+{\left(\nabla V\right)}^T$

$A_n={\left(\nabla V\right)}^T{A}_1+A_1\left(\nabla V\right)+\frac{d{A}_{n-1}}{dt}$

Mathematical formulation

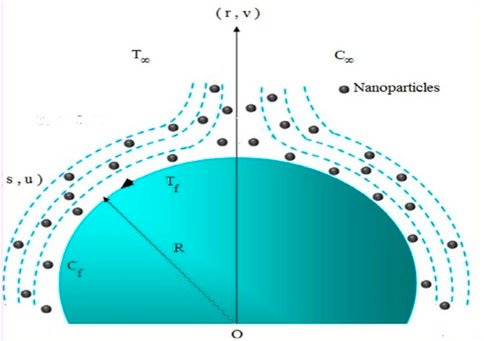
We consider the 2D flow of MHD second-grade nanoliquid flow due to the curved stretched surface. Featuring AE, chemical reaction (binary), and heat generation. We consider (r,s) to be the curvilinear coordinates (see Figure 1). The stretched sheet in s path with $U_w=as$ and r is considered orthogonal to s. Then, B₀ is applied along the transverse path of flow from the magnetic field. Assuming that the moderate magnetic field in the form of ${\mathrm{R}\mathrm{e}}_s$ generated is ignored, a nanostructured materials framework is utilized for erratic motion and thermophoresis. Under the aforementioned assumptions, equations (Mabood and Das, 2016; Imtiaz et al., 2019) are written for the boundary layer as follows:

$\left(r+R\right)\frac{\partial v}{\partial r}+v+R\frac{\partial v}{\partial s}=0(1)$

$\frac{u^2}{r+R}=-\frac{1}{\rho }\frac{\partial p}{\partial r}(2)$

$\begin{array}{l}v\frac{\partial u}{\partial r}+\frac{Ru}{r+R}\frac{\partial u}{\partial s}+\frac{uv}{r+R}=\\ -\frac{1}{\rho }\frac{R}{r+R}\frac{\partial p}{\partial s}+v\left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r+R}\frac{\partial u}{\partial r}-\frac{u}{{\left(r+R\right)}^2}\right)\\ +\frac{{\alpha }_1}{\rho }\{\frac{2R}{r+R}\frac{{\partial }^{2}u}{\partial r^2}\frac{\partial u}{\partial s}-\frac{2R}{{\left(r+R\right)}^2}\frac{\partial u}{\partial r}\frac{\partial u}{\partial s}+\frac{2}{r+R}\frac{\partial v}{\partial r}\frac{\partial u}{\partial r}+\frac{2}{r+R}v\frac{{\partial }^{2}u}{\partial r^2}-\frac{2}{{\left(r+R\right)}^2}v\frac{\partial u}{\partial r}-u\frac{4R}{{\left(r+R\right)}^2}\frac{{\partial }^{2}u}{\partial s\partial r}-u\frac{4}{{\left(r+R\right)}^2}\frac{\partial v}{\partial r}+u\frac{2R}{{\left(r+R\right)}^3}u\frac{\partial u}{\partial s}\}-\frac{\sigma B_0^{2}u}{\rho }\end{array}(3)$

$v\frac{\partial T}{\partial r}+\frac{Ru}{r+R}\frac{\partial T}{\partial s}=\alpha \left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r+R}\frac{\partial T}{\partial r}\right)+\tau \left[D_B\frac{\partial C}{\partial r}\frac{\partial T}{\partial r}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial r}\right)}^2\right]+\frac{Q_0}{\rho c_p}\left(T-T_w\right)(4)$

$v\frac{\partial C}{\partial r}+\frac{Ru}{r+R}\frac{\partial C}{\partial s}=D_B\left(\frac{{\partial }^{2}C}{\partial r^2}+\frac{1}{r+R}\frac{\partial C}{\partial r}\right)+\frac{D_T}{T_{\infty }}\left[\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r+R}\frac{\partial T}{\partial r}\right]-T_r^2{\left(\frac{T}{T_{\infty }}\right)}^n{e}^{-\frac{Ea}{KT}}\left(C-C_{\infty }\right)(5)$

With associated BCs (Mabood and Das, 2016) – (Imtiaz et al., 2019)

$\begin{array}{l}u=U_w=cs,v=0,\frac{\partial T}{\partial r}=-hf\left(T_f-T_{\infty }\right),D_B\frac{\partial C}{\partial y}+\frac{D_T}{T_{\infty }}\frac{\partial T}{\partial y}=0aty=0\\ u\to 0,\frac{\partial u}{\partial r}\to 0,T\to T_{\infty },C\to C_{\infty }asy\to \infty \end{array}\}(6)$

FIGURE 1

FIGURE 1. Geometry of the problem.

Transformation consideration

$\begin{array}{l}\eta =\sqrt{\frac{c}{v}r},u=cs{f}^{\prime }\left(\eta \right),v=-\frac{R}{r+R}\sqrt{cv}f\left(\eta \right),\tau =\frac{{\left({\rho }_c\right)}_p}{{\left({\rho }_c\right)}_f}\\ p=\rho c^2{s}^{2}P\left(\eta \right),\varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }},\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}\end{array}(7)$

Eq. 3 is satisfied, and with the help of the abovemrntioned transformation Eqs 1–5 are reduced

$\frac{\partial P}{\partial \eta }=\frac{f^{\prime 2}}{n+K}(8)$

$\begin{array}{l}\frac{2K}{\eta +K}P=f^{‴}+\frac{1}{\eta +K}f-\frac{1}{{\left(\eta +K\right)}^2}f’+\frac{K}{n+K}f{f}^{″}+\frac{K}{{\left(\eta +K\right)}^2}ff\prime \\ -\frac{K}{\left(\eta +K\right)}f{\prime }^2+\beta \{\frac{2K}{\eta +K}f’f^{″}-\frac{2K}{{\left(\eta +K\right)}^2}f{f}^{‴}-\frac{8K}{{\left(\eta +K\right)}^2}f’f^{″}\\ +\frac{4K}{{\left(\eta +K\right)}^3}f{f}^{″}+\frac{6K}{{\left(\eta +K\right)}^3}f{\prime }^{\mathit{2}}-\frac{4K}{{\left(\eta +K\right)}^4}ff’\}-M{f}^{\prime }\end{array}-\frac{K}{\left(\eta +K\right)}f{\prime }^2+\beta \{\frac{2K}{\eta +K}{f}^{\prime }{f}^{″}-\frac{2K}{{\left(\eta +K\right)}^2}f{f}^{‴}-\frac{8K}{{\left(\eta +K\right)}^2}{f}^{\prime }f″(9)$

${\theta }^{″}+\frac{1}{\eta +K}{\theta }^{\prime }+\mathrm{Pr}\left(\frac{K}{\eta +K}f{\theta }^{\prime }+Nb\theta \prime \varphi \prime +{Nt{\theta }^{\prime }}^{\mathit{2}}\right)+Q\theta =0(10)$

${\varphi }^{″}+\frac{1}{\eta +K}{\varphi }^{\prime }+\frac{K}{\eta +K}Scf\theta \prime +\frac{Nt}{Nb}\left({\theta }^{″}+\frac{1}{\eta +K}{\theta }^{\prime }\right)-Sc\varsigma {\left(1+{\delta }_1\theta \right)}^m\exp \left(\frac{-E}{1+{\delta }_1\theta }\right)\varphi =0(11)$

with transformed BCs

$\begin{array}{l}{f}^{\prime }\left(0\right)=1,\theta \prime \left(0\right)=-\delta \left(1-\theta \left(0\right)\right),Nb\varphi \prime \left(0\right)+Nt\theta \prime \left(0\right)=0at\eta =0\\ f^{\prime }\to 0,\theta \to 0,\varphi \to 0as\eta \to \infty .\end{array}(12)$

We have, $\beta =\frac{{\alpha }_{\mathit{1}}c}{\mu }$, $\delta =\frac{h_f}{k}\sqrt{\frac{v}{a}}$, Nb =$\frac{\tau D_B\left(C_w-C_{\infty }\right)}{v}$, $K=R\sqrt{\frac{c}{v}}$, $Nt=\frac{\tau D_T\left(T_w-T_{\infty }\right)}{T_{\infty }v}$,

Sc = $\frac{v}{D_B}$, E =$\frac{E_a}{k{T}_{\infty }}$, $Q=\frac{Q_{\mathit{0}}}{\rho C_p}$, $\zeta =\frac{k_r^{\mathit{2}}}{c}$, Pr = $\frac{v}{\alpha }$, ${\delta }_{\mathit{1}}=\frac{T_w-T_{\infty }}{T_{\infty }}$.

Now, removing the $P$ between Eqs 8 and 9, we get

$\begin{array}{l}{f}^{⁗}+\frac{2}{\eta +K}{f}^{‴}-\frac{1}{{\left(\eta +K\right)}^2}f″+\frac{1}{{\left(\eta +K\right)}^3}f\prime +\frac{K}{\eta +K}\left(f{f}^{‴}+f\prime f″\right)+\frac{K}{{\left(\eta +K\right)}^2}\left(f{f}^{″}+f{\prime }^{\mathit{2}}\right)\\ -\frac{K}{{\left(\eta +K\right)}^3}f{f}^{\prime }+\beta \{\frac{2K}{\eta +K}{f}^{\prime }{f}^{″}-\frac{2K}{{\left(\eta +K\right)}^2}ff‴-\frac{8K}{{\left(\eta +K\right)}^2}f\prime f″\\ +\frac{4K}{{\left(\eta +K\right)}^3}f{f}^{″}+\frac{6K}{{\left(\eta +K\right)}^3}f{\prime }^{\mathit{2}}-\frac{4K}{{\left(\eta +K\right)}^4}f{f}^{\prime }\}-M{f}^{″}-\frac{M}{\left(\eta +K\right)}{f}^{\prime }\end{array}(13)$

Expressions for the local C_fs and Nu_s gives

$C_{fs}=\frac{\mu }{\frac{1}{2}\rho U_w^2}{\tau }_{rs},{\mathrm{N}\mathrm{u}}_s=\frac{s{q}_w}{k\left(T_w-T_{\infty }\right)}(14)$

${\tau }_{rs}=\mu {\left[\frac{\partial u}{\partial r}-\frac{u}{r+R}+\frac{2{\alpha }_1}{\mu }\left(\frac{R}{r+R}\frac{\partial u}{\partial r}\frac{\partial u}{\partial s}+\frac{v}{r+R}\frac{\partial u}{\partial r}-\frac{2Ru}{{\left(r+R\right)}^2}\frac{\partial u}{\partial s}-\frac{2uv}{{\left(r+R\right)}^2}\right)\right]}_{r=0}(15)$

$q_w=-k{\left(\frac{\partial T}{\partial y}\right)}_{r=0}(16)$

Non-dimensional Nusselt number and friction co-efficient

$\begin{array}{l}{\mathrm{R}\mathrm{e}}_s^{-1/2}{C}_{fs}=\left[f^{″}\left(0\right)-\frac{f^{\prime }\left(0\right)}{K}+\beta \left(f^{\prime }\left(0\right)f^{″}\left(0\right)-\frac{2}{K}f\prime {\left(0\right)}^2\right)\right]\\ {\mathrm{R}\mathrm{e}}_s^{-1/2}N{u}_s=-{\theta }^{\prime }\left(0\right)\end{array}$

where ${\mathrm{R}\mathrm{e}}_s=\frac{c{s}^2}{v}$

Results and discussion

The key emphasis of this article is highlighted via the numerical approach integrated by utilizing the NDSolve technique by using Mathematica. The main emphasis of pertained physical variables on$f^{\prime }\left(\eta \right)$, $\theta \left(\eta \right)$, and $\varphi \left(\eta \right)$ fields, as well as drag fraction and Nusselt number, are elaborated and delineated through Figures 2–20 and Tables 1–3. Table 1 is adorned to check the compatibility of the current analysis by constructing a contrasting $-f^{″}\left(\mathit{0}\right)$. An excellent achievement has been found with a previously published result. 8. The reference values in the current study have been taken as $K=\mathit{5},\delta =\mathit{0.8}$, $Nt=Nb=\mathit{0.4},Sc=\mathit{5}$, Q = 0.1, $\beta =\mathit{0.3},$ M = 1, E = 1, and $\zeta =\mathit{1}$ kept constant throughout the computation, and the variations have been mentioned in the graphs and tables accordingly.

FIGURE 2

FIGURE 2. Disparity of M on $f^{\prime }$.

FIGURE 3

FIGURE 3. Disparity of M on $\theta$.

FIGURE 4

FIGURE 4. Disparity of M on $\varphi$.

FIGURE 5

FIGURE 5. Disparity of $K$ on $f^{\prime }$.

FIGURE 6

FIGURE 6. Disparity of $K$ on $\theta$.

FIGURE 7

FIGURE 7. Disparity of $K$ on $\varphi$.

FIGURE 8

FIGURE 8. Disparity of $\beta$ on $f$.

FIGURE 9

FIGURE 9. Disparity of $\beta$ on $\theta$.

FIGURE 10

FIGURE 10. Disparity of $\beta$ on $\varphi$.

FIGURE 11

FIGURE 11. Disparity of $\delta$ on $\theta$.

FIGURE 12

FIGURE 12. Disparity of $\delta$ on $\varphi$.

FIGURE 13

FIGURE 13. Disparity of $Nt$ on $\theta$.

FIGURE 14

FIGURE 14. Disparity of $Nt$ on $\varphi$.

FIGURE 15

FIGURE 15. Disparity of $Q$ on $\theta$.

FIGURE 16

FIGURE 16. Disparity of $E$ on $\varphi$.

FIGURE 17

FIGURE 17. Disparity of $\zeta$ on $\varphi$.

FIGURE 18

FIGURE 18. Disparity of $Nb$ on $\varphi$.

FIGURE 19

FIGURE 19. Disparity of $Sc$ on $\varphi$.

FIGURE 20

FIGURE 20. Disparity of $\mathit{Pr}$ on $\theta$.

TABLE 1

TABLE 1. Contrasting outputs of $-f\prime \prime \left(\mathit{0}\right)$ for selected values of $M$ when $K=\infty$ and $\beta =\mathit{0}.$

TABLE 2

TABLE 2. Friction co-efficient for various values $M$,$K,and\beta .$

TABLE 3

TABLE 3. Local Nusselt number for various values $K,\delta ,Nt,Nb,Sc,E,andQ.$

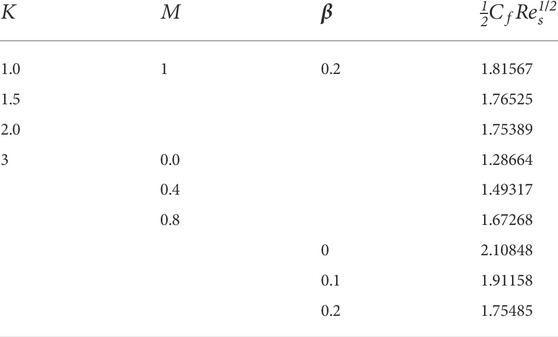
Table 2 is equipped to check the variance in $\frac{\mathit{1}}{\mathit{2}}{C}_f{Re}_s^{\mathit{1}/\mathit{2}}$. For empowered fluid parameter $\beta$ and curvature parameter $K$, friction factor decreases, whereas the reverse trend is observed with$M$. Table 3 is elaborated in variance in Nusselt number for selected values of $K,\delta$,$Nt,Nb,Sc$, Q, and E. It is noticed that N$u{Re}_s^{-\mathit{1}/\mathit{2}}$ rises with uplifting values of $K,\delta$ and E. N$u{Re}_s^{-\mathit{1}/\mathit{2}}$ declines with rising values of $Nt,Sc$ and $Q$ and there are no significant changes with $Nb$.

The impact of $M$ on $f^{\prime }\left(\eta \right)$, $\theta \left(\eta \right)$, and $\varphi \left(\eta \right)$ fields is illustrated in Figures 2–4. It is revealed that velocity diminishes with an escalation in $M$. This notifies that increase in magnetic field obtains the resistive force (Lorentz force) leading to a reduction in the fluid velocity. This also means a reduction in the thickness of the thermal boundary layer. The heat generated causes resistance of the fluid for a greater value of M, which escalates the fluid temperature, and similar behaviour is also seen for the concentration field. Figures 5–7 presents the disparity of curvature parameter $K$ on $f^{\prime }\left(\eta \right)$, $\theta \left(\eta \right)$, and $\varphi \left(\eta \right)$ fields. Figure 5 displays the enhancing values of curvature parameter $K$ on velocity field. Here, velocity escalates with a larger value of $K$. This is because enhancing values of $K$ lessens the kinematic viscosity of the fluid, which causes a reduction in viscosity and, as a result, the velocity of the fluid gains momentum. Temperature and concentration profiles for various values of $K$ are revealed in Figures 6 and 7. It is seen that temperature and concentration decline for augmenting the value of $K$.

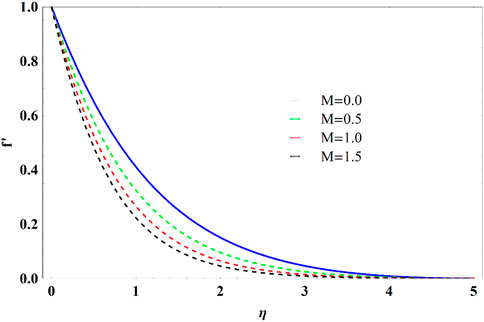
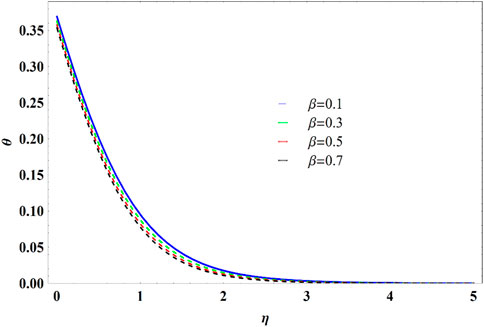
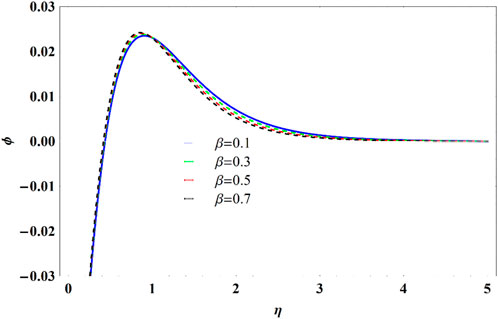
Figures 8–10 analyze the fluid parameter $\beta$ on $f^{\prime }\left(\eta \right)$, $\theta \left(\eta \right)$, and $\varphi \left(\eta \right)$ fields. It can be seen from Figure 8 that velocity profile enhances for a larger value of $\beta$. Physically, fluid parameter $\beta$ has a reverse relation with viscosity. In contrast, temperature and concentration profiles (Figures 9 and 10) offer a reducing behaviour with a rising value of $\beta$. Figures 11 and 12 presented the effect of Biot number $\delta$ on $\theta \left(\eta \right)$ and $\varphi \left(\eta \right)$ fields. Physical involvement of a larger heat transfer coefficient corresponds to enhancement on $\theta \left(\eta \right)$ and $\varphi \left(\eta \right)$ fields. Therefore, $\theta \left(\eta \right)$ and $\varphi \left(\eta \right)$ layer thickness is escalated by increasing Biot number $\delta$.

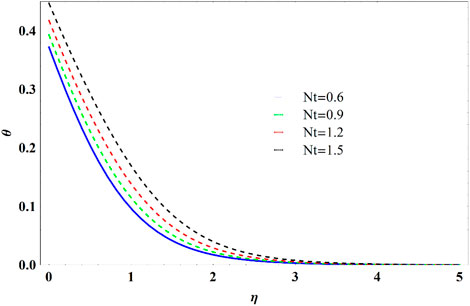
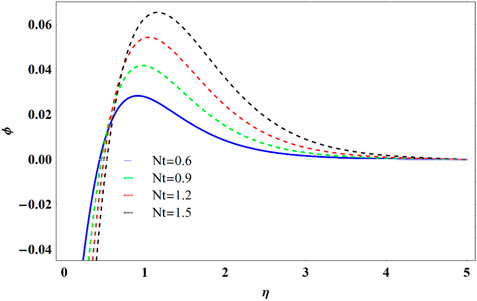
Figure 13 affirms the increasing activity of temperature profile and thermal boundary layer with Nt. The Nt increase produces a much strong thermophoretic force, causing nanoparticles to move away from the plate. This results in the growth of the $\theta \left(\eta \right)$ Figure 14 symbolizes an upsurge in concentration profile for different values of the thermophoresis variable $Nt$. Because microscopic particles move from the hot region towards the cold region during the process of thermophoresis. Figure 15 plotted the numerous values of heat source input Q against the temperature profile. Physically, the existence of Q in the boundary layer improves energy and causes a boost in temperature. Figure 16 explicates the enhancing trend of activation energy E on nanoparticle concentration. The activation energy reduces the modified Arrhenius function and causes boosting generative chemical reaction.

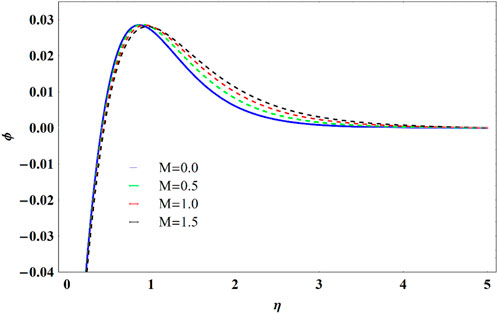
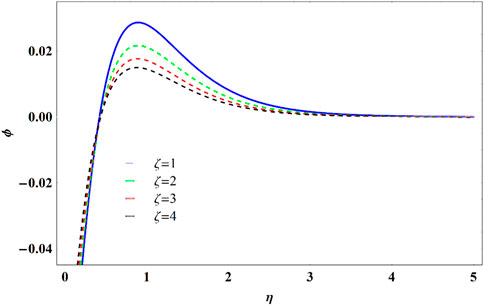
Figure 17 presents the dimensionless concentration on the chemical reaction variable$\zeta$. The concentration of nanoparticle is depreciated on the rise of $\zeta$. This behaviour characterizes the decreasing effect of buoyancy force due to concentration gradient, which causes the reduction of concentration profile.

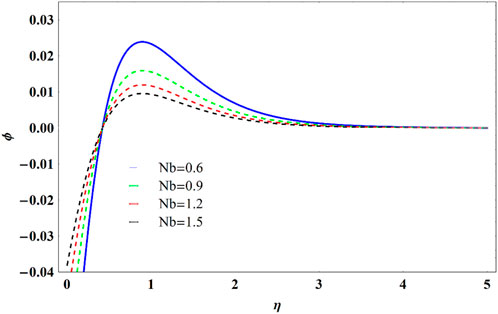
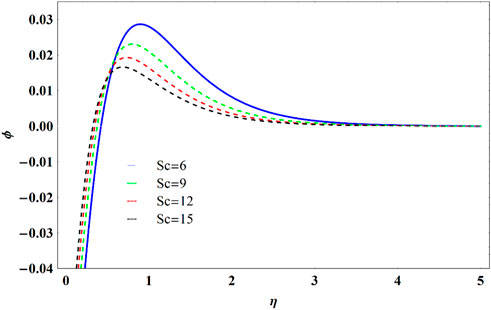
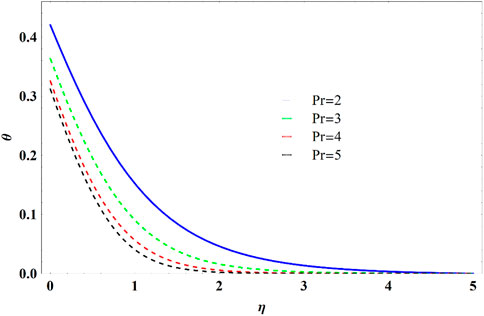
Figure 18 exhibits the variation of the concentration field to diverse values of the Nb. The thickness of the boundary layer and concentration profile decline on increasing Nb input. The reason behind this is that this enriches the pace at which tiny particles drive with various velocities in separate unexpected directions. Figure 19 affirms the declining trend in the concentration field on the escalating values of Sc. This happens because of decaying mass diffusion. Fluctuation for differing values of Prandtl number on temperature is evident in Figure 20. $\theta \left(\eta \right)$ minifies with upshot values of $\mathit{Pr}$ because larger $\mathit{Pr}$ results in lesser thermal diffusivity, thereby bringing about a decrease in temperature.

Conclusion

In this analysis of MHD second^-grade nanoliquid over a curved stretched sheet with activation energy is explored. The observations are concluded as follows:

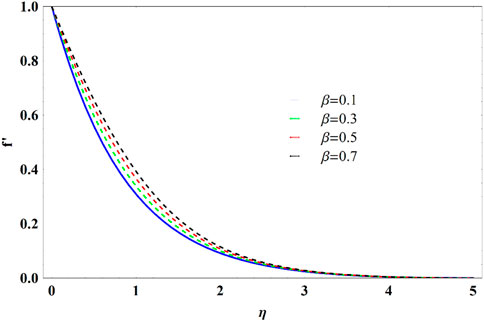
• Increment exists in the momentum and thermal boundary layer thickness when the fluid parameter enhances.

• Velocity distributions show decreasing phenomenon with enhancement in M.

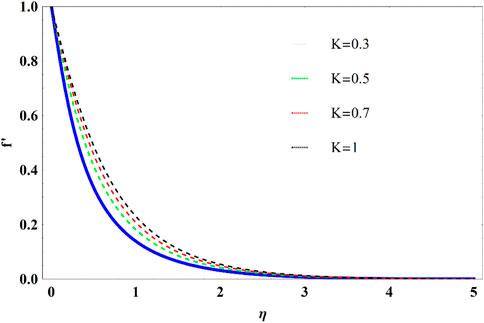
• Both velocity and temperature have increasing behaviour for higher K.

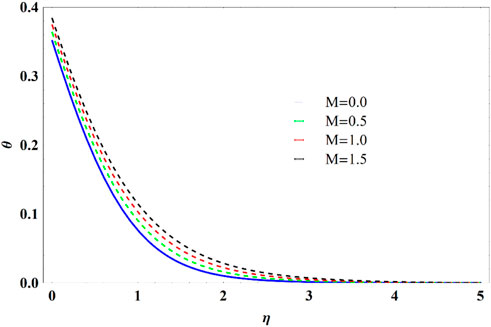
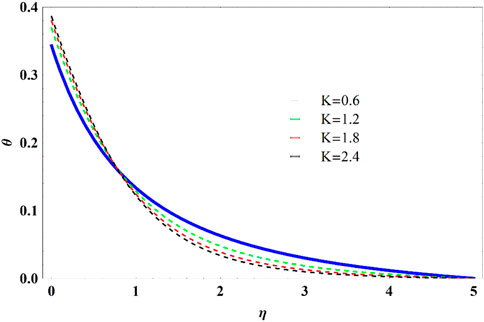
• Convective heating condition enhances the thermal field significantly.

• Brownian movement Nb depreciate for concentration profile.

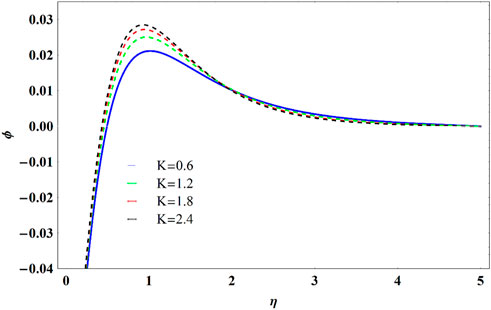
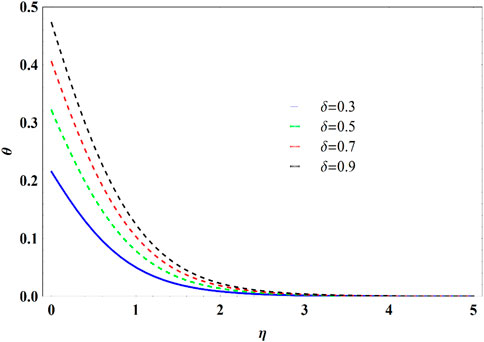
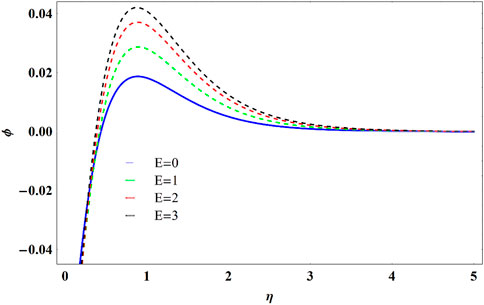
• Concentration is diminished for higher value of$Sc$.

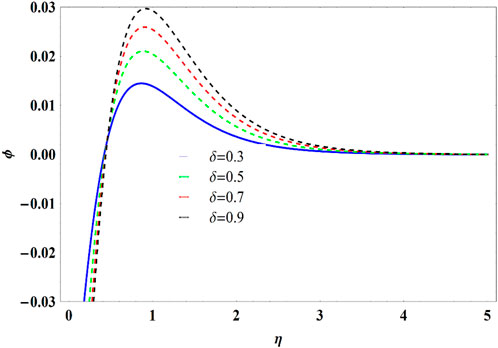
• Increment in fluid parameter $\beta$decreases the friction factor.

• Thermophoresis reduces the volume fraction field and enhances the temperature field.

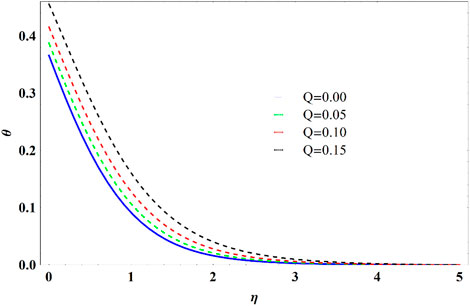
• The temperature profile increases due to temperature heat source Q. An opposite trend is noted in the heat transfer rate.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adnan, A., Khan, I., Shemseldin, A., and Mousa, A. (2022). Numerical energy storage efficiency of MWCNTs-propylene glycol by inducing thermal radiations and combined convection effects in the constitutive model. Front. Chem. 10, 879276. doi:10.3389/fchem.2022.879276

PubMed Abstract | CrossRef Full Text | Google Scholar

Adnan, , and Ashraf, W. (2022). Thermal efficiency in hybrid (Al₂O₃-CuO/H₂O) and ternary hybrid nanofluids (Al₂O₃-CuO-Cu/H₂O) by considering the novel effects of imposed magnetic field and convective heat condition. Waves in Random and Complex Media, 1–16. doi:10.1080/17455030.2022.2092233

CrossRef Full Text | Google Scholar

Adnan, , Ashraf, W., Khan, I., and Andualem, M. (2022). Thermal transport investigation and shear drag at solid-liquid interface of modified permeable radiative-SRID subject to Darcy-Forchheimer fluid flow composed by γ-nanomaterial. Sci. Rep. 12, 3564. doi:10.1038/s41598-022-07045-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Adnan, , Murtaza, R., Hussain, I., Rehman, Z., Khan, I., and Andualem, M. (2022). Thermal enhancement in Falkner-Skan flow of the nanofluid by considering molecular diameter and freezing temperature. Sci. Rep. 12, 9415. doi:10.1038/s41598-022-13423-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Akinbobola, T. E., and Okoya, S. S. (2015). The flow of second grade fluid over a stretching sheet with variable thermal conductivity and viscosity in the presence of heat source/sink. J. Niger. Math. Soc. 34, 331–342. doi:10.1016/j.jnnms.2015.10.002

CrossRef Full Text | Google Scholar

Alamri, S. Z., Khan, A. A., Azeez, M., and Ellahi, R. (2019). Effects of mass transfer on MHD second grade fluid towards stretching cylinder: A novel perspective of cattaneo-christov heat flux model. Phys. Lett. A 383, 276–281. doi:10.1016/j.physleta.2018.10.035

CrossRef Full Text | Google Scholar

Ali, F., Hou, Y., Zahid, M., Rana, M., and Usman, M. (2022). Influence of magnetohydrodynamics and heat transfer on the reverse roll coating of a Jeffrey fluid: A theoretical study. J. Plastic Film Sheeting 38 (1), 72–104. doi:10.1177/87560879211029693

CrossRef Full Text | Google Scholar

Ali, F., Zahid, M., Hou, Y., Manafian, M. A., Rana, M. A., and Hajar, A. (2022). A theoretical study of reverse roll coating for a non-isothermal third-grade fluid under lubrication approximation theory. Math. Problems Eng. 2022, 1–18. Article ID 5029132. doi:10.1155/2022/5029132

CrossRef Full Text | Google Scholar

Ali, F., Hou, Y., Zahid, M., and Rana, M. A. (2020). Theoretical study of the reverse roll coating of non-isothermal magnetohydrodynamics viscoplastic fluid. Coatings 10 (10), 940. MDPI AG. Retrieved from. doi:10.3390/coatings10100940

CrossRef Full Text | Google Scholar

Asogwa, K. K., Alsulami, M. D., Prasannakumara, B. C., and Muhammad, T. (2022). Double diffusive convection and cross diffusion effects on Casson fluid over a Lorentz force driven Riga plate in a porous medium with heat sink: An analytical approach. Int. Commun. Heat Mass Transf. 131, 105761. doi:10.1016/j.icheatmasstransfer.2021.105761

CrossRef Full Text | Google Scholar

Asogwa, K. K., Uwanta, I. J., Momoh, A. A., Omokhuale, E., and Omokhuale, E. (2013). Heat and mass transfer over a vertical plate with periodic Suction and heat sink. Rjaset 5 (1), 07–15. doi:10.19026/rjaset.5.5077

CrossRef Full Text | Google Scholar

Bestman, (1990). Natural convection boundary layer with suction and mass transfer in a porous medium. A. R.Int. J. Energy Res. 14, 389–396. doi:10.1002/er.4440140403

CrossRef Full Text | Google Scholar

Bilal, S., Asogwa, K. K., Alotaibi, H., Malik, M. Y., and Khan, I. (2021). Analytical treatment of radiative Casson fluid over an isothermal inclined Riga surface with aspects of chemically reactive species. Alexandria Eng. J. 60 (5), 4243–4253. doi:10.1016/j.aej.2021.03.015

CrossRef Full Text | Google Scholar

Buongiorono, J. (2006). Convective transport in nanofluid. J. Heat. Trans. 128, 240–250.

Google Scholar

Choi, S. U., and Eastman, J. A. (1995). ASME international mechanical engineering congress & exposition. San Francisco: American Society of Mechanical Engineers (ASME).Enhancing thermal conductivity of fluids with nanoparticles

Google Scholar

Das, K., Sharma, R. P., and Sarkar, A. (2016). Heat and mass transfer of a second grade magnetohydrodynamic fluid over a convectively heated stretching sheet. J. Comput. Des. Eng. 3, 330–336. doi:10.1016/j.jcde.2016.06.001

CrossRef Full Text | Google Scholar

Dawar, A., Shah, Z., and Islam, S. (2020). Mathematical modeling and study of MHD flow of Williamson nanofluid over a nonlinear stretching plate with activation energy. Heat. Trans. 50, 2558–2570. doi:10.1002/htj.21992

CrossRef Full Text | Google Scholar

Dhlamini, M., Mondal, H., Sibanda, P., and Motsa, S. (2022). Activation energy and entropy generation in viscous nanofluid with higher order chemically reacting species. Int. J. Ambient Energy 43, 1495–1507. doi:10.1080/01430750.2019.1710564

CrossRef Full Text | Google Scholar

Eid, M. R., Alsaedi, A., Muhammad, T., and Hayat, T. (2017). Comprehensive analysis of heat transfer of gold-blood nanofluid (Sisko-model) with thermal radiation. Results Phys. 7, 4388–4393. doi:10.1016/j.rinp.2017.11.004

CrossRef Full Text | Google Scholar

Erdogan, M. E., and Imrak, C. E. (2008). Steady flow of a second-grade fluid two coaxial porous cylinders. Mathe. Prob. Engg. doi:10.1155/2007/4265

CrossRef Full Text | Google Scholar

Goud, B. S., Reddy, Y. D., and Asogwa, K. K. (2022). Inspection of chemical reaction and viscous dissipation on MHD convection flow over an infinite vertical plate entrenched in porous medium with Soret effect. Biomass Conv. bioref. doi:10.1007/s13399-022-02886-3

CrossRef Full Text | Google Scholar

Hamid, A., Hashim, K. M., and Khan, M. (2018). Impacts of binary chemical reaction with activation energy on unsteady flow of magneto-Williamson nanofluid. J. Mol. Liq. 262, 435–442. doi:10.1016/j.molliq.2018.04.095

CrossRef Full Text | Google Scholar

Hayat, T., Aziz, A., Muhammad, A., and Alsaedi, A. (2017). On model for flow of Burgers nanofluid with Cattaneo-Christov double diffusion. Chin. J. Phys. 55, 916–929. doi:10.1016/j.cjph.2017.02.017

CrossRef Full Text | Google Scholar

Hayat, T., Aziz, A., Muhammad, T., and Ahmad, B. (20150145332). Influence of magnetic field in three-dimensional flow of couple stress nanofluid over a nonlinearly stretching surface with convective condition. Plos One 10, e0145332. doi:10.1371/journal.pone.0145332

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayat, T., Aziz, A., Muhammad, T., and Ahmad, B. (2016). On magnetohydrodynamic flow of second grade nanofluid over a nonlinear stretching sheet. J. Magnetism Magnetic Mater. 408, 99–106. doi:10.1016/j.jmmm.2016.02.017

CrossRef Full Text | Google Scholar

Hayat, T., Aziz, A., Muhammad, T., and Alsaedi, A. (2018). Effects of binary chemical reaction and Arrhenius activation energy in Darcy-Forchheimer three-dimensional flow of nanofluid subject to rotating frame. J. Therm. Anal. Calorim. 136, 1769–1779. doi:10.1007/s10973-018-7822-6

CrossRef Full Text | Google Scholar

Hayat, T., Muhammad, T., Shehzad, S. A., and Alsaedi, A. (2017). On magnetohydrodynamic flow of nanofluid due to a rotating disk with slip effect: A numerical study. Comput. Methods Appl. Mech. Eng. 315, 467–477. doi:10.1016/j.cma.2016.11.002

CrossRef Full Text | Google Scholar

Hayat, T., Qasim, M., and Mesloub, S. (2011). MHD flow and heat transfer over permeable stretching sheet with slip conditions. Int. J. Numer. Meth. Fluids 66, 963–975. doi:10.1002/fld.2294

CrossRef Full Text | Google Scholar

Hayat, T., Riaz, R., Aziz, A., and Alsaedi, A. (2020). Influence of Arrhenius activation energy in MHD flow of third grade nanofluid over a nonlinear stretching surface with convective heat and mass conditions. Phys. A Stat. Mech. its Appl. 549, 124006. doi:10.1016/j.physa.2019.124006

CrossRef Full Text | Google Scholar

Hsiao, K. (2010). Viscoelastic fluid over a stretching sheet with electromagnetic effects and nonuniform heat source/sink. Math. Problems Eng. 2010, 1–14. Article Article ID 740943. doi:10.1155/2010/740943

CrossRef Full Text | Google Scholar

Ibáñez, G., López, A., Pantoja, J., and Moreira, J. (2016). Entropy generation analysis of a nanofluid flow in MHD porous microchannel with hydrodynamic slip and thermal radiation. Int. J. Heat Mass Transf. 100, 89–97. doi:10.1016/j.ijheatmasstransfer.2016.04.089

CrossRef Full Text | Google Scholar

Imtiaz, M., Mabood, F., Hayat, T., and Alsaedi, A. (2019). Homogeneous-heterogeneous reactions in MHD radiative flow of second grade fluid due to a curved stretching surface. Int. J. Heat Mass Transf. 145, 118781. doi:10.1016/j.ijheatmasstransfer.2019.118781

CrossRef Full Text | Google Scholar

Irfan, M., Khan, W. A., Khan, M., and Gulzar, M. M. (2019). Influence of Arrhenius activation energy in chemically reactive radiative flow of 3D Carreau nanofluid with nonlinear mixed convection. J. Phys. Chem. Solids 125, 141–152. doi:10.1016/j.jpcs.2018.10.016

CrossRef Full Text | Google Scholar

Jamil, M., Rauf, A., Fetecau, C., and Khan, N. A. (2011). Helical flows of second grade fluid due to constantly accelerated shear stresses. Commun. Nonlinear Sci. Numer. Simul. 16, 1959–1969. doi:10.1016/j.cnsns.2010.09.003

CrossRef Full Text | Google Scholar

Jayaprakash, M. C., Asogwa, K. K., Lalitha, K. R., Veeranna, Y., and Sreenivasa, G. T. (2021). Passive control of nanoparticles in stagnation point flow of Oldroyd-B Nanofluid with aspect of magnetic dipole. Proc. Institution Mech. Eng. Part E J. Process Mech. Eng., 095440892110655. doi:10.1177/09544089211065550

CrossRef Full Text | Google Scholar

Khan, A., Shah, Z., Alzahrani, E., and Islam, S. (2020). Entropy generation and thermal analysis for rotary motion of hydromagnetic Casson nanofluid past a rotating cylinder with Joule heating effect. Int. Commun. Heat Mass Transf. 119, 104979. doi:10.1016/j.icheatmasstransfer.2020.104979

CrossRef Full Text | Google Scholar

Khan, S. U., and Shehzad, S. A. (2020). Electrical MHD Carreau nanofluid over porous oscillatory stretching surface with variable thermal conductivity: Application of thermal extrusion system. Phys. A Stat. Mech. It’s Appl. 550, 124–132.

CrossRef Full Text | Google Scholar

Khan, U., Abbasi, A., Ahmed, N., and Mohyud-Din, S. T. (2017). Particle shape, thermal radiations, viscous dissipation and joule heating effects on flow of magneto-nanofluid in a rotating system. Ec 34 (8), 2479–2498. doi:10.1108/EC-04-2017-0149

CrossRef Full Text | Google Scholar

Khan, W. A., and Pop, I. (2010). Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 53, 2477–2483. doi:10.1016/j.ijheatmasstransfer.2010.01.032

CrossRef Full Text | Google Scholar

Khan, W. A., Sultan, F., Ali, M., Shahzad, M., KhanIrfan, M. M., and Irfan, M. (2019). Consequences of activation energy and binary chemical reaction for 3D flow of Cross-nanofluid with radiative heat transfer. J. Braz. Soc. Mech. Sci. Eng. 41, 4. doi:10.1007/s40430-018-1482-0

CrossRef Full Text | Google Scholar

Mabood, F., and Das, K. (2016). Melting heat transfer on hydromagnetic flow of a nanofluid over a stretching sheet with radiation and second-order slip. Eur. Phy. J. Plus 131, 3–42. doi:10.1140/epjp/i2016-16003-1

CrossRef Full Text | Google Scholar

Mahanthesh, B., Gireesha, B. J., and Gorla, R. S. R. (2016). Mixed convection squeezing three-dimensional flow in a rotating channel filled with nanofluid. Int. J. Numer. Methods Heat. Fluid Flow. 26, 1460–1485. doi:10.1108/hff-03-2015-0087

CrossRef Full Text | Google Scholar

Makinde, O. D., and Aziz, A. (2011). Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 50, 1326–1332. doi:10.1016/j.ijthermalsci.2011.02.019

CrossRef Full Text | Google Scholar

Makinde, O. D., Khan, W. A., and Khan, Z. H. (2013). Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. Int. J. Heat Mass Transf. 62, 526–533. doi:10.1016/j.ijheatmasstransfer.2013.03.049

CrossRef Full Text | Google Scholar

Makinde, O. D., Olanrewaju, P. O., and Charles, W. M. (2011). Unsteady convection with chemical reaction and radiative heat transfer past a flat porous plate moving through a binary mixture. Afr. Mat. 22, 65–78. doi:10.1007/s13370-011-0008-z

CrossRef Full Text | Google Scholar

Malvandi, A., Safaei, M. R., Kaffash, M. H., and Ganji, D. D. (2015). MHD mixed convection in a vertical annulus filled with Al2O3-water nanofluid considering nanoparticle migration. J. Magnetism Magnetic Mater. 382, 296–306. doi:10.1016/j.jmmm.2015.01.060

CrossRef Full Text | Google Scholar

Mustafa, M., Hayat, T., Alsaedi, T., and Alsaedi, A. (2017). Buoyancy effects on the MHD nanofluid flow past a vertical surface with chemical reaction and activation energy. Int. J. Heat Mass Transf. 108, 1340–1346. doi:10.1016/j.ijheatmasstransfer.2017.01.029

CrossRef Full Text | Google Scholar

Nadeem, S., Rehman, A., Lee, C., and Lee, J. (2012). Boundary layer flow of second grade fluid in a cylinder with heat transfer. Math. Problems Eng. 2012, 1–13. Article ID 640289. doi:10.1155/2012/640289

CrossRef Full Text | Google Scholar

Rashidi, M. M., and Majid, S. A. (2010). Application of Homotopy Analysis method to the unsteady squeezing flow of second grade fluid between circular plate. Math. Prob 18, 706840.

Google Scholar

Reddy, N. V. B., Kishan, N., and Reddy, C. S. (2019). Melting heat transfer and MHD boundary layer flow of eyring-powell nanofluid over a nonlinear stretching sheet with slip. Int. J. Appl. Mech. Eng. 24, 161–178. doi:10.2478/ijame-2019-0011

CrossRef Full Text | Google Scholar

Shah, Z., Alzahrani, E., Jawad, M., and Khan, U. (2020). Microstructure and inertial characteristics of MHD suspended SWCNTs and MWCNTs based maxwell nanofluid flow with bio-convection and entropy generation past a permeable vertical cone. Coatings 10, 998. doi:10.3390/coatings10100998

CrossRef Full Text | Google Scholar

Shah, Z., Sheikholeslami, M., Ikramullah, K. P., and Kumam, P. (2021). Simulation of entropy optimization and thermal behavior of nanofluid through the porous media. Int. Commun. Heat Mass Transf. 120, 105039. doi:10.1016/j.icheatmasstransfer.2020.105039

CrossRef Full Text | Google Scholar

Sharif, R., Farooq, M. A., and Mushtaq, A. (2019). Magnetohydrodynamic study of variable fluid properties and their impact on nanofluid over an exponentially stretching sheet. J. Nanofluids 8, 1249–1259. doi:10.1166/jon.2019.1671

CrossRef Full Text | Google Scholar

Sheikholeslami, M., Domiri Ganji, D. D., Younus Javed, M. Y., and Ellahi, R. (2015). Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. J. Magnetism Magnetic Mater. 374, 36–43. doi:10.1016/j.jmmm.2014.08.021

CrossRef Full Text | Google Scholar

Sheikholeslami, M., Gorji Bandpy, M. G., Ellahi, R., Hassan, M., and Soleimani, S. (2014). Effects of MHD on Cu-water nanofluid flow and heat transfer by means of CVFEM. J. Magnetism Magnetic Mater. 349, 188–200. doi:10.1016/j.jmmm.2013.08.040

CrossRef Full Text | Google Scholar

Shoaib, M., Raja, M. A. Z., Sabir, M. T., Islam, S., Shah, Z., Kumam, P., et al. (2020). Numerical investigation for rotating flow of MHD hybrid nanofluid with thermal radiation over a stretching sheet. Sci. Rep. 10, 18533. doi:10.1038/s41598-020-75254-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Soid, S. K., Ishak, A., and Pop, I. (2018). MHD flow and heat transfer over a radially stretching/shrinking disk. Chin. J. Phys. 56, 58–66. doi:10.1016/j.cjph.2017.11.022

CrossRef Full Text | Google Scholar

Tan, W., and Masuoka, T. (2005). Stokes' first problem for a second grade fluid in a porous half-space with heated boundary. Int. J. Non-Linear Mech. 40, 515–522. doi:10.1016/j.ijnonlinmec.2004.07.016

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2012). Dual and triple solutions for MHD slip flow of non-Newtonian fluid over a shrinking surface. Comput. Fluids 70, 53–58. doi:10.1016/j.compfluid.2012.01.009

CrossRef Full Text | Google Scholar

Weera, W., Maneengam, A., Saeed, A. M., Aissa, A., Guedri, K., Younis, O., et al. (2022). Effects of branched fins on alumina and N-octadecane melting performance inside energy storage system. Front. Phys. 10, 957025. doi:10.3389/fphy.2022.957025

CrossRef Full Text | Google Scholar

Zuhra, S., Khan, N. S., and Islam, S. (2018). Magnetohydrodynamic second-grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Comp. Appl. Math. 37, 6332–6358. doi:10.1007/s40314-018-0683-6

CrossRef Full Text | Google Scholar

Glossary

${\alpha }_1$ fluid parameter

$\alpha$ thermal diffusivity

s & r

curvilinear co-ordinates

p pressure

Sc Schmidt number

$\sigma$ electrical conductivity

$v$ kinematic viscosity

T fluid temperature

D_B Brownian diffusion coefficient

R radius

$Q$ heat generation/absorption

$T_{\infty }$ ambient temperature

C concentration of the fluid

B₀ magnetic field strength

$D_T$ thermophoretic diffusion coefficient

u and v velocity components

$T_w$ surface temperature

$C_{\infty }$ ambient fluid concentration

$k_r^2$ reaction rate

$\rho$ fluid density

k Boltzmann constant

E_a coefficient of activation energy

$\tau$ nanoparticle heat capacity against base fluid heat capacity

$\mathrm{Pr}$ Prandtl number

$\beta$ fluid parameter

BCs boundary conditions

$K$ curvature parameter

$\delta$ Biot number

Nb Brownian motion

C_w surface concentration

T fluid temperature fluid temperature

${\mathrm{R}\mathrm{e}}_s$ local Reynolds number

$Nt$ thermophoresis

E energy parameter

$\zeta$ reaction rate parameter

${\delta }_1$ temperature difference parameter

t_rs shear stress

q_w heat flux