Research on the Unstable Branch Screening Method for Power System With High-Proportion Wind Power

The sooner the system instability is predicted and the unstable branches are screened, the timelier emergency control can be implemented for a wind power system. In this paper, aiming at the problem that the existing unstable branch screening methods are lack prejudgment, an unstable branch screening method for power system with high-proportion wind power is proposed. Firstly, the equivalent external characteristics model of the wind farm was deduced. And based on this, the out-of-step oscillation characteristics of the power system with high proportion wind power was analyzed. Secondly, based on the oscillation characteristics, line weak-connection index (LWcI) was proposed to quantify the stability margin of a branch. Then an instability prediction method and an unstable branch screening method were proposed based on LWcI and voltage phase angle difference. Finally, the rapidity and effectiveness of the proposed method are verified through the simulation analysis of IEEE-118 system.

1 Introduction

With the proposal of “carbon peaks” and “carbon neutralization” goals, the penetration of renewable energy is increasing rapidly. However, different from synchronous generator, wind power and other renewable energy units have the disadvantages of low inertia and weak poor disturbance immunity, which have a profound impact on the stability of the grid (Liu et al., 2019; Shen and Raksincharoensak, 2021a). Power outage accidents (Nagpal et al., 2018; Alhelou et al., 2019; Liu, 2019; Yang et al., 2021c) in recent years indicate that due to the replacement of synchronous machines by renewable energy sources, the risk of power angle instability is greatly increased, and the development rate of chain fault is greatly accelerated. Therefore, how to prejudge the instability of the system and screen unstable branches as early as possible, so as to reserve more time to guarantee the implementation of emergency control, has become a research hotspot.

Currently, research results about instability criteria are mainly from traditional power systems. For example, Yang (Yang et al., 2006) proposed to use the extended equal area criterion (EEAC) to analyze the transient stability. Yan (Yan et al., 2011) used the maximal Lyapunov exponent (MLE) to prejudge the rotor angle stability. Saunders (Saunders et al., 2014) analyzed transient stability by constructing transient potential energy functions. Yang (Yang et al., 2021b) adopted data-driven method to study power system security and stability problem. This paper was the first study for SCUC problems, it can accommodate the mapping samples of SCUC, and consider the various input factors that affect SCUC decision-making, possessing strong generality, high solution accuracy, and efficiency over traditional methods. The above methods can prejudge the transient stability of the grid quickly using generator information such as rotor angle, but the further application in the emergency control such as the splitting control is limited because the splitting section cannot be determined directly. Therefore, some scholars designed some new instability criterion using the branch response information, such as ucosφ criterion (Yang et al., 2013; Zhang et al., 2021), phase angle criterion (Regulski et al., 2018; Shen et al., 2021a), bus voltage frequency criterion (Zhang et al., 2019; Yang et al., 2022), apparent impedance differential method (Sreenivasachar, 2021; Shen and Raksincharoensak, 2021b) and so on. Compared with methods using generator response information, these methods can not only prejudge the unstable state of the system, but also accurately capture the unstable branches and the splitting section. However, the disadvantage is that these methods do not start until the instability accident has occurred (or approach to instability), thus it is difficult to reserve sufficient time for emergency control.

Research on the instability criterion of the high proportion renewable energy power system is still in the preliminary stage, and relevant work is mainly focused on the influence of wind power integration on transient stability (Ma et al., 2017; Liu et al., 2017; Zheng et al., 2019; Shen et al., 2021b). As for the research on the instability criterion, Wei (Wei et al., 2021; Yang et al., 2021a) and Qin (Li et al., 2021; Qin et al., 2021) respectively analyzed the influence of wind and photovoltaic power integration on oscillation center migration, but failed to propose oscillation center identification method and instability criterion. Chen (Chen et al., 2020; Li et al., 2021) proposed a new transient stability prediction method by defining a new stability index, but still failed to capture the unstable branch. Liu (Liu et al., 2020) proposed to use the slow coherency theory to study the coherency group of wind power system, but the impact of actual faults cannot be fully considered.

Therefore, aiming at the problem that the existing instability criterion lacks prejudgment, a system instability prediction method and an unstable branches screening method are proposed in this paper. which can predict power angle instability earlier and screen unstable branches accurately.

The rest of this paper is organized as follows. In Section 2, the out-of-step oscillation characteristics of the high proportion wind power system is analyzed. In Section 3, the line weak-connection index (LWcI) is proposed to quantify the stability margin, and the unstable branches screening method is proposed. Case study and discussion are shown in Section 4. Section 5 concludes this study by summarizing key findings and contributions of this paper.

2 OUT-OF-STEP Oscillation Characteristics of Wind Power System

2.1 Equivalent External Characteristic Model of Wind Farm

Taking doubly-fed induction generator (DFIG) as an example, the control strategy is shown in Figure 1A (Wang et al., 2015). In steady state, DFIG adopts Maximum Power Point Tracking (MPPT) control strategy. When the system is disturbed, DFIG limits the active power output under the fault ride-through control, and outputs reactive power to support the grid. After the fault is cleared, DFIG switches back to MPPT control.

FIGURE 1

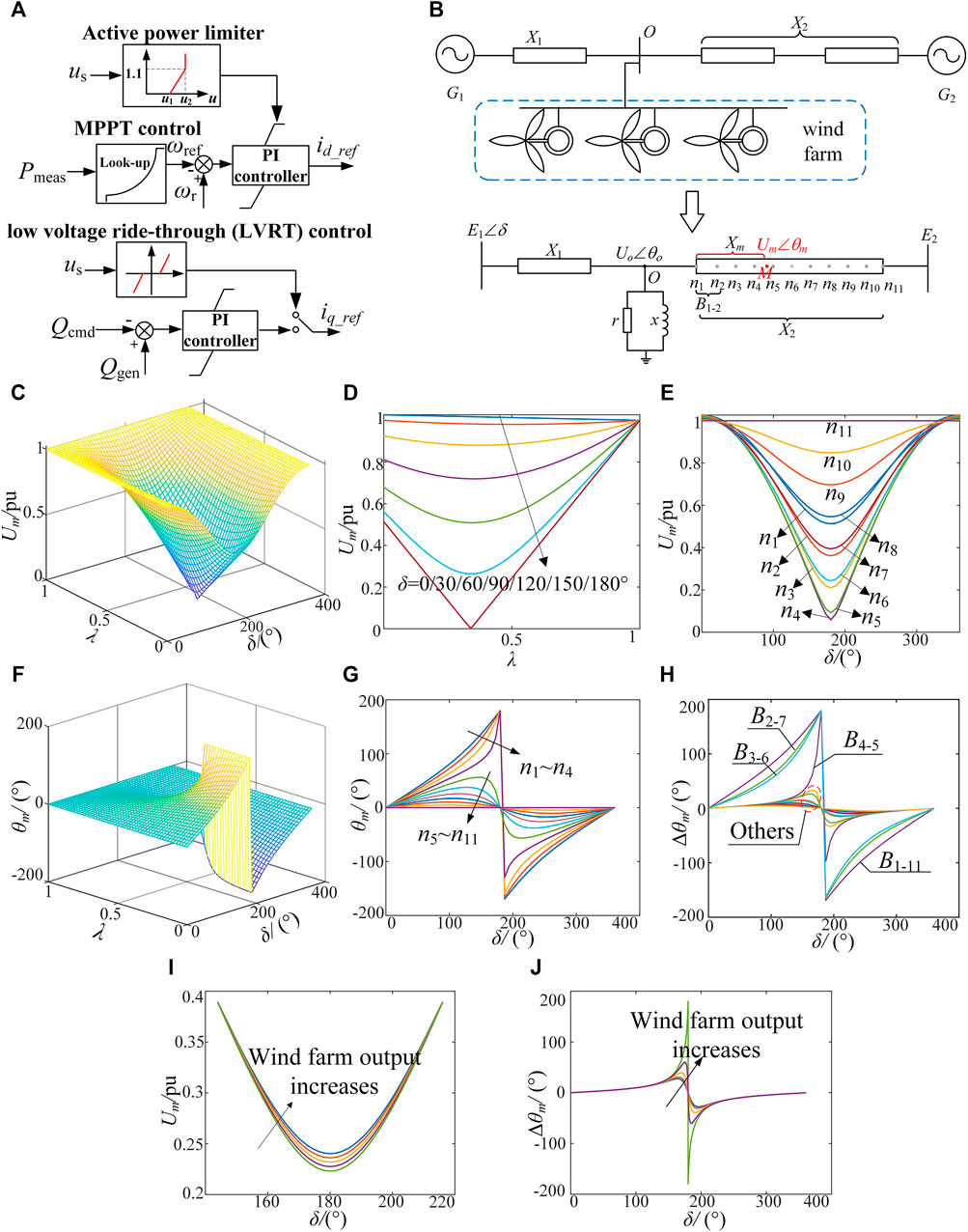
FIGURE 1. Out-of-step oscillation characteristics of wind power system (A) is the control strategy of DFIG (B) is the equivalent two-machine system with DFIG integrated (C) is the distribution law of U_m in δ-λ space (D) is the variation law between U_m and λ (E) is the variation law between U_m and δ (F) is the distribution law of θ_m in δ-λ space (G) is the variation law of θ_m with δ at different position (H) is the variation law between Δθ_m and δ of different branches (I) is the variation law between U_m at point n₄ and δ when wind farm output changes (J) is the variation law between Δθ_m of B_5-6 and δ when wind farm output changes.

Obviously, without additional control, DFIG cannot actively respond to the disturbance of the system. When the system is disturbed, the output power of DFIG do not oscillate like a synchronous generator, but quickly return to the original state. Therefore, there is no power angle swing between DFIG and synchronous generator in electromechanical time scale. Thus, DFIG can be regarded as a power source without inertia, and its equivalent external characteristics can be equivalent to negative resistance and negative reactance in parallel:

$\begin{array}{c}\{\begin{array}{c}r=-\frac{u_s^2}{P_{\mathbf{g}\mathbf{e}\mathbf{n}}}\\ x=-\frac{u_s^2}{Q_{\mathbf{g}\mathbf{e}\mathbf{n}}}\end{array}\end{array}(1)$

Where the negative sign indicates the power injected into the bus.

In addition, if the system is still transient stable after the fault is cleared, DFIG can quickly recover to the pre-fault state and the output power also quickly resumes stability. So the equivalent impedance can be considered constant. If the system is already unstable, the output power of DFIG will oscillate due to the oscillation of the grid voltage. And the equivalent impedance also oscillates. Considering that there is a certain inertia in the system, it takes a certain amount of time from fault removal to complete instability, during which the output power of DFIG does not change dramatically, so it can be simply considered that the equivalent impedance during this period is constant.

2.2 Out-of-step Oscillation Characteristics of Wind Power System

Taking an equivalent two-machine system with a DFIG-based wind farm integrated as an example to analyze the out-of-step oscillation characteristics of wind power system. As shown in Figure 1B, bus O is the common coupling point of the wind farm, and the voltage vector can be expressed as U_o∠θ_o. r and x are equivalent resistance and reactance of the wind farm respectively. E₁ and E₂ are the equivalent potentials of generator G₁ and G₂ respectively, and δ is the rotor angle difference. X₁ and X₂ are equivalent resistance between G₁ and bus O, bus O and G₂, respectively. For convenience analysis, the X₂ is divided into 10 equivalents by points n₁∼n₁₁, and each branch section is represented by B_1-2∼B_10-11. The voltage vector of any point M between the bus O and G₂ is expressed as U_m∠θ_m, and its position function is λ = X_m/X₂, λ∈[0,1].

Based on the node voltage method, the voltage vector of bus O can be expressed as:

$\begin{array}{c}{\dot{\mathit{U}}}_{\mathit{o}}=\frac{{\mathit{Z}}_{\mathbf{\Sigma }}}{\mathit{j}{\mathit{X}}_1}{\mathit{E}}_1{\mathit{e}}^{\mathit{j}\mathit{\delta }}+\frac{{\mathit{Z}}_{\mathbf{\Sigma }}}{\mathit{j}{\mathit{X}}_2}{\mathit{E}}_2\end{array}(2)$

Where $Z_{\Sigma }=\frac{1}{G+\frac{1}{j{X}_1}+\frac{1}{j{X}_2}}$, $G=\frac{1}{r}+\frac{1}{jx}$.

Considering that the active power output of DFIG is limited under low voltage ride-through (LVRT) control, so the $\frac{1}{r}$ is very small, and the real part of $Z_{\Sigma }$ can be ignored. Thus, the expression of the voltage vector at bus O can be rewritten as:

$\begin{array}{c}{\dot{\mathit{U}}}_{\mathit{o}}=\left|{\mathit{Z}}_{\mathbf{\Sigma }}\right|\left(\frac{{\mathit{E}}_1{\mathit{e}}^{\mathit{j}\mathit{\delta }}}{{\mathit{X}}_1}+\frac{{\mathit{E}}_2}{{\mathit{X}}_2}\right)\end{array}(3)$

As shown in Eq. 3, the integration of wind farm changes the amplitude of $Z_{\Sigma }$, thereby changing the voltage amplitude of the common coupling point. The larger the wind farm output power, the greater the $Z_{\Sigma }$, the greater the voltage amplitude of the common coupling point.

In addition, according to Yang (Yang et al., 2013), the unequal voltage on both sides of the branch is one of the reasons for the migration of out-of-step center. When the voltage amplitude on both sides of the branch is unequal, the out-of-step center migrates to the side where the voltage amplitude is smaller. Therefore, the integration of wind power increases the voltage amplitude of the common coupling point, resulting in the unequal voltage amplitude on both sides of the branch, which in turn leads to the migration of the out-of-step center to the side where the voltage amplitude is smaller.

Then, according to Ohm’s law, the following equation exists:

$\begin{array}{c}\frac{{\dot{U}}_o-E_2}{j{X}_2}=\frac{{\dot{U}}_o-{\dot{U}}_m}{j{X}_m}\end{array}(4)$

Therefore, based on Equation 2 and Equation 4, the voltage vector of point M can be expressed as:

$\begin{array}{c}{\dot{U}}_m=\frac{Z_{\mathrm{\Sigma }}}{j{X}_1}(1-\lambda )E_1{e}^{j\delta }+E_2\left[\lambda +\frac{Z_{\mathrm{\Sigma }}}{j{X}_2}(1-\lambda )\right]\end{array}(5)$

Ignoring the real part of $Z_{\Sigma }$, the expression of voltage amplitude and phase angle at point M can be written as:

$\begin{array}{c}\{\begin{array}{c}{U}_m=\sqrt{{\left(\frac{Z_{\mathbf{\Sigma }}(1-\lambda )}{Z_1}{E}_1\mathbf{cos}\mathit{\delta }+E_2\left[\mathit{\lambda }+\frac{Z_{\mathbf{\Sigma }}(1-\mathit{\lambda })}{Z_2}\right]\right)}^2+{\left(\frac{Z_{\mathbf{\Sigma }}(1-\lambda )}{Z_1}{E}_1\sin \delta \right)}^2}\\ {\mathit{\theta }}_m=\mathbf{arctan}\frac{\frac{Z_{\Sigma }}{Z_1}(1-\lambda )E_1\sin \delta }{\frac{Z_{\mathbf{\Sigma }}}{Z_1}(1-\mathit{\lambda })E_1\mathbf{cos}\mathit{\delta }+E_2\left[\mathit{\lambda }+\frac{Z_{\mathbf{\Sigma }}}{Z_2}(1-\mathit{\lambda })\right]}\end{array}\end{array}(6)$

According to Eq. 6, the U_m and θ_m are related to the position function λ, the output power of wind farm, the power angle difference and so on. Thus, assuming that E₁ = E₂ = 1.0, X₂ = 3X₁ = 0.3, and the output power of the wind farm under LVRT control is 0.1 + j0.5, the temporal and spatial distribution law of voltage amplitude U_m and θ_m are shown in Figures 1C–H.

Figures 1C–E show that with the increase of δ, the voltage U_m at any position on the branch decreases and then increases, getting the minimum value when δ = 180°. Meanwhile, the variation amplitude of U_m varies from location to location, so there is always a point where the variation is the most drastic, called the out-of-step center. According to Figure 1E, the out-of-step center is located between n₄ and n₅.

According to Figures 1F–H, when δ increases from 0° to 180°, for the node between the out-of-step center and G₁, θ_m changes monotonically in (0°, 180°). While for the node between the out-of-step center and G₂, θ_m firstly increases and then decreases, and the maximum value is no more than 90°. Therefore, only for the branch where the out-of-step center is located, the voltage phase difference Δθ_m variation rule is consistent with the power angle difference δ.

According to Figures 1I,J, as the output power of wind farm increases, the U_m at point n₄ increases, and the maximum value of Δθ_m at B_5-6 increases until the Δθ_m changes monotonically between (0°, 180°), indicating that the out-of-step center migrates from point n₄ to point n₅, until it completely enters into B_5-6.

In summary, the output power of wind farm changes the flow distribution and voltage level of the system, ultimately affecting the system transient stability and the out-of-step center position. However, the phenomenon that voltage amplitude drops sharply, and the voltage phase angle difference of the branch where the out-of-step center located increases monotonously are still exist, which can be used to predict the transient stability of the system and capture the unstable branch.

3 Instability Prejudgment Criteria and Unstable Branch Screening Method

3.1 Line Weak-Connection Index (LWcI)

According to the conclusion in Section 2, when the out-of-step oscillation occurs, one or more branches loses stability, resulting in a sharp drop of voltage at each point of the branches. Considering that the voltage reduction at the oscillation center is the most severe (Yang et al., 2013), so the voltage of the oscillation center can be used to measure the stability margin of a branch. However, if the oscillation center is not on the branch due to the oscillation center migration, the voltage at one end of the branch is the minimum voltage, which is much greater than the oscillation center voltage. And the result can be conservative and misjudgment can occur. Therefore, in order to prevent misjudgment as the oscillation center migrates outside the branch, the terminal voltage can be used to correct the out-of-step center voltage. Thus, Line weak-connection Index (LWcI) is defined to reflect the stability margin of a branch:

$LWcI =\{\begin{array}{cc}\frac{U_A{U}_B|\mathbf{sin}\mathbf{\Delta }\mathit{\theta }|}{\sqrt{U_A^2+U_B^2-2U_A{U}_B\mathbf{cos}\mathbf{\Delta }\mathit{\theta }}},& U_{AB}>U_{hA} and U_{AB}>U_{hB}\\ \mathbf{min}\left\{U_A,U_B\right\}, & U_{AB}<U_{hA} or U_{AB}<U_{hB}\end{array}(7)$

Where $U_A$ and $U_B$ are terminal voltage amplitude of a branch, $\Delta \theta$ is the voltage angle difference on both sides of a branch, all of which can be obtained through the WAMS system. $U_{AB}=\sqrt{U_A^2+U_B^2-2U_A{U}_B\cos \theta }$, $U_{hA}=\sqrt{U_A^2-U_h^2}$, $U_{hB}=\sqrt{U_B^2-U_h^2}$.

According to Eq. 7, there is a negative correlation between LWCI and Δθ. The larger the Δθ, the smaller the branch stability margin, the smaller the LWcI. Therefore, LWcI can be used to prejudge the transient stability of the wind power system.

Further, according to Section 2.2, only the Δθ of the unstable branch varies monotonously in (−180°, 180°). Thus, there are significant differences in the trajectories between the unstable branches and others in the plane with Δθ as the horizontal axis and LWcI as the vertical axis.

Taking the wind power system in Figure 1B as an example, the trajectory of each branch in LWcI-Δθ plane when the system is stable and unstable is shown in Figure 2.

FIGURE 2

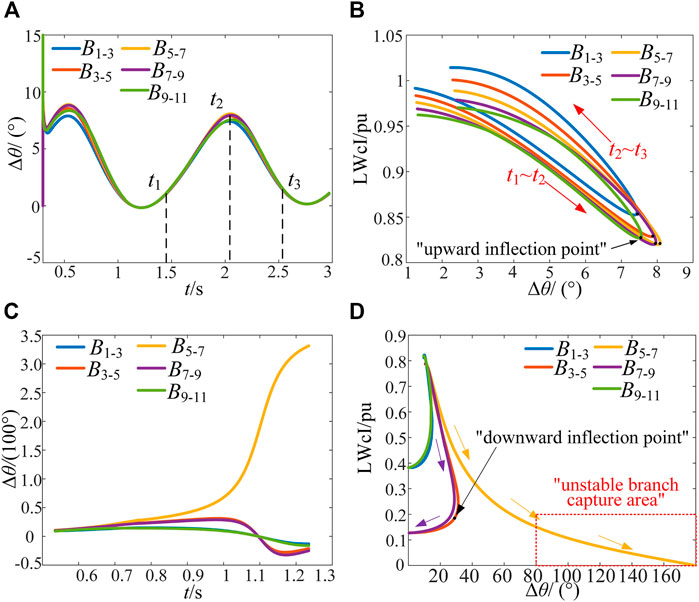
FIGURE 2. Analysis of branch trajectory characteristics (A) is the Δθ-t curve of different branches when the system is stable (B) is the LWcI-Δθ curve of different branches when the system is stable (C) is the Δθ-t curve of different branches when the system is unstable (D) is the LWcI-Δθ curve of different branches when the system is unstable.

As shown in Figures 2A,B, the Δθ of all branches constantly oscillate and decays when the power angle is stable. Taking one period as an example, during t₁∼t₂, the Δθ increases, and the stability margin of all branches decreases, so the trajectories in LWcI-Δθ plane shows a monotonically decreasing trend, that is:

$\begin{array}{c}\{\begin{array}{c}\mathbf{L}\mathbf{W}\mathbf{c}\mathbf{I}\left({\mathit{t}}_{\mathit{i}}\right)-\mathbf{L}\mathbf{W}\mathbf{c}\mathbf{I}\left({\mathit{t}}_{\mathit{i}-1}\right)<0\\ \mathbf{\Delta }\mathit{\theta }\left({\mathit{t}}_{\mathit{i}}\right)-\mathbf{\Delta }\mathit{\theta }\left({\mathit{t}}_{\mathit{i}-1}\right)>0\end{array}\end{array}(8)$

During t₂∼t₃, the Δθ of each branch decreases and the stability margin increases, as shown in Eq. 9. Therefore, an “upward inflection point” appears on the trajectory in LWcI-Δθ plane, indicating that there is no risk of instability in this cycle.

$\begin{array}{c}\{\begin{array}{c}\mathbf{L}\mathbf{W}\mathbf{c}\mathbf{I}\left({\mathit{t}}_{\mathit{i}}\right)-\mathbf{L}\mathbf{W}\mathbf{c}\mathbf{I}\left({\mathit{t}}_{\mathit{i}-1}\right)>0\\ \mathbf{\Delta }\mathit{\theta }\left({\mathit{t}}_{\mathit{i}}\right)-\mathbf{\Delta }\mathit{\theta }\left({\mathit{t}}_{\mathit{i}-1}\right)<0\end{array}\end{array}(9)$

As shown in Figure 2C, only the Δθ of B_5-7 exceeds 180°, which is the unstable branch. Corresponding to Figure 2D, only the trajectory of B_5-7 monotonically decreases, satisfying Eq. 8. While for a branch which is still stable, because the extreme value of Δθ exists, a “downward inflection point” appears. After crossing the “downward inflection point”, as the system is already unstable, the voltage of each node is still decreasing, so the LWcI and Δθ both decrease, as shown in.

$\begin{array}{c}\{\begin{array}{c}\mathbf{L}\mathbf{W}\mathbf{c}\mathbf{I}\left({\mathit{t}}_{\mathit{i}}\right)-\mathbf{L}\mathbf{W}\mathbf{c}\mathbf{I}\left({\mathit{t}}_{\mathit{i}-1}\right)<0\\ \mathbf{\Delta }\mathit{\theta }\left({\mathit{t}}_{\mathit{i}}\right)-\mathbf{\Delta }\mathit{\theta }\left({\mathit{t}}_{\mathit{i}-1}\right)<0\end{array}\end{array}(10)$

Therefore, the “unstable branch capture area”, which is shown in Figure 2D, can be used to prejudge the system instability and screen the unstable branch. If the trajectory of a branch always satisfies Eq. 8 and enters into the “unstable branch capture area”, which can be expressed as in Eq. 11, the stability margin of the branch is significantly reduced and the system is at risk of instability.

$\begin{array}{c}\{\begin{array}{c}\underset{¯}{\mathbf{L}\mathbf{W}\mathbf{c}\mathbf{I}}<\mathbf{L}\mathbf{W}\mathbf{c}\mathbf{I}\left({\mathit{t}}_{\mathit{i}}\right)<\overline{\mathbf{L}\mathbf{W}\mathbf{c}\mathbf{I}}\\ \underset{¯}{\mathbf{\Delta }\mathit{\theta }}<\mathbf{\Delta }\mathit{\theta }\left({\mathit{t}}_{\mathit{i}}\right)<\overline{\mathbf{\Delta }\mathit{\theta }}\end{array}\end{array}(11)$

Where $\underset{¯}{\mathrm{L}\mathrm{W}\mathrm{c}\mathrm{I}}$ and $\overline{\mathrm{L}\mathrm{W}\mathrm{c}\mathrm{I}}$ represent the lower and upper limits of LWCI, respectively. $\underset{¯}{\mathrm{\Delta }\theta }$ and $\overline{\mathrm{\Delta }\theta }$ represent the lower and upper limits of Δθ, respectively.

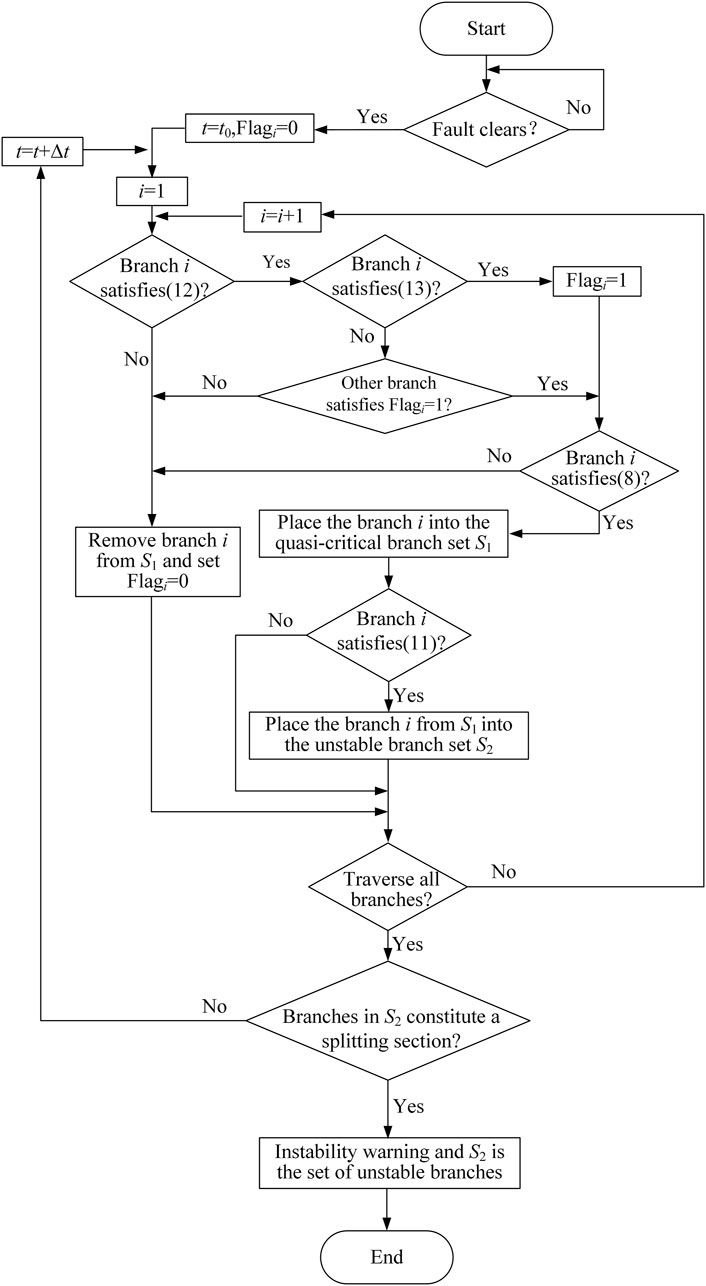
3.2 Unstable Branch Screening Process

The system instability prediction and unstable branch screening process proposed in this paper is shown in Figure 3. After the fault is cleared, the voltage phase angle difference of each branch is firstly calculated. As shown in Eq. 12, if it is greater than the threshold, the stability margin of the branch needs further analysis.

$\begin{array}{c}\mathbf{\Delta }{\mathit{\theta }}_{\mathit{i}}>\mathbf{\Delta }{\mathit{\theta }}_{\mathit{t}\mathit{h}}\end{array}(12)$

FIGURE 3

FIGURE 3. Process of instability prediction and unstable branch screening.

Secondly, calculate LWcI of the branch which satisfies Eq. 12. If the value is lower than the threshold as shown in Eq. 13, the stability margin is already small, and it is necessary to monitor the trajectory in the LWcI-Δθ plane.

$\begin{array}{c}\mathbf{L}\mathbf{W}\mathbf{c}{\mathbf{I}}_{\mathit{i}}\le \mathbf{L}\mathbf{W}\mathbf{c}{\mathbf{I}}_{\mathit{t}\mathit{h}}\end{array}(13)$

Thirdly, if the trajectory of the branch satisfying Equation 12 and Equation 13 in the LWcI-Δθ plane always satisfies Eq. 8, the stability margin of the branch keeps decreasing and the risk of instability keeps increasing. When the trajectory satisfies Eq. 11, that is, it enters into the “unstable branch capture area”, the branch can be considered as an unstable branch.

Finally, traverse all branches in turn, and then repeat the steps above based on the data at the next sampling moment until all unstable branches constitute a splitting section.

4 Case Study

In order to verify the effectiveness of the method proposed in this paper, the IEEE-118 system with wind farm integrated is built on the PSS/E platform. As shown in Figure 4A, the synchronous generators on the bus 89, 100 and 103 are replaced by wind farms, the capacity of which is 450, 300 and 300 MVA, respectively. Meanwhile, another wind farm with capacity of 75MVA is integrated at the bus 25. Assume that the output power of wind farms equals to the rated power, and the load power is 4252 MW, so the penetration rate of wind power is 26.46%.

FIGURE 4

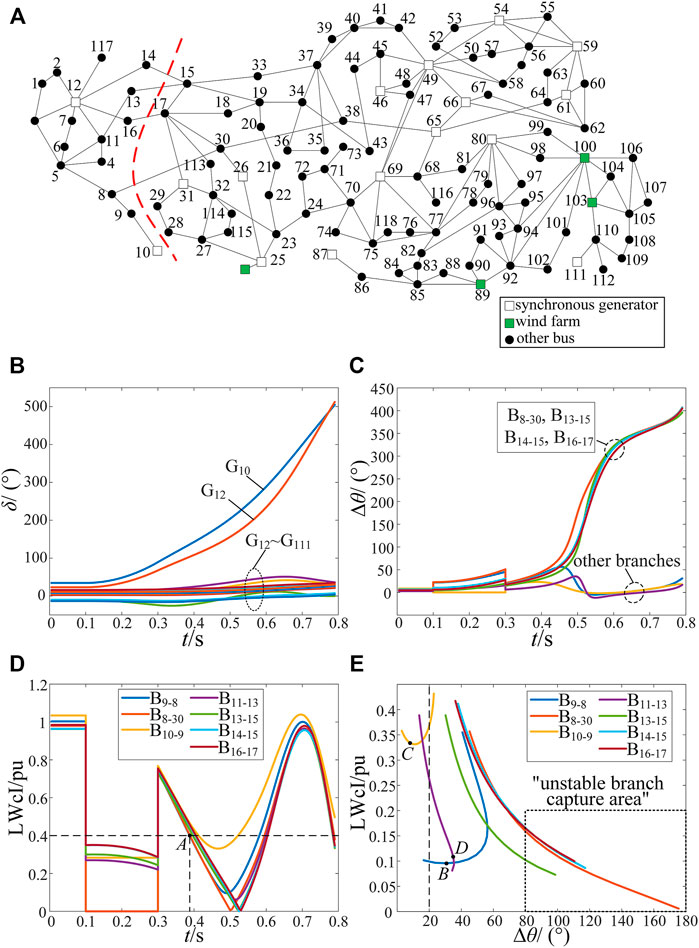
FIGURE 4. The transient response of the IEEE-118 wind power system (A) is the diagram of IEEE-118 system with wind farms (B) is power angle curves of generators (C) is the voltage phase angle difference of branches (D) is the LWcI-t curve of different branches (E) is the LWcI-Δθ curve of different branches during the period of 0.39 and 0.51 s.

According to Eq. 7, when the voltage on both sides is equal and the Δθ is equal to 130°, LWcI = 0.41. Considering that the system is still stable at that time, so set LWcI_th = 0.4,θ_th = 20°. According to the variation rule of Δθ of an unstable branch, set $\underset{¯}{LWcI}=0$, and $\overline{LWcI}=0.2$, $\underset{¯}{\Delta \theta }=80°$ and $\overline{\Delta \theta }=180°$. It is worth mentioning that the setting parameters of the “unstable branch capture area” can be adjusted. The larger the Δθ_m and the smaller the LWcI, the stronger the reliability of the criterion but the worse the speed.

Assume that a three-phase short circuit failure occurs on branch 8–30 at 0.1 s, and lasts 0.2 s. The transient response of the system is shown in Figures 4B–E. Considering that there are too many branches, only the branches whose voltage phase angle difference is greater than 20° are displayed. According to Figures 4B,C, the power angle of G₁₀ and G₁₂ increases rapidly after the fault is cleared, and the voltage phase angle difference of branch 8–30 13–15 14–15 and 16–17 continues to increase, indicating that G₁₀ and G₁₂ lose stability compared with other generators, and the out-of-step center is located on branch 8–30 13–15 14–15 and 16–17.

As shown in Figure 4D, the LWcI of each branch is monotonically decreasing when the fault is removed, indicating that the stability margin of each branch declines continuously. Around 0.39s, the LWcI of branch 8–30 firstly decreases to 0.4, satisfying Eq. 13. And the program begins to monitor the trajectory of each branch in the LWcI-Δθ plane to screen the unstable branches. Corresponding to Figure 4E, the trajectories of the branch 8–30 13–15 14–15 and 16–17 in the LWcI-Δθ plane are always monotonously decreasing, and enter into the " unstable branch capture area” at 0.45, 0.47, 0.48 and 0.49 s respectively. It indicates that the above branches are all unstable and constitute a splitting section, as shown by the red dashed line in Figure 4A. By contrast, at 0.49 s, the trajectories of the branch 9–8, 10–9, 11–13 are located at points B, C and D respectively. Obviously, there have been inflection points in the trajectories of branch 9–8 and 10–9, indicating that there is no out-of-step center on branch 9–8 and 10–9. For branch 11–13, the trajectory still drops monotonically, so it still needs to be monitored. But according to “upward inflection point” in the trajectory during the period of 0.49–0.51 s, it can be judged that branch 11–13 are not unstable branch, either.

In summary, the unstable status of the system can be prejudged and all unstable branches can be accurately screened at 0.49 s using the method in this paper. If the traditional method (Tang et al., 2015) is adopted, the complete splitting section cannot be obtained until the system is already unstable at 0.57 s. Therefore, compared with other methods, the method proposed in this paper can prejudge unstable status of the system and screen all the unstable branches earlier under the premise of ensuring correctness, and thus reserve more time for emergency control such as splitting control.

5 Conclusion

An instability prediction method and an unstable branch screening method are proposed in this paper. Some conclusions are summed up as follows. Firstly, when the wind power system loses stability, the bus voltage amplitude drops, and the voltage phase angle difference of the unstable branch increases, which are the key response information mapped on the branch. Secondly, according to the response information, an indicator called line weak-connection index (LWcI) is built to assess the stability margin of a branch. The smaller the LWcI, the smaller the stability margin of the branch. Thirdly, the trajectories of different branches are different in the plane composed of LWcI and voltage phase angle difference. Only the trajectory of the unstable branch shows a monotonically decreasing trend, while there are “upward inflection points” or “downward inflection points” in the trajectories of other branches. Depending on the difference of trajectory characteristics, the unstable branch can be accurately screened.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

FT was responsible for methodology and revision of the manuscript. XW was responsible for writing the original draft. YG and JQ were responsible for data processing and supervision. JX and XL were responsible for visualization and supervision. All authors contributed, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China under Grant 51977157.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alhelou, H., Hamedani-Golshan, M., Njenda, T., and Siano, P. (2019). A Survey on Power System Blackout and Cascading Events: Research Motivations and Challenges. Energies 12 (4), 682. doi:10.3390/en12040682

CrossRef Full Text | Google Scholar

Chen, Y., Mazhari, S. M., Chung, C. Y., Faried, S. O., and Pal, B. C. (2020). Rotor Angle Stability Prediction of Power Systems with High Wind Power Penetration Using a Stability Index Vector. IEEE Trans. Power Syst. 35 (6), 4632–4643. doi:10.1109/TPWRS.2020.2989725

CrossRef Full Text | Google Scholar

Li, Z., Jiang, W., Abu-Siada, A., Li, Z., Xu, Y., and Liu, S. (2021). Research on a Composite Voltage and Current Measurement Device for HVDC Networks. IEEE Trans. Ind. Electron. 68 (9), 8930–8941. doi:10.1109/TIE.2020.3013772

CrossRef Full Text | Google Scholar

Liu, J., Tang, F., Zhao, J., Liu, D., and Kamwa, I. (2020). Coherency Identification for Wind-Integrated Power System Using Virtual Synchronous Motion Equation. IEEE Trans. Power Syst. 35 (4), 2619–2630. doi:10.1109/TPWRS.2020.2968294

CrossRef Full Text | Google Scholar

Liu, J., Yang, D., Yao, W., Fang, R., Zhao, H., and Wang, B. (2017). PV-based Virtual Synchronous Generator with Variable Inertia to Enhance Power System Transient Stability Utilizing the Energy Storage System. Prot. Control. Mod. Power Syst. 2 (1), 39. doi:10.1186/s41601-017-0070-0

CrossRef Full Text | Google Scholar

Liu, Y. (2019). “Analysis of Brazilian Blackout on March 21st,2018 and Revelations to Security for Hunan Grid,” in 2019 4th International Conference on Intelligent Green Building and Smart Grid (IGBSG), Yichang, China, 06-09 Sep. 2019, 422–426. doi:10.1109/IGBSG.2019.8886219

CrossRef Full Text | Google Scholar

Mosi, L., Zhiyuan, S., Guangshi, L., Mingpo, L., and Xiaoyin, Q. (2019). “Study on the Influence of Large-Scale Wind Power Integration on Transient Stability of Power System,” in 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), Xi'an, China, 21-24 Oct. 2019, 1156–1159. doi:10.1109/APAP47170.2019.9224650

CrossRef Full Text | Google Scholar

Ma, Z., Chen, H., and Chai, Y. (2017). Analysis of Voltage Stability Uncertainty Using Stochastic Response Surface Method Related to Wind Farm Correlation. Prot. Control. Mod. Power Syst. 2 (1), 20. doi:10.1186/s41601-017-0051-3

CrossRef Full Text | Google Scholar

Nagpal, M., Martinich, T. G., Jiao, Z., Manuel, S.-H., Zhang, H. A., and Alimardani, A. (2018). Lessons Learned from a Regional System Blackout and Restoration in BC Hydro. IEEE Trans. Power Deliv. 33 (4), 1954–1961. doi:10.1109/TPWRD.2017.2768046

CrossRef Full Text | Google Scholar

Qin, F., Tang, F., Zhang, T., Wei, X., and Li, Y. (2021). “Impact of Photovoltaic Grid-Connected on Distribution of Power System Disturbed Oscillation Center,” in 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28-30 May 2021. doi:10.1109/CIEEC50170.2021.9510601

CrossRef Full Text | Google Scholar

Regulski, P., Rebizant, W., Kereit, M., and Herrmann, H.-J. (2018). “PMU-based Generator Out-of-step Protection,” in 2018 10th IFAC Symposium on Control of Power and Energy Systems (CPES), Tokyo, Japan, 04-06 Sep. 2018, 79–84. IFAC-PapersOnLine51. doi:10.1016/j.ifacol.2018.11.681

CrossRef Full Text | Google Scholar

Saunders, C. S., Alamuti, M. M., and Taylor, G. A. (2014). “Transient Stability Analysis Using Potential Energy Indices for Determining Critical Generator Sets,” in 2014 IEEE PES General Meeting - Conference & Exposition, National Harbor, MD, USA, 27-31 July. 2014, 1–5. doi:10.1109/PESGM.2014.6939235

CrossRef Full Text | Google Scholar

Shen, X., Ouyang, T., Khajorntraidet, C., Li, Y., Li, S., and Zhuang, J. (2021a). Mixture Density Networks-Based Knock Simulator. Ieee/asme Trans. Mechatron., 1. doi:10.1109/TMECH.2021.3059775

CrossRef Full Text | Google Scholar

Shen, X., Ouyang, T., Yang, N., and Zhuang, J. (2021b). Sample-Based Neural Approximation Approach for Probabilistic Constrained Programs. IEEE Trans. Neural Netw. Learn. Syst., 1–8. doi:10.1109/TNNLS.2021.3102323

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021a). Pedestrian-Aware Statistical Risk Assessment. IEEE Trans. Intell. Transport. Syst., 1–9. doi:10.1109/TITS.2021.3074522

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021b). Statistical Models of Near-Accident Event and Pedestrian Behavior at Non-signalized Intersections. J. Appl. Stat., 1–21. doi:10.1080/02664763.2021.1962263

CrossRef Full Text | Google Scholar

Sreenivasachar, K. (2021). Out-Of-Step Detection on Transmission Lines Using Apparent Impedance Differential Method. IEEE Trans. Power Deliv., 1. doi:10.1109/TPWRD.2021.3125525

CrossRef Full Text | Google Scholar

Tang, F., Yang, J., Liao, Q., Wang, Y., and Jia, J. (2015). Out-of-step Oscillation Splitting Criterion Based on Bus Voltage Frequency. J. Mod. Power Syst. Clean. Energ. 3 (3), 341–352. doi:10.1007/s40565-015-0140-0

CrossRef Full Text | Google Scholar

Wang, Y., Hu, J., Zhang, D., Ye, C., and Li, Q. (2015). “DFIG WT Electromechanical Transient Behaviour Influenced by PLL: Modelling and Analysis,” in International Conference on Renewable Power Generation (RPG 2015), Beijing, China, 17-18 Oct. 2015. doi:10.1049/cp.2015.0331

CrossRef Full Text | Google Scholar

Wei, X., Tang, F., Li, Y., Qin, F., and Zhang, T. (2021). “Study on the Oscillation Center of DFIG-Based Wind Farm Power System,” in 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28-30 May 2021. doi:10.1109/CIEEC50170.2021.9510498

CrossRef Full Text | Google Scholar

Xiaoming, Y., and Dichen, L. (2013). “Research on Dynamic Migration Mechanism of Out-of-step Oscillation center Based on Wide Area Measurement,” in 3rd International Conference on Intelligent System Design and Engineering Applications (ISDEA), Hong Kong, China, 16-18 Jan. 2013. doi:10.1109/ISDEA.2012.275

CrossRef Full Text | Google Scholar

Yan, J., Liu, C.-C., and Vaidya, U. (2011). PMU-based Monitoring of Rotor Angle Dynamics. IEEE Trans. Power Syst. 26 (4), 2125–2133. doi:10.1109/TPWRS.2011.2111465

CrossRef Full Text | Google Scholar

Yang, J., Liao, Q. F., Tang, F., Wang, Y. F., Zhou, Y. T., and Tu, L. (2013). Study on Splitting Criterion Based on Improvement Ucosφ. Amm 433-435, 1313–1319. doi:10.4028/www.scientific.net/AMM.433-435.1313

CrossRef Full Text | Google Scholar

Yang, N., Liu, S., Deng, Y., and Xing, C. (2021a). An Improved Robust SCUC Approach Considering Multiple Uncertainty and Correlation. IEEJ Trans. Elec Electron. Eng. 16 (1), 21–34. doi:10.1002/tee.23265

CrossRef Full Text | Google Scholar

Yang, N., Qin, T., Wu, L., Huang, Y., Huang, Y., Xing, C., et al. (2022). A Multi-Agent Game Based Joint Planning Approach for Electricity-Gas Integrated Energy Systems Considering Wind Power Uncertainty. Electric Power Syst. Res. 204, 107673. doi:10.1016/j.epsr.2021.107673

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Wu, L., Shen, X., Jia, J., Li, Z., et al. (2021b). Intelligent Data-Driven Decision-Making Method for Dynamic Multi-Sequence: An E-Seq2Seq Based SCUC Expert System. IEEE Trans. Ind. Inf., 1. doi:10.1109/TII.2021.3107406

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Xing, C., Ye, D., Jia, J., Chen, D., et al. (2021c). Deep Learning‐based SCUC Decision‐making: An Intelligent Data‐driven Approach with Self‐learning Capabilities. IET Gener. Transm. Distrib. doi:10.1049/gtd2.12315

CrossRef Full Text | Google Scholar

Yang, W., Xue, Y., Song, X., Wu, D., Ge, F., and Xie, D. (2006). “Study on Stability Mechanism for a Typical Fault with EEAC Theory,” in 2006 International Conference on Power System Technology, Chongqing, China, 22-26 Oct. 2006, 1–4. doi:10.1109/ICPST.2006.321621

CrossRef Full Text | Google Scholar

Zhang, L., Xie, Y., Ye, J., Xue, T., Cheng, J., Li, Z., et al. (2021). Intelligent Frequency Control Strategy Based on Reinforcement Learning of Multi-Objective Collaborative Reward Function. Front. Energ. Res. 9, 587. doi:10.3389/fenrg.2021.760525

CrossRef Full Text | Google Scholar

Zhang, S., and Zhang, Y. (2019). Characteristic Analysis and Calculation of Frequencies of Voltages in Out-of-step Oscillation Power System and a Frequency-Based Out-of-step Protection. IEEE Trans. Power Syst. 34 (1), 205–214. doi:10.1109/TPWRS.2018.2866022

CrossRef Full Text | Google Scholar

Zheng, D., Ouyang, J., Xiong, X., and Li, M. (2019). Rotor Angle Stability Control for DFIG‐integrated Power System Considering Phase‐amplitude Characteristics of Transient‐grid Voltage. IET Generation, Transm. Distribution 13 (16), 3549–3555. doi:10.1049/iet-gtd.2018.6960

CrossRef Full Text | Google Scholar