A Fault Signal Processing Method Based on An Improved Prony Algorithm

The fault of power systems introduces a severe challenge in terms of fault recording analysis, and the traditional Prony method cannot perform satisfactorily in the process of signal recordings fitting caused by faults. Therefore, an improved adaptive Prony algorithm is proposed in this article to study the characteristics of fault recordings. Specifically, the search step size is taken as an adaptive variable, and the mean square relative fitting error (MSRFE) is set as the criterion. Then, a large step is employed to rapidly determine an approximate segmentation point in the initial stage of the searching process, and its horizon is gradually reduced to establish an accurate subsegment point. Finally, the Prony algorithm is deployed to analyze the subsegment fitting original signal. The proposed approach has been simulated on an assumed fault signal, and the results validate the accuracy and efficiency of the method.

Introduction

An accurate assessment plays an indispensable role in the safety active control systems (Shen et al., 2021a; Shen and Raksincharoensak, 2021a; Shen and Raksincharoensak, 2021b). Similarly, it is significant to study an effective fault signal analysis method for safe and stable operation in power systems (WangJin et al., 2019; Yang et al., 2019; Yang et al., 2021a; Zhang et al., 2021). Although the technology of fault analysis has already been developed in the existing literature, there are still obstacles to fault identification using the electrical parameters of recording signals. In practice, the state of power systems is monitored using intelligent monitoring terminals in real time. In this way, the fault recording accuracy of the system can be guaranteed, but producing redundant data increases the difficulty of data storage. On the other hand, if only targeted data sampling is carried out for the power grid in case of fault, despite data redundancy can be cut down, it may lead to a lack of recording data and a decrease in recording accuracy. Therefore, the research on fault recording algorithms of power systems has theoretical and practical significance.

For research of signal recordings, it can be analyzed based on steady state and transient (Sajadi et al., 2019). However, the steady-state efficiency of fault identification is bounded. The main reason is that renewable energy to access power systems is becoming increasingly complicated in recent years, and fault analysis has to accord with the requirements of sensitivity, fast, and accurate at the same time (Liao et al., 2018; Zhu et al., 2019; Liu et al., 2020a; Zhu et al., 2020; Wang et al., 2021). These problems have been solved based on transient analysis, showing practical application (Saleh et al., 2015; Yu et al., 2020). In addition, the demand for data is urgent with the rapid development of deep learning technology in power systems (Yang et al., 2018; Yang et al., 2021b). In this context, one of the most critical points is how to extract the characteristic information of transient electrical signals such as voltage, current, and frequency in the research of fault recording. For one thing, the random noise can lightly bury the transient with low energy and small amplitude due to the hybrid of transient and steady state. For another, although the extracted transient characteristics are directly applied in the fault research because the extracted data are massive and irregular (Xu et al., 2017; Shen et al., 2020a; Desai and Makwana, 2021), they still fail to achieve the goal of identifying specific faults. Therefore, the effective extraction of its feature information is crucial to the fault identification problem, which is directly related to the effectiveness and accuracy of fault identification and location.

Numerous works have studied methods to ensure the safety of power grids (Shen et al., 2017; Liu et al., 2020b; Shen et al., 2020b; Li et al., 2021a; Shen et al., 2021b; Hosseini et al., 2021). In the study of Li et al. (2021a), a combined high voltage direct current measurement method is present to improve the extraction accuracy of the measured signal. Besides, some traditional methods such as Hilbert–Huang transform, wavelet transform, and Fourier transform are used in signal processing (Borghetti et al., 2008; Satpathi et al., 2018; Li et al., 2021b). However, the previous methods only separate fault recordings and cannot realize the direct extraction of fault feature information. Its characteristics are obtained directly through the Prony algorithm. In Tawfik and Morcos. (2005), a fault location method integrating the Prony method and artificial neural networks is presented, and the modified scheme provided good accuracy. Yet, when the amplitude of the high-frequency component of the signal is small, the estimation is prone to errors in practice. In Ando. (2020), the difference algorithm is introduced to improve the characteristics of high-frequency components of signals, but its inherent defect has not been tackled. Later, a segmented Prony method is proposed (Jansen and Garoosi, 2000), which divides the signal into different subsegments to ensure good continuity and minor variation in each subsegment, improving the impact on signal characteristics. Nevertheless, the segmented method rarely focused on how to segment to obtain the best analysis results. Based on this, an adaptive Prony method is presented, taking MSRFE as the criterion to realize the adaptive segmentation of the fault signal (Bracale et al., 2007). However, the algorithm searches the subsegment boundary point by enumeration search with a fixed step, resulting in low efficiency. These methods also have the inadequacies of fault signal recognition accuracy for certain signals overall.

In this article, when a power system fault materializes, an improved adaptive Prony method is proposed to describe the accurate variation of electrical parameters. The point of the subsegment is searched by variable step-size strategy, and MSRFE is considered the criterion. The proposed approach has been simulated on an assumed fault signal, and results show that the improved Prony algorithm has higher accuracy and efficiency than the traditional method.

Prony Method Model

The Prony method is formulated as a linear combination of exponential functions to describe the mathematical model of equal distance sampling data and linearized approximate solution. The amplitude, phase, frequency, and attenuation factor of the corresponding signal can be obtained directly by this method. The general solution procedure of the Prony algorithm is as follows.

The continuous signal $x\left(t\right)$ is equidistantly sampled according to the sampling frequency. There are $N$ sampling data obtained and stated as $x\left(0\right),x\left(1\right),\dots ,x(N-1)$, and $x_n$ can be stated in Eqs 1, 2.

$x_n={\displaystyle \sum _{i=1}^p{b}_i{z}_i^n},n=\mathrm{0,1},\dots ,N-1(1)$

$\{\begin{array}{l}{b}_i=A_i{e}^{j{\theta }_i}\\ z_i=e^{(a_i+j2\pi f_i)T_s}\end{array}i=\mathrm{1,2},\cdots ,p,(2)$

where $A_i$, ${\theta }_i$, ${\alpha }_i$, and $f_i$ denote the amplitude, initial phase angle, attenuation factor, and frequency of the ith complex exponential function, respectively; $N$ and $p$ are the number of sampling points and the order, respectively; and $T_s$ is the sampling period.

Then, obtain ${\alpha }_i$ and $z_i$ by constructing the difference equation and its characteristic equation. The singular value decomposition and the least square method should be used to solve ${\alpha }_i$, thereby improving the calculation accuracy (Liu et al., 2008).

Finally, the required parameter can be obtained from previous equations, respectively, as shown in Eq.3.

$\{\begin{array}{l}{A}_i=\left|b_i\right|,\hfill \\ {\theta }_i=\arctan \left(\mathrm{Im}\left(b_i\right)/\mathrm{Re}\left(b_i\right)\right),\hfill \\ {\alpha }_i=\ln \left(z_i\right)/T_s,\hfill \\ f_i=\arctan \left(\mathrm{Im}\left(z_i\right)/\mathrm{Re}\left(z_i\right)\right)/2\pi T_s,\hfill \end{array}(3)$

Improved Prony Algorithm Strategy

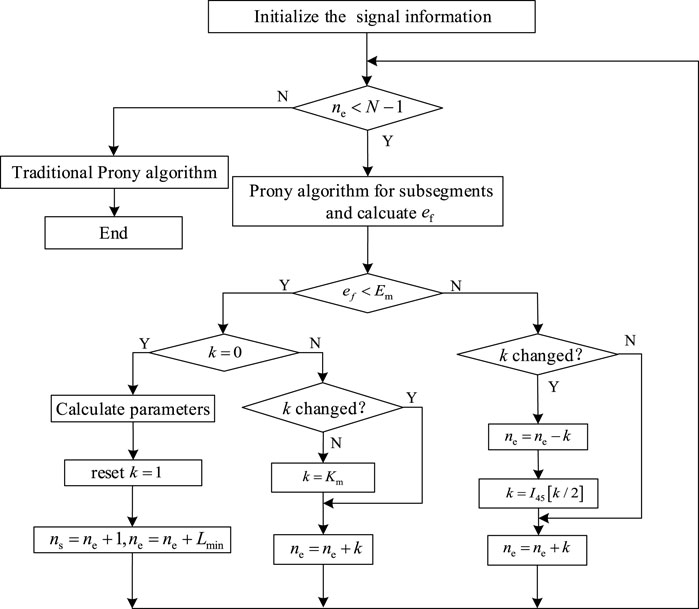
The traditional Prony method has some practical limitations, which may lead to inaccurate fitting results of some specific signals under certain conditions, such as mutation signals when a fault occurs in power systems. Specifically, on the one hand, the search step size of the traditional Prony algorithm is performed with a fixed step. On the other hand, the accuracy of the fitting depends on the selected order. The order is selected artificially by using the traditional method. Although there will be an order to make the fitting accurate, it will take more time for an operation. At the same time, it will also bring extra components. Thus, the method proposed in this article is an improvement in these aspects. The steps involving the parameters of the analysis algorithm are explained as follows.

Step 1: Initialize the original data and parameters, including the signal information, search step $k$, minimum length of subsegment $L_{\min }$, sampling frequency, a maximum value of MSRFE $E_m$, and some remaining parameters.

Step 2: Compare the number of sampling points and the sequence number at the end of the subsegment. When the number of sampling points is greater than the end sequence of the subsegment, the Prony algorithm is directly applied in the subsegment. Otherwise, proceed to step 3.

Step 3: Using the Prony algorithm for subsegments and calculating MSRFE $e_f$. According to MSRFE obtained from the subsegment, whether its value is lower than the maximum value assumed. If MSRFE is lower than its maximum value, proceed to step 4. Otherwise, proceed to step 5.

Step 4: Judge whether the step is equal to 0. If its value is 0, reset the step to 1. Otherwise, judge whether the step was changed, if not changed, then make it set the maximum search step $K_m$.

Step 5: Check the step was changed, and update the corresponding parameters, where $I_{45}$ means rounding.

Step 6: Until the condition of step 2 is met, output the characteristic parameter of signal information.

The detailed procedure is shown in Figure 1, and the expression of MSRFE is shown in Eq. 4.

$MSREF=\frac{1}{n_0}{\displaystyle \sum _{n=n_s,x_n\ne 0}^{n_e}\frac{{\left[x_1\left(n\right)-x\left(n\right)\right]}^2}{x{\left(n\right)}^2}},(4)$

where $x\left(n\right)$ is the real value, $x_1\left(n\right)$ is the estimated value, $n_0$ is the total number of non-zero values in the subsegment, and $n_s$ and $n_e$ are the start sequence number and end sequence number, respectively.

FIGURE 1

FIGURE 1. Flowchart of the proposed, improved adaptive Prony method.

To better evaluate the accuracy of fitting and real value, the root-mean-square error (RMSE) is introduced in this article, which is defined as Eq. 5.

$RMSE=\sqrt{\frac{1}{L}{\displaystyle \sum _{n=1}^N{\left[x_1\left(n\right)-x\left(n\right)\right]}^2}},(5)$

where L is the length of the signal.

Case Study

Instance and Setup

In this article, two types of original voltage signals mimic recordings. The signals under the normal operation and fault are simulated by a smooth and a signal of mutational processes, respectively. The mathematical expression of the smooth voltage signal is shown in Eq. 6, and its parameters are shown in Table 1.

$\begin{array}{c}x\left(t\right)=x_1\left(t\right)+x_2\left(t\right)+x_3\left(t\right)+x_4\left(t\right)\\ =110e^{-2.0t}\cos (2\pi \times 50t+\pi /3)\\ +220e^{-2.0t}\cos (2\pi \times 50t+\pi /6)\\ +220e^{-1.0t}\cos (2\pi \times 80t+\pi /6)\\ +330e^{-0.5t}\cos (2\pi \times 60t+\pi /6),\end{array}(6)$

TABLE 1

TABLE 1. Specific parameters of the smooth signal.

Process Simulation Verification

The total number of sampling points, the sampling period, and the sampling frequency are set 1,000, 0.025 s, and 4 kHz in the simulation, and the start sequence point and the end sequence point are defined as 1 and 20, respectively. The minimum length of the subsegment is 20, and the maximum search step is 20. Figure 2A is plotted to depict the fitting under the normal condition provided by known parameters. We can observe that the simulation results show an excellent agreement is consistent, the order is 230, and the RMSE is so tiny that it can be ignored.

FIGURE 2

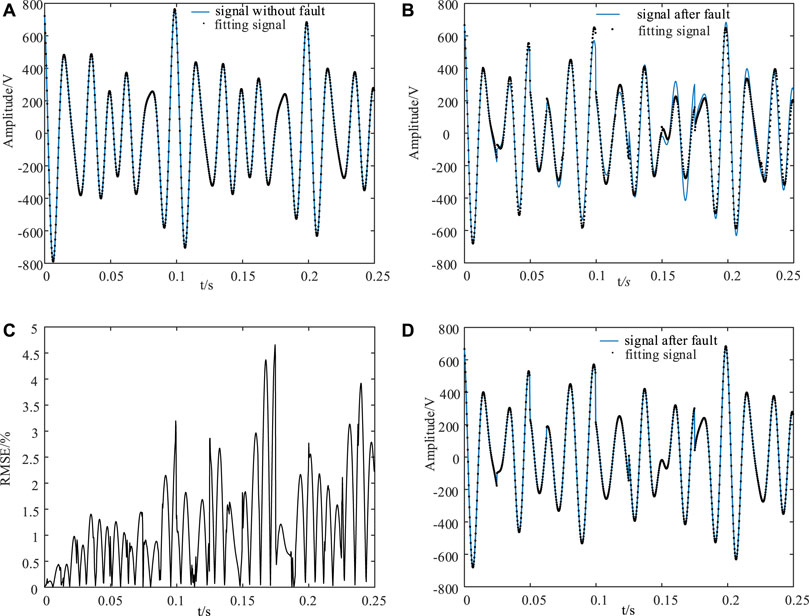
FIGURE 2. Simulation results: (A) Smooth signal simulation based on the traditional Prony method. (B) Mutation signal simulation based on the traditional Prony method. (C) RMSE of the original and fitting signals based on the traditional Prony method. (D) Mutation signal simulation based on the proposed method in this article.

Comparative Simulation Verification

In this case, based on the assumption of the smooth signal, $x_1\left(1:200\right)=0$, $x_2\left(100:500\right)=0$, $x_3\left(200:500\right)=0$, and $x_4\left(400:700\right)=0$ is set in the program to simulate the signal with sudden operation change, and the meaning of $x_1$ from 0 to 0.05 s, $x_2$ from 0.025 to 0.125 s, $x_3$ from 0.05 to 0.125 s, and $x_4$ from 0.1 to 0.175 s all failing to react. The traditional Prony method is used for the fault recording, and the comparison between fitting and the original signal is given in Figure 2B. We can see that the trend of the two signals is deviated. Furthermore, Figure 2C shows the maximum RMSE of both is around 4.5%, and the traditional method is intractable for fitting the signal. The reason for such a difference may be that the traditional method makes decisions by considering the original signal is always continuous and smooth without mutation, and it results in mutagenicity when a fault occurs. It is bound to skip some vital parts while fitting by this method, resulting in some information being ignored. Moreover, the order is often set in advance in the fitting process, and it takes a longer time to manually and continuously adjust the order to fit the original signal.

The previously assumed fault recording signal is analyzed by using the proposed method in this article, and the corresponding result is shown in Figure 2D. We can see that the performance of the proposed method is satisfying, overlapping with the original signal. The reason is that the search step, as a variable, will be segmented when encountering sudden change points in the search stage, avoiding some information being ignored at the critical moment of analysis. On the other hand, the time of fitting is decreased shorter than the traditional Prony method because the order of this method does not need to rule in advance. Meanwhile, to further illustrate the effectiveness of the proposed method, fitting dates are further analyzed. The signal is divided into eight subsegments in total, taking the first two segments of the total date as an example for analysis, as given in Table 2.

TABLE 2

TABLE 2. Component parameters of subsegment based on simulation.

Table 2 indicates that the signal with a component frequency of 50 Hz and an amplitude of 110 V is not present in subsegment 1, so the corresponding data are missing, and the information of other components is accurately extracted. Similarly, the subsegment signal is not affected by components 1 and 2, so there is only relevant information of components 3 and 4 in the subsegment. More specifically, some data obtained through an attenuation process, such as amplitude and initial phase angle, do not get in line with Table 1. By taking the first line of subsegment 2 as an example, the sequence point of subsegment 2 ranges from 100 to 199. After 0.025 s, the accuracy of amplitude becomes $330\times e^{-0.5\ast 0.025}=325.91$, and the initial phase angle transforms from 30 to $\arg \left[30+(2\ast \pi \times 60\times 0.025\times 180)/\pi \right]=-150.0$.

Conclusion

The traditional Prony algorithm is improved in this article. First, the basic model of the Prony algorithm is constructed. On this basis, the mean square relative fitting error is set as the criterion, and the variable step method is used to search the subsegment boundary points. Finally, a fault recording signal processing with an improved adaptive Prony algorithm is proposed. The conclusions based on simulation analysis are as follows.

The improved adaptive Prony algorithm proposed in this article can not only fit the signal under normal conditions but also obtain higher accuracy after the signal characteristics change under abnormal conditions.

In the fault recording signal fitting, the proposed method does not need to set the order in advance. Compared with the traditional Prony algorithm, it can greatly reduce the fitting time and improve the calculation efficiency.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

NY put forward the main research points; YL, JZ, and ZZ contributed to manuscript writing and revision; LD, CY, and ZD performed simulation research; SL, WX, and BZ collected relevant background information; LZ, YH, and XZ revised for grammar and expression. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This article was supported in part by the National Natural Science Foundation of China 51607104.

Conflict of Interest

WX is employed by State Grid Yichang Power Supply Company. XZ is employed by CSG Power Generation Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ando, S. (2020). Frequency-Domain Prony Method for Autoregressive Model Identification and Sinusoidal Parameter Estimation. IEEE Trans. Signal. Process. 68, 3461–3470. doi:10.1109/tsp.2020.2998929

CrossRef Full Text | Google Scholar

Borghetti, A., Bosetti, M., Di Silvestro, M., Nucci, C. A., and Paolone, M. (2008). Continuous-Wavelet Transform for Fault Location in Distribution Power Networks: Definition of Mother Wavelets Inferred from Fault Originated Transients. IEEE Trans. Power Syst. 23 (2), 380–388. doi:10.1109/tpwrs.2008.919249

CrossRef Full Text | Google Scholar

Bracale, A., Caramia, P., and Carpinelli, G. (2007). Adaptive Prony Method for Waveform Distortion Detection in Power Systems. Int. J. Electr. Power Energ. Syst. 29 (5), 371–379. doi:10.1016/j.ijepes.2006.10.005

CrossRef Full Text | Google Scholar

Desai, J. P., and Makwana, V. H. (2021). A Novel Out of Step Relaying Algorithm Based on Wavelet Transform and a Deep Learning Machine Model. Prot. Control. Mod. Power Syst. 6, 40. doi:10.1186/s41601-021-00221-y

CrossRef Full Text | Google Scholar

Hosseini, S. A., Taheri, B., Abyaneh, H. A., and Razavi, F. (2021). Comprehensive Power Swing Detection by Current Signal Modeling and Prediction Using the GMDH Method. Prot. Control. Mod. Power Syst. 6, 15. doi:10.1186/s41601-021-00193-z

CrossRef Full Text | Google Scholar

Jansen, B. H., and Garoosi, V. (2000). Development and Evaluation of the Piecewise Prony Method for Evoked Potential Analysis. IEEE Trans. Biomed. Eng. 47 (12), 1549–1554. doi:10.1109/10.887935

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, D., Ukil, A., Satpathi, K., and Yeap, Y. M. (2021). Hilbert-huang Transform Based Transient Analysis in Voltage Source Converter Interfaced Direct Current System. IEEE Trans. Ind. Electron. 68 (11), 11014–11025. doi:10.1109/tie.2020.3038056

CrossRef Full Text | Google Scholar

Li, Z., Jiang, W., Abu-Siada, A., Li, Z., Xu, Y., and Liu, S. (2021). Research on a Composite Voltage and Current Measurement Device for HVDC Networks. IEEE Trans. Ind. Electron. 68 (9), 8930–8941. doi:10.1109/tie.2020.3013772

CrossRef Full Text | Google Scholar

Liao, S., Xu, J., Sun, Y., Bao, Y., and Tang, B. (2018). Control of Energy-Intensive Load for Power Smoothing in Wind Power Plants. IEEE Trans. Power Syst. 33 (6), 6142–6154. doi:10.1109/TPWRS.2018.2834940

CrossRef Full Text | Google Scholar

Liu, D., Hu, W., and Chen, Z. (2008). SVD-TLS Extending Prony Algorithm for Extracting UWB Radar Target Feature. J. Syst. Eng. Electron. 19 (2), 286–291. doi:10.1016/S1004-4132(08)60080-8

CrossRef Full Text | Google Scholar

Liu, S., Liu, L., Fan, Y., Zhang, L., Huang, Y., Zhang, T., et al. (2020). An Integrated Scheme for Online Dynamic Security Assessment Based on Partial Mutual Information and Iterated Random Forest. IEEE Trans. Smart Grid 11 (4), 3606–3619. doi:10.1109/tsg.2020.2991335

CrossRef Full Text | Google Scholar

Liu, Y., Yang, N., Dong, B., Wu, L., Yan, J., Shen, X., et al. (2020). Multi-Lateral Participants Decision-Making: A Distribution System Planning Approach with Incomplete Information Game. IEEE Access 8, 88933–88950. doi:10.1109/access.2020.2991181

CrossRef Full Text | Google Scholar

Sajadi, A., Kolacinski, R. M., Clark, K., and Loparo, K. A. (2019). Transient Stability Analysis for Offshore Wind Power Plant Integration Planning Studies-Part I: Short-Term Faults. IEEE Trans. Ind. Applicat. 55 (1), 182–192. doi:10.1109/tia.2018.2868550

CrossRef Full Text | Google Scholar

Saleh, S., Aljankawey, A., Errouissi, R., and Castillo-Guerra, E. (2015). Extracting the Phase of Fault Currents: A New Approach for Identifying Arc Flash Faults. IEEE Trans. Ind. Applicat. 52 (2), 1. doi:10.1109/tia.2015.2483698

CrossRef Full Text | Google Scholar

Satpathi, K., Yeap, Y. M., Ukil, A., and Geddada, N. (2018). Short-Time Fourier Transform Based Transient Analysis of VSC Interfaced Point-to-Point DC System. IEEE Trans. Ind. Electron. 65 (5), 4080–4091. doi:10.1109/tie.2017.2758745

CrossRef Full Text | Google Scholar

Shen, X., Ouyang, T., Khajorntraidet, C., Li, Y., Li, S., and Zhuang, J. (2021a). Mixture Density Networks-Based Knock Simulator. Ieee/asme Trans. Mechatron., 1. doi:10.1109/tmech.2021.3059775

CrossRef Full Text | Google Scholar

Shen, X., Ouyang, T., Yang, N., and Zhuang, J. (2021b). Sample-Based Neural Approximation Approach for Probabilistic Constrained Programs. IEEE Trans. Neural Netw. Learn. Syst., 1–8. doi:10.1109/tnnls.2021.3102323

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021). Pedestrian-aware Statistical Risk Assessment. IEEE Trans. Intell. Transport. Syst., 1–9. doi:10.1109/tits.2021.3074522

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021). Statistical Models of Near-Accident Event and Pedestrian Behavior at Non-signalized Intersections. J. Appl. Stat., 1–21. doi:10.1080/02664763.2021.1962263

CrossRef Full Text | Google Scholar

Shen, X., Zhang, X., Ouyang, T., Li, Y., and Raksincharoensak, P. (2020). Cooperative Comfortable-Driving at Signalized Intersections for Connected and Automated Vehicles. IEEE Robot. Autom. Lett. 5 (4), 6247–6254. doi:10.1109/lra.2020.3014010

CrossRef Full Text | Google Scholar

Shen, X., Zhang, Y., Sata, K., and Shen, T. (2020). Gaussian Mixture Model Clustering-Based Knock Threshold Learning in Automotive Engines. Ieee/asme Trans. Mechatron. 25 (6), 2981–2991. doi:10.1109/tmech.2020.3000732

CrossRef Full Text | Google Scholar

Shen, X., Zhang, Y., Shen, T., and Khajorntraidet, C. (2017). Spark advance Self-Optimization with Knock Probability Threshold for Lean-Burn Operation Mode of SI Engine. Energy 122, 1–10. doi:10.1016/j.energy.2017.01.065

CrossRef Full Text | Google Scholar

Tawfik, M., and Morcos, M. (2005). On the Use of Prony Method to Locate Faults in Loop Systems by Utilizing Modal Parameters of Fault Current. IEEE Trans. Power Deliv. 20 (1), 532–534. doi:10.1109/tpwrd.2004.839739

CrossRef Full Text | Google Scholar

Wang, C., Mei, S., Yu, H., Cheng, S., Du, L., and Yang, P. (2021). Unintentional Islanding Transition Control Strategy for Three-/single-phase Multimicrogrids Based on Artificial Emotional Reinforcement Learning. IEEE Syst. J. 15, 5464–5475. doi:10.1109/jsyst.2021.3074296

CrossRef Full Text | Google Scholar

WangJin, Q. T., Jin, T., and Mohamed, M. A. (2019). An Innovative Minimum Hitting Set Algorithm for Model-Based Fault Diagnosis in Power Distribution Network. IEEE Access 7, 30683–30692. doi:10.1109/access.2019.2902598

CrossRef Full Text | Google Scholar

Xu, Y., Sun, Y., Wan, J., Liu, X., and Song, Z. (2017). Industrial Big Data for Fault Diagnosis: Taxonomy, Review, and Applications. IEEE Access 5, 17368–17380. doi:10.1109/access.2017.2731945

CrossRef Full Text | Google Scholar

Yang, N., Huang, Y., Hou, D., Liu, S., Ye, D., Dong, B., et al. (2019). Adaptive Nonparametric Kernel Density Estimation Approach for Joint Probability Density Function Modeling of Multiple Wind Farms. Energies 12 (7), 1356. doi:10.3390/en12071356

CrossRef Full Text | Google Scholar

Yang, N., Liu, S., Deng, Y., and Xing, C. (2021). An Improved Robust SCUC Approach Considering Multiple Uncertainty and Correlation. IEEJ Trans. Elec Electron. Eng. 16 (1), 21–34. doi:10.1002/tee.23265

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Wu, L., Shen, X., Jia, J., Li, Z., et al. (2021). Intelligent Data-Driven Decision-Making Method for Dynamic Multi-Sequence: An E-Seq2Seq Based SCUC Expert System. IEEE Trans. Ind. Inf. 1, 1. doi:10.1109/tii.2021.3107406

CrossRef Full Text | Google Scholar

Yang, N., Ye, D., Zhou, Z., Cui, J., Chen, D., and Wang, X. (2018). Research on Modelling and Solution of Stochastic SCUC under AC Power Flow Constraints. IET Generation, Transm. Distribution 12 (15), 3618–3625. doi:10.1049/iet-gtd.2017.1845

CrossRef Full Text | Google Scholar

Yu, J., Zhang, Z., Xu, Z., and Wang, G. (2020). An Equivalent Calculation Method for Pole-to-Ground Fault Transient Characteristics of Symmetrical Monopolar MMC Based DC Grid. IEEE Access 8, 123952–123965. doi:10.1109/access.2020.3006028

CrossRef Full Text | Google Scholar

Zhang, L., Xie, Y., Ye, J., Xue, T., Cheng, J., Li, Z., et al. (2021). Intelligent Frequency Control Strategy Based on Reinforcement Learning of Multi-Objective Collaborative Reward Function. Front. Energ. Res. 9, 760525. doi:10.3389/fenrg.2021.760525

CrossRef Full Text | Google Scholar

Zhu, B., Ding, F., and Vilathgamuwa, D. M. (2020). Coat Circuits for DC-DC Converters to Improve Voltage Conversion Ratio. IEEE Trans. Power Electron. 35 (4), 3679–3687. doi:10.1109/tpel.2019.2934726

CrossRef Full Text | Google Scholar

Zhu, B., Zeng, Q., Chen, Y., Zhao, Y., and Liu, S. (2019). A Dual-Input High Step-Up DC/DC Converter with ZVT Auxiliary Circuit. IEEE Trans. Energ. Convers. 34 (1), 161–169. doi:10.1109/TEC.2018.2876303

CrossRef Full Text | Google Scholar