Lumped-Circuits Model of Lossless Transmission Lines and Its Numerical Characteristics

Aiming at the lumped-circuits model of the lossless transmission line in the digital simulation, the article discusses and analyzes the unit step response generation of the lumped-circuits model by comparing the numerical simulation results of the implicit trapezoidal method, the implicit Euler method, and a multi-step formula. The root cause of numerical oscillations pointed out that using the L-stable numerical algorithm to indirectly simulate the dynamic response of the lumped-circuits model is a numerical method that does not truly reflect the original model, but it can directly reflect the true dynamic response of the lossless transmission line. In this study, a method for determining the chained number in the digital simulation of a lumped-circuits model is given. The simulation results prove the effectiveness of the method.

Introduction

In the digital simulation model of lossless transmission lines, the model using the circuit equivalent model to study the physical characteristics of transmission lines is called the lumped-circuits model, which is different from the classical finite-difference time-domain algorithm model. As the name suggests, the lumped-circuits is different from the distributed parameter circuit, which uses a partial differential equation to describe the voltage fluctuation process. The former uses lumped inductance and capacitance to approximate the physical characteristics of lossless transmission lines with distributed parameter characteristics. Cui (2018) pointed out that there are fundamental differences between the two, and they cannot be completely equivalent in physical characteristics. Therefore, only appropriate approximation methods (Shen et al., 2020; Shen et al., 2021; Shen and Raksincharoensak, 2021) can be found to ensure that the lumped-circuits of the transmission line can be approximately equivalent to the distributed parameter circuit.

The modeling of the transmission line transient response needs to select an appropriate physical model according to the frequency of the system research signal. The lumped-circuits model is a commonly used approximate model for physical simulation and digital simulation of transmission lines, but its significant problem in digital simulation is numerical oscillation (Ye et al., 2021). In order to solve this problem, various numerical algorithms are used to solve the transient response of transmission lines, but there are different defects in dealing with numerical oscillation. Root-matching techniques (Watson and Irwin, 1998) solve this problem well and are the main algorithm to solve the problem of numerical oscillation at present. Song et al. (2020) proposed an efficient electromagnetic transient simulation method based on the discrete similarity principle, which further expanded the application scope of root-matching techniques. Although the root-matching techniques can better solve the numerical oscillation problem, in a strict sense, these discrete calculation principles cannot ensure that the physical characteristics of the transmission line do not change. Therefore, the research on the numerical algorithm that can keep the physical structure of the transmission line from distortion has become a very important research subject.

In addition, the number of the chained circuits is a key parameter for the lumped-circuits of lossless transmission lines in physical analogy. Cui (2017) gives an estimation formula for determining the chained number of the lumped-circuits in the physical analogy of lossless transmission lines. This formula is also useful for the estimation (Yang et al., 2019a; Yang et al., 2019b; Yang et al., 2021a; Zhang et al., 2021) of the chained number in the digital simulation, but it can not be directly applied. The influence of the approximation error (Yang et al., 2018; Yang et al., 2021b) of the numerical algorithm needs to be considered.

For a long time, the lumped-circuits model of lossless transmission lines was often used as the electromagnetic simulation model of transmission lines (Paul, 1994; Min and Mao, 2007), but little is known about the numerical characteristics of the model. Starting from the characteristics of three lumped-circuits, the numerical characteristics of the lumped-circuits model, including its unit step response and sine excitation response, are studied in detail. The relevant conclusions can provide reference for the application range and method of the lumped-circuits model of lossless transmission lines. In addition, this study pointed out that the numerical algorithm of symplectic conservation can accurately simulate the physical characteristics of lossless transmission lines.

Lumped-Circuits Model of Lossless Transmission Lines

Basic Lumped-Circuits Model

Usually, the state space model is used to solve the dynamic response of lossless transmission lines. First, the lossless transmission lines need to be discretized in space to obtain blocks of $T$-type circuits, $\text{Γ}$-type or inverse $\text{Γ}$- type circuits, and $\text{Π}$-type circuits. As shown in Figure 1, it is a schematic diagram of a lossless transmission line, with an inductance per unit length of $L_0$ and a capacitance per unit length of $C_0$, and the total length of the line is recorded as $l$. If the transmission line is evenly divided into $M$ segments, the inductance parameter of a single circuit segment is $L=L_{0}l\mathrm{∕}M$ and the capacitance parameter is $C=C_{0}l\mathrm{∕}M$.

FIGURE 1

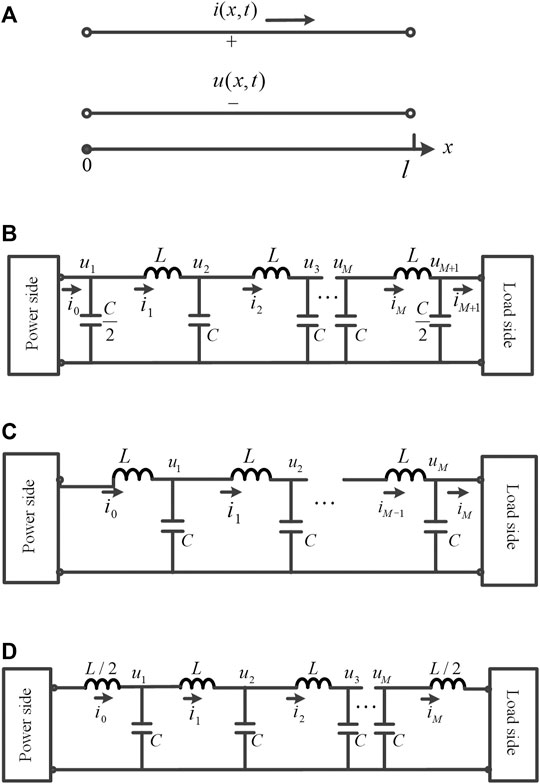
FIGURE 1. Lossless transmission line and its three equivalent lumped-circuits. (A) Lossless transmission line. (B) Lumped-circuits consisted of M $\text{Π}$-type circuits. (C) Lumped-circuits consisted of M inverse $\text{Γ}$-type circuits. (D) Lumped-circuits consisted of M $T$-type circuits.

According to the topological characteristics of the above lumped-circuits, it is not difficult to see that the lumped-circuits consisting of chained inverse $\text{Γ}$-type circuits is suitable for the situation where the ideal power supply is a unit step signal and the load is a pure capacitive load. The lumped-circuits composed of chained $\text{Π}$- type circuits are more suitable for the case that the power supply is a non-ideal power supply, that is, the power supply with internal impedance, and the load is pure capacitive load. However, for ideal power supply, such as the unit step signal, in order to facilitate the application of boundary conditions at the head end during simulation, a small resistance can be artificially inserted in series in the ideal power circuit, so that the step response characteristics of the circuit can be simulated. The lumped-circuit composed of chained $T$-type circuits is more suitable for ideal or non-ideal power supply, and the load is the pure inductance or resistance inductance series branch. It is worth noting that the above discussion is only based on not adding more system state variables. Without this limitation, the above three lumped-circuits are applicable to any form of load combination.

Dynamic Response of the Lumped-Circuits Model

When the lossless transmission line shown in Figure 1A is connected with the characteristic impedance $Z_c$, at this time, the head end voltage source $u_{es}$ is transmitted to the terminal at the traveling wave velocity $v={\left(\sqrt{L_0{C}_0}\right)}^{-1}$, and there is no reverse traveling wave of the voltage, that is, the ending voltage amplitude has no attenuation, but the phase lags behind the head-end voltage wave by a delay time $t_L=l\mathrm{∕}v$. In this case, through the Fourier analysis of the ending voltage, it is obtained that the frequency response characteristic of the ending voltage transfer function when the terminal is matching is as follows:

$H\left(l,j\omega \right)=e^{-j\omega t_L}(1)$

The amplitude-frequency characteristics and phase-frequency characteristics of Eq. 1 are as follows:

$\left|H\left(l,j\omega \right)\right|=1(2)$

$\phi \left(l,j\omega \right)=-\omega t_L(3)$

where $\omega$ is the angle frequency. Eqs. 4, 5 are the necessary conditions for digital simulation of the lossless transmission line and are also the key evaluation indexes to test the quality of the numerical algorithm.

For the lumped-circuits shown in Figures 1B,D, when the terminal is matched, the frequency response characteristic of the ending voltage transfer function is as follows (Cui, 2017; Cui, 2018):

$\left|H_M\left(j\omega t_l\right)\right|=\{\begin{array}{c}1, \omega t_l\le 2rad\\ {\left(\omega t_l\right)}^{-2M}, \omega t_l>2rad\end{array}(4)$

${\phi }_M\left(j\omega t_l\right)=\{\begin{array}{c}-2M arscin\left(\frac{\omega t_l}{2}\right), \omega t_l\le 2rad\\ 0, \omega t_l>2rad\end{array}(5)$

where $t_l$ represents the propagation time of the forward voltage traveling wave along the transmission line with length $l/M$.

As shown in Figure 2A, the amplitude-frequency response curve of the lumped-circuits when $M$ is different is given. It can be seen that when $M$ is greater than or equal to 5, the amplitude-frequency response characteristics of the lumped-circuits show the characteristics of an ideal low-pass filter, and the cut-off frequency is ${\omega }_c=2\mathrm{∕}{t}_l$. In other words, if the frequency of the excitation source is greater than ${\omega }_c$, the voltage signal transmitted to the transmission line terminal will be seriously distorted. In addition, in order to ensure that the phase error of the ending voltage signal is small, $\omega \le 1\mathrm{∕}{t}_l$ must be made. Therefore, when using the numerical method to analyze the lumped-circuits model of lossless transmission lines in the time domain, the frequency of the excitation source $\omega \le {\omega }_c$ must be met to ensure that the amplitude-frequency response is constant 1, $\omega \le {\omega }_c\mathrm{∕}2$ as far as possible to ensure a small phase error, so as to ensure the integrity of the signal in the transmission process.

FIGURE 2

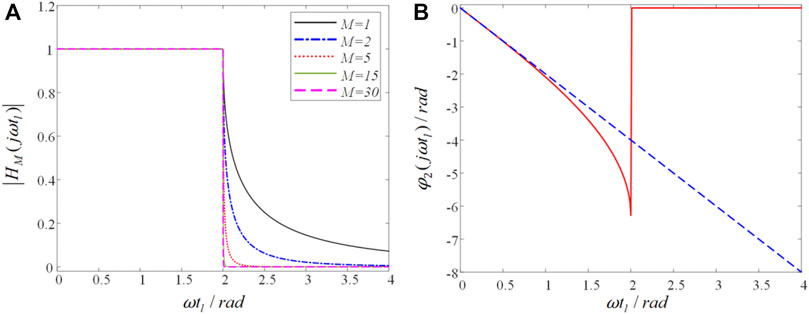
FIGURE 2. Frequency response curve. (A) Amplitude-frequency response curve when $M$ takes different values. (B) Phase-frequency response curve when $M=2$.

Although it is theoretically possible to meet the property that the amplitude-frequency response of the lossless transmission line is always 1 and the phase relative error is 4.72% by physically controlling the frequency of the excitation source, it is inevitable to introduce numerical errors when using the numerical integration algorithm to solve the state space equation of the lumped-circuits (Lei et al., 2009). Therefore, reducing and avoiding the amplitude and phase errors caused by numerical calculation is the problem to be solved in this study.

Numerical Characteristics of the Lumped-Circuits Model

Figure 3A shows an example of a double conductor lossless transmission line. The wave impedance of the lossless transmission line is $Z_0$, the wave velocity is $c$, the total length of the line is $l$, the ideal voltage source $u_{es}$ at the head end of the transmission line is a 100-$V$ step signal with time delay, and the load end is connected with a capacitor $C_L$ of 1,000 $pF$. The lumped-circuits models shown in Figures 1B,D are used for numerical modeling, and the implicit trapezoidal integral formula, the implicit Euler method, and a linear multi-step method in the study by (Wang et al., 2019) are used for numerical simulation, and the respective characteristics of the model and the algorithm are compared and analyzed. The calculation formats of the three numerical algorithms are introduced as follows.

For the Following Initial Value Problems

$\{\begin{array}{c}\dot{x}=f\left(x,t\right)\\ x\left(t=0\right)=x_0\end{array}$

The approximate formula of the implicit trapezoidal integral formula (TR) for approximately solving the state variable $x\left(t\right)$ is as follows:

$x_{j+1}=x_j+\frac{h}{2}\left[f\left(x_{j+1},t_{j+1}\right)+f\left(x_j,t_j\right)\right]$

where $x_{j+1}\approx x\left(t_{j+1}\right),t_{j+1}=t_j+h$, and $h$ is the space between adjacent time grid points.

Similarly, the calculation format of the implicit Euler method (IE) is as follows:

$x_{j+1}=x_j+hf\left(x_{j+1},t_{j+1}\right)$

The calculation format of the four-step method (FM) is as follows:

$\frac{20-8\sqrt{2}}{11}hf\left(x_{j+4},t_{j+4}\right)=\frac{1}{11}{x}_j+\frac{4\sqrt{2}-8}{11}{x}_{j+1}+\frac{4}{11}{x}_{j+2}-\frac{4\sqrt{2}+8}{11}{x}_{j+3}+x_{j+4}$

Table 1 shows the comparison of the three numerical algorithms. It can be seen that the properties of the three algorithms are different, and the solution effect of the actual problem is also different. The time domain response results of a single lossless transmission line will be analyzed in detail below.

TABLE 1

TABLE 1. Comparison of three numerical algorithms.

Taking the lumped model in Figure 1B as an example, a set of linear differential equations can be obtained according to the circuit law as follows:

$\{\begin{array}{c}L\frac{d{i}_k\left(t\right)}{dt}=u_k\left(t\right)-u_{k+1}\left(t\right)-r{i}_k\left(t\right),k\in \left(1,M\right)\\ C\frac{d{u}_k\left(t\right)}{dt}=i_{k-1}\left(t\right)-i_k\left(t\right), k\in \left(1,M+1\right)\end{array}(6)$

$\left[\begin{array}{cc}\mathit{L}& 0\\ 0& \mathit{C}\end{array}\right]\left[\begin{array}{c}\dot{\mathit{I}}\\ \dot{\mathit{U}}\end{array}\right]=\left[\begin{array}{cc}-\mathit{R}& \mathit{P}\\ \mathit{Q}& 0\end{array}\right]\left[\begin{array}{c}\mathit{I}\\ \mathit{U}\end{array}\right]+\left[\begin{array}{c}{\mathit{\mu }}_1\left(t\right)\\ {\mathit{\mu }}_2\left(t\right)\end{array}\right](7)$

In Eq. 7, $\mathit{I}={[i_1\left(t\right),i_2\left(t\right),\cdots ,i_M\left(t\right)]}^T$, $\mathit{U}={[u_1\left(t\right),u_2\left(t\right),\cdots ,u_{M+1}\left(t\right)]}^T$, $\mathit{R}=diag(r,r,\cdots ,r)$, $\mathit{C}=diag(C,C,\cdots ,C)$, $\mathit{L}=diag(L,L,\cdots ,L)$, ${\mathit{\mu }}_1\left(t\right)={[\mathrm{0,0},\cdots ,0]}^T$, ${\mathit{\mu }}_2\left(t\right)={[i_0,0,\cdots ,0]}^T$.

$\begin{array}{l}\mathit{P}={\left[\begin{array}{cc}\begin{array}{cc}\begin{array}{c}1\\ \end{array}& \begin{array}{c}-1\\ \ddots \end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\\ -1\end{array}& \begin{array}{c}\begin{array}{cc}& \end{array}\\ \begin{array}{cc}& \end{array}\end{array}\end{array}\\ \begin{array}{cc}\begin{array}{c}\\ \end{array}& \begin{array}{c}\\ \end{array}\end{array}& \begin{array}{cc}\begin{array}{c}1\\ \end{array}& \begin{array}{c}\begin{array}{cc}-1& \end{array}\\ \begin{array}{cc}1& -1\end{array}\end{array}\end{array}\end{array}\right]}_{M\times (M+1)}\\ \mathit{Q}={\left[\begin{array}{cc}\begin{array}{cc}-1& \end{array}& \begin{array}{cc}& \end{array}\\ \begin{array}{cc}\begin{array}{c}1\\ \begin{array}{c}\\ \\ \end{array}\end{array}& \begin{array}{c}-1\\ \begin{array}{c}\ddots \\ \\ \end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\\ \begin{array}{c}\ddots \\ 1\\ \end{array}\end{array}& \begin{array}{c}\\ \begin{array}{c}\\ -1\\ 1\end{array}\end{array}\end{array}\end{array}\right]}_{(M+1)\times M}\end{array}$

Applying constraints to Eq. 7, we get the following:

$\{\begin{array}{c}{i}_0=\frac{u_{es}-u_1}{r_s}\\ \left(\frac{C}{2}+C_L\right)\frac{d{u}_{M+1}}{\text{d}t}=i_M\end{array}(8)$

In the simulation, the resistance in the ideal voltage source is $r_s=0.000001\text{Ω}$, the chained number of the lumped-circuits model is $M=100$, and the simulation step size is $h=1.0\times {10}^{-7}s$. The lumped-circuits consisted of chained $\text{Π}$-type circuits digitally simulated by using the implicit trapezoidal integral formula, the implicit Euler method, and the four-step method in the study by (Wang et al., 2019), as shown in Figures 3B,D. Since the four-step method cannot start the calculation by itself, the explicit Euler method needs to be used to calculate the header.

It can be seen from Figures 3B,D that under the $\text{Π}$-type lumped-circuits model, when the lossless transmission line is terminated with a capacitor, the ending voltage calculated using the three numerical algorithms with different properties has a certain time delay relative to the head-end voltage (Zhan et al., 2017). According to the research by (Cui, 2017; Cui, 2018), the calculation formula of the delay time is as follows:

$t_M=\frac{M}{\omega }arccos\frac{2-{\omega }^2{t}_l^2}{2}(9)$

Therefore, the relative phase error of the algorithm is defined as follows:

${\epsilon }_{{\phi }_M}=\left[\frac{t_{phase}}{t_M-1}\right]\times 100\%(10)$

where $t_{phase}$ represents the time delay of the ending voltage waveform calculated using the numerical algorithm.

The reason for the signal transmission delay under the lumped-circuits model is due to the charge discharge process of capacitance and inductance and the dissipative process of load energy in the lumped-circuits, which is obviously different from the wave process of lossless transmission lines.

In addition, the ending voltage calculated using the implicit trapezoidal method has obvious numerical oscillation. In order to further study the physical mechanism of numerical oscillation, this study uses the implicit trapezoidal method to solve the ending voltage response of different chained numbers $M$ in the $T$-type lumped-circuits with the unit step signal connected at the head end without delay and characteristic impedance of the lossless transmission line at the end load. The simulation results are shown in Figure 3E, with the increase in the chained number $M$; the greater the step response overshoot of the ending voltage, the higher the frequency of voltage oscillation, the faster the attenuation of amplitude, the shorter the voltage rise time and dynamic time, and the overall waveform of the ending voltage is closer to the unit step voltage waveform in addition to the overshoot. This conclusion has the same physical characteristics as the step response of the lumped-circuits derived by inverse Fourier transform in the study by (Cui, 2018).

The above shows that the implicit trapezoidal integration method retains the dynamic response characteristics of the step response of the lumped-circuits because it does not have numerical L-stable (Noda et al., 2014; Chakraborty and Ramanujam, 2018), which just reflects the real numerical characteristics of the lumped-circuits. On the contrary, because of the L-stable of the implicit Euler method and the four-step method in the study by (Wang et al., 2019), the overshoot and oscillation characteristics of the unit step voltage waveform are suppressed and the details of the dynamic response process of the lumped-circuits are obliterated, so they are impossible for truly simulating the physical process (Wang and Yang, 2016).

The above conclusions show that whether the selection of the numerical algorithm is appropriate is very important to reflect the real dynamic response process of the lumped-circuits. Of course, this numerical oscillation is false for the lossless transmission line itself, which also shows that the lumped-circuits can not be completely equivalent to the lossless transmission line model. Therefore, the lumped-circuits is only a numerical approximation of the lossless transmission line model. In order to truly reflect the numerical characteristics of the lossless transmission line model, it is suggested that the numerical algorithm with L-stable be used to simulate the lumped-circuits. Although the L-stable numerical algorithm dampens the overshoot and oscillation characteristics of the real waveform of the lumped circuit (Gao et al., 2021), it positively reflects the numerical characteristics of the lossless transmission line model.

FIGURE 3

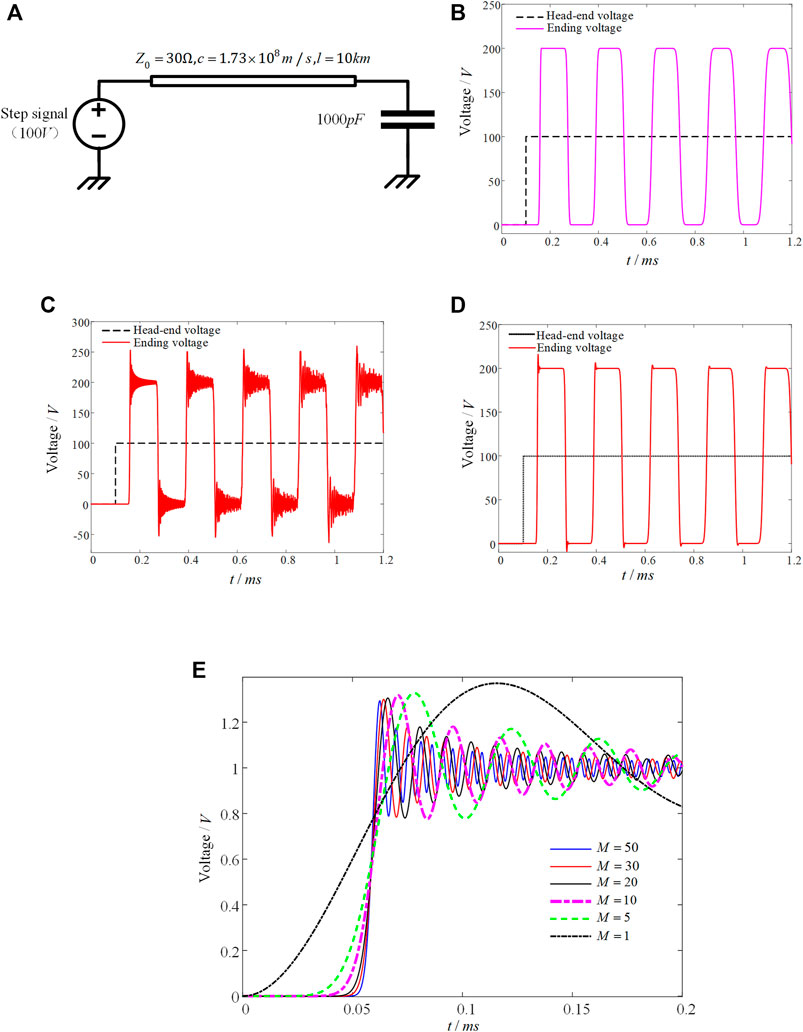
FIGURE 3. Example analysis. (A) Step response model of the lossless transmission line. (B) Calculation results of the implicit Euler method. (C) Calculation results of the implicit trapezoidal method. (D) Calculation results of the four-step method. (E) Unit step response of the $T$-type lumped-circuits.

Sine Excitation Response of the Lumped-Circuits Model

Different numerical algorithms have great differences in the numerical simulation results of the lumped-circuits, but this difference is not very obvious for the sine excitation response without the disturbance term. In addition, although the larger the chained number $M$ is selected, the closer the ending voltage waveform is to the unit step voltage waveform as a whole, from the perspective of numerical calculation efficiency; how to select the appropriate chained number $M$ directly determines the efficiency and accuracy of simulation. Besides, the simulation step size is limited by the accuracy of the numerical algorithm. Therefore, the efficiency of the lumped-circuits simulation depends on the chained number $M$ and the accuracy and stability of the numerical algorithm adopted.

For the lossless transmission line shown in Figure 3A, according to the previous analysis, considering that the ending voltage phase delay is in the linear interval. Assuming that the angular frequency of the sinusoidal excitation source meets $\omega t_l\le 1$, the ending voltage phase delay approximately meets the following:

${\phi }_M\left(j\omega \right)\approx -\omega M{t}_l, \omega =2\pi f(11)$

According to Eq. 11, in order to reduce the phase transmission error of the lumped-circuits model and ensure that the amplitude-frequency response characteristic is constant 1, the chained number $M$ should meet the following:

$M\ge \left[\frac{2\pi f_{max}l}{v}\right](12)$

where the square brackets indicate rounding up. $f_{max}$ represents the maximum frequency of the excitation signal of the lossless transmission line during numerical simulation. $l$ is the total length of the transmission line.

In order to verify the correctness of the above conclusions, the $T$-type lumped-circuits model of the lossless transmission line is considered. The simulation step size shall be less than or equal to the optimal step size as follows:

$h<\frac{l}{Mv}(13)$

Using the numerical example shown in Figures 3A, a sine voltage excitation source with a frequency of 10 $kHz$ is considered, which has a delay of 0.1 $ms$ and a peak value of 10 $kV$. The terminal load is the characteristic resistance of the equivalent lumped-circuits. According to Eq. 12, the transmission line is divided into 4 equal parts. The implicit trapezoidal method is used to solve the model. According to the research by (Cui, 2017), the characteristic impedance of the $T$-type equivalent lumped-circuits is as follows:

$Z_c^T=z_0\sqrt{1-\left(\frac{1}{2}\omega t_l\right)},t_l=\frac{l}{Mv}(14)$

As can be seen from Figure 4, when $M=4$, there is an obvious difference in the amplitude of the head and end voltage waveform, which does not meet the characteristics of the transmission line. After increasing to $M=12$, except for the obvious overshoot of the first wave peak, the subsequent amplitude error is basically stable. This shows that in the actual simulation, the value of $N$ needs to be flexibly selected accordingly. Through a large number of simulations, it is found that $M$ can be 2–3 times the calculated value of Eq. 12. In addition, the characteristics of the numerical algorithm are also one of the factors affecting the amplitude-frequency characteristics of the lumped-circuits model. How to choose an appropriate numerical algorithm is also a direction worthy of further research. Symplectic algorithms (Xing and Yang, 2007; Ye et al.) may be a better choice to accurately simulate the physical characteristics of lossless transmission lines. The amplitude frequency response error curve (absolute value of absolute error) of the commonly used TR and IE algorithms when $N=12$ is calculated below, considering the sinusoidal voltage excitation source with frequency $f$, the excitation source has no delay and the end load is matched. The optimal time domain simulation step is taken according to Eq. 13.

FIGURE 4

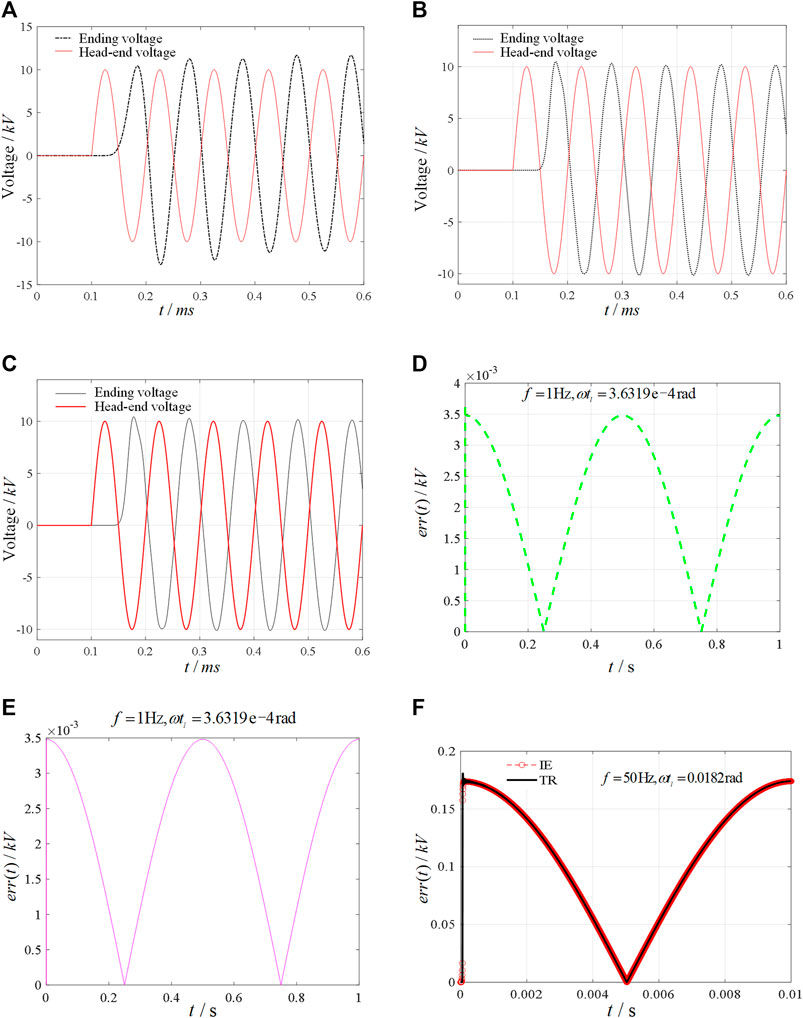
FIGURE 4. Chained number and numerical algorithm analysis of lumped-circuits numerical simulation. (A) M = 4 (the terminal resistance is 30 Ω). (B) M = 12 (the terminal resistance is 30 Ω). (C) M = 12 (the terminal resistance is 29.65 Ω). (D) Amplitude-frequency response error curve of the TR algorithm. (E) Amplitude-frequency response error curve of algorithm IE. (F) Amplitude-frequency response error curve of algorithms TR and IE.

As can be seen from Figures 4D,E, when the system frequency is small, that is, when $\omega t_l$ is close to 0, the amplitude frequency response error of algorithms TR and IE is also small. However, it can be seen from Figure 4F that the amplitude frequency response error of algorithms TR and IE increases sharply with the increase in system frequency. According to Figure 2, the error amplitude frequency response error caused by the model is almost 0, so the error at this time is mainly caused by the numerical algorithm, which also fully shows that it is very necessary to study the application of symplectic algorithms in the high-precision time-domain response simulation of lossless transmission lines.

Conclusion

Starting from the equivalent lumped-circuits model of lossless transmission lines, this article mainly studies the boundary condition application methods of three equivalent lumped-circuits models. Users can flexibly choose the type of the equivalent lumped-circuits model according to the type of excitation source and load. The causes of numerical oscillation in digital simulation of the equivalent lumped-circuits model are explained theoretically, and the L-stable numerical algorithm is proposed to avoid this situation. A determination method of chained number of the equivalent lumped-circuits model is studied, and a specific application example is given. In conclusion, the method proposed in this study can provide the basis for the selection of model and numerical algorithm for the equivalent lumped-circuits model of lossless transmission lines in digital simulation.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

HZ put forward the main research points and mathematical analysis; TL is responsible for the framework formation and revision; SZ collected relevant background information and completed simulation research; XZ completed manuscript writing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chakraborty, S., and Ramanujam, R. (2018). New Numerical Integration Methods for Simulation of Electromagnetic Transients. Int. J. Emerging Electric Power Syst. 19 (4), 122. doi:10.1515/ijeeps-2018-0122

CrossRef Full Text | Google Scholar

Cui, X. (2018). Notes on Lumped-Circuits for Physical Analogy of Transmission Lines[J]. Zhongguo Dianji Gongcheng Xuebao/Proceedings Chin. Soc. Electr. Eng. 38 (1), 1–11. doi:10.13334/j.0258-8013.pcsee.171699

CrossRef Full Text | Google Scholar

Cui, X. (2017). Chained Number of Lumped-Circuits for Physical Analogy of the Lossless Transmission Lines. Proc. Chin. Soc. Electr. Eng. 37 (09), 2561–2571. doi:10.13334/j.0258-8013.pcsee.162633

CrossRef Full Text | Google Scholar

Gao, S., Chen, Y., Song, Y., and Huang, S. (2021). Three-stage Implicit Integration for Large Time-step Size Electromagnetic Transient Simulation with Shifted Frequency-Based Modeling. Electric Power Syst. Res. 198 (11), 107356. doi:10.1016/j.epsr.2021.107356

CrossRef Full Text | Google Scholar

Lei, L., Xiang, C., and Lei, Q. (2009). Simulation of Electromagnetic Transients of the Bus Bar in Substation by the Time-Domain Finite-Element Method[J]. IEEE Trans. Electromagn. Compatibility 51 (4), 1017–1025. doi:10.1109/TEMC.2009.2028691

CrossRef Full Text | Google Scholar

Min, T., and Mao, J. (2007). A Precise Time-step Integration Method for Transient Analysis of Lossy Nonuniform Transmission Lines[J]. IEEE Trans. Electromagn. Compatibility 50 (1), 166–174. doi:10.1109/TEMC.2007.913222

CrossRef Full Text | Google Scholar

Noda, T., Kikuma, T., and Yonezawa, R. (2014). Supplementary Techniques for 2S ⁃DIRK ⁃ Based EMT Simulations[J]. Electric Power Syst. Res. (115), 87⁃93. doi:10.1016/j.epsr.2014.04.011

CrossRef Full Text | Google Scholar

Paul, C. R . (1994). Analysis of Multiconductor Transmission Lines[M. New York: John Wiley & Sons.

Google Scholar

Shen, X., Ouyang, T., Khajorntraidet, C., Li, Y., Li, S., and Zhuang, J. (2021). Mixture Density Networks-Based Knock Simulator. Ieee/asme Trans. Mechatron., 1. doi:10.1109/TMECH.2021.3059775

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021). Pedestrian-aware Statistical Risk Assessment. IEEE Trans. Intell. Transport. Syst., 1–9. doi:10.1109/TITS.2021.3074522

CrossRef Full Text | Google Scholar

Shen, X., Zhang, Y., Sata, K., and Shen, T. (2020). Gaussian Mixture Model Clustering-Based Knock Threshold Learning in Automotive Engines. Ieee/asme Trans. Mechatron. 25 (6), 2981–2991. doi:10.1109/TMECH.2020.3000732

CrossRef Full Text | Google Scholar

Song, W., Yao, S., Chang, L., Zhang, X., and Han, M. (2020). The Research of Electromagnetic Transient Simulation Method Based on Discrete Similarity[J]. Proc. Chin. Soc. Electr. Eng. 40 (21), 9. doi:10.13334/j.0258-8013.pcsee.200249

CrossRef Full Text | Google Scholar

Wang, F., and Yang, M. (2016). Fast Electromagnetic Transient Simulation for over ⁃ Voltages of Transmission Line by High Order Radau Method and V-Transformation [J]. IET Generation Transm. Distribution 2016 10 (14), 3639–3645. doi:10.1049/iet-gtd.2016.0476

CrossRef Full Text | Google Scholar

Wang, Y., Qiang, Li., Zhao, Wei., Zhang, Lei., and Chen, S. (2019). Electromagnetic Transient Simulation Algorithm Based on Improved Critical Damping Adjustment. Automation Electric Power Syst. (15), 180–185. doi:10.7500/AEPS20180413006

CrossRef Full Text | Google Scholar

Watson, N. R., and Irwin, G. D. (1998). Electromagnetic Transient Simulation of Power Systems Using Root-Matching Techniques. IEE Proc. Gener. Transm. Distrib. 145 (5), 481–486. doi:10.1049/ip-gtd:19982173

CrossRef Full Text | Google Scholar

Xing, Y., and Yang, R. (2007). Phase Errors and Their Correction in Symplectic Implicit Single-step Algorithm[J]. Chin. J. Theor. Appl. Mech. 39 (5), 4. doi:10.6052/0459-1879-2007-5-2006-561

CrossRef Full Text | Google Scholar

Yang, N., Huang, Y., and Hou, D. (2019). Adaptive Nonparametric Kernel Density Estimation Approach for Joint Probability Density Function Modeling of Multiple Wind Farms[J]. Energies 12, 356. doi:10.3390/en12071356

CrossRef Full Text | Google Scholar

Yang, N., Ye, Di., Zhou, Zh., Cui, J., Chen, D., and Wang, X. (2018). Research on Modelling and Solution of Stochastic SCUC under AC Power Flow Constraints[J. ].IET Generation, Transm. Distribution 12 (15), 3618–3625. doi:10.1049/iet-gtd.2017.1845

CrossRef Full Text | Google Scholar

Yang, N., Huang, Y., Hou, D., Liu, S., Ye, D., Dong, B., et al. (2019). Adaptive Nonparametric Kernel Density Estimation Approach for Joint Probability Density Function Modeling of Multiple Wind Farms. Energies 12, 1356. doi:10.3390/en12071356

CrossRef Full Text | Google Scholar

Yang, N., Liu, S., Deng, Y., and Xing, C. (2021). An Improved Robust SCUC Approach Considering Multiple Uncertainty and Correlation. IEEJ Trans. Elec Electron. Eng. 16, 21–34. doi:10.1002/tee.23265

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Xing, C., Ye, D., Jia, J., Chen, D., et al. (2021). Deep Learning‐based SCUC Decision‐making: An Intelligent Data‐driven Approach with Self‐learning Capabilities. IET Gener. Transm. Distrib. 1, 12. doi:10.1049/gtd2.12315

CrossRef Full Text | Google Scholar

Ye, J., Zhao, D., and Zhang, L. (2021). Research on Combined Electricity and Heating System Scheduling Method Considering Multi-Source Ring Heating Network[J]. Front. Energ. Res. Early Access.

Google Scholar

Ye, J., Xu, M., Wang, Y., Li, B., Zhang, L., Yi, Z., et al. (2021). Time Domain Response Analyses of Multiconductor Transmission Lines Using L-Stable Single Step Multistage Block Method[J]. J. Xinyang Normal Univ. (Natural Sci. Edition) 34 (4), 639697–640644. doi:10.3969/j.issn.1003-0972.2021.04.022

CrossRef Full Text | Google Scholar

Zhan, R., Li, Y., Jiao, C., Yu, Y., Meng, J., and Wang, B. “Time Delay along a Chained Lumped-Circuits: for the Physical Analogy of Half-Wavelength Power Transmission Lines,” in Proceedings of the 2017 IEEE 5th International Symposium on Electromagnetic Compatibility, EMC-Beijing), October 2017 (IEEE), 012044. doi:10.1088/1757-899x/231/1/012044

CrossRef Full Text | Google Scholar

Zhang, L., Xie, Y., Ye, J., Xue, T., Cheng, J., Li, Z., et al. (2021). Intelligent Frequency Control Strategy Based on Reinforcement Learning of Multi-Objective Collaborative Reward Function. Front. Energ. Res. 9, 525. doi:10.3389/fenrg.2021.760525

CrossRef Full Text | Google Scholar