
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 24 December 2021
Sec. Advanced Clean Fuel Technologies
Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.804094
This article is part of the Research Topic Cleaner Treatment Technologies and Productions in The Energy Industry View all 24 articles
Detailed numerical calculations are performed for investigating the effect of fin number and position on unsteady natural convection heat transfer in internally finned horizontal annulus. The SIMPLER algorithm with Quick scheme is applied for solving the Navier Stokes equations of flow and heat transfer. The results show that the heat transfer rate in annulus with fins increases with the increasing numbers of fin and Rayleigh numbers. For Ra = 2 × 105, the effect of numbers of fins and fins position at the bottom part on the unsteady solutions can be neglected, because the self-oscillation phenomenon is mainly affected by natural convection at the upper part of annulus. Although the fin positions cannot increase heat transfer rate significantly in the case of four fins, the self-oscillated solutions can be suppressed by altering fins position.
Natural convection heat transfer in annulus has been the topic of many investigations until recently, since it has many industrial applications including solar heating, electronic components, and reactor design. A large number of literatures on both experimental and numerical studies were published in the past few decades (Yong et al., 2006; Ghasemi et al., 2012; EI-Maghlany et al., 2015; Gholamalipour et al., 2019). The most fundamental studies were reported by Kuehn and Goldstein (Kuehn and Goldstein, 1976; Kuehn and Goldstein, 1978; Kuehn and Goldstein, 1980) in which experimental and numerical results were obtained for improving the knowledge of heat transfer performance, natural convection, and temperature fields in horizontal annulus. The natural convection heat transfer in annulus is limited by the heat transfer area of the inner cylinder. Therefore, the internal fins are sometimes employed for the purpose of increasing the heat transfer area, leading to an increasing heat transfer rate in annulus.
Numerical investigations of the natural convection heat transfer in annulus with internal fins were studied by many researchers (Chen and Hsu, 2007; Kim et al., 2013; Senapati et al., 2017; Liu et al., 2021). Maakoul (El Maakoul et al., 2020) numerically studied the thermal performance of longitudinal fins in the double-pipe heat exchanger. Their results showed that the smallest internal fins with the size of 166 mm can provide the highest thermal performance and the heat transfer rate with longitudinal fins is higher than other cases under the same flow velocity. Chai and Patankar (1993) numerically investigated flow and heat transfer under gravity in horizontal annulus in the case of six fins. Their results indicated that the effect of the fins orientations is not obvious for improving the rate of averaged heat transfer, and the averaged heat transfer rate can increase with the increasing values of Rayleigh number and decrease with the increasing value of fin height. Farinas et al. (Farinas et al., 1997) investigated the effect of fins with different configurations on the flow pattern, temperature field, and heat transfer rate in annulus. Rahnama et al. (Rahnama et al., 1999; Rahnama and Farhadi, 2004) also studied natural convection heat transfer in annulus with radial fins. The existence of fins can improve the heat transfer rate while high fins resist the development of natural convection and decrease the value of local Nusselt number. Nada and Said (Nada and Said, 2019) studied the effects of Rayleigh numbers, internal cylindrical diameters, fins numbers, shapes, and arrangements on the heat transfer rate, flow pattern and effective thermal conductivity of the annulus. Alshahrani and Zeitoun (2005) numerically investigated the thermal resistance of finned annuli using conduction analysis and the correlation. Their results indicated that the thermal resistance becomes larger when the fin length increases in their parameter scope. Kiwan and Zeitoun (2008) studied the heat transfer rate in the annulus with fins made of porous material and the effect of fin conductivities, Darcy numbers, and Rayleigh numbers on thermal performance. Shadlaghani et al. (2019) studied the effect of internal fins on flow and heat transfer using control volume method. Their results showed that although the heat transfer coefficient between the two fins is reduced, fins increase the total heat transfer rate of both inner and outer walls of annulus and fins efficiencies are decreased with the increasing value of Rayleigh number.
Natural convection may occur in the annulus recurrently, and most of these flows are unsteady even under the steady boundary conditions, especially those encountered in the complex domain (Zhang et al., 2011; Zhang et al., 2014). Many numerical studies have been carried out to investigate the non-linear characteristics of natural convection heat transfer in annulus. Labonia and Guj (2000) experimentally investigated the transition process from steady laminar flow and heat transfer to chaotic state in annulus by increasing the values of Rayleigh numbers. Yoo and Han (Yoo, 1998; Yoo and Han, 2000) numerically studied the bifurcation sequences from steady to chaos of flow in annulus and a transition from a steady flow with the pattern of unicellular to an oscillatory multicellular flow pattern. Borjini et al. (2005) studied a reverse transition of natural convection from the quasi-periodic solutions to the periodic solutions with the increasing value of Rayleigh number in a very narrow annulus. Usman et al. (2021) investigated a transition from steady to oscillated solutions of natural convection in annulus when the Prandtl number is equal to 0.1. The numerical results revealed that the heat transfer rate increases suddenly in a narrow range of Rayleigh numbers, and this increase in heat transfer rate is related to a transition into chaos. Yang and Kong (Yang and Kong, 2019) studied the unsteady natural convection heat transfer in annulus with different Rayleigh numbers and Prandtl numbers.
Comparatively, a few studies have been reported on the non-linear characteristics of flow and heat transfer in annulus with fins. Idrissi et al. (2016) studied the natural convection heat transfer in annulus in the case of two fins attached to the upper surface of inner annulus. Their results indicated that the existence of a bifurcation point can separate two kinds of flow patterns, and the heat transfer rate increases for Rayleigh numbers higher than the critical value. Touzani et al. (2019) investigated the effect of the Rayleigh number from 103 to 104 on the flow pattern and heat transfer rate in the finned internally annulus. A bi-cellular or unicellular flow patterns can be observed, and the overall heat transfer rate is increased by adding fins. Gao et al. (2020) numerically studied the steady state, static branching and self-sustained oscillated solutions of natural convection heat transfer in annuli with fins. A series of critical Rayleigh numbers was obtained when the different initial conditions are selected. However, most of previous studies focus on the process of evolution from steady to chaotic flow for different non-dimensionless parameters such as Rayleigh numbers or Prantal numbers, and only in a few of the works the effect of fin numbers and positions on the non-linear phenomenon of natural convection heat transfer were considered in detail.
The objective of this paper is to study the flow and heat transfer in annulus with different fin number and positions by SIMPLER algorithm with Quick scheme. The effect of fin number and positions on the steady or oscillated phenomenon of flow and heat transfer under the steady boundary conditions will be studied in detail. The space trajectory of velocity at the sample point and the time signal of the average dimensionless equivalent thermal conductivity will be calculated for evaluating the effect of fin position and number on the non-linear characteristics.
A schematic diagram of the horizontal annulus with fins is illustrated in Figure 1. The temperatures of the inner and outer cylinders are maintained at uniform but different values of Ti and To, respectively. The natural convection heat transfer occurs for Ti >To. The radius of the inner cylinder is denoted by ri and at the same time that of the outer cylinder is denoted by ro. The two concentric cylinders, consisting of an annulus, are assumed to be long enough that a two dimensional model can be applied. The natural convection resulting from the temperature difference between the cylinders is assumed to be unsteady and laminar. The fins of height Lf and the thickness of δ are evenly attached to the surface of inner cylinder. The thermo-physical properties of the fluid are assumed to be independent of temperature, and the flow in annulus follows the Boussinesq approximation.
The unsteady-state flow and heat transfer equations for natural convection heat transfer in annulus with fins in this investigation are described in Ref. (Gao et al., 2020). The Quick scheme is employed to discretize the convection terms while the deferred correction method is added into the computational process to improve the convergence of iterations. The SIMPLER algorithm with Quick scheme is selected for solving the Navier-Stokes equations of flow and heat transfer. The whole annulus with fins is considered as the calculating domain and the flow velocities of solid regions are set to zero. The dimensionless governing equations are solved numerically using the control-volume based finite volume method. An alternating direction scheme is applied where all the equations can be solved iteratively until the convergence criteria are met. The iterative calculation can be terminated when the relative residual of all variables is less than 10−6 for each time step.
The local dimensionless equivalent thermal conductivity based on the outer cylindrical envelope is used for evaluating the local heat transfer effect, and its definition formulation is written as follows.
where qθ is the local heat transfer rate along the surface of the outer cylinder at the fin positioned angle θ, and kf is the thermal conductivity of fluid.
To study the overall heat transfer effect, the average dimensionless equivalent thermal conductivity based on the whole outer cylindrical envelope is defined as
The check of grid independence is calculated under the parameters of nfin = 6, δ/L = 0.05, Ra = 105, Pr = 0.701. The dimensionless time step ∆τ = 0.1 is taken to calculate for obtaining time-step independent solutions. The number of grid nodes 160 × 400 is used to achieve grid independence. To verify the numerical code, the average dimensionless equivalent thermal conductivity is calculated numerically with modified Rayleigh numbers. The modified Rayleigh number Ram is defined by Alshahrani and Zeitoun (2005). The calculated solutions are compared with the results from Alshahrani and Zeitoun (2005) and Kiwan and Zeitoun (2008). It can be seen in Figure 2 that the numerical results in this study agreed very well with other experimental and numerical results.
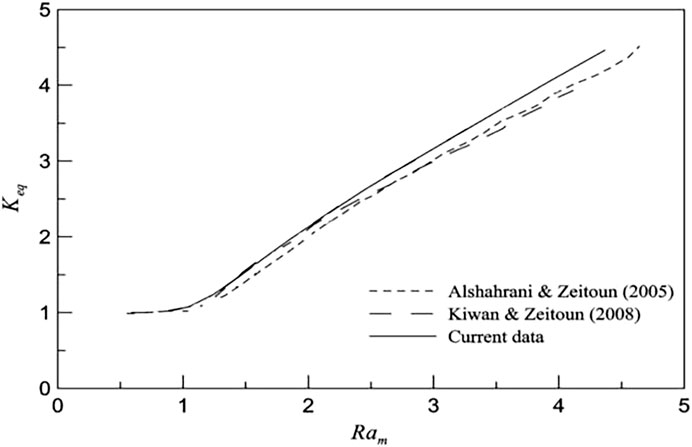
FIGURE 2. Comparison of current and previous results of the average dimensionless equivalent thermal conductivity of whole cylinder (Keq).
The flow pattern, temperature distribution, and heat transfer rate of natural convection heat transfer in annulus with fins will be numerically investigated in detail. The effect of fin positions and number on the nonlinear characteristic of heat transfer will be analyzed in this section.
Numerical simulations of the flow and heat transfer in horizontal annulus with fins are performed in the case of Ra≤5 × 103. The numerical simulations indicate that the steady solution can be obtained from the initial conditions of stationary flow and uniform temperature field.Figures 3, 4 show the flow and temperature fields at lower Rayleigh numbers with different fin numbers and positions for Ra = 5 × 103, respectively. In the case of nfin = 2, the effect of fin angle on the flow fields can be seen in Figures 3A–D. There are two symmetric and big vortices in the case of α = 0 in Figure 3A. The fluid flows up along the inner heated cylinder by the buoyancy forces, as it gets closer to the top of the outer wall, it then moves down along the sidewall of the outer cylinder. The temperature fields in Figure 4A are also symmetrical with respect to the mid axial line accordingly. The existence of fins can increase the heat transfer areas and influence the isotherms. The heat transfer rate is very low at the root of fin and increases along the fin until it arrives at the greatest value on the top of the fin.

FIGURE 3. Flow fields with different fin numbers and positions for Ra = 5 × 103 . (A) α = 0, nfin = 2 (B) α = π/6, nfin = 2 (C) α = π/3, nfin = 2 (D) α = π/2, nfin = 2 (E) α = 0, nfin = 3 (F) α = π/6, nfin = 3 (G) α = π/3, nfin = 3 (H) α = 0, nfin = 4 (I) α = π/6, nfin = 4 (J) α = π/4, nfin = 4 (K) α = 0, nfin = 6 (L) α = π/3, nfin = 6. Ra, Rayleigh number; α, angle of fins; nfin, number of fins.
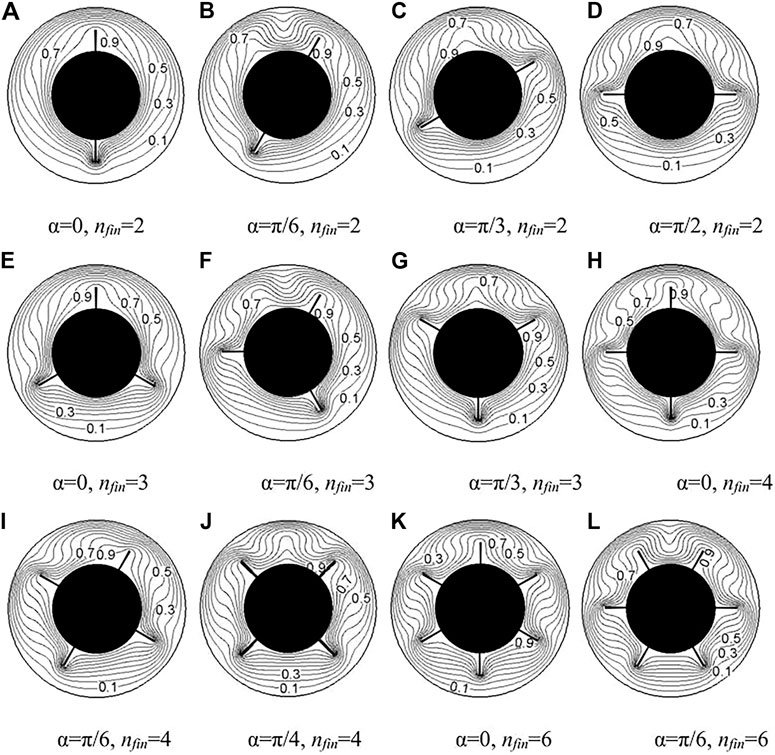
FIGURE 4. Temperature fields with different fin numbers and positions for Ra = 5 × 103. (A) α = 0, nfin = 2 (B) α = π/6, nfin = 2 (C) α = π/3, nfin = 2 (D) α = π/2, nfin = 2 (E) α = 0, nfin = 3 (F) α = π/6, nfin = 3 (G) α = π/3, nfin = 3 (H) α = 0, nfin = 4 (I) α = π/6, nfin = 4 (J) α = π/4, nfin = 4 (K) α = 0, nfin = 6 (L) α=π/6, nfin=6.
In the case of α = π/6, one new vortex appears at the upper part of the annulus and at the same time the right vortex becomes small because of the suppression of the fin at the right side, as shown in Figure 3B. The new vortex becomes larger and the right vortex shrinks gradually as the fin angle increases, as can be seen in Figures 3C, D. At the same time, the left vortex becomes smaller and rises up, providing space for the development of another new vortex. In the case of α = π/2, the fluid flows up and it is forced to alter the orientation when it meets the fins located at the center of the annulus, as shown in Figure 3E. There are four big vortices formed in the horizontal annulus. Two of them are in the right side of the annulus and the other two are in the left side. The isotherms changes obviously especially at the upper part of annulus, as depicted by Figures 4B–E. The isotherm concentration in the upper part of the annulus is more than that in the other places. The largest temperature gradient occurs at the middle top of the outer cylinder. As the number of fins increases, the heat transfer area also increases and the flow structure becomes more complex. When there exists two fins in the lower part of the annulus, the fluid motion in the lower part is very weak due to the fact that high temperature surface is over that with low temperature as shown in Figures 3E, J, L. It is due to the dominated mechanism of conduction heat transfer in the lower part of the annulus.
Table 1 shows the average dimensionless equivalent thermal conductivity Keq for different fin numbers and angles at Ra = 5 × 103. The total heat transfer rate mainly depends on the surface area of the heat transfer, the flow pattern, and the velocity. The values of Keq increases with the increase of the fin number. In the case of α = π/6, the value of Keq with two fins is 1.64, while the corresponding value of Keq with six fins is 2.1. The value of Keq increases by 28% when the fin number increases from two to six. Accordingly, the value of Keq increases by 17% in the case of α = π/3. This result can be expected since the heat transfer area increases obviously with the increasing fin number. It also can be seen in Table 1 that the effect of fin position on the average equivalent thermal conductivity. In the case of the fin number larger than four, the effects of fin position on the heat transfer rate are negligible. In the case of the fin number less or equal to three, the effect of the fin position on the heat transfer rate cannot be neglected. The values of Keq in the case of nfin = 2 increases about 7% from the fin angle 0 to π/6 and it increases about 9.4% in the case of nfin = 3. The results indicate that the fin position has significant effect in convection-dominated regime. The fin attached to the top surface of the inner cylinder resists the development of natural convection in the upper part of the annulus, and therefore, it can alter the flow patterns or heat transfer rate.
Figure 5 shows the variations of local equivalent thermal conductivity Keql around the outer cylinder. The asymmetric solution of Keql can be obtained under the condition of asymmetric geometric structure with α = π/6. The maximum value of Keql occurs at the right top surface of the outer cylinder because of the synthesized effect. In the case of α = π/3, the symmetric solutions of Keql can be obtained on the symmetric boundary condition, as shown in Figure 5B. The maximum value of Keql occurs at the middle top surface of the outer cylinder and its value can be arrived at 4.1 because of the heat transfer dominated by natural convection. The local peak value of Keql is related to the effect of fins attached to the inner cylinder. The results indicated that the heat transfer rate on the upper wall of the outer cylinder is obviously larger than that on the bottom wall because it can be improved by two ways of natural convection and by adding fins.
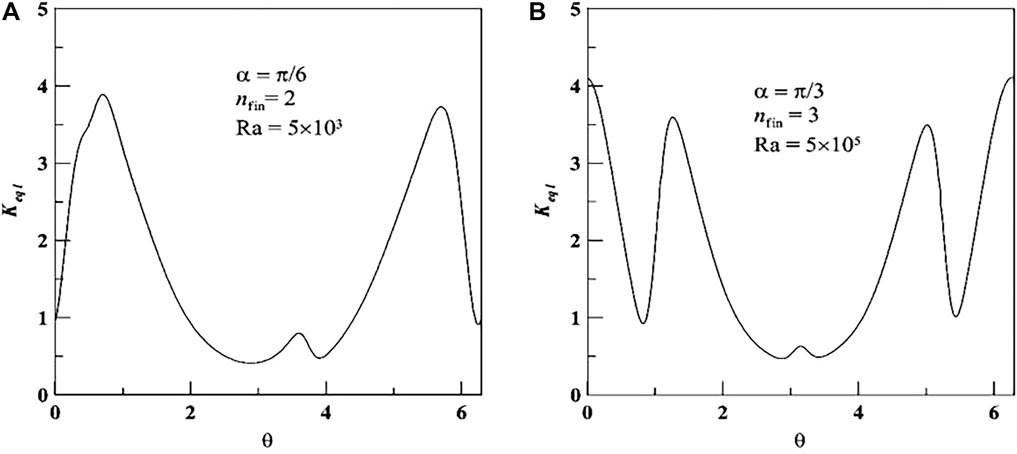
FIGURE 5. Variations of local equivalent thermal conductivity Keql around outer cylinder. (A) α = π/6, (B) α = π/3.
Numerical simulations of natural convection from the zero initial flow field and uniform temperature fields are calculated for different fin numbers. When time required are sufficiently long, self-oscillated solutions can be obtained in the case of Ra = 2 × 105. Figure 6 shows the temperature fields with different fin numbers when the heat transfer rate arrived at maximum. The asymmetric and unsteady solutions can be obtained with the axisymmetric and steady boundary conditions. In the case of nfin = 2, the existence of fins increases the thickness of flow and thermal boundary layer along the bottom part of the inner cylinder and the heat transfer area, and at the same time the fins decrease the thickness of boundary layer along the surface of the outer cylinder, as shown in Figure 6A. The heat transfer rate increases with the increasing number of fins at the lower surface of inner cylinder. However, the temperature distributions on the upper part of annulus for nfin 4 or nfin = 6 are almost the same because of the similar geometric structure on this part. The flow fields for different fins at the maximum value of Keq are shown in Figure 7. The number of flow vortex increases with the increasing fin numbers. There are three big vortices in the whole annulus for nfin = 2. One exists between the two fins at the top of the annulus and the other two are in the middle part of the annulus. The number of vortices increases and the big vortex in the middle part of the annulus is separated by the fins located at the center of the annulus. However, the flow pattern does not change at the top part of the annulus for all the cases. The results indicate that the heat transfer rate at the top of the annulus can be enhanced more obviously than that at the other part of the annulus. The changing of fin number at the bottom part of the annulus does not make obvious effects on the temperature distribution and the flow pattern at the upper part.
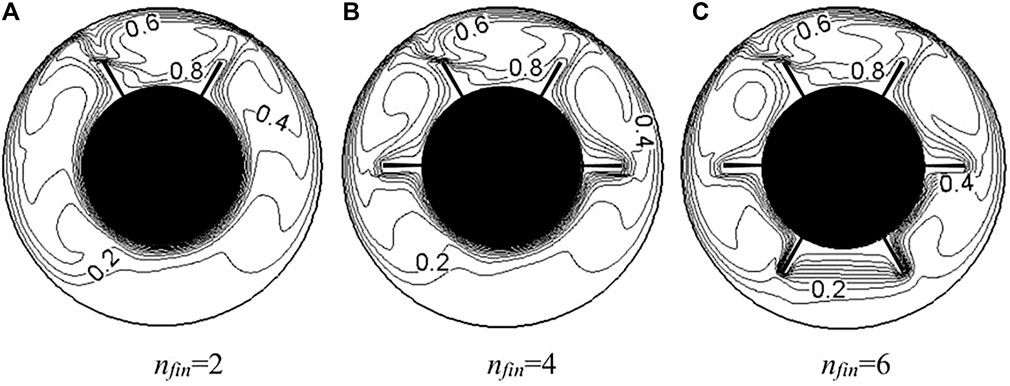
FIGURE 6. Temperature fields with different fin numbers for Ra = 2 × 105. (A) nfin = 2 (B) nfin = 4 (C) nfin = 6.
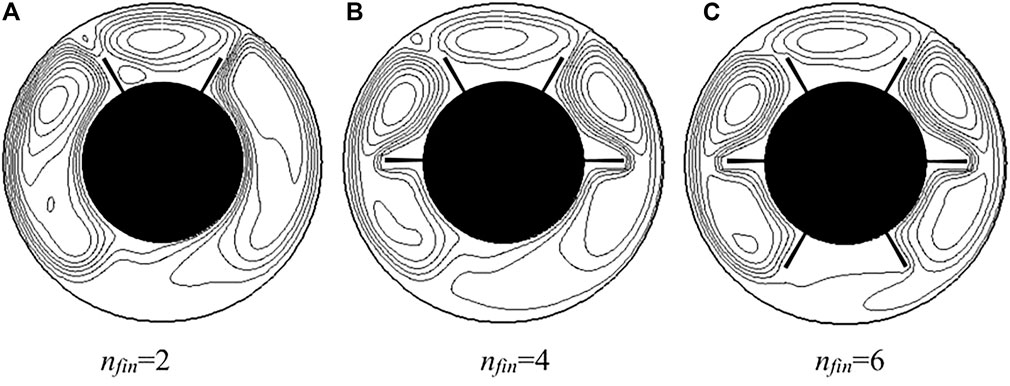
FIGURE 7. Flow fields with different fin numbers for Ra = 2 × 105. (A) nfin = 2 (B) nfin = 4 (C) nfin = 6.
Figure 8 shows the time signal of Keq with different fin numbers for Ra = 2 × 105. The initial condition is given that the temperature and flow fields are at the maximum values of Keq. The value of Keq increases with the increasing area of heat transfer and the oscillated phenomenon occurs at all the cases and the oscillated period can keep almost the same with the increasing number of fins at the bottom surface of the inner cylinder. The nonlinear phenomenon of natural convection heat transfer is analyzed by using phase space of velocity at points (20, 5) and (2, 46). The sample points are selected for evaluating the nonlinear characteristics of natural convection heat transfer. Some points at the lower part of the annulus or near boundary cannot be chosen because of the small amplitudes. When the dimensionless time is less than 1,000, the data of Keq is not given in those figures for the purpose of convenience presentation. The phase trajectories of velocity at the selected points are shown in Figure 9. The system of natural convection heat transfer loses its stability and the phase trajectory of velocity becomes a cycle after the first Hopf bifurcation in the case of Ra = 2 × 105. The result indicated that the heat transfer rate and the amplitude of oscillation increase with the increasing number of fins, while the flow and heat transfer still oscillated with the same period. It means that the oscillation phenomenon of flow and heat transfer are related to the geometric structure at the upper part of the annulus and the natural convection is the most important factor for effecting the nonlinear characteristics.
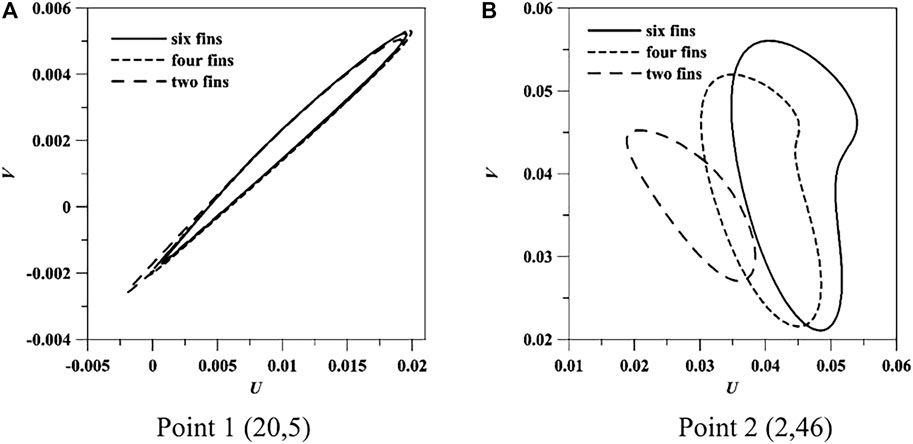
FIGURE 9. Phase space of velocity at different sample points. (A) Point 1 (20,5) (B) Point 2 (2,46).
Numerical simulations of the unsteady natural convection are performed for different fin positions. Figure 10 shows the time signal of Keq for two fins with different positions. The heat transfer rate increases with the increasing value of Rayleigh numbers and the nonlinear phenomenon is also affected by the value of Rayleigh numbers. When the fin is located at the top surface of the inner cylinder in the case of α = 0 and α = π/6, the natural convection is easily limited by the fins and the steady solution can be obtained in the case of Rayleigh number from 2 × 105 to 106. In the case of α = π/3, the natural convection can be developed without obstacles at the upper part of the annulus and the nonlinear phenomenon occurs at Ra = 2 × 105. In the case of α = π/2, the periodic oscillations of flow and heat transfer after a critical Rayleigh numbers between 2 × 105 and 106. The results show that the effect of the fin positions on the nonlinear characteristics is obvious, and the oscillated solution can be easily obtained when there is no fin at the upper part of the annulus. The effect of fins attached to the top surface of the inner cylinder on the natural convection and nonlinear characteristics can be also obtained in the case of four fins, as shown in Figure 11. For Ra = 106, the steady solutions can be calculated for α = 0 and α = π/6 while the unsteady solutions appear for α = 0 and α = π/6. Therefore, the effect of fin position on heat transfer rate is negligible in the case of four fins, but the oscillated phenomenon can be partially suppressed by altering fin positions. This is because the natural convection can be developed easily at the upper part of annulus when the temperature of the bottom surface is higher than that at the other surfaces. When the fins are added at the upper part of the annulus, the temperature distribution can be disturbed and sometimes steady flow and temperature fields can be obtained, as shown in Figure 11A.
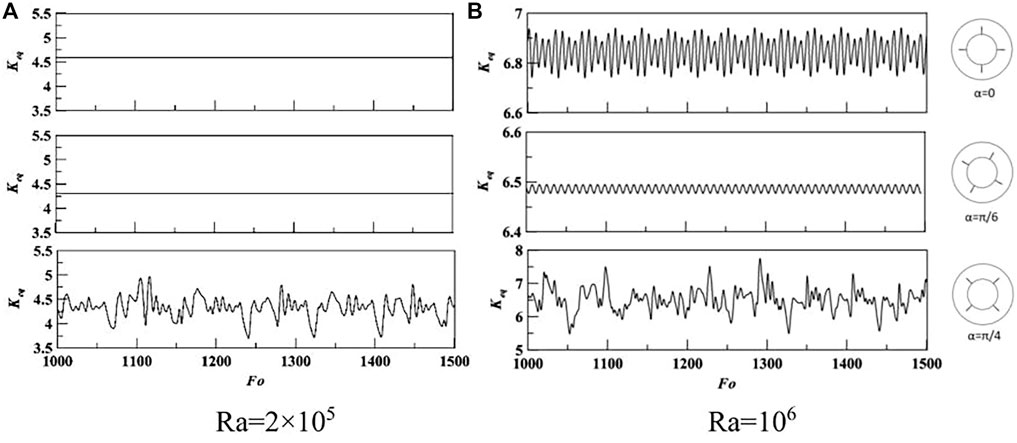
FIGURE 11. Time signal of Keq for four fins with different positions. (A) Ra = 2 × 105 (B) Ra = 106.
In order to investigate further the nonlinear characteristics, the numerical solutions of velocity at the sample point (20, 5) is obtained for different fin positions in Figure 12. It can be seen that the system loses its stability and the phase trajectory of velocity is a circle for α = π/6. A quasi-periodic system can be achieved for α = 0, and the system progresses toward chaos for α = π/4. The numerical investigation revealed that the nonlinear phenomenon of natural convection heat transfer in annulus with fins can be affected by the fin positions and Rayleigh numbers.
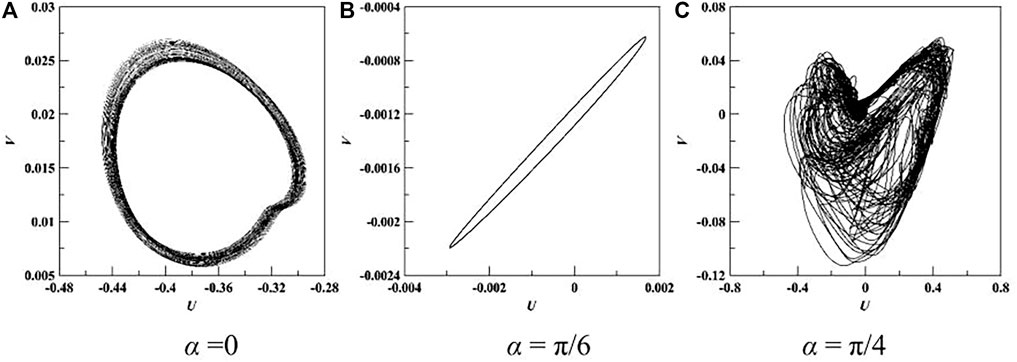
FIGURE 12. Phase space of velocity at the sample point (20, 5) for nfin = 4, Ra = 106. (A) α = 0 (B) α = π/6 (C) α = π/4.
Numerical convection heat transfer in annulus with fins attached to the inner cylinder has been presented. Governing equations are solved using the SIMPLER algorithm with QUICK scheme. The effect of fin numbers and position on non-linear characteristics was investigated in detail.
In the case of Ra ≤5 × 103, the steady and symmetrical solutions can be reached from the initial zero velocity and uniform field for different fin numbers and positions. The heat transfer rate increases with the increasing numbers of fin and Rayleigh numbers. For nfin = 2, α = π/6 and Ra = 2 105, the natural convection heat transfer in the annulus loses its stability and the periodic oscillation solution can be obtained after a sufficient long time. The heat transfer rate and the amplitude of oscillation increase with the increasing fin located at other places while the flow and heat transfer still oscillated with the same period. It means that the oscillation phenomenon of flow and heat transfer is related to the geometric structure at the upper part of the annulus and the development of natural convection is the most important factor for nonlinear characteristics. The effect of fin position on the unsteady natural convection is obvious for the same number of fins. In the case of nfin = 4 and Ra = 106, three different kinds of oscillated solutions can be obtained by changing fin inclination angles. Therefore, the nonlinear characteristics of the whole system mainly depend on the natural convection at the upper part of the annulus, and the oscillated phenomenon can be partially suppressed by altering fin positions.
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The financial support was granted by the Chinese National Natural Science Foundation under Grant No. 51866008 and the Foundation of A Hundred Youth Talents Training Program of Lanzhou Jiaotong University.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
F0, dimensionless time; Keq, average dimensionless equivalent thermal conductivity of whole cylinder; Keql, local dimensionless equivalent thermal conductivity; kf , thermal conductivity for fluid, W/m·K; L, gap width, m; Lf , height of fins, m; nfin, number of fins; Pr, Prandtl number; qθ, local heat transfer rate, W; r, radial coordinate; ri, radius of inner circle, m; r0, radius of envelope circle, m; Ra, Rayleigh number; Ram, modified Rayleigh number; Ti, temperature of inner circle, K; T0, temperature of envelope circle, K; U, dimensionless tangential velocity; V, dimensionless radial velocity; α, angle of fins, rad; δ, thickness of fins; θ, angular coordinate.
Alshahrani, D., and Zeitoun, O. (2005). Natural Convection in Air-Filled Horizontal Cylindrical Annuli. Alexandria Eng. J. 44 (6), 814–824.
Borjini, M. N., Abidi, A., and Aissia, H. B. (2005). Prediction of Unsteady Natural Convection within a Horizontal Narrow Annular Space Using the Control-Volume Method. Numer. Heat Transfer, A: Appl. 48 (8), 811–829. doi:10.1080/10407780500196576
Chai, J. C., and Patankar, S. V. (1993). Laminar Natural Convection in Internally Finned Horizontal Annuli. Numer. Heat Transfer, Part A: Appl. 24 (1), 67–87. doi:10.1080/10407789308902603
Chen, H. T., and Hsu, W. L. (2007). Estimation of Heat Transfer Coefficient on the Fin of Annular Finned Tube Heat Exchangers in Natural Convection for Various Fin Spacings. Int. J. Heat Mass. Tran. 10 (50), 1750–1761. doi:10.1016/j.ijheatmasstransfer.2006.10.021
Ei-Maghlany, W. M., Sorour, M. M., and Hozien, O. (2015). Experimental Study of Natural Convection in an Annulus between Two Eccentric Horizontal Square Ducts. Exp. Therm. Fluid Sci. 65, 65–72. doi:10.1016/j.expthermflusci.2015.03.006
El Maakoul, A., Feddi, K., Saadeddine, S., Ben Abdellah, A., and El Metoui, M. (2020). Performance Enhancement of Finned Annulus Using Surface Interruptions in Double-Pipe Heat Exchangers. Energ. Convers. Manag. 210, 112710. doi:10.1016/j.enconman.2020.112710
Farinas, M.-I., Garon, A., and Saint-Louis, K. (1997). Study of Heat Transfer in a Horizontal cylinder with Fins. Revue Générale de Thermique 36 (5), 398–410. doi:10.1016/s0035-3159(97)81601-7
Gao, Q., Zhang, K., and Wang, L. B. (2020). Numerical Analysis of Natural Convection in Internally Finned Horizontal Annuli. Front. Heat Mass Transfer 14, 29. doi:10.5098/hmt.14.29
Ghasemi, E., Soleimani, S., and Bararnia, H. (2012). Natural Convection between a Circular Enclosure and an Elliptic cylinder Using Control Volume Based Finite Element Method. Int. Commun. Heat Mass Transfer 39, 1035–1044. doi:10.1016/j.icheatmasstransfer.2012.06.016
Gholamalipour, P., Siavashi, M., and Doranehgard, M. H. (2019). Eccentricity Effects of Heat Source inside a Porous Annulus on the Natural Convection Heat Transfer and Entropy Generation of Cu-Water Nanofluid. Int. Commun. Heat Mass Transfer 109, 104367. doi:10.1016/j.icheatmasstransfer.2019.104367
Idrissi, A., Cheddadi, A., and Ouazzani, M. T. (2016). Heat Transfer in an Annular Space Fitted with Heating Isothermal Blocks: Numerical Bifurcation for Low Blocks Height. Case Stud. Therm. Eng. 7, 1–7. doi:10.1016/j.csite.2015.11.002
Kim, H. J., An, B. H., Park, J., and Kim, D.-K. (2013). Experimental Study on Natural Convection Heat Transfer from Horizontal Cylinders with Longitudinal Plate Fins. J. Mech. Sci. Technol. 27 (2), 593–599. doi:10.1007/s12206-012-1236-3
Kiwan, S., and Zeitoun, O. (2008). Natural Convection in a Horizontal Cylindrical Annulus Using Porous Fins. Int. Jnl Num Meth HFF 18 (5), 618–634. doi:10.1108/09615530810879747
Kuehn, T. H., and Goldstein, R. J. (1976). An Experimental and Theoretical Study of Natural Convection in the Annulus between Horizontal Concentric Cylinders. J. Fluid Mech. 74, 695–719. doi:10.1017/s0022112076002012
Kuehn, T. H., and Goldstein, R. J. (1978). An Experimental Study of Natural Convection Heat Transfer in Concentric and Eccentric Horizontal Cylindrical Annuli. J. Heat Transfer 100, 635–640. doi:10.1115/1.3450869
Kuehn, T. H., and Goldstein, R. J. (1980). Numerical Solution to the Navier-Stokes Equations for Laminar Natural Convection about a Horizontal Isothermal Circular cylinder. Int. J. Heat Mass Transfer 23 (7), 971–979. doi:10.1016/0017-9310(80)90071-x
Labonia, G., and Guj, G. (2000). Natural Convection in a Horizontal Concentric Cylindrical Annulus: Oscillatory Flow and Transition to Chaos. J. Fluid Mech. 375 (375), 179–202. doi:10.1017/S0022112098002754
Liu, L., Cao, Z., Shen, T., Zhang, L., and Zhang, L. (2021). Experimental and Numerical Investigation on Flow and Heat Transfer Characteristics of a Multi-Waves Internally Spiral Finned Tube. Int. J. Heat Mass Transfer 172, 121104. doi:10.1016/j.ijheatmasstransfer.2021.121104
Nada, S. A., and Said, M. A. (2019). Effects of Fins Geometries, Arrangements, Dimensions and Numbers on Natural Convection Heat Transfer Characteristics in Finned-Horizontal Annulus. Int. J. Therm. Sci. 137, 121–137. doi:10.1016/j.ijthermalsci.2018.11.026
Rahnama, M., and Farhadi, M. (2004). Effect of Radial Fins on Two-Dimensional Turbulent Natural Convection in a Horizontal Annulus. Int. J. Therm. Sci. 43, 255–264. doi:10.1016/j.ijthermalsci.2003.07.002
Rahnama, M., Mehrabian, M. A., Mansouri, S. H., Sinaie, A., and Jafargholi, K. (1999). Numerical Simulation of Laminar Natural Convection in Horizontal Annuli with Radial Fins. Proc. Inst. Mech. Eng. E: J. Process Mech. Eng. 213 (2), 93–97. doi:10.1243/0954408991529780
Senapati, J. R., Dash, S. K., and Roy, S. (2017). Numerical Investigation of Natural Convection Heat Transfer from Vertical cylinder with Annular Fins. Int. J. Therm. Sci. 111, 146–159. doi:10.1016/j.ijthermalsci.2016.08.019
Shadlaghani, A., Farzaneh, M., Shahabadi, M., Tavakoli, M. R., Safaei, M. R., and Mazinani, I. (2019). Numerical Investigation of Serrated Fins on Natural Convection from Concentric and Eccentric Annuli with Different Cross Sections. J. Therm. Anal. Calorim. 135, 1429–1442. doi:10.1007/s10973-018-7542-y
Touzani, S., Idrissi, A., Cheddadi, A., and Ouazzani, M. T. (2019). Numerical Study of Laminar Natural Convection in a Finned Annulus: Low Isothermal Blocks Positions. J. Eng. Phys. Thermophy 92 (4), 1064–1071. doi:10.1007/s10891-019-02021-6
Usman, M., Son, J. H., and Park, I. S. (2021). A Low-Rayleigh Transition into Chaos for Natural Convection inside a Horizontal Annulus at Prandtl Number 0.1. Int. J. Heat Mass Transfer 179 (2), 121658. doi:10.1016/j.ijheatmasstransfer.2021.121658
Yang, X., and Kong, S.-C. (2019). Numerical Study of Natural Convection in a Horizontal Concentric Annulus Using Smoothed Particle Hydrodynamics. Eng. Anal. Boundary Elem. 102, 11–20. doi:10.1016/j.enganabound.2019.02.007
Yong, S., Zhao, T. S., and Guo, Z. L. (2006). Finite Difference-Based Lattice Boltzmann Simulation of Natural Convection Heat Transfer in a Horizontal Concentric Annulus. Comput. Fluids 35 (1), 1–15. doi:10.1016/j.compfluid.2004.11.003
Yoo, J.-S., and Han, S.-M. (2000). Transitions and Chaos in Natural Convection of a Fluid with Pr = 0.1 in a Horizontal Annulus. Fluid Dyn. Res. 27 (4), 231–245. doi:10.1016/s0169-5983(00)00004-6
Yoo, J.-S. (1998). Natural Convection in a Narrow Horizontal Cylindrical Annulus: Pr ≤ 0.3. Int. J. Heat Mass Transfer 41 (20), 3055–3073. doi:10.1016/s0017-9310(98)00051-9
Zhang, K., Yang, M., Wang, J., and Zhang, Y. (2014). Experimental Study on Natural Convection in a Cylindrical Envelope with an Internal Concentric cylinder with Slots. Int. J. Therm. Sci. 76, 190–199. doi:10.1016/j.ijthermalsci.2013.09.005
Keywords: non-linear characteristic, natural convection, periodic oscillation, fin number, fin position
Citation: Zhang K, Zhang Y, Wang X and Wang L (2021) Effect of Fin Number and Position on Non-linear Characteristics of Natural Convection Heat Transfer in Internally Finned Horizontal Annulus. Front. Energy Res. 9:804094. doi: 10.3389/fenrg.2021.804094
Received: 28 October 2021; Accepted: 22 November 2021;
Published: 24 December 2021.
Edited by:
Xuewen Cao, China University of Petroleum, ChinaReviewed by:
Dongsheng Xia, Dalian Maritime University, ChinaCopyright © 2021 Zhang, Zhang, Wang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kun Zhang, emhhbmdrdW41MjAxNUAxNjMuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.