Short-Term Photovoltaic Power Interval Prediction Based on the Improved Generalized Error Mixture Distribution and Wavelet Packet -LSSVM

The periodicity and non-stationary nature of photovoltaic (PV) output power make the point prediction result contain very little information, increase the difficulty of describing the prediction uncertainty, and it is difficult to ensure the most efficient operation of the power system. Effectively predicting the PV power range will greatly improve the economics and stability of the grid. Therefore, this paper proposes an improved generalized based on the combination of wavelet packet (WP) and least squares support vector machine (LSSVM) to obtain higher accuracy point prediction results. The error mixed distribution function is used to fit the probability distribution of the prediction error, and the probability prediction is performed to obtain the prediction interval. The coverage rate and average width of the prediction interval are used as indicators to evaluate the prediction results of the interval. By comparing with the results of conventional methods based on normal distribution, at 95 and 90% confidence levels, the method proposed in this paper achieves higher coverage while reducing the average bandwidth by 5.238 and 3.756%, which verifies the effectiveness of the proposed probability interval prediction method.

1 Introduction

In recent years, the depletion of fossil fuels and the widespread environmental pollution have become global issues that must be urgently solved. Increasingly more countries and regions are searching for new energy sources to replace fossil fuels. Therefore, renewable energy sources, such as solar energy and wind energy, have attracted more attention worldwide owing to their advantages of being abundant, safe, and clean. In the first half of 2020, China’s newly installed photovoltaic power generation capacity reached 11.52 million kilowatts, including 7.082 million kilowatts of centralized photovoltaic and 4.435 million kilowatts of distributed photovoltaic. By the end of June, the cumulative installed capacity of photovoltaic power generation had reached 216 million kW, including 149 million kilowatts of centralized photovoltaic power and 67.07 million kilowatts of distributed photovoltaic power. The randomness, fluctuation, and intermittent nature of PV power impose enormous obstacles to the integration of solar energy into the power grid (Ueda et al., 2008; Armstrong, 2014; Europe, 2014).

Current research on forecasting short-term PV power generation requires numerical weather prediction (NWP) with consideration to various meteorological factors, combined with different power forecasting models (continuous, physical, statistical, artificial intelligence methods, multiple combined methods, and so on). However, all of these methods use traditional prediction models. The so-called point prediction method consists of inferring the output value of PV power generation at a certain time in the future according to certain laws (Mao et al., 2018; Huang et al., 2019a; Yang et al., 2019; Mao et al., 2020). Owing to the uncertainty of PV output power, the point prediction results do not often achieve the expected accuracy rate. Moreover, the point forecast information is minimal, and the grid dispatcher cannot learn the reliability of the predicted value and make effective decisions with regard to power system dispatching. Interval prediction can obtain the point prediction value of PV power generation, confidence level of the prediction value, and fluctuation range of the output power (Mao and Xin, 2018; Huang et al., 2019b). Obviously, interval prediction is more practical for formulating annual power and maintenance plans, arranging conventional unit combinations, formulating daily power generation plans, optimizing the power system rotation reserve, scheduling in real-time, new energy consumption, enhancing the flexibility of heating system and improving the stability of power system (Li L.-L. et al., 2021; Zhang et al., 2021).

A previous study (Han et al., 2019) proposed a multi-mode PV power generation interval prediction method that considers the seasonal distribution of power fluctuation characteristics. First, the PV output power, absolute power deviation, and relative change rate were analyzed to understand the seasonal distribution characteristics of PV output, which fluctuates over time. Then, multiple seasonal models based on the extreme learning machine (ELM) were established for the deterministic prediction of PV power. The deterministic prediction error was fitted by kernel density estimation to complete the PV power interval prediction. Another study (Xiao-ping and Yang, 2019) proposed an interval state estimation method for active power distribution networks with consideration to the randomness of wind turbines and PV output. This method uses an ELM to model the randomness of wind turbine and PV output in the form of interval numbers, performs ultra-short-term predictions for the wind turbine and PV output intervals, and uses the output interval as a pseudo measurement based on the Application Delivery Network (ADN) particle swarm optimization state estimation. In (Mashud and Irena, 2016), a 2-dimensional (2D) interval prediction method is proposed to predict aggregate statistical data and allocate PV power values in future time intervals. This method is more suitable for predictors compared with point prediction and has high application variability. The proposed method called Neural Network Ensemble for 2D-interval forecasting (NNE2D) combines the selection of variables through mutual information and neural network integration to calculate the 2D interval predictions. The two interval boundaries are expressed in percentiles. In (Luo et al., 2015), a set pair analysis method is proposed to construct prediction intervals based on the scientific division of the meteorological data range. First, the historical data were normalized and similar days were selected for the days to be predicted. Subsequently, pairs were constructed and the Identical Discrepancy Contrary (IDC) distance was calculated. In (Rana et al., 2015), a particular method for 2D interval prediction is proposed to predict a series of expected solar output values for future time intervals. Using the model called Support Vector Regression for 2D-interval forecasting (SVR2D), this method adopts support vector regression as the prediction algorithm, and can directly calculate the 2D interval forecasts from previous historical solar and meteorological data. In (Golestaneh and Gooi, 2017), a non-parametric method is proposed to reliably predict the intervals based on radial basis function (RBF) neural network prediction. The lower upper bound estimation method is suitable for constructing the prediction interval. Based on similar daytime principles, a historical power data record was selected by analyzing the PV power generation factors. Then, strong correlations that favor historical data as a sample model facilitated the convergence. In (Plessis et al., 2021), aiming at the macro-level model to capture the uncertainty of the low-power output dynamic capability of a large multi-megawatt photovoltaic system, a neural network-based aggregate inverter-level prediction method is proposed. In (Liu and Xu, 2020), it is proposed to integrate three different random learning algorithms (extreme learning machine, random vector function chain and random configuration network) into a hybrid prediction model to predict photovoltaic power generation probability. In (Ska et al., 2021), a new type of small model is proposed, which considers the operating status of each part of the photovoltaic system, and is used to predict the photovoltaic temperature, the correlation coefficient of the solar irradiance in the plane, and the power output. In (Li J. et al., 2021), an improved beam group optimization algorithm is proposed to reduce the fuel cost of the power system. The algorithm uses the tent mapping to generate the initial population, and uses the gray wolf optimizer to generate the global search vector to improve the global search ability. The improvement of the algorithm has certain reference significance for the prediction link. In (Ma et al., 2021), the short-term forecast errors of photovoltaic power generation mainly come from numerical weather forecasting and forecasting process, and a short-term photovoltaic power forecasting method based on irradiance correction and error forecasting is proposed to improve the forecasting accuracy from the perspective of correcting NWP information. In the above-mentioned studies, non-parametric estimation methods were used to predict the interval probability. Because non-parametric estimation methods do not assume the function and do not set any parameters, they can avoid the effect of selecting an incorrect prediction error function. However, the specific distribution function of the prediction error cannot be obtained. The parameter estimation method uses an optimized normal distribution to fit the probability distribution of the prediction error and then predicts the probability.

This study introduces an improved generalized error mixture distribution function to fit the probability distribution of the prediction error and perform probability prediction to obtain the prediction interval. Factor analysis (FA) is used to reduce the dimensionality of meteorological factors and reduce the number of input variables. A similar day algorithm is used to select data similar to the weather factors predicted as the training set. Prediction results were obtained for two different weather types. Using the LSSVM to solve small sample data and the ability to approximate nonlinear functions, the obtained fundamental frequency signal and multi-layer high-frequency signal are used as the input of the LSSVM to perform frequency-by-frequency prediction, and finally different scales The output results above are superimposed and synthesized to obtain the predicted value of the output power of the original PV power station. Finally, FCM clustering is used to build the improved generalized error mixture distribution function. According to the previously obtained prediction error of the WP-LSSVM model, the probability density distribution function is used for fitting. The upper and lower bounds are determined according to the error distribution, and interval prediction is carried out. The simulation results reveal that the proposed method performed better compared with the prediction interval. The scale parameters of the improved generalized error mixed distribution function can evaluate the prediction results at different time and space scales, and provide uncertain information and reliability evaluation basis for the safe operation of the power system and the dispatching operation of the power grid.

2 Selection of Similar Days

This study used FA to screen the input variables of the predictive model, find hidden representative factors, and group variables of the same nature into one factor to reduce the number of variables. Then, meteorological factors with a larger contribution rate were selected as the input variables of the prediction model. NWP information contains various meteorological factors in each region, and the amount of data is very large. Adding too much data to the model will reduce the generalization ability of the model. Generally, there is a certain correlation between the factors that affect the power of photovoltaic power generation. The information provided by multiple types of NWP overlaps to a certain extent, which will increase the complexity of calculation. The factor analysis method is used to selectively extract the NWP information, and the main components that have a greater impact on the photovoltaic power are obtained as the input of the prediction model. This method simplifies the network structure and improves the computational efficiency, but does not affect the accuracy of the final result prediction.

This paper presents an example regarding the NWP data of a PV power station. For details on the data used in this study, please refer to subsection B of Section VI. This study considered the radiation, atmospheric density, temperature, and humidity as common factors in the samples. For n-dimensional data, $x=\left(x_1,x_2,\cdots ,x_n\right)\text{'}$, Let its mean value be $u=\left(u_1,u_2,\cdots ,u_n\right)\text{'}$. The general model of factor analysis is:

$x=u+Af+l$

In the formula, $A={\left(a_{ij}\right)}_{n\times m}$ is the factor correlation coefficient matrix; $f=\left(f_1,f_2,\cdots ,f_m\right)\text{'}$ is the common factor; $a_{ij}$ is the correlation coefficient on the common factor $f_j$ of the variable $x_i$; $l=\left(l_1,l_2,\cdots ,l_n\right)$ is the recessive factor, $i=\mathrm{1,2},\cdots ,n;j=\mathrm{1,2},\cdots ,m$. This article defines the common factors of the sample as: radiation factor, atmospheric density factor, temperature factor, humidity factor. The results obtained by performing FA on seven meteorological factors that affect the PV output are presented in Table 1.

TABLE 1

TABLE 1. Correlation coefficients of factor analysis.

As can be seen in Table 1, meteorological factors, such as direct radiation, temperature, and humidity, have a high contribution rate to certain common factors, and the absolute values of their correlation coefficients exceed 0.7. Therefore, the direct normal radiation (corresponding to short-wave radiation), temperature (corresponding to temperature), and humidity (corresponding to humidity) were considered as the input of subsequent models.

Similar days refer to the historical days in a quarter that have the same weather type as the forecast day. Data obtained on similar days can often effectively reflect the output trend under the weather type conditions. The model’s prediction accuracy rate can be greatly improved by selecting a historical day that is strongly correlated with the day to be predicted as the model’s training set. To select the date closest to the predicted weather type and season type from the historical records of PV power generation systems, this study considered three meteorological factors (direct radiation, temperature, and humidity) obtained from FA as the environmental factors to be considered in the similar day selection. The assessment was made by considering the sunny day type as an example. Similar days were selected from the historical data of sunny days, and 14 similar days were selected as the training set of subsequent models. Similarly, data can be obtained for the similar days of other weather types. The similar day selection algorithm steps are as follows:

Step 1. Select a historical record consistent with the forecast weather type and season type to form an “n” sample set $D$.

Step 2. Calculate the Euclidean distance d of the historical record in the day to be predicted, and the sample set $D$; $d$ is calculated as follows:

$\mathit{d}=\mathit{sqrt}\left({\left({\displaystyle \sum _{\mathit{j}=1}^3{\mathit{Y}}_{\mathit{j}}-{\mathit{X}}_{\mathit{ij}}}\right)}^2\right)(1)$

In Eq. 1, $i=\mathrm{1,2},\cdots ,n$ and $Y_1,Y_2,Y_3$ are the daily average direct radiation, average daily temperature, and average daily humidity of the day to be predicted; $X_{i1},X_{i2}$ and $X_{i3}$ denote the average daily direct radiation, average daily humidity, and average daily temperature recorded in the article of sample set $D$.

Step 3. The Euclidean distance set $d=\left\{d_1,d_2,\cdots ,d_n\right\}$ is arranged in descending order, and the date corresponding to the relatively small value of the 14th day of the month is a similar day corresponding to the predicted day.

3 Photovoltaic Output Power Point Prediction

3.1 WP Theory

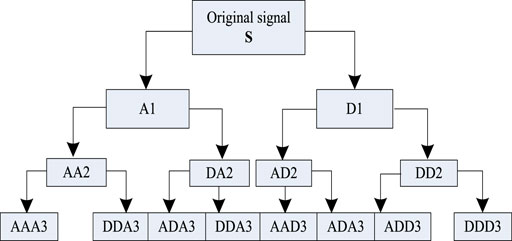
Wavelet Analysis is a signal time-scale (time-frequency) analysis method, and has the characteristics of multi-resolution analysis. Additionally, it is capable of characterizing the local characteristics of the signal in the time and frequency domains, that is, the time window and frequency window. The time-frequency localization analysis method can be changed to detect the instantaneous anomalies entrained in the normal signal, and display the signal components. This method is known to function as a ‘microscope’ for signal analysis (Puthenpurakel and Subadhra, 2016). Moreover, WP analysis can provide a more refined method for signal analysis because it divides the frequency band into multiple levels. Further, it decomposes the high-frequency part, which is not subdivided, using multi-resolution analysis and can consider the characteristics of the analyzed signal. This method selects the corresponding frequency band to match the signal spectrum, and thereby improves the time-frequency resolution and increases the potential for wider application (Liu et al., 2013). Among them, the Haar function is a simple and commonly used orthogonal wavelet function with tight support in wavelet analysis. The Haar WP is a WP that has the Haar function as the wavelet basis function. The three-layer decomposition of the WP decomposition tree is shown in Figure 1.

FIGURE 1

FIGURE 1. WP decomposition algorithm.

In Figure 1, S represents the decomposed signal, A represents the low-frequency part of the signal, $D$ represents the high-frequency part of the signal, and the attached number represents the number of decomposition layers, that is, the number of scales.

The decomposition algorithm and reconstruction algorithm of the WP are described below.

Let us assume that $g_j^n\left(t\right)\in U_j^n$; then, $g_j^n\left(t\right)$ can be expressed as follows:

${\mathit{g}}_{\mathit{j}}^{\mathit{n}}\left(\mathit{t}\right)={\displaystyle \sum _{\mathit{t}}{\mathit{d}}_{\mathit{l}}^{\mathit{j},\mathit{n}}{\mathit{u}}_{\mathit{n}}(2^{\mathit{j}}\mathit{t}-\mathit{l})}(2)$

The WP decomposition algorithm operates as follows: find $\left\{d_l^{j+1,n}\right\}$ and $\left\{d^{j,2n}\right\}$ from $\left\{d_l^{j,2n+1}\right\}$, where

$\{\begin{array}{c}{\mathit{d}}_{\mathit{l}}^{\mathit{j},2\mathit{n}}={\displaystyle \sum _{\mathit{k}}{\mathit{a}}_{\mathit{k}-2\mathit{l}}{\mathit{d}}_{\mathit{k}}^{\mathit{j}+1,\mathit{n}}}\\ {\mathit{d}}_{\mathit{l}}^{\mathit{j},2\mathit{n}+1}={\displaystyle \sum _{\mathit{k}}{\mathit{b}}_{\mathit{k}-2\mathit{l}}{\mathit{d}}_{\mathit{k}}^{\mathit{j}+1,\mathit{n}}}\end{array}(3)$

The WP reconstruction algorithm operates as follows: from $\left\{d_l^{j,2n}\right\}$ and $\left\{d_l^{j,2n+1}\right\}$ find $\left\{d_l^{j+1,n}\right\}$, where

${\mathit{d}}_{\mathit{l}}^{\mathit{j}+1,\mathit{n}}={\displaystyle \sum _{\mathit{k}}\left[{\mathit{h}}_{\mathit{l}-2\mathit{k}}{\mathit{d}}_{\mathit{k}}^{\mathit{j},2\mathit{n}}+{\mathit{g}}_{\mathit{l}-2\mathit{k}}{\mathit{d}}_{\mathit{k}}^{\mathit{j},2\mathit{n}+1}\right]}(4)$

In Eq. (3), $a$ and $b$ are the decomposition filter banks, $j=\mathrm{1,2},\cdots ,J$, and $n=\mathrm{1,2},\cdots ,2^j-1$, $J$ are the WP decomposition layers.

3.2 LSSVM

The LSSVM regression applies the LSSVM to the regression estimation proposed by Suykens in 1999 (Zhu and Wei, 2013). Unlike the two previously mentioned algorithms, the LSSVM uses a quadratic loss function and transforms the optimization problem into a linear equation problem instead of a quadratic programming problem. Additionally, the constraints also become equality constraints instead of inequality constraints. Although the LSSVM does not have the standard high accuracy rate, it can ensure that the obtained solution is the global optimal solution because it solves the linear equation problem using large datasets. Additionally, it has the advantages of requiring less computational resources and achieving faster solution and convergence speed.

The algorithm for LSSVM regression (Miranian and Abdollahzade, 2013) is as follows:

Set a known training set as follows:

$\mathit{T}=\{({\mathit{x}}_1,{\mathit{y}}_1),\mathrm{...},({\mathit{x}}_{\mathit{l}},{\mathit{y}}_{\mathit{l}})\}\in {\left(\mathit{X*Y}\right)}^{\mathit{l}}$

where $x_i\in X=R^n$, $y_i\in Y=R$, $i=\mathrm{1,2},\cdots ,l$.

Select appropriate parameters and appropriate kernel functions. This paper chooses the radial basis function as the kernel function of the SVM.

Construct and solve the following problems:

$\underset{\mathit{w},\mathit{b},\mathit{e}}{\mathit{max}}\mathit{J}(\mathit{w},\mathit{e})=\frac{1}{2}({\mathit{W}}^{\mathit{T}}\mathit{W}+\mathit{\gamma }{\displaystyle \sum _{\mathit{i}=1}^{\mathit{l}}{\mathit{e}}_{\mathit{i}}^2})(5)$

s t. $y_i=W^T\varphi \left(x_i\right)+b+e_i$, $i=\mathrm{1,2},\cdots ,l$where $\varphi (•)$ is the kernel space mapping function, $w$ is the weight vector, $e_i$ is the error variable, $b$ is the deviation, $J$ is the loss function, and $\gamma$ is an adjustable constant.

Constructable Lagrangian function:

$\mathit{L}(\mathit{w},\mathit{b},\mathit{e},\mathit{\alpha })=\mathit{J}(\mathit{w},\mathit{e})-{\displaystyle \sum {}^{\mathit{i}=1}{{\displaystyle \mathit{\alpha }}}_{\mathit{i}}\{{\mathit{W}}^{\mathit{T}}\varphi \left({\mathit{x}}_{\mathit{i}}\right)+\mathit{b}+{\mathit{e}}_{\mathit{i}}-{\mathit{y}}_{\mathit{i}}\}}(6)$

where ${\alpha }_i\in R$ is the Lagrangian multiplier. Find the partial derivatives of Eq. 6 with respect to $e_i$, ${\alpha }_i$, $w$, and $b$, respectively, and then eliminate $w$ and $e_i$ to obtain the following equation:

$\left[\begin{array}{cc}0& 1_{\mathit{u*}1}\\ 1_{1\mathit{*u}}& \varphi {\left({\mathit{x}}^{\mathit{i}}\right)}^{\mathit{T}}\varphi \left({\mathit{x}}_{\mathit{j}}\right)+\frac{1}{\mathit{\gamma }}\mathit{I}\end{array}\right]\left[\begin{array}{c}\mathit{b}\\ \mathit{a}\end{array}\right]=\left[\begin{array}{c}0\\ \mathit{y}\end{array}\right](7)$

where $1_{1\text{*}u}=[\mathrm{1,1},\mathrm{...},1]=1_{u\text{*}1}^T$, $\alpha =[{\alpha }_1,{\alpha }_2,\mathrm{...},{\alpha }_l]$, and $i,j=1,\cdots ,l$. From Eq. 7, ${\alpha }_i$ and $b$ can be solved.

The following decision function is constructed:

$\mathit{f}\left(\mathit{x}\right)={\displaystyle \sum _{\mathit{i}=1}^{\mathit{l}}{\mathit{\alpha }}_{\mathit{i}}\varphi {\left(\mathit{x}\right)}^{\mathit{T}}\varphi \left({\mathit{x}}_{\mathit{i}}\right)+\mathit{b}}(8)$

Eq. 8 is the regression estimation of the problem, where $\varphi {\left(x\right)}^T\varphi \left(x_i\right)$ is the part of the kernel function.

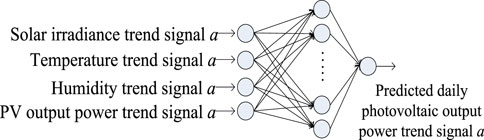
Considering the PV power station output power and trend signal $a$ of the NWP meteorological data as examples, the training process of the LSSVM is as shown in Figure 2. LSSVM maps the input data from low-dimensional to high-dimensional space through nonlinear mapping, thereby constructing the optimal linear regression function. The key of the LSSVM model lies in the choice of the internal kernel function. In this paper, the radial basis function is selected as the kernel function. LSSVM establishes a network model through formulas Eq. 5–8 to capture the nonlinear relationship between input and output.

FIGURE 2

FIGURE 2. Trend signal of LSSVM algorithm prediction model.

In Figure 2, the construction of each other frequency band model also accords with the construction method of the above-mentioned trend signal model. Finally, the results obtained for different scales were superimposed and combined to obtain the final prediction result.

4 The Improved Generalized Error Mixture Distribution Parameter Estimation

4.1 The Improved Generalized Error Distribution Model

The probability density curve can reflect its prediction error range, can also estimate the output of a given confidence interval, so it is very important to choose an appropriate probability density fitting model. Previous research on statistical characteristics of the prediction error is more, such as Beta distribution, Laplace distribution and Cauchy distribution, but the fitting effect is not ideal. Combined with the characteristics of the forecast error spikes and light tails and the more flexible shape, an improved generalized error distribution model is adopted. This study introduced the improved generalized error distribution function to fit the probability distribution of the prediction error and perform probability prediction to obtain the prediction interval. The prediction effect is better compared with that based on the optimized normal distribution and probability prediction. Additionally, the scale parameter of the improved generalized error distribution function can be used to evaluate the size of the prediction error at different time and space scales. The function expression is:

$\mathit{f}\left(\mathit{x},\mathit{v},\mathit{\lambda }\mathrm{,}\mathit{\alpha }\mathrm{,}\mathit{\mu }\right)=\frac{\mathit{v}}{\mathit{\lambda }\mathrm{\Gamma }\left(\frac{1}{\mathit{v}}\right)}\mathit{exp}\left(-{\left|\frac{\mathit{x}-\mathit{\mu }}{\mathit{\lambda }}\right|}^{\mathit{\alpha }}\right)(9)$

$\mathit{\lambda }={{\displaystyle \left\{\frac{{{\displaystyle 2}}^{\left(2-\frac{2}{\mathit{v}}\right)}\mathbf{\Gamma }\left(\frac{1}{\mathit{v}}\right)}{\mathbf{\Gamma }\left(\frac{3}{\mathit{v}}\right)}\right\}}}^{1/2}(10)$

where $\text{Γ}(\cdot )$ is the gamma function, $x$ is the Wind power forecast error per-unit value, $v$ and $\lambda$ are shape parameters, $\alpha$ and $\mu$ are the slope parameters and position parameters that are added in combination with the error distribution characteristics.

4.2 FCM Clustering and Entropy Weight Method

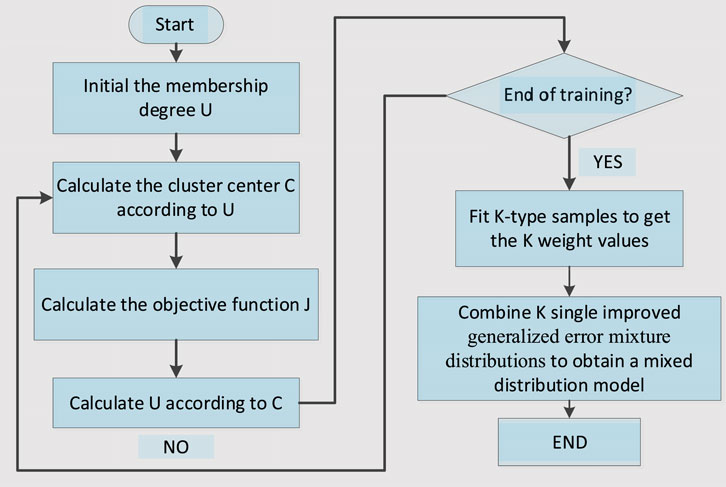
FCM is a partition-based clustering algorithm. Its idea is to maximize the similarity between objects divided into the same cluster and minimize the similarity between different clusters. FCM is an improvement of hard C-means algorithm, which is hard for data partitioning, while FCM is a kind of flexible fuzzy partitioning. Hard clustering classifies each object to be recognized strictly into a class with specific characteristics, while FCM establishes an uncertain description of the sample category. Therefore, FCM can reflect the objective world more accurately and becomes the mainstream method of cluster analysis. The FCM algorithm is described as follows:

Data set: $X=\left\{X_1,X_2\cdots X_n\right\}$to find a partition matrix $U=\left[u_{ji}\right]$ and cluster center $V=\left\{v_1,v_2\cdots v_c\right\}$ from $X$ to make the objective function, while $m$ is a weighted index, $m\in \left[1,+\infty \right]$.

$\mathit{ J}\left(\mathit{U},\mathit{V}\right)=\mathit{min}\left({\displaystyle \sum }_{\mathit{j}=1}^{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{c}}{\mathit{u}}_{\mathit{ji}}^{\mathit{m}}{\mathit{d}}_{\mathit{ji}}^2\right)(11)$

The elements of matrix $U$ meet $u_{ji}\in \left[\mathrm{0,1}\right]j=1,\cdots ,n$,$i=1,\cdots ,c$ and the matrix variable $u_{ji}$ to meet ${\displaystyle \sum }_{i=1}^c{u}_{ji}=1$.

$0<{\displaystyle \sum }_{\mathit{j}=1}^{\mathit{n}}{\mathit{u}}_{\mathit{ji}}<\mathit{n}(12)$

The Euclidean distance ($d$) between data $x_i$ and the cluster center $v_j$ is as follows:

${\mathit{d}}_{\mathit{ji}}=\parallel {\mathit{x}}_{\mathit{j}}-{\mathit{v}}_{\mathit{i}}\parallel (13)$

The Lagrange multiplier was then introduced into 9) to generate an objective function, as follows:

$\mathit{J}\left(\mathit{U},\mathit{V},\mathit{Y}\right)={\displaystyle \sum }_{\mathit{j}=1}^{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{c}}{\mathit{u}}_{\mathit{ji}}^{\mathit{m}}{\mathit{d}}_{\mathit{ji}}^2-{\displaystyle \sum }_{\mathit{j}=1}^{\mathit{n}}{\mathit{y}}_{\mathit{i}}\left({\displaystyle \sum }_{\mathit{i}=1}^{\mathit{c}}{\mathit{u}}_{\mathit{ji}}^{\mathit{m}}-1\right)(14)$

Once an objective function is derived, the membership degree and cluster center formulae are obtained as follows:

${\mathit{u}}_{\mathit{ji}}=\frac{{\left(\frac{1}{{\mathit{d}}_{\mathit{ji}}^2}\right)}^{\frac{1}{\left(\mathit{m}-1\right)}}}{{{\displaystyle \sum }}_{\mathit{k}=1}^{\mathit{c}}{\left(\frac{1}{{\mathit{d}}_{\mathit{jk}}^2}\right)}^{\frac{1}{\left(\mathit{m}-1\right)}}}(15)$

and

${\mathit{v}}_{\mathit{i}}=\frac{{{\displaystyle \sum }}_{\mathit{j}=1}^{\mathit{n}}{\left({\mathit{u}}_{\mathit{ji}}\right)}^{\mathit{m}}{\mathit{x}}_{\mathit{j}}}{{{\displaystyle \sum }}_{\mathit{j}=1}^{\mathit{n}}{\left({\mathit{u}}_{\mathit{ji}}\right)}^{\mathit{m}}}(16)$

Next, execute the steps of FCM clustering algorithm.

1) Calculate the minimum distance between two samples $\alpha$>0. Generates a distance matrix $D$, the two closest samples are placed in a class, and the midpoint of the two samples is used as the center of the first type.

2) Use matrix $D$ to select the distance threshold $\alpha$ to calculate all samples whose distance is greater than $\alpha$ from the two samples in the first category. The two closest points in these samples are then used as a category, while the midpoint of the two points located in the center of the cluster constitutes the second category.

3) Samples with a distance greater than $\alpha$ are extracted from the remaining samples. The two points with the shortest distance are used to define a class, and the midpoints of the two samples define a clustering center.

4) Repeat Step 3 until Class C is determined

5) Use the results of step 4 to set the initial parameters and cluster centers.

6) The degree of membership is calculated by formulas Eqs 13, 15

7) Use formulas Eqs 14, 16 to determine a new cluster center,

8) Use formula Eq. 12 to calculate the objective function. If this judgment is less than the threshold, the cluster ends; otherwise, return to step 6.

The different weighting methods significantly affect the modeling effect of the combined model. The entropy weight method is a method to determine the weight of each indicator in the system through the information entropy theory, which can reduce the influence of subjective factors and improve the credibility and accuracy of the analysis. It relies on the magnitude of entropy to evaluate the degree of dispersion of indicators. The smaller the entropy value, the greater the dispersion, the smaller the uncertainty, and the greater the amount of information, the greater the role of this indicator in the comprehensive evaluation, and the greater the weight. This study uses the entropy method to determine the weight of each sub-model.

Suppose there are $n$ objects and $m$ evaluation indicators. $X_{ij}$ is the data of object $i$ under index $j$, calculate the proportion of object $i$ under index $j$ in the index.

${\mathit{P}}_{\mathit{ij}}=\frac{{\mathit{X}}_{\mathit{ij}}}{{{\displaystyle \sum }}_{\mathit{i}=1}^{\mathit{n}}{\mathit{X}}_{\mathit{ij}}} \mathit{j}=\mathrm{1,2},\dots ,\mathit{m}(17)$

Calculate the information entropy of index $j$:

${\mathit{e}}_{\mathit{j}}=-\frac{1}{\ln \mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{P}}_{\mathit{ij}}\ln {\mathit{P}}_{\mathit{ij}}(18)$

If $P_{ij}=0$ , then $\underset{P_{ij}\to 0}{\lim }{P}_{ij}\ln P_{ij}=0$.

Determine the weight of index $j$:

${\mathit{\omega }}_{\mathit{j}}=\frac{{\mathit{d}}_{\mathit{j}}}{{{\displaystyle \sum }}_{\mathit{j}=1}^{\mathit{m}}{\mathit{d}}_{\mathit{j}}}=\frac{1-{\mathit{e}}_{\mathit{j}}}{\mathit{m}-{{\displaystyle \sum }}_{\mathit{j}=1}^{\mathit{m}}{\mathit{e}}_{\mathit{j}}}(19)$

Where the coefficient of difference of index $j$ is $d_j=1-e_j$. The larger the $d_j$, the more important the indicator.

The composite score of object $i$:

${\mathit{s}}_{\mathit{i}}={\displaystyle \sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}{\mathit{X}}_{\mathit{ij}}(20)$

4.3 Establishment of the Improved Generalized Error Distribution Model

The improved generalized error mixture distribution model is obtained by linearly combining multiple improved generalized error distribution models. The sum of the weights of every single model is 1. The distribution mixture has the advantages of simple structure, flexible shape, and good fitting performance; its parameter weights are obtained by FCM clustering. Figure 3 shows the flowchart for the construction of the distribution model.

FIGURE 3

FIGURE 3. Establishment of the improved generalized error mixture distribution model.

5 Short-Term PV Power Generation Probability Interval Prediction Process Based on WP-LSSVM and the Improved Generalized Error Distribution

The WP analysis can decompose the randomness and uncertainty of the signal to separate the prediction and analysis, which enables the prediction and analysis of the trend part that does not include interference. Simultaneously, support vector machines can solve small sample size, nonlinear, and high dimensional pattern recognition problems. The LSSVM has faster convergence speed and is more suitable for short-term prediction. Therefore, the authors used a forecasting method that combines the WP and LSSVM to forecast the PV output interval. The general process is shown in Figure 4.

FIGURE 4

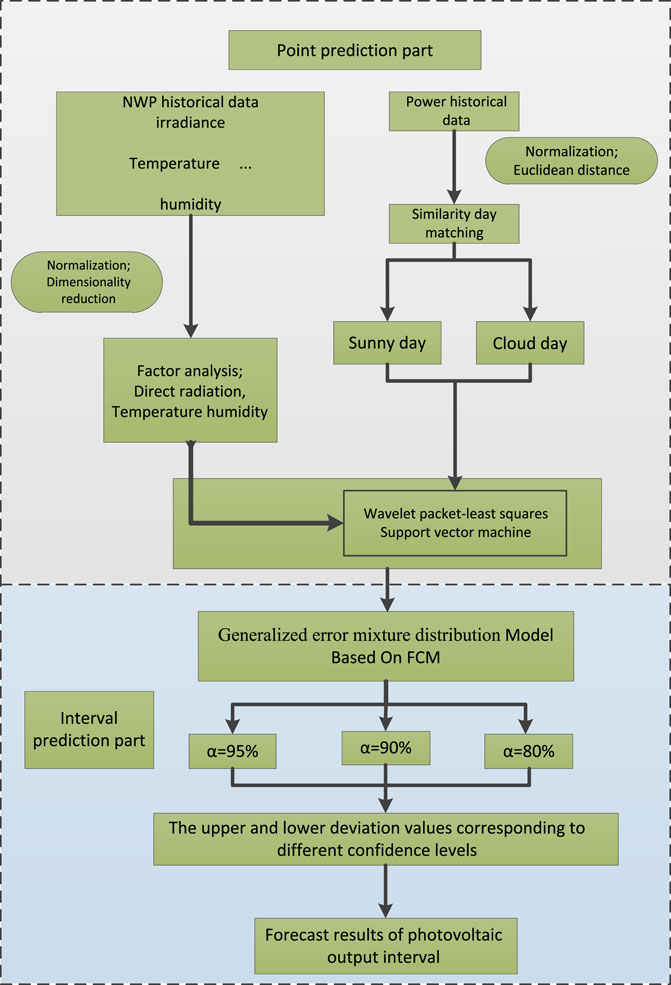
FIGURE 4. Flow chart of short-term PV power generation probability interval prediction based on mixture of WP-LSSVM and the improved generalized error distribution.

The basic principles of the PV output interval prediction based on the WP and LSSVM are divided into the following steps with Haar as the wavelet basis function:

Step 1. Normalize the NWP data and power data, obtain the main factors that affect the power by carrying out FA, and obtain the training sets using the Euclidean distance for different weather types;

Step 2. Input the training set data into the WP-LSSVM, and analyze the point prediction error results;

Step 3. The improved generalized error distribution model based on the FCM algorithm is used to fit the prediction error. The corresponding interval prediction results are obtained according to different confidence levels.

6 Analysis of Prediction Results Based on WP-LSSVM Point Prediction Model

6.1 Evaluation Indicators

6.1.1 Evaluation Indicators for Point Prediction

By considering the advantages and disadvantages of point prediction results, this study used relevant indicators, in the following order: root mean square error (RMSE), qualified rate (QR), mean relative error (MRE), correlation coefficient, and accuracy rate. The indices are expressed by Eqs 21–26.

$\mathit{RMSE}=\sqrt{\frac{1}{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{{\mathit{P}}_{\mathit{Mi}}-{\mathit{P}}_{\mathit{Pi}}}{\mathit{Ca}{\mathit{p}}_{\mathit{i}}}\right)}^2}(21)$

$\mathit{QR}=\frac{1}{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{B}}_{\mathit{i}}\times 100\mathit{\%}(22)$

${\mathit{B}}_{\mathit{i}}=\{\begin{array}{cc}1& \left(1-\frac{\left|{\mathit{P}}_{\mathit{Mi}}-{\mathit{P}}_{\mathit{Pi}}\right|}{\mathit{Cap}}\right)\ge 0.75\\ 0& \left(1-\frac{\left|{\mathit{P}}_{\mathit{Mi}}-{\mathit{P}}_{\mathit{Pi}}\right|}{\mathit{Cap}}\right)<0.75\end{array}(23)$

$\mathit{MRE}=\frac{{{\displaystyle \sum }}_{\mathit{i}=1}^{\mathit{n}}\left|{\mathit{P}}_{\mathit{Mi}}-{\mathit{P}}_{\mathit{Pi}}\right|}{\mathit{Cap}•\mathit{n}}(24)$

The correlation coefficient is expressed as follows:

$\mathit{r}=\frac{{{\displaystyle \sum }}_{\mathit{i}=1}^{\mathit{n}}[({\mathit{P}}_{\mathit{Mi}}-\overline{{\mathit{P}}_{\mathit{M}}})•({\mathit{P}}_{\mathit{Pi}}-{\overline{\mathit{P}}}_{\mathit{P}})]}{\sqrt{{{\displaystyle \sum }}_{\mathit{i}=1}^{\mathit{n}}{({\mathit{P}}_{\mathit{Mi}}-\overline{{\mathit{P}}_{\mathit{M}}})}^2•{{\displaystyle \sum }}_{\mathit{i}=1}^{\mathit{n}}{({\mathit{P}}_{\mathit{Pi}}-{\overline{\mathit{P}}}_{\mathit{P}})}^2}}(25)$

The accuracy rate is expressed as follows:

${\mathit{r}}_1=\left[1-\sqrt{\frac{1}{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{{\mathit{P}}_{\mathit{Mi}}-{\mathit{P}}_{\mathit{Pi}}}{\mathit{Cap}}\right)}^2}\right](26)$

where $P_{Mi}$ is the actual power at time $i$; $P_{Pi}$ is the predicted power at time $i$; $\overline{P_M}$ is the average value of the actual power of all samples; ${\overline{P}}_P$ is the average of all predicted power samples; $CA{P}_i$ is the daily average boot capacity; $n$ is the number of daily samples.

6.1.2 Evaluation Indicators for Interval Prediction

The prediction interval’s coverage probability represents the probability of the target value falling within the prediction interval and is a key indicator for evaluating the interval’s prediction reliability. A high coverage probability indicates that more target values will fall within the constructed prediction interval and vice versa. The definition formula is expressed as follows:

${\mathit{P}}_{\mathit{c}}=\frac{1}{\mathit{N}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{N}}{\mathit{\epsilon }}_{\mathit{i}}(27)$

where $P_C$ is the coverage probability of the prediction interval; $N$ is the total number of samples; ${\epsilon }_i$ is a variable. If the target value $y_i$ is between the upper boundary $U_i$ and the lower boundary $L_i$ of the prediction interval, then, ${\epsilon }_i$ is 1; otherwise ${\epsilon }_i$ is 0.

${\mathit{\epsilon }}_{\mathit{i}}=\{\begin{array}{c}1\mathit{ }{\mathit{y}}_{\mathit{i}}\in \left[{\mathit{L}}_{\mathit{i}},{\mathit{U}}_{\mathit{i}}\right]\\ 0 {\mathit{y}}_{\mathit{i}}\in \left[{\mathit{L}}_{\mathit{i}},{\mathit{U}}_{\mathit{i}}\right]\end{array}(28)$

Generally, the indicator for evaluating the performance of interval prediction is the interval prediction coverage probability. If the target value limit is used as the upper and lower boundary of the prediction interval, then, the 100% interval prediction coverage probability can be easily realized. If an interval is too wide, this will increase the uncertainty of the prediction results, which will in turn reduce the prediction result for system scheduling and lead to the loss of decision-making value. Therefore, it is necessary to quantitatively evaluate the prediction interval width. The commonly used interval prediction average width measurement index is abbreviated as PINAW and expressed as follows:

${\mathit{W}}_{\mathit{A}}=\frac{1}{\mathit{NR}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{N}}({\mathit{U}}_{\mathit{i}}-{\mathit{L}}_{\mathit{i}})(29)$

where $W_A$ is the average interval prediction width, and $R$ is the variation range of the target value. By using $R$, we can ensure that $W_A$ is normalized between [0, 1].

6.2 Data Sources

The data set for the calculation example presented in this paper comprises the measured PV power data, historical weather data, and related NWP data of a PV power station in Jilin, China. The time span of the training set is from January 1, 2017, to December 31, 2017. The time span of the test set is from June 1st to June 5th, 2018. The installed capacity of the PV power station is 30 MW, and the data sampling interval is 15 min.

To summarize the unified sample statistical distribution, the problem of the network training time increasing as a result of the singular sample data and dimensional inconsistency of the original data was eliminated. In this regard, the original PV power plant data must be normalized as expressed by the normalized Eq. 30:

$\mathit{ }{\mathit{x}}_{\mathit{i}}^{\mathit{\text{'}}}=\frac{{\mathit{x}}_{\mathit{i}}-{\mathit{x}}_{\mathit{min}}}{{\mathit{x}}_{\mathit{max}}-{\mathit{x}}_{\mathit{min}}}(30)$

where $x_i^{\text{'}}$ denotes the normalized data; xi denotes the original PV data; $x_{min}$ and $x_{max}$ are the minimum and maximum values of the original PV data, respectively.

Based on the above discussion, FA reveals that the direct radiation, temperature, and humidity are the main factors affecting the PV power.

6.3 WP Decomposition and Reconstruction

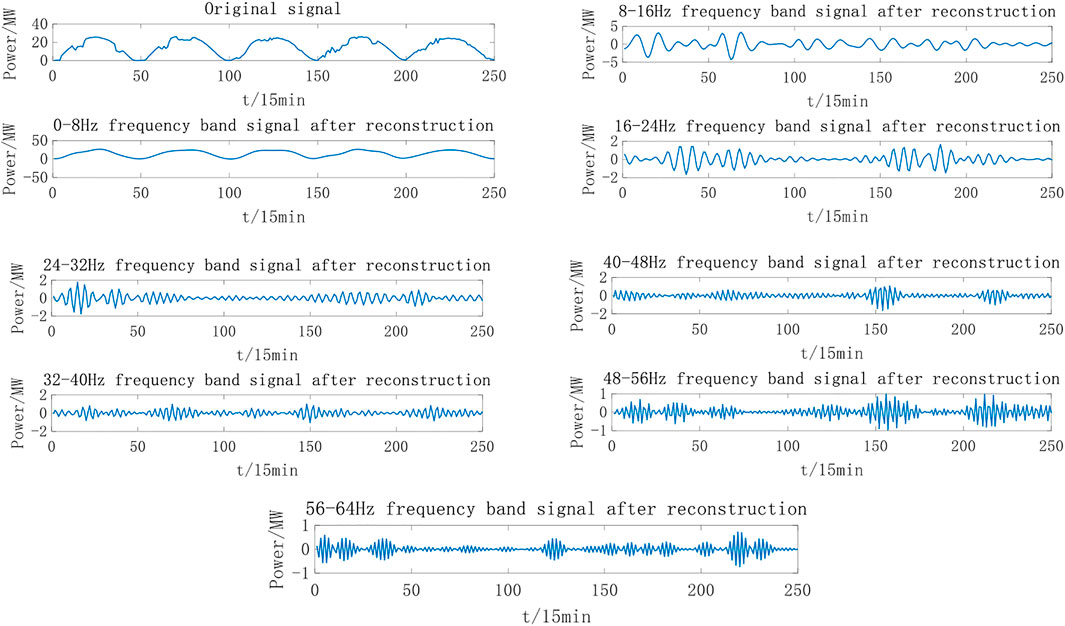
In this study, raw data for the solar irradiance, ambient temperature, ambient humidity, and output power of PV power plants were obtained by FA, selected as WP decomposition objects, and reconstructed for model training and prediction. Considering the raw data of the PV power plant output power from April 1st to April 5th as an example, the time interval for collecting three-layer WP decomposition data is 15 min, as shown in Figure 5. Each sub-picture in Figure 5 is the original signal; reconstructed 0-8HZ; 8-16HZ; 16-24HZ; 24-32HZ; 32-40HZ; 40-48HZ; 48-56HZ; 56-64HZ frequency band signal.

FIGURE 5

FIGURE 5. Frequency components of PV power plant output power processed by WP.

As can be seen, after the multi-scale WP decomposition and reconstruction, each frequency signal part is stable and the image trend in some periods is approximately the same.

6.4 WP-LSSVM Point Prediction Results

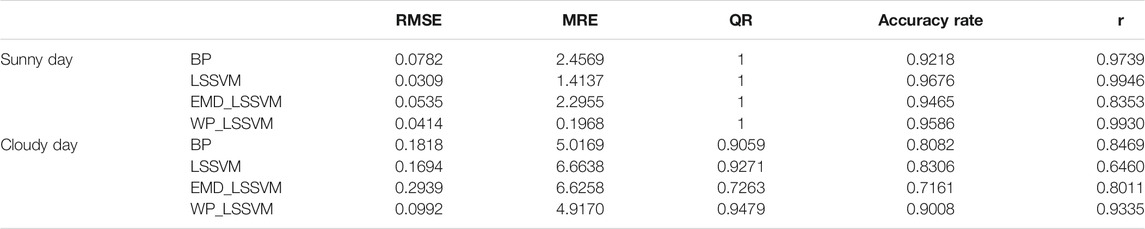
According to the NWP weather data and original PV power generation system’s output power data as the training sample set, the two weather types for the forecast day are April 9th (cloudy) and April 30th (clear). The NWP meteorological data (solar irradiance, temperature, and humidity) of the weather forecast day were selected as the prediction model input to predict the future PV power generation. Compared with the traditional LSSVM forecasting method, BP neural network forecasting method, and combined EMD-LSSVM forecasting method, the use of five evaluation methods, namely, the RMSE, MRE, accuracy rate, QR, and correlation coefficient, can intuitively reflect the model’s value effectiveness.

Figure 6 shows the power prediction curves and actual PV power generation of the four prediction models under two different weather types: April 9th (cloudy) and April 30th (sunny). It compares the PV power prediction values of the two weather types under different methods, including the prediction values using wavelet decomposition, combined empirical mode decomposition, and no wavelet decomposition. It can be seen that the predicted value of PV power after decomposition and reconstruction using wavelet packet is closer to the true value curve, and the accuracy rate is higher. By intuitively analyzing the prediction effect of four different prediction methods, namely, the MRE, RMSE, QR, and correlation coefficient for April 9th (cloudy) and April 30th (cloudy), it can be seen that the accuracy rate of the five evaluation methods’ power curve generation trend is essentially the same. The indicators for evaluating the model’s effectiveness are listed in Table 2.

FIGURE 6

FIGURE 6. PV power forecast values for different weather types. (A) April 30th (Sunny) (B) April 9th (Cloudy).

TABLE 2

TABLE 2. Comparison of prediction results obtained by five models.

As can be seen in Table 2, regardless of the day being sunny or cloudy, the combined WP-LSSVM prediction method performed better than the single LSSVM and BP neural network according to the five prediction model evaluation indices (RMSE, MRE, QR, correlation coefficient, and accuracy rate). Considering the prediction results of the network and EMD-LSSVM, this study selected a point prediction method combining the WP and LSSVM to analyze the actual PV output and prediction results in preparation for the subsequent interval probability prediction.

6.5 PV Power Prediction Error Probability Density Fitting

In this study, the point prediction error of the sunny set and cloudy sky set for Jilin in 2017 was used as the analysis object to obtain the forecast error distribution of PV power generation. Considering the single-step prediction as an example, the WP-LSSVM prediction method was applied. In this study, seven distribution models, including the normal distribution, generalized error distribution, and generalized error mixture distribution, were used to calculate the single-step forecast error of PV power generation and obtain statistical samples for the forecast error as shown in Figure 7.

FIGURE 7

FIGURE 7. Comparison of fitting effects of five error distribution models. (A) Sunny day (B) Cloudy day

As can be seen from Figure 7, the fitting effect of the mixed distribution model is better than that of the single distribution model, overcoming the defects of strong dependence on sample data, single distribution form and poor fitting effect of a single distribution. The fitting effect of generalized error mixed distribution model is better than Gaussian distribution model in peak, waist and tail. The generalized error mixed distribution model has good fitting effect, which intuitively reflects its advantage in sensitivity.

6.6 PV Power Probability Interval Prediction

To ensure the safe and reliable operation of the power system, a high confidence level is required. To obtain more reliable and effective information based on the generalized error mixture distribution model, three sizes were considered (95, 90, and 80%) to determine the predicted value’s confidence interval and realize the PV power interval prediction as presented in Table 3.

TABLE 3

TABLE 3. Upper and lower deviation values of prediction interval corresponding to Different Confidence Levels.

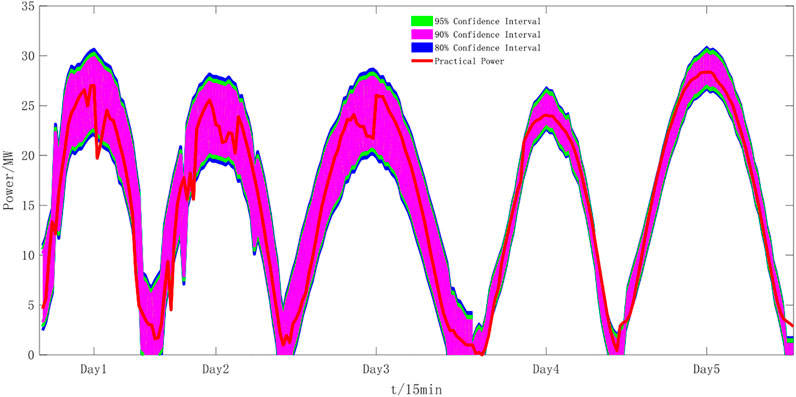
The proposed method combining the WP and LSSVM was applied with consideration from June 1st to June 5th, 2018. Single-point forecasting was performed on the PV data of a single step to obtain the single-step prediction absolute error, and the improved generalized error mixture distribution fitting was performed on the prediction error to obtain the prediction interval. Figure 8 shows the PV power prediction interval with 95% confidence.

FIGURE 8

FIGURE 8. Comparison of fitting effects of five error distribution models.

As can be seen in Figure 8, the PV power probability prediction based on the improved generalized error mixture distribution can effectively obtain the fluctuation range for a future time period and the prediction interval. The interval covers most of the true values and the prediction bandwidth is within a reasonable range. The double standard of a small average interval width based on the high coverage of the prediction interval is achieved. After the calculation, the results of each evaluation index were obtained with 95% confidence. The probability prediction evaluation index based on the normal distribution in parameter estimation is provided for comparison, as presented in Tables 4, 5, 6. With a 95% confidence level, the prediction bandwidth of a single generalized error distribution is reduced by 2.524% compared with the normal distribution, and the prediction bandwidth of the mixed model is reduced by 2.714% compared with the single model.

TABLE 4

TABLE 4. Indicator results based on the improved generalized error mixture distribution.

TABLE 5

TABLE 5. Indicator results based on generalized error distribution.

TABLE 6

TABLE 6. Indicator results based on normal distribution.

In terms of interval coverage, if the prediction interval of the two-interval prediction methods is sufficiently wide, all point predictions can be easily covered. However, the corresponding information cannot be obtained accordingly. Although the proposed method cannot perfectly cover every true value, its interval coverage is still high. Additionally, the interval coverage greatly improves as the confidence decreases. Compared with the interval prediction results under the traditional normal distribution, the proposed method obtained more satisfactory results, regardless of the interval coverage or average interval prediction width.

7 Conclusion

Since various NWP meteorological data have different degrees of influence on the output power of PV power plants, this study used a FA method to screen various meteorological factors affecting the power generation of PV power plants. Temperature, ambient temperature, and ambient humidity can reduce the number of input variables and the complexity of point prediction models and algorithms.

Because the output power sequence of PV power plants has periodic and non-stationary characteristics, and WPs can effectively extract non-linear and non-stationary signals, deep analysis can be performed on PV data to reduce the autocorrelation of each frequency signal, and thereby improve the sample data. In the analysis carried out by five point prediction methods, the quality of the results was evaluated by comparing four indices, namely, the RMSE, MRE, QR, correlation coefficient, and accuracy rate. The WP-LSSVM PV power station output power point prediction method was selected because it has a higher prediction accuracy rate, and accurate point prediction provides a good basis for probability prediction.

This study compared multiple probability density fittings (logistic, generalized error mixture distribution, normal, generalized error distribution, and so on) on the point prediction error obtained by the WP-LSSVM method. A method based on the generalized error mixture distribution is proposed. The distributed PV power probability prediction method uses the generalized error mixture distribution function to describe the PV power prediction error probability distribution, and uses the generalized error mixture distribution to establish the error distribution. Based on the improved generalized error regression, the hybrid model of FCM and entropy weight method can achieve better results. At 95% confidence level, the coverage rate increased by 0.01% on average while the average bandwidth decreased by 5.238%. At 90% confidence level, the coverage rate has increased by 0.23% on average while the average bandwidth has dropped by 3.756%. At 80% confidence level, the coverage rate increased by 1.39% on average while the average bandwidth decreased by 3.308%. The proposed method provides a practical and effective method for predicting the probability interval of the output power of PV power plants. At present, most of the research on interval prediction uses the method of probability function fitting, which weakens the timing of point prediction sequence to a certain extent. In the next stage of research, we can try to innovate an interval prediction method that retains the timeliness.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors contributed to this research. TP conducted the experiments, performed the experiments, and wrote the draft of this paper. MY, XS, and MM suggested the study idea and shared in writing and revising the paper.

Funding

This work was supported by the State Grid Corporation of China Science and Technology project ‘‘The Research and Demonstration of the Technology of Probabilistic Optimal Dispatch Considering the Electric/Thermal Load and the New Energy Uncertainty’’ under Grant 52230020002J.

Conflict of Interest

Authors YS, ZL and BL are employed by State Grid Jilin Electric Power Company Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Armstrong, K. (2014). Big Data: A Revolution that Will Transform How We Live, Work, and Think. Maths. Comput. Educ. 47 (10), 181–183. doi:10.1080/1369118x.2014.923482

CrossRef Full Text | Google Scholar

Europe, S. P. (2014). Global Market Outlook for Solar Power 2015-2019. Brussels, Belgium: Solar Power Europe.

Google Scholar

Golestaneh, F., and Gooi, H. B. (2017). “Multivariate Prediction Intervals for Photovoltaic Power Generation,” in 2017 IEEE Innovative Smart Grid Technologies - Asia (ISGT-Asia), Auckland, December 4-7, 2017.

CrossRef Full Text | Google Scholar

Han, Y., Wang, N., Ma, M., Zhou, H., Dai, S., and Zhu, H. (2019). A PV Power Interval Forecasting Based on Seasonal Model and Nonparametric Estimation Algorithm. Solar Energy 184 (MAY), 515–526. doi:10.1016/j.solener.2019.04.025

CrossRef Full Text | Google Scholar

Huang, N., Wang, D., Lin, L., Cai, G., Huang, G., Du, J., et al. (2019a). Power Quality Disturbances Classification Using Rotation forest and Multi‐resolution Fast S‐transform with Data Compression in Time Domain. IET Generation, Transm. Distribution 13 (22), 5091–5101. doi:10.1049/iet-gtd.2018.5439

CrossRef Full Text | Google Scholar

Huang, N., Wu, Y., Cai, G., Zhu, H., and Xing, E. (2019b). Short-term Wind Speed Forecast with Low Loss of Information Based on Feature Generation of OSVD. IEEE Access 7, 81027–81046. doi:10.1109/access.2019.2922662

CrossRef Full Text | Google Scholar

Li, J., Fu, Y., Li, C., Li, J., Xing, Z., and Ma, T. (2021b). Improving Wind Power Integration by Regenerative Electric Boiler and Battery Energy Storage Device. Int. J. Electr. Power Energ. Syst. 131 (10), 107039. doi:10.1016/j.ijepes.2021.107039

CrossRef Full Text | Google Scholar

Li, L.-L., Liu, Z.-F., Tseng, M.-L., Zheng, S.-J., and Lim, M. K. (2021a). Improved Tunicate Swarm Algorithm: Solving the Dynamic Economic Emission Dispatch Problems. Appl. Soft Comput. 108 (5), 107504. doi:10.1016/j.asoc.2021.107504

CrossRef Full Text | Google Scholar

Liu, H., Tian, H.-q., Pan, D.-f., and Li, Y.-f. (2013). Forecasting Models for Wind Speed Using Wavelet, Wavelet Packet, Time Series and Artificial Neural Networks. Appl. Energ. 107 (jul), 191–208. doi:10.1016/j.apenergy.2013.02.002

CrossRef Full Text | Google Scholar

Liu, W., and Xu, Y. (2020). Randomized Learning-Based Hybrid Ensemble Model for Probabilistic Forecasting of PV Power Generation. IET Generation Transm. Distribution 14, 5909–5917. doi:10.1049/iet-gtd.2020.0625

CrossRef Full Text | Google Scholar

Luo, M., Sun, Z., Liu, Q., Luo, Y., Zhu, J., Li, W., et al. (2015). Solar Irradiance Interval Prediction Based on Set Pair Analysis Theory. Baoding City: Electric Power Science and Engineering.

Google Scholar

Ma, Y., Lv, Q., Zhang, R., Zhu, H., and Yin, W. (2021). Short-term Photovoltaic Power Forecasting Method Based on Irradiance Correction and Error Forecasting. Energ. Rep. 7, 5495–5509. doi:10.1016/j.egyr.2021.08.167

CrossRef Full Text | Google Scholar

Mao, Y. A., Cs, A., and Hl, B. (2020). Day-ahead Wind Power Forecasting Based on the Clustering of Equivalent Power Curves. Energy 218, 119515. doi:10.1016/j.energy.2020.119515

CrossRef Full Text | Google Scholar

Mao, Y., Chen, X., Jian, D., and Yang, C. (2018). Ultra-short-term Multi-step Wind Power Prediction Based on Improved EMD and Reconstruction Method Using Run-Length Analysis. IEEE Access 6, 31908–31917. doi:10.1109/access.2018.2844278

CrossRef Full Text | Google Scholar

Mao, Y., and Xin, H. (2018). Ultra-short-term Prediction of Photovoltaic Power Based on Periodic Extraction of PV Energy and LSH Algorithm. IEEE Access s, 51200–51205. doi:10.1109/access.2018.2868478

CrossRef Full Text | Google Scholar

Mashud, R., and Irena, K. (2016). Neural Network Ensemble Based Approach for 2D-Interval Prediction of Solar Photovoltaic Power. Energies 9 (10), 829.

Google Scholar

Miranian, A., and Abdollahzade, M. (2013). Developing a Local Least-Squares Support Vector Machines-Based Neuro-Fuzzy Model for Nonlinear and Chaotic Time Series Prediction. IEEE Trans. Neural Netw. Learn. Syst. 24 (2), 207–218. doi:10.1109/tnnls.2012.2227148

PubMed Abstract | CrossRef Full Text | Google Scholar

Plessis, A., Strauss, J. M., and Rix, A. J. (2021). Short-term Solar Power Forecasting: Investigating the Ability of Deep Learning Models to Capture Low-Level Utility-Scale Photovoltaic System Behaviour. Appl. Energ. 285, 116395. doi:10.1016/j.apenergy.2020.116395

CrossRef Full Text | Google Scholar

Puthenpurakel, S. P., and Subadhra, P. R. (2016). “Identification and Classification of Microgrid Disturbances in a Hybrid Distributed Generation System Using Wavelet Transform,” in 2016 International Conference on Next Generation Intelligent Systems (ICNGIS), Kottayam, India, September 1-3, 2016. doi:10.1109/icngis.2016.7854066

CrossRef Full Text | Google Scholar

Rana, M., Koprinska, I., and Agelidis, V. G. (2015). 2D-interval Forecasts for Solar Power Production. Solar Energy 122 (DEC), 191–203. doi:10.1016/j.solener.2015.08.018

CrossRef Full Text | Google Scholar

Ska, C., Ek, B., and Jkk, A. (2021). PV Temperature and Performance Prediction in Free-Standing, BIPV and BAPV Incorporating the Effect of Temperature and Inclination on the Heat Transfer Coefficients and the Impact of Wind, Efficiency and Ageing. Renew. Energ. 181, 235–249. doi:10.1016/j.renene.2021.08.124

CrossRef Full Text | Google Scholar

Ueda, Y., Kurokawa, K., Tanabe, T., Kitamura, K., and Sugihara, H. (2008). Analysis Results of Output Power Loss Due to the Grid Voltage Rise in Grid-Connected Photovoltaic Power Generation Systems. IEEE Trans. Ind. Electron. 55 (7), 2744–2751. doi:10.1109/tie.2008.924447

CrossRef Full Text | Google Scholar

Xiao-ping, Y., and Yang, G. (2019). “Interval State Estimation Considering Randomness of Multiple Distributed Generations in Active Distribution Networks,” in Proceedings of the 2nd International Conference on Electrical and Electronic Engineering (EEE 2019), Hangzhou, May 26, 2019.

CrossRef Full Text | Google Scholar

Yang, M., Zhang, L., Cui, Y., Zhou, Y., and Yan, G. (2019). Investigating the Wind Power Smoothing Effect Using Set Pair Analysis. IEEE Trans. Sustain. Energ. 11, 1161–1172. doi:10.1109/tste.2019.2920255

CrossRef Full Text | Google Scholar

Zhang, L., Li, Y., Zhang, H., Xu, X., Yang, Z., and Xu, W. (2021). A Review of the Potential of District Heating System in Northern China. Appl. Therm. Eng. 188 (16), 116605. doi:10.1016/j.applthermaleng.2021.116605

CrossRef Full Text | Google Scholar

Zhu, B., and Wei, Y. (2013). Carbon price Forecasting with a Novel Hybrid ARIMA and Least Squares Support Vector Machines Methodology. Omega 41 (3), 517–524. doi:10.1016/j.omega.2012.06.005

CrossRef Full Text | Google Scholar