- 1Key Laboratory of Smart Grid of Ministry of Education, Tianjin University, Tianjin, China
- 2State Grid Economic and Technological Research Institute Co., Ltd., Beijing, China
The optimal operation model of AC/DC distribution network with energy router (ER) is essentially a nonconvex nonlinear programming (NLP) problem. In order to improve the feasibility of solving the model, a convex approximation algorithm is proposed in this work. The steady-state model of ER is developed with considering the loss characteristics and multiport coordinated control strategy. It is embedded in the optimization formulations of AC/DC network as basic operating equations. Then, using second-order cone relaxation technology, the power flow equations of AC and DC distribution networks are convexly relaxed. On this basis, the highly nonlinear operating model of ER is linearized by introducing a successive approximation approach. Therefore, the original NLP problem is transformed into the convex programming problem and the solution efficiency is improved. Meanwhile, an iterative solution algorithm is developed to ensure the accuracy of the convex approximation approach. Simulation results verify the feasibility and efficiency of the proposed algorithm.
Introduction
The development of renewable energy technology poses new challenges for flexible access and effective regulation of the power system (Guo et al., 2019). Energy router (ER) is also known as power electronic transformer (PET), and solid-state transformer. It has the functions of voltage conversion and power flow routing (Chen et al., 2020; Li et al., 2021; Liu et al., 2018). The AC/DC hybrid distribution network with ER (ER-based AC/DC HDN) can interconnect networks with multiple voltage levels and frequencies. It is conducive to the flexible access and consumption of distributed generations (DGs), and has attracted extensive attention (Zhang et al., 2020). However, flexible device access, AC/DC hybrid connection, three-phase asymmetrical, and active and reactive power coupling make the analysis and solution of ER-based AC/DC HDN face great challenges (Meng et al., 2018; Tang et al., 2021; Zhang et al., 2021).
The existing literatures have carried out research on the establishment of the ER steady-state model and its application in the distribution network. In (Miao et al., 2016), each port of ER is equivalent to the voltage source converter. On this basis, taking into account the loss characteristics of the converter, a power flow model for ER has been proposed in (Dong et al., 2019). Then, in order to reduce network losses, operating costs, and improve the voltage distribution, a multi-objective optimization model for AC network with ER was developed in (Miao et al., 2018). To take advantage of flexible regulation capabilities of ER, an optimization method for voltage imbalanced suppression is studied in (Dong et al., 2018). The above literatures have improved the operating performance of the ER based distribution networks from various aspects. However, the coordination control capability among multiport of ER needs to be further researched. Furthermore, the optimization model in the above literatures includes power flow constraints and highly nonlinear ER operation constraints. It is essentially a nonconvex nonlinear programming (NLP) problem, and obtaining the solution with an acceptable time is a great challenge (Deng et al., 2021)- (Soofi et al., 2021).
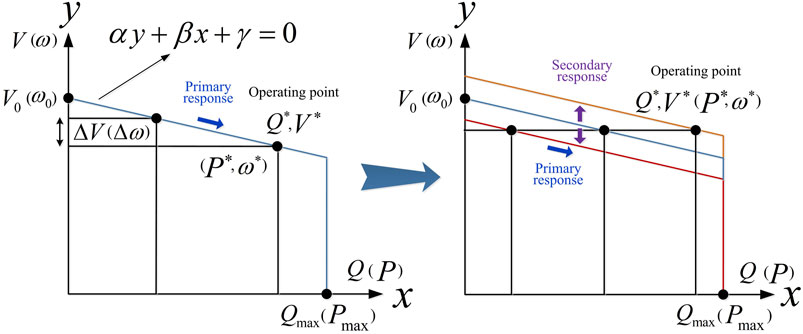
ER contains an intermediate DC/DC link. It isolates the distribution network into multiple AC and DC subnetworks with independent voltages and frequencies (Li et al., 2020). While operation, an appropriate coordinated control strategy is important to satisfy the power exchange demands of the ER and the subnetworks. For this issue, an optimal combination of operation strategy based on generalized droop control is introduced in (Rouzbehi et al., 2015). The switching of different operating modes (constant voltage control, constant power control, and droop control) of ER is determined by optimizing the droop coefficient. It is worth noting that the droop control strategy has been extensively studied in islanded system. In (Yu et al., 2018), a peer-to-peer control strategy for islanded networks is developed. In order to be apply to the asymmetric low voltage AC network, a three-phase droop control strategy has been studied in (Abdelaziz et al., 2013). On this basis, a secondary control strategy is introduced in (Allam et al., 2018) to improve the utilization efficiency of DGs. Applying these control methods to ER-based AC/DC HDN can improve the operating performance of the network, which has not been studied yet.
Generally, converting the original NLP problem into a convex programming problem can improve the efficiency of the solution. Using the second-order cone relaxation technology, an optimal operation model for AC distribution network is proposed in (Ji et al., 2017), which improves the feasibility of the solution. In (Gan and Low, 2014) a second-order cone programming (SOCP) model for DC network is introduced. These researches provide a basis for convex programming modeling of AC/DC network. However, several limitations can be found. 1) The highly nonlinear loss characteristic equation of ER is a quadratic function involving current. The existing SOCP approach cannot effectively deal with it. 2) The square of the voltage in SOCP model is the optimization variable. The droop control strategy involves the first-order term of voltage, which cannot be transformed in the form of SOCP manner.
In order to improve the feasibility of solving the optimization model of ER-based AC/DC HDN, a convex approximation algorithm is proposed in this work. The main contributions are summarized as follows.
1) An optimal operation model for ER-based AC/DC HDN is devolved in this paper. The multiport coordinated control strategy of ER is considered. Thus, the power balanced of ET and the system can be guaranteed. On this basis, a hierarchical droop control strategy is introduced, which improves the utilization efficiency of DGs.
2) The second-order cone relaxation method is adopted to handle the nonlinear power flow equations. Then, combined with the linear approximation approach, the operation constraints of ER are successfully linearized. The original NLP problem is converted into a convex programming problem, which improves the efficiency of the solution. Furthermore, the successive iteration algorithm is proposed to ensure the accuracy of the solution.
Steady-State Model and Coordinated Control Strategy of ER
Steady-State Model of Multiport ER
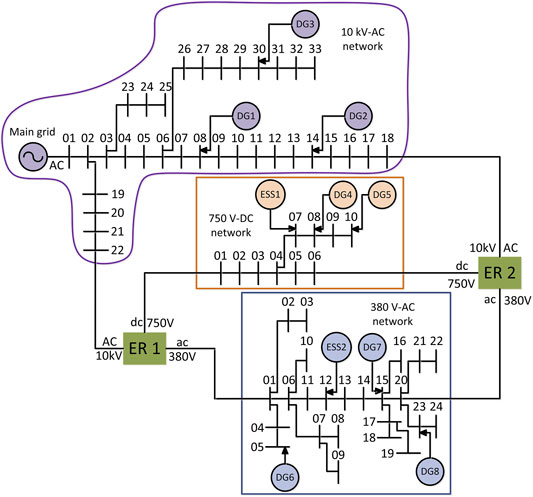
The equivalent structure diagram of ER based on PET is shown in Figure 1. It includes M AC ports and N DC ports. Each port is composed of AC/DC or DC/DC converter, which is used to connect AC and DC networks, respectively.
While operation, the active power balanceed of ER should be satisfied, as described in Eq. 1.
The power loss of each ER port
Then, the total loss of ER
Coo rdinated Control Strategy of Multiport ER
The AC and DC subnetworks are connected via ER coupling. Due to the intermediate DC/DC isolation link of ER, multiple AC subnetworks operate at different frequencies. To maintain the power balanced of ER, AC, and DC subnetworks, an appropriate coordinated control strategy is necessary. In (Rouzbehi et al., 2015), a generalized droop control strategy is proposed, which is the integration of constant voltage control, constant power control and droop control. The control mode is determined by the generalized droop coefficient. The simulation results show that the droop control strategy (
The steady-state model of multiport ER is summarized by Eqs 1–6. It is embedded in the asymmetric AC/DC network optimization model as basic formulas in next section.
Optimal Operation Model and Convex Approximation Conversion
Optimal Operation Model for ER-Based AC/DC HDN
Objective Function
This work takes the minimum active power loss as the objective function, shown as follows:
Constraints
The Distflow branch equations of AC/DC distribution networks include power flow constraints, branch voltage constraints, and current constraints (Zhang et al., 2018). It is relaxed by the cone relaxation technique, shown as follows:
Droop control characteristic constraints of DGs in the low voltage AC/DC networks are expressed as Eqs 10–12.
Operational constraints of the network are formulated as:
The allowable range of variables is shown in Eq. 13, in which
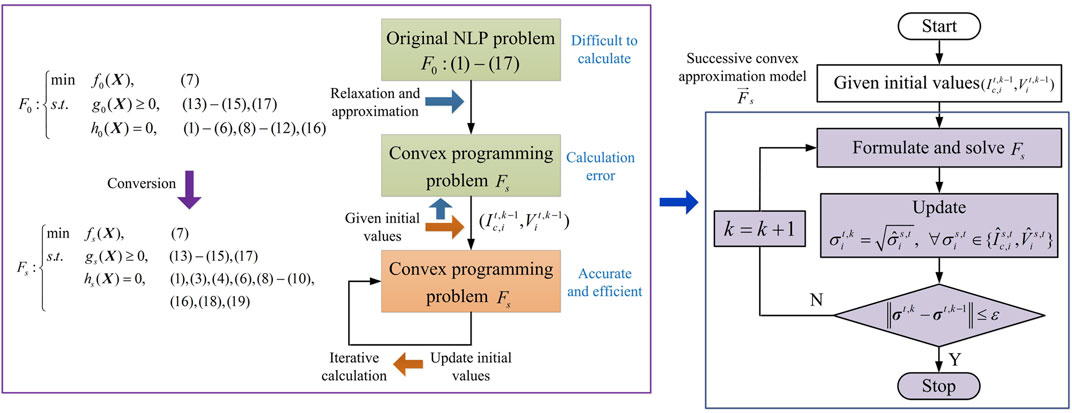
Eqs 7–17 together with the steady-state model of ER Eqs 1–6 form the original optimal operation model
Successive Convex Approximation Conversion to NLP Problem
Linear Approximation
In section Optimal Operation Model for ER-Based AC/DC HDN, the second-order cone relaxation technique is adopted to linearize the Distflow branch equations, as shown in Eqs 8, 9. The square of the branch current is introduced as the optimization variable. Thus, the constant term
Using Eq. 18, the ER loss characteristic constraint in Eq. 2 can be transformed into linear expression. Furthermore, the square of the node voltage is the optimization variable. The droop control constraints Eqs 5, 6, 11, 12 involve the first-order term of voltage, which are approximately linearized using Eq. 19.
where,
Successive Convex Approximation Algorithm
The optimal values of branch current and node voltage (
The diagram of the successive convex approximation algorithm is shown in Figure 3.
The solution process is as follows:
Step 1: Given initial values (
Step 2: The initial values are updated according to the current optimal values of
Step 3: If the difference between initial values in two adjacent iterations is less than the given threshold
Case Studies
In order to verify the effectiveness of the approach proposed in this work, the solver Cplex is used to solve the optimization program based on Matlab-Yalmip platform. The network topology of ER-based AC/DC HDN is shown in Figure 4. 10 kV high voltage AC network (Zhu, 2002), 380 V low voltage AC network, and 750 V low voltage DC network (Dong et al., 2019) are coupled through ER. The no load voltage in AC network is
Results of Optimal Power Flow
The original NLP problem
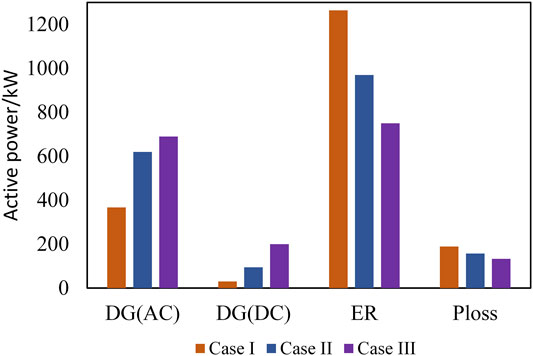
Table 1 shows the active power loss and solution time of model
To verify the effectiveness of the introduced secondary control strategy, three cases are studied here.
Case I: Droop control strategy without secondary layer is adopted by ER and DGs;
Case II: Droop control strategy without secondary layer is adopted by ER and secondary droop control strategy is adopted by DGs;
Case III: Secondary droop control strategy is adopted by ER and DGs.
Active power output by DGs and ER in the low voltage network and the total power loss are demonstrated in Figure 5. Droop control characteristic is shifted by introducing the secondary droop control layer. The regulation performance of the controller is improved. The active power output of DGs is increased, and the active power injected by ER is reduced. Thus, the utilization efficiency of DGs in Case III is 55.4 and 19.7% higher than Case I and Case II, respectively. Compared with Case I and Case II, the total power loss in Case III is reduced by 29.6 and 15.5%, respectively.
Results of Day-Ahead Optimal Scheduling
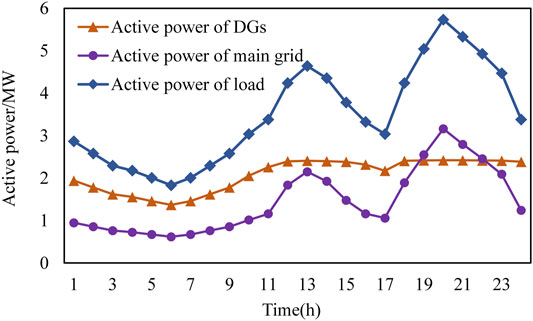
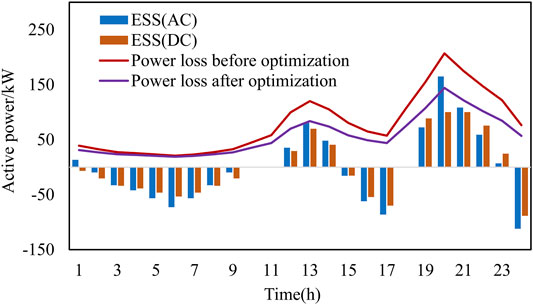
As demonstrated in Figure 6, the power output of DGs and main grid changes with the load curve. The ESS is charged at 1:00–10:00 and 15:00–17:00 during the low load period, and discharged at 12:00–14:00 and 19:00–23:00 during the peak load period, as shown in Figure 7. Compared with before optimization, the total power loss after optimization has been reduced by 27.2%. Meanwhile, the active power loss of ER decreased from 331.9 to 300.3 kWh. The operating efficiency of the network is improved.
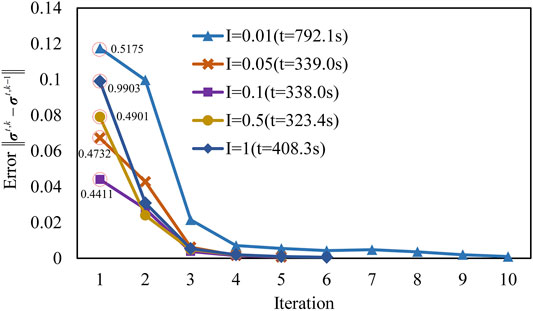
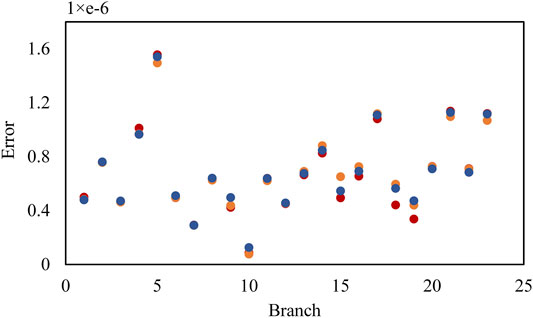
The node voltage is typically around 1p.u. To verify the convergence of the proposed successive convex approximation algorithm, various initial current values are analyzed here. As demonstrated in Figure 8, the convergence is obtained in all scenes. The solution time varies from 323.4 to 792.1 s, which is more than 5 h in the original NLP model. The number of iterations varies from 6 to 10. Furthermore, the relaxation error of branch current is 1e-6 order of magnitude, as depicted in Figure 9. These results reveal that the proposed approach in this work has good convergence and accuracy while improving the efficiency of the calculation.
Conclusion
The multi-period optimal operation model for ER-based AC/DC HDN is proposed in this work. The multiport coordinated control strategy of ER is considered in this paper. The introduction of a secondary droop control strategy improves the performance of the controller, which is conducive to enhance the utilization efficiency of DGs. On this basis, the operational efficiency of the network can be improved by coordinating and optimizing the active power output of DGs and ER. The second-order cone relaxation technique and successive linear approximation approach are adopted to converter the original NLP problem into a convex programming model. The proposed successive convex approximation algorithm has good convergence and accuracy. Ensure that the optimal solution of ER-based AC/DC HDN is obtained within an acceptable time.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author Contributions
TZ: conceptualization, writing-review and editing. YM: formal analysis, writing-review and editing. XW: data curation, and software. YD: data curation, and software. YS: writing-original draft, and review. KY: data curation, and review. HJ: methodology, software, and supervision.
Funding
The authors gratefully acknowledge the project supported by Science and Technology Project of State Grid Corporation (SGSDJY00GPJS1900058).
Conflict of Interest
Authors YS and KY were employed by the company State Grid Economic and Technological Research Institute Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdelaziz, M. M. A., Farag, H. E., El-Saadany, E. F., and Mohamed, Y. A.-R. I. (2013). A Novel and Generalized Three-Phase Power Flow Algorithm for Islanded Microgrids Using a newton Trust Region Method. IEEE Trans. Power Syst. 28, 190–201. doi:10.1109/tpwrs.2012.2195785
Allam, M. A., Hamad, A. A., Kazerani, M., and El-Saadany, E. F. (2018). A Novel Dynamic Power Routing Scheme to Maximize Loadability of Islanded Hybrid AC/DC Microgrids under Unbalanced AC Loading. IEEE Trans. Smart Grid 9, 5798–5809. doi:10.1109/tsg.2017.2697360
Chen, Y., Wang, P., Elasser, Y., and Chen, M. (2020). Multicell Reconfigurable Multi-Input Multi-Output Energy Router Architecture. IEEE Trans. Power Electron. 35, 13210–13224. doi:10.1109/tpel.2020.2996199
Deng, Y., Zhang, Y., Luo, F., and Mu, Y. (2021). Operational Planning of Centralized Charging Stations Utilizing Second-Life Battery Energy Storage Systems. IEEE Trans. Sustain. Energ. 12, 387–399. doi:10.1109/tste.2020.3001015
Dong, L., Zhang, T., Pu, T., Chen, N., and Sun, Y. (2019). A Decentralized Optimal Operation of AC/DC Hybrid Microgrids Equipped with Power Electronic Transformer. IEEE Access 7, 157946–157959. doi:10.1109/access.2019.2949378
Dong, L., Zhang, T., Pu, T. J., Chen, N. S., and Sun, Y. Y. (2018). “Optimal Scheduling of Asymmetrical AC/DC Micro-grid Based on PET,” in International Conference on Power System Technology, Guangzhou, China, November 6-8, 2018, 1757–1763.
Gan, L., and Low, S. H. (2014). Optimal Power Flow in Direct Current Networks. IEEE Trans. Power Syst. 29, 2892–2904. doi:10.1109/tpwrs.2014.2313514
Guo, H., Wang, F., Zhang, L., and Luo, J. (2019). A Hierarchical Optimization Strategy of the Energy Router-Based Energy Internet. IEEE Trans. Power Syst. 34, 4177–4185. doi:10.1109/tpwrs.2019.2907323
Ji, H., Li, P., Wang, C., Song, G., Zhao, J., Su, H., et al. (2017). A Strengthened SOCP-Based Approach for Evaluating the Distributed Generation Hosting Capacity with Soft Open Points. Energ. Proced. 142, 1947–1952. doi:10.1016/j.egypro.2017.12.394
Khan, S., and Bhowmick, S. (2019). A Generalized Power-Flow Model of VSC-Based Hybrid AC-DC Systems Integrated with Offshore Wind Farms. IEEE Trans. Sustain. Energ. 10, 1775–1783. doi:10.1109/tste.2018.2870914
Li, K., Wen, W., Zhao, Z., Yuan, L., Cai, W., Mo, X., et al. (2021). Design and Implementation of Four-Port Megawatt-Level High-Frequency-Bus Based Power Electronic Transformer. IEEE Trans. Power Electron. 36, 6429–6442. doi:10.1109/tpel.2020.3036249
Li, P., Sheng, W., Duan, Q., Li, Z., Zhu, C., and Zhang, X. (2020). A Lyapunov Optimization-Based Energy Management Strategy for Energy Hub with Energy Router. IEEE Trans. Smart Grid 11, 4860–4870. doi:10.1109/tsg.2020.2968747
Liu, C., Li, X. J., Zhi, Y. M., and Cai, G. W. (2018). New Breed of Solid-State Transformer Mainly Combing Hybrid Cascaded Multilevel Converter with Resonant DC-DC Converters. Appl. Energ. 210, 724–736. doi:10.1016/j.apenergy.2017.08.052
Meng, F., Chowdhury, B., and Chamanamcha, M. (2018). Three-phase Optimal Power Flow for Market-Based Control and Optimization of Distributed Generations. IEEE Trans. Smart Grid 9, 3691–3700. doi:10.1109/tsg.2016.2638963
Miao, J. Q., Zhang, N., and Kang, C. Q. (2016). “Generalized Steady-State Model for Energy Router with Applications in Power Flow Calculation,” in IEEE Power and Energy Society General Meeting, Boston, MA, USA, July 17-21, 2016, 1–5.
Miao, J., Zhang, N., Kang, C., Wang, J., Wang, Y., and Xia, Q. (2018). Steady-State Power Flow Model of Energy Router Embedded AC Network and its Application in Optimizing Power System Operation. IEEE Trans. Smart Grid 9, 4828–4837. doi:10.1109/tsg.2017.2672821
Rouzbehi, K., Miranian, A., Candela, J. I., Luna, A., and Rodriguez, P. (2015). A Generalized Voltage Droop Strategy for Control of Multiterminal DC Grids. IEEE Trans. Ind. Applicat. 51, 607–618. doi:10.1109/tia.2014.2332814
Soofi, A. F., Manshadi, S. D., Liu, G., and Dai, R. (2021). A SOCP Relaxation for Cycle Constraints in the Optimal Power Flow Problem. IEEE Trans. Smart Grid 12, 1663–1673. doi:10.1109/tsg.2020.3023890
Sun, Y., Hu, L., Malik, S. M., Chen, N., and Pu, T. (2019). Unified Method for Optimal Power Flow of AC/DC System with PET Based on Extended branch Model. J. Eng. 2019, 1942–1946. doi:10.1049/joe.2018.8707
Tang, K., Dong, S., Ma, X., Lv, L., and Song, Y. (2021). Chance-constrained Optimal Power Flow of Integrated Transmission and Distribution Networks with Limited Information Interaction. IEEE Trans. Smart Grid 12, 821–833. doi:10.1109/tsg.2020.3021829
Yu, M., Huang, W., Tai, N., Zheng, X., Wu, P., and Chen, W. (2018). Transient Stability Mechanism of Grid-Connected Inverter-Interfaced Distributed Generators Using Droop Control Strategy. Appl. Energ. 210, 737–747. doi:10.1016/j.apenergy.2017.08.104
Zhang, H., Moura, S. J., Hu, Z., Qi, W., and Song, Y. (2018). A Second-Order Cone Programming Model for Planning PEV Fast-Charging Stations. IEEE Trans. Power Syst. 33, 2763–2777. doi:10.1109/tpwrs.2017.2754940
Zhang, S., Pei, W., Xiao, H., Yang, Y., Ye, H., and Kong, L. (2020). Enhancing the Survival Time of Multiple Islanding Microgrids through Composable Modular Energy Router after Natural Disasters. Appl. Energ. 270, 115138. doi:10.1016/j.apenergy.2020.115138
Zhang, Y., Meng, X., Shotorbani, A. M., and Wang, L. (2021). Minimization of AC-DC Grid Transmission Loss and DC Voltage Deviation Using Adaptive Droop Control and Improved AC-DC Power Flow Algorithm. IEEE Trans. Power Syst. 36, 744–756. doi:10.1109/tpwrs.2020.3020039
Zhu, J. Z. (2002). Optimal Reconfiguration of Electrical Distribution Network Using the Refined Genetic Algorithm. Electric Power Syst. Res. 62, 37–42. doi:10.1016/s0378-7796(02)00041-x
Nomenclature
Sets
Variables
Parameters
Keywords: AC/DC distribution network, energy router, steady-state model, second-order cone relaxation, successive approximation
Citation: Zhang T, Mu Y, Wang X, Deng Y, Song Y, Yuan K and Jia H (2021) Convex Approximation Algorithm for AC/DC Distribution Network With Energy Router. Front. Energy Res. 9:731944. doi: 10.3389/fenrg.2021.731944
Received: 28 June 2021; Accepted: 12 July 2021;
Published: 23 July 2021.
Edited by:
Bo Yang, Kunming University of Science and Technology, ChinaReviewed by:
Ke Peng, Shandong University of Technology, ChinaYingyun Sun, North China Electric Power University, China
Copyright © 2021 Zhang, Mu, Wang, Deng, Song, Yuan and Jia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yunfei Mu, yunfeimu@tju.edu.cn
 Tao Zhang
Tao Zhang