
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 23 July 2021
Sec. Nuclear Energy
Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.705823
This article is part of the Research Topic Reactor Physics: Methods and Applications View all 27 articles
Monte Carlo (MC) methods have been widely used to solve the particle transport equation due to their high accuracy and capability of processing complex geometries. History-based and event-based algorithms that are applicable to different architectures are two methods for parallelizing the MC code. There is a large work on evaluating and optimizing parallel algorithms with continuous-energy schemes. In this work, we evaluate the single-node performance of history-based and event-based algorithms for multigroup MC methods on both CPUs and GPUs with Quicksilver, a multigroup MC transport code that has already implemented the history-based algorithms. We first implement and optimize the event-based algorithm based on Quicksilver and then perform the evaluation work extensively on the Coral2 benchmark. Numerical results indicate that contrary to continuous-energy schemes, the history-based approach with multigroup schemes outperforms the event-based algorithm on both architectures in all cases. We summarize that the performance loss of the event-based algorithm is mainly due to: 1) extra operations to reorganize particles, 2) batched atomic operations, and 3) poor particle data locality. Despite the poor performance, the event-based algorithm achieves higher memory bandwidth utilization. We further discuss the impact of memory access patterns and calculation of cross sections (xs) on the performance of the GPU. Built on the analytics, and shed light on the algorithm choice and optimizations for paralleling the MC transport code on different architectures.
Particle transport problems such as shielding radiations and power reactor calculations require solving the Boltzman equation, which describes how particles transport through and interact with materials. Deterministic methods solve such problems by numerical calculations to obtain the required physical quantities. Different from deterministic methods, Monte Carlo (MC) methods (Metropolis and Ulam, 1949) construct a stochastic model through statistical sampling and particle weighting and are capable of handling complex geometry and physics models. The expected value of a physical quantity is then estimated by the weighted average of behaviors of numerous independent particles. Random numbers following the specific probability distributions are used to model various events (collision, fission, capture, etc.), thus causing statistical uncertainty. Increasing the number of particle histories is usually used to reduce uncertainty, but meanwhile, it comes at a significant computational cost. To reduce the runtime, MC transport codes such as Shift (Pandya et al., 2016), OpenMC (Romano and Forget, 2013), and MCNP (Forster and Godfrey, 1985) are usually targeted at large-scale parallelization on high-performance supercomputers with tens of thousands of computing nodes.
There are two parallel algorithms for MC methods, history-based and event-based algorithms. History-based algorithms loop over a large number of independent particles, each of which is simulated from the birth to the death by a fixed thread. Because each particle has an independent trajectory and a different history length, history-based algorithms are appropriate for multiple-instruction multiple-data (MIMD) architectures. The MC transport loop over particles is not suitable for vectorization because different instructions are required at different times. To exploit the vectorization capabilities of computing architectures, the event-based MC method was proposed in the 1980s (Brown and Martin, 1984). This approach processes a batch of particles based on the next event that particles will undergo. Particles that have the same next event will be processed together.
Traditionally, MC codes are parallelized on CPU-based machines. To achieve higher floating-point operations per second (FLOPS), supercomputers tend to rely on vectorized, single-instruction multiple-data (SIMD) or single-instruction multiple-threads (SIMT) architectures such as graphical processing unit (GPU) and Intel Xeon Phi processors (MIC). A large amount of research uses vectorized architectures to obtain better performance. Li et al. (2017) proposed a multi-stream approach based on GPU for matrix factorization to accelerate stochastic gradient descent and achieved 5–10× speedup. Yan et al. (2020) presented an optimized implementation for single-precision Winograd convolution on GPUs. Its implementation achieved up to 2.13× speedup on Volta V100 and up to 2.65× speedup on Turing RTX2070. Existing research shows that computation-intensive programs can obtain a significant performance improvement.
A number of MC codes on vectorized architectures (Du et al., 2013; Liu et al., 2014; Bergmann and Vujić, 2015) have been developed. Most recent studies of GPU-based MC methods (Choi et al., 2019; Hamilton and Evans, 2019) have focused on event-based algorithms. The WARP code (Bergmann and Vujić, 2015) adapted event-based algorithms to the new GPU hardware and realized a generalized GPU-based implementation for continuous-energy MC transport. Substantial gains in performance are achieved by using event-based algorithms in the Shift code (Hamilton and Evans, 2019), a continuous-energy MC neutron transport solver. All of the GPU-based studies above are based on continuous energy, on which the event-based approach outperforms the history-based method by a large margin.
We consider the single-node performance of the history-based and event-based algorithms for multigroup MC methods. Compared with continuous-energy MC methods, the multigroup scheme has a simpler logic. The energy ranges in the multigroup energy spectrum are usually subdivided into a few hundred groups and averaged in different ways over the continuous-energy schemes, thus avoiding the need to carry out a lookup over very large cross section tables, which constitute a significant fraction of runtime. Therefore, multigroup MC methods have extremely different memory access patterns and conditional branches. To further optimize the performance of the multi-group MC programs, it is necessary to evaluate the performance of history-based and event-based algorithms on modern architectures. Hamilton et al. (2018) provided a comparison of history-based and event-based algorithms for multigroup MC methods on GPUs. However, it lacks a comparative analysis of the multigroup and continuous energy schemes, as well as a comparative analysis of performance on the CPU and GPU.
This article is aimed at providing a detailed analysis of the single-node performance difference between different parallel algorithms with different cross section schemes on both CPUs and GPUs. The studies were performed using Quicksilver (Richards et al., 2017), a proxy application for the MC transport code Mercury (LLNL, 2017). It implements the history-based algorithm on both CPUs and GPUs through a thin-threads approach (Bleile et al., 2019).
The main contributions of this work are that:
• We implement the event-based algorithm for multigroup MC methods in the Quicksilver code on both CPUs and GPUs. The implementation details, including modification of data structures, loop organization, and optimization on the GPU, are provided.
• We explore the performance difference of the history-based and event-based algorithms for multigroup MC methods on both CPUs and GPUs. The results show that the event-based algorithm for multigroup MC methods is over 1.5× slower than the history-based algorithm on both architectures, but achieves a higher memory bandwidth.
• We analyze the performance-affecting factors, including memory access patterns and xs schemes. Built on the analytics, we provide suggestions for optimizations and algorithm choices for the MC transport code on different architectures.
MC methods are very different from deterministic transport methods. MC methods solve the transport equation by simulating individual particles and recording some aspects (tallies) of their average behavior. The average behavior of particles in the physical systems is then inferred (using the central limit theorem) from the average behavior of the simulated particles. Deterministic methods typically give fairly complete information throughout the phase space of the problem, while MC methods supply information only about specific tallies requested by the user.
MC methods transport particles between events (for example, collisions) that are separated in space and time. The individual probabilistic events that comprise a process are simulated sequentially. The probability distributions governing these events are statistically sampled to describe the total phenomenon. Probability distributions are randomly sampled using transport data to determine the outcome at each step of its life.
As the particle histories are independent, it is natural to achieve parallelism over individual particles. This means each thread or process will process a single particle for its whole life cycle until it is absorbed, escapes from the system, or reaches the end of a time step. Algorithm 1 is the basic history-based algorithm with a loop over simulated particles. The loop body sequentially processes particle histories that would alternate between moving particle to collision site and processing particle collision. Moving particle to collision site involves calculating several distances, including sampling distance to next collision and other geometric operations. Processing particle collision encompasses the most sophisticated control flow, which involves sampling the nuclide to interact with the reaction type.
In the GPU implementation, the loop is replaced by a CUDA kernel launch where the total number of CUDA threads is equal to the number of particles. The number of particles is much larger than the number of threads the device can physically execute simultaneously to hide the latency of accessing global memory. Owing to the limited GPU resources, particles are usually simulated in batches. In Algorithm 1, each particle has a different history length and therefore will collide at different times, which represents a thread divergence of MC methods at the highest level.
This work was performed in the Quicksilver code (Bleile et al., 2019; Richards et al., 2017), a proxy application of the full production code Mercury developed and maintained by Lawrence Livermore National Laboratory (LLNL). Quicksilver is designed to represent the key features of Mercury and offers an approximation of the critical physical routines that form the essential part of the full production code. It only implements some of the most common physical interactions but keeps enough to represent crucial computational patterns. Mercury supports meshes with multiple types and solid geometry, while Quicksilver is limited to only a 3D polyhedral mesh. Additionally, Mercury uses both continuous and multigroup cross sections, while Quicksilver only supports the multigroup nuclear data.
Quicksilver offers only two types of predefined tallies: balance tallies and a cell-based scalar flux tally. Balance tallies record the total number of times specific events occur (such as collisions, facet crossings). Scalar flux tally scores the flux of particles through each mesh cell. In addition, Quicksilver implements history-based algorithms on both CPUs and GPUs. Thread safety is handled by using atomic operations. In this article, we implement the event-based approach.
In this section, we implement the basic event-based algorithm on both CPUs and GPUs and present some optimizations on GPUs. Instead of being simulated by a fixed task from the creation to completion, event-based transport processes particles with the same next event (e.g., calculate total macro cross section) together. It offers an opportunity to exploit vectorization capabilities. As discussed in Ozog et al. (2015), employing an event-based algorithm to the MC transport code is not trivial because nearly all the data structures and loop organization require to be modified.
The notations used in this work are listed in Table 1.
Suppose there are N particles to be simulated in a cycle. N particles form the initial particle vector. Because storing the attributes of N particles simultaneously is not feasible on a GPU, the number of particles in a given batch is often limited to at most B particles. We refer to a vector of particles to be processed in a batch as a particle bank. We denote the initial particle vector and particle bank by
Algorithm 2 is the basic event-based algorithm on CPUs. The algorithm begins by getting a batch of particles from the initial particle vector (line 2). The next step is an initialization (line 4) of event queues that correspond to four event types: computing cross sections, advancing, collision, and crossing facet. Four event queues are abbreviated as
Before generating trajectories, all particles must first calculate the cross sections, which is the first event of the particle. Therefore, the initialization of event queues is to put all particles in the bank into
The basic event-based algorithm on GPUs is still as shown in Algorithm 2, but all the events are processed through GPU kernels. Compared with the large kernel in the history-based algorithm, a smaller event kernel means that most branching logic is handled outside the kernel, resulting in less thread divergence within kernels and therefore an improved utilization of vectorization. In addition, smaller kernels are capable of providing the reduced computational complexity and therefore each thread occupies fewer GPU resources (registers, etc.). Because of a fixed amount of resources available, more threads can be executed simultaneously to achieve a higher occupancy, which is an important consideration for improving GPU performance. The performance of multigroup MC methods on GPUs is affected by many factors, one of which is thread divergence. Reducing thread divergence results in an improved arithmetic performance, but may also bring some changes in other aspects, such as memory access patterns, which may cause more serious performance losses.
An essential concern is the update of tallies. Quicksilver only provides two kinds of tallies, one of which is the scalar flux tally. One way to update the scalar flux tally is to allocate a copy for each particle in
The particle’s basic information, including position, energy, direction, velocity, etc., is represented by a data structure. One approach for storing the initial particle vector and particle bank is to allocate an array of these structures, which is known as AOS. The second method is to store each data component of these structures in distinct arrays, which is usually called SOA. On CPUs, AOS is often used to improve cache efficiency due to its better locality. The SOA pattern is usually recommended to be used for GPU so that coalesced memory accesses can be efficiently utilized. We explored the performance difference between AOS and SOA on the GPU. The results in Figure 1 demonstrate that, on the GPU, the SOA pattern performs better on both problem 1 and problem 2 (see Section 4.1 for the introduction of these two problems), but only brings very little performance gains. In the following experiments, we use AOS for CPU implementations and SOA for GPU.
Figure 2 shows the memory management of the event-GPU algorithm. Since all operations of event queues, including event kernels and initialization, can be handled on the GPU, the memory of event queues only needs to be allocated on the GPU, avoiding data movement between host and device. Data on geometry, materials, and multigroup cross sections are all transferred from the CPU to the GPU during the initialization of Quicksilver and will not be modified in the subsequent execution. The initial particle vector
The kernel that handles events in the longest queue (this means that GPU can concurrently simulate a maximum number of particles) is launched each time. To know which queue is the longest, we allocate memory for an array of length four using cudaMallocManaged and maintain it to represent current lengths of event queues. Then the maximum length can be determined on the host. Kernels are switched over and over until all the particles in that batch are simulated.
In the basic event-GPU algorithm, particles will be terminated when it is absorbed, escapes from the system (or subdomain), or reaches the end of a time step, leading to a gradual decrease in the number of active particles in
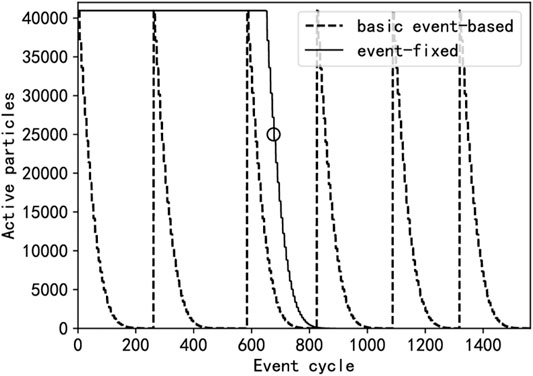
FIGURE 3. The number of active particles as a function of event cycles for the basic event-based algorithm and the event-fixed algorithm with
Hamilton et al. (2018) proposed to replace terminated particles with new particles to maximize GPU occupancy, which keeps the number of active particles in a cycle for a significant fraction of cycle runtime. To achieve this, instead of killing terminated particles directly, we replace terminated particles in
It should be noted that the meaning of “batch” is no longer the same as the original meaning. The difference is that “batch” in the event-fixed method is based on the number of terminated particles, not source particles. Specifically, a global counter is maintained and incremented atomically when particles are terminated. Once the counter rises above B, it is considered that a batch of particles has been processed.
At the conclusion of event processing atomic operations are utilized to redistribute active particles. However, the atomic operation would have a great impact on the overall performance because the GPU will typically execute many more threads simultaneously and the redistribution operation will occur frequently. We consider another method based on prefix sum to collect the indices of active particles, thus avoiding atomic operations on queues.
For event queue
When the number of active particles falls below a threshold. For example, from the circle in Figure 3, the cost of multiple event kernel startups will exceed the benefits brought by the event-based algorithm itself. The main reason is that the event kernel cannot be executed efficiently for a small number of particles in flight. From the threshold, we switch to the history-based algorithm to track the residue particles. We refer to this method as an event-hybrid approach. Before switching to the history-based algorithm each particle may be going to undergo a different next event, which means that all event queues are not empty. Performing the following three steps, all particles will be merged into
• Execute advancing kernel. After this step, surviving particles in
• Execute collision kernel. After colliding with sampled nuclides, survive particles will enter
• Execute crossing kernel. Particles in
Finally, we perform a history-based algorithm on all particles in
In this section, we present a single-node performance comparison of the history-based and event-based algorithms of Quicksilver on both CPUs and GPUs. In addition, some experiments were conducted to further explain the reasons for the performance evaluation results.
For performance evaluations, we perform some experiments on the Tianjin HPC1 system, each node of which contains two fourteen-core Intel Xeon E5-2690 v4 CPUs operating at 2.6 GHz along with four NVIDIA Tesla K80 GPUs. L1 cache is one of the factors that can affect performance on GPUs. On the Kepler architecture, all memory transactions only use an L2 cache, but the L1 cache is disabled by default and must be enabled using the compiler flag “-Xptxas -dlcm –ca.” In the following experiments on GPUs, L1 cache is enabled. To simplify the execution within a rank, we use one rank for a GPU and 4 ranks per node as a result of running on 4 Tesla K80 GPUs.
We utilize a single problem, Godiva in water (Cullen et al., 2003), as the basis of our study. This problem was generated to be used as a Cora 2 benchmark in Quicksilver due to its balanced reactions and balanced nature to match a classic MC test problem. The benchmark is defined by multiple parts, including cross sections, materials, and geometries. The cross sections define the detailed information to describe reactions that will occur when colliding with different isotopes. Materials mainly define physical information, such as the number of isotopes and the number of reactions considered in the corresponding material. Geometries contain the size of the mesh and the size of subdomains related to domain decomposition.
This benchmark defines a Cartesian mesh with

TABLE 2. Problem definition in the Cora 2 benchmark. Two problems have different numbers of isotopes and reactions.
We describe the implementation details of the basic event-based algorithm on GPUs in Section 3.1.2 and implement three optimized methods (event-fixed, event-hybrid, and event-prefix) for enhancing the GPU performance. We now perform a comparison of these algorithms. Besides, we also investigate the performance gains by enabling L1 cache (event-based, L1). Figure 4 shows the average cycle runtime for different GPU algorithms on both problem 1 and problem 2, respectively. Results are obtained using 100 cycles and
The results indicate that there is a big gap between the performance of the atomic-based and prefix-sum-based methods. The prefix sum method outperforms the atomic method by a factor of approximately two on the problems considered. This proves that there is a significant benefit to replacing atomic operations with the prefix sum method when redistributing survive particles. The event-fixed approach achieves an obvious performance increase. This is because GPU efficiency is reduced multiple times within a cycle due to the decrease in the number of particles in each batch, which keeps the GPU not fully occupied for a large fraction of the calculation. Replacing terminated particles with new source particles allows the GPU to maintain a high occupancy rate until the end of each cycle. Compared with the event-fixed approach, the event-hybrid algorithm brings little performance gains, which is not surprising. The tracking using the hybrid algorithm at the end of each cycle only accounts for very few calculations; therefore, the performance gains by using event-hybrid are very limited.
It is worth noting that the L1 cache only brings a slight advantage due to the event-based algorithm’s inability to efficiently exploit the L1 cache. There are several reasons. One reason is that the light kernel offers little opportunity for event-based methods to reuse data. Particle data are only used during the execution of short-lived event kernels, the data required by the previous kernel are often different from the next event kernel, leading to frequent invalidation of the cache of earlier loaded data. Another reason is that the particle redistribution results in less spatial locality. In event-based methods, although the first access to a particle data will cause the particle to be cached in the L1 cache, very few components of a particle data would be accessed later in the same event kernel. Therefore, the event-GPU algorithms obtain a small performance increase by enabling the L1 cache due to its insensitivity to the L1 cache.
This article now explores the single-node performance of the history-based and event-based algorithms on both CPUs and GPUs. All experiments on GPUs are based on event-hybrid algorithm and L1 cache is enabled.
Table 3 provides the particle-tracking rate for the history-based and event-based algorithms on both CPUs and GPUs. It can be seen from Table 3 that, on the CPU, the history-based algorithm is over 1.5x faster than the event-based algorithm in all cases. The serious performance degradation of event-CPU relative to history-CPU is mainly caused by the following reasons:
1) Extra operations: Event-CPU requires extra operations to organize the particles periodically to ready them for the different event-processing routines. These additional operations introduce extra overhead compared to the history-based algorithm on the CPU.
2) Atomic operations: The atomic operations in history-CPU are randomly distributed along the history of each particle, whereas the atomic operations in event-CPU are batched into a single-event loop. Therefore, more threads are waiting for atomic operations in the event-CPU.
3) Particle data locality: There are more opportunities for history-CPU to reuse data. In history-CPU, particle data can be cached in registers; thus consecutive particle data access can be hit directly in registers. However, in event-CPU, data required by the current event loop are often part of the complete particle data and are often different from the previous loop. Very few components of particle data would be accessed later in the current event loop.

TABLE 3. Tracking rate (
It should be noted that the event-GPU algorithm did not achieve the speedup as expected and only provides 19–23 equivalent CPU cores that are 3x slower than history-GPU. Different from previous studies on the continuous-energy MC code (Bergmann and Vujić, 2015; Choi et al., 2019; Hamilton and Evans, 2019) where the lookup of energy grids occupies a very large portion of the calculation. Table 3 shows the remarkably superior performance of the history-based method relative to the event-based approach on the GPU. The main advantage of event-GPU is that the top level branches of history-GPU are removed, which decreases thread divergence on the GPU. Nevertheless, event-GPU has many disadvantages that would significantly affect the performance of the event-GPU algorithm for the multigroup transport code. Apart from the drawbacks related to extra operations, atomic operations, and particle data locality, memory access pattern is another factor. We will design several experiments in Section 4.4 to analyze the factor in detail.
MC transport is a random memory access problem, and the memory bandwidth of each algorithm requires to be measured. We measured the memory bandwidth using the perf and nvprof tools. On the Intel Xeon E5-2690 v4 CPU, the available memory bandwidth is measured by the STREAM benchmark. Table 3 shows the achievable memory bandwidth of the history-based and event-based algorithms on the CPU and GPU. On problem 1, the history-based algorithm achieves approximately 9 GB/s or roughly 9% of available memory bandwidth on the CPU, while the event-based algorithm achieves roughly 15%. The result on the GPU is similar to that on the CPU. The history-based algorithm achieves 95 GB/s memory bandwidth, whereas the event-based algorithm achieves 140 GB/s or roughly 40% of the available memory bandwidth. The results on both architectures demonstrate that despite the poor performance, the event-based algorithm can achieve higher memory bandwidth.
It should be noted that the memory bandwidth cannot be saturated by the MC code due to its random memory access patterns, especially for the history-based algorithm. In most cases, only one item in the cache line can be used, because of which the performance of MC methods is bounded by memory access latency. The ability of GPU to support more concurrent memory requests and to hide memory access latency makes the performance on the GPU better (Table 3 shows two algorithms are faster on the GPU).
Figure 5 shows the parallel efficiency as the thread count (one process) is increased on the CPU. We can see that both the history-based and event-based algorithms achieve over 60% parallel efficiency when using less than 14 threads (within one socket), while the parallel efficiency drops rapidly when the second socket is used. This is because nonunified memory access occurs when the second socket is consumed. Compared to the event-based algorithm, the parallel efficiency of the history-based algorithm drops and becomes slower since more threads are waiting for the atomic operations in the event-based algorithm, as demonstrated in Section 4.3.1. We further use two processes with 14 threads per rank and find that the parallel efficiency of the two algorithms increases to more than 50% when scaling to 28 threads. This shows that the MC particle transport code is sensitive to memory access latency and using MPI across sockets reduces the impact of nonunified memory access.
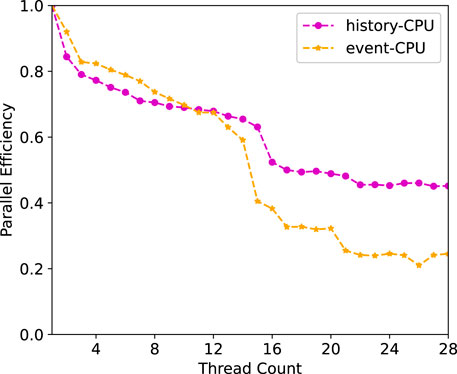
FIGURE 5. Thread parallel efficiency of problem 1 on the two-sockets of Intel Xeon E5-2690 v4 14 core CPU. Only one process is used.
Table 4 provides a comparison of time spent on different event subroutines on both CPUs and GPUs. The experiments were carried out using one rank. The process of generating source particles is excluded during the measurement. As observed, xs calculation only occupies less than 8%. This is because in the multigroup MC simulation, macroscopic cross section corresponding to a specific energy group is computed only once and subsequent calls to the function of xs calculation directly return the cached value. The results indicate that calculating cross sections in the multigroup scheme is not as time-consuming as in the continuous-energy scheme. The time spent on xs calculation for problem 2 constitutes a larger fraction than problem 1 on both two architectures due to more isotopes and reactions in problem 2.
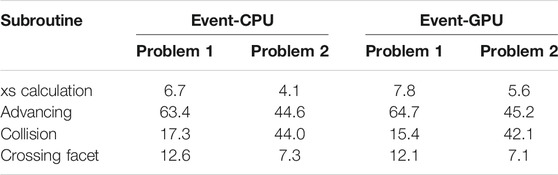
TABLE 4. Percentage (%) of time spent on subroutines of event-based algorithm on CPU and GPU for problem 1 and problem 2.
The intra-node results provided in Section 4.3.1 indicate that for the multigroup particle transport code, history-GPU outperforms event-GPU by factors of three to four across a range of the problems considered, whereas previous studies on continuous-energy schemes demonstrate that event-GPU is faster than history-GPU. The reasons for this performance difference mainly contain two factors: memory access pattern and calculation of cross sections. In this section we will design several experiments to answer the following two questions:
1) How does the memory access pattern affect the performance of the history-based and event-based algorithms for multigroup MC transport methods on the GPU?
2) Why is the event-based algorithm for continuous-energy MC transport methods faster than the history-based algorithm on the GPU?
On the GPU, a good coalesced access can be achieved when the neighboring threads access neighboring locations in memory. Memory coalescing offers an opportunity to combine multiple memory accesses into a single transaction, greatly improving efficiency.
In the history-based algorithm, contiguously stored particles are assigned to neighboring threads, leading to a good coalesced access. In the event-based algorithm, however, disjoint memory accesses are encountered because of the reallocation of particles to different threads at the conclusion of each event cycle. This prevents the event-based algorithm from utilizing memory coalescing. Therefore, the cost caused by poor memory access patterns may outweigh the benefit of reducing thread divergence.
To demonstrate the impact of disjoint memory accesses, we modify the memory access patterns of event-GPU. We sort the particle bank before executing each event kernel so that contiguously stored particles are assigned to neighboring threads. Then we compare the runtime of the original and sorted event kernel. Figure 6 shows the runtime of the original and sorted xs kernel. The sorted xs kernel achieves lower runtime on both two problems every time the cross sections are calculated, indicating that there is a significant performance loss for the original xs kernel. However, the performance of sorted xs kernel cannot be achieved as sorting the particle bank is very expensive.
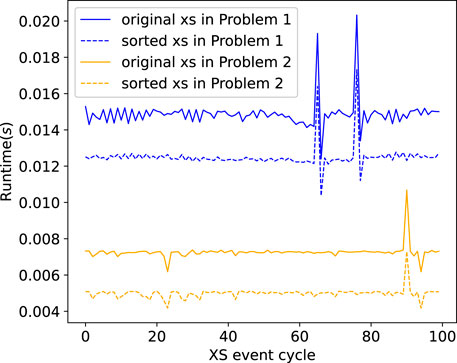
FIGURE 6. Runtime of original and sorted xs kernel on Problem 1 and Problem 2. The x-axis represents the number of xs events in the execution of event-GPU.
Numerous studies on continuous-energy MC methods achieve the opposite results to the conclusion of this article that is based on multigroup schemes. The major difference between the continuous-energy and multigroup schemes is the former needs time-consuming energy lookups. Several algorithms for accelerating energy lookups have been proposed, such as the unionized grid method (Leppänen, 2009) and hash-based approach (Brown, 2014; Walsh et al., 2015), which can provide speedups of up to 20x over conventional schemes.
In the history-based algorithm, it would take much more time to calculate cross sections in the continuous-energy scheme than that in the multigroup scheme. Fortunately, there are some existing optimization techniques on the GPU to accelerate the continuous-energy xs event kernel in the event-based algorithm, such as sort event queue by material or energy, and kernel splitting, etc. For the continuous-energy scheme, the speedup of accelerating xs event kernel would exceed the cost caused by poor memory access patterns. Therefore, the event-GPU is faster than history-GPU with the continuous-energy scheme.
We will design experiments with XSBench (Tramm et al., 2014), a mini app representing continuous-energy cross section kernel, to investigate the impact of calculations of cross sections. XSBench has already implemented both conventional and optimized energy lookup algorithms. To show the difference in the time of xs calculation between continuous-energy and multigroup MC, we also performed an experiment with OpenMC.
Experiment with XSBench and OpenMC. To verify the theoretical analysis, we first test XSBench on the GPU to show the significant speedup of the continuous-energy xs kernel. Table 5 shows the runtime of three algorithms implemented in XSBench on the CPU and GPU. The history-based and event-based methods are used on the CPU and GPU respectively. The results are obtained on the same CPU and GPU shown in Section 4.1. On the CPU, the number of particles is set to
OpenMC has implemented the event-based algorithm with the continuous-energy scheme. We simulated Pincell case (Horelik et al., 2013) using OpenMC to show the percentage of time spent on different subroutines when using continuous-energy cross sections. Table 6 shows the results. Compared with the results in Table 4, it can be seen that the time percentage needed to compute xs in the continuous-energy scheme is much larger than that in the multigroup scheme.

TABLE 6. Percentage (%) of time spent on different subroutines in the Pincell case, which is simulated using event-based implementation in OpenMC with the continuous-energy scheme.
Experiment with XSBench and Quicksilver. We modify Quicksilver by adding accesses to continuous-energy cross sections for each particle. The modified code is aimed at approximating the program features of the continuous-energy MC code by bridging the major gap between the multigroup scheme and the continuous-energy scheme. For history-CPU and history-GPU, it is only necessary to add relative implementation in XSBench at the location where the distance to the next collision is computed. For event-GPU, an event kernel that performs calculations of continuous-energy cross sections is called.
Table 7 shows the tracking rate of modified algorithms for problem 1 and problem 2. Event-GPU outperforms other algorithms by factors of approximately 1.2–1.5 after adding accesses to continuous-energy cross sections. The superior performance of event-GPU relative to history-based algorithms is dominantly due to two factors. On the one hand, calculating continuous-energy cross sections on the GPU using the event-based method is capable of obtaining a significant speedup as shown in Table 5. The speedup of computing continuous-energy cross sections exceeds the cost of disjoint access to particle data. On the other hand, the calculation of continuous-energy cross sections is much more time-consuming than the multigroup scheme, causing more serious thread divergence in history-GPU. This means that continuous-energy event-GPU would reduce much more thread divergence than multigroup, that is to say, the corresponding benefit would be larger.
We have characterized history-based and event-based algorithms for multigroup MC transport code. Built on the analytics, we make the following summaries.
For multigroup MC transport methods, the event-based algorithm suffers from performance loss caused by extra operations to organize particles, batched atomic operations, and poor particle data locality. Besides, memory access pattern is another factor that weakens the performance of event-GPU. The history-based algorithm outperforms the event-based algorithm on both two architectures in all cases. Thus the history-based algorithm is recommended on both the CPU and GPU for multigroup MC transport methods.
For continuous-energy MC methods, the event-based algorithm is faster on the GPU due to the overwhelming speedup of the cross section kernel. We recommend using the history-based algorithm on the CPU and the event-based algorithm on the GPU.
The history-based algorithm suffers from serious thread divergence on the GPU. One reason is that each particle has a different history length. To reduce branches, we can limit each particle to a prescribed number of collisions. In addition, the proposed optimizations, including event-fixed and event-hybrid, can also be applied to event-based implementation with continuous-energy schemes.
Despite the fact that the event-based algorithm can achieve higher memory bandwidth utilization on both the CPU and GPU, the memory bandwidth cannot be saturated since the majority of the memory access patterns are random. We have characterized the MC transport code as memory latency bound. GPU can hide the latency to access memory by executing many more threads than the device can physically execute simultaneously, which helps GPU provides higher performance. In terms of memory access, a suitable architecture for executing the MC transport code should be a many-core architecture that can support a large number of simultaneous memory requests and hide memory access latency. The more the number of cores, the better the performance. Considering the issue of power consumption, each core requires to be specially designed in accordance with the characteristics of the MC particle transport code. To obtain a hundredfold speedup on a single node, an MC-specified architecture should be designed.
This article evaluates the performance of the history-based and event-based algorithms for the multigroup MC particle transport on CPUs and GPUs using Quicksilver, a multigroup MC code with only the history-based implementation. In this article, we first implement and optimize the event-based algorithm. The queue-based method is used to implement the event-based algorithm. To improve the performance on the GPU, terminated particles are replaced with new particles so that the number of active particles will remain fixed for most of the time. A hybrid history and event-based method is also implemented. The results show that both two methods benefit the basic event-based algorithm.
Then we used the Coral2 benchmark to evaluate the intra-node performance and other factors of history-based and event-based algorithms. The event-based algorithm suffers from performance loss due to extra operations to reallocate particles, batched atomic operations, and poor particle data locality. We further focus on the performance affecting factors on the GPU and the performance difference between the multigroup and continuous-energy MC code. Different from the results on continuous-energy MC codes, the history-based algorithm on the GPU with the multigroup scheme outperforms the event-based algorithm by a factor of around three. This is because the disjointed memory accesses are encountered in the event-based algorithm, which prevents the kernel from utilizing memory coalescing. The cost of poor memory access patterns outweighs the benefit of reducing thread divergence. For continuous-energy MC code, the speedup of accelerating xs event kernel would exceed the cost by poor memory access patterns, thus the event-based algorithm for the continuous-energy MC code obtains a superior performance.
The evaluation results build on our analytics. For multigroup MC codes, despite the poor performance, the event-based algorithm can achieve higher memory bandwidth utilization on both CPU and GPU. Compared with the CPU, the GPU is more suitable for executing the MC transport code due to its capability of supporting a large number of simultaneous memory requests and hiding memory access latency. In future research, we plan to optimize the MC transport code on modern architectures and develop MC-specified architecture.
Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/LLNL/Quicksilver/tree/master/Examples/CORAL2_Benchmark.
DM designed the research. TL and JL guided the research. DM drafted the manuscript. BY helped perform experiments and organize the manuscript. QZ helped revise the paper. DM revised and finalized the paper.
This research work was supported in part by the National Key Research and Development Program of China (2017YFB0202104 and 2018YFB0204301).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Bergmann, R. M., and Vujić, J. L. (2015). Algorithmic Choices in WARP - A Framework for Continuous Energy Monte Carlo Neutron Transport in General 3D Geometries on GPUs. Ann. Nucl. Energ. 77, 176–193. doi:10.1016/j.anucene.2014.10.039
Bleile, R., Brantley, P., Richards, D., Dawson, S., McKinley, M. S., and O'Brien, M. (2019). “Thin-threads: An Approach for History-Based Monte Carlo on Gpus,” in 2019 International Conference on High Performance Computing & Simulation (HPCS), Dublin, Ireland (Tentative), June 15–19, 2019 (IEEE), 273–280. doi:10.1109/HPCS48598.2019.9188080
Brown, F. B., and Martin, W. R. (1984). Monte Carlo methods for radiation transport analysis on vector computers. Progress in Nuclear Energy 14 (3). (Elsevier), 269–299. doi:10.1016/0149-1970(84)90024-6
Brown, F. B. (2014). New Hash-Based Energy Lookup Algorithm for Monte Carlo Codes. Technical Report. Los Alamos, NM (United States). Los Alamos National Lab.(LANL).
Choi, N., Kim, K. M., and Joo, H. G. (2019). “Initial Development of Pragma–A Gpu-Based Continuous Energy Monte Carlo Code for Practical Applications,” in Transactions of the Korean Nuclear Society Autumn Meeting, Goyang, Korea, October 24–25, 2019 (Goyang, Korea), 24–25.
Cullen, D. E., Clouse, C. J., Procassini, R., and Little, R. C. (2003). Static and Dynamic Criticality: Are They Different?. Technical Report.
Du, X., Liu, T., Ji, W., Xu, X. G., and Brown, F. B. (2013). “Evaluation of Vectorized Monte Carlo Algorithms on Gpus for a Neutron Eigenvalue Problem,” in Proceedings of International Conference on Mathematics and Computational Methods Applied to Nuclear Science & Engineering, Sun Valley, Idaho, May 5–9, 2014 (Sun Valley, Idaho, USA), 2513–2522.
Forster, R., and Godfrey, T. (1985). Mcnp-a General Monte Carlo Code for Neutron and Photon Transport 77, 33–55. doi:10.1007/BFb0049033
Hamilton, S. P., and Evans, T. M. (2019). Continuous-energy Monte Carlo Neutron Transport on Gpus in the Shift Code. Ann. Nucl. Energ. 128, 236–247. doi:10.1016/j.anucene.2019.01.012
Hamilton, S. P., Slattery, S. R., and Evans, T. M. (2018). Multigroup Monte Carlo on Gpus: Comparison of History-And Event-Based Algorithms. Ann. Nucl. Energ. 113, 506–518. doi:10.1016/j.anucene.2017.11.032
Horelik, N., Herman, B., Forget, B., and Smith, K. (2013). “Benchmark for Evaluation and Validation of Reactor Simulations (Beavrs), V1. 0.1,” in Proceedings of International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, Sun Valley, Idaho, May 5–9, 2014. 5–9
Leppänen, J. (2009). Two Practical Methods for Unionized Energy Grid Construction in Continuous-Energy Monte Carlo Neutron Transport Calculation. Ann. Nucl. Energ. 36, 878–885. doi:10.1016/j.anucene.2009.03.019
Li, H., Li, K., An, J., and Li, K. (2017). Msgd: A Novel Matrix Factorization Approach for Large-Scale Collaborative Filtering Recommender Systems on Gpus. IEEE Trans. Parallel Distributed Syst. 29, 1530–1544. doi:10.1109/TPDS.2017.2718515
Liu, T., Du, X., Wei, J., Xu, X. G., and Brown, F. B. (2014). “A Comparative Study of History-Based versus Vectorized Monte Carlo Methods in the Gpu/cuda Environment for a Simple Neutron Eigenvalue Problem,” in SNA + MC 2013 - Joint International Conference on Supercomputing in Nuclear Applications + Monte Carlo, Paris, October 27–31, 2013. doi:10.1051/snamc/201404206
[Dataset] LLNL (2017). Mercury. Available at: https://wci.llnl.gov/simulation/computer-codes/mercury (Accessed February 18, 2020).
Metropolis, N., and Ulam, S. (1949). The Monte Carlo Method. J. Am. Stat. Assoc. 44, 335–341. doi:10.1080/01621459.1949.10483310
Ozog, D., Malony, A. D., and Siegel, A. R. (2015). “A Performance Analysis of Simd Algorithms for Monte Carlo Simulations of Nuclear Reactor Cores,” in 2015 IEEE International Parallel and Distributed Processing Symposium, Hyderabad, India, May 25–29, 2015 (IEEE), 733–742. doi:10.1109/IPDPS.2015.105
Pandya, T. M., Johnson, S. R., Evans, T. M., Davidson, G. G., Hamilton, S. P., and Godfrey, A. T. (2016). Implementation, Capabilities, and Benchmarking of Shift, a Massively Parallel Monte Carlo Radiation Transport Code. J. Comput. Phys. 308, 239–272. doi:10.1016/j.jcp.2015.12.037
Richards, D. F., Bleile, R. C., Brantley, P. S., Dawson, S. A., McKinley, M. S., and O’Brien, M. J. (2017). “Quicksilver: a Proxy App for the Monte Carlo Transport Code Mercury,” in 2017 IEEE International Conference on Cluster Computing (CLUSTER), Hawaii, United States, September 5–8, 2017 (IEEE), 866–873. doi:10.1109/CLUSTER.2017.121
Romano, P. K., and Forget, B. (2013). The Openmc Monte Carlo Particle Transport Code. Ann. Nucl. Energ. 51, 274–281. doi:10.1016/j.anucene.2012.06.040
Romano, P. K., and Siegel, A. R. (2017). Limits on the Efficiency of Event-Based Algorithms for Monte Carlo Neutron Transport. Nucl. Eng. Techn. 49, 1165–1171. doi:10.1016/j.net.2017.06.006
Tramm, J. R., Siegel, A. R., Islam, T., and Schulz, M. (2014). Xsbench-the Development and Verification of a Performance Abstraction for Monte Carlo Reactor Analysis. PHYSOR 2014 - The Role of Reactor Physics Toward a Sustainable Future, The Westin Miyako, Kyoto, Japan, September 28, 2014.
Walsh, J. A., Romano, P. K., Forget, B., and Smith, K. S. (2015). Optimizations of the Energy Grid Search Algorithm in Continuous-Energy Monte Carlo Particle Transport Codes. Comput. Phys. Commun. 196, 134–142. doi:10.1016/j.cpc.2015.05.025
Keywords: parallel computing, performance evaluation, history-based, event-based, particle transport
Citation: Ma D, Yang B, Zhang Q, Liu J and Li T (2021) Evaluation of Single-Node Performance of Parallel Algorithms for Multigroup Monte Carlo Particle Transport Methods. Front. Energy Res. 9:705823. doi: 10.3389/fenrg.2021.705823
Received: 06 May 2021; Accepted: 25 June 2021;
Published: 23 July 2021.
Edited by:
Qian Zhang, Harbin Engineering University, ChinaReviewed by:
Rongliang Chen, Shenzhen Institutes of Advanced Technology (CAS), ChinaCopyright © 2021 Ma, Yang, Zhang, Liu and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tiejun Li, dGpsaUBudWR0LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.