Event-Triggered Forecasting-Aided State Estimation for Active Distribution System With Distributed Generations

In this study, the forecasting-aided state estimation (FASE) problem for the active distribution system (ADS) with distributed generations (DGs) is investigated, considering the constraint of data transmission. First of all, the system model of the ADS with DGs is established, which expands the scope of the ADS state estimation from the power network to the DGs. Moreover, in order to improve the efficiency of data transmission under the limited communication bandwidth, a component-based event-triggered mechanism is employed to schedule the data transmission from the measurement terminals to the estimator. It can efficiently reduce the amount of data transmission while guaranteeing the performance of system state estimation. Second, an event-triggered unscented Kalman filter (ET-UKF) algorithm is proposed to conduct the state estimation of the ADS with mixed measurements. To this end, the unscented transform (UT) technique is employed to approximate the probability distribution of the state variable after nonlinear transformation, which can reach more than second order, and then, an upper bound of the filtering error covariance is derived and subsequently minimized at each iteration. The gain of the desired filter is obtained recursively by following a certain set of recursions. Finally, the effectiveness of the proposed method is demonstrated by using the IEEE-34 distribution test system.

1 Introduction

With the widespread integration of distributed generations (DGs) in the power system, the conventional passive distribution system is being transformed into the active distribution system (ADS) (Ehsan and Yang, 2018; Ge et al., 2020a; Li et al., 2020; Luo et al., 2020). It is common that the inherent intermittence and variability of DG generation increase the complexity and uncertainty of the operation state for the ADS (Ge et al., 2021b; 2020b). In this regard, it is necessary to ensure the accuracy and efficiency of state estimation for the ADSs, which is prerequisite for the safe and reliable operation of the power distribution system (Chen Y. et al., 2017; Zhang et al., 2020; Ge et al., 2021a). In general, the traditional static state estimation (SSE) methods are mainly based on the weighted least square (WLS) that cannot meet the estimation requirements of ADSs, because it ignores the dynamics of the system. For this reason, the forecasting-aided state estimation (FASE) is proposed to improve the accuracy and speed of the estimator effectively for the ADSs (Do Coutto Filho and Stacchini de Souza, 2009; Wang et al., 2020). The FASE method takes into consideration the time evolution of the ADS states that can make the state prediction of the next time instant, so as to provide the information required for a security analysis and preventive control functions. Moreover, when the measurement data of ADS are flawed or even unavailable due to certain reasons, the state prediction values can be used to provide a set of pseudo states of the ADS, thus improving the robustness of the estimator to external interference.

Due to the advantages of the FASE method and its promising prospect of practical application, it has attracted increasing attention for research, and there have been plenty of remarkable achievements made in addressing FASE problems for the ADS (Ćetenović and Ranković, 2018; Macii et al., 2020; Cheng and Bai, 2021; Geetha et al., 2021). For instance, a novel approach in assessing the process noise covariance matrix for FASE in ADS has been proposed by Ćetenović and Ranković (2018), which contributes in improving the accuracy of estimation. The asynchronous hierarchical FASE method has been proposed by Geetha et al. (2021). According to this method, the global estimation values are calculated by collating the estimates of smaller reduced order subsystems to reduce the overall level of computational complexity. Cheng and Bai (2021) put forward the robust FASE for ADSs by using a strict linearization method for the purpose of dealing with the nonlinear measurements, which can reduce the nonlinear error for the state estimation. However, in the prior literature, the monitoring scope of the state estimation system is often limited to the power network part of the ADS. In general, the DGs are modeled as equivalent power injection, but they are not monitored and modeled in detail. In fact, when there are a large number of DGs connected to the distribution network, the accurate estimation of real-time DG states plays a crucial role in the flexible control and dispatch of the ADS (Yang et al., 2018). Meanwhile, with the development of smart sensor, more information of the DG system is allowed to be collected to the monitoring center (Fang et al., 2020). The information redundancy can be improved by considering the measurement of DG system in the context of ADS state estimation, thereby facilitating to enhance the estimation performance. Therefore, it is of much practical significance to construct an adequate model of the ADSs with DGs for expanding the scope of state estimation and improving the estimation performance of ADSs.

In addition, due to economic constraint and the complexity of reconstruction, it is impractical to replace all distribution remote terminal units (DRTUs) with phasor measurement units (PMUs) within a short period of time (Yang et al., 2017). In the foreseeable future, both PMUs and DRTUs will provide measurement data for the FASE of the ADSs collectively (Dobakhshari et al., 2021). Therefore, the FASE algorithm is based on PMU/DRTU mixed nonlinear measurements. In practice, it is significant to deal with nonlinear measurement, which would seriously affect the performance of FASE for the ADSs. In this regard, there are various nonlinear filtering algorithms developed to handle the nonlinear system state estimation, such as the particle filter (PF), the extended Kalman filter (EKF), and the unscented Kalman filter (UKF). The PF algorithm can carry out the recursive Bayesian estimation using the nonparametric Monte Carlo simulation method. Due to the high dimension of the distribution system, however, a considerable amount of particles are required, which would give rise to a huge computational workload. The EKF algorithm linearizes the nonlinear system through the Taylor series expansion but ignores the higher order terms (Sun et al., 2017, 2018), which cannot guarantee the high estimation accuracy. As for the UKF algorithm, the unscented transform (UT) technique is applied to approximate the probability distribution of the state variable after nonlinear transformation (Zhao and Mili, 2019; Dang et al., 2020). The UKF algorithm produces better estimation performance than the EKF algorithm, and it is more suitable to realize the online application of estimation.

Furthermore, with the rapid increase in the number of power users and the extensive connection of DGs, the scale of the ADS is also expanding. In order to meet the monitoring requirements of the ADS, it is necessary to install more measurement devices. As a result, a considerable amount of measurement data would be transmitted to the estimator. Due to the limited network communication resources, the transmission of numerous data may contribute to the network-induced phenomena, for example, data loss and transmission delay, which makes it likely to lose useful information, thus affecting the estimation performance of the ADS (Ding et al., 2017; Cheng et al., 2018; Xing et al., 2018). In order to reduce the transmission of redundant data, the communication strategy based on the event-triggered mechanism has been proposed. According to this strategy, the measurement will be transmitted to the data center for processing only when the preset event-triggering conditions are satisfied. Compared with the traditional time-triggered one, the event-triggered mechanism has the advantage in alleviating the communication burden with ensuring the expected estimation performance. Therefore, the estimation problem based on the event-triggered mechanism has recently attracted much attention (Liu et al., 2018; Li et al., 2019; Kooshkbaghi et al., 2020; Shanmugam et al., 2020; Zhu et al., 2020). For instance, an event-triggered PF algorithm has been proposed by Liu et al. (2018) to estimate the state of the synchronous generator in real time, and the UKF algorithm has been used as the local estimator to provide trigger information in the study by Li et al. (2019), which reduces the computational burden of the intelligent terminal. So far, to our knowledge, the FASE of the ADS based on the event-triggered mechanism has not been considered as carefully as required.

As motivated by the above discussion, this study is purposed to address the FASE problem for the ADS with DGs under the constraints of communication resource, and the main contributions of it are detailed as follows.

1) The system model of the ADSs with DGs is established by considering the state variables and measurements of DGs in detail, which expands the estimation scope of the ADS and facilitates the accurate FASE of the ADS.

2) An appropriate component-based event-triggered mechanism is adopted to reduce “unnecessary” data transmissions from the measuring terminals to the monitoring center, thus alleviating the burden placed on the network transmission.

3) Given the nonlinear mixed measurement of the ADS and the intermittent observation attributed to the event-triggered mechanism, the event-triggered UKF (ET-UKF) algorithm is proposed to ensure the performance of the state estimation.

The rest of this article is organized as follows. The state and measurement models of the ADS are built by incorporating the state and measurement information of DGs into the distribution system in System Model of ADS with DGs section. In FASE with Component-Based Event-Triggered Mechanism section, the component-based event-triggered mechanism is introduced, and the ET-UKF algorithm is designed. In Simulation Results and Analysis section, the IEEE-34 distribution test system is taken as an example to verify the effectiveness of the proposed method.

2 System Model of the Active Distribution System With Distributed Generations

For the FASE of ADSs, the system model is composed of the state model and the measurement model. The state model is linear, which represents the transition trajectory between consecutive states (Zhao et al., 2019). The measurement model expresses the functional relationship between measurements and state variables. In this study, considering the widespread connection of DGs in the ADS, the system model is built by combining the state and measurement variables of power networks and DGs.

2.1 State Model

The system state $x_k\in {\mathrm{ℝ}}^n$ is composed of the state of the network part of the ADS and the DGs connected to the distribution system, and $x_k={[x_{DG,k}^T,x_{DN,k}^T]}^T$. In reality, there are many types of DGs, including DGs that are directly connected to the distribution network such as synchronous generators and asynchronous generators (as shown in Figure 1A), and DGs that are connected to the grid through power electronic converters, such as photovoltaic cells and energy storage batteries (Chen S. et al., 2017). The most common DGs connected to the grid via power electronic devices are the direct current DGs, which are connected to the grid via a chopper-inverter device (as shown in Figure 1B).

FIGURE 1

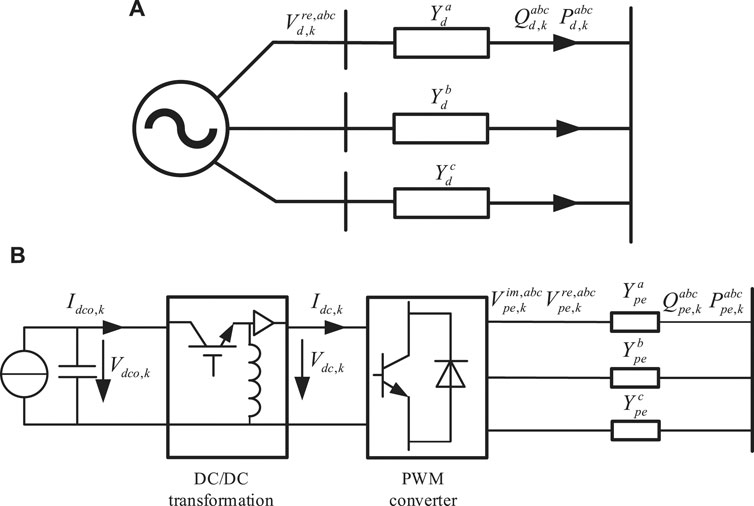
FIGURE 1. The models of the two most commonly used DGs: (A) model of DGs connected to the grid directly and (B) model of direct current type DGs connected to grid via a chopper-inverter device.

For the DGs connected to the grid directly, the state variables are selected as $x_{d,k}={\left[V_{d,k}^{re,a},V_{d,k}^{re,b},V_{d,k}^{re,c},V_{d,k}^{im,a},V_{d,k}^{im,b},V_{d,k}^{im,c}\right]}^T$, where $V_{d,k}^{re,p}$ and $V_{d,k}^{im,p}$ ($p\in \left\{a,b,c\right\}$) represent the real and imaginary parts of the alternating current voltage output by the DGs, respectively. For the direct current–type DGs connected to grid via a chopper-inverter device, the state variables are set as $x_{pe,k}={\left[V_{dco,k},I_{dco,k},V_{dc,k},V_{pe,k}^{re,a},V_{pe,k}^{re,b},V_{pe,k}^{re,c},V_{pe,k}^{im,a},V_{pe,k}^{im,b},V_{pe,k}^{im,c}\right]}^T$, where $V_{dco,k}$ and $I_{dco,k}$ are the voltage and current output by the direct current–type DGs, respectively, and $V_{dc,k}$ represents the direct current voltage output by the DC/DC transformation. Therefore, $x_{DG,k}={\left[x_{d,1,k}^T,\dots ,x_{d,n_d,k}^T,x_{pe,1,k}^T,\dots ,x_{pe,n_{pe},k}^T\right]}^T\in {\mathrm{ℝ}}^{n_{DG}}$. In addition, the state vector of the distribution network part $x_{DN,k}={\left[V_{1,k}^T,\dots ,V_{\iota ,k}^T,\dots ,V_{n_{DN},k}^T\right]}^T\in {\mathrm{ℝ}}^{n_{DN}}$ is consisted of the real and imaginary parts of bus voltage in the distribution network, where $V_{\iota ,k}={\left[V_{\iota ,k}^{re,a},V_{\iota ,k}^{re,b},V_{\iota ,k}^{re,c},V_{\iota ,k}^{im,a},V_{\iota ,k}^{im,b},V_{\iota ,k}^{im,c}\right]}^T$ is a vector representing the state of the $\iota -\text{th}$ bus.

Then, the state model of the ADS with DGs can be described as

$x_k=F_{k-1}{x}_{k-1}+g_{k-1}+w_{k-1},(1)$

where $F_{k-1}$ is the transition matrix that represents the speed of the state transition process, and vector $g_{k-1}$ is associated with the trend behavior of the state trajectory. $w_{k-1}\in {\mathrm{ℝ}}^n$ represents the process noise that obeys Gaussian distribution, which satisfies $\mathbb{E}\left\{w_{k-1}\right\}=0$ and $\mathbb{E}\left\{w_{k-1}{w}_{k-1}^T\right\}=Q_{k-1}$. In this study, with the consideration of the adequacy and parsimony of the state model, we adopt the Holt–Winters double exponential smoothing method in Eq. 1 to update $F_{k-1}$ and $g_{k-1}$ as follows:

$F_{k-1}={\alpha }_H\left(1+{\beta }_H\right)I,(2)$

$g_{k-1}=\left(1+{\beta }_H\right)\left(1-{\alpha }_H\right){\widehat{x}}_{k-1|k-2}-{\beta }_H{a}_{k-2}+\left(1-{\beta }_H\right)b_{k-2},(3)$

where I is the identity matrix; ${\alpha }_H$ and ${\beta }_H$ are smoothing parameters, which are commonly in the range from 0 to 1; ${\widehat{x}}_{k-1|k-2}$ is the predicted state at instant $k-1$; and $a_k$ and $b_k$ are recursively defined as

$a_k={\alpha }_H{\widehat{x}}_{k|k}+\left(1-{\alpha }_H\right){\widehat{x}}_{k|k-1},(4)$

$b_k={\beta }_H\left(a_k-a_{k-1}\right)+\left(1-{\beta }_H\right)b_{k-1},(5)$

2.2 Measurement Model

The measured data of the ADS primarily originate from alternating current voltage, power, other measurement information of the network part, and the measurement information provided by sensors in DGs.

In general, the measurements obtained from different types of DGs are different. For the DGs directly connected to the grid, the measurement information is $y_{d,k}={\left[P_{d,k}^a,P_{d,k}^b,P_{d,k}^c,Q_{d,k}^a,Q_{d,k}^b,Q_{d,k}^c,{\mathrm{V}}_{d,k}^a,{\mathrm{V}}_{d,k}^b,{\mathrm{V}}_{d,k}^c\right]}^T$. Assuming the DG is connected to the $\iota -\text{th}$ bus in the ADS, according to the equivalent model shown in Figure 1A, the measurement equation can be obtained as

$\{\begin{array}{c}{P}_{d,k}^p=-V_{d,k}^{re,p}\left(G_d^p{\overrightarrow{V}}_{d-\iota ,k}^{re,p}-B_d^p{\overrightarrow{V}}_{d-\iota ,k}^{im,p}\right)+V_{d,k}^{im,p}\left(G_d^p{\overrightarrow{V}}_{d-\iota ,k}^{im,p}+B_d^p{\overrightarrow{V}}_{d-\iota ,k}^{re,p}\right)\\ Q_{d,k}^p=-V_{d,k}^{re,p}\left(G_d^p{\overrightarrow{V}}_{d-\iota ,k}^{im,p}+B_d^p{\overrightarrow{V}}_{d-\iota ,k}^{re,p}\right)+V_{d,k}^{im,p}\left(G_d^p{\overrightarrow{V}}_{d-\iota ,k}^{re,p}-B_d^p{\overrightarrow{V}}_{d-\iota ,k}^{im,p}\right)\end{array},(6)$

${\mathrm{V}}_{d,k}^p=\sqrt{{\left(V_{d,k}^{re,p}\right)}^2+{\left(V_{d,k}^{im,p}\right)}^2},(7)$

where ${\overrightarrow{V}}_{d-\iota ,k}^{re,p}=V_{d,k}^{re,p}-V_{\iota ,k}^{re,p}$, ${\overrightarrow{V}}_{d-\iota ,k}^{im,p}=V_{d,k}^{im,p}-V_{\iota ,k}^{im,p}$. $G_d^p$ and $B_d^p$ are the real and imaginary parts of equivalent admittance $Y_d^p$, respectively. $P_{d,k}^p$ and $Q_{d,k}^p$ represent the active and reactive power outputs by the DGs, and ${\mathrm{V}}_{d,k}^p$ is the voltage amplitude of the DGs.

For the direct current DGs connected to the grid by the chopper-inverter device, according to the data that can be measured by the chopper-inverter device sensors, the measurement is $y_{pe,k}={\left[V_{dco,k},I_{dco,k},V_{dc,k},I_{dc,k},{\mathrm{V}}_{pe,k}^a,{\mathrm{V}}_{pe,k}^b,{\mathrm{V}}_{pe,k}^c,P_{pe,k}^a,P_{pe,k}^b,P_{pe,k}^c,Q_{pe,k}^a,Q_{pe,k}^b,Q_{pe,k}^c\right]}^T$. From the equivalent model shown in Figure 1B, the measurement equation can be expressed as

$\{\begin{array}{l}{V}_{dco,k}=V_{dco,k}\\ I_{dco,k}=I_{dco,k}\\ V_{dc,k}=V_{dc,k}\\ I_{dc,k}=\frac{I_{dco,k}{V}_{dco,k}{\eta }_{dc}}{V_{dc,k}}\end{array}(8)$

${\mathrm{V}}_{pe,k}^p=\sqrt{{\left(V_{pe,k}^{re,p}\right)}^2+{\left(V_{pe,k}^{im,p}\right)}^2},(9)$

$\{\begin{array}{c}{P}_{pe,k}^p=-V_{pe,k}^{re,p}\left(G_{pe}^p{\overrightarrow{V}}_{pe-\iota ,k}^{re,p}-B_{pe}^p{\overrightarrow{V}}_{pe-\iota ,k}^{im,p}\right)+V_{pe,k}^{im,p}\left(G_{pe}^p{\overrightarrow{V}}_{pe-\iota ,k}^{im,p}+B_{pe}^p{\overrightarrow{V}}_{pe-\iota ,k}^{re,p}\right)\\ Q_{pe,k}^p=-V_{pe,k}^{re,p}\left(G_{pe}^p{\overrightarrow{V}}_{pe-\iota ,k}^{im,p}+B_{pe}^p{\overrightarrow{V}}_{pe-\iota ,k}^{re,p}\right)+V_{pe,k}^{im,p}\left(G_{pe}^p{\overrightarrow{V}}_{pe-\iota ,k}^{re,p}-B_{pe}^p{\overrightarrow{V}}_{pe-\iota ,k}^{im,p}\right)\end{array},(10)$

where ${\overrightarrow{V}}_{pe-\iota ,k}^{re,p}=V_{pe,k}^{re,p}-V_{\iota ,k}^{re,p}$, ${\overrightarrow{V}}_{pe-\iota ,k}^{im,p}=V_{pe,k}^{im,p}-V_{\iota ,k}^{im,p}$. $I_{dc,k}$ is the DC/DC converter output current, ${\eta }_{dc}$ is the efficiency of the DC/DC converter, and ${\mathrm{V}}_{pe,k}^p$ represents the voltage amplitude at the ports of power electronic grid–connected devices. $G_{pe}^p$ and $B_{pe}^p$ are the real and imaginary parts of equivalent admittance $Y_{pe}^p$, respectively.

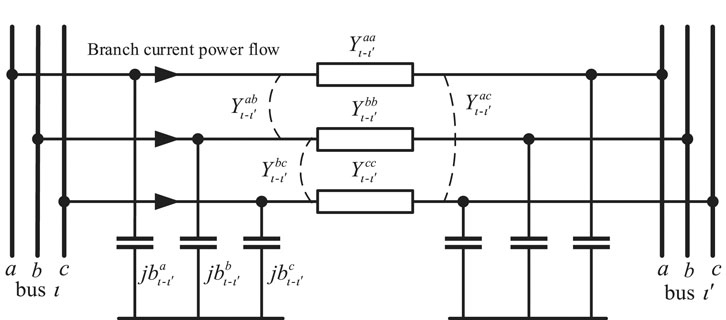
The measurement information of the network part is mainly provided by the PMUs and the DRTUs. The PMU can measure the real and imaginary parts of bus voltage and branch current, respectively. Moreover, the DRTU can measure the voltage amplitude, injected power of the bus, and the power flow of the branch. Figure 2 shows the three-phase line model of the distribution system. Combined with the circuit theorem, the functional relationship between measurement variable and state variable can be calculated.

FIGURE 2

FIGURE 2. Three-phase line model of the distribution system.

Then, the PMU measurements are expressed as

$\{\begin{array}{l}{V}_{\iota ,k}^{re,p}=V_{\iota ,k}^{re,p}\\ V_{\iota ,k}^{im,p}=V_{\iota ,k}^{im,p}\end{array},(11)$

$\{\begin{array}{l}{I}_{\iota -\iota \prime ,k}^{re,p}=\frac{1}{2}{b}_{\iota -\iota \prime }^p{V}_{\iota ,k}^{im,p}+{\displaystyle \sum }_{q\in \left\{a,b,c\right\}}{G}_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{re,q}-B_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{im,q}\\ I_{\iota -\iota \prime ,k}^{im,p}=\frac{1}{2}{b}_{\iota -\iota \prime }^p{V}_{\iota ,k}^{re,p}+{\displaystyle \sum }_{q\in \left\{a,b,c\right\}}{G}_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{im,q}-B_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{re,q}\end{array},(12)$

and the DRTU measurements are expressed as

${\mathrm{V}}_{\iota ,k}^p=\sqrt{{\left(V_{\iota ,k}^{re,p}\right)}^2+{\left(V_{\iota ,k}^{im,p}\right)}^2},(13)$

$\{\begin{array}{c}{P}_{\iota ,k}^p=V_{\iota ,k}^{re,p}{\displaystyle \sum }_{\iota \prime \in N_{\iota }}{\displaystyle \sum }_{q\in \left\{a,b,c\right\}}{G}_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{re,q}-B_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{im,q}\\ +V_{\iota ,k}^{im,p}{\displaystyle \sum }_{\iota \prime \in N_{\iota }}{\displaystyle \sum }_{q\in \left\{a,b,c\right\}}{G}_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{im,q}+B_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{re,q}\\ Q_{\iota ,k}^p=-\frac{1}{2}{\displaystyle \sum }_{\iota \prime \in N_{\iota }}{b}_{\iota -\iota \prime }^p[{\left(V_{\iota ,k}^{re,p}\right)}^2+{\left(V_{\iota ,k}^{im,p}\right)}^2]\\ -V_{\iota ,k}^{re,p}{\displaystyle \sum }_{\iota \prime \in N_{\iota }}{\displaystyle \sum }_{q\in \left\{a,b,c\right\}}{G}_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{im,q}+B_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{re,q}\\ +V_{\iota ,k}^{im,p}{\displaystyle \sum }_{\iota \prime \in N_{\iota }}{\displaystyle \sum }_{q\in \left\{a,b,c\right\}}{G}_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{re,q}-B_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{im,q}\end{array},(14)$

$\{\begin{array}{c}{P}_{\iota -\iota \prime ,k}^p=-V_{\iota ,k}^{re,p}{\displaystyle \sum }_{q\in \left\{a,b,c\right\}}{G}_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{re,q}-B_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{im,q}\\ +V_{\iota ,k}^{im,p}{\displaystyle \sum }_{q\in \left\{a,b,c\right\}}{G}_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{im,q}+B_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{re,q}\\ Q_{\iota -\iota \prime ,k}^p=-\frac{1}{2}{b}_{\iota -\iota \prime }^p[{\left(V_{\iota ,k}^{re,p}\right)}^2+{\left(V_{\iota ,k}^{im,p}\right)}^2]\\ -V_{\iota ,k}^{re,p}{\displaystyle \sum }_{q\in \left\{a,b,c\right\}}{G}_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{im,q}+B_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{re,q}\\ +V_{\iota ,k}^{im,p}{\displaystyle \sum }_{q\in \left\{a,b,c\right\}}{G}_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{re,q}-B_{\iota -\iota \prime }^{pq}{\overrightarrow{V}}_{\iota -\iota \prime ,k}^{im,q}\end{array},(15)$

where ${\mathrm{V}}_{\iota ,k}^p$ represents the p-phase voltage amplitude at the $\iota -\text{th}$ bus. $P_{\iota ,k}^p$ and $Q_{\iota ,k}^p$ represent the p-phase–injected active power and reactive power at the $\iota -\text{th}$ bus, respectively. $P_{\iota -\iota \prime }^p$ and $Q_{\iota -\iota \prime }^p$ represent the p-phase active power and reactive power flow at the $\iota -\iota \prime$ branch, respectively. $N_{\iota }$ represents the set of bus directly connected to the $\iota -\text{th}$ bus.

Combining all measurements of PMUs, DRTUs, and DGs’ sensors, the measurement output $y_k\in {\mathrm{ℝ}}^m$ is composed as follows:

$y_k=h\left(x_k\right)+v_k,(16)$

where $y_k={\left[y_{DG,k}^T,y_{DN,k}^T\right]}^T$, and $y_{DG,k}={\left[y_{d,1,k}^T,\dots ,y_{d,m_d,k}^T,y_{pe,1,k}^T,\dots ,y_{pe,m_{pe},k}^T\right]}^T$ is the measurement vector of DGs, $y_{DN,k}={\left[y_{DRTU,k}^T,y_{PMU,k}^T\right]}^T$ represents the measurement vector of the network part, $h(\cdot )$ is a high-order nonlinear function, and $v_k\in {\mathrm{ℝ}}^m$ is the measurement noise subject to the Gaussian distribution, which satisfies $\mathbb{E}\left\{v_k\right\}=0$ and $\mathbb{E}\left\{v_k{v}_k^T\right\}=R_k$.

Remark 1: In this study, the system model of ADS with DGs is established by considering the state variables and measurements of DGs in detail, which expands the scope of ADS state estimation from the network to the DGs and improves estimated accuracy. It should be noted that the two most commonly used DGs are taken as examples for modeling in this study. The modeling methods of other DGs are similar to it. In practical applications, the models can be established according to the specific structure of the DGs.

Remark 2: According to the IEEE standard c37.118–2005, the PMUs ought to provide data in both the angular form (i.e., the phasor angles and magnitudes) and the rectangular form (i.e., the real and imaginary parts of voltages of the buses) (Martin et al., 2008). In this study, both the state and measured variables are presented in the rectangular form to build a linear PMU measurement model. In doing so, the complexity of the estimator is reduced, and the estimation performance is improved.

3 FASE With the Component-Based Event-Triggered Mechanism

3.1 Component-Based Event-Triggered Mechanism

With the event-triggered mechanism, the event generator determines whether the newly obtained measurement is sent to the estimator or not, which is based on the difference between the previously transmitted measurement and the latest measurement. To reduce the amount of data transmissions from measurement terminals to the estimator and ensure the desired estimation performance, each measurement terminal examines the event generator independently, and the consistency with other measurement terminals in the ADS is not required. As such, the component-based event-triggered mechanism is adopted in the data transmission of the ADS (Figure 3). The measured data are obtained by the measurement terminals (e.g., the DRTUs, the PMUs, and the DGs’ sensors) and screened by the event generator with the triggering condition. Then, the measured data meeting the triggering conditions are transited to the communication system. Moreover, the trigger detector determines which terminals have triggered and which terminals have not, and then the “zero-order hold” strategy is adopted to update the measurement data in the detector. Last, the data are passed into the estimator for processing.

FIGURE 3

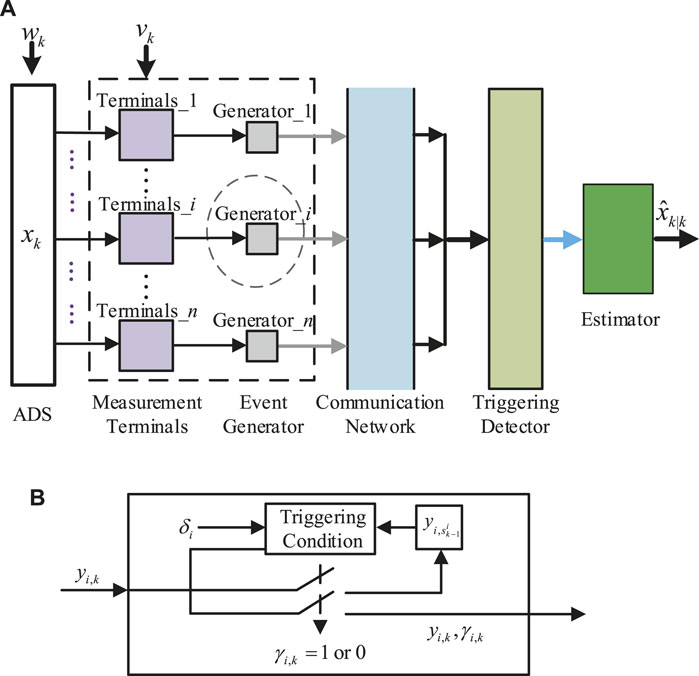
FIGURE 3. State estimation with the event-triggered mechanism in the ADS: (A) flow of the event-triggered mechanism and (B) event generator.

The event-triggered condition is described as

${\gamma }_{i,k}=\{\begin{array}{c}1,l_i\left(y_{i,s_{k-1}^i},y_{i,k}\right)>0\\ 0,l_i\left(y_{i,s_{k-1}^i},y_{i,k}\right)\le 0\end{array},(17)$

where $l_i\left(y_{i,s_{k-1}^i},y_{i,k}\right)=\left|\right|y_{i,s_{k-1}^i}-y_{i,k}\left|\right|-{\delta }_i$, $\left\{s_k^i\right\}$ represents the triggering instants sequence, $s_0^i=0$ and $s_k^i=\underset{k\ge s_{k-1}^i}{\text{min}}\left\{k\in N^{+}|l_i\left(y_{i,s_{k-1}^i},y_{i,k}\right)>0\right\}$.

In this study, the “zero-order hold” strategy is used to update the measurement ${\stackrel{⌣}{y}}_k$ received by the estimator subject to the component-based event-triggered mechanism, where ${\stackrel{⌣}{y}}_k={\left[{\stackrel{⌣}{y}}_{1,k}^T,\cdots ,{\stackrel{⌣}{y}}_{i,k}^T,\cdots ,{\stackrel{⌣}{y}}_{m_1,k}^T\right]}^T$ and ${\stackrel{⌣}{y}}_{i,k}$ is the received measurement data associated with the ith measuring device.

${\stackrel{⌣}{y}}_{i,k}=\{\begin{array}{c}{y}_{i,k},{\gamma }_{i,k}=1\\ {\stackrel{⌣}{y}}_{i,k-1},{\gamma }_{i,k}=0\end{array}.(18)$

Based on the above analysis, we can get ${\stackrel{⌣}{y}}_{i,k-1}=y_{s_{k-1}^i}$. $y_{s_k}={\left[y_{1,s_k^1}^T,y_{2,s_k^2}^T,\cdots ,{\stackrel{⌣}{y}}_{m_1,s_k^{m_1}}^T\right]}^T$ is defined to the measurement transmitted under the event-triggered mechanism, and the matrix ${\varphi }_k=diag\left\{{\gamma }_{1,k}{I}_1,\dots ,{\gamma }_{i,k}{I}_i,\dots {\gamma }_{m_1,k}{I}_{m_1}\right\}$ is defined, where $I_i$ is an identity matrix. Then, the measurement received by the estimator at instant k can be expressed as

${\stackrel{⌣}{y}}_k={\varphi }_k{y}_k+\left(I-{\varphi }_k\right)y_{s_{k-1}}.(19)$

It is possible for the component-based event-triggered mechanism to make the measurement information transmitted in the communication network incomplete. Despite the “zero-order hold” strategy being used to update the measurement in the triggering detector, the non-triggering error would bring about serious effect on the estimation performance of the ADS. As such, it is necessary to design a suitable filter algorithm for reducing the impact of the non-triggering error. Fortunately, with the component-based event-triggered mechanism, the estimator can acquire some valuable information that will facilitate the effective design of the filter. On the one hand, the triggering sequence of the triggering generator is known. On the other hand, the non-triggering error would fall into a certain range.

Remark 3: In order to save network communication resources of the ADS, the component-based event-triggered mechanism is employed, with which the measurement transmission of each component is scheduled individually according to its own triggering condition. The component-based event-triggered mechanism pays attention on the individual change of each component of the system output, while the usual one focuses on the output vector. Considering that there are the characteristics of extremely different operating states between the busses, complex structure, and wide distribution in the ADS, the component-based event-triggered mechanism is more suitable for the ADS.

3.2 Event-Triggered UKF Algorithm

In order to ensure the state estimation performance of the ADS with DGs under the event-triggered mechanism, a filter is designed based on the framework of the UKF algorithm. First, the one-step prediction and filtering error covariances are calculated. Second, some parameters were adjusted by using some lemmas to find the upper bound of the covariance. Last, such an upper bound is minimized by designing an appropriate filter gain.

For the state model Eq. 1 and event-triggered measurement model Eq. 19, the filter is designed as follows:

${\widehat{x}}_{k|k-1}=F_{k-1}{\widehat{x}}_{k-1|k-1}+g_{k-1},(20)$

${\widehat{x}}_{k|k}={\widehat{x}}_{k|k-1}+K_k\left({\stackrel{⌣}{y}}_k-{\widehat{y}}_{k|k-1}\right),(21)$

where ${\widehat{x}}_{k-1|k-1}$ denotes the estimation of the state $x_{k-1}$, ${\widehat{x}}_{k|k-1}$ is the one-step state prediction at time instant k, $K_k$ is the filter gain to be deigned, and ${\widehat{y}}_{k|k-1}$ is the predicted value of the measurement. Then we define ${\tilde{e}}_{k|k-1}=x_k-{\widehat{x}}_{k|k-1}$ and ${\tilde{e}}_{k|k}=x_k-{\widehat{x}}_{k|k}$ that represent the one-step prediction and filtering error, respectively, and the corresponding covariance matrices are defined as $P_{k|k-1}=\mathbb{E}\left\{{\tilde{e}}_{k|k-1}{\tilde{e}}_{k|k-1}^T\right\}$ and $P_{k|k}=\mathbb{E}\left\{{\tilde{e}}_{k|k}{\tilde{e}}_{k|k}^T\right\}$.

Before proceeding, the following lemma is recalled, which will be used in later developments.

Lemma 1 (Cheng and Bai, 2021): For any two vectors $X,Y\in {\mathrm{ℝ}}^n$, the following inequality holds:

$X{Y}^T+Y{X}^T\le aX{X}^T+a^{-1}Y{Y}^T,(22)$

where a is a positive scalar.Combining Eqs 19, 21, we can get the state estimation at instant k:

${\widehat{x}}_{k|k}={\widehat{x}}_{k|k-1}+K_k\left(y_k-{\widehat{y}}_{k|k-1}\right)+K_k{\epsilon }_k,(23)$

where ${\epsilon }_k=\left(I-{\varphi }_k\right)\left(y_{s_{k-1}}-y_k\right)$ represents the non-triggered error. The estimation error at instant k can be expressed as

${\tilde{e}}_{k|k}={\tilde{e}}_{k|k-1}-K_k\left(y_k-{\widehat{y}}_{k|k-1}\right)-K_k{\epsilon }_k.(24)$

Then, covariance of the filtering error can be calculated as following:

$\begin{array}{c}{P}_{k|k}=\mathbb{E}\left\{{\tilde{e}}_{k|k}{\tilde{e}}_{k|k}^T\right\}\\ =\mathbb{E}\left\{{\tilde{e}}_{k|k-1}{\tilde{e}}_{k|k-1}^T\right\}\\ -\mathbb{E}\left\{{\tilde{e}}_{k|k-1}{\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}{K}_k^T-K_k\mathbb{E}\left\{\left(y_k-{\widehat{y}}_{k|k-1}\right){\tilde{e}}_{k|k-1}^T\right\}\\ +K_k\mathbb{E}\left\{\left(y_k-{\widehat{y}}_{k|k-1}\right){\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}{K}_k^T\\ -\mathbb{E}\left\{{\tilde{e}}_{k|k-1}{\epsilon }_k^T\right\}{K}_k^T-K_k\mathbb{E}\left\{{\epsilon }_k{\tilde{e}}_{k|k-1}^T\right\}\\ +K_k\mathbb{E}\left\{\left(y_k-{\widehat{y}}_{k|k-1}\right){\epsilon }_k^T\right\}{K}_k^T+K_k\mathbb{E}\left\{{\epsilon }_k{\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}{K}_k^T\\ +K_k\mathbb{E}\left\{{\epsilon }_k{\epsilon }_k^T\right\}{K}_k^T.\end{array}(25)$

Theorem 1: Consider the system described by Eqs 1, 19 with filter Eqs 20, 21 and define the following two Riccati-like different equations.

${\overline{P}}_{k|k-1}=F_{k-1}{\overline{P}}_{k-1|k-1}{F}_{k-1}+Q_{k-1},(26)$

$\begin{array}{c}{\overline{P}}_{k|k}={\mu }_{1,k}{\overline{P}}_{k|k-1}-\mathbb{E}\left\{{\tilde{e}}_{k|k-1}{\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}{K}_k^T\\ -K_k\mathbb{E}\left\{\left(y_k-{\widehat{y}}_{k|k-1}\right){\tilde{e}}_{k|k-1}^T\right\}+{\mu }_{2,k}{K}_k\mathbb{E}\left\{\left(y_k-{\widehat{y}}_{k|k-1}\right){\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}{K}_k^T\\ +{\mu }_{3,k}{K}_k\left({\displaystyle \sum }_{i\in N_{\gamma =0}}{\delta }_i^{2}I\right)K_k^T,\end{array}(27)$

where ${\mu }_{1,k}=1+a_{1,k}$, ${\mu }_{2,k}=1+a_{2,k}$, and ${\mu }_{3,k}=1+a_{1,k}^{-1}+a_{2,k}^{-1}$, $a_{1,k}$, and $a_{2,k}$ are positive scalar. If there exist positive-definite solutions ${\overline{P}}_{k|k-1}$ and ${\overline{P}}_{k|k}$ with initial conditions ${\overline{P}}_{0|0}=P_{0|0}$, the matrix ${\overline{P}}_{k|k}$ is the upper bound of covariance matrix $P_{k|k}$, namely, ${\overline{P}}_{k|k}\ge P_{k|k}$.

Proof: According to Lemma 1, the following inequalities are obtained:

$-\mathbb{E}\left\{{\tilde{e}}_{k|k-1}{\epsilon }_k^T\right\}{K}_k^T-K_k\mathbb{E}\left\{{\epsilon }_k{\tilde{e}}_{k|k-1}^T\right\}\le a_{1,k}{P}_{k|k-1}+a_{1,k}^{-1}{K}_k\mathbb{E}\left\{{\epsilon }_k{\epsilon }_k^T\right\}{K}_k^T,(28)$

$\begin{array}{ccccccccccccccccccccccccccccccc}{K}_k\mathbb{E}\left\{\left(y_k-{\widehat{y}}_{k|k-1}\right){\epsilon }_k^T\right\}{K}_k^T+K_k\mathbb{E}\left\{{\epsilon }_k{\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}{K}_k^T& & & & & & & & & & & & & & & & & & & & & & & & & & & & & & \\ \le a_{2,k}{K}_k\mathbb{E}\left\{\left(y_k-{\widehat{y}}_{k|k-1}\right){\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}{K}_k^T+a_{2,k}^{-1}{K}_k\mathbb{E}\left\{{\epsilon }_k{\epsilon }_k^T\right\}{K}_k^T.& & & & & & & & & & & & & & & & & & & & & & & & & & & & & & \end{array}(29)$

According to the event-triggered condition Eq. 17, we can obtained

${\epsilon }_k{\epsilon }_k^T\le {\epsilon }_k^T{\epsilon }_{k}I\le {\displaystyle \sum }_{i\in N_{\gamma =0}}{\delta }_i^{2}I,(30)$

where $N_{\gamma =0}$ represents a set of measurement devices that are not triggered by an event.Then

$-\mathbb{E}\left\{{\tilde{e}}_{k|k-1}{\epsilon }_k^T\right\}{K}_k^T-K_k\mathbb{E}\left\{{\epsilon }_k{\tilde{e}}_{k|k-1}^T\right\}\le a_{1,k}{P}_{k|k-1}+a_{1,k}^{-1}{K}_k\left({\displaystyle \sum }_{i\in N_{\gamma =0}}{\delta }_i^{2}I\right)K_k^T,(31)$

$\begin{array}{c}{K}_k\mathbb{E}\left\{\left(y_k-{\widehat{y}}_{k|k-1}\right){\epsilon }_k^T\right\}{K}_k^T+K_k\mathbb{E}\left\{{\epsilon }_k{\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}{K}_k^T\\ \le a_{2,k}{K}_k\mathbb{E}\left\{\left(y_k-{\widehat{y}}_{k|k-1}\right){\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}{K}_k^T+a_{2,k}^{-1}{K}_k\left({\displaystyle \sum }_{i\in N_{\gamma =0}}{\delta }_i^{2}I\right)K_k^T.\end{array}(32)$

This completes the proof.After that, the filter gain $K_k$ can be obtained by the ${\overline{P}}_{k|k}$.

$\begin{array}{c}\frac{\partial tr\left({\overline{P}}_{k|k}\right)}{\partial K_k}=-2\mathbb{E}\left\{{\tilde{e}}_{k|k-1}{\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}\\ +2{\mu }_{2,k}{K}_k\mathbb{E}\left\{\left(y_k-{\widehat{y}}_{k|k-1}\right){\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}\\ +2{\mu }_{3,k}{K}_k{\displaystyle \sum }_{i\in N_{\gamma =0}}{\delta }_i^{2}I.\end{array}(33)$

Let $\partial tr\left({\overline{P}}_{k|k}\right)/\partial K_k=0$, and through some algebraic operations, the filter gain can be obtained.

$K_k=P_{xy,k|k-1}{P}_{\delta ,k|k-1}^{-1},(34)$

subject to

$P_{\delta ,k|k-1}={\mu }_{2,k}{P}_{yy,k|k-1}+{\mu }_{3,k}{\displaystyle \sum }_{i\in N_{\gamma =0}}{\delta }_i^{2}I,(35)$

where $P_{yy,k|k-1}=\mathbb{E}\left\{\left(y_k-{\widehat{y}}_{k|k-1}\right){\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}$ and $P_{xy,k|k-1}=\mathbb{E}\left\{{\tilde{e}}_{k|k-1}{\left(y_k-{\widehat{y}}_{k|k-1}\right)}^T\right\}$ represent the predicted measurement covariance matrix and state-measurement cross-covariance matrix, respectively. Then the upper bound of the covariance matrix can be expressed as

${\overline{P}}_{k|k}={\mu }_{1,k}{\overline{P}}_{k|k-1}-K_k{P}_{\delta ,k|k-1}{K}_k.(36)$

Next, the UT technology is employed to calculate the prediction of measurement and predicted measurement covariance matrix and state-measurement cross-covariance matrix. Considering the high-dimensional nonlinearity of the ADS, in order to ensure the accuracy of the algorithm, while avoiding non-local effects and high-order term errors, in this study, the proportional symmetric sampling strategy is selected as the sigma point sampling strategy of the UT (Wang et al., 2019). The calculation method of the sigma points and its weight is as follows:

${\chi }_{j,k|k-1}=\{\begin{array}{l}{\widehat{x}}_{k|k-1},j=0\hfill \\ {\widehat{x}}_{k|k-1}+{\psi }_{j,k|k-1},j=1,\dots ,n\hfill \\ {\widehat{x}}_{k|k-1}-{\psi }_{j-n,k|k-1},j=n+1,\dots ,2n\hfill \end{array},(37)$

where ${\psi }_{j,k|k-1}={\left(\sqrt{\left(n+\lambda \right){\overline{P}}_{k|k-1}}\right)}_j$ represents the jth column of the square root of the positive definite matrix $\left(n+\lambda \right){\overline{P}}_{k|k-1}$. In order to obtain the prediction of measurement and covariance matrix, we define two set weighted coefficient ${\theta }_j^m$ and ${\theta }_j^{\text{c}}$ as follows:

$\{\begin{array}{l}{\theta }_j^{\text{m}}=\frac{\lambda }{n+\lambda },j=0\hfill \\ {\theta }_j^{\text{c}}=\frac{\lambda }{n+\lambda }+\left(1-a^2+\beta \right),j=0\hfill \\ {\theta }_j^{\text{m}}={\theta }_j^{\text{c}}=\frac{1}{2\left(n+\lambda \right)},j=\mathrm{1,2},\cdots ,2n\hfill \end{array},(38)$

where $\lambda ={\alpha }^2\left(n+\kappa \right)-n$. κ is used to capture the information of higher-order moments of a given probability distribution, and the value of κ is usually 0 or $3-n$. α is the scale correction factor to determine the distribution range of sigma points, and for the Gaussian distribution, commonly $\alpha \in [{10}^{-4},1]$. β is a parameter related to the prior distribution of the state vector, and for the Gaussian distribution, $\beta =2$ is optimal.The prediction of measurement and covariance matrix can be calculated as follows:

${\widehat{y}}_{j,k|k-1}=h\left({\chi }_{j,k|k-1}\right),j=\mathrm{0,1},\dots ,2n,(39)$

${\widehat{y}}_{k|k-1}={\displaystyle \sum }_{j=0}^{2n}{\theta }_j^m{\widehat{y}}_{j,k|k-1},(40)$

$P_{xy,k|k-1}={\displaystyle \sum }_{j=0}^{2n}{\theta }_j^c\left({\chi }_{j,k|k-1}-{\widehat{x}}_{k|k-1}\right){\left({\widehat{y}}_{j,k|k-1}-{\widehat{y}}_{k|k-1}\right)}^T,(41)$

$P_{yy,k|k-1}={\displaystyle \sum }_{j=0}^{2n}{\theta }_j^c\left({\widehat{y}}_{j,k|k-1}-{\widehat{y}}_{k|k-1}\right){\left({\widehat{y}}_{j,k|k-1}-{\widehat{y}}_{k|k-1}\right)}^T+R_k.(42)$

In order to show the proposed filtering algorithm more clearly, the ET-UKF algorithm is summarized as in Algorithm 1.

Algorithm 1ET-UKF Algorithm.

1: Initialization: select the initial values of ${\widehat{x}}_{0|0}$ and $P_{0|0}$, set $k=0$ and the maximum computation step $k_{max}$, and set $a_{\mathrm{1,0}}$, $a_{\mathrm{2,0}}$, and ${\delta }_i$.

2: At time k, compute the state prediction value ${\widehat{x}}_{k|k-1}$ and the upper bound of state prediction error covariance matrix ${\overline{P}}_{k|k-1}$ by Eqs 20, 26.

3: Compute $2n+1$ sigma points and weigh coefficients by using Eqs 37, 38. Then compute the prediction of measurement ${\widehat{y}}_{k|k-1}$ and the covariances $P_{xy,k|k-1}$ and $P_{yy,k|k-1}$ by using Eqs 39–42.

4: Calculate filter gain $K_k$ by using Eq. 34.

5: With the obtained $K_k$, compute ${\widehat{x}}_{k|k}$ and ${\overline{P}}_{k|k}$ by using Eqs 21, 36.

6: Set $k=k+1$, if $k>k_{max}$, exit. Otherwise, go to step 2.

Remark 4: In this study, for the purpose of saving network communication resources of the ADS, the component-based event-triggered transmission mechanism is adopted to reduce the unnecessary data transmission. However, this method makes it difficult to calculate the error covariance matrix recursively. To this issue, an alternative approach is proposed to introduce some adjustable parameters (e.g., $a_{1,k}$ and $a_{2,k}$) through some lemmas to obtain the upper bound of the covariance matrix. Next, the upper bound is minimized by designing appropriate filtering gain, and the minimized bound of the covariance matrix is closely related to the parameters. For this reason, with these parameters selected appropriately, the possible conservatism of the upper bound can be reduced. Fortunately, the research on optimization is a significantly active field of applied mathematics, which helps determine the optimal parameters.

4 Simulation Results and Analysis

4.1 Simulation Settings

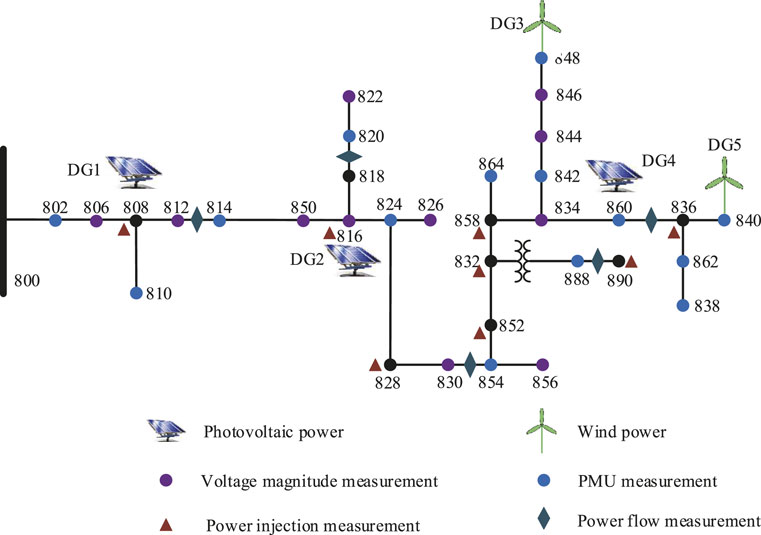
In this section, the IEEE-34 distribution test system is adopted to simulate and verify the effectiveness of the proposed state estimation algorithm. The topology structure and line parameters of the IEEE-34 distribution test system are originated from the study by Kersting (1991). The simulation is implemented in MATLAB R2019b. The dynamic variation of the ADS is simulated by changing the load dynamically. The law of load change is assumed to be $S_{L,k+1}=(1+0.1\text{rands}(\cdot ))S_{L,k}$, and $S_{L,0}$ represents the initial load provided in the study by Kersting (1991). The measuring devices consist of the DRTUs, the PMUs, and the DGs’ sensors. Figure 4 illustrates the installation positions of the measuring devices and DGs in the test system.

FIGURE 4

FIGURE 4. Configuration of measurement devices and DGs in the IEEE-34 distribution test system.

In the simulation, the parameters are set to $a_{1,k}=a_{2,k}=0.5$. The process noise parameter is expressed as $Q_k=4\times {10}^{-3}I$. In the Holt–Winters double exponential smoothing method, the parameters ${\alpha }_H$ and ${\beta }_H$ are selected as ${\alpha }_H=0.9$ and ${\beta }_H=0.1$. The initial value of the covariance matrix is set to $P_{0|0}=4\times {10}^{-6}I$. Moreover, in order to further evaluate the effectiveness of the proposed state estimation method under different scenarios, four measurement noise scenarios are set in the simulation, and their noise parameters are shown in Table 1.

TABLE 1

TABLE 1. Measurement noise in different scenarios.

4.2 Result Analysis

1) Verification of the proposed ADS system model.

In this section, the ET-UKF algorithm (${\delta }_i=0$) is applied for state estimation under different scenarios, so as to validate the system model proposed in this study. The estimation results will be compared between the model proposed and the conventional model where DGs are not modeled in detail. Figure 5 shows the root-mean-square error (RMSE) of state variables associated with the network obtained by the two models under different noise scenarios, where $\text{RMSE}\left(k\right)=\sqrt{\frac{1}{n}{\displaystyle \sum _{j=1}^n{\left({\tilde{e}}_{j,k|k}\right)}^2}}$. It can be found out that the estimated result produced by the proposed model is more accurate than the conventional model in all scenarios. To make the estimation results more intuitive, Figure 6 plots the state tracking curves of the a-phase voltage at the 816 bus. Figure 7 presents the state tracking curves of the DG2. Obviously, the proposed model can not only improve the accuracy of the state estimation but also expand the scope of state estimation, which is effective in monitoring the operation states of the IEEE-34 distribution test system and the DGs.

FIGURE 5

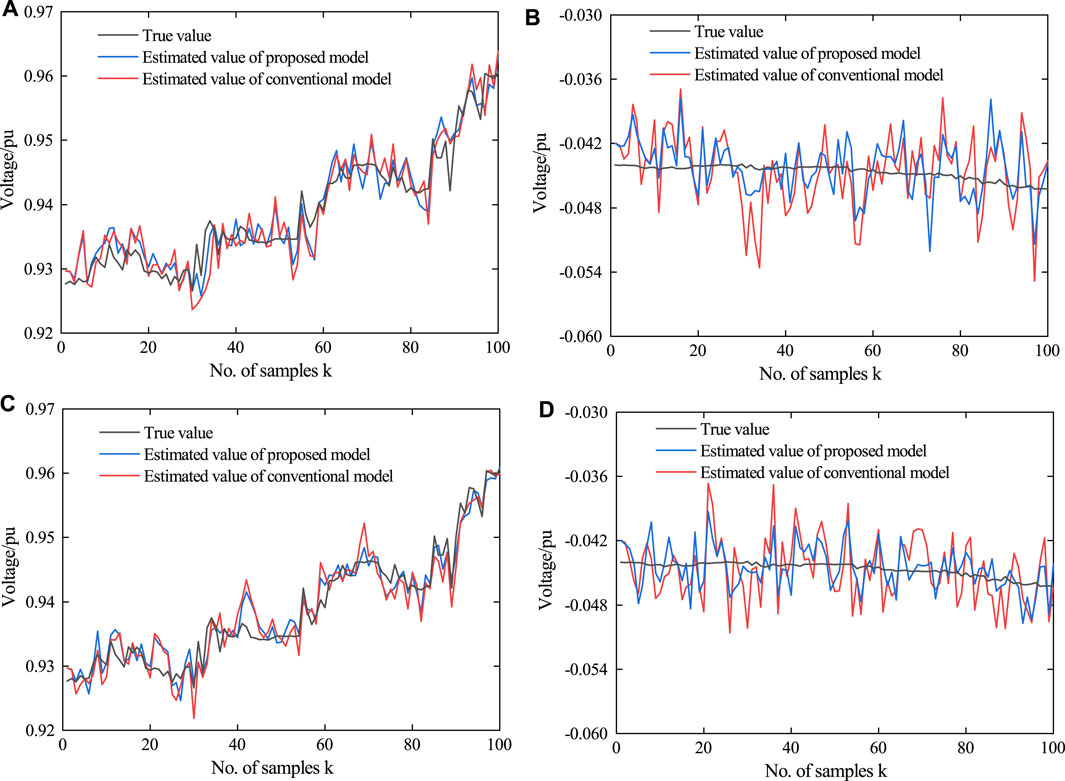
FIGURE 5. Actual state and its estimation of a-phase voltage at the 816 bus. (A) Real part of bus voltage in the case of Scenario 1, (B) imaginary part of bus voltage in the case of Scenario 1, (C) real part of bus voltage in the case of Scenario 2, and (D) imaginary part of bus voltage in the case of Scenario two.

FIGURE 6

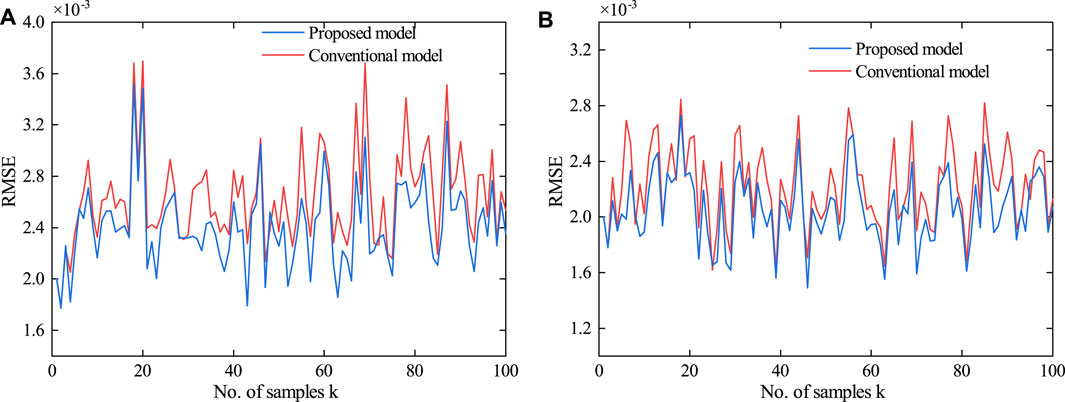
FIGURE 6. RMSE between the estimation and true values under the proposed and conventional models. (A) Scenario 1 and (B) Scenario 2.

FIGURE 7

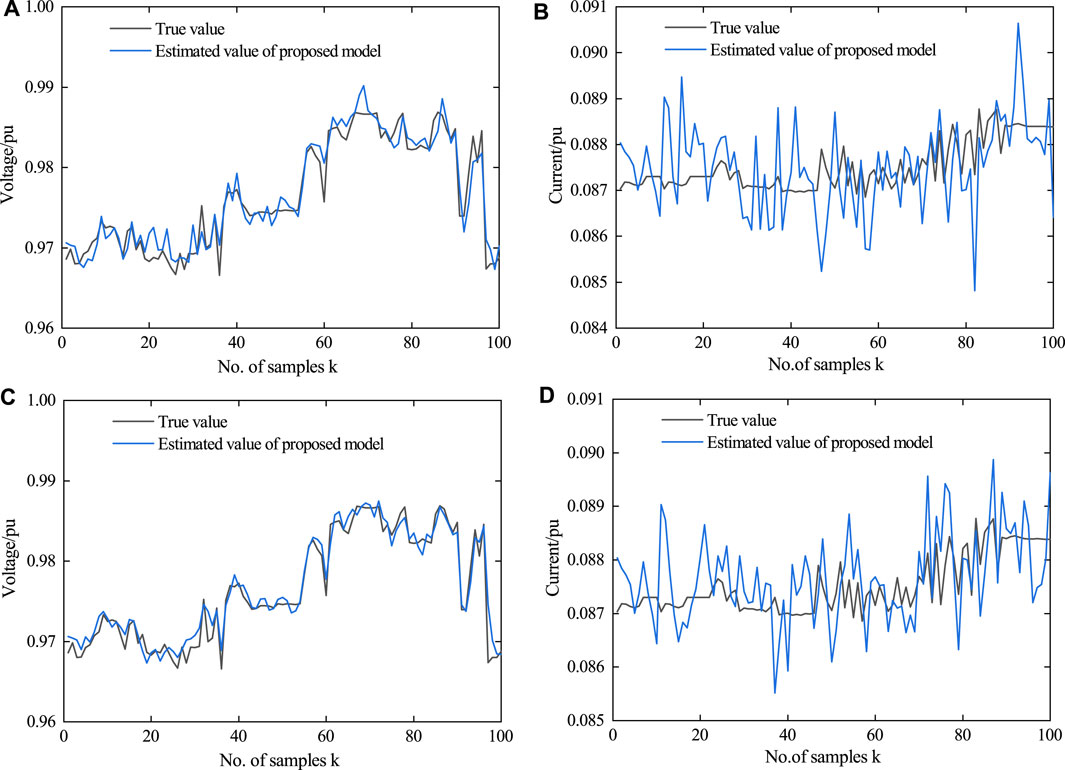
FIGURE 7. Actual state and its estimation of DG2. (A) Voltage output by the DG2 in the case of Scenario 1, (B) current output by the DG2 in the case of Scenario 1, (C) voltage output by the DG2 in the case of Scenario 2, and (D) current output by the DG2 in the case of Scenario 2

2) Verification of the ET-UKF algorithm.

In order to demonstrate the performance of the event-triggered mechanism, a data transmission ratio (DTR) is defined as a transmission performance index by $J_{drt}=\frac{1}{m{k}_{\text{max}}}{\displaystyle \sum _{j=1}^{j=m}{\displaystyle \sum _{k=1}^{k=k_{\text{max}}}{\gamma }_{j,k}\times 100\text{\%}}}$. In particular, to demonstrate the superior performance of the ET-UKF algorithm, simulation is performed with the event-triggered threshold ${\delta }_i=5\times {10}^{-3}$ under the two noise scenarios. In the case of scenarios 3 and 4, the DTRs are $J_{drt}=61.60\text{\%}$ and $J_{drt}=55.81\text{\%}$, respectively. Figure 8 shows the state tracking curves of the a-phase voltage at the 816 bus. From this figure, it can be seen that the ET-UKF algorithm is capable to track the changes in the system state in real time and make accurate estimates even if only a part of the measurement data is received, which is attributed to the non-triggering error getting well handled by the ET-UKF algorithm. In Figure 9, the RMSE of estimated results is compared between the ET-UKF algorithm and the ET-EKF algorithm. It is evident that the estimation accuracy of the ET-UKF algorithm is higher than that of the ET-EKF algorithm under any situation, which is because the UT technology is advantageous over the linearization method applied by the EKF algorithm.

FIGURE 8

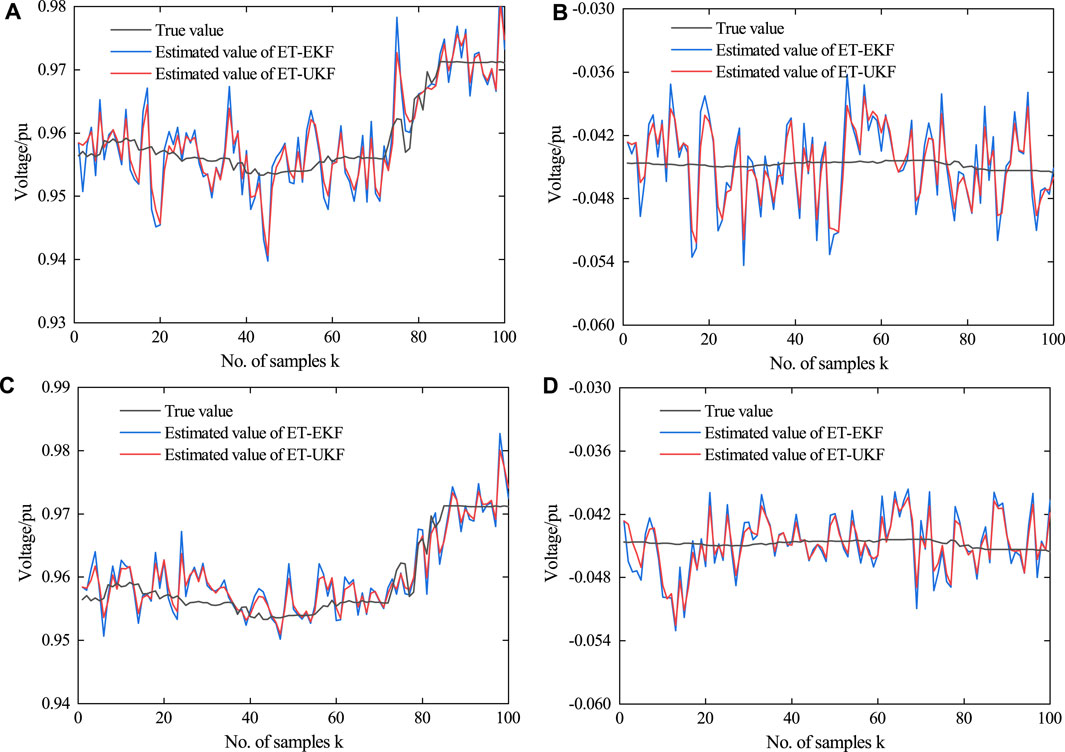
FIGURE 8. Actual state and its estimation of a-phase voltage at 864 bus. (A) Real part of bus voltage in the case of Scenario 3, (B) imaginary part of the bus voltage in the case of Scenario 3, (C) real part of bus voltage in the case of Scenario 4, and (D) imaginary part of bus voltage in the case of Scenario 4.

FIGURE 9

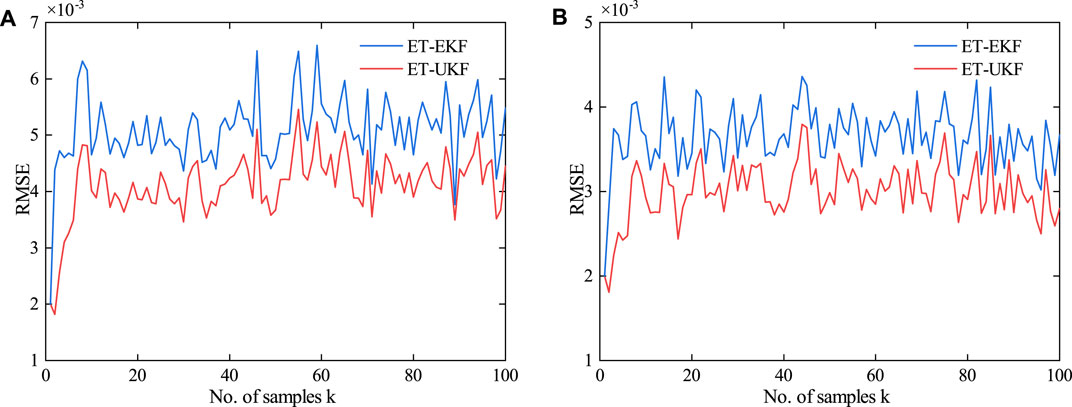
FIGURE 9. RMSE between the estimated and true values for ET-UKF and ET-EKF algorithms. (A) Scenario 3 and (B) Scenario 4.

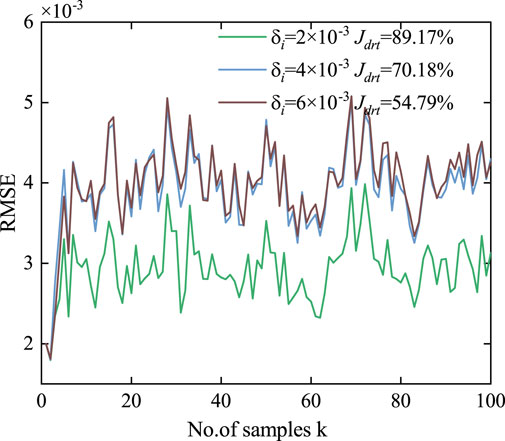
3) The impact from the different triggering thresholds on estimation performance.

In order to figure out the impact of various triggering thresholds on estimation performance, simulations are conducted with ${\delta }_i=2\times {10}^{-3}$, ${\delta }_i=4\times {10}^{-3}$, and ${\delta }_i=6\times {10}^{-3}$, respectively. Figure 10 shows the RMSE of estimation results and DTR with different triggering thresholds. In order to view the estimation results more intuitively, Figures 11, 12 show the state tracking curve and measuring device trigger sequence of the 814 bus c-phase with different event-triggering thresholds, respectively. It can be found out from these figures that the DTR decreases sharply with the increase in the triggering threshold, which is because the large triggering threshold prevented more measurement data from being transmitted to the remote estimation center, suggesting that the event-triggered mechanism contributes to reducing data transmission in the communication network and alleviating the communication pressure. With the increase in the threshold, however, the RMSE for the estimation results of the ET-UKF algorithm would also rise. Therefore, choosing an appropriate threshold in the practical ADS is effective in relieving the communication pressure and ensuring the performance of state estimation.

FIGURE 10

FIGURE 10. Variation of the RMSE and $J_{drt}$ with the trigger threshold (in the case of Scenario 3).

FIGURE 11

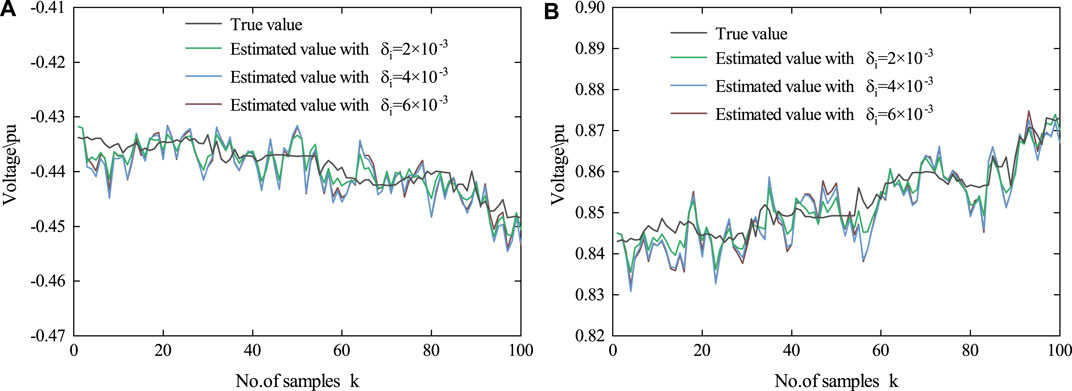
FIGURE 11. Actual state and its estimation of c-phase voltage at the 814 bus (in the case of Scenario 3). (A) Real part of bus voltage and (B) imaginary part of bus voltage.

FIGURE 12

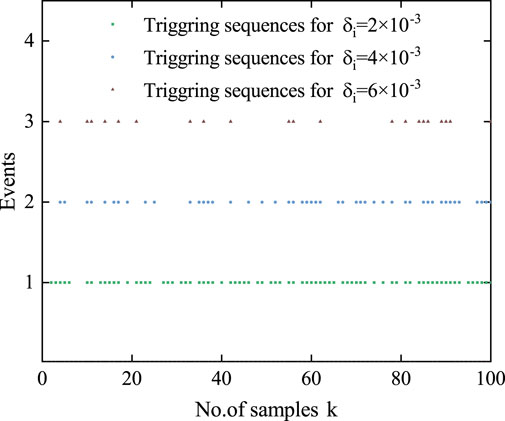
FIGURE 12. Triggering sequences of the measurement device installed at the 814 bus (in the case of Scenario 3).

5 Conclusion

In this study, a FASE method for the ADS with DGs has been developed under the condition of limited communication resources. First, the system model of the ADS has been built to improve the accuracy and extend the scope of state estimation. Moreover, in order to solve the network-induced phenomena attributed to considerable data transmission in ADS, the component-based event-triggered mechanism has been adopted to reduce the amount of data transmitted through communication network and save the communication resources. Besides, the ET-UKF algorithm has been designed to guarantee the estimation performance of the system. Finally, the effectiveness of the proposed method has been verified by the simulation. In view of the importance of the integrated energy system as a development trend in the energy field, the development of high-performance state estimation algorithms for the integrated energy system has become a top priority. Future study will consider the dynamic characteristics and time scales of different systems in the integrated energy system (Chen et al., 2020; Chen et al., 2021) and apply the algorithm proposed in this study to integrated energy systems.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

XB designed the component-based event-triggered mechanism. XZ designed the ET-UKF algorithm for the FASE of the ADSs. LG proposed the state space model of ADS with DGs. FQ and YL conducted the simulation verification.

Funding

This research was supported by the National Natural Science Foundation of China (Grant No. 51807134) and the Shandong Provincial Natural Science Foundation, China (Grant No. ZR2020MF071).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank the project team members of the National Natural Science Foundation of China and the Shandong Provincial Natural Science Foundation who encouraged this research.

References

Ćetenović, D. N., and Ranković, A. M. (2018). Optimal Parameterization of Kalman Filter Based Three-phase Dynamic State Estimator for Active Distribution Networks. Int. J. Electr. Power Energ. Syst. 101, 472–481. doi:10.1016/j.ijepes.2018.04.008

CrossRef Full Text | Google Scholar

Chen, S., Wei, Z., Sun, G., Lu, N., Sun, Y., and Zhu, Y. (2017a). Multi-area Distributed Three-phase State Estimation for Unbalanced Active Distribution Networks. J. Mod. Power Syst. Clean Energ. 5, 767–776. doi:10.1007/s40565-016-0237-0

CrossRef Full Text | Google Scholar

Chen, Y., Ma, J., Zhang, P., Liu, F., and Mei, S. (2017b). Robust State Estimator Based on Maximum Exponential Absolute Value. IEEE Trans. Smart Grid 8, 1537–1544. doi:10.1109/TSG.2015.2485280

CrossRef Full Text | Google Scholar

Chen, Y., Yao, Y., Lin, Y., and Yang, X. (2020). Dynamic State Estimation for Integrated Electricity-Gas Systems Based on Kalman Filter. CSEE J. Power Energ. Syst., 1–11. doi:10.17775/CSEEJPES.2020.02050

CrossRef Full Text | Google Scholar

Chen, Y., Yao, Y., and Zhang, Y. (2021). A Robust State Estimation Method Based on Socp for Integrated Electricity-Heat System. IEEE Trans. Smart Grid 12, 810–820. doi:10.1109/TSG.2020.3022563

CrossRef Full Text | Google Scholar

Cheng, C., and Bai, X. (2021). Robust Forecasting-Aided State Estimation in Power Distribution Systems with Event-Triggered Transmission and Reduced Mixed Measurements. IEEE Trans. Power Syst., 1. doi:10.1109/TPWRS.2021.3062386

CrossRef Full Text | Google Scholar

Cheng, C., Bai, X., Zhang, Q., and Huang, C. (2018). Set-membership Filtering for Generator Dynamic State Estimation with Delayed Measurements. Syst. Sci. Control. Eng. 6, 35–43. doi:10.1080/21642583.2018.1531794

CrossRef Full Text | Google Scholar

Dang, L., Chen, B., Wang, S., Ma, W., and Ren, P. (2020). Robust Power System State Estimation with Minimum Error Entropy Unscented Kalman Filter. IEEE Trans. Instrumentation Meas. 69, 8797–8808. doi:10.1109/TIM.2020.2999757

CrossRef Full Text | Google Scholar

Ding, F., Wang, X., Mao, L., and Xu, L. (2017). Joint State and Multi-Innovation Parameter Estimation for Time-Delay Linear Systems and its Convergence Based on the Kalman Filtering. Digital Signal. Process. 62, 211–223. doi:10.1016/j.dsp.2016.11.010

CrossRef Full Text | Google Scholar

Do Coutto Filho, M. B., and Stacchini de Souza, J. C. (2009). Forecasting-aided State Estimation––part i: Panorama. IEEE Trans. Power Syst. 24, 1667–1677. doi:10.1109/TPWRS.2009.2030295

CrossRef Full Text | Google Scholar

Dobakhshari, A. S., Abdolmaleki, M., Terzija, V., and Azizi, S. (2021). Robust hybrid linear state estimator utilizing scada and pmu measurements. IEEE Trans. Power Syst. 36, 1264–1273. doi:10.1109/TPWRS.2020.3013677

CrossRef Full Text | Google Scholar

Ehsan, A., and Yang, Q. (2018). Optimal integration and planning of renewable distributed generation in the power distribution networks: A review of analytical techniques. Appl. Energ. 210, 44–59. doi:10.1016/j.apenergy.2017.10.106

CrossRef Full Text | Google Scholar

Fang, Z., Lin, Y., Song, S., Song, C., Lin, X., and Cheng, G. (2020). Active distribution system state estimation incorporating photovoltaic generation system model. Electric Power Syst. Res. 182, 106247. doi:10.1016/j.epsr.2020.106247

CrossRef Full Text | Google Scholar

Ge, L., Li, Y., Li, S., Zhu, J., and Yan, J. (2021a). Evaluation of the situational awareness effects for smart distribution networks under the novel design of indicator framework and hybrid weighting method. Front. Energ. 15, 143–158. doi:10.1007/s11708-020-0703-2

CrossRef Full Text | Google Scholar

Ge, L., Song, Z., Xu, X., Bai, X., and Yan, J. (2021b). Dynamic networking of islanded regional multi-microgrid networks based on graph theory and multi-objective evolutionary optimization. Int. Trans. Electr. Energ. Syst. 35, e12687. doi:10.1002/2050-7038.12687

CrossRef Full Text | Google Scholar

Ge, L., Xian, Y., Yan, J., Wang, B., and Wang, Z. (2020a). A hybrid model for short-term pv output forecasting based on pca-gwo-grnn. J. Mod. Power Syst. Clean Energ. 8, 1268–1275. doi:10.35833/MPCE.2020.000004

CrossRef Full Text | Google Scholar

Ge, L., Zhang, S., Bai, X., Yan, J., Shi, C., and Wei, T. (2020b). Optimal capacity allocation of energy storage system considering uncertainty of load and wind generation. Math. Probl. Eng. 2020, 2609674. doi:10.1155/2020/2609674

CrossRef Full Text | Google Scholar

Geetha, S. J., Chakrabarti, S., and Rajawat, K. (2021). Asynchronous hierarchical forecasting-aided state estimator with sub-area data validation for power systems. IEEE Sensors J. 21, 2124–2133. doi:10.1109/JSEN.2020.3017920

CrossRef Full Text | Google Scholar

Kersting, W. (1991). Radial distribution test feeders. IEEE Trans. Power Syst. 6, 975–985. doi:10.1109/59.119237

CrossRef Full Text | Google Scholar

Kooshkbaghi, M., Marquez, H. J., and Xu, W. (2020). Event-triggered approach to dynamic state estimation of a synchronous machine using cubature kalman filter. IEEE Trans. Control. Syst. Tech. 28, 2013–2020. doi:10.1109/TCST.2019.2923374

CrossRef Full Text | Google Scholar

Li, S., Li, L., Li, Z., Chen, X., Fernando, T., Iu, H. H.-C., et al. (2019). Event-trigger heterogeneous nonlinear filter for wide-area measurement systems in power grid. IEEE Trans. Smart Grid 10, 2752–2764. doi:10.1109/TSG.2018.2810224

CrossRef Full Text | Google Scholar

Li, Y., Wang, C., and Li, G. (2020). A mini-review on high-penetration renewable integration into a smarter grid. Front. Energ. Res. 8, 84. doi:10.3389/fenrg.2020.00084

CrossRef Full Text | Google Scholar

Liu, X., Li, L., Li, Z., Chen, X., Fernando, T., Iu, H. H.-C., et al. (2018). Event-trigger particle filter for smart grids with limited communication bandwidth infrastructure. IEEE Trans. Smart Grid 9, 6918–6928. doi:10.1109/TSG.2017.2728687

CrossRef Full Text | Google Scholar

Luo, F., Yang, X., Wei, W., Zhang, T., Yao, L., Zhu, L., et al. (2020). Bi-level load peak shifting and valley filling dispatch model of distribution systems with virtual power plants. Front. Energ. Res. 8, 305. doi:10.3389/fenrg.2020.596817

CrossRef Full Text | Google Scholar

Macii, D., Fontanelli, D., and Barchi, G. (2020). A distribution system state estimator based on an extended kalman filter enhanced with a prior evaluation of power injections at unmonitored buses. Energies 13, 6054. doi:10.3390/en13226054

CrossRef Full Text | Google Scholar

Martin, K. E., Hamai, D., Adamiak, M. G., Anderson, S., Begovic, M., Benmouyal, G., et al. (2008). Exploring the ieee standard c37.118–2005 synchrophasors for power systems. IEEE Trans. Power Deliv. 23, 1805–1811. doi:10.1109/TPWRD.2007.916092

CrossRef Full Text | Google Scholar

Shanmugam, L., Mani, P., and Joo, Y. H. (2020). Stabilisation of event-triggered-based neural network control system and its application to wind power generation systems. IET Control. Theor. Appl. 14, 1321–1333. doi:10.1049/iet-cta.2019.0246

CrossRef Full Text | Google Scholar

Sun, Y., Wang, Y., Wu, X., and Hu, Y. (2018). Robust extended fractional kalman filter for nonlinear fractional system with missing measurements. J. Franklin Inst. 355, 361–380. doi:10.1016/j.jfranklin.2017.10.030

CrossRef Full Text | Google Scholar

Sun, Y., Wu, X., Cao, J., Wei, Z., and Sun, G. (2017). Fractional extended kalman filtering for non-linear fractional system with lévy noises. IET Control. Theor. Appl. 11, 349–358. doi:10.1049/iet-cta.2016.1041

CrossRef Full Text | Google Scholar

Wang, S., Lyu, Y., and Ren, W. (2019). Unscented-transformation-based distributed nonlinear state estimation: Algorithm, analysis, and experiments. IEEE Trans. Control. Syst. Tech. 27, 2016–2029. doi:10.1109/TCST.2018.2847290

CrossRef Full Text | Google Scholar

Wang, Y., Sun, Y., and Dinavahi, V. (2020). Robust forecasting-aided state estimation for power system against uncertainties. IEEE Trans. Power Syst. 35, 691–702. doi:10.1109/TPWRS.2019.2936141

CrossRef Full Text | Google Scholar

Xing, Z., Xia, Y., Yan, L., Lu, K., and Gong, Q. (2018). Multisensor distributed weighted kalman filter fusion with network delays, stochastic uncertainties, autocorrelated, and cross-correlated noises. IEEE Trans. Syst. Man, Cybernetics: Syst. 48, 716–726. doi:10.1109/TSMC.2016.2633283

CrossRef Full Text | Google Scholar

Yang, Q., Jiang, L., Ehsan, A., Gao, Y., and Guo, S. (2018). Robust power supply restoration for self-healing active distribution networks considering the availability of distributed generation. Energies 11, 210. doi:10.3390/en11010210

CrossRef Full Text | Google Scholar

Yang, Q., Jiang, L., Hao, W., Zhou, B., Yang, P., and Lv, Z. (2017). Pmu placement in electric transmission networks for reliable state estimation against false data injection attacks. IEEE Internet Things J. 4, 1978–1986. doi:10.1109/JIOT.2017.2769134

CrossRef Full Text | Google Scholar

Zhang, Y., Wang, J., and Li, Z. (2020). Interval state estimation with uncertainty of distributed generation and line parameters in unbalanced distribution systems. IEEE Trans. Power Syst. 35, 762–772. doi:10.1109/TPWRS.2019.2926445

CrossRef Full Text | Google Scholar

Zhao, J., Gómez-Expósito, A., Netto, M., Mili, L., Abur, A., Terzija, V., et al. (2019). Power system dynamic state estimation: Motivations, definitions, methodologies, and future work. IEEE Trans. Power Syst. 34, 3188–3198. doi:10.1109/TPWRS.2019.2894769

CrossRef Full Text | Google Scholar

Zhao, J., and Mili, L. (2019). A theoretical framework of robust h-infinity unscented kalman filter and its application to power system dynamic state estimation. IEEE Trans. Signal Process. 67, 2734–2746. doi:10.1109/TSP.2019.2908910

CrossRef Full Text | Google Scholar

Zhu, C., Su, Z., Xia, Y., Li, L., and Dai, J. (2020). Event-triggered state estimation for networked systems with correlated noises and packet losses. ISA Trans. 104, 36–43. doi:10.1016/j.isatra.2019.11.038

PubMed Abstract | CrossRef Full Text | Google Scholar