
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res., 11 February 2021
Sec. Electrochemical Energy Storage
Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.606313
This article is part of the Research TopicMaterial and Composition Screening Approaches in Electrocatalysis and Battery ResearchView all 11 articles
The oxygen evolution reaction (OER) plays a key role in the determination of overall water-splitting rate. Lowering the high overpotential of the OER of transition metal oxides (TMOs), which are used as conventional OER electrocatalysts, has been the focus of many studies. The OER activity of TMOs can be tuned via the strategic formation of a heterostructure with another TMO substrate. We screened 11 rutile-type TMOs (i.e., MO2; M = V, Cr, Mn, Nb, Ru, Rh, Sn, Ta, Os, Ir, and Pt) on a rutile (110) substrate using density functional theory calculations to determine their OER activities. The conventional volcano approach based on simple binding energies of reaction intermediates was implemented; in addition, the electrochemical-step symmetry index was employed to screen heterostructures for use as electrode materials. The results show that RuO2 and IrO2 are the most promising catalysts among all candidates. The scaling results provide insights into the intrinsic properties of the heterostructure as well as materials that can be used to lower the overpotential of the OER.
Green hydrogen production remains a challenge that must be overcome to achieve a hydrogen economy (Turner, 2004). Water electrolysis is one of the approaches toward hydrogen eco-friendliness. It is based on the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER) as cathodic and anodic reactions, respectively. However, the slow kinetics of the OER limit the commercialization of this approach. Oxide systems based on Ir or Ru (i.e., IrOx or RuOx) are known to have the best OER performances (Lee et al., 2012; Frydendal et al., 2014; Suen et al., 2017). However, these materials are expensive. Therefore, many studies have been conducted to identify a cost-effective alternative oxide material with high activity. For example, transition-metal substitution (García-Mota et al., 2011) and the introduction of oxygen vacancies (Xiao et al., 2020) have been studied as means to control the compositions of expensive materials. However, transition-metal substitution and oxygen vacancies only locally affect the active sites.
To activate the metal oxide, support materials are mixed with the oxide to enhance the electrical conductivity and activity of the electrocatalytic reaction (Kumar et al., 2016; Qingxiang et al., 2018; Bu et al., 2019; Lu et al., 2019). In addition, research on heterostructures is conducted with the goal of activating the material on the substrate. Modifications are mainly based on the strain effect and charge transfer due to the formation of an interface between the support material and catalyst. For instance, the heterostructure of La0.5Sr0.5CoO3-δ and MoSe2 induces the phase transition of MoSe2 from the 2H to the 1T phase (Oh et al., 2019). In addition, the charge transfer from the Co ion to Mo ion improves the electrochemical activity. The results of another study showed that the heterostructure of IrOx and SrIrO3 outperforms iridium or ruthenium oxide systems (Seitz et al., 2016). Based on density functional theory (DFT) calculations, IrO3 or anatase IrO2 motifs are formed during strontium leaching in the outermost surface layers of SrIrO3 and contribute to the high activity. Another strength of the heterostructure is that it can possibly contribute to reducing the use of precious metals by replacing them into low-cost metals while maintaining similar intrinsic activity of each active site (Esposito et al., 2010; Zhou et al., 2014; Wang et al., 2015; Jin et al., 2016). Rutile (TiO2) is a well-known substrate material for metal oxide systems because of its high structural stability and simple structure (Hanaor et al., 2012). It is suitable for the growth of oxide films, facilitating the fabrication of heterostructures with various metal oxides. In addition, rutile affects the catalytic activity of metal oxides and has a high cost effectiveness (Seitsonen and Over, 2010; Stacchiola et al., 2013; Wei et al., 2015; Sun et al., 2016; Li et al., 2017). However, the effect of the rutile support on the activity remains unclear due to difficulties with respect to the characterization of the heterostructure during experiments (Stacchiola et al., 2013).
In this study, we performed DFT calculations to theoretically investigate the effect of the TiO2 substrate on the heterostructure and thus on the OER. We screened the OERs of heterostructures consisting of various rutile-type metal oxides (i.e., VO2, CrO2, MnO2, NbO2, RuO2, RhO2, SnO2, TaO2, OsO2, IrO2, and PtO2) and a TiO2 substrate. The results show that these rutile heterostructures follow the universal scaling relations of metals and oxides; however, the binding strengths of the O* intermediates increase due to the TiO2 substrate. The volcano plot and electrochemical-step symmetry index (ESSI) show that the RuO2 and IrO2 are the closest to an ideal catalyst. The results of our computational screening provide insights into the effects of support materials on electrocatalytic reactions.
Spin-polarized DFT calculations were performed with the projector-augmented wave (PAW) method (Blochl, 1994) and Vienna Ab initio Simulation Package (VASP) (Kresse and Furthmiiller, 1996). The electron exchange–correlation energy was treated within the generalized gradient approximation (GGA) and the Perdew–Burke–Ernzerhof functional (Perdew et al., 1997). To determine the trend of the OER activity, the DFT + U method within Liechtenstein’s approach (Anisimovdag et al., 1997) was used and the following correction parameters were employed: U = 4.95 eV for Ti, 2 eV for V, 7.15 eV for Cr, 6.63 eV for Mn, 3.32 eV for Nb, 6.73 eV for Ru, 5.97 eV for Rh, 5.91 eV for Ir, and 6.25 eV for Pt (Xu et al., 2015). The energy cutoff for the plane wave basis set was set at 520 eV. The geometry was optimized using the residual minimization method and the direct inversion in the iterative subspace method (RMM–DIIS) algorithm until the net force on each atom was below 0.02 eV·Å−1, and the total energy was 10–6 eV per atom. Dipole slab corrections were also applied to all slab model calculations. The k-point sampling of the Brillouin zone was done with a 4 × 4 × 1 for bulk calculations and 6 × 6 × 8 for slab calculations.
To theoretically investigate the OER activities of rutile-type heterostructures, we considered the heterostructures of 11 rutile-type oxides (i.e., MO2, where M = V, Cr, Mn, Nb, Ru, Rh, Sn, Ta, Os, Ir, and Pt) with a TiO2 substrate. To accurately illustrate the OER activity, the following magnetic structures were used for all calculations according to Xu et al.’s work: nonmagnetic (NM) for TiO2, NbO2, RuO2, RhO2, IrO2, and PtO2, and ferromagnetic (FM) for CrO2 and MnO2 (Xu et al., 2015). Furthermore, the ground state magnetic configurations of the other candidate models were identified as FM for VO2 and NM for SnO2, TaO2, and OsO2, respectively (Supplementary Figure S1). Surface models, that is, six-layer stoichiometric slabs, were built by using the 2 × 1 supercell of the optimized unit cell. The vacuum of ∼15 Å was applied in the (110) direction, which is the most stable facet of rutile-type oxides (Figure 1A; Kung, 1989). Note that a tri-layer consisting of oxygen–metal–oxygen (O–M–O) atomic layers was considered to be a single layer in our slab models. The top four layers of the slab models were allowed to fully relax. The two layers at the bottom were fixed to represent the bulk state. For heterostructures, the top three layers of the TiO2 slab model were replaced with MO2 layers while maintaining the cell dimensions of the TiO2 substrate. The coordinatively unsaturated sites (CUS) of the metal atoms at the top surface were considered to be the adsorption sites for each intermediate (i.e., OH*, O*, and OOH*) for the OER. To examine the oxygen coverage effect on the OER activity, the pristine and fully O* covered surfaces were representatively compared (i.e., denoted as 2Ob and 2Ob 2Oc, where the subscripts “b” and “c” represent the bridge sites and CUS, respectively).
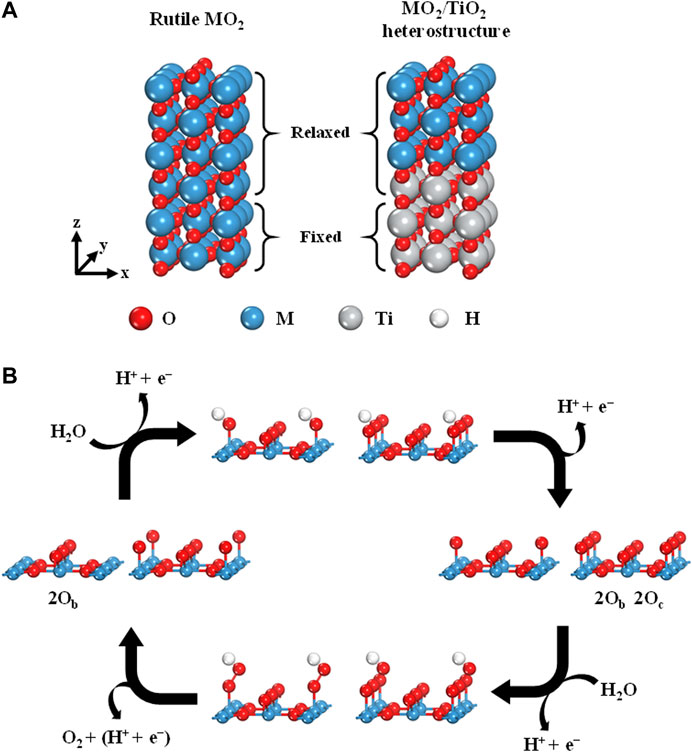
FIGURE 1. (A) Six-layered (110) surface of rutile-type MO2(left) and MO2/TiO2 heterostructure (right). (B) OER scheme of four elementary reaction steps on the rutile-type (110) surface with 2Ob and 2Ob 2Oc.
The overall OER process consists of four elementary steps involving proton-coupled electron transfer (PCET; Figure 1B) (Hammes-Schiffer, 2015; Costentin and Savéant, 2017). In this study, we followed the conventional four-electron pathways with respect to the OER of rutile heterostructures, which can be described as follows:
The adsorption free energy was calculated using the following equation:
where
where
Finally, the theoretical overpotential of the OER
where
We examined the scaling relations between the adsorption free energies of the reaction intermediates (i.e., OH*, O*, and OOH*; Supplementary Table S2) for all rutile-type catalysts of interest (Figure 2A). The binding energies of OOH* and OH* are linearly correlated, with an offset of 3.20 eV. Note that our scaling trend is similar to the “universal” scaling relation reported by Man et al. [i.e., ΔEOOH* = ΔEOH* + 3.20 (±0.20 eV)] (Man et al., 2011), implying that all rutile-type systems, including heterostructures, follow the conventional scaling relations for metals and oxide surfaces. Based on the best fit, 68% of the points are within ±0.35 eV (1σ) and 95% are within ±0.70 eV (2σ). The scaling relationship between ΔEO* and ΔEOH* exhibits a slope of 1.39 (blue solid line), that is, it is much less steep than the slope of two (blue dashed line), which is the indicator line of the double bonding nature of O* (Rossmeisl et al., 2007).
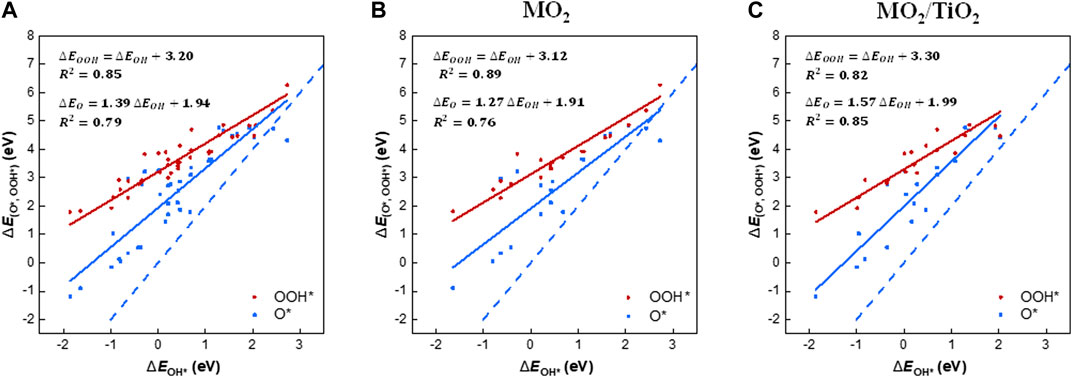
FIGURE 2. Scaling relations of the binding energies of the OER intermediates (i.e., OH*, O*, and OOH*) with the binding energy of OH*, which is the first intermediate for the OER. The diagrams contain the binding energies on the (110) surface of (A) all rutile-type oxides in this study, (B) MO2, and (C) MO2/TiO2 heterostructures, respectively. The solid lines are the linear trends of the binding energies of OOH* (red) and O* (blue) with respect to the binding energy of OH*. The blue dashed line in all diagrams is the guideline of the O* intermediate, which indicates the double bonding nature on the surface, with a slope of 2.
To analyze the substrate effect of TiO2 on the heterostructures, we divided the scaling relations into two groups, that is, (110) surfaces of MO2 and MO2/TiO2 heterostructures (Figure 2B,C). Notably, the binding energies of OOH* and O* on the MO2/TiO2 (110) surface are more concentrated than those of MO2. The scaling relation between OOH* and OH* of MO2/TiO2 (red solid line) shows an increased intercept by 0.18 compared with the corresponding scaling relation of MO2, implying slightly weakened interactions between OOH* and the surface. Note that the scaling relations between the binding strengths of O* and OH* species on MO2 and MO2/TiO2 (blue solid lines) apparently differ. The slopes of MO2/TiO2 (110) heterostructures are closer to 2 (i.e., double bonding nature of O*) than those of MO2 (110) surfaces (Rossmeisl et al., 2007). This is due to the intensified binding strengths of O* intermediates in heterostructures compared with MO2 surfaces (Divanis et al., 2020). This indicates that the TiO2 substrate generally stabilizes the O* intermediates, which might lead to a decrease in
Based on the scaling relations between the binding energies of the reaction intermediates, a volcano plot was constructed, as shown in Figure 3A. We chose
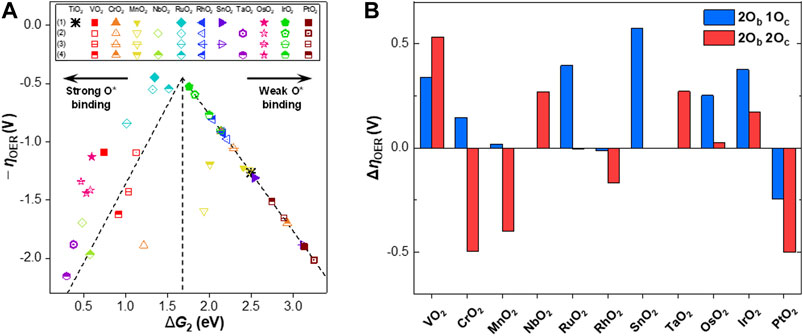
FIGURE 3. (A) Volcano plot for the negative overpotential of the OER
Similar to the previous studies (Rossmeisl et al., 2007; Man et al., 2011), RuO2 and IrO2 were both identified as the active OER catalysts among the MO2 candidates (i.e.,
The changes in
To determine the promising free-energy regime for the OER, we further analyzed the free energies of the steps in terms of the ESSI, as suggested by Calle-Vallejo and coworkers (Govindarajan et al., 2018). The ESSI is an energetic descriptor that indicates the degree of similarity with an ideal catalyst, where all OER steps are perfectly symmetric at 1.23 eV. The ESSI is defined by the following equation and is only applied to steps with
Figure 4A shows
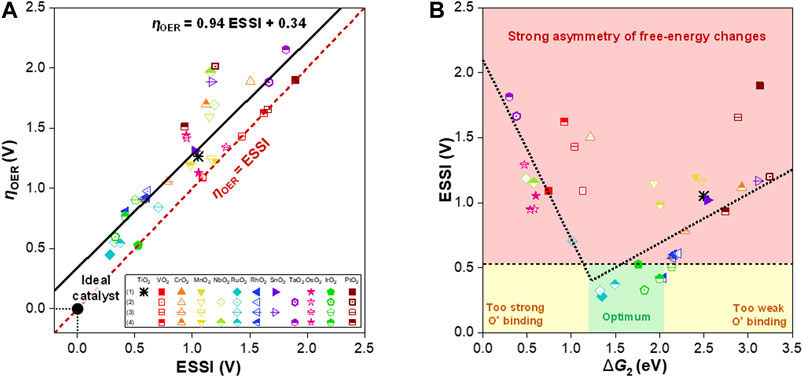
FIGURE 4. (A)
Based on the scaling relation between the ESSIs and
We screened a variety of rutile oxide heterostructures based on a TiO2 substrate using scaling relations and relevant descriptors to identify a promising OER catalyst. The scaling relations between the reaction intermediates demonstrate that the rutile-type MO2 heterostructures follow the universal scaling relationship of metal oxides. In addition, the TiO2 substrate stabilizes the O* bond on the (110) metal oxide surface. Based on the conventional volcano plot, RuO2 and IrO2 are found to be highly active OER catalysts as previously reported. Based on the ESSI descriptor, the superior activity of the RuO2 can be attributed to the high symmetry of the reaction steps. Furthermore, based on the ESSI-ΔG2 activity map, the candidates can be classified into an optimum group, a second promising group of OER catalysts with potential for optimization, and an inferior group that does not require particular attention.
The results of our computational screening using the scaling relations of rutile-type heterostructures provide valuable insights into the effect of the support material on the overpotential and thus guidelines for the design of a promising OER catalyst.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
All calculations and data analyses were performed by HYL. All authors contributed to the discussion of the results and wrote and revised the manuscript. SKK and GYJ supervised the project.
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (Ministry of Science and ICT) (NRF-2019M1A2A2065614) and the Global PhD Fellowship Program (NRF-2019H1A2A1076827 and NRF-2016H1A2A1908137). SKK acknowledges the UNIST grant (2.200487.01) for the support of the publication. Computational resources were provided by UNIST High Performance Computing (HPC) systems and Korea Institute of Science and Technology Information (KISTI) (KSC-2019-CRE-0255).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.606313/full#supplementary-material.
Anisimovdag, V. I., Aryasetiawan, F., and Lichtenstein, A. I. (1997). First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA + U method. J. Phys. Condens. Matter 9, 767–808. doi:10.1088/0953-8984/9/4/002
Blochl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953. doi:10.1103/PhysRevB.50.17953
Bu, Y., Jang, H., Gwon, O., Kim, S. H., Joo, S. H., Nam, G., et al. (2019). Synergistic interaction of perovskite oxides and N-doped graphene in versatile electrocatalyst. J. Mater. Chem. A 7 (5), 2048–2054. doi:10.1039/c8ta09919g
Costentin, C., and Savéant, J.-M. (2017). Theoretical and mechanistic aspects of proton-coupled electron transfer in electrochemistry. Curr. Opin. Electrochem. 1, 104–109. doi:10.1016/j.coelec.2016.11.001
Divanis, S., Kutlusoy, T., Boye, I. M. I., Man, I. C., and Rossmeisl, J. (2020). Oxygen evolution reaction: a perspective on a decade of atomic scale simulations. Chem. Sci. 11, 2943. doi:10.1039/c9sc05897d
Esposito, D. V., Hunt, S. T., Stottlemyer, A. L., Dobson, K. D., McCandless, B. E., Birkmire, R. W., et al. (2010). Low-cost hydrogen-evolution catalysts based on monolayer platinum on tungsten monocarbide substrates. Angew. Chem. Int. Ed. 49, 9859–9862. doi:10.1002/anie.201004718
Exner, K. S. (2019). Design criteria for oxygen evolution electrocatalysts from first principles: introduction of a unifying material-screening approach. ACS Appl. Energy Mater. 2, 11. doi:10.1021/acsaem.9b01480
Exner, K. S., and Over, H. (2019). Beyond the rate-determining step in the oxygen evolution reaction over a single-crystalline IrO2 (110) model electrode: kinetic scaling relations. ACS Catal. 9, 6755–6765. doi:10.1021/acscatal.9b01564
Frydendal, R., Paoli, E. A., Knudsen, B. P., Wickman, B., Malacrida, P., Stephens, I. E. L., et al. (2014). Benchmarking the stability of oxygen evolution reaction catalysts: the importance of monitoring mass losses. ChemElectroChem. 1, 2075–2081. doi:10.1002/celc.201402262
García‐Mota, M., Vojvodic, A., Metiu, H., Man, I. C., Su, H.‐Y., Rossmeisl, J., et al. (2011). Tailoring the activity for oxygen evolution electrocatalysis on rutile TiO2(110) by transition-metal substitution. ChemCatChem. 3, 1607–1611. doi:10.1002/cctc.201100160
Govindarajan, N., Garcia-Lastra, J. M., Meijer, E. A., and Calle-Vallejo, F. (2018). Does the breaking of adsorption-energy scaling relations guarantee enhanced electrocatalysis? Curr. Opin. Electrochem. 8, 110–117. doi:10.1016/j.coelec.2018.03.025
Govindarajan, N., Koper, M. T. M., Meijer, E. J., and Calle-Vallejo, F. (2019). Outlining the scaling-based and scaling-free optimization of electrocatalysts. ACS Catal. 9, 4218–4225. doi:10.1021/acscatal.9b00532
Hammes-Schiffer, S. (2015). Proton-coupled electron transfer: moving together and charging forward. J. Am. Chem. Soc. 137, 8860–8871. doi:10.1021/jacs.5b04087
Hanaor, D. A. H., Xu, W., Ferry, M., and Sorrell, C. C. (2012). Abnormal grain growth of rutile TiO2 induced by ZrSiO4. J. Cryst. Growth 359, 83–91. doi:10.1016/j.jcrysgro.2012.08.015
Jin, B., Zhou, X., Huang, L., Licklederer, M., Yang, M., and Schmuki, P. (2016). Aligned MoOx/MoS2 core–shell nanotubular structures with a high density of reactive sites based on self-ordered anodic molybdenum oxide nanotubes. Angew. Chem., Int. Ed. Engl. 55, 12252. doi:10.1002/anie.201605551
Kresse, G., and Furthmiiller, J. (1996). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0
Krishnamurthy, D., Sumaria, V., and Viswanathan, V. (2018). Maximal predictability approach for identifying the right descriptors for electrocatalytic reactions. J. Phys. Chem. Lett. 9, 588–595. doi:10.1021/acs.jpclett.7b02895
Kumar, K., Canaff, C., Rousseau, J., Arrii-Clacens, S., Napporn, T. W., Habrioux, A., et al. (2016). Effect of the oxide−carbon heterointerface on the Activity of Co3O4/NRGO nanocomposites toward ORR and OER. J. Phys. Chem. C 120 (15), 7949–7958. doi:10.1021/acs.jpcc.6b00313
Kung, H. H. (1989). Transition metal oxides: surface chemistry and catalysis. Amsterdam: Elsevier Science.
Kuo, D. Y., Kawasaki, J. K., Nelson, J. N., Kloppenburg, J., Hautier, G., Shen, K. M., et al. (2017). Influence of surface adsorption on the oxygen evolution reaction on IrO2(110). J. Am. Chem. Soc. 139, 3473–3479. doi:10.1021/jacs.6b11932
Kuo, D. Y., Paik, H., Kloppenburg, J., Faeth, B., Shen, K. M., Schlom, D. G., et al. (2018). Measurements of oxygen electroadsorption energies and oxygen evolution reaction on RuO2(110): a discussion of the sabatier principle and its role in electrocatalysis. J. Am. Chem. Soc. 140, 17597–17605. doi:10.1021/jacs.8b09657
Lee, Y., Suntivich, J., May, K. J., Perry, E. E., and Shao-Horn, Y. (2012). Synthesis and activities of rutile IrO2 and RuO2 nanoparticles for oxygen evolution in acid and alkaline solutions. J. Phys. Chem. Lett. 3 (3), 399–404. doi:10.1021/jz2016507
Li, X., Sun, X., Xu, X., Liu, W., Peng, H., Fang, X., et al. (2017). CO oxidation on PdO catalysts with perfect and defective rutile-TiO2 as supports: elucidating the role of oxygen vacancy in support by DFT calculations. Appl. Surf. Sci. 401, 49–56. doi:10.1016/j.apsusc.2016.12.210
Lu, X. F., Chen, Y., Wang, S. B., Gao, S. Y., and Lou, X. W. (2019). Interfacing manganese oxide and cobalt in porous graphitic carbon polyhedrons boosts oxygen electrocatalysis for Zn–Air batteries. Adv. Mater. 31 (39), 1902339. doi:10.1002/adma.201902339
Man, I. C., Su, H.‐Y., Calle‐Vallejo, F., Hansen, H. A., Martínez, J. I., Inoglu, N. G., et al. (2011). Universality in oxygen evolution electrocatalysis on oxide surfaces. ChemCatChem. 3, 1159–1165. doi:10.1002/cctc.201000397
Oh, N. K., Kim, C., Lee, J., Kwon, O., Choi, Y., Jung, G. Y., et al. (2019). In-situ local phase-transitioned MoSe2 in La0.5Sr0.5CoO3-δ heterostructure and stable overall water electrolysis over 1000 hours. Nat. Commun. 10, 1723. doi:10.1038/s41467-019-09339-y
Perdew, J. P., Burke, K., and Ernzerhof, M. (1997). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865. doi:10.1103/PhysRevLett.77.3865
Qingxiang, W., Dastafkan, K., and Chuan, Z. (2018). Design strategies for non-precious metal oxide electrocatalysts for oxygen evolution reactions. Curr. Opin. Electrochem. 10, 16–23. doi:10.1016/j.coelec.2018.03.015
Rossmeisl, J., Qu, Z.-W., Zhu, H., Kroes, G.-J., and Nørskov, J. K. (2007). Electrolysis of water on oxide surfaces. Electroanal. Chem. 607, 83. doi:10.1016/j.jelechem.2006.11.008
Seitsonen, A. P., and Over, H. (2010). Oxidation of HCl over TiO2-supported RuO2: a density functional theory study. J. Phys. Chem. C 114, 22624–22629. doi:10.1021/jp108603a
Seitz, L. C., Dickens, C. F., Nishio, K., Hikita, Y., Montoya, J., Doyle, A., et al. (2016). A highly active and stable IrOx/SrIrO3 catalyst for the oxygen evolution reaction. Science 353 (6303), 1011–1014. doi:10.1126/science.aaf5050
Stacchiola, D. J., Senanayake, S. D., Liu, P., and Rodriguez, J. A. (2013). Fundamental studies of well-defined surfaces of mixed-metal oxides: special properties of MOx/TiO2(110) {M = V, Ru, Ce, or W}. Chem. Rev. 113, 4373–4390. doi:10.1021/cr300316v
Suen, N.-T., Hung, S.-F., Quan, Q., Zhang, N., Xu, Y.-J., and Chen, H. M. (2017). Electrocatalysis for the oxygen evolution reaction: recent development and future perspectives. Chem. Soc. Rev. 46 (337), 337–365. doi:10.1039/c6cs00328a
Sun, X., Peng, X., Xu, X., Jin, H., Wang, H., and Wang, X. (2016). H2 adsorption and dissociation on PdO(101) films supported on rutile TiO2(110) facet: elucidating the support effect by DFT calculations. J. Mol. Model. 22, 204. doi:10.1007/s00894-016-3072-3
Turner, J. A. (2004). Sustainable hydrogen production. Science 305, 972–974. doi:10.1126/science.1103197
Valdes, A., Qu, Z.-W., Kroes, G.-J., Rossmeisl, J., and Norskov, J. K. (2008). Oxidation and photo-oxidation of water on TiO2 surface. J. Phys. Chem. C 2, 9872–9879. doi:10.1021/jp711929d
Vojvodic, A., Calle-Vallejo, F., Guo, W., Wang, S., Toftelund, A., Studt, F., et al. (2011). On the behavior of Brønsted-Evans-Polanyi relations for transition metal oxides. J. Chem. Phys. 134, 244509. doi:10.1063/1.3602323
Wang, D. Y., Gong, M., Chou, H. L., Pan, C. J., Chen, H. A., Wu, Y., et al. (2015). Highly active and stable hybrid catalyst of cobalt-doped FeS2 nanosheets–carbon nanotubes for hydrogen evolution reaction. J. Am. Chem. Soc. 137, 1587. doi:10.1021/jacs.5b07788
Wei, W., Dai, Y., Huang, B., Li, X., Nagele, F., Over, H., et al. (2015). Density functional characterization of the electronic structures and band bending of rutile RuO2/TiO2(110) heterostructures. J. Phys. Chem. C 119, 12394–12399. doi:10.1021/acs.jpcc.5b01884
Xiao, Z., Huang, Y.-C., Dong, C.-L., Xie, C., Liu, Z., Du, S., et al. (2020). Operando identification of the dynamic behavior of oxygen vacancy-rich Co3O4 for oxygen evolution reaction. J. Am. Chem. Soc. 142, 12087. doi:10.1021/jacs.0c00257
Xu, Z., Rossmeisl, J., and Kitchin, J. R. (2015). A linear response DFT+U study of trends in the oxygen evolution activity of transition metal rutile dioxides. J. Phys. Chem. C 119, 4827–4833. doi:10.1021/jp511426q
Keywords: density functional theory, oxygen evolution reaction, rutile-type oxide, heterostructure, scaling relation
Citation: Lim HY, Park SO, Kim SH, Jung GY and Kwak SK (2021) First-Principles Design of Rutile Oxide Heterostructures for Oxygen Evolution Reactions. Front. Energy Res. 9:606313. doi: 10.3389/fenrg.2021.606313
Received: 14 September 2020; Accepted: 05 January 2021;
Published: 11 February 2021.
Edited by:
Kai S. Exner, Sofia University, BulgariaReviewed by:
Marko Melander, University of Jyväskylä, FinlandCopyright © 2021 Lim, Park, Kim, Jung and Kwak. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gwan Yeong Jung, Z3lqdW5nQHVuaXN0LmFjLmty; Sang Kyu Kwak, c2trd2FrQHVuaXN0LmFjLmty
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.