Comparative analysis of force sensitive resistor circuitry for use in force myography systems for hand gesture recognition

Wearable technologies for hand gesture classification are becoming increasingly prominent due to the growing need for more natural, human-centered control of complex devices. This need is particularly evident in emerging fields such as virtual reality and bionic prostheses, which require precise control with minimal delay. One method used for hand gesture recognition is force myography (FMG), which utilizes non-invasive pressure sensors to measure radial muscle forces on the skin’s surface of the forearm during hand movements. These sensors, typically force-sensitive resistors (FSRs), require additional circuitry to generate analog output signals, which are then classified using machine learning to derive corresponding control signals for the device. The performance of hand gesture classification can be influenced by the characteristics of this output signal, which may vary depending on the circuitry used. Our study examined three commonly used circuits in FMG systems: the voltage divider (VD), unity gain amplifier (UGA), and transimpedance amplifier (TIA). We first conducted benchtop testing of FSRs to characterize the impact of this circuitry on linearity, deadband, hysteresis, and drift, all metrics with the potential to influence an FMG system’s performance. To evaluate the circuit’s performance in hand gesture classification, we constructed an FMG band with 8 FSRs, using an adjustable Velcro strap and interchangeable circuitry. Wearing the FMG band, participants (N = 15) were instructed to perform 10 hand gestures commonly used in daily living. Our findings indicated that the UGA circuit outperformed others in minimizing hysteresis, drift and deadband with comparable results to the VD, while the TIA circuit excelled in ensuring linearity. Further, contemporary machine learning algorithms used to detect hand gestures were unaffected by the circuitry employed. These results suggest that applications of FMG requiring precise sensing of force values would likely benefit from use of the UGA. Alternatively, if hand gesture state classification is the only use case, developers can take advantage of benefits offered from using less complex circuitry such as the VD.

1 Introduction

There is a variety of measurable physiological activity at all levels of the central and peripheral nervous systems, as well as in the muscles of the extremities, which can be used to infer motor intentions and derive control signals for external devices. Recording of muscle and physiological activity to derive control signals has become a prominent practice in part due to the growing market of virtual and augmented reality (VR and AR, respectively), bionic prostheses, and robotic assistive devices, among many other technologies. A common method of deriving control signals for external and assistive devices is the measurement of hand movements and gestures. Our hands are critical to how we interact with our environment and communicate with others, leading to growing interest in non-invasive techniques to reliably decode hand gestures for various consumer, rehabilitation, and assistive device applications. A prominent approach to achieving this task is to capture and analyze muscle activity in the muscles responsible for actuating hand and wrist movements (muscle in the forearm and sometimes intrinsic hand muscles) (Tchantchane et al., 2023). Myoelectric (Scheme and Englehart, 2011), optical (Fujwara et al., 2019), and even acoustic (Nazari and Zheng, 2023) sensors can detect muscle activity; each coming with its own benefits and disadvantages.

An emerging and relatively low-cost, experimental sensing modality used for hand gesture recognition is force myography (FMG) (Belyea et al., 2019). These FMG systems measure muscle activity by employing an array of pressure sensors placed along the circumference of the forearm (Radmand et al., 2016). Here, muscle activation during hand and wrist movements results in changes in muscle configuration and volume that collectively present as local changes in the outward radial forces measured by each forces sensor. This force information can in turn be processed and used to derive device control signal.

There are many types of pressure sensors that can effectively serve force myography systems (Xiao and Menon, 2019), however, among the most common is the force sensitive resistor (FSR). FSRs are passive, two terminal devices that decrease in resistance when a force is applied. This inverse relationship of force to resistance is derived from the FSRs polymer thin film composition (Saadeh et al., 2017). Two interwoven patterns of metal lie on a thermoplastic base just above semiconductive ink-coated layer. Solder tabs connect to the patterned metal, and as the layers of ink and metal are pressed together under the application of force, their resistance decreases. These sensors offer the benefits of affordability, commercial availability, and simplicity of implementation (Lebosse et al., 2011; Young et al., 2023). However, inherent variances exist in the manufacturing process of semiconductive ink, resulting in a unique force-resistance response from each FSR (FSRTEK, 2024). This leads to no two FSRs having the same force-resistance curve, even for units of the same model, which can be mitigated during integration using signal acquisition and conditioning circuitry (Velásquez and Flórez, 2010; Ohmite, 2024).

While conditioning circuitry varies per use case it has the potential to significantly impact an FSR’s output signal. Across literature, there are three prominent circuits most typically employed when FSRs are being used in FMG systems: the voltage divider (VD) (Sadeghi et al., 2018; Sadarangani et al., 2017; Shaikh et al., 2015; Barnea et al., 2012; Cho et al., 2016; Rehman et al., 2023), the unity gain amplifier (UGA) (Velásquez and Flórez, 2010; Godiyal et al., 2018), and the transimpedance amplifier (TIA) (Giovanelli and Farella, 2016; Prakash et al., 2020; Esposito et al., 2018; Prakash et al., 2021). Despite the variety of circuitry employed, little work has been performed to characterize the influence of circuitry choices in this unique context of hand gesture classification. Thus, our objective was to quantitively assess the effects of circuit choices on the performance of FSR-based FMG systems, specifically in the context of signal quality during data acquisition and hand gesture classification performance.

2 Materials and methods

We performed two separate experiments to determine the benefits and limitations of three circuit types (VD, UGA, and TIA) as relevant to hand gesture classification applications. In the first experiment, FSR signal quality metrics were quantified and compared across circuit types. The metrics evaluated included signal drift, hysteresis, deadband, and linearity. In the second experiment, we conducted human testing with a custom multi-sensor FMG band worn on participants’ forearms to examine the performance of the circuits when the measured force data were used with machine learning techniques to classify hand gestures.

2.1 Circuit design

We examined the performance of the VD (Barnea et al., 2012; Shaikh et al., 2015; Cho et al., 2016; Sadarangani et al., 2017; Sadeghi et al., 2018; Rehman et al., 2023), UGA (Godiyal et al., 2018; Velásquez and Flórez, 2010) and TIA (Giovanelli and Farella, 2016; Prakash et al., 2020; Esposito et al., 2018; Prakash, Sharma, and Sharma, 2021); acquisition circuits as shown in Figure 1. This figure represents a single channel of each circuit type, highlighting the signal acquisition components, summarizing the circuits used in the previously stated works.

Figure 1

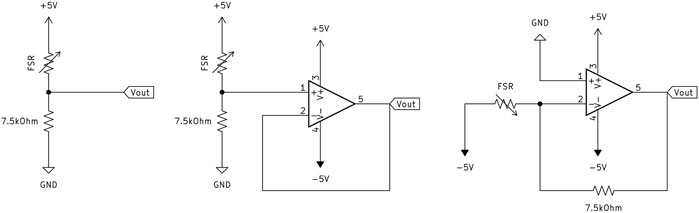
Figure 1. From left to right: Voltage Divider (VD), Unity Gain Amplifier (UGA), Transimpedance Amplifier (TIA). This is a representative diagram of the circuitry used for a single channel. Note, in FMG systems with multiple sensing elements, this circuitry would be repeated for each element along with accompanying system specific componentry to accommodate the additional channels.

Of the three circuits, the VD was the least complex from a circuit design perspective as it employs only two components. In this configuration, one lead of the FSR is tied to positive voltage and the other to a load resistor tied to ground. Per the FSR manufacturer suggestion, the value chosen for this resistor was 7.5kOhm (±1%) as it was suggested to provide the most linear voltage response in the force range most applicable to our work (0–4 N) (Interlink, 2024).

The UGA builds upon the VD such that it incorporates a voltage follower at the output of the VD. The voltage follower is a subcircuit containing an operational amplifier (Op-Amp) whose negative input is tied to its output. This differs from the typical use of an Op-Amp as it maintains a gain of 1, offering the unique benefit of maintaining a signal while isolating the low-impedance output of the voltage follower from the high-impedance output of the VD. A high-impedance input to any analog to digital converter (ADC) may cause imprecise measurements, thus voltage followers are used to transfer high-impedance signals to low-impedance inputs.

The most complex of the three circuits was the TIA. In this configuration, the FSR was fixed at -5 V at one lead and the other feeds a signal to the positive input of an Op-Amp. Due to the negative voltage input fed into the FSR, the output signal of the circuit varied from 0 to -5 V. A load resistor of 7.5kOhm (±1%) tied the negative terminal of the Op-Amp to the output, as suggested by the manufacturer for the most linear response within our force range. The TIA is unique in that it offers a low impedance output regardless of set gain, making it ideal for FSR applications involving amplification.

2.2 Experiment 1 - signal metric analysis

We assessed four signal quality performance metrics across the three circuit types. These included: 1) Drift, which was evaluated as the amount that a sensor’s voltage output varies over time when statically loaded; 2) Hysteresis, as calculated as the difference in the voltage output when a sensor was being load compared to unloaded; 3) Deadband, which quantified the required input force needed to be applied to the FSR prior to registering a voltage change, expressed as a percentage of its force measurement range; 4) Linearity, which was defined as the system’s ability to respond (voltage output) linearly to an input force, which affects the proportionality of the input forces from the muscle to voltage output measured. These metrics impact real-world performance of an FMG system. Drift affects FMG systems that are intended to be used over sustained periods of time. A higher drift may result in deviations of voltage over time, potentially impacting hand gesture classification accuracy during sustained grasps. It is ideal for FMG systems to minimize hysteresis as they would respond similarly when in both loading and unloading phases (for example, during the hand closing and opening). This property may affect the system’s ability to identify grasp states depending on if users are contracting or relaxing their forearm muscles (ex. partially closing or opening the hand to arrive at a position). An FMG system with smaller deadband would be more responsive during low force phases of hand movements, enabling the FSRs to more rapidly detect changes, for example, this would allow a more rapid detection of the onset of hand movements. A more linear system would result in a predictable sensor output, as voltage output would more linearly correspond to an applied force.

2.2.1 Touch tactor

To collect data for the assessment of our signal quality metrics, we employed a custom setup that allowed for controlled application of force to a Force Sensitive Resistor (FSR) using a tissue analog. This setup was designed to facilitate easy connection of the FSR to each of the three tested circuit types, and a load cell was employed to compare the voltage output from the FSR and circuitry against a known reference force.

Our force applicator device, or Force Tactor, was attached to a custom MakerBeam aluminum extrusion frame as shown in Figure 2. The Force Tactor received control input signals from a Python script that commanded the rotation of a pinion gear on a servo motor (DS3235, DS servo), causing linear movement of an FSR mounted to a toothed rack. The FSR was connected to one of the three circuit types. Motors were controlled via an Arduino Uno R3, and the current draw was recorded using an ASC723 current sensor. A Polydimethylsiloxane (PDMS) dome was adhered to the FSR’s surface to distribute pressure across the entire sensing surface (Jensen et al., 1991; Velásquez and Flórez, 2010). Therefore, with rotation of the servo and downward movement of the rack, the FSR was pushed into a commercially purchased Syndaver skin, muscle, and fat tissue analog (Figure 2, below) (Kho et al., 2023). A 3D printed platform supported the tissue analog and sat above a calibrated parallel beam loadcell (TAL220B 5 kg, HT Sensor Technology Co.) wired to an Op-Amp (INA126, Texas Instruments) that acted as a force reference. Signal output from the FSR and reference circuitry was recorded by a National Instrument USB 6210 Data Acquisition System (NI DAQ) connected to and recorded by a lab PC running a custom script in MATLAB software.

Figure 2

Figure 2. The designed Force Tactor. A cubic MakerBeam assembly housed a 35 kg servo mounted to a rack and pinion gear. The gear assembly translated rotational servo movement to linear downward movement of a FSR400 into a Syndaver Abdominal Tissue Plate 10 cm × 5 cm. A 3D printed stabilizer supported the skin and sat atop a loadcell used for applied force reference. Loadcell and FSR voltages were measured through supplemental circuitry not shown.

2.2.2 Data collection and analysis

Data collection and subsequent analysis of drift, hysteresis, deadband and linearity were collected in accordance with ANSI/ISA-51.1-1979 (R1993) standards (ANSI/ISA Process Instrumentation Terminology, 1979). We first defined the testing voltage range for each circuit. This was accomplished by identifying the maximum voltage achieved by each circuit during the participant trials described below to define a testing range between zero and the identified maximum, or minimum values (2.539, 2.465, and −2.495 V for the VD, UGA, and TIA circuits, respectively). Each circuit was individually connected to the same FSR and experimental setup, then loaded and unloaded through their respective voltage range as determined by the active test. Sensor metric tests were conducted in accordance with the ANSI/ISA protocol similar to Schofield et al. (Schofield et al., 2016), with each being performed in a randomized order and repeated 5 times.

Sensor drift data was collected by loading the FSR to its maximum voltage and then holding this load for 45 s. Drift was then calculated by finding the difference between the starting voltage and the voltage after the sustained loading period and reported as a percentage of the input. Hysteresis testing involved loading the FSR to its maximum voltage and then unloading it. Hysteresis was calculated by finding the maximum difference between a loading and unloading state within the tested voltage range of each circuit as described above. This value was then reported as a percent of the tested range. Deadband was tested by loading the FSR at a slow rate (servo output of 5° per second) into the synthetic skin until a non-zero voltage reading was first registered. The deadband was then calculated by finding the minimum voltage registered due to any input, then reporting the range of 0 to the found value as a percentage of input span. Linearity testing involved the downward movement of the FSR into synthetic skin at an increasing pressure until the maximum voltage was met. Linearity was calculated by applying a linear line of best fit to the measured voltage versus applied force, then generating a coefficient of determination as the desired linearity metric. All results were averaged among all participants of the same circuit type and reported in Table 1. Figure 3 shows the experimental setup of this testing.

Table 1

Table 1. Drift, Hysteresis, Deadband and Linearity metrics for all three circuit types.

Figure 3

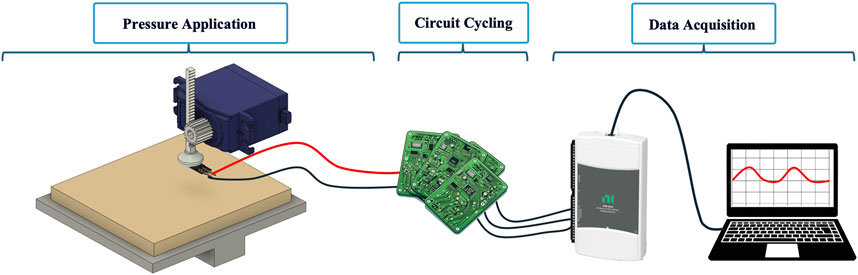
Figure 3. Experimental setup of Force Tactor system. The FSR was moved into the synthetic skin at a variable rate until a goal voltage, determined by the selected test (drift, hysteresis, deadband, linearity), was met. FSR voltage drop was measured by the selected circuit (VD, UGA, TIA) and fed into an NI DAQ for data acquisition. A lab computer recorded raw voltages for offline analysis.

2.3 Experiment 2 - hand gesture classification

In this second experiment, we sought to determine each circuit’s influence on hand gesture classification accuracies. Here participant testing was performed with the same three VD, UGA, and TIA circuits and an FMG armband that incorporated 8 FSRs. Offline pattern classification and cross validation analysis were then employed to examine the impacts of circuitry on hand gesture classification performance.

2.3.1 FMG band design

We used eight of Interlink Electronics’ FSR400 short tail sensors to measure radial muscle forces (Sadeghi et al., 2018; Cho et al., 2016; Li et al., 2012; Prakash et al., 2021; Sadarangani et al., 2017). These FSRs were placed into 3D-printed sensor cradles which offered support to the sensors, ensuring muscle forces were translated directly to the sensing surface. A PDMS plastic dome was adhered to the surface of each FSR to evenly distribute pressure (Jensen et al., 1991; Velásquez and Flórez, 2010). Adhesive Velcro-backings were attached to the back of each cradle such that they could be fit to a Velcro strap. Wiring management was addressed using a 10 pin DuPont connector located in the middle of the band’s length, enabling modular use with different circuits during testing by simply unplugging and plugging in each circuit via this connector. The band is shown in Figure 4.

Figure 4

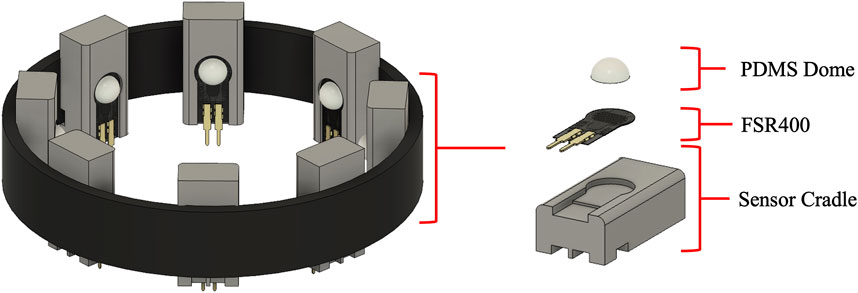
Figure 4. The designed FMG band. Eight FSR400 sensors with PDMS caps rested within ABS plastic cradles connected to a Velcro strap. Velcro was used such that the device was adjustable and could be tightened to the participant’s forearm with wiring run outside of the band.

2.3.2 Circuit design

Interchangeability of the three circuits was necessary to allow for consistency during testing in which the FMG band could be continuously worn by participants and the circuits tested by simply unplugging and plugging in each. To achieve this, each circuit was built on separate protoboards with isolated power and ground sources and plugged into the FMG band using a detachable 10 pin DuPont connector. The VD circuit was designed as depicted in Figure 1 however, given the eight FSRs employed in the arm band, eight 7.5 kOhm (±1%) resistors were used with voltage inputs of +5 V and GND. The UGA circuit implemented 2, 4-channel Op-Amps following the output of the 8 FSRs from the VD. We chose to use the LM324 Op-Amp (Texas Instruments) for its fast response rate and frequent use in literature (Interlink, 2024; Torres et al., 2015; Chen et al., 2023). The LM324N through-hole model required a bipolar voltage range for proper functionality, thus ±5 V was chosen. The same model Op-Amp was also used for the TIA circuit. Here, FSR input connections fed directly to the input of the Op-Amp and reference resistors jumped the connection of the input and output of the Op-Amp.

2.3.3 Experimental procedure

Fifteen able-bodied participants between of 20–32 years of age were recruited (mean age 23 ± 3.2 years). Six participants identified as female and nine identifying as male, with 14 participants being right hand dominant and one ambidextrous as identified using an Edinburgh handedness survey (Charman et al., 2013). The testing protocol was approved by the UC Davis Institutional Review Board and participants provided written informed consent.

Pre-testing procedures began with the handedness survey and forearm measurements (circumference, length). The investigator then fit the FMG band around the muscle bulk of the participant’s dominant forearm (determined by the survey), approximately 2/3 the distance from the distal end of the forearm (Figure 5) (Sakr and Menon, 2017; Battraw et al., 2024). Next, the FMG band was connected to one of the three circuits, in a randomized order. Power was supplied to the selected circuit via a TekPower TP-3005D-3 DC power supply, connected to a 120 V 60 Hz medical grade isolation transformer (Tripp Lite IS1800HG). The output of the selected circuit, ground, and signal pins were connected to the analog input channels of an NI DAQ (described above). The NI DAQ was connected to a lab computer running a custom MATLAB script that recorded all 8 FSR raw voltages and accompanying time stamp. Once the FMG band was fit and wired, participants were instructed to sit in a relaxed position with their arm at a 90-degree angle. A preliminary test was run where the participant would perform a maximum voluntary contraction such that we could verify sensor activation to ensure FMG band fit and acquisition of data. After verification, testing began.

Figure 5

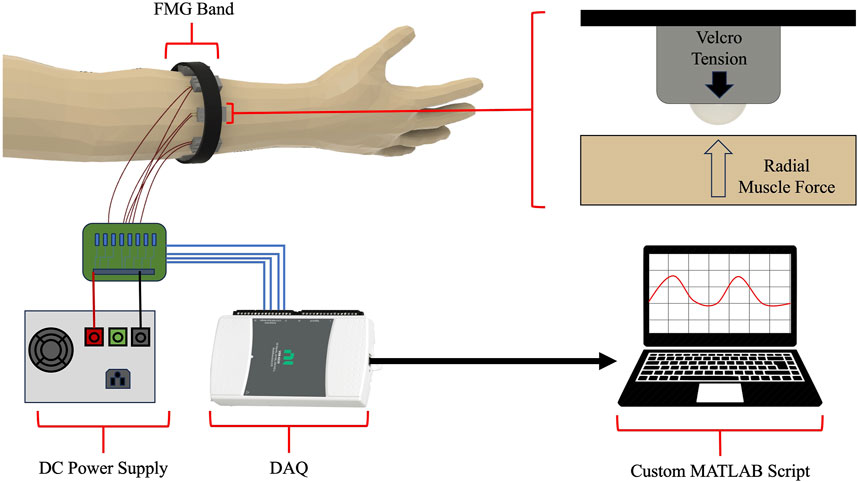
Figure 5. The experimental setup. The FMG band was fit 2/3 the length of a participant’s forearm from the wrist and the participant was instructed to perform hand gestures timed to an auditory tone. Upon muscle contraction, radial muscle forces at the surface of the skin caused changes in FSR resistances, which were measured and recorded via the band’s wire outputs by benchtop equipment.

2.3.4 Testing

Participants were tasked with making one of ten hand gestures: Cylindrical Rotation (CR), Cylindrical Wrap (CW), Index Flexion (IF), Index Point (IP), Key Pinch (KP), Pulp Pinch (PP), Tripod Pinch (TP), Wrist Extension (WE), Wrist Flexion (WF), and Wrist Rotation (WR) (illustrated in Figure 6) (Battraw et al., 2024). These gestures were chosen as they account for a wide range of hand movements which included individual digit flexion, pronation and supination, along with those commonly used in activities of daily living (Feix et al., 2016). Our custom MATLAB script was then run, which visually prompted participants to perform a hand movement followed by an auditory tone for 3 s, signaling the participant to perform the gesture, followed by silence for 3 s, signaling the participant to rest. This was repeated two more times for a given hand gesture and repeated for all 10 hand gestures resulting in three contractions and relaxations per hand gesture and 30 contractions per circuit type. Hand gesture order was randomized and after all gestures were completed, the active circuit was disconnected and the next circuit would connect in its place, repeating until all circuits were tested.

Figure 6

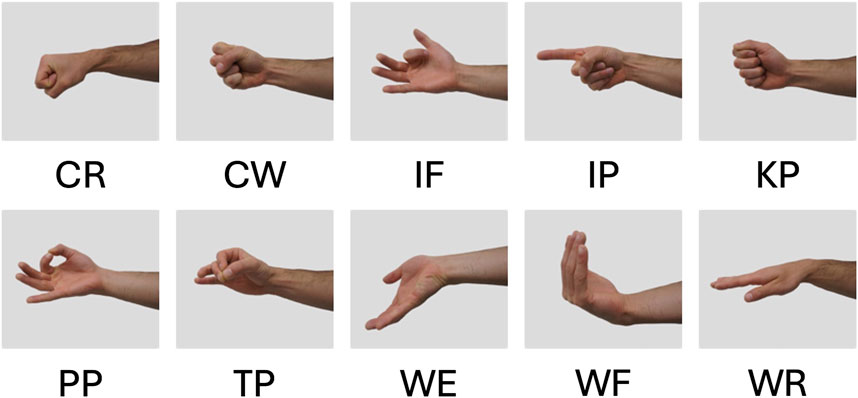
Figure 6. The ten hand gestures that were performed in the experiment: Cylindrical Rotation (CR), Cylindrical Wrap (CW), Index Flexion (IF), Index Point (IP), Key Pinch (KP), Pulp Pinch (PP), Tripod Pinch (TP), Wrist Extension (WE), Wrist Flexion (WF), and Wrist Rotation (WR).

2.3.5 Data analysis

Hand gesture classification accuracy was the primary metric used to evaluate circuit performance. This measure was defined as our system’s ability to correctly predict an executed hand gesture from the patterns in the muscle-force data. To achieve this, we performed an offline analysis using linear discriminant analysis (LDA) paired with leave-one-out cross validation (LOOCV). As is consistent with prior literature the mean absolute value (MAV) of the voltages produced by the 8 FSRs served as the primary feature used to compute classification accuracies (Ahmadizadeh et al., 2019; Scheme and Englehart, 2011). As defined by literature, the MAV was calculated by averaging the absolute value of the signal produced by the FSR. This feature was used as it makes changes in voltage during contraction more discernible from periods of rest (Abbaspour et al., 2020). For our pattern classification model, we segmented the FSR voltages using 200 ms windows with a 50 ms time increment (Smith et al., 2010). The MAV of these windows were then calculated and used as our feature vectors to train and test the LDA classifier using LOOCV through a custom Python script, utilizing the LDA function from the sklearn package. Each feature vector contained a label attached to it that represent a specific hand gesture. These labels were stored in an array and used as the model’s ground truth. We then used LOOCV which removed a single feature vector from the data set and trained the classifier on the remaining features. Afterwards, the classifier made a prediction on the “left out” feature. This process was repeated for all feature vectors and afterwards, the predictions from the classifier were compared to the ground truth values to create a classification accuracy, the percent at which the classifier correctly predicted the feature vectors. Hand gesture classification accuracies were plotted in confusion matrices (see results, Figure 7), which display the percentage of accurate predictions and the likelihood of each hand gesture being misclassified as other gesture types. Figure 8 details the overall process that data flows from initial windowing to confusion matrix generation. A Python script was written to average classification accuracies across participants for each circuit. Additionally, we analyzed these classification data in feature space using the following measures:

- Interclass Nearest Neighbors (IDNN) which quantified the distance between hand gesture clusters within feature space (Kristoffersen et al., 2019), and thus served as a metric to describe the distinguishability between hand gestures.

- Within-Class Distance (WD) compared the distance in non-dimensional space between repetitions of the same gesture (Kristoffersen et al., 2019), offering a quantitative measure of the consistency of each hand gesture.

- Mean Semi-Principal Axis (MSA) measured the overall variance of grasp clusters determined through means of ellipsoid radius estimations (Bunderson and Todd, 2012), providing a measure of the variability in the semi-principal axis, and thus quantitative insights into the distinct clustering of gestures in feature space.

Figure 7

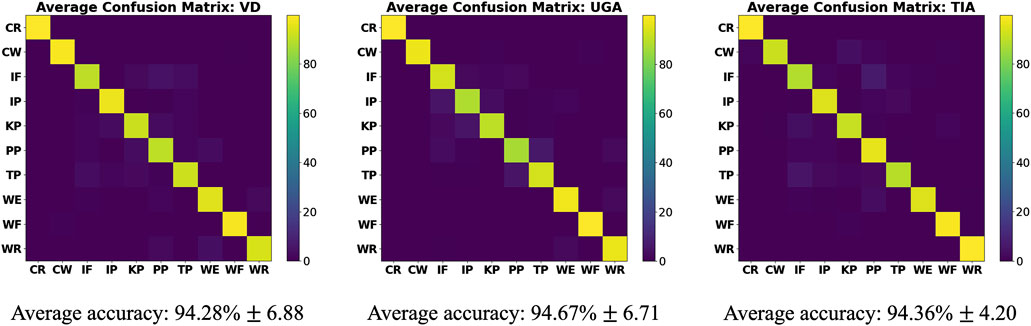
Figure 7. Confusion matrices averaged over all participants for each circuit type. The vertical axis represents actual grasps, and the horizontal represents predicted grasps. A color closer to yellow indicates a higher proportion of instances that a prediction was made, and purple indicates lower. The most important region is the diagonal which shows the correct predictions for actual grasps. All values of the diagonal were averaged, producing an average accuracy reported for each circuit type.

Figure 8

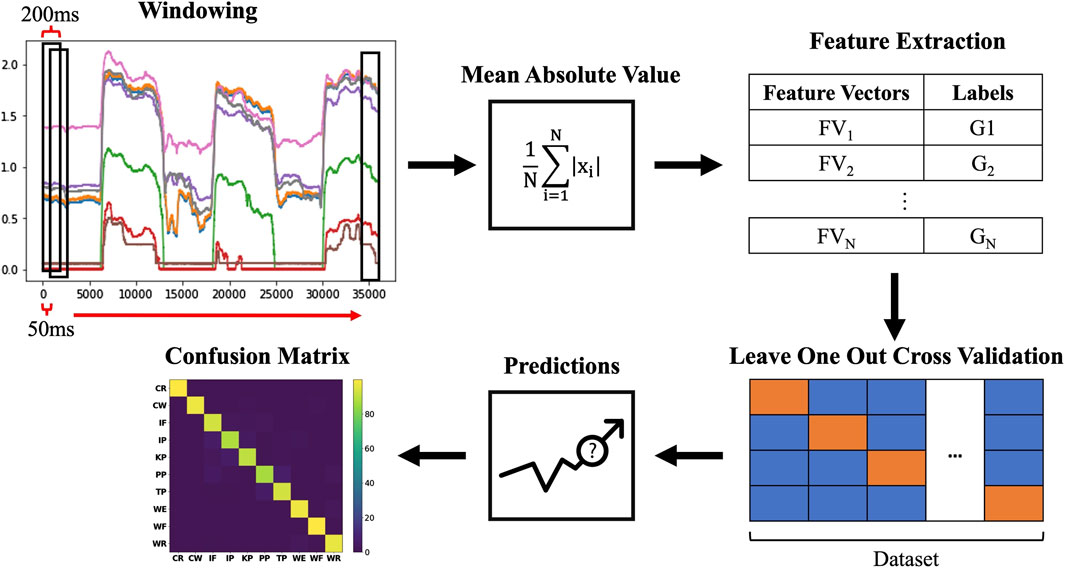
Figure 8. Raw voltages to confusion matrix data pipeline. Raw FSR data was first segmented in 200 ms windows with 50 ms time increments. The MAV of these windows was found and used as feature vectors to train and test the LDA classifier using LOOCV. Resultant predictions from the classifier were displayed in a series of confusion matrices for each input dataset.

The resultant values were averaged among all participants, assigning an average to each circuit type for all three metrics. Data were tested for normality and sphericity using Shapiro-Wilk and Mauchly tests, respectively, were found to be non-normal and spherical. Non-parametric Friedman and Wilcoxon signed-rank tests were conducted to check for statistical differences between resultant circuit type data (Kim, 2014). We also calculated the variance of the classification accuracy of each hand gesture across participants. These variances were found to be non-normal and spherical, thus were examined using the same non-parametric tests to determine if a statistical difference was present.

3 Results

3.1 Experiment 1

3.1.1 Pressure application

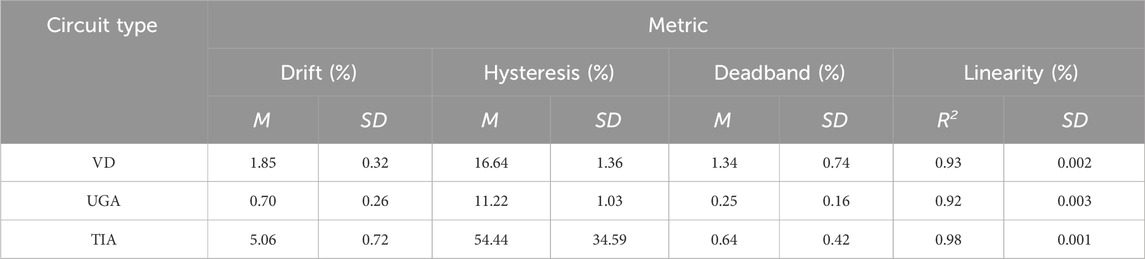
For all three circuit types, measured values of drift, hysteresis, deadband, and linearity and their standard deviations are shown in Table 1. Drift, hysteresis and deadband were reported as a percentage of their tested voltage range. Linearity was reported as a coefficient of determination value, R². In these results, the UGA demonstrated the lowest drift at 0.7% and the TIA the highest at 5.06%. Hysteresis results were similar to drift with the UGA producing the lowest values at 11.22% and TIA the highest at 54.44%. Deadband followed a similar trend demonstrating lowest with the UGA at 1.13% and highest with the VD at 2.44%. TIA demonstrated the most linear response with R² = 0.98 and UGA the least with an R² = 0.92.

3.2 Experiment 2

3.2.1 Gesture classification

Confusion matrices generated from hand grasp classification accuracies are shown in Figure 7, noting the diagonal for correct classifications. The overall accuracy score is the average of the values along this diagonal, resulting in an average accuracy of 94.28% (SD 6.88%) for the VD, 94.67% (SD 6.71%) for the UGA, and 94.36% (SD 4.20) for the TIA.

3.2.2 Feature space metrics

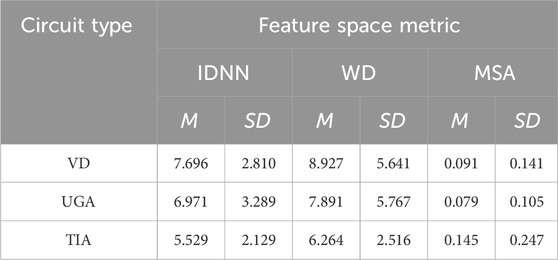
Feature space metrics of Interclass Distance Nearest Neighbors, Within-Class Distance and Mean Semi-Principal Axis were computed for each participant then averaged over all participants per circuit as follows in Table 2. In the IDNN metric, the VD reported the highest averaged distance of 7.696 while the TIA yielded the lowest of 5.529. In WD, the TIA reported the lowest average distance between grasp repetitions of 6.264 and the VD yielded the highest of 8.927. In the MSA metric, the UGA produced the lowest average variance between grasps with a value of 0.091 while the TIA yielded a higher value of 0.145.

Table 2

Table 2. Computed feature space metrics for each circuit type, averaged over all participants.

3.2.3 Statistical analyses

Friedman and Wilcoxon signed-rank tests were used to find statistical differences between the average classification accuracies of each circuit type. No statistical differences were found, results are shown in Table 3. Additionally, the same tests were run on the population variances for each grasp between all circuit types, shown in Table 4. No statistical differences were found between population variances.

Table 3

Table 3. Computed Friedman and Wilcoxon signed-rank tests for circuit type classification accuracies.

Table 4

Table 4. Computed Friedman and Wilcoxon signed-rank tests for circuit type classification variances.

4 Discussion

This work highlights the differences found between FSR signal acquisition circuits and their impact on FMG system performance in a hand gesture classification application. The signal quality analyses showed that of the three circuits, the UGA produced favorable results in most metrics, scoring lowest in drift, hysteresis and deadband, seen in Table 1. As it is not uncommon in daily tasks to grasp and hold objects for extended periods of time, a low drift circuit may help improve an FMG system’s performance during such sustained grasping activities. Conversely, drift-related changes in FSR signal output over long contraction periods may result in erroneous gesture classification, which may be further magnified by the presence of multiple FSR signals (8 in our experimental setup). As FMG has the potential to extend beyond simple state classifications to proportional control, hysteresis becomes a critical consideration (Belyea et al., 2018). While there is inherent hysteresis in muscle activation, lower sensor hysteresis will support the accurate measurement of radial muscle forces during both muscle contraction and relaxation phases (i.e., sensor loading and unloading). Interestingly, hysteresis measures illustrated the greatest differences in standard deviation between circuits as the UGA had the lowest of 1.03%, while the TIA reported 34.59%. Greater deadband performance makes the UGA more sensitive to minute changes in skin deflection at lower forces and better at detecting subtle hand movements. This may help FMG systems to be more capable of detecting partial hand gestures that do not fully contract forearm muscles due to a greater low-end resolution. While the VD did not achieve the highest performance in any category, its results among these metrics was highly comparable to that of the UGA. The TIA demonstrated the most linear force to voltage response at a 5% increase over the next most linear circuit, the VD. If an FSR in an FMG system is nonlinear and is placed on a large bulk of muscle, output voltage may either quickly saturate or not be registered, leading to an overall decreased resolution in given force ranges. The TIA provides the most linear response to a given force input within the desired force range; thus, it is more likely to resolve accurate force values over the sensor’s voltage range.

The VD, UGA, and TIA all independently predicted hand gestures at an average of 94.28% (SD 6.88%), 94.67% (SD 6.71%), and 94.36% (SD 4.20%), respectively, across all 10 gestures, seen in Figure 7. Despite investigators carefully fitting the FMG band to each participant’s forearm as consistently as possible, inherent variabilities related to the dimensions of each person’s arm and their comfort tolerance to the tightness of the band likely introduced individual variability into our data. Despite this variability, these high classification rates were consistently achieved with minimal deviation, demonstrating the robustness of the system. No statistical differences were found between the classification accuracies of each circuit type, as seen in Table 3. When examining each circuit type and comparing variances between grasps across our participants similar results were found (Table 4), demonstrating a consistent classification of hand gestures regardless of circuit type. Practically, our findings suggest that in offline hand gesture classification applications, each of the three tested circuits offers nearly the same performance in terms of classification accuracy.

Our feature space analysis offers a more nuanced understanding of the gesture classification data. The VD circuit produced the largest IDNN value, illustrating a greater separation between hand gesture clusters. This suggests that if used in control applications the VD circuit may produce a control signal that leverages a more unique representation of gestures in feature space. While there were no significant differences found between classification accuracies, real-world applications could potentially benefit from this property as the greater distance between grasps in feature space allows classification algorithms to distinguish between grasp types more accurately and reliably (Franzke et al., 2021). This may be particularly advantageous in real-time control applications as a larger IDNN value may correspond with more distinct features. Real-time gesture classification inherently produces less accurate results (Abbaspour et al., 2021) and nuanced differences in feature space have the potential to significantly impact the overall accuracy and consistency of predictions. The TIA reported the lowest value for WD, demonstrating the least variance for repetitions of the same grasp. In feature space, hand grasp repetitions are clustered in a smaller region for the TIA than other circuit types. However, even though the TIA resulted in the lowest WD value, it yielded the smallest distance between grasp types in feature space (IDNN), indicating that grasp clusters are closer together, perhaps mitigating this effect. The distribution within feature space, as measured by the MSA, produced the largest results from the UGA. The UGA yielded the lowest MSA value, indicating the lowest intra-class variability within the gesture dataset when compared to those of other circuit types (Franzke et al., 2021). This represents a lower signal variability and tighter clustering over all hand gestures in feature space. Practically in hand gestures classification applications, this has the potential for improved robustness to noise and minor signal variations from biological or electrical sources.

Finally, it is worth noting that there may be interrelationships among our signal performance metrics and the feature space metrics. For example, one would anticipate sensor drift and MSA to be closely related as increases in sensor drift tend to cause greater variance in recorded data. This, in turn, results in a greater spread of data in feature space, leading to a higher variance in the grasp clusters, as quantified by MAS. Similar relationships may likely be observed with other metric pairs, such as linearity and WD. From this, we note that further investigation into the causal impact of sensor characteristics on feature space metrics is likely important in future work.

Our findings have a variety of implications for design the design of FMG hand gesture recognition systems. Collectively they suggest that the voltage divider, unity gain amplifier, and transimpedance amplifier all offer similar hand gesture classification performance in a single-limb position offline classification task yet differ in the signal characteristics and feature space that each circuit outputs. The UGA demonstrated the lowest measures of drift, hysteresis, and deadband. The TIA produced the most linear voltage response to an applied force but exhibits large amounts of hysteresis. Finally, the VD showed similar results as the UGA, with slightly larger measures of drift, hysteresis, and deadband. While feature space metrics offer further insight into the separation of gesture related muscle activity and the spread of these data, there was ultimately no significant differences in classification accuracies and standard deviation across circuit types. While not statistically relevant in this work, these feature space metrics and their relation to signal characteristics could be more impactful in real-time applications. Future work in FMG systems with FSRs should be completed with these performance metrics in mind when choosing a signal acquisition circuit. For a more comprehensive understanding of signal metric impact on FMG system performance, investigations of real-time gesture classification performance are a critical next step. This may provide assessment of circuit performance in applications more closely reflective of real-world use. For example, although the UGA outperformed other circuits across most metrics, its dependency on a bipolar power supply can limit its application in untethered, free-moving systems, like the inevitable challenges a TIA circuit will face. Although additional circuit design can address this issue, it will introduce further complexity into the system’s design. However, this work suggests that if the FMG application is being performed for the purposes of simple gesture classification in offline applications, less complex circuitry such as a VD circuit can produce high accuracy results. However, if precise readings of the forces introduced to the FMG sensors is a priority, more complex circuit designs may be useful to help produce linear force-voltage responses and mitigate challenges such as hysteresis, drift, and deadbands. Ultimately, the choice of circuit should align with the application or objectives of the study being performed.

In future work, we intend on fabricating a system capable of conducting real-time gesture classification. The results presented here represent offline classification accuracies, which differ from real-time gesture classification, a model more reflective of real-world applications. Testing our systems in real-time may demonstrate nuances in driving FMG circuitry that are not present in offline classification. Further, these future experiments may point to different circuitry options that are more robust for real-time use. Thus, creating an FMG system capable of on-board real-time classification is necessary to conduct this work.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/BEAR-Labs?tab=repositories.

Ethics statement

The studies involving humans were approved by UC Davis Institutional Review Board. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

GS: Formal Analysis, Investigation, Writing–original draft, Writing–review and editing. PY: Conceptualization, Investigation, Software, Writing–original draft, Writing–review and editing. MB: Conceptualization, Writing–review and editing. JK: Formal Analysis, Investigation, Writing–review and editing. JS: Conceptualization, Funding acquisition, Resources, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Funding for this research project was provided by UC Davis Next Level Research Award.

Acknowledgments

The authors would like to thank the participants for their patience during testing.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbaspour, S., Lindén, M., Hamid, G., Naber, A., and Ortiz-Catalan, M. (2020). Evaluation of surface EMG-based recognition algorithms for decoding hand movements. Med. Biol. Eng. Comput. 58 (1), 83–100. doi:10.1007/s11517-019-02073-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbaspour, S., Naber, A., Ortiz-catalan, M., Gholamhosseini, H., and Lindén, M. (2021). Real-time and offline evaluation of myoelectric pattern recognition for the decoding of hand movements. Sensors Basel, Switz. 21 (16), 5677. doi:10.3390/S21165677

CrossRef Full Text | Google Scholar

Ahmadizadeh, C., Pousett, B., and Menon, C. (2019). Investigation of channel selection for gesture classification for prosthesis control using force myography: a case study. Front. Bioeng. Biotechnol. 7 (December), 331. doi:10.3389/FBIOE.2019.00331

PubMed Abstract | CrossRef Full Text | Google Scholar

ANSI/ISA Process Instrumentation Terminology (1979). ANSI/ISA standard 51.1.

Google Scholar

Barnea, A., Olaru, D., Asachi, G., and Oprisan, C. (2012). “Force sensitive resistors calibration for the usage,” in gripping devices the 3 rd international conference on diagnosis and prediction in mechanical engineering systems dipre 12 the 3 r d internationa l conference on diagnosis and prediction in mech anical engineering systems force sensitive resistors calibration for the usage in gripping devices. Available at: https://www.researchgate.net/publication/335754343.

Google Scholar

Battraw, M. A., Fitzgerald, J., James, M. A., Bagley, A. M., Joiner, W. M., and Schofield, J. S. (2024). Understanding the capacity of children with congenital unilateral below-elbow deficiency to actuate their affected muscles. Sci. Rep. 2024 14 (1), 4563–4616. doi:10.1038/s41598-024-54952-7

CrossRef Full Text | Google Scholar

Belyea, A. T., Kevin, B. E., and Erik, J. S. (2018). A proportional control Scheme for high density force myography. J. Neural Eng. 15 (4), 046029. doi:10.1088/1741-2552/AAC89B

PubMed Abstract | CrossRef Full Text | Google Scholar

Belyea, A. (2019). FMG vs emg: a comparison of usability for real-time pattern recognition based control. TBME. 66 (11), 3098–3104. doi:10.1109/TBME.2019.2900415

PubMed Abstract | CrossRef Full Text | Google Scholar

Bunderson, N. E., and Todd, A. K. (2012). Quantification of feature space changes with experience during electromyogram pattern recognition control. IEEE Trans. Neural Syst. Rehabilitation Eng. 20 (3), 239–246. doi:10.1109/TNSRE.2011.2182525

PubMed Abstract | CrossRef Full Text | Google Scholar

Charman, T., Hepburn, S., Lewis, M., Lewis, M., Steiner, A., Rogers, S. J., et al. (2013). Edinburgh handedness inventory. Encycl. Autism Spectr. Disord., 1051–1054. doi:10.1007/978-1-4419-1698-3_877

CrossRef Full Text | Google Scholar

Chen, P., Li, Z., Togo, S., Yokoi, H., and Jiang, Y. (2023). A layered SEMG-FMG hybrid sensor for hand motion recognition from forearm muscle activities. IEEE Trans. Human-Machine Syst. 53 (5), 935–944. doi:10.1109/THMS.2023.3287594

CrossRef Full Text | Google Scholar

Cho, E., Chen, R., Karim Merhi, L., Xiao, Z., Pousett, B., and Menon, C. (2016). Force myography to control robotic upper extremity prostheses: a feasibility study. Front. Bioeng. Biotechnol. 4 (MAR), 18. doi:10.3389/fbioe.2016.00018

PubMed Abstract | CrossRef Full Text | Google Scholar

Esposito, D., Andreozzi, E., Fratini, A., Gargiulo, G. D., Savino, S., Niola, V., et al. (2018). A piezoresistive sensor to measure muscle contraction and mechanomyography. Sensors Switz. 18 (8), 2553. doi:10.3390/s18082553

PubMed Abstract | CrossRef Full Text | Google Scholar

Feix, T., Romero, J., Schmiedmayer, H. B., Dollar, A. M., and Kragic, D. (2016). The GRASP taxonomy of human grasp types. IEEE Trans. Human-Machine Syst. 46 (1), 66–77. doi:10.1109/THMS.2015.2470657

CrossRef Full Text | Google Scholar

Franzke, A. W., Kristoffersen, M. B., Jayaram, V., Van Der Sluis, C. K., Murgia, A., and Bongers, R. M. (2021). Exploring the relationship between EMG feature space characteristics and control performance in machine learning myoelectric control. IEEE Trans. Neural Syst. Rehabilitation Eng. 29, 21–30. doi:10.1109/TNSRE.2020.3029873

CrossRef Full Text | Google Scholar

FSRTEK (2024). FSR 101 force sensing resistor theory and applications. Available at: https://www.fsrtek.com/standard-sensor/fa101-force-sensing-resistor (Accessed July 17, 2024).

Google Scholar

Fujwara, E., Wu, Y. T., Villela, C. S., Gomes, M. K., Soares, M. C. P., Suzuki, C. K., et al. (2019). “Design and application of optical fiber sensors for force myography,” in 2018 SBFoton International Optics and Photonics Conference, SBFoton IOPC, January, 2018.

Google Scholar

Giovanelli, D., and Farella, E. (2016). Force sensing resistor and evaluation of Technology for wearable body pressure sensing. J. Sensors 2016, 1–13. doi:10.1155/2016/9391850

CrossRef Full Text | Google Scholar

Godiyal, A. K., Mondal, M., Joshi, S. D., and Joshi, D. (2018). Force myography based novel strategy for locomotion classification. IEEE Trans. Human-Machine Syst. 48 (6), 648–657. doi:10.1109/THMS.2018.2860598

CrossRef Full Text | Google Scholar

Interlink (2024). FSR® integration guide Interlink Electronics FSR ® force sensing resistors ® FSR ® integration guide. Available at: www.interlinkelectronics.com.

Google Scholar

Jensen, T. R., Radwint, R. G., and Webster, J. G. (1991). A conductive polymer sensor for measuring external finger forces. J. Biomchanics. 24, 851–858. doi:10.1016/0021-9290(91)90310-j

PubMed Abstract | CrossRef Full Text | Google Scholar

Kho, A. S. K., Béguin, S., O’Cearbhaill, E. D., and Annaidh, A.N. (2023). Mechanical characterisation of commercial artificial skin models. J. Mech. Behav. Biomed. Mater. 147 (November), 106090. doi:10.1016/J.JMBBM.2023.106090

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, H.-Y. (2014). Statistical notes for clinical researchers: nonparametric statistical methods: 2. Nonparametric methods for comparing three or more groups and repeated measures. Restor. Dent. and Endod. 39 (4), 329. doi:10.5395/RDE.2014.39.4.329

PubMed Abstract | CrossRef Full Text | Google Scholar

Kristoffersen, M. B., Franzke, A. W., Van Der Sluis, C. K., Murgia, A., and Bongers, R. M. (2019). The effect of feedback during training sessions on learning pattern-recognition-based prosthesis control. IEEE Trans. Neural Syst. Rehabilitation Eng. 27 (10), 2087–2096. doi:10.1109/TNSRE.2019.2929917

CrossRef Full Text | Google Scholar

Lebosse, C., Renaud, P., Bayle, B., and De Mathelin, M. (2011). Modeling and evaluation of low-cost force sensors. IEEE Trans. Robotics 27 (4), 815–822. doi:10.1109/TRO.2011.2119850

CrossRef Full Text | Google Scholar

Li, N., Yang, D., Jiang, L., Liu, H., and Cai, H. (2012). Combined use of FSR sensor array and SVM classifier for finger motion recognition based on pressure distribution map. J. Bionic Eng. 9 (1), 39–47. doi:10.1016/S1672-6529(11)60095-4

CrossRef Full Text | Google Scholar

Nazari, V., and Zheng, Y. P. (2023). Controlling upper limb prostheses using sonomyography (smg): a review. Sensors. MDPI 23, 1885. doi:10.3390/s23041885

CrossRef Full Text | Google Scholar

Ohmite (2024). Ohmite FSR series integration guide: force sensing resistor integration guide force sensing resistor. Available at: www.ohmite.com.

Google Scholar

Prakash, A., Kumar Sahi, A., Sharma, N., and Sharma, S. (2020). Force myography controlled multifunctional hand prosthesis for upper-limb amputees. Biomed. Signal Process. Control 62 (September), 102122. doi:10.1016/J.BSPC.2020.102122

CrossRef Full Text | Google Scholar

Prakash, A., Sharma, N., and Sharma, S. (2021). An affordable transradial prosthesis based on force myography sensor. Sensors Actuators A Phys. 325, 112699. doi:10.1016/j.sna.2021.112699

CrossRef Full Text | Google Scholar

Radmand, A., Scheme, E., and Kevin, E. (2016). High-density force myography: a possible alternative for upper-limb prosthetic control. J. Rehabilitation Res. Dev. 53 (4), 443–456. doi:10.1682/JRRD.2015.03.0041

PubMed Abstract | CrossRef Full Text | Google Scholar

Rehman, M.U., Shah, K., Haq, I.U., Iqbal, S., Ismail, M. A., and Fatih, S. (2023). Assessment of low-density force myography armband for classification of upper limb gestures. Sensors 23 (5), 2716. doi:10.3390/s23052716

PubMed Abstract | CrossRef Full Text | Google Scholar

Saadeh, M. Y., Carambat, T. D., and Arrieta, A. M. (2017). Evaluating and modeling force sensing resistors for low force applications. Available at: http://asmedigitalcollection.asme.org/SMASIS/proceedings-pdf/SMASIS2017/58264/V002T03A001/2568042/v002t03a001-smasis2017-3703.pdf.

CrossRef Full Text | Google Scholar

Sadarangani, G. P., Jiang, X., Simpson, L. A., Eng, J. J., and Menon, C. (2017). Force myography for monitoring grasping in individuals with stroke with mild to moderate upper-extremity impairments: a preliminary investigation in a controlled environment. Front. Bioeng. Biotechnol. 5, 42. doi:10.3389/fbioe.2017.00042

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadeghi, C., Rana, , and Menon, C. (2018). Regressing grasping using force myography: an exploratory study. Biomed. Eng. Online 17 (1), 159. doi:10.1186/s12938-018-0593-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakr, M., and Menon, C. (2017). “Study on the force myography sensors placement for robust hand force estimation,” in 2017 IEEE International Conference on Systems, Man, and Cybernetics, SMC 2017, 2017-January, 1387–1392. doi:10.1109/smc.2017.8122807

CrossRef Full Text | Google Scholar

Scheme, E., and Englehart, K. (2011). Electromyogram pattern recognition for control of powered upper-limb prostheses: state of the art and challenges for clinical use. J. Rehabilitation Res. Dev. 48 (6), 643–660. doi:10.1682/JRRD.2010.09.0177

PubMed Abstract | CrossRef Full Text | Google Scholar

Schofield, J. S., Evans, K. R., Hebert, J. S., Marasco, P. D., and Carey, J. P. (2016). The effect of biomechanical variables on force sensitive resistor error: implications for calibration and improved accuracy. J. Biomechanics 49 (5), 786–792. doi:10.1016/j.jbiomech.2016.01.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Shaikh, M. F., Salcic, Z., and Wang, K. (2015). “Analysis and selection of the force sensitive resistors for gait characterisation,” in 2015 6th International Conference on Automation, Robotics and Applications (ICARA), 370–375.

CrossRef Full Text | Google Scholar

Smith, L. H., Hargrove, L. J., Lock, B. A., and Kuiken, T. A. (2010). Determining the optimal window length for pattern recognition-based myoelectric control: balancing the competing effects of classification error and controller delay. IEEE Trans. Neural Syst. Rehabilitation Eng. A Publ. IEEE Eng. Med. Biol. Soc. 19 (2), 186–192. doi:10.1109/TNSRE.2010.2100828

PubMed Abstract | CrossRef Full Text | Google Scholar

Tchantchane, R., Zhou, H., Zhang, S., and Alici, G. (2023). A review of hand gesture recognition systems based on noninvasive wearable sensors. Adv. Intell. Syst. 5 (10), 2300207. doi:10.1002/AISY.202300207

CrossRef Full Text | Google Scholar

Torres, M., Sagaró, R., Broche, L., Delisle, D., Reyes, A., López, A., et al. (2015). Robotic system for upper limb rehabilitation. IFMBE Proc. 49, 948–951. doi:10.1007/978-3-319-13117-7_240

CrossRef Full Text | Google Scholar

Velásquez, A., and Flórez, J. A. (2010). Calibration of force sensing resistors (fsr) for static and dynamic applications. IEEE ANDESCON, 1–6. doi:10.1109/andescon.2010.5633120

CrossRef Full Text | Google Scholar

Xiao, Z. G., and Menon, C. (2019). A review of force myography research and development. Sensors Basel, Switz. 19 (20), 4557. doi:10.3390/S19204557

CrossRef Full Text | Google Scholar

Young, P. R., Hebert, J. S., Marasco, P. D., Carey, J. P., and Schofield, J. S. (2023). Advances in the measurement of prosthetic socket interface mechanics: a review of Technology, techniques, and a 20-year update. Expert Rev. Med. Devices 20, 729–739. doi:10.1080/17434440.2023.2244418

PubMed Abstract | CrossRef Full Text | Google Scholar