94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
Daniel Walter1*
Andreas Bergmann2Meike Maibach1Lara Huethorst1Lea Reinartz2Nina Grünewald1
Christoph Selter1
Andreas Harrer2- 1Institute for Development and Research in Mathematics Education, TU Dortmund University, Dortmund, Germany
- 2Faculty of Computer Science, University of Applied Sciences and Arts, Dortmund, Germany
One key training objective of pre-service teachers is to develop their diagnostic skills in order to enable them to support their students adequately. This article describes the conception and evaluation of the digital learning platform FALEDIA. Researchers from different perspectives of mathematics education on the one hand and of computer science on the other report on design principles and concrete realizations which intend to support the needs of the targeted user group. A pre-post-test about diagnostic skills with 695 pre-service teachers from two universities provides insights into their gains of knowledge. A questionnaire about learning styles was conducted and the pre-service teachers’ interactions with the digital learning plattform were tracked to get insights into their usage of the FALEDIA plattform. It is shown that pre-service teachers—from first-year to experienced—achieved significant performance gains in terms of diagnostic skills through the learning platform. With regard to usage, it could be shown that the self-assessed learning style has only little effect on usage behavior.
1 Introduction
It is repeatedly found internationally that a considerable proportion of learners—in Germany about 25%—leave primary school with below-average mathematical competencies (Mullis et al., 2020). Difficulties in learning mathematics in the secondary school forms are expected as a consequence for these children especially. It seems essential to professionalize teachers in such a way that they are able to support the children’s learning processes in a better way as early as primary school (Hoth et al., 2016; Leuders et al., 2018). Enabling future teachers—so called pre-service teachers—to appropriately support students has traditionally been considered a key issue in university education (Prediger and Selter, 2008).
Teachers must develop diagnostic skills and apply them in their own teaching. This is a central task for university teaching. However, there is often a problem, particularly in large-scale courses. While pre-service teachers are made aware of the importance of individual support, it is difficult for a single lecturer to exemplify this in a university course with sometimes several hundred participants. This is because it is challenging to provide individual support to all pre-service teachers when they are learning and thinking differently.
Digitally prepared learning offers for the teaching at universities could provide new impulses and contribute to the professionalization of teachers. However, with regard to the training of students who want to pursue the profession of primary school teachers in mathematics, the availability of subject-related learning platforms seems to be limited and should be expanded (Hollebrands et al., 2021). Until recently, there has been rarely any digital platform for the training of primary mathematics teachers that utilizes the potential of digital media—for example, feedback with an adaptive character (Reinhold et al., 2020) or linked representations (Lisarelli, 2023).
At this point, the FALEDIA project (ger.: fallbasierte Lernplattform zur Steigerung von Diagnosefähigkeiten; eng.: case-based learning platform to increase diagnostic skills)1 ties in. The FALEDIA learning platform aims to improve the diagnostic skills of prospective teachers by linking subject-specific and didactic knowledge with digitally implemented case-based learning situations. In this way, digital learning opportunities are available to increase diagnostic skills for various central arithmetic topics in a subject-specific manner.
The aim of this article is to describe the conceptual design of the FALEDIA learning platform and to present empirical findings related to pre-service teachers’ performance in the area of diagnostic skills before and after using the digital learning platform as well as pre-service teachers’ usage behavior. To this end, the article is structured as follows: section 2 first provides the theoretical background relevant to the design of the platform while section 3 reveals the design process. Section 4 deals with the conceptual design of the learning platform by presenting design principles from a computer science and mathematics education perspective as well as their concrete realization. Section 5 provides empirical findings on the evaluation of the concept by describing empirically recorded diagnostic skills of pre-service teachers and their usage of the platform. Finally, the article closes with a conclusion and outlook.
2 Theoretical background
In this section, the theoretical background to the conceptual design of the learning platform is presented by addressing the most relevant research. Section 2.1 deals with learning with learning platforms in university education, followed by section 2.2, which addresses the area of diagnostic skills.
2.1 Learning with learning platforms for teacher education
Learning Management Systems (LMS) such as Moodle or ILIAS are currently the central point of contact in the training of (pre-service) teachers, especially for accessing the materials provided for a particular course. This type of learning platform usage is an important part of university teacher training, as learning materials can be made available as files and collaboration can be coordinated (Lwande et al., 2021; Nagy, 2016). At the same time, however, LMS offer rather limited opportunities for subject-specific professionalization. For example, LMS provide only limited feedback with an adaptive and subject-related character. Furthermore, usage data can hardly be collected for research purposes. In many cases—including FALEDIA—these points lead to the decision to develop an own digital learning platform that is not based on a LMS and does not mainly emphasize organizational aspects but is intended for the training and research of professional subject-specific competencies. Key research findings on projects that have this focus are summarized below:
• In a quasi-experimental study, Enenkiel et al. (2022) investigated whether the video-based learning environment ViviAn can be suitable for promoting diagnostic skills of pre-service secondary school teachers. The pre-service teachers were presented with videotaped classroom situations, after which they were asked to assess students’ competencies. Compared to the control group, a significant learning development of the pre-service teachers could be identified in relation to their diagnostic skills.
• In addition, Wildgans-Lang et al. (2020) study of pre-service elementary school teachers suggests that documents of ‘virtual third graders’ embedded in a learning platform were perceived as authentic by the participants.
• This finding can also be supported by the study of Codreanu et al. (2020), which shows that learning platforms, if designed appropriately, can be helpful in diagnosing learners’ current levels of knowledge and highlighting learning potentials.
Learning platforms can thus be a tool that is seen as authentic by pre-service teachers and can potentially be used for the promotion of diagnostic skills. However, it seems to depend on the concrete design of the learning platforms to actually achieve this. In terms of the concrete design of web-based learning platforms, a broad distinction can be made between two variants, which differ primarily in terms of the activity of the users:
• Worked-examples (WE): Well-structured examples are presented, whereby the users mostly perceive the content receptively and not so actively (Garces et al., 2023). Renkl (2017) was able to show that worked-examples can also have a positive effect on the learning of mathematical concepts, especially in the introductory phase of studies.
• Problem-based learning (PBL): The users are encouraged to be active on their own, for example, through work assignments. The assignments are processed on the learning platform, which also provides the learners with individual feedback for constructive further work, e.g., through intelligent tutoring systems (Hursen, 2019; Koedinger et al., 1997, Booth et al., 2013).
Both approaches offer learning opportunities for (pre-service) teacher training. However, recent work integrates WE and PBL and could demonstrate promising performance developments (Neubrand et al., 2016; Loibl et al., 2017)—for larger cohorts as well (Booth et al., 2013; Saatz and Kienle, 2013). This aspect is also reflected in metareviews in the setting of technology-based learning (Bond et al., 2018).
Largely unexplored remain the questions, if rather WE or PBL have greater learning effects on different kinds of subjects of the teacher training curriculum for mathematics education in primary school, to what extent WE or PBL are subjectively perceived by pre-service teachers as conducive to learning, and how WE and PBL can be meaningfully related to each other when dealing with different domains. These questions will be addressed later (see section 4.3).
2.2 Learning of diagnostic skills of (pre-service) teachers
Major international comparative studies such as PISA or TIMSS have highlighted the need for individual support as one of the central responsibilities of schools (Mullis et al., 2020; OECD, 2019). However, to be able to support children adequately according to their individual needs, it is a necessary prerequisite that teachers are able to diagnose the knowledge, problems and ideas—summarized learning levels—of their students. Therefore, it is a common demand that (pre-service) teachers build up diagnostic skills already in pre-service teacher education (Loibl et al., 2020; Selter et al., 2017; Wagner and Ehlert, 2019).
Diagnostic activities are widely summarized as “all information that provides information about students’ learning opportunities, learning status, learning processes, and learning outcomes” (Steffens and Höfer, 2013, p. 24). Following this, in order to support learners, teachers need to be aware of children’s individual ways of thinking and learning levels (Hattie, 2009). However, research has shown that teachers are often able to predict which tasks are particularly difficult for children: It is also difficult for them to analyze why a particular task potentially causes difficulties for students. Additionally, (pre-service) teachers have difficulties identifying typical challenges to learning and misconceptions or describing mistakes in a student’s solution as well as finding reasons for these mistakes (Blömeke et al., 2014; Brunner et al., 2021; Carpenter et al., 1988; Hoth et al., 2016; Tirosh, 2000). Moreover, (pre-service) teachers sometimes select fostering tasks which are not matching the diagnosed difficulties (Barnhart and van Es, 2015; Schulz, 2014). Teachers therefore need well-trained skills in the area of diagnosis, which resembles a lifelong learning process. These skills are indispensable so that, on the one hand diagnoses can be carried out adequately and on the other hand appropriate consequences can be derived from them (Schiefele et al., 2019, p. 130). This poses significant challenges for teachers since the complexity and variety can hardly be thoroughly covered within pre-service teacher education and must therefore be addressed in teacher education.
The usage of cases is a sensible and frequently applied method for this, as they “can be used as prototypes to develop essential knowledge” (Doyle, 1990, p. 14). A case is considered a descriptive research document based on a real-life situation, problem or incident (Merseth, 1990, p. 54). Different types of cases such as videos, transcripts, audio files or written documents can be used. Casework has received increasing attention in pre-service teacher training since the 1980s (Sato and Rogers, 2010). The long tradition of cases in teacher education can be attributed to several advantages of cases:
“Cases and case methods offer a particularly promising possibility for teacher educators, teacher education programs, and those who wish to understand more deeply the human endeavor called teaching” (Merseth, 1990, p. 722).
One of these frequently mentioned reasons—among numerous others—for using cases in teacher education and training is the bridging between theory and practice (Doyle, 1990; Helleve et al., 2023; Sato and Rogers, 2010). Therefore, “cases have an essential role in teacher education as pedagogical tools for helping teachers practice the basic professional processes of analysis, problem-solving, and decision-making” (Doyle, 1990, p. 10). Practicing with cases enables the (pre-service) teachers to establish the relationship between the general and the specific in the used cases, realize several different ways to interpret one situation and offers the time for multiple perceptions of a situation—without immediate pressure to act (Hebenstreit et al., 2016; Helleve et al., 2023; Krammer et al., 2012).
Diagnostic skills, which are often acquired through practical teaching experience in traditional university teacher training programs, can be promoted through targeted case-based learning in the initial phase of teacher training (Prediger, 2010). These skills can also be applied in large-scale course settings. The detailed analysis of cases in form of vignettes deepens the understanding of complex teaching and learning situations and lays the foundation for reflective and practice-oriented teaching (Brandt, 2022).
Since diagnostic skills are topic-specific (Schulz, 2014), they should be built up using authentic examples from the respective topic. In the FALEDIA learning platform, case work is used to enable (pre-service) teachers to deal with student documents and to learn diagnostic skills on the basis of these documents, depending on a specific mathematical topic in primary education. The extent to which domain-specific casework in a digital implementation as a learning platform with individualized feedback in university teacher training can contribute to increasing the diagnostic skills of pre-service teachers has not yet been sufficiently researched and is therefore covered by the evaluation (see section 5).
3 The human-centered design process to develop the learning platform
After describing the background relevant to the development of the learning platform, the design process for developing the learning platform is presented below. It was iteratively developed as an interactive (web based) system within a multidisciplinary team. For the system to be most beneficial for its users—which is a common goal for interactive systems—it must be developed with the users’ needs and expectations in mind and likewise be based on current knowledge of human factors and ergonomics. To reach that goal there is a standardized process model (International Organization for Standardization, 2019) called the human-centered design (HCD) for interactive systems. Using a human-centered approach while designing learning solutions is widely established (Biabdillah et al., 2021; Chaves and Bittencourt, 2018; Zaharias and Poulymenakou, 2005) so we consider it an appropriate instrument for the target audience of pre-service mathematics teachers. In the following section the HCD is presented in detail and how it was implemented in the project. The process is divided into five phases (see Figure 1).
Figure 1
Figure 1. Human-centered design process based on International Organization for Standardization (2019).
Following these phases, the presented project was realized. It is essential to consider all phases to ensure the success of the project—bearing in mind that both disciplines (mathematics education as well as computer science) had different perspectives and requirements. The phases in the diagram are described in detail in the following:
3.1 Plan the human-centered design process
To enable the HCD it was necessary to plan regular meetings to ensure collaboration between the project partners. Therefore, all project partners met to exchange ideas and to discuss the project progress biweekly. In addition, several smaller and more focused meetings were established to develop and refine the discussed ideas.
3.2 Understand and specify the context of use
To understand and specify the context of use it is necessary to identify stakeholders, learn about specific characteristics and goals, and the environment in which the solution will most likely be used. The context of use was specified based on the experience the project partner in mathematics education have in regard of teaching courses in the relevant topics (here: diagnostic skills). While teaching those courses, an active exchange with the targeted audience is necessary and therefore a broad understanding of the difficulties and needs of the targeted audience was available.
3.3 Specify the user requirements
Based on the context of use the user requirements need to be specified. This was accomplished in this project by using personas (Cooper, 1999), a method to abstract specific characteristics of the targeted audience into fake persons to help the design team to understand and consider their needs and requirements. Examples of user requirements include the creation of self-directed learning opportunities or the combination of worked examples and problem-based learning.
3.4 Produce design solutions
All the previous work was considered to produce the design solutions. During development, it was important to maintain a constant exchange with all the stakeholders within the project team and to work iteratively on the design solutions in order to implement it in the best possible way and meet the specified user requirements. In this project, a mixture of paper prototypes (Snyder, 2003) and mockups of user interfaces was used to produce design solutions, which allows testing without software implementation. Each artifact was discussed with all stakeholders.
3.5 Evaluate the designs
Another important aspect is the evaluation of the design solutions. On the one hand evaluations with the targeted audience were conducted (see section 5). On the other hand, experts from six different universities and five government institutes with different backgrounds were consulted in order to receive multifaceted feedback to improve the design solutions.
Overall, the HCD is iterative. Each activity must be completed at least once, but each activity can be repeated several times when appropriate and it is possible to move from one activity to the next. In our case all phases were completed at least once and the phases specify the user requirements, produce design solutions, and evaluate the designs were repeated one time. It was necessary to repeat these phases because the first iteration did not fully meet the user requirements which uncovered during evaluation. One example is the input of free text, which has proven to be more complex on the technical side. On the other hand, the activity called paths (see Figure 2) was initially planned to be much more technically sophisticated than was necessary in the actual application. The division into modules was also developed in an iterative process. In general, the design team should do this for as long as necessary to produce design solutions that meets the user requirements. If the design solutions meet the user requirements the process is completed. This is usually checked by means of user evaluations and experts.
Figure 2
Figure 2. Element to stimulate exploration: paths (A: Instruction and children case to work with; B: selection of two diagnostic tasks; C: children solution of selected diagnostic tasks; D: selection of a fostering task with corresponding feedback).
4 Conceptual design of the learning platform
On the basis of the theoretical background, design principles are derived from a computer science and mathematics education perspective. Subsequently, the implementation of the principles is reported in the context of the presentation of the learning platform.
4.1 Design principles from a computer science perspective
When developing new interactive systems, it is common to build on the principles of how such systems should be designed in order to be suitable to users. Several principles need to be considered. The so-called eight golden rules of interface design by Shneiderman et al. (2017) are a widely accepted set of rules to improve the way interfaces are designed. In addition to Norman (2013) formulated seven design principles to ensure a sufficient human-centered design. The minimization of the cognitive load is essential in order to improve the chance for learning. Therefore, the insights of the cognitive load theory by Sweller et al. (2011) and Mayer’s Cognitive Theory of Multimedia Learning (CTML) (e.g., Mayer, 2005, 2017) were considered. Below, the most relevant principles (in short P) regarding the research questions (see section 5) are described:
4.1.1 P1 strive for consistency
In order to reduce the cognitive load and avoid possible irritations, it is advisable to ensure a high degree of consistency in the implementation (Shneiderman et al., 2017). This applies to the areas of structure, design, and usage. For example, on the learning platform the elements to stimulate exploration (see section 4.3) are an essential part in the project and are used at several places—with changing content but similar interaction. After learning how to interact with the elements users are able to focus on the content presented and the chances for learning are therefore improved.
4.1.2 P2 reduce short-term memory load
In the area of cognitive load, short-term memory load plays an important role. The less that needs to be retained in short-term memory, the better to improve chances for learning (Shneiderman et al., 2017). This aspect is also emphasized in the CTML, which points out, among other things, the need to consider the modality principle, the coherence principle and the contiguity principle. On the learning platform, when implementing the elements to stimulate exploration, attention was paid to making all necessary information accessible and visible on one screen to reduce the short-term memory load.
4.1.3 P3 discoverability
To be able to use the learning platform, it is necessary that the user can discover the possibilities of interaction (Norman, 2013). In relation to the learning platform in the case of elements to stimulate exploration it was ensured to highlight actionable items to help the user identify those and therefore be able to take action.
4.1.4 P4 conceptual model
On the learning platform, the different topics were divided into modules to enable the user to construct a conceptual model, which leads to understanding and a feeling of control (Norman, 2013). The structure remains consistent for each module. A unified navigation is realized as well as a specific navigation for the content within. The user selects an intended content and engages with it at their own pace. After finishing the first module the user should have a conceptual model that enables them to focus on the content while working with the next modules, which reduces the cognitive load and therefore improves the chances for learning.
4.2 Design principles from a mathematics education perspective
After the design principles have been examined from a computer science perspective, a mathematics education perspective will now follow. It will be described what a (virtual) learning environment is, which criteria usually are applied in mathematics education when designing learning environments, and finally how these criteria are implemented on the learning platform.
In school contexts, the term “learning environment” can be used in very different ways, ranging from the idea of creating an atmosphere conducive to learning in the classroom to the subject-specific design of teaching-learning settings (Hannafin, 1995). With regard to the latter, the concept of Reinmann and Mandl (2006) is often applied, who understand a learning environment as an overall arrangement that supports learners in their learning processes.
Certainly, the above understanding of the term is very general—the question of how such an overarching arrangement should be designed remains unclear. Wollring (2008) describes six central guiding ideas for this, which he originally established with regard to mathematics learning in primary school. However, they can also be applied to the university level and be used as criteria in the evaluation of virtual learning environments (Roth, 2022). Below, the criteria (in short C) are outlined and it is described how they were considered in FALEDIA.
4.2.1 C1 subject matter and meaning
Learning environments should have a mathematical subject matter that is ‘meaningful’ to and valued by the respective learners. The learning platform addresses core contents of primary school mathematics, such as operation and place value understanding, which every teacher will be confronted with in their daily work. In this respect, coherence of the contents on the learning platform with the later profession as a teacher is established.
4.2.2 C2 articulation, communication, social organization
Learning environments should allow multiple ways of working and articulating, as well as being able to retain individual or cooperatively generated learning products in a non-volatile way. This can be realized by spaces for designing (areas in which mathematical representations can be used flexibly) and for retaining (documentation function). This criterion is particularly fulfilled on the learning platform by the exploration elements, especially since they include areas that can be used flexibly in the learning process. The documentation function is fulfilled on the learning platform through the so-called state logging. The users log in to the platform with accounts created specifically by each person. The respective processing status is saved after logging out and is retrieved after logging in again.
4.2.3 C3 differentiate
Learning environments should offer the possibility to meet different learning requirements of learners and thus to differentiate. This criterion is fulfilled on the learning platform especially by the feedback functions with adaptive character. The processing of the digital elements is followed by subject-related feedback adapted to the respective input of the user, which encourages constructive further work. In addition, users can optionally call up further information through collapsible content. Furthermore, the learning platform provides user-friendly navigation to view content from the background knowledge section and/or content from the “Diagnosis and Fostering” section that is individually regarded as being of interest.
4.2.4 C4 logistics
The concern of the criterion “logistics” is that the contents addressed in the learning environments should be assessed as feasible in the respective educational field. Accordingly, concepts that are out of the ordinary do not fulfill this criterion. In relation to the developed learning platform, the contents should therefore be designed in such a way that they can easily be embedded in existing university structures. Since the contents addressed on the learning platform represent common learning subjects at universities with teacher training programs and are at the same time prescribed by educational policy, this criterion can be regarded as fulfilled on the content level. Furthermore, the learning platform can be embedded in existing course structures at different universities with moderate effort, as already demonstrated in the course of the project by a university transfer.
4.2.5 C5 evaluation
Learning environments should be evaluable on several levels with adequate effort. A positive evaluation can be considered as given if the learning success of the users is evidenced. In the accompanying research of the FALEDIA project it was proven that learners from different universities can significantly increase their diagnostic skills with the platform (see section 5).
4.2.6 C6 interconnection to other learning environments
Although learning environments usually address a specific mathematical subject, they should not be isolated. Rather, in the sense of relationship-based mathematics, they should also be designed in relation to several different mathematical objects, forms of representation, or patterns of argumentation. The learning platform addresses this criterion by connecting the presented contents to each other. For example, it can be helpful to use the learning content on the topic of understanding operations when working on the topic of place value understanding, since an understanding of multi-digit numbers is always required when calculating in the four basic arithmetic operations.
4.3 Realization on the learning platform
4.3.1 Module structure
The learning platform’s content is divided into modules, each addressing a selected topic of the primary school pupils’ mathematics learning trajectories (Clements and Sarama, 2019). This module structure supports user interaction and clarifies the structure. While developing the module structure the principles mentioned in 4.1 and 4.2 have been considered. Every module is structured equally (P1), and the different topics within a module are separated on specific pages (P2, P4).
Every module has a start page to inform the user about the content of the upcoming pages, a short motivation why exactly this content is discussed, and an overview over this module’s structure. The next page introduces the background knowledge that is needed to proceed in the module. This page acts as an outline for the background knowledge content that will follow, and an extended motivation is given why the discussed topics are necessary for the targeted audience.
On the following page, the content of the background knowledge, for example in the module place value understanding (C1), is divided into three parts (here: Bundling and unbundling, Place value and numerical value, Linking representations). However, depending on the thematic focus, there can also be any number of pages. By dividing the background knowledge into smaller pieces, it can be perceived more easily by the users and embedded in existing university course structures at different universities (C4). The theoretical background provided serves as the basis for being able to work on the following pages, which focus on practicing diagnosis and fostering, since well-founded mathematical knowledge is considered a prerequisite to interpret cases appropriately.
The next pages serve as the transition into the diagnosis and fostering area. A short description is given which facets of the background knowledge were discussed and which topics concerning diagnosis and fostering will follow (P2).
The diagnosis and fostering content is combined on one page. Based on the provided background knowledge the users are asked to interpret cases in order to enhance their diagnosis and fostering skills.
Every module ends with a competency list that contains competencies that are important in regard of the topics discussed in this module. The user has the possibility to rate their own knowledge based on the different competencies on a scale of one to four from insecure to confident and write a comment that is saved for possible later usage. By using these competence lists, prospective teachers can become aware of the topics in which they can still improve themselves—and in which they subjectively feel confident (Gutscher, 2018).
4.3.2 Balancing worked-examples and problem-based learning
As previously stated, both WE and PBL provide learning opportunities. Nevertheless, the relative merits and drawbacks of both concepts have been and continue to be a matter of considerable debate. Kirschner et al. (2006) have expressed reservations about PBL, citing a lack of sufficient guidance for users as a potential drawback. Hmelo-Silver et al. (2007) contend that PBL does not inherently require excessive guidance. Rather, the degree of guidance provided depends on the specific implementation. To achieve an optimal balance between user engagement and the presentation of structured examples, it may be beneficial to integrate WE and PBL. The existing body of research on learning platforms for the training of prospective primary school mathematics teachers has yet to demonstrate how a coordinated balance of WE and PBL can be designed.
A pilot study was conducted in order to obtain answers to the question of balancing WE and PBL. Individual interviews with prospective teachers, who had used two different variants of the learning platform (either solely WE or solely PBL) for two subjects of different complexity (place value understanding or operation understanding), were conducted and analyzed quantitatively. As part of the research, 21 prospective teachers were asked to express their individual preferences regarding the design of the platform in the subject areas. The interview data provides information on how to balance WE and PBL in a target-oriented manner for different topics of learning. The results are documented in detail in Böttcher et al. (2022). Here, only four essential findings are summarized, which were implemented into the design of the final version.
• Initial contact with new content as WE, deepening as PBL: According to the assessment of the prospective teachers, content that is unknown to them should first be prepared as a WE in order to support an introduction to the content. On the other hand, the prospective teachers argued that topics they were familiar with should be presented as PBLs in order to deepen and secure their existing knowledge.
• Complex content as WE, less complex content as PBL: The same situation applies to the question of how to deal with complex or less complex topics. Here, the data indicate that less complex content can certainly be connected with self-activities as PBL, while learning subjects classified as difficult should rather correspond to the design of WE.
• Getting an overview and refresher on WE: WE are perceived as helpful by prospective teachers especially when they are used with content that has an interwoven system (e.g., characterizing the different basic ideas in the topic of understanding operations). This also applies to those prospective teachers who should already know the content but would like to refresh their knowledge.
• Importance of PBL in diagnostic skills activities: The prospective teachers voted in unison for those activities to be set up as PBL, in which, for example, student errors had to be analyzed and support tasks had to be selected appropriately. They justified this with the fact that exactly these activities represent typical everyday activities for teachers in the classroom and that preparation for this should already take place accordingly during the university course.
The findings that students prefer instructions for complex content go along with the position of Kirschner et al. (2006). They state that new topics in particular, and those that are too complex to work out for yourself, can be introduced particularly well via explanations. However, there are findings by Wittwer and Renkl (2008) which indicate that explanatory interventions may be perceived as superfluous by learners who possess a substantial foundation of prior knowledge in the given domain.
This survey results indicating a student preference for PBL in diagnostic content—specifically, practical applications—should be interpreted as a target group-specific finding, for which, to the best of our knowledge, there are no further findings in the literature to date that have investigated this question precisely, yet.
The results were taken into account in the implementation of the final version of the learning platform, which contains both PBL and WE elements.
4.3.3 Elements to stimulate exploration
A core part of the project was the design and implementation of elements to stimulate exploration (C2) to enable self-directed learning. Their goal is to make the content accessible to the user in order to enhance conceptual understanding and its application. In total five distinguishable elements were created. The challenge was to create elements that are on the one hand meaningful for the targeted audience (C1) and on the other hand operational in terms of usability.
4.3.4 Element to stimulate exploration: groups
The basic idea behind this element is to find similar items in different representation forms and to divide them into groups (C6). Figure 3 shows groups with content from the diagnosis and fostering area. The assigned task is to check the 12 children documents (given cases) and to look for similarities regarding mistakes. Three cases belong to each group and the goal is to find the related documents and assign them into one group. The current progress in Figure 2 is that three cases are assigned to one group. The user checked this constellation and received positive feedback that the assignment was correct and a label is provided as a groups’ name. To complete the task the other cases must be assigned to the remaining—here still empty—groups.
Figure 3
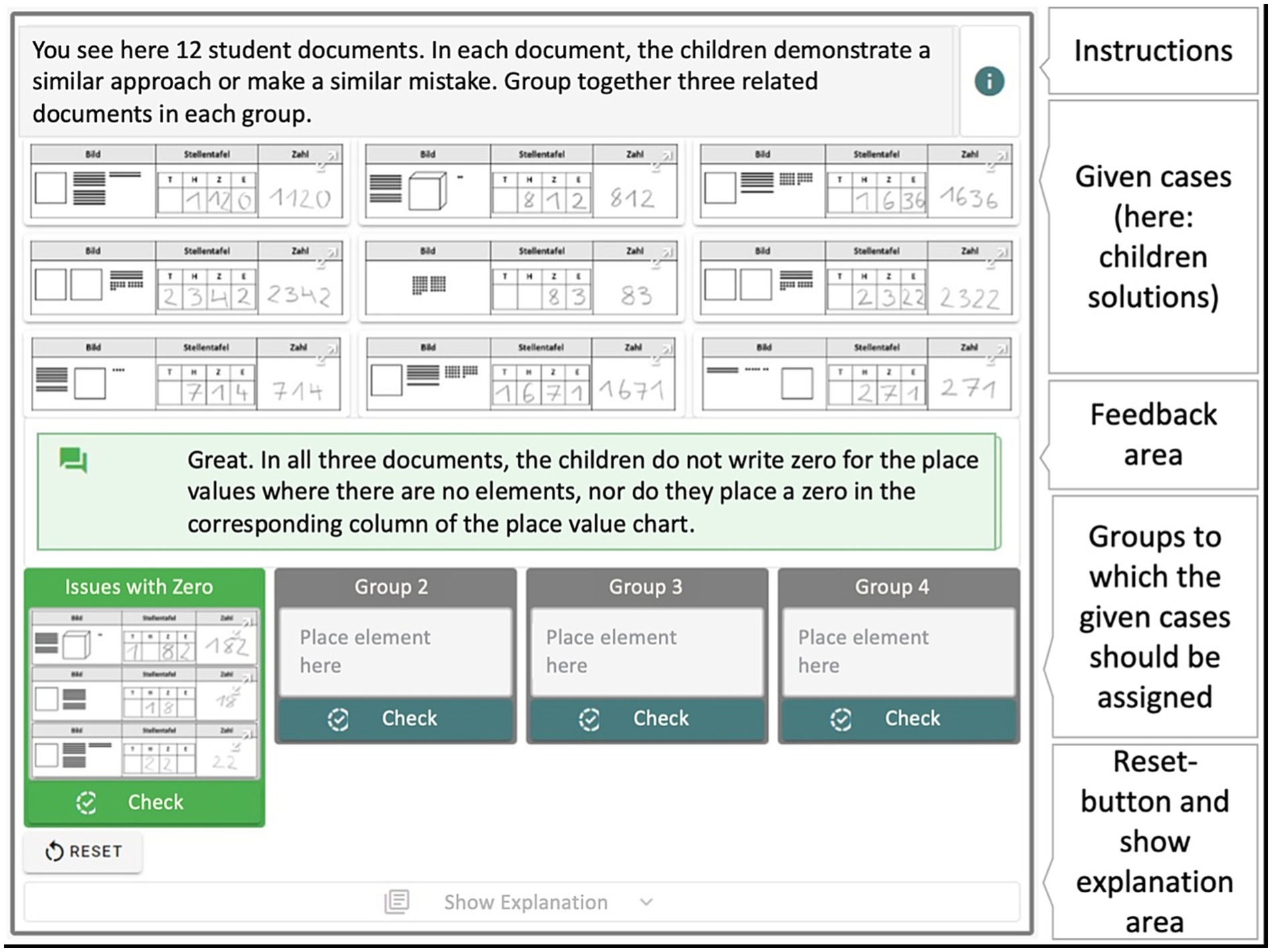
Figure 3. Element to stimulate exploration: groups [screenshot of the learning platform (left) with additional explanation of the relevant areas (right)].
The user is able to check, at any time, if the constructed groups contain items that belong together. After the check is performed, customized feedback is given based on the user’s classification of items. For example, if it is necessary to find three items but only two out of three belong together, and a check is requested, the system gives feedback that two items belong together, but one item is different. To enrich this feedback for the user it will mention to which kind of groups the items belong, but not exactly which item belongs to which group. The feedback is therefore based on the relationship between items inside an assigned group.
Groups can be setup in two modes, whether the group names should be hidden or displayed. When authoring the specific example this design decision has to be made by the author. If the group names are hidden items that belong together can be placed in any available group and the corresponding group name will be revealed with an additional success message if the check was successful.
Regarding the freedom of interaction (C3), the user has an extensive amount of possibilities to interact in this task. Because the user can check the assigned items at any time and the given feedback is based on the relationship between the items inside the group a lot of unique combinations can occur. For example, there are 12 items to choose from and always three items belong to one group. Now, if it was possible to receive feedback after one item is assigned to a group up until all 12 items are assigned, there would be 255 unique feedback combinations. While the technical implementation is capable of handling all feedback combinations, it is appropriate to reduce this number in order to minimize the associated work for creating the feedback and as well as to concentrate on the feedback that is meaningful for the user. In this particular case, a constraint is added that feedback is only given when at least three elements are assigned. A benefit associated with this constraint is to prevent the check of random combination to force the solution. This reduced the unique combinations to 241. Then, the feedback was constrained to appear only when exactly three items are assigned. This results in a total of 20 meaningful feedback messages: Four messages if all items belong to the correct group, 12 messages if two items belong to the correct group but one item is from a different group, and four messages if all items are from different groups. In addition to that two generic messages are added, one when no item is assigned and one when more than three items are assigned resulting in 22 feedback messages. In summary, the given feedback is limited depending on the minimum and maximum number of items in a group. Using these limitations, it was feasible to realize meaningful feedback for the user.
4.3.5 Element to stimulate exploration: paths
The basic idea behind paths is to practice the selection of appropriate diagnosis and fostering tasks based on a children’s document. Figure 2 shows paths with content from the diagnosis and fostering area.
Users are asked to analyze a case and make assumptions about the possible mistake (A). Based on the assumption the users have to choose two diagnosis tasks (out of four) they would let the child solve to gain more insight (B). After the two diagnosis tasks are chosen the users see the children’s solutions (C). Now the users are asked to choose one (out of four) fostering tasks they would let the child solve to resolve possible issues of understanding. Finally, the users receive feedback on how well suited the fostering task was considering the two selected diagnosis tasks and the corresponding children’s solution (D). This feedback approach is unique because it does not evaluate if the selection is right or wrong, which is generally difficult to achieve in the area of diagnosis and fostering, it describes whether the selected fostering task was appropriate for the children’s solution of the diagnosis tasks.
Regarding the freedom of interaction (C3), the user has a considerable number of possibilities to interact in this task. The user is able to choose any two tasks, but the number of tasks is limited to four. The combination of two out of four diagnosis tasks and one additional fostering task (out of four) results in 24 unique feedback messages. The design of this element reflects the tight connection between diagnosis and fostering.
4.3.6 Element to stimulate exploration: slider
The idea of slider is to visualize a process and let the user make decisions on the next step on several decision points. For example, the user has to select how an iconic representation will be displayed in the place value chart after adding and bundling further counters for number representation in various place value systems, for example in base 5 (see Figure 4). Depending on which of the three answer options is selected, the user receives specific feedback and, if the answer is incorrect, is given the opportunity to select another option.
Figure 4
Figure 4. Element to stimulate exploration: slider (screenshot of the learning platform).
The other two elements to stimulate exploration available on FALEDIA are only presented in outline form for reasons of limited space:
4.3.7 Element to stimulate exploration: order
While interacting with order the user should arrange a set of items (i.e., four numbers from different place value systems) on a scale.
4.3.8 Element to stimulate exploration: stamping
Stamping is a multilevel quiz based on a case. The purpose of the example is to analyze a case where a child consistently makes the same mistake, and then to indicate how the child is likely to complete the final task. It is necessary to answer all questions assigned to one level correctly to unlock the next level. The knowledge needed for the next level is based upon the previous level.
5 Evaluation of the concept
After the conceptual design of the digital learning platform has been presented in the previous parts of this paper, the evaluation of the concept will now follow. For this purpose, design decisions of the conducted study are revealed first, before the evaluation results are presented.
5.1 Study design
The learning platform was developed with the aim of contributing to the enhancement of diagnostic skills. In order to be able to explain possible learning effects, the way pre-service teachers use the platform is also of interest from the perspective of platform designers: The design of a learning platform can be tailored to specific design principles, such as navigational structure, with effects on usage and cognitive load on the learners. Depending on different learning styles (see below in section 5.2. for more details of our chosen learning style model), the effect of the design choices can influence system use and potentially also learning effects. Therefore, two research questions were posed as part of the study:
• RQ 1: Which diagnostic skills do pre-service teachers show before and after using the digital learning platform?
• RQ 2: How does the usage behavior on the digital learning platform of pre-service teachers differ based on the self-disclosed learning style?
The research questions primarily focus on examining indications of the learning platform’s effectiveness in terms of its potential to enhance diagnostic skills across various locations and different phases of the degree program. It is important to note that this study does not claim to demonstrate that the platform is more effective in developing diagnostic skills than other interventions. Furthermore, the study acknowledges that factors beyond pre-existing knowledge may contribute to the development of diagnostic abilities. A direct comparison of target groups from different universities is explicitly not intended, as the prerequisites and types of prior knowledge vary significantly between institutions and therefore cannot be directly compared. The study aims to evaluate potential indicators of the platform’s overall effectiveness rather than compare outcomes between specific institutions or student groups or assert superiority over further educational approaches.
In order to answer the research questions, the digital learning platform was used in the winter semester of 2021/2022 in three obligatory university courses at two universities in Germany (TU Dortmund University and University of Münster) as part of teacher training in mathematics education for primary schools. The courses differ in particular with regard to their positioning in the program of study:
1. “Learning and applying arithmetic”: A course for first-semester students (Bachelor’s program) at the University of Münster, attended by 338 pre-service teachers.
2. “Basic Ideas of Mathematics Education”: A course for 306 pre-service teachers in the Bachelor’s program at the TU Dortmund University in the third or fifth semester.
3. “Mathematical Kaleidoscope”: A course for pre-service teachers in the Master’s program at the University of Münster in which 51 students participated.
The sample thus comprises a total of 695 pre-service teachers. The learning platform was used in the courses listed above to gain insights into the extent to which the learning platform impacts on the diagnostic skills of pre-service teachers at different settings and time points in the course of their studies.
In the absence of an appropriate instrument for measuring diagnostic skills with regard to place value understanding, a new and piloted instrument—a written test—was developed to fill this gap. Participation was anonymous, so that no demographic data of the participants can be provided. All pre-service teachers were obligated to participate in the evaluation study by completing written tests before and after using the learning platform. With these tests, the diagnostic skills of the pre-service teachers were assessed using the example of the content area place value understanding. The test consisted of two tasks. The starting point for task 1 was a case study in which a second grader was asked to transfer a pictorial representation into the number representation. The error here is that the number of base-ten-blocks was determined column by column (here: one hundred, ten tens, and two tens) and then the individual numbers (1, 10, 2) were written down one after the other, which led to the number 1102, that does not match the pictoral representation—since the pictorial represents the number 220 (see Figure 5). Based on this case, the prospective teachers were asked to (1a) describe what the child did correctly, (1b) describe what the child did not do correctly, and (1c) explain possible causes of the error. The tasks outlined represent key elements of diagnostic skills (Hill et al., 2008; Wuttke and Seifried, 2017).
Figure 5
Figure 5. Case study used for task 1.
In task 2, the prospective teachers are given another case in which a different error is made. Although the base-ten-blocks given in the pictorial representation had been transferred correctly to the place value chart, no bundling process was carried out during the transfer to the number representation. Instead of the number 252, the number 2322 was written down (see Figure 6). Based on this case, the prospective teachers were presented with a total of four consecutive tasks for which they were asked to assess whether these tasks appeared suitable for gaining more information about the child’s thinking. The assessment had to be given on a Likert scale (from “very suitable” to “not suitable at all”) and also explained in a written explanation. For example, the task “You have 8 tens and 7 ones. What is the number? You get another 5 ones. What is the number now? Write down the number,” as it also requires bundling in one place (here: the ones), which can be identified as an obvious cause of the error in the case study. In contrast, the task “Place the number 283 with base-ten-blocks” can be regarded as less suitable, as no bundling activities are necessary here.
Figure 6
Figure 6. Case study used for task 2.
The analysis was based on a system of categories developed in which the categories describing mistakes, analyzing the causes of mistakes, and assessing diagnostic tasks were distinguished according to the tasks used. Points were given if the participants addressed the relevant subject-specific and subject-didactic background facets in their answers. Bundling and unbundling, place value and numerical value and change of representations are particularly relevant for understanding place value. For task 1 a/b (max. 6 points) or c (max. 6 points), two points were awarded for each background facet, depending on whether they were addressed appropriately, partially appropriately, inappropriately or not at all. In task 2, a maximum of 15 points could be collected, whereby 3 points were awarded for a suitable analysis of the case and a maximum of 3 points per diagnostic task for a suitable assessment of each of the four proposed diagnostic tasks. In total, a maximum of 27 points could be achieved in the test. Each test was analyzed by two people. A Krippendorff’s alpha of 𝛼 =0.86 could be determined and confirms a satisfactory intercoder reliability. Significances were calculated using Anovas.
In order to be able to identify possible learning effects of the students on the learning platform, the pre-service teachers were instructed to use the learning platform exclusively for self-study. Furthermore, there was no input on the topic of place value understanding in the respective course during the intervention phase. In this way, it should be ensured that potential learning gains are due to the learning platform and not, for example, to a lecture on the topic of place value understanding or other support activities, such as accompanying exercises and exchanges with other students. Naturally, it cannot be guaranteed that the participants did not obtain information on the topic in other ways during the intervention. However, for reasons of research methodology, the subjects were advised in detail not to deal with other sources that address place value understanding—though a stronger integration of the learning platform for example with lecture and exercise content would of course seem both conceivable and sensible. The learning platform is not intended to replace face-to-face learning or exchange between students on the one hand and exchange with lecturers on the other.
For analyzing RQ 2 the pre-service teachers were asked to complete a survey on learning styles. Learning style models help to differentiate a population of learners according to specific differences in learning behavior and preferences; thus using an instrument to identify learning styles in addition to other metrics of interaction with the system can help to identify if the learning platform is suitable generally and/or with specific sub-populations of learners.
The learning platform was built in its current form with little personalized features that address different learners’ characteristics. Therefore, it is necessary to gain insights if learners show different user behavior based on their self-disclosed learning style while using the same learning platform to figure out if the platform needs a more adaptive approach.
The Felder-Silverman Learning Style Model (Felder, 1988) was chosen as a survey instrument because it is well established and frequently used (Raj and Renumol, 2022) in science education. In addition to that, the user behavior was tracked using logfiles to be able to correlate the user behavior to the self-disclosed learning style.
For ethical reasons, the authors of this paper decided not to create a control group, as the surveys were conducted as part of required courses in the elementary teacher education programs, which students attend only once. It therefore does not seem justifiable to deliberately withhold information and learning opportunities from a potential control group.
6 Empirical findings
6.1 Diagnostic skills
This section reports results for RQ 1, which addresses pre-service teachers’ diagnostic skills before and after engagement with the learning platform. Table 1 shows the pre-and post-test data for each of the three pre-service teachers cohorts.
Table 1
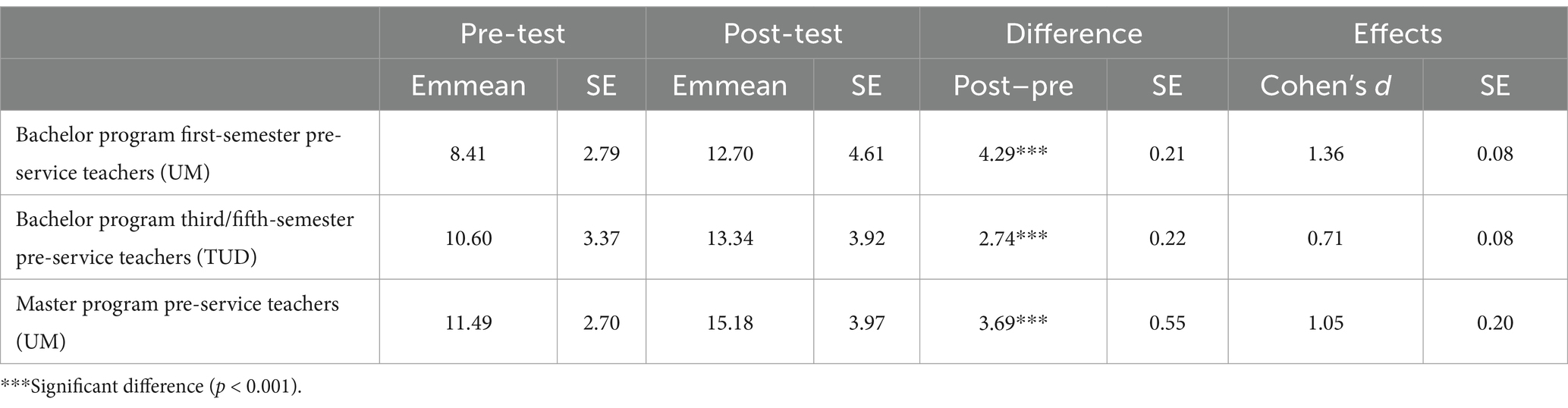
Table 1. Diagnostic skills of pre-service teachers of different courses before and after the use of the learning platform.
The results show that pre-service teachers at all three points in their studies achieved higher test scores after using the learning platform than before. First-semester Bachelor’s pre-service teachers at the University of Münster scored an average of 8.41 points in the pre-test and 12.7 points in the post-test, pre-service teachers in their third and fifth bachelor’s semester at TU Dortmund University scored an average of 10.6 points in the pre-test and 13.34 points in the post-test. The most experienced pre-service teachers in the Master’s program at University of Münster achieved 11.49 points in the pre-test and 15.18 points in the post-test.
The performance gains are significant for all three cohorts, each with p < 0.05. Furthermore, the effect sizes determined with Cohen’s d show a medium effect in the Bachelor’s course at the TU Dortmund University (d2 = 0.71) and strong effects in both the Bachelor’s first semester course and the Master’s course at the University of Münster (d1 = 1.36, d3 = 1.05).
Despite the statistically significant increases in performance as well as medium and strong effects, it should be pointed out that on average, the pre-service teachers show diagnostic skills that need improvement after using the learning platform. It is to be noted that the average scores of the pre-service teachers after using the learning platform are far from the maximum possible 27 points across all courses, so that there still seems to be a need for professionalization even after using the learning platform. However, the post-tests also identified pre-service teachers who were able to achieve all points. This could not be determined in the pretest, in which a maximum of 22 points were achieved across all courses (see Figure 7).
Figure 7
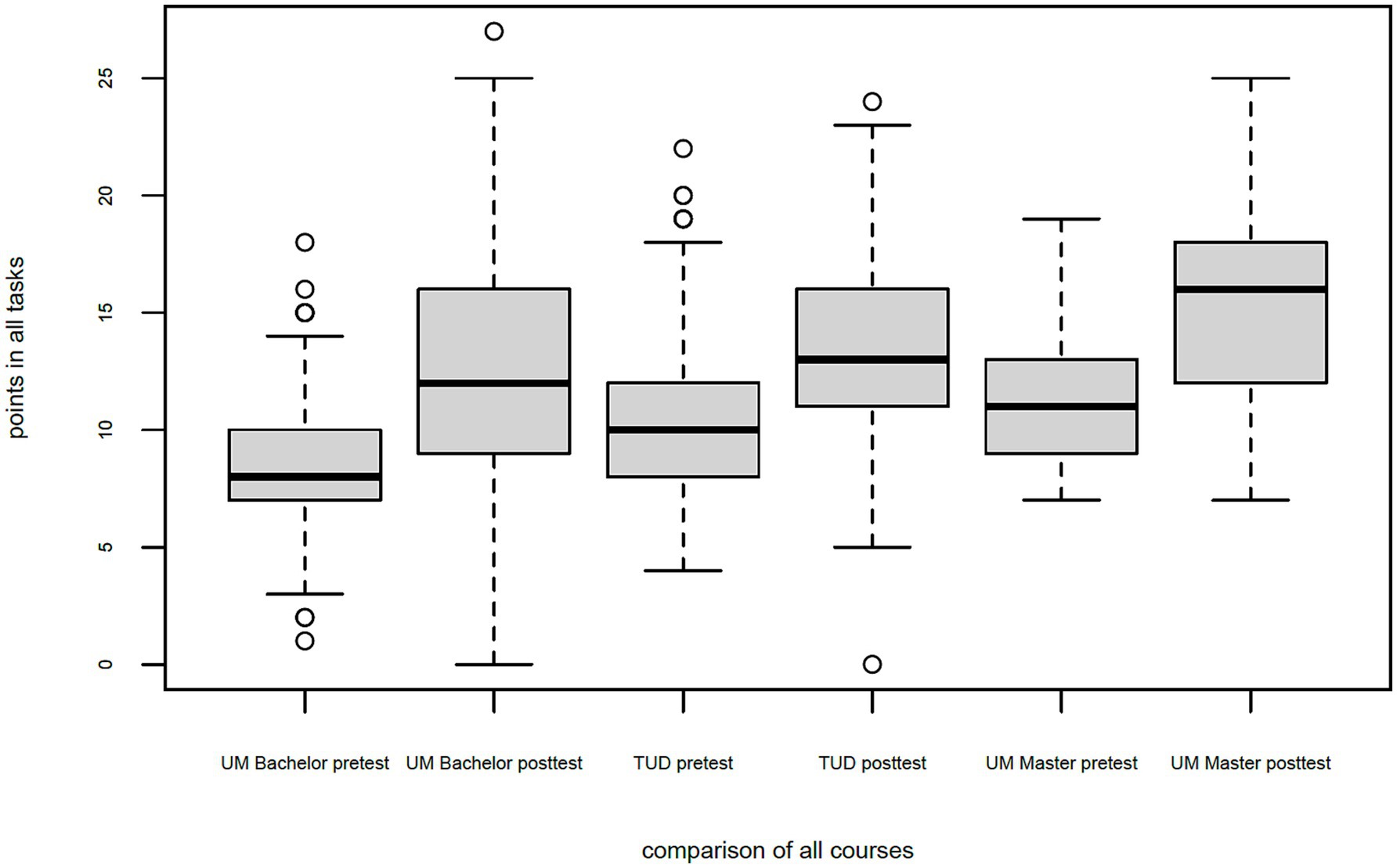
Figure 7. Diagnostic skills of pre-service teachers of different courses before and after the use of the learning platform—Boxplot.
The increase in diagnostic skills due to the learning platform, which combines informative and exploration-stimulating elements, can be classified as profitable, especially in the light of a preliminary study that was carried out. In the pilot study, the pre-service teachers were presented with variants of the learning platform that contained only informative or exploration-stimulating elements. Accordingly, there was neither a balance between the elements nor were the criteria outlined in section 3 fulfilled. Although the results of the preliminary study also demonstrate significant increases in pre-service teachers’ performance, the effect sizes are smaller than in the data reported here (d = 0.59) (Böttcher et al., 2022). This finding points to the particular importance of a matched, subject-related combination of informative and exploration-stimulating elements of a learning platform. Furthermore, it can also be assumed that the considerable performance gains in the study presented here are not necessarily attributable to floor effects due to low performance in the pretest and inevitably expected high performance gains in the posttest. This requires a (digital) learning platform that is appropriate to the target group and adequately designed in terms of subject didactics.
6.2 Learning styles and user behavior
The following analysis focuses on the data set of rather experienced pre-service teachers in the third and fifth bachelor’s semesters at the TU Dortmund University, which had the same setup as in our first studies.
To answer RQ2 we investigate how the usage behavior differs based on the self-disclosed learning style. The Felder-Silverman Learning Style Model (Felder, 1988) is employed and correlated with tracked user behavior within the platform. This learning style model has four dimensions that can be seen as continuums: (1) active or reflective, (2) visual or verbal, (3) sensing or intuitive, and (4) sequential or global. The data collected from the abbreviated survey instrument (Graf et al., 2007) was used to cluster the individual pre-service teachers to find groups with different learning styles using k-means (MacQueen, 1967). Figure 8 shows the clusters according to differences in learning styles. Clusters 1 (turquoise) and 5 (light green) with mainly active and sensing learning style represent the pre-service teachers that we consider—within the learning style framework—to be most likely to use elements to stimulate exploration. In contrast cluster 2 (orange) represents the pre-service teachers with reflective behavior which we consider are least likely to use elements to stimulate exploration. Clusters 3 (blue) and 4 (pink) represent a combination of dimensions that does not allow a straightforward hypothesis with respect to exploration.
Figure 8
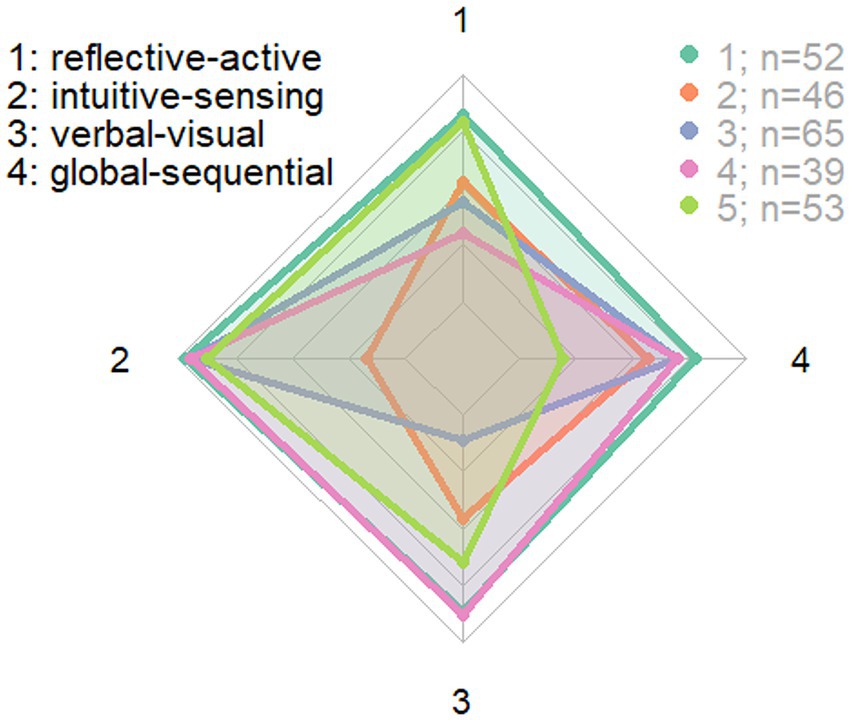
Figure 8. Clusters according to the four dimensions of Felder-Silverman in a spider diagram: each dimension is shown with the first adjective on the inner side and the second on the outer side scaled according to the users’ answers: e.g., “reflective-active” means that values at the outermost belong to active and at the innermost to reflective style.
Figure 8 shows metrics of pre-service teachers’ usage behavior in one of the modules (place value understanding) of the learning platform. The picture is split according to the clusters with the same color coding. It shows violin plots2: on the upper part the total time in seconds the pre-service teachers spent on the module, on the lower part the interaction factor, which represents the degree of explorative behavior. The interaction factor is calculated by dividing the time spent on the elements to stimulate exploration by the total time spent with the platform as a percentage. For all violin plots the probability is high around the median, which shows that the distribution is not skewed and does not require further analysis. All plots also have a similar interquartile range. The whiskers of the box plots have about the same reach. The median varies between the different clusters, so some effects of the learning style are visible: we have some indication that the active/sensing clusters [1 (turquoise), 5 (light green)] spend more time on the learning platform than cluster 2 (orange), yet a detailed investigation of these differences is needed. Furthermore, the shape of the probability density changes for each cluster, e.g., the peculiar shape of cluster 2 (orange) on the upper part requires deeper analysis.
In order to analyze the interaction and behavior with the elements to stimulate exploration the bar plot in Figure 9 was created. It shows the percentage of how many pre-service teachers of each cluster interacted with any elements to stimulate exploration, with all the mandatory3 elements to stimulate exploration, have solved all the mandatory elements to stimulate exploration, interacted with all elements to stimulate exploration and have solved all elements to stimulate exploration.
Figure 9
Figure 9. Violin plots with time spent (top) and interaction factor (bottom) for each cluster.
The data shows that there are some minor differences between the clusters within the categories. Further examination using the Bonferroni-Holm procedure (Holm, 2024) showed that the differences are not significant. This means that different learning styles do not significantly change the way the learning platform is used. Because the level of interaction is generally substantial and especially for the mandatory elements of the module very high (cf. the first two segments of bars in Figure 10) the design of the elements to stimulate exploration can be considered as an inviting interaction regardless of specific learning styles.
Figure 10
Figure 10. Percentage of interaction with elements to stimulate exploration for each cluster.
The evaluation thus provides arguments to the effect that the interdisciplinary collaboration consisting of a team of researchers from computer science and mathematics education led to a product that takes into account the specific needs of the focused user group. As a consequence of the results on user behavior and learning styles the learning platform seems to be suitable and activating for a wide range of different users. This does not yet answer if the preferences expressed in a learning style actually help learners when content is adapted to that learning style. The combination of the effects on diagnostic skills on different populations of learning styles is a next step in the data analysis to find out if a more adaptive approach is needed with respect to content and elements to stimulate exploration.
7 Discussion
This paper presented the conceptual design of the FALEDIA learning platform and empirical findings related to the diagnostic skills of pre-service primary mathematics teachers before and after using the learning platform, as well as results on learning styles and user behavior. The data indicate that using the learning platform in self-study can help to increase the diagnostic skills of pre-service teachers at different university locations and at different points in their studies—from first-year to experienced in the Master’s degree program. These results are in accordance with the findings of meta-analyses conducted, which integrate studies from various disciplines and corroborate the efficacy of digital learning opportunities with balanced proportions of PBL and WE (Barbieri et al., 2023; Gijbels et al., 2005; Walker & Leary, 2009).
With regard to usage, it was shown that the self-assessed learning style has hardly any effect on usage behavior, yet across different learning styles a substantial level of interaction with the elements to stimulate interaction was detected. Overall, our findings support a positive evaluation of the concept. However, a more comprehensive study of the interactions between different user groups with FALEDIA would appear to be beneficial in order to provide suggestions for improving the user experience.
During the implementation of the learning platform, a framework was provided through the use of the HCD in which a design solution was developed that meets the user requirements of the targeted audience of pre-service mathematics teachers. The use of the HCD can therefore be classified as successful regarding the evaluation.
With regard to the concrete design of learning platforms, a balanced combination of WE and PBL also proved to be beneficial to learning in the research project described here. Accordingly, the recommendation formulated in the literature to combine PBL and WE was confirmed. Thereby, casework seems to play an essential role, which enables teachers to increase their diagnostic skills. Casework should thus not only be considered in the context of non-digital university learning opportunities, but also and especially in digital learning opportunities, such as FALEDIA.
In this way, it was possible to pave new ways to increase the diagnostic skills of pre-service teachers. Through the associated professionalization of teachers, a contribution is also made indirectly to increasing the mathematics performance of primary school pupils, because teacher who have adequate diagnostic skills will be able to support students more adequately than those who are less professional in this area.
While the empirical results demonstrate how pre-service teachers’ diagnostic skills can be developed, the present study’s methodological decisions impose specific limitations that indicate potential avenues for future research. The most pertinent of these are outlined below:
• Local instead of global proof of efficacy: The data outlined refer to the use of an exemplary module of the learning platform on the topic of place value understanding. Seven further modules have been implemented on the basis of the study results described here on various topics, which are also relevant to primary school. In the context of future studies, a similar investigation to the one described in this article is desirable for other selected subject areas, so that the concept can be evaluated across various topics.
• Cross section instead of longitudinal section: The performance data of the pre-service teachers was collected at an interval of just 1 week, which limits the representativeness of the data to a cross-section rather than a longitudinal one. Consequently, it is unclear whether the observed performance developments are representative of long-term trends.
• Pre-service instead of in-service teachers: The present study was designed to examine the efficacy of FALEDIA in facilitating the professional development of pre-service teachers. However, it did not address whether experienced in-service teachers could also benefit from using FALEDIA and subsequently apply their enhanced skills in everyday classroom support situations, thereby enabling students to develop more pronounced competencies.
• Self-study instead of embedding in the course organization: In order to ascertain the extent to which FALEDIA can be attributed as a contributing factor to the observed learning effects, the pre-service teachers were required to utilize FALEDIA exclusively for self-study. This raises the question of how FALEDIA can be integrated into learning events in order to promote performance.
• Potential self-assessment bias: The learning styles identified were derived from data reported by the preservice teachers themselves, which may have introduced a degree of subjectivity into the process. Such an approach would be beneficial in order to circumvent self-assessment bias. However, this approach was not feasible within the context of this study, particularly given the necessity for multiple versions of the learning platform to accommodate diverse learning styles. This would have necessitated a completely different design for the learning platform, which would have significantly complicated the collection of performance data.
Finally, it should be pointed out that FALEDIA is by no means associated with the vision of creating pre-service teachers learning at the university exclusively within the framework of learning platforms. Rather, the aim is to meaningfully supplement existing course structures with empirically approved and conceptually appropriate digitally supported teaching-learning concepts. The fact that the learning platform was used in the evaluation solely for self-study by the pre-service teachers is primarily justified by research methodology, since learning effects can be attributed to the learning platform and not to other external stimulation on the topics. Of course, the learning platform is equally suitable for collaborative work and for making them the subject of university teaching.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
Ethical approval was not required for the studies involving humans because the aim of the study is to support prospective teachers in developing the diagnostic skills in mathematics that they urgently need for their work as teachers, as stipulated by the teacher training laws in Germany. All subjects explicitly agreed to participate in the study and used the same supportive learning materials, so that no individual prospective teachers were favored or disadvantaged. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Author contributions
DW: Writing – original draft. AB: Writing – review & editing. MM: Writing – review & editing. LH: Writing – review & editing. LR: Writing – review & editing. NG: Writing – review & editing. CS: Writing – review & editing. AH: Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This FALEDIA project was funded by the Federal Ministry of Education and Research (BMBF) in the Federal Republic of Germany (funding reference number: 16DHB3017).
Acknowledgments
For parts of this contribution, the following consulting/analysis services were used by the Statistical Consulting and Analysis Unit (SBAZ) of the Center for Higher Education at TU Dortmund University: statistical questioning and data collection, data mask/data entry/data processing, statistical methodology, selection of statistical software or statistical programming, data analysis, statistical formulation of text passages.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The authors declare that no Gen AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
2. ^Violin plots contain box plots and show the probability density of the values.
3. ^Mandatory elements are directly visible on the corresponding pages in regard to elements that are hidden behind an expandable items labeled “display additional exercise.”
References
Barbieri, C. A., Miller-Cotto, D., Clerjuste, S. N., and Chawla, K. (2023). A meta-analysis of the worked examples effect on mathematics performance. Educ. Psychol. Rev. 35:11. doi: 10.1007/s10648-023-09745-1
Barnhart, T., and Van Es, E. (2015). Studying teacher noticing: examining the relationship among pre-service science teachers’ ability to attend, analyze and respond to student thinking. Teach. Teach. Educ. 45, 83–93. doi: 10.1016/j.tate.2014.09.005
Biabdillah, F., Tolle, H., and Bachtiar, A. (2021). Go story: design and evaluation educational Mobile learning podcast using human centered design method and gamification for history. J. Infor. Technol. Comput. Sci. 6, 308–318. doi: 10.25126/jitecs.202163345F
Blömeke, S., König, J., Busse, A., Suhl, U., Benthien, J., Döhrmann, M., et al. (2014). Von der Lehrerausbildung in den Beruf–Fachbezogenes Wissen als Voraussetzung für Wahrnehmung, Interpretation und Handeln im Unterricht. Z. Erziehungswiss 17, 509–542. doi: 10.1007/s11618-014-0564-8
Bond, M., Bedenlier, S., Buntins, K., Kerres, M., and Zawacki-Richter, O. (2018). Systematic. Reviews in educational technology research: Potential and pitfalls. Paper Presented at EdMedia Conference, Amsterdam.
Booth, J. L., Lange, K. E., Koedinger, K. R., and Newton, K. J. (2013). Using example problems to improve student learning in algebra: differentiating between correct and incorrect examples. Learn. Instr. 25, 24–34. doi: 10.1016/j.learninstruc.2012.11.002
Böttcher, M., Huethorst, L., Walter, D., Gutscher, A., Selter, C., Bergmann, A., et al. (2022). “FALEDIA–design and research of a digital case-based learning platform for primary pre-service teachers” in Proceedings of the Twelfth Congress of the European Society for Research in Mathematics Education (CERME12). eds. J. Hodgen, E. Geraniou, G. Bolondi, and F. Ferretti (Bozen-Bolzano, Italy: Free University of Bozen-Bolzano and ERME), 1–8.
Brandt, J. (2022). Diagnose und Förderung erlernen: Untersuchung zu Akzeptanz und Kompetenzen in einer universitären Großveranstaltung. Wiesbaden: Springer Fachmedien Wiesbaden.
Brunner, K., Obersteiner, A., and Leuders, T. (2021). How prospective teachers detect potential difficulties in mathematical tasks – an eye tracking study. RISTAL 4, 109–126. doi: 10.23770/rt1845
Carpenter, T. P., Fennema, E., Peterson, P. L., and Carey, D. A. (1988). Teachers’ pedagogical content knowledge of students’ problem solving in elementary arithmetic. J. Res. Math. Educ. 19, 385–401. doi: 10.5951/jresematheduc.19.5.0385
Chaves, I. G., and Bittencourt, J. P. (2018). Collaborative learning by way of human-centered design in design classes. Strat. Design Res. J. 11, 27–33. doi: 10.4013/sdrj.2018.111.05
Clements, D. H., and Sarama, J. (2019). Learning and teaching with learning trajectories [LT]2. Marsico institute, Morgridge College of Education, University of Denver. Available online at: learningtrajectories.org.
Codreanu, E., Sommerhoff, D., Huber, S., Ufer, S., and Seidel, T. (2020). Between authenticity and cognitive demand: finding a balance in designing a video-based simulation in the context of mathematics teacher education. Teach. Teach. Educ. 95:103146. doi: 10.1016/j.tate.2020.103146
Cooper, A. (1999). “The inmates are running the asylum” in Software-Ergonomie’99. eds. U. Arend, E. Eberleh, and K. Pitschke (Wiesbaden: Vieweg+Teubner Verlag), 17.
Enenkiel, P., Bartel, M.-E., Walz, M., and Roth, J. (2022). Diagnostische Fähigkeiten mit der videobasierten Lernumgebung Vivi An fördern. J. Math. Didakt 43, 67–99. doi: 10.1007/s13138-022-00204-y
Felder, R. (1988). Learning and teaching styles in engineering education. J. Eng. Educ. 78, 674–681.
Garces, S., Vieira, C., Ravai, G., and Magana, A. J. (2023). Engaging students in active exploration of programming worked examples. Educ. Inf. Technol. 28, 2869–2886. doi: 10.1007/s10639-022-11247-6
Gijbels, D., Dochy, F., Van Den Bossche, P., and Segers, M. (2005). Effects of problem-based learning: a meta-analysis from the angle of assessment. Rev. Educ. Res. 75, 27–61. doi: 10.3102/00346543075001027
Graf, S., Viola, S. R., Leo, T., and Kinshuk,. (2007). In-depth analysis of the Felder-Silverman learning style dimensions. J. Res. Technol. Educ. 40, 79–93. doi: 10.1080/15391523.2007.10782498
Gutscher, A. (2018). Kompetenzlisten und Lernhinweise zur Diagnose und Förderung. Wiesbaden: Springer Fachmedien Wiesbaden.
Hannafin, M. J. (1995). “Open learning environments. Foundations, assumptions, and implications for automated design” in Automating instructional design: computer-based development and delivery tools. eds. R. D. Tennyson and A. E. Baron (Berlin, Heidelberg: Springer), 101–130.
Hattie, J. (2009). Visible learning: a synthesis of over 800 meta-analyses relating to achievement. London; New York: Routledge.
Hebenstreit, A., Hinrichsen, M., Hummrich, M., and Meier, M. (2016). “Einleitung – eine Reflexion zur Fallarbeit in der Erziehungswissenschaft” in Was ist der Fall? eds. M. Hummrich, A. Hebenstreit, M. Hinrichsen, and M. Meier (Wiesbaden: Springer Fachmedien Wiesbaden), 1–9.
Helleve, I., Eide, L., and Ulvik, M. (2023). Case-based teacher education preparing for diagnostic judgement. Eur. J. Teach. Educ. 46, 50–66. doi: 10.1080/02619768.2021.1900112
Hill, H. C., Ball, D. L., and Schilling, S. G. (2008). Unpacking pedagogical content knowledge: conceptualizing and measuring teachers’ topic-specific knowledge of students. J. Res. Math. Educ. 39, 372–400.
Hmelo-Silver, C. E., Duncan, R. G., and Chinn, C. A. (2007). Scaffolding and achievement in problem-based and inquiry learning: a response to Kirschner, Sweller, and Clark (2006). Educ. Psychol. 42, 99–107. doi: 10.1080/00461520701263368
Hollebrands, K., Anderson, R., and Oliver, K. (Eds.) (2021). Online learning in mathematics education. Cham: Springer International Publishing.
Hoth, J., Döhrmann, M., Kaiser, G., Busse, A., König, J., and Blömeke, S. (2016). Diagnostic competence of primary school mathematics teachers during classroom situations. ZDM 48, 41–53. doi: 10.1007/s11858-016-0759-y
Hursen, C. (2019). The effect of technology supported problem-based learning approach on adults’ self-efficacy perception for research-inquiry. Educ. Inf. Technol. 24, 1131–1145. doi: 10.1007/s10639-018-9822-3
International Organization for Standardization. (2019). Ergonomics of human-system interaction—part 210: Human-centred design for interactive systems (ISO standard no. 9241–210: 2019). Available online at: https://www.iso.org/standard/77520.html (Accessed October 13, 2024).
Kirschner, P. A., Sweller, J., and Clark, R. E. (2006). Why minimal guidance during instruction does not work: an analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educ. Psychol. 41, 75–86. doi: 10.1207/s15326985ep4102_1
Koedinger, K. R., Anderson, J. R., Hadley, W. H., and Mark, M. A. (1997). Intelligent tutoring goes to school in the big City. Int. J. Artif. Intell. Educat. 8, 30–43.
Krammer, K., Lipowsky, F., Pauli, C., Schnetzler, C., and Reusser, K. (2012). “Unterichtsvideos als Medium zur Professionalisierung und als Instrument der Kompetenzerfassung von Lehrpersonen” in Lehrerprofessionalisierung wissenschaftlich begleiten – Strategien und Methoden. eds. M. Kobarg, C. Fischer, I. Dalehefe, F. Trepke, and M. Menk (Münster, u.a.: Waxmann), 69–86.
Leuders, T., Dörfler, T., Leuders, J., and Philipp, K. (2018). “Diagnostic competence of mathematics teachers: unpacking a complex construct” in Diagnostic competence of mathematics teachers. eds. T. Leuders, K. Philipp, and J. Leuders (Cham: Springer International Publishing), 3–31.
Lisarelli, G. (2023). Transition tasks for building bridges between dynamic digital representations and Cartesian graphs of functions. Digit. Exp. Math. Educ. 9, 31–55. doi: 10.1007/s40751-022-00121-2
Loibl, K., Leuders, T., and Dörfler, T. (2020). A framework for explaining teachers’ diagnostic judgements by cognitive modeling (Dia CoM). Teach. Teach. Educ. 91:103059. doi: 10.1016/j.tate.2020.103059
Loibl, K., Roll, I., and Rummel, N. (2017). Towards a theory of when and how problem solving followed by instruction supports learning. Educ. Psychol. Rev. 29, 693–715. doi: 10.1007/s10648-016-9379-x
Lwande, C., Oboko, R., and Muchemi, L. (2021). Learner behavior prediction in a learning management system. Educ. Inf. Technol. 26, 2743–2766. doi: 10.1007/s10639-020-10370-6
MacQueen, J. (1967). “Some methods for classification and analysis of multivariate observations” in Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Statistics, 5.1 (University of California, Los Angeles: University of California Press), 281–297.
Mayer, R. E. (2005). “Cognitive theory of multimedia learning” in The Cambridge handbook of multimedia learning. ed. R. E. Mayer (Cambridge: Cambridge University Press), 31–48.
Mayer, R. E. (2017). Using multimedia for e-learning. Comput. Assist. Learn. 33, 403–423. doi: 10.1111/jcal.12197
Mullis, I. V. S., Martin, M. O., Foy, P., Kelly, D. L., and Fishbein, B. (2020). TIMSS 2019 international results in mathematics and science. Available at: https://timssandpirls.bc.edu/timss2019/international-results/ (Accessed October 13, 2024).
Nagy, J. T. (2016). Using learning management systems in business and economics studies in Hungarian higher education. Educ. Inf. Technol. 21, 897–917. doi: 10.1007/s10639-014-9360-6
Neubrand, C., Borzikowsky, C., and Harms, U. (2016). Adaptive prompts for learning evolution with worked examples - highlighting the students between the “novices” and the “experts” in a classroom. Int. J. Environ. Sci. Educ. 11, 6774–6795. doi: 10.25656/01:12680
Norman, D. (2013). The design of everyday: revised and expanded edition. Hachette UK, Cambridge, Mass: MIT Press.
OECD (2019), PISA 2018 results (volume I): what students know and can do. Paris: PISA, OECD Publishing. Available at: https://www.oecd.org/en/publications/2019/12/pisa-2018-results-volume-i_947e3529.html (Accessed October 13, 2024).
Prediger, S. (2010). How to develop mathematics-for-teaching and for understanding: the case of meanings of the equal sign. J. Math. Teacher. Educ. 13, 73–93. doi: 10.1007/s10857-009-9119-y
Prediger, S., and Selter, C. (2008). Diagnose als Grundlage für individuelle Förderung im Unterricht. Schule NRW 60, 113–116.
Raj, N. S., and Renumol, V. G. (2022). A systematic literature review on adaptive content recommenders in personalized learning environments from 2015 to 2020. J. Comput. Educ. 9, 113–148. doi: 10.1007/s40692-021-00199-4
Reinhold, F., Hoch, S., Werner, B., Richter-Gebert, J., and Reiss, K. (2020). Learning fractions with and without educational technology: what matters for high-achieving and low-achieving students? Learn. Instr. 65:101264. doi: 10.1016/j.learninstruc.2019.101264
Reinmann, G., and Mandl, H. (2006). “Unterrichten und Lernumgebungen gestalten” in Pädagogische Psychologie. Ein Lehrbuch. eds. A. Krapp and B. Weidenmann (Weinheim: Beltz). 613–658.
Renkl, A. (2017). Learning from worked-examples in mathematics: students relate procedures to principles. ZDM 49, 571–584. doi: 10.1007/s11858-017-0859-3
Roth, J. (2022). “Digitale Lernumgebungen–Konzepte, Forschungsergebnisse und Unterrichtspraxis” in Digitales Lehren und Lernen von Mathematik in der Schule. eds. G. Pinkernell, F. Reinhold, F. Schacht, and D. Walter (Berlin: Springer Berlin Heidelberg). 109–136.
Saatz, I., and Kienle, A. (2013). Increasing quality in large scale university courses–Eflashcards as an approach to support active learning and individual facilitation. J. E-learn. Educ. Hagen. 9.
Sato, M., and Rogers, C. (2010). “Case methods in teacher education” in International encyclopedia of education (Elsevier), 592–597.
Schiefele, C., Streit, C., and Sturm, T. (2019). Pädagogische Diagnostik und Differenzierung in der Grundschule. Mathe und Deutsch inklusiv unterrichten. München: Ernst Reinhardt Verlag.
Schulz, A. (2014). Fachdidaktisches Wissen von Grundschullehrkräften. Wiesbaden: Springer Fachmedien Wiesbaden.
Selter, C., Hußmann, S., Hößle, C., Knipping, C., Lengnink, K., and Michaelis, J. (2017). Diagnose und Förderung heterogener Lerngruppen. Münster: Waxmann.
Shneiderman, B., Plaisant, C., Cohen, M., Jacobs, S., Elmqvist, N., and Diakopoulos, N. (2017). Designing the user Interface: Strategies for effective human-computer interaction. Sixth Edn. Boston, MA: Pearson Education (US).
Snyder, C. (2003). Paper prototyping: the fast and easy way to design and refine user interfaces. Burlington: Morgan Kaufmann Publishers.
Steffens, U., and Höfer, D. (2013). “Die Hattie-Studie–Forschungsbilanz und Handlungsperspektiven” in Die Hattie Studie, Ergebnisse und Perspektiven. ed. H. Börner (Bad Berka: Thüringer Institut für Lehrerfortbildung). 10–35.
Tirosh, D. (2000). Enhancing prospective teachers’ knowledge of children’s conceptions: the case of division of fractions. J. Res. Math. Educ. 31:5. doi: 10.2307/749817
Wagner, L., and Ehlert, A. (2019). “Diagnostic competence of math teacher students - an important skill in inclusive settings,” in Inclusive mathematics education: Research results from Brazil and Germany, eds M. Knigge, D. Kollosche, O. Skovsmose, R. M. José Souzade, and M. G. Penteado, Cham: Springer International Publishing) 561–579.
Walker, A., and Leary, H. (2009). A problem based learning meta-analysis: differences across problem types, implementation types, disciplines, and assessment levels. Interdiscipl. J. Probl. Based Learn. 3, 6–28. doi: 10.7771/1541-5015.1061
Wildgans-Lang, A., Scheuerer, S., Obersteiner, A., Fischer, F., and Reiss, K. (2020). Analyzing prospective mathematics teachers’ diagnostic processes in a simulated environment. ZDM 52, 241–254. doi: 10.1007/s11858-020-01139-9
Wittwer, J., and Renkl, A. (2008). Why instructional explanations often do not work: a framework for understanding the effectiveness of instructional explanations. Educ. Psychol. 43, 49–64. doi: 10.1080/00461520701756420
Wollring, B. (2008). “Kennzeichnung von Lernumgebungen für den Mathematikunterricht in der Grundschule” in Lernumgebungen auf dem Prüfstand–Zwischenergebnisse aus den Forschungsprojekten ed Kasseler Forschergruppe (Kassel: Kassel University Press).
Wuttke, E., and Seifried, J. (2017). “Competence, teacher competence and professional error competence: an introduction” in Professional error competence of preservice teachers. eds. E. Wuttke and J. Seifried (Cham: Springer International Publishing), 1–14.
Keywords: diagnostic skills, mathematics education, learning platform, usage, online higher education, learning style
Citation: Walter D, Bergmann A, Maibach M, Huethorst L, Reinartz L, Grünewald N, Selter C and Harrer A (2025) How pre-service teachers can be supported to increase their diagnostic skills in mathematics—design and evaluation of a learning platform for university teacher training. Front. Educ. 10:1510828. doi: 10.3389/feduc.2025.1510828
Edited by:
Raja Nor Safinas Raja Harun, Sultan Idris University of Education, MalaysiaReviewed by:
Nia Wahyu Damayanti, Surabaya State University, IndonesiaImam Rofiki, State University of Malang, Indonesia
Copyright © 2025 Walter, Bergmann, Maibach, Huethorst, Reinartz, Grünewald, Selter and Harrer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daniel Walter, ZGFuaWVsLndhbHRlckB0dS1kb3J0bXVuZC5kZQ==