Disadvantaged by chance? Examining the persistence of relative age effects on educational achievement

Most education systems have arbitrarily chosen annual cut-off dates for school enrolment, which create age differences of up to a year within a cohort of pupils. Prior research has shown that the oldest in a cohort systematically outperform their relatively younger peers. Yet, little is known about the temporal persistence of relative age effects in education. In this article, we investigate how relative age effects on educational achievement evolve over different stages of compulsory education. Drawing on administratively linked test score data comprising entire student cohorts in Northwestern Switzerland, we employ two complementary analytical approaches to examine for how long the advantages of relatively older pupils prevail. The results indicate that relative age effects diminish the more pupils progress in their educational careers. However, effects of relative age at school enrolment are still identifiable beyond sixth grade, which marks the transition into secondary education in Switzerland.

1 Introduction

Age-based school entry laws employed in most education systems create systematic age differences by introducing yearly cut-off dates that define an interval of eligible birth dates for a new cohort of pupils to enter school. These arbitrarily set cut-off dates are important as they cause children born right after the cut-off date to be up to a year older than their counterparts born right before the subsequent cut-off date. To put this into perspective, in education systems where children must be five years old to enter school, the age difference created by cut-off dates accounts for up to twenty per cent of the total lifespan of those enrolled. Given the magnitude of these age differences, one would expect that relatively older children find it easier to adapt to the school environment due to their more advanced cognitive and psycho-social development (Duncan et al., 2007; Black et al., 2011; Dhuey et al., 2019). Scholars from various scientific fields—such as sports science, epidemiology, or educational research—have come to demonstrate that relative age within a cohort provides advantages to the relatively older while disadvantaging the relatively younger. The consequential outcomes resulting from age differences within annual age-grouped cohorts are commonly termed as relative age effects (Bedard and Dhuey, 2006; Baker et al., 2010).

Educational research has repeatedly underlined the importance of early childhood in shaping future educational outcomes and pathways. Gaps in educational performance that emerge when children enter school are critical as they prove persistent over time (Cunha and Heckman, 2007; Skopek and Passaretta, 2021). Several studies found that children who enter school relatively old compared to their classmates tend to achieve higher test scores (e.g., Bedard and Dhuey, 2006; Smith, 2009), are less likely to experience grade retention (e.g., Dicks and Lancee, 2018; Jerrim et al., 2022) and are overrepresented in more demanding educational programmes at the secondary level (e.g., Mühlenweg and Puhani, 2010; Ponzo and Scoppa, 2014). However, there are conflicting findings on the longevity of relative age effects in education. While some work indicates that later life outcomes such as earnings (e.g., Solli, 2017) or fertility behavior (e.g., Peña, 2017) can be traced back to relative age at school enrolment, other studies show that relative age effects diminish the more learners progress on their educational pathways (e.g., Thoren et al., 2016; Mavilidi et al., 2022).

The present study contributes to this strand of literature by investigating the temporal persistence of relative age effects on educational achievement. Specifically, we analyse whether and to what extent pupils' relative age at school enrolment affects their performance in different subjects across different grades of compulsory education. In doing so, this study informs about whether—and no less importantly when—actions should be taken to address the implications of relative age effects. Determining if and when relative age effects diminish is particularly relevant for highly stratified education systems—such as the case of Switzerland portrayed here—since pupils are sorted into tracks with designated educational pathways at a young age.

Identifying the impact of relative age on educational achievement is a complex endeavor, as the effect of relative age is a composite with several channels through which this effect may unfold. In this paper, we employ two complementary identification strategies, namely a regression discontinuity design and an instrumental variable approach, enabling us to rule out specific components of the effect of relative age and allowing for a nuanced investigation of relative age effects on educational achievement. Due to a record linkage, we can analyse data from standardized assessments comprising entire student cohorts in Northwestern Switzerland across different subjects and grades. Our results provide evidence of substantial relative age effects in the early stages of compulsory school that diminish the more pupils progress through compulsory education.

The present study proceeds as follows. The next section introduces an analytical framework of relative age effects in education. Following a mapping of the state of research, we describe the data used and expound on the methodological approach. Subsequently, we present our results and conclude by critically discussing our findings and their implications.

2 Background

2.1 Theoretical considerations

Relative age effects refer to differential outcomes resulting from age differences within annual age-grouped cohorts (Baker et al., 2010). These age differences are caused by arbitrarily chosen cut-off dates that determine eligibility for an annual cohort based on the date of birth of individuals in the target group. In most of Switzerland, for instance, the cut-off date for school enrolment is the 31st of July.¹ Every year, children who turn 4 years old between the 1st of August and the 31st of July make up a cohort of school entrants. If all families comply with the admission rule, children born on the 1st of August are the oldest in a cohort and twelve months older than their counterparts born on the 31st of July. In reality, a non-negligible share of families opts to delay their child's school entry by a year (SCCRE, 2023), a practice that is discussed in the literature as academic red-shirting (e.g., Bassok and Reardon, 2013; Lenard and Peña, 2018; Dhuey et al., 2019).²

Conceptually, relative age effects are manifestations in a given outcome, such as performance in school, that can be attributed to initial age differences within a cohort that interact with social mechanisms over time. The link between children's biological age and their physical maturity and socio-emotional development (Eisenberg et al., 2010) grants relatively old children a head start for learning in school. This initial advantage among older children may unleash cumulative processes in a developmental environment where credit and support are allocated among individuals according to their performance.

What Merton (1968) coined as the Matthew effect is one example of a cumulative process leading up to relative age effects. If relatively old students benefit more from schooling early on, they will outperform their younger counterparts. And if skill begets skill, these pupils can follow a steeper learning curve, causing the differences between the oldest and the youngest of a cohort to grow over time. Complementing this view, Hancock et al. (2013) argue that gaps due to relative age endure and are propagated through self-fulfilling prophecies. While the Matthew effect identifies initial age-related disparities as the driver of relative age effects, the concept of self-fulfilling prophecies focuses on subsequent relative age (dis)advantages and emphasizes the role of expectations and beliefs that arise from them. Self-fulfilling prophecies occur when (false) beliefs lay the ground for a new behavior that eventually makes previous (false) beliefs come true (Jussim, 1986).

Self-fulfilling prophecies may drive relative age effects when involved actors—namely teachers, parents, and pupils—falsely associate differences in physical maturity and socio-emotional development with actual differences in abilities and talent. According to Rosenthal and Jacobson (1968) seminal example on Pygmalion effects, teachers may (unconsciously) treat relatively older pupils preferentially if they mistake pupils' relative age for academic aptitude. For example, they might support older children with preferential resources such as more challenging assignments, additional learning opportunities or encouragement while the relatively younger children are denied such treatment. Consequently, pupils with a relative age advantage are better positioned to improve their academic abilities.

Complementary to Pygmalion effects, the notion of Galatea effects postulates that once pupils are aware of the expectations placed upon them, they begin to act in accordance with these expectations (Eden and Kinnar, 1991). Relatively old pupils who, through the confusion between ability and age by their teachers, believe they are more gifted than their younger peers develop higher self-efficacy and are motivated to keep outperforming their younger peers. In a similar vein, Marsh (2016) and Parker et al. (2019) proposed the Negative-Year-in-School-Effect as an extension of the Big-Fish-Little-Pond-Effect. This model hypothesizes that being relatively young in a given grade negatively affects pupils' academic self-concept since pupils perceive their relative age as a reflection of their academic prowess. This effect endures over time through continuous social comparison with in-grade peers. Over the long run, Marsh (2016) argues that the Negative-Year-in-School-Effect on educational outcomes supersedes the effects of mere age differentials created during school enrolment.

2.2 Epistemological challenges

While social mechanisms help explain the emergence and persistence of relative age effects, estimating the consequences of relative age at school enrolment on later educational achievement poses two types of epistemological challenges. The first of these challenges relates to the inseparability of concurring causal links between age and educational outcomes. On the one hand, it cannot be ruled out that children who entered school older relative to their peers simply perform better because they are older when they take the test (e.g., Black et al., 2011). On the other hand, it may not be relative age but rather the absolute age at school enrolment that is predictive of later educational outcomes (e.g., Dhuey et al., 2019). Assuming that all families comply with school enrolment regulations and that all pupils follow a linear educational career, pupils' relative age, absolute age at enrolment, and age at measurement are perfectly collinear, making it impossible to disentangle which effect actually determines educational outcomes. Thus, the estimate of relative age at enrolment is likely to be a composite effect. Nonetheless, this composite effect is integral to the social reality in schools as pupils, their teachers, and parents still act upon the age differences they observe. To align our findings with the established terminology used in previous research, we refer to differential outcomes resulting from age differences within age-grouped cohorts as relative age effects while acknowledging that effects of absolute age and age at measurement are inseparably involved as well.

The second challenge arises from factors that affect a pupil's relative position in the age distribution and may open competing channels through which educational outcomes are affected, thus potentially inducing endogeneity. These factors either stem from non-compliance with school enrolment regulations or non-linear progressions through grades (Sprietsma, 2010). On the one hand, delayed school enrolment, so-called academic red-shirting, or more infrequent early school enrolment, induces age differences that transcend the ones created by cut-off dates. On the other hand, pupils who skip or repeat a grade based on their performance in school experience a sudden shift in their age relative to others in a cohort. As selection happens in both situations—for instance, delayed school enrolment is more common among well-off families (e.g., Bassok and Reardon, 2013; Lenard and Peña, 2018) and low-performing pupils are more likely to suffer from grade retention (e.g., Dicks and Lancee, 2018; Jerrim et al., 2022)—the effect of relative age at school enrolment may be biased for these specific groups of pupils. The same applies to so-called season of birth effects when the season a child is born is related to parents' socio-demographic characteristics or specific developmental risks (e.g., Buckles and Hungerman, 2013). Given the multitude of channels that may be in play when analyzing the effects of relative age on educational outcomes, it is vital to follow a methodological approach that limits potential distortions.

2.3 Empirical evidence

Previous empirical work on the relationship between pupils' relative age at school enrolment and academic outcomes generally revealed positive short-term effects of being older relative to the rest of the cohort. Several studies provide evidence that individuals born in the first few months after the cut-off date for school enrolment achieve higher test scores than their younger peers in various subjects (Smith, 2009; Ponzo and Scoppa, 2014; Thoren et al., 2016; Peña, 2017; Bjerke et al., 2022; Mavilidi et al., 2022). As international comparative studies show, this effect is identifiable across different education systems with varying intensity (Bedard and Dhuey, 2006; Sprietsma, 2010). Moreover, scholars have come to demonstrate the positive effect of relative age on academic achievement using different methodological approaches, ranging from common regression frameworks to quasi-experimental designs such as regression discontinuity (e.g., Smith, 2009) or instrumental variables (e.g., Bedard and Dhuey, 2006).

The advantages of relatively old pupils also become apparent concerning educational pathways. Research from Germany (Mühlenweg and Puhani, 2010), Austria (Schneeweis and Zweimüller, 2014), or Italy (Ponzo and Scoppa, 2014) finds that pupils with a relative age disadvantage are less likely to be tracked into academic programmes at the secondary level rather than vocational programmes. Evidence suggests that relative age affects educational pathways even beyond secondary education, with findings suggesting that those with a relative age disadvantage at the time of school enrolment are less likely to attend tertiary education (Peña, 2017; Solli, 2017). Furthermore, recent studies from France (Dicks and Lancee, 2018) and Spain (Jerrim et al., 2022) find that children who were relatively young at school enrolment show a higher likelihood of repeating a grade.

Several studies identify relative age effects within the context of compulsory schooling that transcend mere performance-related outcomes. Using different data sources from the United States, Dhuey and Lipscomb (2008) find that relatively older high school students are 4–11 per cent more likely to become captains in sports teams or presidents in clubs. Instrumental variable estimates from Fumarco and Baert (2019) indicate that pupils with a relative age disadvantage have fewer friends in school and meet with them less often. In line with the notion of Pygmalion effects, results from Dhuey and Lipscomb (2010) indicate that relatively young pupils are over-referred to special educational needs services, with each additional month in relative age decreasing the likelihood of receiving these services by 2–5 per cent.

While persuasive evidence on relative age effects on educational achievement and attainment exists, there are mixed results on how enduring and persistent these effects are. On the one hand, some studies suggest that the effects of relative age at school enrolment persist through their educational careers. Others indicate substantial relative age effects on educational achievement in primary school and that these effects still prevail in secondary education, although the effect sizes slightly decrease (Bedard and Dhuey, 2006; Smith, 2009; Ponzo and Scoppa, 2014). Moreover, scholars provide evidence of modest wage penalties for individuals who entered school relatively young, even when educational achievement and attainment are accounted for (Schneeweis and Zweimüller, 2014; Peña, 2017; Solli, 2017).

On the other hand, some more recent studies fail to underline the persistence of relative age effects by showing that these effects vanish over time. Using longitudinal data, some studies find that while substantial relative age effects on educational achievement can be identified in primary education, these effects consistently diminish in size and vanish completely once pupils reach the end of compulsory education (Thoren et al., 2016; Bjerke et al., 2022; Mavilidi et al., 2022). Nam (2014), for instance, shows for Korea that the effect of relative age at enrolment in school does not persist by the time pupils graduate from upper secondary education. On the contrary, pupils with an initial relative age disadvantage showed higher engagement with academic studies upon entering upper secondary school, thereby compensating for their subpar achievement in lower secondary school. Findings from Bernardi and Grätz (2015) using English data suggest, however, that the negative effects of being relatively young at school enrolment vanish sooner for pupils whose parents are highly educated. Contradicting the findings described above, some studies do not find any indications that the relative age at which children enter school affects their labor market outcomes, such as wages or the probability of employment (Dobkin and Ferreira, 2010; Nam, 2014; Pehkonen et al., 2015).

2.4 Our study

The aim of the present study is to investigate the persistence of relative age effects on educational achievement throughout compulsory education. Examining how relative age effects unfold over different stages in pupils' educational careers may offer new insights to untangle conflicting findings in the literature on the long-term implications of relative age at school enrolment. From a practical perspective, uncovering the temporal development of how relative age affects educational outcomes informs policymakers and teachers on whether and at which educational stage efforts to mitigate relative age effects should be taken. If it would transpire that relative age effects on educational achievement prevail until the end of compulsory school, this would not only underline that chance is integral part of educational processes but also challenge assertions of meritocracy in education.

This study examines the effect of relative age at school enrolment on test scores for the case of Switzerland. Switzerland's education system is characterized by early tracking, high stratification at the secondary level and marked differences in learning outcomes by the time students leave compulsory school (e.g., Buchmann et al., 2016), making an examination of relative age effects all the more relevant. Usually, children in Switzerland enter compulsory school after turning 4 years old, beginning with 2 years of kindergarten, followed by 6 years of primary education (grades 1–6) and 3 years of lower secondary education (grades 7–9). In the latter, pupils are allocated to one of several school types that differ by academic requirements. Compulsory education ends with completing ninth grade. At this point, almost all children either continue school in general education (in 2020: 31.3%) or take up vocational training (in 2020: 64.4%) (FSO, 2022a).

3 Materials and methods

3.1 Data

The persistence of relative age effects on educational outcomes can best be studied using test scores from standardized performance assessments. This study relies on test score data from Northwestern Switzerland, the so-called Checks (BR NWCH, 2021), covering the period from 2015 to 2020. The Checks are administered annually in four cantons of Switzerland (Aargau, Basel-Landschaft, Basel-Stadt, and Solothurn) measuring pupils' competence in various subjects in third, fifth (2018–2020), sixth (2015–2017), eighth, and ninth grade. Due to the gradual implementation of the Checks across cantons, there are gaps in data coverage in specific canton-year-grade combinations (see Appendix A). In our analyses, we pool the test score data from different years by grade. As participation in the Checks is generally mandatory, the data covers entire student cohorts in cantons of Northwestern Switzerland. Overall, the region of Northwestern Switzerland comprises approximately one-sixth of all students in Switzerland. Since many employers, particularly host companies in the vocational sector of upper secondary education, request a portfolio of their applicants' results in the Checks from eighth and ninth grade, the Checks can be regarded as high-stakes tests, which likely contributes to the external validity of the data.

3.2 Measures

The dependent variables are test scores in German reading, German writing, and algebra. The test scores are measured in terms of weighted likelihood estimates (WLE), which were scaled by two-parameter logistic models in the cases of German reading and algebra and multi-facet Rasch models in the case of German writing (König and Berger, 2021). For ease of interpretation, we standardized the WLE, so they have a mean of zero and a standard deviation of one across subjects, years, and grades.

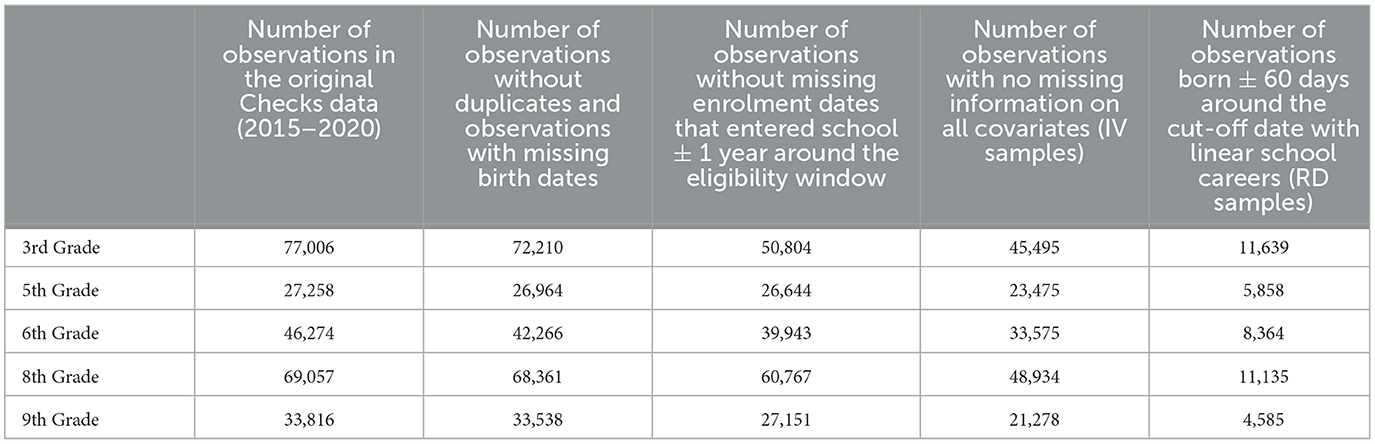
Apart from test scores, the Checks provide minimal information about the test takers. Only due to a record linkage to administrative data provided by Switzerland's Federal Statistical Office (FSO, 2022b,c,d,e,f,g,h,i,j,k,l,m) and the Central Compensation Office (CCO, 2022a,b,c,d,e,f,g,h,i,j), we were able to obtain information on pupil characteristics. Next to their exact birth dates, we gathered information on pupils' sex (male or female), migration background (native or first- or second-generation migrant), parental income (mean taxable income of parents as deciles), and household characteristics, namely the living area per capita (in square meters) in the parental household and whether a pupil lives in a single-parent household. From the Checks, we have information about the canton, grade, the year in which the pupil took the test and foreign language use at home. Table 1 provides an overview of the analytical samples by grade and analytical approach.³ We obtained information on the cut-off dates by contacting cantonal administrations (see Appendix Table A2).

Table 1

Table 1. Overview of sample sizes.

3.3 Analytical samples

Three factors limit the analytical samples used in our study. First, since we have duplicates for some children in the data and because we cannot identify a small number of children unambiguously in the administrative records, 4.0 per cent of all observations are excluded from the analyses. Second, we exclude observations for specific cohorts in the cantons of Aargau and Basel-Landschaft where information on the exact cut-off date for school enrolment is unavailable. Yet, the federalist structure of Switzerland's education system offers an analytical benefit. Since the cantons retain extensive jurisdiction over the modalities of school enrolment, there is variation in cut-off dates between cantons and years, which minimizes concerns about potential endogeneity due to season of birth effects. Lastly, the number of observations is further restricted by missing information on the variables used in the models, and we limit the observations to pupils who were born one year before or after the legal enrolment dates per canton and year. Pupils that skipped a grade or were retained twice resemble a particular population which we exclude from our analysis. These observations resemble about 0.6 per cent in third grade up to 4.4 per cent in ninth grade.

3.4 Empirical strategy

Given the various channels through which relative age can be affected and influenced (Sprietsma, 2010), it is vital to establish a methodological approach that allows unequivocal inference on relative age effects on educational performance. Bedard and Dhuey (2006) made a convincing case by showing that estimating relative age effects via OLS would yield downwardly biased estimates. In the present study, we opt for two complementary approaches to address these endogeneity concerns.

3.4.1 Regression discontinuity

As the first identification strategy, we exploit random variation in relative age caused by the arbitrarily set cut-off dates as a quasi-experiment. Using a regression discontinuity (RD) design (e.g., Lee and Lemieux, 2010), we compare pupils whose birthday lies right after the cut-off date for school enrolment—the oldest in a cohort—to those born right before the cut-off date. Given that the variation in birthdays is random, a discontinuity in test scores around the cut-off date can be attributed to the difference in relative age. In light that the randomness of birthdays is a compelling assumption, several previous studies have exploited the discontinuity around the cut-off date as an exogenous source of variation for causal inference on relative age effects (e.g., Smith, 2009; Crawford et al., 2014; Dicks and Lancee, 2018).

The absence of manipulation of treatment status is an essential pre-requisite in an RD design (Lee and Lemieux, 2010). Delayed or early school entry, as well as grade retention or skipping, likely pose a threat to this identification assumption as these practices—rather than the day of birth in relation to the cut-off date—determine a pupil's relative age, thus introducing endogeneity to the model. This violation is particularly striking when there is self-selection among specific groups into these practices (e.g., Bassok and Reardon, 2013; Lenard and Peña, 2018; Dicks and Lancee, 2018; Jerrim et al., 2022), potentially creating systematic differences in academic outcomes among complying and non-complying individuals. Since our data neither provides information on the year of school enrolment nor on grade retention or skipping, we cannot distinguish pupils who enrolled in school outside the envisaged school year from those who skipped or repeated a grade. In light of these constraints, we opt for a sharp RD design limiting the analytical samples to pupils who—in retrospect—complied with the enrolment regulations and who did not repeat or skip a grade (see Table 1). Hence, our estimate of the relative age effect only applies to individuals born a given number of days around the cut-off date who complied with the enrolment regulations and were able to sustain a linear school career.

By counting the number of days between the birthday of a pupil i and the cut-off date that was in place for a given year and canton (Birthday), we define a bandwidth before and after the cut-off date to assign treatment status (Treatment), namely being relatively old at school enrolment. To account for the fact that the functional form may differ before and after the cut-off date, we allow for separate slopes by introducing an interaction term, which yields the following equation to be estimated in OLS:

$\begin{array}{r}Scor{e}_i=\alpha +{\beta }_{1}Birthda{y}_i+{\beta }_{2}Treatmen{t}_i\\ +{\beta }_{3}Birthda{y}_i\times Treatmen{t}_i+\gamma X_i+{\epsilon }_i\end{array}$

where Score_i represents a pupil's test score in a given subject, β₂ is the causal effect of interest and γX_i denotes the set of control variables.

Guided by optimal bandwidth selectors (Imbens and Kalyanaraman, 2012; Calonico et al., 2020), we find that 60 days on each side of the cut-off date is an appropriate bandwidth to address the bias-variance trade-off (see Table 1). In light of the sensitivity of confidence intervals to the bandwidth and functional form assumptions in an RD design, we complement our results with a non-parametric estimation of the treatment effect (Calonico et al., 2018).

Based on observable characteristics in our data, we find no indication that observations on both sides of the cut-off date are systematically different. The variance in the cut-off dates by canton and year additionally helps to rule out season of birth effects potentially caused by environmental factors and differences in gestational preferences by specific socio-economic groups. What we do observe is that there are fewer pupils born just before the cut-off in higher grades, particularly in grades eight and nine. We consider the possibility that, over time, grade retention becomes more likely among pupils born before the cut-off date (Dicks and Lancee, 2018; Jerrim et al., 2022). Since we restrict our analytical samples in the RD approach to pupils who sustained a linear school career, the pupils born before the cut-off date who remain the analytical samples in later grades may represent a particularly gifted subpopulation. In this case, we would expect an underestimation of the RD estimates in later grades.

3.4.2 Instrumental variables

While our estimates using a sharp RD design provide valuable insights into the extent to which relative age differentials induced by the cut-off date for school enrolment manifest in educational performance, the exclusion of pupils that enter school outside the envisaged school year or did not sustain a linear school career might provide an inaccurate reflection of the reality in schools. Furthermore, if treatment status is related to educational performance, the results may be downwardly biased—particularly in later grades—as we potentially exclude relatively young pupils who were not able to sustain a linear school trajectory because of their subpar performance. Therefore, we complement our findings using an instrumental variable (IV) approach, which allows us to consider observations with non-linear school careers and who did not comply with the enrolment regulations.

Once we include pupils whose relative age exceeds the possible range of an enrolment window in the analyses, a solution is needed to overcome the issue that unobservable factors may confound the observed age at school enrolment and thus the effect of relative age on school performance. For instance, a fraction of pupils is relatively old because they repeated a grade, while another fraction is relatively old because they positively selected into delayed school entry. To resolve this problem, we follow an approach introduced by Bedard and Dhuey (2006) and use assigned relative age as an instrument of observed relative age. Assigned relative age refers to the age at enrolment children would have in the absence of early or late enrolment and grade retention or grade skipping, respectively. In practice, assigned relative age is calculated using a child's birthday relative to the cut-off date without considering the birth year. Using assigned relative age as an instrumental variable for observed age is an established approach employed in several previous studies (e.g., Nam, 2014; Ponzo and Scoppa, 2014; Peña, 2017).

More specifically, we estimate the following equations using 2SLS:

$\begin{array}{l}\text{First stage: }\widehat{ObservedAg{e}_i}={\pi }_{10}+{\pi }_{11}AssignedAg{e}_i+\gamma X_i+{\upsilon }_i\\ \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}Second stage: }Scor{e}_i={\pi }_{20}+{\pi }_{21}\widehat{ObservedAg{e}_i}+\gamma X_i+{\upsilon }_i\end{array}$

where π₁₁ captures the effect of assigned relative age on children's observed age, adjusting for covariates γX_i, and π₂₁ captures the effect of relative age on test scores.

If consistent, the IV approach produces an estimate that resembles an unbiased estimator of the effect of entering school 1 year older (Bedard and Dhuey, 2006), which is comparable to the estimate of the treatment status in the RD design. However, three conditions must hold for the IV estimate to be interpretable as a local average treatment effect (LATE). First, a sufficient correlation between pupils' actual age at enrolment and their assigned age is needed. Since most observations (75.9%) start school in the envisaged school year and never skip or repeat a grade, this first requirement is satisfied.

Second, assigned relative age is required to be uncorrelated with unobserved covariates of educational achievement in the error term. While this condition cannot be evaluated empirically, there are approaches to corroborate that this condition is satisfied. For instance, Ponzo and Scoppa (2014), which use a similar IV approach, regress all individual controls of the model on assigned age and conduct joint F-tests. Although this test does not validate the exogeneity of the instrument, it makes it more credible that the instrument is uncorrelated with unobservable confounders. In our case, we find no significant F-statistics in any of our analytical samples. Moreover, we find that the main effect is substantially robust to the inclusion of the control variables (see Appendix E3). Furthermore, as outlined above, we are confident to rule out season of birth effects as potential confounders.

Third, as discussed by Barua and Lang (2016), the IV approach needs to satisfy the monotonicity assumption in relation to essential heterogeneity. Essential heterogeneity refers to the fact that treatment effects can vary across groups (e.g., children with higher academic aptitude could benefit even more from being relatively older) and that there is some degree of sorting based on treatment status (Fiorini and Stevens, 2021). Monotonicity means switching treatment status between two counterfactuals should always affect the treatment in the same direction. We find empirical evidence that pupils in the same grade and born in the same month either enroll late or are retained, enroll early or skip a grade, while most enroll on time. Although these observations have the same assigned relative age, their observed age at enrolment—and thus their treatment status—varies. This circumstance supports that the monotonicity assumption is violated (see Appendix E5 for a detailed discussion). Fiorini and Stevens (2021) analyze the consequences of a violation of the monotonicity assumption regarding the use of assigned age as an instrument for observed age. They conclude that a violation of the monotonicity assumption results in a potential overestimation of the treatment effect, although this effect still fairly reflects a LATE. While the IV approach likely produces upper-bound effects, the estimates still allow for a meaningful interpretation, especially in comparison to estimates from previous research or the RD estimates.

4 Results

4.1 Regression discontinuity estimates

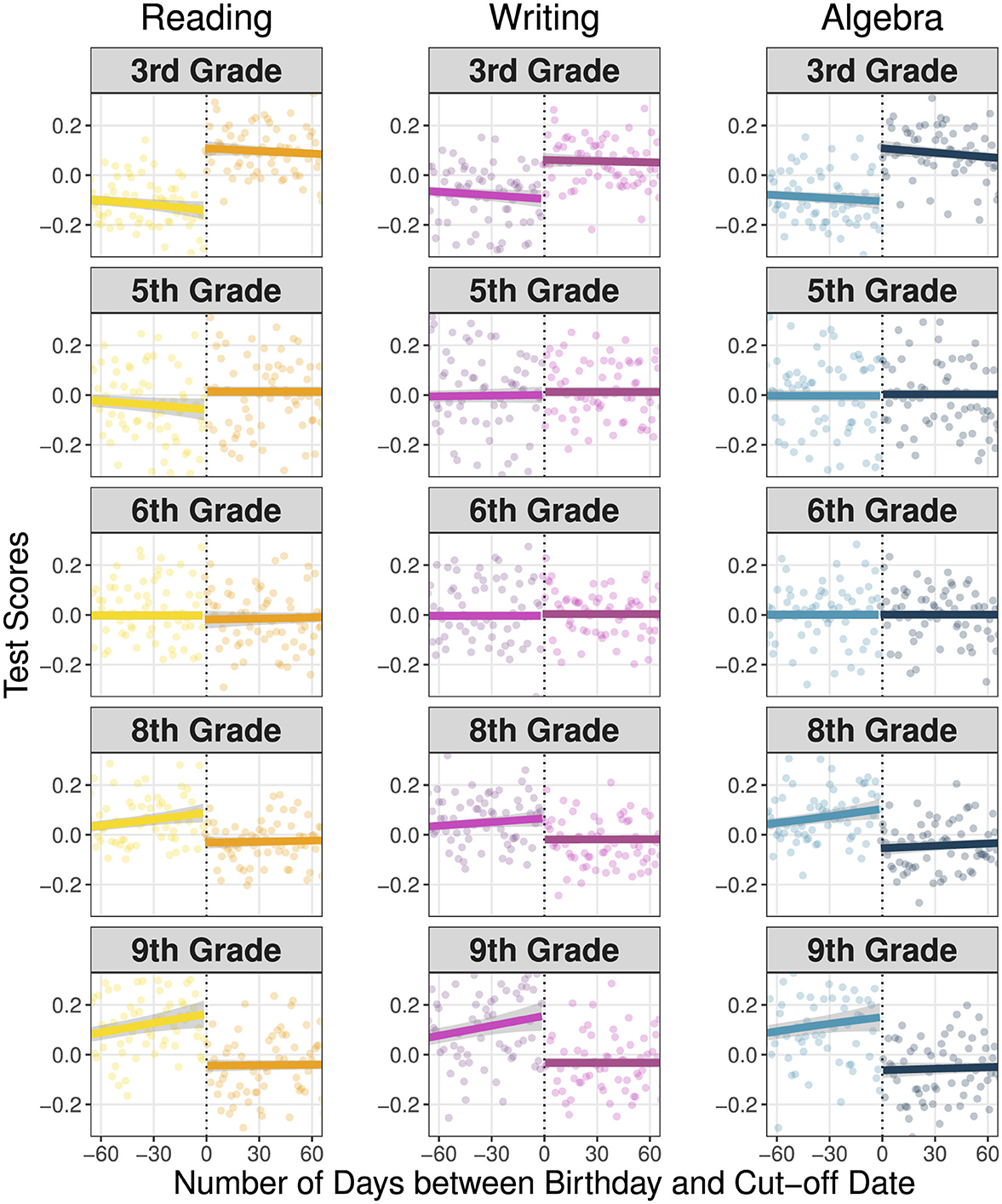
Figure 1 displays the bivariate relationship between pupils' birthdays relative to the cut-off date for school enrolment and test scores in the three subjects by grade. In each graph, the dotted vertical line indicates the cut-off date and the horizontal axis shows the number of days between the cut-off date and a pupil's birthday. The points represent binned sample means of test scores, through which a local polynomial model along with a 95 per cent confidence band is fitted.

Figure 1

Figure 1. Discontinuity in test scores around the cut-off date by grade.

A clear and substantial discontinuity around the cut-off date is apparent among third graders in all competence domains. Pupils who entered school relatively old achieve considerably higher test scores than their younger counterparts whose birthdays lie before the cut-off date. In fifth grade, the discontinuity around the cut-off date diminished in size and there is considerably more variation in test scores. In sixth grade, the test scores before and after the cut-off date converge and there is no clear evidence of a discontinuity anymore. Visual inspection of test scores around the cut-off date in grades 8 and 9 yields interesting yet unexpected insights. The discontinuity around the cut-off date reappears, but this time inverted. Among eighth and ninth graders, pupils who entered school relatively young outperform their older counterparts across all competence domains. The discontinuity around the cut-off date is more pronounced among ninth graders than among eighth graders.

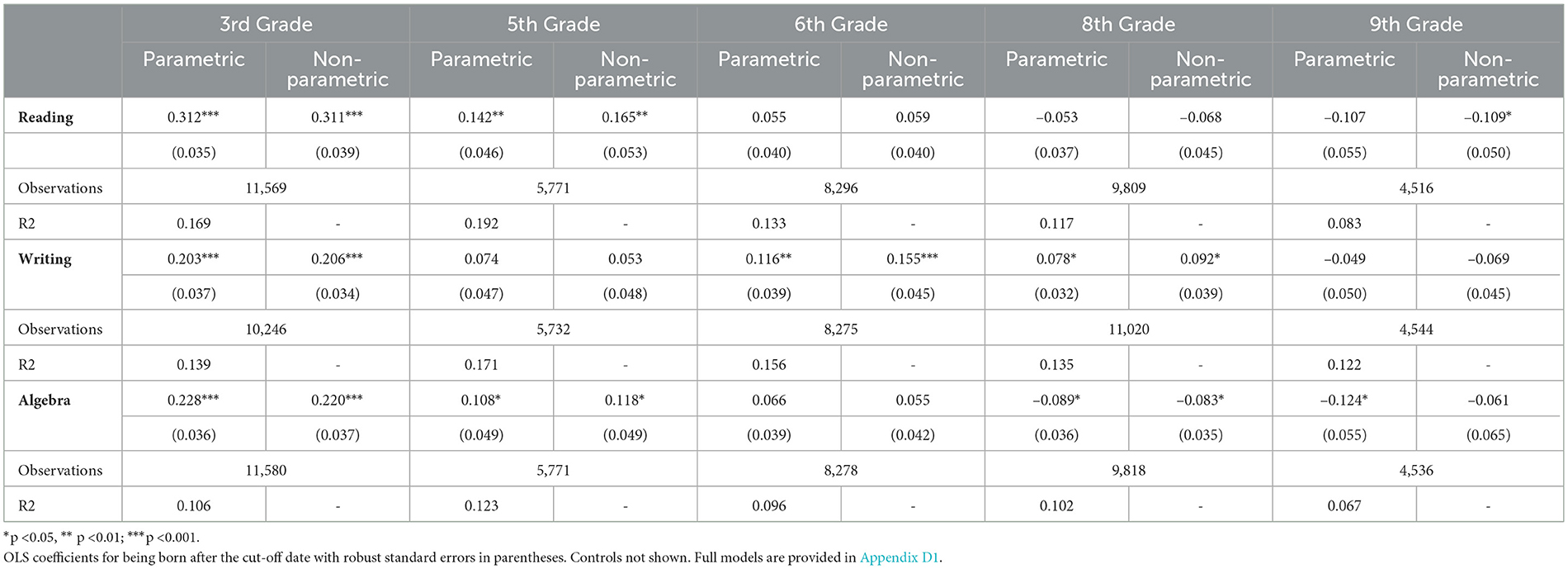
We estimate parametric and non-parametric RD models to determine whether the observed gaps in test scores depicted in Figure 1 can be attributed to relative age differences created by the cut-off date for school enrolment. Table 2 presents RD estimates across grades for the three competence domains. Each coefficient represents the estimated difference in test scores of pupils born shortly after the cut-off date compared to their younger counterparts whose birthdays lie before the cut-off date. All estimates are adjusted for covariates and apply only to individuals who complied with the enrolment regulations and sustained a linear school trajectory.

Table 2

Table 2. Parametric and non-parametric regression discontinuity estimates by grade.

In line with the visual evidence presented in Figure 1, the multivariate models estimate a positive and statistically significant effect of being born shortly after the cut-off date on test scores among third graders. The effect sizes are marginally higher for reading (β = 0.312, p < 0.001) than for writing (β = 0.203, p < 0.001) and algebra (β = 0.228, p < 0.001). Notably, the estimates for third graders are similar in size to those presented in previous studies employing an RD design. For instance, Smith (2009) presents RD estimates for fourth graders of around 0.25 SD higher test scores in numeracy and reading.

For fifth graders, the estimates decrease in size. In the case of writing competence, neither the parametric (β = 0.074, p > 0.05) nor the non-parametric (β = 0.053, p > 0.05) estimates of entering school at a relatively older age are distinguishable from zero. Among pupils in sixth grade, the effect sizes further decrease. Being born shortly after the cut-off date for school enrolment accounts for less than 0.1 SD higher test scores in reading and algebra, with neither estimate being statistically significant at a 95 per cent confidence level. A statistically significant discontinuity around the cut-off date is only found in the case of test scores in writing.

In eighth grade, for test scores in reading (β = −0.053, p > 0.05) and algebra (β = −0.089, p < 0.05), the estimated effects even turn negative. In contrast, the models on test scores in writing suggest that relative age effects prevail in favor of relatively old children in eighth grade (β = 0.078, p < 0.05). Once pupils are in their last year of compulsory school, in ninth grade, the estimated effects on test scores are generally negative, mirroring the unexpected finding based on visual inspection of Figure 1. However, except for test scores in algebra using a parametric estimation (β = −0.124, p < 0.05) and test scores in reading using a non-parametric estimation (β = −0.109, p < 0.05), the estimated discontinuity in test scores is statistically insignificant.

Additional analyses generally indicate robustness of the findings presented in Table 2. Parametric models using smaller bandwidths around the cut-off date, namely 30 and 15 days, yield very similar results regarding point estimates and statistical significance (see Appendix D3). We further conducted subgroup analyses separating pupils based on their sex, language spoken at home and parental income. These analyses reveal that the discontinuities in test scores around the cut-off date do not systematically differ between foreign language and German-speaking pupils as well as pupils whose parental income lies in the upper versus lower half of the income distribution. In contrast, we find greater discontinuities in test scores for males in writing and for females in algebra, particularly in eighth and ninth grade (see Appendix D4). Moreover, we find nearly identical estimates when using matching samples created by coarsened exact matching (see Appendix D5).

In the early phases of compulsory school, the RD approach provides evidence of substantial relative age effects in favor of those whose birthdays lie shortly after the cut-off date for school enrolment. Yet, the more pupils proceed in their educational careers, relative age differentials created by cut-off dates diminish. This finding aligns with what some research has previously discovered (e.g., Thoren et al., 2016; Mavilidi et al., 2022). By the time pupils have reached the end of compulsory school, the RD models yield negative coefficients suggesting that pupils who entered school at a relatively younger age outperform their older peers. A study by Nam (2014) using Korean data also finds that relatively young pupils achieve higher test scores than their older peers. However, several of our estimates for eighth and ninth graders lack statistical significance.

4.2 Instrumental variable estimates

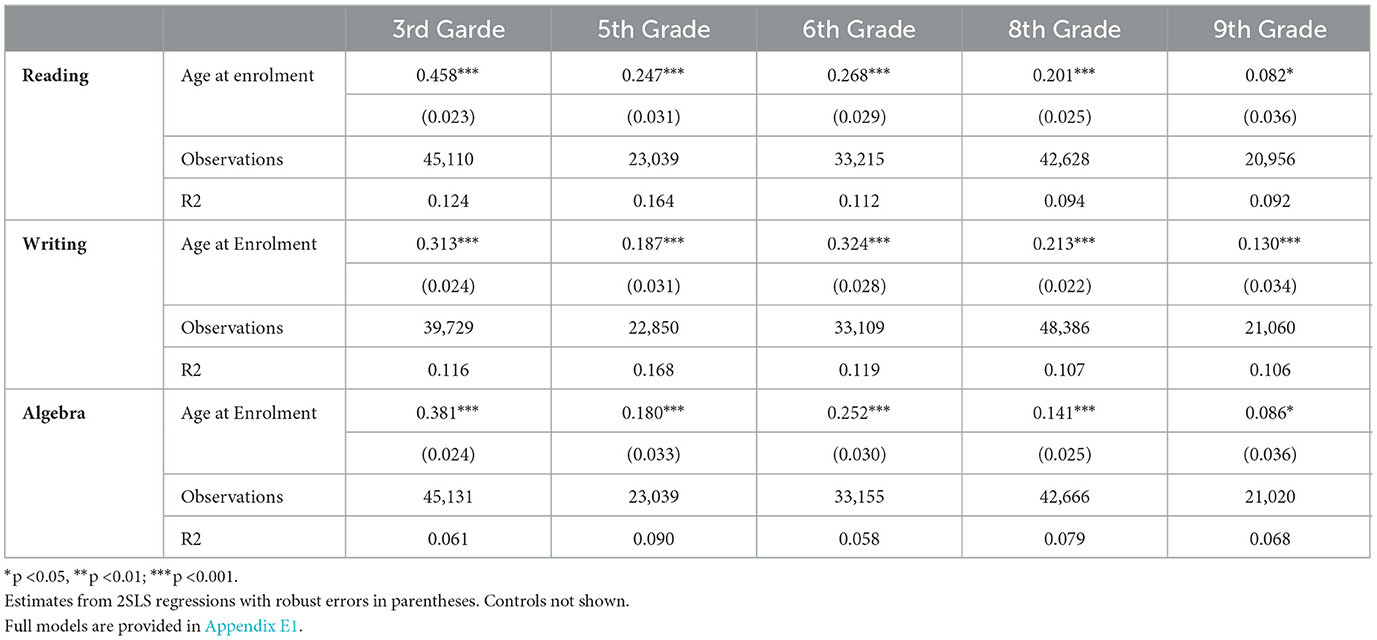
Pursuing an instrumental variable approach allows us to investigate relative age effects in a less confined way since pupils with non-linear educational careers can also be considered. Table 3 depicts the estimates of the IV regressions across grades and subjects. The estimates are adjusted for covariates and represent the effect on test scores of being one year older at school enrolment. For all models in Table 3, F-tests allow rejecting the null hypothesis of weak instruments. Furthermore, all models yield highly significant Wu-Hausman test statistics, indicating that OLS estimates would be inconsistent and 2SLS estimation is preferable.

Table 3

Table 3. Instrumental variable estimates by grade.

Similar to the results from the RD design, the estimates from the multivariate IV models find statistically significant positive effects of being one year older on test scores among pupils in third grade in all subjects. The effect is largest in reading (π = 0.458, p < 0.001), followed by algebra (π = 0.381, p < 0.001) and writing (π = 0.313, p < 0.001). Smith (2009) and Peña (2017) report IV estimates of similar magnitude on the same subjects for fourth and third-graders, respectively.

Despite a decrease in size, the effects of age at enrolment remain statistically significant throughout fifth and sixth grade. The estimated effects in sixth grade of being one year older at the time of school enrolment amount to 0.324 SD (p < 0.001) higher test scores in writing and 0.252 SD (p < 0.001) higher test scores in algebra. Similar to these results, Ponzo and Scoppa (2014) find an apparent reduction of relative age effects between fourth and eighth graders regarding test scores in mathematics using Italian data.

In contrast to the RD estimates, the models using an IV approach indicate for all subjects that relative age effects in favor of relatively older pupils persist into lower secondary education. In eighth grade, we once more find a reduction in effect sizes across all subjects. Nonetheless, pupils in eighth grade that were one year older at the time of school enrolment have, on average, 0.213 SD (p < 0.001) higher test scores in writing, 0.201 SD (p < 0.001) higher test scores in reading, and 0.141 SD (p < 0.001) higher test scores in algebra. In ninth grade, the estimated effect sizes decrease again and remain statistically significant for the domain of writing (π = 0.130, p < 0.001), reading (π = 0.082, p < 0.05), and algebra (π = 0.086, p < 0.05). This aligns with findings from Smith (2009) who reports a decrease in relative age effects from fourth to tenth grade while the estimates also remain statistically significant. According to their findings, writing is also the subject that shows the smallest decrease in effect size over time.

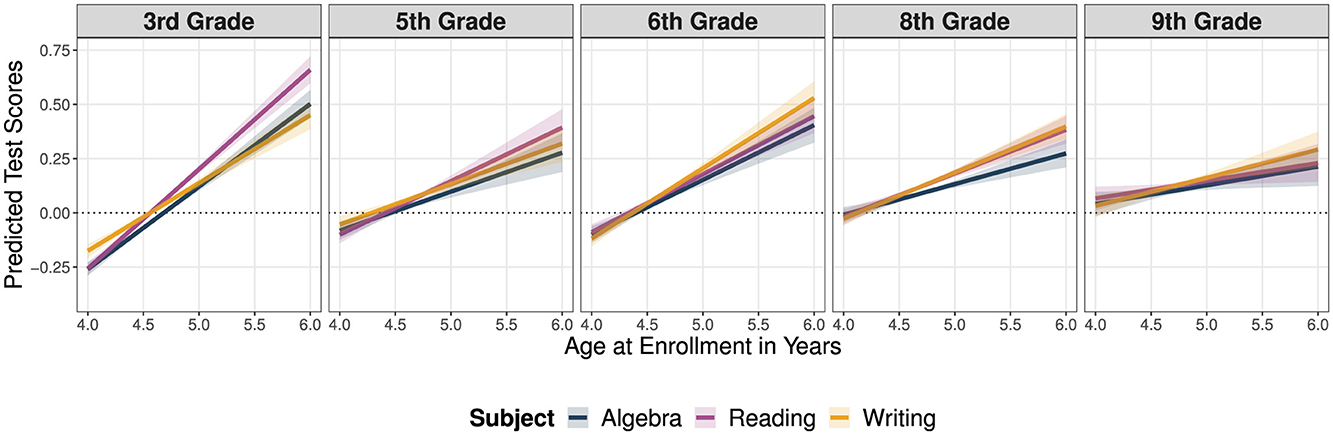
To illustrate the main results of the IV models, Figure 2 depicts predictive margins of the age at enrolment on test scores across all grades. Mirroring the RD models, the IV models indicate that the advantage of being relatively older at school enrolment decreases throughout the compulsory school. In contrast, however, the IV models suggest that relative age effects persist into lower secondary education and that the effects of relative age at school enrolment do not change direction among eighth and ninth graders.

Figure 2

Figure 2. Predicted test scores by age at enrolment and grade.

As an additional check for the IV models we ran subgroup analyses, analogous to the RD approach, which indicate overall robustness of our findings (see Appendix E2). Only in ninth grade, we find that the relative age effect is insignificant for males, foreign language-speaking pupils, and pupils from lower-income households in reading. Similarly, in ninth grade, the effect is insignificant for females, foreign language-speaking pupils, and pupils from upper-income households regarding algebra. The relative age effect on writing vanishes only for the sample that speaks a foreign language at home. Further, we compared our IV estimates with estimates from OLS models using the same samples and covariates. The OLS results indicate a consistent negative relationship between being one year older at school enrolment and test scores across all subjects and grades while being highly significant, except for reading in third grade (see Appendix F). This underlines that OLS is unsuitable for identifying relative age effects as they are subject to endogenous factors such as red-shirting or grade retention.

4.3 Persistent relative age effects?

In this study, we investigated the temporal persistence of relative age effects in education with two different identification strategies. To compare the estimates of the two analytical approaches, we must clarify and recall what effects they identify. On the one hand, the RD models determine the difference in test scores between pupils born up to 60 days after and those born up to 60 days before the cut-off date for school enrolment for pupils who complied with school enrolment regulations and did not repeat or skip a grade. Thus, the RD models refer to a LATE around the cut-off, which only apply to these pupils.

The reversal of the discontinuity around the cut-off date toward the end of compulsory school found in the RD models contradicts the theoretical expectations on the persistence of relative age effects. However, the results of the RD models might reflect a statistical artifact due to unobserved processes that systematically induce selectivity around the cut-off date. Since the RD models only consider students who were able to sustain a linear school career, the higher learning outcomes among relatively young students in lower secondary education may be driven by grade retention. Granted that the relatively young tend to perform sub-par in school, these pupils may be retained more often, leaving particularly gifted and resilient pupils whose birthdays lie shortly before the cut-off date in the analytical sample. The assumption that relatively young students suffer from grade retention more often finds empirical support in previous studies (Dicks and Lancee, 2018; Jerrim et al., 2022). Due to the selectivity among those born before the cut-off date, the RD approach likely underestimates relative age effects, particularly in higher grades.

In comparison, the IV approach allows us to consider pupils with non-linear school trajectories or who enrolled in school early or late as well. However, its estimates only refer to a LATE of being one year older at school enrolment if all conditions of an IV are met. As outlined previously, as our instrument likely violates the monotonicity assumption, the IV approach likely produces upper-bound effects (Fiorini and Stevens, 2021).

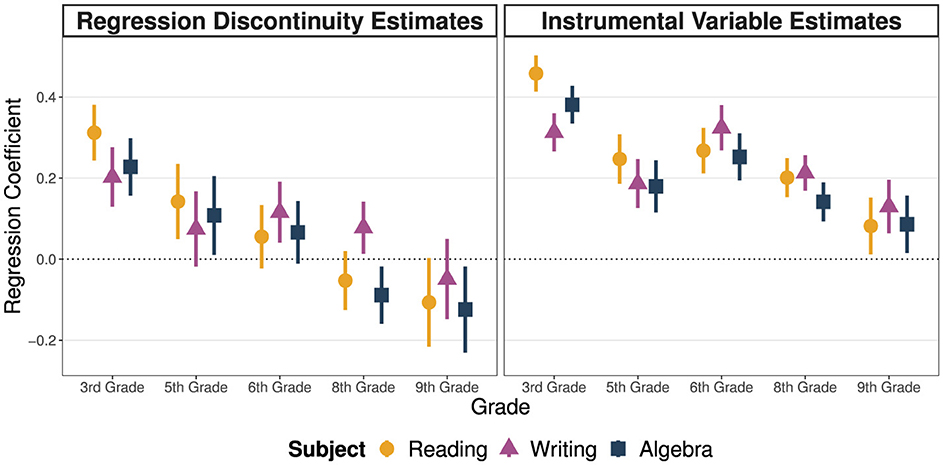
When putting the results of both empirical approaches together, we can draw a nuanced picture of the temporal dynamics of relative age effects throughout compulsory education although our estimates only allow for an approximation of the true causal effect. For a graphical overview, Figure 3 depicts the point estimates of the RD and IV models for each subject and grade along with 95 per cent confidence intervals. We find substantial relative age effects for both identification strategies in third grade, which diminish in subsequent grades. Albeit the similarity between the estimates from the RD models and the IV models for grades in primary education, the deflation of effect sizes is more apparent in the RD framework. The RD models' effects for pupils in lower secondary education even contradict the IV estimates and the theoretical implications of relative age effects as they indicate that relatively young pupils outperform older pupils.

Figure 3

Figure 3. Estimates of relative age at school enrolment on test scores across grades.

Both identification strategies make compelling cases that the advantages of pupils who entered school relatively old diminish over time. The RD approach finds that—among those who can sustain a linear school career—children born right before the cut-off even outperform their counterparts born right after the cut-off in lower secondary education. The IV approach contradicts this finding, as the relative age effects in favor of those who entered school relatively old remain significant until the end of compulsory education. Considering the potential underestimation in the RD framework and that the IV results resemble upper-bound estimates, we cannot rule out that the effects of relative age at school enrolment are still marked in sixth grade, when pupils are allocated to educational tracks based on their abilities. Hence, it is plausible that relative age affects track placement, as suggested in previous studies (e.g., Mühlenweg and Puhani, 2010; Ponzo and Scoppa, 2014).

If the relative disadvantage for young pupils through primary education is large enough, these pupils might be compelled, via social and institutional mechanisms, to repeat a grade and trade in an additional year of schooling to minimize the externalities of the relative age disadvantages. The systematic exclusion of such observations from the sample could explain the steeper reduction and, in lower secondary education, even the inversion of relative age effects estimated in the RD approach. The imbalance of the samples regarding treatment status supports this conjecture. Such an argumentation, although not testable with our data, is in line with research which shows that grade retention is more frequent among relatively younger pupils (Dicks and Lancee, 2018; Jerrim et al., 2022). Furthermore, alternative explanations for pupils born before the cut-off date to drop out of the sample more frequently than their counterparts who entered school relatively old, namely, to enter a private school or to move outside Northwestern Switzerland, are less compelling.

5 Discussion

Pupils who did not start learning on the same level as their peers might subsequently fall behind throughout their educational careers. Age-based school entry laws based on cut-off dates may contribute to early gaps in educational performance as they create relative age differences within a cohort of pupils, affecting their school readiness. Previous studies from various countries have come to demonstrate that the youngest in a cohort fall behind their relatively older peers. However, evidence on the longevity of relative age effects remains inconclusive. The present article aims to contribute to this strand of literature by investigating the temporal persistence of relative age effects on educational achievement. In this study, we used administratively linked test score data encompassing entire student cohorts in Northwestern Switzerland to examine the effects of relative age at school enrolment on test scores at different points of compulsory school. To identify these effects, we employed two complementary empirical strategies, which provide a nuanced picture of relative age effects.

Estimates from a sharp RD design indicate that the initial advantages of relatively older pupils diminish over time. This is supported by the results from the IV approach, which allows us to consider pupils who entered school outside the envisaged school year or who repeated or skipped a grade. Neither do these results support the conjecture that initial age-related achievement disparities induce divergent achievement gains over time, nor do the results provide evidence that subsequent age-related expectations hinder pupils who entered school relatively young from catching up to their older peers. It appears that schooling effectively counteracts the adverse implications of being relatively young at school enrolment. Just as the age differences become proportionally smaller over time, so do the age-related disadvantages of those who entered school relatively young. It may also be plausible that pupils who entered school relatively young develop efficient learning strategies to compensate for their initial relative age disadvantage.

However, the results differ between the two identification strategies as the RD models suggest that pupils who entered school relatively old achieve lower test scores than their younger peers in lower secondary education, while the IV models indicate a greater temporal persistence of relative age effects. Notably, in the IV models, these effects persist over the transition into lower secondary education. One convincing explanation for the sooner vanishing and even reversed relative age effects in eighth and ninth grade in the RD design is that the relative age disadvantage to the detriment of relatively young pupils during primary school might be powerful enough that these pupils are more likely to be retained. If this is the case, relatively young pupils who repeated a grade drop out of the RD samples in later grades, leaving only a resilient—and presumably particularly gifted—subpopulation of pupils born before the cut-off date in the samples, which would result in an underestimation of the effect. Consequently, if the educational system would not allow grade retention, we would expect more persistent relative age effects in an RD approach. In contrast, the IV approach still shows noticeable effects of relative age at school enrolment after the transition into lower secondary education. However, these effects should be interpreted as upper-bound estimates.

Hence, we argue that the combination of the two results informs us best about the gradations of relative age effects, as both identification strategies imply that relative age effects lessen as pupils progress through compulsory education. However, when interpreting the RD results as lower-bound and the IV results as upper-bound estimates, relative age effects are potentially still at play when students are allocated to performance-based tracks in sixth grade.

One caveat of this study is that the data used does not allow the creation of panel-like data, where individual pupils' learning trajectories could be traced throughout compulsory education. Another limitation stems from the fact that we cannot distinguish between pupils who enrolled in school late or were retained and those who entered school early or skipped a grade, respectively. This would have been very informative to test our argument for more frequent grade retention among relatively younger pupils. Furthermore, despite being widely applied in the literature on relative age effects, the approach of using assigned relative age as an instrument is not free of methodological criticism (Barua and Lang, 2016; Fiorini and Stevens, 2021). The comparison of the two strategies, however, yields valuable insights into the persistence of relative age effects. Like most previous research on relative age effects in education, this study is no exception to the epistemological problem regarding the inseparability of relative age, absolute age at enrolment, and age at test-taking. Similarly, we cannot explicitly model the social mechanisms that give rise to relative age effects. While our results contradict the conjecture of the Matthew effect, it would be very promising for future research to investigate the role of self-fulfilling prophecies in the emergence and temporal development of relative age effects.

6 Conclusion

Our study shows that time works against the relative age effect, but likely too slowly. In primary education, the effect is still evident and might cause a biased evaluation of performance by teachers. Further, poor evaluations can motivate parents to reconsider their educational goals for and their investment in their children. This becomes more evident when considering that in Switzerland and other stratified education systems such as Germany or the Netherlands, the transition into performance-based tracks happens at the end of primary education. Parents and teachers might be enticed into considering grade retention to facilitate the allocation into more advanced tracks. However, from a pupil's perspective, grade retention exerts a strong ability signal accompanied by the risk of stigma and decreased self-efficacy (Marsh, 2016; Parker et al., 2019). Furthermore, if track placement is subject to relative age effects, they play a role in determining educational pathways and subsequently affect outcomes later in life. Therefore, particularly during the critical phase of primary education, relative age poses a threat to equity in educational outcomes that should be addressed.

Recognizing that relative age effects might partially shape educational pathways, we can draw a line to findings on outcomes later in life. If relative age disadvantages translate into distinct educational pathways where younger students are more likely to face less favorable learning conditions, this can cause diverging outcomes later in life. Additionally, if students compensate for their relative age disadvantages with an additional year of schooling, this will ultimately delay their labor market entry, which can partially explain differences in labor market outcomes.

We acknowledge that cut-off dates for school enrolment are a practical and widely accepted practice to group children into school cohorts. However, the implications of arbitrarily set cut-off dates for pupils' learning outcomes are non-negligible. In view of our results, the adverse effects of age-based school entry laws warrant a policy response to overcome or at least mitigate relative age effects. Webdale et al. (2020) recently published an overview of proposed solutions to the relative age effect. One possible approach would be to consider learning gains over time to capture the general aptitude of students rather than performance on a test day. Another approach implies changing the institutional setting by either decreasing the number of months between cut-off dates or clustering pupils with similar birth dates in classes, ultimately reducing relative age differentials. A further—and likely more feasible—approach concerns the social mechanisms that give rise to enduring relative age effects. Teachers should be made more aware that relative age affects their pupils' learning and should adjust their grading practices and means of support accordingly.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: the large scale assessment data (“Checks”) used in this study is available upon request and free of charge for all interested researchers (via the “SWISSUbase” repository). The “Checks” data was linked to register data provided from Switzerland's Federal Statistical Office and the Central Compensation Office. The linked data set used in this study cannot be made publicly available due to privacy regulations stated in the data user agreement with the Federal Statistical Office and the Central Compensation Office. Nonetheless, we enable replications of our study in two ways: First, Appendix B outlines the exact data linkage procedure and mentions the contract number with the Federal Statistical Office and the Central Compensation Office. Using this contract number, an identical data linkage can be established. Second, we provide additional information on data linkage and all our code files on an Open Science repository (see https://osf.io/9ceya/). Requests to access these datasets should be directed to https://www.swissubase.ch/en/catalogue/studies/13889/18123/overview.

Ethics statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent from the (patients/ participants OR patients/participants legal guardian/next of kin) was not required to participate in this study in accordance with the national legislation and the institutional requirements.

Author contributions

RB: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. TA: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The article is published with support from the Bern University of Teacher Education. Robin Benz discloses receipt of the following financial support: this work has received funding from the European Union's 2020 research and innovation programme under grant agreement no. 101004392 (PIONEERED).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2025.1463619/full#supplementary-material

Footnotes

1. ^Due to the federalist structure of Switzerland's education system, the sub-national units, the cantons, retain extensive jurisdiction over educational policy in compulsory education. Among other things, cantons have autonomy over school entry laws, including cut-off dates for school enrolment. Starting in 2007, the cantons were mandated to gradually adopt the nationwide cut-off date of the 31st of July. For more information, see Appendix A.

2. ^The rates of delayed school enrolments in the four cantons that make up Northwestern Switzerland are as follows: Out of all children who reached school eligibility, 14% in Aargau, 14% in Solothurn, 6% in Basel-Landschaft, and 6% in Basel-Stadt enter school at least one year late (SCCRE, 2023, 61f.)

3. ^More information on the record linkage and the analytical samples is provided in Appendix B. See Appendix C for descriptive statistics of the variables.

References

Baker, J., Schorer, J., and Cobley, S. (2010). Relative age effects: an inevitable consequence of elite sport? Sportwissenschaft 40, 26–30. doi: 10.1007/s12662-009-0095-2

Crossref Full Text | Google Scholar

Barua, R., and Lang, K. (2016). School entry, educational attainment, and quarter of birth: a cautionary tale of a local average treatment effect. J. Hum. Cap. 10, 347–376. doi: 10.1086/687599

Crossref Full Text | Google Scholar

Bassok, D., and Reardon, S. F. (2013). “Academic redshirting” in kindergarten: prevalence, patterns, and implications. Educ. Eval. Policy Anal. 35, 283–297. doi: 10.3102/0162373713482764

PubMed Abstract | Crossref Full Text | Google Scholar

Bedard, K., and Dhuey, E. (2006). The persistence of early childhood maturity: international evidence of long-run age effects. Q. J. Econ. 121, 1437–1472. doi: 10.1162/qjec.121.4.1437

Crossref Full Text | Google Scholar

Bernardi, F., and Grätz, M. (2015). Making up for an unlucky month of birth in school: causal evidence on the compensatory advantage of family background in England. Sociol. Sci. 2, 235–251. doi: 10.15195/v2.a12

Crossref Full Text | Google Scholar

Bjerke, A. H., Smestad, B., Eriksen, E., and Rognes, A. (2022). Relationship between birth month and mathematics performance in Norway. Scandinavian J. Educ. Res. 66, 1038–1048. doi: 10.1080/00313831.2021.1958371

PubMed Abstract | Crossref Full Text | Google Scholar

Black, S. E., Devereux, P. J., and Salvanes, K. G. (2011). Too young to leave the nest? The effects of school starting age. Rev. Econ. Stat. 93, 455–467. doi: 10.1162/REST_a_00081

Crossref Full Text | Google Scholar

BR NWCH (2021). Checks im BR NWCH 2013–2020. Universität Zürich - Institut für Bildungsevaluation - IBE.

Google Scholar

Buchmann, M., Kriesi, I., Koomen, M., Imdorf, C., and Basler, A. (2016). “Differentiation in secondary education and inequality in educational opportunities: the case of Switzerland,” in Models of Secondary Education and Social Inequality – An International Comparison (Cheltenham, UK; Northampton, MA, USA: Edward Elgar Publishing), 111–128. doi: 10.4337/9781785367267.00016

Crossref Full Text | Google Scholar

Buckles, K., and Hungerman, D. (2013). Season of birth and later outcomes: old questions, new answers. Rev. Econ. Stat. 95, 711–724. doi: 10.1162/REST_a_00314

PubMed Abstract | Crossref Full Text | Google Scholar

Calonico, S., Cattaneo, M. D., and Farrell, M. H. (2018). On the effect of bias estimation on coverage accuracy in nonparametric inference. J. Am. Stat. Assoc. 113, 767–779. doi: 10.1080/01621459.2017.1285776

PubMed Abstract | Crossref Full Text | Google Scholar

Calonico, S., Cattaneo, M. D., and Farrell, M. H. (2020). Optimal bandwidth choice for robust bias-corrected inference in regression discontinuity designs. Econom. J. 23, 192–210. doi: 10.1093/ectj/utz022

Crossref Full Text | Google Scholar

CCO (2022a). Data From: Statistik der Zentralenausgleichsstelle (ZAS) [Statistics From the Central Compensation Office] - as of 31.12.2011. Central Compensation Office.

Google Scholar

CCO (2022b). Data From: Statistik der Zentralenausgleichsstelle (ZAS) [Statistics from the Central Compensation Office] - as of 31.12.2012. Central Compensation Office.

Google Scholar

CCO (2022c). Data From: Statistik der Zentralenausgleichsstelle (ZAS) [Statistics from the Central Compensation Office] - as of 31.12.2013. Central Compensation Office.

Google Scholar

CCO (2022d). Data From: Statistik der Zentralenausgleichsstelle (ZAS) [Statistics from the Central Compensation Office] - as of 31.12.2014. Central Compensation Office.

Google Scholar

CCO (2022e). Data From: Statistik der Zentralenausgleichsstelle (ZAS) [Statistics from the Central Compensation Office] - as of 31.12.2015. Central Compensation Office.

Google Scholar

CCO (2022f). Data From: Statistik der Zentralenausgleichsstelle (ZAS) [Statistics from the Central Compensation Office] - as of 31.12.2016. Central Compensation Office.

Google Scholar

CCO (2022g). Data From: Statistik der Zentralenausgleichsstelle (ZAS) [Statistics from the Central Compensation Office] - as of 31.12.2017. Central Compensation Office.

Google Scholar

CCO (2022h). Data From: Statistik der Zentralenausgleichsstelle (ZAS) [Statistics from the Central Compensation Office] - as of 31.12.2018. Central Compensation Office.

Google Scholar

CCO (2022i). Data From: Statistik der Zentralenausgleichsstelle (ZAS) [Statistics from the Central Compensation Office] - as of 31.12.2019. Central Compensation Office.

Google Scholar

CCO (2022j). Data From: Statistik der Zentralenausgleichsstelle (ZAS) [Statistics from the Central Compensation Office] - as of 31.12.2020. Central Compensation Office.

Google Scholar

Crawford, C., Dearden, L., and Greaves, E. (2014). The drivers of month-of-birth differences in children's cognitive and non-cognitive skills. J. R. Stat. Soc. 177, 829–860. doi: 10.1111/rssa.12071

PubMed Abstract | Crossref Full Text | Google Scholar

Cunha, F., and Heckman, J. (2007). The technology of skill formation. Am. Econ. Rev. 97, 31–47. doi: 10.1257/aer.97.2.31

Crossref Full Text | Google Scholar

Dhuey, E., Figlio, D., Karbownik, K., and Roth, J. (2019). School starting age and cognitive development. J. Policy Anal. Manag. 38, 538–578. doi: 10.1002/pam.22135

Crossref Full Text | Google Scholar

Dhuey, E., and Lipscomb, S. (2008). What makes a leader? Relative age and high school leadership. Econ. Educ. Rev. 27, 173–183. doi: 10.1016/j.econedurev.2006.08.005

Crossref Full Text | Google Scholar

Dhuey, E., and Lipscomb, S. (2010). Disabled or young? Relative age and special education diagnoses in schools. Econ. Educ. Rev. 29, 857–872. doi: 10.1016/j.econedurev.2010.03.006

Crossref Full Text | Google Scholar

Dicks, A., and Lancee, B. (2018). Double disadvantage in school? Children of immigrants and the relative age effect: a regression discontinuity design based on the month of birth. Eur. Sociol. Rev. 34, 319–333. doi: 10.1093/esr/jcy014

Crossref Full Text | Google Scholar

Dobkin, C., and Ferreira, F. (2010). Do school entry laws affect educational attainment and labor market outcomes? Econ. Educ. Rev. 29, 40–54. doi: 10.1016/j.econedurev.2009.04.003

Crossref Full Text | Google Scholar

Duncan, G. J., Dowsett, C. J., Claessens, A., Magnuson, K., Huston, A. C., Klebanov, P., et al. (2007). School readiness and later achievement. Dev. Psychol. 43, 1428–1446. doi: 10.1037/0012-1649.43.6.1428

PubMed Abstract | Crossref Full Text | Google Scholar

Eden, D., and Kinnar, J. (1991). Modeling galatea: boosting self-efficacy to increase volunteering. J. Appl. Psychol. 76, 770–780. doi: 10.1037/0021-9010.76.6.770

Crossref Full Text | Google Scholar

Eisenberg, N., Spinrad, T. L., and Eggum, N. D. (2010). Emotion-related self-regulation and its relation to children's maladjustment. Annu. Rev. Clin. Psychol. 6, 495–525. doi: 10.1146/annurev.clinpsy.121208.131208

PubMed Abstract | Crossref Full Text | Google Scholar

Fiorini, M., and Stevens, K. (2021). Scrutinizing the monotonicity assumption in IV and fuzzy RD designs. Oxf. Bull. Econ. Stat. 83, 1475–1526. doi: 10.1111/obes.12430

Crossref Full Text | Google Scholar

FSO (2022a). Der Übergang am Ende der obligatorischen Schule - 2017–2020. Available at: https://www.bfs.admin.ch/asset/de/23487437 (accessed May 30, 2023).

Google Scholar

FSO (2022b). Data From: Gebäude- und Wohnungsstatistik (GWS) [Federal Buildings and Dwellings Statistic] - as of 31.12.2015. Federal Statistical Office.

Google Scholar

FSO (2022c). Data From: Gebäude- und Wohnungsstatistik (GWS) [Federal Buildings and Dwellings Statistic] - as of 31.12.2016. Federal Statistical Office.

Google Scholar

FSO (2022d). Data From: Gebäude- und Wohnungsstatistik (GWS) [Federal Buildings and Dwellings Statistic] - as of 31.12.2017. Federal Statistical Office.

Google Scholar

FSO (2022e). Data From: Gebäude- und Wohnungsstatistik (GWS) [Federal Buildings and Dwellings Statistic] - as of 31.12.2018. Federal Statistical Office.

Google Scholar

FSO (2022f). Data From: Gebäude- und Wohnungsstatistik (GWS) [Federal Buildings and Dwellings Statistic] - as of 31.12.2019. Federal Statistical Office.

Google Scholar

FSO (2022g). Data From: Gebäude- und Wohnungsstatistik (GWS) [Federal Buildings and Dwellings Statistic] - as of 31.12.2020. Federal Statistical Office.

Google Scholar

FSO (2022h). Data From: Statistik der Bevölkerung und der Haushalte (STATPOP) [Population and Households Statistics] - as of 31.12.2020. Federal Statistical Office.

Google Scholar

FSO (2022i). Data From: Statistik der Bevölkerung und der Haushalte (STATPOP) [Population and Households Statistics] - as of 31.12.2016. Federal Statistical Office.

Google Scholar

FSO (2022j). Data From: Statistik der Bevölkerung und der Haushalte (STATPOP) [Population and Households Statistics] - as of 31.12.2017. Federal Statistical Office.

Google Scholar

FSO (2022k). Data From: Statistik der Bevölkerung und der Haushalte (STATPOP) [Population and Households Statistics] - as of 31.12.2018. Federal Statistical Office.

Google Scholar

FSO (2022l). Data From: Statistik der Bevölkerung und der Haushalte (STATPOP) [Population and Households Statistics] - as of 31.12.2019. Federal Statistical Office.

Google Scholar

FSO (2022m). Data From: Statistik der Bevölkerung und der Haushalte (STATPOP) [Population and Households Statistics] - as of 31.12.2020. Federal Statistical Office.

Google Scholar

Fumarco, L., and Baert, S. (2019). Relative age effect on European adolescents' social network. J. Econ. Behav. Organ. 168, 318–337. doi: 10.1016/j.jebo.2019.10.014

Crossref Full Text | Google Scholar

Hancock, D. J., Adler, A. L., and Côté, J. (2013). A proposed theoretical model to explain relative age effects in sport. Eur. J. Sport Sci. 13, 630–637. doi: 10.1080/17461391.2013.775352

PubMed Abstract | Crossref Full Text | Google Scholar

Imbens, G., and Kalyanaraman, K. (2012). Optimal bandwidth choice for the regression discontinuity estimator. Rev. Econ. Stud. 79, 933–959. doi: 10.1093/restud/rdr043

PubMed Abstract | Crossref Full Text | Google Scholar

Jerrim, J., Lopez-Agudo, L. A., and Marcenaro-Gutierrez, O. D. (2022). Grade retention and school entry age in Spain: a structural problem. Educ. Assess. Eval. Account. 34, 331–359. doi: 10.1007/s11092-021-09375-7

Crossref Full Text | Google Scholar

Jussim, L. (1986). Self-fulfilling prophecies: a theoretical and integrative review. Psychol. Rev. 93, 429–445. doi: 10.1037/0033-295X.93.4.429

Crossref Full Text | Google Scholar

König, N., and Berger, S. (2021). Checks in BR NWCH. Standardised School Performance Assessments on Primary and Lower Secondary Level. Institute for Educational Evaluation, Zürich.

Google Scholar

Lee, D. S., and Lemieux, T. (2010). Regression discontinuity designs in economics. J. Econ. Lit. 48, 281–355. doi: 10.1257/jel.48.2.281

Crossref Full Text | Google Scholar

Lenard, M. A., and Peña, P. A. (2018). Maturity and minorities: the impact of redshirting on achievement gaps. Educ. Econ. 26, 593–609. doi: 10.1080/09645292.2018.1468873

Crossref Full Text | Google Scholar

Marsh, H. W. (2016). Cross-cultural generalizability of year in school effects: negative effects of acceleration and positive effects of retention on academic self-concept. J. Educ. Psychol. 108, 256–273. doi: 10.1037/edu0000059

Crossref Full Text | Google Scholar

Mavilidi, M. F., Marsh, H. W., Xu, K. M., Parker, P. D., Jansen, P. W., and Paas, F. (2022). Relative age effects on academic achievement in the first ten years of formal schooling: a nationally representative longitudinal prospective study. J. Educ. Psychol. 114, 308–325. doi: 10.1037/edu0000681

Crossref Full Text | Google Scholar

Merton, R. K. (1968). The matthew effect in science. Science 159, 56–63. doi: 10.1126/science.159.3810.56

Crossref Full Text | Google Scholar

Mühlenweg, A., and Puhani, P. (2010). The evolution of the school-entry age effect in a school tracking system. J. Hum. Resour. 45, 407–438. doi: 10.1353/jhr.2010.0020

PubMed Abstract | Crossref Full Text | Google Scholar

Nam, K. (2014). Until when does the effect of age on academic achievement persist? Evidence from Korean data. Econ. Educ. Rev. 40, 106–122. doi: 10.1016/j.econedurev.2014.02.002

Crossref Full Text | Google Scholar

Parker, P. D., Marsh, H. W., Thoemmes, F., and Biddle, N. (2019). The negative year in school effect: extending scope and strengthening causal claims. J. Educ. Psychol. 111, 118–130. doi: 10.1037/edu0000270

Crossref Full Text | Google Scholar

Pehkonen, J., Viinikainen, J., Böckerman, P., Pulkki-Råback, L., Keltikangas-Järvinen, L., and Raitakari, O. (2015). Relative age at school entry, school performance and long-term labour market outcomes. Appl. Econ. Lett. 22, 1345–1348. doi: 10.1080/13504851.2015.1031864

PubMed Abstract | Crossref Full Text | Google Scholar

Peña, P. A. (2017). Creating winners and losers: date of birth, relative age in school, and outcomes in childhood and adulthood. Econ. Educ. Rev. 56, 152–176. doi: 10.1016/j.econedurev.2016.12.001

Crossref Full Text | Google Scholar

Ponzo, M., and Scoppa, V. (2014). The long-lasting effects of school entry age: evidence from Italian students. J. Policy Model. 36, 578–599. doi: 10.1016/j.jpolmod.2014.04.001

Crossref Full Text | Google Scholar

Rosenthal, R., and Jacobson, L. (1968). Pygmalion in the classroom. Urban Rev. 3, 16–20. doi: 10.1007/BF02322211

Crossref Full Text | Google Scholar

SCCRE (2023). Education Report Switzerland 2023. Swiss Coordination Centre for Research in Education, Aarau.

Google Scholar

Schneeweis, N., and Zweimüller, M. (2014). Early tracking and the misfortune of being young. Scand. J. Econ. 116, 394–428. doi: 10.1111/sjoe.12046

Crossref Full Text | Google Scholar

Skopek, J., and Passaretta, G. (2021). Socioeconomic inequality in children's achievement from infancy to adolescence: the case of Germany. Soc. Forces 100, 86–112. doi: 10.1093/sf/soaa093

PubMed Abstract | Crossref Full Text | Google Scholar

Smith, J. (2009). Can regression discontinuity help answer an age-old question in education? The effect of age on elementary and secondary school achievement. BE J. Econ. Anal. Policy 9, 1–30. doi: 10.2202/1935-1682.2221

Crossref Full Text | Google Scholar

Solli, I. F. (2017). Left behind by birth month. Educ. Econ. 25, 323–346. doi: 10.1080/09645292.2017.1287881

Crossref Full Text | Google Scholar

Sprietsma, M. (2010). Effect of relative age in the first grade of primary school on long-term scholastic results: international comparative evidence using PISA 2003. Educ. Econ. 18, 1–32. doi: 10.1080/09645290802201961

Crossref Full Text | Google Scholar

Thoren, K., Heinig, E., and Brunner, M. (2016). Relative age effects in mathematics and reading: investigating the generalizability across students, time and classes. Front. Psychol. 7:679. doi: 10.3389/fpsyg.2016.00679

PubMed Abstract | Crossref Full Text | Google Scholar

Webdale, K., Baker, J., Schorer, J., and Wattie, N. (2020). Solving sport's “relative age” problem: a systematic review of proposed solutions. Int. Rev. Sport Exerc. Psychol. 13, 187–204. doi: 10.1080/1750984X.2019.1675083

Crossref Full Text | Google Scholar