Rong Guo
Yan Zheng2- 1Department of Education, Shaanxi Normal University, Xi’an, China
- 2Xi’an Wuhuan Middle School, Xi’an, China
Computational thinking is regarded as an essential skill for students in the 21st century, and programming is one of the means to cultivate it. This study introduces mind mapping into graphical programming to visualize the cognitive process of computational thinking, aiming to enhance students’ computational thinking skills. After a semester of teaching experiments, independent-sample t-tests and paired-sample t-tests were conducted on the data, revealing significant improvements in both computational thinking skills and self-efficacy among the students in the experimental group. Further analysis of the data showed significant enhancements in their algorithmic thinking and modeling, as well as pattern recognition and evaluation sub-skills, while abstraction and decomposition sub-skills did not show significant improvement. Additionally, the experimental group demonstrated significant improvements to varying degrees in five dimensions of computational thinking self-efficacy: creativity, algorithmic thinking, collaboration skills, critical thinking, and problem-solving abilities.
1 Introduction
The development of digital technology has created many new job opportunities while also posing a certain impact on the traditional employment structure, requiring enterprises to have more talents with digital technology and knowledge. As the digital society transforms the way people work and live, it also sets new requirements for citizens’ digital literacy (Silva et al., 2021). Consequently, in today’s era of rapid information technology development, understanding the fundamental principles of computer science is no longer solely the domain of programmers and computer scientists. Applying computer science to solve problems has become an essential skill for everyone, which also embodies the essence of computational thinking (Yang and Lin, 2024). Computational thinking is defined as a way of thinking that utilizes computer science concepts to solve problems, design systems, and understand human behavior (Wing, 2006). It is a fundamental skill essential for successful learners in the 21st century.
Against this backdrop, countries worldwide have recognized the importance of fostering computational thinking and have introduced policies to advance its education. Scholars are actively exploring strategies to enhance students’ computational thinking skills and have proposed that programming is an ideal tool for nurturing computational thinking (Hsu et al., 2018). This is because programming provides avenues for applying computational concepts and practices while also supporting the development of cognitive abilities related to computational thinking (Basogain Olabe et al., 2017). Research has found that visual programming can significantly boost students’ computational thinking skills (Aksit and Wiebe, 2020). However, for younger students, programming poses certain challenges due to difficulties in comprehending abstract and generalizing concepts, as well as the prerequisite knowledge of basic concepts, syntax, and commands (Mladenović et al., 2021).
In response, scholars point out that learners’ prior knowledge is a crucial factor influencing programming learning, as students often lack a programming background and related knowledge, leading to difficulties in grasping programming concepts and practical operations (Demir, 2022). Establishing a systematic mindset to comprehend programming concepts and principles is key to learning programming (Cui and Ng, 2021). In programming, the process of using computational thinking to solve problems is a systematic thought process involving a series of cognitive steps such as analyzing problems, decomposing them, extracting essences, selecting algorithms, and implementing programming. Therefore, through systematic thinking training, students’ computational thinking and programming abilities can be effectively enhanced.
However, in current programming education, the teaching organization often proceeds directly from problem identification and understanding to code implementation, with the research focus on the realization of projects/works/functions (e.g., Atmatzidou and Demetriadis, 2016; Sullivan et al., 2017). There is a lack of developing students’ process-oriented thinking in problem-solving, i.e., a lack of a thinking training process. The existing teaching places emphasis on the debugging phase of programming, with less emphasis on the most essential thinking processes in computational thinking, such as abstraction and decomposition. Furthermore, students’ thinking is implicit in their programming works, making it difficult for teachers to identify issues. As a result, some scholars suggest that when teaching programming, in addition to using block-based programming with graphical interfaces, it is also crucial to help students articulate their programming logic to arrange appropriate programming blocks (Barr and Stephenson, 2011). We need tools to assist students in training their thinking, expressing their ideas, and visualizing their implicit thinking.
Research has shown that visual representations of thinking can help students express the relationships between complex ideas, showcasing internal cognitive structures in a visual form, which aids in recalling key components (Davies, 2011). Thus, organizing thoughts and supplementing ideas through relevant graphics (e.g., flowcharts, mind maps, graphic organizers) can significantly enhance students’ learning outcomes (Batdi, 2015; Shi et al., 2023; Stokhof et al., 2020; Zhao et al., 2022). Scholars have empirically confirmed that using mind maps in teaching can positively impact students’ academic performance, attitudes, conceptual learning, and critical thinking. Similarly, in research related to computational thinking, the use of mind maps has been proven to significantly improve primary school students’ computational thinking skills. However, there is a lack of empirical research on the impact of mind maps on middle school students’ computational thinking skills and self-efficacy in graphical programming. Therefore, this study aims to explore the effects of mind maps on middle school students’ computational thinking skills and self-efficacy in graphical programming.
2 Literature review
2.1 Definition of computational thinking
Different scholars have defined computational thinking from various perspectives. Papert was the first to propose the concept of computational thinking, which he saw as a process of using computational representations to articulate important ideas, making them clearer and more explicit (Atmatzidou and Demetriadis, 2016). Wing defined computational thinking as “a process of solving problems, designing systems, and understanding human behavior by drawing on the concepts fundamental to computer science” (Wing, 2006). Brennan et al. believed that computational thinking encompasses three dimensions: computational concepts, computational practices, and computational perspectives (Brennan and Resnick, 2012). Many other scholars have understood computational thinking as a cognitive process that integrates multiple thinking processes (Israel-Fishelson and Hershkovitz, 2022; Selby, 2013), including decomposition (breaking down problems into smaller, manageable parts), abstraction (identifying and extracting key information from real-world situations), algorithmic thinking (solving problems through a series of steps and instructions), pattern recognition (the ability to identify similarities in problems and situations), and programming debugging (converting instructions into computer programs, identifying errors, and debugging for corrections). In this study, computational thinking is viewed as a cognitive process, and thus, enhancing computational thinking can be seen as training and nurturing this series of thinking processes.
Enhancing students’ computational thinking is not about turning them into programmers, but empowering them to apply the thought processes of computer science to solve problems. As such, in nurturing computational thinking, it is crucial to train students’ minds and equip them with a comprehensive set of thought processes. As mentioned earlier, a prevailing issue in current computational thinking education is the overemphasis on programming and debugging, while neglecting other cognitive processes like decomposition, abstraction, algorithmic thinking, and pattern recognition. This one-sided approach hinders students from developing a systematic computational thinking framework.
Furthermore, when students are coding, their thought processes are implicitly embedded in their work, making it challenging for teachers to pinpoint which specific aspect of the cognitive process is problematic for individual students. Consequently, it becomes difficult to identify students’ weaknesses across different dimensions. To address these challenges, we must leverage tools that enhance students’ capabilities in all dimensions of computational thinking and visualize these thought processes. By doing so, not only can teachers better understand the intricacies of each student’s cognitive journey, but they can also tailor instruction to address specific weaknesses, thereby fostering a more holistic and effective development of computational thinking skills.
2.2 Tools for cultivating computational thinking
While there are numerous tools available for fostering computational thinking, given the advantages of programming in this regard, our focus lies primarily on programming-related tools. Programming learning tools focused on computational thinking primarily encompass graphical programming (such as Scratch, APP Inventor), text-based programming (such as Python, C), open-source hardware programming (such as Arduino), gaming (such as Penguin Go), and more. Additionally, mathematical teaching tools like wxMaxima can be utilized to cultivate students’ problem-solving and modeling abilities (Karjanto, 2021; Karjanto and Husain, 2021). Among these, research on graphical programming holds an absolute advantage (Tikva and Tambouris, 2021). This is due to the “low floor, high ceiling” nature of graphical programming, which encapsulates code within blocks, allowing students to create programs simply by dragging and dropping these blocks. Consequently, graphical programming does not require extensive knowledge of programming syntax rules, enabling students to complete a project in mere minutes. This ease of use and brevity make it highly accessible for students. By eliminating the need for strict syntax and foundational programming prerequisites, students can devote more energy to honing their thinking skills. This type of tool is particularly well-suited for primary and secondary school students looking to enhance their computational thinking abilities.
Existing research has demonstrated that utilizing graphical programming tools can significantly enhance students’ computational thinking skills. Graphical programming exerts a notable influence on students’ computational concepts, practices, and perspectives. Specifically, it has been shown to be highly effective in mastering computational concepts such as sequence, loop, condition, and event that are integral to computational thinking (Meerbaum-Salant et al., 2010; Sevillano García and Sáez López, 2016; Giordano and Maiorana, 2014). Furthermore, graphical programming significantly promotes computational practices related to computational thinking, including abstraction and debugging (Statter and Armoni, 2017; Webb and Rosson, 2013). Tsai, C. Y. conducted a quasi-experimental study, where the experimental group used graphical programming tools while the control group received traditional instruction. The results revealed that the experimental group had a better understanding of programming concepts compared to the control group (Tsai, 2019). Additionally, numerous studies have confirmed the positive impact of graphical programming on computational thinking from perspectives such as creative thinking, critical thinking, and problem-solving abilities (Ma et al., 2021).
It can be seen that existing research on computational thinking primarily unfolds from two perspectives. The first perspective explores students’ learning outcomes in terms of creative thinking, critical thinking, algorithmic thinking, and other dimensions. The second perspective examines the learning outcomes of computational thinking based on the three dimensions proposed by Brennan and others. In the empirical research conducted so far, there has been little examination of the cultivation effects of different tools from the angle of the cognitive processes involved in computational thinking. Therefore, this study analyzes the cultivation effects of various tools and strategies by focusing on the cognitive processes associated with computational thinking, such as abstraction, decomposition, algorithmic thinking, pattern recognition, and programming debugging.
2.3 Mind mapping
Mind mapping is defined as “a visual, nonlinear representation of ideas and their relationships” (Biktimirov and Nilson, 2003). It is a method invented by Buzan to concretize and visualize divergent thinking, enabling the visualization and expression of the cognitive structures within the brain (Buzan, 2006). Mind mapping employs shapes, images, and keywords to represent the relationships between conceptual ideas (Rostron, 2002). This approach aids in knowledge retention, organization, nurturing creative thinking, and assisting students in describing the relationships between complex ideas. When students can express complex thought relationships graphically, they are more likely to comprehend those relationships, further analyze their components, and facilitate deeper learning. Thus, processing or supplementing ideas through mind mapping can enhance students’ learning outcomes. Research indicates that taking notes using mind mapping positively impacts students’ conceptual learning and their attitudes towards courses (Al-Jarf, 2009).
Recent studies have shown that incorporating mind mapping into graphical programming significantly improves students’ creative thinking, critical thinking, and algorithmic thinking, thereby enhancing computational thinking skills among primary school students. Some research has also confirmed the impact of mind mapping on the computational thinking of university students. However, there is a lack of empirical studies investigating the role of mind mapping in graphical programming among middle school students, as well as its effects on computational thinking skills and self-efficacy (Sari et al., 2021).
2.4 Self-efficacy
Bandura defines self-efficacy as an individual’s belief in their ability to master or accomplish a task, which influences the choices they make, the effort they exert, and their perseverance in the face of difficulties when completing tasks (Bandura and Wessels, 1997). Research indicates that students with high self-efficacy perceive difficulties as challenges that arise during task completion, thereby affecting their level of effort in various contexts (Gandhi and Varma, 2010). Bandura emphasizes the existence and significance of domain-specific self-efficacy. Consequently, analyzing programming self-efficacy is crucial in fostering computational thinking through graphical programming. Programming is a complex and challenging process, and programming self-efficacy emerges as a pivotal variable in the learning journey when tackling problems through programming. Studies reveal that negative attitudes and low self-efficacy in programming training can act as barriers to learning (Hongwarittorrn and Krairit, 2010), whereas higher programming self-efficacy ensures success in programming endeavors (Yağcı, 2016). Hence, in utilizing programming to cultivate computational thinking among students, our primary focus should be on exploring strategies to enhance their programming self-efficacy.
Studies have confirmed that the application of mind mapping strategies in flipped classrooms significantly enhances academic performance and self-efficacy among second-year university students (Zheng et al., 2020). Helen Semilarski and colleagues utilized mind maps and concept maps to support students in integrating interdisciplinary learning, and their findings revealed that the employment of such visualization strategies notably boosted students’ self-efficacy in the domains of life and earth sciences, as well as in the utilization of models and systems (Semilarski et al., 2022). Based on these findings, we hypothesize that the use of mind mapping strategies in the cultivation of computational thinking can elevate students’ programming self-efficacy. Currently, there is a lack of empirical evidence demonstrating the impact of mind mapping on students’ self-efficacy specifically within the context of computational thinking development. Therefore, in this study, we conduct an experiment to investigate whether mind mapping can enhance students’ domain-specific self-efficacy in the process of fostering computational thinking.
2.5 Research objectives and questions
This study primarily explores the impact of different strategies on students’ computational thinking from the perspective of its cognitive processes, including abstraction, decomposition, pattern recognition, algorithmic thinking, programming debugging, and so forth. Additionally, existing research has confirmed that the use of mind maps in programming can enhance computational thinking skills among primary school students and university students. However, there have been few experimental studies examining the influence of mind maps on middle school students’ computational thinking skills and their self-efficacy in computational thinking. Therefore, this study aims to investigate the impact of mind maps on middle school students’ computational thinking skills and self-efficacy in the context of graphical programming. The following questions are posed to guide the research:
Question 1: Can mind mapping enhance middle school students’ computational thinking skills from the perspective of its cognitive processes (dimensions of abstraction, decomposition, pattern recognition, algorithmic thinking, and programming debugging)?
Question 2: Can mind mapping improve middle school students’ self-efficacy in computational thinking?
3 Method
3.1 Research hypotheses
Based on the above discussion, the following research hypotheses are formulated for this study:
a. When using mind mapping for programming learning, students’ computational thinking skills will show more significant improvement, with effects observed across all dimensions of the cognitive processes of computational thinking (including abstraction, decomposition, pattern recognition, algorithmic thinking, and programming debugging).
b. When using mind mapping for programming learning, students’ self-efficacy in computational thinking will experience a more significant enhancement.
3.2 Experimental subject
This study was conducted in the spring of 2024 at an urbanized junior high school. The participants were first-year junior high school students enrolled in the programming club during the semester, with an average age of 13 years old. The study involved an experimental group of 20 students and a control group of 17 students. None of the students in either the experimental or control group had prior exposure to graphical programming during their primary school years or before.
Prior to the instructional experiment, a pre-test was administered to both the experimental and control groups on March 21st, 2024, using the Computational Thinking Skills and Self-Efficacy Measurement Scale via an online survey platform. A total of 37 questionnaires were collected for both the computational thinking skills and attitude sections, all of which were deemed valid, resulting in a 100% response rate.
After the completion of twelve 1-h sessions, a post-test was conducted on June 20th, 2024, using the same measurement scales. Again, 37 questionnaires were collected from both groups for both sections, all of which were considered valid, maintaining a 100% response rate.
The collected data were statistically analyzed using SPSS 20.0 software. In the measurement scale for computational thinking skills, the independent sample t-test revealed a p-value of 0.075, indicating that there is no significant difference in computational thinking skills between the experimental group and the control group. Similarly, in the measurement scale for self-efficacy in computational thinking, the independent sample t-test showed a p-value of 0.094, suggesting that there is no significant difference in self-efficacy in computational thinking between the experimental group and the control group. Moreover, both the experimental and control groups completed programming tasks in groups of two to three students.
3.3 Learning content
As previously mentioned, this study conceptualizes computational thinking as a cognitive process encompassing five dimensions: decomposition, abstraction, algorithmic thinking, pattern recognition, and programming debugging. Therefore, fostering computational thinking necessitates a focus on these five components. The research plan leverages mind mapping as a tool to aid students in understanding and mastering the cognitive processes of computational thinking.
Students first gain an understanding of the project to be completed in each activity. Subsequently, under the guidance of the teacher, they engage in discussions to analyze the roles, variables, and contexts of the project. The outcomes of this decomposition are then presented using mind maps (as illustrated in Figures 1, 2). This step helps students break down complex projects, thereby fostering their ability to decompose problems, a key aspect of computational thinking.
Figure 1. Mind map illustrating the cognitive processes of computational thinking.
Figure 2. Students using mind maps to train their thinking process.
Next, students articulate the functions and roles of the decomposed parts based on the teacher’s demonstrations. This activity aims to encourage students to abstract phenomena, stripping away non-essential details to grasp the essence of the problem, thereby nurturing their ability to abstract. Students are then prompted to analyze which building blocks or modules should be used to implement the different roles and functions. The process of recalling and imagining suitable building blocks fosters algorithmic thinking and pattern recognition skills. Finally, students work in groups to write code and complete the project.
By using mind maps to decompose tasks, students are guided to think about problems step-by-step, abstract the essence of the problem, match the problem with specific building blocks or modules, and ultimately solve the problem. By unfolding the cognitive processes of computational thinking through mind mapping, this experimental approach aims to cultivate students’ computational thinking abilities.
Furthermore, the 12 projects selected for the experiment were designed by the researchers, taking into account the students’ proficiency levels. These projects encompass various program structures and building blocks in graphical programming, including “Big Fish Eats Little Fish,” “Guess Idioms from Pictures,” “Flappy Bird,” “Fruit Crush,” “Whack-a-Mole,” “Tank Battle,” “Pole Climbing Race,” “Racing Game,” “Monster Hunt,” “Dress-Up Game,” “Jump Game,” and “Airplane Battle.”
3.4 Experimental procedure
The experimental procedures are illustrated in Figure 3. Both the experimental group and the control group were taught by the same instructor, with sessions held once a week, each lasting for an hour, over a total of 16 weeks. During the first 2 weeks, students were introduced to the Scratch graphical programming interface and building blocks, as well as the X-mind mind mapping software. In the third week, pre-tests were conducted to assess students’ computational thinking skills and self-efficacy.
Figure 3. Experimental procedure.
From the fourth week to the fifteenth week, the teaching experiments commenced. For the experimental group, the teaching process entailed the following steps: the instructor demonstrated case studies, then the instructor and students jointly analyzed and decomposed these cases using mind maps, guiding students to identify key logics and Scratch blocks. Students engaged in discussions among themselves to refine their mind maps, and subsequently collaborated to write the program based on the prompts from the mind maps. Finally, they presented their work and summarized their learning.
The teaching process for the control group was largely similar to that of the experimental group, with the notable exception of the absence of mind mapping. Specifically, the instructor demonstrated case studies, and then the instructor and students analyzed the cases together. Students then collaborated to complete the cases, followed by presentations and summaries.
3.5 Instrument
3.5.1 Computational thinking skills
To assess students’ computational thinking skills, we employed The Bebras CT Challenge as our measurement tool. The Bebras CT Challenge is an internationally renowned online competition designed to promote computer science and computational thinking among students aged 10 to 19, and it has proven to be highly effective (Boom et al., 2022; Dagiene and Jevsikova, 2012; Román-González et al., 2017). This competition categorizes students into six age groups. Given that the average age of the students in our experiment was 13, we selected questions from the 12–14 age group. Each age group’s questions are divided into three levels of difficulty: A-level, B-level, and C-level, each targeting different sub-skills of computational thinking. Specifically, A-level comprises 6 questions worth 2 points each, assessing algorithmic thinking and modeling capabilities; B-level includes 4 questions worth 4 points each, evaluating pattern recognition and evaluation skills; and C-level consists of 2 questions worth 6 points each, measuring abstraction and decomposition abilities. We first translated the questions into Chinese and then had two students read through them to analyze any potential linguistic barriers in comprehension. It was found that the Chinese translations did not pose any comprehension difficulties for the students.
3.5.2 Computational thinking self-efficacy
To measure students’ self-efficacy in computational thinking, we utilized the Computational Thinking Scale adapted by Korkmaz and Bai (2019). The original Computational Thinking Self-Efficacy Scale developed by Korkmaz and colleagues has gained widespread application globally. For this study, we employed the Chinese version of the CTS, which has been extensively used in China and recognized for its effectiveness in measuring self-efficacy in computational thinking. The Computational Thinking Self-Efficacy Scale employs a Likert five-point scale ranging from 1 = Strongly Disagree to 5 = Strongly Agree. It assesses five dimensions of computational thinking: creativity, algorithmic thinking, collaboration ability, critical thinking, and problem-solving ability, with a total of 22 items.
4 Results
4.1 Analyzing the impact of mind mapping on computational thinking skills
Regarding the first research question, we first conducted independent sample t-tests on the pre-test and post-test data from the experimental and control classes to determine whether there were any differences in computational thinking skills between the two classes before the teaching experiment began and whether there were any differences after the teaching experiment was implemented. The results are presented in Tables 1, 2. Subsequently, we performed paired sample t-tests on the pre-test and post-test data of both the experimental and control classes separately to verify the effectiveness of the teaching experiment’s intervention. The results of these analyses are shown in Tables 3, 4.
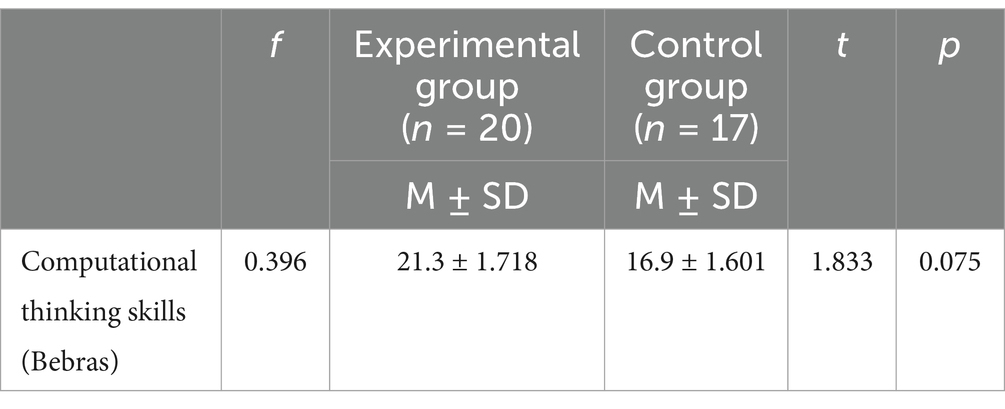
Table 1. Measurement of computational thinking skills in experimental group and control group (Bebras) pre-test comparison (df = 35).
Table 2. Measurement of computational thinking skills in experimental group and control group (Bebras) post-test comparison (df = 35).
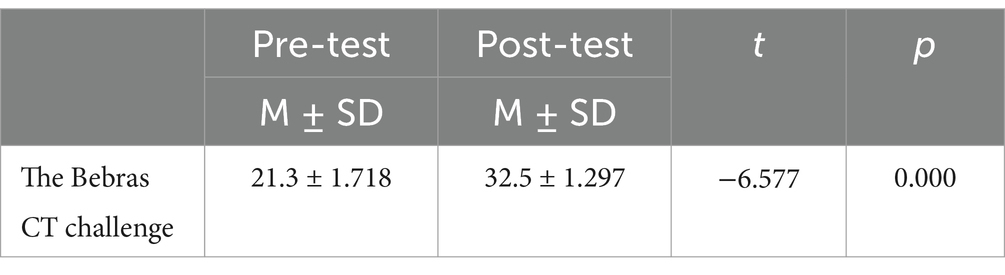
Table 3. Comparison of pre and post tests of the computational thinking skills measurement scale in the experimental group (n = 20, df = 19).
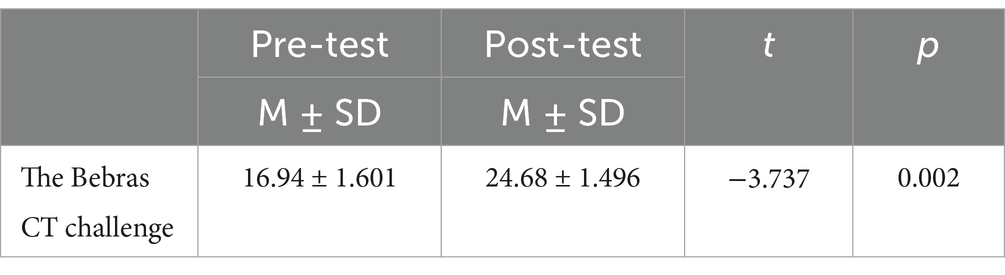
Table 4. Comparison of pre and post tests of the computational thinking skills measurement scale in the control group (n = 17, df = 16).
Before the experiment, through conducting an independent sample t-test on the pre-test data, we can conclude (as shown in Table 1) that the levels of computational thinking skills between the experimental class and the control class were essentially the same, with no significant difference (p = 0.075 > 0.05). After a semester of instruction, we performed paired sample t-tests on the pre-test and post-test data of both groups. The data indicated (as shown in Tables 3, 4) that within the experimental class, there was a significant difference before and after the experiment (p < 0.001), indicating an extremely significant improvement in computational thinking skills as a result of the teaching experiment. Similarly, within the control class, there was also a significant difference (p = 0.002), suggesting a notable enhancement in computational thinking skills following the teaching experiment, albeit to a lesser extent compared to the experimental group.
When conducting an independent sample t-test on the post-test data, the results (as shown in Table 2) indicated an extremely significant difference (p < 0.001) between the experimental class and the control class, suggesting that the experimental class outperformed the control class in computational thinking skills. We further analyzed the differences across the three dimensions of computational thinking and found that the experimental group significantly surpassed the control group in two dimensions: algorithmic thinking and modeling capabilities (p = 0.046), as well as measurement, pattern recognition, and evaluation abilities (p = 0.004). However, there was no significant difference in the dimension of abstraction and decomposition (p = 0.059).
4.2 Analyzing the impact of mind mapping on self-efficacy in computational thinking
Addressing the second research question, we employed the Computational Thinking Scale to conduct both independent sample t-tests and paired sample t-tests to detect whether there were significant differences between the experimental group and the control group before and after the experiment. Prior to the experiment, we conducted a pre-test on both the experimental and control groups. The results of the independent sample t-test (as shown in Table 5) indicated that the experimental group and the control group were essentially the same in terms of self-efficacy in computational thinking, with no significant difference (p = 0.094). After the teaching experiment, paired sample t-tests were performed separately on the experimental and control groups to analyze the changes in both groups. The data revealed (as shown in Table 6) that there was a significant difference in the experimental class before and after the experiment (p < 0.001), indicating a remarkable enhancement in the attitudes toward computational thinking among the experimental group through the teaching experiment. In contrast, no significant difference was found in the control class (p = 0.092). Although the average score of self-efficacy in computational thinking among the control group increased slightly compared to the pre-test, this improvement did not reach statistical significance (Table 7).
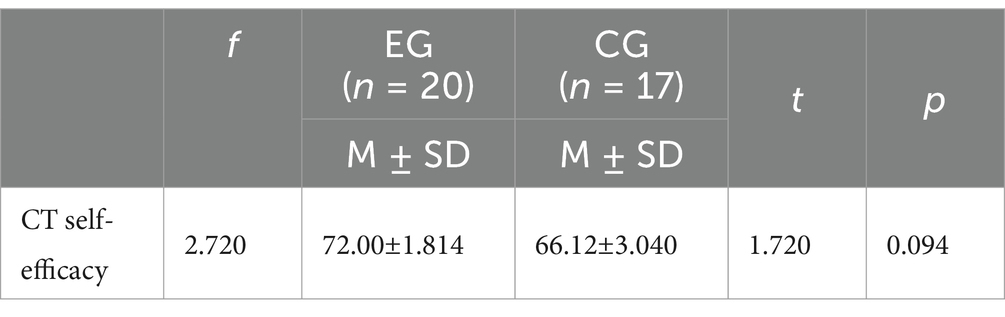
Table 5. Comparison of pre-test scores on the computational thinking self-efficacy scale (CTS) between the experimental group and the control group (df = 35).
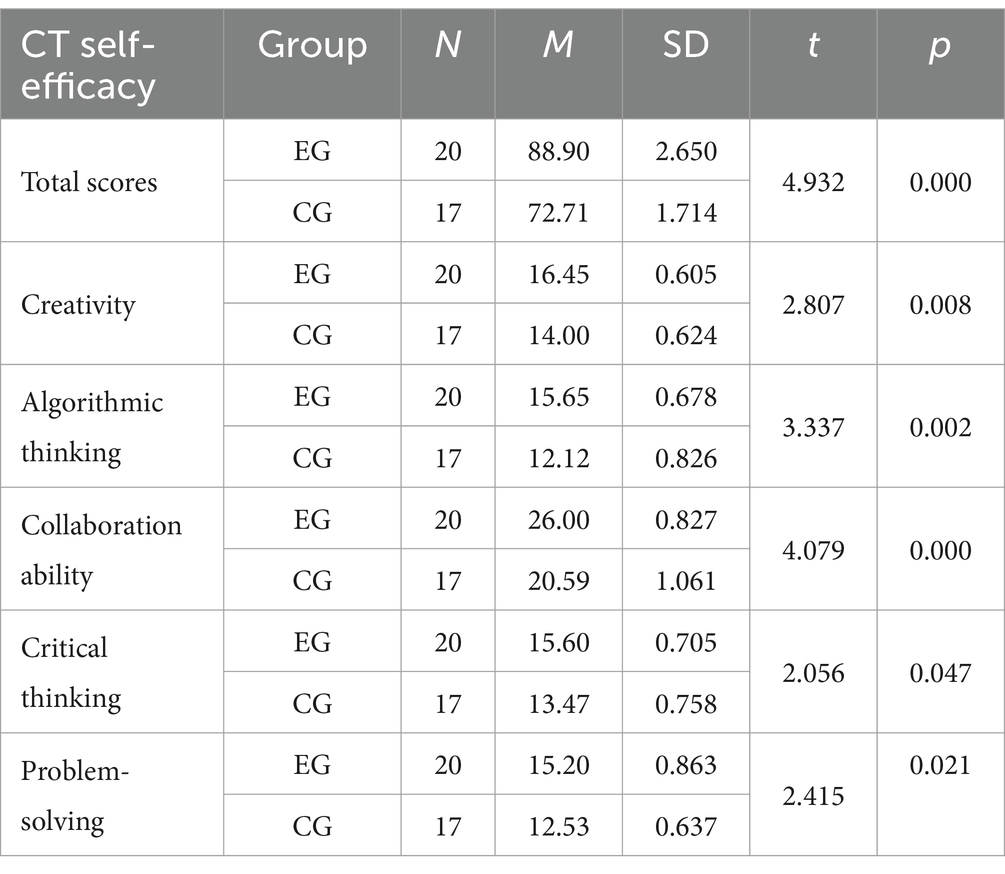
Table 6. Comparison of post-test scores on the computational thinking self-efficacy scale (CTS) between the experimental group and the control (df = 35).
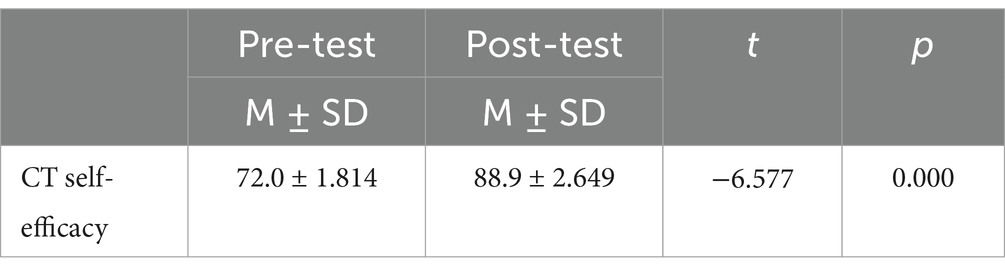
Table 7. Comparison of pre-test and post-test scores on the computational thinking self-efficacy scale (CTS) for the experimental group (n = 20, df = 19).
Further analysis was conducted to examine the differences between the two groups across various dimensions. Based on the results of the independent sample t-test (as shown in Table 8), it can be observed that there was an extremely significant difference (p < 0.001) between the experimental class and the control class after the implementation of the teaching experiment. Specifically, significant differences of varying degrees were found in five dimensions: creativity, algorithmic thinking, collaboration ability, critical thinking, and problem-solving.
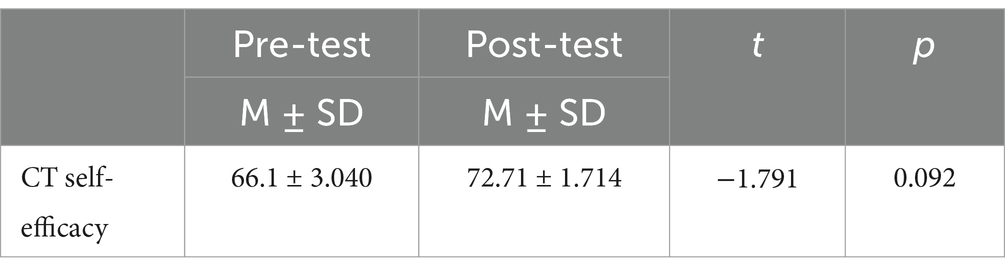
Table 8. Comparison of pre-test and post-test scores on the computational thinking self-efficacy scale (CTS) for the control group (n = 17, df = 16).
5 Discussion
Programming serves as an ideal tool for enhancing students’ computational thinking, and through specific strategic support in this process, students can attain a higher level of proficiency (Hooshyar, 2022; Rodríguez-Martínez et al., 2020; Zhang et al., 2023). Furthermore, each step in the cognitive process of computational thinking has a crucial impact on problem-solving abilities, making it significant to leverage tools to advance students’ cognitive processes related to computational thinking. Thus, it is necessary to explore supportive strategies for fostering the cognitive processes of computational thinking.
In this study, mind mapping was employed as a supportive strategy and a cultivation tool for the cognitive processes of computational thinking, to investigate its impact on computational thinking skills and self-efficacy. After a 12-week experiment, post-test data revealed that both the experimental group and the control group showed improvements in computational abilities, but the effect was more pronounced in the experimental group. The control group utilized graphical programming tools to cultivate students’ computational thinking, demonstrating that visual programming can significantly enhance students’ computational thinking skills. This finding corroborates existing research, reinforcing the positive influence of programming tools on computational thinking through data. Below is a discussion on the research questions based on the study’s findings.
Research Question 1: Can mind mapping enhance middle school students’ computational thinking skills from the perspective of the cognitive processes of computational thinking (dimensions of abstraction, decomposition, pattern recognition, algorithmic thinking, and programming debugging)? The results indicate that the experimental group supported by mind mapping exhibited more significant improvements in computational thinking skills. Further analysis reveals that, compared to the control group, students showed notable differences in the dimensions of algorithms and modeling, as well as pattern recognition and evaluation. However, there were no significant differences in the dimensions of abstraction and decomposition.
As mentioned earlier, during the teaching process, students in both the experimental and control groups were led by teachers to analyze and decompose cases, with the teachers’ explanations predominating. However, in the experimental group, after presenting the decomposed results using mind maps, students continued to use mind maps to analyze the specific steps for implementing each small problem. This process was crucial for enhancing their algorithmic modeling skills. Additionally, during this process, students also associated the specific code blocks they used with previously learned cases, serving as a form of recall and cognitive reinforcement, ultimately improving their pattern recognition abilities. Upon further analysis of the experimental process, it was observed that after presenting cases, teachers led students to decompose the cases and analyze the problems together. Therefore, no significant differences were observed in the dimensions of decomposition and abstraction. In the future, an attempt could be made to allow students to use mind maps independently to decompose cases and analyze problems, thereby fostering their abilities in decomposition and abstraction. The experiment confirmed previous research findings (Basu et al., 2017; Ismail et al., 2010) that mind mapping has a positive impact on the computational thinking skills of university students and primary school students. Simultaneously, this study extended this discovery to middle school students.
Research Question 2: Can mind mapping enhance middle school students’ self-efficacy in computational thinking? We have obtained a positive answer to this question. The data indicated that the experimental group showed significant improvements across all five dimensions of computational thinking self-efficacy. This result aligns with previous research (Malycha and Maier, 2017; Rahmidani, 2019), suggesting that mind mapping positively impacts students’ creativity, critical thinking, algorithmic thinking, problem-solving skills, and collaboration abilities. In the context of this experiment, when students used mind maps to analyze project-based tasks, they generated diverse ideas and multiple solutions to the same problem. This process effectively promoted their creative thinking, algorithmic thinking, and collaboration skills. Furthermore, the variety of approaches to solving the same problem necessitated analysis, discussion, and selection among students, which contributed to the development of their critical thinking. In contrast, in the control group, individual ideas were implicit within the programming modules, hindering students from analyzing the differences between various methods. Consequently, using mind maps to discuss algorithms and visualizing thinking facilitated student communication and discussion, ultimately enhancing their computational thinking self-efficacy.
This finding corroborates previous research, demonstrating that mind mapping can significantly enhance students’ self-efficacy in flipped classrooms and interdisciplinary teaching. The current study extends these results by showing that mind mapping can also improve students’ computational thinking self-efficacy in the context of graphical programming. Furthermore, research indicates that low self-efficacy is a significant barrier in programming learning, whereas students with high self-efficacy tend to perform better in programming. This explanation sheds light on why the experimental group students demonstrated superior computational thinking skills compared to the control group. By fostering a sense of accomplishment and confidence through the use of mind maps, students in the experimental group likely felt more empowered to tackle programming challenges, leading to their improved performance.
6 Conclusion and limitations
This study explored the strategy of utilizing mind maps to enhance middle school students’ computational thinking skills and self-efficacy in graphical programming. By visualizing the cognitive processes of computational thinking through mind maps, the teaching experiment conducted over a semester revealed that this strategy significantly improved students’ computational thinking skills, particularly in the dimensions of algorithmic modeling and pattern recognition and evaluation. Regarding computational thinking self-efficacy, students demonstrated notable enhancements across five dimensions: creativity, algorithmic thinking, critical thinking, collaboration skills, and problem-solving abilities. This research holds significant theoretical and practical implications. Theoretically, this study validates the role of mind mapping as an instructional strategy in fostering computational thinking in programming education. By experimentally verifying the positive impact of mind mapping on computational thinking self-efficacy, it expands upon previous research on mind mapping. Practically, this experiment was conducted in an authentic teaching environment, making it feasible for frontline teachers to adopt and implement the strategy in their own classrooms. This finding offers a practical tool for educators to enhance students’ computational thinking skills and self-efficacy, ultimately leading to improved learning outcomes in programming education.
There are several limitations to this study that warrant consideration. Firstly, the sample was drawn from urban schools in western China, where students had no prior exposure to graphical programming before middle school. Future research could expand to economically developed provinces in central and eastern China to increase the diversity of the sample. Secondly, the sample students were voluntarily enrolled in the graphical programming club, indicating a high likelihood of their interest in computer-related activities. Additionally, the majority of the participants were male, and the study did not account for gender factors. Future research should broaden the scope of participants and consider multiple factors such as interest and gender. Thirdly, different forms of mind mapping, such as digital creation versus hand-drawn, can influence student learning. However, this study only utilized digital mind mapping. Further research could explore the effects of various mind mapping methods on students’ learning outcomes. Lastly, the study found no significant difference in the decomposition and abstraction dimensions of computational thinking. Further investigation is needed to explore potential reasons for this outcome and refine the experimental design. Addressing these limitations in future research will contribute to a more comprehensive understanding of the effectiveness of mind mapping in enhancing computational thinking skills and self-efficacy among students.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Ethics statement
Ethical approval was not required for the study involving human samples in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin. Ethical approval was not required for the study involving animals in accordance with the local legislation and institutional requirements. Written informed consent was obtained from the individual(s), and minor(s)’ legal guardian/next of kin, for the publication of any potentially identifiable images or data included in this article.
Author contributions
RG: Writing – original draft, Writing – review & editing. YZ: Writing – original draft, Data curation. HM: Writing – original draft.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aksit, O., and Wiebe, E. N. (2020). Exploring force and motion concepts in middle grades using computational modeling: a classroom intervention study. J. Sci. Educ. Technol. 29, 65–82. doi: 10.1007/s10956-019-09800-z
Al-Jarf, R. (2009). Enhancing freshman students’ writing skills with a mind-mapping software. In Conference proceedings of eLearning and Software for Education (eLSE) (Vol. 5, No. 01, pp. 375–382). Available at: https://ssrn.com/abstract=3901075
Atmatzidou, S., and Demetriadis, S. (2016). Advancing students’ computational thinking skills through educational robotics: a study on age and gender relevant differences. Robot. Auton. Syst. 75, 661–670. doi: 10.1016/j.robot.2015.10.008
Barr, V., and Stephenson, C. (2011). Bringing computational thinking to K-12: what is involved and what is the role of the computer science education community? ACM Inroads 2, 48–54. doi: 10.1145/1929887.1929905
Basogain Olabe, X., Olabe Basogain, M. Á., Olabe Basogain, J. C., and Rico, M. J. (2017). Computational thinking in pre-university blended learning classrooms
Basu, S., Biswas, G., and Kinnebrew, J. S. (2017). Learner modeling for adaptive scaffolding in a computational thinking-based science learning environment. User Model. User-Adap. Inter. 27, 5–53. doi: 10.1007/s11257-017-9187-0
Batdi, V. (2015). A meta-analysis study of mind mapping techniques and traditional learning methods. Anthropologist 20, 62–68. doi: 10.1080/09720073.2015.11891724
Biktimirov, E. N., and Nilson, L. B. (2003). Mapping your course: designing a graphic syllabus for introductory finance. J. Educ. Bus. 78, 308–312. doi: 10.1080/08832320309598618
Boom, K. D., Bower, M., Siemon, J., and Arguel, A. (2022). Relationships between computational thinking and the quality of computer programs. Educ. Inf. Technol. 27, 8289–8310. doi: 10.1007/s10639-022-10921-z
Brennan, K., and Resnick, M. (2012). New frameworks for studying and assessing the development of computational thinking. In Proceedings of the 2012 annual meeting of the American educational research association, Vancouver, Canada (Vol. 1, p. 25).
Cui, Z., and Ng, O. L. (2021). The interplay between mathematical and computational thinking in primary school students’ mathematical problem-solving within a programming environment. J. Educ. Comput. Res. 59, 988–1012. doi: 10.1177/0735633120979930
Dagiene, V., and Jevsikova, T. (2012). Reasoning on the content of informatics education for beginners. Soc. Sci. 78, 84–90. doi: 10.5755/j01.ss.78.4.3233
Davies, M. (2011). Concept mapping, mind mapping and argument mapping: what are the differences and do they matter? High. Educ. 62, 279–301. doi: 10.1007/s10734-010-9387-6
Demir, F. (2022). The effect of different usage of the educational programming language in programming education on the programming anxiety and achievement. Educ. Inf. Technol. 27, 4171–4194. doi: 10.1007/s10639-021-10750-6
Gandhi, H., and Varma, M. (2010). Strategic content learning approach to promote self-regulated learning in mathematics. Proceed. epiSTME 3, 119–124.
Giordano, D., and Maiorana, F. (2014). “Use of cutting edge educational tools for an initial programming course” in In 2014 IEEE global engineering education conference (EDUCON). 3–5 April 2014, Military Museum and Cultural Center, (Harbiye, Istanbul, Turkey: IEEE) 556–563.
Hongwarittorrn, N., and Krairit, D. (2010). Effects of program visualization (jeliot3) on students’ performance and attitudes towards java programming. In The spring 8th international conference on computing, communication and control technologies (Vol. 69).
Hooshyar, D. (2022). Effects of technology-enhanced learning approaches on learners with different prior learning attitudes and knowledge in computational thinking. Comput. Appl. Eng. Educ. 30, 64–76. doi: 10.1002/cae.22442
Hsu, T. C., Chang, S. C., and Hung, Y. T. (2018). How to learn and how to teach computational thinking: suggestions based on a review of the literature. Comput. Educ. 126, 296–310. doi: 10.1016/j.compedu.2018.07.004
Ismail, M. N., Ngah, N. A., and Umar, I. N. (2010). The effects of mind mapping with cooperative learning on programming performance, problem solving skill and metacognitive knowledge among computer science students. J. Educ. Comput. Res. 42, 35–61. doi: 10.2190/EC.42.1.b
Israel-Fishelson, R., and Hershkovitz, A. (2022). Studying interrelations of computational thinking and creativity: a scoping review (2011–2020). Comput. Educ. 176:104353. doi: 10.1016/j.compedu.2021.104353
Karjanto, N. (2021). Calculus and digital natives in rendezvous: wxMaxima impact. Educ. Sci. 11:490. doi: 10.3390/educsci11090490
Karjanto, N., and Husain, H. S. (2021). Not another computer algebra system: highlighting wxMaxima in calculus. Mathematics 9:1317. doi: 10.3390/math9121317
Korkmaz, Ö., and Bai, X. (2019). Adapting computational thinking scale (CTS) for chinese high school students and their thinking scale skills level. Participatory Educ. Res. 6, 10–26. doi: 10.17275/per.19.2.6.1
Ma, H., Zhao, M., Wang, H., Wan, X., Cavanaugh, T. W., and Liu, J. (2021). Promoting pupils’ computational thinking skills and self-efficacy: a problem-solving instructional approach. Educ. Technol. Res. Dev. 69, 1599–1616. doi: 10.1007/s11423-021-10016-5
Malycha, C. P., and Maier, G. W. (2017). Enhancing creativity on different complexity levels by eliciting mental models. Psychol. Aesthet. Creat. Arts 11, 187–201. doi: 10.1037/aca0000080
Meerbaum-Salant, O., Armoni, M., and Ben-Ari, M. (2010). Learning computer science concepts with scratch. In Proceedings of the Sixth international workshop on Computing education research (pp. 69–76).
Mladenović, M., Žanko, Ž., and Aglić Čuvić, M. (2021). The impact of using program visualization techniques on learning basic programming concepts at the K–12 level. Comput. Appl. Eng. Educ. 29, 145–159. doi: 10.1002/cae.22315
Rahmidani, R. (2019) Improving students’ motivation and learning creativity through mind mapping learning method. In 2nd Padang International Conference on Education, Economics, Business and Accounting (PICEEBA-2 2018) (pp. 881–889)
Rodríguez-Martínez, J. A., González-Calero, J. A., and Sáez-López, J. M. (2020). Computational thinking and mathematics using scratch: an experiment with sixth-grade students. Interact. Learn. Environ. 28, 316–327. doi: 10.1080/10494820.2019.1612448
Román-González, M., Pérez-González, J. C., and Jiménez-Fernández, C. (2017). Which cognitive abilities underlie computational thinking? Criterion validity of the computational thinking test. Comput. Hum. Behav. 72, 678–691. doi: 10.1016/j.chb.2016.08.047
Rostron, S. S. (2002). Accelerating performance: Powerful new techniques to develop people. London: Kogan Page Publishers.
Sari, R., Sumarmi, S., Astina, I., Utomo, D., and Ridhwan, R. (2021). Increasing students critical thinking skills and learning motivation using inquiry mind map. Int. J. Emerg. Technol. Learn. 16, 4–19. doi: 10.3991/ijet.v16i03.16515
Selby, C. (2013). Computational thinking: the developing definition. University of Southampton. Available at: https://eprints.soton.ac.uk/356481/1/Selby_Woollard_bg_soton_eprints.pdf (Accessed January, 2013).
Semilarski, H., Soobard, R., Holbrook, J., and Rannikmäe, M. (2022). Expanding disciplinary and interdisciplinary core idea maps by students to promote perceived self-efficacy in learning science. Int. J. STEM Educ. 9:57. doi: 10.1186/s40594-022-00374-8
Sevillano García, M. L., and Sáez López, J. M. (2016). Sensors, programming and devices in art education sessions. One case in the context of primary education. Cult. Educ. 29, 350–384. doi: 10.1080/11356405.2017.1305075
Shi, Y., Yang, H., Dou, Y., and Zeng, Y. (2023). Effects of mind mapping-based instruction on student cognitive learning outcomes: a meta-analysis. Asia Pac. Educ. Rev. 24, 303–317. doi: 10.1007/s12564-022-09746-9
Silva, R., Fonseca, B., Costa, C., and Martins, F. (2021). Fostering computational thinking skills: a didactic proposal for elementary school grades. Educ. Sci. 11:518. doi: 10.3390/educsci11090518
Statter, D., and Armoni, M. (2017). Learning abstraction in computer science: a gender perspective. In Proceedings of the 12th Workshop on Primary and Secondary Computing Education (5–14).
Stokhof, H., De Vries, B., Bastiaens, T., and Martens, R. (2020). Using mind maps to make student questioning effective: learning outcomes of a principle-based scenario for teacher guidance. Res. Sci. Educ. 50, 203–225. doi: 10.1007/s11165-017-9686-3
Sullivan, A. A., Bers, M. U., and Mihm, C. (2017). Imagining, playing, and coding with KIBO: Using robotics to foster computational thinking in young children. Hong Kong: Siu-cheung KONG The Education University of Hong Kong, 110.
Tikva, C., and Tambouris, E. (2021). Mapping computational thinking through programming in K-12 education: a conceptual model based on a systematic literature review. Comput. Educ. 162:104083. doi: 10.1016/j.compedu.2020.104083
Tsai, C. Y. (2019). Improving students’ understanding of basic programming concepts through visual programming language: the role of self-efficacy. Comput. Hum. Behav. 95, 224–232. doi: 10.1016/j.chb.2018.11.038
Webb, H., and Rosson, M. B. (2013). Using scaffolded examples to teach computational thinking concepts. In Proceeding of the 44th ACM technical symposium on Computer science education (pp. 95–100).
Yağcı, M. (2016). Effect of attitudes of information technologies (IT) preservice teachers and computer programming (CP) students toward programming on their perception regarding their self-sufficiency for programming Bilişim teknolojileri (BT) öğretmen adaylarının ve bilgisayar programcılığı (BP) öğrencilerinin programlamaya karşı tutumlarının programlama öz yeterlik algılarına etkisi. J. Human Sci. 13, 1418–1432. doi: 10.14687/ijhs.v13i1.3502
Yang, T. C., and Lin, Z. S. (2024). Enhancing elementary school students’ computational thinking and programming learning with graphic organizers. Comput. Educ. 209:104962. doi: 10.1016/j.compedu.2023.104962
Zhang, X., Tlili, A., Guo, J., Griffiths, D., Huang, R., Looi, C. K., et al. (2023). Developing rural Chinese children’s computational thinking through game-based learning and parental involvement. J. Educ. Res. 116, 17–32. doi: 10.1080/00220671.2023.2167798
Zhao, L., Liu, X., Wang, C., and Su, Y. S. (2022). Effect of different mind mapping approaches on primary school students’ computational thinking skills during visual programming learning. Comput. Educ. 181:104445. doi: 10.1016/j.compedu.2022.104445
Keywords: mind mapping, computational thinking skills, self-efficacy, computational thinking, t-test
Citation: Guo R, Zheng Y and Miao H (2024) The influence of mind mapping on computational thinking skills and self-efficacy in students’ learning of graphical programming. Front. Educ. 9:1479729. doi: 10.3389/feduc.2024.1479729
Edited by:
Pedro Tadeu, CI&DEI-ESECD-IPG, PortugalReviewed by:
Natanael Karjanto, Sungkyunkwan University, Republic of KoreaFina Fakhriyah, University of Muria Kudus, Indonesia
Cathy Ringstaff, WestEd, United States
Copyright © 2024 Guo, Zheng and Miao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rong Guo, MTE5MjcyNDc4QHFxLmNvbQ==