- 1College of Engineering and Technology, American University of the Middle East, Egaila, Kuwait
- 2Department of Computer Science and Mathematics, School of Arts and Sciences, Lebanese American University (LAU), Beirut, Lebanon
AI systems are now capable of providing accurate solutions to questions presented in text format, causing a major problem in assessment integrity. To address this issue, interactive material can be integrated with the questions, preventing current AI systems from processing the requirements. This study proposes a novel approach that combines two important tools: GeoGebra and Moodle. GeoGebra is a widely used tool in schools and universities for creating dynamic and interactive material in the STEM field. On the other hand, Moodle is a popular learning management system with integrated tools capable of generating multiple versions of the same question to enhance academic integrity. We combine these two tools to automatically create unique interactive questions for each student in a computer-based assessment. Detailed implementation steps that do not require prior coding experience or the installation of additional plugins are presented, making the technique accessible to a wider range of instructors. The proposed approach was tested on a group of students and showed enhanced performance in animation-based questions compared to traditional question formats. Moreover, a survey exploring the students’ opinions on the proposed approach reported strong student endorsement of animated questions.
1 Introduction
Assessments are an integral component of the educational process in traditional and online environments. These assessments manifest in many forms, from paper-based to computer-delivered (Spivey and McMillan, 2014). Regardless of the format, the primary purpose of assessments is to evaluate students’ performance in their courses, measure their learning outcomes, and monitor their academic progress (Newton, 2007). With the onset of the COVID-19 pandemic, educational institutions worldwide had to shift to an online environment and adapt new assessment methods accordingly. This shift prompted the integration of new educational tools within various learning management systems (LMSs). Simultaneously, instructors invested time and effort in modifying their teaching methodologies to fit the online setting. They familiarized themselves with these new educational tools used in delivering and organizing course materials, facilitating online interactions and communication with students, as well as designing and managing online assessments (Alamri, 2023). For the latter, instructors explored a range of existing and emerging tools to create their assessments, many of which were previously unfamiliar to them. Consequently, they were able to guide the students to use them, evaluate the students’ performance, and maintain the continuity of the educational process during remote learning (Peimani and Kamalipour, 2021; Rodriguez et al., 2022). Even when the pandemic subsided, many instructors recognized the effectiveness of integrating these online assessment tools into their teaching and learning journey. These tools can provide immediate results and timely personalized feedback to students, helping in a continuous self-assessment to perform better academically (Sancho-Vinuesa et al., 2018; Ramanathan et al., 2020). Moreover, the data acquired and analyzed from the online assessments offers the instructors valuable instantaneous feedback on the needs of their students and identifies areas of improvement in their teaching methods.
While integrating the online solution in assessments, instructors have faced a serious challenge in ensuring academic integrity (Holden et al., 2021; Reedy et al., 2021). Although cheating and plagiarism issues have been widely discussed in traditional teaching environments (McCabe, 2016), they were always limited due to face-to-face proctored sessions. During the COVID era, the shift to online assessments further facilitated cheating and plagiarism (Peytcheva-Forsyth et al., 2018). Students are not closely supervised by instructors with easy online connections to communicate with peers and share answers and solutions (Elkhatat et al., 2021). Additionally, students had access to websites, forums, and platforms providing services to assist in completing assessments (Lancaster and Cotarlan, 2021). Students can post the questions and wait for responses from tutors, or they can look for questions that have already been solved. Consequently, instructors were not able to evaluate the real performance of students, reflecting both their understanding and their level of effort.
While there is no single assessment approach that would be appropriate for all courses, several studies have addressed the issue to find out how cheating and plagiarism can be minimized (Nigam et al., 2021; Noorbehbahani et al., 2022). Educational institutions have adopted tech-based solutions, for example, limiting IP addresses for the students during online assessments (Tiong and Lee, 2021), locking and securing the browser while running the assessments (Adesemowo et al., 2016), using software for face and voice recognition and verification (Garg et al., 2020; Harish and Tanushri, 2022) or using software to detect plagiarism (Eshet, 2024). In the same context, some institutions have imposed online assessments in an invigilated room, as a way to control cheating and plagiarism (Gamage et al., 2022). The latter could be logistically challenging if applied in every assessment for a large number of students and it highly depends on the IT infrastructure of the institution. An alternative scenario proposed the creation of multiple versions of the same assessment (Pang et al., 2022). It means that the questions in an assessment will not only be shuffled, but they will be completely different between students. For the best practice, the instructors create a database of questions classified based on different criteria (e.g., topic, level of difficulty, time required to solve the question) and generate multiple versions of the same assessment, all while maintaining equity between students. One should be careful with this solution as it can be applied at the expense of increasing the load on the instructors, as the preparation of authentic online assessments requires more time and effort compared to paper-based assessments (Szopiński and Bachnik, 2022).
In this paper, we propose a framework that facilities the process of creating multiversion assessments for instructors. Our framework makes use of two well-known platforms for online assessments, which are GeoGebra and Moodle. We describe how our tool enables instructors to create dynamic animated questions on GeoGebra without the need for coding knowledge. In addition, we illustrate how our system integrates the multiversion questions into Moodle in a smooth manner. The deployment of the proposed system paves the way for instructors to create complete multi-version interactive assessments for a large number of students in a very short time. In the next section, we discuss the existing solutions and the unique features that are added by our proposed system. After that, we describe the details of our system and its components.
2 Literature review
2.1 Evaluation systems
The evaluation processes in education exhibit both similarities and differences across various international contexts, influenced by cultural, political, and institutional factors. The Programme for International Student Assessment (PISA), conducted by the Organization for Economic Co-operation and Development (OECD), provides a global perspective by assessing 15-year-old students’ performance in reading, mathematics, and science. PISA offers insights into how different educational systems equip students with the knowledge and skills needed for real-world challenges. Students from countries like Australia, Canada, the United Kingdom, and Russia showing similar learning trajectories while students from the United States and China have different trajectories, highlighting the diverse educational approaches across countries (Wu et al., 2020).
Various forms of assessments can be utilized to evaluate student learning effectively. These include but not limited to:
• Polls can quickly gauge understanding during a lesson (Price, 2022) and improve student engagement. However, careful management and clear instructions are needed to prevent overuse and reduced motivation (Nguyen et al., 2019; Zhao, 2023).
• Project-based assessments offer significant benefits, including enhanced student engagement, interdisciplinary collaboration, and the development of real-world problem-solving skills (Yayu et al., 2023). These assessments allow students to apply theoretical knowledge in practical settings, which can lead to deeper learning and better preparation for future careers (Evenddy et al., 2023). However, challenges include the complexities of curriculum design, time constraints, and the need for effective project management strategies to ensure that all students benefit equally (Tain et al., 2023).
• Portfolio reviews are another method, where a collection of a student’s work is assessed over time, providing a comprehensive view of their progress (Darmiyati et al., 2023). They encourage active learning and can be particularly effective in subjects that demand a demonstration of knowledge, skills, and attitudes (Deeba et al., 2023). However, in addition to being labor-intensive and time-consuming for both students and educators, consistency and objectivity in portfolio evaluation can be challenging, especially when multiple evaluators are involved (Carraccio and Englander, 2004).
• Peer assessments involve students evaluating each other’s work, fostering critical thinking (Hwang et al., 2023). Nonetheless, the reliability of peer assessments can vary, with students sometimes providing overly lenient or harsh evaluations. Additionally, there can be a lack of consistency between peer and teacher assessments, leading to discrepancies in grading (Chang et al., 2012).
• Online assessment in education offers significant benefits, including flexibility, accessibility, and the ability to provide immediate feedback, which can enhance student engagement and learning outcomes (Heil and Ifenthaler, 2023; Huber et al., 2024). Despite their benefits, online assessments may face issues related to technical reliability, student engagement, and the authenticity of assessments. Moreover, they require significant infrastructure and may pose challenges in terms of academic integrity (Benjamin et al., 2006).
This work will focus on online assessments, with a primary emphasis on enhancing academic integrity through question randomization.
2.2 Randomization in question creation
Many educational platforms support the feature of creating automatically graded and randomized assessments. Several tools and plugins, discussed in the next part, have been integrated within LMSs to meet the needs of multiple disciplines, especially in science, technology, engineering, and mathematics (STEM) courses. Instructors can generate an assessment with “static” questions, selected from a pool of multiple-choice, short-answer, or numerical exercises. In other scenarios, some tools offer the possibility to create “dynamic” questions enabling the instructor to automatically generate numerous versions of the same question. For clarity within the context of this paper, the terms dynamic and static are used to describe different types of questions in assessments. When we refer to a dynamic question, it indicates a change of a set of parameters in a question, like numbers or variables, to create many different versions of a question. Conversely, static question indicates changeless parameters, meaning that the question remains identical across all versions of the assessment. Although dynamic questions require some specific scripting knowledge, they have advantages over multiple static questions, mainly for the reason of bug fixes, which will be easily applied to a single question instead of a series of questions (Kraska, 2022).
LMSs have gained a lot of attention in recent years, especially after the COVID-19 pandemic. One of the most widely used LMSs is Moodle (Wang et al., 2020) known for its open-source nature, flexibility, and extensive community support. Several extensions to the Moodle platform can be added through plugins to enable more advanced features. For the creation of “dynamic” questions, several tools are available. These tools offer several educational benefits, particularly in STEM courses. They enable the instructors to design complex mathematical and scientific randomized questions, with an automated grading process, and prompt feedback to students. In addition, these tools can play a crucial role in maintaining academic integrity. By offering question randomization, each student faces a unique given, which makes it more challenging for students to engage in unauthorized assistance. Students perceive randomizing questions as a highly effective tool in the exam logistics to reduce cheating and is reported as the least stress-inducing method (Novick et al., 2022). Thus, these tools not only enhance the quality of assessments and learning experiences but also contribute significantly to upholding academic integrity in digital education environments.
Under the Moodle platform, the most common tools/plugins are WIRIS, STACK (System for Teaching and Assessment of Mathematics using a Computer Algebra Kernel), and formula question types.
WIRIS is known for its user-friendly interface. The questions format of WIRIS is like the ones available by default in Moodle (short answer, multiple choice, essay, cloze…). Additionally, WIRIS enables the creation of dynamic graphs, enabling a unique plot for every student (Mora et al., 2011; Ballon and Gomez, 2022). The example shown in Figure 1, developed under WIRIS, changes the vector (direction and magnitude) every time a student attempts the quiz.
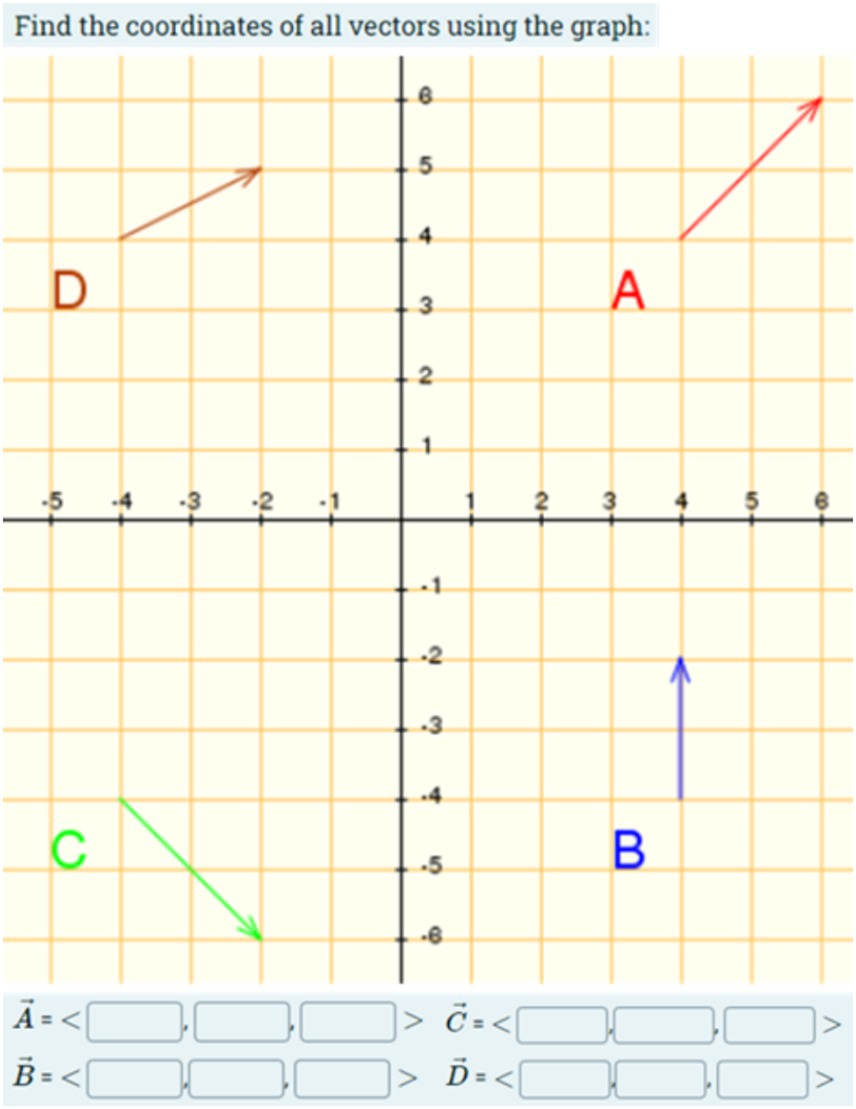
Figure 1. A dynamic question created by WIRIS. The direction and magnitude of the vectors change for each student.
An alternative approach is to use the STACK question type (Sangwin, 2004; Smit, 2022; Ahmed and Seid, 2023). STACK is an open-source online assessment system for mathematics, science, and engineering based on the computer algebra system Maxima. Although it is compatible with Moodle, integration, and question authoring are considered to be more complex when compared to the aforementioned plugins. On the other hand, STACK can create randomized questions with graph plotting. It also offers advanced grading criteria and validity feedback with specific information to students based on the so-called potential response trees.
In addition to STACK and WIRIS, the Formula-type question is an alternative, easy to install, plugin that can be easily integrated with Moodle. It provides all the functionalities needed to create dynamic questions. Although question authoring is relatively simple when compared to STACK, Formula lacks the ability to create dynamic graphs. However, this drawback can be resolved using an interactive graphics library, JSXGraph. The latter is a cross-browser JavaScript (JS) library for mathematical visualizations, including interactive geometry, function plotting, charting, and data visualization (Beharry, 2023; Hooper and Jones, 2023). Its capabilities in creating dynamic animations and interactive materials go beyond the built-in features in WIRIS and STACK. Combining JSXGraph with WIRIS, STACK or Formula enables the creation of dynamic visual questions (Kraska, 2022). Such questions can include dynamic animations and interactive materials. Unfortunately, the use of JSXGraph requires coding experience and the plugin has to be installed on the Moodle server running the assessment.
2.3 AI and the importance of animation/video assessments
The rapid advancements in AI tools present significant advantages for education, yet they also pose numerous challenges. AI systems are now capable of providing personalized learning experience for students (Chen et al., 2020; Harry, 2023), reduce workload for educators by automating administrative tasks (Chhatwal et al., 2023; Pisica et al., 2023), create dynamic and interactive learning environments (Adiguzel et al., 2023; Negoiță and Popescu, 2023), and holds promise for students with special educational needs, offering tailored learning experiences that cater to their individual requirements (Reiss, 2021).
AI is increasingly being utilized in the field of assessments, particularly in creating assessment questions, providing feedback, and grading. AI-driven tools can generate a variety of question types, such as multiple-choice and short answer, with various difficulty, by analyzing existing content to ensure alignment with learning objectives (Lu et al., 2021; Nasution, 2023; Kic-Drgas and Kılıçkaya, 2024). This automation not only saves educators time but also ensures diversity and coverage across topics. Additionally, AI systems offer immediate, personalized feedback to students, helping them understand and learn from their mistakes in real-time, which supports their learning process (Porter and Grippa, 2020; Wongvorachan et al., 2022; Chien et al., 2024). In grading, AI can improve consistency and reduce human error, with studies showing that AI systems outperform human graders in maintaining uniform evaluations, leading to fairer outcomes (Gobrecht et al., 2024). While AI models like ChatGPT can simulate grading tasks, their effectiveness is still limited, suggesting the need for a balanced approach where AI supports but does not replace human judgment (Kooli and Yusuf, 2024).
On the other hand, With the difficulty in detecting AI-generated content (Sullivan et al., 2023) and the proficiency of AI tools in completing students’ assignments (Perkins, 2023; Yang and Stivers, 2024), the traditional notions of academic integrity are fundamentally challenged (Komáromi, 2023; Duvignau, 2024). To address this issue, the limitation of AI in processing unstructured data (Lin et al., 2023) can be leveraged. Animations, simulations, or videos can be embedded within assessment to reduce the chances of AI use.
A very well-known tool used to show animations and interactive content in the domain of STEM is GeoGebra (Iwani Muslim et al., 2023; Mazlan and Zulnaidi, 2023; Seloane et al., 2023). The use of GeoGebra has proved to enhance conceptual understanding (Kllogjeri, 2010; Dahal et al., 2022), increase student engagement (Zutaah et al., 2023), enhance academic performance (Arbain and Shukor, 2015; Arini and Dewi, 2019). Moreover, GeoGebra’s user-friendly interface allows easy integration into teaching, even for instructors with limited computer skills (Solvang and Haglund, 2021).
Typically, these materials remain static in a question, meaning they stay unchanged for every student during an assessment. Although static visual materials are practical in some cases, all the students will get the same answer with the same answer key. Unfortunately, creating multiple versions of an animation requires a lot of time and effort. The integration between STACK and GeoGebra has been reported to facilitate the creation of multiple versions of a specific animation (Lutz, 2018; Pinkernell et al., 2023). Unfortunately, it is mentioned that the installation of STACK can be complex and might require substantial technical effort (Sangwin, 2010; Nakamura et al., 2018; Juma et al., 2022).
2.4 Objectives of this study
This research will try to tackle the following research questions:
RQ1: Is it possible to integrate Moodle Formula with GeoGebra to create dynamic animated questions leveraging the features of both tools?
RQ2: How would such integration affect the student’s performance in online assessments.
3 Materials and methods
In this study, we explore the integration of Moodle Formula, a free plugin capable of generating multiple versions of the same question, with GeoGebra, a dynamic mathematics software that allows users to freely copy, distribute, and transmit content for non-commercial purposes. By leveraging the complementary strengths of these tools, we demonstrate a method for creating varied and dynamic assessment questions at no cost.
Figure 2 shows a high-level representation of the integration between Moodle Formula question and GeoGebra. The traditional formula question that is normally used to generate multiple versions of a question is used in this work. A random number is generated at the beginning, then in the question text the GeoGebra animation/simulation is called and fed with the random value generated previously. Afterwards, the answer key is added based on the random value for automatic grading. To reproduce this work, detailed steps are available in section 3.1.
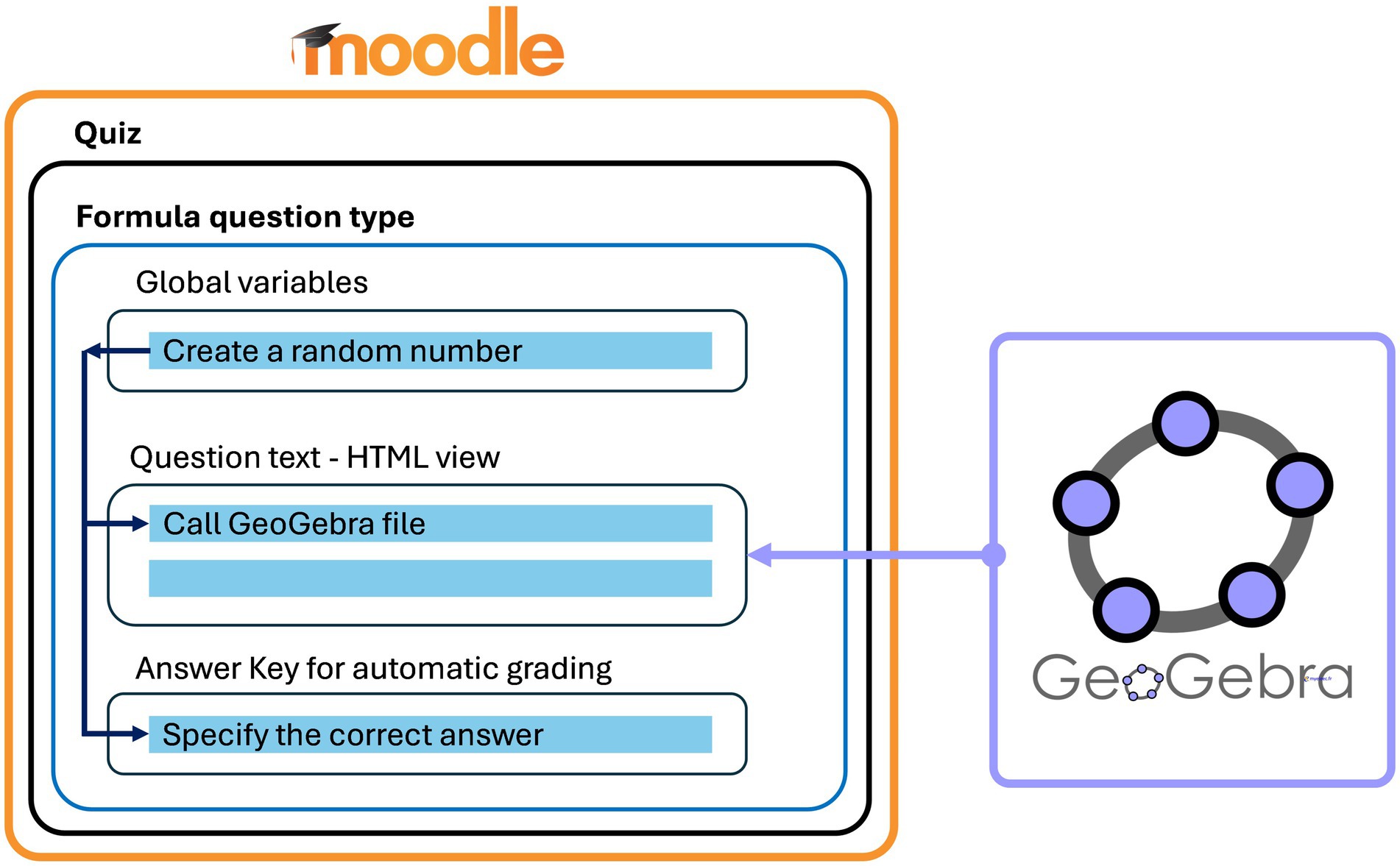
Figure 2. High-level representation of integrating GeoGebra with Moodle’s Formula Question Type: Generate random variables, call the GeoGebra file, and specify the correct answer for automated grading.
This study comprises three major parts: first, a novel integration of GeoGebra with Moodle Formula to create multi-version animated questions; second, a specialized quiz to assess the impact on student performance; and third, a survey to gather student perceptions. Together, these elements provide a thorough evaluation of the educational enhancements.
3.1 Integrating Moodle formula with GeoGebra
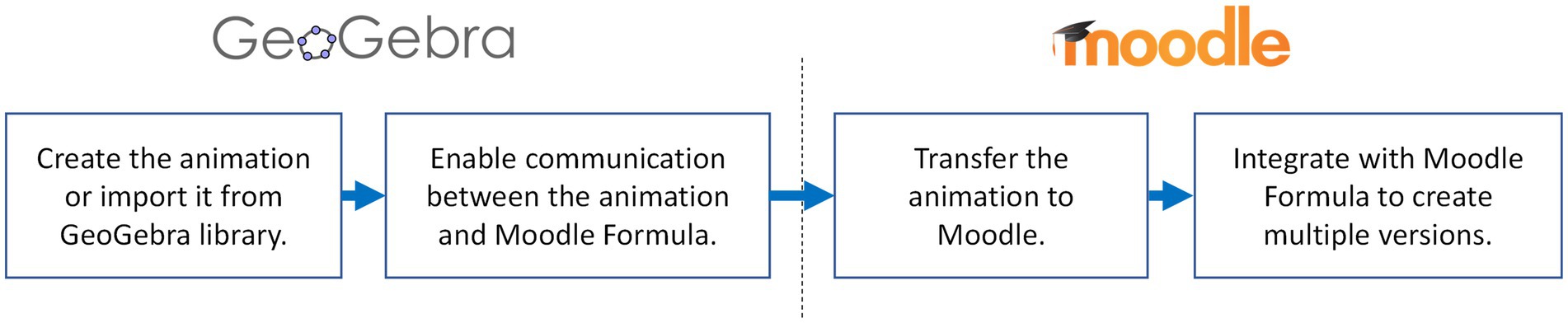
The novel integration technique between GeoGebra and Moodle Formula proposed in this work can be divided into 4 steps as shown in Figure 3.
3.1.1 Step 1: creating/importing the animation from GeoGebra library
Creating an animation can be done using GeoGebra’s graphing calculator which has an intuitive user interface and does not require coding for the creation of basic graphs and animations; named applets. In addition to that, users can benefit from the huge library containing many examples in different fields. In this example, we are creating our own applet from scratch. Starting from a blank applet, users can add expressions, functions, animations, images, buttons … The applet created for this study is shown in Figure 4. On the left, the objects in the animation are shown, in the middle, the applet is presented and to the right, the settings for the object selected are displayed. The applet contains 2 images (the browser clipart and a book cover) and 2 buttons (Reset and start). The image position and size can be determined by up to three points located at three corners of the image. Changing the coordinates of these points results in animating the image. For the image of the book cover, only two points are enough to create the desired animation (enlarging the image). The points used are A and B, located at the bottom corners of the image. For this example, the aim is to change the size of the book cover image at various speeds. For that, two sliders are added: slider “a” and slider “b.” Slider “a” will be responsible for changing the size while slider “b” will be used to change the speed. For the values of the slider parameters, the user can set the range (start and end values), the step, and the speed of the step increment if an automatic increase in the slider value is set.
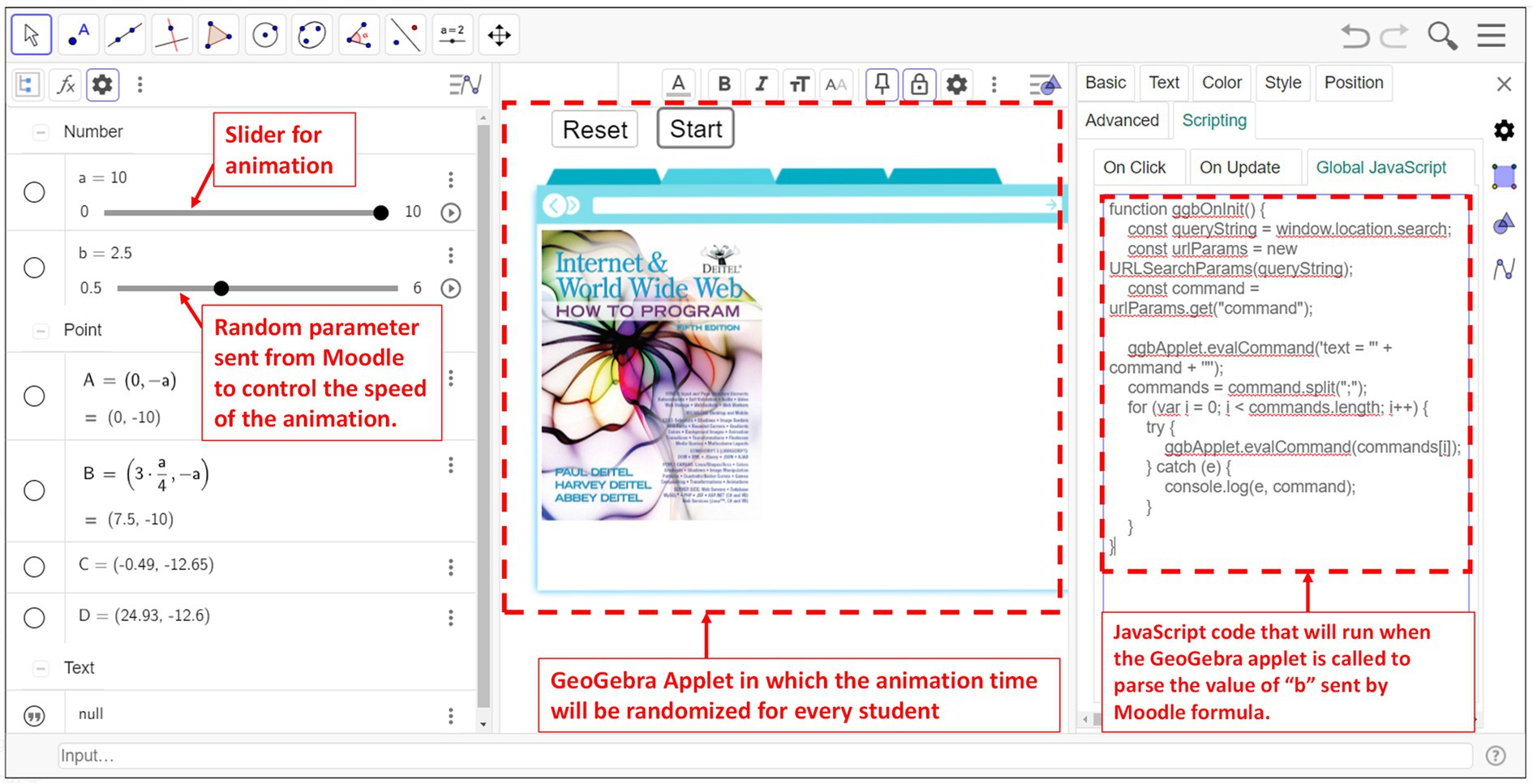
Figure 4. A screenshot from GeoGebra showing the animation objects (left), the animation itself called applet (middle), and the code used to parse the parameters sent from Moodle which is discussed in Step 2 (right).
For this example, the coordinates of A and B are (0, −a) and (3a/4, −a). So, if “a” changes from 1 to 10, the coordinates of A:B will change from (0, −1):(3/4, −1) to (0, −10):(30/4, −10) respectively. This will result in an increase in the picture size while maintaining the same aspect ratio. The speed of slider “a” is taken from the slider “b.” For slider “a,” if the speed is 1 (b = 1), the animation will take 10 s to complete. If the animation speed is 5 (b = 5), the animation will take 2 s to finish.
3.1.2 Step 2: enable communication between the animation and Moodle formula
To create multiple versions of the animation, a certain slider parameter can be given a random number. This random number will be communicated from Moodle Formula at a later stage (step 4). To enable this communication, a specific code snippet is inserted into the “Global Javascript” section within the “Scripting” settings. This code remains constant and does not vary with the type of animation employed. Its primary function is to facilitate the communication process, and it is implemented by simply copying and pasting the code into the designated setting.
3.1.3 Step 3: transfer the animation to Moodle
The animation is transferred to Moodle by downloading it as a “Web page (.html)” and then uploading it to the Moodle course page as a “File.” This will give the file a unique web address. Communication between Moodle and the GeoGebra applet will be done through this unique web address (step 4).
3.1.4 Step 4: integrate with Moodle formula to create multiple versions
In this work, the slider parameter b, which is responsible for setting the speed of the animation will be given a random number. In step one, upon the creation of the animation, a range (minimum and maximum value) and a specific value were given to parameter b. The range was set from 0.5 to 5, and the specific value was 2.5. However, the specific value will now be replaced by a random number generated in the Moodle Formula question.
Figure 5 shows a screenshot from the Moodle formula question. In the random variables box, the parameter “v” varies between 0.5 and 5 with a 0.5 step. This parameter will be passed to the animation to override the value of slider parameter “b” and hence create multiple versions of the animation.
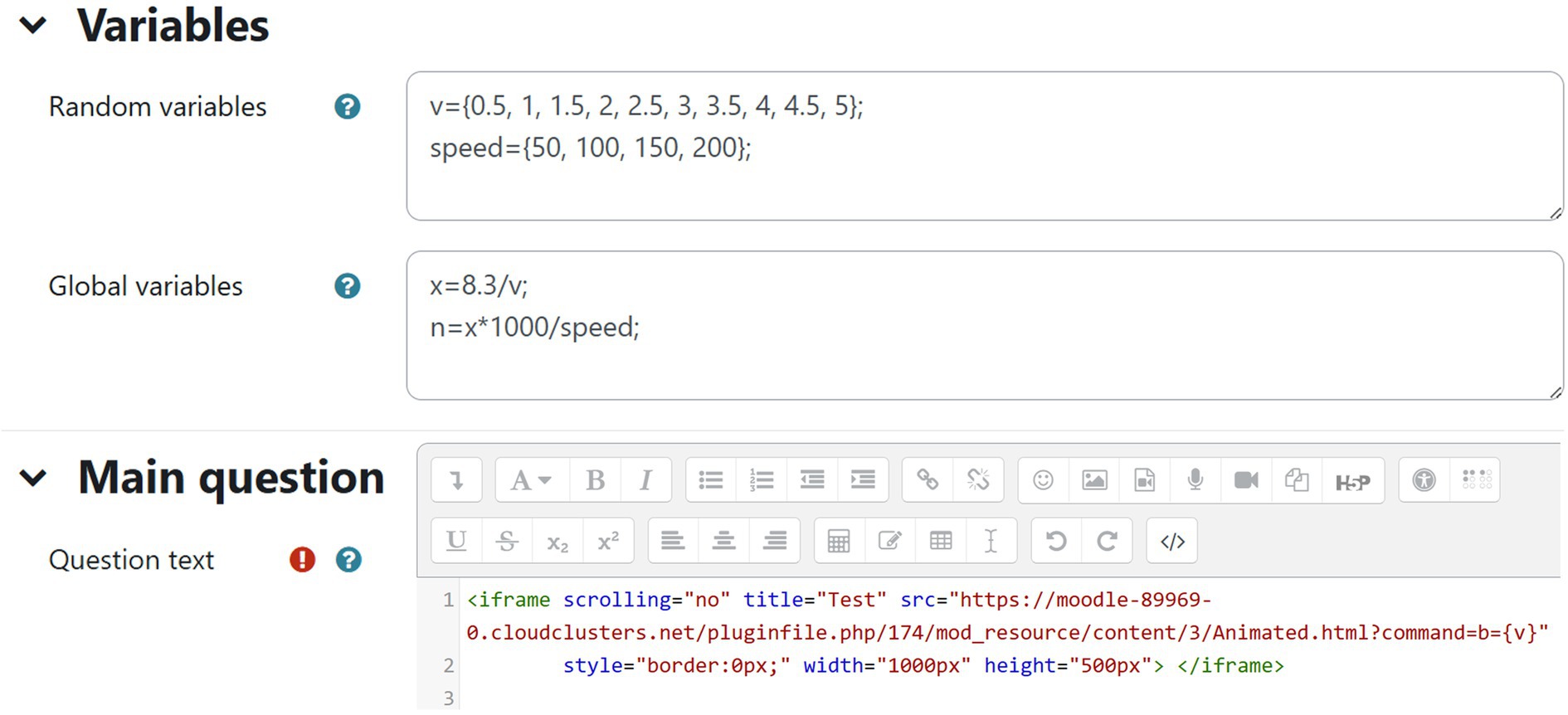
Figure 5. A screenshot from Moodle formula question type. Random variables are defined here and passed later to the animation in the main question text.
To pass the parameter, the web address of the Moodle file obtained in step 3 is concatenated with the word “?command=” followed by the “the name of GeoGebra slider (in our case b) = name of the Moodle Formula random variable (in our case {v})” as shown in Figure 6. The resulting web address is placed in the question text as the source (src) inside an iframe to display the animation within the question. Figure 5 shows the link used in this study.
In this work, the code will execute b = {v}. Since within the Moodle formula question, v is a random number, each student will see an animation with a different value for b. This will result in changing the speed of the animation.
3.2 The multi-version assessment in Moodle
To test the feasibility and effectiveness of the proposed technique, we conducted an experiment that targeted a group of 26 computer science students who took the “Web Programming” course at the Lebanese American University during the Spring and Fall 2022 semesters. The students are divided into 21 males and 5 females. The age of the participating students ranges between 18 and 21. Among the 26 students, there were 22 Lebanese, 3 Syrians, and one Palestinian student. The experiment contains a quiz for the student and a follow-up survey which will be discussed in section 3.3.
The quiz contains the same question asked in two different formats with different versions. The traditional question format is used for question 1 which is text and images. For question two the animation approach discussed in section 3.1 is used. In both cases, multiple versions are created using Moodle formula. The aim is to see the impact of animated questions on the student’s performance.
The quiz was conducted as one of the online course assessments that the students are required to do after finishing the JavaScript chapter. In the two questions of the quiz, the student is asked to complete a JavaScript code to reproduce a certain animation. The execution of the JavaScript program results in animating an image that starts with a small size and grows gradually to reach its full size at the end. In this work, the random factor added to the animation is the speed at which the image grows.
Figure 7 shows a screenshot of the two questions. Question 1 (Figure 7A) was asked in a traditional way. The requested animation was described using text and several screenshots taken at different instances during the animation. The animation time is given to the student as conducting measurements in such a format is not possible.

Figure 7. A screenshot of (A) the static question (question1) and (B) the dynamics question (question 2).
Question 2 is presented using the animated dynamic approach discussed in section 3.1 (Figure 7B). The animation can be visualized using the start button. The student is asked in this question to calculate the animation time using a stopwatch and then use that time along with the interval value to deduce the speed of the animation. The animation will differ from one student to another as the speed is randomly assigned to each version. In question 2, the animation is developed under GeoGebra and its integration within Moodle.
The same code to be completed for Question 1 (c) and Question 2 (d) is shown in Figure 8.
Once the students attempt the quiz, they can freely navigate between the questions. Multiple attempts are allowed and the attempt with the highest score is recorded and analyzed in section 3. To ensure reliable results, the propagation of errors across connected subparts was carefully examined and rectified. Specifically, if a student’s incorrect response in one part is due only to an error made in a previous subpart, measures were implemented to mark the subsequent part as correct. This approach helps in isolating the impact of errors to their original context, thereby preventing a single mistake from affecting the entire assessment. This also ensures that evaluations are both accurate and fair by considering each subpart independently.
3.3 The follow-up survey
After the student answers the questions, they are requested to fill out a survey that we created to collect their feedback. The main purpose of this quiz was to discover the students’ ability to understand and solve the animated question, and to see whether they would prefer exams that contain animated questions to traditional static questions that contain only text and images. In addition, we wanted to test the success of the main target of the animated question, which is preventing cheating. Hence, the survey was designed to focus on these aspects. The survey contained eight questions that were answered via the traditional 5-point Likert Scale, and four open-ended questions.
The first set of questions are:
1. I understood well the question that I solved.
2. The level of the question is easy (I was able to easily calculate the correct answer)
3. I was able to easily perform the steps required to answer the question.
4. I liked the animation-based style of the question.
5. This type of question evaluates my understanding better than static questions do.
6. This type of question is excellent for scientific majors.
7. I prefer to have animation-based questions more than regular static questions in exams.
8. I should perform better in the exam if it contains animation-based questions.
On the other hand, the four open-ended questions are:
1. What valuable experience did you gain by experimenting with this new type of question?
2. What do you think are the advantages of such types of questions?
3. Do you think this type of question can help reduce students’ cheating in online exams?
4. What are your suggestions to improve this type of questions?
4 Results and discussion
4.1 GeoGebra - Moodle formula integration
To implement the proposed technique Moodle 4.0 was installed on an online server with 2 CPU Cores, 2GB RAM, and 60GB SSD. Using the novel technique discussed in section 3.1, the integration of the GeoGebra web application with Moodle was successfully implemented, ensuring seamless connectivity and functionality. All animations were manually tested after the quiz started, confirming different animations were created and randomly allocated for each student.
As mentioned in section 3.1.1, educators can benefit from the extensive GeoGebra library to create such multi-version interactive assessments. Any animation/simulation in GeoGebra’s library can be randomized and integrated within Moodle Formula. For instance, Figure 9 shows the successful integration of the simulation developed by optowiki.info (Michael Schaefer) in GeoGebra with Moodle Formula using our proposed technique. In this question, students are asked to find a physical property of mediums 1 and 2 (index of refraction). To do this, they must interact with the simulation (move the laser) and apply the correct set of equations to find the answer. With this integration, the simulation environment behaves differently for each student resulting in an automatically graded interactive question with a unique solution for each student.
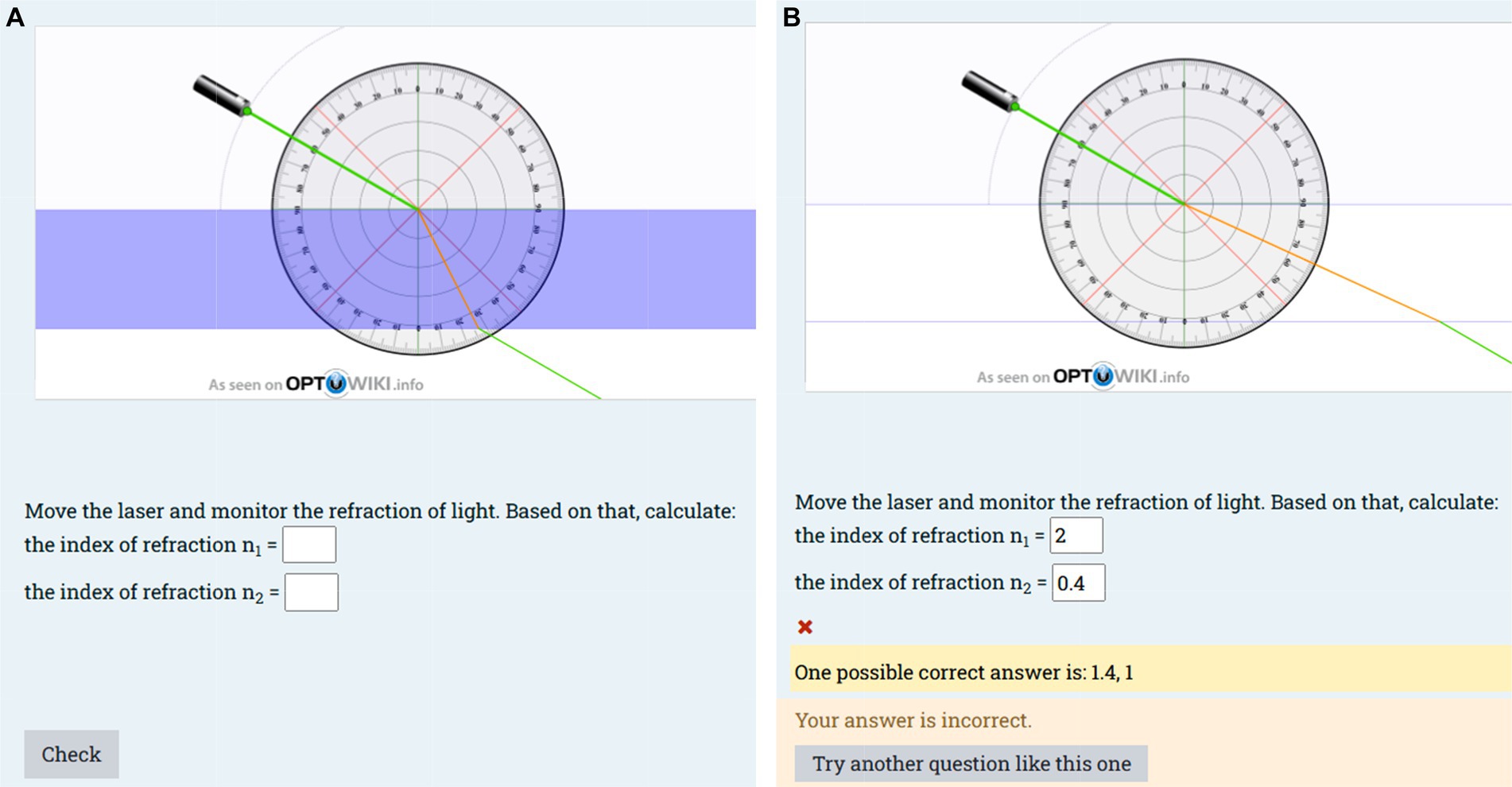
Figure 9. (A) A simulation from GeoGebra library developed by optowiki.info (Michael Schaefer) integrated with Moodle Formula using the proposed technique with a check button for training purposes. (B) An option to “Try another question like this one” which will provide the same experiment but within a different environment in which the light will behave differently.
While this integration has been used primarily for assessment purposes in this work, its applications can be extended to train students in answering questions based on the behavior of a system under different conditions. Figure 9 illustrates a training scenario implemented using the proposed technique while leveraging Moodle’s interactive features in the quiz setting. In this scenario, students can interact with the question, answer the related questions, and check their answer to receive immediate feedback on their responses (Figure 9A). They also have the option to redo the question (“try another question like this one” in Figure 9B) under different circumstances to reinforce their understanding.
4.2 Quiz results
The results of the Moodle quiz are shown in Figure 10. As mentioned in section 3.2, 26 students attempted the survey. Students not answering both questions were excluded from the study. The data is organized into two main categories, each relating to how the quiz questions were presented: Static question (pictures and text) and dynamic question (dynamic animation). Question 1 contains three subparts asking about the interval, frequency, and code while question 2 asks for one additional subpart which is the duration of the animation. Student responses are marked with a ‘1’ for correct answers (green) and ‘0’ for incorrect answers (light red).
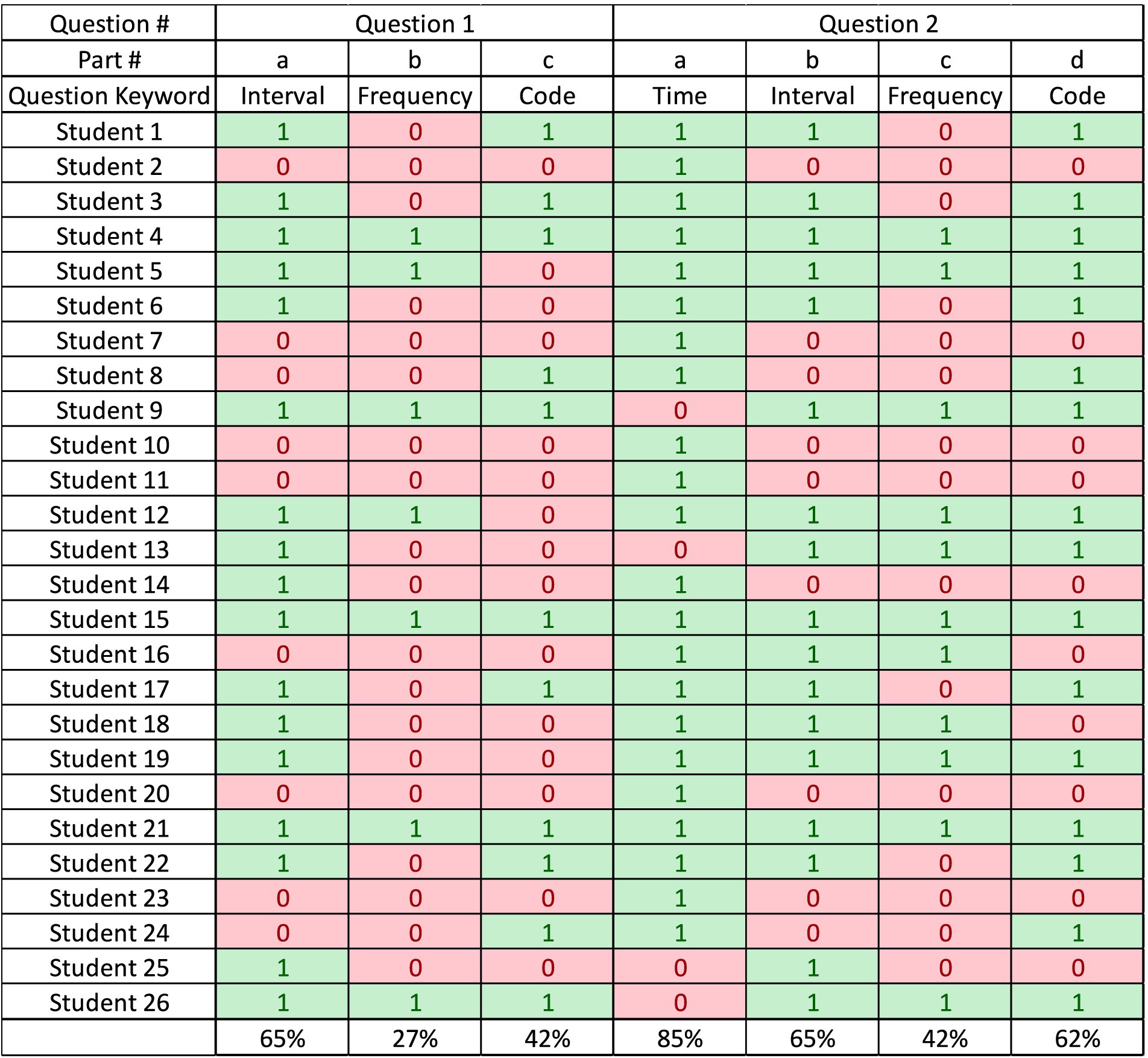
Figure 10. Results of the Moodle quiz showing students’ performance in the traditional question format versus the dynamic animation format.
Students who consistently performed well in text-based questions generally also did well in animation-based questions (e.g., Student 4, 15, 21). This suggests some students might be strong across multiple formats.
There are students (e.g., Students 2, 7, 10, 11, 20, 23) who struggled with both formats, indicating difficulties that are likely independent of the medium of question presentation.
The average of each subpart is shown at the bottom of the table. For question 1, the averages are 65, 27, and 42% for the interval, frequency, and code, respectively. On the other hand, for question 2, the averages are 85, 65, 42, and 62% for the time, interval, frequency, and code, respectively.
For Question 1 - part a, asking about the interval, the same performance was obtained between the two formats (65%). Parts asking about the frequency and the code showed improved performance with the animation format compared to the traditional one where the average increased from 27 to 42% in the frequency question, and from 42 to 62% in the code question.
The improvement in Parts b and c in the dynamic format might suggest that these concepts were better understood when animation/video explanation was used or that students engage more effectively with animation content.
When distributing the grades equally on each subpart the average of students in question 1 is 44.87% while the average in question 2 (for the last 3 subparts) is 56.41% indicating 25.7% improvement. To confirm the improvements achieved in animation-based format the Wilcoxon signed-rank test is performed to determine if the difference is statistically significant.
Null hypothesis: There is no significant difference between the averages of questions 1 and 2.
Alternative hypothesis: There is a significant difference between the averages of questions 1 and 2.
For the student’s average in each question:
• The sum of positive ranks W+ = 31
• The sum of negative ranks W− = 2.5
• The test statistic W is the smaller of W+ and W−, so W = 2.5.
• Number of non-zero difference: n = 8
For a typical significance level of α = 0.05 (two-tailed test), the critical value would be 3 (based on standard Wilcoxon signed-rank test tables). Since our test statistic (2.5) is less than the critical value (3), we would reject the null hypothesis. The Wilcoxon signed-rank test reveals a statistically significant difference between student performance on Question 1 (traditional format) and Question 2 (animation format).
The substantially larger sum of positive ranks (31) compared to negative ranks (2.5) strongly suggests that students generally performed better on Question 2, which utilized an animation format, than on Question 1, which used a traditional format.
This result implies that the animation format may be more effective in enhancing student engagement through visual stimuli or improving comprehension of the question.
4.3 Survey results
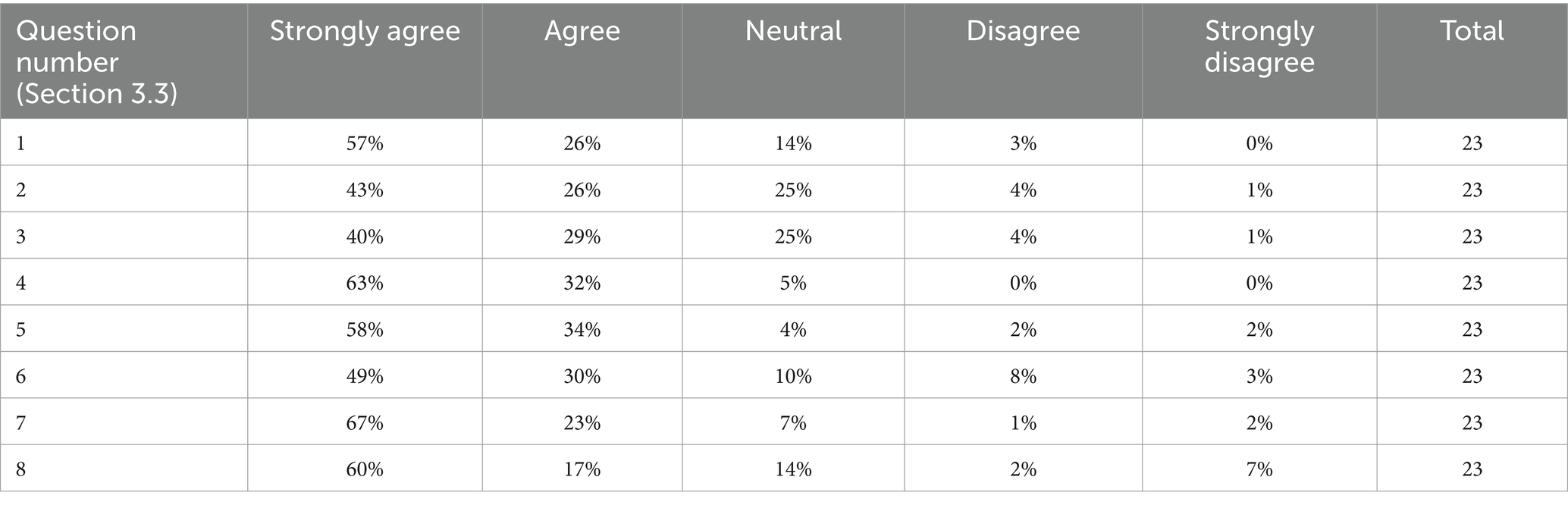
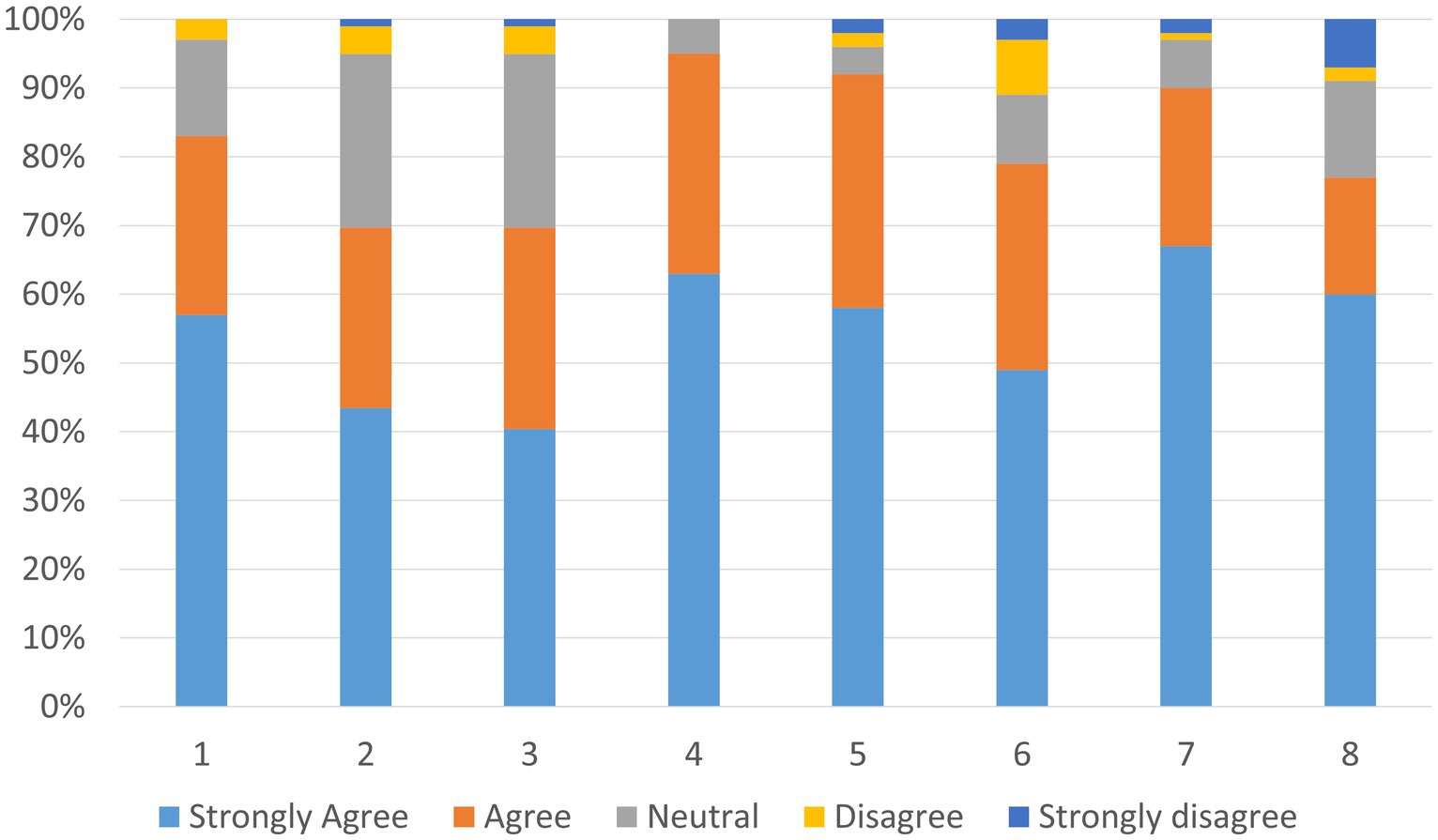
As mentioned in Section 3.3, to gain insights from a different perspective, the same students who took the quiz were asked to provide their feedback after completing the quiz. All the students who responded except 3 resulting in an 88.5% participation rate (23/26 students). The results of the closed-ended questions are shown in Table 1 and their distribution is illustrated in Figure 11. Taking into consideration that students of different levels in the two classes took the survey, the results are encouraging. Most of the students liked the animated question style and agreed that this type of question evaluates the student’s understanding better than static questions do (Questions 4 and 5). In addition, the majority of the students found the question easy and were able to follow up with the steps that are required to find.
The answer without difficulty (Questions 1, 2, and 3). A minor percentage of students (5%) faced difficulties in understanding the question and finding the correct answer, which could be solved by adding more explanation to the question given. Moreover, 79% of the students agreed that this type of question is excellent for scientific majors. Most importantly, approximately all the students stated that they prefer this type of question over static questions and that they would do better in exams that contain animated questions. In general, the results of the closed-ended questions reflect the students’ satisfaction and willingness to accept animated questions and their ability to comprehend and perform better in exams that are based on these types of questions.
With respect to the open-ended questions, we highlight here the most relevant answers that were stated by several students for each question. For the first question, the students stated that the most valuable experiences they gained from the quiz are: “I was able to understand the question and identify what is required to answer faster and better” (16 answers), “enjoyable and fun to work with and solve” (13 answers), “the interface makes the question very user friendly” (8 answers), “this style of questions reflects more if the student is knowledgeable of the material or not” (7 answers), “it felt like a real-life demo that helped me better visualize the problem before and during solving it” (4 answers). For the second question, the most important advantages that were mentioned by the students include: “better to understand,” “easier to solve,” “more user-friendly,” “attracts the attention of students,” “provides assistance to the student,” “engages the student more in the exam,” “makes the experience much livelier,” and “increases the student’s confidence.”
The answers to the third question were diverse. Some students stated that they believe these types of questions could reduce cheating in online exams if the questions are designed properly. The majority of students confirmed that animated questions with random values should “reduce cheating to a high degree since every student gets different values.” Some students were not sure whether it helps in reducing cheating or not. Other students stated that cheating will still occur since a student can give the required formula to another student and the latter will apply the formula to the values that he/she has to find the answer. Note that although the last observation is true, the animated question type will still reduce blind cheating and assist in making the student acquire the intended learning outcomes, since the cheating student needs to understand and apply the formula that he obtained from his/her classmate in order to get the answer and confirm its correctness.
With respect to the last question, some students mentioned several important suggestions for improvement. We pinpoint the most important answers here, such as “replacing the manual stopwatch with an automatic method to calculate the animation time,” “shortening the length of the code,” “giving hints to the student when they are confused,” “using integer values instead of decimals,” “clarifying the JS code,” “using nonfunctional codes and trying to fix them while testing them,” “make the question MCQ,” and “ask about functionality not just numbers.”
4.4 Limitations and future work
While the proposed technique offers significant benefits in enhancing assessment integrity and the overall learning experience, some potential limitations should be considered. The approach requires the use of a Learning Management System (LMS) such as Moodle, or a similar platform capable of generating multiple versions of the same question. Additionally, basic proficiency in GeoGebra is necessary for the effective implementation of this tool.
This technique is particularly advantageous in science and engineering disciplines, as it allows students to engage with questions based on animations or simulations under varying conditions. However, it may be less applicable in fields that do not rely on such dynamic visualizations. Moreover, implementing this technique requires access to a computer and a stable internet connection, which could pose accessibility challenges for some users. With the rapid evolution of AI systems, our future direction will focus on exploring their potential to solve questions presented in interactive or animated formats. Additionally, this integration has been tested on a group of students for evaluation purposes. In the future, the effectiveness of this technique in training students through specific experiments or simulations under varying circumstances can be further assessed.
5 Conclusion
Aiming to enhance students’ engagement and reduce cheating in online assessments, an approach is proposed to integrate multi-version animations into questions. With this approach, the problem is presented to the students as an animation that should be observed and analyzed. In addition to that, the animation changes from one student to another. The implementation was done through a novel technique that enables the integration of Moodle formula question type and GeoGebra. The advantages of this technique are that no prior coding skills are required, no additional plugins are needed, and instructors can benefit from the huge GeoGebra animation library.
The new approach was tested on a group of university computer science students. The analysis of the provided data shows that animation-based questions might be more effective for teaching and evaluating certain types of content, particularly where understanding might benefit from visual representation or where engagement is crucial.
A survey exploring the students’ opinions on the proposed approach reported a strong student endorsement of animated questions. The positive feedback also supports the initiative to integrate more dynamic elements into exams, particularly in fields that benefit from visual and interactive content.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
SH: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. KM: Data curation, Formal analysis, Methodology, Resources, Software, Supervision, Validation, Writing – original draft, Writing – review & editing. BJ: Investigation, Supervision, Validation, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adesemowo, A. K., Johannes, H., Goldstone, S., and Terblanche, K. (2016). The experience of introducing secure e-assessment in a south African university first-year foundational ICT networking course. Africa Educ. Rev. 13, 67–86. doi: 10.1080/18146627.2016.1186922
Adiguzel, T., Kaya, M. H., and Cansu, F. K. (2023). Revolutionizing education with AI: exploring the transformative potential of ChatGPT. Contemp. Educ. Technol. 15:ep429. doi: 10.30935/cedtech/13152
Ahmed, A. M., and Seid, A. M. (2023). Enhancing students’ linear algebra I learning using assessment through STACK. Int. J. Emerg. Technol. Learn. 18, 4–12. doi: 10.3991/ijet.v18i19.42371
Alamri, H. (2023). Instructors’ self-efficacy, perceived benefits, and challenges in transitioning to online learning. Educ. Inf. Technol. 28, 15031–15066. doi: 10.1007/s10639-023-11677-w
Arbain, N., and Shukor, N. A. (2015). The effects of GeoGebra on students achievement. Proc. Soc. Behav. Sci. 172, 208–214. doi: 10.1016/j.sbspro.2015.01.356
Arini, F. Y., and Dewi, N. R. (2019). GeoGebraAs a tool to enhance student ability in Calculus. KnE Soc. Sci. 2019, 205–212. doi: 10.18502/kss.v3i18.4714
Ballon, E. M. M., and Gomez, F. L. R. (2022). Exploring the use of Wiris in the evaluation at an online course., in 2022 XII international conference on virtual campus (JICV), (IEEE), 1–4.
Beharry, A. (2023). Demo: a functional EDSL for mathematics visualization that compiles to JavaScript., in Proceedings of the 11th ACM SIGPLAN international workshop on functional art, music, modelling, and design, (New York, NY, USA: ACM), 21–24.
Benjamin, S., Robbins, L. I., and Kung, S. (2006). Online resources for assessment and evaluation. Acad. Psychiatry 30, 498–504. doi: 10.1176/APPI.AP.30.6.498/METRICS
Carraccio, C., and Englander, R. (2004). Analyses/literature reviews: evaluating competence using a portfolio: a literature review and web-based application to the ACGME competencies. Teach. Learn. Med. 16, 381–387. doi: 10.1207/S15328015TLM1604_13
Chang, C. C., Tseng, K. H., and Lou, S. J. (2012). A comparative analysis of the consistency and difference among teacher-assessment, student self-assessment and peer-assessment in a web-based portfolio assessment environment for high school students. Comput. Educ. 58, 303–320. doi: 10.1016/J.COMPEDU.2011.08.005
Chen, L., Chen, P., and Lin, Z. (2020). Artificial intelligence in education: a review. IEEE Access 8, 75264–75278. doi: 10.1109/ACCESS.2020.2988510
Chhatwal, M., Garg, V., and Rajput, N. (2023). Role of AI in the education sector. Lloyd Bus. Rev. II, 1–7. doi: 10.56595/lbr.v2i1.11
Chien, C. C., Chan, H. Y., and Hou, H. T. (2024). Learning by playing with generative AI: design and evaluation of a role-playing educational game with generative AI as scaffolding for instant feedback interaction. J. Res. Technol. Educ. 1:2338085. doi: 10.1080/15391523.2024.2338085
Dahal, N., Pant, B. P., Shrestha, I. M., and Manandhar, N. K. (2022). Use of GeoGebra in teaching and learning geometric transformation in school mathematics. Int. J. Interact. Mobile Technol. 16, 65–78. doi: 10.3991/ijim.v16i08.29575
Darmiyati, D., Sunarno, S., and Prihandoko, Y. (2023). The effectiveness of portfolio assessment based problem based learning on mathematical critical thinking skills in elementary schools. Int. J. Curric. Dev. Teach. Learn. Innov. 1, 42–51. doi: 10.35335/CURRICULUM.V1I2.65
Deeba, F., Raza, M. A., Gillani, I. G., and Yousaf, M. (2023). An investigation of role of portfolio assessment on students’ achievement. J. Soc. Sci. Rev. 3, 149–161. doi: 10.54183/JSSR.V3I1.125
Duvignau, R. (2024). ChatGPT has eaten my assignment: a student-centric experiment on supervising writing processes in the AI era. IEEE Global Engineering Education Conference, EDUCON.
Elkhatat, A. M., Elsaid, K., and Almeer, S. (2021). Some students plagiarism tricks, and tips for effective check. Int. J. Educ. Integr. 17:15. doi: 10.1007/s40979-021-00082-w
Eshet, Y. (2024). The plagiarism pandemic: inspection of academic dishonesty during the COVID-19 outbreak using originality software. Educ. Inf. Technol. 29, 3279–3299. doi: 10.1007/s10639-023-11967-3
Evenddy, S. S., Gailea, N., and Syafrizal, S. (2023). Exploring the benefits and challenges of project-based learning in higher education. PPSDP Int. J. Educ. 2, 458–469. doi: 10.59175/PIJED.V2I2.148
Gamage, S. H. P. W., Ayres, J. R., and Behrend, M. B. (2022). A systematic review on trends in using Moodle for teaching and learning. Int. J. STEM Educ. 9:9. doi: 10.1186/s40594-021-00323-x
Garg, K., Verma, K., Patidar, K., Tejra, N., and Patidar, K. (2020) Convolutional neural network based virtual exam controller. in 2020 4th international conference on intelligent computing and control systems (ICICCS), (IEEE), 895–899.
Gobrecht, A., Tuma, F., Möller, M., Zöller, T., Zakhvatkin, M., Wuttig, A., et al. (2024). Beyond human subjectivity and error: a novel AI grading system. Available at : http://arxiv.org/abs/2405.04323
Harish, B. G., and Tanushri, G. K. (2022). Online proctoring using Aritficial intelligence. Int. J. Sci. Res. Eng. Manag. 6:462. doi: 10.55041/IJSREM14462
Harry, A. (2023). Role of AI in education. Interdicipl. J. Humman. 2, 260–268. doi: 10.58631/injurity.v2i3.52
Heil, J., and Ifenthaler, D. (2023). Online assessment in higher education: a systematic review. Online Learn. 27, 187–218. doi: 10.24059/OLJ.V27I1.3398
Holden, O. L., Norris, M. E., and Kuhlmeier, V. A. (2021). Academic integrity in online assessment: a research review. Front. Educ. 6:639814. doi: 10.3389/feduc.2021.639814
Hooper, C., and Jones, I. (2023). Conceptual statistical assessment using JSXGraph. Int. J. Emerg. Technol. Learn. 18, 269–278. doi: 10.3991/ijet.v18i01.36529
Huber, E., Harris, L., Wright, S., White, A., Raduescu, C., Zeivots, S., et al. (2024). Towards a framework for designing and evaluating online assessments in business education. Assess. Eval. High. Educ. 49, 102–116. doi: 10.1080/02602938.2023.2183487
Hwang, G. J., Zou, D., and Wu, Y. X. (2023). Learning by storytelling and critiquing: a peer assessment-enhanced digital storytelling approach to promoting young students’ information literacy, self-efficacy, and critical thinking awareness. Educ. Technol. Res. Dev. 71, 1079–1103. doi: 10.1007/s11423-022-10184-y
Iwani Muslim, N. E., Zakaria, M. I., and Yin Fang, C. (2023). A systematic review of GeoGebra in mathematics education. Int. J. Acad. Res. Prog. Educ. Dev. 12:133. doi: 10.6007/IJARPED/v12-i3/19133
Juma, Z. O., Ayere, M. A., Oyengo, M. O., and Osang, G. (2022). Evaluating engagement and learning based on a student categorization using STACK, exam data, key informant interviews, and focus group discussions. Int. J. Emerg. Technol. Learn. 17, 103–114. doi: 10.3991/ijet.v17i23.36619
Kic-Drgas, J., and Kılıçkaya, F. (2024). Using artificial intelligence (AI) to create language exam questions: a case study. XLinguae 17, 20–33. doi: 10.18355/XL.2024.17.01.02
Kllogjeri, P. (2010). “GeoGebra: a global platform for teaching and learning math together and using the synergy of mathematicians” in Communications in Computer and Information Science. eds. A. Ghosh and L. Zhou (Berlin, Heidelberg: Springer), 681–687.
Komáromi, G. (2023). Designing assignments for university students in the age of AI: examples from business finance education. J. Educ. Pract. 14, 106–111. doi: 10.7176/JEP/14-18-15
Kooli, C., and Yusuf, N. (2024). Transforming Educational Assessment: Insights Into the Use of ChatGPT and Large Language Models in Grading. Int. J. Hum. Comput. Interact, 1–12. doi: 10.1080/10447318.2024.2338330
Kraska, M. (2022). Meclib: dynamic and interactive figures in STACK questions made easy. Int. J. Emerg. Technol. Learn. 17, 15–27. doi: 10.3991/ijet.v17i23.36501
Lancaster, T., and Cotarlan, C. (2021). Contract cheating by STEM students through a file sharing website: a Covid-19 pandemic perspective. Int. J. Educ. Integr. 17:3. doi: 10.1007/s40979-021-00070-0
Lin, Y., Luo, Q., and Qian, Y. (2023). Investigation of artificial intelligence algorithms in education. Appl. Comput. Eng. 16, 180–184. doi: 10.54254/2755-2721/16/20230886
Lu, O. H. T., Huang, A. Y. Q., Tsai, D. C. L., and Yang, S. J. H. (2021). Expert authored and machine generated short answer questions for assessing students learning performance : Educational Technology and Society.
Lutz, T. (2018). Geogebra and Stack. Creating tasks with randomized interactive objects with the GeogebraStack_helpertool. In 1st international STACK conference, (Fürth, Germany).
Mazlan, Z. Z., and Zulnaidi, H. (2023). The nature of gender difference in the effectiveness of GeoGebra. ASM Sci. J. 18, 1–10. doi: 10.32802/asmscj.2023.1044
McCabe, D. (2016). “Cheating and honor: lessons from a long-term research project” in Handbook of academic integrity. ed. S. E. Eaton (Singapore: Springer Singapore), 187–198.
Mora, Á., Mérida, E., and Eixarch, R. (2011). Random learning units using WIRIS quizzes in Moodle. Int. J. Math. Educ. Sci. Technol. 42, 751–763. doi: 10.1080/0020739X.2011.583396
Nakamura, Y., Yoshitomi, K., Kawazoe, M., Fukui, T., Shirai, S., Nakahara, T., et al. (2018). Effective use of math E-learning with questions specification. Cham: Springer, 133–148.
Nasution, N. E. A. (2023). Using artificial intelligence to create biology multiple choice questions for higher education. Agric. Environ. Educ. 2:em002. doi: 10.29333/AGRENVEDU/13071
Negoiță, D. O., and Popescu, M. A. M. (2023). “The use of artificial intelligence in education” in International Conference of Management and Industrial Engineering, 11:208–214. doi: 10.56177/11ICMIE2023.43
Newton, P. E. (2007). Clarifying the purposes of educational assessment. Assess Educ. 14, 149–170. doi: 10.1080/09695940701478321
Nguyen, L. D., O’Neill, R., and Komisar, S. J. (2019). Using poll app to improve active learning in an engineering project management course offered to civil and environmental engineering students., in ASEE annual conference and exposition, conference proceedings.
Nigam, A., Pasricha, R., Singh, T., and Churi, P. (2021). A systematic review on AI-based proctoring systems: past, present and future. Educ. Inf. Technol. 26, 6421–6445. doi: 10.1007/s10639-021-10597-x
Noorbehbahani, F., Mohammadi, A., and Aminazadeh, M. (2022). A systematic review of research on cheating in online exams from 2010 to 2021. Educ. Inf. Technol. 27, 8413–8460. doi: 10.1007/s10639-022-10927-7
Novick, P. A., Lee, J., Wei, S., Mundorff, E. C., Santangelo, J. R., and Sonbuchner, T. M. (2022). Maximizing academic integrity while minimizing stress in the virtual classroom. J. Microbiol. Biol. Educ. 23:21. doi: 10.1128/jmbe.00292-21
Pang, D., Wang, T., Ge, D., Zhang, F., and Chen, J. (2022). How to help teachers deal with students’ cheating in online examinations: design and implementation of international Chinese online teaching test anti-cheating monitoring system (OICIE-ACS). Electron. Commer. Res. 1:14. doi: 10.1007/s10660-022-09649-2
Peimani, N., and Kamalipour, H. (2021). Online education in the post COVID-19 era: students’ perception and learning experience. Educ. Sci. 11:633. doi: 10.3390/educsci11100633
Perkins, M. (2023). Academic integrity considerations of AI large language models in the post-pandemic era: ChatGPT and beyond. J. Univ. Teach. Learn. Pract. 20:07. doi: 10.53761/1.20.02.07
Peytcheva-Forsyth, R., Aleksieva, L., and Yovkova, B. (2018). The impact of technology on cheating and plagiarism in the assessment – the teachers’ and students’ perspectives. Perspectives., in AIP conference proceedings, (American Institute of Physics Inc.).
Pinkernell, G., Diego-Mantecón, J. M., Lavicza, Z., and Sangwin, C. (2023). AuthOMath: combining the strengths of STACK and GeoGebra for school and academic mathematics. Int. J. Emerg. Technol. Learn. 18, 201–204. doi: 10.3991/IJET.V18I03.36535
Pisica, A. I., Edu, T., Zaharia, R. M., and Zaharia, R. (2023). Implementing artificial intelligence in higher education: pros and cons from the perspectives of academics. Societies 13:118. doi: 10.3390/soc13050118
Porter, B., and Grippa, F. (2020). A platform for AI-enabled real-time feedback to promote digital collaboration. Sustain. For. 12:10243. doi: 10.3390/SU122410243
Price, T. J. (2022). Real-time polling to help corral university-learners’ wandering minds. J. Res. Innovat. Teach. Learn. 15, 98–109. doi: 10.1108/JRIT-03-2020-0017
Ramanathan, R., Shivalingaih, J., Nanthakumar, R., Ravindran, K., Shanmugam, J., Nadu, T., et al. (2020). Effect of feedback on direct observation of procedural skills in estimation of RBC count among first year medical students. Int. J. Theor. Phys. 8, 126–130. doi: 10.37506/ijop.v8i2.1260
Reedy, A., Pfitzner, D., Rook, L., and Ellis, L. (2021). Responding to the COVID-19 emergency: student and academic staff perceptions of academic integrity in the transition to online exams at three Australian universities. Int. J. Educ. Integr. 17:9. doi: 10.1007/s40979-021-00075-9
Reiss, M. J. (2021). The use of AI in education: practicalities and ethical considerations. Lond. Rev. Educ. 19, 1–14. doi: 10.14324/LRE.19.1.05
Rodriguez, R., Martinez-Ulloa, L., and Flores-Bustos, C. (2022). E-portfolio as an evaluative tool for emergency virtual education: analysis of the case of the university Andres Bello (Chile) during the COVID-19 pandemic. Front. Psychol. 13:892278. doi: 10.3389/fpsyg.2022.892278
Sancho-Vinuesa, T., Masià, R., Fuertes-Alpiste, M., and Molas-Castells, N. (2018). Exploring the effectiveness of continuous activity with automatic feedback in online calculus. Comput. Appl. Eng. Educ. 26, 62–74. doi: 10.1002/cae.21861
Sangwin, C. (2004). Assessing mathematics automatically using computer algebra and the internet. Teach. Math. Appl. 23, 1–14. doi: 10.1093/teamat/23.1.1
Sangwin, C. (2010). Who uses STACK? A report on the use of the STACK CAA system. Available at: https://www.researchgate.net/publication/228948202 (Accessed May 28, 2024).
Seloane, P. M., Ramaila, S., and Ndlovu, M. (2023). Developing undergraduate engineering mathematics students’ conceptual and procedural knowledge of complex numbers using GeoGebra. Pythagoras 44:14. doi: 10.4102/pythagoras.v44i1.763
Smit, W. J. (2022). A case study: using STACK questions in an engineering module., in 2022 IEEE IFEES world engineering education forum-global engineering deans council (WEEF-GEDC), (IEEE), 1–5.
Solvang, L., and Haglund, J. (2021). How can GeoGebra support physics education in upper-secondary school—a review. Phys. Educ. 56:055011. doi: 10.1088/1361-6552/ac03fb
Spivey, M. F., and McMillan, J. J. (2014). Classroom Versus Online Assessment. J. Educ. Bus. 89, 450–456. doi: 10.1080/08832323.2014.937676
Sullivan, M., Kelly, A., and McLaughlan, P. (2023). ChatGPT in higher education: considerations for academic integrity and student learning. J. Appl. Learn. Teach. 6, 31–40. doi: 10.37074/jalt.2023.6.1.17
Szopiński, T., and Bachnik, K. (2022). Student evaluation of online learning during the COVID-19 pandemic. Technol. Forecast. Soc. Change 174:121203. doi: 10.1016/j.techfore.2021.121203
Tain, M., Nassiri, S. H., Meganingtyas, D. E. W., Sanjaya, L. A., and Bunyamin, M. A. H. (2023). The challenges of implementing project-based learning in Physics. J. Phys. Conf. Ser. 2596, 012068.
Tiong, L. C. O., and Lee, H. J. (2021). E-cheating prevention measures: Detection of cheating at online examinations using deep learning approach a case study. Available at: http://arxiv.org/abs/2101.09841 (Accessed July 28, 2023).
Wang, X., Chen, W., Qiu, H., Eldurssi, A., Xie, F., and Shen, J. (2020). A survey on the E-learning platforms used during COVID-19. in 2020 11th IEEE annual information technology, electronics and Mobile communication conference (IEMCON), (IEEE), 0808–0814.
Wongvorachan, T., Lai, K. W., Bulut, O., Tsai, Y.-S., and Chen, G. (2022). Artificial intelligence: transforming the future of feedback in education. J. Appl. Test. Technol. 23, 1–7.
Wu, X., Wu, R., Chang, H. H., Kong, Q., and Zhang, Y. (2020). International comparative study on PISA mathematics achievement test based on cognitive diagnostic models. Front. Psychol. 11:563344. doi: 10.3389/FPSYG.2020.02230/BIBTEX
Yang, C., and Stivers, A. (2024). Investigating AI languages’ ability to solve undergraduate finance problems. J. Educ. Bus. 99, 44–51. doi: 10.1080/08832323.2023.2253963
Yayu, I., Hizqiyah, N., Nugraha, I., Cartono, C., Ibrahim, Y., Nurlaela, I., et al. (2023). The project-based learning model and its contribution to life skills in biology learning: a systematic literature network analysis. JPBI 9, 26–35. doi: 10.22219/JPBI.V9I1.22089
Zhao, X. (2023). The Impact of Live Polling Quizzes on Student Engagement and Performance in Computer Science Lectures. Available at: http://arxiv.org/abs/2309.12335
Keywords: digital assessments, artificial intelligence, integrity, interactive assessment, animated questions, GeoGebra, Moodle formula
Citation: Hamady S, Mershad K and Jabakhanji B (2024) Multi-version interactive assessment through the integration of GeoGebra with Moodle. Front. Educ. 9:1466128. doi: 10.3389/feduc.2024.1466128
Edited by:
Raman Grover, Consultant, Vancouver, CanadaReviewed by:
Dennis Arias-Chávez, Continental University, PeruK. Sathish Kumar, Alagappa University, India
Copyright © 2024 Hamady, Mershad and Jabakhanji. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Saleem Hamady, U2FsZWVtLmhhbWFkeUBhdW0uZWR1Lmt3
 Saleem Hamady
Saleem Hamady Khaleel Mershad
Khaleel Mershad Bilal Jabakhanji
Bilal Jabakhanji