Connecting mathematics and sports in informal learning spaces

Turner, Erin; Buxner, Sanlyn; Miller, Seneca B.; Baze, Christina; Valerdi, Ricardo

doi:10.3389/feduc.2024.1456653

ORIGINAL RESEARCH article

Front. Educ., 21 August 2024

Sec. STEM Education

Volume 9 - 2024 | https://doi.org/10.3389/feduc.2024.1456653

This article is part of the Research Topic Mathematical Thinking, Practices, and Processes in Non-formal Learning Environments View all 7 articles

Connecting mathematics and sports in informal learning spaces

Erin Turner¹^*

¹College of Education, Department of Teaching, Learning and Sociocultural Studies, University of Arizona, Tucson, AZ, United States
²College of Education, Department of STEM Education, Northern Arizona University, Flagstaff, AZ, United States
³Department of Systems and Industrial Engineering, University of Arizona, Tucson, AZ, United States

Introduction: There is a critical need to develop innovative educational strategies that engage youth in meaningful mathematics learning, particularly students from groups that have been historically marginalized in science, technology, engineering, and mathematics (STEM). In this study, we explore youths’ participation in two collaborative projects from the Growing Mathletes curriculum which combines baseball contexts and mathematics. Our goal was to understand the potential of these projects to support youths’ engagement with mathematical ideas and practices, and the extent to which youth leveraged a range of resources, including prior experiences and funds of knowledge, to inform their decisions and understanding.

Methods: The Design a Stadium and Baseball Team Roster projects were implemented in two afterschool setting sites and two summer program sites with 102 youth of all genders in grades 3 to 8. Data sources included video recordings of youth participation in the project, project artifacts, and youth interviews.

Results: We found the projects contained specific features that supported youths’ engagement in three specific mathematical practices: (1) make sense of problems and persevere in solving them, (2) reason abstractly and quantitatively, and (3) construct viable arguments and critique the reasoning of others. Additionally, there is evidence that while engaging in these projects youth drew on their own funds of knowledge to inform their decisions and understanding.

Conclusion: Our findings point to key implications for researchers, educators, and curriculum developers in informal STEM learning spaces.

Introduction

There is a critical need to develop innovative educational strategies that engage youth from diverse racial, cultural and linguistic backgrounds in meaningful mathematics learning (Celedón-Pattichis et al., 2018). The decontextualized and procedure-oriented nature of traditional, school-based mathematics instruction often fails to capture the interest of students (Boaler and Greeno, 2000; Ellis and Berry, 2005; Walkington, 2013). This is particularly true for students from groups that have been historically marginalized in science, technology, engineering, and mathematics (STEM; e.g., African American, Indigenous, and Latinx youth), as even contextualized mathematics activities from traditional school curricula often fail to reflect their identities, experiences, and perspectives (Ladson-Billings, 2009). This disconnect separates students’ cultural strengths and experiences from their mathematics learning (Leonard, 2008; Celedón-Pattichis et al., 2018), and for some youth, leads to disengagement and lower achievement (Spencer, 2009), particular in comparison to settings that build on students’ interests and identities (Clark et al., 2013; Walkington, 2013).

Informal learning spaces, such as after-school programs and community centers, provide unique opportunities to support STEM learning (McCombs et al., 2017), in part because they can offer flexible, interest-based, collaborative activities (Afterschool Alliance, 2013). Informal learning spaces are also often community-centered and can provide more positive STEM experiences for youth who have had negative experiences in school (McCreedy and Dierking, 2013; Bathgate and Schunn, 2017). Project-Based Learning (PBL), an approach that emphasizes real-world problem solving (Capraro et al., 2013), has been shown to be effective in informal learning settings, particularly when projects are grounded in culturally responsive, meaningful contexts (Lipka et al., 2005; Enyedy et al., 2011). For example, PBL activities that connect mathematics and sports such as baseball have the potential to be high-interest, relevant contexts for engaging mathematical ideas (e.g., averages, data analysis) and practices (e.g., problem solving; Kirk and Kinchin, 2003; Casey and Quennerstedt, 2015). Despite the promise of such activities, there is a lack of curricular resources for PBL in informal learning spaces (Pattison et al., 2017a). Moreover, given that most research on informal STEM learning spaces focuses on science, technology or engineering, rather than mathematics, there is a need to better understand how youths’ participation in mathematics-focused PBL supports their engagement with mathematical ideas and practices (National Governors Association Center for Best Practices and Council of Chief State School Officers, 2010). In the Growing Mathletes Project, we aimed to address these research needs and challenges, through the design, implementation and study of baseball and mathematics PBL activities in informal learning environments that serve youth from diverse backgrounds, including youth from groups historically marginalized in STEM (Latinx, African-American youth). Our study adds mathematics learning-focused findings to research on informal STEM education, and provides insights for informal educators and curriculum developers.

Focus of our study

In this study, we explore youths’ participation in two collaborative project-based activities that were implemented in afterschool and summer camp programs focused on connecting baseball and mathematics. Our goal was to understand the potential of these projects to support youths’ engagement with mathematical ideas and practices, and the extent to which youth leveraged a range of resources, including prior experiences and funds of knowledge, to inform their decisions and understanding. Specifically, our study addressed the following research questions:

RQ1: How do youth engage key mathematical practices (National Governors Association Center for Best Practices and Council of Chief State School Officers, 2010) as they participate in the Baseball Team Roster and Design a Stadium project projects in informal learning settings?

RQ2: What resources do youth draw upon to support their decision making and understanding?

Literature review

In the following sections, we discuss research on informal environments and their potential for supporting mathematics learning, and then introduce STEM focused PBL as a specific strategy for informal spaces such as afterschool programs and summer camps. We end by discussing the importance of grounding projects in relevant, meaningful contexts, and propose that connections between sports and mathematics hold promise for engaging youth typically underserved and underrepresented in STEM fields.

Informal learning spaces and mathematics learning

While most research in mathematics education focuses on formal, classroom-based learning, there is growing interest in the diverse ways that youth participate in mathematical practices and develop mathematical understandings in contexts outside of school. Informal learning spaces include more structured spaces such as afterschool programs or summer camps, and more open-ended spaces such as museum exhibits, nature centers, and playgrounds. Informal mathematics learning environments are often designed with specific goals in mind, such as supporting mathematical reasoning and learning (National Research Council, 2009). Yet in comparison to schools, these settings reflect a more relaxed and collaborative atmosphere which can increase student engagement and motivation (Vadeboncoeur and Padilla-Petry, 2017; Falk and Dierking, 2018). In addition, informal learning spaces that promote engagement and learning are typically characterized by interactive activities, opportunities for collaboration (e.g., Werner et al., 2009) and open-ended projects that include choice and creativity (e.g., Denner and Werner, 2007; Tan et al., 2013; Sager et al., 2023).

Research suggests that informal learning environments support youths’ curiosity toward STEM, their engagement in STEM-related activities, and understandings about the relevance of STEM disciplines in their lives (Noam et al., 2003; Afterschool Alliance, 2013), all of which can buffer against potentially negative experiences with STEM in school (McCreedy and Dierking, 2013; Bathgate and Schunn, 2017). Specific to mathematics, research on play in informal learning spaces has shown that youth engage in mathematics strategically and flexibly as a way to solve authentic problems that arise in the setting (Fisch et al., 2009; Martin et al., 2009). For example, Nasir (2012) found that youth set and pursued emergent goals as they played basketball, many of which involved complex mathematical reasoning such as calculating shooting averages and using those metrics to improve their game. Notably, while youth engage with mathematical ideas and strategies in informal spaces, via practices such as visualization, estimation and analyzing outcomes (Nasir and Hand, 2008) they do not always view their practices as mathematical, because of narrow, school-based conceptions of mathematics that privilege computation (Kliman et al., 2013). This suggests that informal learning settings designed to support mathematics learning need to call attention to mathematical ideas and help youth to see their practices as mathematical.

Another pressing challenge is ensuring that informal learning spaces are accessible to youth from diverse backgrounds. Some research suggests that community-based afterschool and summer camp programs may benefit youth who may not be well-served by other informal settings (Dawson, 2016). For instance, while museums are powerful levers to advance interest in STEM, they are less visited by culturally and linguistically diverse families, potentially because of fiscal barriers or feelings of not belonging (Falk, 1993; Melber, 2007; Dawson, 2014). In contrast, community-based centers such as Major League Baseball (MLB) Youth Academies, which host both afterschool and summer camp programs, were built in under-resourced neighborhoods with the explicit purpose of attracting African American and Latinx youth, a goal that they have successfully met (MLB.com, 2015; ESPN.com, 2017). Another example are Boys and Girls Clubs which work with youth over sustained periods of time, supporting multiple aspects of development (e.g., intellectual, socio-emotional; National Research Council, 2009). While these types of informal learning spaces are positioned to engage youth who have been historically marginalized in STEM fields (Dawson, 2016), they also face challenges, including a lack of high-quality curricula for informal STEM learning, and a lack of preparation to support STEM content (Afterschool Alliance, 2013). The next section describes one strategy, PBL, to address these challenges.

Project-based learning in informal learning spaces

Several strategies have been identified to enhance mathematics learning in informal settings. Perhaps the most-cited approach is the integration of project-based learning (PBL), in which youth develop strategies and solutions to address broad, real-world questions (Capraro et al., 2013). There are several critical components of PBL, including activities that are guided by a driving question (Darling-Hammond et al., 2008), opportunities for collaboration, discussion, and reflection (Larmer et al., 2015), and the creation of a final artifact or model to showcase learning (Krajcik et al., 2022). The openness, choice and relevance of PBL projects allows youth to draw on prior experiences and knowledge to generate unique strategies and solutions (Darling-Hammond et al., 2008). Benefits of STEM-focused PBL in informal learning settings include enhanced engagement and learning (Capraro et al., 2017), and increased interest in STEM and STEM-related careers (Tseng et al., 2013; Mohr-Schroeder et al., 2014; Kwon et al., 2021). PBL also encourages the development of critical thinking and problem-solving skills (Bevan et al., 2015; Schukajlow et al., 2018).

Despite strong consensus on the benefits of PBL in STEM-focused informal learning settings, most studies have investigated science (e.g., Mateos-Nuñez et al., 2020), robotics (e.g., Newton et al., 2020), or engineering-focused projects (e.g., Yilmaz et al., 2010), rather than mathematics. Mathematics-focused PBL involves students in complex, real-world projects, to promote a deeper understanding of mathematical concepts and practices (Pattison et al., 2017a). For example, Cross et al. (2012) described a statistics focused project in which elementary age youth in an afterschool program collected and analyzed data to explore school breakfast options that would both encourage students to eat breakfast and also support their learning. They found that the project was relevant and connected to students’ interests, while addressing important statistical ideas such as sampling, distribution of data, and data representations. In related school-based research, Özdemir et al. (2015) found that middle school students improved their mathematical understanding and their attitudes toward STEM following a project-based unit that included ratios, proportions, and percentages. Similarly, Holmes and Hwang (2016), documented the impact of mathematics PBL projects with racially and economically diverse 8th and 9th graders; participating students evidenced increased motivation, critical thinking, and understanding of mathematics concepts.

To document the impact of STEM-focused PBL in informal learning settings, researchers often focus on outcomes such as beliefs or attitudes (Marshall et al., 2021; Bicer and Lee, 2023), or content knowledge (Han et al., 2014). There is a need for more robust, qualitative assessment tools that can capture the multifaceted impacts of PBL (Thomas, 2000; Vadeboncoeur and Padilla-Petry, 2017), including how PBL supports engagement in disciplinary practices. While not specific to informal learning settings, various researchers have suggested that rubrics may be particularly well suited to capture the complex outcomes of PBL activities (Brodie and Gibbings, 2009; Petrosino, 2023). Developing and investigating such tools is particularly important for mathematics-focused PBL, given the limited number of studies that have specifically examined mathematics-related outcomes. Mathematics-focused PBL activities, which include complex, real-world questions that allow for multiple strategies and solutions, have the potential to support students’ engagement in the Standards for Mathematical Practice (National Governors Association Center for Best Practices and Council of Chief State School Officers, 2010), fostering skills such as problem-solving, reasoning, and communication. For example, PBL creates opportunities for youth to make sense of open-ended problems and persevere in solving them (Mathematical Practice 1; Capraro et al., 2013). Similarly, in mathematics-focused projects youth may draw on data to develop mathematical arguments, and they may consider, critique, and respond to the reasoning of others (Mathematical Practice 3). Despite the promise of PBL for supporting students’ engagement in mathematical practices, research in this area is extremely limited, particularly in informal learning spaces that serve youth from diverse and underrepresented backgrounds. The next section focuses specifically on the importance of grounding projects in relevant contexts that draw on youths’ experiences and interests.

Relevant projects that connect mathematics and sports

PBL activities that connect to youths’ interests and to relevant, culturally responsive contexts have shown particular promise for engaging youth who have been historically marginalized in STEM (Nasir, 2012; Krajcik et al., 2022). When PBL activities are grounded in familiar contexts, and to questions that relate to youths’ interests and experiences, this encourages youth to draw on what they know, including funds of knowledge from their communities and everyday activities (González et al., 2005; Simic-Muller et al., 2009; Turner et al., 2009). One promising context for PBL in informal learning settings are sports related activities, both because of the STEM connections and the fact that many youth participate or express interest in sports (Aspen Institute, 2018; Jones et al., 2020). For example, Marshall et al. (2021) engaged underrepresented middle school youth (African American, Latinx, multi-racial) interested in sports in a summer camp that combined basketball, analysis of basketball performance data, and biomechanics related activities. They found that youth demonstrated enhanced STEM-identities (i.e., familiarity, interest, perceived importance) on post-camp surveys (see also Drazan et al., 2017). Similarly, Jones et al. studied a sports and computing summer camp for elementary grade Black and Latinx youth and found that youth expressed strong interest in sports, and on post camp surveys, evidenced increased understanding of the utility of technology in athletics.

Baseball in particular provides rich contexts for the application of mathematical concepts and practices (Casey and Quennerstedt, 2015). As noted by Quinn (1996), baseball statistics such as batting averages, earned run averages (ERAs), and on-base percentages provide practical examples for teaching concepts like ratios, percentages, and probability. Similarly, using baseball contexts in mathematics activities creates opportunities for students to engage in mathematical practices (National Governors Association Center for Best Practices and Council of Chief State School Officers, 2010), such as problem solving, and to develop critical analysis skills. For example, a study by Kirk and Kinchin (2003) shows that analyzing baseball data requires students to interpret statistical information, make predictions, and solve complex problems. According to Wang et al. (2017) middle school students who played a sports-related computer game about running races demonstrated problem solving and quantitative reasoning skills (i.e., reasoning about relationships between speed, time and distance), and a willingness to accept challenges.

The use of sports contexts to explore mathematics can also foster collaboration and a sense of community among youth. A study by Nasir (2012) found that peer collaboration in sports-related activities helped students develop a deeper understanding of mathematical concepts through shared problem-solving and discussion. This is important, because when learning settings support collaboration and risk-tasking, engagement is enhanced (Boaler and Greeno, 2000; Boaler, 2002; Nasir, 2012). However, a key challenge in using sports contexts, such as baseball, to teach mathematics is the availability of relevant resources. Informal learning settings may lack access to relevant materials to effectively integrate these contexts into their programming (Afterschool Alliance, 2013). Additionally, while connecting sports and mathematics can enhance youth engagement, ensuring that the activities are educationally valuable can be challenging. As McCombs et al. (2017) emphasize, educators must carefully design activities to balance sports-related content with mathematical learning objectives. Our work in the Growing Mathletes program aims to address this challenge, through the design, implementation and study of sports and mathematics PBL activities in informal learning environments that serve youth from diverse backgrounds. This study will contribute mathematics education focused findings to the growing body of research on informal STEM education, and provide research-based insights for informal educators and program designers.

Methods

Growing Mathletes Program context

The Growing Mathletes program is an National Science Foundation-funded research and design project aimed at broadening participation in STEM for youth from underrepresented backgrounds. The curriculum consists of 21 sessions for youth in grades 3 through 8, each of which include activities that connect sports (primarily baseball and softball), mathematics concepts, and growth mindset concepts. For example, in the Strike Zone session youth learn about the concept of strike zones (the area above home plate that is used to determine whether a pitch is a strike or a ball) in baseball. They measure the height of their individual strike zones, create a representation on chart paper, and calculate and plot the area. Next, they use their chart paper representations to practice pitching balls toward their strike zone, calculating the number of “strikes” and “balls” thrown in a set of 10 attempts. The session concludes with a discussion of mistakes, and how reflection on mistakes can support learning and performance improvements in sports, school and other areas of life. Other sessions introduce youth to additional baseball performance statistics such as batting average, earned run average, hits and home runs, and provide youth with opportunities to generate, represent and analyze their own data. Analysis of program outcomes across multiple implementations has shown that youth demonstrate a small but statistically significant increase in their growth mindset for mathematics on post program surveys, and report increases in understanding of specific mathematics concepts, such as fractions, decimals and percents, in post session interviews (Baze et al., 2024).

The Growing Mathletes curriculum also includes two projects which are the focus of this study: Baseball Team Roster, and Design a Baseball Stadium. In both projects, youth work in small groups to plan, create, and present a final product (see Appendices A,B). In the Baseball Team Roster project (Roster project), the driving question is: How can we create a 9-player MLB baseball team roster that meets salary requirements and maximizes performance? In the project, youth use various batting and pitching statistics from a recent season (e.g., batting average, hits, homeruns, earned run average, strike outs, wins) to select players for their own 9-player roster, within a specified salary cap. As they plan their rosters, youth interpret the relative importance of different player statistics (i.e., which statistics are most important when selecting a pitcher, vs. a position player), and they work collaboratively to optimize multiple criteria (maximum performance among the players on their team, for minimum cost). They present their rosters to the group, justifying their selection of players and explaining the criteria they used to make decisions. As a whole group, youth compare their rosters by analyzing the batting averages of players on their teams, and comparing the total hits or homeruns achieved by players on their roster to the salary dollars spent.

In the Design a Stadium project (Stadium project), the driving question is: How can we design a MLB stadium that will attract fans, including youth, and meet their needs? Youth research some of the 30 Major League Baseball stadiums and develop a proposal for their new stadium. Their stadium plans must include the distances of the outfield wall (which are different for every ballpark), unique stadium features to attract fans (giant scoreboards, recreational areas, etc.), seating capacity (overall and by section), and ticket prices. As part of their design proposals, youth estimate how much it would cost for their family (or a group of friends) to attend a game at their stadium. Youth present their stadium plans to the group, justifying their decisions and how they used different criteria and priorities to guide their designs.

Participants

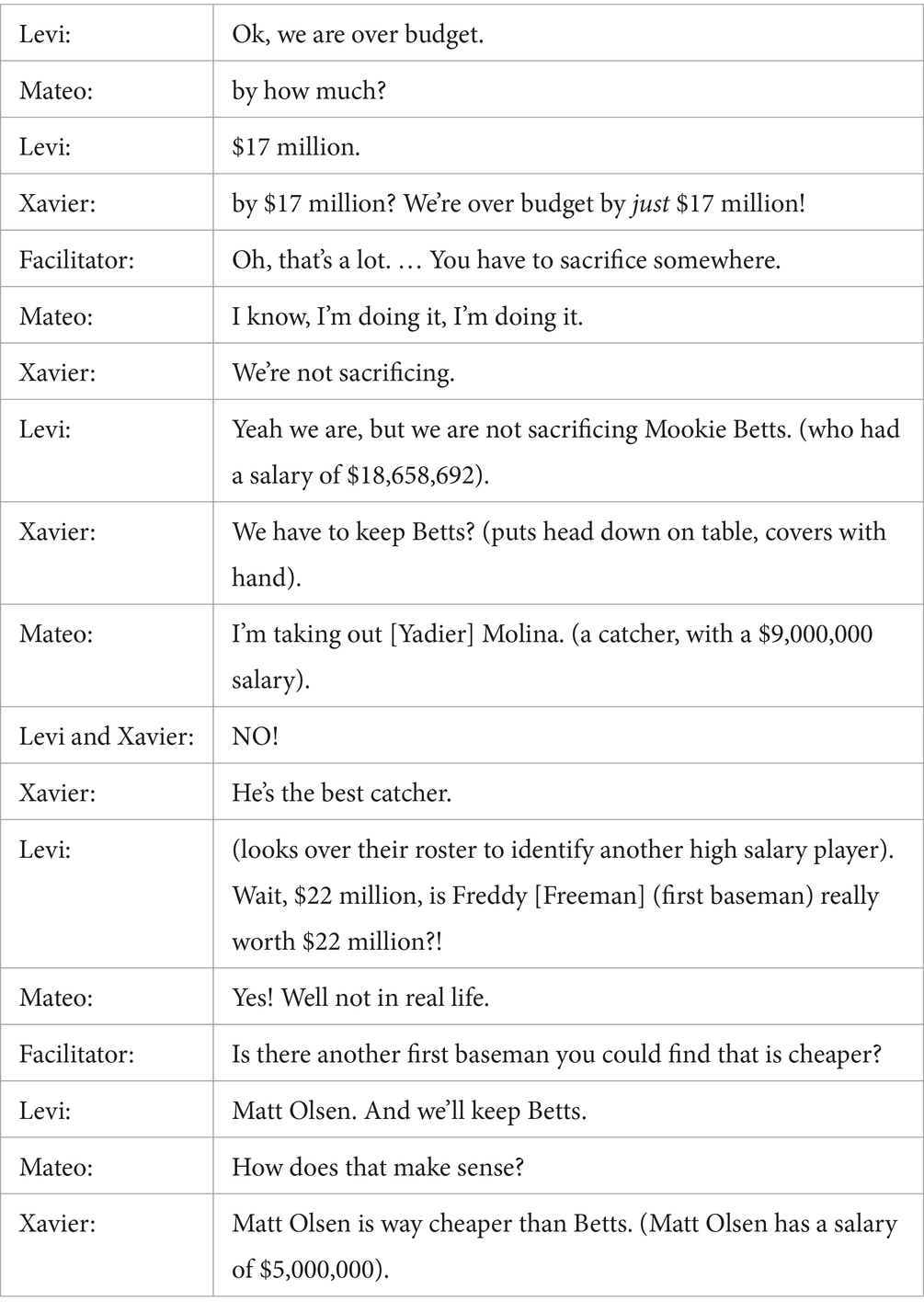
The Growing Mathletes program has been implemented in various informal learning settings, including Boys and Girls Club afterschool programs, and sports and STEM related summer camps at MLB academies. For each implementation, our project team provided professional learning support to adult facilitators (initial training, opportunities to engage in sessions as learners, ongoing coaching during implementation) at each of the sites. In this analysis, we draw on data collected from two afterschool sites in the Southwest region of the United States, and two summer camp sites in the Southwest and Central regions of the United States. An overview of the youth participants (total = 102) from each site is provided in Table 1. Information about age and gender was self-reported by youth on surveys.

Table 1

Table 1. Overview of youth participants at each informal learning site.

At all sites, youth participants reflected the racial/ethnic background of the surrounding schools and communities. At the two Southwest afterschool sites, youth participants attended schools within walking distance of the Boys and Girls Clubs. The schools predominantly served students from minoritized backgrounds [Latinx (45% Site 1, 57% Site 2), Black/African American (17% Site 1, 21% Site 2), White (24% Site 1, 14% Site 2), two or more races (7% Site 1, 3% Site 2), American Indian (3% Site 1, 4% Site 2)].¹ The Southwest summer camp site also drew youth from the surrounding community, though some youth attended from other parts of the city. The community population was 55% White, 31% Latinx, 6% 2 or more races and 3% Black/African American, based on census tract data (FRB Census Geocoder, 2024). The Central summer camp also drew youth from the surrounding community, which was 48% Black/African American, 43% Latinx, 5% White, and 2% two or more races (FRB Census Geocoder, 2024). At the Boys and Girls club sites, some youth participants had experiences with sports, including baseball, but for most, their primary source of knowledge was the Growing Mathletes program. In contrast, the two summer camp sites drew youth with interest in baseball; many camp participants played baseball or softball in local leagues.

Data collection

The primary data sources for this study were (a) video recordings of 20 small groups as they worked on the projects outlined above (14 Baseball Team Roster groups, and 6 Design a Stadium groups), and (b) the artifacts they produced (i.e., planning notes, final project posters). We selected these data sources given our research focus on how program activities supported youths’ engagement in mathematical practices; video recordings of youths’ interactions in extended projects allowed detailed documentation of youths’ participation in these practices, including evidence of youths’ actions, decisions, and discussions. Members of our research team reviewed each video and created detailed content logs that described the small groups’ activity in 5 min increments. Stopping the videos after each 5 min increment allowed research team members to capture the details of youths’ interactions, including exchanges with the facilitators, specific examples of the reasoning youth used to make decisions, conversations or debates among youth in the group, and descriptions of mathematical concepts or practices employed. While the logs did not include a full transcript of the interactions, we transcribed specific excerpts to capture youths’ activity and reasoning related to key group decisions. Secondary data sources included (a) detailed field notes taken by project team members as they observed these sessions and (b) transcripts of interviews with a subset of youth participants following each project session. This included interviews with 12 of the 50 youth from small groups included in the analysis of the Roster project, and 8 of the 23 youth from small groups included in our analysis of the Stadium project. Interviewed youth included 12 girls and 8 boys, and all but 2 youth were from Latinx, African American or mixed-race backgrounds. While the broader purpose of these interviews was to elicit youths’ feedback to inform iterative revision of program activities, for this analysis we used segments of the interviews that included youths’ descriptions of their participation in the Roster or Stadium projects to add additional context to the video recordings and collected artifacts.

Analysis

Data analysis was organized around three phases. In Phase 1, we used the video recordings, detailed content logs, and group artifacts to score each small group’s project work using an analysis rubric. The analysis rubric included dimensions focused on use of mathematics concepts including number sense and operations, and mathematical practices such as MP 2: Reason abstractly and quantitatively, and MP 3: Construct viable arguments and critique the reasoning of others (see Table 2 for selected dimensions in the analysis rubric). A final dimension of the analysis rubric focused on the resources and supports youth drew upon to inform their decision making including prior experiences and knowledge, facilitator suggestions, and peer support. For each dimension of the analysis rubric, we noted whether the small group interactions reflected limited evidence (i.e., a single, isolated instance, or evidence from a single youth in the group, or several instances which were brief and lacking in depth), strong evidence (i.e., repeated, meaningful instances, evidence from multiple youth in the group), or a lack of evidence. To ensure credibility of our interpretations (Lincoln and Guba, 1985), two members of the research team individually scored each small group using the analysis rubric, and then met to compare their analyses. Differences in scores were resolved via discussion. When necessary, we consulted videos for additional information. In Phase 2, we triangulated the evidence on each small group’s analysis rubric against relevant secondary data sources including segments of researcher field notes that focused on the interactions of that specific group, or interviews with youth participants. We noted instances when secondary data sources confirmed evidence already recorded on the group’s rubric, and added additional evidence (e.g., interview quotes) as appropriate. In Phase 3, we analyzed the small group rubric evidence across groups to identify themes related to our two research questions. Following a process of thematic analysis (Creswell, 2009), we first reviewed evidence for a given dimension (i.e., Making Sense of Problems, Problem Solving) across groups and generated initial codes to label different ways that groups evidenced that dimension, including how they enacted mathematical practices and the resources and supports that they drew upon to support decision making. When multiple dimensions related to the same mathematical practice (i.e., the dimensions Communicating Reasoning and Mathematical Arguments and Considering, Responding, Critiquing the Ideas of Peers both related to MP 3: Construct viable arguments and critique the reasoning of others) we reviewed the evidence across these dimensions to generate initial codes. Next, we reviewed codes and associated evidence to identify themes related to how small groups evidenced specific mathematical practices, including similarities and differences (RQ1), and related to the resources or supports youth drew upon to inform their decision making (RQ2). This process involved drafting themes, checking the theme against relevant evidence across different small groups, and then creating a detailed memo for each research question that described prominent themes and illustrative examples. Our findings are organized around these key themes.

Table 2

Table 2. Description of selected dimensions from analysis rubric for small group projects.

Findings

Our findings are organized around our two research questions. For research question 1, we highlight themes related to the mathematical practices that were most prominent (MP 1, MP 2, and MP 3) as youth worked on collaborative projects in the informal learning environments. Of the 20 small groups, all but 1 or 2 demonstrated at least “limited evidence” of these mathematical practices, and approximately half of the groups demonstrated strong evidence. In comparison, other mathematical practices, such as MP 5 and 6 were less evident; approximately one-third of groups lacked evidence for these practices, while half demonstrated limited evidence, and several groups had strong evidence. Our findings are organized around themes related to the mathematical practices most salient in our analysis (MP 1, 2, and 3), offering evidence for the role of specific project features to promote meaningful engagement of these practices. For research question 2, we outline the range of resources that youth leveraged to support their work, and then highlight the varied ways that youth drew on knowledge from other experiences and contexts to inform their work. All youth names used are pseudonyms. We end with a discussion of our findings, and implications for further research and curriculum development for informal STEM learning environments.

Findings for RQ1: youths’ engagement with specific mathematical practices

Our analysis of small group interactions on the Roster and Stadium projects demonstrated that youth engaged in six of the eight mathematical practices (National Governors Association Center for Best Practices and Council of Chief State School Officers, 2010). Before we turn to the three practices that were most prominent (MP1, MP2, and MP3), we briefly describe youths’ engagement with other practices. In both projects youth evidenced MP 5: Use Appropriate Tools Strategically, and MP 6: Attend to Precision in complementary ways as they used calculators to execute, check or revise calculations, or used rulers to sketch accurate models of their field design (e.g., using rulers to ensure an equal distance between bases in the infield). MP 4: Model with Mathematics was also evident in small groups’ work, as youth used equations to model the total salary of their MLB roster, or the cost of attending a game in their stadiums. Youth also engaged in MP 4 as they identified and related important quantities (e.g., size and location of seating sections, compared to ticket prices in the Stadium project), and interpreted their mathematical results in the context of the real-world situation. These instances of modeling with mathematics typically involved other mathematical practices, such as problem solving (MP1) or quantitative reasoning (MP2), and thus are discussed in the corresponding findings sections below. Two mathematical practices related to the use of patterns and structures (MP7) and the recognition of repeated reasoning (MP8) were less evident in youth interactions, likely due to the lack of focus on mathematical patterns and structures in the projects, and thus are not a focus in the findings sections that follow.

MP1: make sense of problems and persevere in solving them

As youth engaged with each of the project-based tasks (Baseball Team Roster and Design a Stadium) they evidenced specific practices related to MP1: Make sense of problems and persevere in solving them. First, as youth made sense of the goals of each project and considered possible problem solving approaches, they made strategic decisions that facilitated calculations and helped them to keep track of their progress. For example, in the Roster project, multiple groups opted to select the most important, and potentially most expensive players first, such as the pitcher, and to track their spending along the way so they were aware of how much money was left after each player selection. Group P from the Southwest Summer Camp site started by selecting the team pitcher and catcher (positions that they deemed most important), and then calculated their remaining salary funds.

They continued this process as they selected the remaining 6 players, calculating available funds after each selection to ensure that they did not overspend the allotted salary budget.

In the Stadium project, youth made purposeful decisions about quantities to facilitate calculations with larger numbers, which supported efficient progress through the task. For instance, Group D from a Southwest afterschool program site strategically used multiples of 5,000 or 10,000 as they planned the seating sections in their stadium so that they could easily ensure that the capacity of their sections equaled the total capacity of the stadium (100,000). Initially, they designated 20,000 seats to each of 5 seating sections (because they knew 5 times 20,000 is 100,000). Later, they revised this plan to allow for more seats in the “cheaper sections,” but continued to use quantities that facilitated efficient mental calculation. Another small group of elementary grade students at the same Southwest site, Group F, used a similar approach, explaining to the program facilitator that they used “friendly numbers” for their seating capacity and ticket prices of each section to make it easier to review and keep track of calculations.

Second, as youth worked on the projects, they evaluated their progress, reflected on whether their approaches to the problem made sense, and made adjustments as needed. In some instances, these adjustments were based on the constraints of the project, and other times based on their real-world reasoning about the situation. For example, in the Roster project, some groups spent less than the allowed salary dollars on their team roster, and decided to use the remaining funds on additional players to strengthen the team. Group R at the Southwest summer camp site decided to draft a second pitcher, given the importance of this position. One youth in the group explained, “after we picked and had all the [required] players. We had more extra salary and thought that it would be helpful to have an extra pitcher just in case.”

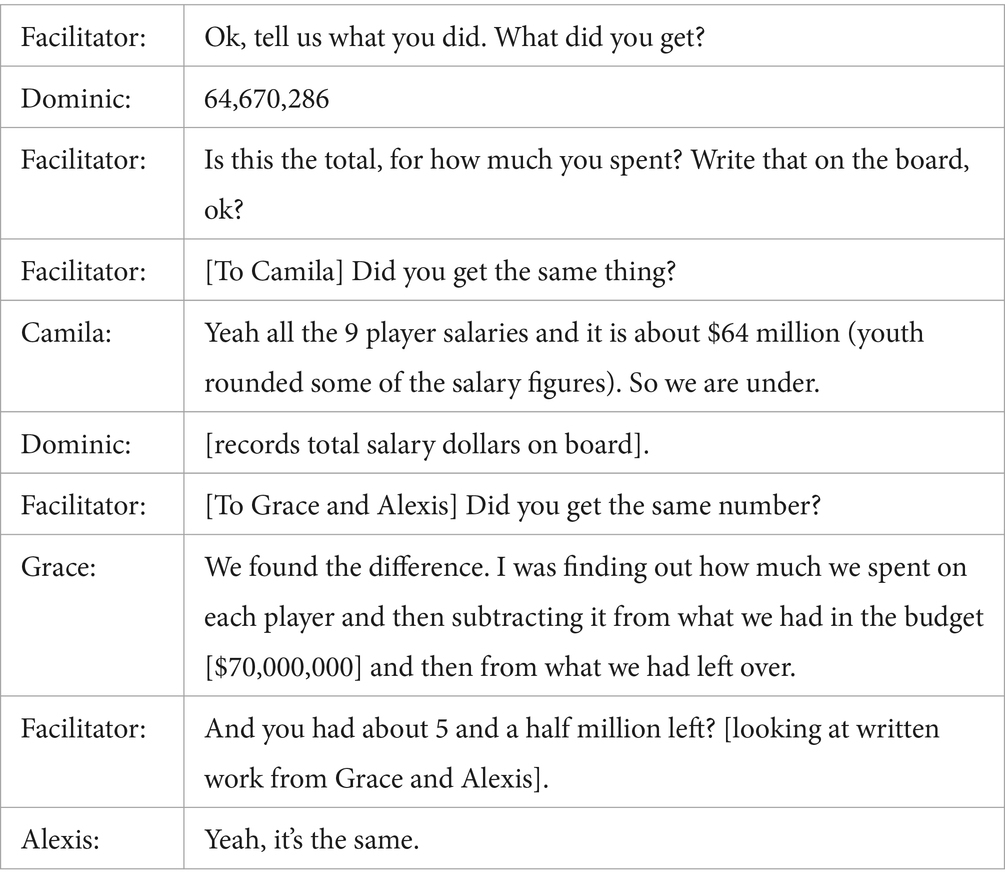
In other cases, youth found that their selected players exceeded the salary limit, and they had to make adjustments to their selections. For example, Group K from the Southwest summer camp site totaled their selected player salaries and discovered that their roster was $17 million over budget. They debated which player to “lose” in favor of another, less expensive option.

The group tested out this plan and found that by removing Freddy Freeman they had a little over 5 million salary dollars remaining, enough to add in a different first baseman, Matt Olsen. These adjustments allowed them to honor the budgetary constraints of the task, while still retaining their favorite player, Mookie Betts.

In the Stadium project, youth also tracked their progress and made adjustments as needed, in some instances based on real-world considerations related to the project context. For example, Group J at a Southwest afterschool site initially planned to only offer 4-packs packs of tickets for their exclusive VIP section, reasoning that attendees would want to enjoy the special VIP offerings with family and friends. But when asked by the facilitator whether she could purchase a single ticket to join a group in the VIP section, the girls decided that the 4-pack option was too limited and they added a per person ticket pricing structure to their plan.

In both projects, multiple groups of youth engaged in making sense of problems (MP1) as they generated and enacted problem solving approaches, made purposeful decisions that supported their progress, and strategic adjustments to their approach when needed. The balance between the openness and choice built into the project, combined with the requirements and constraints, seemed to support these practices, a point which we return to in the discussion.

MP2: reason abstractly and quantitatively

Across both projects, youth consistently attended to the meaning of quantities in relation to the real-world scenario. As youth performed operations, compared quantities, and selected values, they did so in ways that clearly evidenced understanding of how the quantities related to specific components of the project context. For example, in the Stadium project, youth performed multi-step calculations as they planned the seating capacity and ticket prices for their stadium, and projected the total cost for a group of family members or friends to attend a game. At one of the Southwest afterschool sites, multiple groups (H, I, and J) labeled their calculations in ways that evidenced understanding of meaning of each quantity and solution in relation to the context (e.g., they labeled equations that represented the total cost of ticket prices, food purchases and parking for a group of 4 people attending the game). One group designed a very small, personal stadium that included only 1,100 seats. When they shared their design, they explained the meaning of the quantities in each seating section (number of seats, and ticket prices), and the meaning of their computations (i.e., Youth: “we put 100, 100, 300, 500 and then another 100…. for the number of seats in each section. We added those together and we got 1,100 …[which was] the total number of seats in the stadium.”).

At the other Southwest afterschool site, Group E identified and operated on quantities related to seating capacity and ticket practices in ways that reflected understanding of the meaning of the values in context. For example, they divided the 75,000 seats in their stadium across three seating sections of varying sizes and ticket prices to create accessible options for stadium attendees. One youth explained the half/double ratios they used to set ticket prices for each section:

In other words, as these youth identified and operated on quantities, they consistently attended to the meaning of the quantities and operations in the real world situation.

Just as youth contextualized quantities throughout their work on the Roster and Stadium projects, they also demonstrated the ability to decontextualize—to represent and manipulate situations symbolically, flexibly using properties of operations to support their work. For example, in the Roster project, multiple groups of youth reasoned that they could use two different mathematical operations, addition or subtraction, to determine whether their team roster exceeded the allowable salary budget. Some youth opted to repeatedly subtract each player’s strategy from the $70,000,000 budget, understanding that the result of each operation represented the amount of salary dollars remaining. Other youth successively added each player’s strategy, understanding that the result of each sum represented the number of salary dollars spent. In some small groups, such as Group G at a Southwest afterschool site, youth explored both approaches in parallel, explaining how they each verified that the team roster met the salary requirements.

While the facilitator did not further probe the youths’ explanation, the youth concurred that each of their operations “proved” that the team roster met the $70,000,000 salary limit requirement, and seemed to understand how their addition and subtraction calculations related to one another, each providing key information about their situation.

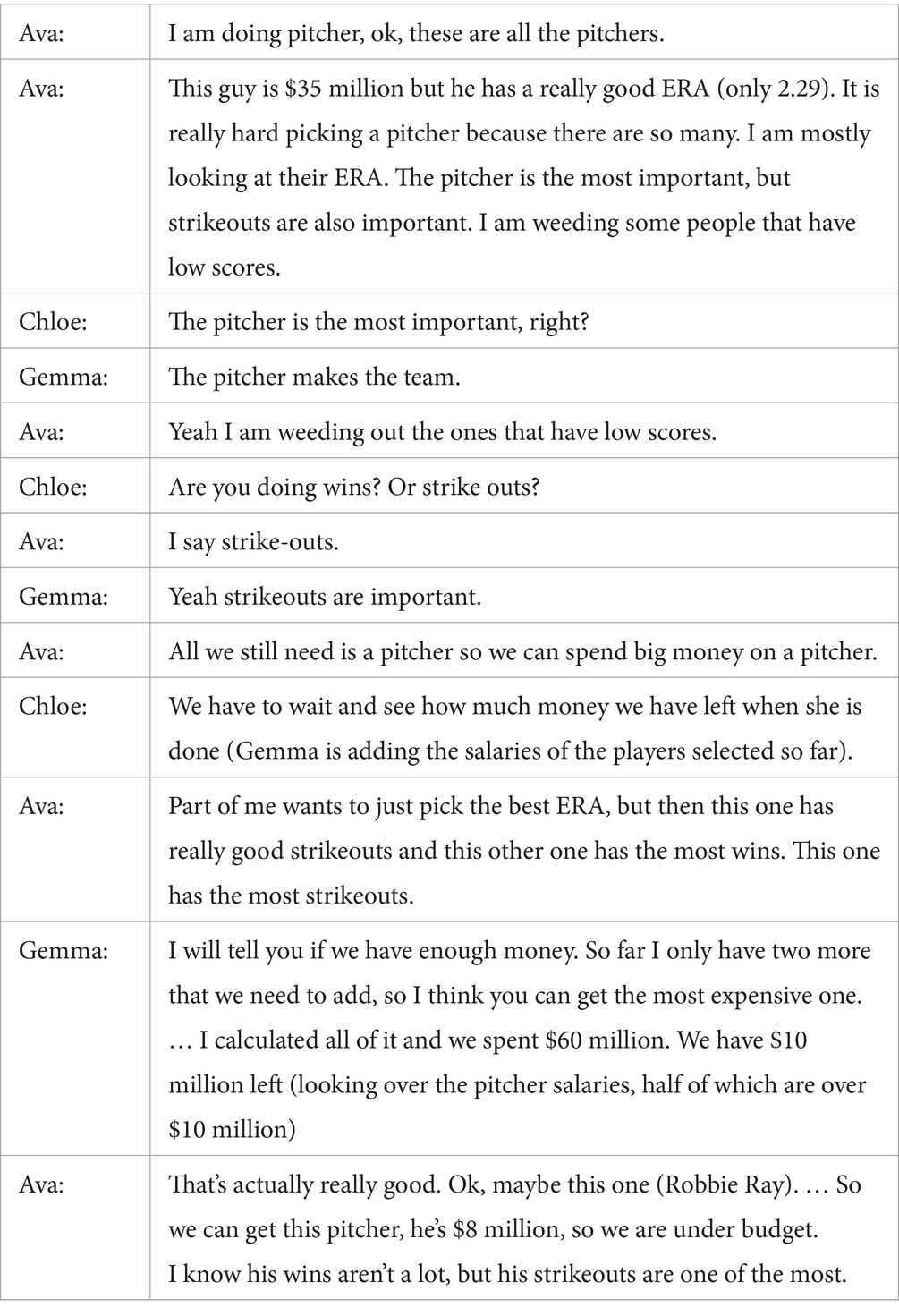
Another way that youth reasoned abstractly and quantitatively as they engaged in the projects was by reasoning across different quantities to inform the decisions they made. This primarily occurred in the Roster project as youth compared quantities abstractly (i.e., comparing decimal values, whole numbers, or percentages) and then contextualized the meaning of those quantities and relationships in terms of baseball player statistics. For example, Group N at the Southwest summer camp site used multiple player statistics to compare players at each position as they made their team roster. In the discussion excerpt below, the youth debated which first baseman to select. Gemma shared the first baseman statistics with the rest of the group, while Chloe compared the first baseman statistics to those of the second baseman she was reviewing.

Once the group selected all field players, they proceeded to select a pitcher, leaving the pitcher to the end so they could spend all remaining salary funds on this position. In the discussion below, the youth leading the pitcher selection (Ava) debated the relative importance of different pitcher statistics, including ERA (Earned Run Average), wins, and strikeouts.

Throughout this discussion, the girls compared quantities expressed as whole numbers (salaries, hits, homeruns) and as decimals (ERA, batting average). They not only compared the quantities abstractly, but reasoned about the relative importance of each quantity for a particular player (i.e., they concluded that strikeouts were critical for a pitcher, while hits and home runs were focal points for the first baseman.) In addition, they correctly interpreted whether higher or lower values for a given statistic indicated strong performance (e.g., with ERA, a lower value is better because it indicates that a pitcher gives us fewer runs, while with strikeouts, a higher value is better). In other words, as youth reasoned about different statistics they decontextualized and recontextualized each value to inform their roster decisions.

Across both projects, though more prominent in the Roster project, youth engaged in quantitative reasoning as they compared and found relationships among values, debated the relative importance of different player statistics, and reasoned about how different operations related to the problem context. We suspect that the different kinds of quantitative data included in the Roster project was particularly supportive of these practices, a point which we elaborate in the discussion.

MP3: construct viable arguments and critique the reasoning of others

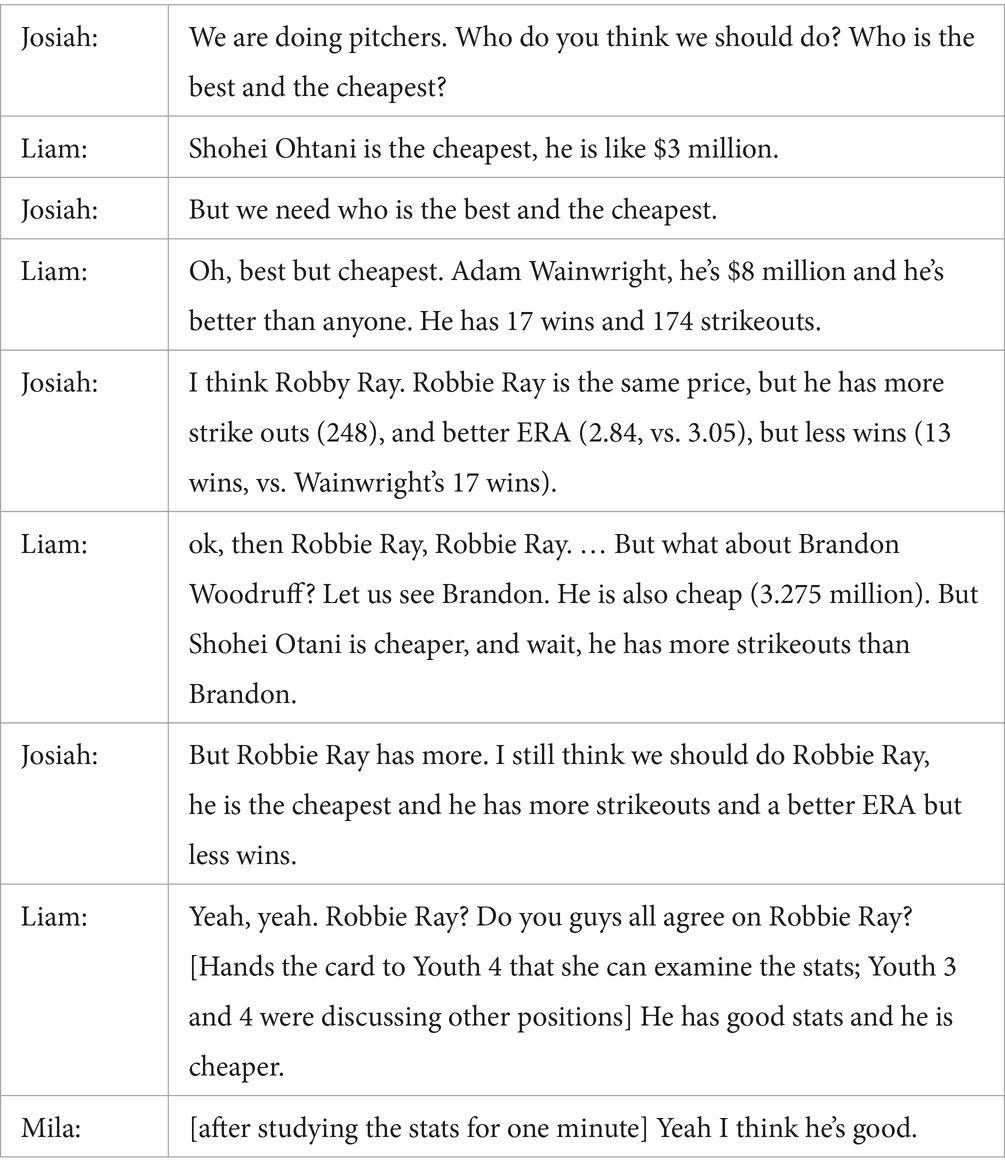
As youth communicated their reasoning about the meaning of quantities in the project, they also engaged in MP3: constructing and critiquing augments. In the Roster project, this most often occurred as youth argued for selecting a particular player. As evidenced in the excerpts above, they often considered how a player’s statistics compared to those of others that played the same position. For example, in the discussion below, two boys from Group R from the Southwest summer camp site engaged in a lively debate about which player they should select for pitcher. Their goal was to optimize multiple criteria in their pitcher selection (maximum performance for the minimum cost).

Following this session, Josiah reflected on the project with a member of our team, and specifically described his group’s process for communicating and critiquing arguments for specific players.

Notable in Josiah’s reflection is how the project created opportunities for students to present and justify their own arguments, but also opportunities to consider other’s reasoning, and to revise their arguments in response to critique.

In the Stadium project, youth also engaged in communicating and critiquing arguments, most often related to decisions about seating capacity and ticket prices for different sections of their stadium. For example, groups H, I and J each had spirited debates about which seating section would be the most desirable, and therefore the most expensive. Two groups presented conventional arguments for a small section of expensive, exclusive, “close to the field” seats for “VIP” attendees. But one group (Group I), argued that the lower seats were less desirable, because they only provided a partial view of the field, and included a higher risk of “getting hit” by a ball. Instead, they argued that the VIP section should be located in the top rows of the stadium, as those seats allowed a wide view of the entire field.

In summary, both projects created opportunities for youth to communicate their reasoning and to construct, consider, and respond to the ideas of others. Mathematical argumentation was most evident in the Roster project, as youth strove to optimize multiple criteria so that players had maximum performance for minimal cost. When students constructed arguments in the Stadium project, the focus was mostly on youths’ reasoning for their choices and preferences in their stadium design.

Findings for RQ2: youth leverage resources to support their decision making and understanding

This section focuses on the varied resources that youth drew upon to support their understanding and decision making as they completed the two projects. We found that almost all groups evidenced use of social resources (peers and/or facilitators) to support their decision making. In both projects, youth asked group members for ideas and suggestions as they made decisions about ticket prices, seating capacity, and player selection. Often, discussions were collaborative where several youth introduced and debated ideas, as shown in the excerpts from groups K and I above. In other instances, a single youth drove the decision making, often because this youth was older and positioned as a group leader. While all groups collaborated, in some instances the collaboration was less focused on considering peers’ ideas and more focused on delegation of tasks (i.e., one youth selected players, one youth added salaries to keep track of totals, and a third youth recorded their selections on a team poster). We found these cases to be less productive, as opportunities to engage in mathematical practice were focused on a subset of youth. While it was more common for youth to draw on ideas from peers as they made decisions, groups also leveraged suggestions from facilitators to inform their work. Consistent with the norms of informal learning spaces (Vadeboncoeur and Padilla-Petry, 2017), facilitators allowed youth to drive small group work, as they circulated among groups, asking questions and offering tips as needed (see groups G, K and I above). While use of social resources was a prominent pattern across groups, we focus the remainder of this findings section on how youth drew on their experiences and funds of knowledge (González et al., 2005) from settings outside the informal learning space to inform their decisions.

Youth draw on their own funds of knowledge to inform their decisions and understanding

In both projects, but in particular the Baseball Team Roster project, youth demonstrated and utilized knowledge of baseball and of specific players that was beyond what was included in the activity. For example, some groups drew on their understanding of team rosters or “line-ups” to make sense of the goals of the project. When a younger youth in Group S at the Central summer camp site expressed confusion about the project, a peer in the group referenced an outside experience to support his understanding.

Following this exchange, the younger youth leaned into the group conversation, and even took the lead on the selection of a player for one of the field positions.

In other cases, youth drew on their knowledge in ways that informed how they interpreted provided player statistics. For example, as highlighted in the extended example from Group N above (Section on MP2), youth used their knowledge of baseball to debate the relative importance of different statistics for a given position (i.e., ERA vs. strikeouts for pitchers), or the importance of different positions (i.e., selecting a pitcher first, or spending the most salary dollars on a pitcher). In these instances, youth used their knowledge of baseball as a resource to correctly interpret whether “higher” or “lower” values for a given statistic indicate better performance (i.e., a low ERA is optimal, while a high value for strikeouts is preferred), which then guided their player selection.

Sometimes, youths’ knowledge of players complemented the provided statistics, providing additional data points to consider. This included real time information about players (i.e., injuries), or knowledge of players’ abilities from youths’ experience watching baseball. For example, when Group P from the Southwest summer camp site was comparing center fielders, they considered how the player salaries compared to batting average and home runs, and whether cheaper players actually had weaker statistics. They initially settled on Mike Trout, who in the 2021 season had generally stronger statistics than the other options, but then reconsidered when one youth in the group recalled that Trout was injured.

Ultimately, this youth’s knowledge influenced the group decision and they selected a different (non-injured) player for the center field position.

While youths’ use of their prior knowledge and experiences to inform decisions was most common in the Roster project, some groups leveraged outside experiences to inform their Design a Stadium decisions, particularly related to ticket pricing. For example, in Group E from a Southwest afterschool site, youth prioritized full attendance at games in their stadium, and reasoned that if they made ticket prices too high, people would opt to view the game on television instead of attending in person. As these two youth explained during a post project interview:

Other groups had similar reasoning, arguing that considering “their friends and family” helped them determine reasonable prices for tickets and concessions in their stadium. As a youth from Group D explained, “if we were to do it, then we were to invite our friends or our family, [we thought about] would we want them to pay a lot? or, do we want them to pay a little bit?”

Interestingly, in some instances youths’ use of their prior knowledge about specific players to inform decisions meant that the group only engaged minimally with the provided player statistics. For example in Group K from the Southwest summer camp site, youth were debating between two players for the right field position (Aaron Judge and Mookie Betts). Rather than comparing their statistics (hits, homeruns, batting average, salary, etc.), one youth claimed that they knew Mookie Betts was “faster” and should be selected.

While Aaron Judge outperformed Mookie Betts on multiple statistics (higher batting average, more hits and homeruns in 2022), the group selected Mookie Betts because of one youth’s claim and they knew he was “faster.” As the group continued to select players, they again relied on their prior knowledge of players, instead of player statistics, to inform choices. For example, when selecting a second baseman, Mateo referenced their experience watching one player on television to justify the choice: “Let us take this guy [Adam Fraiser]. I’ve seen him play before. He hit a ball, and I do not even know how [but] he hit a homerun.” Without further discussion, the group selected this player. Notably, youth could have used various player statistics to justify this choice (i.e., Adam Fraiser’s batting average was comparable to that of other second baseman, and his salary was considerably less), but their reliance on one group member’s knowledge of the player backgrounded this information.

We noted similar patterns in other groups, wherein youth who had more prior experience with baseball used this knowledge to inform and justify their decisions, often with minimal use of the provided player statistics. For example, Efran, a youth from Group A explained that he led the selection process for his group, based on his experience watching players on television. He noted:

I picked those baseball players because I watch baseball and I picked the players I know. I know that they are good, but they are cheap. So I just told the people sitting at the table to choose those people. Because I’ve seen them play before and they are pretty good when I watch them on TV…. So I’m like, “just get him.” And there was a baseball player with 39 home runs so I said, “choose him. He′s really good (post project interview).

Other youth used their knowledge of specific teams (but not the statistics of particular players) to select or eliminate players from their roster. For example, a youth in Group L at the Southwest summer camp site selected a pitcher because he played for the Angels (the youth’s favorite team), and other groups at this site eliminated players from the Dodgers, and selected players from the Blue Jays, primarily based on their team affiliations.

In summary, youth leveraged social resources (peers and facilitators), in addition to their own knowledge and experiences from settings outside of the informal learning space to inform their understanding and decisions, particularly during the Roster project. While in most instances these connections to outside funds of knowledge enhanced youth’s engagement with the provided statistics, in some cases, youth leveraged outside knowledge in ways that limited opportunities to engage in mathematical reasoning. We revisit this potential challenge in the discussion.

Discussion

Overall, we found that both of the projects implemented in informal learning sites contained specific features that supported youths’ engagement in mathematical practices including problem solving (MP1), quantitative reasoning (MP2) and argumentation (MP3). First, the openness and choice built into the projects not only encouraged creativity but also required youth to generate problem solving approaches (MP1), and to build arguments to support their choices and decisions (MP3). At the same time, the given constraints (i.e., salary limit), required youth to monitor their overall progress and make adjustments to ensure compliance. This monitoring and revision of approach led to further engagement in key problem solving practices (MP1). In other words, the balance of choice and constraints in the projects seemed particularly generative for supporting youth engagement in key mathematical practices. This was most apparent in the Roster project, as youth were able to choose criteria and processes for selecting players, but were constrained by the parameters of a salary limit and the need to construct (at a minimum) a 9-player roster. These constraints led to a more challenging problem, which prompted youth to iteratively review and reflect on their choices until they completed the task. In contrast, in the Stadium project, youth were able to make choices about the overall size of their stadium, the capacity and ticket prices of different seating sections, and unique stadium features. While the project emphasized choice, few constraints were provided. For example, youth had to include different seating sections but could design stadiums of any size. Similarly, youth were asked to include features that they thought would attract fans, but without consideration of budgetary limits. Given the relative lack of constraints in the Stadium project, youth were not prompted to monitor or adjust their approaches (MP 1), or to mathematically justify their design decisions (MP 3) in the way that was evident in the Roster project. This finding related to the importance of balancing choice and constraint in mathematics-focused PBL activities is in part consistent with prior research which has highlighted youth voice and choice as essential design elements for PBL (Tan et al., 2013; Larmer et al., 2015). Yet our findings about the role of constraints extends this prior work, by showing that a key component of designing challenging and authentic questions (Larmer et al., 2015) is ensuring that those questions include sufficient, real-world constraints.

Another project feature that supported youth engagement in mathematical practices was the included quantitative data about player performance (in the Roster project) and the contextual information about sample stadiums (in the Stadium project). In the Roster project in particular we found that the player statistics supported youths’ engagement in quantitative reasoning (MP 2) and their opportunities to develop, communicate and critique mathematical arguments (MP 3), as they used the various sources of data to defend their player selections. In the Stadium project, while youth occasionally used the sample stadium information to justify their choices about stadium capacity or outfield distances, the lack of constraints limited youths’ need for this information. If the project had included budget limits along with information about potential costs of different stadium features, youth may have drawn on this information as engaged in quantitative reasoning (MP 2) or communicated mathematical arguments (MP 3). While PBL activities often include sustained inquiries where youth generate information on their own (Cross et al., 2012; Larmer et al., 2015), we found that including authentic player statistics in the project materials allowed youth to focus their attention on comparing the values and interpreting the relative importance of different statistics. Given the fluidity of activity in informal learning settings and the fact that time for sustained inquiries may be limited, providing youth with a diverse set of authentic data seemed like a productive way to maximize opportunities to engage in mathematical practices.

Finally, we found that both projects created opportunities for youth to draw on outside knowledge and experiences, including knowledge of baseball and understanding about the needs and interests of potential baseball fans to support their project decisions. In the Roster project, youth leveraged knowledge of player positions and the importance of specific statistics as they selected players for their team roster. This was particularly true for youth in the summer camp implementations, as those settings drew more youth with prior baseball experiences (e.g., Groups P and S above). In the Stadium project, there were fewer instances when youth drew on baseball-related knowledge to inform their decisions, which may reflect a lack of experience attending live sporting events in stadiums, particularly among youth who did not play team sports. When youth did leverage outside knowledge, they often considered what they knew about the interests and needs of friends, family, and other potential fans while designing unique stadium features, determining reasonable ticket prices, and arranging seating sections (e.g., Group E). Notably, in the Roster project there were several instances when youths’ use of their knowledge about specific players to inform roster selections meant that the group only engaged minimally with the provided player statistics (e.g., Groups A and K), which then limited their opportunities to engage in mathematical reasoning. While youths’ engagement in the projects invited connections to their experiences and funds of knowledge, a practice which has been shown to enhance STEM learning (Simic-Muller et al., 2009; Turner et al., 2009; Nasir, 2012; Krajcik et al., 2022), our findings also suggest that informal learning educators may need to support youth to use their real world knowledge to complement and enhance their engagement in mathematical reasoning, rather than limiting such opportunities.

Our work answers a call for additional research on the impact of informal learning settings and PBL activities on youths’ mathematics engagement and learning, particularly for youth from groups underserved and underrepresented in STEM fields (Condliffe et al., 2017; Pattison et al., 2017b). Additionally, by documenting the potential of PBL activities that integrate sports and mathematics to support youths’ engagement in mathematical practices (National Governors Association Center for Best Practices and Council of Chief State School Officers, 2010), we address additional calls that research on PBL (Thomas, 2000), and in STEM informal learning spaces to attend to a range of outcomes.

Implications and conclusion

Our study has important implications for educators, curriculum developers, and researchers who work in informal STEM learning spaces. First, there is the need for additional informal learning curricula that integrate sports and mathematics, given the positive outcomes demonstrated in our findings (i.e., engagement in mathematical practices, connections to outside knowledge and experiences). Additionally, our findings suggest that curriculum developers attend to the complementary roles of choice and creativity alongside constraints to support youths’ engagement in problem solving and mathematical reasoning and to encourage reflection and discussion.

Second, our findings have implications for professional learning and support for informal STEM learning facilitators. Youth in informal afterschool and summer settings have varied backgrounds and interests, and facilitators need to seek connections to youth who may have limited prior experiences with project contexts. Our findings also suggest that professional learning programs for informal STEM educators should include strategies for supporting youths’ sustained focus on mathematical learning goals, such as reminding youth of project guidelines or supporting youth to use data to support decisions and arguments. This is consistent with other research that has highlighted the professional learning needs of informal STEM facilitators (Hladik, 2022).

An important limitation of our research is that our team offered professional learning support (i.e., initial training, ongoing coaching) for facilitators who implemented the program. While materials from our professional learning sessions will be broadly disseminated via our project website, future research should explore the effectiveness of the Growing Mathletes program, including how the culminating projects support youths’ engagement in mathematical practices, when implemented by facilitators who do not participate in sessions with our team, but are instead supported by our online materials and/or by other professional learning supports in their contexts. An added limitation is that our research focused on informal learning spaces that offered a more structured learning program (i.e., a week long summer camp, or designated time for Growing Mathletes during an afterschool program). Future research should explore the applicability of Growing Mathletes activities, and particularly their potential to engage youth in mathematical practices, in less structured informal learning spaces such as community centers or museums.

Finally, our findings raise key questions and topics for future research on mathematics learning in informal settings. Specifically, studies should explore additional aspects of integrating sports and mathematics to better understand the learning impacts for youth with varying levels of interest and prior knowledge about sports. Research should also continue to investigate how specific features of mathematics-focused PBL activities support mathematical understanding, and the application of different mathematical practices.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by the University of Arizona Institutional Review Board. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin.

Author contributions

ET: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Supervision, Writing – original draft, Writing – review & editing. SB: Data curation, Formal analysis, Investigation, Writing – review & editing. SM: Data curation, Formal analysis, Investigation, Writing – review & editing. CB: Data curation, Formal analysis, Investigation, Writing – review & editing. RV: Funding acquisition, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This material is based upon work supported by the National Science Foundation under Grant #2005793. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1456653/full#supplementary-material

Footnotes

1. ^www.usnews.com/education/k12/

References

Afterschool Alliance . (2013). Defining youth outcomes for STEM learning in afterschool. Washington, DC. Available online at: http://www.afterschoolalliance.org/STEM_Outcomes_2013.pdf (Accessed April 15, 2024)