A systematic review and meta-analysis of intervention studies on mathematics and science pedagogical content knowledge

Fukaya, Tatsushi; Nakamura, Daiki; Kitayama, Yoshie; Nakagoshi, Takumi

doi:10.3389/feduc.2024.1435758

SYSTEMATIC REVIEW article

Front. Educ., 19 September 2024

Sec. Teacher Education

Volume 9 - 2024 | https://doi.org/10.3389/feduc.2024.1435758

A systematic review and meta-analysis of intervention studies on mathematics and science pedagogical content knowledge

$\r\nTatsushi Fukaya$ Tatsushi Fukaya^*

Daiki Nakamura

Yoshie Kitayama

Takumi Nakagoshi

Graduate School of Humanities and Social Sciences, Hiroshima University, Higashihiroshima, Japan

Pedagogical content knowledge (PCK) has been considered as professional knowledge that teachers need to effectively instruct students. Empirical studies have been conducted to enrich teachers' PCK through interventions such as professional development programs. In this study, we conducted a systematic review and meta-analysis of studies about PCK interventions and their quantitative evaluation among mathematics or science teachers at the elementary and secondary education levels. We identified 101 effect sizes (42 for multiple group comparison designs and 59 for multiple time point comparison designs) and found that the interventions had a positive effect in both designs. The results of the meta-regression analysis showed that in the multiple group design, the effects differed by intervention target, with higher scores for the PCK intervention than for the CK-only intervention, and in the multiple time point design, the effects differed by subjects treated, with higher scores for the science materials than for the mathematics materials. These results not only demonstrate the average effectiveness of previous studies aimed at improving teachers' PCK but also provide insights into effective designs for professional development methods that promote PCK acquisition.

Systematic review registration: https://osf.io/vf4hq/?view_only=068483e4e82c42cd994e2c8174bd0a64.

Background of the study

The influence from teachers in the classroom may be one of the most important factors affecting student learning (Darling-Hammond, 2000; Hattie, 2009; Wayne and Youngs, 2003). A review of rigorously conducted studies examining the impact of teacher training programs on student achievement reported that enhancing teachers' instructional expertise increased student achievement by the 21^st percentile (Yoon et al., 2007). Research on teacher quality and its connection to student learning (also known as teaching effectiveness) has been conducted from the 1970s (Brophy and Good, 1986; Doyle, 1977; Rosenshine, 1976) to the 2000s (Darling-Hammond, 2000; Seidel and Shavelson, 2007; Wayne and Youngs, 2003). Among these studies, since the flourishing of cognitive psychology in the 1980s, research has been particularly focused on teacher knowledge (Ball et al., 2001; Fennema and Franke, 1992; Hogan et al., 2003).

Currently, teacher professional knowledge is considered to be one of the core competencies of teachers (Baumert and Kunter, 2013). Within this knowledge, pedagogical content knowledge (PCK) proposed by Shulman (1986, 1987), which conceptualizes teacher-specific knowledge, has received particular attention. PCK is defined as follows: “It represents the blending of content and pedagogy into an understanding of how particular topics, problems, or issues are organized, represented, and adapted to the diverse interests and abilities of learners, and presented for instruction” (Shulman, 1987, p. 8). Shulman (1986) posited that PCK comprises two elements. The first is knowledge of instructional representations, which is considered to be the knowledge that effectively explains certain subject matter content. The second is knowledge of learners, which is the knowledge to judge what misconceptions or bugs students show about a subject's content and how difficult (or easy) the content is.

Since Shulman's original proposition, there have been efforts to expand upon the components of PCK, as evidenced by reviews conducted by Chan and Hume (2019) for science and Depaepe et al. (2013) for mathematics. Notably, mathematical knowledge for teaching (MKT) is a well-known example of such a concept. MKT pertains to the mathematical knowledge that educators require to effectively teach mathematics and is primarily composed of content knowledge (CK) and PCK (Ball et al., 2001). One of the distinguishing features of MKT is its subdivision of the CK essential to teachers into three subcategories: common content knowledge, specialized content knowledge, and horizon content knowledge. Additionally, aside from the two elements proposed by Shulman, knowledge of content and curriculum are also regarded as elements of PCK within the context of MKT. The concept of curriculum knowledge has also been proposed as a PCK element in other studies (e.g., Kind, 2009).

Great strides have been made, not only conceptually but also methodologically, toward attempting to examine teachers' PCK empirically since Shulman's proposal. Although qualitative studies based on limited classroom observations have been conducted (e.g., Alonzo and Kim, 2016; Oh and Kim, 2013; Seymour and Lehrer, 2006), quantitative studies have also been carried out with numerous participants through test sets measuring PCK in various domains of a subject since the 2000s. Ball and colleagues have employed MKT as a framework for empirical validation, and multiple quantitative studies have been reported to date (Hill et al., 2004, 2005, 2008). Additionally, tests designed for middle school mathematics (Baumert et al., 2010), biology, and physics (Großschedl et al., 2015; Sorge et al., 2019) have been developed. Large-scale projects such as the Cognitive Activation in the Classroom (COACTIV) project, conducted in Germany as a complementary survey to the PISA program (Baumert et al., 2013), and the Teacher Education and Development Study in Mathematics (TEDS-M) project, an international survey organized by the International Association for the Evaluation of Educational Achievement (IEA; Blömeke and Kaiser, 2014), have also been undertaken.

Quantitative research utilizing the PCK test has demonstrated that students achieve higher academic results when taught by teachers who exhibit greater PCK scores (Callingham et al., 2016; Keller et al., 2016; Lenhart, 2010). A longitudinal study was conducted in Germany as part of PISA 2003, with 4,353 9th grade students and 181 mathematics teachers participating (Baumert et al., 2010). The analysis revealed a positive relationship between teachers' PCK and students' mathematics performance at grade 10, with PCK having a larger impact on students' performance than CK [it should be noted, however, that studies such as those by Fauth et al. (2019) and Förtsch et al. (2018) reported no significant correlation between teachers' PCK and students' academic performance].

While PCK research has made progress, there have also been criticisms of the concept (see Depaepe et al., 2013 for a summary). For example, some researchers criticize that PCK is too static a view of teacher professionalism, and view PCK as more dynamic and more closely tied to actual classroom behaviors (Bednarz and Proulx, 2009; Mason, 2008; Petrou and Goulding, 2011). Cochran et al. (1993) proposed the concept of pedagogical content knowing (PCKg) instead of PCK and emphasized its dynamic nature. Although the authors acknowledge that the criticisms of PCK are important perspectives, we believe that they do not immediately invalidate the findings of PCK research. In response to the criticism of PCK static nature, recent studies have examined the relationship between static PCK and more dynamic teaching acts. These studies have found that PCK and teaching behaviors are positively related; namely, having rich PCK enables teachers to assess students' subject-based thinking and to provide effective instructions (Dreher and Kuntze, 2015; Kulgemeyer et al., 2020; Meschede et al., 2017). Thus, we suggest that PCK, even when measured statically, is important knowledge that serves as a basis for the dynamic performance of teachers.

Interventions for PCK and the purpose of this study

Considering the significant role of PCK, there have been numerous efforts to enhance the acquisition of PCK among teachers. Evens et al. (2015) conducted a systematic review of both quantitative and qualitative PCK intervention studies and found that most of these studies reported positive outcomes, indicating that the interventions had a beneficial effect on PCK development. The authors also identified five sources of PCK, namely:

(1) Educational experience: Having experience teaching actual students. In particular, early career teaching experiences are believed to promote the development of PCK (e.g., Simmons et al., 1999).

(2) PCK courses: Interventions that directly target PCK, such as thinking about what kind of misconceptions students might have and how teachers can address them (e.g., Haston and Leon-Guerrero, 2008).

(3) CK: Interventions targeting CK have also been used because having accurate and rich CK on the subject is a prerequisite for having PCK (e.g., Brownlee et al., 2001).

(4) Collaboration with peers: Collaboration among teachers, such as working together with other teachers to develop lessons and giving advice to each other (e.g., Dalgarno and Colgan, 2007).

(5) Reflection: Reflecting on one's own experiences and gaining new insights (e.g., Kenney et al., 2013).

Of these, educational experiences, PCK courses, collaboration with colleagues, and reflection were the methods most frequently mentioned in the studies, while CK was the least frequently mentioned (Evens et al., 2015).

Previous reviews have suggested the effectiveness of PCK interventions based on most studies reporting positive outcomes (e.g., Depaepe et al., 2013; Evens et al., 2015; Kind, 2009). However, these reviews failed to quantitatively measure the degree of effectiveness of such interventions. Given the problem that narrative reviews, in which researchers subjectively summarize the results of studies, lead to subjective interpretation of results (Borenstein et al., 2009), there is a need to quantify the effects of PCK interventions using meta-analysis, which can statistically integrate the results of prior studies and derive objective results. Although the development of quantitative studies examining the effects of interventions using the PCK test set has made it possible to conduct meta-analyses, no attempts have been made so far to integrate the results of the effects of PCK interventions.

To address the issue identified in previous studies that only conducted narrative reviews on PCK interventions, the first research question of this study was established: How effective have PCK interventions conducted in previous studies been? Specifically, we conduct a meta-analysis of intervention studies that have used the PCK test set to evaluate the effects of interventions on teachers of mathematics and science at the primary and secondary education stages. Previous studies on the PCK test have mainly focused on mathematics and science (Ball et al., 2008), and this study targets the same subject areas in primary and secondary education. We will include studies that use pre- and post-test comparisons at multiple time points, and multiple group comparisons such as experimental and control groups. As these are different study designs, we will integrate effect sizes based on these designs separately.

Furthermore, among studies that have conducted PCK interventions, some have reported positive effects (Rosenkränzer et al., 2017; Suma et al., 2019), while others have disclosed no effects (Luft and Zhang, 2014; Smit et al., 2017). This suggests that there may be variability in the effectiveness of PCK interventions across different studies. Therefore, this study examines the second research question: If high heterogeneity in effect sizes is observed, what factors explain this heterogeneity? Investigating this question will likely provide insights into the characteristics of effective intervention designs and materials that can promote the acquisition of PCK more effectively. To answer the second question, we also conduct meta-regression analysis examining the effects of moderators that may explain the variability of effect sizes for variables with a certain number of effect sizes. These moderators include teacher-related differences such as pre-service or in-service status and subject area and intervention-related differences such as intervention targets and duration.

Method

Recently, there has been an emphasis on the adoption of methods that improve transparency and reproducibility in conducting systematic reviews and meta-analyses, as highlighted by Polanin et al. (2020). The current study adheres to the Preferred Reporting Items for Systematic Review and Meta-Analyses (PRISMA; Pigott and Polanin, 2020) guidelines, which prioritize transparency and reproducibility in systematic reviews.

This study was conducted as part of a project focusing on quantitative studies of PCK, which included two groups of studies: (1) a survey study examining the association between PCK and other teachers' and students' variables and (2) an intervention study evaluating the efficacy of educational interventions in enhancing PCK (this study). While the integrative statistical analyses of the survey and intervention studies were conducted separately, the literature search and coding were conducted simultaneously without distinguishing between the two.

Review protocol

Prior to conducting the literature search, a review protocol was created and registered with the Open Science Framework (OSF). The protocol is available in Appendix A at the following URL: https://osf.io/vf4hq/?view_only=068483e4e82c42cd994e2c8174bd0a64. Next, the databases and search strings for the literature search were determined. Finally, we determined the procedures for screening titles and abstracts, coding the text, and performing the meta-analysis. However, these were modified as necessary during the course of the work.

Inclusion and exclusion criteria

This study employed the following seven inclusion and exclusion criteria.

Population

The population of interest in this study was teachers responsible for mathematics and natural science education in primary and secondary schools or students pursuing relevant teaching licenses. Thus, studies that targeted teachers in charge of subjects other than mathematics and natural sciences in primary and secondary education, such as early childhood education, higher education (university), and special-needs schools, were excluded.

PCK

Included in this study are studies that quantitatively measured PCK through tests or assignments, with scores treated as a continuous variable. However, studies that did not conduct quantitative scoring, even if they included PCK tasks, as well as qualitative studies consisting solely of episodes and qualitative analysis were excluded. Furthermore, the respondents in the studies were pre- or in-service teachers, and responses measured through third-party evaluations were not included.

PCK is a unique category of teacher knowledge in that it is a mixture of CK and pedagogical knowledge (PK). Therefore, studies that only measured CK or PK, despite being referred to as PCK, were excluded. Additionally, studies that employed abstract Likert-type questionnaires that lacked specific subject content were also excluded. However, studies using MKT, the test set developed by Ball and Hill for elementary school teachers (Hill et al., 2004, 2005, 2008), were included because it consisted of both CK and PCK items. Nonetheless, studies that combined CK and PCK scores into one score were excluded from the analysis. It should be noted that what is being discussed here is the criterion for the measurement of PCK and not the intervention. In other words, if PCK was accurately measured, studies that only intervened in CK were also included herein.

Study design

For this study, we included intervention studies that compared PCK scores using multiple measurements, such as studies with an experimental group that received an intervention and a control group that did not, or studies that measured PCK scores at pre-intervention and post-intervention time points. We excluded review articles or studies that relied on secondary data, as well as studies that measured PCK but only described its characteristics without conducting intervention. Studies explicitly aimed at enhancing professional knowledge other than PCK were excluded even if they conducted interventions (Harr et al., 2014, 2015). Studies measuring developmental changes in PCK across university years were included, as they can be considered broad intervention studies reflecting the effects of university education (e.g., Blömeke et al., 2014).

Statistics

The studies that provided information on the mean and standard deviation (or standard error and sample size) for each group or pre- and post-period were included in our analysis. Studies that did not report the necessary statistics were not automatically excluded, but we attempted to contact the authors to obtain the statistics or raw data. When the contact information for the first or corresponding author was not available online or if the author did not respond or declined to provide information, the study was excluded.

Time frame

The review included studies that were published after the proposal of PCK by Shulman in 1986.

Publication status

To avoid publication bias, the review included non-published papers such as conference proceedings and doctoral dissertations in addition to papers published in academic journals. However, conference presentations, master's theses, and books were excluded from the analysis. Books were excluded from the analysis due to their lack of original data and potential overlap with journal papers.

Language

The study included papers written in English and Japanese, the latter being the native language of the research group.

Literature search, screening, and data extraction

A systematic review was conducted to identify intervention studies examining the effectiveness of an education program to promote PCK acquisition among pre- or in-service teachers, in addition to survey studies. To this end, the literature search initially collected both intervention and survey studies on mathematics and science, which were later classified separately after screening.

Search targets

The primary search for relevant studies was conducted using online databases. To supplement this search, manual searches were conducted on the reference lists of PCK review articles and books with PCK in the title to ensure that all relevant references were identified.

Databases used

To gather a comprehensive collection of studies, we utilized representative databases (Web of Science) and a search engine (Google Scholar), as well as ProQuest Dissertations and Theses, which enables the exploration of doctoral dissertations, and Citation Information by the National Institute of Informatics (CiNii) for Japanese-language articles.

Search string

Electronic searches in Web of Science, ProQuest, and Google Scholar were conducted using the following character strings: (“pedagogical content knowledge” OR PCK OR “mathematical knowledge for teaching” OR “content knowledge for teaching mathematics”) AND (science OR sciences OR scientific OR chemistry OR chemical OR biology OR biological OR physics OR mathematics OR mathematic OR mathematical OR math) NOT (“technological pedagogical content knowledge” OR TPCK OR “technological pedagogical and content knowledge” OR TPACK OR “pedagogical technology integration content knowledge” OR PTICK). In CiNii, the following strings were used: (“pedagogical content knowledge” OR PCK OR “mathematical knowledge for teaching” OR “content knowledge for teaching mathematics” OR “授業を想定した教材内容知識” OR “授業を想定した教科内容の知識”).

Procedures

Figure 1 depicts the search process and its outcomes, which was conducted according to the PRISMA 2020 guidelines for systematic reviews (Page et al., 2021). The searches were conducted between April 13 and 23, 2021, using the Web of Science, Google Scholar, ProQuest, and CiNii databases. The first and fourth authors searched Google Scholar and CiNii, while the second and third authors searched Web of Science and ProQuest. The search results were cross-checked by two authors. Additionally, we conducted a manual search of the reference lists of relevant review articles and books. The search terms used in the database were also used to scrutinize the reference lists, leading to the identification of 33 papers. The searches resulted in a total of 7,409 hits; 3,257 duplicates and 929 ineligible records were removed, and 3,258 references were screened by adding the 33 references found through the hand search.

Figure 1

Figure 1. Search and results flow chart.

From May 21 to October 6, 2021, the titles and abstracts were reviewed by the members of the research team. After 10 papers were screened as practice, the remaining papers were distributed among the four authors for screening. Any uncertainties or disagreements were discussed by all team members, and the final decision was made by consensus. A total of 726 references were chosen for full-text preservation, of which 176 references were excluded because they were either inaccessible or behind a paywall in databases that were not covered by the authors' university contract. However, considering that the authors' university entered into a new database contract in June 2023, we reattempted to access the full texts of these 176 references from October 1 to 11, 2023. As a result, we were able to access the full texts of 121 of the 176 references, reducing the number of reports not retrieved to 55; thus, we conducted a full-text screening of 671 references.

From October 6, 2021 to January 14, 2022, we screened the full texts. After practicing the screening procedures for 15 references together, the four authors divided the references among themselves and worked on them separately. Then, all members discussed the cases in which there were doubts, and the final value was determined by consensus. The 121 references that were added later were screened by the first author between October 11 and October 30, 2023. Consequently, 598 articles were deemed ineligible for the following reasons: not in English or Japanese (Reason 1, n = 27), not empirical papers (Reason 2, n = 24), not the target sample (Reason 3, n = 20), PCK not quantitatively measured (Reason 4, n = 218), PCK not scored as a continuous variable (Reason 5, n = 136), and others. The remaining 74 articles were subject to coding for main texts.

From January 14 to February 4, 2022, the first round of coding was carried out. As we mentioned, in this study, we conducted a systematic review of both intervention studies that investigated the impact of interventions targeting PCK and survey studies that examined the relationship between PCK and other teachers' and students' related variables. Therefore, we first coded the type of studies to distinguish between intervention and survey studies. Between February 4 and April 8, 2022, the main coding process was carried out. When the coding method was confirmed with all members, three papers were coded as a practice to verify the coding method. Then, the papers were divided between the first and fourth author and the second and third authors, who discussed and coded the papers in pairs. Finally, the first, second, and third authors met to discuss and confirm the results of the coding. The literature added later was coded by the first author between February 14 and 29, 2024, during which nine articles met the screening criteria and five studies were coded. The data that were coded by the second and third authors were independently coded by the first author to determine the inter-rater agreement. Upon coding 11 studies and 42 effect sizes, the range of agreement was 88% to 100%, with kappa coefficients ranging from 0.81 to 1.00 (M = 0.98, SD = 0.05). Discrepancies were resolved through discussion between the first and second authors.

Six papers lacked the necessary statistics for the meta-analysis. The authors attempted to contact the authors of all six papers for which they could confirm the first author's contact information on the internet and received responses from three of them, one of whom provided raw data. This study (Luft and Zhang, 2014) was included in the meta-analysis. Note that when a longitudinal study design with three or more time points was used (e.g., Luft and Zhang, 2014), multiple effect sizes were extracted based on the difference between Time 3 and Time 2 in addition to the difference between Time 2 and Time 1. For studies with three or more groups (e.g., Rosenkränzer et al., 2017), we assigned experimental and control groups based on the description in the paper. As a result, of the 74 studies, 49 were survey studies; therefore, 25 intervention studies were included in this study.

Coding variables

The main coding variables of the study were as follows.

Variables related to the surface characteristics of the study: (1) the year of publication of the article, (2) the country in which the study was conducted, and (3) the publication status of the study.

Characteristics related to the sample: (1) teacher status (pre- or in-service teachers), (2) school type of the teachers (classified according to the notation in the paper), (3) subject specialization of the teachers, and (4) years of teaching experience of the teachers.

Characteristics related to the measurement of PCK: (1) elements of PCK (knowledge of instructional representations, knowledge of learners, or others), (2) subject domain (number and computation, functions, physics, chemistry, etc.), (3) test format (multiple choice, free description, or others), (4) level of representations measured (memory level or transfer level), and (5) number of PCK test items. Note, however, that for a majority of the effect sizes (92%), information regarding the level of representation (transfer level vs. memory level) assessed in the PCK test was unavailable and hence was not considered in the subsequent analyses.

Characteristics related to the intervention of PCK: (1) intervention target (CK, knowledge of instructional representations, knowledge of learners, or others) and (2) intervention method. For the intervention methods, based on a review by Evens et al. (2015), we addressed four activities as follows. The first is collaborative activities that involve peer collaboration, such as discussions among participants. The second is practical activities that involve one's own or others' educational practices, such as mock classes or classroom observations. The third is theoretical activities that provide theoretical knowledge about subjects or education, such as lectures by researchers. Fourth is reflection, which involves ex post discussions of one's own or others' practice. (3) Intervention duration. The duration of the intervention was coded as follows based on the description in the article: several hours (1–6 h), several days (6–10 h), several weeks (10–30 h), several months (30 h or more per month), and years (a period of more than 1 year). (4) Study design (one group pre-post comparison design, or two groups post comparison design, and others).

Statistics: (1) mean, SD, sample size, and others for the posttest of the experimental group, (2) mean, SD, sample size, and others for the posttest of the control group, (3) mean, SD, sample size, and others for the pretest of the experimental group.

Analytical procedures

We employed the dmerat (version 0.0.9000), meta (version 6.0-0), and metafor (version 3.8-1) packages for R (version 4.2.1) to conduct statistical analyses. The R script containing all the reported analyses (Appendix B) and the raw data file used in the analyses (Appendix C) can be accessed from the aforementioned URL of OSF.

Criteria for integration of effect sizes and the model to be employed

To calculate the effect size, Hedges' g was used, which represents the effect size between two independent groups. Hedges' g is calculated by adding a small sample correction to Cohen's d. The effect of the correction is particularly large when the sample size is small (n < 20). Note that in studies with multiple time point comparisons, the data between time points are not independent because the same individual was measured several times. To calculate the effect size using paired data, we need not only the mean and standard deviation of each time point but also the correlation coefficient between time points, which was not reported in most studies. Therefore, in this study, Hedges' g was used as the effect size even for studies with designs based on multiple time point comparisons.

The effect sizes obtained were synthesized using the random-effects model to estimate the overall effect size of the study. Borenstein et al. (2009) state that it is generally appropriate to apply a random-effects model, unless the researchers, populations, and procedures are all the same. Additionally, Harrer et al. (2021) point out that in the field of social sciences, a random-effects model is often employed because heterogeneity in studies is always assumed; therefore, it is customary to always use a random-effects model.

Methods of analysis in the integration of effect sizes

The study used four methods to calculate the integrated effect size: (1) baseline method (simple random-effects model), (2) trim-and-fill method, (3) outlier removal method, and (4) three-level model method. The first method (baseline method) integrated all effect sizes based on a random-effects model (Borenstein et al., 2009). The second method (trim-and-fill method) was employed when the asymmetry test (Egger test) was significant (Egger et al., 1997), where pseudo data were added to create a symmetrical distribution of the effect size around the mean, followed by integration. The outlier removal method excluded effect sizes outside the 95% confidence interval of the mean effect size of the baseline as outliers before integration (Viechtbauer and Cheung, 2010).

The second and third methods address the issues of asymmetry or outliers in the collected effect sizes. However, a related issue caused by the nested structure of effect sizes has been recognized by researchers in the field of meta-analysis. In many meta-analyses, effect sizes are nested within studies, resulting in non-independent data when multiple effect sizes are reported within a study. To address this issue, the fourth method (the three-level model method) was employed to calculate integrated effect sizes while accounting for the nested structure of effect sizes (Harrer et al., 2021). Ignoring the nested structure of data within study clusters is known to introduce bias in effect size estimation (Becker, 2000). Therefore, the fourth method was used to integrate effect sizes while taking the nested structure into account.

Evaluating heterogeneity

To assess the heterogeneity in effect sizes across studies, we utilized the I² statistic (Higgins et al., 2003). The study by Higgins et al. (2003) proposed that I² values equal to 25%, 50%, and 75% indicate low, moderate, and high heterogeneity, respectively. We estimated the heterogeneity variance τ² using REML estimators (Viechtbauer, 2005). To calculate the confidence intervals for the pooled effects, we employed the Knapp-Hartung adjustment (Knapp and Hartung, 2003).

Meta-regression analysis

When high heterogeneity was observed and there were more than 10 effect sizes available for each level of the variables, the researchers conducted a meta-regression analysis to investigate the study characteristics (moderators) that caused the heterogeneity (Borenstein et al., 2009). The model for the meta-regression analysis is represented by Equation 1.

\begin{array}{l} {\hat{θ}}_{k} = θ + β_{1} x_{1 k} + \dots + β_{n} x_{n k} + ϵ_{k} + ζ_{k} & (1) \end{array}

Equation 1 corresponds to a random-effects model in which the estimated effect size ${\hat{θ}}_{k}$ of study k is expressed by a linear combination of the intercept θ, the product of the moderation variable x_nk and regression coefficient β_n, and the sampling error ζ_k. The researchers used the maximum likelihood method to estimate the models. If the regression coefficient test in the adopted model is significant at the 5% level, the moderation variable is considered to have a significant effect. In the meta-regression analysis, data containing missing values were subject to list wise deletion. Therefore, note that the number of sample size in meta-regression analysis is smaller compared to other analyses.

Results

Characteristics of the collected studies

Table 1 provides an overview of the key characteristics of the 25 studies that were included in this study. The majority of the studies were published after 2010, and there has been a noticeable increase in the number of quantitative PCK intervention studies in recent years. The United States was the most common country of publication, contributing nearly half of the total studies, with Germany being the second most common location, with five studies. The studies were predominantly published in academic journals. Approximately half of the studies involved pre-service teachers, while the other half included in-service teachers. There was an almost equal number of studies focused on mathematics and on science. The most common intervention design was a one-group pre-post comparison design, which was used in 15 studies. In contrast, a total of 10 studies used multiple groups comparison designs.

Table 1

Table 1. Characteristics of the sampled studies (n = 25).

In the subsequent sections, we divided the analysis into effect sizes based on multiple group comparison designs and those based on multiple time point comparison designs and analyzed each effect size separately. Initially, we provided a summary of the descriptive features of the tests and interventions and then reported results regarding the integration of effect sizes and meta-regression analysis.

Analysis of effect sizes based on multiple group comparison design

First, we focused on the characteristics of PCK tests and interventions in the effect sizes presented in multiple group comparison designs (k = 42). In Table 2, we outlined the features of the PCK tests, with many studies measuring a single component of PCK (k = 27) and about 30% studies measuring multiple components (k = 14). The majority of the effect sizes came from science tests, with fewer from mathematics. This disparity was because the majority of papers that reported a significant number of effect sizes were from science studies. While half of the test formats were descriptive tests, only a small number were multiple-choice or interview tests. The number of items on the PCK test varied significantly, ranging from 2 to 58, with 5 being the most common.

Table 2

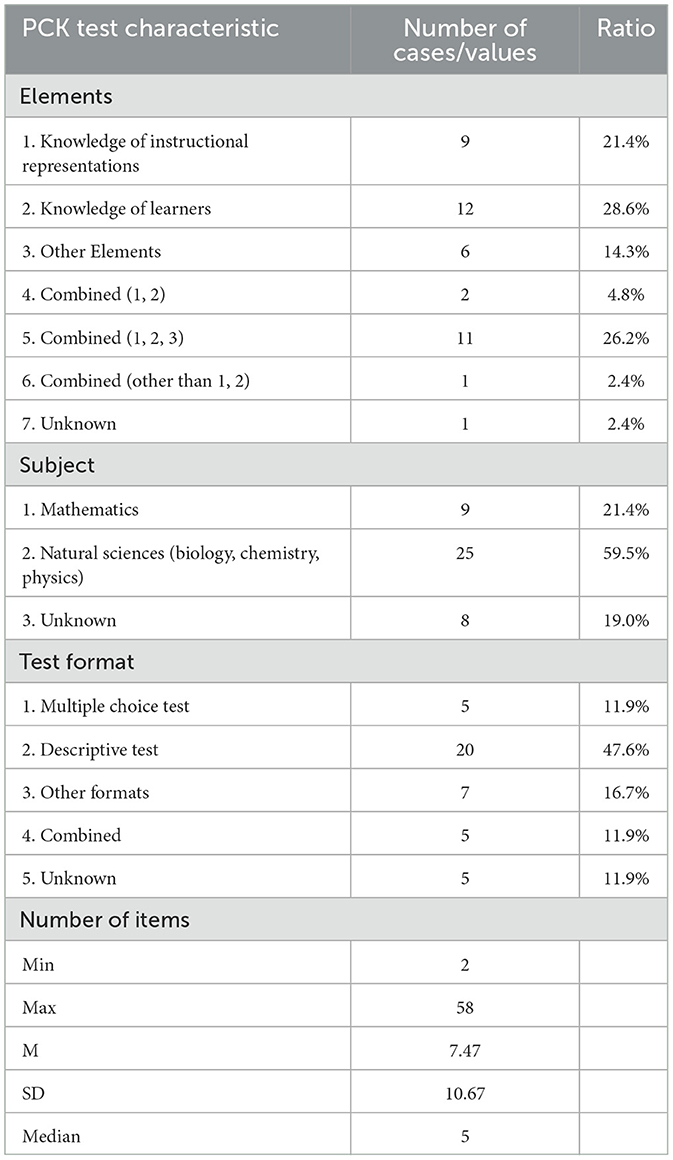
Table 2. Characteristics of the PCK test in effect sizes reported in multiple group comparison designs (k = 42).

Table 3 presents the characteristics of interventions used in the effect sizes. While few educational methods used in the interventions were classified in terms of specific characteristics, many of them combined multiple characteristics. Thus, in addition to the number of effect sizes classified only as specific characteristics, we reported the number of effect sizes with individual characteristics among those that combined multiple characteristics. As a result, the ratios in the intervention targets and educational methods in Table 3 exceeded 100%. Of the 42 effect sizes, 15 targeted only CK in their interventions. On the other hand, many of the studies that had multiple types of knowledge as their intervention target, directly targeted PCK as well as CK. Of these, knowledge of learners were the most frequently targeted components of PCK. The majority of interventions were designed using multiple methods, with lectures by researchers being the most common (29 cases), followed by collaborative activities (27 cases), practical activities (15 cases), and reflection (12 cases). There were no studies that conducted interventions over short periods such as hours or days; the most common duration for interventions was in weeks. More than 20% of each variable was unknown, and many of the studies did not specify the details of the intervention.

Table 3

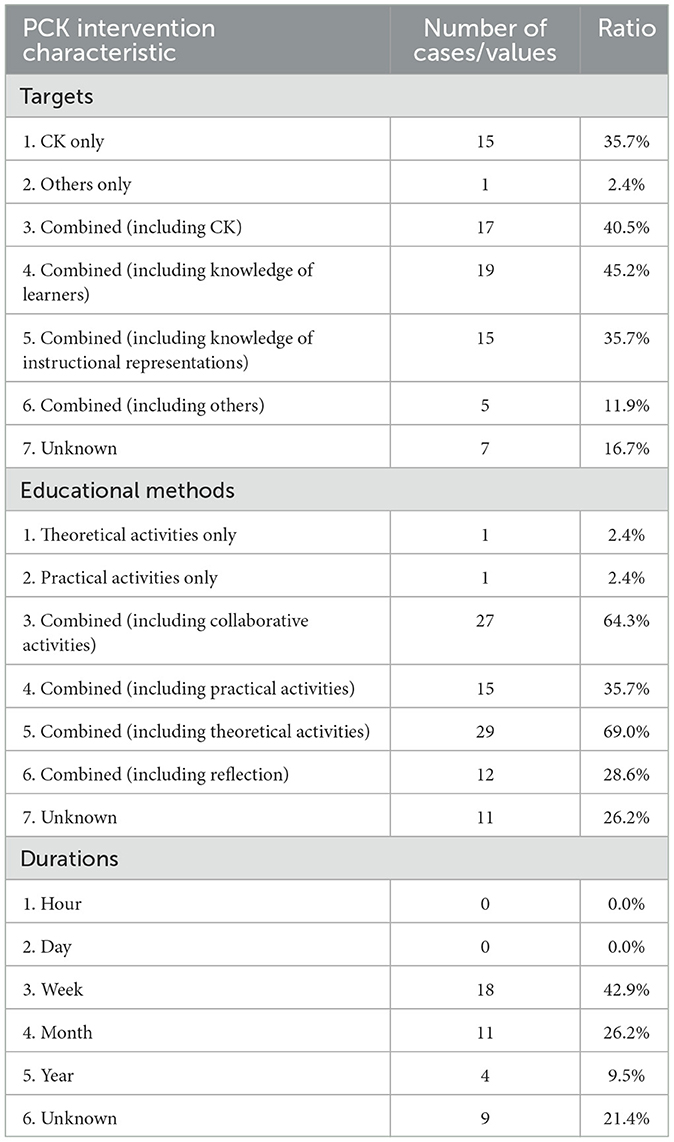
Table 3. Characteristics of the PCK intervention in effect sizes reported in multiple group comparison designs (k = 42).

Furthermore, an analysis was conducted to synthesize the effect sizes obtained from studies that utilized multiple group comparison designs. The forest plot is shown in Figure 2, and the statistics based on the four models are shown in Table 4. In the forest plot, the effect sizes extracted from the included studies are displayed in ascending order. The squares and the horizontal lines represent each effect size and its 95% confidence interval, respectively. The diamond at the bottom of the plot indicates the overall effect size and its 95% confidence interval, as aggregated by the random-effects model. The vertical line at the center of the plot represents an effect size of 0, which serves as the reference line for determining the significance of the effect sizes. In Figure 2, the left edge of the diamond crosses this reference line, indicating that the effect of the intervention is significant.

Figure 2

Figure 2. Forest plot of effect sizes based on multiple group comparison design.

Table 4

Table 4. Results of the integration of effect sizes of multiple group comparison design based on four models.

Table 4 presents the results of effect size integration for each of the four models. The table sequentially displays the sample size (k), the effect size (g) with its 95% confidence interval, and the significance probability (p). The 95% prediction interval (PI) indicates the range within which future observations are expected to fall. This interval predicts the range of effect sizes that may be observed in subsequent studies based on the results obtained from the meta-analysis (Borenstein et al., 2009). The I² statistic measures the extent of heterogeneity in the meta-analysis. As shown in Table 4, the integration of effect sizes using the random-effect model indicated that the intervention in the experimental group led to higher performance on the PCK test than the control group, with an expected effect size of g = 0.74 (95% CI [0.51, 0.97]). However, high heterogeneity was confirmed between the studies, with an I² value of 84% (95% CI [79%, 88%]).

The Egger test yielded a significant result [t₍₄₀₎ = 2.12, p < 0.05], indicating asymmetry in the effect size distribution. Thus, the trim-and-fill method was employed, which yielded a lower expected effect size of g = 0.59 (95% CI [0.33, 0.85]) than the baseline model. Additionally, an analysis that excluded outliers based on confidence intervals yielded an expected effect size of g = 0.67 (95% CI [0.48, 0.85]). Although the expected effect size was slightly lower than the baseline model, the difference was not substantial. Finally, the three-level model produced a mean effect size of g = 0.63 (95% CI [0.28, 0.98]). Although the effect size was smaller than the other two models, it may be attributed to the study-level variation caused by large effect sizes reported by some studies such as Rosenkränzer et al. (2017), as indicated by estimated variance components of τ² Level 3= 0.17 and τ² Level 2= 0.23. This indicates that I² Level 3 = 36% and I² Level 2 = 48% of the variation were attributed to intercluster and intracluster heterogeneity, respectively. The three-level model provided a better fit than the two-level model (χ² = 11.93, p < 0.001).

To account for the substantial heterogeneity in the effect sizes observed across studies, a meta-regression analysis was conducted to identify the variables that may explain these differences. The study included independent variables of teachers' countries (USA teachers vs. German teachers), teachers' teaching experience (in- vs. pre-service teachers), PCK test components (single vs. multiple components), intervention targets (CK only vs. multiple elements including PCK), and intervention duration (less than weeks vs. longer than months) for the more than 10 samples under each condition. Table 5 presents the results of the meta-regression analyses of the variables accordingly. The effect of intervention targets (CK plus PCK Intervention) was significant (Table 5), indicating that interventions targeting PCK were found to enhance the effectiveness of the intervention compared to interventions that focused on CK alone (p = 0.01). On the other hand, differences in teachers' countries, teaching experience, PCK test components, and intervention duration did not have a significant effect on the results.

Table 5

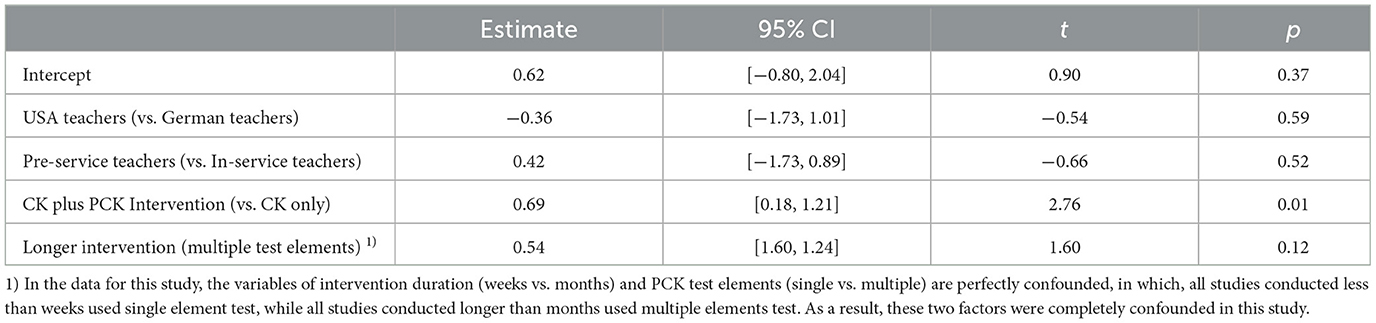
Table 5. Results of the meta-regression analysis for the effect sizes of multiple group comparison design (k = 29).

Analysis of effect sizes based on multiple time point comparison design

We also summarized the characteristics of PCK tests and interventions in the effect sizes reported in multiple time point comparison designs. Table 6 shows the characteristics of the PCK tests. The data showed that approximately 60% of the PCK tests evaluated a single element (37 cases), while the rest assessed multiple elements (22 cases). Science was the main subject, but mathematics accounted for about 20% of the PCK tests, similar to those in the multiple group comparison design studies. The most common test format was descriptive tests, and there were few multiple-choice or other types of tests, such as interviews. The number of PCK items varied considerably from 2 to 58, with 5 being the most commonly used.

Table 6

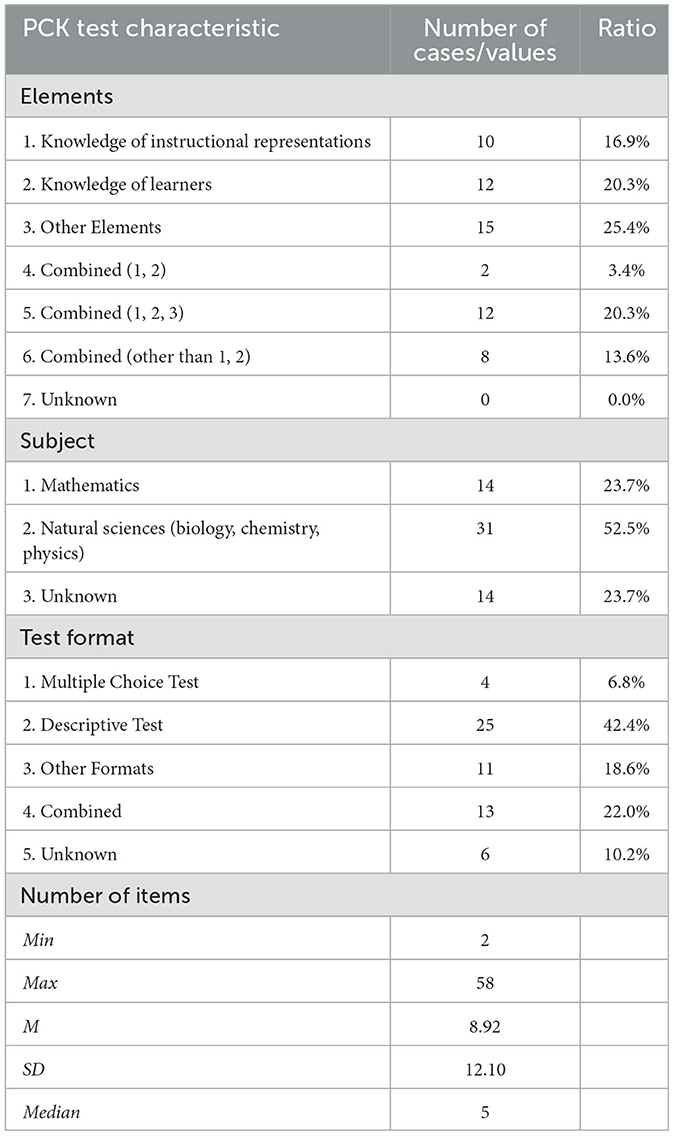
Table 6. Characteristics of the PCK test in effect sizes reported in multiple time comparison designs (k = 59).

Table 7 provides a summary of the characteristics of interventions used in the targeted effect sizes. On the intervention targets, 11 cases solely focused on CK, while the remaining interventions targeted multiple types of knowledge, with many of them directly addressing both PCK and CK. Of these, knowledge of instructional representations and knowledge of learners were addressed in 24 cases each. Furthermore, all interventions utilized more than one educational method, with collaborative activities being the most commonly used (39 cases). The second most common were theoretical activities led by researchers (30 cases), followed by practical activities such as class observation (25 cases) and teacher reflection (16 cases). The majority of interventions lasted for weeks, but some were conducted over several months or years. As with the group comparison design, many variables were unknown, such as the intervention targets in 34% of the effect sizes.

Table 7

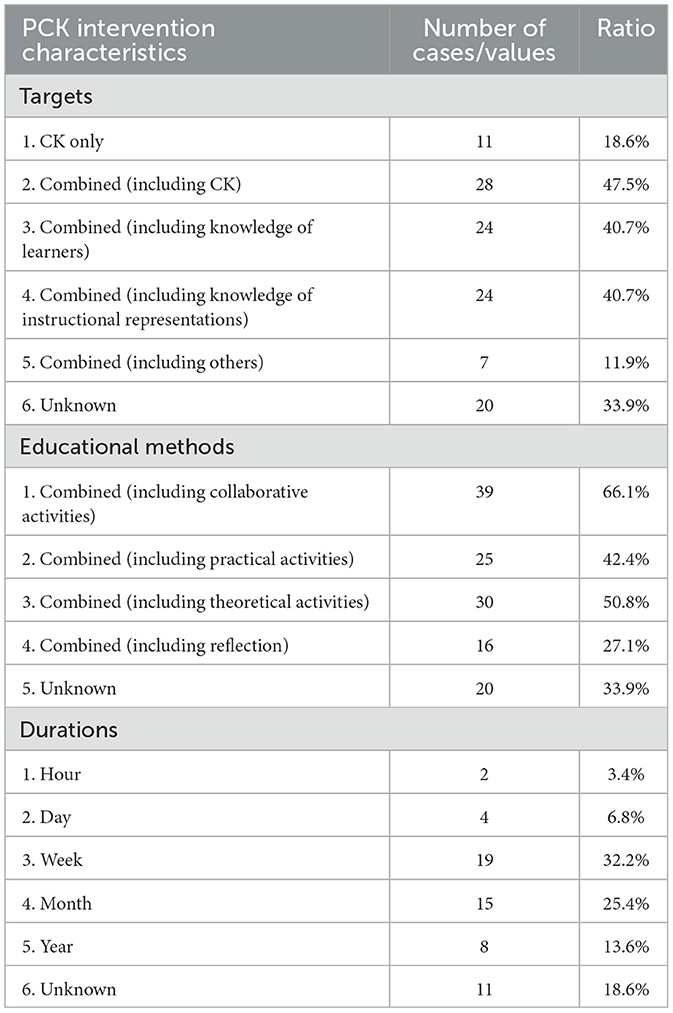
Table 7. Characteristics of the PCK intervention in effect sizes reported in multiple time comparison designs (k = 59).

Furthermore, an analysis to combine the effect sizes obtained from the studies in the multiple time point comparison design was conducted. The forest plot for this analysis is presented in Figure 3, and the statistics for the four models are displayed in Table 8. As shown in Table 8, the results of random-effects model indicated an expected improvement in PCK scores from pre- to post-intervention, with an effect size of g = 0.90 (95% CI [0.71, 1.10]). However, the high I² value of 87% (95% CI [85%, 90%]) indicated significant heterogeneity among the studies. Additionally, the Egger test yielded a significant result [t₍₅₁₎ = 5.25, p < 0.001], indicating asymmetry in the effect size distribution. Thus, the trim-and-fill method was employed, which yielded a lower expected effect size of g = 0.44 (95% CI [0.18, 0.69]) than the baseline model. A subsequent analysis that excluded outliers based on confidence intervals yielded an expected effect size of g = 0.91 (95% CI [0.73, 1.09]), which was similar to the baseline model.

Figure 3

Figure 3. Forest plot of effect sizes based on multiple time comparison design.

Table 8

Table 8. Results of the integration of effect sizes of multiple time comparison design based on four models.

The effect sizes obtained from the three-level meta-analytic model had a mean value of g = 0.79 (95% CI [0.49, 1.09]). Although this effect size was smaller than that obtained from the other two models, this was likely due to accounting for variation between studies that report several high effect sizes. The estimated variance components were τ² Level 3 = 0.33 and τ² Level 2 = 0.11, indicating that I² Level 3 = 68% of the variation was due to intercluster heterogeneity, and I² Level 2 = 22% was due to intracluster heterogeneity. The three-level model showed a better fit than the two-level model (χ² = 29.96, p < 0.001). The magnitude of the effect sizes differed among the models, with the trim-and-fill and three-level model analysis methods yielding lower effect sizes than the other models. This suggests the need for more studies, including those in which sufficient intervention effects were not obtained. However, all models indicated a positive effect size, indicating that the intervention was effective in improving teachers' PCK.

To account for the high level of heterogeneity observed across the studies, a meta-regression analysis was conducted to identify the variables that may explain the variations in the effect sizes. The meta-regression analysis included more than 10 studies for each condition, and the following independent variables were entered into the analysis: teachers' countries (USA teachers vs. German teachers), teachers' teaching experience (in- vs. pre-service teachers), PCK test components (single vs. multiple components), subject measured by PCK test (mathematics vs. science), intervention targets (CK only vs. multiple elements including PCK), and intervention duration (less than weeks vs. longer than months). Only the regression coefficient for the subject measured by PCK test (Science PCK vs. Math PCK) was statistically significant (Table 9), indicating that interventions had a greater effect when the subject was science compared to mathematics (p = 0.04). On the other hand, differences in teachers' countries, teaching experience, PCK test components, intervention targets, and intervention duration did not have a significant effect on the results.

Table 9

Table 9. Results of the meta-regression analysis for the effect sizes of multiple time comparison design (k = 33).

Discussion

This study conducted a systematic review and meta-analysis of quantitative PCK studies to investigate the effects of teacher PCK interventions in mathematics and science education at elementary and secondary levels. The review involved searching representative research databases and collecting 101 effect sizes from 25 studies, including 42 effect sizes for multiple group comparison designs and 59 effect sizes for multiple time point comparison designs. While several studies have examined PCK interventions since their proposal by Shulman (1986), most of the studies included in this review were conducted after 2010, and studies that quantitatively examined the effects of PCK interventions using PCK tests were relatively recent. Therefore, the number of effect sizes collected was not extensive, which is a limitation of this study that will be further discussed.

When effect sizes were integrated, the expected effect size for the multiple group comparison design was 0.74 (baseline model), with higher PCK scores for the experimental group receiving the intervention than for the control group not receiving the intervention. The expected effect size for the multiple time point comparison design was 0.90 (baseline model), indicating higher scores on the PCK test measured after the intervention compared to the scores measured a priori. This result confirms the claim in previous reviews (e.g., Depaepe et al., 2013; Evens et al., 2015; Kind, 2009) that have argued for the effectiveness of PCK interventions. However, these reviews did not quantify the extent to which PCK interventions were effective. The results of the present study show that the PCK intervention has a large effect in both designs. On the other hand, estimates based on the three-level model tended to be smaller than the baseline model, with g = 0.63 for the multiple group comparison design and g = 0.79 for the multiple time point comparison design. This is because a large number of effect sizes were reported in a single study. For example, Rosenkränzer et al. (2017) reported 18 effect sizes in each design, which included very high effect sizes. The three-level model takes into account the study level, which relatively weakens the effect of studies reporting more than multiple effect sizes. Therefore, the multilevel model can be interpreted as having lower effect sizes than the baseline model.

Comparing the two designs, higher effect sizes were found in the multiple time point comparison design than in the between-group comparison design. In many cases of multiple group comparison designs, teachers, even in a control group, participated in some learning programs (e.g., Luft and Zhang, 2014; Strawhecker, 2005; Yang et al., 2018). For example, in Roth et al. (2019), teachers in the control group participated in a program to deepen their content knowledge, as opposed to those in the experimental group who engaged in activities to analyze their own and others' classroom videos over a 1-year period. Control group teachers engaged in a variety of content-deepening learning activities that they then implemented in their classrooms. Thus, in the multiple group comparison design, the difference between the two groups tended to be smaller. On the other hand, in the multiple time point comparison design, the scores before receiving the intervention are used as the point of comparison, so the intervention effect is likely to be more pronounced.

On the other hand, there was large heterogeneity in each intervention, as expressed in the I² values. Therefore, in this study, we conducted a meta-regression analysis to test which factors could explain the variation in effect sizes. The analysis of multiple group comparison design revealed effects across intervention targets (CK-only vs. CK plus PCK intervention), with higher effects for the intervention including PCK as well compared to the CK-only intervention. Many studies on PCK have targeted CK based on the assumption that CK is necessary for teachers to acquire PCK (Abell, 2008; Gess-Newsome, 2013). However, studies that rigorously tested this hypothesis through experiments reported that teaching CK to teachers had minimal effects on PCK and that direct instruction in PCK was more effective (Evens et al., 2018; Tröbst et al., 2018). The results of this study can be seen as corroborating these experimental findings through meta-analysis.

On the other hand, the result with data of multiple time point comparison design showed the effect of subject measured by PCK tests, indicating that interventions had a greater effect when the subject was science compared to mathematics. This result can be attributed to educational activities specific to the science domain that are not typically conducted in mathematics. Hands-on activities, whereby teachers themselves conduct scientific experiments or computer simulations, are used more frequently in professional development for science education than for mathematics education. Several studies have actually introduced these activities to enhance teachers' PCK (Kanter and Konstantopoulos, 2010; Rosenkränzer et al., 2017; Yang et al., 2018). However, various other differences exist between PCK studies in mathematics and science. In studies focusing on mathematics, for example, tests often cover a wide range of topics, such as functions and quantities, rather than specific contents (e.g., Copur-Gencturk and Lubienski, 2013). In contrast, science studies often focus on specific domains such as biology or chemistry, and within those domains, some of the studies address specific topics like photosynthesis (e.g., Gess-Newsome et al., 2019). This difference may lead to more pronounced effects of the interventions in science rather than mathematics.

Finally, we discuss the remaining issues of this study. First, it is necessary to clarify the effects of interventions that were not addressed in the meta-regression analysis of this study, such as the characteristics of the intervention method. Even if the interventions have the same elements and duration, their effects are expected to vary depending on the method used in the intervention. For example, in Roth et al. (2019), one feature of the intervention in the experimental group was a video recording of a model lesson or their own lesson and an activity to watch it. However, this study has not been able to examine the effects of these activities. It has been noted that even in the whole area of professional development research of teachers, demonstrating the effectiveness of intervention methods has not always been successful (Garet et al., 2001; Hill et al., 2013). Although we were unable to examine the effects of methods in the studies included in this study because the number of effect sizes were limited, future studies should clarify the effects of characteristics in the intervention methods on the acquisition of PCK.

Second, it is assumed that not only the characteristics of the intervention but also the characteristics of the evaluation (how PCK is assessed) might affect the effect size of the intervention on PCK (e.g., Copur-Gencturk and Lubienski, 2013). In addition to the elements of PCK, the present study also reported the proportion of PCK formats (multiple-choice, open-ended, and other formats). Since it is assumed that the degree to which teachers themselves have to utilize their knowledge is great in the open-ended format (e.g., Fukaya and Uesaka, 2018), the effect of the intervention could be evaluated more clearly in the non-multiple-choice format. However, we were not able to examine such effects in this study, so further studies are expected in the future.

In addition, the transfer of learning needs to be examined as an perspective that has not been focused on in previous studies (for literature on the transfer of learning, see Bransford et al., 1999; Haskell, 2001; Mestre, 2005). Transfer of learning goes beyond simply remembering what has been learned and refers to applying what has been learned in a new task. In teacher education, teachers are expected to apply the knowledge and skills acquired in training and university to content not covered in their classroom. Therefore, what is expected in PCK interventions is not just recall but transfer of what they learn in the interventions. It would be important to distinguish in intervention studies whether the index used for evaluation is at the mere memory level or at the transfer level (i.e., whether it includes content not covered in the intervention). As revealed in this study, few studies to date have explicitly explained how the measures used in the evaluation relate to the intervention, so we could not determine whether the evaluation index was at the transfer level or not. It seems essential for future studies to specify the key features of the intervention or evaluation in the paper, including whether they evaluated the transfer of learning.

Author's note

References marked with an asterisk indicate studies included in the meta-analysis.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

TF: Conceptualization, Data curation, Investigation, Methodology, Supervision, Writing – original draft, Writing – review & editing. DN: Data curation, Investigation, Methodology, Software, Writing – original draft, Writing – review & editing. YK: Data curation, Investigation, Writing – original draft, Writing – review & editing. TN: Data curation, Investigation, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by JSPS KAKENHI Grant Number 19K21773.

Acknowledgments

We are grateful to Dr. Julie A. Luft for her help with providing the raw data. During the preparation of this work the authors used DeepL and Chat GPT (GPT-4, OpenAI) in order to improve language and readability. After using these services, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abell, S. K. (2008). Twenty years later: does pedagogical content knowledge remain a useful idea? Int. J. Sci. Educ. 30, 1405–1416. doi: 10.1080/09500690802187041