
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Educ. , 31 July 2024
Sec. STEM Education
Volume 9 - 2024 | https://doi.org/10.3389/feduc.2024.1425307
This article is part of the Research Topic Mathematical Thinking, Practices, and Processes in Non-formal Learning Environments View all 8 articles
Introduction: Prior research has documented students’ struggles in conceiving of angle and angle measurement, which may stem from textbook and curriculum representations of angles as static. In this study, we examined grade 3-5 students’ mathematical thinking of angle during an educational robotics task implemented within a making space learning environment in a school setting (i.e., hybrid making space).
Methods: Our analysis included 19 video recordings of six groups of students in grades 3-5.
Results: Results from this study demonstrate how students negotiated a shared understanding of angle through multiple epistemic tools (e.g., gestures, bodily actions, language) that were situated and contextualized within the task. This included developing a shared language, conceptualizing angle as a dynamic entity, and perceiving angle through directionality and degree measures.
Discussion: We contend that learning experiences within a hybrid making space provide young students with opportunities to engage in mathematics as a social phenomenon and human activity.
Mathematics classrooms are often environments that marginalize learners who are not able to express their mathematical thinking and reasoning with precision or accuracy (Civil and Hunter, 2015; de Araujo et al., 2018; Ryan and Chronaki, 2020). This in return leads to feelings of isolation and an underdeveloped STEM identity, loss of confidence and efficacy, reduced access to advanced mathematics courses, and limited exposure to non-traditional instructional strategies (Danielak et al., 2014; Berry, 2015; Collins et al., 2020; Rittle-Johnson et al., 2021). With an increase of making spaces in formal school settings on an international scale (Hynes and Hynes, 2018), it is worth considering the potential of these learning environments for supporting students’ growth as mathematics learners. Making spaces are broadly defined as a physical environment that provides a variety of materials and tools to support individuals or groups to collaborate, to make things, to create new knowledge, or to solve problems” (Mersand, 2021, p. 175). Recent research highlights how making spaces can serve as sites to engage students in mathematical practices (e.g., problem solving) and cultural and intuitive approaches to mathematics (e.g., informal measurement) that are foundational for students’ thinking about and understanding of mathematical concepts (Doorman et al., 2019; Komarudin et al., 2021; Simpson and Kastberg, 2022).
As such, our initial analysis of students’ mathematical participation in a making space focused on examining student’s mathematical play through failure and feedback loops in making space contexts (Shokeen et al., 2020). However, through our ongoing analysis, we observed other mathematical phenomenon such as students’ language and perception around angle, their intuitive ideas of length measurements as long and short, and algorithmic thinking through trial and error experiences. Prior research has documented students struggles in conceiving of angle and angle measurement (Tanguay and Venant, 2016; Rahayu and Jupri, 2021), which may be due to the static definition of angle more commonly introduced in textbooks and curriculum (Keiser, 2004; Alyami, 2020). Therefore, we revisited the video data to address the following research question: How do students in grades 3–5 utilize epistemic tools to negotiate a shared understanding of the concept of angle within a non-formal learning environment?
In this study, epistemic tools include a variety of representations and models (e.g., symbolic, gestures, tangible objects) utilized by students for knowledge construction (Kelly and Cunningham, 2019; Mathayas et al., 2019; Ke et al., 2020). Results from this study demonstrate how students negotiated a shared understanding of a complex mathematical concept (Alyami, 2020) - angle -through multiple epistemic tools that were situated and contextualized within an educational robotics task. We argue that learning experiences within a hybrid making space1 provide young students with opportunities to engage in mathematics as a social phenomenon and human activity. Students should be provided with joint opportunities and a range of tools and manipulatives, including their bodies, to support and facilitate their understanding of mathematical concepts. Moreover, we contend that such mathematics is likely hidden within the process of the task as it differs from most school classrooms that are bounded by academic assessments and void of authentic problems (Nemirovsky et al., 2017). Therefore, the significance of this study lies in the potential for hybrid making spaces to support the learning of mathematics in school environments.
To situate this study, we considered prior scholarship on educational robots, the complex nature of angle, and various ways to think about epistemic tools to facilitate knowledge-building practices.
Educational robots in this study are defined as the conception and implementation of robots as a pedagogical tool for the development of students’ understanding of disciplinary content, skills, and practices (Muñoz et al., 2020), and a common feature of making spaces (Oliver, 2016). Research has highlighted the potential for educational robots to develop K-8 students understanding of a variety of mathematical concepts and practices including proportional reasoning (Alfieri et al., 2015), algebra concepts (Ardito et al., 2014), computational thinking (Angeli and Valanides, 2020), and spatial, measurement, and number concepts (Shumway et al., 2023). Research regarding educational robots and students’ understanding of angle can be traced back to LOGO, a programming language designed for young learners to control the movement of a turtle (Filippaki and Papamichael, 1997; Clements and Burns, 2000). This research highlighted the benefits of LOGO in the development of students understanding of turn concepts (e.g., rotation and direction) and turn or angle measurements (Clements and Battista, 1989). For example, Clements and Burns (2000) described students’ ability to transition from physical movements to represent rotations to a mental image. More recently, Min-Chi et al. (1996) and Kim et al. (2021) has argued for the inclusion of educational robots to support students’ development of angle as a mathematical concept. The inclusion of a hands-on approach of manipulating a robot, as well as using a digital measurement compass to program the robot, afforded students the ability to understand special angle pairs (e.g., complementary angles; Kim et al., 2021) and angle as a dynamic entity (Min-Chi et al., 1996).
Angle is a prominent feature of two-dimensional figures, which make it important to provide students with opportunities to carefully explore the idea of angle prior to beginning elementary grades. As suggested by Mitchelmore and White (1998), understanding angle as a concept involves three stages: (a) situated angle concepts developed through play and social experiences prior to formal schooling (e.g., walking up and down inclines), (b) contextual angle concepts in which children notice commonalities of an angle concept in a variety of contexts (e.g., sloping situations), and (c) abstract angle concepts that involves developing a standard general angle concept that represents more than one context (e.g., recognizing right angles in several angle contexts).
However, developing the understanding of angle concept is complex (Keiser, 2004; Tanguay and Venant, 2016; Alyami, 2020). Common Core State Standards Initiative, 2021 in the United States places ‘angle’ measure in fourth grade. Students are expected to recognize angle measure in degrees as “the fraction of the circular arc between the points where two rays intersect the circle” (p. 31). Students are then expected to measure angles using a protractor (Common Core State Standards). Similar standards can be found in other countries such as Year 5 in Australia (Australian Curriculum, Assessment and Reporting Authority, 2024) and England (Government Digital Services, 2021). But many upper-elementary students struggle in understanding the concept of angle (Browning et al., 2007). For instance, if only sharpness is considered as the quality of angle, then students may consider an obtuse angle as “less of an angle” (Keiser, 2004, p. 292). Or focusing on the rays of an angle lead students to perceive the size of the angle as affected by the rays’ length (Mitchelmore and White, 1998; Tanguay and Venant, 2016). Or students have a difficult time conceptualizing turning within rotation and hinge situations as features of the angle concept (Michtelmore, 1998). Further, students’ misconceptions and struggles with angle as a mathematical concept may stem from textbook representations and presentations of angle (Keiser, 2004; Alyami, 2020). For example, Tanguay and Venant (2016) noted the obscurity between angle as a static geometric figure and angle as a magnitude of a rotational motion in their analysis of two textbook collections from primary schooling in Quebec (grades K-6).
Due to students’ misunderstandings of angle, as well as students lack of understanding regarding how angle is represented in everyday situations, researchers have developed and/or implemented different approaches to support the development of students’ understanding of angle such as visual field activities and spatial representations (Bustang et al., 2013), variations in a teaching sequence – one dynamic and one static (Devichi and Munier, 2013), an on-line Logo programming environment (Latsi and Kynigos, 2022), and a body-based angle task (Smith et al., 2014). Results from these studies indicated how student-centered and/or authentic tasks that utilize different modalities or representation, such as movement of one’s body (Clements and Burns, 2000) and/or the manipulation of materials (e.g., rope; Devichi and Munier, 2013), have positive impacts in terms of students’ understanding of angle. In particular, findings highlight students’ ability to understand that the length of the rays do not influence the angle measure (Devichi and Munier, 2013; Crompton, 2015) – a common misconception as noted above (Tanguay and Venant, 2016) – as well as develop dynamic and flexible mental images of angle through multiple modalities such as body movements and manipulation of digital objects (Clements and Burns, 2000; Latsi and Kynigos, 2022). Further, Smith et al. (2014) found that third and fourth grade students’ engagement in a motion-controlled angle task improved their ability to estimate the size of an angle and draw angles of specified measures.
Broadly speaking, epistemic tools encompass artifacts, resources, and processes that support and facilitate learners in knowledge-building practices, making learners’ thinking visible for shared discourse and collaborative knowledge production as situated within specific physical, cultural, and social contexts (Wendell et al., 2019). Prior research in science and engineering contexts underscore the role of epistemic tools to engage learners in sense-making and decision-making (Tan et al., 2019; Wendell et al., 2019), increase learners’ proficiency in engineering practices (e.g., define a problem) and content knowledge (Bernhard et al., 2019; Kelly and Cunningham, 2019; Tan et al., 2019), and systems thinking (Ke et al., 2020). In this study, the epistemic tools include a variety representations and artifacts that learners use to express and negotiate their mathematical thinking of angle - objects, drawings, oral and written language, and our bodies, to name a few (Abrahamson and Bakker, 2016; Fonger, 2019; Kelly and Cunningham, 2019; Mathayas et al., 2019). In addition, these representations and artifacts emerge as knowledge construction tools, as opposed to being supplied (e.g., digital design notebooks; Wendell et al., 2019), through their collaborative interactions and negotiated discourse around an educational robotics tasks in an informal learning environment (Radford, 2016a; Settlage and Southerland, 2019).
In this study, we employed Radford’s (2016a, 2016b) notion of joint labor, which highlights the teaching and learning process as a single and same activity, one where teachers and students “… engage together, intellectually and emotionally, toward the production of common work. Common work is the sensuous appearance of knowledge” (Radford, 2016b, pp. 1412–1413) expressed through actions, language, gestures, perception, and tools. As implied, students are not viewed as passive learners receiving information from a teacher who possess all the knowledge to transmit to students. Joint labor allows for the creation, negotiation, and production of knowledge (i.e., processes of objectification), as well as the development of individuals as subjects in education (i.e., processes of subjectification). Nakawa et al. (2023) utilized this perspective to understand the role of finger gestures in learning addition of two numbers. These researchers highlighted the joint labor of a teacher and 15 children aged 5–6 years to perceive their fingers as a tool for solving addition problems, particularly through an episode of struggle when a child proposed adding the numbers 12 and 5 and realized that they could not represent 12 using their 10 fingers. In our study, we adopted this idea to consider the joint labor among students working together on a robotics task within a hybrid making space. Through their joint labor, we consider how they engaged with historically constituted knowledge specific to the concept of angle.
Embodied cognition is based on the radical hypothesis that human cognition is deeply intertwined between body and brain (Kirsh, 2013; Nathan, 2022), i.e., to solve problems humans use their brain as well as their body. Bodily actions, such as gestures, are critical components to shape an individual’s thinking. Research on embodied cognition has highlighted the role of gestures in shaping and representing student’s thinking, reasoning, and understanding of concepts (Kirsh, 2013), as well as supporting their ability to communicate ideas that may be challenging for students to describe through other forms of representations such as spoken language (Katirci et al., 2022). Prior research in formal classrooms has shown that gestures play an integral role in interpersonal communication, especially in the case where core problem domain concepts may be difficult to explicate verbally (Reynolds and Reeve, 2001; Nathan et al., 2013). Further, gestures disclose how a student orients to and utilizes concrete and symbolic representations from their environment while communicating their mathematical thinking to another (Bieda and Nathan, 2009). For example, Alibali and Nathan (2012) included an example of a student using pointing gestures to explain or communicate their thinking regarding how they solved the problem 6 + 3 + 4 = ___ + 4 (i.e., symbolic representation). Beyond gestures, actions of the body matter for cognitive performance and learning of mathematical concepts (Alibali and Nathan, 2018). For example, elementary students were tasked with walking the sides and interior angles of a Euclidean triangle to experience and understand that the sum of the interior angles is 180° (Soto, 2022).
The data for this study was collected from the TinkerLab, a making space within an intermediate school (i.e., grades 3–5, ages 9–11) located in the northeast region of the United States. At the time of the study (May 2019), this local school district provided access to making activities for every student in grades K-5 as part of their school curriculum, which included exposure to educational robotics. The making activity in this study was designed by the TinkerLab educator to engage students in the integration of collaboration, communication, computational practices, and mathematical concepts during a free period during the school day. It was presented in two phases. The goal of Phase 1 was to make a path for Dash (Figure 1A), an educational robot, by placing tape on the floor from one side of the room to the other. This path was to be traversed by another group in Phase 2. To accomplish this goal, the group was provided with a roll of wide yellow tape. With the broad goal of Phase 1, members of the group had to negotiate how to create a path that was often framed by groups as “challenging, but doable.” The goal of Phase 2 was for each group to program Dash (Figure 1A) to stay on the path (Figure 1 – PATH) placed by another group. This was completed through composing a series of block codes on the iPad app Blockly (Figure 1B). In addition, groups were provided with two other tools - a pencil (Figure 1C) and a measuring tape (Figure 1D). Unlike prior research that highlights the use of educational robots within an authentic and worldly context that would elicit students’ participation in mathematics (Doorman et al., 2019; Komarudin et al., 2021), this task was not designed with an intent of developing and/or engaging students in the mathematical concept angle.

Figure 1. Illustration of the tools used in both phases of the task. Image was originally published in Shokeen et al. (2020).
The students’ mathematical thinking about angle was void of a physical protractor as this tool was not provided by the teacher. However, the Blockly app included what we referred to as a digital protractor in which students were able to program Dash to rotate between left 90-degrees and right 90-degrees in 15-degree increments. Yet, this feature did not use formal notation and/or mathematical language such as degree or angle. As seen in Figure 2, Dash was programmed to turn right at a 90-degree angle.
The data source for this study included video data from a wide-angle camera, as well as Go-Pro™ cameras worn on the chest of randomly chosen two students per group. Researchers that gather data through go-pro cameras extend the advantages of video data through enabling a more subjective, collaborative, and participatory approach (Pink, 2015; Burbank et al., 2018), as well as opportunities to enter spaces that might otherwise be difficult to follow (Burris, 2017). The utilization of multiple cameras for any one group afforded the research team an opportunity to “see” different perspectives to form a larger possibility space of an event (Kastberg et al., 2023). As this data was collected for each of six groups, we collected 19 videos. Each video lasted the length of the activity, approximately 20 min. Similar to Nakawa et al. (2023), our data and analysis included short observations of one activity as opposed to longitudinal research recommended by Radford (2015) when utilizing a joint labor perspective. Table 1 includes demographic information of each group and the total duration of videos analyzed per group.
The video data was analyzed using five possible forms of representations developed and described by Lesh et al. (1987): (a) concrete, (b) pictorial, (c) symbolic, (d) language, and (e) realistic. Lesh et al. (1987) emphasized the understanding of concepts through student’s ability to represent their thinking and activity through the five different representations, as well as their ability to move and translate between and within these forms of representations (Lesh et al., 1987; Moore et al., 2013). In addition, as argued by Katirci et al. (2022) and Moore et al. (2020), we included gestures and the body as an additional representation as they too serve as a tool to shape students’ reasoning, as well as allow students to convey their mathematical thinking to others.
In this study, we modified the six forms of representations to align with the educational robotics task (see Table 2). For example, we included digital diagrams and models as a pictorial representation and the various block or lines of code as a symbolic representation. These were refined through our ongoing analysis.
Analysis began with the first two authors independently analyzing a video from Grade 4 – Group A. One of the common disagreements was between symbolic representation and language representation as an epistemic tool. For example, one author coded the use of “zig-zag” (e.g., “Just make a zig-zag.”) as symbolic while the other author coded this a language representation. While we have argued elsewhere how the use of informal terminology to form and communicate ideas and reasoning regarding the use of angles and length of rays (Shokeen et al., 2021), it is not considered as a formal notation of angles in mathematics (Alyami, 2020). Therefore, we distinguished oral communication that included mathematical notation (i.e., symbolic) from oral communication that did not (i.e., language). As we continued to independently analyze and collectively discuss videos from Grade 4 – Group A, additional questions regarding forms of representation was raised such as how to categorize a student who used a strip a tape to point in a particular direction as opposed to using their finger, which we agreed was a gesture representation as opposed to a concrete representation as holding the tape served as a pointing mechanism and limited the student’s ability to actually point using their finger.
Once consensus was reached, Author 1 coded the videos for Grade 3 – Group A, Grade 3 – Group B, and Grade 4 – Group B while Author 2 analyzed Grade 5 – Group A and Grade 5 – Group B. We placed our analysis in an excel sheet in 15-s increments (Figure 3). This allowed us to examine students’ shared understanding of mathematical thinking of angle through six different representations (i.e., epistemic tools; Kelly and Cunningham, 2019). The alignment of the text within each cell was also used to indicate when representations occurred simultaneously or in a linear fashion. In addition, we were able to examine students’ use of epistemic tools to develop a shared understanding of the concept of angle across the videos of any one group (i.e., joint labor).

Figure 3. Image of analysis in an excel sheet similar to Moore et al. (2013).
Before addressing how students negotiated an understanding of angle through their joint labor, we provide a visual overview of the epistemic tools used during two phases by different grades students (see Figure 3). For readability, we only included the frequency of those that were observed within each phase and grade. As an example of how to read the different images, consider Phase 2, Grade 3. Through our analysis, we observed eight instances in which a student communicated their thinking of angle through language (e.g., “turn left 45”). This is represented in the arrow below Language. Further, the bi-directional arrows between two epistemic tools are included to note instances when more than one tool was employed within the joint labor process. Continuing with the example from Phase 2, Grade 3, we observed six instances of language-pictorial. This is seen on the arrow connecting Language and Pictorial tools. This indicates that third grade students in this study negotiated their understanding of angle through moving between non-symbolic oral and 2-D representations, particularly digital representations as they were programming Dash using the Blockly app. The dashed arrows indicate the joint tool use that we did not observe (e.g., pictorial-realistic).
Language was a common tool as phrases such as “turn 45,” “drive left,” “tight angle,” “try 20,” and “it does not turn enough” were utilized in creating and traversing the path. Beyond language as a common epistemic tool, we observed students across the three grade bands commonly utilize epistemic tools through moving back and forth between representations, or even layered as simultaneous representations – (a) language-gesture, (b) language-concrete, and (c) language-pictorial. Examples of these will be included throughout the results.
When looking across phases, symbolic representation was not a common epistemic tool in Phase 1, but more prevalent in Phase 2. We hypothesize this was by nature of programming Dash’s movement to traverse the path in Phase 2. The Blockly app, used in Phase 2 to program Dash, has a drive command that includes “turn left” or “turn right” and students are required to enter the degree amount for Dash to turn left or right. Therefore, students were more likely to negotiate Dash’s movements through symbolic tools such as “turn left 90 degrees” or “180 degrees. We need to do 180 degrees.” In Phase 1, students rarely used the word degree when negotiating the path. In the few instances (n = 3) in which students communicated about angle through a symbolic tool in Phase 1, it was still in reference to Dash’s potential to traverse the path. For example, “Dash cannot do a ten-degree angle.”
Similarly, pictorial representation as an epistemic tool, as well as the movement between pictorial-language and pictorial-symbolic, was only observed in Phase 2. Again, we contend this was by nature of the Blockly app as the angle measure Dash turned was selected through manipulating the digital protractor as described above. As an example, after testing Dash’s movement along the path, Travis stated, “Nope, that’s not enough of a turn right there.” Travis’s language triggered Fawn, who was in possession of the iPad, to select line of code that noted, “turn right 60.” Travis then stated, “90 degrees. We need to do 90 degrees.” This symbolic representation was next taken up by Fawn as she used the digital protractor (i.e., pictorial representation) to rotate the dial from 60-degrees to 90-degrees.
Lastly, realistic representations as an epistemic tool were only used in Phase 1 when describing the path. For example, a group of fourth graders used real-world metaphors (e.g., wire, crazy roads) to express their understanding of angle as alternating left and right turns in the path. Gabby noted, “This is starting to look like some crazy shape.” “It’s like a machine. It’s like a wire,” stated Almond. Ryan added, “It is like one of the crazy roads that you see in movies.” Alex agreed, “yeah, there’s like all these different roads.” In this episode, students demonstrated their mathematical thinking of angle by connecting their observation of angle as reflected in real-life scenarios to their creation of angle in the making of the path.
In considering how students used different epistemic tools as part of their joint labor, we observed three ways in which they developed a shared understanding of angle: (a) language, (b) dynamic representations, and (c) directionality and degree measure. For each, we include a range of examples and images from videos from across the data set. Pseudonyms are used throughout to maintain the anonymity of the participants.
We observed several instances in which students utilized gestures as an epistemic tool to exemplify the meaning of a particular word used to describe angles such as strict or tight or wide. We provide two examples of students using different gestures as a way to share their mathematical thinking of the word “wide” within the context of laying a taped path. First, after laying a strip a tape to form an acute angle with another piece of tape, a fourth-grade group decided that the angle formed was too small or too tight for Dash to traverse the path (see Figure 4A). Gabby suggested they make the angle wider through both verbal (i.e., “a little wider”) and gestural (i.e., moved her hands wider; expanding one hand up and one hand down in front of her body) representations (see Figure 4B). This was taken up by Billie, as she ripped up one strip of tape forming the “too tight” angle and rotated the strip of tape to form a larger or “wider” angle measure (see Figure 4C). As implied, Gabby and Billie are negotiating the meaning of a wide angle, particularly within the context of Dash being able to rotate its body when the angle formed between two strips of tape is too tight.
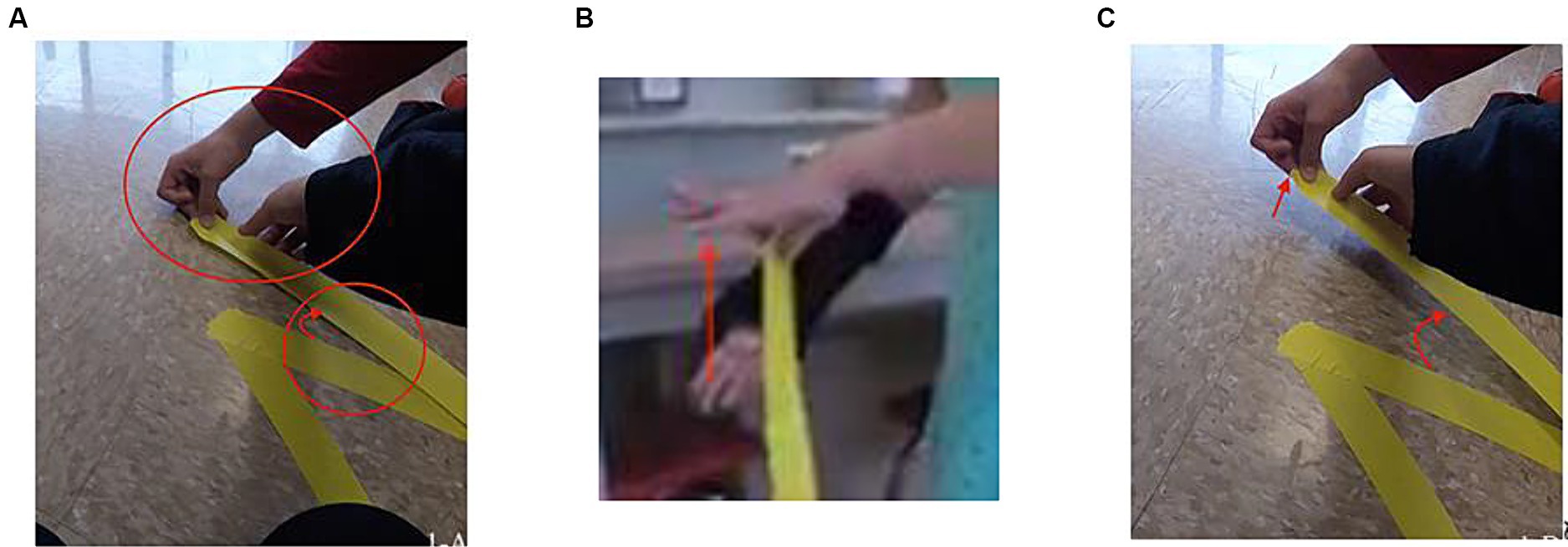
Figure 4. Images of joint labor around creating a wide angle. (A) shows the angle formed was too small or tight for Dash to traverse the path. (B) shows Gabby’s suggestion of making the angle wider. (C) illustrates Billie rotating the strip of tape to make the angle wider. (A-C) Image was originally published in Shokeen et al. (2020).
As a second example, when negotiating laying strips of tape for the next part of the path, Kelley suggested the following to his third-grade peers. “I thought we would go wide. Wide.” He moved his arms out from the middle of his body forming what Kelley perceived to be a wide angle. Kelley’s arms served as the two rays and his chest as the common endpoint. Grace took up this idea (i.e., “Yeah.”) but seemed to think about it differently than a wide angle. “Yeah, we should make one that goes in two directions. Like one goes this way … and one goes that way.” Using the piece of tape between her hands, Grace pointed in one direction for “this way” and another direction for “that way” (see Figure 5). When the tape was laid in two directions, we observed the creation of an obtuse angle (see Figure 5).
Zigzag was a “special” case of their joint labor around angle, particularly in laying the path from one side of the room to the other. There are different colloquial descriptions associated with the term zigzag, such as “one of a series of short sharp turns, angles, or alterations in a course” (Merriam-Webster, 2021) or “a line, course, or progression characterized by sharp turns first to one side and then to the other” (LLC, 2024). These descriptions use words (e.g., short, sharp, turn) that are often closely aligned to angles (Clements and Burns, 2000). We found that students in each group used ‘zig-zag’ at multiple times to share their perceptions of angles and lengths. Students used the term both in reference to a single angle and to the broader patterns in a path composed of multiple angles and lengths. In order to develop and negotiate an understanding around this non-formal word, students used varying epistemic tools of language, gesture, and action (e.g., ripping tape).
Students were observed regularly communicating about a specific angle between two adjacent section of tapes. In order to form an angle, students negotiated about two parameters – the length of the tape (i.e., length of rays) and direction of connection between two section of tape (i.e., the angle between the rays). For example, in the Grade 5 group, Olivia used colloquial language to communicate about rays and an angle, beginning by saying “No, make it jagged. That’s way too long.” In order to explain what she meant and perceived, she performed an action of pulling up the last tape section from the floor, ripping it into two parts and laid one piece of the ripped tape back down. She then stated, “keep doing that pattern,” and pointed toward a specific angle on the path (see Figure 6). Olivia pointed toward that specific angle to illustrate what she meant by ‘jagged,’ as the group had not understood what she was trying to communicate. In other words, her perception of a desirable angle composed by two rays, was not being communicated accurately through language. Later, Olivia changed her suggestion from ‘jagged’ to ‘zigzag’, saying “We can do zigzags,.” Sahil agreed with her and added, “Make it zigzag.” Sahil repeating the term ‘zigzag’ demonstrated that he had now aligned with Olivia’s perception of desirable angles and rays and was able to follow the meaning of zigzag. This example describes how the Grade 5 group used a specific angle to develop a shared perceptual understanding of ‘zigzag’ to guide their activity.

Figure 6. A representation of zig-zag. Image was originally published in Shokeen et al. (2021).
The term ‘zigzag’ was also used to communicate about a broader pattern and was particularly powerful and useful for discussing multiple twists and turns (i.e., angles and rays). In this situation, unlike the example of Olivia, the use of ‘zig-zag’ did not require all of them to be talking about the same piece of tape. It allowed students to communicate about the path without referring to a particular section of tape as a base arc for the angle or about a particular angle composed of rays. For instance, in the Grade 4 group, students were engaged in joint labor as they examined the path from different directions while discussing how to continue the path (see Figure 7); thus, indicating angle is directional based on one’s position relative to the strip of tape being referred to. Ryan introduced the term ‘zig-zag’ by suggesting, “Go forward a little longer and then we can do a couple of zig-zags.” Here, Ryan is not talking about a single angle, but he was describing his strategy of laying a broader pattern of tape. Alex responded, “Just do zig-zag” and he moved his foot to indicate a zig-zag pattern (Figure 7C), using gesture to illustrate what he means by ‘zig-zag.’ Paul followed with a more specific suggestion, saying, “Yeah, 45-degree angle(s)” and made a zig-zag pattern with his right arm (Figure 7B). Adding to the discussion Ryan suggested, “Dude, go one more backward and then start doing zig-zag,” moving his finger rapidly back and forth (Figure 7A). In this discussion Alex, Paul, and Ryan each used the epistemic tools of language and gestures, but in different ways, to communicate about the same pattern of ‘zig-zag’ without restraining their discussion to any specific angle or ray within the path. Their discussion illustrates the use of ‘zig-zag’ to discuss a broader pattern, rather than a single angle or piece of tape.
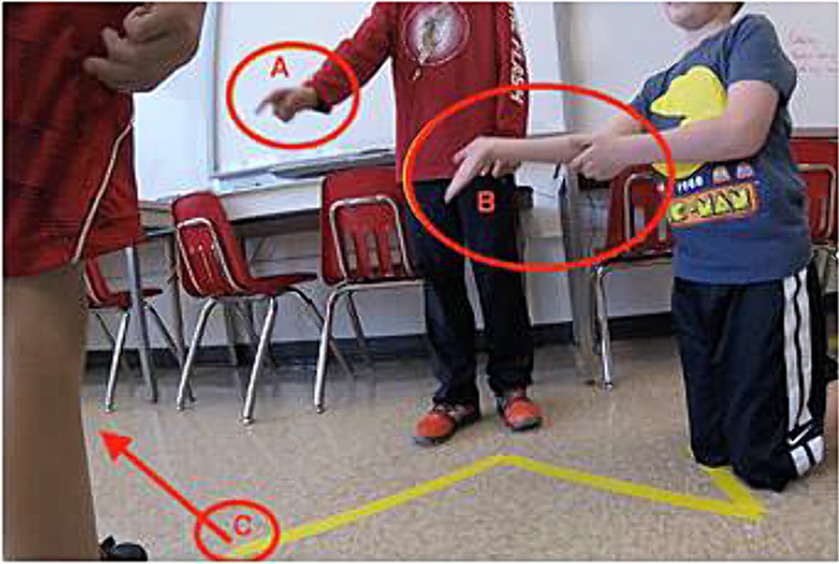
Figure 7. Negotiation of zig-zag as a broader pattern. Image was originally published in Shokeen et al. (2021).
As exemplified in our findings, students considered the rotation of the angle, often in reference to a common point where two rays meet to form an angle, but further considering angle as a dynamic figure (Alyami, 2020). In these instances, students sought out clarification of how and where to lay a strip of tape on the path using a variety of epistemic tools, such as the concrete nature of the tape. For example, Page encouraged his third-grade peers to make a zigzag pattern, “Make it a zigzag.” This meaning of zigzag was indicated by Page pointing to the end of the path and moving his finger across the floor towards his body, forming what we observed to be about a 90-degree angle. Yet Page’s mathematical thinking was either not heard/witnessed or not understood by Penny as she expressed uncertainty. Penny was observed dynamically manipulating the strip of tape along the arc of a circle before she stopped and asked, “like that?” In Figure 8, Penny’s left hand remained as the center of a circle, while her right hand moved along the arc as she considered how to lay the tape as to form a zig-zag pattern. Page disapproved by stating, “No, no, no. Like diagonal…diagonal rate.” Page’s gesture indicated that the strip of tape laid by Penny should form a smaller angle measure. In this example, Penny and Page are engaged in joint activity as they develop a dynamic understanding of angle through manipulating (and observing) a strip of tape to create a zig-zag pattern.
As another example, we observed Paul and Alex communicating and negotiating about adding a strip of tape at some angle measure through concrete and symbolic tools. Alex was hovering a piece of tape above the floor that would form an obtuse angle with the piece of tape already on the floor. Paul stated from a distance, “Make it more complex, right there. Make it like a…” Alex rotated the tape with his left arm to form a smaller angle with the piece of tape, using the strip of tape as a dynamic tool to form a shared understanding of angle. Paul confirmed this change in the angle through a verbal, symbolic statement: “Yeah, like a 45-degree angle like that.”
One way we observed students developing a shared understanding of angle was through Dash’s movement along the path, both in terms of the direction (e.g., “turn left”) and magnitude (e.g., “try 45 degrees”). But unlike above, students were observed substituting their body in place of Dash to consider Dash’s perspective along the path, as well as through physically rotating Dash. In other words, they utilized their bodies and the physical nature of Dash as knowledge building tools. For example, in determining the direction that Dash needed to turn to navigate the second strip of tape, Addie, a third-grade student, considered the perspective of Dash through positioning her body at the end of the first strip of tape (i.e., parallel with the second strip of tape). She pointed to the path and swung her arms back-and-forth along the strip of tape (see Figure 9). Addie determined that the next line of code should indicate the direction that Dash should turn, namely right. “This is right. He has to turn right.” This countered one of her group member’s earlier statement that Dash should turn left. In this instance, Samuel did not position his body as Addie, but only pointed in the direction of the second strip of tape with his left hand from where he stood in the classroom. This indicated how taking on the perspective of Dash may help in determining directionality of the angle in this situation.

Figure 9. Addie’s position on the path from two different cameras. Image on the left is from Addie’s perspective. The arrow is to illustrate the movement of her arm.
Another example exemplifies a student’s mathematical thinking after not programming Dash to successfully turn an appropriate amount to be positioned to traverse the next strip of tape or path. Paul and Alex discussed the angle size and direction in which Dash should be programmed when Alex created a border of the path with his hands (see Figure 10A), then next placed his body/head over Dash as if he trying to get the perspective of Dash in relation to Dash’s body position on the path (see Figure 10B). From his perspective and estimation, Alex stated through language, “So let us do like 35, 35.”

Figure 10. (A) illustrates Alex creating a border of the path with his hands. (B) highlights Alex’s embodying Dash’s perspective by placing his body/head over Dash.
There were also instances in which students physically manipulated Dash to clarify their meaning regarding angle. In the physical manipulation of Dash, they were able to consider Dash’s perspective. For example, Alex rotated Dash as he stated, “We only have to do like a tiny turn.” This indicated that Dash was positioned appropriately along the path and a tiny turn was the next line to enter into the program. As another example, one group of fourth grade students noted after a test that Dash “did not turn all the way,” indicating that the angle measure entered into the program was less than the angle measure between two strips of tape on the floor. Billie suggested 90-degrees. Jackie bent down and moved Dash left to right and right to left at the angle formed by the two strips of tape and stated, “I feel like it’s less than that. Try 60 or 75.” In this case, Jackie used Dash and her perspective of what constitutes a 90-degree angle to determine that Dash should turn at a 60- or 75-degree angle.
In addition, we observed one instance in which a group of third-grade students physically manipulated Dash to negotiate the direction in which Dash should turn next as it is positioned at the end of the first strip of tape along the path (see Figure 11A). Before entering the next line of code, Kelley asked, “Should he go right or left?” Bella and Grace both shifted or rotated Dash on the path while simultaneously noting the direction Dash should rotate - “right turn” (see Figure 11B). Grace added, “This way is right…that he is turning himself.” In this instance, rotating Dash some amount was a dynamic representation or a “process of change of direction” (Freudenthal, 1983, p. 327).

Figure 11. (A) illustrates students physically manipulating Dash to negotiate the direction of the next turn on the path. (B) shows students rotating Dash right.
In this study, we illustrated how students in grades 3–5 negotiated a shared understanding of angle through multiple epistemic tools that were situated and contextualized through the use of an educational robot within a hybrid making space. This included developing a shared language, conceptualizing angle as a dynamic entity, and perceiving angle through directionality and degree measures. Our examples further highlighted specific moments in which students communicated their thinking and negotiated an understanding about angle through either a single tool or through coordinating and building upon their mathematical thinking about angle simultaneously and collaboratively. As such, the results of this study highlight the potential for hybrid making spaces to serve as sites to engage students in complex mathematical concepts (e.g., angle) that are foundational to students’ thinking and conceptual understanding (Alyami, 2020), but not privileged in school settings (e.g., “tight angle”) (Nemirovsky et al., 2017; Simpson and Kastberg, 2022). The results further underscored how the different phases of the activity, as well as the available tools (i.e., roll of tape, Dash, and the app/iPad), afforded the use of different epistemic tools. For example, the app in Phase 2 created opportunities for students to use their body as a substitute for Dash that were non-existent in Phase 1. As another example, students were more likely to use more formal mathematical notation in oral forms of communication (i.e., symbolic representations) in Phase 2 than Phase 1, which we attribute to Dash.
Formal (e.g., 45-degrees) and informal (e.g., turn 45) language was a common tool used to generate a shared knowledge base about angles. We contend that the flexibility of the hybrid making space allowed students the opportunity to discuss their ideas using language that was not only familiar, but situational. For example, “turn” was used in relation to Dash’s movement along the path as if driving a car. This is in contrast to standards documents that uses the term “turn” to indicate the measure an angle rotates through n one-degree angles of a circle (Common Core State Standards Initiative, 2021), which children do not readily understand (Mitchelmore and White, 1998). The use of zig-zag also emerged within the context of laying the path for Dash to traverse. Sometimes the word zig-zag was used to refer to a single sharp angle, whereas other times the focus was on the tape that created the arc of the angle. Thus, the use of ‘zig-zag’ also involved co-creating situated understandings about the meaning of angle within the activity. This particular finding adds to our understanding of possible ways elementary students may communicate and think about angle as prior research on this notion of zig-zag is scant, if non-existent.
The results from this study also highlighted the different uses of bodily movements (e.g., gestures) as a knowledge-building tool among students. As noted in prior research (Alibali and Nathan, 2012; Nathan et al., 2013), students in this study used gestures such as pointing gestures and representational gestures to clarify vague language (e.g., “this”) and exemplify the meaning of a particular word used to describe angles such as “tight.” As described by Nathan et al. (2013), the use of gestures may have supported these students in communicating their thinking around a mathematical concept that may be difficult to explain verbally. In Phase 2, students were observed using more of their entire bodies to take the perspective and position of Dash along the path, and use their bodies to then verbally communicate the direction and amount of turn to enter into the app (e.g., turn left 45-degrees). The use of their body may have supported students in developing an understanding of angle as turn, including direction (Freudenthal, 1983; Clements et al., 1996; Kaur, 2020), and in this case, was supported through the use of an educational robot. According to Clements and Burns (2000) this is done through the synthesis of two schemes.
To conceptualize a turn and its measure, students have to maintain a record of both the initial heading and final heading of an object, using a frame of reference to fix these headings. They have to analyze motor activity of rotation of the object from the former to the latter, and compare that rotation to internalized benchmarks or to iterations of an internalized image of a unit of turn. As they develop this ability, students curtail physical movements that fix the headings and represent the rotation from one to the other (p. 42).
In addition, the use of the tape afforded students the opportunity to physically rotate the strip of tape about a point and along the arc of a circle. Similarly, physically rotating Dash left and right provided students an opportunity to internalize the intended rotation of Dash. Viewing the dynamic feature of angles was more than likely cognitively “hidden” from students, but embodied within their bodily movement of the strip of tape and rotation of Dash. As such, through their joint labor, students conceptualized and reasoned about angle within a frame of reference (Joshua et al., 2015); first by thinking of the measure as degrees and trying to assign a value to the angle in relation to too much or too little (i.e., committing to the unit), second by committing to a direction in relation to Dash’s movement on the path, and lastly through rotating the strip of tape or Dash about a point (i.e., commitment to a reference point).
In addition, as the strip of tape was laid on the floor, it became a static representation. Alyami (2020) differentiates the qualitative view of angle (i.e., attending to properties of an angle) from the quantitative view of angle (i.e., attending to a quality that is measurable), which we argue aligns with the static and dynamic representation of the tape. Therefore, students were engaged with two representations of angle that are both needed to understanding angle concepts, but often a source of struggle when learning about angles (Scally, 1986; Alyami, 2020). This is important as prior research has shown textbooks often provide a static definition of angle (Keiser, 2004; Alyami, 2020) and that teachers too lack a clear and thorough understanding of angles to support the dynamic view of angle (Browning et al., 2007; Thanheiser et al., 2010).
Broadly, the significance of this study lies in the potential for hybrid making spaces and/or educational robots to support students’ mathematical development. In particular, the use of educational robots, such as Dash, may promote and/or reinforce students’ conceptual understanding of angle as both a static and dynamic representation. The results from this study also shed light on how the design of activities and the tools that are made available may foster the use of multiple representations for students to communicate with one another around a particular mathematical concept, as well as develop their own understanding of the mathematical concept. In this study, the activity had a goal to accomplish in each phase (e.g., create a path to Dash to traverse from one end of the room to other) but allowed for students’ agency and creativity in how they met this goal. It was designed to promote teamwork or joint labor while the teacher sat on the peripheral as an observer. The tools – roll of tape, Dash, and an iPad – afforded opportunities to think and build a shared understanding about angle within the context of the activity and hybrid making space. We argue that providing a protractor would have changed the way students negotiated their understanding of angle through the various epistemic tools. Collectively, these design elements highlight how an educator’s decisions regarding what to include (or not), how to structure (e.g., individual or small group), what tools and materials to provide (or not), whether students should be using mathematical notation (or not), and so forth has the potential to shape how students communicate their mathematical thinking with one another and develop a shared understanding. This line of educational design thinking can inform professional development opportunities around making spaces, as well as pedagogical courses involving prospective teachers.
Further, the goal of the activity presented in this paper was not to engage students in mathematical activity, which illustrates the “hidden” nature of mathematics within hybrid making spaces, and through educational robots, as a humanistic and authentic approach to mathematics (Simpson and Kastberg, 2022). Being able to “see,” name, and make sense of the mathematics that is happening in hybrid making spaces can become a powerful formative assessment for educators to make sense of student thinking and learning. The question becomes, how do we support educators in observing students’ mathematical thinking and learning that is not a focus of early mathematics standards and benchmarks (e.g., spatial reasoning, Uttal et al., 2013) or potentially not age- or grade appropriate (e.g., inverse proportional relationships, Simpson et al., 2021)? How might we make sense of and/or build upon the mathematics as conceptualized by the three stages of angle as a concept developed by Mitchelmore and White (1998)? Future research endeavors can begin to explore these questions.
Methodologically, we included the body as an epistemic tool, an important component that has gained traction in recent years in terms of student’s thinking and learning (Shapiro and Stolz, 2019). Gestures, in particular, are not only a tool to shape students’ thinking or reasoning, but it is an important representation to communicate about ideas which are challenging for youth to describe through other forms of representation. As we have discussed in the empirical evidence from the study, during both phases of the activity, students relied on their bodies and bodily gestures to negotiate their thinking about angle, as well as gain a perspective of an inanimate object, Dash. Hence, we argue for the inclusion of the body (e.g., gestures) as a representation to prior models (e.g., representational fluency, Lesh et al., 1987) as it adds a deeper and more nuanced understanding of students’ communication, thinking and reasoning within activities that encourage joint labor. Additionally, we adapted the definitions, such as symbolic representation, to meet the digital workspace of the Blockly app. As digital mathematical environments continue to be a part of our learning, research may need to consider additional and/or alternative representations.
The findings from this study are grounded in a particular educational robot, Dash. Therefore, generalizing the influence of different educational robots for supporting students’ understanding of angle across hybrid making spaces is beyond the scope of this study. However, we contend this is a ripe area of research to continue to build upon, particularly with a variety of educational robots (e.g., Sphero, Ozobot) that are being utilized in classrooms, making spaces in out-of-school contexts, and hybrid making spaces. Future research could also replicate the activity within a similar context as a way to consider transferability of results (Lincoln and Guba, 1985). Individuals may also argue that another limitation was our approach to the analysis in that the first two authors did not establish inter-rater agreement. As described by Denzin (1984), we rather employed investigator triangulation as we examined the same phenomenon from different backgrounds and experiences. We found this to be a more useful approach to analyzing multiple forms of representations within interactions among five students.
Lastly, as observed in Figure 12, there are differences in terms of the different forms of representations used by children in different grade bands. For example, in Phase 1, 5th grade students use more language representation than 3rd and 4th grade students in our study. As another example, in Phase 2, 4th grade students used less gesture-language representations, but more pictorial-symbolic representations, than the other two grade levels. Future research could focus on where differences exist in terms of representations, but more specifically, why and the implications this may have on their shared understanding of angle (or other mathematical concepts).
Our findings highlight how the use of an educational robot within a hybrid making space afforded students an opportunity to negotiate an understanding of angle through multiple epistemic tools. As such, the utilization of such tools was situated and contextualized in the nature of the making activity, and was often done as part of their joint labor. We argue that attending to the nature of different epistemic tools used by students in hybrid making spaces have the potential to highlight their understanding about the static and dynamic nature of angles. The flexible nature of hybrid making space activities can provide students an opportunity to apply the mathematical concepts that they read about in their textbook; sometimes it even prepares students to learn about the formal notations of a concept.
The datasets presented in this article are not readily available. As included in consent and assent documents, “identifying information might be removed from identifiable private information and, after such removal, the information could be used for future research studies, but only studies in which Dr. S is involved.” Requests to access the datasets should be directed to AS, YXNpbXBzb25AYmluZ2hhbXRvbi5lZHU=.
The studies involving humans were approved by Binghamton University Institutional Review Board. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin. Written informed assent for participation in this study was provided by participants. Written informed consent was obtained from the minor(s)’ legal guardian/next of kin for the publication of any potentially identifiable images or data included in this article.
AS: Conceptualization, Formal analysis, Methodology, Project administration, Writing – original draft, Writing – review & editing. ES: Conceptualization, Formal analysis, Writing – original draft, Writing – review & editing. NK: Formal analysis, Methodology, Writing – review & editing. CW-P: Formal analysis, Methodology, Writing – review & editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
We thank the students, teacher, and school who shared their collaborative experiences with the first author.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. ^We define a hybrid making space as a third space (Gutiérrez et al., 1999) where the norms and expectations of a formal learning environment (e.g., school) and the norms and expectations of a non-formal learning environment (e.g., summer camp) co-exist (Simpson and Feyerabend, 2022).
Abrahamson, D., and Bakker, A. (2016). Making sense of movement in embodied design for mathematics learning. Cogn. Res. Princ. Implic. 1:33. doi: 10.1186/s41235-016-0034-3
Alfieri, L., Higashi, R., Shoop, R., and Schunn, C. D. (2015). Case studies of a robot-based game to shape interests and hone proportional reasoning skills. Int. J. STEM Educ. 2, 1–13. doi: 10.1186/s40594-015-0017-9
Alibali, M. W., and Nathan, M. J. (2012). Embodiment in mathematics teaching and learning: evidence from learners' and teachers' gestures. J. Learn. Sci. 21, 247–286. doi: 10.1080/10508406.2011.611446
Alibali, M. W., and Nathan, M. J. (2018). “Embodied cognition in learning and teaching: action, observation, and imagination” in International Handbook of the Learning Sciences. eds. F. Fischer, C. E. Hmelo-Silver, S. R. Goldman, and P. Reimann (New York, NY, USA: Routledge), 75–85.
Alyami, H. (2020). Textbook representations of radian angle measure: the need to build on the quantitative view of angle. Sch. Sci. Math. 120, 15–28. doi: 10.1111/ssm.12380
Angeli, C., and Valanides, N. (2020). Developing young children's computational thinking with educational robotics: an interaction effect between gender and scaffolding strategy. Comput. Hum. Behav. 105:105954. doi: 10.1016/j.chb.2019.03.018
Ardito, G., Mosley, P., and Scollins, L. (2014). We, robot: using robotics to promote collaborative and mathematics learning in a middle school classroom. Middle Grades Res. J. 9, 73–88.
Australian Curriculum, Assessment and Reporting Authority. (2024). Australian Curriculum: Mathematics (Version 8.4). Available at: https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/ (Accessed May 29, 2024).
Bernhard, J., Carstensen, A. K., Davidsen, J., and Ryberg, T. (2019). Practical epistemic cognition in a design project—engineering students developing epistemic fluency. IEEE Trans. Educ. 62, 216–225. doi: 10.1109/TE.2019.2912348
Berry, R. Q. (2015). “Addressing the needs of the marginalized students in school mathematics: a review of policies and reforms” in Proceedings of North American Chapter of the International Group for the Psychology of Mathematics Education. eds. T. G. Bartell, K. N. Bieda, R. T. Putnam, K. Bradfield, and H. Donimguez (PME-NA), 19–32.
Bieda, K. N., and Nathan, M. J. (2009). Representational disfluency in algebra: evidence from student gestures and speech. ZDM 41, 637–650. doi: 10.1007/s11858-009-0198-0
Browning, C. A., Garza-Kling, G., and Sundling, E. H. (2007). What's your angle on angles? Teach. Child. Math. 14, 283–287. doi: 10.5951/TCM.14.5.0283
Burbank, B., McGregor, D., and Wild, M. (2018). ‘My special, my special thing, and my camera!’ Using GoPro™ as a complementary research tool to investigate young children’s museum experiences. Museum Soc. 16, 311–333. doi: 10.29311/mas.v16i3.2792
Burris, A. (2017). A child’s eye-view: an examination of point-of-view camera use in four informal education settings. Visitor Stud. 20, 218–237. doi: 10.1080/10645578.2017.1404352
Bustang, B., Zulkardi, Z., Darmawijoyo, D., Dolk, M. L. A. M., and Van Eerde, H. A. A. (2013). Developing a local instruction theory for learning the concept of angle through visual field activities and spatial representations. Int. Educ. Stud. 6, 58–70. doi: 10.5539/ies.v6n8p58
Civil, M., and Hunter, R. (2015). Participation of non-dominant students in argumentation in the mathematics classroom. Intercult. Educ. 26, 296–312. doi: 10.1080/14675986.2015.1071755
Clements, D. H., and Battista, M. T. (1989). Learning of geometrical concepts in a Logo environment. J. Res. Math. Educ. 20, 450–467. doi: 10.2307/749420
Clements, D. H., Battista, M. T., Sarama, J., and Swaminathan, S. (1996). Development of turn and turn measurement concepts in a computer-based instructional unit. Educ. Stud. Math. 30, 313–337. doi: 10.1007/BF00570828
Clements, D. H., and Burns, B. A. (2000). Students' development of strategies for turn and angle measure. Educ. Stud. Math. 41, 31–45. doi: 10.1023/A:1003938415559
Collins, K. H., Joseph, N. M., and Ford, D. Y. (2020). Missing in action: gifted black girls in science, technology, engineering, and mathematics. Gift. Child Today 43, 55–63. doi: 10.1177/1076217519880593
Common Core State Standards Initiative. (2021). Geometry. Available at: https://www.thecorestandards.org/Math/Content/G/ (Accessed January 23, 2024).
Crompton, H. (2015). Understanding angle and angle measure: a design-based research study using context aware ubiquitous learning. Int. J. Technol. Math. Educ. 22, 19–30. doi: 10.1564/tme_v22.1.02
Danielak, B. A., Gupta, A., and Elby, A. (2014). Marginalized identities of sense-makers: reframing engineering student retention. J. Eng. Educ. 103, 8–44. doi: 10.1002/jee.20035
de Araujo, Z., Roberts, S. A., Willey, C., and Zahner, W. (2018). English learners in K–12 mathematics education: a review of the literature. Rev. Educ. Res. 88, 879–919. doi: 10.3102/0034654318798093
Devichi, C., and Munier, V. (2013). About the concept of angle in elementary school: misconceptions and teaching sequences. J. Math. Behav. 32, 1–19. doi: 10.1016/j.jmathb.2012.10.001
Doorman, M., Bos, R., de Haan, D., Jonker, V., Mol, A., and Wijers, M. (2019). Making and implementing a mathematics day challenge as a makerspace for teams of students. Int. J. Sci. Math. Educ. 17, 149–165. doi: 10.1007/s10763-019-09995-y
Filippaki, N., and Papamichael, Y. (1997). Tutoring conjunctions and construction of geometry concepts in the early childhood education: the case of the angle. Eur. J. Psychol. Educ. 12, 235–247. doi: 10.1007/BF03172873
Fonger, N. L. (2019). Meaningfulness in representational fluency: an analytic lens for students’ creations, interpretations, and connections. J. Math. Behav. 54:100678. doi: 10.1016/j.jmathb.2018.10.003
Government Digital Services. (2021). Statutory Guidance: National Curriculum in England: Mathematics Programmes of Study. Available at: https://www.gov.uk/government/publications/national-curriculum-in-england-mathematics-programmes-of-study (Accessed May 29, 2024).
Gutiérrez, K. D., Baquedano-López, P., and Tejeda, C. (1999). Rethinking diversity: hybridity and hybrid language practices in the third space. Mind Cult. Act. 6, 286–303. doi: 10.1080/10749039909524733
Hynes, M. M., and Hynes, W. J. (2018). If you build it, will they come? Student preferences for makerspace environments in higher education. Int. J. Technol. Des. Educ. 28, 867–883. doi: 10.1007/s10798-017-9412-5
Joshua, S., Musgrave, S., Hatfield, N., and Thompson, P. W. (2015). “Conceptualizing and reasoning with frames of reference” in Proceedings of the 18th Annual Conference on Research in Undergraduate Mathematics Education. eds. T. Fukawa-Connelly, N. E. Infante, K. Keene, and M. Zandieh (Pittsburgh, PA, USA: SIGMAA), 31–44.
Katirci, N., Shokeen, E., Simpson, A., and Williams-Pierce, C. (2022). Attending to the missing role of gestures in representational fluency. Roundtable presentation presented at the annual research meeting of the American Educational Research Association: San Diego, CA.
Kastberg, S., Simpson, A., and Williams-Pierce, C. (2023). “Perspective taking and design features” in Formative Design in Learning: Design Thinking, Growth Mindset and Community. eds. B. Hokanson, M. Schmidt, M. E. Exter, A. A. Tawfik, and Y. Earnshaw (Cham, Switzerland: Springer), 157–166.
Kaur, H. (2020). Introducing the concept of angle to young children in a dynamic geometry environment. Int. J. Math. Educ. Sci. Technol. 51, 161–182. doi: 10.1080/0020739X.2020.1717657
Ke, L., Sadler, T. D., Zangori, L., and Friedrichsen, P. J. (2020). Students’ perceptions of socio-scientific issue-based learning and their appropriation of epistemic tools for systems thinking. Int. J. Sci. Educ. 42, 1339–1361. doi: 10.1080/09500693.2020.1759843
Keiser, J. M. (2004). Struggles with developing the concept of angle: comparing sixth-grade students' discourse to the history of the angle concept. Math. Think. Learn. 6, 285–306. doi: 10.1207/s15327833mtl0603_2
Kelly, G. J., and Cunningham, C. M. (2019). Epistemic tools in engineering design for K-12 education. Sci. Educ. 103, 1080–1111. doi: 10.1002/sce.21513
Kim, Y. R., Park, M. S., and Tjoe, H. (2021). Discovering concepts of geometry through robotics coding activities. Int. J. Educ. Math. Sci. Technol. 9, 406–425. doi: 10.46328/ijemst.1205
Komarudin, K., Suherman, S., and Anggraini, A. (2021). Analysis of mathematical concept understanding capabilities: the impact of makerspace STEM learning approach models and student learning activities. J. Innov. Educ. Cultur. Res. 2, 35–43. doi: 10.46843/jiecr.v2i1.21
Kirsh, D. (2013). Embodied cognition and the magical future of interaction design. ACM Trans Comput Hum Interact. 20, 1–30.
Latsi, M., and Kynigos, C. (2022). Mathematical assemblages around dynamic aspects of angle in digital and physical space. Int. J. Sci. Math. Educ. 20, 1677–1698. doi: 10.1007/s10763-021-10225-7
Lesh, R., Post, T., and Behr, M. (1987). “Representations and translations among representations in mathematics learning and problem solving” in Problems of Representations in the Teaching and Learning of Mathematics. ed. C. Janvier (Hillsdale, NJ, USA: Lawrence Erlbaum Associates), 33–40.
Lincoln, Y., and Guba, E. (1985). Naturalistic Inquiry, vol. 9. Newberry Park, CA, USA: Sage, 438–439.
LLC. (2024). Zigzag. Available at: https://www.dictionary.com/browse/zigzag (Accessed May 30, 2024).
Mathayas, N., Brown, D. E., Wallon, R. C., and Lindgren, R. (2019). Representational gesturing as an epistemic tool for the development of mechanistic explanatory models. Sci. Educ. 103, 1047–1079. doi: 10.1002/sce.21516
Merriam-Webster. (2021). Zigzag. Available at: https://www.merriam-webster.com/dictionary/zigzag (Accessed November 7, 2021)
Mersand, S. (2021). The state of makerspace research: a review of the literature. TechTrends 65, 174–186. doi: 10.1007/s11528-020-00566-5
Michtelmore, M. (1998). Young students’ concepts of turning and angle. Cogn. Instr. 16, 265–284. doi: 10.1207/s1532690xci1603_2
Min-Chi, K., Cheng-Ling Alice, C., and Chi-Min, K. (1996). Using Robot in Developing the Concept of Angle for Elementary School Children [Paper Presentation]. 37th Annual ASEE/IEEE Frontiers in Education Conference, Milwaukee, WI, United States.
Mitchelmore, M., and White, P. (1998). Development of angle concepts: a framework for research. Math. Educ. Res. J. 10, 4–27. doi: 10.1007/BF03217055
Moore, T. J., Brophy, S. P., Tank, K. M., Lopez, R. D., Johnston, A. C., and Hynes, M. M. (2020). Multiple representations in computational thinking tasks: A clinical study of second-grade students. J Sci Educ Technol, 29, 19–34. doi: 10.1007/s10956-020-09812-0
Moore, T. J., Miller, R. L., Lesh, R. A., Stohlmann, M. S., and Kim, Y. R. (2013). Modeling in engineering: the role of representational fluency in students’ conceptual understanding. J. Eng. Educ. 102, 141–178. doi: 10.1002/jee.20004
Muñoz, L., Villarreal, V., Morales, I., Gonzalez, J., and Nielsen, M. (2020). Developing an interactive environment through the teaching of mathematics with small robots. Sensors 20:1935. doi: 10.3390/s20071935
Nathan, M. J. (2022). Foundations of embodied learning: A paradigm for education. New York, NY, USA: Routledge.
Nakawa, N., Uegatani, Y., Otani, H., and Fukuda, H. (2023). Young Japanese children’s subjectification and objectification through the lens of joint labor in a mathematical activity at a preschool: a case study. Early Childhood Educ. J. 1, –13. doi: 10.1007/s10643-023-01493-9
Nathan, M. J., Srisurichan, R., Walkington, C., Wolfgram, M., Williams, C., and Alibali, M. W. (2013). Building cohesion across representations: a mechanism for STEM integration. J. Eng. Educ. 102, 77–116. doi: 10.1002/jee.20000
Nemirovsky, R., Kelton, M. L., and Civil, M. (2017). “Toward a vibrant and socially significant informal mathematics education” in Compendium for Research in Mathematics Education. ed. J. Cai (Reston, VA, USA: NCTM), 968–979.
Oliver, K. M. (2016). Professional development considerations for makerspace leaders, part one: addressing “what?” and “why?”. TechTrends 60, 160–166. doi: 10.1007/s11528-016-0028-5
Pink, S. (2015). Going forward through the world: thinking theoretically about first person perspective digital ethnography. Integr. Psychol. Behav. Sci. 49, 239–252. doi: 10.1007/s12124-014-9292-0
Radford, L. (2015). Methodological aspects of the theory of objectification. Perspectivas da Educação Matemática 8, 547–567.
Radford, L. (2016a). “Mathematics education as a matter of labor” in Encyclopedia of Educational Philosophy and Theory. ed. M. A. Peters (Springer), 1409–1413.
Radford, L. (2016b). The theory of objectification and its place among sociocultural research in mathematics education. RIPEM Int. J. Res. Math. Educ. 6, 187–206.
Rahayu, S., and Jupri, A. (2021). Geometrical thinking of junior high school students on the topic of lines and angles according to Van Hiele theory. J. Phys. Conf. Ser. 1806:012089. doi: 10.1088/1742-6596/1806/1/012089
Reynolds, F. J., and Reeve, R. A. (2001). Gesture in collaborative mathematics problem-solving. J. Math. Behav. 20, 447–460. doi: 10.1016/S0732-3123(02)00091-3
Rittle-Johnson, B., Farran, D. C., and Durkin, K. L. (2021). Marginalized students’ perspectives on instructional strategies in middle-school mathematics classrooms. J. Exp. Educ. 89, 569–586. doi: 10.1080/00220973.2020.1728513
Ryan, U., and Chronaki, A. (2020). A joke on precision? Revisiting “precision” in the school mathematics discourse. Educ. Stud. Math. 104, 369–384. doi: 10.1007/s10649-020-09963-2
Scally, S. P. (1986). A clinical investigation of the impact of a LOGO learning environment on students' van Hiele levels of geometric understanding. In L. Burton and C Hoyles (Eds.), Proceedings of the 10th International Conference on the Psychology of Mathematics Education. Thousand Oaks, CA, USA: University of London. 123–128.
Settlage, J., and Southerland, S. A. (2019). Epistemic tools for science classrooms: the continual need to accommodate and adapt. Sci. Educ. 103, 1112–1119. doi: 10.1002/sce.21510
Shapiro, L., and Stolz, S. A. (2019). Embodied cognition and its significance for education. Theory Res. Educ. 17, 19–39. doi: 10.1177/1477878518822149
Shokeen, E., Katirci, N., Bih Fofang, J., Simpson, A., and Williams-Pierce, C. (2020). Unpacking mathematical play within makerspaces using embodied cognition. In P. Mirza-Babaei, V. McArthur, V. Abeele Vanden, and M. Birk (Eds.), Extended Abstracts of the 2020 Annual Symposium on Computer-Human Interaction in Play Association for Computing Machinery. eds. P. Mirza-Babaei, V. McArthur, AbeeleV. Vanden and M. Birk (New York, NY, USA: PME-NA). 365–369.
Shokeen, E., Simpson, A., Williams-Pierce, C., and Katirci, N. (2021). “Use of zig-Zag to represent mathematical thinking about angle” in Proceedings of the 43rd Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. eds. D. Olanoff, K. Johnson, and S. Spitzer (Philadelphia, PA), 323–324.
Shumway, J. F., Welch, L. E., Kozlowski, J. S., Clarke-Midura, J., and Lee, V. R. (2023). Kindergarten students’ mathematics knowledge at work: the mathematics for programming robot toys. Math. Think. Learn. 25, 380–408. doi: 10.1080/10986065.2021.1982666
Simpson, A., and Feyerabend, M. (2022). Tug-of-war: the pull of formal institutional practices and structures and the desire for personal change. Int. J. Sci. Math. Educ. 20, 149–168. doi: 10.1007/s10763-020-10139-w
Simpson, A., and Kastberg, S. (2022). Mathematical practices for making: legitimizing youth’s informal ways of doing mathematics. J. Hum. Math. 12, 40–75. doi: 10.5642/jhummath.202201.05
Simpson, A., Kim, J., and Yang, J. (2021). “Caregiver-child interactions: informal ways of doing mathematics during engineering tasks” in Proceedings of the 43rd Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. eds. D. Olanoff, K. Johnson, and S. Spitzer (Philadelphia, PA: PME-NA), 807–811.
Smith, C. P., King, B., and Hoyte, J. (2014). Learning angles through movement: critical actions for developing understanding in an embodied activity. J. Math. Behav. 36, 95–108. doi: 10.1016/j.jmathb.2014.09.001
Soto, H. (2022). Feeling the Angle Sum of a Triangle: An Introduction to Embodied Learning in Mathematics. Math Circular. Available at: https://medium.com/math-circular/feeling-the-angle-sum-of-a-triangle-c9a3e654df3f (Accessed May 30, 2024)
Tan, E., Calabrese Barton, A., and Benavides, A. (2019). Engineering for sustainable communities: epistemic tools in support of equitable and consequential middle school engineering. Sci. Educ. 103, 1011–1046. doi: 10.1002/sce.21515
Tanguay, D., and Venant, F. (2016). The semiotic and conceptual genesis of angle. ZDM 48, 875–894. doi: 10.1007/s11858-016-0789-5
Thanheiser, E., Browning, C. A., Moss, M., Watanabe, T., and Garza-Kling, G. (2010). Developing mathematical content knowledge for teaching elementary school mathematics. Issues Undergr. Math. Preparation Sch. Teach. 1, 1–13.
Uttal, D. H., Meadow, N. G., Tipton, E., Hand, L. L., Alden, A. R., Warren, C., et al. (2013). The malleability of spatial skills: a meta-analysis of training studies. Psychol. Bull. 139, 352–402. doi: 10.1037/a0028446
Keywords: angle, educational robotics, epistemic tools, joint labor, making space
Citation: Simpson A, Shokeen E, Katirci N and Williams-Pierce C (2024) Elementary students’ shared understanding of angle during an educational robotics task. Front. Educ. 9:1425307. doi: 10.3389/feduc.2024.1425307
Received: 29 April 2024; Accepted: 19 June 2024;
Published: 31 July 2024.
Edited by:
Gladys Sunzuma, Bindura University of Science Education, ZimbabweReviewed by:
Lucio Negrini, University of Applied Sciences and Arts of Southern Switzerland (SUPSI), SwitzerlandCopyright © 2024 Simpson, Shokeen, Katirci and Williams-Pierce. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Amber Simpson, YXNpbXBzb25AYmluZ2hhbXRvbi5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.