- Department of Special Education, The University of Texas at Austin, Austin, TX, United States
Read-alouds provide teachers with an efficacious method for introducing vocabulary and content to young children. In this study, kindergarten teachers were randomly assigned to implement a mathematics-focused extended read-aloud program called TEMPLE (Teaching Early Math by Providing Language Exploration) with kindergarten children ages 5–6 (19 teachers with 169 children) or to a business-as-usual (BaU) condition (17 teachers and 146 children). With TEMPLE, teachers used read-alouds with storybooks to introduce mathematics vocabulary and content with each read-aloud accompanied by a brief mathematics activity for a period of up to 18 weeks. At posttest, TEMPLE children demonstrated an advantage on two measures of mathematics, but the difference between TEMPLE and BaU children was not significant. In an analysis related to implementation fidelity, we identified a positive and significant association between the number of book readings that TEMPLE teachers reported and scores on one of the mathematics measures. Limited implementation of the program may have led to these results.
Introduction
Children begin kindergarten with many things in hand: a backpack, crayons, and early mathematics skills. However, upon kindergarten entry, children may already differ in their mathematics knowledge (von Hippel et al., 2018; Throndsen et al., 2020). These differences in mathematics knowledge may impact the later academic success of children. Evidence from the longitudinal data supports that school-entry mathematics skills are predictive of fifth-grade achievement (Claessens et al., 2009). Similarly, Duncan et al. (2007) findings support that mathematics skills at school entry are associated with higher academic performance in later grades. Success in early mathematics requires knowledge of numbers, operations, and vocabulary (Krajewski and Schneider, 2009; Toll and Van Luit, 2014). Due to initial skill differences at the start of kindergarten (von Hippel et al., 2018), children may not have the same chance to develop the interdisciplinary skills they need to succeed in mathematics. To provide children with access to early mathematical language and content, we developed an extended read-aloud routine to be used with mathematics-focused trade books (i.e., story books that can be purchased online or in a bookstore and found in a school or community library, a teacher’s classroom, or in the home).
In this introduction, we provide an overview of early mathematics language and review read-aloud efforts in early education settings. Then we discuss the implementation of read-aloud studies. Finally, we provide the purpose and research questions guiding this study.
Early mathematics language
Children learn and communication through language. As children start to participate in school, there is an academic language that children learn. This academic language may overlap with everyday spoken language that children hear in the home and in their community. However, academic language may differ from the language that children use in their home environments. In either case, some children need support with the learning of academic language (Schleppegrell, 2012). Within the language of mathematics, children learn about mathematics through language, whether that language is words (e.g., three, more, triangle), symbols (e.g., 4, =), drawings, or gestures. In this study, we focus on mathematics language presented primarily with words.
Children hear and use mathematics language very early in their lives, and this language is related to an understanding of mathematics (Turan and De Smedt, 2022). For example, Susperreguy and Davis-Kean (2016) determined that high-quality mathematics language used by caregivers at mealtimes was predictive of children’ mathematics performance 1 year later. In other research, Levine et al. (2010) noted the caregiver talk about numeracy in the home related to child-level understanding of cardinality.
With preschoolers, Purpura et al. (2017a) identified mathematics language as a mediator between mathematics performance and literacy scores. Hornburg et al. (2018) noted mathematics language shared significant correlations with a variety of preschool mathematics tasks, including counting, numeral identification, cardinality, comparison, ordering numbers, and story problems. Importantly, mathematics language appears to predict later success with mathematics. As such, Toll and Van Luit (2014) identified mathematics language as a predictor of early numeracy growth for a wide distribution of children (i.e., children who demonstrated typical or weak mathematics performance). Purpura and Logan (2015) determined mathematics language as a predictor of later mathematics scores, and King and Purpura (2021) suggested mathematics language explained some of the variance in later mathematics performance in preschool. In fact, mathematics language has been identified as one of the strongest predictors of early childhood mathematical success (Purpura et al., 2017a). Therefore, extra efforts supporting early mathematics language could prove useful for acquiring early mathematical skills. One approach for focusing on early mathematics language is through read-alouds, which we explore in the next section.
Mathematics-focused read-alouds
The combination of mathematics and literacy can be a useful strategy for enhancing mathematical language skill for children. Specifically, mathematics-focused read-alouds can be used to develop mathematical knowledge and build mathematical language (Casey et al., 2008; Van den Heuvel-Panhuizen et al., 2016; Purpura et al., 2017b). In this study, we use the term “read-aloud” to refer to this activity even as it is sometimes referred to as “dialogic reading” or “shared book reading” (Anders et al., 2012; Hassinger-Das et al., 2015). A read-aloud is defined as a book or book passage read aloud to a child or group of children, often by an adult (Alatalo and Westlund, 2021).
An interactive read-aloud is defined by Johnston (2016, p. 40) as a practice where teachers or caregivers read text to children while incorporating “pitch, tone, pace, volume changes, questions, and comments to produce a fluent and engaging delivery.” These interactive components engage children and promote oral language by eliciting and reinforcing verbal responses (Mol et al., 2009). Additionally, literacy-focused read-alouds help develop content knowledge, grammar, syntax, and vocabulary knowledge (Biemiller, 2001; Santoro et al., 2008; Heisey and Kucan, 2010; Stevens et al., 2010; Strachan, 2015). Similar tenets of engagement and content-focused talk lend themselves to mathematic-specific read-alouds. Within mathematics, read-alouds can enhance mathematics content knowledge as well as mathematics language (Purpura et al., 2021).
While much of the literature about read-alouds has focused on literacy topics, multiple research teams have investigated mathematics-focused efforts (Casey et al., 2008; Green et al., 2018; McGuire et al., 2021). For example, Casey et al. (2008) developed an intervention for kindergarten children using read-alouds to improve geometry concepts like part-whole relations. Teachers implemented the intervention for 63 kindergarten children over 8 sessions. The read-aloud plus geometry intervention group’s progress (n = 35) was compared to children who received geometry instruction without the read-alouds (n = 28). Teachers using the read-aloud program worked from the book, Tan and the Shape Changer (Schiro et al., 2002), and systematically introduced geometric concepts to children. Teachers received a brief training session from the researchers where they watched video clips of how to best use the materials and activities in their classes. The read-aloud plus geometry incorporated poems, chants, puppets, an interactive storyline, and activities (i.e., combining isosceles triangles to make the body of a dragon) for children to engage with geometry content. At posttest, children who participated in the read-aloud plus geometry condition significantly outperformed those in the geometry-alone condition on near (ES [effect size] = 0.09) and far transfer (ES = 0.12) tasks about triangles. These findings provided support for the use of interactive storytelling as a method for teaching mathematics content related to geometry.
Also at kindergarten, Hassinger-Das et al. (2015) implemented mathematics-focused read-alouds and compared the read-alouds to mathematics instruction without read-alouds. Their primary goal was to increase kindergarten mathematics vocabulary knowledge of children who exhibited low number sense scores on a screening measure. Children (n = 124) from 17 kindergarten classrooms were randomly assigned to participate in small-group instruction using read-alouds, small-group number sense instruction, or a business-as-usual (BaU). In the two conditions with small-group instruction, children participated in 24 sessions (30 min each) with researchers. With the read-alouds condition, researchers used each of seven storybooks over three sessions; researchers read and re-read the books, provided explicit instruction on vocabulary within the books, and engaged children in activities and games related to the mathematics content of the books. With the number sense instruction condition, children engaged in learning about counting, number relations, and operations without read-alouds. At posttest, children who participated in instruction with the read-alouds demonstrated stronger mathematics vocabulary knowledge than children in the other two conditions (ESs = 0.51–0.57). However, the authors identified no significant differences between conditions on a posttest measure of applied problem solving. Children who received number sense instruction demonstrated higher scores on a posttest calculation measure than children in the read-alouds condition or BaU (ESs = 0.58–0.59). Results demonstrated the promise of read-alouds for increasing mathematics-vocabulary knowledge but without transfer to overall mathematics performance.
At preschool, McGuire et al. (2021), investigated the efficacy of a 10-week program focused on early mathematics. Their program, Booked on Math, utilized mathematics-focused book readings and inquiry-based lesson plans. The researchers chose 10 books that aligned with the targeted mathematics domains of number concepts and operations, spatial relationships and shapes, comparison and measurement, and patterns. The program was implemented at a university-based family development center with 6 teachers and 74 children. Two of the teachers voluntarily agreed to be in the BaU condition. Teachers who implemented Booked on Math did not receive specific training on implementing the program before implementing it with their classrooms. At posttest, across seven mathematics constructs, McGuire et al. noted a significant impact on two of the seven constructs (i.e., quantifies and knowledge of patterns) for the children who participated in Booked on Math.
With a focus on children with disabilities, Green et al. (2018) examined the effects of an integrated mathematics and literacy intervention on the early numeracy skills of 50 preschool children (aged 3 to 5) with disabilities (Green et al., 2018). The intervention was implemented by trained researchers and took place 3 times a week for 6 weeks. This quasi-experimental study consisted of two conditions, treatment and BaU. The intervention condition utilized read-alouds and integrated mathematical content through scripted questions. Children engaged in mathematics-related activities after each story was read aloud to them. Children in the BaU were read the same books without the extra mathematical content or activities. At posttest, children who received the intervention significantly outperformed the control group in overall mathematics ability (ES = 0.22), comparison (ES = 0.12), oral counting (ES = 0.15), and one-to-one correspondence (ES = 0 0.13).
While there are more studies about mathematics-focused read-alouds for young children, these studies represent a sample of studies and their approaches to combining mathematics and literacy to promote early numeracy skills. This research establishes how read-aloud interventions can act as a vessel for content such as geometric reasoning (Casey et al., 2008), counting (Green et al., 2018), and shape knowledge (McGuire et al., 2021). As mentioned, many other efforts within this area, particularly with parents and their children, have produced positive results for early childhood mathematics development (Hojnoski et al., 2014; Purpura et al., 2017b; Hendrix et al., 2019; Uscianowski et al., 2020; Purpura et al., 2021).
Purpose and research questions
Because mathematics language is important to concurrent and later mathematics performance (Turan and De Smedt, 2022), we wanted to investigate the initial feasibility of an extended read-alouds program designed to help teachers focus on both mathematics language and mathematics content. Toward this end, we designed the TEMPLE (Teaching Early Mathematics by Providing Language Exploration) project which relied on mathematics-focused read-alouds. We describe this as an extended read-alouds program because each TEMPLE teacher used a read-aloud routine paired with a mathematics activity.
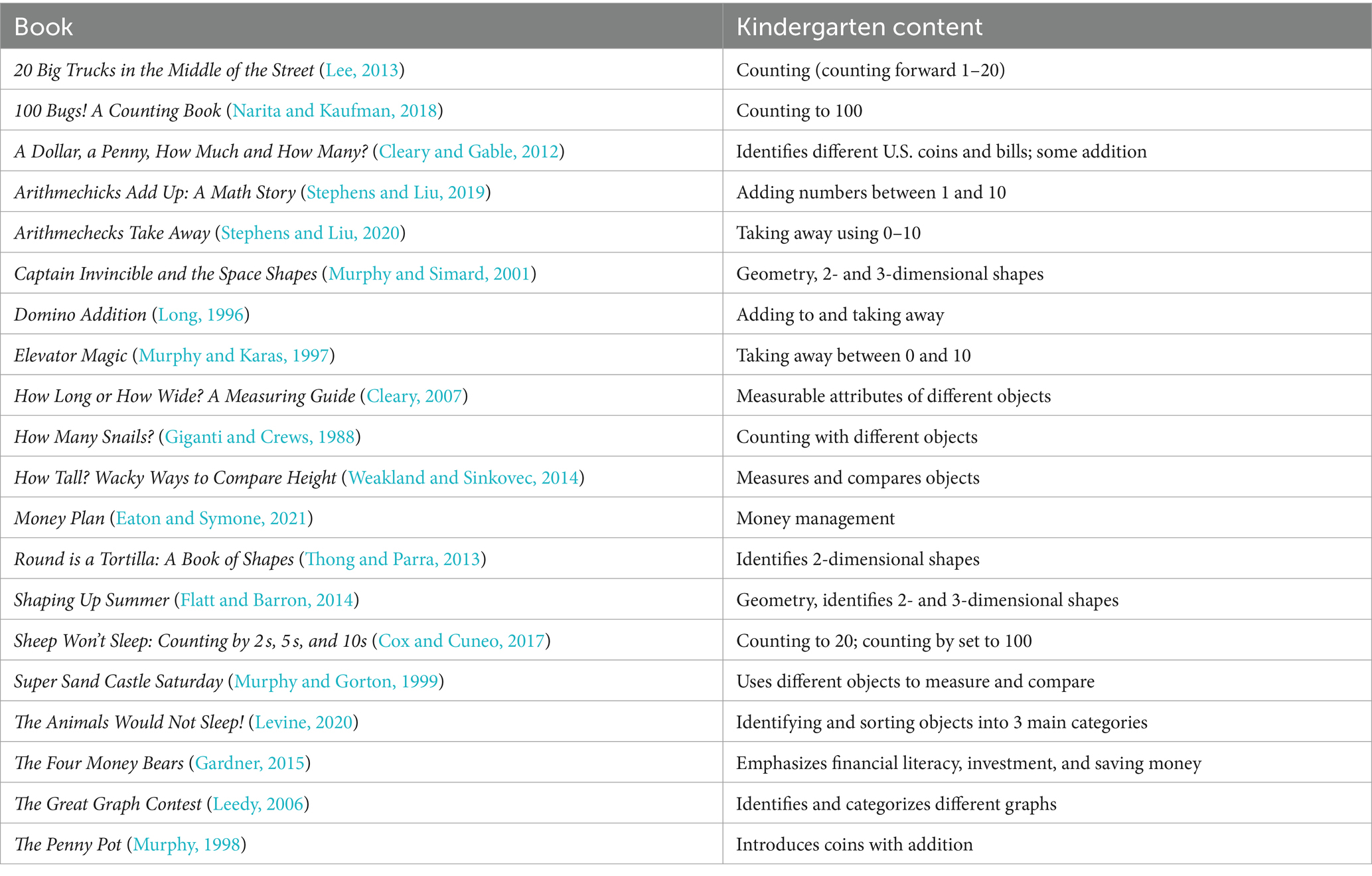
With TEMPLE read-alouds, we relied on previous read-aloud efforts but with slight differences in execution and design. Similar to Booked on Math, developed by McGuire et al. (2021), we designed TEMPLE for implementation at the whole-class level. While other read-aloud studies employed a quasi-experimental design (Casey et al., 2008; Green et al., 2018), we used a randomized controlled trial in which we assigned teachers to participate in TEMPLE read-alouds or a BaU. Past research has investigated similar mathematics read-alouds with smaller sample sizes (i.e., 50 to 84 children; Casey et al., 2008; Green et al., 2018; McGuire et al., 2021; Purpura et al., 2021). Therefore, we aimed to increase the sample size of participating teachers and children. Furthermore, we developed the TEMPLE read-aloud routine for use with any mathematics-focused trade book by adapting a routine previously developed to increase pre-reading skills (i.e., Read-Aloud Routine for Building Vocabulary and Comprehension Skills in Prekindergarten; The Meadows Center for Preventing Educational Risk, 2014). In contrast to McGuire et al. (2021), we trained teachers to implement and use the read-aloud routine with the children in their classrooms. But similar to McGuire et al. (2021), we selected 20 mathematics-focused trade books and considered their match to the Texas mathematics standards for kindergarten as well as each book’s mathematics-related vocabulary, quality of mathematics concepts, and appeal to kindergarten children. We planned for each teacher to select one book each week for at least 18 weeks during the school year.
We explored the following research questions. (1) Does participation in the TEMPLE read-alouds lead to improved child outcomes at posttest on two measures (i.e., one researcher created measure and one commercially available measure) of early mathematics? (2) Do TEMPLE children perform better on mathematics measures when they participated in more book readings with their teacher?
Method
Context and setting
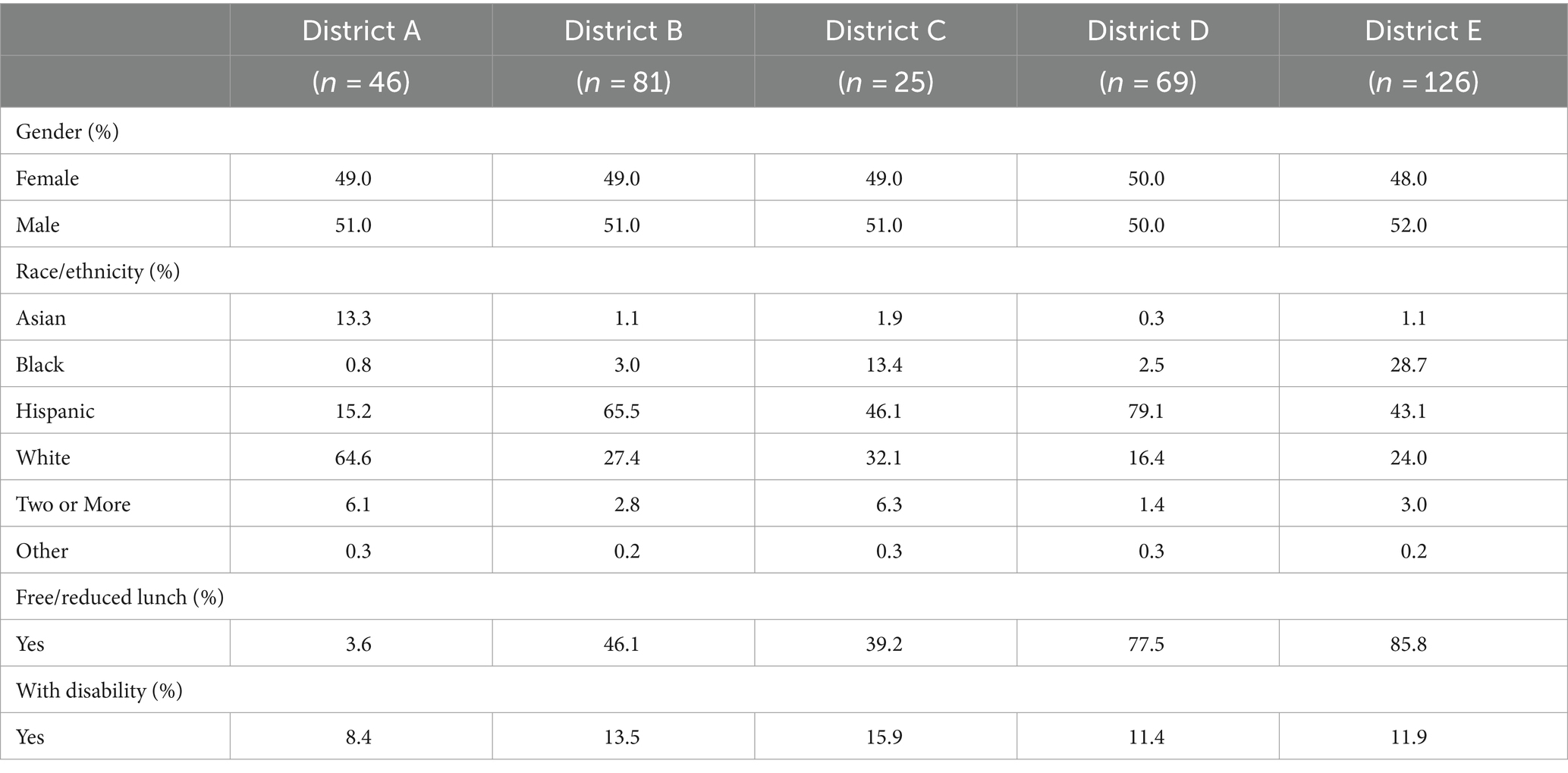
Five school districts in a state in the south central of the U.S. participated in this study. A school district is an organization bound by a geographical area that provides educational services to students across preschool through high school. Our 5 school districts oversaw 15 elementary schools (23,000 students in district), 7 elementary schools (9,000 students), 6 elementary schools (8,000 students), 6 elementary schools (7,000 students), and 5 elementary schools (6,000 students).
Across the 5 districts, we recruited 36 kindergarten teachers from 8 elementary schools. Table 1 presents the demographics of the participating school districts. One district with 15 participating teachers was in a mid-sized city on the eastern side of the state. Three districts were in a rural area of the central portion of the state and had a combined total of 17 teachers. All three of these districts met the federal definition for rural school districts (i.e., census-defined rural territory more than 25 miles from an urbanized area). One district, with four teachers, was in a suburban area adjacent to a large metropolitan city in the central portion of the state.
Participants
Before beginning the study, we received Institutional Review Board approval from our university. All 36 teachers signed written consent forms for participation. Teachers sent home consent forms to the caregivers of all children in each of their classrooms. We collected caregiver consent from 347 children ages 5 to 6 years old. Blocking by school, we randomly assigned 19 teachers to implement the TEMPLE Read-Aloud routine (n = 179 children) or 17 teachers to participate in kindergarten BaU (n = 154 children). Of the classrooms randomized, none dropped out of the study.
Teachers as implementers
Before the program began, we provided one 2 h professional development session to TEMPLE teachers in a synchronous virtual workshop. The virtual workshop allowed teachers to ask questions and clarify important aspects of the project in a collaborative environment. The session was recorded and provided to teachers so they could reference it later. The workshop had the dual purpose of introducing teachers to the idea of mathematics as a language-based activity and teaching them how to use the TEMPLE Read-Aloud routine. A key feature of the TEMPLE Read-Aloud routine was that teachers used mathematics-focused children’s books to increase children’s familiarity with mathematics vocabulary. We provided each teacher with a binder that contained TEMPLE Read-Aloud routine materials we developed for use with any mathematics-focused children’s trade book and a set of 20 books we selected for use during the study period. Table 2 provides an overview of the 20 books. We asked teachers to try to use the TEMPLE Read-Aloud routine for 18 weeks (with 18 books).
During this initial workshop, we addressed the following. (a) We discussed the predictive nature of kindergarten mathematics skills on future academic success in both mathematics and reading (Pagani et al., 2010). (b) We presented research indicating that proficiency with mathematical language is an underlying factor that facilitates both numeracy and reading skills (Purpura et al., 2017a). (c) We highlighted categories of mathematics-related terminology [e.g., terms related to precise quantities (one, two, three), imprecise quantities (a little bit, many, all), spatial location (in, out, above, below), movement or direction (come, go, into, left, right), comparisons (more, less, equal, bigger), and measurement (minute, inch, pound), etc.]. (d) We provided examples of common mathematics-related vocabulary terms that may cause confusion. (e) We discussed various groups of mathematics-related terminology represented on a list of early sight words. (f) We demonstrated how to use the TEMPLE Read-Aloud routine to introduce and explore mathematics content and mathematics vocabulary terms in the kindergarten classroom.
Components of the TEMPLE read-aloud routine
When using the weekly TEMPLE Read-Aloud routine, children participated in interactive read-alouds and activities with one mathematics-focused book over 3 days each week. It was intended for the classroom teacher to use the extended read-aloud routine for approximately 45 min per week of classroom time over those 3 days (i.e., about 20 min, 15 min, and 10 min for the first, second, and third days, respectively).
We selected books that covered as many of the objectives in the Mathematics Texas Essential Knowledge and Skills at Kindergarten as possible. Objectives in this mathematics standards document included: represent and compare whole numbers; describe the relative positive and magnitude of whole numbers; explore relationships within the number system; develop an understanding of addition and subtraction; identify coins; recite numbers to 100 by ones and tens; analyze attributes of two-dimensional shapes and three-dimensional figures; compare measurable attributes; and collect and organize data to interpret information.
For each book, we also considered the mathematics-related vocabulary terms presented, the probable appeal to kindergarten children, and the quality of the presentation of mathematics concepts (e.g., illustrations supported mathematical understanding or the book contained multiple exposures to a concept). Figure 1 provides an overview of the three-day TEMPLE framework used each week.
Day one of TEMPLE read-aloud routine
For the first session each week, the teacher introduced the book and three to five target vocabulary terms from the story. Each week, the classroom teacher selected the target vocabulary terms from the book based on a list of suggested early mathematics terminology. For example, for 20 Big Trucks in the Middle of the Street, vocabulary terms and child-friendly definitions may have included: (a) middle: in between two things, (b) count: find the number, (c) big: not small but large, and (d) small: not big but little. Teachers received a set of vocabulary cards (see Figure 2) they could use with the book. The teacher provided both a kindergarten-friendly definition and a non-verbal representation (e.g., a hand gesture, picture, or object) for each term, and invited children to listen for these words in the story and to give a thumbs-up (or other gesture) when the words were read by their teacher.
Based on best practice recommendations for read-alouds (Giroir et al., 2015), teachers read the selected book straight through the first time, without stopping for discussion, to allow children to focus on understanding the storyline. After completing this first reading, children talked to one another about the story and what they learned with prompting, if needed, from the teacher. The same day, either immediately or later in the day, the teacher read the book a second time, pausing to interact with children about the story, the selected vocabulary terms, and the mathematics content addressed. During this second reading, the teacher also showed children how the pictures supported the story and the mathematics content. After the second reading, the teacher and children engaged in a conversation about how the story and the mathematics concepts addressed related to the children’s everyday lives. Within the routine materials, we provided suggestions on common ways kindergartners use mathematics for each strand in the preschool guidelines (see Figure 2). We asked teachers to elicit ideas from the children in their classroom and to add their own ideas about how everyday connections can be made to the book they read each week.
Finally, children participated in a hands-on activity targeting the mathematics-related terms and concepts in the story. This activity gave children opportunities for further exploration of the concepts and vocabulary terms encountered during the read-aloud time (Massey, 2013). We developed a variety of activity ideas and included these suggestions in the TEMPLE Read-Aloud materials (see Figure 3). We encouraged teachers to use our suggestions as a starting point but to be creative when planning activities related to each book (i.e., a different activity for each day of the routine week, for a total of three extension activities across the week). We emphasized incorporating playfulness, concrete items, and body movements into the activities. We also encouraged teachers to use items already in the classroom to help children connect the mathematics-related content and vocabulary terms to children’s everyday lives. We did not plan specific activities for each book because we designed the TEMPLE Read-Aloud routine to be a framework to be used with any mathematics-focused children’s book. We intended to support teachers in developing their own skills at helping kindergartners connect to the mathematics-related content and vocabulary terms in any mathematics-focused children’s book.
Day two of TEMPLE read-aloud routine
On the second day of the extended read-aloud routine, teachers read the story for a third time, again pausing to interact with the children about the story, pictures, mathematics-related vocabulary terms, and mathematical content. Children then participated in a second hands-on activity connecting to the story’s mathematics content and target vocabulary terms.
Day three of TEMPLE read-aloud routine
For the third day in the weekly routine, teachers provided a third hands-on activity and had the option of rereading the book depending upon child interest. To strengthen the kindergartners’ connections to target vocabulary terms and mathematics concepts, we asked teachers to leave related materials in their mathematics-play center over the week and to make connections to the target terminology and mathematics content as the children went through their everyday routines and activities.
Business-as-usual
Teachers in the BaU continued their kindergarten mathematics instruction with the children in their classroom as originally planned. We did not provide any training to the BaU teachers, and they did not receive any TEMPLE materials from our research team.
Fidelity of implementation
We collected data on fidelity of TEMPLE implementation via survey and direct observations. Each week, we asked each TEMPLE teacher to complete a self-report survey via Qualtrics. Note, every week we sent each teacher an email about filling out the survey but did not follow-up when teachers did not complete the survey. We made this decision because of restrictions related to visitors in school buildings and to see how well teachers implemented the program without much interference from the research team. On the survey, TEMPLE teachers (a) named the book they used during the week; (b) described the number of times they read the book with their class; (c) provided a rating of the book on a scale of 1 (would not recommend this book) to 10 (would highly recommend the book); (d) explained the strengths of the book and activities; and (e) described the weaknesses of the book and activities.
We also conducted direct fidelity observations of those TEMPLE teachers who worked at participating schools within an hour’s proximity to our university (n = 11) in Districts A, B, C, and D. Research staff developed an observation form that could be used to gather observational data specific to each day’s expectations of the TEMPLE read-aloud routine (i.e., Day 1, Day 2, Day 3). For instance, if a teacher was doing the read-aloud for the first time that week (i.e., Day 1), the observer noted whether the teachers activated prior knowledge and introduced the vocabulary terms according to the procedure in the routine. If a teacher was observed reading the book on the second or third day that week, the observer noted how vocabulary was reviewed and how the connecting questions and enrichment activities were implemented.
Measures
We tested consented children in both conditions at pretest and posttest. We used one brief measure with all children: the Kindergarten Texas Early Assessment of Mathematics (KTEAM; Powell and Moore, 2021). We also randomly selected and tested approximately four children in each classroom using the Test of Early Mathematics Ability, 3rd edition (TEMA-3; Ginsberg and Baroody, 2003). We tested these same randomly selected children with the TEMA-3 at pre- and posttest. Children were not administered the KTEAM and the TEMA-3 on the same day.
KTEAM
We developed the KTEAM (Powell and Moore, 2021) to measure child knowledge of the mathematics objectives listed in the Texas Essential Knowledge and Skills (TEKS). These objectives fell into the categories of number and operations, algebraic reasoning, geometry and measurement, data analysis, and personal financial literacy. The KTEAM had two parts. In Part A, examiners tested children in a whole class setting. Children received a paper booklet and drew or circled responses to 37 items in the booklet. The questions focused on an understanding of mathematics vocabulary with questions that asked about more (2 questions), most, greatest, less, least (3 questions), taller, longest, shortest, one more, one less, equal, add, subtract, take away, group of 10, penny, nickel, dime, quarter, pattern (2 questions), rectangle (2 questions), triangle (2 questions), square, circle, sphere, cone, cylinder, cube, and three questions about number writing of three, sixteen, and forty-five. Some questions asked children to circle an option (e.g., “Circle the jug that holds the least water.”). Other questions asked children to draw (e.g., “Draw a triangle.”) or write (“What’s next in this pattern? 1 3 5 1 3 5 1 3 5 ___). In Part B, examiners tested children individually on an additional 10 items. For four items, children looked at pictures and named the number of dots, apples, or bears. On two items, children counted forward from 1 to 20 or backwards from 20 to 1. The final four questions were orally presented word problems (e.g., “You have 3 pennies. I have 8 pennies. How many pennies do we have together?”). Children earned one point for each correct response for a total possible score of 47. At pretest, the range of scores was from 10 to 45. At posttest, the range was from 16 to 47, with only one student scoring a perfect 47. Cronbach’s alpha for this sample was 0.82.
TEMA-3
We used the commercially available TEMA-3 (Ginsberg and Baroody, 2003) to measure mathematics performance across a broad range of early numerical skills including: subitizing, counting, discerning more and less, addition and subtraction, recognizing and writing numerals, and solving word problems with manipulatives. Examiners read from the TEMA-3 administration booklet and administered this measure individually to children. On the TEMA-3, children demonstrated their mathematics understanding using fingers, pictures, manipulatives, pencil and paper, and verbal responses. Testing began at a point determined by the child’s age and stopped when a child scored five consecutive incorrect responses. Because of time constraints, we randomly selected four children in each classroom to take the TEMA-3. In classrooms with four or fewer consented children, we tested all children with consent. Reliability was reported as 0.98. Test–retest reliability, as reported by the manual, was 0.82 to 0.93.
Data collection and scoring
The second author and three additional examiners administered the two measures. We trained the examiners on administration of the KTEAM in one 2 h initial training session and, later, one 1 h review session. The four examiners responsible for testing also administered the more complex TEMA-3, and we provided one 2 h training and practice of the administration of this measure. We required each examiner to demonstrate accuracy in scoring before administering the measures to children in school settings.
We double coded all scoring for the KTEAM and TEMA-3. For these measures, two examiners, working independently, scored measures, and entered data into two separate databases. Upon the completion of data entry, we ran a comparison of the two databases to identify the discrepancies between the two sets of scores. We used the discrepancies to calculate the inter-rater reliability of the scoring as 96.6%. We resolved all discrepancies to ensure almost 100% accuracy in the database.
Procedure
We recruited districts and trained teachers in the early fall of the school year. Pretesting of children occurred in November and December. We asked TEMPLE teachers to use the TEMPLE read-aloud routine in their classrooms for up to 18 weeks, selecting one of the 20 mathematics-focused children’s books each week. Posttesting of all children occurred in April and May.
Data analysis
Children were nested within teachers and teachers were nested within schools. Given the clustered nature of the data, we used multilevel models to examine the effect of TEMPLE read-alouds on child-level outcomes. Multilevel models account for dependencies in nested data structures by estimating residual components at each level and by partitioning total variance into its level-specific component parts, yielding unbiased parameter estimates (Singer and Willett, 2003). We estimated treatment effects at the teacher-level using dummy codes for experimental conditions (1 = TEMPLE, 0 = BaU). We included pretest scores as covariates to optimize statistical power and to aid the interpretation of model parameters (Bloom et al., 2007). Specifically, child-level scores were centered on teacher means (Enders and Tofighi, 2007) in level 1 of the model and class-level means were centered on the grand mean and included as a teacher-level covariate to optimize precision (Hoffman, 2015). The reduced-form equation is:
Here, i represents children, j represents classrooms, and k represents schools. Parameter γ000 refers to the average child-level outcome across all classrooms and schools; represents child-level pretest scores centered around the classroom mean; is the classroom-level pretest aggregate centered around the grand mean; is classroom-level dummy variable representing TEMPLE program; residuals are Level 1, 2, and 3 random effects, respectively. We estimated effect sizes (Hedges’ g) for the main effect of TEMPLE as the ratio of the model-derived treatment coefficient and the unadjusted pooled within-group standard deviation across conditions at posttest (What Works Clearinghouse, 2020).
Our second research question focused on the association between the number of book readings by teachers and children’s math achievement. We evaluated this research question using data from treatment children only because this information was not collected from the teachers in the BaU classes. The three-level model failed to converge, and we removed the random intercept at the school level and estimated a two-level model with the children at Level 1 and teachers at Level 2. The clustering of teachers within schools was accounted for using the design-based correction of standard errors implemented in Mplus (type = complex; McNeish et al., 2017). We estimated the effect of number of book readings at the teacher-level with child-level pretest data centered on classroom means as a level 1 covariate and with classroom-level aggregates centered on the grand means at level 2. We fit models using Mplus 8.7 (Muthén and Muthén, 2023). We handled missing data using the full information maximum likelihood (FIML) estimation, which uses all available information in the data and provides unbiased results with either missing completely at random or missing at random data (Enders, 2010).
Results
Fidelity of TEMPLE implementation and social validity
We had complete TEMPLE survey data in 144 instances (with 17 of the 19 TEMPLE teachers responding at least once; M = 8.0 surveys, SD = 4.3); range of completed surveys by teacher was 1 to 15. During implementation of TEMPLE, we encouraged teachers to use 18 of the 20 books in any order. Teachers reported reading each book an average of 2.5 times during the week (SD = 0.9). Over the course of TEMPLE, teachers reported that children participated in 21.2 read-alouds (SD = 9.0), with a range of 4 to 39 reported total read-alouds.
We collected in-person fidelity of TEMPLE implementation from 11 (of 19) TEMPLE teachers on 32 occurrences, with 11 observations for Day 1, seven for Day 2, and 14 for Day 3. The observation checklist for Day 1 contained 10 items, the Day 2 checklist contained four items, and the checklist for Day 3 contained five items. For Day 1 TEMPLE implementation, we noted 78.9% fidelity. Day 2 adherence was 89.3%. The fidelity for teachers we observed implementing Day 3 was 88.8%.
On the weekly survey, we asked teachers to rate each book on a scale of 1 (terrible) to 10 (amazing), with an average score of 6.6 (SD = 2.8) across the books. When teachers provided strengths of the books and activities, they mentioned “They liked the different shoes and they LOVED hearing the words they had not heard before,” “They like anything with cars and trucks,” “It was engaging and easy for students to understand,” “The students loved the illustrations,” “The loved how they used silly objects to measure the height of the objects and they liked the activities that went with the lesson,” and “This book was super engaging and made it fun and easy to teach multiple concepts!” When teachers gave books a lower rating, they provided comments such as “the book was too long for this age group,” “This book did not seem to keep the students’ attention as well,” or “It included other math/science terms that our students were not familiar with.”
Attrition, baseline equivalence, and variance
Overall attrition ranged from 1.2 to 5.4% at posttest. Rates of attrition were comparable across treatment conditions. At posttest, the difference in attrition rates ranged from 0.4 to 2.4% across outcomes. After the posttest, the potential for bias due to attrition is considered acceptable when following the cautious guidelines provided by the What Works Clearinghouse (2020). The two groups were very similar on pretest scores (Hedges’ g ranged from 0.03 to 0.07; p-values ranged from 0.76 to 0.77), suggesting equivalence prior to onset of TEMPLE.
We estimated an unconditional three-level model with random intercepts to estimate the intraclass correlation (ICC) and to examine the proportion of total variance due to differences between teachers and schools. The estimate of ICC indicated most of the total variance was at the child-level (0.83 for KTEAM and 0.77 for TEMA-3) with smaller amounts at the teacher-level (0.11 for KTEAM and 0.06 for TEMA-3) and the school-level (0.06 for KTEAM and 0.17 for TEMA-3). We fit a three-level conditional model to estimate the main effect of TEMPLE.
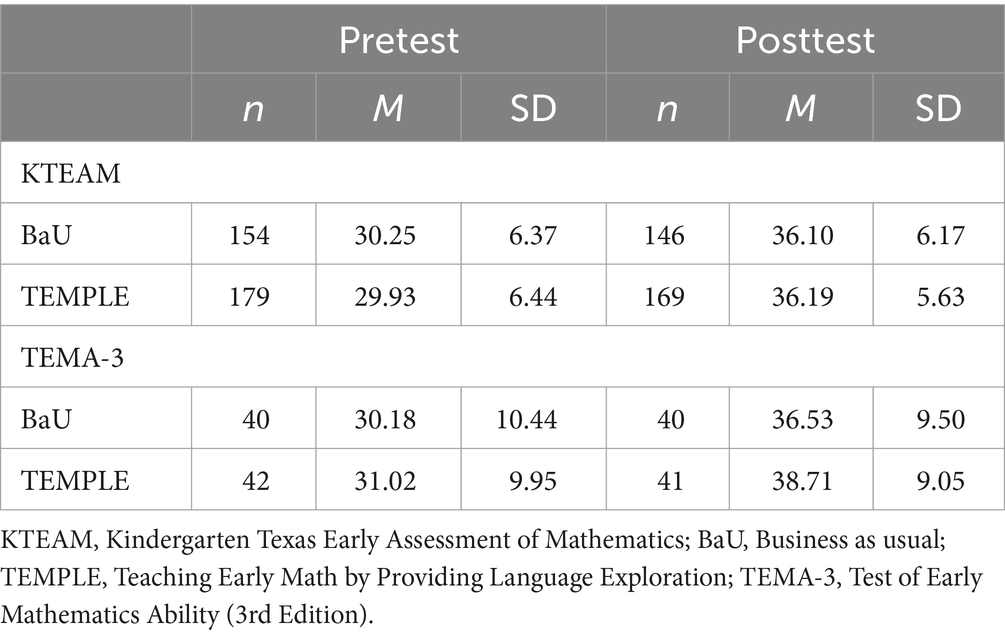
Main effect of TEMPLE
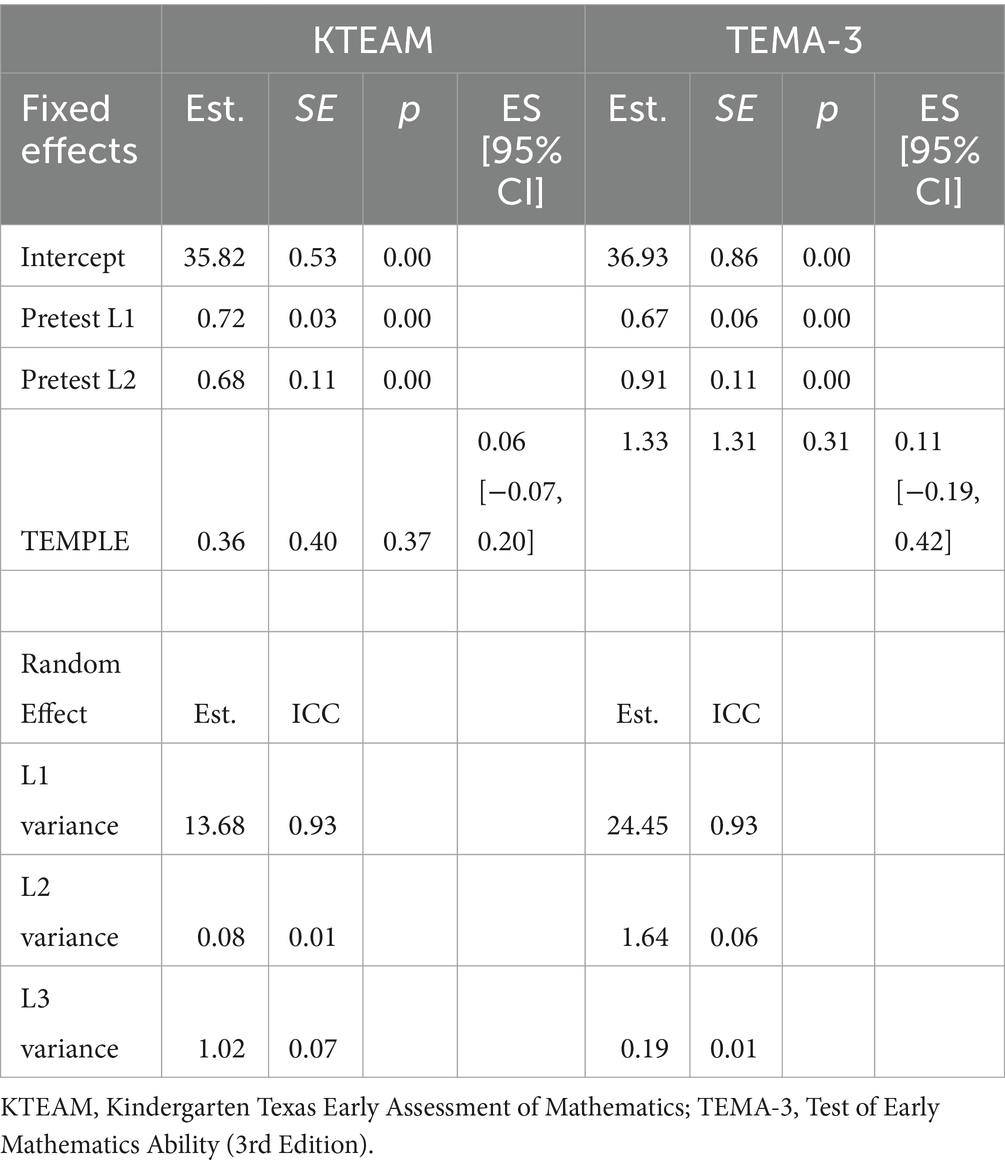
Table 3 displays observed pretest and posttest means and standard deviations for each measure by treatment conditions. The estimated effects of the TEMPLE program on mathematics outcomes are reported in Table 4. Children in classes assigned to the TEMPLE program outperformed children in the control classrooms; however, the difference was not significant on the TEMA-3 (ES = 0.11, 95% CI [−0.19, 0.42]) or on the KTEAM outcome measures (ES = 0.06, 95% CI [−0.07, 0.20]).
Effect of number of book readings on child outcomes
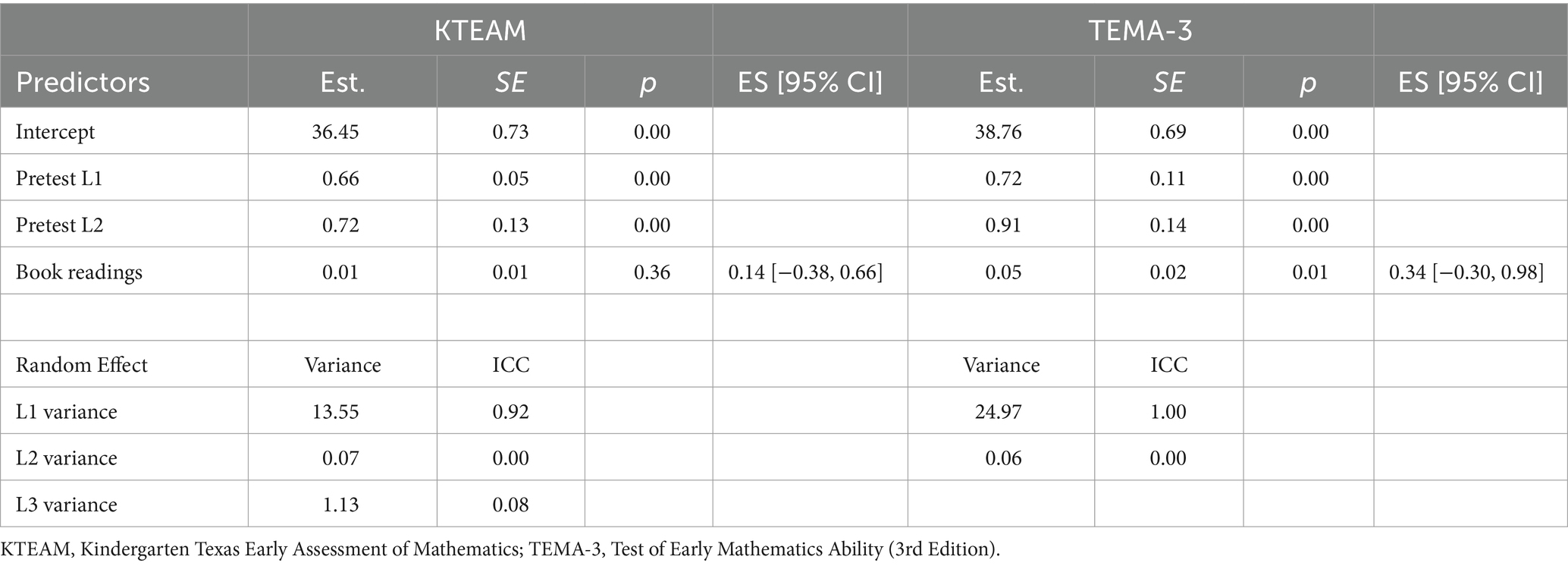
Next, we examined the number of book readings completed by TEMPLE teachers (i.e., the number of times a TEMPLE teacher reported reading any books during the TEMPLE program). We calculated this based on the weekly surveys that teachers completed with the survey question of “how many times did you read the book this week?” We investigated whether the number of total book readings by a TEMPLE teacher was associated with child outcomes, and we estimated a multilevel model with total number of book readings as the between-teacher predictor. Results presented in Table 5 indicate a positive and significant association between number of book readings and children’s scores on the TEMA-3 ( = 0.05, SE = 0.02, p = 0.01). It is important to note that although the regression coefficient was significant, the ES was not (ES = 0.34, 95% CI [−0.30, 0.98]).
Our analysis suggests that there may be an effect of the total number of book readings on TEMA-3 scores, as indicated by an ES of 0.34. However, it’s important to interpret these results with caution due to the wide confidence interval, which ranges from −0.30 to 0.98. This wide range suggests considerable uncertainty surrounding the estimated effect. Given our small sample size (n = 38), it is plausible that our analysis lacks the statistical power to detect effects. Therefore, while the observed effect provides some evidence for the impact of number of book readings, further research with larger sample sizes is needed to provide a more conclusive finding. The association between number of book readings and KTEAM scores was positive but not significant ( = 0.01, SE = 0.01, p = 0.36, ES = 0.14, 95% CI [−0.38, 0.66]).
Discussion
In this study, we investigated the initial feasibility of mathematics-focused extended read-alouds (i.e., TEMPLE) implemented by kindergarten teachers with their entire classrooms of kindergarten children. First, we examined the impact of the TEMPLE Read-Alouds on two measures of mathematics, and we compared children who participated in TEMPLE versus children in a BaU. Based on those results, we investigated whether teachers who reported book use of TEMPLE materials had differential results within the TEMPLE condition.
Effect of TEMPLE read-alouds
With our first research question, we asked whether teacher and child participation in TEMPLE led to improved child outcomes at posttest on two different mathematics measures. We determined baseline equivalence between the two conditions (i.e., TEMPLE and BaU); therefore, we could attribute any posttest differences to participation in TEMPLE. Our analysis, however, suggested no significant difference on either the KTEAM (for which we had scores for all children) or the TEMA-3 (for which we had scores for approximately 4 children in each classroom). We noted that the TEMPLE children had greater posttest scores than BaU children on both measures, but these scores, while positive, were not significant.
Our effect size on the TEMA-3 of 0.11 was fairly similar to that in other read-aloud research studies, such as Casey et al. (2008, ESs = 0.09, 0.12) and Green et al. (2018, ESs = 0.12, 0.13, 0.15, 0.22). But this was not similar to the effects (0.51, 0.57) of Hassinger-Das et al. (2015), perhaps because the outcome in Hassinger-Das was a mathematics language measure whereas our KTEAM emphasized both mathematics vocabulary and mathematics content. In a preschool evaluation of TEMPLE (Powell et al., under review), we determined the TEMPLE read-aloud routine as efficacious for improving child-level mathematics outcomes. That we did not replicate the TEMPLE results from preschool (i.e., children ages 3 and 4) in kindergarten (i.e., children ages 5 and 6) could indicate that read-alouds are not as appropriate in kindergarten as preschool; but prior research shows that is not the case. For that reason, we turned our attention – with our second research question – toward teacher implementation of TEMPLE as an explanation for this difference in results.
Effect of TEMPLE read-alouds with fidelity
With our second research question, we pursued the idea that teacher implementation of TEMPLE may have had a differential impact on child-level mathematics outcomes. Our analysis suggested that fidelity of TEMPLE implementation had some effect of the results from our study. When teachers reported doing more book readings, the association between the number of readings and scores on the TEMA-3 was both positive and significant. We saw the same positive trend for scores on the KTEAM yet this was not significant.
It was important to investigate this research question for several reasons. First, we relied on teachers to fill in a brief weekly survey to report which book they read during the week. Even with a few gentle reminders from the research team, teachers did not submit surveys regularly. In fact, two teachers never submitted a single survey, but 17 teachers submitted a total of 144 surveys. The average number of returned surveys from each teacher was 8, which was less than half of the expected number of weeks of TEMPLE implementation (i.e., 18 weeks).
In prior read-aloud research, researchers often implemented the read-alouds in classrooms (e.g., Hassinger-Das et al., 2015; Purpura et al., 2017b; Green et al., 2018). Given that researchers would drive to schools for the project, all read-aloud sessions would have been implemented as planned. As such, both Green et al. (2018) and Hassinger-Das et al. (2015) measured fidelity of implementation of the researchers (not teachers) who implemented their read-aloud intervention. Fidelity for such studies is important to learn about whether the program was implemented and the quality of that implementation (O’Donnell, 2008). In Casey et al. (2008), kindergarten teachers implemented the read-alouds with one book for eight sessions. However, the authors provided no information about fidelity of intervention implementation. This is similar to no information about fidelity from the classroom teachers who implemented read-alouds in McGuire et al. (2021). While our return rate from the weekly teacher surveys was underwhelming, it does provide a snapshot as to how many teachers implemented a read-alouds program when provided with initial training but then, for the most part, left to implement the program on their own.
Second, in the small number of in-person fidelity observations we conducted, we noted fidelity for Day 1 of each week’s TEMPLE implementation to average 78.9%. This percentage is almost identical to Peltier et al. (2021) study in which a classroom teacher implemented a word-problem intervention with 78.6% fidelity. We would expect this percentage to be higher, particularly for the day in which each book and its vocabulary would be introduced. Our fidelity rate might be acceptable, but there is room for improvement. As fidelity of implementation for mathematics interventions has been identified as an important predictor of child-level outcomes (Nelson et al., 2019), not only should future research investigate whether teachers are doing the TEMPLE read-alouds but whether they are using the materials effectively.
Third, we provided all TEMPLE teachers with a brief (i.e., 2 h) professional development workshop about the TEMPLE read-alouds and routine. Teachers attended this session before implementation. Due to constraints on school visits, we did not provide any follow-up workshops or embedded coaching. As described in the literature, coaching is often an integral companion to professional development (Rudd et al., 2009; Wood et al., 2016) which may or may not be important to embed in future iterations of this research (Kennedy, 2016). Beyond including follow-up professional development and coaching, however, teachers, schools, and districts may need to be open to a change in routines and practices for teachers to incorporate a new practice into their regular weekly teaching routine (Thoonen et al., 2011).
Limitations
Before concluding, we note several limitations to this research study. First and foremost, we did not have regular implementation of TEMPLE from all teachers. Teachers did not fill in surveys regularly, even with a weekly email reminder from our research team. We also did not conduct regular in-person checks of implementation fidelity. Much of our hands-off approach was due to COVID-related protocols still in place in schools with schools excluding or limiting visitors in the school building. But without this information, we do not know if TEMPLE teachers were implementing TEMPLE and not filling in the weekly survey or if they were not implementing TEMPLE at all. We also have a limited understanding of the mathematics activities that teachers used alongside each book. Future research should focus on the initial efficacy of the extended TEMPLE Read-Alouds when implemented with high levels of fidelity. Furthermore, future research should investigate TEMPLE Read-Alouds with a prescribed mathematics activity for each session or a teacher-selected activity. And if teachers select the activity to accompany each book reading, more information should be collected on the type of activity, duration of activity, and emphasis on vocabulary within each activity. In the future, researchers may also want to collect observational data on how children used the target vocabulary terms within the TEMPLE Read-Alouds program and across the school day.
Second, we did not administer the TEMA-3 to all participating children. We randomly selected four children in each classroom to participate in the TEMA-3 to limit the in-person interaction with our research staff in school buildings. In the future, we would administer this assessment to all children as it is a standardized assessment of early mathematics knowledge. Third, our KTEAM measure produced higher average scores at pretest, which may have contributed to ceiling effects at posttest. In the future, we would revise this assessment and include more mathematics vocabulary terms appropriate for the early elementary grades.
Conclusion
We learned of no differences between TEMPLE children and BaU children after participation in TEMPLE read-alouds; however, we did see a significant different between conditions when we considered the number of book readings conducted by TEMPLE teachers. If we were to describe this study, we would suggest that we conducted an initial feasibility study in which we learned about implementation fidelity, or lack thereof. To determine the efficacy of the extended TEMPLE read-alouds for kindergarten children, we would need to provide better training to teachers, and we would need to better monitor fidelity related to dosage and quality of the instruction.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving humans were approved by The University of Texas at Austin Institutional Review Board. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Author contributions
SP: Writing – original draft, Writing – review & editing. CM: Project administration, Writing – original draft. MVT: Writing – original draft. A-MF: Formal analysis, Writing – original draft. GR: Formal analysis, Methodology, Writing – original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported in part by a grant from the T.L.L. Temple Foundation.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alatalo, T., and Westlund, B. (2021). Preschool teachers’ perceptions about read-alouds as a means to support children’s early literacy and language development. J. Early Child. Lit. 21, 413–435. doi: 10.1177/1468798419852136
Anders, Y., Rossbach, H.-G., Weinert, S., Ebert, S., Kuger, S., Lehrl, S., et al. (2012). Home and preschool learning environments and their relations to the development of early numeracy skills. Early Child. Res. Q. 27, 231–244. doi: 10.1016/j.ecresq.2011.08.003
Biemiller, A. (2001). Teaching vocabulary: early, direct, and sequential. Am. Educ. 25, 24–28, 47. Available at: https://www.aft.org/ae/spring2001/biemiller
Bloom, H. S., Richburg-Hayes, L., and Black, A. R. (2007). Using covariates to improve precision for studies that randomize schools to evaluate educational interventions. Educ. Eval. Policy Anal. 29, 30–59. doi: 10.3102/0162373707299550
Casey, B., Erkut, S., Ceder, I., and Young, J. M. (2008). Use of a storytelling context to improve girls’ and boys’ geometry skills in kindergarten. J. Appl. Dev. Psychol. 29, 29–48. doi: 10.1016/j.appdev.2007.10.005
Claessens, A., Duncan, G., and Engel, M. (2009). Kindergarten skills and fifth-grade achievement: evidence from the ECLS-K. Econ. Educ. Rev. 28, 415–427. doi: 10.1016/j.econedurev.2008.09.003
Cleary, B. P., and Gable, B. (2012). A dollar, a penny, how much and how many?. Kildare, Ireland: Millbrook Press.
Cox, J., and Cuneo, N. (2017). Sheep won't sleep: Counting by 2s, 5s, and 10s. New York, NY: Holiday House.
Duncan, G. J., Dowsett, C. J., Claessens, A., Magnuson, K., Huston, A. C., Klebanov, P., et al. (2007). School readiness and later achievement. Dev. Psychol. 43, 1428–1446. doi: 10.1037/0012-1649.43.6.1428
Enders, C. K., and Tofighi, D. (2007). Centering predictor variables in cross-sectional multilevel models: a new look at an old issue. Psychol. Methods 12, 121–138. doi: 10.1037/1082-989x.12.2.121
Giganti, P., and Crews, D. (1988). How many snails?: A counting book. New York, NY: Greenwillow Books.
Ginsberg, H. P., and Baroody, A. J. (2003). Test of early mathematics ability (3rd Ed). Austin, TX: Pro-ed.
Giroir, S., Grimaldo, L. R., Vaughn, S., and Roberts, G. (2015). Interactive read-alouds for English learners in the elementary grades. Read. Teach. 68, 639–648. doi: 10.1002/trtr.1354
Green, K. B., Gallagher, P. A., and Hart, L. (2018). Integrating mathematics and children’s literature for young children with disabilities. J. Early Interv. 40, 3–19. doi: 10.1177/1053815117737339
Hassinger-Das, B., Jordan, N. C., and Dyson, N. (2015). Reading stories to learn math: mathematics vocabulary instruction for children with early numeracy difficulties. Elem. Sch. J. 116, 242–264. doi: 10.1086/683986
Heisey, N., and Kucan, L. (2010). Introducing science concepts to primary students through read-alouds: interactions and multiple texts make the difference. Read. Teach. 63, 666–676. doi: 10.1598/RT.63.8.5
Hendrix, N. M., Hojnoski, R. L., and Missall, K. N. (2019). Shared book reading to promote math talk in parent-child dyads in low-income families. Top. Early Child. Spec. Educ. 39, 45–55. doi: 10.1177/0271121419831762
Hoffman, L. (2015). Longitudinal analysis: modeling within-person fluctuation and change. London, England: Routledge.
Hojnoski, R. L., Columba, H. L., and Polignano, J. (2014). Embedding mathematical dialogue in parent-child shared book reading: a preliminary investigation. Early Educ. Dev. 25, 469–492. doi: 10.1080/10409289.2013.810481
Hornburg, C. B., Schmitt, S. A., and Purpura, D. J. (2018). Relations between preschoolers’ mathematical language understanding and specific numeracy skills. J. Exp. Child Psychol. 176, 84–100. doi: 10.1016/j.jecp.2018.07.005
Johnston, V. (2016). Successful read-alouds in today’s classroom. Kappa Delta Pi Rec. 52, 39–42. doi: 10.1080/00228958.2016.1123051
Kennedy, M. M. (2016). How does professional development improve teaching? Rev. Educ. Res. 86, 945–980. doi: 10.3102/0034654315626800
King, Y. A., and Purpura, D. J. (2021). Direct numeracy activities and early math skills: math language as a mediator. Early Child. Res. Q. 54, 252–259. doi: 10.1016/j.ecresq.2020.09.012
Krajewski, K., and Schneider, W. (2009). Exploring the impact of phonological awareness, visual-spatial working memory, and preschool quantity-number competencies on mathematics achievement in elementary school: findings from a longitudinal study. J. Exp. Child Psychol. 103, 516–531. doi: 10.1016/j.jecp.2009.03.009
Levine, S. C., Suriyakham, L. W., Rowe, M. L., Huttenlocher, J., and Gunderson, E. A. (2010). What counts in the development of young children’s number knowledge? Dev. Psychol. 46, 1309–1319. doi: 10.1037/a0019671
Massey, S. L. (2013). From the reading rug to the play center: enhancing vocabulary and comprehensive language skills by connecting storybook reading and guided play. Early Childhood Educ. J. 41, 125–131. doi: 10.1007/s10643-012-0524-y
McGuire, H. B., Clayton, G., Yoo, M., and Logue, M. E. (2021). Booked on math: developing math concepts in pre-k classrooms using interactive read-alouds. Early Childhood Educ. J. 49, 313–323. doi: 10.1007/s10643-020-01073-1
McNeish, D., Stapleton, L. M., and Silverman, R. D. (2017). On the unnecessary ubiquity of hierarchical linear modeling. Psychol. Methods 22, 114–140. doi: 10.1037/met0000078
Mol, S. E., Bus, A. G., and de Jong, M. T. (2009). Interactive book reading in early education: a tool to stimulate print knowledge as well as oral language. Rev. Educ. Res. 79, 979–1007. doi: 10.3102/0034654309332561
Murphy, S. J., and Simard, R. (2001). Captain invincible and the space shapes. New York, NY: HarperCollins.
Muthén, L., and Muthén, M. (2023). Mplus. Available at: https://www.statmodel.com/index.shtml.
Nelson, P. M., Van Norman, E. R., Parker, D. C., and Cormier, D. C. (2019). An examination of interventionist implementation fidelity and content knowledge as predictors of math intervention effectiveness. J. Appl. Sch. Psychol. 35, 234–256. doi: 10.1080/15377903.2019.1568334
O’Donnell, C. L. (2008). Defining, conceptualizing, and measuring fidelity of implementation and its relationship to outcomes in K–12 curriculum intervention research. Rev. Educ. Res. 78, 33–84. doi: 10.3102/0034654307313793
Pagani, L. S., Fitzpatrick, C., Archambault, I., and Janosz, M. (2010). School readiness and later achievement: a French-Canadian replication and extension. Dev. Psychol. 46, 984–994. doi: 10.1037/a0018881
Peltier, C., Lingo, M. E., Autry, F., Deardorff, M. E., and Palacios, M. (2021). Schema-based instruction implemented under routine conditions. J. Appl. Sch. Psychol. 37, 246–267. doi: 10.1080/15377903.2020.1821273
Powell, S. R., and Moore, C. (2021). Kindergarten Texas early assessment of mathematics. Austin, TX: S. R. Powell, 1912 Speedway, 78712.
Powell, S. R., Moore, C. E., Forsyth, S. R., Fall, A.-M., and Roberts, G. (under review). The impact of mathematics-focused read-alouds on mathematics outcomes for preschool children.
Purpura, D. J., and Logan, J. A. R. (2015). The nonlinear relations of the approximate number system and mathematical language to early mathematics development. Dev. Psychol. 51, 1717–1724. doi: 10.1037/dev0000055
Purpura, D. J., Logan, J. A. R., Hassinger-Das, B., and Napoli, A. R. (2017a). Why do early mathematics skills predict later reading? The role of mathematical language. Dev. Psychol. 53, 1633–1642. doi: 10.1037/dev0000375
Purpura, D. J., Napoli, A. R., Wehrspann, E. A., and Gold, Z. S. (2017b). Causal connections between mathematical language and mathematical knowledge: a dialogic reading intervention. J. Res. Educ. Effect. 10, 116–137. doi: 10.1080/19345747.2016.1204639
Purpura, D. J., Schmitt, S. A., Napoli, A. R., Dobbs-Oates, J., King, Y. A., Hornburg, C. B., et al. (2021). Engaging caregivers and children in picture books: a family-implemented mathematical language intervention. J. Educ. Psychol. 113, 1338–1353. doi: 10.1037/edu0000662
Rudd, L. C., Lambert, M. C., Satterwhite, M., and Smith, C. H. (2009). Professional development + coaching = enhanced teaching: increasing usage of math mediated language in preschool classrooms. Early Childhood Educ. J. 37, 63–69. doi: 10.1007/s10643-009-0320-5
Santoro, L. E., Chard, D. J., Howard, L., and Baker, S. K. (2008). Making the “very” most of classroom read-alouds to promote comprehension and vocabulary. Read. Teach. 61, 396–408. doi: 10.1598/RT.61.5.4
Schiro, M., Casey, B., and Anderson, K. (2002). Tan and the shape changer. St. Petersburg, FL: The Wright.
Schleppegrell, M. J. (2012). Academic language in teaching and learning: introduction to the special issue. Elem. Sch. J. 112, 409–418. doi: 10.1086/663297
Singer, J. D., and Willett, J. B. (2003). Applied longitudinal data analysis: modeling change and event occurrence. Oxford, England: Oxford University Press.
Stephens, A. M., and Liu, J. (2019). Arithmechicks add up: a math story. Honesdale, PA: Boyds Mills Press.
Stevens, R. J., Van Meter, P., and Warcholak, N. D. (2010). The effects of explicitly teaching story structure to primary grade children. J. Lit. Res. 42, 159–198. doi: 10.1080/10862961003796173
Strachan, S. L. (2015). Kindergarten students’ social studies and literacy learning from interactive read-alouds. J. Soc. Stud. Res. 39, 207–223. doi: 10.1016/j.jssr.2015.08.003
Susperreguy, M. I., and Davis-Kean, P. E. (2016). Maternal math talk in the home and math skills in preschool children. Early Educ. Dev. 27, 841–857. doi: 10.1080/10409289.2016.1148480
The Meadows Center for Preventing Educational Risk (2014). Read-aloud routine for building vocabulary and comprehension skills in prekindergarten : Author.
Thoonen, E. E. J., Sleegers, P. J. C., Oort, F. J., Peetsma, T. T. D., and Geijsel, F. P. (2011). How to improve teaching practices: the role of teacher motivation, organizational factors, and leadership practices. Educ. Adm. Q. 47, 496–536. doi: 10.1177/0013161X11400185
Throndsen, J. E., Shumway, J. F., and Moyer-Packenham, P. S. (2020). The relationship between mathematical literacy at kindergarten entry and public preschool attendance, type, and quality. Early Childhood Educ. J. 48, 473–483. doi: 10.1007/s10643-019-01014-7
Toll, S. W. M., and Van Luit, J. E. H. (2014). Explaining numeracy development in weak performing kindergartners. J. Exp. Child Psychol. 124, 97–111. doi: 10.1016/j.jecp.2014.02.001
Turan, E., and De Smedt, B. (2022). Mathematical language and mathematical abilities in preschool: a systematic literature review. Educ. Res. Rev. 36:100457. doi: 10.1016/j.edurev.2022.100457
Uscianowski, C., Almeda, M. V., and Ginsberg, H. P. (2020). Differences in the complexity of math and literacy questions parents pose during storybook reading. Early Child. Res. Q. 50, 40–50. doi: 10.1016/j.ecresq.2018.07.003
Van den Heuvel-Panhuizen, M., Elia, I., and Robitzsch, A. (2016). Effects of reading picture books on kindergartners’ mathematics performance. Educ. Psychol. 36, 323–346. doi: 10.1080/01443410.2014.963029
von Hippel, P. T., Workman, J., and Downey, D. B. (2018). Inequality in reading and math skills forms mainly before kindergarten: a replication, and partial correct, or “are schools to great equalizer?”. Sociol. Educ. 91, 323–357. doi: 10.1177/0038040718801760
Weakland, M., and Sinkovec, I. (2014). How tall?: wacky ways to compare height. Bloomington, MN: Picture Window Books.
What Works Clearinghouse (2020). What works clearinghouse procedures handbook, version 4.1 : U.S. Department of Education, Institute of Education Sciences, National Center for Education Evaluation and Regional Assistance. Available at: https://ies.ed.gov/ncee/wwc/handbooks.
Keywords: mathematics, read-alouds, kindergarten, mathematics vocabulary, numeracy
Citation: Powell SR, Moore CE, Vander Tuin M, Fall A-M and Roberts G (2024) Investigation of the initial feasibility of extended mathematics read-alouds used by kindergarten teachers. Front. Educ. 9:1379491. doi: 10.3389/feduc.2024.1379491
Edited by:
Martin Schöfl, University of Education Upper Austria, AustriaReviewed by:
Michael Schurig, Technical University Dortmund, GermanyVerena Dresen, University of Innsbruck, Austria
Copyright © 2024 Powell, Moore, Vander Tuin, Fall and Roberts. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sarah R. Powell, c3Jwb3dlbGxAdXRleGFzLmVkdQ==
†ORCID: Sarah R. Powell, orcid.org/0000-0002-6424-6160
Clinton E. Moore, orcid.org/0000-0002-1757-1892
Mackenna Vander Tuin, orcid.org/0009-0002-7027-0236
Anna-Maria Fall, orcid.org/0000-0002-6257-6684
Greg Roberts, orcid.org/0000-0001-6333-7442
 Sarah R. Powell
Sarah R. Powell Clinton E. Moore†
Clinton E. Moore†