
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Educ., 16 July 2024
Sec. Teacher Education
Volume 9 - 2024 | https://doi.org/10.3389/feduc.2024.1367076
Background: Teacher instructional practices play crucial roles not only in shaping the happenings in the classrooms but also in facilitating students’ understanding and success rates in mathematics. However, previous studies on teachers’ factors that bolster or undermine instructional practices often consider the influence of these factors on instructional practices in isolation.
Objective: On the contrary, we took an inclusive approach in the present study to quantify and disentangle the complex relationship between self-efficacy, job satisfaction, stress, cooperation, and instructional practices with a focus on mathematics teachers.
Methods: We used structural equation modelling to analyze the generated data from 1,304 Norwegian secondary school mathematics teachers.
Results: The results showed that teacher self-efficacy contributes the most to teacher instructional practices through direct and mediating effects. It mediates the effects of stress and cooperation on teachers’ practices. The contribution of teacher cooperation to instructional practices supersedes teacher stress while the effect of job satisfaction is not substantial. Also, instructional practices that include frequent use of techniques of cognitive activation, clarity of instruction, and classroom management are more prevalent among female than male mathematics teachers in Norway.
Conclusion: By implications, these findings revealed that teacher self-efficacy and teacher cooperation are prime factors which interventions could bring about the desired improvement in classroom practices among mathematics teachers.
The role of teachers in conducting and shaping happenings in the classrooms cannot be over-emphasized especially when it concerns the teaching and learning of mathematics. Depaepe and König (2018) refer to these eventual happenings in the classrooms as teacher instructional practices. In response to the development of 21st-century knowledge and skills, several educational institutions around the world are seeking instructional practices that facilitate creativity and innovation, critical thinking, problem-solving, communication and collaboration among students. Thus, research into the happenings in the classrooms has witnessed increased attention in the international context over the last few decades (Schiefele and Schaffner, 2015; Larsen and Jang, 2021). There is an accumulation of evidence that suggests that teacher instructional practices form a substantial part of quality instruction and implicates the former in students’ success rates in mathematics (Rasmussen and Kwon, 2007; Yu and Singh, 2016; König et al., 2021; Larsen and Jang, 2021). Beyond the influence of instructional practices on students’ learning outcomes, it would be interesting to identify teachers’ personal or interpersonal factors that foster or mar their practices in the classrooms. This identification would be useful for possible interventions. Researchers have launched investigations into this line of thought and identified teacher self-efficacy, teacher competence knowledge, teacher beliefs, and teacher cooperation as important contributors to teacher practices in the classroom (Depaepe and König, 2018; Yang et al., 2020; Bellibaş et al., 2021; Sulla and Rollo, 2023). Building on this foundation, attempts are made in the present study to investigate the influence of teacher self-efficacy, teacher cooperation, teacher job satisfaction, and teacher stress on teacher instructional practices in mathematics classrooms.
Teacher self-efficacy entails teachers’ self-evaluation of their competence to teach such that given educational attainment is achieved. As Skaalvik and Skaalvik (2007) rightly put it, teacher self-efficacy from a social cognitive perspective encapsulates “individual teachers’ beliefs in their abilities to plan, organise, and carry out activities required to attain given educational goals” (p. 612). It is a matter of teachers’ beliefs in what they can do in a situation to achieve a certain level of accomplishment. This situation-specificity of teachers’ self-efficacy makes it different from self-concept which captures a stable form of beliefs and attributes (Bong and Clark, 1999; Bong and Skaalvik, 2003). It follows logically that teacher self-efficacy is multidimensional given the multidimensional nature of the situation (in this case the teaching and learning activities). As such, researchers have identified self-efficacy in instruction, self-efficacy in classroom management, and self-efficacy in student engagement as three dimensions of teacher self-efficacy (Tschannen-Morana and Hoy, 2001; Klassen et al., 2009). Next to self-efficacy, in the present study, as a multidimensional construct is teacher job satisfaction. Teacher job satisfaction is “the sense of fulfilment and gratification that teachers experience through their work as a teacher” (Ainley and Carstens, 2018, p. 43). It entails teachers’ self-evaluations of their teaching jobs. The evaluation could be positive, negative, or mixed feelings depending on the circumstances. Teacher job satisfaction is relatively high in Norway as compared with some countries around the world with 93% overall job satisfaction, 48% satisfaction with salaries, and 66% satisfaction with teaching contracts (OECD, 2020). The relationship between teacher self-efficacy and job satisfaction has been extensively studied with several studies (e.g., Skaalvik and Skaalvik, 2014; Aldridge and Fraser, 2016; Zakariya, 2020) suggesting that high self-efficacy bolsters teacher job satisfaction.
The relationship between teacher instructional practices and the techniques they use in sharing, coordinating, and collaborating on instructional activities forms an important block of the present study. This collective action of sharing, coordinating, and collaborating among teachers to achieve instructional learning outcomes is regarded as teacher cooperation (Bellibaş et al., 2021). It is expected that teacher cooperation is a multidimensional construct since teachers cooperate in different ways using different techniques. Empirical evidence has been put forth to justify the multidimensionality of the construct. A typical example is the OECD Teaching and Learning International Survey (TALIS) technical report that operationalised teacher cooperation using two dimensions: “exchange and co-ordination among teachers” and “professional collaboration in lessons among teachers” (OECD, 2019, p. 251). The extent to which teachers cooperate among themselves has been linked with teacher job satisfaction, especially for men (Toropova et al., 2021). Teacher cooperation being an important construct makes it interesting, in the present study, to quantify the extent to which it relates to teacher instructional practices either directly or through other constructs such as self-efficacy and job satisfaction. Teacher stress, in the present study, encapsulates stress associated with teaching, work-induced stress on the physical and mental health conditions of teachers, as well as the number of hours devoted to teaching. It may influence not only the cooperation among teachers but also their instructional practices. However, limited studies are available in the literature to buttress such a claim. In parts, teacher stress is negatively associated with self-efficacy and job satisfaction (e.g., Collie et al., 2012) but its influence on teacher instructional practices requires further investigation.
The present study seeks to provide empirical evidence for a relationship between teacher self-efficacy, teacher job satisfaction, teacher stress, teacher cooperation, and instructional practices with a focus on mathematics teachers. Admittedly, there have been similar attempts in literature. However, such attempts suffer one or more defects that necessitate a renewed investigation. For instance, researchers (e.g., Aldridge and Fraser, 2016; Zakariya, 2020) have quantified the relations between teacher self-efficacy and job satisfaction without relating the subsequent effect to instructional practices. On the other hand, researchers have also investigated teacher instructional practices (e.g., Yu and Singh, 2016; Larsen and Jang, 2021) without considering the effect of teacher self-efficacy and teacher job satisfaction on the construct. These partial or rather separated studies of factors that influence teacher instructional practices expose a gap in the literature. This gap necessitates an investigation into the relationship between and within the constructs of interest in the present study. Further, several studies have been conducted with a focus on neither Norwegian teachers (e.g., Collie et al., 2012; Yu and Singh, 2016) nor teachers of mathematics (e.g., Paulick et al., 2013; Bellibaş et al., 2021). The findings of such studies may not be generalizable to the context of the present study given the differences in culture, economics, classroom norms and practices.
Thus, we deem it necessary in the present study to provide empirical evidence of the relationship between the research constructs which is relatively comprehensive (by studying multiple relations, simultaneously) and more relevant to the teaching of mathematics (by focusing on mathematics teachers). We contend that this approach to examining the relationship will offer an opportunity to investigate not only the dependent-independent relations but also the dependent-dependent relations between the research constructs. As such, the findings of the present study will offer a basis for interventions that bolster instructional practices with several implications for educational administrators and practitioners. Furthermore, it is of prime interest to us in the present study to investigate the variability of teachers’ instructional practices across genders, age groups, and years of teaching experience. This is necessary to determine which gender, age groups, and experience levels of teachers we should prioritise while designing interventions targeted at improving teacher instructional practices in mathematics. We argue that the results of this variability investigation will be useful to gauge differences in instructional practices based on teachers’ gender, age, and teaching experience. In clear terms, we attempt to address the following research questions:
What is the relationship between and within instructional practices, self-efficacy, job satisfaction, stress, and cooperation among mathematics teachers?
Do instructional practices of mathematics teachers differ with their gender, age groups, and teaching experience?
It is crucial to remark that we focus on teacher instructional practice in the second research question because the former constitutes the outcome variable in this study. The whole study was designed to investigate factors that predict teacher instructional practices. All other variables, e.g., self-efficacy, job satisfaction, stress, and cooperation among mathematics teachers are predictors whose contributions to teacher instructional practices we aimed to investigate. The remaining parts of this article are arranged such that we present theoretical backgrounds for the conceptualisation, operationalisation, and measurement of teacher instructional practices including the formulation of the research hypotheses in the next section. Then, we present issues related to methodology such as the sample of the study, measuring instruments, and the procedure for data collection, analysis, and interpretation. We present and interpret the results in a section. Then, we discuss important findings. We conclude the present article by highlighting important findings, their implications for practices and limitations of the study.
The theoretical background of instructional practices can be traced to theories of learning such as cognitive theory, constructivism, distributed cognition, and social-cultural theory. Meanwhile, the transition from the descriptive purposes of these learning theories to the prescriptive nature of instructional practices is not a smooth one. Nonetheless, two theoretical perspectives of teacher-centred and student-centred instructional practices have emerged in the teaching and learning of mathematics over the years (Hopkins et al., 1997; Morgan et al., 2015; Hann, 2020). However, the distinctions between these theoretical perspectives have become ambiguous, lately. Yet, teacher-centred instructional practices have come under different names such as traditional instruction, direct instruction, and conventional method of teaching with teachers taking the lead role and the focus is on what the teacher does and not on what the students do in the classroom (Rittle-Johnson, 2006; Biggs, 2012). The student-centred instructional practices (e.g., inquiry-based instruction and active learning), on the other hand, shift the classroom focus from the teacher’s doings to students’ doings and the teacher’s role is reduced to being a facilitator in the classroom (Biggs, 2012; Hann, 2020). Despite the inconclusive results on the effectiveness of both theoretical perspectives on instructional practices on students’ performance in mathematics (Morgan et al., 2015), there is consistent advocacy for the adoption of student-centred instructional practices in mathematics education (Cai and Howson, 2012; Theobald et al., 2020). That is, a type of instructional practice that fosters students’ engagement with mathematics and encourages peer-to-peer interaction in the classroom.
Based on the student-centred theoretical perspective of instructional practices, researchers have conceptualised and operationalised instructional practices with an emphasis on cognitive activation, clarity of instruction, and classroom management as prime dimensions of the construct (Lipowsky et al., 2009; Charalambous and Praetorius, 2018; Schlesinger et al., 2018). Cognitive activation characterises teachers’ practices that focus on organising and selecting tasks that require students’ ability to implement, differentiate, criticise, and generate knowledge within the context of solving problems (Lipowsky et al., 2009). As it relates to mathematics classrooms, cognitive activation practices include the use of tasks that have multiple solutions, that engage the students mathematically, and encourage student–student interactions (Schlesinger et al., 2018). The clarity of instruction characterises teachers’ practices that focus on stating the learning outcomes before each teaching activity, making genuine efforts such as preparing content summary to ensure the expected learning outcomes are met, and facilitating relatedness of old and new topics (Ainley and Carstens, 2018). The hallmark of the clarity of instruction is to ensure there is a clear direction for students on what is expected at the end of each lesson. Closely related to the clarity of instruction is the classroom management dimension of the teacher instructional practices. This dimension characterises teachers’ practices with a focus on managing the classroom atmosphere by setting and ensuring classroom rules and regulations, controlling unruly behaviours, and managing classroom time (Schlesinger et al., 2018). Interestingly, each of the three dimensions of instructional practices has been investigated and found to contribute substantially to students’ affect and performance in mathematics (Lipowsky et al., 2009; Charalambous and Praetorius, 2018).
Research on operationalisation and measures of teacher instructional practices or their broadly conceived instructional quality can be delineated along a continuum depending on the content-specificity of the measures. Towards one extreme of the continuum are generic measures that are designed with little or no consideration for the content-specificity of teaching activity, and they are used to measure teacher instructional practices in all the subject matter (Charalambous and Praetorius, 2018). Examples of these generic measures are the dynamic model of educational effectiveness (Creemers and Kyriakides, 2008), the classroom assessment scoring system (Pianta and Hamre, 2009), and the three basic dimensions measure (Klieme et al., 2009). The strength of the generic measures lies in their suitability for inter-content assessments of instructional practices and possible cross-country comparisons. However, this strength comes at a price of deficiency in accounting for the content specificity of the classroom context.
Towards the other extreme of the continuum, are subject-specific measures of instructional practices such as the mathematics scan (Walkowiak et al., 2014), the elementary mathematics classroom observation form (Thompson and Davis, 2014), and the reformed teaching observation protocol (Sawada et al., 2002). It is crucial to remark that the mathematics scan was originally validated using a small sample of 60 third and fourth-grade teachers. Further, the reformed teaching observation protocol has been criticised for not being inherently mathematical (Boston et al., 2015). These observations, among other things, led Gleason et al. (2017) to develop and validate a more mathematics-inherent measure of teacher instructional practices (called mathematics classroom observation protocol for practices) using a multistage iterative process over three years that involved a large sample of mathematics teachers. The strength of the subject-specific measures lies in their focus on relatively exclusive practices of a subject matter such as the problem-solving strategies in mathematics, mathematical sense-making, constructing multi-solution tasks, and focusing on correct uses of representations, symbols, and procedures in mathematics arguments (Schlesinger and Jentsch, 2016).
Researchers (e.g., Walkington and Marder, 2014; Schlesinger et al., 2018) have attempted to combine the strength of both the generic and subject-specific measures by developing a hybrid type that may be placed in the middle of the continuum. In developing the hybrid measures, the researchers supplement the generic items with subject-specific items. For instance, Schlesinger et al. (2018) build on the three basic dimensions measure (Klieme et al., 2009) by incorporating two additional mathematics-specific dimensions which they called subject-related and teaching-related quality of mathematics instructional practices. The merit of simultaneous capturing of both generic and subject-specific instructional practices by the hybrid measures is appealing. However, such measures are unsuitable for comparing teacher instructional practices across multiple subject matters, and they are prone to deficits in validity and reliability for cross-country comparisons. Considering the data source of the present study, we operationalised and measured teacher instructional practices using the generic perspective. Meanwhile, the measure used in the presented study may not be considered to be at the extreme end of the teacher instructional practice continuum because we restricted our generated data to teachers who teach mathematics at the time of the data collection.
Regardless of the content-specificity of the measures of teacher instructional practices, researchers have broadly captured classroom practices using one or a combination of classroom observations, students’ ratings, and teachers’ self-report instruments. The process involved in the classroom observation instruments entails a researcher(s) rating teachers’ practices against some pre-set criteria on the instruments. This observation can happen either with the researchers present in the classroom synchronously or they are watching a videotape of the lectures, asynchronously (Casabianca et al., 2013). The advantage of the observation method lies in reducing bias that could stem from self-reported instruments. However, it could be cumbersome or rather impossible when there are numerous lessons to observe and rate. Both students’ and teachers’ ratings, on the other hand, rely on a self-reported process with students rating their teachers’ instructional practices and teachers’ self-reporting their practices, respectively (Wagner et al., 2016). These modes of measuring teacher instructional practices may be suitable for large-scale purposes. However, they are equally susceptible to biases stemming from teacher popularity, students’ characteristics, and social desirability with teachers and/or students reporting what they perceive as being socially desirable (Kunter and Baumert, 2007). For the present study, data were generated using teacher self-reported measures, and the social desirability bias was mitigated by using the frequency response scale rather than the Likert scale of agreement which is more prone to such bias (Ainley and Carstens, 2018).
The rationale for establishing the relationships between teacher instructional practices and other constructs such as self-efficacy, job satisfaction, stress, and cooperation among teachers may be theoretically argued from a social cognitive perspective. The social cognitive theory posits that human functioning (e.g., teachers’ instructional practices) is constantly being shaped by a dynamic interaction between environmental (e.g., teacher stress), personal (e.g., teacher self-efficacy), and behavioural (e.g., teacher cooperation) factors (Bandura, 2001). Researchers (e.g., Bellibaş et al., 2021; Toropova et al., 2021), though in parts or rather in isolated cases, have provided empirical evidence to complement this theoretical argument for the relations between our research constructs. Despite the lack of a holistic approach to studying the relations between and within these constructs, previous studies have implications in formulating the research hypotheses of the present study. For instance, Schiefele and Schaffner (2015) showed that teacher self-efficacy has a substantial influence on teacher instructional practices. In a larger sample study, Bellibaş et al. (2021) showed that teacher cooperation and teacher job satisfaction influence the classroom practices of over 100 thousand teachers in over six thousand schools across 32 countries. As we argued in the introduction section of this article, we expect teacher stress to have a negative influence on teacher instructional practices based on its previously established relations (e.g., Collie et al., 2012) with teacher self-efficacy and job satisfaction. Building on the social cognitive theoretical perspective and insights from previous studies, we formulate the following hypotheses:
H1: Teacher self-efficacy, job satisfaction and teacher cooperation positively predict teacher instructional practices.
H2: Teacher stress negatively predicts teacher instructional practices.
In addition to the individual (direct) predictive effects of the research constructs on teacher instructional practices, as formulated in hypotheses one and two, there are possibilities of interaction (mediating) effects through these constructs on the teacher instructional practices. These mediating effects are plausible following the dynamic relationship between the teachers’ personal, behavioural, and environmental factors as postulated by the social cognitive theory. Moreover, there is an accumulation of evidence (e.g., Zakariya, 2020; Bellibaş et al., 2021) that suggests that both teacher self-efficacy and teacher cooperation have a non-trivial effect on teacher job satisfaction. Such evidence corroborates the plausibility of the mediating effects of teacher job satisfaction between both teacher self-efficacy and teacher cooperation on teacher instructional practices. In addition, since the extent to which teachers are confident of their ability to teach successfully is shaped by cooperation among themselves (Gil-Flores, 2016), we expect teacher self-efficacy to mediate the effect of teacher cooperation on teacher instructional practices. Building on research (e.g., Collie et al., 2012; Molero Jurado et al., 2019) that shows that teacher stress could undermine teacher self-efficacy, teacher job satisfaction and, indeed, the extent of cooperation among the teachers, we expected the latter constructs to mediate the effect of teacher stress on the instructional practices. As such, we formulate the following hypotheses:
H3: Teacher self-efficacy, teacher job satisfaction, and teacher cooperation mediate the effect of teacher stress on teacher instructional practices.
H4: Teacher self-efficacy and teacher job satisfaction mediate the effect of teacher cooperation on teacher instructional practices.
Figure 1 presents a comprehensive view of the hypotheses and constitutes a conceptual model of relationships between the research constructs of the present study. In Figure 1, the oval shapes represent the research constructs, and the single-ended arrows indicate the directions of the effect of one construct on another. Each of the single-ended arrows or a combination of them carries the hypotheses of the present study. Further, the positive or negative signs on the arrows indicate either the hypothesized effects are bolstering or undermining, respectively. Each of these hypotheses points towards addressing the research question one of investigating the relationship between and within instructional practices, self-efficacy, job satisfaction, stress, and cooperation among mathematics teachers. Hypotheses one and two examine the relationship between teacher self-efficacy, job satisfaction, teacher cooperation, and teacher stress as predictors of teacher instructional practices in mathematics classrooms. Within these predictors, hypotheses three and four examine the mediating roles played by teacher self-efficacy, teacher job satisfaction, and teacher cooperation between teacher stress and instructional practices.
In the present study, we draw on the most recent publicly available TALIS data on lower secondary school teachers. TALIS is the leading international survey that focuses on the working conditions of teachers and school leaders in primary, lower secondary, and upper secondary schools around the world. It was first conducted in 2008 and was later run in 2013 and 2018. The 2018 edition comprises 48 participating countries in which 200 schools were randomly selected as the primary sampling unit in each country with 20 teachers chosen within each school using a probabilistic sampling procedure (OECD, 2019; Zakariya, 2021). Our focus is on Norwegian lower secondary school teachers who taught mathematics at the time the TALIS 2018 was conducted. 1,304 mathematics teachers participated in the study including 708 (54.29%) women and 596 (45.71%) men. Their age distribution is such that 15 teachers were under 25 years, 25–29 years (157), 30–29 years (345), 40–49 years (427), 50–59 years (214), and 146 teachers were 60 years or older. The average teaching experience is 14 years for all the teachers. For ease of mean comparisons, we categorised teachers under 40 years 517 (39.65%) as young and those who are 40 years and above 787 (60.35%) as old. Further, we categorised teachers into two based on the average teaching experience. Those with less than 14 years of teaching experience were 688 (52.76%) and categorised as less experienced, those with 14 years or more teaching experience were 613 (47.00%) and categorised as experienced, and three teachers had missing values on the experience variable.
The TALIS 2018 team conceptualised teacher instructional practices as a multidimensional construct that comprised three dimensions “clarity of instruction,” “cognitive activation,” and “classroom management” (OECD, 2019, p. 234). The scores on these dimensions form a composite score (i.e., the mean of the standardised dimension scores) for the overall teacher instructional practices. Further, each of these dimensions has four items in which teachers answered the leading question: “Thinking about your teaching in the [mathematics class], how often do you do the following?” using one of these options: never or almost never, occasionally, frequently, and always (OECD, 2019, p. 234). Sample items of the respective dimensions are “I set goals at the beginning of instruction,” “I give tasks that require students to think critically,” and “I calm students who are disruptive” (OECD, 2019, p. 234). The validity and reliability of the teacher instructional practices measure were extensively studied and found to be valid and reliable with respective coefficient omega (Zakariya, 2022) of 0.790, 0.723, and 0.889 for each dimension of the measure using the Norwegian lower secondary school teachers (OECD, 2019).
The TALIS 2018 team conceptualised teacher self-efficacy as a multidimensional construct that comprised three dimensions, i.e., self-efficacy in classroom management, instruction, and student engagement. The scores on these dimensions form a composite score for the overall teacher self-efficacy. Further, each of these dimensions has four items in which the teachers answered the leading question: “In your teaching, to what extent can you do the following?” using one of these options: not at all, to some extent, quite a bit, and a lot. Sample items of the respective dimensions are “Get students to follow classroom rules,” “Craft good questions for students,” and “Help students think critically” (OECD, 2019, p. 258). The validity and reliability of the teacher self-efficacy measure were extensively studied and found to be valid and reliable with respective coefficient omega of 0.814, 0.706, 0.642 for each dimension of the measure using the Norwegian lower secondary school teachers (OECD, 2019).
The TALIS 2018 team also conceptualised teacher job satisfaction as a multidimensional construct that comprised two dimensions, i.e., job satisfaction with work environment and profession (OECD, 2019). The scores on these dimensions form a composite score for overall teacher job satisfaction. Further, each of these dimensions has four items in which teachers answered the leading question: “We would like to know how you generally feel about your job. How strongly do you agree or disagree with the following statements?” using one of these options: strongly disagree, disagree, agree, strongly agree (OECD, 2019, p. 302). Sample items of these dimensions are “All in all, I am satisfied with my job” and “If I could decide again, I would still choose to work as a teacher,” respectively (OECD, 2019, p. 302). The validity and reliability of the teacher job satisfaction measure were extensively studied and found to be valid and reliable with respective coefficient omega of 0.854 and 0.885 for each dimension of the measure using the Norwegian lower secondary school teachers (OECD, 2019).
The TALIS 2018 team also conceptualised teacher cooperation as a multidimensional construct that comprised two dimensions: “exchange and co-ordination among teachers” and “professional collaboration in lessons among teachers” (OECD, 2019, p. 252). The scores on these dimensions form a composite score for overall teacher cooperation. Further, each of these dimensions has four items in which teachers answered the leading question: “On average, how often do you do the following in this school?” using one of these options: never, once a year or less, 2–4 times a year, 5–10 times a year, 1–3 times a month, and once a week or more (OECD, 2019, p. 252). Sample items of these dimensions are “Attend team conferences” and “Participate in collaborative professional learning,” respectively (OECD, 2019, p. 252). The validity and reliability of the teacher cooperation measure were extensively studied and found to be valid and reliable with respective coefficient omega of 0.721 and 0.563 for each dimension of the measure using the Norwegian lower secondary school teachers (OECD, 2019).
For the teacher stress, it was a single-dimensional measure that comprised four items on a four-point Likert scale from not at all to a lot and the teachers respond to the leading question: “In your experience as a teacher at this school, to what extent do the following occur?” (OECD, 2019, p. 319). A sample item of the measure is “My job negatively impacts my mental health” and the measure was found to be valid and reliable with a coefficient omega of 0.815 (OECD, 2019, p. 319). The full items for all the measures are available on the respective pages of the referenced TALIS 2018 technical report. It is crucial to remark that all the research measures in this study have been subjected to rigorous and comprehensive validity investigations before data collection in Norwegian. For the initial validity check, the TALIS technical team combined research theories, expert reviews, and their experience from the previous administration of the measures to justify the validity of the scale items (OECD, 2019). The initial check was followed by pilot testing as well as field trials of the scale in many countries before the questionnaire expert group, the TALIS international consortium, and the OECD technical team modified the scale items. Finally, the generated data from the pilot testing and field trials of the scale were used to investigate and confirm multiple aspects of validity such as content validity, construct validity, predictive validity, item analysis, and measurement invariance for the scale (OECD, 2019).
We screened the composite scores (self-efficacy, job satisfaction, cooperation, stress, and instructional practices) for the pattern and the significance of the missing values using little’s missing completely at random (MCAR) tests. The proportions of missing values are 2.4, 3.4, 1.8, 3.1, and 16.6% for self-efficacy, job satisfaction, cooperation, stress, and instructional practices, respectively. We found the missing patterns to be random for all the composite scores ( = 31.479, df = 28, p-value = 0.296). Thus, following Zakariya (2021), we used a full information maximum likelihood estimation with a maximum expectation algorithm instead of multiple imputations to handle the missing values. Supplementary Appendices A–C present the basic descriptive statistics, correlation matrix, and covariance matrix for all the research variables, respectively.
To address the first research question and its associated hypotheses, we analysed the data using structural equation modelling of the composite scores (i.e., we ran path analysis). This was done by evaluating the structural model (Figure 1) for its consistency with the generated data obtained from Norwegian mathematics teachers using path analysis with a robust maximum likelihood (MLR) estimator. Figure 1 is a standard path analysis model typical of the structural equation modelling method of statistical analysis. It carries the hypotheses of the direct and indirect (mediating) effects between and within the research constructs. The strength of this type of statistical analysis is that it allows for evaluating the consistency of the hypothesised model with the generated data while testing all the hypotheses simultaneously. This will not only increase the efficiency of the analysis but also increase the accuracy of the estimated parameters. Therefore, this type of statistical analysis is given preference over the traditional multiple regression analysis that requires the solution of an equation to estimate the solution of another, typical of solving simultaneous equations with many unknowns (Byrne, 2012). Then, we investigated the partial mediation analysis in the model to separate the specific mediating effects of the endogenous constructs from the total effects in the model. We assessed the global fit of the hypothesised model with the data by using a combination of cut-off values for the goodness of fits indices: comparative fit index (CFI), Tucker-Lewis’s index (TLI), root mean square error of approximation (RMSEA), and standardised root mean square residual (SRMR). Following insights from the literature (e.g., Hu and Bentler, 1999; Byrne, 2012), we contend that there is an excellent model fit of the data if both CFI and TLI are greater than 0.95, RMSEA is less than 0.06, and SRMR is less than 0.08. These analyses were performed in Mplus 8.4, and the syntax for path analysis and mediation analysis is presented in Supplementary Appendix D. Further, we used independent sample t-tests to examine mean differences in teacher instructional practices instead of addressing the second research question. These analyses were performed in SPSS 20 software.
The first set of results concerns the evaluation of the hypothesised relationship of the research constructs as presented in Figure 1. The results show an excellent global fit of the evaluated model with the generated data (chi-squared CFI =1.000, TLI = 1.000, SRMR =0.001, and RMSEA = 0.001). That is, there is consistency between the hypothesised model of the research constructs and the generated data. Figure 2 presents the standardized estimates of some parameters of the evaluated model with significant estimates (i.e., p < 0.05) in boldfaces.
The presented results in Figure 2 show that all the estimated effects of one construct on another in the evaluated model are significant except for the effect of teacher job satisfaction on instructional practices ( ). As postulated in Hypothesis One Figure 2 confirms the substantial positive effects of teacher self-efficacy ( ) and teacher cooperation ( ) on teacher instructional practices. However, contrary to our postulation in Hypothesis One the positive of effect teacher job satisfaction on teacher instructional practices is not significant. On the one hand, these findings revealed that teachers who often use multiple assessment methods, engage students in critical thinking, and maintain decorum in the classroom frequently use the techniques of instructional practices. Similarly, teachers who often share ideas on teaching materials, engage in joint meetings and collaborate on professional training are linked with frequent use of instructional practices. On the other hand, there is not enough evidence in the present study to justify such a substantial relation between teacher job satisfaction and instructional practices. Contrary to our expectation as postulated in Hypothesis two Figure 2 shows that the effect of teacher stress on teacher instructional practices is positive ( ). This finding reveals that despite the stress, mental and physical drains of teaching, teachers manage to engage in frequent use of instructional practices. This finding is a surprise to us and worth further investigation.
In addition, Figure 2 confirms some expected positive and negative effects within the research constructs. For instance, both teacher self-efficacy ( ) and teacher cooperation ( ) have substantial positive effects on teacher job satisfaction, while teacher stress has a substantial negative effect ( ) on teacher job satisfaction. That is, teachers with high self-efficacy and those who cooperate and collaborate on teaching matters are highly satisfied with their teaching job. On the contrary, teachers who perceive mathematics teaching as often stressful and draining on their physical and mental health are highly dissatisfied with the teaching job. Figure 2 also shows that teacher cooperation has a substantial positive effect ( ) on teacher self-efficacy, while teacher stress has a substantial negative effect ( ) on the construct. These findings suggest that teacher cooperation bolsters self-efficacy while teachers’ perceived stress and burnout undermine their self-efficacy. Finally, Figure 2 reveals a substantial negative effect of teacher stress ( ) on teacher cooperation. That is, teachers’ stress and burnout undermine the level of cooperative and collaborative practices among the teachers.
To address hypotheses three and four of the present study, we investigated the partial mediation analysis of the presented evaluated model in Figure 2. This partial mediation analysis avails the opportunity to estimate both the indirect and total effects of each of the research constructs on teacher instructional practices. By indirect effect, we mean the product of regression coefficients along the path(s) from a target predictor variable through the meditator(s) to an outcome variable in the evaluated model. The direct effect is the regression coefficient from a target predictor variable to an outcome variable in the model. Further, the total effect is the sum of both the direct and indirect effects from a target predictor to the outcome variable in the model. Table 1 presents the standardised estimates of these effects as revealed by the mediation analysis.
In addition to the presented direct effects in Figure 1 and Table 1 shows the estimates of the indirect effects within the research constructs of the present study. The presented results in Table 1 show a significant negative indirect effect ( ) of teacher stress on teacher instructional practices. This total indirect effect is a combination of effects through mediators such as teacher cooperation, teacher self-efficacy and teacher job satisfaction. The results of the specific indirect effect analysis show that each of these mediators, but teacher job satisfaction, carries a substantial negative effect from teacher stress to teacher instructional practices despite the positive effect of the former on the latter as shown in Figure 1. Thus, the total effect (i.e., the direct effect plus the total indirect effect) of teacher stress is still positive and significant ( ). Table 1 also shows that there is a significant total indirect effect ( ) of teacher cooperation on teacher instructional practices. This total indirect effect is a combination of effects through two mediators: teacher self-efficacy and teacher job satisfaction. The results of the specific indirect effect analysis show that only teacher self-efficacy substantially mediates the effect of teacher cooperation on teacher instructional practices. That is, teacher job satisfaction is not a substantial mediator between teacher cooperation and teacher instructional practices. These findings can be interpreted as teachers whose extent of cooperation bolsters their self-efficacy often linked with frequent use of instructional practices. On the other hand, teachers whose extent of cooperation undermines their self-efficacy are less frequently linked with frequent use of instructional practices. However, similar interpretations cannot be substantiated in the present study for the mediating roles of teacher job satisfaction. Moreover, the total effect of teacher cooperation on teacher instructional practices as revealed in Table 1 is higher than reported in Figure 1 and substantial ( ).
Further, Table 1 shows that the indirect effect of teacher self-efficacy through teacher job satisfaction on teacher instructional practices is not significant ( ). This insignificant indirect effect is expected considering the insignificant direct effect of teacher job satisfaction on teacher instructional practices as revealed in Figure 1. That is, regardless of the bolstering effect of teacher self-efficacy on their job satisfaction there is no substantial contribution of the latter to teacher instructional practices. Nevertheless, the non-significant indirect effect strengthens the total effect of teacher self-efficacy on teacher instructional practices ( ). This is a crucial finding which might have been ignored if we had not investigated the mediation analysis in the present study. The presented results in the last two sections of this article provide empirical evidence for the extent of the relationship between and within teacher instructional practices, self-efficacy, job satisfaction, stress, and cooperation among mathematics teachers. We contend that the direct and indirect effects between and within the research constructs as reported shed light on the complex relation of the research constructs. Thus, addressing the first research question of the present study.
To address the second research question, we analyse the generated data using independent sample t-tests with gender, age groups, and years of teaching experience as grouping variables while teacher instructional practices are the dependent variable. This analysis enabled us to examine whether significant differences exist between teacher instruction practices among male and female, young and old, and less experienced and experienced mathematics teachers. We present the results of these analyses in Table 2.
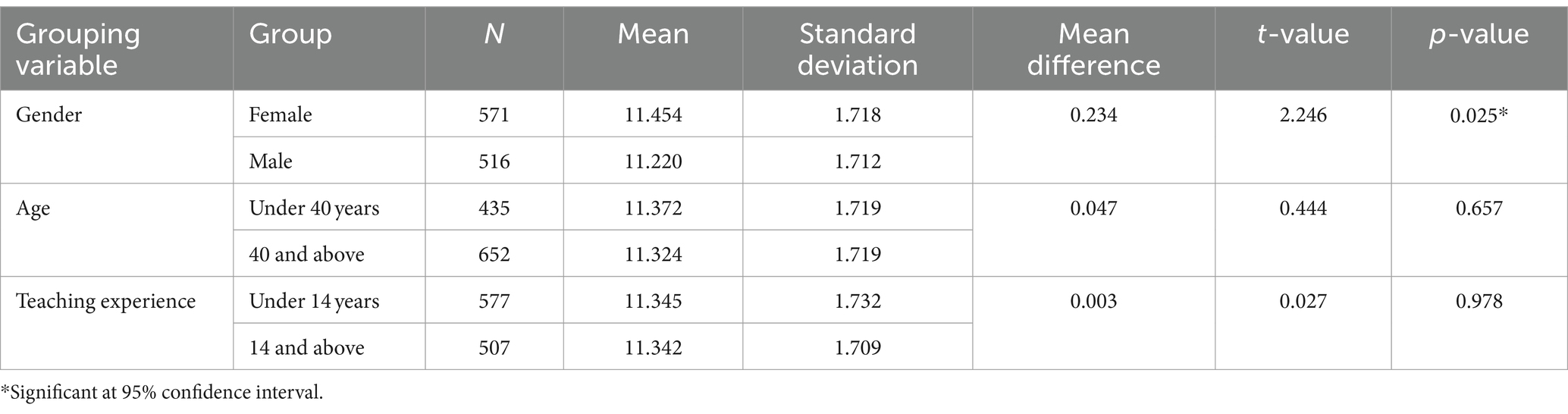
Table 2. Mean difference tests of teacher instructional practices across gender, age, teaching experience.
The presented results in Table 2 show that gender is the only grouping variable that exhibits a significant mean difference (0.234) in teacher instructional practices . That is, the mean differences because of age[ ] and years of teaching experience ( ) are not significant. The significant result shows that the frequent use of instructional practices is more prevalent among female mathematics teachers than their male counterparts. On the other hand, the non-significant results show that age and the number of years of teaching mathematics have no substantial role in determining the frequent use of instructional practices among mathematics teachers. These findings are interesting as we expected, at least, the teaching experience to play a decisive role in teacher instructional practices but our results show otherwise. Going back to the second research question of the present study, the results only confirm that teachers’ gender is the only variable upon which teacher instructional practices are substantially different with female teachers reporting better practices.
We build on the social cognitive theory and insights from the literature to hypothesise and investigate a dynamic relationship between and within teacher self-efficacy, teacher cooperation, teacher job satisfaction, and teacher stress, as it concerns instructional practices of lower secondary mathematics teachers in Norwegian schools. The findings are revealing and may be discussed under two headings: main effects; mediating effects and mean differences.
The findings of the present study confirm that teacher self-efficacy and teacher cooperation influence the frequency of instructional practices among mathematics teachers in Norway. These findings suggest a cue for educational stakeholders on the benefits of improving teacher self-efficacy and encouraging teacher cooperation as a proxy to bolster frequent use of instructional practices among mathematics teachers. These findings corroborate the reports by Depaepe and König (2018); Schiefele and Schaffner (2015) who identified teacher self-efficacy as an important predictor of teacher instructional practices. Furthermore, these findings strengthen the earlier report by Bellibaş et al. (2021) who showed that teacher collaboration plays a role in teacher instructional practices. Meanwhile, our study provides a fresh perspective on the relationship between teacher self-efficacy, teacher cooperation, and teacher instructional practices in two ways. First, our focus on teachers of mathematics gives a clearer perspective on what happens in mathematics classrooms as compared to generic classrooms used in previous studies (e.g., Schiefele and Schaffner, 2015; Bellibaş et al., 2021). Second, the large sample size and robust analytical tools constitute an advantage over previous studies (e.g., Schiefele and Schaffner, 2015; Depaepe and König, 2018) by providing relatively generalisable and more accurate estimates of the relationship between the research constructs.
In contrast to our expectation, teacher job satisfaction has a non-substantial influence on the frequency of instructional practices among mathematics teachers in Norway. That is, the extent to which Norwegian mathematics teachers enjoy teaching and retain their work environment has no appreciable influence on their instructional practices. This finding is contrary to the report by Bellibaş et al. (2021) which showed that teacher job satisfaction has a substantial influence on teacher instructional practices. However, we can provide two perspectives to explain this contrary finding. First, it could be that the earlier report on the substantial influence of job satisfaction on teacher instructional practices is not generalizable to our context due to lack of focus on mathematics teachers in the report. Another plausible explanation is that the resultant influence of teachers’ job satisfaction on their instructional practices is not significant because Norwegian lower secondary teachers are relatively highly satisfied with their teaching job as shown in the literature (Zakariya et al., 2020). A more surprising finding in the present study is the substantial positive relation between teacher stress with teacher instructional practises. We argue that this surprising finding is a novel contribution of the present study to the literature given the scarcity of studies on the relation between the two constructs. Thus, we recommend further investigations on this relation in an independent sample from that of the present study.
Despite the unexpected positive relation between teacher stress and teacher instructional practices, the former has substantial undermining effects on teacher cooperation, teacher self-efficacy, and teacher job satisfaction. The finding shows that teachers’ perceived stress and strains stemming from mathematics teaching weaken their level of cooperation, their self-efficacy, and their satisfaction with the teaching job. This finding corroborates previous studies that reported such undermining effect of teacher stress on teacher self-efficacy and teacher job satisfaction (e.g., Collie et al., 2012; Molero Jurado et al., 2019) while offering a novel contribution to the literature on the effect of the construct on teacher cooperation. As an implication to educational stakeholders, we contend that this finding highlights the significance of protecting teachers’ physical and mental health not only to undermine teachers’ stress but also to strengthen teachers’ cooperation, self-efficacy, and job satisfaction. In a similar manner to previous studies (e.g., Bellibaş et al., 2021; Toropova et al., 2021), we also found that the extent to which teachers cooperate and collaborate on teaching-related affairs enhances their self-efficacy and job satisfaction. Finally, the finding of the present study emphasises the crucial role of teacher self-efficacy in bolstering teacher job satisfaction. Unlike previous studies that investigate this relation among generic teachers (e.g., Aldridge and Fraser, 2016; Zakariya, 2020), this finding sieves out what is applicable to teachers of mathematics within the Norwegian borders.
Apart from the main effects between and within the research constructs, the findings of the present study also revealed exciting mediators between the research constructs. First, we found that teacher cooperation and teacher self-efficacy are crucial mediators of the effect of teacher stress on instructional practices. By implication, these findings show that teachers with high perceptions of stress and strain in teaching mathematics can be supported to frequently use instructional practices by enhancing their cooperation and self-efficacy. This finding, in parts, corroborates studies in the literature that have identified the mediating roles of teacher self-efficacy (e.g., Zakariya, 2020) and teacher cooperation (e.g., Bellibaş et al., 2021), while establishing the non-substantial mediating role of teacher job satisfaction. We contend that our finding is a prime opportunity for education stakeholders to intervene on any of these mediators as a proxy to enhance the frequent use of instructional practices in mathematics classrooms. Besides, our finding reveals that not only does teacher self-efficacy serve as a mediator between teacher stress and instructional practices but also between teacher cooperation and the latter construct. This finding highlights the significance of teacher self-efficacy as it concerns teacher support for frequently using instructional practices in mathematics classrooms. Furthermore, the finding of the present study reveals that the frequent use of instructional practices is more predominant among female than male lower secondary school mathematics teachers in Norway. This finding suggests that more deliberate effort is needed to bolster the frequent use of instructional practices among male teachers than female teachers.
In sum, the present study provides tentative evidence to quantify and disentangle the complex relationship between and within teacher instructional practices, teacher job satisfaction, self-efficacy, teacher cooperation, and teacher stress. We have identified teacher self-efficacy, among the research constructs, as the most contributing factor to frequent use of instructional practices. Teacher self-efficacy does not only bolster teacher instructional practices directly but also play crucial mediating roles between teacher cooperation, teacher stress and teacher instructional practices. Next to teacher self-efficacy in the present study is the substantial contribution of teacher cooperation to instructional practices which is then followed by teacher stress. Meanwhile, both the direct and the mediating effects of teacher job satisfaction on teacher instructional practices are not substantial. Moreover, the frequent use of instructional practices is more prevalent among female than male mathematics teachers in Norway. These findings provide the quantification of a relationship between the research constructs and mathematics teacher instructional practices in Norway. They also expose factors such as teacher self-efficacy and teacher cooperation which interventions may bring about the desired improvement in classroom practices that promote creativity, critical thinking, problem-solving, communication and collaboration among students. By implication, pre-service and in-service mathematics teachers in Norway can leverage cooperation among themselves and enhanced self-efficacy to improve their classroom instructional practices. Also, educational stakeholders in Norway can take a cue from the findings of this study to design and implement targeted interventions that foster teacher self-efficacy and teacher cooperation as a proxy to encourage effective instructional practices among mathematics teachers. Further, researchers around world can replicate this study to validate or falsify our tested hypotheses in their samples. This will provide appropriate guidance to educational stakeholders in their countries.
Despite the novel contributions of the present study to the literature, there are limitations that are worth mentioning. First, we used secondary and cross-sectional dataset in this study which makes it difficult to claim deterministic causal relations between and within the research constructs. As such, our study has only provided tentative evidence of the relationship between and within the research constructs. We recommend further longitudinal or experimental studies to explore the established relationship. The use of a secondary dataset in this study delimits our investigation to constructs in which data are available. Other crucial constructs such as teacher competence knowledge and teacher beliefs which may influence teacher instructional practices are unaccounted for in this study. Also, the use of the self-reported questionnaire to generate the data is susceptible to desirability bias (Kunter and Baumert, 2007). We agree that the frequency response scale used by the TALIS team to generate the data can only reduce but not eliminate this bias. Moreover, for each hypothesized and tested relation in Figure 1, there is a possibility of the corresponding reversed relation. For instance, it is possible for job satisfaction to influence either self-efficacy or teacher cooperation. However, such relations are not considered in the present study. We recommend that future studies should explore these possibilities. Finally, we restricted our focus to the influence of teachers’ factors on their instructional practices. Admittedly, this approach undermines the effects of other crucial factors such as school climate conditions, leadership support, curriculum constraints, and students’ factors. It would be interesting to investigate the effects of these factors as complements to the findings of the present study.
Publicly available datasets were analyzed in this study. This data can be found at: https://www.oecd.org/education/talis/talis-2018-data.htm.
The studies involving humans were approved by the Teaching and Learning Internal Survey Committee, Oslo Centre, Norway. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
YZ: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. NA: Methodology, Validation, Writing – original draft, Writing – review & editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
YZ acknowledges the support of the University of Agder Library for paying the APC of the manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1367076/full#supplementary-material
Ainley, J., and Carstens, R. (2018). Teaching and learning international survey (TALIS) 2018 conceptual framework, OECD working papers, no. 187 Paris: OECD Publishing.
Aldridge, J. M., and Fraser, B. J. (2016). Teachers’ views of their school climate and its relationship with teacher self-efficacy and job satisfaction. Learn. Environ. Res. 19, 291–307. doi: 10.1007/S10984-015-9198-X
Bandura, A. (2001). Social cognitive theory: an agentic perspective. Annu. Rev. Psychol. 52, 1–26. doi: 10.1146/Annurev.Psych.52.1.1
Bellibaş, M. Ş., Gümüş, S., and Liu, Y. (2021). Does school leadership matter for teachers’ classroom practice? The influence of instructional leadership and distributed leadership on instructional quality. Sch. Eff. Sch. Improv. 32, 387–412. doi: 10.1080/09243453.2020.1858119
Biggs, J. B. (2012). What the student does: teaching for enhanced learning. High. Educ. Res. Dev. 31, 39–55. doi: 10.1080/07294360.2012.642839
Bong, M., and Clark, R. E. (1999). Comparison between self-concept and self-efficacy in academic motivation research. Educ. Psychol. 34, 139–153. doi: 10.1207/S15326985ep3403_1
Bong, M., and Skaalvik, E. M. (2003). Academic self-concept and self-efficacy: how different are they really? Educ. Psychol. Rev. 15, 1–40. doi: 10.1023/A:1021302408382
Boston, M., Bostic, J., Lesseig, K., and Sherman, M. (2015). A comparison of mathematics classroom observation protocols. Math. Teach. Educ. 3, 154–175. doi: 10.5951/Mathteaceduc.3.2.0154
Byrne, B. M. (2012). Structural equation modeling with Mplus: Basic concepts, applications, and programming. New York: Routledge, Taylor & Francis Group.
Cai, J., and Howson, G. (2012). Toward an International Mathematics Curriculum. In: Third International Handbook of Mathematics Education. Springer International Handbooks of Education, vol 27. Eds. Clements, M., Bishop, A., Keitel, C., Kilpatrick, J., Leung, F. (New York, NY: Springer). doi: 10.1007/978-1-4614-4684-2_29
Casabianca, J. M., Mccaffrey, D. F., Gitomer, D. H., Bell, C. A., Hamre, B. K., and Pianta, R. C. (2013). Effect of observation mode on measures of secondary mathematics teaching. Educ. Psychol. Meas. 73, 757–783. doi: 10.1177/0013164413486987
Charalambous, C. Y., and Praetorius, A.-K. (2018). Studying mathematics instruction through different lenses: setting the ground for understanding instructional quality more comprehensively. ZDM Math. Educ. 50, 355–366. doi: 10.1007/S11858-018-0914-8
Collie, R. J., Shapka, J. D., and Perry, N. E. (2012). School climate and social–emotional learning: predicting teacher stress, job satisfaction, and teaching efficacy. J. Educ. Psychol. 104, 1189–1204. doi: 10.1037/A0029356
Creemers, B. P. M., and Kyriakides, L. (2008). The dynamics of educational effectiveness: a contribution to policy, practice, and theory in contemporary schools. London: Routledge.
Depaepe, F., and König, J. (2018). General pedagogical knowledge, self-efficacy and instructional practice: disentangling their relationship in pre-service teacher education. Teach. Teach. Educ. 69, 177–190. doi: 10.1016/J.Tate.2017.10.003
Gil-Flores, J. (2016). Variables associated to the self-efficacy perceived by secondary school science teachers. Revista De Educ. 372, 80–102. doi: 10.4438/1988-592X-RE-2016-373-322
Gleason, J., Livers, S., and Zelkowski, J. (2017). Mathematics classroom observation protocol for practices (MCOP2): a validation study. Investig. Math. Learn. 9, 111–129. doi: 10.1080/19477503.2017.1308697
Hann, T. (2020). Investigating the impact of teacher practices and noncognitive factors on mathematics achievement. Res. Educ. 108, 22–45. doi: 10.1177/0034523719842601
Hopkins, K. B., Mcgillicuddy-De Lisi, A. V., and De Lisi, R. (1997). Student gender and teaching methods as sources of variability in Children's computational arithmetic performance. J. Genet. Psychol. 158, 333–345. doi: 10.1080/00221329709596672
Hu, L. T., and Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: conventional criteria versus new alternatives. Struct. Equ. Model. Multidiscip. J. 6, 1–55. doi: 10.1080/10705519909540118
Klassen, R. M., Bong, M., Usher, E. L., Chong, W. H., Huan, V. S., Wong, I. Y. F., et al. (2009). Exploring the validity of a teachers’ self-efficacy scale in five countries. Contemp. Educ. Psychol. 34, 67–76. doi: 10.1016/J.Cedpsych.2008.08.001
Klieme, E., Pauli, C., and Reusser, K. (2009). “The Pythagoras study: investigating effects of teaching and learning in Swiss and German mathematics classrooms” in The power of video studies in investigating teaching and learning in the classroom. eds. T. Janik and T. Seidel (New York: Waxmann), 137–160.
König, J., Blömeke, S., Jentsch, A., Schlesinger, L., Née Nehls, C. F., Musekamp, F., et al. (2021). The links between pedagogical competence, instructional quality, and mathematics achievement in the lower secondary classroom. Educ. Stud. Math. 107, 189–212. doi: 10.1007/S10649-020-10021-0
Kunter, M., and Baumert, J. (2007). Who is the expert? Construct and criteria validity of student and teacher ratings of instruction. Learn. Environ. Res. 9, 231–251. doi: 10.1007/S10984-006-9015-7
Larsen, N. E., and Jang, E. E. (2021). Instructional practices, students’ self-efficacy and math achievement: a multi-level factor score path analysis. Can. J. Sci. Math. Technol. Educ. 21, 803–823. doi: 10.1007/S42330-021-00181-3
Lipowsky, F., Rakoczy, K., Pauli, C., Drollinger-Vetter, B., Klieme, E., and Reusser, K. (2009). Quality of geometry instruction and its short-term impact on Students' understanding of the Pythagorean theorem. Learn. Instr. 19, 527–537. doi: 10.1016/J.Learninstruc.2008.11.001
Molero Jurado, M. D. M., Perez-Fuentes, M. D. C., Atria, L., Oropesa Ruiz, N. F., and Gazquez Linares, J. J. (2019). Burnout, perceived efficacy, and job satisfaction: perception of the educational context in high school teachers. Biomed. Res. Int. 2019, 1–10. doi: 10.1155/2019/1021408
Morgan, P. L., Farkas, G., and Maczuga, S. (2015). Which instructional practices Most help first grade students with and without mathematics difficulties? Educ. Eval. Policy Anal. 37, 184–205. doi: 10.3102/0162373714536608
OECD (2020). TALIS 2018 results (volume II): Teachers and school leaders as valued professionals. Paris: TALIS, OECD Publishing.
Paulick, I., Retelsdorf, J., and Möller, J. (2013). Motivation for choosing teacher education: associations with teachers’ achievement goals and instructional practices. Int. J. Educ. Res. 61, 60–70. doi: 10.1016/J.Ijer.2013.04.001
Pianta, R. C., and Hamre, B. K. (2009). Conceptualization, measurement, and improvement of classroom processes: standardized observation can leverage capacity. Educ. Res. 38, 109–119. doi: 10.3102/0013189x09332374
Rasmussen, C., and Kwon, O. N. (2007). An inquiry-oriented approach to undergraduate mathematics. J. Math. Behav. 26, 189–194. doi: 10.1016/J.Jmathb.2007.10.001
Rittle-Johnson, B. (2006). Promoting transfer: effects of self-explanation and direct instruction. Child Dev. 77, 1–15. doi: 10.1111/J.1467-8624.2006.00852.X
Sawada, D., Piburn, M. D., Judson, E., Turley, J., Falconer, K., Benford, R., et al. (2002). Measuring reform practices in science and mathematics classrooms: the reformed teaching observation protocol. Sch. Sci. Math. 102, 245–253. doi: 10.1111/J.1949-8594.2002.Tb17883.X
Schiefele, U., and Schaffner, E. (2015). Teacher interests, mastery goals, and self-efficacy as predictors of instructional practices and student motivation. Contemp. Educ. Psychol. 42, 159–171. doi: 10.1016/J.Cedpsych.2015.06.005
Schlesinger, L., and Jentsch, A. (2016). Theoretical and methodological challenges in measuring instructional quality in mathematics education using classroom observations. ZDM 48, 29–40. doi: 10.1007/S11858-016-0765-0
Schlesinger, L., Jentsch, A., Kaiser, G., König, J., and Blömeke, S. (2018). Subject-specific characteristics of instructional quality in mathematics education. ZDM 50, 475–490. doi: 10.1007/S11858-018-0917-5
Skaalvik, E. M., and Skaalvik, S. (2007). Dimensions of teacher self-efficacy and relations with strain factors, perceived collective teacher efficacy, and teacher burnout. J. Educ. Psychol. 99, 611–625. doi: 10.1037/0022-0663.99.3.611
Skaalvik, E. M., and Skaalvik, S. (2014). Teacher self-efficacy and perceived autonomy: relations with teacher engagement, job satisfaction, and emotional exhaustion. Psychol. Rep. 114, 68–77. doi: 10.2466/14.02.PR0.114k14w0
Sulla, F., and Rollo, D. (2023). The effect of a short course on a group of Italian primary school teachers’ rates of praise and their pupils’ on-task behaviour. Educ. Sci. 13. doi: 10.3390/Educsci13010078
Theobald, E. J., Hill, M. J., Tran, E., Agrawal, S., Arroyo, E. N., Behling, S., et al. (2020). Active learning narrows achievement gaps for underrepresented students in undergraduate science, technology, engineering, and math. Proc. Natl. Acad. Sci. 117, 6476–6483. doi: 10.1073/Pnas.1916903117
Thompson, C. J., and Davis, S. B. (2014). Classroom observation data and instruction in primary mathematics education: improving design and rigour. Math. Educ. Res. J. 26, 301–323. doi: 10.1007/S13394-013-0099-Y
Toropova, A., Myrberg, E., and Johansson, S. (2021). Teacher job satisfaction: the importance of school working conditions and teacher characteristics. Educ. Rev. 73, 71–97. doi: 10.1080/00131911.2019.1705247
Tschannen-Morana, M., and Hoy, A. W. (2001). Teacher efficacy: capturing an elusive construct. Teach. Teach. Educ. 17, 783–805. doi: 10.1016/S0742-051X(01)00036-1
Wagner, W., Göllner, R., Werth, S., Voss, T., Schmitz, B., and Trautwein, U. (2016). Student and teacher ratings of instructional quality: consistency of ratings over time, agreement, and predictive power. J. Educ. Psychol. 108, 705–721. doi: 10.1037/Edu0000075
Walkington, C., and Marder, M. (2014). “Classroom observation and value-added models give complementary information about quality of mathematics teaching” in Designing teacher evaluation systems: New guidance from the measuring effective teaching project. Eds. T. Kane, K. Kerr, and R. Pianta (Wiley), 234–277.
Walkowiak, T. A., Berry, R. Q., Meyer, J. P., Rimm-Kaufman, S. E., and Ottmar, E. R. (2014). Introducing an observational measure of standards-based mathematics teaching practices: evidence of validity and score reliability. Educ. Stud. Math. 85, 109–128. doi: 10.1007/S10649-013-9499-X
Yang, X., Kaiser, G., König, J., and Blömeke, S. (2020). Relationship between pre-service mathematics teachers’ knowledge, beliefs and instructional practices in China. ZDM Math. Educ. 52, 281–294. doi: 10.1007/S11858-020-01145-X
Yu, R., and Singh, K. (2016). Teacher support, instructional practices, student motivation, and mathematics achievement in high school. J. Educ. Res. 111, 81–94. doi: 10.1080/00220671.2016.1204260
Zakariya, Y. F. (2020). Effects of school climate and teacher self-efficacy on job satisfaction of mostly STEM teachers: a structural multigroup invariance approach. Int. J. STEM Educ. 7. doi: 10.1186/S40594-020-00209-4
Zakariya, Y. F. (2021). Application of an innovative alignment optimisation method to a cross-cultural mean comparison of teacher self-efficacy: a cross-country study. Heliyon 7, 1–10. doi: 10.1016/J.Heliyon.2021.E08212
Zakariya, Y. F. (2022). Cronbach's alpha in mathematics education research: its appropriateness, overuse, and alternatives in estimating scale reliability. Front. Psychol. 13:1074430. doi: 10.3389/Fpsyg.2022.1074430
Keywords: teacher self-efficacy, teacher cooperation, mathematics teachers, TALIS 2018, teacher job satisfaction
Citation: Zakariya YF and Adegoke NA (2024) Teacher instructional practices: untangling their complex relations with self-efficacy, job satisfaction, stress, and cooperation among mathematics teachers. Front. Educ. 9:1367076. doi: 10.3389/feduc.2024.1367076
Received: 08 January 2024; Accepted: 05 July 2024;
Published: 16 July 2024.
Edited by:
Mei-Shiu Chiu, National Chengchi University, TaiwanReviewed by:
Francesco Sulla, University of Foggia, ItalyCopyright © 2024 Zakariya and Adegoke. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yusuf Feyisara Zakariya, eXVzdWYuemFrYXJpeWFAdWlhLm5v
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.