Including neurodiversity in computational thinking

Introduction: The foundational practices of Computational Thinking (CT) present an interesting overlap with neurodiversity, specifically with differences in executive function (EF). An analysis of CT teaching and learning materials designed for differentiation and support of EF show promise to reveal problem-solving strengths of neurodivergent learners.

Methods: To examine this potential, studies were conducted using a computer-supported, inclusive, and highly interactive learning program named INFACT that was designed with the hypothesis that all students, including neurodivergent learners, will excel in problem solving when it is structured through a variety of CT activities (including games, puzzles, robotics, coding, and physical activities) and supported with EF scaffolds. The INFACT materials were used in 12 treatment classrooms in grades 3–5 for at least 10  h of implementation. Pre-post assessments of CT were administered to treatment classes as well as 12 comparison classes that used 10  h of other CT teaching and learning materials. EF screeners were also used with all classes to disaggregate student results by quartile of EF.

Findings: Students using INFACT materials showed a significant improvement in CT learning as compared to comparison classes. Students with EF scores in the lower third of the sample showed the greatest improvement.

Discussion: This study shows promising evidence that differentiated activities with EF scaffolds situated across several contexts (e.g., games, puzzles, physical activities, robotics, coding) promote effective CT learning in grades 3–5.

1 Introduction

This paper reports on a study of teaching and learning materials designed for the inclusion of neurodivergent learners in computational thinking (CT) in grades 3–8. We define an inclusive classroom as one that has at least 20% of students with individual education plans (IEPs) or equivalent alternative programming for cognitive differences. The study examines how materials supported executive function (EF) and differentiated teaching and learning, specifically in inclusive classrooms in grades 3–5.

Inclusive classrooms are typically general education classrooms where neurodivergent and neurotypical students learn together. Inclusive classrooms often do not include learners with profound needs that cannot be accommodated in a general classroom. As of 2017, in the US, approximately 65% of learners receiving special education services were spending 80% or more of the school day in inclusive classrooms (Horowitz et al., 2017; McFarland et al., 2019). While there are varying levels of severity of many of the conditions requiring special education, inclusive classrooms typically include learners who need light or moderate supports, but not those who need more intensive supports to accomplish daily tasks (Polirstok, 2015). As today’s classrooms are becoming more inclusive of neurodiversity—the differences in the ways students think and learn—teachers and those designing for classroom settings need to look for new approaches to engage all learners.

The term neurodiversity refers to a growing perspective that variation in human brain activities is comparable to the natural variation in race, sexuality, and other human factors (Blume, 1998; Singer, 1998). Terms such as neurodiversity and neurodivergence are often used to steer away from labels such as autism, ADHD, and dyslexia, which come from a medical perspective. The diagnostic labels may be useful in identifying potential interventions as well as crucial for accessing potential educational resources for some learners, but they may also come with prejudice and stigmatization that ignore the talents of these learners. Focusing on strengths, and taking an asset-based approach to education, offers each learner a chance to reveal their strengths and supports equity in the classroom (Bang, 2020; Madkins et al., 2020).

Inclusive classrooms often include students who demonstrate outstanding talents in specific areas related to problem solving, while also requiring supports for EF (Asbell-Clarke, 2023). EF is the set of processes the brain uses to coordinate sensory, emotional, and cognitive aspects of learning (Antshel et al., 2014; Varvara et al., 2014; Bellman et al., 2015; Meltzer, 2018; Meltzer et al., 2018; Demetriou et al., 2019). These processes include attention, working memory, and self-regulation, which are required when organizing and prioritizing information and tasks and when conducting tasks such as setting goals and designing and implementing a plan to achieve those goals (Brown, 2006; Diamond, 2013). EF is considered essential for deeper learning and developing transferable skills for success in school, college, and one’s career (Pellegrino and Hilton, 2012).

EF is rapidly being recognized as a key area of focus for education for all learners, not just those in special education (Immordino-Yang et al., 2018; Meltzer, 2018). EF is responsible for regulating attention, emotions, and impulse control, which enables persistence and motivation to achieve these goals (Meltzer et al., 2018; Semenov and Zelazo, 2018). EF can be a struggle for many neurodivergent learners, as well as learners undergoing stress, trauma, and/or anxiety (Immordino-Yang et al., 2018), all of which are on the rise in today’s schools (Hawes et al., 2022; Rodriguez and Burke, 2023). Overall, supporting EF in learning activities may produce better performance which can, in turn, increase motivation, causing a positive learning cycle and improved self-efficacy (Semenov and Zelazo, 2018).

CT is an emerging area of education that may reveal the strengths of many neurodivergent learners and also support their EF. CT is a problem-solving approach that leads to generalized and replicable solutions that can be implemented by computers and information-processing systems (Shute et al., 2017), and is attracting increased attention in K–12 education, prompting calls for new models of pedagogy, instruction, and assessment, particularly in younger grades (Wing, 2008; Cuny et al., 2010; Barr and Stephenson, 2011; Grover and Pea, 2017; Shute et al., 2017). The fundamental practices of CT are also foundational to everyday problem solving (e.g., making a meal or cleaning up the classroom), as well as many school-based learning activities (e.g., solving a math problem, conducting a science experiment, or writing an essay). Foundational CT practices include Problem Decomposition: breaking up a complex problem into smaller, more manageable problems; Pattern Recognition: seeing patterns among problems that may have similar types of solutions; Abstraction: generalizing problems into groups by removing the specific information and finding the core design of each problem; and Algorithmic Thinking: thinking of problem-solutions as a set of general instructions that can be reused in different settings. Additionally, the CSTA (2017) outlines a number of dispositions or attitudes essential to CT, including confidence in dealing with complexity, persistence in working with difficult problems, tolerance for ambiguity in dealing with open-ended problems, and the ability to work in collaborative groups towards a common goal.

The practices and dispositions associated with CT present an interesting overlap with the strengths and needs of many neurodivergent learners. For example, some neurodivergent learners such as autistic learners may not demonstrate high cognitive flexibility (i.e., they are very rigid in their thinking) yet excel in recognizing patterns within complex situations and paying attention to close detail (Jolliffe and Baron-Cohen, 1997; Fugard et al., 2011). Pattern recognition has also been proposed as a primary basis for particular talents and savant behaviors in autism, such as calendar calculating, mathematics, and other specialized skills (Baron-Cohen, 2008; Mottron et al., 2009). Research also suggests that some other learners who may struggle to focus attention on details in pattern recognition (e.g., some people with ADHD) may be more open to ambiguity and collaborations than their peers, often making innovative connections between ideas and abstractions that are not seen by others (Beaty et al., 2015). Similarly, the differences in the brains of individuals with dyslexia may be beneficial for spatial reasoning, interconnectedness, and abstraction (Eide and Eide, 2012).

CT has the potential dual advantage of tapping into some of the specific cognitive strengths (e.g., pattern recognition, systematic thinking, and abstraction) associated with neurodiversity, while also structuring problems in a clear and generalizable way to assist all learners. Students who struggle with EF challenges may benefit from a problem-solving approach that emphasizes breaking up problems into smaller chunks to support working memory, and generalization of patterns in problem solutions to apply to a variety of different situations that may support cognitive flexibility. In addition, the emphasis on developing algorithms, or problem-solving tools, that can be named and re-used, is a mechanism to support metacognition and explicit reflection on the problem-solving steps (Ocak et al., 2023). A systematic review of the effects of CT interventions on children’s EF (Montuori et al., 2023) showed significant effects on students’ planning and core EF skills. For example, children aged 5–7 showed increased planning skills after using Code.org (an introductory coding environment) for a month. The largest effects were observed on children’s problem solving and complex EFs such as planning, but significant positive effects emerge also for core EFs like cognitive inhibition and working memory.

Coding and robotics programs were shown to be effective when they addressed the various components of CT, such as problem analysis, planning, evaluating and debugging, where CT interventions that focused on just one component or on programming skills solely were less effective (Oluk and Saltan, 2015). Robotics activities have been shown to improve the inhibition in terms of speed and accuracy of information processing for a broad array young children who were categorized as having “special needs” (identified as having cognitive and behavioral differences) (Di Lieto et al., 2020).

2 Materials and methods

The challenges many neurodivergent learners face in school are often related to executive function processes in the brain, which include working memory, cognitive flexibility, and inhibitory control (which is closely related to self-regulation of attention) (Meltzer, 2018). In an effort to support a broad range of neurodivergent (and neurotypical) learners in CT, the INFACT project provides differentiated teaching and learning materials using CT in a variety of contexts and modalities with embedded supports for learners’ executive function. To support and study the potential intersection between CT and EF in grades 3–5, a consortium of learning scientists and developers designed a program called Including Neurodiversity in Foundational and Applied Computational Thinking (INFACT).

2.1 Overview of INFACT teaching and learning materials

The INFACT teaching and learning materials for grades 3–8 introduce CT practices such as Problem Decomposition, Pattern Recognition, Abstraction, and Algorithm Design in a variety of contexts like mazes, music, art, puzzles, and sports to provide many real-life examples of CT.

The INFACT activities are delivered in topical sequences that build foundational and applied CT knowledge through a multitude of off-line and online activities. The sequences are:

• Sequence 1: Introduction to CT focuses on introducing learners to CT practices such as Problem Decomposition, Pattern Recognition, Abstraction, and Algorithm Design.

• Sequence 2: Clear Commands focuses on clear and unambiguous communication and devising a common set of commands to give instructions for a task.

• Sequence 3: Conditional Logic focuses on the use of IF-THEN (and IF-THEN-ELSE) commands with the introduction of Boolean operators such as AND, OR, and NOT.

• Sequence 4: Repeat Loops uses REPEAT commands to group together patterns of commands to make repetitive instructions more efficient.

• Sequence 5: Variables focuses on the use of variables to make commands and algorithms modifiable and reusable.

• Sequence 6: Functions focuses on the creation and use of functions to build sets of commands into reusable algorithms.

Each INFACT learning sequence consists of a number of different possible Activation activities, Foundational activities, Applied activities, and Wrap Up activities that the teacher can choose according to their students’ interests and their classroom needs. Each sequence also has a default set of activities for a quick start. Activation activities motivate and prepare learners for the sequence topical activities. The Foundational activities build conceptual knowledge associated with CT topics and practices. The Applied activities have students apply CT topics and practices in supported tasks. The Wrap Up activities allow students to reflect upon the sequence and focus on the main take-aways. These materials are available through Open Access (INFACT, 2024).

2.2 Supporting differentiated instruction in INFACT materials

For effective inclusive education, educators need to differentiate their teaching strategies to draw on the unique strengths of all learners, including neurodivergent learners, while also supporting the different EF needs of all students (Tomlinson and Strickland, 2005; Van Garderen et al., 2009; Brownell et al., 2010; Armstrong, 2012; Immordino-Yang et al., 2018). Differentiated instruction presents all learners with the same learning goal but provides students varied pathways to reach that goal and also allows students to demonstrate knowledge in different ways by adapting activities to support multiple modalities (Galiatsos et al., 2019). The Universal Design for Learning (UDL) framework (Rose, 2000) provides guidance on differentiating for neurodiversity by offering multiple means of representation, multiple means of action and expression, and multiple means of engagement. Some neurodivergent students may need additional supports with EF, as well as with navigating social interactions, sensory demands, and barriers posed by disability-related bias or social stigma (Schindler et al., 2015; Chandrasekhar, 2020; Mellifont, 2021). Students’ need for differentiated learning, particularly around EF, has only grown during COVID (Myung et al., 2020). Without these supports, neurodivergent learners may “underperform” because extraneous barriers mask their problem-solving talents (Shattuck et al., 2012; Gottfried et al., 2014; Austin and Pisano, 2017; Galiatsos et al., 2019).

Differentiation strategies for inclusive classrooms that are embedded in the overall design of INFACT include:

• Clean and consistent interface design

• Activation strategies to engage and prepare learners

• Multiple entry points into an activity

• Alternate representations and modes of learning.

The INFACT activities are delivered through a teacher differentiation portal that allows teachers to select activities based upon availability of technology, student grouping (e.g., pairs or whole class), and interest area or theme. The portal also offers multiple versions of many activities allowing for different entry points and scaffolds for different learners. The INFACT themes include game-based learning, robotics, and/or coding, as well as activities that allow a more general exploration of CT. Robotics activities are designed for use with Spheros, and a guide is provided to “translate” the activities for other popular robotics systems. The game-based learning theme of INFACT focuses on Zoombinis, a popular and award-winning CT puzzle game that has been shown to support teaching and learning of CT practices in grades 3–8 (Asbell-Clarke et al., 2021). Unplugged activities, puzzles, and games are used to build CT concepts before (or instead of) jumping into coding activities. Many of the INFACT activities include “get up and go” embodied activities, where students physically act out a puzzle or walk through a maze. Unplugged and digital CT activities complement robotics and gameplay to help build foundational understanding of problem decomposition, pattern recognition, abstraction, and algorithm design.

2.3 Supporting executive function in INFACT materials

Robertson et al. (2020) argue that the link between EF and CT is worth exploring for two reasons. First, EF is a predictor of academic success in general, including in the development of mathematical skills and science learning (Gilmore and Cragg, 2014). Second, there is some evidence that the development of CT practice may support the improvement of EF. Castro et al. (2022) found that an 8-week CT intervention program had a favorable effect on metacognitive processes, as well as cognitive processes such as working memory. DePryck (2016) suggests that “the metacognitive abilities required for CT (including connecting new information to former knowledge, deliberately selecting thinking strategies, planning, monitoring and evaluating thinking processes, breaking down complex actions into a conditional sequence) rely on executive function.” Other recent research shows that teaching coding and robotics may have an impact on students’ planning abilities (Gerosa et al., 2019; Arfé et al., 2020; Di Lieto et al., 2020). This research is just emerging and generally has small study numbers, so these linkages merit further investigation.

The INFACT online and offline activities are designed with embedded supports for EF. Supports for EF that are offered alongside offline and online INFACT activities include:

• Vocabulary cards to support working memory by introducing and keeping key terms and phrases at hand during activities (Figure 1).

• CT learning checkpoints to support metacognition and foster explicit expression of understandings (Figure 2).

• “Set up for success” teaching strategies to support working memory and attention through differentiation (Figure 3).

• Prompts to support metacognition including reflection and connections to other contexts (Figure 4).

Figure 1

Figure 1. INFACT Vocabulary Cards help teachers support vocabulary in just-in-time learning.

Figure 2

Figure 2. Metacognitive “I Can” Statements.

Figure 3

Figure 3. Teacher tips on when and how to use scaffolds are accompanied by suggested offline strategies for inclusive implementation of INFACT.

Figure 4

Figure 4. Prompts for reflection and connection.

In addition, digital supports for EF that are embedded within online puzzles from the CT learning game Zoombinis include:

• A flashlight tools to support attention by highlighting salient information (Figure 5).

• Graphical organizers to support working memory by enabling visual recording of information (Figure 6).

• Expression tools to support metacognition by promoting explicit expression of learning (Figure 7).

Figure 5

Figure 5. Screenshot of flashlight tool to scaffold attention in Zoombinis puzzle Allergic Cliffs.

Figure 6

Figure 6. Screenshot of bookkeeping tool to scaffold working memory in Zoombinis puzzle called Pizza Pass.

Figure 7

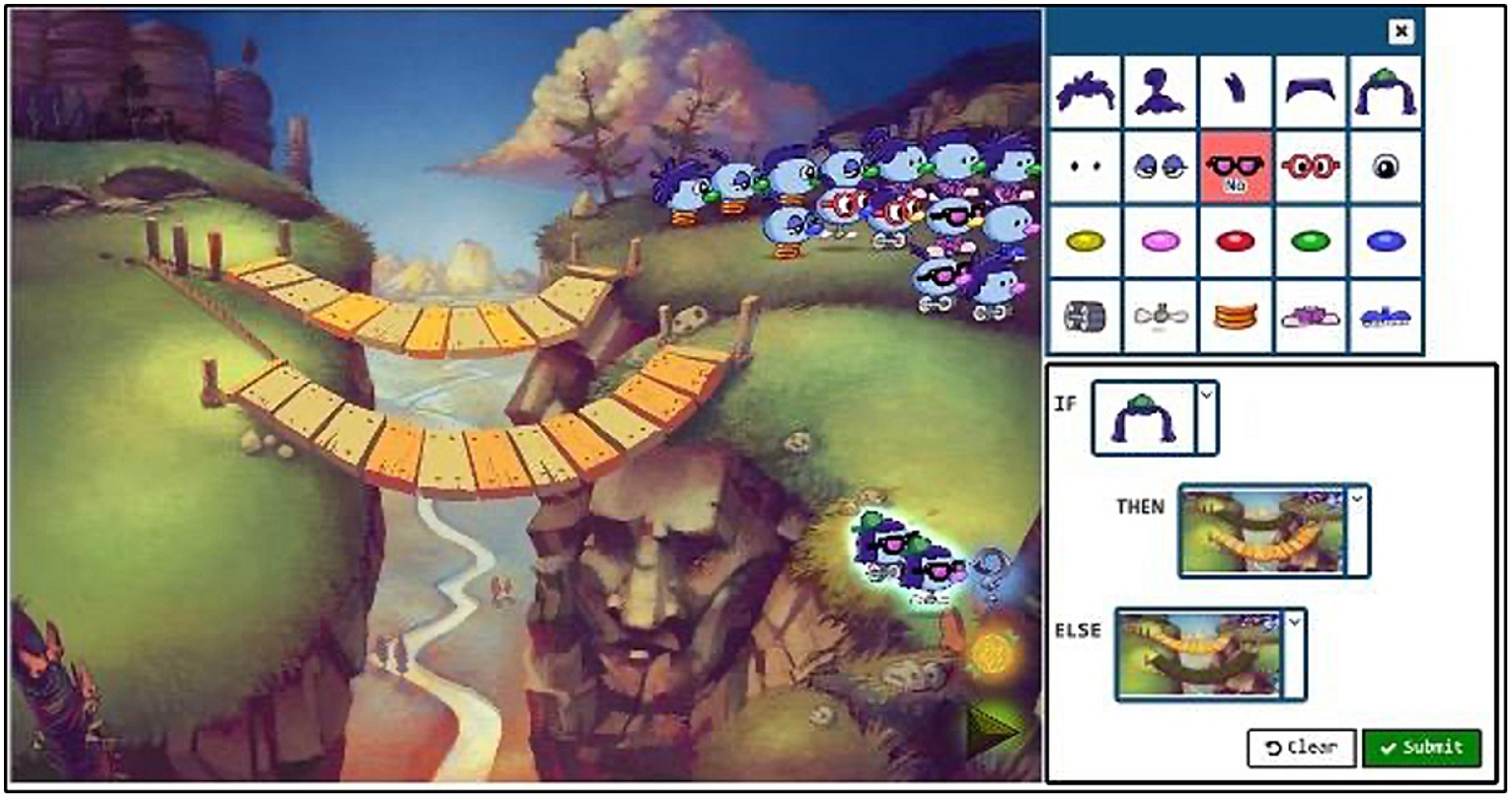
Figure 7. Screenshot of expression tool to scaffold metacognition in Zoombinis puzzle called Allergic Cliffs.

2.4 Research questions

The goal of this study was to address three research questions during the implementation of INFACT in inclusive classrooms in grades 3–5:

• Research Question 1 (RQ1): To what extent does a CT program designed for inclusion (e.g., with built-in differentiation strategies and EF supports) impact foundational CT learning?

• Research Question 2 (RQ2): To what extent does a CT program designed for inclusion moderate the effects of individual EF differences for learners?

• Research Question 3 (RQ3): What connections between CT and EF do teachers recognize and use when implementing a CT program designed for inclusion?

2.5 Research sample

Our independent research team studied the implementation of INFACT in 12 inclusive classes in grades 3–5. Another 12 comparison classes used other CT materials for the same duration. Pre-post CT proficiency assessments and EF assessment screeners were administered to INFACT and comparison classes.

2.5.1 Student participants

In most inclusive classrooms, neurodivergent learners may receive an individual education plan (IEP) or equivalent. Our study included classrooms with at least 20% of students having an IEP. The provision of IEPs, however, is often complicated by unequal access to diagnostic resources as a function of social economic strata and cultural disparities in what behavior is considered problematic or disruptive (Rucklidge, 2010; Russell et al., 2016; Shi et al., 2021). Therefore, we use a screener test with EF tasks rather than IEP status to get a more direct and equitable, albeit limited, measure of student neurodivergence for disaggregation of our sample. We divided the student population into thirds so that we were able to compare students who demonstrated low, medium, and high levels of EF.

A total of 1,009 students (515 treatment and 494 comparison) in grades 3–8 had consent to participate in the study. We obtained full pre-and post-assessment data for 659 (307 treatment and 352 comparison) of these students. However, due to the impact of COVID on recruitment, pre-instruction assessment scores for middle school (grades 6–8) students differed too significantly between the treatment and comparison participants for rigorous comparison, so the final analytic sample consisted of matched data from 364 students (182 treatment and 182 comparison) in grades 3–5.

2.5.2 Teacher participants

To obtain the student sample, INFACT recruited individual teachers through social media and teacher mailing lists. Eligible teachers could work at any kind of school (public, private, etc.) and teach any subject, but had to confirm 20% or more of the students they typically teach had IEP/other classification or teacher/parent designation as needing learning support. Each teacher could enroll up to five grade 3–8 classes in the study.

A comparison group was recruited from teachers who were already teaching CT. For this group, we purposely selected experienced CT teachers so they had an established curriculum they considered business-as-usual for CT teaching and learning. Many of the control teachers were focusing on CT activities that related specifically to coding. These included using introductory coding activities from Code.Org (e.g., hour of code) or having students build games and animations using Scratch (scratch.mit.edu). None of the control teachers reported specific EF supports used in the other materials. The treatment group was notably less experienced in CT. To participate as part of either group, teachers needed to commit to 10 h of CT instruction (using either INFACT or their existing curriculum) during a specific 10-week time period in Fall 2021 or in Spring 2022. Across both implementation periods, a total of 14 teachers participated in the treatment condition and 13 in the comparison condition.

2.5.3 Research design 

To address RQ1 (To what extent does a CT program designed for inclusion (e.g., using differentiation strategies and EF supports) impact foundational CT learning?), we examined the difference in CT proficiency of students in grades 3–5 who have had 10 instruction hours with INFACT teaching and learning materials compared to equivalent students who have had 10 instruction hours with business-as-usual CT activities.

To address RQ2 (To what extent does a CT program designed for inclusion moderate the effects of individual EF differences for learners in grades 3–5?), we examined the difference in CT proficiency for students who had the lowest third of EF scores in grades 3–5, comparing students who were in the INFACT program with equivalent students in the business-as-usual condition.

To address RQ3 (What connections between CT and EF do teachers recognize and use when implementing a CT program designed for inclusion in grades 3–5?) we studied teachers’ perspectives on CT and EF through their descriptions of their experience of teaching INFACT. We included the perspectives of all 14 teachers who implemented the program for RQ3, since this question did not include a comparative element. That means that RQ3 includes the perspectives of teachers working in grades 3–8, though the samples for RQ1 and RQ2 only included students in grades 3–5.

2.6 Data sources

2.6.1 CT measures

Assessment of CT practices is challenging due to a lack of standard measures, particularly at the elementary level. Compounding that complexity is the issue that CT is a thinking process, and measuring thinking processes can be more nuanced than assessing whether a learner can demonstrate knowledge components of a concept. Measuring learners’ abilities to plan, design, and solve complex problems is not done by a typical school test (Ritchhart et al., 2011). Even when CT performance is measured in a natural setting, such as in a coding environment, the final product may not reveal the CT practices or thinking processes involved in designing code (Grover and Pea, 2017). Current assessments often rely heavily on text comprehension and/or prerequisite knowledge of coding, which may preclude adequate measurement of these CT concepts (Kite et al., 2021; Rowe et al., 2021).

The Computational Thinking test (CTt) (Román-González, 2015) and Bebras Tasks (Dagienė and Futschek, 2008; Dagienė et al., 2016) have shown promise as general assessments of core CT constructs for K–12 students (Wiebe et al., 2019). At the time this research was conducted, the psychometric properties of these instruments had not been fully demonstrated, however, and most research was only conducted at the middle-school level. Also, some Bebras tasks were considered too peripheral to core CT skills to stand alone as a standard assessment for CT in K–12 education (Román-González et al., 2019). Additionally, many Bebras questions are coding-centric, a common critique of many CT assessments (Huang and Looi, 2021). The CTt test is more generalizable and also has been since adapted and validated for elementary-aged students in the form of the BCTt and the cCTt (El-Hamamsy et al., 2022), but those findings were not available for this research opportunity.

Learning assessments that include irrelevant barriers such as text or other heavy symbolic notation may also create an undue cognitive load for learners, particularly for those who struggle with areas of EF including attention and working memory (Haladyna and Downing, 2004; Sireci and O’Riordan, 2020; Rowe et al., 2021). For equitable assessments of CT, assessments should be differentiated in terms of “engagement, representation, and action & expression” in line with UDL principles (Rose, 2000) so that each learner is able to learn and demonstrate knowledge on their own terms (Armstrong, 2012; Rowe et al., 2017; Murawski and Scott, 2019). For these reasons, we have used the Interactive Assessments of Computational Thinking (IACT) assessment in our study of INFACT (Figures 8–10). We developed and validated the IACT items in previous research, where they showed a strong test–retest validity and a moderate concurrent validity with select comparable Bebras items (Rowe et al., 2021). At the time of this research, the IACT items presented the best option for CT measures for grades 3–8 without many of the extraneous barriers presented by other CT assessments.

Figure 8

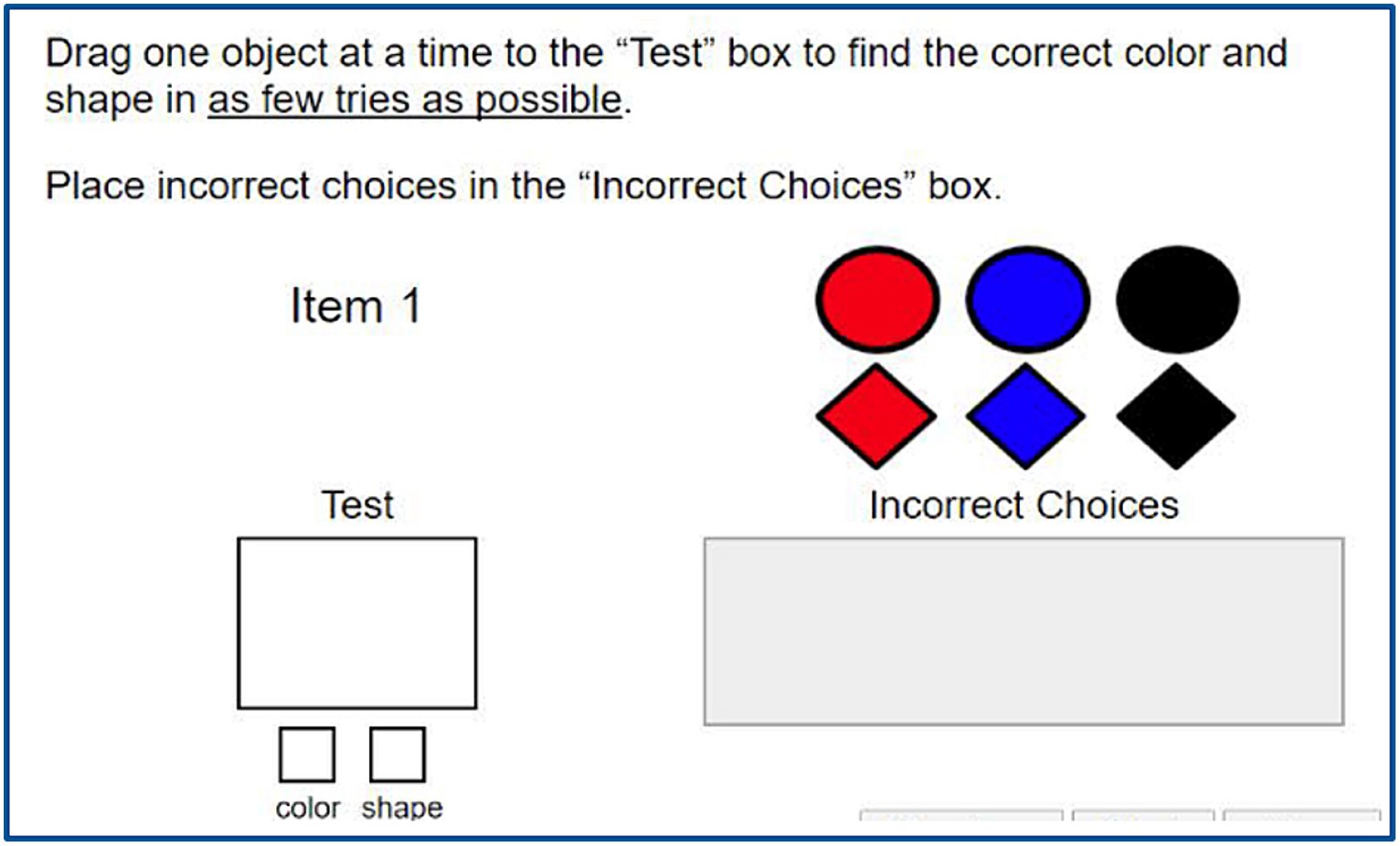
Figure 8. Example Problem Decomposition task in IACT assessments (Rowe et al., 2021).

Figure 9

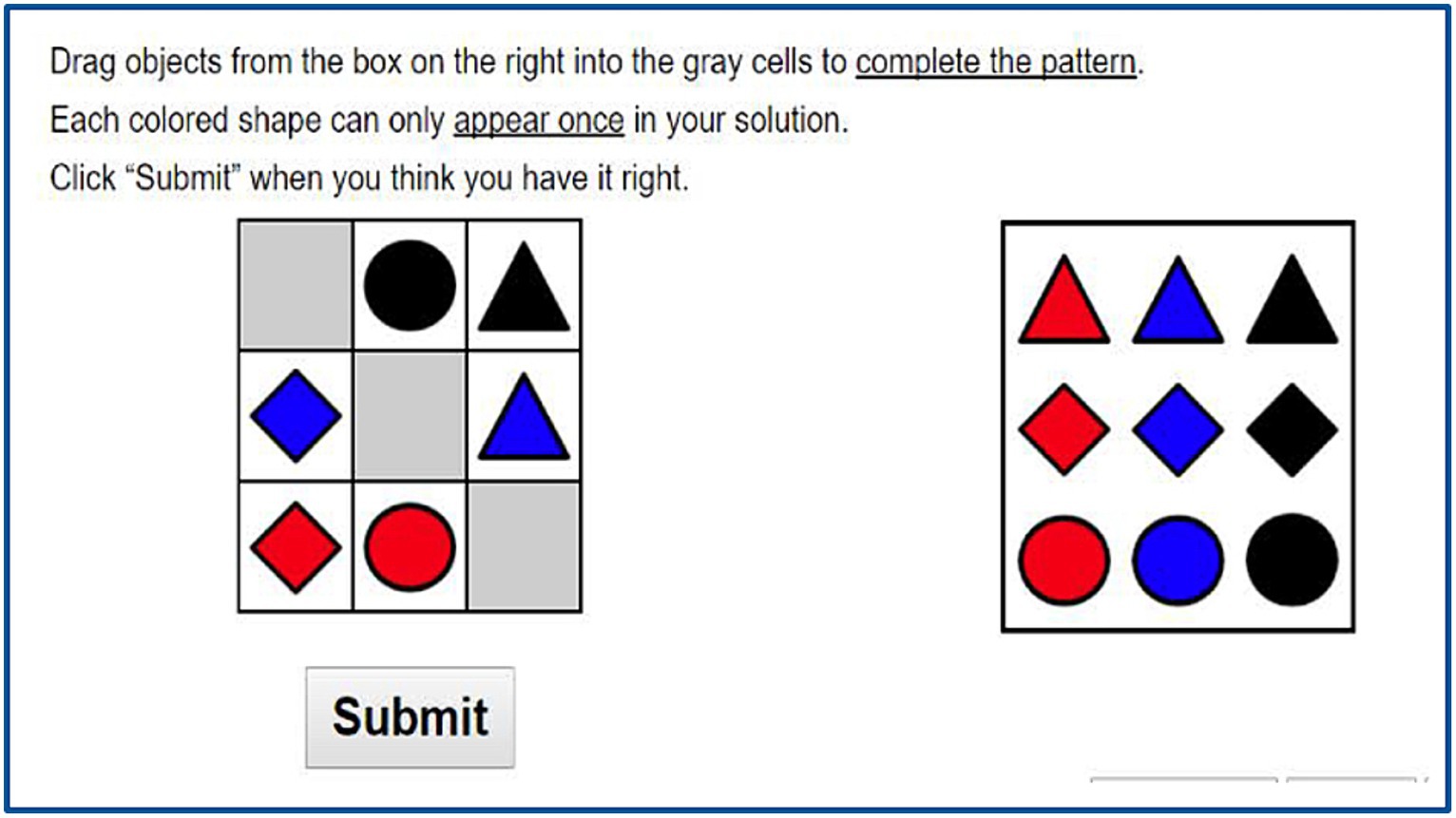
Figure 9. Example Abstraction task in IACT assessments (Rowe et al., 2021).

Figure 10

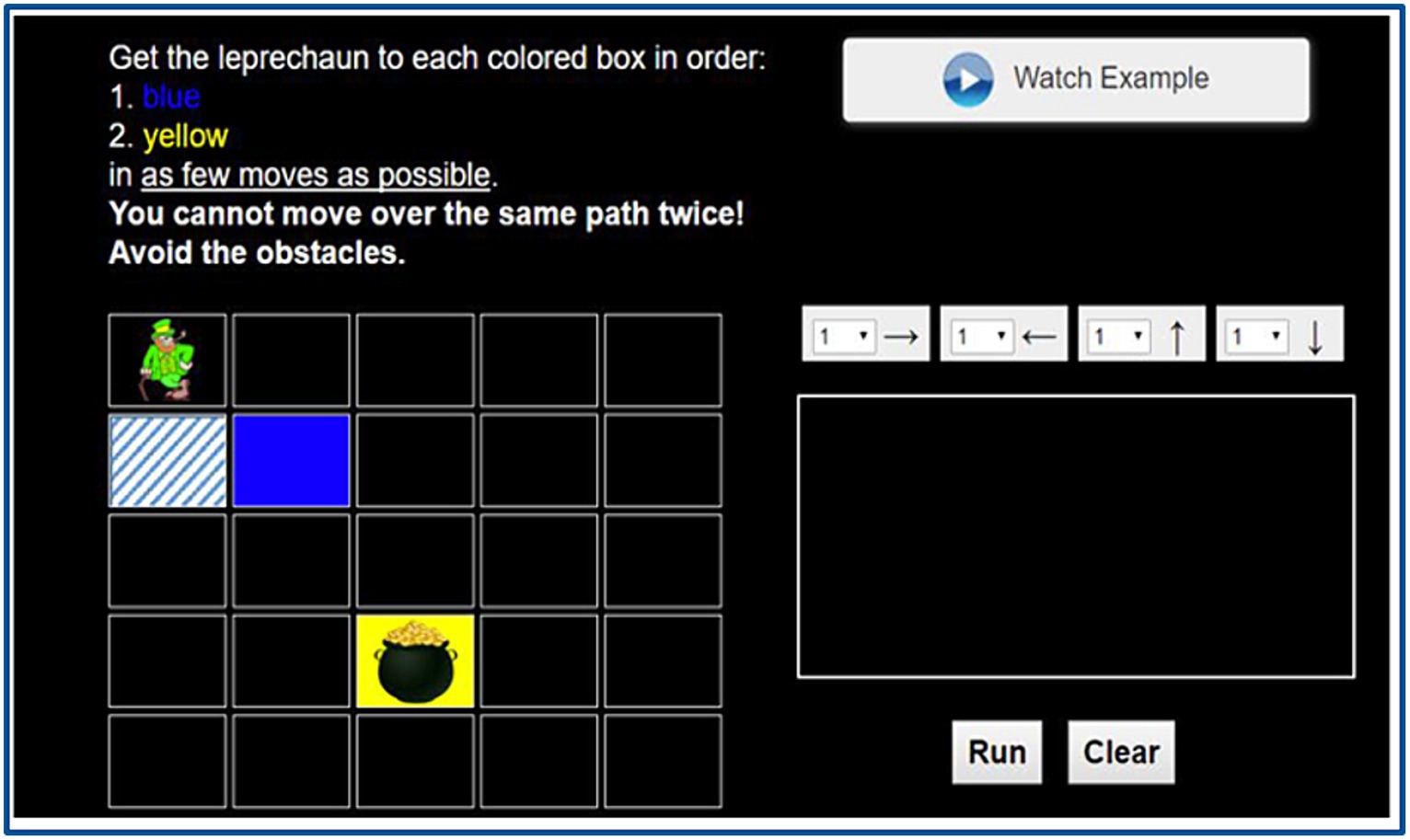
Figure 10. Example Algorithm Design task in IACT assessments (Rowe et al., 2021).

The IACT items were delivered at the beginning and end of the 10-h CT-instruction period, as a pre-and post-test of CT proficiency. IACT consists of four modules, each containing multiple logic puzzles. Because each module is scored differently, z-scores are calculated for each separately, using all data available (including from previous large studies). To prepare to use the IACT items in the INFACT research study, we conducted an initial validation study of 167 students with similar but separate participants in grades 3–8. We observed that the variation in participants’ scores on the first (pattern recognition) module was much lower than for the other modules, with most scoring close to the maximum. Accordingly, we chose to use a modified IACT score based on the remaining three modules, where we observed wider variation. (Data from the first module were still collected during the research study, and they exhibited the same pattern as observed during the validation study.)

The IACT scores were computed based on the performance of participants on a set of CT-related tasks relative to a total norming sample of 4,168 students in grades 3–8 in previous research (Rowe et al., 2021). This was done so that we could place the current study in the context of the full distribution of possible IACT scores. A z-score was computed for each student on each subscale of IACT and then amalgamated into a single overall z-score. Therefore, an IACT score of zero means average performance relative to the sample, a negative score indicates below average performance in units of standard deviations, and a positive score indicates above average performance in units of standard deviations. One should note that students in the present sample generally scored above the overall mean score on the IACT, which may be attributable to the increase in CT in schools since the time of the data collection of the norming sample.

2.6.2 EF measures

In addition to the IACT pre-test, students completed a set of EF tasks at the beginning of the implementation period. These tasks were taken from Neuroscape’s Adaptive Cognitive Evaluation (ACE), a game-like implementation of standard instruments to measure working memory, cognitive flexibility, and attention regulation (Younger et al., 2021). The tasks selected for the research study were Go/No-Go, Flanker, Task Switching, and Backwards Spatial Span. The results of scores on these four tasks were standardized and amalgamated into a single ACE score. ACE data were processed using the aceR package provided by Neuroscape, and the scoring metrics for each individual task were chosen based on the developers’ recommendations (Rate Correct Score for Flanker and Task Switching, Mean Response Time for Go/No-Go, and Maximum Object Span for Backwards Spatial Span). Neuroscape does not currently provide guidance on combining scores from different modules to create a composite measure. However, since scores on each module were weakly to moderately correlated with the other modules (after normalization to account for the different scoring metrics), we used a combined measure. We tested several methods of creating this summary score, including Mahanalobis distance from a theoretical student who obtained the maximum score observed for each module and principal components analysis, but these did not significantly improve model fit over a basic mean of z-scores on the four modules. Accordingly, we proceeded with the mean score for analysis.

2.6.3 Teacher interviews

To address RQ3 and understand how teachers implemented INFACT, we interviewed each teacher in the Treatment condition 3–4 times over the course of the term. Teachers in the comparison group were not interviewed throughout the term, but did fill out a survey after their participation concluded, which included items on the types of activities used and time spent on CT, as well as open-ended items on the meaning and value of CT.

Three interviewers conducted these conversations, with each interviewer assigned to a small number of teachers for continuity. In the first interview, we asked about teachers’ reasons for participating and the planning process, in addition to gathering information about the activities they had already used and their experience. In subsequent interviews, we continued to ask about their experience with the activities used to date. In the final interview, we also asked about their overall INFACT experience, including curricular connections, impact on their teaching, and impact on their students.

2.7 Data analysis

Linear mixed-effects models were used for the quantitative analysis. The models included terms to control for the fixed effects of pre-instruction IACT score, composite ACE score, and grade level. The model also controlled for teacher-and school-level random effects; that is, it accounted for the fact that students with the same teacher or in the same school might show comparable outcomes. There was only one case in which two teachers from the same school participated, and both were in the comparison condition. Meanwhile qualitative analysis began with overarching themes identified from project goals, with additional themes identified iteratively through analysis.

2.7.1 Analysis for RQ1 and RQ2

2.7.1.1 Apriori analysis

See Table 1 for the equations used to model the data for analysis of RQ1 and RQ2. Note that these models were developed apriori in anticipation of the predicted structure and potential sources of noise ahead of data collection. We present the results of the pre-registered study (Attaway and Voiklis, 2022) here, with additional analyses in the next section. Model 1 provides a test for RQ1 by looking for a statistically significant impact for the treatment condition while controlling for the other factors. Model 2 addressed RQ2 and included all the same variables as Model 1 but added an interaction effect between the ACE score used as an EF screener and treatment condition.

Table 1

Table 1. Linear mixed-effects models used to analyze the full sample.

2.7.1.2 Post hoc analysis

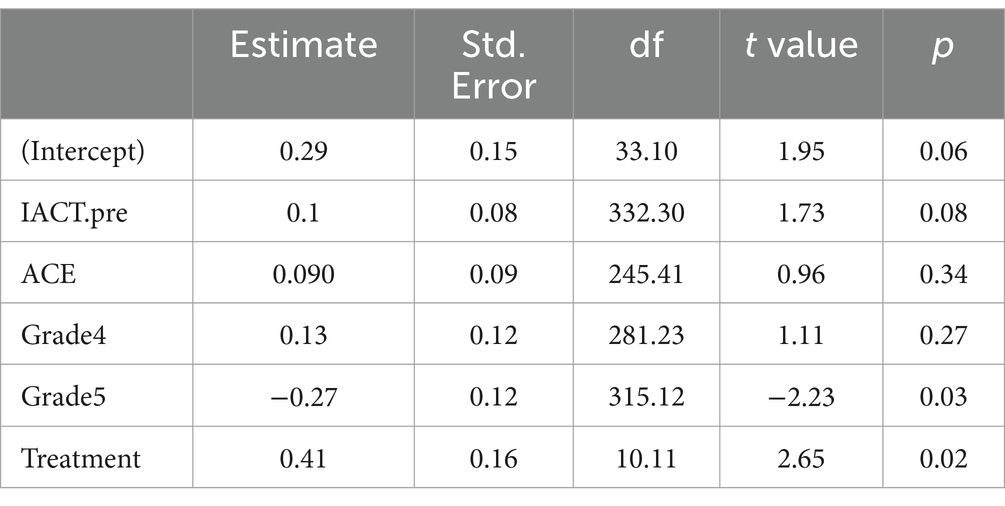
In addition to the apriori models, to address RQ2, we conducted a post hoc analysis to look at the impact of the intervention on students in the lowest third of ACE scores. This provided a better sense of how well INFACT worked for students who struggle the most with EF barriers. As shown in Figure 11, we grouped the data by ACE score thirds rather than continuous ACE scores because the impact of the intervention on ACE scores was not linear. We also recoded time as a binary variable rather than including IACT prescores as a fixed effect. This resulted in a new model using only those students in the lowest third of ACE scores. Table 2 includes the model used.

Figure 11

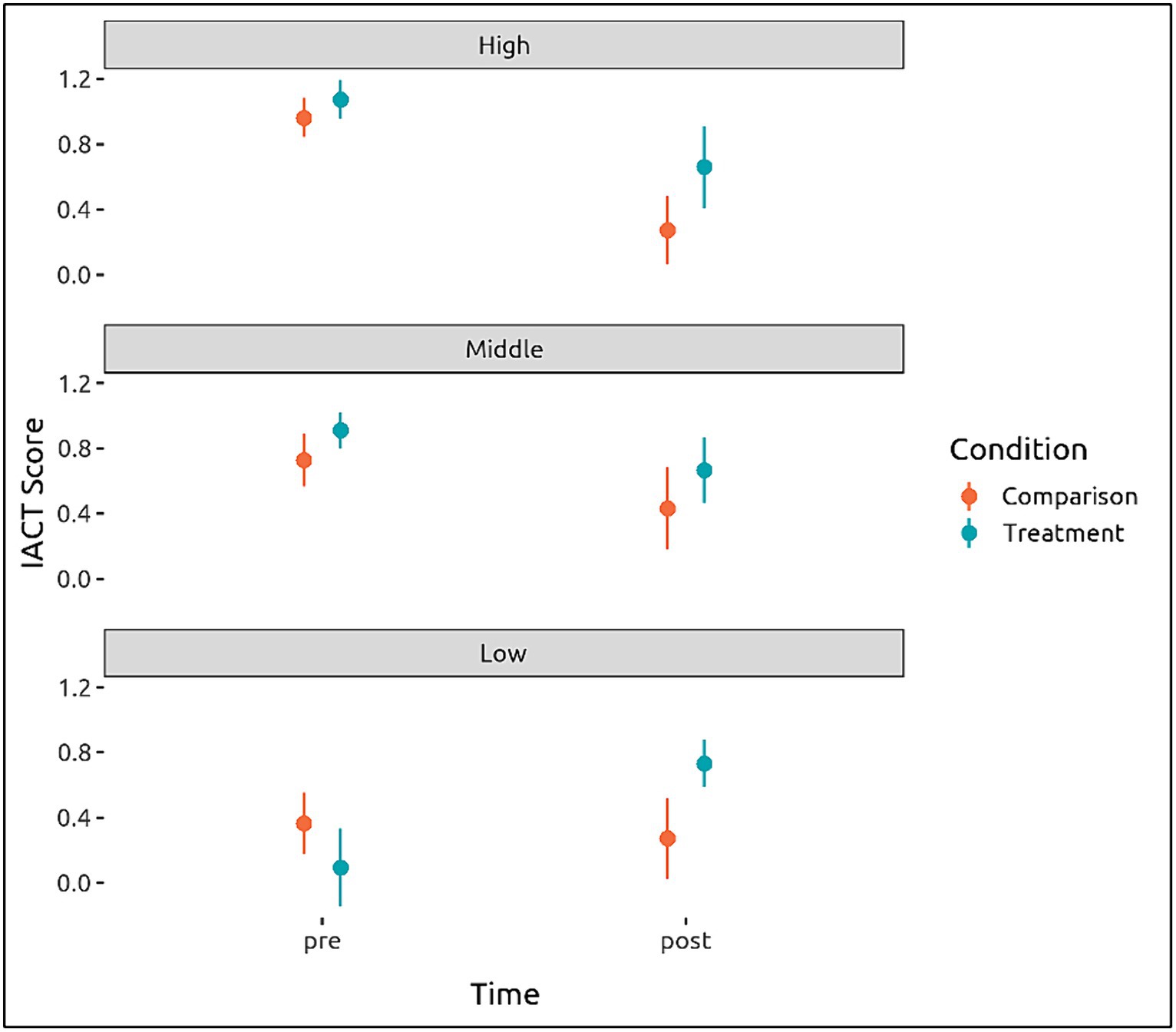
Figure 11. Performance on pre-and post-assessments of CT by group, for students divided by ACE thirds.

Table 2

Table 2. Linear mixed-effects model used to analyze performance of students in the lowest third of ACE scores.

2.7.2 Analysis of interviews

We conducted the full qualitative analysis of the teacher interviews using nVivo. Overarching themes were identified based on project goals with additional themes developed through iteration. We treated each individual teacher as a case study in that we coded all interviews with a single teacher before moving on to the next teacher. Participating educators reviewed these portraits as a form of validation, We also considered demographic and institutional factors (e.g., grade level [s] and school type) but saw relatively little variation patterned along these lines. For portraits of each individual teacher, see Attaway and Voiklis (2022) and Barchas-Lichtenstein et al. (2023).

3 Results

3.1 RQ1: impacts of INFACT on CT proficiency

The difference in CT proficiency between students in grades 3–5 who used INFACT as compared to those who used other CT activities showed a substantial advantage to using INFACT (Table 3). Average IACT scores for students in classes using INFACT were one-third of a standard deviation (β = 0.41) higher than average scores for students in classes using other CT programs. This difference between instructional conditions appears to exceed chance occurrence (p = 0.02). However, because this implementation study occurred during COVID, the study was underpowered; post hoc power analysis indicates that a sample of the same size would only have a 55% chance of detecting an effect of this size. The comparison of INFACT to other CT programs was also limited by the lack of variation in the other programs. Many were coding-centric and did not include the kinesthetic and hands-on activities that were a core part of INFACT teaching and learning activities. Further testing is needed to confirm the reliability of the effect and how INFACT compares to other programs.

Table 3

Table 3. Fixed effects for research question 1 model.

3.2 RQ2: Moderating effect of EF scores and INFACT on CT performance

To study the moderating effects of individual differences in EF and participation in INFACT on external CT assessments, we examined the relationship among IACT scores and ACE scores for students using INFACT compared to those using other CT activities. This analysis included only students who had a complete set of data for both the pre/post IACT assessments and the ACE EF tasks. Pre-assessment scores showed a significant predictive effect of ACE score on IACT performance, with students scoring lower on ACE tending to score lower on IACT as well. However, this effect disappeared at post-assessment for both INFACT and comparison students.

While we did not observe a statistically significant interaction between ACE score and experimental condition (INFACT vs. comparison) in our analysis of RQ2, there were interesting findings when we looked at students scoring in the lowest third on the ACE tests in our post hoc analysis. Upon closer inspection, there was indication that the intervention was quite effective for students with low ACE scores. In fact, the post hoc analysis indicates that the intervention may have a large impact on students who struggle most due to EF barriers. We observed significant increases in scores on the IACT post-assessment for students in the INFACT group (see Figure 11) with Model 3 indicating that the lowest third of ACE scorers exhibited statistically significant gains (see Table 4). Students in the highest and middle thirds on the EF scores did not show this improvement. This was true for the INFACT and the control groups. This may be caused by ceiling effects in the assessment instrument or by an unrelated impact that the pandemic or other extraneous factor had on high EF students during that time. Further research is needed to understand the differential effects of INFACT on low EF and high EF students.

Table 4

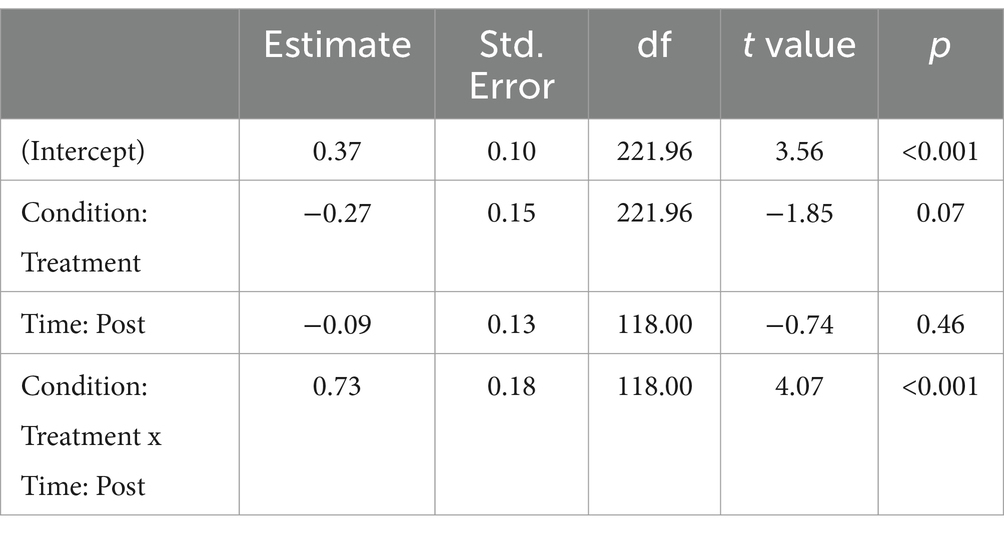
Table 4. LMEM results for post hoc analysis model described in Table 2.

3.3 RQ3: teachers’ perceptions of CT and EF

Interviews with teachers provided insight into the linkages they saw between CT and their neurodivergent learners as they used the INFACT materials. While teachers rarely used the term “executive function,” these interviews illustrate the many ways that using CT as a general problem-solving strategy helped teachers support neurodivergent learners across disciplines (Barchas-Lichtenstein et al., 2023).

Teachers used offline activities in complement with online coding and games to reach learners in different ways and reinforce the foundational CT concepts through related tasks. For example, we consistently heard teachers say that their high-energy students benefited from embodied, movement-based activities that helped them focus, while both visual and movement tasks were a valuable way to help less proficient readers participate alongside their peers.

Activities where students worked in pairs or small groups, rather than individually, were also advantageous in neurodiverse classrooms because teachers could encourage students with complementary strengths to work together; for example, a student who excelled at systematic thinking but who did not read as well could work with a strong reader who was more scattershot in their approach to problems. However, partnered activities required additional scaffolding for some students with social difficulties. Teachers also asked for additional physical and auditory adaptations (e.g., speech to text) for some of their students.

More than one teacher told us that some of their high-achieving students had a harder time connecting with INFACT. Often these students could complete a task correctly but had a harder time explaining their process. The INFACT materials required more metacognition and explicit expression of their problem-solving practices, which seemed to be a struggle for some of these students.

4 Discussion

The findings in this study help show that as CT continues to evolve as an educational discipline, innovative strategies can be used to broaden its appeal and impact. In particular, this study examined how embedding differentiation strategies and EF supports in CT teaching and learning materials can support CT learning, particularly for neurodivergent learners. The INFACT teaching and learning materials were designed to scaffold EF while engaging learners (in grades 3–8) in differentiated CT activities. While inclusive teaching methods used during INFACT are documented in the study, further development and research is suggested to support teacher professional development in the types of innovative teaching strategies required for inclusive CT learning.

CT has interesting connections with identified cognitive strengths of many neurodivergent learners and may be a rich area to broaden participation and nurture much-needed talent in the STEM workforce and in our society (Austin and Pisano, 2017). Systematic thinking and pattern recognition have been observed as extraordinary talents of some neurodivergent learners (Jolliffe and Baron-Cohen, 1997; Baron-Cohen, 2008; Mottron et al., 2009; Fugard et al., 2011), as has divergent thinking and abstraction of ideas (Beaty et al., 2015). INFACT was designed specifically with the hypothesis that these problem-solving talents may be revealed and nurtured through CT education, providing an avenue for neurodivergent learners to excel.

Our study of students in grades 3–5 who used INFACT showed a significant improvement on CT measures as compared to students in similar classes that used other CT teaching and learning activities (RQ1). This finding, while potentially unstable because of the small number of classes in each condition, shows promise and suggests further investigating how supporting neurodiversity in CT may improve participation in STEM problem-solving for a broad range of learners.

To address RQ2, which examined the impact of INFACT on neurodivergent learners, we explored the relationship between students’ performance on ACE tasks (used to measure EF) and their performance on IACT items (used to measure CT) in both the INFACT and the comparison classes. We found that the ACE scores had a high correlation to the pre-assessment IACT scores, with students scoring lower on ACE tending to score lower on IACT as well. This provides further evidence that CT and EF may be related. Interestingly, however, this effect disappeared in the post-assessment scores for both INFACT and comparison students. To examine why the effect disappeared, we conducted a post-hoc analysis of students with the lowest third of ACE scores. The analysis revealed that students scoring in the lowest ACE third on the pre-assessment exhibited a dramatic improvement in CT after implementation of INFACT. This effect was not observed in the comparison condition.

What is clear from the disaggregated EF data is that INFACT dramatically improved the CT scores of learners in the lowest third of EF, compared to other forms of CT instruction. This finding presents an interesting start towards the inclusion of neurodiversity in CT. Supporting EF and differentiating teaching and learning for students, in CT and in STEM problem-solving in general, is not only a strategy for better inclusive education, it also may be critical for our future STEM workforce. Many STEM companies and research labs are starting to recognize the talent of neurodiversity, and opportunities are becoming more widely available for neurodivergent STEM problem solvers to be recognized for the contributions and innovative perspectives they bring to our workforce and society (Austin and Pisano, 2017).

In the examination of RQ3, we found that teachers attributed INFACT’s success with neurodivergent learners, in part, to its variety of modalities of activities (e.g., offline activities, puzzles, games, and robotics) to help learners build foundational conceptual understandings in CT and apply those practices to new contexts. Teachers reported this flexibility helped them reach a wide range of learners and tap into the individual strengths of their students. Differentiation strategies such as allowing multiple entry points into an activity, and offering many different modalities for the activity were also seen to be important factors in the success of INFACT students. Because one of the foci of CT in INFACT is Clear Commands, the curriculum allows natural openings to discuss communications differences in class, and having different forms of activities that could be done individually, in small groups, or as an entire class enabled differentiation for students with social communication differences. These differentiation strategies are aligned with UDL principles and build on the teaching recommendations for an asset-perspective to education, where activities are designed to reveal and nurture individual learners’ strengths while supporting their challenges (Tomlinson and Strickland, 2005).

Teachers noted in particular that “get-up-and-go” offline activities were important to engage their high energy students and were harder to find in other CT programs. Teachers reported that many of their students benefited from that physical engagement. Teachers also noted that while INFACT was designed with UDL principles, further accommodations were needed to reach some of the students with physical and auditory challenges. INFACT was primarily designed for in-classroom use with a group, so the activities were studied in that venue. The activities were also designed, however, during COVID lockdowns, and many of the early users were trying the activities at home and with families. The embedded differentiation of the activities made this transition easy and effective. Finally, we saw that differentiation to include all learners includes not only scaffolding for EF, but also an emphasis on vocabulary development and offering multiple contexts and entry points. In particular, some teachers suggested we also provide more choice and complexity for students who want to dig deeper into CT. These are some of our next steps for future design and development of INFACT.

There were limitations to this research compounded by the fact that it was conducted during the 2021–2022 school year when schools were still heavily impacted by the COVID pandemic, including lasting impacts of previous closures and restrictions. It was extremely difficult to find teachers who were able to commit to the rigid timeframe of the study, and to do all that was required to collect a complete set of student data. Because of this, the study was underpowered, and the effects should continue to be verified with more teachers and learners in the coming years. The comparison between treatment and comparison conditions also was limited by the lack of a standard CT teaching and learning experience outside of INFACT. In addition, a lack of standard CT assessment, particularly for this age group and without extraneous barriers for neurodivergent learners, limits the interpretation of the results. Finally, because of our limited sample size, we were unable to disaggregate data further by race, gender, or other demographics that may impact students’ engagement in CT (Ardito et al., 2020; Leonard et al., 2021), as well as the likelihood they identify or have been identified as a neurodivergent learner (Asbell-Clarke, 2023).

Even with the limitations, the findings suggest that CT teaching and learning materials that support differentiation and scaffold executive function are worth further study. CT is an area where many neurodivergent learners may discover their own talents and interests. Supporting working memory, attention, and metacognition with CT activities may help reveal those talents and support innovative problem solving among this often marginalized group.

Features of INFACT teaching and learning materials that may be most responsible for supporting young neurodivergent learners include offering multiple entry points and modalities for learning activities, supporting clear communication and vocabulary, and using “get up and go” activities to engage high energy learners. While CT may be a particularly beneficial area to support neurodivergent learners, these types of supports may work well in other disciplines as well and should be explored, particularly in other areas of STEM problem solving.

Because CT is, at its root, simply a form of STEM problem solving (Weintrop et al., 2016; Shute et al., 2017), the findings of this research on INFACT may illustrate how these supports can be expanded and integrated into other areas of STEM.

Data availability statement

The datasets presented in this article are not readily available because Data are restricted by confidentiality of minor students’ data. Requests to access the datasets should be directed to jodi_asbell-clarke@terc.edu.

Ethics statement

The studies involving humans were approved by TERC Institutional Review Board, TERC. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin.

Author contributions

JA-C: Conceptualization, Funding acquisition, Investigation, Project administration, Resources, Supervision, Writing – original draft, Writing – review & editing. ID-H: Data curation, Formal analysis, Investigation, Methodology, Supervision, Writing – review & editing. JV: Data curation, Formal analysis, Investigation, Methodology, Supervision, Validation, Writing – review & editing. BA: Data curation, Investigation, Methodology, Writing – review & editing. JB-L: Data curation, Investigation, Methodology, Supervision, Validation, Writing – review & editing. TE: Conceptualization, Funding acquisition, Project administration, Supervision, Writing – review & editing. EB: Conceptualization, Resources, Visualization, Writing – review & editing. TR: Resources, Visualization, Writing – review & editing. KP: Project administration, Resources, Writing – review & editing. SG: Resources, Writing – review & editing. MI: Conceptualization, Resources, Writing – review & editing. FK: Writing – review & editing. DW: Resources, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by a US Department of Education EIR Early-Phase Research Grant (#U411C190179).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Antshel, K. M., Hier, B. O., and Barkley, R. A. (2014). “Executive functioning theory and ADHD” in Handbook of executive functioning. eds. S. Goldstein and J. A. Naglieri (New York, NY: Springer Science + Business Media), 107–120.

Google Scholar

Ardito, G., Czerkawski, B., and Scollins, L. (2020). Learning computational thinking together: effects of gender differences in collaborative middle school robotics program. TechTrends 64, 373–387. doi: 10.1007/s11528-019-00461-8

Crossref Full Text | Google Scholar

Arfé, B., Vardanega, T., and Ronconi, L. (2020). The effects of coding on children's planning and inhibition skills. Comput. Educ. 148:103807. doi: 10.1016/j.compedu.2020.103807

Crossref Full Text | Google Scholar

Armstrong, T. (2012). Neurodiversity in the classroom: Strength-based strategies to help students with special needs succeed in school and life. Alexandria, VA, United States: ASCD.

Google Scholar

Asbell-Clarke, J. (2023). Reaching and teaching Neurodivergent learners in STEM; strategies for embracing uniquely talented problem solvers. New York, NY: Taylor & Francis.

Google Scholar

Asbell-Clarke, J., Rowe, E., Almeda, M., Edwards, T., Bardar, E., Gasca, S., et al. (2021). The development of students’ computational thinking practices in elementary and middle-school classes using the learning game, Zoombinis. Comput. Hum. Behav. 115, 106587–106514. doi: 10.1016/j.chb.2020.106587

Crossref Full Text | Google Scholar

Attaway, B., and Voiklis, J. (2022). INFACT efficacy report. Knology Publication # EDU.051.602.03. Knology.

Google Scholar

Austin, R. D., and Pisano, G. P. (2017). Neurodiversity as a competitive advantage. Harv. Bus. Rev. 95, 96–103. Available at: https://hbr.org/2017/05/neurodiversity-as-a-competitive-advantage

Google Scholar

Bang, M. (2020). Learning on the move toward just, sustainable, and culturally thriving futures. Cogn. Instr. 38, 434–444. doi: 10.1080/07370008.2020.1777999

Crossref Full Text | Google Scholar

Barchas-Lichtenstein, J., Laursen Brucker, J., Asbell-Clarke, J., Attaway, B., Voiklis, J., Field, S., et al. (2023). Portraits of “thinking” in the classroom: how teachers talk about computational thinking and executive function. Submitted for review.

Google Scholar

Baron-Cohen, S. (2008). Autism and Asperger syndrome. Oxford, UK: Oxford University Press.

Google Scholar

Barr, V., and Stephenson, C. (2011). Bringing computational thinking to K-12: what is involved and what is the role of the computer science education community? ACM Inroads 2, 48–54. doi: 10.1145/1929887.1929905

Crossref Full Text | Google Scholar

Beaty, R. E., Benedek, M., Silvia, P. J., and Schacter, D. L. (2015). Creative cognition and brain network dynamics. Trends Cogn. Sci. 20, 87–95. doi: 10.1016/j.tics.2015.10.004

PubMed Abstract | Crossref Full Text | Google Scholar

Bellman, S., Burgstahler, S., and Hinke, P. (2015). Academic coaching: outcomes from a pilot group of postsecondary STEM students with disabilities. J. Postsecond. Educ. Disabil. 28, 103–108.

Google Scholar

Blume, H. (1998). Neurodiversity: on the neurological underpinnings of geekdom The Atlantic Available at: https://www.theatlantic.com/magazine/archive/1998/09/neurodiversity/305909/.

Google Scholar

Brown, S. W. (2006). Timing and executive function: bidirectional interference between concurrent temporal production and randomization tasks. Mem. Cogn. 34, 1464–1471. doi: 10.3758/BF03195911

PubMed Abstract | Crossref Full Text | Google Scholar

Brownell, M. T., Sindelar, P. T., Kiely, M. T., and Danielson, L. C. (2010). Special education teacher quality and preparation: exposing foundations, constructing a new model. Except. Child. 76, 357–377. doi: 10.1177/001440291007600307

Crossref Full Text | Google Scholar

Castro, C. R., Castillo-Ossa, L. F., and Hederich-Martínez, C. (2022). Effects of a computational thinking intervention program on executive functions in children aged from 10 to 11. SSRN Electron. J. doi: 10.2139/ssrn.4095691

Crossref Full Text | Google Scholar

Chandrasekhar, T. (2020). Supporting the needs of college students with autism spectrum disorder. J. Am. Coll. Heal. 68, 936–939. doi: 10.1080/07448481.2019.1686003

PubMed Abstract | Crossref Full Text | Google Scholar

CSTA (2017). CSTA K-12 computer science standards, Revised 2017. Available at: http://www.csteachers.org/standards

Google Scholar

Cuny, J., Snyder, L., and Wing, J. M. (2010). Demystifying computational thinking for non-computer scientists. Unpublished manuscript in progress, referenced in Available at: http://www.cs.cmu.edu/~ CompThink/resources/TheLinkWing.pdf

Google Scholar

Dagienė, V., and Futschek, G. (2008). “Bebras international contest on informatics and computer literacy: criteria for good tasks” in Informatics education—Supporting computational thinking. eds. R. T. Mittermeir and M. M. Sysło (New York, NY: Springer), 19–30.

Google Scholar

Dagienė, V., Stupurienė, G., and Vinikienė, L. (2016). Promoting inclusive informatics education through the Bebras challenge to all K-12 students. Proceedings of the 17th international conference on computer systems and technologies 2016, 407–414.

Google Scholar

Demetriou, E. A., DeMayo, M. M., and Guastella, A. J. (2019). Executive function in autism Spectrum disorder: history, theoretical models, empirical findings, and potential as an endophenotype. Front. Psych. 10:753. doi: 10.3389/fpsyt.2019.00753

PubMed Abstract | Crossref Full Text | Google Scholar

DePryck, K. (2016). From computational thinking to coding and back. Proceedings of the Fourth International Conference on Technological Ecosystems for Enhancing Multiculturality, 27–29.

Google Scholar

Di Lieto, M. C., Castro, E., Pecini, C., Inguaggiato, E., Cecchi, F., Dario, P., et al. (2020). Improving executive functions at school in children with special needs by educational robotics. Front. Psychol. 10:2813. doi: 10.3389/fpsyg.2019.02813

PubMed Abstract | Crossref Full Text | Google Scholar

Diamond, A. (2013). Executive functions. Annu. Rev. Psychol. 64, 135–168. doi: 10.1146/annurev-psych-113011-143750

PubMed Abstract | Crossref Full Text | Google Scholar

Eide, B. L., and Eide, F. F. (2012). The dyslexic advantage: unlocking the hidden potential of the dyslexic brain. New York, NY: Plume.

Google Scholar

El-Hamamsy, L., Zapata-Cáceres, M., Marcelino, P., Bruno, B., Dehler Zufferey, J., Martín-Barroso, E., et al. (2022). Comparing the psychometric properties of two primary school computational thinking (CT) assessments for grades 3 and 4: the Beginners' CT test (BCTt) and the competent CT test (cCTt). Front. Psychol. 13:1082659. doi: 10.3389/fpsyg.2022.1082659

PubMed Abstract | Crossref Full Text | Google Scholar

Fugard, A. J. B., Stewart, M. E., and Stenning, K. (2011). Visual/verbal-analytic reasoning bias as a function of self-reported autistic-like traits: a study of typically developing individuals solving Raven’s advanced progressive matrices. Autism 15, 327–340. doi: 10.1177/1362361310371798

PubMed Abstract | Crossref Full Text | Google Scholar

Galiatsos, S., Kruse, L., and Whittaker, M. (2019). Forward together: Helping educators unlock the power of students who learn differently National Center for Learning Disabilities Available at: https://www.ncld.org/wp-content/uploads/2019/05/Forward-Together_NCLD-report.pdf.

Google Scholar

Gerosa, A., Koleszar, V., Gómez-Sena, L., Tejera, G., and Carboni, A. (2019) Educational robotics and computational thinking development in preschool. In 2019 XIV Latin American conference on learning technologies (LACLO) (pp. 226–230). San Jose Del Cabo, Mexico: IEEE.

Google Scholar

Gilmore, C., and Cragg, L. (2014). Teachers’ understanding of the role of executive functions in mathematics learning. Mind Brain Educ. 8, 132–136. doi: 10.1111/mbe.12050

PubMed Abstract | Crossref Full Text | Google Scholar

Gottfried, M. A., Bozick, R., Rose, E., and Moore, R. (2014). Does career and technical education strengthen the STEM pipeline? Comparing students with and without disabilities. J. Disabil. Policy Stud. 26, 232–244. doi: 10.1177/1044207314544369

Crossref Full Text | Google Scholar

Grover, S., and Pea, R. (2017). Computational thinking: a competency whose time has come. Computer science education: Perspectives on teaching and learning in school, 19, 19–38

Google Scholar

Haladyna, T. M., and Downing, S. M. (2004). Construct-irrelevant variance in high-stakes testing. Educ. Meas. Issues Pract. 23, 17–27. doi: 10.1111/j.1745-3992.2004.tb00149.x

Crossref Full Text | Google Scholar

Hawes, M. T., Szenczy, A. K., Klein, D. N., Hajcak, G., and Nelson, B. D. (2022). Increases in depression and anxiety symptoms in adolescents and young adults during the COVID-19 pandemic. Psychol. Med. 52, 3222–3230. doi: 10.1017/S0033291720005358

PubMed Abstract | Crossref Full Text | Google Scholar

Horowitz, S. H., Rawe, J., and Whittaker, M. C. (2017). The state of learning disabilities: understanding the 1 in 5. National Center for Learning Disabilities. Available at: https://www.ncld.org/the-state-of-learning-disabilities-understanding-the-1-in-5

Google Scholar

Huang, W., and Looi, C. K. (2021). A critical review of literature on “unplugged” pedagogies in K-12 computer science and computational thinking education. Comput. Sci. Educ. 31, 83–111. doi: 10.1080/08993408.2020.1789411

Crossref Full Text | Google Scholar

Immordino-Yang, M. H., Darling-Hammond, L., and Krone, C. (2018). The brain basis for integrated social, emotional, and academic development National Commission on Social, Emotional, and Academic Development Available at: https://www.aspeninstitute.org/publications/the-brain-basis-for-integrated-social-emotional-and-academic-development/.

Google Scholar

INFACT (2024). Available at: https://www.terc.edu/ndinstem/resources/infact-materials/

Google Scholar

Jolliffe, T., and Baron-Cohen, S. (1997). Are people with autism and Asperger syndrome faster than normal on the embedded figures test? J. Child Psychol. Psychiatry 38, 527–534. doi: 10.1111/j.1469-7610.1997.tb01539.x

PubMed Abstract | Crossref Full Text | Google Scholar

Kite, V., Park, S., and Wiebe, E. (2021). The code-centric nature of computational thinking education: a review of trends and issues in computational thinking education research. SAGE Open 11:215824402110164. doi: 10.1177/21582440211016418

Crossref Full Text | Google Scholar

Leonard, J., Thomas, J. O., Ellington, R., Mitchell, M. B., and Fashola, O. S. (2021). Fostering computational thinking among underrepresented students in STEM: Strategies for supporting racially equitable computing. New York, NY: Routledge.

Google Scholar

Madkins, T. C., Howard, N. R., and Freed, N. (2020). Engaging equity pedagogies in computer science learning environments. J. Comput. Sci. Integr. 3:1. doi: 10.26716/jcsi.2020.03.2.1

PubMed Abstract | Crossref Full Text | Google Scholar

McFarland, J., Hussar, B., Zhang, J., Wang, X., Wang, K., Hein, S., et al. (2019). The condition of education 2019. Washington, DC: National Center for Education Statistics.

Google Scholar

Mellifont, D. (2021). Facilitators and inhibitors of mental discrimination in the workplace: a traditional review. Stud. Soc. Justice 15, 59–80. doi: 10.26522/ssj.v15i1.2436

Crossref Full Text | Google Scholar

Meltzer, L. (Ed.) (2018). Executive function in education: From theory to practice. 2nd Edn. New York, NY: The Guilford Press.

Google Scholar

Meltzer, L., Dunstan-Brewer, J., and Krishnan, K. (2018). “Learning differences and executive function: understandings and misunderstandings” in Executive function in education: From theory to practice. ed. L. Meltzer (New York, NY: The Guilford Press), 109–141.

Google Scholar

Montuori, C., Gambarota, F., Altoé, G., and Arfé, B. (2023). The cognitive effects of computational thinking: a systematic review and meta-analytic study. Comput. Educ. 210, 1–23.

Google Scholar

Mottron, L., Dawson, M., and Soulières, I. (2009). Enhanced perception in savant syndrome: patterns, structure and creativity. Philos. Trans. R. Soc. B Biol. Sci. 364, 1385–1391. doi: 10.1098/rstb.2008.0333

PubMed Abstract | Crossref Full Text | Google Scholar

Murawski, W. W., and Scott, K. L. (Eds.) (2019). What really works with universal design for learning. Thousand Oaks, CA: Corwin, a SAGE Publications Company.

Google Scholar

Myung, J., Gallagher, A., Cottingham, B., Gong, A., Kimner, H., Witte, J., et al. (2020). Supporting learning in the COVID-19 context: Research to guide distance and blended instruction Policy Analysis for California Education, PACE.

Google Scholar

Ocak, C., Yadav, A., Vogel, S., and Patel, A. (2023). Teacher education Faculty’s perceptions about computational thinking integration for pre-service education. J. Technol. Teach. Educ. 31, 299–349.

Google Scholar

Oluk, A., and Saltan, F. (2015). Effects of using the scratch program in 6th grade information technologies courses on algorithm development and problem solving skills. Particip. Educ. Res. 2, 10–20. doi: 10.17275/per.15.spi.2.2

Crossref Full Text | Google Scholar

Pellegrino, J. W., and Hilton, M. L. (2012). “Education for life and work: Developing transferable knowledge and skills in the 21st century” in Committee on defining deeper learning and 21st century skills. (Washington DC: National Research Council of the National Academies)

Google Scholar

Polirstok, S. (2015). Classroom management strategies for inclusive classrooms. Creat. Educ. 6, 927–933. doi: 10.4236/ce.2015.610094

Crossref Full Text | Google Scholar

Ritchhart, R., Church, M., and Morrison, K. (2011). Making thinking visible: How to promote engagement, understanding, and independence for all learners. 1st Edn. Hoboken, NJ: Jossey-Bass.

Google Scholar

Robertson, J., Gray, S., Toye, M., and Booth, J. (2020). The relationship between executive functions and computational thinking. Int. J. Comput. Sci. Educ. Schools 3, 35–49. doi: 10.21585/ijcses.v3i4.76

Crossref Full Text | Google Scholar

Rodriguez, Y., and Burke, R. V. (2023). “Impacts of COVID-19 on children and adolescent well-being” in COVID-19, frontline responders and mental health: A playbook for delivering resilient public health systems post-pandemic (Leeds, England: Emerald Publishing Limited), 43–54.

Google Scholar

Román-González, M. (2015). “Computational thinking test: design guidelines and content validation” in EDULEARN15 proceedings (Barcelona, Spain: IATED), 2436–2444.

Google Scholar

Román-González, M., Moreno-León, J., and Robles, G. (2019). “Combining assessment tools for a comprehensive evaluation of computational thinking interventions” in Computational thinking education. eds. S. C. Kong and H. Abelson (Springer)

Google Scholar

Rose, D. (2000). Walking the walk: universal design on the web. J. Spec. Educ. Technol. 15, 45–49. doi: 10.1177/016264340001500307

Crossref Full Text | Google Scholar

Rowe, E., Asbell-Clarke, J., Almeda, M. V., Gasca, S., Edwards, T., Bardar, E., et al. (2021). Interactive assessments of CT (IACT): digital interactive logic puzzles to assess computational thinking in grades 3–8. Int. J. Comput. Sci. Educ. Schools 5, 28–73. doi: 10.21585/ijcses.v5i1.149

Crossref Full Text | Google Scholar

Rowe, E., Asbell-Clarke, J., Baker, R., Eagle, M., Hicks, A., Barnes, T., et al. (2017). Assessing implicit science learning in digital games. Comput. Hum. Behav. 76, 617–630. doi: 10.1016/j.chb.2017.03.043

Crossref Full Text | Google Scholar

Rucklidge, J. J. (2010). Gender differences in attention-deficit/hyperactivity disorder. Psychiatr. Clin. North Am. 33, 357–373. doi: 10.1016/j.psc.2010.01.006

Crossref Full Text | Google Scholar

Russell, A. E., Ford, T., Williams, R., and Russell, G. (2016). The association between socioeconomic disadvantage and attention deficit/hyperactivity disorder (ADHD): a systematic review. Child Psychiatry Hum. Dev. 47, 440–458. doi: 10.1007/s10578-015-0578-3

PubMed Abstract | Crossref Full Text | Google Scholar

Schindler, V., Cajiga, A., Aaronson, R., and Salas, L. (2015). The experience of transition to college for students diagnosed with Asperger’s disorder. Open J. Occup. Ther. 3:1129. doi: 10.15453/2168-6408.1129

Crossref Full Text | Google Scholar

Semenov, A. D., and Zelazo, P. D. (2018). “The development of hot and cool executive function: a foundation for learning in the preschool years” in Executive function in education: From theory to practice. ed. L. Meltzer (New York, NY: The Guilford Press), 109–141.

Google Scholar

Shattuck, P. T., Narendorf, S. C., Cooper, B., Sterzing, P. R., Wagner, M., and Taylor, J. L. (2012). Postsecondary education and employment among youth with an autism spectrum disorder. Pediatrics 129, 1042–1049. doi: 10.1542/peds.2011-2864

PubMed Abstract | Crossref Full Text | Google Scholar

Shi, Y., Hunter Guevara, L. R., Dykhoff, H. J., Sangaralingham, L. R., Phelan, S., Zaccariello, M. J., et al. (2021). Racial disparities in diagnosis of attention-deficit/hyperactivity disorder in a US national birth cohort. JAMA Netw. Open 4:e210321. doi: 10.1001/jamanetworkopen.2021.0321

PubMed Abstract | Crossref Full Text | Google Scholar

Shute, V. J., Sun, C., and Asbell-Clarke, J. (2017). Demystifying computational thinking. Educ. Res. Rev. 22, 142–158. doi: 10.1016/j.edurev.2017.09.003

Crossref Full Text | Google Scholar

Singer, J. (1998). Odd people in: the birth of community amongst people on the autistic spectrum: a personal exploration of a new social movement based on neurological diversity. [Honours dissertation]. University of Technology, Sydney.

Google Scholar

Sireci, S. G., and O’Riordan, M. (2020). Comparability of large-scale educational assessments: Issues and recommendations National Academy of Education, 177–204 Available at: https://naeducation.org/comparability/.

Google Scholar

Tomlinson, C. A., and Strickland, C. A. (2005). Differentiation in practice: A resource guide for differentiating curriculum, grades 9–12. Washington DC: ASCD.

Google Scholar

Van Garderen, D., Scheuermann, A., Jackson, C., and Hampton, D. (2009). Supporting the collaboration of special educators and general educators to teach students who struggle with mathematics: an overview of the research. Psychol. Sch. 46, 56–78. doi: 10.1002/pits.20354

Crossref Full Text | Google Scholar

Varvara, P., Varuzza, C., Sorrentino, A. C. P., Vicari, S., and Menghini, D. (2014). Executive functions in developmental dyslexia. Front. Hum. Neurosci. 8:120. doi: 10.3389/fnhum.2014.00120

PubMed Abstract | Crossref Full Text | Google Scholar

Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., et al. (2016). Defining computational thinking for mathematics and science classrooms. J. Sci. Educ. Technol. 25, 127–147. doi: 10.1007/s10956-015-9581-5

Crossref Full Text | Google Scholar

Wiebe, E., London, J., Aksit, O., Mott, B. W., Boyer, K. E., and Lester, J. C. (2019). “Development of a lean computational thinking abilities assessment for middle grades students” in Proceedings of the 50th ACM technical symposium on computer science education, 456–461.

Google Scholar

Wing, J. M. (2008). Computational thinking and thinking about computing. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 366, 3717–3725. doi: 10.1098/rsta.2008.0118

PubMed Abstract | Crossref Full Text | Google Scholar

Younger, J., O’Laughlin, K. D., Anguera, J. A., Bunge, S., Ferrer, E. E., Hoeft, F., et al. (2021). Development of executive function in middle childhood: a large-scale, in-school, longitudinal investigation. PsyArXiv. doi: 10.31234/osf.io/xf489

Crossref Full Text | Google Scholar