- Institute for Mathematics and its Didactics, Leuphana University Lüneburg, Lüneburg, Germany
Authenticity is considered a central feature in the context of teaching and learning mathematical modelling and is often demanded for both learning tasks and test items. Although large-scale studies hark back to this construct for years, it is largely unclear how a theoretical and empirically robust model for the description and practical operationalization of authenticity in modelling test items might look like. The article addresses this research desideratum and aims at deriving such a model based on existing theoretical concepts in mathematics education. The article provides a broad theoretical overview of the status quo of the construct and presents the “Model for Authenticity in Modelling Test Items” (MAMTI) as a result of those theoretical considerations. The model is based on the ideas of constructivist object authenticity and comprises a total of 8 aspects: real-world context, events, objects, question/assignment, data, figures, use of mathematics and purpose. The model enables further empirical studies to analyze and classify modelling test items or to vary them in terms of authenticity expression.
1 Introduction
Mathematical modelling is of great importance in mathematics education (Stillman, 2019). The competence of mathematical modelling, i. e. solving real-world problems by using mathematics, is especially significant with regard to the challenges of the 21st century and the skills required to master these challenges (Lu and Kaiser, 2022; Luczak and Erwin, 2023). In order to ensure that those modelling problems are close to reality and are not artificially created for educational purposes, authenticity is regularly demanded being an indispensable property of modelling tasks in mathematics education (Kaiser, 2017; Greefrath, 2018). This special claim for the presence of authenticity is not only a normative one, but also empirical studies indicate that the use of authentic resources in teaching mathematics can increase learners’ performance and motivation (Vos et al., 2007; Palm, 2008; Mahler et al., 2020). Therefore, authenticity is not only mentioned as an essential characteristic of modelling tasks being designed for learning, but also of those (standardized) test items1 used for diagnosing and assessing students’ modelling competences (Stacey, 2015; Tout and Spithill, 2015; Greefrath and Maaß, 2020). Within the discussions in the modelling community, authenticity has become a prominent “domain issue” (Galbraith, 2013). Unfortunately, a major concern regarding the concept of authenticity both in modelling learning tasks and modelling test items is that authenticity is often conceptualized differently and sometimes not defined at all (Vos, 2011). However, within recent years, the theoretical considerations of Vos (2011, 2018) have had a significant influence on the current international discourse about authenticity in modelling tasks. She describes authenticity in mathematical modelling tasks in a binary and atomistic way and defines it from a sociological perspective as a social construct. While her approach is already being used to analyze authenticity in learning tasks, it is rarely found in analyses of test items. In particular, a theoretical and empirically robust model for the practical description and operationalization of authenticity in modelling test items represents a research desideratum – although large-scale studies like PISA hark back to this construct for years. Taking this into account, the present study pursues the following aim: Deriving a theoretical model that can be used as a basis for the empirical assessment of authenticity in (standardized) modelling test items.
For doing so, the theoretical article briefly introduces the key role of authenticity in mathematical modelling and presents some conceptual understandings of authenticity in general as well as in mathematics education in particular (section 2). Next, the research aim of the study is stated, the “Model for Authenticity in Modelling Test Items” (MAMTI) is derived theoretically, and the benefit of this model is demonstrated exemplarily by analyzing a sample test item (section 3). Finally, the added value of the obtained model is discussed and further steps are highlighted (section 4).
2 Theoretical background
2.1 Mathematical modelling
2.1.1 Brief introduction to mathematical modelling
With respect to the concept of “mathematical literacy” (OECD, 2018), a central aim of modern mathematics education is to enable students to recognize and understand the role of mathematics in the real world and to be able to use mathematics in it. An essential component in the realization of this basic idea is the conscious consideration of applications and modelling in mathematics education. While applications are thought of from mathematical content in the direction of reality and focus more on the products, mathematical modelling is thought of in the opposite direction from reality to mathematics and focuses more on the processes (Niss et al., 2007). Based on this, modelling in mathematics education (despite many different perspectives, see Kaiser, 2017) is basically understood being the process of working on and solving real-world problems by using mathematics (Niss et al., 2007; Maaß, 2010; Kaiser, 2017; Greefrath, 2018). In line with these ideas, key aspects of mathematical modelling are given by translation processes from reality to mathematics and vice versa (Leiss et al., 2019). The entire modelling process itself comprising all those single steps is often idealized as a cycle describing different sub-competences (see e. g. Blum and Leiss, 2007; Kaiser and Stender, 2013). In this way, mathematical modelling is considered being a 21st century skill and is embedded as an important competence in many curricula around the world (Lu and Huang, 2021).
2.1.2 Discourses around modelling tasks and the key role of authenticity
In the context of modelling, mathematical tasks are crucial for implementing modelling activities into mathematics education (at school) (Blum, 2007). However, the question of whether a given task can be considered being a modelling task is a complex one. A simplified distinction can be made between two perspectives: On the one hand, there are authors (such as Kaiser, 2017) arguing for a clear distinction between so called word problems and modelling tasks. While authenticity is substantially inherent in a modelling task, i. e. because it involves a real-world question or a problem with importance in a genuine out-of-school context, word problems are those text-based tasks with problems that are not important for the real world, but only for the school context. On the other hand, authors and researchers (such as Verschaffel et al., 2020) argue that authenticity can vary even within a modelling task and that there will always be a difference between an authentic out-of-school problem and a problem dealt with at school. According to this last idea, modelling tasks can be located on a continuum of authenticity, with modelling tasks (according to Kaiser, 2017) representing the positive pole and traditional word problems the negative pole.
Looking at the discourse at stake, it becomes clear that authenticity has a key role to play in it. The importance of authenticity in mathematical modelling is further emphasized by the fact that it is named as a central characteristic of modelling tasks by many more authors (Steen et al., 2007; Geiger, 2017; Borromeo Ferri, 2018; Siller and Greefrath, 2020; among others). However, a closer look at the concept of authenticity in mathematics education highlights that the term is often interpreted very differently and sometimes not defined at all (Vos, 2011). Following on from this, the next section is devoted to a theoretical review of conceptual understandings of authenticity both in general as well as in mathematics education.
2.2 Conceptual understandings of authenticity
One of the difficulties in dealing with the term authenticity is that there is no clear definition (not only in education) from both a historical and a contemporary perspective. Etymologically, the terms authenticity and authentic come from ancient Greek: While αύθέvτης can express terms such as executor, autocrat or originator, the adjectival use αύθεντιχός can mean reliable, correct, original (Knaller and Müller, 2005). The late Latin term authenticus, like the original Greek word, refers primarily to written documents. Starting from this word origin, there have been different etymological developments in many different fields, with some facets of meaning disappearing and others gradually being added (Knaller and Müller, 2005). The fields in which the concept of authenticity has been and is used include, for instance, art, law, marketing, philosophy or rhetoric. In these disciplines, the term is used to refer either to objects or to subjects, which is why Knaller (2006) makes a simplified distinction between two forms: Object authenticity and subject/personal authenticity (p. 21). In the following, both forms are presented using scientific disciplines relevant to the discourse in mathematics education exemplarily: On the one hand, the material understanding of concepts in relation to objects in archeology and, on the other hand, the personal understanding of concepts in psychology.
2.2.1 Object authenticity in archeology – part of a binary pair of terms
According to Knaller (2017), the concept of authenticity in relation to objects results mostly from traceability to an originator or to affiliation and is thereby verifiable through institutions or authorities that authorize authenticity (pp. 8–9). Such object authenticity, for instance, is integral to the discipline of archeology. Here, the pursuit of authenticity is at the heart of archaeological knowledge production, as evidenced by activities such as distinguishing between real artefacts and forgeries, or reconstructing the actual origin or past (Mickel, 2018). Basically, in archeology, artefacts are considered authentic if they truthfully originate from human activities in the past, which is ensured by analysts with archaeological expertise. There are certain requirements, for instance, in modern archeology it is a requirement for excavated artefacts that the excavation has been fully documented (Joyce, 2013). But even in archeology, there are discussions and controversies about the understanding of the term, whereby two main approaches can be identified: A materialist and a constructivist one (Holtorf, 2013). According to the materialist understanding, authenticity is understood as an intrinsic property. Objects possess this inherent property (or not) and there is a recognizable basis for determining authenticity. In contrast, the constructive approach understands authenticity not as a naturally inherent quality, but as the result of a process of interpretation and attribution (see in this regard Saupe, 2014; Warnke, 2022). Here, the term is described as “variable, negotiable and relative to a specific social and cultural context” (Holtorf, 2013, p. 428). When considering the conceptual understanding of historical authenticity in the context of archeology, it is striking that the term is often defined by establishing the binary pair of terms original (authentic) and forgery/copy (inauthentic). This binary definition of authenticity is widely used in archeology, but is also critically discussed in parts (e.g., Eser et al., 2017, p. 3).
2.2.2 Subject authenticity in positive psychology – conceptualization as a continuum
While object authenticity focuses on the traceability to authorship, subject authenticity (or sometimes personal authenticity) refers to personal characteristics of persons. With respect to Knaller (2017), subject authenticity encompasses the notion of an empirical, social, psychological subject that distinguishes truthfulness (p. 8–9). In contrast to object authenticity, the attribution of authenticity is not based on universally valid or easily verifiable principles (Knaller, 2017, p. 22). Personal authenticity understood in this way can be found, among other disciplines, in positive psychology. In contrast to the traditionally deficit-oriented psychology, this scientific discipline deals with the positive aspects of being human. Authenticity plays a significant role in this context and is considered being one of the 24-character strengths of a person according to the classification by Peterson and Seligman (2004). In positive psychology, the authenticity of a person plays a role in two facets. On the one hand, authenticity involves “owning one’s personal experiences” (Harter, 2002, p. 382) such as emotions, wants or beliefs. Besides the taking of ownership of one’s own experiences, on the other hand authenticity here also includes an individual’s authentic behavior. This means that one “acts in accord with the true self, expressing oneself in ways that are consistent with inner thoughts and feelings” (Harter, 2002, p. 382).
In this discipline, as well, authenticity is often defined by distinguishing it from the antonym, in this case from a lack of authenticity or false-self behavior. Such false-self behavior involves compromising one’s true self and acting in a way that is experienced as phony or artificial (Harter, 2002). Unlike archeology, a binary definition of authenticity is not an issue in positive psychology. Instead, authenticity is conceptualized as a continuum in which inauthenticity or false behavior represents the lower end and authenticity the upper end (e.g., Wood et al., 2008; Thomaes et al., 2017). To measure an individual authenticity score, which can be located on this scale in the sense of a higher or lower level of authenticity, instruments based on self-assessments are used (e. g. the Authenticity Inventory by Kernis and Goldman (2006), for an exemplary study harking back to authenticity measurement see Borawski (2021)).
2.3 Authenticity in mathematics education: summarizing the status quo of an often used construct
Based on those considerations about object and subject authenticity as outlined above, some very central ideas about authenticity in mathematics education will be described in detail below.
2.3.1 Niss: authenticity as attribution by experts
The definition by Niss (1992) of an authentic extra-mathematical situation, which he formulates in connection to his demand that these should be included in school mathematics, represents a landmark in the understanding of authenticity in mathematics education. He defines an extra-mathematical situation as authentic, “which is embedded in a true existing practice or subject area outside mathematics, and which deals with objects, phenomena, issues, or problems that are genuine to that area and are recognized as such by people working in it” (Niss, 1992, p. 353). He further emphasizes that the situation does not necessarily have to do anything with everyday life or that the mathematical models involved do not have to be correct at all. However, central is the prerequisite that the situation is taken seriously by those persons being addresses in the respective extra-mathematical field. Thus, a situation remains authentic even in spite of modifications, as long as these were made before implementation in the mathematics lesson and as long as people in practice continue to recognize them as authentic. When examining an example task, Niss implicitly mentions some special aspects that can be authentic in the context of a school task. These include the given data, the use of mathematics or a model, the question addressed and the purpose mentioned in the task (Niss, 1992).
2.3.2 Palm: authenticity as a simulation – a holistic approach, located on a continuum
Palm (2007) goes on to define an authentic task in mathematics education as one in which “the situation described in the task including a question or assignment […] is a situation from real life outside mathematics itself that has occurred or that might very well happen” (p. 203). Moreover, according to Palm the task situation should be described truthfully and the conditions of the task processing should be simulated reasonably close to reality. While Palm refers to the concept of authenticity as an extra-curricular situation that should be described truthfully (like Niss does as well), the social component considered being central by Niss is missing here. Rather, what is significant in Palm’s understanding is that authentic tasks involve simulations of real situation and that something that could happen is already to be assessed as being authentic. Based on this construct of authenticity as a simulation, Palm (2009) formulates a “Framework for Authentic Tasks” as an operationalization of his understanding (see Table 1). The components of this framework are so called main- and sub-aspects of real-life task situations that can be simulated with more or less fidelity.
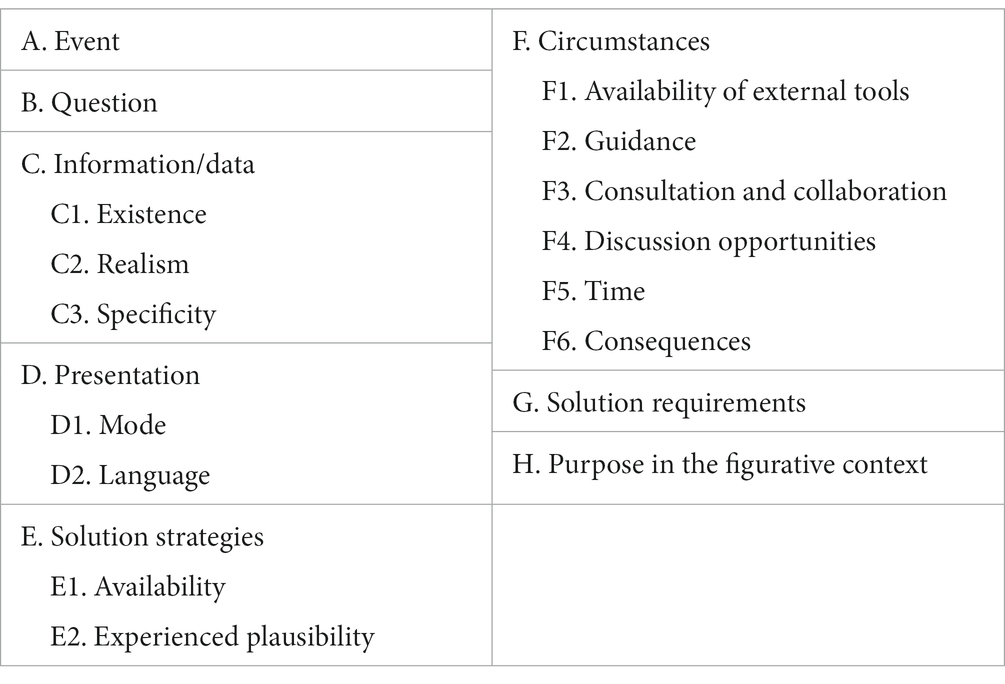
Table 1. “Framework for Authentic Tasks” in the style of Palm (2009, p. 9).
The aspects listed in Palm’s framework are based on his assumptions that the simulation of these can have an influence on the extent to which students engage in mathematical activities when working on word problems (Palm, 2007, p. 203). In addition, Palm highlights empirical arguments for the validity of his theory and his aspect compilation, as the application of the framework proved itself in analyses of tasks (Palm, 2009, pp. 15–16). However, in relation to the framework, he qualifies that it is impossible to simulate all aspects in such a way that they match the extra-curricular aspects completely, so there will always be a gap between the school task and the extra-curricular situation. But the simulation of the aspects suggested by Palm can influence the extent of the gap and thus the authenticity itself, from which it can be deduced that a holistic perspective can be identified in Palm’s consideration of authenticity. Despite the obvious division into different aspects, he applies the term to the overall task, which is also reflected, among other things, in the fact that Palm (2009) writes of “more authentic” and “more inauthentic” tasks (p. 15). In this holistic view, in which something is not classified in a binary way but can assume a higher or lower level on a certain scale, a connection can be made to the authenticity continuum from positive psychology.
This understanding is also reflected in the applications of Palm’s framework in different task analyses (e.g., Wernet, 2017; Paredes et al., 2020). Here, selected aspects of Palm’s framework are assigned binary or ordinal authenticity and then transferred into an overall judgement. In doing so, the authenticity of the overall task is ordinally located on a continuum, for instance in Paredes et al. (2020) as “Fictitious, Believable, Authentic” or in Wernet (2017) as “low, partial or full authenticity.”
2.3.3 Vos: authenticity as a social construct – a binary, atomistic, and social approach
Vos elaborates on existing conceptual understandings in mathematics education and offers her own theoretical foundation for describing authenticity in modelling tasks. Her understanding is based on a definition from a study of Mozambican mathematics classrooms by Vos et al. (2007), in which they considered individual aspects of tasks to be authentic only if they were “clearly not created for educational purposes” (Vos, 2011, p. 715). On this basis, Vos establishes three central determinations for assessing authenticity in modelling tasks, which manifest themselves in the following questions:
(1) Should a binary or an ordinal qualification be used?
(2) Should a holistic or an atomistic approach be chosen?
(3) Should authenticity be expressed dependently or independently of an actor’s viewpoint?
With regard to the first question, Vos (2018) emphasizes that the definition of authenticity in education is blurred, as philosophers and psychologists have used the term to ordinally characterize a person’s existential feelings or expressions. Here, Vos implicitly refers to the dominance of a conceptual understanding of authenticity in education in the sense of the subject authenticity described above. In this context, Vos (2018) mentions that the use of the term authentic is “unsuitable” in relation to the description of mathematics tasks, because tasks are precisely not persons or individuals (p. 4). Consequently, Vos insists on tasks being objects and therefore implicitly refers to the perspective of object authenticity. By doing so, Vos (2011) falls back on the archaeological understanding of the term. And since there is no differentiation between more authentic and less authentic artefacts, she argues analogously for assessing authenticity in modelling tasks in a binary form.
Based on this and referring to question 2, from a holistic perspective an authentic task would have to include the original situation from the real world together with, for instance, responsibility for life or material. However, as the removal of aspects such as this responsibility is imperative for pedagogical purposes to ensure safe learning environments, by Vos it is not possible to describe tasks being authentic by an holistic approach, as this process of reduction makes the task an incomplete copy of reality. In this context, Vos (2018) is in line with other authors (e. g. Büchter and Leuders, 2016, p. 87), who understand education at school as a didactic sanctuary, and thus it never attains full authenticity. Nevertheless, in order to being able to use the term constructively in mathematics education, Vos advocates an atomistic approach: only individual aspects within a task should be ascribed authenticity, which would then of course have to be defined in detail. According to Vos (2011, 2018), tasks in mathematical modelling can contain many different authentic aspects, but not all conceivable aspects must be authentic, otherwise students take on the full responsibility of a professional.
Regarding the third question, she once again harks back to object authenticity consequently, or more precisely, she invokes the constructivist approach from archeology already presented here. Vos (2011) defines authenticity as a social construct, by which she understands “agreements pertaining perceptions, norms and values, and these are developed and sustained in relations between actors and objects” (p. 714), following the sociological studies of Berger and Luckmann (1966). Vos transfers this understanding to mathematical modelling and thus explicitly argues for expressing authenticity in terms of such a social construct as independent of an actor’s viewpoint. As a community which agrees on certain standards for when something is considered being authentic, she considers students, teachers, academics and out-of-school stakeholders. As such a standard, Vos (2018) suggests that for any single authentic task aspect the following two requirements must be met: “1. an out-of-school origin; 2. a certification of provenance” (p. 8). The certification mentioned in the second requirement can, for instance, be given by a photo, a newspaper article or a confirmation of a person with out-of-school expertise.
In order to being able to analyze and categorize tasks using this approach (binary, atomistic, social construct), Vos suggests focusing on a certain set of aspects and examining tasks in terms of the authenticity of these aspects. A concrete example of such a model of operationalization can be found in Figure 1, here Vos (2018) names three central aspects: “task context, question and solution methods & tools” (p. 12).
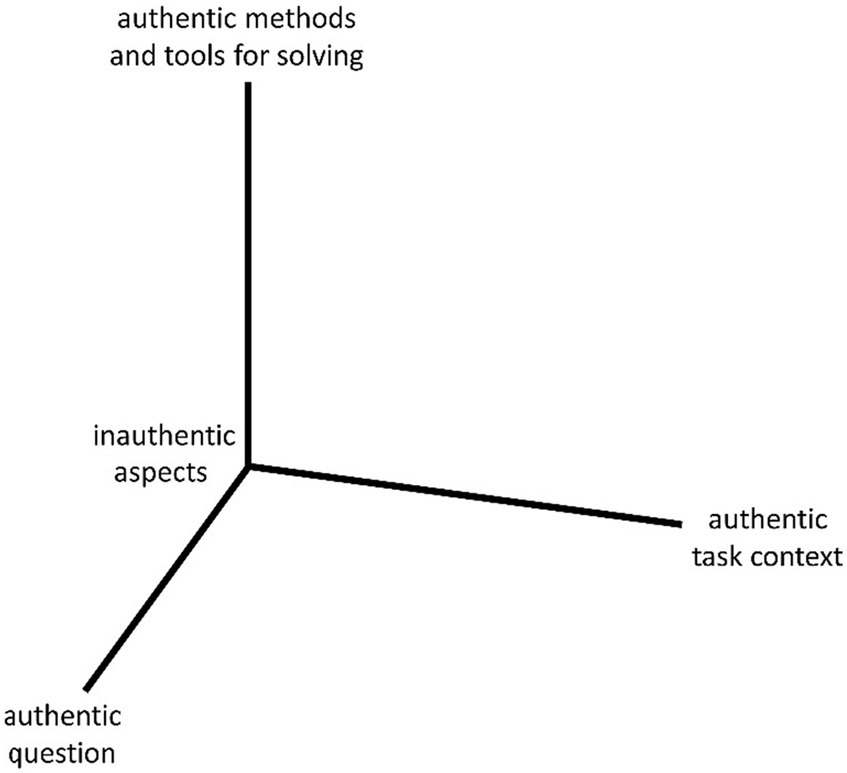
Figure 1. Suggested operationalization according to Vos (adapted from Vos, 2018, p. 12).
Vos (2015) itself considers her definition being in line with the landmark definition given by Niss presented at the beginning – and expands it in two respects. Whereas Niss refers to an extra-mathematical area, Vos speaks of an out-of-school origin, whereby the origin may also be a mathematical one, as long as it is an out-of-school one. In addition, she expands the group of experts in that now, for instance, also stakeholders and not only “people working in it” can confirm the real origin, whereby e. g. also consumer problems can be seen as authentic. Other authors (e. g. Maaß, 2010) also make this extension of everyday life as another arena. The reference to Niss is also strengthened by the fact that Niss’ social component (authenticity as attribution) is reflected in the social construct defined by Vos. In contrast, the comparison of Vos’ and Palms’ theories indicates that in both theories partly opposing assumptions are made. While Palm uses the construct of simulation in his understanding of the term, according to Vos such simulations are precisely not authentic, since a simulation is a copy and thus the opposite of the original. Based on this opposite fundamental assumption, Palm defines authenticity in relation to a task holistically with gradations, while Vos, in contrast, does so binarily and automictically.
2.3.4 Relation to related terms
The term authenticity is defined in the literature partly as a synonym, in connection with or as a distinction from other terms.
Firstly, this concerns the word pair authentic and realistic. On the one hand, there are authors such as Greefrath (2018), for whom a task is authentic if it is credible for the students and at the same time realistic in relation to the environment. Following on from this, the term “realistic” is used in task analyses to assess authenticity (Greefrath et al., 2017; Siller and Greefrath, 2020). In contrast, an explicit distinction between the two terms can be found at authors such as Maaß (2010) or Vos (2020). Whereas according to Vos (2020), as already mentioned, something is authentic if it is clearly not constructed for educational purposes, “realistic means: as if from real-life, close to reality, or could be imagined as real” (p. 38). An aspect understood in this way is therefore “realistic,” but unlike authentic aspects, it does not actually have to exist in this form. This type of distinction is also implicitly found at Niss (1992), who distinguishes between authentic situations and “as if” situations (p. 354).
Secondly, definitions of authenticity can be found in the literature in connection with the term relevance. Some authors (Jablonka, 2007; Turner et al., 2009) talk about the sense of relevance being a prerequisite for authenticity in mathematical modelling. Thus Jablonka (2007): “However, authentic (i. e. actual, not imitated, not false or adulterated) mathematical modelling takes place, when students and teachers are bona fide engaging in a modelling or application activity about an issue relevant to them or to their community” (emphasis in original, p. 196). Other authors, such as Greefrath (2018) or Vos (2011), emphasize that authenticity does not mean that students actually need the corresponding applications or that it is relevant to their present or future lives, but only that something is real and not constructed for school. Thus Vos (2011): “I claim that the term authenticity can be a qualification clear to all actors, even if the aspect has no meaning or relevance to them” (p. 720). According to Vos, the terms already differ in that in her approach authenticity is defined as a social construct in contrast to the actor-dependent term “relevance.”
2.3.5 Authenticity in modelling test items
Regardless of which understanding of the term is followed, it becomes apparent that the realization of authenticity in the construction of modelling tasks is challenging, especially for tasks in standardized test situations (Tout and Spithill, 2015; Greefrath and Maaß, 2020). In the following, the authors understand a standardized test to be an assessment procedure in which reliability and validity can be demonstrated, so that conclusions about the knowledge or skills of the participants can be drawn from the test results (Morrison and Embretson, 2018). Here, it is common practice (with exception of adaptive testing, see Frey, 2023) that each participant receives the same instructions, has the same amount of time, and all answers are scored in the same way. Since authenticity, as shown at the beginning of the article, is considered being a central feature of modelling tasks in general, this also must apply to such tasks in standardized tests that measure modelling competence (“modelling test items”). This requirement is also reflected internationally in the frameworks of various performance tests.
Prominent reference can be made to the OECD’s “Programme for International Student Assessment” (PISA). The programme’s studies measure mathematical performance at regular intervals in the sense of the concept of “mathematical literacy.” PISA defines “mathematical literacy as the ability to formulate and solve mathematical problems in situations encountered in life” (OECD, 2001, p. 22). Here, mathematical modelling is a “cornerstone” of the PISA framework and the OECD (2018) makes conceptual use of a modelling cycle as a “key feature” to measure mathematical literacy (p. 4, 11). In the context of these modelling activities, authenticity has since been demanded in the PISA Frameworks. With regard to task characteristics, the original OECD (1999) Framework explicitly emphasizes that only superficial-looking real-world contexts should be avoided and that the focus is on authentic contexts (p. 51). The OECD’s understanding of authenticity reflects the understanding of Niss (co-author of the Framework): “A context is considered authentic if it resides in the actual experiences and practices of the participants in a real-world setting” (OECD, 1999, p. 51). Confirmation of this requirement for PISA test items can be found at OECD (2001), which again explicitly calls for authentic test items, adding that they may sometimes be fictional as long as they represent the kinds of problem encountered in real life (p. 23). The demand for authenticity is also further reflected in the current OECD (e.g., 2018) frameworks. Authenticity is given such a high priority in PISA that it forms one of the main criteria by which test item adequacy is judged in all countries (Stacey, 2015).
The requirement for authenticity in real-life mathematical test items is also present in various national performance assessment programs. The “National Assessment of Educational Progress” from the United States can be cited as an example: “We recommend developing authentic assessment items with multiple access points that provide diverse populations of students with opportunities to demonstrate their mathematical knowing and reasoning in creative, authentic ways” (National Assessment Governing Board, 2021, p. 128).
While authenticity is explicitly called for in various frameworks of significant performance tests in reality-based mathematics tasks, few studies have been devoted to the analysis of authenticity in such test items. One example is the study by Palm and Burman (2004), which analyzed test items from Finnish and Swedish national evaluations. Here, they do not explicitly state that they are investigating authenticity, but they draw on a previous version of Palm’s framework (Palm, 2006) and implicitly focus on authenticity to be understood in Palm’s sense. Mahler et al. (2020) opted for a small set of aspects of Palm’s (2009) framework when developing mathematics test items in order to make the items as authentic as possible. The authors pointed out that future studies should examine to what extent the authenticity in such test items is related to the probability of solving them and from which aspects students differentially benefit. Other important studies in the context of the investigation of authenticity in test items are those by Greefrath et al. (2017) and Siller and Greefrath (2020). In both studies, authenticity is analogously divided and examined in two aspects: The authenticity of the context and the authenticity of the use of mathematics.
The previous studies mentioned here have looked at the authenticity in test items from different angles, but they do not use a model specifically developed to test items that has been theoretically derived and empirically tested in this context. For example, in the PISA assessment process, only the context of test items is rated on a five point scale in terms of authenticity (Tout and Spithill, 2015). Thus, it is largely unclear how a theoretical and empirically robust model for the description and practical operationalization of authenticity in modelling test items might look like. Moreover, it is striking that Vos’ approach, which is significant for the international discourse, is already used for the analysis of learning tasks (e.g., Turner et al., 2022) but is still unconsidered in analyses of test items.
3 Deriving a theoretical model for assessing authenticity in modelling test items
3.1 Research aim
The desideratum described above is addressed in this article and the following research question is posed in this article: “Which theoretical model can be derived from existing discussions on the authenticity in modelling tasks that can be used for empirically describing and operationalizing modelling items that are used in standardized tests in later steps?”
Based on theoretical considerations (see section 2) as well as expert interviews, a theory-based model was developed which is presented here for the first time. In the following, the central features of the model are presented and the aspects are described in detail.
3.2 Central features of the model
The theoretical analysis gives rise to the following central features of the theoretical model.
(1) Recourse to object authenticity: Firstly, the model is based on the central idea that modelling test items (as well as modelling tasks in general) are objects, rather than subjects, which is why object authenticity forms the foundation. As has been demonstrated, something is considered being authentic if a standardized analysis shows that an object is genuine as opposed to a forgery. Since modelling test items comprise real-world problems, the authenticity of these objects can be assessed with respect to the extra-mathematical reference to reality. Consequently, an object is authentic according to the present model if an analysis (for further details see section 4) proves that it is genuinely derived from reality.
(2) Distinction from related terms: The term authentic is distinguished in the model from the terms realistic and relevant. The definition of authenticity in the model shown above in (1) is derived from object authenticity and does not correspond to the basic idea of a realistic object. Whereas with a realistic object it is merely conceivable that it could exist in reality, an authentic object actually exists. Likewise, it is obvious that the present definition of authenticity (an object is genuine) can be clearly distinguished from the concept of relevance (i.e., whether an object has a meaning for the current or future life of the students).
(3) Binary distinction: Following the idea of object authenticity, authenticity is defined in a binary way in the model: If evidence of an object’s out-of-school origin can be found, it is considered authentic; if no evidence can be found, the aspect is considered not being authentic.2 Although authenticity is normatively demanded for modelling test items, the classification as not authentic is necessarily to be understood as descriptive and value-free for two reasons. Firstly, to date there is little evidence on which use of which resources in modelling test items yields positive effects. Secondly, non-authentic objects can cover a wide spectrum: from artificial disguises to strong simplifications to realistic representations, which should not be devalued across the board.
(4) Atomistic approach: The basis for this is the assumption elaborated in the theoretical part that modelling tasks, especially modelling test items in standardized tests, can only simulate real out-of-school situations. Since simulations of objects are the opposite of the originals, a modelling test item cannot achieve complete authenticity from a holistic perspective. Therefore, in order to operationalize authenticity in the model, an atomistic distinction is made between aspects that can be authentic or not.
(5) A social construct: Since it is not possible to look into the minds of the test item developers involved at the time when analyzing existing test items, the authenticity of individual aspects cannot be identified as an inherent property of the item. Consequently, the model uses the constructive approach of object authenticity: A test item aspect is authentic if researchers attribute authenticity to an aspect in an intersubjectively comprehensible manner based on a theoretically sound method (see section 4). This approach corresponds with Vos’ concept of the social construct, which is why this serves as the basis for the model and the requirements formulated by Vos are used: For an aspect to be attributed authenticity, an extracurricular origin must be present and demonstrable.
(6) Selection of aspects: For the model, a set of aspects was compiled that were identified through the literature review or discussions with experts as central aspects to assess authenticity in modelling test items (see Table 2). Palm’s (2009) framework forms the central basis here, as it was explicitly intended by Palm for aspect compilations in “use-inspired basic research” and as the aspects it contains were found to be useful in previous studies (p. 14). Thus, in the form of a synergistic effect, the model makes it possible to link Vos’ approach with Palm’s considerations. Following Vos (2018), the model deliberately speaks of “aspects,” since other terms such as “elements” or “parts” have stronger dualistic connotations and “aspects” can vary in size and overlap. The total of 8 selected aspects form the core of the model (and thus also the basis for future empirical work based on this model) and are described in detail below.
3.3 Explanation and operationalization of the aspects in the model
Two aspects of Palm’s framework are not reflected at all in the present model because of its specialization in test items. Firstly, the “circumstances,” since standardized testing situations are characterized by the subject being the only source of variation and all other conditions being controlled so as not to act as confounding variables. This is usually associated with time constraints and low-stimulus environments. As this does not correspond to such circumstances as can be found in reality-based situations to which modelling items refer, the aspect is not considered here. Secondly, the “solution requirements” are not entered in the model. In standardized tests, the answer is usually marked by a gap, an answer sentence or a cross. This aspect also does not correspond to those that occur in the reality addressed by modelling items. The final aspects of the model are described in more detail below, including its origins.
3.3.1 Real-world context
The real-world context aims at the overarching reality-based frame of reference to which the test item relates. This first, initially very broad aspect was derived from the discussions with various experts as well as from Siller and Greefrath (2020): “Authenticity refers to an extra-mathematical context which must be discussed by mathematical means in the respective situation. The extra mathematical context should be authentic instead of just being constructed for this special mathematical task” (p. 386). Usually only one object is to be identified as a coding unit here. These can be everyday factual contexts, professional factual contexts or social discourses. The aspect of an item is authentic if – irrespective of the concrete events, data or similar – the overarching real-world context verifiably genuinely originates from reality, i.e., if the context exists outside of school. For instance, the real-world context roofing is authentic, the cloning of the globe is not authentic, and in an intra mathematical test item no object can be defined as a coding unit.
3.3.2 Events
This aspect refers to the event-related happenings presented in the test item. In contrast to the context, the focus is not on the overarching frame of reference, but on the concrete events. The aspect originates from Palm’s (2009) framework, whereby the events are understood in the plural here. This is done because quite often several events are reported in modelling test items and it should be possible to record several objects as a coding unit. Possible objects of the coding unit are described initial situations, events that have occurred as well as planned or performed activities. The events are understood as objects of the coding unit in a generalized way without the information about specific persons, specific objects or specific data. The aspect is authentic if all events from the test item can be proven to actually happen outside of school. Securing a bicycle with a lock or emptying a trash can are therefore considered authentic events. Not authentic are processes like counting the legs of a herd of animals or making the rule that a basketball team wins a game only if the score has a certain mathematical divisor.
3.3.3 Objects
In this aspect, the reality-based objects addressed in the test item are analyzed. This consideration is based on Vos’ understanding of a context: Referring to a study by Djepaxhija (2012) in which calculations have to be made on a real existing marketplace, Vos (2018) identifies this as an authentic context. In the current model, however, this authentic marketplace neither corresponds to the real-world context nor to the events but can be identified as an additional aspect. In the case of an authentic aspect, all reality-based objects are genuinely derived from reality and thus exist outside of school. Prototypical examples of authentic objects are buildings such as the Taj Mahal in India or things such as a dice cup; not authentic objects are, for instance, a fair seven-sided playing dice or a fictitious television model.
3.3.4 Question/assignment
This aspect refers to the question or, alternatively, the work assignment posed in the test item. This aspect was adapted from Palm’s (2009) framework. Furthermore, Niss (1992) and Vos (2018) also explicitly point out that the question can be seen as a central aspect in the issue of task authenticity. To assess this aspect, the question/assignment to which the processing of the test item relates to is the object of the coding unit. Following Vos (2018), an authentic question is one that “people within the context would ask” (p. 3). It becomes evident that the present aspect is inextricably linked to the real-world context. Thus, a question/assignment is classified as authentic if it is formulated by people in the real-world context defined in the first aspect and if this out-of-school origin can be proven. For instance, in the context of tree cutting, it is an authentic question to ask about the height of a tree. In contrast, in the context of candy consumption, it is not an authentic question to ask for the probability of pulling a certain candy out of the bag.
3.3.5 Data
This aspect includes the data presented in the test item (quantities, numbers, sizes, dates, coding, or formulas). It is found implicitly at Niss (1992) as well as explicitly in Palm’s (2009) framework. With Palm, the aspect is divided into 3 sub-aspects, but in the present model, the aspect is combined into one aspect and adapted in terms of the ideas underlying the model. For the identification of the coding unit, analogous to the aspect “objects,” only reality-related data is considered. Inner mathematical statements such as “Calculate with pi equal to 3″ are thus not recorded here, since this does not refer to the data from reality, but to the processing path. The reality-related data can be textual, tabular or graphical and are always understood in the context of the objects and events to which they refer. The decisive factor for the attribution of authenticity is whether the data is genuinely derived from reality, which means that people actually encounter it outside of school. An example of an authentic data value is the height of the Eiffel Tower of 324 meters, since an out-of-school origin can be found for this. The area measurement of 4 by 5 meters for a children’s room is also classified as authentic, as evidence can be found that this was not artificially constructed for educational purposes, but meets people outside of school. On the other hand, for a throw distance in a javelin throwing competition of 100 meters, no evidence can be found that people encounter this data value outside of school, since the world record is less than 100 meters. The same applies to smooth numbers for price quotations of products that never cost smooth amounts outside of school.
3.3.6 Figures
This aspect relates to the figures that are presented in the test item. It implicitly refers to the “presentation” aspect from Palm’s (2009) framework and considers the mode of presentation. In the present aspect, only figures from the item stem are identified as coding units and not those that occur in the answer options. This is due to the fact that, in general, the figures of the distractors must necessarily be created artificially and cannot be authentic. Analogous to the data aspect before, for the attribution of authenticity it is decisive whether the figures are those that people actually encounter outside of school. It consequently does not make a figure non-authentic just because it has been chosen or photographed for the test item. A figure becomes non-authentic when people outside school do not encounter it, e. g. because it has been artificially created or because an original figure has been edited. Examples of authentic illustrations are a photographed/scanned bus map, a city map or a sketch of a garden from a brochure. Not authentic, on the other hand, would be the illustration of a chip bag in which the height was drawn for the test item, or the illustration of such a simplified city map which people do not encounter outside school.
3.3.7 Use of mathematics
This aspect refers to the expected use of mathematics to process the test item. On the one hand, the aspect has its origin at Niss (1992), who addresses the aspect indirectly in an exemplary authenticity analysis of a task. On the other hand, the aspect originates from Siller and Greefrath (2020), who consider this aspect as one of two central ones for the assessment of authenticity in their task analysis. For the model, the aspect was adapted with regard to the ideas underlying it. The coding unit shall be defined as the expected mathematical use in processing the question or assignment of the test item. All parts of the sampling unit that could provide information about this can be used as a basis: The item stem, the sub-question, the answer options or, if applicable, the solution sketch. References to processing such as “Calculate with pi equals three,” which were excluded in the previous aspects, are thus included in the coding unit for this aspect. An authentic aspect exists if the identified mathematical use corresponds to an out-of-school use of mathematics in the real-world context. As with the question/assignment aspect, it becomes apparent that here is again a link to the real-world context aspect. It must be possible to actually prove the use in the real-world context; if the use is completely taken over by an instrument or tool in practice and therefore no longer plays a role, it is not an authentic aspect. An example is the use of the area formula of the rectangle to calculate the size of a wall in the context of painting. Although there are already devices that do this work or make it easier, there is proof that this use continues to exist outside of school and is thus clearly not created for educational purposes. As a counter-example, the use of the arithmetic mean to create a ranking is not an authentic aspect in the context of long jumping. No evidence can be found for the out-of-school origin of the use in the real-world context, as in practice other methods are used (e. g. sorting the best attempts by size).
3.3.8 Purpose
This aspect is about the processing purpose of the test item. The origin of the aspect is implicitly based on Niss (1992) and explicitly based on Palm (2009), who describes “purpose in a figurative context” as an aspect in his framework. Coding unit shall be defined as those components of the test item in which the intent and purpose of the processing required by the test item is described or presented. The purpose must not be the processing itself, so the purpose of an area calculation must not be the calculation of an area itself, but why the area should be calculated in the real-world context. To the extent that such a purpose can be identified in the test item, it is authentic if it corresponds to an out-of-school purpose of an activity in the real-world context and thus is demonstrably genuinely derived from reality. As with the previous aspect or with the aspect of question/assignment, a link with the aspect of real-world context becomes obvious. An example of an authentic purpose is to estimate the wall area so that enough wallpaper is purchased, as evidence can be seen for this extracurricular origin in the real-world context of wallpapering. A non-authentic purpose in the real-world context of playing table tennis is calculating the table tennis table surface in order to improve the quality of the game, since a search for this does not find any out-of-school evidence.
4 Application of the model
The model developed and theoretically legitimized here in the article can now be used to analyze such test items in terms of authenticity that claim to measure modelling competencies. The basic ideas for the application of the model are outlined below and then concretized using a selected example.
4.1 Basic ideas for the application of the model
In order to use the model, the test item must first be defined as a parent object in the form of a sampling unit. The model is designed in a way that a test item consists of an item stem with information (text, data, figures, etc.) and an associated question or work assignment. If there is an item stem with several associated questions or assignments (as it appears quite often in standardized tests), the item stem together with one question or assignment is to be selected as the sampling unit. If available, the desired or expected item solutions issued by the test should also be included as data material in the sampling unit. But is not sufficiently necessary, since this is only an additional help for one single aspect (use of mathematics).
Subsequently, for the assessment of authenticity of the aspects in the sense of the atomistic approach and object authenticity, the object of each of the eight aspects must always be defined as a coding unit in a first step. There are concrete specifications for each aspect and, based on these, the objects must be specified to the raters. Depending on the aspect, this coding unit can be one object or several objects, and it is also possible that no object can be identified. If several objects are identified as a coding unit, the following applies in principle: Authenticity must be attributed to all objects in the coding unit for an aspect to be considered authentic. If authenticity cannot be attributed to at least one single object, the aspect does not originate genuinely from reality and is thus considered not authentic in the sense of the model. The determination of the objects of the coding units should be done consensually by several scientists.
After specifying the objects of each aspect, raters can evaluate the aspects in terms of authenticity. Here the question arises under which conditions authenticity can be attributed. Explicit reference is made to Vos’ requirements for an authentic aspect (2018): (1) an out-of-school origin must be established and this (2) must be demonstrable. This evidence can be given by the test item itself (e. g., source evidence or illustrations) or can be found by purposeful search by the raters. In this regard, scientists should provide raters with comparable and standardizable guidelines.3 In principle, it may be the case that an aspect was genuinely taken from reality, but this is neither evident from the test item itself nor demonstrable through search by several raters. In this case, in the sense of object authenticity and the idea of a social construct, it is consciously accepted that the aspect is classified as not authentic because an out-of-school origin is not apparent to a community (in this case, the scientific raters).
With the help of the coding of the individual aspects, test items can finally be classified with regard to authenticity. However, there are two important restrictions to be mentioned: Firstly, a test item in which all aspects are authentic may not be called holistically authentic. It should be noted that this is only a compilation of aspects central to modelling test items. Other possible aspects such as the availability of tools, processing circumstances or responsibility for material and life are not examined, which is why we should not speak of “authentic test items” in the sense of the assumptions made. Secondly, while test items can be compared in terms of authenticity and considered on an authenticity continuum in the sense of Verschaffel et al. (2020), this should only happen in terms of “more or less” authentic aspects, and not holistically in the way of “more authentic or inauthentic” items.
4.2 Assessing authenticity in the test item “Climbing Mount Fuji”
The unit “Climbing Mount Fuji” serves to demonstrate an exemplary application of the model (see Figure 2 for item stem and question 1). The unit is one of the main survey items from the 2012 PISA study (OECD, 2013) and is suitable for the first exemplary application of the model for several reasons. (1) PISA items in general (as elaborated in the theory) are such test items that have references to reality and are explicitly related to the concept of mathematical modelling. (2) The unit was published as one of two sample units to assess mathematical student performance in the OECD results report OECD (2014) and is thus publicly available. (3) The test item development process and the authenticity assessment within the test development process can be accessed in Tout and Spithill (2015). In the following, we exemplarily consider the first question on the unit “Climbing Mount Fuji,” whose cognitive effort explicitly consists in taking pieces of a real-world situation and establishing a mathematical problem to be solved.

Figure 2. (A) Test Item “Climbing Mount Fuji” (PM942Q01) adapted from OECD, 2013 (B) Identified coding units of the test item “Climbing Mount Fuji”.
In the authenticity assessment within the item creation process of PISA, the context of the first question received an average authenticity rating of 4.32 (range 1–5, with 5 best) from the national program managers (Tout and Spithill, 2015). What an authenticity assessment looks like using the model is shown below.
For the real-world context (aspect I), the topic of mountain climbing can be identified as the overarching reality-based frame of reference. The obvious out-of-school origin cannot initially be derived from evidence in the test item itself. However, purposeful search quickly generates evidence that this is an out-of-school topic. Our key question, whether the overarching real-world context actually exists outside school, can thus be verifiably answered in the affirmative.
Three text parts can be identified as events (aspect II): (1) There is a dormant volcano in Japan, (2) a mountain is opened to the public for climbing only during certain periods and (3) a number of people climb a mountain. Evidence can quickly be found that the events are actually taking place outside of school. Consequently, the key question can be answered in the affirmative for all events, which makes the aspect being authentic.
In the test item there is one reality-based object (aspect III): Mount Fuji. A search quickly proves that Mount Fuji exist outside of school and the aspect is authentic.
The question (aspect IV) referred to in the item processing is “On average, how many people climb Mount Fuji each day?.” This is a question that demonstrably arises in the real-world context of mountain climbing. Once again, this does not emerge from the test item itself but from a purposeful search. In this regard, it is evident that municipalities managing public trails are looking into such an issue. Thus, the question was genuinely derived from reality and the aspect is authentic.
Two values can be identified as data (aspect V): (1) Mount Fuji is only open for climbing from 1 July to 27 August each year and (2) about 200,000 people climb Mount Fuji during this time. Not only is there no evidence about these dates of the opening period, but there is even explicit evidence to the contrary. Firstly, a brief purposeful search shows that Mount Fuji is always opened depending on the weather. Consequently, the opening dates are variable every year and are usually from the beginning of July to the beginning/middle of September. Therefore, given data value (1) from the test item is possibly realistic (imaginable, close to reality), but it is not a value genuinely derived from reality in the sense of the key question, because one finds no evidence that people actually encounter the value outside school. Even though this aspect is already not authentic, we still consider the authenticity of given data value (2) for exemplary discussion. Search shows that the number of climbers per year varies between 200,000 and 400,000. The value of 200,000 from the test item thus demonstrably originates from reality and is authentic. However, the entire aspect includes inauthentic data, making it not genuinely derived from reality and not considered authentic in terms of model logic.
The drawing of the volcano is taken as the coding unit of the figures (aspect VI). Once again, we cannot look into the developers’ minds, whether the graphics in the processing of creating the test item were genuinely taken from reality. In the sense of a social construct, we examine in an intersubjectively comprehensible way whether there is evidence that people actually encounter such an illustration outside school. We again see no evidence in the test item itself, but find out through search that such a drawing of Mount Fuji is a popular out of school vector graphic. Thus, the aspect considered being authentic.
The expected use of mathematics (aspect VII) in the example test item is the calculation of the arithmetic mean. A search quickly reveals evidence that this use is common in the real-world context of mountain climbing. To determine the average climbers of certain trails, municipalities as well as reporting agencies usually use the same method. Since both uses coincide, the aspect is considered being authentic.
A purpose as to why the calculation should be carried out in context cannot be identified at any point within the item. Thus, the coding unit of the purpose (aspect VIII) is missing and cannot be assessed for authenticity.
5 Discussion and outlook
5.1 Added value/novelties
The aim of the study was to address the desideratum identified in the theoretical background and to derive a theoretical model for describing and operationalizing such modelling tasks that are used in standardized tests. The “Model for Authenticity in Modelling Test Items” presented and theoretically legitimated in the article in detail can be considered as the result of the study. The model enables the analysis of authenticity in modelling test items in an intersubjectively comprehensible manner using transparent formation of a coding unit and specific criteria for assessment. Here there are two central novelties: In contrast to certain existing approaches, the present model is both based on object authenticity and is tailored to test items.
The added value of the model becomes evident in the exemplary analysis of the “Climbing Mount Fuji” test item. In the PISA item development process, authenticity is related only to the overall context with a five-point scale, and the test item receives an average rating of 4.32. However, it remains an open question which aspects of the test item are authentic and precisely which are not. In contrast, the model analysis differentially shows that the test item already contains certain authentic aspects (real-world context, events, objects, question, figure, use of mathematics), but for the data no authenticity can be stated and the purpose is not mentioned at all. This increased informative value makes the model an additional support for the acquisition, assessment and (further) development of modelling test items.
Furthermore, the model can be used for assessing the authenticity in test items of standardized tests and thus for comparing multiple tests. Here, well-founded statements can be made about which aspects are particularly frequently or also less frequently authentic in which tests.
5.2 Limitations
A limitation regarding the application of the model is the fact that the assessment of the aspects regarding authenticity is a social attribution. Biases can always occur in the assessment process, for instance, different information may be found or perceived differently in the search. However, this possibility is counteracted by the prior identification of a coding unit and the clearest possible operationalization of the individual aspects. In addition, as mentioned in the article, to reduce bias as much as possible, it should be ensured that each test item is assessed independently by multiple raters. Furthermore, at this point it should be emphasized that the attribution by the raters should not be mistaken with the formation of a subjective opinion. Whereas in the case of a personal opinion a subjective decision is made, in the case of assessment in terms of the model, the raters check in an intersubjectively comprehensible way whether theoretically founded criteria are fulfilled.
Furthermore, the model initially only aims at assessing the authenticity of central aspects of modelling test items. The model thus opens itself to different approaches to how the results obtained by the model can be interpreted after the assessment. This includes questions about how missing coding objects are classified for which aspect or about whether the aspects should be weighted differently. For instance, in line with previous analyses (Greefrath et al., 2017; Siller and Greefrath, 2020), the number of authentic aspects across a large set of tasks (e. g., a set of modelling test items from a standardized test) could be given in the form of percentages and conclusions could be drawn about test item quality. However, two key remarks need to be made regarding the interpretation of the assessment. (1) It is not in the intention of the model to form an overall score from the assessment of the individual aspects. As described in the article and theoretically legitimated, the model follows an atomistic approach, which excludes a holistic final evaluation in the form of a score. (2) Accordingly, the situation that only authentic aspects are measured in a test item does not mean that it is a completely authentic item. It is both only a selection of central aspects and, as theoretically derived in the article, a mathematical school task cannot attain holistic authenticity in the sense of object authenticity.
5.3 Outlook: empirical application
In a next step, the model will be used to gain insights into the extent to which modelling test items in existing standardized tests contain aspects which could be labelled being “authentic.” For this purpose, it is useful to compile a database with test items from significant national and international tests. Authenticity in the test items can then be assessed using the model and the results analyzed qualitatively as well as quantitatively to draw conclusions about the test items as well as the tests in general. In such further studies, it is also important to investigate the extent to which the fundamental model can be applied to all levels of education in the same way, or whether adaptations are necessary in single cases.
In addition to this examination of the status quo, it remains an open question which effects are associated with the normatively required authenticity of different aspects. Here, the model can be used to edit or create modelling test items based on the model and to explore effects on cognitive and motivational-emotional disposition of students when varying individual aspects. In this context, it still remains an open question to what extent authenticity as a task and test item criterion has direct effects or to what extent the students’ perception of this authenticity mediates effects of authenticity. When looking at the sample test item “Climbing Mount Fuji,” it is noticeable that the authenticity could only be proven by external search and that no evidence was apparent to the students from the item itself. The examination of these issues (which are significant for the further development of modelling test items) is made possible by the development of the present model and will be advanced in the coming future.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
DS: Writing – original draft. MB: Writing – review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This publication was supported by the German Research Foundation (DFG).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^The article uses the term “modelling tasks” for learning tasks and “modelling test items” for assessment tasks.
2. ^In the model, the word inauthentic is deliberately not used as the opposite of authentic, since discussions with experts indicated that this is already connoted with a negative valuation. Instead, the term “not authentic” is used, which merely means descriptively that no authenticity could be verified in the sense of the model logic.
3. ^It is recommended that this evaluation be conducted by multiple independent reviewers, as it was found in a pilot study that multiple independent studies complemented each other with important information. After the aspects have been coded independently, a consensus is reached together.
References
Berger, P. L., and Luckmann, T. (1966). The social construction of reality: a treatise in the sociology of knowledge. Garden City, NY: Anchor Books.
Blum, W., and Leiss, D. (2007). “How do students and teachers Deal with modelling problems?” in Mathematical modelling: Education, engineering and economics. eds. C. Haines, P. Galbraith, W. Blum, and S. Khan (Cambridge, UK: Woodhead Publishing), 222–231.
Borawski, D. (2021). Authenticity and rumination mediate the relationship between loneliness and well-being. Curr. Psychol. 40, 4663–4672. doi: 10.1007/s12144-019-00412-9
Borromeo Ferri, R. (2018). Learning how to teach mathematical modeling in school and teacher education. Cham: Springer International Publishing.
Büchter, A., and Leuders, T. (2016). Mathematikaufgaben selbst entwickeln: Lernen fördern - Leistung überprüfen. Berlin: Cornelsen.
Djepaxhija, B. (2012). An exploratory study of grade 8 Albanian students’ solution processes in mathemathics word problems. Kristiansand, Norway: University of Agder.
Eser, T., Farrenkopf, M., Kimmel, D., Saupe, A., and Warnke, U. (2017). “Einleitung: Authentisierung im Museum” in Authentisierung im Museum: Ein Werkstatt-Bericht. eds. T. Eser, M. Farrenkopf, D. Kimmel, A. Saupe, and U. Warnke (Mainz, Germany: Verlag des Römisch-Germanischen Zentralmuseums).
Frey, A. (2023). “Computerized adaptive testing and multistage testing” in International encyclopedia of education(fourth edition) (Elsevier)
Galbraith, P. (2013). “From conference to community: an ICTMA journey—the ken Houston inaugural lecture” in Teaching mathematical modelling: Connecting to research and practice. eds. G. A. Stillman, G. Kaiser, W. Blum, and J. P. Brown (Dordrecht: Springer Netherlands), 27–45.
Geiger, V. (2017). “Designing for mathematical applications and modelling tasks in technology rich environments” in Digital Technologies in Designing Mathematics Education Tasks. eds. A. Leung and A. Baccaglini-Frank (Cham: Springer International Publishing), 285–301.
Greefrath, G. (2018). Anwendungen und Modellieren im Mathematikunterricht. Berlin, Heidelberg: Springer.
Greefrath, G., and Maaß, K. (2020). “Diagnose und Bewertung beim mathematischen Modellieren” in Modellierungskompetenzen – Diagnose und Bewertung. eds. G. Greefrath and K. Maaß (Berlin, Heidelberg: Springer Berlin Heidelberg), 1–19.
Greefrath, G., Siller, H.-S., and Ludwig, M. (2017). “Modelling problems in German grammar school leaving examinations (abitur) – theory and practice” in CERME 10: Proceedings of the tenth congress of the European Society for Research in mathematic education. eds. T. Dooley and G. Gueudet (Dublin: Institute of Education Dublin City University), 932–939.
Harter, S. (2002). “Authenticity” in Handbook of positive psychology. eds. C. R. Snyder and S. J. Lopez (London: Oxford University Press), 382–394.
Holtorf, C. (2013). On Pastness: a reconsideration of materiality in archaeological object authenticity. Anthropol. Q. 86, 427–443. doi: 10.1353/anq.2013.0026
Jablonka, E. (2007). “The relevance of modelling and applications: relevant to whom and for what purpose?” in Modelling and applications in mathematics education. eds. W. Blum, P. L. Galbraith, H.-W. Henn, and M. Niss (Boston, MA: Springer US), 193–200.
Joyce, R. (2013). “When is authentic?” in creating authenticity: Authentication processes in ethnographic museums, eds. A. Geurds and L. Broekhovenvan (Leiden: Sidestone Press), 39–57.
Kaiser, G. (2017). “The teaching and learning of mathematical modelling” in Compendium for research in mathematics education. ed. J. Cai (Reston, VA: National Council of Teachers of Mathematics), 267–291.
Kaiser, G., and Stender, P. (2013). “Complex modelling problems in co-operative, self-directed learning environments” in Teaching mathematical modelling: Connecting to research and practice. eds. G. A. Stillman, G. Kaiser, W. Blum, and J. P. Brown (Dordrecht: Springer Netherlands), 277–293.
Kernis, M. H., and Goldman, B. M. (2006). “A multicomponent conceptualization of authenticity: theory and research” in Advances in experimental social psychology. ed. M. P. Zanna, vol. 38 (New York: Academic Press), 283–357.
Knaller, S. (2006). “Genealogie des ästhetischen Authentizitätsbegriffs” in Authentizität: Diskussion eines ästhetischen Begriffs. eds. S. Knaller and H. Müller (München: Fink), 17–35.
Knaller, S. (2017). Ein Wort aus der Fremde: Geschichte und Theorie des Begriffs Authentizität. Heidelberg, Neckar: Universitätsverlag Winter GmbH Heidelberg.
Knaller, S., and Müller, H. (2005). “Authentisch/Authentizität” in Ästhetische Grundbegriffe: Historisches Wörterbuch in sieben Bänden. Band 7: Register und Supplemente. eds. K. Barck, M. Fontius, D. Schlenstedt, B. Steinwachs, and F. Wolfzettel (Stuttgart: J.B. Metzler), 40–65.
Leiss, D., Plath, J., and Schwippert, K. (2019). Language and mathematics - key factors influencing the comprehension process in reality-based tasks. Math. Think. Learn. 21, 131–153. doi: 10.1080/10986065.2019.1570835
Lu, X., and Huang, J. (2021). “Mathematical modelling in China: how it is described and required in mathematical curricula and what is the status of students’ performance on modelling tasks” in Beyond Shanghai and PISA. eds. B. Xu, Y. Zhu, and X. Lu (Cham: Springer International Publishing), 209–233.
Lu, X., and Kaiser, G. (2022). Can mathematical modelling work as a creativity-demanding activity? An empirical study in China. ZDM 54, 67–81. doi: 10.1007/s11858-021-01316-4
Luczak, R., and Erwin, R. (2023). Mathematical modeling: a study of multidisciplinary benefits in the math classroom. Teach. Math. Applic. Int. J. IMA 42, 325–342. doi: 10.1093/teamat/hrac021
Maaß, K. (2010). Classification scheme for modelling tasks. J. Math. Didakt. 31, 285–311. doi: 10.1007/s13138-010-0010-2
Mahler, N., Kölm, J., and Werner, B. (2020). “Entwicklung von Mathematiktestaufgaben für Schüler*innen mit einem sonderpädagogischen Förderbedarf im Lernen – Konzeption und empirische Ergebnisse” in Schüler*innen mit sonderpädagogischem Förderbedarf in Schulleistungserhebungen. eds. C. Gresch, P. Kuhl, M. Grosche, C. Sälzer, and P. Stanat (Wiesbaden: Springer Fachmedien Wiesbaden), 109–146.
Mickel, A. (2018). “Authenticity in archaeological writing and representation” in Encyclopedia of global archaeology. ed. C. Smith (Cham: Springer), 1–12.
Morrison, K. M., and Embretson, S. E. (2018). “Standardized tests” in The SAGE encyclopedia of educational research, measurement, and evaluation. ed. B. B. Frey (Thousand Oaks: SAGE Publications, Inc)
National Assessment Governing Board (2021). Mathematics framework for the 2026 National Assessment of educational Progress. Washington: National Assessment Governing Board.
Niss, M. (1992). “Applications and modeling in school mathematics – directions for future development” in Developments in school mathematics education around the world. eds. I. Wirszup and R. Streit (Reston, Virginia, USA: National Council of Teachers of Mathematics)
Niss, M., Blum, W., and Galbraith, P. (2007). “Introduction” in Modelling and applications in mathematics education. eds. W. Blum, P. L. Galbraith, H.-W. Henn, and M. Niss (Boston, MA: Springer US), 3–32.
OECD (2013). PISA 2012 released mathematics items. Available at: https://www.oecd.org/pisa/pisaproducts/pisa2012-2006-rel-items-maths-ENG.pdf
OECD (2014). PISA 2012 results: what students know and can do - student performance in mathematics, reading and science. Paris: OECD Publishing.
OECD (2018). PISA 2022 mathematics framework (draft). Available at: https://pisa2022-maths.oecd.org/files/PISA%202022%20Mathematics%20Framework%20Draft.pdf
Palm, T. (2007). “Features and impact of the authenticity of applied mathematical school tasks” in Modelling and applications in mathematics education. eds. W. Blum, P. L. Galbraith, H.-W. Henn, and M. Niss (Boston, MA: Springer US), 201–208.
Palm, T. (2008). Impact of authenticity on sense making in word problem solving. Educ. Stud. Math. 67, 37–58. doi: 10.1007/s10649-007-9083-3
Palm, T. (2009). “Theory of authentic task situations,” in Words and worlds, eds. L. Verschaffel, B. Greer, W. Doorenvan, and S. Mukhopadhyay (Reston, Virginia, USA: BRILL), 1–19.
Palm, T., and Burman, L. (2004). Reality in mathematics assessment: an analysis of task-reality concordance in Finnish and Swedish national assessment. Nordic Stud. Math. Educ. 9, 1–33.
Paredes, S., Cáceres, M. J., Diego-Mantecón, J.-M., Blanco, T. F., and Chamoso, J. M. (2020). Creating realistic mathematics tasks involving authenticity, cognitive domains, and openness characteristics: a study with pre-service teachers. Sustainability 12:9656. doi: 10.3390/su12229656
Peterson, C., and Seligman, M. E. P. (2004). Character strengths and virtues: A handbook and classification. New York: Oxford University Press.
Saupe, A. (2014). “Empirische, materiale, personale und kollektive Authentizitätskonstruktionen und die Historizität des Authentischen” in Authentizität: Artefakt und Versprechen in der Archäologie; Workshop vom 10. bis 12. Mai 2013, Ägyptisches Museum der Universität Bonn. ed. M. Fitzenreiter (London: Golden House Publ), 19–26.
Siller, H.-S., and Greefrath, G. (2020). “Modelling tasks in central examinations based on the example of Austria” in Math. Model. Educ. Sense-MAKING. eds. G. A. Stillman, G. Kaiser, and C. E. Lampen (Cham: Springer International Publishing), 383–392.
Stacey, K. (2015). “The real world and the mathematical world” in Assessing mathematical literacy. eds. K. Stacey and R. Turner (Cham: Springer International Publishing), 57–84.
Steen, L. A., Turner, R., and Burkhardt, H. (2007). “Developing mathematical literacy” in Modelling and applications in mathematics education. eds. W. Blum, P. L. Galbraith, H.-W. Henn, and M. Niss (Boston, MA: Springer US), 285–294.
Stillman, G. A. (2019). “State of the art on modelling in mathematics education—lines of inquiry” in Lines of inquiry in mathematical modelling research in education. eds. G. A. Stillman and J. P. Brown (Cham: Springer International Publishing), 1–20.
Thomaes, S., Sedikides, C., van den Bos, N., Hutteman, R., and Reijntjes, A. (2017). Happy to be “me?” authenticity, psychological need satisfaction, and subjective well-being in adolescence. Child Dev. 88, 1045–1056. doi: 10.1111/cdev.12867
Tout, D., and Spithill, J. (2015). “The challenges and complexities of writing items to test mathematical literacy” in Assessing mathematical literacy. eds. K. Stacey and R. Turner (Cham: Springer International Publishing), 145–171.
Turner, E. E., Bennett, A. B., Granillo, M., Ponnuru, N., Roth Mcduffie, A., Foote, M. Q., et al. (2022). Authenticity of elementary teacher designed and implemented mathematical modeling tasks. Math. Think. Learn. 26, 47–70. doi: 10.1080/10986065.2022.2028225
Turner, E. E., Gutiérrez, M. V., Simic-Muller, K., and Díez-Palomar, J. (2009). “Everything is math in the whole world”: integrating critical and community knowledge in authentic mathematical investigations with elementary Latina/o students. Math. Think. Learn. 11, 136–157. doi: 10.1080/10986060903013382
Verschaffel, L., Schukajlow, S., Star, J., and van Dooren, W. (2020). Word problems in mathematics education: a survey. ZDM 52, 1–16. doi: 10.1007/s11858-020-01130-4
Vos, P. (2011). “What is ‘authentic’ in the teaching and learning of mathematical modelling?” in Trends in teaching and learning of mathematical modelling. eds. G. Kaiser, W. Blum, R. B. Ferri, and G. Stillman (Dordrecht: Springer Netherlands), 713–722.
Vos, P. (2015). “Authenticity in extra-curricular mathematics activities: researching authenticity as a social construct” in Mathematical modelling in education research and practice. eds. G. A. Stillman, W. Blum, and M. Salett Biembengut (Cham: Springer International Publishing), 105–113.
Vos, P. (2018). “How real people really need mathematics in the real world”—authenticity in mathematics education. Educ. Sci. 8:195. doi: 10.3390/educsci8040195
Vos, P. (2020). “Task contexts in Dutch mathematics education,” in National Reflections on the Netherlands didactics of mathematics, ed. M. Heuvel-Panhuizenvan den (Cham: Springer International Publishing), 31–53.
Vos, P., Devesse, T. G., and Pinto, A. A. R. (2007). Designing mathematics lessons in Mozambique: starting from authentic resources. Afri. J. Res. Math.tion 11, 51–66. doi: 10.1080/10288457.2007.10740621
Warnke, U. (2022). “Bergung und Befund” in Handbuch Historische Authentizität. eds. M. Sabrow and A. Saupe (Göttingen: Wallstein Verlag)
Wernet, J. L. W. (2017). Classroom interactions around problem contexts and task authenticity in middle school mathematics. Math. Think. Learn. 19, 69–94. doi: 10.1080/10986065.2017.1295419
Keywords: authenticity, mathematical modelling, test items, standardized tests, theoretical model, theoretical research, mathematics education
Citation: Schlüter D and Besser M (2024) Assessing authenticity in modelling test items: deriving a theoretical model. Front. Educ. 9:1343510. doi: 10.3389/feduc.2024.1343510
Edited by:
Kotaro Komatsu, University of Tsukuba, JapanReviewed by:
Wahyu Widada, University of Bengkulu, IndonesiaRina Durandt, University of the Witwatersrand, South Africa
Copyright © 2024 Schlüter and Besser. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dominik Schlüter, ZG9taW5pay5zY2hsdWV0ZXJAbGV1cGhhbmEuZGU=
 Dominik Schlüter
Dominik Schlüter Michael Besser
Michael Besser