- The Science and Technology Education Program, Faculty of Education, Bar-Ilan University, Ramat Gan, Israel
Few scholarly studies have examined gender gaps vis-à-vis various types of mathematical problems by controlling for individual factors (e.g., general intelligence and self-regulated learning [SRL]) and social factors (e.g., the school’s socioeconomic status [SES]) among elementary school students, as addressed in this study. Achievements on three types of mathematical tasks (operations with numbers, geometry, and word problems) and general intelligence scores were obtained from elementary school students. Information regarding students’ SRL was obtained from a rating scale designed for the teachers. Results showed that boys’ achievements were significantly higher in word problem-solving and geometry tests but not in operation with numbers tests. The results concerning word problems suggest that the effect of the school’s SES level on the gender gap decreased in accordance with the increase in the school’s SES level. The significant interaction between gender and SRL indicated that the effect of students’ SRL level on the gender difference in the students’ performance on the geometry test increased in accordance with the increase in the SRL level. General intelligence contributed to individual differences in word problems and geometry, but not on operations with numbers. The analyses showed that SRL contributed to mathematical performance in all tasks. Directions for future research and implications for narrowing these gender gaps are discussed.
1 Introduction
The academic literature is abundant with research exploring the factors that impact students’ mathematics achievements. Researchers around the world have been seeking to understand how various factors impact directly or indirectly—or even intersect—to influence the mathematical performance of students of all ages (Sakiz et al., 2012; Ghasemi et al., 2019). Over the past decade, many studies have investigated the magnitude and variables explaining mathematical achievements. Given that mastering mathematical manipulations and problem-solving requires higher-order thinking, factors relating to cognitive abilities have been widely examined. Intelligence is a prominent factor that has been repeatedly investigated (e.g., Semeraro et al., 2020). Self-regulated learning (SRL), wherein the students plan how to solve a mathematical task, monitor their own processes, and then reflect on the outcome, is an essential factor in successful mathematics learning (Cleary and Kitsantas, 2017). Students’ beliefs have also been found to impact mathematical achievements. Some studies revealed that positive attitudes have been linked to increased school achievement and higher scores on standardized tests (Chen et al., 2018). Another factor is students’ motivation and self-efficacy in mathematics, which were also determined to be predictors of students’ mathematics achievements (Pinxten et al., 2014; Seaton et al., 2014; Cleary and Kitsantas, 2017).
Many variables relating to the students’ developmental and social environment have been identified as dominant predictors of students’ performance in mathematics. One of the best indicators of school performance in general and mathematical achievement in particular is family SES. In 95% of the countries, students with higher family SES performed significantly better on the PISA mathematics test (Chiu and Xihua, 2008; Levpušček et al., 2013). Students from more educated homes performed better on TIMSS than those from less-educated homes (Wiberg, 2019). Parental education and professional occupation are used as SES measures across studies and are considered highly influential factors in students’ mathematical education (Sirin, 2005). Mathematical performance is also related to other SES components, such as family income and educational resources available to the student at home. Moreover, parental involvement has a well-documented role in children’s education (Fan and Williams, 2010). Students with parents who are involved in school events, tend to be more motivated to study and perform better academically than their counterparts with less involved parents (Fan and Williams, 2010). Student-perceived parental and teacher mathematics behavior are influential factors in math achievements (Sakiz et al., 2012). Teachers’ affective and academic support was found to be related to students’ mathematics achievement (Yu and Singh, 2018). School context and the students’ background have an impact on the students’ TIMSS mathematics results (Wiberg, 2019). We have not yet mentioned other factors that impact students’ mathematical performance, such as culture, mathematics anxiety and/or test anxiety, and classroom climate.
A thorough review of the literature shows that very little research examines the relationship between individual and social factors in predicting achievement in mathematics (Levpušček et al., 2013). Therefore, the main aim of this study was to comprehensively examine the gender differences in mathematical achievements and to explore whether individual (i.e., general intelligence and SRL) and social (i.e., SES) factors are related to these differences. The unique feature of this study was the investigation of the gender differences in elementary students’ performance in three types of mathematical tasks: operations with numbers, geometry, and word problems. Investigation of these combined relationships is rare in literature. We chose to conduct this study among young elementary school students. There is broad scholarly agreement that students who do not meet the required learning standards in mathematics by the end of elementary school have a lower chance of succeeding in general mathematics courses in upper secondary school and beyond (Levpušček et al., 2013).
1.1 Gender gaps and mathematical achievements
Gender gaps in mathematical achievements constitute a long-standing, worrisome issue, as scientists attempt to understand the reasons for the low number of women at the top levels in the fields of science, technology, engineering, and mathematics (STEM; Halpern et al., 2007; Cheryan et al., 2017; O’Dea et al., 2018). The existence and magnitude of gender gaps in mathematical performance vary due to numerous factors, including socioeconomic status, nationality, ethnicity, and age (Else-Quest et al., 2010; Steinmayr et al., 2014; Reilly et al., 2015; Hutchison et al., 2019). Moreover, there is evidence that the detection of gender gaps may depend on how mathematics problems are presented to the students, how skills are measured, and the sociocultural experiences children are exposed to (Else-Quest et al., 2010; Miller and Halpern, 2014; Ghasemi and Burley, 2019; Borgonovi and Greiff, 2020). Ghasemi and Burley (2019) conducted a comprehensive study exploring vast international data sets. Their analyses revealed that, there are generally very small differences between genders when it comes to how much they value, enjoy, and are confident in mathematics. The researchers observed that the magnitude of the differences varied among the nations. In addition, an increase in the gender gap was observed between the fourth and eighth grades. Even though the differences were minimal, and the growth was very small, it might indicate a rising trend in gender differences as students grow.
The origin of gender differences in mathematics has also been attributed to sociological influences. Stereotype threat has been shown to have damaging effects on girls’ mathematical performance (Jones and Wheatley, 1990; Doyle and Voyer, 2016). For example, it is possible that girls’ exposure to mathematics differs from boys’, leading to differences in mathematical abilities among school-age children. According to earlier studies (Duffy et al., 2001; Leyva, 2017), math teachers are more likely to encourage boys to ask questions, respond, and explain concepts. There has also been an association between gender gaps in mathematics and parental assessments of their children’s abilities. According to several studies parental expectations of their children’s abilities have been linked to their self-perception of their own abilities and subsequent performance (Jacobs and Eccles, 1992; Bleeker and Jacobs, 2004; Del Río et al., 2019).
Little empirical evidence exists regarding gender gaps in various types of mathematical problems by addressing general intelligence, SES, and SRL capabilities among elementary school students (e.g., Spinath et al., 2014). Addressing these issues is critical, given the importance of understanding how these factors intersect to influence the mathematical performance of young schoolchildren (Ghasemi et al., 2019). Moreover, such an investigation may yield insights into how SES levels are related to gender differences in mathematical achievements.
1.2 Gender differences and similarities in elementary school mathematics
A large corpus of research has documented differences in the mathematical performance of girls and boys. However, these studies’ findings are inconsistent: According to certain research, boys generally did better than girls on mathematical tasks (e.g., Halpern et al., 2007; Zhu, 2007; Gilleece et al., 2010; Robinson and Lubienski, 2011; Reilly et al., 2015; Stoet and Geary, 2018), while others showed a diverse range of gender differences depending on the type of mathematical tasks (e.g., Voyer et al., 1995). Meta-analyses have indicated no differences (Hyde et al., 2008) or only negligible differences (Reilly et al., 2015) in mathematics achievements between boys and girls in Grades 4, 8, and 12. Reilly et al. (2019) presented findings from the 2011 Trends in Mathematics and Science Study (TIMSS), a comprehensive worldwide evaluation of students’ performance in the eighth grade. In the majority of countries, the meta-analysis found minor to moderate gender differences (from d = −0.60 to +0.31). However, several studies did point out the existence of gender differences in mathematical problem-solving (Ben-Chaim et al., 1988; Royer et al., 1999; Gallagher et al., 2000; Zhu, 2007).
According to research, there are age-dependent gender differences in mathematics. When kindergarten begins, there is no discernible difference in boys’ and girls’ mathematical abilities; however, by the end of the year, boys have an obvious advantage (Penner and Paret, 2008; Lubienski et al., 2013). According to Robinson and Lubienski (2011), the average gap between girls and boys peaks at roughly 0.24 standard deviations in the third and fifth grades. Reilly et al.’s (2015) meta-analysis indicated only very slight gender differences in elementary and middle school years, which grew more significant by the last year of high school.
1.3 Gender differences and the type of mathematical problem
Contextual factors, including the type of the mathematical problem being evaluated, may influence gender differences.
1.3.1 Operations with numbers
Prior research suggested that when it came to calculation and arithmetic examinations (i.e., complicated multiplication, simple subtraction, etc.) requiring relatively easy cognitive processes, girls might do just as well as, or perhaps better than, boys (e.g., Hyde et al., 1990; Fennema et al., 1998; Else-Quest et al., 2010; Wei et al., 2012). Girls in the sixth grade outperform boys not only in arithmetic tasks but also in numerosity comparison, number comparison, number series completion, choice reaction time, and word-rhyming tasks (Wei et al., 2012). According to Fennema et al.’s (1998), boys tended to employ more abstract techniques that show conceptual knowledge, whereas girls tended to use more concrete strategies (i.e., modeling and counting) that explain the problem and symbolize its solution. Other studies show that by the end of the third grade, girls use more standard algorithms than boys do (Fennema and Carpenter, 1998; Che et al., 2012; Laski et al., 2013). However, Wei et al. (2016) found that gender differences in arithmetic performance disappeared after controlling for spatial ability.
1.3.2 Word problem-solving
Studies revealed that boys’ advantages in mathematics emerged on tasks requiring higher order cognitive processing, such as complex problem-solving (e.g., Benbow and Stanley, 1983; Hyde et al., 1990; Geary, 1996; Zhu, 2007; Hyde et al., 2008; Else-Quest et al., 2010; Wei et al., 2012). Björn et al.’s (2016) study investigated the gender differences in the relationships between text comprehension and word problem solving in mathematics. The findings demonstrated that proficient reading comprehension in Grade 4 predicted proficient word problem solving in arithmetic at subsequent grade levels. Girls’ success on arithmetic word problems in Grade 9 was predicted by their strong text comprehension abilities in Grade 4. Fatqurhohman’s (2021) study also determined gender differences on mathematical word-problem skills in the seventh grade, indicating that boys outperformed girls. The author suggested that boys comprehension skills, and accuracy regarding word problems are better than that of girls.
1.3.3 Geometry
Geometry is defined as the mathematics of space (Bishop, 1986). Mathematical educators have addressed spatial ability as the element of geometry and suggested that spatial ability is a key determinant in geometry achievement and problem-solving abilities in geometry (Battista, 1990; Gorgorió, 1998; Ubuz et al., 2009; Erdoğan et al., 2011). One domain where gender differences favoring boys are evident is in spatial processing (e.g., Halpern et al., 2007; Levine et al., 2016; Gilligan et al., 2017; Hutchison et al., 2019). Hutchison et al. (2019) suggested that boys (ages 6 to 13) are more prone to rely on spatial strategies while solving fundamental numerical problems. Battista (1990) suggested that in high school geometry, boys and girls differ in spatial visualization and in their performance. The differences emerge in comprehension of basic concepts, techniques, and principles, as well as in the ability to apply comprehension to new situations. However, other studies revealed no gender differences in students thinking levels in geometry in elementary (Bal, 2014) and high school (Alex and Mammen, 2014).
1.4 Factors that contribute to gender gaps in elementary school mathematics
1.4.1 Socioeconomic status
Scholarly literature has defined socioeconomic status (SES) in various ways. SES is commonly represented as the level of parents, income and education and family resources (Sirin, 2005). A majority of academic studies have focused on individual or family SES, corroborating a strong and consistent relationship between SES and learning achievements (Gabriel et al., 2016; White et al., 2016).
SES has been found to be strongly related to achievements in mathematics (Jordan et al., 2007; Penner and Paret, 2008; Cheema and Kitsantas, 2014; Garon-Carrier et al., 2018; Zhu et al., 2018). Recent studies have indicated that students from low SES families outperform those from middle SES families on a range of cognitive tasks related to mathematical achievement (Lee et al., 2016; Zhu et al., 2018). Compared to their low SES peers, children from high SES families typically possess more sophisticated number skills, such as counting, ordering, and comparing numbers, even before entering kindergarten (Starkey et al., 2004). Compared to their peers from high SES backgrounds, children from low SES significantly underperform on tasks involving spatial orientation and spatial visualization (Levine et al., 2005; Dearing et al., 2012; Elliott and Bachman, 2018).
Preschoolers from low SES are less proficient than their higher SES counterparts in naming, manipulating, and reproducing patterns (Starkey et al., 2004). Few studies examined gender variations in spatial abilities among children from low-income families (Levine et al., 2005; Tzuriel and Egozi, 2010; Garon-Carrier et al., 2018).
School SES is the total SES of all students enrolled at a specific school. Research suggests that school SES is a stronger predictor of academic achievement than home SES (Perry and McConney, 2010; Marchant and Finch, 2016). Therefore, this study focused on school SES and examined the relationship between different levels of school SES and young students’ mathematical performances. This study also sought to further examine the differential relationship between different SES groups, and other factors related to student mathematics performance, such as general intelligence and self-regulated learning capabilities.
1.4.2 General intelligence
General intelligence, measured by childhood psychometric test scores, strongly predicts academic achievements (Deary et al., 2007; Calvin et al., 2010; Paz-Baruch, 2020). Intelligence is viewed as a relatively stable characteristic that is influenced by environment and heredity (Sternberg, 1999). Cattell (1963) submitted that general intelligence is a combination of fluid intelligence and crystalized intelligence. Fluid intelligence, the reasoning and problem-solving ability, is strongly related to cognitive abilities such as comprehension and learning, but it does not rely on prior knowledge. Fluid intelligence has been defined as the ability to solve new and complicated problems through mental processes like inference-drawing, concept formation, classification, relation identification, problem-solving, and so forth (Cattell, 1963; Newton and McGrew, 2010).
On the other hand, crystallized intelligence relies on previous experiences, learned procedures, and knowledge. According to several studies, the correlation between fluid intelligence and academic achievements has an effect size of moderate to large (correlation of around 0.50; Neisser et al., 1996; Peng et al., 2019). In their study, Calvin et al. (2010) demonstrated that after controlling for the variance derived from general intelligence, boys’ mean scores on the quantitative residual factor was higher than that of girls (d = 0.28). The authors suggested that gender differences in educational achievements cannot be explained by general cognitive ability. However, boys showed a slight advantage in quantitative reasoning abilities while girls had the advantage in verbal ability. It was these cognitive specializations that contributed to gender differences in elementary school grades.
1.5 Self-regulated learning
The terms metacognition, self-regulation, and self-regulated learning (SRL) are commonly discussed and examined in educational literature (Dinsmore et al., 2008). Metacognition refers to an individual’s knowledge, regulation, and control of the processes of their own cognitive system (Flavell, 1976). Self-regulation pertains to the process by which individuals control their own behavior, thoughts, or emotions (Bandura, 1991). SRL is a complex concept that emphasizes a learner’s proactive engagement (Pintrich, 2004; Zimmerman and Schunk, 2011).
Self-regulated learning emphasizes the active role of the learner (Boekaerts, 1996; Pintrich, 2004; Zimmerman, 2008). SRL involves establishing personal learning goals and working to achieve them. Cognition, metacognition, motivation, affect, and volition are key elements of SRL (Boekaerts, 1996). Different theoretical models of SRL emphasize various components, yet they unanimously define SRL as a comprehensive process encompassing the monitoring and controlling of behavior, cognition, motivation, and the environment (Efklides, 2011).
Numerous SRL frameworks detail how students manage their learning processes (Boekaerts and Niemivirta, 2000; Azevedo et al., 2010). While these models offer varied insights into SRL, they all agree that self-regulated learners are actively involved in constructing knowledge and employ a range of cognitive and metacognitive strategies to oversee and direct their academic achievements (Zimmerman, 2000). Self-regulated students are characterized as those who effectively manage their learning by using strategies that help them succeed in the learning task and are able to assess the usefulness of those strategies (Zimmerman, 2000). Students are described as being self-regulated to the extent that they know and employ a variety of learning strategies, as well as deciding on when, why, and how to use these strategies in appropriate contexts (Zimmerman, 2000; Dent and Koenka, 2016). According to studies, students who practice SRL strategies also score higher on academic tests and other evaluations of their performance and accomplishment (Zimmerman, 2008; Rosário et al., 2013). Studies show that when it comes to completing academic assignments, SRL students are more involved, consistent, and persistent than their low SRL peers (Zimmerman, 2008; Eilam et al., 2009).
Most theoretical models of SRL include distinctive phases (e.g., Pintrich and Zusho, 2002). In the first stage, motivational beliefs and values are employed as students plan their course of action. Setting goals is an important part of this process (Pintrich, 1999). During the second phase, the self-regulated learner chooses and adjusts cognitive strategies suitable for the current task (Pintrich and Zusho, 2002). Additionally, the learner engages in metacognitive processes that provide feedback on the efficacy of a given strategy. The third phase involves the students putting the strategies into practice and monitoring their progress. During the fourth phase, a link between the learning achievement and the strategic process is made. At last, students return to the initial phase and monitor their progress.
Studies on gender differences in students’ use of SRL strategies often favor girls (Pokay and Blumenfeld, 1990; Wolters and Pintrich, 1998; Pajares and Valiante, 2001; Pajares, 2002; Khanal, 2017). For example, Zimmerman and Martinez-Pons (1990), who examined gender differences in students’ use of SRL strategies, revealed that compared to boys, girls were more likely to keep records, use goal-setting and planning techniques, and self-monitor more often. Pokay and Blumenfeld (1990) examined how high school geometry students used SRL strategies. They found that girls reported using more specific, metacognitive, and general cognitive strategies than boys. Girls also reported stronger effort management. Khanal’s (2017) study examined gender differences in learning strategies in mathematics. The results showed that boys preferred to employ elaboration (i.e., summarizing information and putting ideas into their own words), effort management, and critical thinking strategies, whereas girls preferred to use peer learning, help-seeking, and rehearsal strategies. Bezzina’s (2010) study among eleventh-grade students examined gender differences in mathematical performance and in SRL. The study results suggested that the effect of gender on mathematical performance is no longer significant after controlling for students’ use of SRL strategies.
Considerable research has linked SRL strategies and academic achievements (Zimmerman and Schunk, 2011; Dent and Koenka, 2016), but some researchers have started to doubt the suitability of using self-report questionnaires to measure SRL strategy use (Winne and Jamieson-Noel, 2002). Researchers consider new methods as more valid for assessing students SRL in real time (Schellings and Van Hout-Wolters, 2011). Alternative SRL assessment tools include, for example, direct observations (Whitebread et al., 2009; Spektor-Levy et al., 2017), tracing think-aloud protocols (Vandevelde et al., 2015), and rating scales designed for teachers (Cleary and Callan, 2014). For these reasons, we used teachers’ ratings of student SRL capabilities in the current study.
1.6 The current study
This study is a cross-sectional study type in which we analyzed the relations between various data variables gathered from an elementary student population, at a specific point in time (Levin, 2006). The main aim of this study was to comprehensively examine the gender differences in mathematical achievements (in three types of mathematical tasks) and to explore whether they are related to individual (i.e., general intelligence and SRL) and social (i.e., school SES) factors. Our research questions were as follows:
1. Whether and to what extent are there gender differences in mathematical achievements in three types of mathematical tasks among elementary school students?
2. What are the relations between individual factors (i.e., general intelligence and SRL), social factors (i.e., school SES) and gender differences in mathematical achievements in different types of mathematical tasks?
The first research hypothesis was that differences would be found between boys and girls in the three types of mathematical tasks. We hypothesized that girls’ achievements in operations with numbers tasks would be higher than boys. This hypothesis is based on previous studies demonstrating that girls may do as well as, or even better than boys on tests of computation and arithmetic tasks (e.g., Fennema et al., 1998; Else-Quest et al., 2010; Wei et al., 2012; Räsänen et al., 2021). We also assumed that boys’ achievements in word problems and geometry would be higher than girls. This hypothesis is based on previous studies regarding boys’ higher spatial processing, which affect their geometry performance (e.g., Levine et al., 2016; Gilligan et al., 2017) and studies regarding boys higher mathematical word problems skills (Fatqurhohman, 2021).
The second research hypothesis was that the gender gaps would be related to individual (i.e., general intelligence and SRL) and social (i.e., school SES) factors. We assumed that SES, students’ general intelligence, and SRL capabilities would impact the gender gaps on each mathematical task, which means that SES, SRL, and general intelligence will moderate the gender gaps on each mathematical task. This hypothesis is based on previous studies addressing the relations between SES and students’ mathematical performance (Lee et al., 2016; Zhu et al., 2018) and studies regarding the importance of SRL strategy use and the impact of general intelligence on gender gaps in mathematical performance (Bezzina, 2010; Peng et al., 2019).
This study may contribute to the large body of studies in this field based on our deliberate attempt to include individual and social factors that may contribute to gender gaps in various mathematical tasks. To date, only a few studies have examined elementary students’ mathematics achievements through a multidimensional lens (Moon et al., 2022). Very few studies have included individual factors such as general intelligence and SRL capabilities to elucidate certain gender differences in a variety of elementary school mathematical tasks. Some studies have separately examined the contribution of SES (e.g., Lee et al., 2016) or SRL (Pokay and Blumenfeld, 1990; Bezzina, 2010) to gender gaps in mathematics. The present study investigated the relations between these variables (general intelligence, SRL capabilities, and SES) and gender differences in various areas of mathematical achievement among young students. Moreover, the results of this study may inform researchers and policymakers on how to narrow the gender gap in mathematics education in elementary grades and beyond.
2 Method
2.1 Participants
The sample size was determined a priori by using the G*power software. For conducting a one-way MANOVA analysis, using the test parameters (low effect size = 0.10, α error = 0.05, power = 0.90, two study groups and three response variables), the total sample size required was 146 participants. In order to increase the power and sensitivity, the present study included 170 participants (91 boys and 79 girls; mean age = 10.70, SD = 0.4).
The study had a negligible percentage of outliers, which were removed from the sample (5 participants). Another 4 participants were removed because not all the tests were completed.
The students were sampled from seven elementary schools: two schools from low SES areas (n = 42, 24.7%), three schools from middle SES areas (n = 83, 48.8%), and two schools from high SES areas (n = 45, 26.5%).
The students were from an urban area in Israel. In Israel, there are distinct educational programs for Jewish and secular students as well as for Arab students. Both public and private schools are included in each sector. The students in the study were from the Jewish secular sector. The participants had no learning disabilities or visual impairment.
We obtained the schools’ SES levels from the Ministry of Education’s Nurturing Index, a social and economic status index that rates schools based on a combination of factors including parental education, immigration status, geographic location, and a school-level income measure (i.e., the median parental income of families in the school). The index values range from 1 to 10. The higher the school’s score, the more funding the school is eligible for. Accordingly, in the present study, school values of 1–2 represented high SES, school values of 3–7 represented middle SES, and school values of 8–10 represented low SES. No significant difference in the gender distribution was found between the three SES levels, χ2(1) = 1.55, p = 0.460.
2.2 Measures
2.2.1 Raven’s standard progressive matrix
The Raven’s Standard Progressive Matrices (RSPM; Raven et al., 2000) test is used to evaluate mental ability related to abstract reasoning and is recognized as a nonverbal evaluation of fluid intelligence. The short version of the test was used to examine students’ general intelligence. Correlations (from r = 0.66 to r = 0.91) between the shortened version and the full version were found in previous studies (Arthur and Day, 1994; Bors and Stokes, 1998; Hamel and Schmittmann, 2006; Bilker et al., 2012).
In the RSPM, participants are presented with puzzles containing visual patterns with a piece missing. For each item, the participant is instructed to identify the missing piece from a given selection of eight possibilities. The short version of the RSPM contains 30 items. The time limit is 15 min. The score for each correct response is one point and for incorrect response, zero point.
2.2.2 Teacher’s rating scale of students’ SRL capabilities
The teacher’s rating scale was based on the short version of the Nuremberg Gifted Identification Checklist (NGIC; Harder et al., 2015). The reliability, objectivity, and validity of the rating scale were previously investigated by Harder et al. (2015), who revealed that it is of a high diagnostic quality.
10 NGIC items examining self-regulated learning capabilities were used for this study. Each item was presented as a statement of positive learning capability. For example: “The student has above-average verbal skills of expression”; “This student has effective learning strategies”; “This student has the necessary resources (e.g., time management capabilities and learning opportunities) to improve their skill level in a new domain”; “This student sets personally challenging learning goals and is motivated to attain them.” Teachers could choose one of three responses: “not true,” “partly true,” and “totally true.” The Cronbach’s alpha reliability coefficient in this study was 0.923.
2.2.3 Mathematical achievement
The mathematical achievement tests included three types of mathematical tasks: operations with numbers, word problems, and geometry. The tests were specially designed for this study and were based on the national mathematics curriculum and a nationwide standardized test. Some of the tasks were adapted from the Growth and Effectiveness Measures for Schools exams, the National Authority for Measurement and Assessment in Education (RAMA), Ministry of Education, Israel (see Table 1).
2.2.3.1 Operations with numbers
Operations with numbers included seven tasks of four operations with whole numbers (addition, subtraction, multiplication, and division); comprehension of the place value system and mixed operations (where different operations need to be coordinated). The scoring of each task was based on the difficulty level: low-level exercises received lower scores (i.e., simple addition and subtraction), moderate-level exercises received higher scores (i.e., multiplication and division), and high-level tasks received the highest score (i.e., mixed operations: multiplying first and then adding). The total score for the test was 100. The Cronbach’s alpha reliability of this subtest was 0.61.
2.2.3.2 Word problems
The test included eight word problems: multistep word problems, inquiry problems, process-thinking questions (including the ability to connect concepts, adapt a mathematical model to a verbal situation, and find the solution based on insight), open search, and reasoning problems. The scoring of each word problem was based on the difficulty level: low-level word problems received lower scores (i.e., adapt a mathematical model to a verbal situation and multistep word problems), and high-level word problems received the highest score (i.e., open search, and reasoning problems). The total score for the test was 100. The Cronbach’s alpha reliability of this subtest was 0.74.
2.2.3.3 Geometry
The test included five questions that required identifying the area and perimeter of a square and triangles and recognizing angles by using process thinking (application and insight). The scoring of each task was based on the difficulty level: low-level tasks received lower scores (i.e., recognizing types of angles) and high-level tasks received the highest score (i.e., identifying the area and perimeter of a square by using process thinking). The total score for the test was 100. The Cronbach’s alpha reliability of this subtest was 0.70.
2.3 Procedures
Mathematical measures and general intelligence tests were administered to the participants in two 50-min sessions. The tests were administered to the participants in small groups of (5–6 students) during school hours in a quiet classroom at school. The students could not use calculators during the mathematical test. School teachers completed the rating scale of students’ SRL capabilities after receiving parental approval.
The study was approved by the Ministry of Education’s ethical committee. All participants were volunteers and could withdraw from the study at any point. The students and their parents signed informed consent forms.
3 Results
Prior to examining the research questions, we used Shapiro–Wilk tests to determine whether these variables were normally distributed, because the three mathematical tasks had large standard deviations. The results showed that the variables were not normally distributed among both boys and girls (p < 0.05). Therefore, we conducted both non-parametric and parametric analyses. The Mann–Whitney test served as the non-parametric analysis to examine the differences between boys and girls in each mathematical task. The findings and the significance level of the non-parametric analysis matched the findings of the parametric analysis. Therefore, we presented the findings of the MANOVAs and reported the Means and Standard Deviations instead of the Means and Sum ranks among each gender group. In addition, Levene’s test of equality indicated that the assumption of equality of variance was confirmed. Furthermore, multicollinearity testing revealed no multicollinearity problem between the independent variables (the tolerance was greater than 0.1, and VIF was smaller than 10).
In order to examine the first question in the current study regarding whether significant differences would be found between boys and girls in mathematical achievements, one-way MANOVA analysis was conducted. In order to examine the second research question regarding the relations between individual (i.e., general intelligence and SRL) and social (i.e., school SES) factors and the gender gaps in mathematical achievements, first, we examined the correlations between these factors and the students’ mathematical achievements. Afterwards, mixed effect modeling analyses (MLM analyses) were conducted to examine the contribution of both individual and social factors to students’ mathematical achievements. MLM analyses were conducted since the school is a random factor with students nested by school.
3.1 Gender differences in mathematical achievements in three types of mathematical tasks
Prior to examining the first research question regarding the gender differences in mathematical achievements, the gender differences were examined for the students’ performance on general intelligence and their SRL level. No significant gender differences were found in both general intelligence and SRL measures, F(1,168) = 0.00, p = 0.979, ηp2 = 0.00 and F(1,168) = 0.43, p = 0.512, ηp2 = 0.00, respectively. Namely, the students’ performance on general intelligence and their SRL level did not differ between boys and girls (Table 2).
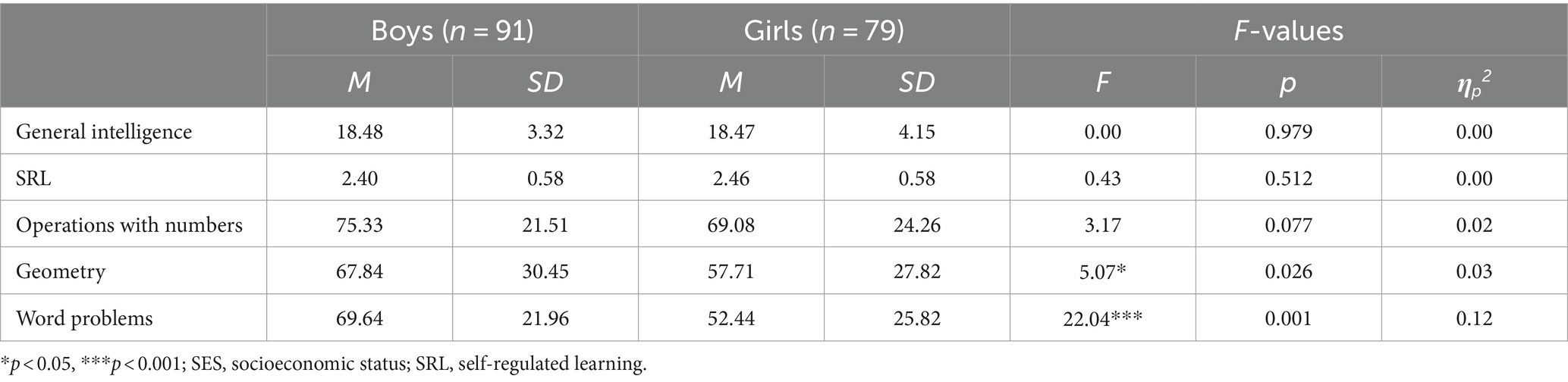
Table 2. Mean, SD, and F-values of students’ general intelligence, SRL, and performance on the three mathematical performance tests, by gender.
In order to examine whether significant differences would be found between boys and girls in the three mathematical tests, one-way MANOVA analysis was conducted. The independent variable was gender, and the dependent variables were the students’ performance on the operations with numbers, geometry, and word problems tests. A significant gender difference was found in the performance on the overall score of the combined mathematical test, F(3,166) = 7.54, p < 0.001, ηp2 = 0.12. A separate one-way ANOVA for each mathematical test indicated that boys outperformed girls in word problem solving test and in the geometry test, [F(1,168) = 22.04, p < 0.001, ηp2 = 0.12 and F(1,168) = 5.07, p = 0.026, ηp2 = 0.03, respectively]. The difference between boys and girls in the performance on the operation with numbers test did not reach a level of significance, F(1,168) = 3.17, p = 0.077, ηp2 = 0.02 (see Table 2).
3.2 Relations between individual factors, social factors, and gender differences in mathematical achievements in different types of mathematical tasks
Prior to examining the second research question regarding the relations between individual (i.e., general intelligence and SRL), social (i.e., school SES) factors and gender differences, Pearson correlation analyses were conducted between the students’ performance on general intelligence and their SRL level and their performance on the three mathematical tests (see Table 3).
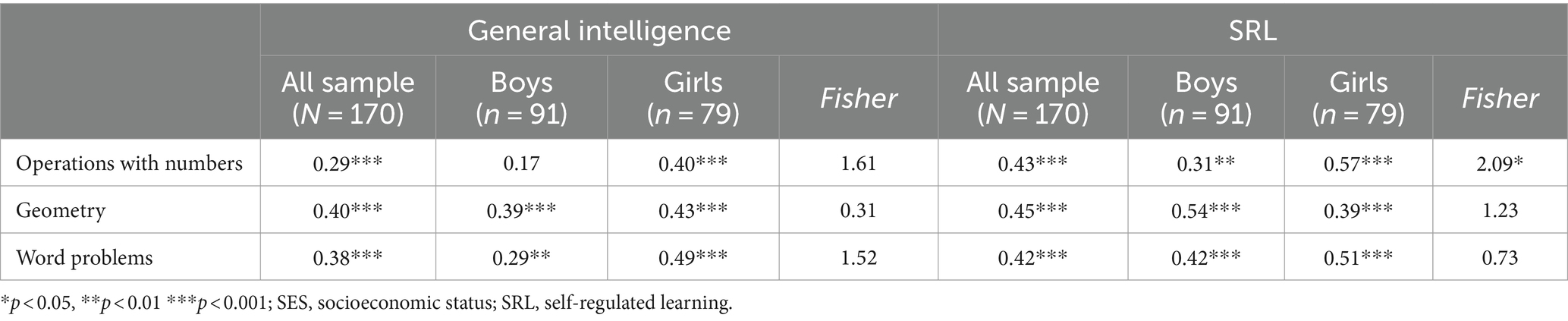
Table 3. Pearson correlation coefficients between students’ general intelligence, SRL, and performance on the three mathematical tests.
As can be seen in Table 3, the students’ performance on the general intelligence test and their SRL level significantly correlated with their performance on the three mathematical tests. In addition, Fisher r-to-z transformation indicated that the correlation coefficient between the students’ SRL level and their performance on the operation with numbers test was significantly higher among girls compared to boys (Fisher z = 2.09, p = 0.037). However, Fisher r-to-z transformation indicated that the correlation coefficient of the three mathematical tests and students’ general intelligence were not significant.
In order to examine the relations between the individual (general intelligence and SRL), social (school SES), and gender differences in mathematical achievements, we conducted mixed-effect modeling (MLM analysis) using the package lme4 in R. The students’ gender, their performance on the general intelligence test, and their SRL level were the fixed factors and the students’ level, and SES was the fixed factor at the school level. The school was the random factor, with students nested by school. For each mathematical test, we examined three models. The zero-model was conducted to assess the effect size for random effects, which was demonstrated using the ICC value (Lorah, 2018). The zero-model indicated ICC of almost 10% and above, which is considered high enough for MLM to be used. The first model examined only the gender differences in each mathematical test, controlling for the school random effect. The results of the first model indicated the same results of the one-way ANOVA analysis, which is presented in this section. This result indicated that boys outperformed girls in the word problem-solving and the geometry tests after controlling for the school random effect. The second model examined the effect of all fixed factors (at the student and school levels) on each mathematical test, controlling for the school random effect. The results of the second model regarding gender differences indicated the same results of the ANOVA analysis, according to which boys outperformed girls on the word problem-solving and geometry tests after controlling for the school random effect. Per the results of the Pearson correlation analyses, the students’ SRL level significantly correlated with their performance on all three mathematical tests. In addition, the students’ performance on the general intelligence test significantly correlated with their performance on the geometry and word problems tests. Finally, the SES of the school significantly correlated with the students’ performance on the word problem test, indicating that higher SES schools performed better on the word problem test.
Because we sought to explore the relations between individual (general intelligence and SRL), social (school SES) factors and gender differences, the final model (the third model) examined the interaction effects between these three factors and gender. The results indicated a significant interaction between gender and SRL regarding the students’ performance on the geometry test and a significant interaction between gender and SES regarding the students’ performance on the word problems test. The significant interaction between gender and SRL indicated that the coefficient of the effect of the students’ SRL level on the gender difference in the students’ performance on the geometry test increased in accordance with the increase in the SRL level (For 1SD below average in the SRL level: B = −22.60, S.E. = 20.21; for average in the SRL level: B = −32.19, S.E. = 22.10 and for 1SD above average in the SRL level: B = −41.78, S.E. = 24.63). The significant interaction between gender and SES indicated that the coefficient of the effect of the school SES level on the gender difference in the students’ performance on the word problems test decreased in accordance with the increase in the school’s SES level (For low SES: B = −43.74, S.E. = 16.37; for mediocre SES level: B = −30.90, S.E. = 17.43 and for high SES level: B = −18.07, S.E. = 19.45) (Table 4).
4 Discussion
Scholarly literature offers a plethora of studies on the stereotypic masculine nature of mathematics. This stereotype affects how teachers teach and how well students learn (Steffens and Jelenec, 2011; OECD, 2015). Thus, it is crucial to understand the factors that may lead to gender gaps in mathematics achievement as early as elementary school, as well as how these factors intersect (Ghasemi et al., 2019).
4.1 Gender differences in different mathematical tasks
Our study is unique in that we examined gender differences in various types of mathematical problems and how they are related to individual (i.e., general intelligence and SRL) and social (i.e., school SES) factors among young students. Our results revealed gender differences in elementary school mathematical performance on word problem-solving and geometry tests but not on the operation with numbers test. As we assumed, boys outperformed girls in the word problem-solving and geometry tests. These findings are in line with the variability hypothesis which holds that men represent more variability than women on various psychological constructs. More male variability indicates that often, more boys reach extremely high scores (Stevens and Haidt, 2017). Further studies are needed to explore gender differences in achievements in various types of mathematical tasks among young students.
Our results suggest that boys were similar to girls on operations with numbers tasks. These results corroborate previous studies indicating that girls perform as well as, or better than boys on tests of calculation and arithmetic tasks that require relatively simple cognitive processes (e.g., Hyde et al., 1990; Fennema et al., 1998; Else-Quest et al., 2010; Wei et al., 2012; Räsänen et al., 2021). Our study results support previous conclusions of previous studies that boys and girls are equally equipped with basic numerical competencies, which could assist them in acquiring complex mathematical skills (Hutchison et al., 2019; Räsänen et al., 2021).
As revealed in previous studies (e.g., Kikas et al., 2020), gender differences in students’ word problem-solving were also found in our study. Previous studies suggested that the gender disparity in mathematical problem-solving derives from the fact that girls use more concrete strategies that illustrate the problem and represent its solution, while boys occasionally use more abstract strategies, and tend to be more flexible in using strategies for complex and challenging problems compare to girls (Fennema et al., 1998; Zhu, 2007).
In the current study, boys’ performance on geometry tasks was greater than girls’. These results corroborate previous studies showing that as boys’ visual–spatial ability is better than girls’, and that boys usually perform better on geometry tasks (Gilligan et al., 2017; Hutchison et al., 2019). The results of the current study add to the existing literature concerning elementary school children, as most of the previous studies were conducted among junior high and high school children.
4.2 The interrelations between general intelligence, SRL, school SES, and gender differences in mathematical achievements
Our results partly support our second hypothesis that the gender gap increases when the level of school SES increases. The gender differences on word problems are especially prevalent among low SES students. A possible explanation may be related to low SES girls’ mathematics self-perception. Previous studies found that girls from high SES have higher mathematics self-perception than girls from low SES (del Río et al., 2019). The results concur with those of other studies (e.g., Penner and Paret, 2008; Wang et al., 2014; Zhu et al., 2018) that reported a strong SES influence on students’ mathematical achievements across all age groups. Bessudnov and Makarov’s (2015) study showed that boys’ advantage in mathematical performance tests was significantly greater in schools of a higher SES, with more advanced curricula. We suggest that future studies further examine the impact of low SES girls’ mathematics self-efficacy on their mathematics problem-solving abilities. It seems that the role of gender in students’ mathematics learning can be modified when considering societal factors. Furthermore, the results highlight the need for intervention programs in mathematics for girls from low-SES environments, or guidance for parents from low-SES environments. Such early interventions may have profound effects on the children’s future development.
Surprising results were found regarding the interactions between gender and SRL regarding geometry tasks. The results indicated that the gender gap increases when the level of SRL increases. It seems that high SRL capabilities assist boys’ geometry performance in particular compared to girls’. These results are inconsistent with Bezzina’s (2010) study, which suggested that using SRL strategies diminishes gender differences in mathematical performance among high school students. As previous studies suggested that boys usually use fewer SRL strategies during mathematical tasks (Guo et al., 2021), the current study’s findings strengthen the existing theoretical knowledge concerning the contribution of SRL capabilities to boys’ geometry performance in elementary school and offer valuable information to mathematics teachers that using SRL strategies in geometry tasks could narrow the gap between boys and girls.
The study results revealed no interaction between gender and SES regarding geometry achievements. This contradicts our hypothesis and previous reports on differences between children from low and high SES backgrounds on visual–spatial abilities (Starkey et al., 2004; Levine et al., 2005; Tzuriel and Egozi, 2010; Johnson et al., 2022). The discrepancy can be attributed to the fact that the geometry tasks used in the study were based on the fifth-grade curriculum and did not include mental rotation or highly demanding visual–spatial processing. Future studies should examine the impact of SES on students’ performance in geometry using tasks of varied levels of difficulty.
We found that general intelligence contributed to individual differences on word problems and geometry but not on operations with numbers. One possible explanation for this finding is that operations with numbers tasks require only technical procedures and not the higher-order thinking skills posed by word problems and geometry tasks, which also require strategic thinking. Previous research has shown that preschool children’s performance in arithmetic computation and word problems was predicted by nonverbal intelligence (Wong and Ho, 2017). However, in another study by Campos et al. (2013) on elementary school children, general cognitive ability was not significant in the regression analysis predicting word problem scores. The authors suggested that selective attention play significant role in solving word problems. Accordingly, we recommend that future studies examine the contribution of working memory, selective attention, and executive functions to student performance on diverse mathematical tasks.
Our study’s analyses showed that SRL capabilities contribute to student performance in all mathematical tasks. These results underscore the importance of SRL in determining successful learning experiences in mathematics (Montague, 2008; Rosenzweig et al., 2011; Schunk and Greene, 2018). Previous studies have also suggested that one way to promote mathematical problem-solving is to help students regulate their learning (De Corte et al., 2000; Zimmerman and Schunk, 2011; Desoete and De Craene, 2019; Gidalevich and Kramarski, 2019). Word problem-solving is considered a major obstacle for students as it involves reading comprehension and the activation of various executive function components; that is, to solve word problems, a student must have a conceptual understanding of the problem and then translate the concept into the relevant arithmetical exercise (Lewis and Mayer, 1987; Hegarty et al., 1992; Nortvedt, 2011; Viterbori et al., 2017; Pongsakdi et al., 2020). It seems that students’ abilities to plan ahead before starting to solve the problem, choose the right strategy, and self-monitor the solution process are critical for the attainment of high mathematical performance (Mevarech et al., 2018; Kramarski et al., 2021). Because SRL capabilities are still developing at the age of 10 years (about fifth grade; Dignath et al., 2008; Hanin and Van Nieuwenhoven, 2020) and may differ between boys and girls (Heirweg et al., 2019), future studies should further examine the relationship between SRL capabilities and word problem-solving in arithmetic at this age with a larger sample of children.
4.3 Limitations
It is important to recognize some limitations of the current study. First, because only one cohort of seven schools was tested in the current study, it would be interesting to conduct an extended study designed with a large number of children, in which a variety of mathematical abilities are assessed. Second, we were able to assess students’ performance across a range of mathematical domains thanks to the utilization of diverse mathematical tasks. However, in order to fully understand gender differences in students’ learning strategies during problem-solving in mathematics, it is recommended that future studies use qualitative research tools such as interviews and observations with students.
Furthermore, this study did not examine other factors that impact students’ mathematical performance, such as culture, mathematics anxiety, test anxiety, and classroom climate. Although the scope of this paper cannot cover every eventuality, further studies may explore the interrelations between other factors that may relate to elementary students’ achievements in various types of mathematical problems.
Finally, in the study, we intentionally used teachers’ ratings of students’ SRL capabilities and not students’ self-report questionnaires to avoid overreliance on student reports. However, it is possible that the teachers’ ratings were biased due to prior knowledge of their students’ skills and/or anticipated performance. We suggest that future research employ thinking-aloud methods, interviews, and observations to investigate SRL components in different ways. Such methods could support findings concerning the impact of SRL components on mathematical achievement.
4.4 Educational implications
The following educational implications and recommendations on how to modify and narrow the gender gap in mathematics can be inferred from the study’s findings: First, we suggest designing an intervention program for in-service educators in mathematics. The program should address the variables leading to gender differences in mathematics. It is recommended that program instructors will collaborate with teachers to devise effective teaching strategies aimed at reducing gender differences in mathematics across various areas of mathematics. Second, seminars and lectures should be designed for parents (especially from a low SES environment). These parental programs should explain the impact of stereotypes on gender differences in mathematics and address the importance of the home environment in reducing gender differences in mathematics, such as playing mathematical games from an early age and engaging young children in mathematical discourse. Third, the current study’s findings underscore the importance of providing teachers with guidance to generate a class climate that encourages students to ask questions in class and exposes all students to female role models in STEM disciplines. Furthermore, as mentioned above in the Discussion, the study underscores the necessity of intervention programs in mathematics, adapted to address learning strategies for girls from low SES environments (Russo and Hopkins, 2017; Wang and Degol, 2017). Thus, we recommend the following teaching strategies: teaching mathematics via the lens of a story, providing practical math activities that students can relate to everyday situations, and adopting cooperative learning strategies that enhance confidence in mathematics abilities.
5 Conclusion
Identifying key factors of success plays an important role in efforts to improve academic performance. This study provides new insights related to gender heterogeneity, effective factors and the importance of these factors to ensure gender equality in mathematics achievements. In general, the present study highlights the importance of developing effective learning strategies while solving mathematical tasks. The findings could provide educators and instructional designers with new insights, allowing them to enhance their planning of effective educational programs tailored to improve all students’ achievements and narrow the gender gaps in elementary school mathematical performance.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving humans were approved by Ministry of Education ethical committee. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin.
Author contributions
NP-B: Conceptualization, Formal analysis, Investigation, Methodology, Project administration, Supervision, Validation, Writing – original draft, Writing – review & editing. OS-L: Conceptualization, Formal analysis, Investigation, Methodology, Project administration, Supervision, Validation, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alex, J. K., and Mammen, K. J. (2014). Gender differences amongst south African senior secondary school learners' geometric thinking levels. Mediterr. J. Soc. Sci. 5, 1908–1915. doi: 10.5901/mjss.2014.v5n20p1908
Arthur, W. Jr., and Day, D. V. (1994). Development of a short form for the Raven advanced progressive matrices test. Educ. Psychol. Meas. 54, 394–403. doi: 10.1177/0013164494054002013
Azevedo, R., Moos, D. C., Johnson, A. M., and Chauncey, A. D. (2010). Measuring cognitive and metacognitive regulatory processes during hypermedia learning: issues and challenges. Educ. Psychol. 45, 210–223. doi: 10.1080/00461520.2010.515934
Bal, A. P. (2014). Predictor variables for primary school students related to van Hiele geometric thinking. J. Theory Practice Educ. 10, 259–278.
Bandura, A. (1991). Social cognitive theory of self-regulation. Organ. Behav. Hum. Decis. Process. 50, 248–287. doi: 10.1016/0749-5978(91)90022-L
Battista, M. T. (1990). Spatial visualization and gender differences in high school geometry. J. Res. Math. Educ. 21, 47–60. doi: 10.2307/749456
Benbow, C., and Stanley, J. (1983). Sex differences in mathematical reasoning ability: more facts. Science 222, 1029–1031. doi: 10.1126/science.6648516
Ben-Chaim, D., Lappen, G., and Houang, R. T. (1988). The effect of instruction on spatial visualization skills of middle school boys and girls. Am. Educ. Res. J. 25, 51–71. doi: 10.3102/00028312025001051
Bessudnov, A., and Makarov, A. (2015). School context and gender differences in mathematics performance among school graduates in Russia. Int. Stud. Sociol. Educ. 25, 63–81. doi: 10.1080/09620214.2014.1000937
Bezzina, F. H. (2010). Investigating gender differences in mathematics performance and in self-regulated learning. Equal. Divers. Inclus. 29, 669–693. doi: 10.1108/02610151011074407
Bilker, W. B., Hansen, J. A., Brensinger, C. M., Richard, J., Gur, R. E., and Gur, R. C. (2012). Development of abbreviated nine-item forms of the Raven's standard progressive matrices test. Assessment 19, 354–369. doi: 10.1177/1073191112446655
Bishop, A. J. (1986). What are some obstacles to learning geometry. Studies in Mathematics Education. 5, 141–159.
Björn, P. M., Aunola, K., and Nurmi, J. E. (2016). Primary school text comprehension predicts mathematical word problem-solving skills in secondary school. Educ. Psychol. 36, 362–377. doi: 10.1080/01443410.2014.992392
Bleeker, M. M., and Jacobs, J. E. (2004). Achievement in math and science: do mothers' beliefs matter 12 years later? J. Educ. Psychol. 96, 97–109. doi: 10.1037/0022-0663.96.1.97
Boekaerts, M. (1996). Self-regulated learning at the junction of cognition and motivation. Eur. Psychol. 1, 100–112. doi: 10.1027/1016-9040.1.2.100
Boekaerts, M., and Niemivirta, M. (2000). “Self-regulated learning: finding a balance between learning goals and ego-protective goals” in Handbook of self-regulation (Cambridge, MA: Academic Press), 417–450.
Borgonovi, F., and Greiff, S. (2020). Societal level gender inequalities amplify gender gaps in problem solving more than in academic disciplines. Intelligence 79:101422. doi: 10.1016/j.intell.2019.101422
Bors, D. A., and Stokes, T. L. (1998). Raven's advanced progressive matrices: norms for first-year university students and the development of a short form. Educ. Psychol. Meas. 58, 382–398. doi: 10.1177/0013164498058003002
Calvin, C. M., Fernandes, C., Smith, P., Visscher, P. M., and Deary, I. J. (2010). Sex, intelligence and educational achievement in a national cohort of over 175,000 11-year-old schoolchildren in England. Intelligence 38, 424–432. doi: 10.1016/j.intell.2010.04.005
Campos, I. S., Almeida, L. S., Ferreira, A. I., Martinez, L. F., and Ramalho, G. (2013). Cognitive processes and math performance: a study with children at third grade of basic education. Eur. J. Psychol. Educ. 28, 421–436. doi: 10.1007/s10212-012-0121-x
Cattell, R. B. (1963). Theory of fluid and crystallized intelligence: a critical experiment. J. Educ. Psychol. 54, 1–22. doi: 10.1037/h0046743
Che, M., Wiegert, E., and Threlkeld, K. (2012). Problem solving strategies of girls and boys in single-sex mathematics classrooms. Educ. Stud. Math. 79, 311–326. doi: 10.1007/s10649-011-9346-x
Cheema, J. R., and Kitsantas, A. (2014). Influences of disciplinary classroom climate on high school student self-efficacy and mathematics achievement: a look at gender and racial–ethnic differences. Int. J. Sci. Math. Educ. 12, 1261–1279. doi: 10.1007/s10763-013-9454-4
Chen, L., Bae, S. R., Battista, C., Qin, S., Chen, T., Evans, T. M., et al. (2018). Positive attitude toward math supports early academic success: Behavioural evidence and neurocognitive mechanisms. Psychol. Sci. 29, 390–402. doi: 10.1177/0956797617735528
Cheryan, S., Ziegler, S. A., Montoya, A. K., and Jiang, L. (2017). Why are some STEM fields more gender balanced than others? Psychol. Bull. 143, 1–35. doi: 10.1037/bul0000052
Chiu, M. M., and Xihua, Z. (2008). Family and motivation effects on mathematics achievement: analyses of students in 41 countries. Learn. Instr. 18, 321–336. doi: 10.1016/j.learninstruc.2007.06.003
Cleary, T. J., and Callan, G. L. (2014). Student self-regulated learning in an urban high school: predictive validity and relations between teacher ratings and student self-reports. J. Psychoeduc. Assess. 32, 295–305. doi: 10.1177/0734282913507653
Cleary, T. J., and Kitsantas, A. (2017). Motivation and self-regulated learning influences on middle school mathematics achievement. Sch. Psychol. Rev. 46, 88–107. doi: 10.1080/02796015.2017.12087607
De Corte, E., Verschaffel, L., and Op'tEynde, P. (2000). “Self-regulation: a characteristic and a goal of mathematics education” in Handbook of self-regulation. eds. M. Boekaerts, P. R. Pintrich, and M. Zeidner (Cambridge, MA: Academic Press), 687–722.
Dearing, E., Casey, B. M., Ganley, C. M., Tillinger, M., Laski, E., and Montecillo, C. (2012). Young girls' arithmetic and spatial skills: the distal and proximal roles of family socioeconomics and home learning experiences. Early Child. Res. Q. 27, 458–470. doi: 10.1016/j.ecresq.2012.01.002
Deary, I. J., Strand, S., Smith, P., and Fernandes, C. (2007). Intelligence and educational achievement. Intelligence 35, 13–21. doi: 10.1016/j.intell.2006.02.001
del Río, M. F., Strasser, K., Cvencek, D., Susperreguy, M. I., and Meltzoff, A. N. (2019). Chilean kindergarten children's beliefs about mathematics: family matters. Dev. Psychol. 55, 687–702. doi: 10.1037/dev0000658
Dent, A. L., and Koenka, A. C. (2016). The relation between self-regulated learning and academic achievement across childhood and adolescence: a meta-analysis. Educ. Psychol. Rev. 28, 425–474. doi: 10.1007/s10648-015-9320-8
Desoete, A., and De Craene, B. (2019). Metacognition and mathematics education: an overview. ZDM 51, 565–575. doi: 10.1007/s11858-019-01060-w
Dignath, C., Buettner, G., and Langfeldt, H. P. (2008). How can primary school students learn self-regulated learning strategies most effectively? A meta-analysis on self-regulation training programmes. Educ. Res. Rev. 3, 101–129. doi: 10.1016/j.edurev.2008.02.003
Dinsmore, D. L., Alexander, P. A., and Loughlin, S. M. (2008). Focusing the conceptual lens on metacognition, self-regulation, and self-regulated learning. Educ. Psychol. Rev. 20, 391–409. doi: 10.1007/s10648-008-9083-6
Doyle, R. A., and Voyer, D. (2016). Stereotype manipulation effects on math and spatial test performance: a meta-analysis. Learn. Individ. Differ. 47, 103–116. doi: 10.1016/j.lindif.2015.12.018
Duffy, J., Warren, K., and Walsh, M. (2001). Classroom interactions: gender of teacher, gender of student, and classroom subject. Sex Roles J. Res. 45, 579–593. doi: 10.1023/A:1014892408105
Efklides, A. (2011). Interactions of metacognition with motivation and affect in self-regulated learning: the MASRL model. Educ. Psychol. 46, 6–25. doi: 10.1080/00461520.2011.538645
Eilam, B., Zeidner, M., and Aharon, I. (2009). Student conscientiousness, self-regulated learning, and science achievement: an explorative field study. Psychol. Sch. 46, 420–432. doi: 10.1002/pits.20387
Elliott, L., and Bachman, H. J. (2018). SES disparities in early math abilities: the contributions of parents' math cognitions, practices to support math, and math talk. Dev. Rev. 49, 1–15. doi: 10.1016/j.dr.2018.08.001
Else-Quest, N. M., Hyde, J. S., and Linn, M. C. (2010). Cross-national patterns of gender differences in mathematics: a meta-analysis. Psychol. Bull. 136, 103–127. doi: 10.1037/a0018053
Erdoğan, A., Baloğlu, M., and Kesici, Ş. (2011). Gender differences in geometry and mathematics achievement and self-efficacy beliefs in geometry. Eurasian J. Educ. Res. 2, 1–10.
Fan, W., and Williams, C. M. (2010). The effects of parental involvement on students' academic self-efficacy, engagement and intrinsic motivation. Educ. Psychol. 30, 53–74. doi: 10.1080/01443410903353302
Fatqurhohman, F. (2021). Characteristics of students in resolving word problems based on gender. J. Educ. Learn. Math. Res. 2, 1–10. doi: 10.37303/jelmar.v2i1.42
Fennema, E., and Carpenter, T. P. (1998). New perspectives on gender differences in mathematics: an introduction. Educ. Res. 27, 4–5. doi: 10.3102/0013189X027005004
Fennema, E., Carpenter, T. P., Jacobs, V. R., Franke, M. L., and Levi, L. W. (1998). A longitudinal study of gender differences in young children's mathematical thinking. Educ. Res. 27, 4–5.
Flavell, J. (1976). “Metacognitive aspects of problem solving” in The nature of intelligence. ed. L. Resnick (Hillsdale, NJ: Lawrence Erlbaum), 231–236.
Gabriel, M., Muasya, I., Mwangi, J., Mukhungulu, M., and Ewoi, L. (2016). The influence of parental socioeconomic status, involvement in learning activities and its influence on children's academic performance in urban informal settlements in Westlands division—Nairobi County. Int. J. Educ. Soc. Sci. 3, 54–65.
Gallagher, A. M., DeLisi, R., Holst, P. C., McGillicuddy-DeLisi, A. V., Morely, M., and Cahalan, C. (2000). Gender differences in advanced mathematical problem solving. J. Exp. Child Psychol. 75, 165–190. doi: 10.1006/jecp.1999.2532
Garon-Carrier, G., Boivin, M., Lemelin, J. P., Kovas, Y., Parent, S., Séguin, J. R., et al. (2018). Early developmental trajectories of number knowledge and math achievement from 4 to 10 years: low-persistent profile and early-life predictors. J. Sch. Psychol. 68, 84–98. doi: 10.1016/j.jsp.2018.02.004
Geary, D. (1996). Sexual selection and sex differences in mathematical abilities. Behavi. Brain Sci. 19, 229–247. doi: 10.1017/S0140525X00042400
Ghasemi, E., and Burley, H. (2019). Gender, affect, and math: a cross-national meta-analysis of trends in international mathematics and science study 2015 outcomes. Large-scale Assess. Educ. 7, 1–25. doi: 10.1186/s40536-019-0078-1
Ghasemi, E., Burley, H., and Safadel, P. (2019). Gender differences in general achievement in mathematics: an international study. New Waves Educ. Res. Dev. J. 22, 27–54.
Gidalevich, S., and Kramarski, B. (2019). The value of fixed versus faded self-regulatory scaffolds on fourth graders' mathematical problem solving. Instr. Sci. 47, 39–68. doi: 10.1007/s11251-018-9475-z
Gilleece, L., Cosgrove, J., and Sofroniou, N. (2010). Equity in mathematics and science outcomes: characteristics associated with high and low achievement on PISA 2006 in Ireland. Int. J. Sci. Math. Educ. 8, 475–496. doi: 10.1007/s10763-010-9199-2
Gilligan, K. A., Flouri, E., and Farran, E. K. (2017). The contribution of spatial ability to mathematics achievement in middle childhood. J. Exp. Child Psychol. 163, 107–125. doi: 10.1016/j.jecp.2017.04.016
Gorgorió, N. (1998). Exploring the functionality of visual And non-visual strategies in solving rotation problems. Educ. Stud. Math. 35, 207–231.
Guo, W., Lau, K. L., Wei, J., and Bai, B. (2021). Academic subject and gender differences in high school students' self-regulated learning of language and mathematics. Curr. Psychol. 42, 7965–7980. doi: 10.1007/s12144-021-02120-9
Halpern, D. F., Benbow, C. P., Geary, D. C., Gur, R. C., Hyde, J. S., and Gernsbacher, M. A. (2007). The science of gender differences in science and mathematics. Psychol. Sci. Public Interest 8, 1–51. doi: 10.1111/j.1529-1006.2007.00032.x
Hamel, R., and Schmittmann, V. D. (2006). The 20-minute version as a predictor of the Raven advanced progressive matrices test. Educ. Psychol. Meas. 66, 1039–1046. doi: 10.1177/0013164406288169
Hanin, V., and Van Nieuwenhoven, C. (2020). An exploration of the cognitive, motivational, emotional and regulatory behaviours of elementary-school novice and expert problem solvers. Can. J. Sci. Math. Technol. Educ. 20, 312–341. doi: 10.1007/s42330-020-00092-9
Harder, B., Trottler, S., Vialle, W., and Ziegler, A. (2015). Diagnosing resources for effective learning via teacher and parent checklists. Psychol. Test Assess. Model. 57, 201–221.
Hegarty, M., Mayer, R. E., and Green, C. E. (1992). Comprehension of arithmetic word problems: evidence from students' eye fixations. J. Educ. Psychol. 84, 76–84. doi: 10.1037/0022-0663.84.1.76
Heirweg, S., De Smul, M., Devos, G., and Van Keer, H. (2019). Profiling upper primary school students' self-regulated learning through self-report questionnaires and think-aloud protocol analysis. Learn. Individ. Differ. 70, 155–168. doi: 10.1016/j.lindif.2019.02.001
Hutchison, J. E., Lyons, I. M., and Ansari, D. (2019). More similar than different: gender differences in children's basic numerical skills are the exception not the rule. Child Dev. 90, 66–79. doi: 10.1111/cdev.13044
Hyde, J., Fennema, E., and Lamon, S. (1990). Gender differences in mathematics performance: a meta-analysis. Psychol. Bull. 107, 139–155. doi: 10.1037/0033-2909.107.2.139
Hyde, J., Lindberg, S., Linn, M., Ellis, A., and Williams, C. (2008). Gender similarities characterize math performance. Science 321, 494–495. doi: 10.1126/science.1160364
Jacobs, J. E., and Eccles, J. S. (1992). The impact of mothers' gender-role stereotypic beliefs on mothers' and children's ability perceptions. J. Pers. Soc. Psychol. 63, 932–944. doi: 10.1037/0022-3514.63.6.932
Johnson, T., Burgoyne, A. P., Mix, K. S., Young, C. J., and Levine, S. C. (2022). Spatial and mathematics skills: similarities and differences related to age, SES, and gender. Cognition 218:104918. doi: 10.1016/j.cognition.2021.104918
Jones, M. G., and Wheatley, J. (1990). Gender differences in teacher-student interactions in science classrooms. J. Res. Sci. Teach. 27, 861–874. doi: 10.1002/tea.3660270906
Jordan, N. C., Kaplan, D., Locuniak, M. N., and Ramineni, C. (2007). Predicting first-grade math achievement from developmental number sense trajectories. Learn. Disabil. Res. Pract. 22, 36–46. doi: 10.1111/j.1540-5826.2007.00229.x
Khanal, B. (2017). Preference of mathematics learning strategies based on gender. Int. Educ. Res. J. 3, 43–45.
Kikas, E., Mädamürk, K., and Palu, A. (2020). What role do comprehension-oriented learning strategies have in solving math calculation and word problems at the end of middle school? Br. J. Educ. Psychol. 90, 105–123. doi: 10.1111/bjep.12308
Kramarski, B., Tzohar-Rozen, M., and Gadasi, Z. (2021). “Metacognition and meta-emotion in kindergarten: is the combination necessary for self-regulation in mathematical problem solving?” in Trends and prospects in metacognition research across the life span. eds. D. Moraitou and P. Metallidou (Cham: Springer)
Laski, E. V., Casey, B. M., Yu, Q., Dulaney, A., Heyman, M., and Dearing, E. (2013). Spatial skills as a predictor of first grade girls' use of higher-level arithmetic strategies. Learn. Individ. Differ. 23, 123–130. doi: 10.1016/j.lindif.2012.08.001
Lee, Y. S., Park, Y. S., and Ginsburg, H. (2016). Socio-economic status differences in mathematics accuracy, strategy use, and profiles in the early years of schooling. ZDM 48, 1065–1078. doi: 10.1007/s11858-016-0783-y
Levin, K. A. (2006). Study design III: cross-sectional studies. Evid. Based Dent. 7, 24–25. doi: 10.1038/sj.ebd.6400375
Levine, S. C., Foley, A., Lourenco, S., Ehrlich, S., and Ratliff, K. (2016). Sex differences in spatial cognition: advancing the conversation. Wiley Interdiscip. Rev. Cogn. Sci. 7, 127–155. doi: 10.1002/wcs.1380
Levine, S. C., Vasilyeva, M., Lourenco, S. F., Newcombe, N. S., Huttenlocher, J., Report, R., et al. (2005). Socioeconomic status modifies the sex difference in spatial skill. Psychol. Sci. 16, 841–845. doi: 10.1111/j.1467-9280.2005.01623.x
Levpušček, M. P., Zupančič, M., and Sočan, G. (2013). Predicting achievement in mathematics in adolescent students: the role of individual and social factors. J. Early Adolesc. 33, 523–551. doi: 10.1177/0272431612450949
Lewis, A. B., and Mayer, R. E. (1987). Students' miscomprehension of relational statements in arithmetic word problems. J. Educ. Psychol. 79, 363–371. doi: 10.1037/0022-0663.79.4.363
Leyva, L. A. (2017). Unpacking the male superiority myth and masculinization of mathematics at the intersections: a review of research on gender in mathematics education. J. Res. Math. Educ. 48, 397–433. doi: 10.5951/jresematheduc.48.4.0397
Lorah, J. (2018). Effect size measures for multilevel models: definition, interpretation and TIMSS example. Large Scale Assess. Educ. 6, 2–11. doi: 10.1186/s40536-018-0061-2
Lubienski, S. T., Robinson, J. P., Crane, C. C., and Ganley, C. M. (2013). Girls' and boys' mathematics achievement, affect, and experiences: findings from ECLS-K. J. Res. Math. Educ. 44, 634–645. doi: 10.5951/jresematheduc.44.4.0634
Marchant, G. J., and Finch, W. H. (2016). Student, school, and country: the relationship of SES and inequality to achievement. J. Global Res. Educ. Soc. Sci. 6, 187–196.
Mevarech, Z. R., Verschaffel, L., and De Corte, E. (2018). “Metacognitive pedagogies in mathematics classrooms: from kindergarten to college and beyond” in Handbook of self-regulation of learning and performance. eds. D. H. Schunk and J. A. Greene (New York: Routledge/Taylor & Francis Group), 109–123.
Miller, D. I., and Halpern, D. F. (2014). The new science of cognitive sex differences. Trends Cogn. Sci. 18, 37–45. doi: 10.1016/j.tics.2013.10.011
Montague, M. (2008). Self-regulation strategies to improve mathematical problem solving for students with learning disabilities. Learn. Disabil. Q. 31, 37–44. doi: 10.2307/30035524
Moon, C. Y., Larke, P. J., and James, M. C. (2022). Examining mathematics achievement: an analysis of fourth and eighth grade TIMSS US data by ethnicity, gender, and sociocultural variables. J. Ethnic Cult. Stud. 9, 226–243. doi: 10.29333/ejecs/942
Neisser, U., Boodoo, G., Bouchard, T. J., Boykin, A. W., Brody, N., Ceci, S. J., et al. (1996). Intelligence: knowns and unknowns. Am. Psychol. 51, 77–101. doi: 10.1037/0003-066X.51.2.77
Newton, J. H., and McGrew, K. S. (2010). Introduction to the special issue: current research in Cattell–horn–Carroll– based assessment. Psychol. Sch. 47, 621–634. doi: 10.1002/pits.20495
Nortvedt, G. A. (2011). Coping strategies applied to comprehend multistep arithmetic word problems by students with above-average numeracy skills and below-average reading skills. J. Math. Behav. 30, 255–269. doi: 10.1016/j.jmathb.2011.04.003
O’Dea, R. E., Lagisz, M., Jennions, M. D., and Nakagawa, S. (2018). Gender differences in individual variation in academic grades fail to fit expected patterns for STEM. Nat. Commun. 9, 3777–3778. doi: 10.1038/s41467-018-06292-0
OECD (2015). The ABC of gender equality in education: Aptitude, behaviour, confidence. Berlin: OECD Publishing.
Pajares, F. (2002). Gender and perceived self-efficacy in self-regulated learning. Theory Pract. 41, 116–125. doi: 10.1207/s15430421tip4102_8
Pajares, F., and Valiante, G. (2001). Gender differences in writing motivation and achievement of middle school students: a function of gender orientation? Contemp. Educ. Psychol. 26, 366–381. doi: 10.1006/ceps.2000.1069
Paz-Baruch, N. (2020). Educational and learning capital as predictors of general intelligence and scholastic achievements. High Abil. Stud. 31, 75–91. doi: 10.1080/13598139.2019.1586656
Peng, P., Wang, T., Wang, C., and Lin, X. (2019). A meta-analysis on the relation between fluid intelligence and reading/mathematics: effects of tasks, age, and social economics status. Psychol. Bull. 145, 189–236. doi: 10.1037/bul0000182
Penner, A. M., and Paret, M. (2008). Gender differences in mathematics achievement: exploring the early grades and the extremes. Soc. Sci. Res. 37, 239–253. doi: 10.1016/j.ssresearch.2007.06.012
Perry, L., and McConney, A. (2010). School socio-economic composition and student outcomes in Australia: implications for educational policy. Aust. J. Educ. 54, 72–85. doi: 10.1177/000494411005400106
Pintrich, P. R. (1999). The role of motivation in promoting and sustaining self-regulated learning. Int. J. Educ. Res. 31, 459–470. doi: 10.1016/S0883-0355(99)00015-4
Pintrich, P. R. (2004). A conceptual framework for assessing motivation and self-regulated learning in college students. Educ. Psychol. Rev. 16, 385–407. doi: 10.1007/s10648-004-0006-x
Pintrich, P. R., and Zusho, A. (2002). “The development of academic self-regulation: the role of cognitive and motivational factors” in Development of achievement motivation. eds. A. Wigfield and J. S. Eccles (Cambridge, MA: Academic Press), 249–284.
Pinxten, M., Marsh, H. W., De Fraine, B., Van Den Noortgate, W., and Van Damme, J. (2014). Enjoying mathematics or feeling competent in mathematics? Reciprocal effects on mathematics achievement and perceived math effort expenditure. Br. J. Educ. Psychol. 84, 152–174. doi: 10.1111/bjep.12028
Pokay, P., and Blumenfeld, P. C. (1990). Predicting achievement early and late in the semester: the role of motivation and use of learning strategies. J. Educ. Psychol. 82, 41–50. doi: 10.1037/0022-0663.82.1.41
Pongsakdi, N., Kajamies, A., Veermans, K., Lertola, K., Vauras, M., and Lehtinen, E. (2020). What makes mathematical word problem solving challenging? Exploring the roles of word problem characteristics, text comprehension, and arithmetic skills. ZDM 52, 33–44. doi: 10.1007/s11858-019-01118-9
Räsänen, P., Aunio, P., Laine, A., Hakkarainen, A., Väisänen, E., Finell, J., et al. (2021). Effects of gender on basic numerical and arithmetic skills: pilot data from third to ninth grade for a large-scale online dyscalculia screener. Front. Educ. 6:683672. doi: 10.3389/feduc.2021.683672
Raven, J., Raven, J. C., and Court, J. H. (2000). Manual for Raven's progressive matrices and vocabulary scales. Oxford: Oxford Psychologists Press.
Reilly, D., Neumann, D. L., and Andrews, G. (2015). Sex differences in mathematics and science achievement: a meta-analysis of National Assessment of educational Progress assessments. J. Educ. Psychol. 107, 645–662. doi: 10.1037/edu0000012
Reilly, D., Neumann, D. L., and Andrews, G. (2019). Investigating gender differences in mathematics and science: results from the 2011 trends in mathematics and science survey. Res. Sci. Educ. 49, 25–50. doi: 10.1007/s11165-017-9630-6
Robinson, J. P., and Lubienski, S. T. (2011). The development of gender achievement gaps in mathematics and reading during elementary and middle school: examining direct cognitive assessments and teacher ratings. Am. Educ. Res. J. 48, 268–302. doi: 10.3102/0002831210372249
Rosário, P., Núñez, J. C., Valle, A., González-Pienda, J., and Lourenço, A. (2013). Grade level, study time, and grade retention and their effects on motivation, self-regulated learning strategies, and mathematics achievement: a structural equation model. Eur. J. Psychol. Educ. 28, 1311–1331. doi: 10.1007/s10212-012-0167-9
Rosenzweig, C., Krawec, J., and Montague, M. (2011). Metacognitive strategy use of eighth-grade students with and without learning disabilities during mathematical problem solving: a think-aloud analysis. J. Learn. Disabil. 44, 508–520. doi: 10.1177/0022219410378445
Royer, J. M., Tronsky, L. N., Chan, Y., Jackson, S. J., and Marchant, H. I. (1999). Math-fact retrieval as the cognitive mechanism underlying gender differences in math test performance. Contemp. Educ. Psychol. 24, 181–266. doi: 10.1006/ceps.1999.1004
Russo, J., and Hopkins, S. (2017). Student reflections on learning with challenging tasks: ‘I think the worksheets were just for practice, and the challenges were for maths’. Math. Educ. Res. J. 29, 283–311. doi: 10.1007/s13394-017-0197-3
Sakiz, G., Pape, S. J., and Woolfolk Hoy, A. (2012). Does perceived teacher affective supports matter for middle school students in mathematics classrooms? J. Sch. Psychol. 50, 235–255. doi: 10.1016/j.jsp.2011.10.005
Schellings, G., and Van Hout-Wolters, B. (2011). Measuring strategy use with self-report instruments: theoretical and empirical considerations. Metacogn. Learn. 6, 83–90. doi: 10.1007/s11409-011-9081-9
Schunk, D. H., and Greene, J. A. (2018). Handbook of self-regulation of learning and performance. New York: Routledge.
Seaton, M., Parker, P., Marsh, H. W., Craven, R. G., and Yeung, A. S. (2014). The reciprocal relations between self-concept, motivation and achievement: juxtaposing academic self-concept and achievement goal orientations for mathematics success. Educ. Psychol. 34, 49–72. doi: 10.1080/01443410.2013.825232
Semeraro, C., Giofrè, D., Coppola, G., Lucangeli, D., and Cassibba, R. (2020). The role of cognitive and non-cognitive factors in mathematics achievement: the importance of the quality of the student-teacher relationship in middle school. PLoS One 15:e0231381. doi: 10.1371/journal.pone.0231381
Sirin, S. R. (2005). Socioeconomic status and academic achievement: a meta-analytic review of research. Rev. Educ. Res. 75, 417–453. doi: 10.3102/00346543075003417
Spektor-Levy, O., Basilio, M., Zachariou, A., and Whitebread, D. (2017). Young children’s spontaneous manifestation of self-regulation and metacognition during constructional play tasks. Teach. Coll. Rec. 119, 1–28. doi: 10.1177/016146811711901314
Spinath, B., Eckert, C., and Steinmayr, R. (2014). Gender differences in school success: what are the roles of students' intelligence, personality and motivation? Educ. Res. 56, 230–243. doi: 10.1080/00131881.2014.898917
Starkey, P., Klein, A., and Wakeley, A. (2004). Enhancing young children's mathematical knowledge through a pre-kindergarten mathematics intervention. Early Child. Res. Q. 19, 99–120. doi: 10.1016/j.ecresq.2004.01.002
Steffens, M. C., and Jelenec, P. (2011). Separating implicit gender stereotypes regarding math and language: implicit ability stereotypes are self-serving for boys and men, but not for girls and women. Sex Roles 64, 324–335. doi: 10.1007/s11199-010-9924-x
Steinmayr, R., Wirthwein, L., and Schöne, C. (2014). Gender and numerical intelligence: does motivation matter? Learn. Individ. Differ. 32, 140–147. doi: 10.1016/j.lindif.2014.01.001
Sternberg, R. J. (1999). The theory of successful intelligence. Rev. Gen. Psychol. 3, 292–316. doi: 10.1037/1089-2680.3.4.292
Stevens, S., and Haidt, J. (2017). The greater male variability hypothesis-An addendum to our post on google memo. Retrieved from: https://heterodoxacademy.org/the-greater-male-variabilityhypothesis
Stoet, G., and Geary, D. C. (2018). The gender-equality paradox in science, technology, engineering, and mathematics education. Psychol. Sci. 29, 581–593. doi: 10.1177/0956797617741719
Tzuriel, D., and Egozi, G. (2010). Gender differences in spatial ability of young children: the effects of training and processing strategies. Child Dev. 81, 1417–1430. doi: 10.1111/j.1467-8624.2010.01482.x
Ubuz, B., Üstün, I., and Erbaş, A. K. (2009). Effect of dynamic geometry environment on immediate and retention level achievements of seventh grade students. Eurasian J. Educ. Res. 35, 147–164.
Vandevelde, S., Van Keer, H., Schellings, G., and Van Hout-Wolters, B. (2015). Using think-aloud protocol analysis to gain in-depth insights into upper primary school children's self-regulated learning. Learn. Individ. Differ. 43, 11–30. doi: 10.1016/j.lindif.2015.08.027
Viterbori, P., Traverso, L., and Usai, M. C. (2017). The role of executive function in arithmetic problem-solving processes: a study of third graders. J. Cogn. Dev. 18, 595–616. doi: 10.1080/15248372.2017.1392307
Voyer, D., Voyer, S., and Bryden, M. P. (1995). Magnitude of sex differences in spatial abilities: a meta-analysis and consideration of critical variables. Psychol. Bull. 117, 250–270. doi: 10.1037/0033-2909.117.2.250
Wang, M. T., and Degol, J. L. (2017). Gender gap in science, technology, engineering, and mathematics (STEM): current knowledge, implications for practice, policy, and future directions. Educ. Psychol. Rev. 29, 119–140. doi: 10.1007/s10648-015-9355-x
Wang, L., Li, X., and Li, N. (2014). Socio-economic status and mathematics achievement in China: a review. ZDM 46, 1051–1060. doi: 10.1007/s11858-014-0617-8
Wei, W., Chen, C., and Zhou, X. (2016). Spatial ability explains the male advantage in approximate arithmetic. Front. Psychol. 7, 1–9. doi: 10.3389/fpsyg.2016.00306
Wei, W., Lu, H., Zhao, H., Chen, C., Dong, Q., and Zhou, X. (2012). Gender differences in children's arithmetic performance are accounted for by gender differences in language abilities. Psychol. Sci. 23, 320–330. doi: 10.1177/0956797611427168
White, G. W., Stepney, C. T., Hatchimonji, D. R., Moceri, D. C., Linsky, A. V., Reyes-Portillo, J. A., et al. (2016). The increasing impact of socioeconomics and race on standardized academic test scores across elementary, middle, and high school. Am. J. Orthopsychiatry 86, 10–23. doi: 10.1037/ort0000122
Whitebread, D., Coltman, P., Pasternak, D. P., Sangster, C., Grau, V., Bingham, S., et al. (2009). The development of two observational tools for assessing metacognition and self-regulated learning in young children. Metacogn. Learn. 4, 63–85. doi: 10.1007/s11409-008-9033-1
Wiberg, M. (2019). The relationship between TIMSS mathematics achievements, grades, and national test scores. Educ. Inq. 10, 328–343. doi: 10.1080/20004508.2019.1579626
Winne, P. H., and Jamieson-Noel, D. (2002). Exploring students' calibration of self reports about study tactics and achievement. Contemp. Educ. Psychol. 27, 551–572. doi: 10.1016/S0361-476X(02)00006-1
Wolters, C. A., and Pintrich, P. R. (1998). Contextual differences in student motivation and self-regulated learning in mathematics, English, and social studies classrooms. Instr. Sci. 26, 27–47. doi: 10.1023/A:1003035929216
Wong, T. T. Y., and Ho, C. S. H. (2017). Component processes in arithmetic word-problem solving and their correlates. J. Educ. Psychol. 109, 520–531. doi: 10.1037/edu0000149
Yu, R., and Singh, K. (2018). Teacher support, instructional practices, student motivation, and mathematics achievement in high school. J. Educ. Res. 111, 81–94. doi: 10.1080/00220671.2016.1204260
Zhu, Z. (2007). Gender differences in mathematical problem solving patterns: a review of literature. Int. Educ. J. 8, 187–203.
Zhu, Y., Kaiser, G., and Cai, J. (2018). Gender equity in mathematical achievement: the case of China. Educ. Stud. Math. 99, 245–260. doi: 10.1007/s10649-018-9846-z
Zimmerman, B. J. (2000). “Attaining self-regulation: a social-cognitive perspective” in Handbook of self-regulation. eds. M. Boekaerts, P. R. Pintrich, and M. Zeidner (Cambridge, MA: Academic Press), 13–39.
Zimmerman, B. J. (2008). Investigating self-regulation and motivation: historical background, methodological developments, and future prospects. Am. Educ. Res. J. 45, 166–183. doi: 10.3102/0002831207312909
Zimmerman, B. J., and Martinez-Pons, M. (1990). Student differences in self-regulated learning: relating grade, sex, and giftedness to self-efficacy and strategy use. J. Educ. Psychol. 82, 51–59. doi: 10.1037/0022-0663.82.1.51
Keywords: gender gaps, general intelligence, mathematical achievements, self-regulated learning, socioeconomic status
Citation: Paz-Baruch N and Spektor-Levy O (2024) How the relationship between individual and social factors informs the narrowing of gender gaps in elementary mathematical achievements. Front. Educ. 9:1339040. doi: 10.3389/feduc.2024.1339040
Edited by:
Joaquin Marc Veith, University of Hildesheim, GermanyReviewed by:
Maria Sofologi, University of Ioannina, GreeceIan Thacker, University of Texas at San Antonio, United States
Copyright © 2024 Paz-Baruch and Spektor-Levy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nurit Paz-Baruch, bnVyaXQucGF6QGJpdS5hYy5pbA==
 Nurit Paz-Baruch
Nurit Paz-Baruch Ornit Spektor-Levy
Ornit Spektor-Levy