
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Educ. , 26 April 2024
Sec. Educational Psychology
Volume 9 - 2024 | https://doi.org/10.3389/feduc.2024.1335957
This article is part of the Research Topic The important role of the early school years for reading, writing and math development: Assessment and Intervention at school entry View all 14 articles
Reading and arithmetic are distinct academic skills that share similarities in skill acquisition and use. Previous research investigated the cognitive basis of associations and dissociations between reading and arithmetic by using either subtyping or dimensional approaches. In the current study, we aim to bridge the gap between these two approaches by investigating common and distinct predictors of reading and arithmetic at different performance levels with quantile regression models. This allowed us to look more closely at the lower tail of the ability distributions, and to test whether predictions for children with low reading and arithmetic fluency differed from the typical performance range. We analyzed longitudinal data of 357 children speaking English or German. Outcome variables were reading and arithmetic fluency assessed at the end of Grade 1, 2, and 3. Predictors were assessed in Grade 1. Results confirmed nonverbal IQ and working memory as domain-general predictors of reading and arithmetic. The association of reading and arithmetic was mainly explained by nonverbal IQ, phonological awareness, RAN and multi-digit transcoding. Across grades and performance levels, phonological awareness and RAN made a specific contribution to reading. Magnitude processing and multi-digit transcoding were specific predictors of arithmetic. Counting also made a specific prediction to arithmetic in Grade 3, but only in the low performance range. Our findings indicate partly distinct underlying cognitive mechanisms for reading and arithmetic. Shared predictors are involved in retrieval efficiency, language processing and cross-format integration. These results have important implications, as they suggest that most predictors are equally relevant for children with low, typical or even excellent reading and arithmetic fluency.
Reading and arithmetic are core academic skills that provide fundamental tools for everyday-life and learning more complex abilities. They may seem like different skill sets. But there are many similarities. To start with, reading and arithmetic are both symbol-based systems in which visual stimuli (letters, Arabic digits) are put in relation with sounds (phonemes, number words; Dehaene, 1992; Coltheart et al., 2001; Barrouillet et al., 2004). In the early stages of skill acquisition, both abilities require reliance on algorithms to obtain a consistent output: For reading, this refers to grapheme-phoneme conversion, which enables reading by serial decoding strategies (Frith, 1985; Coltheart et al., 2001). In the field of arithmetic, young children are able to compute simple additions and subtractions by serial counting (Peters and De Smedt, 2018). Repeated decoding of the same word or computing of the same multiplication enables the build-up of memory traces, i.e., associations between orthographic and phonological representations or between arithmetic problems and solutions. These facts can be retrieved quickly and effortlessly, enabling efficient use of the learnt skills as in lexico-orthographic reading and arithmetic fact retrieval.
Skillful use of reading and arithmetic abilities requires the efficient integration of visual, verbal and semantic representations. There is a parallelism between the cognitive structure of models for reading and number processing, as recently highlighted by Jöbstl et al. (2023) and depicted in Figure 1. The Lexical Quality Hypothesis (Perfetti and Hart, 2001) postulates that interindividual differences in reading are related to the degree in which the three main constituents of a word are integrated, namely orthography (word form), phonology (word sound) and semantics (word meaning). Fluent, skilled reading requires well specified and connected orthographic, phonological and semantic representations of the same word. The Triple Code Model for number processing (Dehaene, 1992) builds on a similar structure. The basic tenet is that numbers are represented by three codes: The visual Arabic code (for Arabic digits; e.g., 3), the verbal word frame (number words; e.g., “three”) and the analog magnitude representation (quantities; e.g., ■■■). These three codes are connected and get activated during numerical and arithmetic computations.
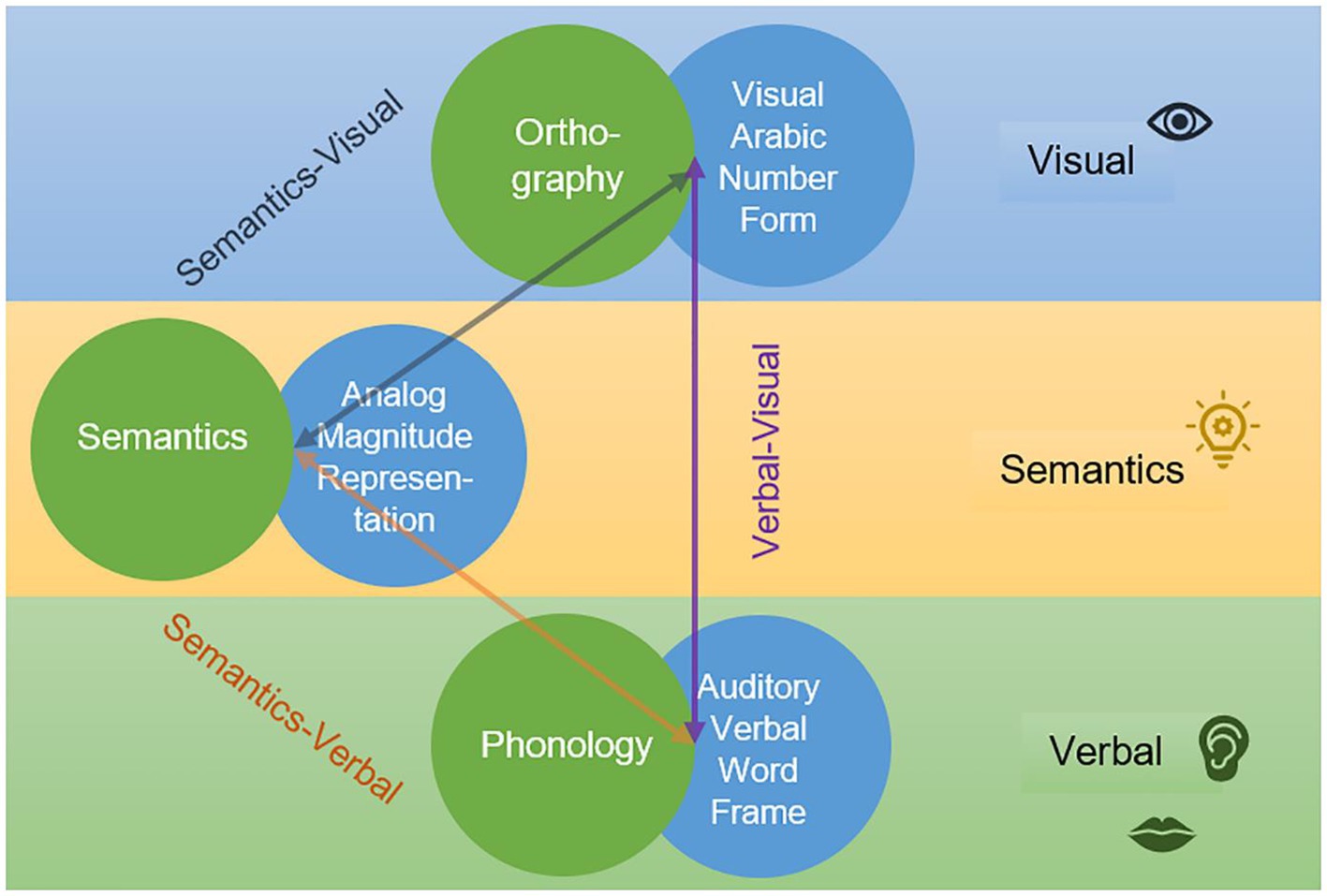
Figure 1. Similarity in the cognitive architecture of the lexical quality hypothesis (green circles) and the triple code model (blue circles). From “A-B-3—Associations and dissociations of reading and arithmetic: is domain-specific prediction outdated?,” by V. Jöbstl, A. F. Steiner, P. Deimann, U. Kastner-Koller, K. Landerl, 2023, PlosOne, 18 (5): e0285437 (doi: 10.1371/journal.pone.0285437). CC BY-NC.
Empirical research reported associations of varying strength between reading and arithmetic, with correlation coefficients between 0.14 and 0.77 (Dirks et al., 2008; Landerl and Moll, 2010; Moll et al., 2014; Peterson et al., 2017; Willcutt et al., 2019; Zoccolotti et al., 2021). This variability is driven by different sources: Studies used different operationalizations of reading (word, text, accuracy, speed, fluency, comprehension) and arithmetic (oral/written format, problems, computations, fact accuracy, fact fluency). Note that when reading and arithmetic were consistently assessed as fluency measures, correlation coefficients were moderate to high [r = 0.44 in Moll et al. (2014); r = 0.66 in Willcutt et al. (2019)]. Participants’ age also varies substantially in the reported studies (between 7 and 18 years old) and this may affect the strength of the associations. Furthermore, studies were carried out in countries with different languages (Dutch, German, English, Italian). It is possible that linguistic and orthographic characteristics modulate the associations among academic skills.
In line with the notion that acquired skills are related in typical samples, learning disorders in these two skill domains (namely, dyslexia and dyscalculia) co-occur three to five times more often than what would be expected based on individual prevalence rates (Landerl and Moll, 2010; Moll et al., 2014; Koponen et al., 2018; Joyner and Wagner, 2020). These associations suggest the existence of a common basis of the two skills. Studies investigating common and distinct cognitive underpinnings of reading and arithmetic have mostly implemented two different methodological approaches. In one approach, specific profiles of individuals with either isolated deficits (e.g., only reading vs. arithmetic problems) or combined deficits (co-occurring reading and arithmetic problems) are identified and compared (Siegel and Heaven, 1986). This approach is based on the subtyping classification scheme. Studies based on this approach often reported a selective pattern of impaired cognitive performance specifically related to reading but not to arithmetic problems or vice versa (Willburger et al., 2008; Landerl et al., 2009; Willcutt et al., 2013; Cirino et al., 2015; Moll et al., 2015; Raddatz et al., 2017). Landerl et al. (2009) for instance showed that 8- to 10-year-old children with impaired reading fluency and age-adequate arithmetic skills displayed lower performance in phonological processing and rapid naming (RAN) tasks, but not in numerical processing paradigms. Children in the group with impaired arithmetic performance and age-adequate reading skills showed the opposite pattern of impaired number processing performance but age-adequate phonological and rapid naming skills. Importantly, the vast majority of studies in this field consistently reported an additive pattern of cognitive deficits in the group with comorbid reading and arithmetic problems, which means that children with a combined deficit profile manifested the sum of the deficits reported in each single-deficit group and did not show substantial qualitative differences in the cognitive profile compared to single-deficit groups. The subtyping approach is informative, because it provides clear-cut comparisons between matched deficit groups that are specifically selected to show a deficit in one skill domain while controlling for performance in the other skill domain. However, as recently suggested (Peters and Ansari, 2019; Astle and Fletcher-Watson, 2020), this approach has some limitations: (1) Group membership is based on arbitrary cut-offs which differ from study to study, thus impairing replicability and comparability; (2) Participants are selected on the basis of very specific inclusion, exclusion criteria and performance cut-offs. This in turn makes the samples less ecologically valid, in the sense that they do not reflect the full range of variability observed in the general population; (3) Group size is often low, with a clear impact on statistical power.
A more recent, alternative approach assesses reading and arithmetic as continuous dimensions and tests the contribution of different cognitive predictors by means of linear relationships. This dimensional approach has the advantage of being free from the definition of arbitrary cut-offs, as it considers the whole spectrum of possible performance in the skill domain of interest, and is usually implemented in large, unselected samples, thus potentially overcoming the problem of power and generalizability. This approach is in line with the basic tenet of the multiple deficit model (Pennington, 2006; McGrath et al., 2020) and with recent theoretical accounts (Protopapas and Parrila, 2018) that assume quantitative but no qualitative differences in the underlying cognitive skills of individuals with poor vs. typical skill performance. Research using a dimensional approach identified a broad range of skills that similarly predict reading and arithmetic. These include working memory, visuo-spatial memory, phonological awareness, RAN, language skills, processing speed, attention, reasoning, counting and number naming (Durand et al., 2005; Geary, 2011; Fuchs et al., 2016; Cirino et al., 2018; Child et al., 2019; Vanbinst et al., 2020; Zoccolotti et al., 2020; Amland et al., 2021; Bernabini et al., 2021). Longitudinal studies in Finnish children investigated dimensions that predict the co-variation of reading and arithmetic and consistently found that RAN and counting made an important contribution (Koponen et al., 2007, 2020; Korpipää et al., 2017). This evidence was partly replicated in a recent longitudinal study with German-speaking children (Jöbstl et al., 2023). However, uncovering the cognitive underpinnings driving the association of reading and arithmetic, as reported in the above-mentioned studies, is just as relevant as researching the substrates of dissociations (Landerl et al., 2013a). In line with this reasoning, the cross-sectional study by Bernabini et al. (2021) investigated the contribution of a set of cognitive predictors (nonverbal IQ, phonological awareness, magnitude processing and number system knowledge) to reading while controlling for arithmetic performance and vice versa. They collected a sample of 97 Italian speaking children attending 4th and 5th grade of primary school. Results of linear regressions indicated counting as the only dimension predicting both reading and math controlling for the other outcome measures. Magnitude processing, number transcoding and number repetition measures made a specific contribution to arithmetic but not to reading. In a longitudinal study following 885 German-speaking children from kindergarten to Grade 2, Jöbstl et al. (2023) performed a series of fully latent structural equation models. Their results showed that RAN was a significant predictor of reading after controlling for arithmetic skills. In contrast, variance in arithmetic was predicted by magnitude processing independent of reading performance.
To sum up, the available literature indicates distinct as well as common cognitive predictors of reading and arithmetic. Findings are so far controversial and this could be due to different designs, methodological and statistical approaches, languages of participants, age ranges and operationalizations of predictive and outcome measures. There are inconsistencies especially between studies classifying subtypes compared to studies using a dimensional approach. This might be due to the fact that studies using the dimensional approach mostly predicted one skill-domain without controlling for the other skill-domain. Studies that predicted variance in reading controlling for arithmetic and vice versa (Bernabini et al., 2021; Jöbstl et al., 2023) indeed found a more consistent picture which broadly mimics findings by studies with deficit groups.
The current study investigates the cognitive contributions to low- and high-achievement performance in reading and arithmetic fluency in a longitudinal sample of English- and German-speaking children followed across the first 3 years of elementary school. This developmental period is particularly informative, as it spans the time in which children switch from relying on procedures such as decoding and counting to - at least in part – retrieving verbal facts to read and do arithmetic.
In a previous study (Jöbstl et al., 2024), we showed that there is a degree of specificity in the cognitive predictors of reading and arithmetic fluency. We conducted Ordinary Least Squares (OLS) regression analyses in the same longitudinal sample as in the present study and predicted reading controlling for arithmetic and vice versa. Phonological awareness was a specific predictor of reading fluency, magnitude comparison made a specific contribution to arithmetic fluency. Our results revealed that there are cognitive substrates for associations among skill domains: RAN and multi-digit transcoding explained shared variance between skills. Yet, it is unclear whether these relations hold across the whole continuum of performance. The present study aims to fill this gap by testing whether cognitive predictors of reading and arithmetic have a different importance depending on the skill-level of the criterion variable. We addressed the cognitive basis of associations between reading and arithmetic fluency by modeling their shared variance and, in line with our previous analysis, we inspected specific relations, thus predicting reading after partialling out the influence of arithmetic and vice versa. Importantly, we used the method of quantile regression as a way to overcome the existing controversy related to the methodological inconsistencies of studies with a subtyping vs. dimensional approach. This statistical method will provide us with insight into the question of whether there is a qualitative difference in the pattern of cognitive predictors for high- vs. low-level performance in reading and arithmetic. We aimed to test two competing hypotheses: (1) According to the multiple deficit model, we would expect similar predictive trends in low- and high-achievement ranges. The multiple deficit model theorizes that the distribution of risk factors for a particular disorder is continuous and quantitative (Pennington, 2006), thus implying underlying linear relations between cognitive predictors and outcome variables. (2) Alternatively, we tested whether the predictive pattern differed at different performance levels. It is still possible, that certain predictors are non-linearly related to the criterion variables. This was reported for instance for RAN- and PA-reading associations (de Groot et al., 2015; McIlraith, 2018; Ozernov-Palchik et al., 2022) and also for the association between numerical predictors and arithmetic (Devlin et al., 2022). This research question is particularly relevant in light of literature on low-achieving individuals with dyslexia or dyscalculia. Accordingly, low-level performance was modeled at the 16th percentile of the distribution of reading and arithmetic fluency skills. This percentile corresponds to one standard deviation from the mean and is particularly relevant, as it is defined as the clinical cutoff for identifying reading, spelling and math difficulties in evidence-based guidelines for diagnosing learning disorders in German-speaking countries (Galuschka and Schulte-Körne, 2016; Haberstroh and Schulte-Körne, 2019).
We focused on fluency measures with the aim of having consistent operationalizations in the reading and arithmetic domains, so that regression models would predict different academic competences measured in a similar format.
In the following, we present the cognitive predictors examined in this study and reason on potential differences in their predictive role depending on the performance level. We investigated the role of so-called “domain-general” predictors, dimensions that play a role in a broad spectrum of abilities, including reading and arithmetic; and “domain-specific” predictors, dimensions that are particularly relevant for only one skill domain but not for the other.
We included nonverbal intelligence and working memory as domain-general predictors. These dimensions underpin a wide range of cognitive skills (reasoning, problem-solving, visuo-spatial processing, storage and manipulation of visuo-spatial and verbal information) that are related to the outcome variables reading and arithmetic (Geary, 2011; Fuchs et al., 2016; Korpipää et al., 2017) as well as to the predictor variables (Clayton et al., 2020; Koponen et al., 2020). These dimensions were included for two reasons: (1) as nonspecific cognitive predictors of reading and arithmetic; (2) to control for general cognitive functioning related to both outcome and predictor variables. This way, we ensured that relations observed between predictors and outcomes are specific and not due to co-variance with general cognitive abilities.
Among domain-specific predictors, phonological awareness and RAN were expected to be preferentially associated with reading measures. Phonological awareness supports grapheme-phoneme mapping during decoding and is one of the strongest predictors of reading in samples with typical development (Caravolas et al., 2012) and with reading deficits (Landerl et al., 2013b). Studies reporting an association of phonological awareness with arithmetic (Vanbinst et al., 2020; Amland et al., 2021) or with the covariance between reading and arithmetic (Korpipää et al., 2017; Cirino et al., 2018; Koponen et al., 2020) at the beginning of formal schooling suggest that phonological awareness might share some verbal processing features with arithmetic early on. These verbal processing features are related for instance to the manipulation of verbal number words in number reading and writing and to the build-up of arithmetic facts. Phonological awareness can be considered a proxy for language skills in its association with arithmetic. As different language skills make different contributions to arithmetic over the course of development, the contribution of phonological awareness is likely to change over time. Overall, we expected to find a consistent pattern as in our previous analysis (Jöbstl et al., 2024), revealing a large contribution of phonological processing to reading and a minor contribution to arithmetic fluency. With reference to reading, we anticipated a stronger contribution of this predictor in the low- vs. high-performance range due to a higher relevance of phonological processing skills in less automatized and thus more decoding-prone reading styles. Note that this hypothesis has already been confirmed in a previous study based on a subtyping approach (de Groot et al., 2015) but the finding was not replicated in a more recent study that adopted a dimensional approach (McIlraith, 2018).
RAN is a prominent predictor of reading fluency (Landerl et al., 2022). While there is no clear consensus on the theoretical basis of RAN (Kirby et al., 2010), researchers have argued that rapid naming shares many features with reading, as for instance serial processing and access from a visual input to a verbal output (Moll et al., 2009; Georgiou et al., 2013). RAN is considered a proxy for the efficiency of serial retrieval of visual-verbal associations across skill domains. Indeed, a number of studies consistently showed that RAN is not unique to reading but predicts also arithmetic as well as reading-arithmetic co-variation (Balhinez and Shaul, 2019; Georgiou et al., 2020; Koponen et al., 2020). Notwithstanding a clear cross-domain contribution, RAN can be expected to be more strongly related to reading than to arithmetic, as Jöbstl et al. (2023) previously pointed out, because there are more subcomponents of the task that are in common with reading (such as serial processing and naming) than with arithmetic. In line with this reasoning, our former analysis (Jöbstl et al., 2024) revealed a specific contribution of RAN to reading and, to a lesser extent, to arithmetic. In the current study, we anticipated that RAN would predict more strongly the high- vs. low-performance range, because retrieval-related mechanisms as measured by RAN are engaged at highly automated levels of performance. This hypothesis has been confirmed in previous studies (McIlraith, 2018; Ozernov-Palchik et al., 2022).
Counting, magnitude processing and multi-digit number transcoding were included as domain-specific predictors with an anticipated preferential importance for arithmetic. These dimensions have a straightforward relevance for number processing and are established predictors of arithmetic (Starr et al., 2013; Göbel et al., 2014; Banfi et al., 2022; Träff et al., 2023). Evidence about their contribution to reading and reading-arithmetic covariance is mixed.
Knowledge of the counting chain is an important prerequisite to correctly enumerate quantities, a numerical ability that enables to grasp the cardinality principle (the last number word of the counting chain reflects the counted quantity), which in turn boosts the understanding and the connection of different number codes (Geary and VanMarle, 2018). Reciting the counting chain also supports arithmetic early on, as it allows to solve simple additions and subtractions by counting up- or downward from a given number (Peters and De Smedt, 2018). Counting fluency was found to be highly correlated with RAN and to account for variance in reading (Koponen et al., 2013; Bernabini et al., 2021) and covariance in reading and arithmetic (Korpipää et al., 2017; Koponen et al., 2020). This evidence was taken as an indication that counting (together with RAN) measures the efficiency of serial retrieval skills, that is, the speed with which verbal traces are retrieved from memory. Another study (Cirino et al., 2018), however, showed that counting was more strongly predictive of arithmetic than reading. Cirino et al. (2018) did not control for reading while predicting arithmetic and it is therefore unclear whether the contribution of counting was specific to arithmetic or not. Note that in our previous analysis (Jöbstl et al., 2024), counting made a very marginal, specific contribution to arithmetic fluency (a not significant trend), and it did not reliably predict reading. Against this background and given its foundational role in supporting number processing and basic calculation strategies, we anticipated a prominent prediction of counting to arithmetic at the beginning of formal schooling and especially among children with low arithmetic fluency. Its contribution to reading fluency is expected to be minor.
Magnitude processing refers to the ability to compare or judge quantities such as dots or Arabic numbers. According to the triple code model, it requires understanding of quantities as analog representations and (for symbolic magnitude processing) to connect these to their symbolic counterpart in the visual Arabic code. There is evidence indicating unique prediction of symbolic and of non-symbolic magnitude comparison to arithmetic but not to reading (Durand et al., 2005; Jöbstl et al., 2023). Other studies, however, found that symbolic magnitude processing explained variance in reading comprehension, but not fluency (Cirino et al., 2018) and it also explained reading and arithmetic covariance (Koponen et al., 2020), although to a small extent. The reason for the involvement of magnitude processing in reading is not straightforward. It can be assumed that, similar to word reading, magnitude processing requires cross-format integration of the visual and semantic codes. In this sense, magnitude processing and reading might share similar symbolic processing strategies. Note that our former analysis (Jöbstl et al., 2024) revealed a reliable, specific contribution of magnitude processing to arithmetic fluency but not to reading. In the current study we tested the hypothesis that magnitude processing skills are more relevant in the low vs. high arithmetic fluency range. The ability to compare dots and single digits reflects basic numerical processing skills related to understanding quantities and being able to map Arabic digits onto number semantic. As arithmetic skills develop, access to and use of these basic number processing skills get more and more automatized. At the same time, symbolic number processing and especially knowledge of arithmetic facts become essential to efficiently solve calculations and thus retrieval of verbal number traces from memory supersedes the understanding of the meaning of numbers. Note that a previous longitudinal study with 209 Dutch-speaking children followed from kindergarten to Grade 1 already tested a similar hypothesis and did not confirm it (Bartelet et al., 2014). Bartelet et al. found a comparable contribution of symbolic magnitude processing to arithmetic across performance levels, thus suggesting a linear relation between these variables. It will be highly relevant to consider whether the results by Bartelet et al. (2014) can be confirmed in the current study, which investigates an older cohort.
Multi-digit number transcoding refers to the ability to shift between spoken number words (e.g., “thirty-two”) and Arabic digits (e.g., 32) and requires mastery of two number codes. On the one hand, understanding of morpho-syllabic structures enables to build-up and understand complex spoken number words in the verbal code (e.g., “sixty” is made up of two morphemes: “six,” indicating the magnitude, and “ty” indicating the place-value class). On the other hand, Arabic digit knowledge and place-value understanding are fundamental to grasp the Arabic number code. Accordingly, previous evidence suggests that multi-digit transcoding explains variance in tasks requiring place-value understanding (Cheung and Ansari, 2021). Multi-digit transcoding was reported to predict reading and reading-arithmetic co-variation (Cirino et al., 2018; Koponen et al., 2020; Amland et al., 2021). The underlying sources of shared variance between multi-digit transcoding and reading may be twofold: (1) Matching of verbal number words and Arabic digits in number transcoding parallels letter-sound binding during reading. These two dimensions may thus share variance related to cross-format mapping; (2) Reading words and transcoding numbers involves also higher-level language resources like morpho-syllabic processing of verbal codes, which is necessary for word construction and analysis. Against this background, we developed two competing hypotheses. The first hypothesis assumes that multi-digit transcoding and reading fluency co-vary due to shared cross-format mapping. Being grapheme-phoneme conversion a foundational skill of reading, we anticipated a contribution of multi-digit transcoding in children with low reading skills at the start of formal schooling, a time window in which some children are still struggling with decoding procedures. Our alternative hypothesis posits that multi-digit transcoding predicts high-level reading fluency, due to shared resources related to morpho-syllabic processing. The use of morpho-syllabic features of words during reading emerges after grapheme-phoneme conversion routines have been consolidated (Ehri, 2005, 2014). A recent review highlighted that reading strategies based on morpho-syllabic processing can be observed as early as in Grade 1 (Levesque et al., 2021). We therefore anticipated to observe a contribution of multi-digit transcoding to high-level reading fluency already in Grade 1.
This study reports the analysis of data from a cross-linguistic project that examined the development of numerical and reading skills in English- and German-speaking primary school children followed from Grade 1 to Grade 3 (Göbel et al., 2020). Longitudinal data relevant for the current study variables was available from a total of 357 children: 191 English-speaking children (t1: Mage = 6 years, 2 months; SDage = 4 months; 50% female; 97% monolingual) and 166 German-speaking children (t1: Mage = 7 years, 2 months; SDage = 3 months; 47% female; 87% monolingual). German-speaking children in Graz (Austria) came from a middle-income urban school district. English-speaking children in Yorkshire (United Kingdom) came from four urban, three town, and four rural schools, with a mean deprivation index decile score of 8 (indicating the 30% of least deprived neighborhoods) (Department for Communities and Local Government, 2015) and an average of 11% of free school meals.
The use of a cross-linguistic design resulted in differences between the samples: (1) English-speaking children were on average one year younger than German-speaking children because compulsory education starts earlier in the UK as compared to Austria; (2) The decade-unit inversion in number transcoding tasks is an additional challenge for German- as compared to English-speaking children. We accounted for language-related differences in the statistical analysis (see data preparation and analysis section for more details). Note that the cognitive dimensions were correlated to the outcome variables in both samples, language group had no substantial impact on these associations. The correlation table is reported in Jöbstl et al. (2024). As language did not impact associations, we merged the two language samples to increase the statistical power of the multivariate quantile regression models.
The study adhered to the principles outlined in the Declaration of Helsinki, and consent was obtained from both the children and their guardians. The ethics committees of the Universities of York and Graz approved the study (Reference number, University of York: 559; University of Graz: 39/23/63 ex 2016/17).
Reading and arithmetic fluency tasks were administered at each time point with similar tasks (t1: Fall of Grade 1, April–July 2017; t2: Fall of Grade 2, April–July 2018; t3: Fall of Grade 3, April–July 2019). Reading fluency was assessed by means of standardized timed tests with words and pseudowords [English: TOWRE-2, Torgesen et al. (2012); German: SLRT-II; Moll and Landerl (2010)]. Arithmetic fluency was measured with one-minute timed tasks including additions and subtractions at t1 and t2, multiplication and division subtasks were added at t3. The assessment of predictors of reading and arithmetic skills took place at t1. These included: (1) Nonverbal IQ, measured with the Raven’s Standard Progressive Matrices Plus (Raven et al., 1998) adapted for group use; (2) Working memory, assessed with Digit Recall Forward, Backward and Block Recall Forward from the Working Memory Test Battery for Children (Pickering and Gathercole, 2001) and a non-standardized Block Recall Backward task; (3) Phonological awareness, collected with phoneme deletion tasks. The English-speaking sample was administered the York Assessment of Reading Comprehension (Snowling et al., 2009), the German-speaking sample was administered a comparable task developed within our lab; (4) RAN tasks with letters and digits from the Comprehensive Test of Phonological Processing [CTOPP; Wagner et al. (2013)]; (5) Counting fluency, administered by means of a timed forward counting task; (6) Magnitude processing, assessed with dots and digits comparison tasks; (7) Multi-digit transcoding, measured with three indicators: number identification, number reading, and number writing. A full description of the tasks is available in the Supplementary Appendix and can also be found in Jöbstl et al. (2024).
Predictors consisting of only one dimension were z-standardized separately in each language group. This was done for two reasons: (1) some measures as for example phonological awareness were assessed with slightly different tasks in the two language groups and therefore raw scores were not on the same scale; (2) The English- and German-speaking groups were matched on duration of formal education. English children, however, start school 1 year earlier than Austrian children, resulting in about 1 year age difference between language groups. Z-standardizing the data in each language group prevented a bias due to this age gap.
For tasks with multiple conditions, principal component analysis (PCA) was employed to derive a composite score. PCAs were conducted in each language group, separately (see Supplementary Appendix for further details). A comprehensive summary of factor loadings can be found in Jöbstl et al. (2024).
We employed quantile regression models to investigate whether prediction patterns depend on the skill level of reading fluency and arithmetic fluency. Quantile regression models enable the investigation of prediction patterns at different performance levels, thus testing for non-linear relationships between variables. Like Bartelet et al. (2014), we performed quantile regressions at the 16th, 50th, and 84th quantiles, which correspond to criterion scores below one standard deviation from the sample mean, the median, and above one standard deviation from the mean, respectively.
We computed two sets of quantile regression models: (1) To address the cognitive basis of the association between reading and arithmetic fluency, we predicted shared variance in reading and arithmetic fluency at each time point. The dependent variables in this set of models were computed by means of PCA on reading and arithmetic fluency variables in each grade (see Supplementary Table S1); (2) To investigate prediction patterns specific to either reading or arithmetic, we included the respective other domain in each regression model (e.g., arithmetic in models predicting reading and vice versa). This enabled us to specifically target one skill domain by controlling for shared variance between the two skill domains. The anova() function (Chambers and Hastie, 1992) was used to compare significant slopes between different quantile models. Specifically, it performs an analysis of variance (ANOVA) to test the equality of distinct slopes across the different quantile models. Goodness of fit was reported as pseudo-R2 for quantile regression (R1, Koenker and Machado, 1999).
Note that the grouping variable referring to the language spoken by participants was not included in any of the regression models. Data were z-standardized separately in each sample and therefore language-related differences in intercepts were controlled for. We also performed OLS regression models, in which we tested whether language group predicted shared and specific variance in reading and arithmetic. Results indicated no significant contribution of this variable (β ≤ 0.15, p ≥ 0.285), which also yielded moderate collinearity with age (VIF = 3.6) and was thus redundant in the models.
We additionally conducted sensitivity analyses to ensure that the results of the quantile regression models conducted in the whole sample were robust against differences in the distribution of variables in the two language groups. We computed quantile regression models in the two language samples separately and then pooled regression coefficients using meta-analysis methods in SPSS (fixed effects). Results are reported in the supplement.
The analysis was run in IBM SPSS Statistics (Version 29) and in R (R Core Team, 2024), p-values <0.05 were considered significant.
Descriptive statistics, including raw scores of the administered tasks, and the correlation matrix can be found in Jöbstl et al. (2024). Quantile regression models predicting shared variance in reading and arithmetic fluency are reported in Table 1. Table 2 displays results of the regression model predicting specific variance in reading fluency, the prediction of arithmetic fluency is in Table 3.
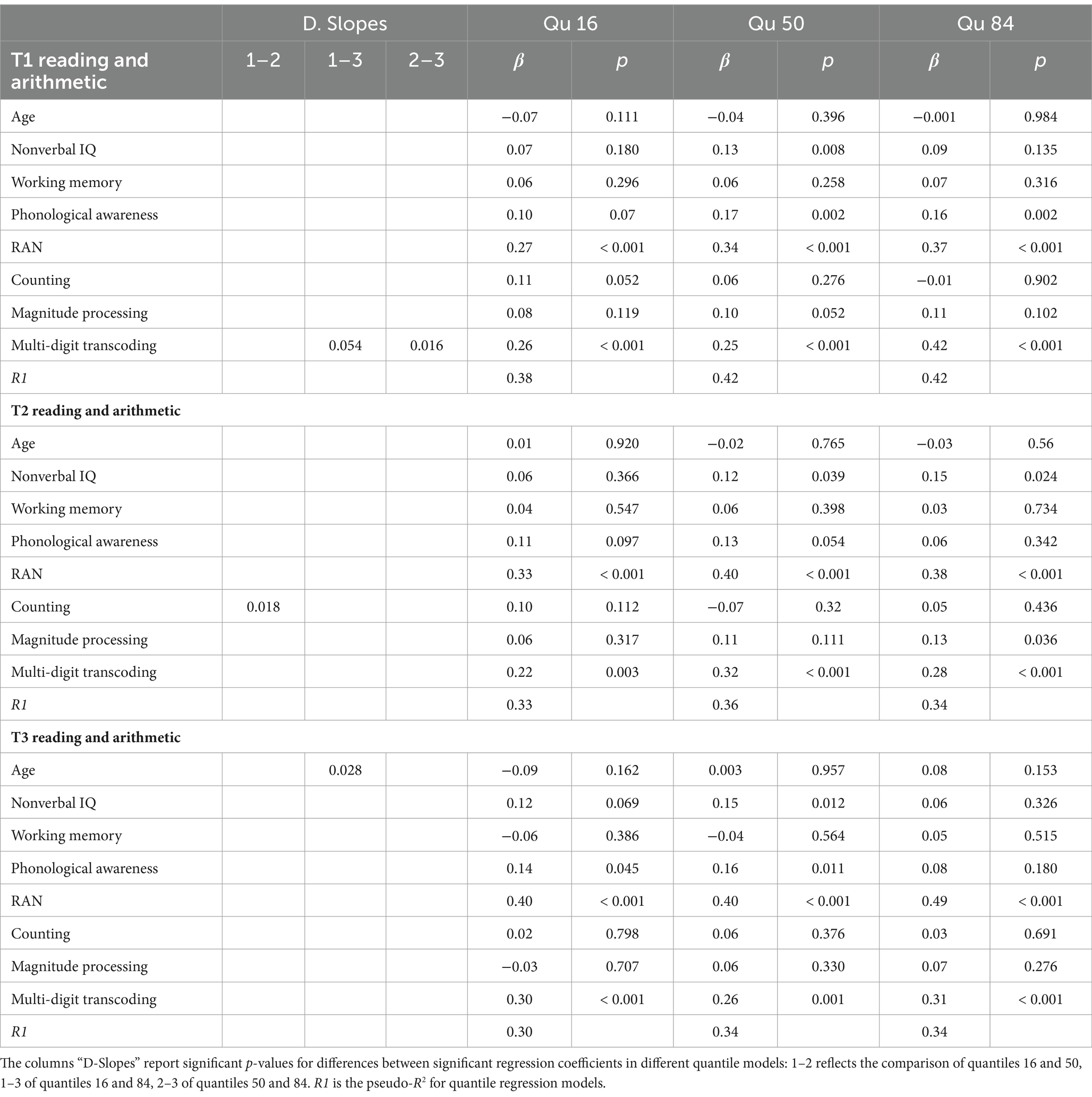
Table 1. Quantile regression models predicting common variance in reading and arithmetic fluency in Grade 1, 2, and 3.
Nonverbal IQ predicted common variance in reading and arithmetic fluency in Grade 1 at percentile 50, in Grade 2 at percentiles 50 and 84, in Grade 3 again only at percentile 50. Slopes did not differ significantly. Working memory made no significant contribution.
Phonological awareness predicted common variance in reading and arithmetic at Grade 1 across performance levels. In Grade 2, this predictor showed only a trend for a significant contribution to quantile 50 (p = 0.054). In Grade 3, phonological awareness predicted performance at percentile 16 and 50. There was no significant difference among slopes across performance levels at any grade. RAN was a robust predictor of common variance in fluency tasks across grades and performance levels, with no difference in slopes.
Counting made no significant contribution. Magnitude processing showed a trend for a significant prediction in Grade 1 at percentile 50 (p = 0.052), and was a significant predictor in Grade 2 at percentile 84. Finally, multi-digit transcoding predicted reading and arithmetic fluency in all grades and across all performance levels. The slope in Grade 1 at percentile 84 was significantly higher than percentile 50 and percentile 16, though as a trend in the latter (p = 0.054).
Age did not uniquely predict reading fluency in any grade or at any quantile level.
Nonverbal IQ predicted 1st grade reading fluency at quantile 84, but not in subsequent grades or at quantile levels 16 and 50. Working memory predicted 2nd grade reading at quantile 16 and 3rd grade reading at quantile level 50. However, the effect of working memory on reading was negative, indicating a suppressor effect. This negative effect is due to the overlap of working memory with other predictors, such as RAN, multi-digit transcoding and arithmetic fluency, which accounted for shared variance while working memory explained criterion-irrelevant variance.
Phonological awareness and RAN were consistent predictors of reading fluency across different performance levels and grades. Counting and magnitude processing, generally considered to be domain-specific to arithmetic, did not explain variance in reading at any quantile or in any grade. Multi-digit transcoding explained variance above arithmetic at quantile levels 50 and 84, but only in 1st grade.
Arithmetic fluency was a significant predictor of reading fluency in each grade. In 1st grade, there was a significant effect at quantiles 16 and 84. In 2nd and 3rd grade, arithmetic fluency consistently explained variance across all quantiles.
It is important to note that while different predictors showed varying effects depending on quantile models, there were no significant differences between slopes.
There was a significant effect of age in 2nd grade arithmetic fluency at quantile level 84, which differed significantly from quantile level 16.
Nonverbal IQ predicted arithmetic fluency in 2nd grade at quantile levels 16 and 50, and in 3rd grade at quantile level 16. While there was no significant difference in slopes in 1st or 2nd grade, there was a significant difference in 3rd grade. The effect at quantile16 was significantly higher than the effect at quantile 84. Working memory was a significant predictor in 1st grade and marginally 3rd grade (quantile 16; p = 0.052). In 1st grade, working memory predicted arithmetic fluency at quantiles 16 and 50, but there was no significant difference among slopes.
Phonological awareness, an established predictor of reading, did not predict arithmetic fluency significantly. Phonological awareness acted as a suppressor variable, likely due to shared variance with reading fluency. RAN accounted for variance in 1st grade arithmetic performance at quantile 16, and marginally quantile 50 (p = 0.055), with no significant differences between slopes.
Counting, a domain-specific predictor of arithmetic, did not predict 1st or 2nd grade arithmetic fluency. However, it predicted 3rd grade arithmetic fluency at quantile 16, with a significant difference compared to quantiles 50 and 84. Magnitude comparison was generally a stable predictor of arithmetic performance across various quantiles, with no significant differences between quantile levels. Multi-digit transcoding was a significant predictor of arithmetic fluency across grades. In 1st grade, multi-digit transcoding predicted arithmetic performance across skill levels, with the largest effects at quantile 84 compared to quantiles 16 and 50. In 2nd grade, multi-digit transcoding was again significant across performance levels, with no differences between slopes. In 3rd grade, multi-digit transcoding predicted significant variance at quantiles 50 and 84, with a significant difference between slopes in favor of quantile 84.
Reading fluency predicted arithmetic fluency across grades and quantiles, except for 1st grade. In 1st grade, only the effect at quantile 50 was significant with no significant differences between slopes in any grade.
Sensitivity analyses with pooled regression coefficients are reported in the Supplementary Tables S2–S4. Results are very consistent with the quantile regression models conducted in the whole sample.
The current study investigated cognitive dimensions that contribute to reading and arithmetic fluency through the first 3 years of primary school, examining whether these contributions differed at different levels of performance. We ran quantile regression models that fitted low-, median- and high-performance in the outcome variables, referring to the 16th, 50th, and 84th percentile, respectively. Note that the 16th percentile is recognized as the clinical cutoff for identifying reading, spelling and arithmetic difficulties in evidence-based guidelines for diagnosing dyslexia and dyscalculia in German-speaking countries (Galuschka and Schulte-Körne, 2016; Haberstroh and Schulte-Körne, 2019). Our analyses aimed to unravel whether there is a substantial difference in the predictive pattern of cognitive dimensions in low-achieving individuals as compared to individuals with typical development and thus represent an important first step in reconciling seemingly inconsistent evidence from two research streams, namely the subtyping and the dimensional approaches.
We addressed the cognitive basis of associations between reading and arithmetic fluency by predicting their shared variance. In a second set of models, we aimed at unveiling the cognitive basis of dissociations between academic skills by introducing arithmetic as a covariate while modeling reading and vice versa, thus addressing the specificity of cognitive predictors for one skill domain.
In a previous analysis of the same data based on OLS multiple regression models Jöbstl et al. (2024), phonological awareness was identified as a reading-specific predictor and magnitude processing as arithmetic-specific predictor. Rapid naming and multi-digit transcoding explained shared variance in reading and arithmetic fluency. Our findings are broadly consistent with this analysis. Importantly, the current study shows that most cognitive dimensions contribute similarly to reading and arithmetic at different levels of attainment, suggesting the existence of linear relations, as the multifactorial perspective would predict. There were few exceptions to this general pattern. We discuss these results in detail in the next sections.
Regression models investigating the cognitive basis of shared variance in reading and arithmetic fluency are consistent with the previous partial correlation analysis by Jöbstl et al. (2024), which indicated a minor contribution of domain-general predictors and a major contribution of domain-specific predictors to covariance in reading and arithmetic fluency, with an important portion of it explained by RAN and multi-digit transcoding.
In the current study, five dimensions predicted shared variance in reading and arithmetic: Nonverbal IQ, phonological awareness, RAN, magnitude processing and multi-digit transcoding. Nonverbal IQ is a domain-general dimension, its involvement in reading-arithmetic covariance indicates that visuo-spatial and reasoning skills are relevant for both literacy and math skills.
The contribution of phonological awareness to shared variance in reading and arithmetic fluency highlights that language processing underpins the covariation between these domains. The fact that this dimension predicted shared variance in Grade 1, was not significant in Grade 2, and again made a reliable contribution in Grade 3 suggests that the language processing dimensions subtended by phonological awareness differ at different levels of instruction. Cross-format mapping as in grapheme-phoneme conversion (reading) and number transcoding (arithmetic) are probably the most likely candidates to explain the contribution of this predictor to shared variance in Grade 1. Note that phonological awareness did not predict low-level shared performance in Grade 1. This may indicate a non-linear relation, although this interpretation is highly unlikely given the robust linear pattern observed in the prediction of specific variance in reading fluency (see further for a discussion of this result). Alternatively, it is possible that the slope in the low-performance range just missed the threshold for significant results (p = 0.07). The role of phonological awareness in Grade 3 may be related to the manipulation of verbal material as for example during memory retrieval of orthographic representations and of arithmetic facts. The prediction did not hold in the high-performance range, indicating that this kind of language processing resources are no longer required once reading and arithmetic competences are highly automatized. Note, however, that our interpretations are very speculative. The observational design of this study and the assessed variables do not allow us to address more precisely the nature of this association. Furthermore, phonological awareness is an intrinsically multifactorial dimension with a complex and bidirectional relation with reading (Landerl et al., 2019). Future studies should investigate in more detail the linguistic features that underlie the covariation between reading and arithmetic, perhaps moving beyond the concept of phonological awareness.
RAN contributed to shared variance in reading and arithmetic fluency across grades and performance levels. Our findings are consistent with a number of previous studies in Finnish- and German-speaking children (Koponen et al., 2007, 2020; Korpipää et al., 2017; Jöbstl et al., 2023). According to the model proposed by Jöbstl et al. (2023), associations between reading and arithmetic can be explained by shared integration mechanisms of visual, verbal and semantic information. Rapid naming is supposed to measure serial retrieval fluency and is therefore a good candidate for measuring these integration processes especially between visual and verbal codes.
Magnitude comparison made a small and isolated contribution to high-level shared performance in Grade 2. This might be an indication of the role of symbolic processing resources in reading-arithmetic covariation. Note, however, that this scattered significant finding may as well be driven by the high number of regression models performed (see limitation section for a more in-depth consideration of this problem). It should thus be interpreted with caution until replicated.
Multi-digit transcoding was a reliable predictor of shared variance at all grades and performance levels, with the strongest prediction in Grade 1 at high-level performance. There are two likely explanations for the involvement of this dimension in reading and arithmetic covariance. First, multi-digit transcoding requires cross-format mapping, that is, mapping of Arabic digits onto number words and vice versa, a feature that is necessary to do arithmetic and that parallels letter-sound binding in reading. Second, multi-digit transcoding requires morpho-syllabic processing, which enables to convert spoken number words into Arabic numbers (and vice versa) using the so-called transcoding routines (Barrouillet et al., 2004). This form of higher-level language processing is relevant for reading too and therefore it may represent a second important source of shared variance between reading and arithmetic fluency.
Nonverbal IQ predicted high-level performance in Grade 1. Its minor contribution suggests a marginal involvement of general cognitive resources in reading fluency. Working memory predicted reading fluency in Grade 2 at percentile 16 and in Grade 3 at percentile 50. Note that all significant and non-significant beta coefficients were negative for this regressor, meaning that higher working memory resources were related to lower reading fluency. This is unexpected given that working memory was positively correlated with reading fluency (rs between 0.22 and 0.29). The pattern reflects a suppression effect due to the association of working memory with RAN, multi-digit transcoding and arithmetic fluency. This suppressor effect indicates that the four dimensions share a common component, most likely related to the central executive resources of working memory (Baddeley, 2012). The central executive includes sustained, selective attention and monitoring skills that are transversal to many tasks and situations of cognitive effort. These resources are not specific to the prediction of reading fluency, and probably enhanced the effect of other variables.
Our hypothesis that phonological awareness and RAN would preferentially contribute to reading fluency was confirmed. The two dimensions made specific contributions throughout performance levels and time points. This finding is in line with our previous analysis Jöbstl et al. (2024) and with a number of previous studies [see Landerl et al., 2022 for a recent review] and highlights the importance of these two components for reading fluency and its development through the first 3 years of school in a less (English) and a more transparent orthography (German). Our results indicate the existence of a linear relation between the two constructs and reading fluency, thus suggesting that phonological awareness and RAN predict low and high reading fluency skills to the same extent. Our findings are partly in line with a previous longitudinal study based on a dimensional approach (McIlraith, 2018). This study used quantile regression to predict Grade 1 reading performance from preschool and kindergarten predictors in 293 English-speaking children. They found reliable contributions of RAN and PA measured in kindergarten to reading at median and high-performance levels but not at low-performance level. There may be multiple reasons for the existing inconsistencies between our study and previous evidence, as for instance differences in the statistical analysis, the type of tasks, the assessment time point and the level of instruction. Future studies should aim to disentangle these confounding effects in the attempt to understand these inconsistencies.
As to cross-domain contributions, multi-digit transcoding predicted reading fluency in Grade 1 at median and high-level performance. This pattern of specific contribution does not align well with the idea that cross-format mapping is the primary source of co-variation between the two skills. If that was the case, we should have found a reliable contribution of multi-digit transcoding to reading at low-performance level. Our findings are more consistent with the hypothesis that multi-digit transcoding and reading share morpho-syllabic processing resources that are particularly relevant for high-level reading fluency. Note, however, that this hypothesis would have predicted a reliable contribution of transcoding to reading throughout grades, which was not found. The lack of contribution at higher grades is difficult to explain. We might speculate that the morpho-syllabic processing skills shared between the two dimensions are simple, mostly consisting in derivational rules for word assembly (as in “friend-ship” and “six-ty”), and these may be well consolidated already at the end of Grade 1, thus being not relevant for reading fluency in higher grades.
Counting and magnitude processing made no significant prediction to reading fluency, thus suggesting that these dimensions are not relevant for reading fluency once variance in arithmetic is controlled for.
Nonverbal IQ predicted low- and median-level arithmetic fluency in Grade 2 and low-level arithmetic fluency in Grade 3. The nonverbal IQ task involved reasoning and visuospatial processing, characteristics that are intrinsic to number processing (Cipora et al., 2020). This pattern of prediction suggests that the involvement of these skills in arithmetic becomes relevant above Grade 1, probably coinciding with more mature processing of multi-digit numbers and understanding of the positional system. The fact that nonverbal IQ contributed to low/median performance indicates that resources like reasoning and visuospatial processing are engaged by children who do not yet rely upon efficient verbal retrieval skills for arithmetic facts and need these resources as a support for effortful calculation strategies based on algorithms.
Working memory predicted arithmetic fluency at low- and median-level performance in Grade 1 (there was a similar trend also in Grade 3). These findings suggest that working memory resources play a more prominent role in young children with rather low arithmetic fluency skills. This is in line with previous evidence reporting a working memory deficit in dyscalculia (Szucs et al., 2013). Low performance on speeded addition and subtraction tasks can either derive from erroneous fact retrieval due to interfering memory traces (De Visscher and Noël, 2013) or from limited availability of arithmetic facts, which results in the use of simple counting strategies as an alternative method to achieve a correct solution. In both cases, children require an important engagement of storage and manipulation of numerical information, thus taxing working memory resources. In contrast, children with high performance in speeded addition and subtraction tasks most likely rely on robust memory traces that can be effortlessly accessed with no need for any further manipulation.
Among numerical predictors, counting predicted arithmetic fluency in Grade 3 in the low-level performance range. This result is only partly in line with our hypotheses. We expected counting to be preferentially related to arithmetic, with a more important contribution at the beginning of formal schooling. The fact that counting predicted arithmetic fluency in Grade 3 but not in Grade 1 is difficult to reconcile with our hypothesis. Our results are also against the idea that counting is related to serial retrieval mechanisms, as it should predict high-level arithmetic fluency performance, which is supposed to rely heavily on retrieving facts from memory. In contrast, counting only contributed to low-level performance in Grade 3. Our findings rather suggest that counting is used as a compensatory strategy to solve arithmetic problems in children that cannot fluently retrieve arithmetic facts. This interpretation is in line with clinical descriptions of children with dyscalculia that mention preponderant use of counting instead of fact retrieval strategies in solving math problems (Kucian and von Aster, 2015; Haberstroh and Schulte-Körne, 2019).
With sparse exceptions, magnitude processing was a reliable predictor of arithmetic fluency throughout grades and performance levels. This is consistent with previous literature reporting a specific contribution of magnitude processing to arithmetic (Jöbstl et al., 2023). In line with Bartelet et al. (2014), we found no difference in the predictive pattern depending on performance level. Our results thus highlight that magnitude processing makes a similar contribution at any level of arithmetic achievement during the first 3 years of formal schooling. This is in line with the assumption of the multiple deficit model and highlights that the ability to understand non-symbolic and symbolic number semantic contributes to arithmetic fluency at any level of proficiency.
Multi-digit number transcoding contributed robustly to arithmetic through grades and performance levels (the only exception being its non-significant contribution to low-level performance in Grade 3). In line with our previous analysis Jöbstl et al. (2024), the current findings indicate that the contribution of multi-digit number transcoding to arithmetic fluency is specific, as it holds after controlling for variance in reading fluency. This finding adds up to previous evidence indicating multi-digit number transcoding as one of the most important predictors of arithmetic over and above other numerical predictors (Göbel et al., 2014; Habermann et al., 2020; Banfi et al., 2022). Across grades, the increase in the slopes of the transcoding-predictors with increasing levels of arithmetic fluency likely indicates that these two skills co-vary more strongly when both are highly efficient and automated.
As to cross-domain predictors, we found that RAN predicted Grade 1 arithmetic fluency at the low-performance level and, as a trend, at median-performance level. The significant contribution of RAN to Grade 1 arithmetic fluency was already reported in our previous analysis with OLS regression. Our results partly support previous literature reporting rapid naming as a predictor of arithmetic fluency (Koponen et al., 2013, 2020; Korpipää et al., 2017), and extends it by showing that the association between RAN and arithmetic fluency holds after controlling for reading. However, the reason why in the present study this variable contributed to low-level reading performance is unclear. We expected RAN to predict high-performance level, as it is supposed to measure serial retrieval efficiency relevant for automatized and retrieval-based skills. One possible explanation for the current results is that RAN captured variance in arithmetic fluency that was not already explained by reading fluency. Beginning readers with low reading fluency are unlikely to engage in serial retrieval skills, as they are still committed in training grapheme-phoneme conversion rules. It is thus possible that, at low-level reading performance, arithmetic shares more similarity with RAN than with reading.
Our analysis consisted of 27 multivariate regression models (three main dependent variables investigated over three time points and three levels of performance). Given that the likelihood of committing Type I errors increases with the number of outcome variables investigated, we cannot rule out the possibility that some of our significant results were actually driven by chance. All regression coefficients and the corresponding p-values are reported in the tables of regression results. We invite the reader to interpret the most scattered findings with caution, because these may not be robust. Beside p-values, it is important to consider the magnitude of the effects and whether these will be replicated by future studies with a comparable design.
Due to power constraints related to the sample size, only a limited number of domain-general dimensions (nonverbal intelligence and working memory) were included in the current study. Research evidence suggests that other domain-general dimensions as for instance different executive functions explain variance in reading, arithmetic and their overlap (Balhinez and Shaul, 2019; Koponen et al., 2020; Zoccolotti et al., 2020). Note, however, that these domain-general predictors were shown to be indirectly related to the outcome variables (Koponen et al., 2020) and their contribution was smaller than the one of reading- and arithmetic-specific predictors (Moll et al., 2014; Peterson et al., 2017; Cirino et al., 2018; Koponen et al., 2020; Malone et al., 2020). Nevertheless, literature on the role and importance of these dimensions to reading, arithmetic and their overlap is scattered. Future studies with large sample sizes should systematically test the contribution of these dimensions.
The current study based on an analysis of longitudinal data highlights that dimensions contributing to reading and arithmetic fluency have a similar predictive role across time points and performance levels. This indicates that the prediction in the low-performance range does not differ substantially from the prediction in the typical performance range. One relevant exception to this trend is counting fluency, which may serve compensatory calculation strategies for children with low arithmetic fluency in Grade 3.
Dimensions that explain shared variance in reading and arithmetic fluency or that make specific cross-domain contributions relate to retrieval efficiency, language/symbolic processing and cross-format mapping, skills that are necessary for successful integration of visual, verbal and semantic information relevant for both reading and arithmetic fluency.
The existence of a general linear prediction pattern suggests that the investigated cognitive dimensions are relevant for children with very different attainment in reading and arithmetic fluency. The results of the present study therefore highlight the benefits of early assessment of literacy and numeracy skills, as in currently available screening tools [see for example Jöbstl et al., 2022]. Having shown that cognitive dimensions in Grade 1 predict both high and low levels of performance later on, risk factors for reading and arithmetic difficulties can be identified at an early stage, which in turn makes it possible to design support programs that focus on strengthening below-average skills. Similarly, the early identification of skilled cognitive resources enables to target children with exceptionally high literacy and arithmetic skills and support them appropriately throughout formal schooling.
Publicly available datasets were analyzed in this study. This data can be found here: https://reshare.ukdataservice.ac.uk/854335/.
The studies involving humans were approved by the ethics committees of the Universities of Graz and York. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin.
CB: Data curation, Formal analysis, Investigation, Methodology, Visualization, Writing – original draft. VJ: Data curation, Formal analysis, Investigation, Methodology, Visualization, Writing – original draft. SG: Conceptualization, Funding acquisition, Investigation, Project administration, Resources, Supervision, Writing – review & editing. KL: Conceptualization, Funding acquisition, Investigation, Project administration, Resources, Supervision, Writing – review & editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded in part by the Austrian Science Fund (FWF; I 2778-G16) and by the Economic and Social Research Council (ESRC; ES/N014677/1, ES/W002914/1). For the purpose of open access, the authors have applied a CC BY public copyright license to any author accepted manuscript version arising from this submission.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1335957/full#supplementary-material
Amland, T., Lervåg, A., and Melby-Lervåg, M. (2021). Comorbidity between math and reading problems: is phonological processing a mutual factor? Front. Hum. Neurosci. 14:e577304. doi: 10.3389/fnhum.2020.577304
Astle, D. E., and Fletcher-Watson, S. (2020). Beyond the core-deficit hypothesis in developmental disorders. Curr. Dir. Psychol. Sci. 29, 431–437. doi: 10.1177/0963721420925518
Baddeley, A. D. (2012). Working memory: theories, models, and controversies. Annu. Rev. Psychol. 63, 1–29. doi: 10.1146/annurev-psych-120710-100422
Balhinez, R., and Shaul, S. (2019). The relationship between reading fluency and arithmetic fact fluency and their shared cognitive skills: a developmental perspective. Front. Psychol. 10:1281. doi: 10.3389/fpsyg.2019.01281
Banfi, C., Clayton, F. J., Steiner, A. F., Finke, S., Kemény, F., Landerl, K., et al. (2022). Transcoding counts: longitudinal contribution of number writing to arithmetic in different languages. J. Exp. Child Psychol. 223:105482. doi: 10.1016/j.jecp.2022.105482
Barrouillet, P., Camos, V., Perruchet, P., and Seron, X. (2004). ADAPT: a developmental, asemantic, and procedural model for transcoding from verbal to Arabic numerals. Psychol. Rev. 111, 368–394. doi: 10.1037/0033-295X.111.2.368
Bartelet, D., Vaessen, A., Blomert, L., and Ansari, D. (2014). What basic number processing measures in kindergarten explain unique variability in first-grade arithmetic proficiency? J. Exp. Child Psychol. 117, 12–28. doi: 10.1016/j.jecp.2013.08.010
Bernabini, L., Bonifacci, P., and de Jong, P. F. (2021). The relationship of reading abilities with the underlying cognitive skills of math: a dimensional approach. Front. Psychol. 12:577488. doi: 10.3389/fpsyg.2021.577488
Caravolas, M., Lervåg, A., Mousikou, P., Efrim, C., Litavský, M., Onochie-Quintanilla, E., et al. (2012). Common patterns of prediction of literacy development in different alphabetic orthographies. Psychol. Sci. 23, 678–686. doi: 10.1177/0956797611434536
Cheung, P., and Ansari, D. (2021). Cracking the code of place value: the relationship between place and value takes years to master. Dev. Psychol. 57, 227–240. doi: 10.1037/dev0001145
Child, A. E., Cirino, P. T., Fletcher, J. M., Willcutt, E. G., and Fuchs, L. S. (2019). A cognitive dimensional approach to understanding shared and unique contributions to Reading, math, and attention skills. J. Learn. Disabil. 52, 15–30. doi: 10.1177/0022219418775115
Cipora, K., He, Y., and Nuerk, H. C. (2020). The spatial–numerical association of response codes effect and math skills: why related? Ann. N. Y. Acad. Sci. 1477, 5–19. doi: 10.1111/nyas.14355
Cirino, P. T., Child, A. E., and Macdonald, K. T. (2018). Longitudinal predictors of the overlap between reading and math skills. Contemp. Educ. Psychol. 54, 99–111. doi: 10.1016/j.cedpsych.2018.06.002
Cirino, P. T., Fuchs, L. S., Elias, J. T., Powell, S. R., and Schumacher, R. F. (2015). Cognitive and mathematical profiles for different forms of learning difficulties. J. Learn. Disabil. 48, 156–175. doi: 10.1177/0022219413494239
Clayton, F. J., Copper, C., Steiner, A. F., Banfi, C., Finke, S., Landerl, K., et al. (2020). Two-digit number writing and arithmetic in year 1 children: does number word inversion matter? Cogn. Dev. 56, 1–14. doi: 10.1016/j.cogdev.2020.100967
Coltheart, M., Rastle, K., Perry, C., Langdon, R., and Ziegler, J. (2001). DRC: a dual route cascaded model of visual word recognition and reading aloud. Psychol. Rev. 108:204. doi: 10.1037//0033-295X.108.1.204
de Groot, B. J. A., van den Bos, K. P., Minnaert, A. E. M. G., and van der Meulen, B. F. (2015). Phonological processing and word reading in typically developing and reading disabled children: severity matters. Sci. Stud. Read. 19, 166–181. doi: 10.1080/10888438.2014.973028
De Visscher, A., and Noël, M. P. (2013). A case study of arithmetic facts dyscalculia caused by a hypersensitivity-to-interference in memory. Cortex 49, 50–70. doi: 10.1016/j.cortex.2012.01.003
Department for Communities and Local Government (2015). The English indices of deprivation 2015 [statistical release]. Available at: https://www.gov.uk/government/statistics/english-indices-of-deprivation-2015.
Devlin, B. L., Jordan, N. C., and Klein, A. (2022). Predicting mathematics achievement from subdomains of early number competence: differences by grade and achievement level. J. Exp. Child Psychol. 217:105354. doi: 10.1016/j.jecp.2021.105354
Dirks, E., Spyer, G., Van Lieshout, E. C. D. M., and De Sonneville, L. (2008). Prevalence of combined reading and arithmetic disabilities. J. Learn. Disabil. 41, 460–473. doi: 10.1177/0022219408321128
Durand, M., Hulme, C., Larkin, R., and Snowling, M. (2005). The cognitive foundations of reading and arithmetic skills in 7- to 10-year-olds. J. Exp. Child Psychol. 91, 113–136. doi: 10.1016/j.jecp.2005.01.003
Ehri, L. C. (2005). Learning to read words: theory, findings, and issues. Sci. Stud. Read. 9, 167–188. doi: 10.1207/s1532799xssr0902_4
Ehri, L. C. (2014). Orthographic mapping in the acquisition of sight word reading, spelling memory, and vocabulary learning. Sci. Stud. Read. 18, 5–21. doi: 10.1080/10888438.2013.819356
Frith, U. (1985). “Beneath the surface of developmental dyslexia” in Surface dyslexia: Neuropsychological and cognitive studies of phonological reading. eds. K. Patterson, J. C. Marshall, and M. Coltheart (Erlbaum), 301–330.
Fuchs, L. S., Geary, D. C., Fuchs, D., Compton, D. L., and Hamlett, C. L. (2016). Pathways to third-grade calculation versus word-reading competence: are they more alike or different? Child Dev. 87, 558–567. doi: 10.1111/cdev.12474
Galuschka, K., and Schulte-Körne, G. (2016). The diagnosis and treatment of reading and / or spelling disorders in children and adolescents. Dtsch. Arztebl. Int. 113, 279–286. doi: 10.3238/arztebl.2016.0279
Geary, D. C. (2011). Cognitive predictors of achievement growth in mathematics. Dev. Psychol. 47, 1539–1552. doi: 10.1037/a0025510.Cognitive
Geary, D. C., and VanMarle, K. (2018). Growth of symbolic number knowledge accelerates after children understand cardinality. Cognition 177, 69–78. doi: 10.1016/j.cognition.2018.04.002
Georgiou, G. K., Parrila, R., Cui, Y., and Papadopoulos, T. C. (2013). Why is rapid automatized naming related to reading? J. Exp. Child Psychol. 115, 218–225. doi: 10.1016/j.jecp.2012.10.015
Georgiou, G. K., Wei, W., Inoue, T., and Deng, C. (2020). Are the relations of rapid automatized naming with reading and mathematics accuracy and fluency bidirectional? Evidence from a 5-year longitudinal study with Chinese children. J. Educ. Psychol. 112, 1506–1520. doi: 10.1037/edu0000452
Göbel, S. M., Watson, S. E., Lervåg, A., and Hulme, C. (2014). Children’s arithmetic development: it is number knowledge, not the approximate number sense, that counts. Psychol. Sci. 25, 789–798. doi: 10.1177/0956797613516471
Göbel, S., Wesierska, M., and Landerl, K. (2020). Three-hundred-and-twenty-eight and 328: Cross-format number integration and its relationship to mathematics performance 2017–2020 [data set].
Habermann, S., Donlan, C., Göbel, S. M., and Hulme, C. (2020). The critical role of Arabic numeral knowledge as a longitudinal predictor of arithmetic development. J. Exp. Child Psychol. 193:104794. doi: 10.1016/j.jecp.2019.104794
Haberstroh, S., and Schulte-Körne, G. (2019). The diagnosis and treatment of dyscalculia. Deutsches Arzteblatt Int. 116, 107–114. doi: 10.3238/arztebl.2019.0107
Jöbstl, V., Banfi, C., Göbel, S. M., and Landerl, K. (2024). Cognitive predictors of reading-arithmetic associations and dissociations: A longitudinal study from Grade 1 to Grade 3. [Manuscript submitted for publication].
Jöbstl, V., Steiner, A. F., Deimann, P., Kastner-Koller, U., and Landerl, K. (2023). A-B-3-associations and dissociations of reading and arithmetic: is domain-specific prediction outdated? PLoS One 18:e0285437. doi: 10.1371/journal.pone.0285437
Jöbstl, V., Steiner, A. F., Kastner-koller, U., Deimann, P., Kaltenberger, A., Wagner, V., et al. (2022). Entwicklung eines förderorientierten Schuleingangsscreenings. Erste Befunde zur prognostischen Validität. [development of support-oriented school entrance screening. First results about prognostic validity]. Frühe Bildung 11, 194–200. doi: 10.1026/2191-9186/a000585
Joyner, R. E., and Wagner, R. K. (2020). Co-occurrence of reading disabilities and math disabilities: a meta-analysis. Sci. Stud. Read. 24, 14–22. doi: 10.1080/10888438.2019.1593420
Kirby, J. R., Georgiou, G. K., Martinussen, R., and Parrila, R. (2010). Naming speed and reading: from prediction to instruction. Read. Res. Q. 45, 341–362. doi: 10.1598/RRQ.45.3.4
Koenker, R., and Machado, J. A. F. (1999). Goodness of fit and related inference processes for quantile regression. J. Am. Stat. Assoc. 94, 1296–1310,
Koponen, T., Aro, M., Poikkeus, A. M., Niemi, P., Lerkkanen, M. K., Ahonen, T., et al. (2018). Comorbid fluency difficulties in reading and math: longitudinal stability across early grades. Except. Child. 84, 298–311. doi: 10.1177/0014402918756269
Koponen, T., Aunola, K., Ahonen, T., and Nurmi, J. E. (2007). Cognitive predictors of single-digit and procedural calculation skills and their covariation with reading skill. J. Exp. Child Psychol. 97, 220–241. doi: 10.1016/j.jecp.2007.03.001
Koponen, T., Eklund, K., Heikkilä, R., Salminen, J., Fuchs, L., Fuchs, D., et al. (2020). Cognitive correlates of the covariance in reading and arithmetic fluency: importance of serial retrieval fluency. Child Dev. 91, 1063–1080. doi: 10.1111/cdev.13287
Koponen, T., Salmi, P., Eklund, K., and Aro, T. (2013). Counting and RAN: predictors of arithmetic calculation and reading fluency. J. Educ. Psychol. 105, 162–175. doi: 10.1037/a0029285
Korpipää, H., Koponen, T., Aro, M., Tolvanen, A., Aunola, K., Poikkeus, A. M., et al. (2017). Covariation between reading and arithmetic skills from grade 1 to grade 7. Contemp. Educ. Psychol. 51, 131–140. doi: 10.1016/j.cedpsych.2017.06.005
Kucian, K., and von Aster, M. (2015). Developmental dyscalculia. Eur. J. Pediatr. 174, 1–13. doi: 10.1007/s00431-014-2455-7
Landerl, K., Castles, A., and Parrila, R. (2022). Cognitive precursors of reading: a cross-linguistic perspective. Sci. Stud. Read. 26, 111–124. doi: 10.1080/10888438.2021.1983820
Landerl, K., Freudenthaler, H. H., Heene, M., De Jong, P. F., Desrochers, A., Manolitsis, G., et al. (2019). Phonological awareness and rapid automatized naming as longitudinal predictors of reading in five alphabetic orthographies with varying degrees of consistency. Sci. Stud. Read. 23, 220–234. doi: 10.1080/10888438.2018.1510936
Landerl, K., Fussenegger, B., Moll, K., and Willburger, E. (2009). Dyslexia and dyscalculia: two learning disorders with different cognitive profiles. J. Exp. Child Psychol. 103, 309–324. doi: 10.1016/j.jecp.2009.03.006
Landerl, K., Göbel, S. M., and Moll, K. (2013a). Core deficit and individual manifestations of developmental dyscalculia (DD): the role of comorbidity. Trends Neurosci. Educ. 2, 38–42. doi: 10.1016/j.tine.2013.06.002
Landerl, K., and Moll, K. (2010). Comorbidity of learning disorders: prevalence and familial transmission. J. Child Psychol. Psychiatry Allied Discip. 51, 287–294. doi: 10.1111/j.1469-7610.2009.02164.x
Landerl, K., Ramus, F., Moll, K., Lyytinen, H., Leppänen, P. H. T., Lohvansuu, K., et al. (2013b). Predictors of developmental dyslexia in European orthographies with varying complexity. J. Child Psychol. Psychiatry Allied Discip. 54, 686–694. doi: 10.1111/jcpp.12029
Levesque, K. C., Breadmore, H. L., and Deacon, S. H. (2021). How morphology impacts reading and spelling: advancing the role of morphology in models of literacy development. J. Res. Read. 44, 10–26. doi: 10.1111/1467-9817.12313
Malone, S. A., Burgoyne, K., and Hulme, C. (2020). Number knowledge and the approximate number system are two critical foundations for early arithmetic development. J. Educ. Psychol. 112, 1167–1182. doi: 10.1037/edu0000426
McGrath, L. M., Peterson, R. L., and Pennington, B. F. (2020). The multiple deficit model: Progress, problems, and prospects. Sci. Stud. Read. 24, 7–13. doi: 10.1080/10888438.2019.1706180
McIlraith, A. L. (2018). Predicting word reading ability: a quantile regression study. J. Res. Read. 41, 79–96. doi: 10.1111/1467-9817.12089
Moll, K., Fussenegger, B., Willburger, E., and Landerl, K. (2009). RAN is not a measure of orthographic processing. Evidence from the asymmetric German orthography. Sci. Stud. Read. 13, 1–25. doi: 10.1080/10888430802631684
Moll, K., Göbel, S. M., and Snowling, M. J. (2015). Basic number processing in children with specific learning disorders: comorbidity of reading and mathematics disorders. Child Neuropsychol. 21, 399–417. doi: 10.1080/09297049.2014.899570
Moll, K., Kunze, S., Neuhoff, N., Bruder, J., and Schulte-Körne, G. (2014). Specific learning disorder: prevalence and gender differences. PLoS One 9:e103537. doi: 10.1371/journal.pone.0103537
Moll, K., and Landerl, K. (2010). SLRT-II: Lese-und Rechtschreibtest [SLRT-II: Reading and spelling test] : Huber.
Moll, K., Ramus, F., Bartling, J., Bruder, J., Kunze, S., Neuhoff, N., et al. (2014). Cognitive mechanisms underlying reading and spelling development in five European orthographies. Learn. Instr. 29, 65–77. doi: 10.1016/j.learninstruc.2013.09.003
Ozernov-Palchik, O., Sideridis, G. D., Norton, E. S., Beach, S. D., Wolf, M., Gabrieli, J. D. E., et al. (2022). On the cusp of predictability: disruption in the typical association between letter and word identification at critical thresholds of RAN and phonological skills. Learn. Individ. Differ. 97:102166. doi: 10.1016/j.lindif.2022.102166
Pennington, B. F. (2006). From single to multiple models of developmental disorders. Cognition 101, 385–413. doi: 10.1016/j.cognition.2006.04.008
Perfetti, C. A., and Hart, L. (2001). “The lexical quality hypothesis” in Precursors of functional literacy2. eds. L. Verhoeven, C. Elbro, and P. Reitsma (Amsterdam: John Benjamins Publishing Company), 189–213.
Peters, L., and Ansari, D. (2019). Are specific learning disorders truly specific, and are they disorders? Trends in Neuroscience and Education 17:100115. doi: 10.1016/j.tine.2019.100115
Peters, L., and De Smedt, B. (2018). Arithmetic in the developing brain: a review of brain imaging studies. Dev. Cogn. Neurosci. 30, 265–279. doi: 10.1016/j.dcn.2017.05.002
Peterson, R. L., Boada, R., Mcgrath, L. M., Willcutt, E. G., Olson, R. K., and Pennington, B. F. (2017). Cognitive prediction of reading, math, and attention: shared and unique influences. J. Learn. Disabil. 50, 408–421. doi: 10.1126/science.1249098.Sleep
Pickering, S., and Gathercole, S. E. (2001). Working memory test battery for children (WMTB-C) : Psychological Corporation.
Protopapas, A., and Parrila, R. (2018). Is dyslexia a brain disorder? Brain Sci. 8, 1–18. doi: 10.3390/brainsci8040061
Raddatz, J., Kuhn, J. T., Holling, H., Moll, K., and Dobel, C. (2017). Comorbidity of arithmetic and Reading disorder: basic number processing and calculation in children with learning impairments. J. Learn. Disabil. 50, 298–308. doi: 10.1177/0022219415620899
Raven, J., Raven, J. C., and Court, J. H. (1998). Raven’s standard progressive matrices and vocabulary scales. Oxford (UK): Oxford Psychologists Press.
R Core Team (2024). R: A language and environment for statistical computing_. Vienna, Austria: R Foundation for Statistical Computing. Available at: https://www.R-project.org/.
Siegel, L. S., and Heaven, R. K. (1986). “Categorization of learning disabilities” in Handbook of cognitive, social and neuropsychological aspects of learning disabilities (Routledge), 95–122.
Snowling, M. J., Stothard, S. E., Clarke, P., Bowyer-Crane, C., Harrington, A., Truelove, E., et al., (2009). York assessment of Reading for comprehension (YARC). GL Assessment.
Starr, A., Libertus, M. E., and Brannon, E. M. (2013). Number sense in infancy predicts mathematical abilities in childhood. Proc. Natl. Acad. Sci. USA 110, 18116–18120. doi: 10.1073/pnas.1302751110
Szucs, D., Devine, A., Soltesz, F., Nobes, A., and Gabriel, F. (2013). Developmental dyscalculia is related to visuo-spatial memory and inhibition impairment. Cortex 49, 2674–2688. doi: 10.1016/j.cortex.2013.06.007
Torgesen, J. K., Wagner, R. K., and Rashotte, C. A. (2012). Test of word reading efficiency – Second edition (TOWRE-2). Pro-Ed.
Träff, U., Skagerlund, K., Östergren, R., and Skagenholt, M. (2023). The importance of domain-specific number abilities and domain-general cognitive abilities for early arithmetic achievement and development. Br. J. Educ. Psychol. 93, 825–841, e12599. doi: 10.1111/bjep.12599
Vanbinst, K., van Bergen, E., Ghesquière, P., and De Smedt, B. (2020). Cross-domain associations of key cognitive correlates of early reading and early arithmetic in 5-year-olds. Early Child. Res. Q. 51, 144–152. doi: 10.1016/j.ecresq.2019.10.009
Wagner, R. K., Torgesen, J. K., Rashotte, C. A., and Pearson, N. A. (2013). Comprehensive test of phonological processing 2nd ed. (CTOPP-2). Pro-Ed.
Willburger, E., Fussenegger, B., Moll, K., Wood, G., and Landerl, K. (2008). Naming speed in dyslexia and dyscalculia. Learn. Individ. Differ. 18, 224–236. doi: 10.1016/j.lindif.2008.01.003
Willcutt, E. G., McGrath, L. M., Pennington, B. F., Keenan, J. M., DeFries, J. C., Olson, R. K., et al. (2019). “Understanding comorbidity between specific learning disabilities” in Models for innovation: Advancing approaches to Higher-Rick and Higher-impact Learnig disabilities science. New directions for Child and adolescent development. eds. L. S. Fuchs and D. L. Compton, vol. 165, 91–109.
Willcutt, E. G., Petrill, S. A., Wu, S., Boada, R., DeFries, J. C., Olson, R. K., et al. (2013). Comorbidity between reading disability and math disability: concurrent psychopathology, functional impairment, and neuropsychological functioning. J. Learn. Disabil. 46, 500–516. doi: 10.1038/jid.2014.371
Zoccolotti, P., Angelelli, P., Marinelli, C. V., and Romano, D. L. (2021). A network analysis of the relationship among reading, spelling and maths skills. Brain Sci. 11:656. doi: 10.3390/brainsci11050656
Keywords: arithmetic, development, longitudinal, quantile regression, reading
Citation: Banfi C, Jöbstl V, Göbel SM and Landerl K (2024) Longitudinal predictors of reading and arithmetic at different attainment levels. Front. Educ. 9:1335957. doi: 10.3389/feduc.2024.1335957
Received: 14 November 2023; Accepted: 16 April 2024;
Published: 26 April 2024.
Edited by:
Christoph Weber, University of Education Upper Austria, AustriaReviewed by:
Steffen Zitzmann, University of Tübingen, GermanyCopyright © 2024 Banfi, Jöbstl, Göbel and Landerl. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chiara Banfi, Y2hpYXJhLmJhbmZpQHVuaS1ncmF6LmF0
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.