Edith Debrenti- Department of Economics, Faculty of Economics and Social Science, Partium Christian University, Oradea, Romania
Using game-based learning (GBL), especially digital game-based learning (DGBL), as a teaching and learning environment can be a pedagogical resource and a good strategy in the classroom to support mathematical learning. Effective manipulatives and games play a crucial role in promoting mathematical understanding. They support students in building, reinforcing and connecting varied representations of mathematical concepts. High-quality games are particularly valuable for learners as they provide them with control and adaptability. These games have properties that are adapted to cognitive and mathematical structures, facilitating the development of connections between different pieces and forms of knowledge. Digital games can help to achieve the same effects. In this paper, we conduct a quasi-experiment using games developed for this purpose. Our aim is to investigate whether non-digital games vs. digital games yield different results. Our results indicate that while students enjoyed themselves and found the task-solving enjoyable during both types of game-based learning, the use of non-digital games vs. digital games can sometimes lead to different outcomes.
1 Introduction
According to Rosli et al. (2015) prekindergarten, kindergarten, and elementary school teachers use both tangible and virtual manipulatives as instructional aides to facilitate student understanding of concepts in numbers, operations, geometry, algebra, measurements, data analysis, and probability. Tangible manipulatives assist students in constructing, reinforcing, and linking diverse mathematical concepts. From literature, engaging in concrete activities serves as a beneficial mental exercise (Clements, 1989; Kamii, 1989). Clements (1999) found that for teachers to actively engage children's thinking, manipulatives must be integrated into educational tasks to provide meaningful context and support, alone they are not enough. “Games are effective not because of what they are, but because of what they embody and what learners are doing as they play a game” (Van Eck, 2006, p. 18). According to Russo and Russo (2018) and Russo et al. (2023), the six principles of educationally rich mathematical games in the literature are: 1. Students are engaged; 2. There is a balance of skill and luck. 3. Mathematics is central. 4. Flexibility in learning and teaching. 5. Promotes home-school connections. 6. Games into studies. The educational value of a game depends on the extent to which teachers perceive that a game is appropriately challenging, engaging, enjoyable, adaptable to support different learners, and adaptable to inquiry or broader mathematical investigations. Likewise, perceived levels of student enjoyment and engagement, as well as the potential of a game leads to rich mathematical inquiry, were important features in assessing how likely a teacher would be using a particular game with students in the future if given the opportunity, as was the game's ability to support mathematical discussion. Research by Bordás (2016) shows that in order to motivate students and adapt to their individual needs, teachers at both lower and upper secondary level consider it important to use interactive methods, game-based teaching and the use of the internet and digital tools.
In practice, primary school teachers tend to use non-digital mathematical games to support maths learning (board, dice, and card games). According to Russo and Russo (2020) and Russo et al. (2021) almost all the primary teachers admitted playing mathematical games in their classrooms a minimum of once a week, they view games as highly effective for developing all four proficiencies highlighted in the Mathematics Curriculum: fluency, understanding, problem-solving, and reasoning. According to Dienes (2015), activities, games and concrete experiences should be the base of learning mathematics, that could be a joyful experience with the use of tools that enhance efficiency. In primary school, children establish connections between abstract concepts and practical experiences in a more tangible manner, experiencing them through games. Manipulatives are “objects designed to represent explicitly and concretely mathematical ideas that are abstract” (Moyer, 2001, p. 176). Rosli et al. (2015) said that manipulatives help students to see the connections between concepts and improve their knowledge in problem solving and problem posing, even in the case of real-life problems. The incorporation of games serves as a compelling tool in the process of learning mathematics. Di Sia (2017) found that the association with games stimulates children's imagination, providing an enjoyable approach to mathematics, that is perceived as a helpful and enjoyable discipline. Students enjoy the tasks, where they have to invest mental effort in the use of games, didactic materials (Yung and Paas, 2015).
The virtual tool does not seem suitable for this. Öztop (2022) examining the impact of using games in primary school mathematics education on learning outcomes and comparing effect sizes by game type finds that the effect of digital games is small (0.436) and that of non-digital games is large (1.032). The results show that non-digital games are much more effective on learning outcomes than digital games in primary school mathematics education.
According to the literature, there is a contrast between the frequency that teachers prefer to use non-digital games with students vis-a-vis the tendency in the literature to focus on digital games, where the majority of research focused on game-based learning in mathematics, specifically tend to explicitly focus on digital games, rather than non-digital games (Hainey et al., 2016; Hussein et al., 2022). The large scale of quantitative studies involving non-digital games are comparatively rare, with most studies into games occurring within a single school context, generally involving students from a limited range of specific grade levels.
Guiding the pedagogical practice of teacher trainees as their supervisor, we created our own development games and we implemented together with the students in classrooms where they teach, and then we examined the experiences and results together. Our question is: whether non-digital games vs. digital games are different?
2 Digital games, digital game-based learning and achievements in learning of mathematics
According to the literature, numerous studies have identified positive impacts associated with the use of games in learning mathematics (Suh et al., 2005; Steen et al., 2006; Moyer-Packenham et al., 2008). Such activities are typically interactive, motivating, and practical, contributing to maintaining students' interest and enhancing their understanding of mathematical concepts. The aim is to integrate games into the educational environment to enhance students' mathematical learning, expanding the use of games based on higher-order thinking can diversify the educational benefits of games and serve a wider range of learning objectives. Kailani et al. (2019) found that the games, by themselves, do not automatically imply positive impact. One must consider the diverse factors that work in tandem with game-based learning. Such factors include the technical aptitude and attitudes of the people—classroom teachers, faculty members, parents, and researchers—implementing the technology. Not only should there be an effective implementation plan that is well-executed, but the content of that execution needs to be well-designed with thorough curricula relevance.
Game-based learning means the use of games for educative purposes and aimed to improve the user knowledge and experience. The main benefit of these educational games is they focus on improving children's life-essential abilities such as problem solving and critical thinking. GBL aimed to improve the user's knowledge and experience.
Digital game-based learning (DGBL) is learning by using certain computer games for educational purposes. It is a type of game-based learning (GBL; Prensky, 2001). Computer games can be used as a “learning tool” (Ke, 2008, p. 1609) that “simulate real-life social networks” (Neville et al., 2009, p. 410; Ferguson, 2014) and motivational situations such as the use of real-world and computer-generated data to perform math operations.
The contemporary epistemological and pedagogical viewpoints in mathematical education highlight the importance of incorporating realistic mathematical practices and sense-making experiences. Problem solving is a major component of “thinking mathematically” (Schoenfeld, 2020). A DGBL activity engages students in the process of problem solving or knowledge acquisition when facing the challenges presented by the game (Huang et al., 2010). Literature suggests that DGBL stands out as a promising approach for enhancing students' learning motivation and achievement in mathematics. The computer games in terms of being interactive, based on a set of agreed rules and constraints, and directed toward a clear goal and constantly provide feedback, either as a score, toenable players to monitor their progress toward the goal (Clark et al., 2016) DGBL demonstrates positive impacts on learning across diverse subjects and for various types of learners. Its motivational aspect significantly engages and captivates learners. Additionally, DGBL actively supports, reinforces, and expedites the learning process, contributing to the development of higher-order cognitive skills (Hong et al., 2009). “The game playing process therefore supports the learning process by allowing players to acquire learning experiences in games, encouraging interactions between learners and the game system, and situating learners in complex learning environments” (Huang, 2011, p. 694). Twigg (2011) emphasized the essential integration of technology into mathematics curriculum, asserting its necessity for student learning in contemporary society. Accordingly, the utilization of interactive software and computers emerges as crucial tools in facilitating math learning through practical engagement. Ferguson (2014) found that DGBL can offer students the opportunity to enhance their current knowledge when teachers provide the right DGBL environment relevant to the curriculum being learned. Hung et al. (2014) stated that supplying practice opportunities along with immediate feedback through the use of computer and information technologies proves to be effective in encouraging students to enhance their understanding of mathematics.
Teed (2012) asserts that DGBL or GBL unfolds within a virtual environment enriched with fantasy elements, involving participants in educational activities through the utilization of technological tools like computers. DGBL specifically employs digital games to instigate competition, captivate learners, and provide challenges, ultimately serving as a motivational and engaging medium for learning.
Trybus (2015) claims that GBL has many advantages. It offers cost-effectiveness, minimal physical risk or liability to learners, standardized assessments for facilitating student-to-student comparisons, high levels of engagement, a learning pace customized to individual student needs, immediate feedback responses to errors, seamless transfer of learning to real-world scenarios, and an overall engaging experience for the learner.
Gillispie et al. (2010) observed that students exhibited an average increase of 17% in math achievement when 500 middle school students were examined regarding their achievement and attitudes while using problem-based digital games that incorporated concepts in prealgebra and algebra. The study found that students were not only receptive to repeating GBL missions but were also willing to engage in them to enhance their scores on the computer.
In a quantitative study (Roschelle et al., 2010) the aim was to assess whether the utilization of computer software led to increased student engagement in mathematics class and enhanced learning for fourth-grade students. The results indicated that students in the experimental group, those exposed to the computer software, achieved higher scores on the post-test compared to students in the control group. In a mixed-methods study, Sardone and Devlin-Scherer (2010) involving 25 undergraduate students in teacher education to identify twenty-first-century skills utilized in educational games. The participants evaluated 50 games based on specific criteria such as motivation, critical thinking, problem-solving, collaboration, and communication. The findings revealed that digital games inherently incorporate many of these twenty-first-century skills. Ke (2008) identified that game design plays a crucial role in shaping students' interaction with the game.
In their meta-analysis, Li and Ma (2010) explored the impact of computer technology on the learning of mathematics in kindergarten through 12th grade students. Their findings revealed a generally positive correlation between students' academic achievement and the utilization of GBL, particularly among special needs students, elementary students, and those in a constructivism classroom setting.
Several studies have examined the effects of GBL teaching method on students' achievements, emphasizing the significance of its effects on the development of students' affective domain, which is closely linked to the subject and its instruction. A systematic review by Divjak and Tomic (2011) of 27 studies identified from the years 1995 to 2010, focusing on game-based learning (GBL) in mathematics education. Their findings indicated that math learning games not only facilitated the achievement of specific learning objectives but also enhanced students' motivation and fostered positive attitudes toward learning mathematics.
In a one-shot case study (Khan and Chishti, 2011) the objective was to examine the impact of students' active participation on math achievement. Employing a posttest-only design, the study revealed a significant correlation, indicating that students' active engagement in math class had a considerable influence on their math achievement. In his study Ferguson (2014) presented statistical significance for the use of traditional mathematics teaching methods over the use of DGBL in combination with traditional mathematics teaching methods.
Wouters et al. (2013) found that serious games were more effective than conventional instruction in terms of learning and retention, but found no evidence that they were more motivating.
Clark et al. (2016) suggests that game environments support overall improvements in intrapersonal learning outcomes compared to non-game educational environments, and that game designers and educational researchers should collaborate on designs to keep game graphics, environments, and narratives optimally aligned with assessed learning objectives. In an action research study (White and McCoy, 2019) which explored game-based learning as fifth grade mathematics students utilizing game-based lessons, results revealed that student attitudes improved both toward the lessons and toward math in general. Indriani et al. (2019) aimed to describe the quality of problem based learning assisted by Monopoly games on students critical thinking skill for seventh grade students shows that implementation PBL assisted by Monopoly game improve the students' mathematical critical thinking skills.
The results of a systematic review (Vankúš, 2021) with the use of 57 journals, indicate that 54% of the articles consider the affective domain in the measurement of the effects of game-based learning in mathematics education. These articles report mostly (84%) the positive influences of game-based learning on students' motivation, engagement, attitudes, enjoyment, and state of flow.
Manzano-León et al. (2021) in their systematic review in three multidisciplinary databases, on quantitative experimental studies that explore the impact of educational gamification on student motivation and academic performance in the last 5 years (40 studies), most of them report gamification as a valid learning strategy and the results support the conclusion that educational games have a potential impact on the academic performance, commitment, and motivation of students.
Erşen and Ergül (2022) analyzed 80 research studies conducted between 2017 and 2021 on games and mathematical teaching using qualitative methods. As a result, studies aimed at determining effect gained importance, and in the methodological context, quantitative studies were frequently preferred and experimental designs were used accordingly. It was also found that secondary school students were preferred as participants, that the most common type of game used was digital computer games, that the games were mostly associated with the learning area of “numbers and operations,” and that the research studies had mostly positive results for the use of games in mathematics education.
According to Pan et al. (2022), in the recent decade, over 20 major literature reviews have explored the effects of learning games on students' performances, only six of these reviews focused on mathematical education. Mathematics educators generally agree that teaching and learning mathematics requires different skills compared to other subject matters. As such, games designed and employed for mathematics education can differ from those for other subject matters.
In a quantitative meta-analysis review of 24 studies, Tokac et al. (2019) investigated the effects of learning video games on mathematics achievement of PreK-12th grade students compared to traditional classroom methods. Results showed heterogeneity among effect sizes, both in magnitude and direction and suggested that mathematics video games contributed to higher learning gains as compared to traditional instructional methods.
Kailani et al. (2019) in a sistematic review of the literature found that in 12 out of the 14 studies had participants from the age group of 6–14, while two studies had a sample population of undergraduate students between the ages of 17–20. The focus of research on games is mainly in the early years of primary school, as games are rarely used in secondary school mathematics and with university students.
3 Research methodology
Our aim is to investigate whether non-digital games vs. digital games yield different results. Our research was based on three mathematical games. Random sampling was used: a group of students used non-digital (card-based) games, the other group used a DGBL test on computers in the informatics lab. All participants worked an hour and were supervised during the test by us. Participation in the experiment was voluntary. For the elementary school students, the teacher requested parental consent, and all of them agreed.
3.1 Participants
The data was collected in 2022 and 103 individuals, 9–11-year-old elementary school students participated from three schools in Western Region of Romania. Distribution of elementary students according to methods: 49 students (47.57%) used DGBL and 54 (52.42%) used non-digital games.
3.2 Instrument
In the literature we found that majority of teachers prefer arithmetic operations with numbers focused games in their classes. Therefore, we wanted to choose a less used area (e.g., measurement and logic).
The games designed by us could be classified to different mathematical content areas: 1st problem: focuses on numbers, logic, strategy; 2nd problem: geometry, strategy, and measurement, 3rd problem: propositional logic and reasoning.
The universal online platform that was used for the DGBL test was created within JavaScript, PHP, HTML, and CSS, which made screenshots of the final solutions. As non-digital games we used different paper cards. For assessment we analyzed the screenshots. The maximum points the participants could reach was 100 for each problem. Once students clicked the “Completed” button, the solution was saved in the database as screenshots. Participants also had the option to use the “Start “gain” button.
Our research tool included the following tasks:
1. The hexagon problem (Figure 1). Place the small hexagons into the large shape so that adjacent triangles contain the same number (triangles are considered adjacent if they share a side). The hexagons cannot be rotated (Marchis, 2013, p. 64).
2. The cake problem (Figure 2). The figure represents a lattice cake consisting of 20 equal- size squares. Five friends wish to share the cake in such manner that each of them gets a differently shaped four-square piece. Could you help them out? (Matlap, 2018a, p. 308).
3. The house problem (Figure 3). There are five houses in five different colors. Each house is inhabited by a person of a different nationality. Each owner prefers a certain beverage, has a different hobby and keeps a certain pet. No owner drinks the same beverage, has the same pet, or has the same hobby as their neighbor. What we know is:
1. The British lives in a red house.
2. The Swedish has a dog.
3. The Danish drinks tea.
4. The German plays the piano.
5. The Norwegian lives in the first house.
6. The green house's owner drinks coffee.
7. The owner who plays golf likes juice.
8. The owner of the yellow house plays football in his free time.
9. The owner who dances has a parrot.
10. The man who lives in the middle house drinks tea.
11. The owner who plays board games lives next to the one that has a cat.
12. The man who has a horse, lives next to the one who plays football.
13. The Norwegian lives next to the blue house.
14. The owner who plays board games is the neighbor of the one who drinks water.
15. The green house is next to the white house, on the left.
Figure 1. The hexagon problem.
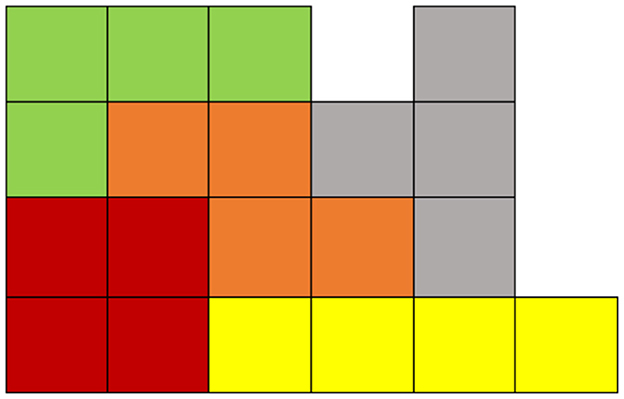
Figure 2. The correct solution of the cake problem (Matlap, 2018b, p. 384).
Figure 3. The solution for the house problem.
Who owns the fish? (Székely, 2012, p. 53). The problems and their solutions can be found in the Supplementary file.
3.3 Hypotheses
The research questions of the study is: whether non-digital games vs. digital games are different? The assigned null hypothesis was as follows: H0: There will be no statistically significant difference in student achievement between students assessed with non-digital games and students assessed with digital games.
4 Results
4.1 Results of the first problem
The first task was to arrange seven hexagon-shaped pieces in accordance with specific rules. Various strategies can be employed to solve this problem; participants may attempt to locate the middle piece, initiate the arrangement from the sides, or employ trial-and-error methods. Despite placing significant emphasis on carefully reading and following the rules, many students, including undergraduates, failed to adhere to the instructions (e.g., they want to rotate pieces).
Majority of participants, 61 individuals (59.22%), successfully solved the problem, while 42 participants (40.77%) did not.
Among the elementary school students who worked with cards (54 students), 18 students (33.33%) successfully solved the problem, while two-thirds (36 students, 66.66%), were unsuccessful. On the other hand, of the elementary school students engaged in DGBL, a substantial majority (43 students, 87.76%), solved the problem, only six students (12.24%) failed. There was a significant difference in achievement between digital games and cards for elementary school students, as indicated by the statistical analysis [t(103) = 6.67, p < 0.05].
The Table 1 shows the results.
Table 1. Results of the first problem.
4.2 Results of the second problem
The second problem serves as a prime example of manipulating plane shapes, with only one correct solution. Nearly all participants correctly interpreted the problem, but the challenge lay in finding the perfect solution. The task required participants to put five different shapes into the grid, essentially cutting the “cake” into five pieces. Consequently, the maximum score was 5, which was transformed into a percentage. For instance, achieving 5/5 corresponded to 100%, 4/5 to 80%, and so forth. The detailed results are presented in Table 2, revealing that the majority (76 students, 73.78%) achieved scores between 60 and 80%.
Table 2. Results of the second problem.
Table 2 also indicates that perfect results were attained by six elementary students: five working with non- digital games (9.25%) and one student with DGBL (2.04%). In comparison of the averages presented in Table 2, with F-tests and t-tests applied, the results achieved by the two groups of elementary school students are significantly different: DGBL solvers outperformed non-digital solvers, as indicated by t(103) = 2.08, p < 0.05.
4.3 Results of the third problem
The final task involved a logic puzzle that measured propositional logic thinking. There are five houses of different colors next to each other and houses have to arranged in a particular order. Only two participants (1.94%) successfully solved the problem, while 6 (5.82%) either failed or gave up. The remaining students demonstrated varying degrees of success in solving the problem. Some students who use non-digital game, employed interesting problem-solving methods, such as placing cards in a chart, while others used the floor space, stating the need for more room to process the task.
Table 3 provides detailed data on the results obtained by the groups of participants, revealing that 89.32% of them (92 students) achieved < 50%.
Table 3. Results of the third problem.
5 Discussion
In our experiment two different groups was tested: a group of students used non-digital (card-based) games, the other group used a DGBL test. The large scale quantitative studies involving non-digital games are comparatively rare, in our case majority, 54 participants use non-digital games (52.42% of students involved).
The games designed by us could be classified to different content areas: numbers, geometry, strategy and measurement, propositional logic, and reasoning. These tasks are problem-type, hence more challenging, from a topic that is encountered less frequently and can be solved by elementary school students. However, when designing the games, it was possible to represent them in a plane, which is why we chose these.
The hypothesis: there will be no statistically significant difference in student achievement between students assessed with non-digital games and students assessed with digital games.
In case of the first problem: elementary school students demonstrated better results with DGBL, 43 students (87.76%) solved the problem. With non-digital games 18 elementary students (33.33%) solved the problem. There is a significant difference in achievement between digital and non-digital games for elementary school students, as indicated by the statistical analysis [t(103) = 6.67, p < 0.05]. In their case, for this problem the digital game resulted in better solutions.
In case of the second problem, perfect results were attained by six elementary students: five working with non- digital games (9.25%) and one student with DGBL (2.04%). The average of elementary students who worked with non-digital games was 60.74, while for those who used digital games, the average was 68.98. There is a significant difference in the averages of the two groups of elementary school students: DGBL solvers outperformed non-digital solvers. In their case, the DGBL was the best game to resolve the problem.
In case of the third problem: two participants (1.94%) solved the problem, 89.32% (92 students) achieved < 50%, while 6 (5.82%) either failed or gave up. The average of elementary students who worked with non-digital games was 32.15, while for those who used digital games, the average was 25.96. F-tests and t-tests were conducted on the achievements of the two groups of elementary students, revealing no significant difference: t(103) = 1.62, p < 0.05 between their achievements.
When solving the third problem, we observed the following about the way of thinking: young schoolchildren treated logical statements more rigidly (they considered them in sequence, one after the other, if they encountered an obstacle, they did not overturn their previous assumptions). We observed that young schoolchildren were not flexible; they thought strictly in sequence, not preferring any particular statements, and did not pair statements. Some students who use non-digital game, employed interesting problem-solving methods.
Consequently, it can be concluded that the hypothesis is not confirmed for the 1st and 2nd problem, in case of elementary students for these problems the digital games were more effective. In case of the 3rd problem the null hypothesis was confirmed, is no statistically significant difference in student achievement between students assessed with non-digital games and students assessed with digital games.
During the experiment, we noticed that most of the participants enjoyed working both with the cards and with the digital games. The games were useful in engaging students in solving tasks. We conclude that can be a difference between the performance of students using non-digital games vs. students assessed digital games, there are tasks for which digital games help the learner, enabling them to solve them more successfully. Our results indicate that while students enjoyed themselves and found the task-solving enjoyable during both types of game-based learning, the use of non-digital games vs. digital games can sometimes lead to different outcomes.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
Ethical approval was not required for the study involving humans in accordance with the local legislation and institutional requirements. Written informed consent for participation in the study was not required from the participants and/or their legal guardians/next of kin in accordance with the national legislation and the institutional requirements.
Author contributions
ED: Conceptualization, Data curation, Investigation, Methodology, Supervision, Visualization, Writing – original draft.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
The content of this manuscript has been presented in part at the 8th International Scientific Colloquium Mathematics and Children, Osijek, Croatia, May 28–29, 2021 (Debrenti and Back, 2022). Visualization in the Teaching and Learning of Mathematics, 8th International Scientific Colloquium Mathematics and Children 2021, Osijek, Croatia, 28–29 May. The author would like to thank her student, Annamaria Back, who helped her in developing the research instrument and for her valuable support in the research.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1331312/full#supplementary-material
References
Bordás, A. (2016). A szituatív tanulás szerepe partiumi magyar pedagógusok szakmai fejlődésében. [The role of situational learning in the professional development of Hungarian teachers in Partium]. REGIO 24, 211–239. doi: 10.17355/rkkpt.v24i4.143
Clark, D. B., Tanner-Smith, E. E., and Killingsworth, S. S. (2016). Digital games, design, and learning. Rev. Educ. Res. 86, 79–122. doi: 10.3102/0034654315582065
Clements, D. H. (1989). Computers in Elementary Mathematics Education. Englewood Cliffs, NJ: Prentice-Hall.
Clements, D. H. (1999). “Concrete” manipulatives, concrete ideas. Contempor. Iss. Early Childh. 1:45. doi: 10.2304/ciec.2000.1.1.7
Debrenti, E., and Back, A. (2022). “Visualization in the teaching and learning of mathematics,” in Advances in Research on Teaching Mathematics, eds Z. Kolar-Begovic, R. Kolar-Super, and A. Katalenic (Zagreb), 72–89.
Di Sia, P. (2017). Learning mathematics through games in primary school: an applicative path. Edutainment 1, 127–132. doi: 10.15503/edut.2016.1.127.133
Divjak, B., and Tomic, D. (2011). The impact of game-based learning on the achievement of learning goals and motivation for learning mathematics-literature review. J. Inform. Org. Sci. 35, 15–30.
Erşen, Z. B., and Ergül, E. (2022). Trends of game-based learning in mathematics education: a systematic review. Int. J. Contempor. Educ. Res. 9, 603–623. doi: 10.33200/ijcer.1109501
Ferguson, T. (2014). Mathematics Achievement with Digital Game-Based Learning in High School Algebra 1 Classes. Doctoral Dissertations and Projects, 794. Available online at: https://digitalcommons.liberty.edu/doctoral/794 (accessed January 14, 2024).
Gillispie, L., Martin, F., and Parker, M. A. (2010). Effects of a 3-D video game on middle school student achievement and attitude in mathematics. Electr. J. Math. Technol. 4, 68–79.
Hainey, T., Connolly, T. M., Boyle, E. A., Wilson, A., and Razak, A. (2016). A systematic literature review of games-based learning empirical evidence in primary education. Comput. Educ. 102, 202–223. doi: 10.1016/j.compedu.2016.09.001
Hong, J. C., Cheng, C. L., Hwang, M. Y., Lee, C. K., and Change, H. Y. (2009). Assessing the educational values of digital games. J. Comput. Assist. Learn. 25, 423–437. doi: 10.1111/j.1365-2729.2009.00319.x
Huang, W. H. (2011). Evaluating learners' motivational and cognitive processing in an online game-based learning environment. Comput. Hum. Behav. 27, 694–704. doi: 10.1016/j.chb.2010.07.021
Huang, W. H., Huang, W. Y., and Tschopp, J. (2010). Sustaining iterative game playing processes in DGBL: the relationship between motivational processing and outcome processing. Comput. Educ. 55, 789–797. doi: 10.1016/j.compedu.2010.03.011
Hung, C. M., Huang, I., and Hwang, G. J. (2014). Effects of digital game-based learning on students' self-efficacy, motivation, anxiety, and achievements in learning mathematics. J. Comput. Educ. 1, 151–166. doi: 10.1007/s40692-014-0008-8
Hussein, M. H., Ow, S. H., Elaish, M. M., and Jensen, E. O. (2022). Digital game-based learning in K-12 mathematics education: a systematic literature review. Educ. Inform. Technol. 27, 2859–2891. doi: 10.1007/s10639-021-10721-x
Indriani, M. N., Isnarto, I., and Mariani, S. (2019). The implementation of PBL (problem based learning) model assisted by monopoly game media in improving critical thinking ability and self confidence. J. Prim. Educ. 8, 200–208. doi: 10.15294/jpe.v8i2.25991
Kailani, S., Newton, R., and Pedersen, S. (2019). “Game-based learning and problem-solving skills: a systematic review of the literature,” in Conference Paper: EdMedia + Innovate Learning 2019. Amsterdam.
Kamii, C. K. (1989). Young Children Continue to Reinvent Arithmetic: 2nd Grade. Implications of Piaget's Theory. New York, NY: Teachers College Press.
Ke, F. (2008). A case study of computer gaming for math: engaged learning from gameplay? Comput. Educ. 51, 1609–1620. doi: 10.1016/j.compedu.2008.03.003
Khan, S. B., and Chishti, S. H. (2011). Learners' errors: supporting learners for participating in mathematics classroom. Int. J. Acad. Res. 3, 656–659.
Li, Q., and Ma, X. (2010). A meta-analysis of the effects of computer technology on school students' mathematics learning. Educ. Psychol. Rev. 22, 215–243. doi: 10.1007/s10648-010-9125-8
Manzano-León, A., Camacho-Lazarraga, P., Guerrero, M. A., Guerrero-Puerta, L., Aguilar-Parra, J. M., Trigueros, R., et al. (2021). Between level up and game over: a systematic literature review of gamification in education. Sustainability 13:2247. doi: 10.3390/su13042247
Marchis, J. (2013). Matematika óvó- és tanítóképzős hallgatóknak [Mathematics for Kindergarten- and Elementary School Teachers]. Kolozsvár: Galaxia Guttenberg Press.
Moyer, P. (2001). Are we having fun yet? How teachers use manipulatives to teach mathematics. Educ. Stud. Math. 47, 175–197. doi: 10.1023/A:1014596316942
Moyer-Packenham, P. S., Salkind, G., and Bolyard, J. J. (2008). Virtual manipulatives used by K-8 teachers for mathematics instruction: considering mathematical, cognitive, and pedagogical fidelity. Contempor. Iss. Technol. Teach. Educ. 8, 202–218.
Neville, D. O., Shelton, B. E., and McInnis, B. (2009). Cybertext redux: using digital game-based learning to teach L2 vocabulary, reading, and culture. Comput. Assist. Lang. Learn. 22, 409–424. doi: 10.1080/09588220903345168
Öztop, F. (2022). Effectiveness of using digital and non-digital games in primary mathematics teaching: a meta-analysis study. Int. Prim. Educ. Res. J. 6, 65–80. doi: 10.31235/osf.io/bc7er
Pan, Y., Ke, F., and Xu, X. (2022). A systematic review of the role of learning games in fostering mathematics education in K-12 settings. Educ. Res. Rev. 36:100448. doi: 10.1016/j.edurev.2022.100448
Prensky, M. (2001). Digital natives, digital immigrants. On The Horizon 9, 1–6. doi: 10.1108/10748120110424816
Roschelle, J., Rafanan, K., Bhanot, R., Estrella, G., Penuel, B., Nussbaum, M., et al. (2010). Scaffolding group explanation and feedback with handheld technology: impact on students' mathematics learning. Educ. Technol. Res. Dev. 58, 399–419. doi: 10.1007/s11423-009-9142-9
Rosli, R., Goldsby, D., and Capraro, M. M. (2015). Using manipulatives in solving and posing mathematical problems. Creat. Educ. 6, 1718–1725. doi: 10.4236/ce.2015.616173
Russo, J., Bragg, L., and Russo, T. (2021). How primary teachers use games to support their teaching of mathematics. Int. Electr. J. Element. Educ. 13, 407–419. doi: 10.26822/iejee.2021.200
Russo, J., Bragg, L., Russo, T., and Minas, M. (2023). Identifying the characteristics of non-digital mathematical games most valued by educators. Educ. Sci. 13:30. doi: 10.3390/educsci13010030
Russo, J., and Russo, T. (2018). “What makes a 'good' mathematical game?,” in Proceedings of the 55th annual conference of the Mathematics Association of Victoria. Bundoora; Melbourne.
Russo, J., and Russo, T. (2020). Transforming mathematical games into investigations. Austr. Prim. Math. Classr. 25, 14–19. doi: 10.3316/aeipt.229363
Sardone, N. B., and Devlin-Scherer, R. (2010). Teacher candidate responses to digital games: 21st-century skills development. J. Res. Technol. Educ. 42, 409–425. doi: 10.1080/15391523.2010.10782558
Schoenfeld, A. H. (2020). Mathematical practices, in theory and practice. ZDM Math. Educ. 52, 1163–1175. doi: 10.1007/s11858-020-01162-w
Steen, K., Brooks, D., and Lyon, T. (2006). The impact of virtual manipulatives on first grade geometry instruction and learning. J. Comput. Math. Sci. Teach. 25, 373–391.
Suh, J., Moyer, P. S., and Heo, H. J. (2005). Examining technology uses in the classroom: developing fraction sense using virtual manipulative concept tutorials. J. Interact. Onl. Learn. 3, 1–20.
Székely, Z. (2012). Eszezo, agypörgeto feladványok [Mind Games -Brain Teasers] (Déva: Corvin Kiadó), 53.
Teed, R. (2012). Game-Based Learning. Carleton College. Available online at: http://serc.carleton.edu/introgeo/games/index.html (accessed January 18, 2024).
Tokac, U., Novak, E., and Thompson, C. G. (2019), Effects of game-based learning on students' mathematics achievement: a meta-analysis. J. Comput. Assist. Learn. 2019, 1–14. doi: 10.1111/jcal.12347
Trybus, J. (2015). Game-Based Learning: What It Is, Why It Works, and Where It's Going (Miami: New Media Institute). Available online at: https://www.google.com/search?client=safariandrls=enandq=Retrieved+from+http%3A%2F%2F%2F+game-based-learning–what-it-is-why-it-works-and-where-its-going.html&ie=UTF-8&oe=UTF-8 (accessed January 24, 2024).
Twigg, C. A. (2011). The Math Emporium: Higher Education's Silver Bullet. Change Magazine Higher Learn. 43, 25–34.
Van Eck, R. (2006). Digital game-based learning: it's not just the digital natives who are restless. Educause Rev. 41, 16–30.
Vankúš, P. (2021). Influence of game-based learning in mathematics education on students' affective domain: a systematic review. Mathematics 9:986. doi: 10.3390/math9090986
White, K., and McCoy, L. P. (2019). Effects of game-based learning on attitude and achievement in elementary mathematics. Networks 21, 1–20. doi: 10.4148/2470-6353.1259
Wouters, P., van Nimwegen, C., van Oostendorp, H., and van der Spek, E. D. (2013). A meta-analysis of the cognitive and motivational effects of serious games. J. Educ. Psychol. 105, 249–265. doi: 10.1037/a0031311
Keywords: game-based learning, digital game-based learning, digital games, non-digital games, STEM, manipulatives, concrete, virtual
Citation: Debrenti E (2024) Game-Based Learning experiences in primary mathematics education. Front. Educ. 9:1331312. doi: 10.3389/feduc.2024.1331312
Received: 31 October 2023; Accepted: 26 February 2024;
Published: 08 March 2024.
Edited by:
Vanda Santos, University of Aveiro, PortugalReviewed by:
José Cravino, University of Trás-os-Montes and Alto Douro, PortugalRichard Van Eck, University of North Dakota, United States
Copyright © 2024 Debrenti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Edith Debrenti, debrenti.edit@partium.ro