
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Educ. , 09 May 2024
Sec. Teacher Education
Volume 9 - 2024 | https://doi.org/10.3389/feduc.2024.1325083
 Petra Scherer1,2†
Petra Scherer1,2† Katrin Rolka1,3*†
Katrin Rolka1,3*†In-service courses for teachers are often provided by so called facilitators who function as teacher trainers and whose tasks in the education system are multifaceted. The professional development (PD) of facilitators is of great importance, and the complex process of scaling up might lead to unexpected constraints, and influence the effectiveness of a program. In general, more research is needed concerning facilitators’ PD with respect to their different roles and functions. In this paper, a project will be presented that focused on qualifying facilitators for the topic “inclusive mathematics” and accompanied the process of scaling up. In the end, unexpectedly, five out of 15 facilitators did not finish the program. Therefore, the challenges and concrete reasons for dropout were investigated in detail. The paper will present a case analysis, where Facilitators’ multifaceted roles, functions, and tasks emerged as the central category. Moreover, conclusions for professionalization programs and research will be derived and discussed.
In-service courses for teachers are often provided by so called facilitators or teacher trainers who take different functions and tasks in the education system (see Dengerink et al., 2015; Barzel et al., 2024). As facilitators play a central role with respect to teachers’ professional development (PD), their own PD is of major importance. Apart from informal learning, internationally, there exist different models for formal professionalization (Koster and Dengerink, 2001; Thomas, 2004; Schoenfeld, 2015; Smith, 2020; Karsenty, 2021). However, especially for Germany where the study reported in this paper took place, there do not exist coherent standards for facilitators’ professionalization, and in particular, more research is needed in this field (Roesken-Winter et al., 2021; Prediger et al., 2022).
Within the German Center for Mathematics Teacher Education (DZLM) and in cooperation with a statewide agency for teacher education, a PD course was developed for qualifying a group of facilitators for “inclusive mathematics” and accompanying the further process of scaling up. The process of scaling up within such programs is per se challenging (cf. Krainer, 2015; Roesken-Winter et al., 2015b; see section 2.4) and may lead to unexpected constraints that influence a project and the effectiveness of a program. It will be illustrated what changes in the reported project occurred and what might be learnt with respect to facilitators’ PD.
The paper, initially, elucidates the theoretical background to facilitators’ PD in section 2. The complexity and challenges of facilitators’ PD will be illustrated by their different roles and functions (section 2.1), PD courses’ specific design principles and importance of quality (section 2.2), the meaning of support within the PD context (section 2.3), and the complex process of scaling up (section 2.4). In section 3, the concrete project with materials and methods will be outlined. The concrete PD course will be described (section 3.1), followed by the methods giving relevant information concerning the research questions, participants as well as data collection and data analysis (section 3.2). Section 4 will present the results. After an overview and some general remarks (section 4.1), the analysis will be given from a case-oriented view, focusing one key case (section 4.2), as well as from a category-oriented view (section 4.3). The contribution ends in section 5 with a discussion of the findings and further perspectives for PD programs and PD research.
Within the complex field of teacher education, so called “facilitators” are of great importance. Concrete programs for their PD and their roles in the complex educational system have to consider different theoretical foundations that will be addressed in this section. Those fields are not to be seen separately but show interdependencies and might influence each other.
When trying to clarify the PD of facilitators, it firstly turns out that there exists a variety of names for this group: teacher trainers, moderators, didacticians, facilitators, multipliers, coaches, teacher leaders or teacher educators (Even, 2014; Dengerink et al., 2015; Krainer, 2015). This variety of naming correlates to diverse roles, functions, and tasks, for example pre-service or in-service teaching, general adviser for schools, coaching of teachers or of professional communities of practice. In summary, one can say that the lack of an agreed-upon name and the diverse roles and functions in this field indicate “that these people are not recognized as members of an identifiable group whose members share a profession” (Even, 2014, p. 330).
In the following, we concentrate on persons responsible for providing PD courses, and use the term “facilitator” for them. Focusing on the selected task of providing PD courses, however, facilitators as such are an extremely heterogeneous group: They usually have different backgrounds, different tasks and functions in different working contexts, teach different subjects, and teach different types of learners (Dengerink et al., 2015, p. 335; see also Smith, 2020). Being a facilitator is not a profession as such and, in Germany, facilitators often work as regular teachers at school at the same time. Moreover, in Germany, the work as teacher educator in the second phase1 of pre-service teacher education is also subsumed under the notion “facilitator”, even though their functions and the persons to be qualified differ clearly (pre-service teachers in the second phase vs. in-service teachers). Indeed, in many cases, for concrete PD courses, heterogeneous groups of participants can be found, ranging from novices to experienced facilitators or persons with even different professions. Not least, the heterogeneity within the group of facilitators can be traced back to the fact that there do not yet exist coherent standards for the professionalization of this group in all countries. In fact, there are efforts for developing and implementing standards. However, these standards do not cover the full range of functions and tasks of facilitators as some of them focus, for example, on teacher educators at university and explicitly do not consider in-service-training as their core task (Koster and Dengerink, 2001). Overall, more research is needed for facilitators’ PD (Zaslavsky, 2008; Roesken-Winter et al., 2015a; Prediger et al., 2019).
Concerning facilitators’ required knowledge and competencies with regard to providing PD courses themselves, it has been worked out that these go far beyond the teacher level (see Zaslavsky, 2008; Borko et al., 2014). “Going beyond the classroom-level, expanded knowledge refers not only to the new knowledge of mathematical content and the relevant didactic aspects aimed at continuing education, but also to the didactic knowledge of adult education” (Peters-Dasdemir et al., 2020, p. 459). For example, taking Shulman’s (1987) categories content knowledge (CK), pedagogical content knowledge (PCK) and pedagogical knowledge (PK) as a starting point, a transmission from the classroom level to the facilitator PD level leads to the corresponding categories on the PD level CK-PD, PCK-PD, and PK-PD for facilitators (Peters-Dasdemir et al., 2020).
Against the background of these extended competencies, the so called Three-Tetrahedron Model (3 T-Model, see Prediger et al., 2019; Figure 1) is of major importance when it comes to qualifying facilitators. For the professionalization process, all three levels of the 3 T-Model are relevant: The tetrahedron on the classroom level – comprising students, teachers, classroom mathematical content, and classroom resources – will be transposed to the teacher PD level as well as to the facilitator PD level. On the facilitator PD level, facilitators are learners, the facilitator PD content comprises the whole tetrahedron on the teacher PD level which, again, comprises as teacher PD content the complete tetrahedron on the classroom level. The main level of acting concerns the facilitator PD level, but teacher PD level as well as classroom level are touched.
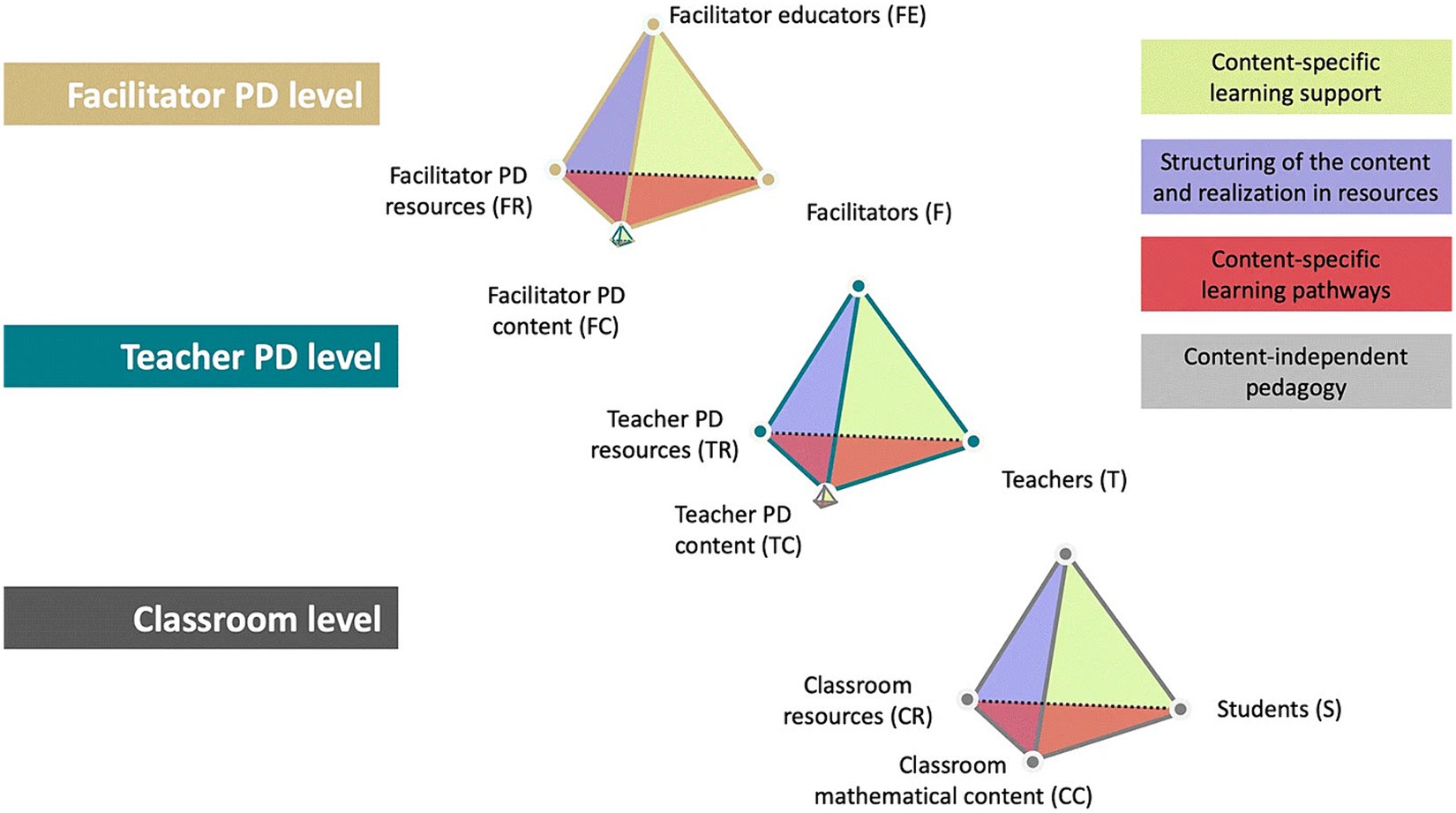
Figure 1. Three-tetrahedron model (3 T-model) for content-related PD research (Prediger et al., 2019, p. 410; CC BY 4.0).
For linking the three tetrahedron levels with respect to design and research questions, Prediger et al. (2019) formulate three main strategies (see also Prediger et al., 2022; Barzel et al., 2024):
• Lifting: design principles and research questions must be transferred from the classroom level to the teacher PD level and, finally, to the facilitator PD level.
• Nesting: when designing and carrying out a PD course for facilitators, all relevant aspects of the other tetrahedrons should be considered.
• Unpacking: in contrast to the first two strategies that are central for developing courses on the facilitator PD level, here, the reverse way is taken into account: For the classroom level, the tetrahedron on the facilitator PD level has to be unpacked for the teacher PD level, and finally the tetrahedron on the teacher PD level has to be unpacked for the classroom level.
In this paper, the lifting-strategy will be looked at in more detail. As will be explained in section 2.2, central design principles for PD courses that are valid for the teacher PD level, have to be transferred and possibly adapted for the facilitator PD level.
There exist different models aiming at facilitators’ PD (Thomas, 2004), and with respect to successful design and effectiveness of subject specific PD courses research findings mainly concern the teacher level (Timperley et al., 2007; Darling-Hammond et al., 2017): as important factors for PD courses on the teacher level, the duration of courses, practice-oriented or case-related activities, as well as teachers’ reflections are stressed (Lipowsky and Rzejak, 2015). Based on this research, the DZLM has brought out the following six design principles: “Competence-orientation”, “Participant-orientation”, “Various instruction formats”, “Case-relatedness”, “Stimulating cooperation”, and “Fostering (self)reflection” (Barzel and Selter, 2015; Roesken-Winter et al., 2015a).
For the facilitators’ PD level, corresponding research findings are rare (Roesken-Winter et al., 2015a) but one might assume that the effectiveness of facilitators’ PD depends on similar factors that have to be transposed to the facilitators’ level by lifting (see section 2.1). For some of the design principles, the lifting is quite obvious and not particularly challenging for facilitators, like for example “Various instruction formats” as this design principle aims at making use of various instruction formats like face-to-face teaching, online teaching, self-study, etc. However, for other design principles, the lifting is more challenging. Exemplarily, the realization of this lifting is illustrated for the design principle “Fostering (self)reflection”: Facilitators like other practitioners have to be stimulated to become reflective in their practice (Schön, 1988). For instance, reflections should refer to concrete PD courses and facilitators’ different roles on facilitator PD level as well as teacher PD level.
Besides these design principles derived by lifting them from the teacher PD level to the facilitator PD level, a seventh principle “level-linking” becomes obvious, as for facilitators all three levels (classroom, teacher PD, facilitator PD, Figure 1) are of great importance (Barzel et al., 2024): Facilitators have to be prepared for their new tasks, functions, and role as a facilitator. Their professional perspective has to be extended, as they have to be aware of all three levels, know the characteristics and connect the three levels (Barzel et al., 2024).
Within processes of PD, the specific conditions are of major importance, and the underlying structural and systemic situations are relevant. Although the specific context on the facilitator PD level differs from the teacher PD level, research findings for the latter one should be considered. Only a few findings on the teacher PD level focusing on support of school exist, and these findings “indicate that the school context can have positive effects on implementing training contents into practice if school administrators give teachers the time required to participate actively, if participation is actively supported and promoted by school administrators, and if the school administrators practice a transformational leadership style” (Lipowsky and Rzejak, 2015, p. 31; see also Tirosh et al., 2015; Darling-Hammond et al., 2017; Smith, 2020; Roesken-Winter et al., 2021). Furthermore, sustainability as well as learning and transfer processes seem to be influenced positively when training objectives are in accordance with school-related reform processes (Lipowsky and Rzejak, 2015; Tirosh et al., 2015).
It seems plausible that, also on the facilitator PD level, support from the relevant context is of major importance. On the one hand, systemic conditions have to be considered: On the facilitator PD level, the improvement of systemic context conditions in which the facilitator PD takes place, and the cooperation with responsible stakeholders are desirable (see Roesken-Winter et al., 2021). On the other hand, taking into account facilitators’ multifaceted functions and tasks, also teacher PD level and classroom level matters, as in Germany facilitators often also work as regular teachers at school (see section 2.1). A teacher working part-time as a facilitator providing PD courses might be more successful if he or she is supported by relevant persons and if the specific content related objectives are in line on the different levels. In contrast, contradictory objectives on the different levels and lack of support might impede facilitators’ PD (see for teachers’ PD Tirosh et al., 2015).
A prominent model for scaling up PD is the so called “cascade model” (see for example Kennedy, 2005, p. 240): “experienced teacher educators provide PD for future teacher educators (mostly experienced teachers), who in turn provide PD for teachers, and so on” (Krainer, 2015, p. 96). Using the terms of section 2.1 and the illustration in Figure 1, within the scaling up process facilitator educators provide PD courses for teachers to become facilitators, and these facilitators will offer PD courses for teachers.
Following the cascade model, the process of scaling up is very complex and might produce challenges on different levels (see Roesken-Winter et al., 2021). Krainer and Zehetmeier (2013) stress a necessary framework that is general enough to be used in different contexts, and bring out the term “learning system” “where action, reflection, autonomy and networking are regarded as important dimensions to consider when analyzing educational practice, as well as educational research and policy” (Krainer and Zehetmeier, 2013, p. 877). Based on their research, they identify key measures focusing on local, regional, and national level of the educational system (p. 880 ff.), and they set out the respective requirements on the different levels. Also, Schoenfeld (2015, p. 162) stresses that “for any system of professional development to function effectively, it must be coherent” and especially, the different levels like classroom, district or national need to be aligned.
It seems likely that these complexities and probable difficulties are connected with the aforementioned characteristics of the facilitator’s professional role (section 2.1) and the necessary support of the PD context (see section 2.3). As explained in section 2.1, facilitators usually have various functions and at least have one or more other professional jobs, and work part-time as a facilitator. For example, working as a teacher at school and being part-time exempted for providing PD courses does not guarantee a sufficient flexibility for working as a facilitator or facilitator educator. Within a scaling up program from the district to the state level, following the cascade model, the temporal or local conditions might change completely and make it difficult to reconcile the different jobs with each other, probably making the required support impossible (see section 2.3).
Within an entire PD program “Coping with heterogeneity in inclusive settings”, a subject specific PD course containing four mathematics modules has been developed by the authors, aiming at qualifying a group of facilitators for primary and lower secondary mathematics. This PD course was planned and carried out within the DZLM in cooperation with a statewide agency for teacher education. The PD course was offered in 2018 over a period of ten months by both authors and tried out with 15 facilitators.
Planned as a scaling up process, these qualified facilitators should offer the course to other facilitators or teachers for qualifying them as facilitators. Within the process of scaling up, these future courses should be designed by the facilitators based on the materials developed by the authors for the original PD course. The concrete preparation and adaptation of materials was planned as a working process of the whole facilitators’ group in teams of three to four persons being responsible for a specific module, in the sense of adaptation and reproduction (Karsenty, 2021). Moreover, in the process of carrying out the courses, it was intended that the facilitator educators go on working as a community of practice (e.g., offering concrete courses in pairs and reflecting experiences and insights in small groups).
Initially, the process of scaling up was planned by the statewide agency as an overlapping model (future courses to be given by the facilitators were planned to start between module 4 and 5), but changed in between to a successive model: Due to structural and systemic reasons and to the Covid-19 pandemic, the first courses provided by the facilitator educators started in September 2020, almost two years after the end of the original PD course given by the authors.
The research-based course design was grounded on a variety of evaluated course concepts for teachers and facilitators, done by the authors before (Scherer et al., 2019; Bertram and Rolka, 2022). For the concrete design, firstly, a selection of relevant contents was necessary with regard to time, as the number and length of the modules was fixed as a systemic guideline. As mentioned above, the mathematics modules were embedded in an entire program with a broader concept of adult learning, starting with module 1, focusing on the general role of facilitators and adult learning, and followed by module 6, given by the statewide agency, representing their general objectives and strategies with respect to subject specific PD (for the entire program overview see also Figure 2 in section 4.3).
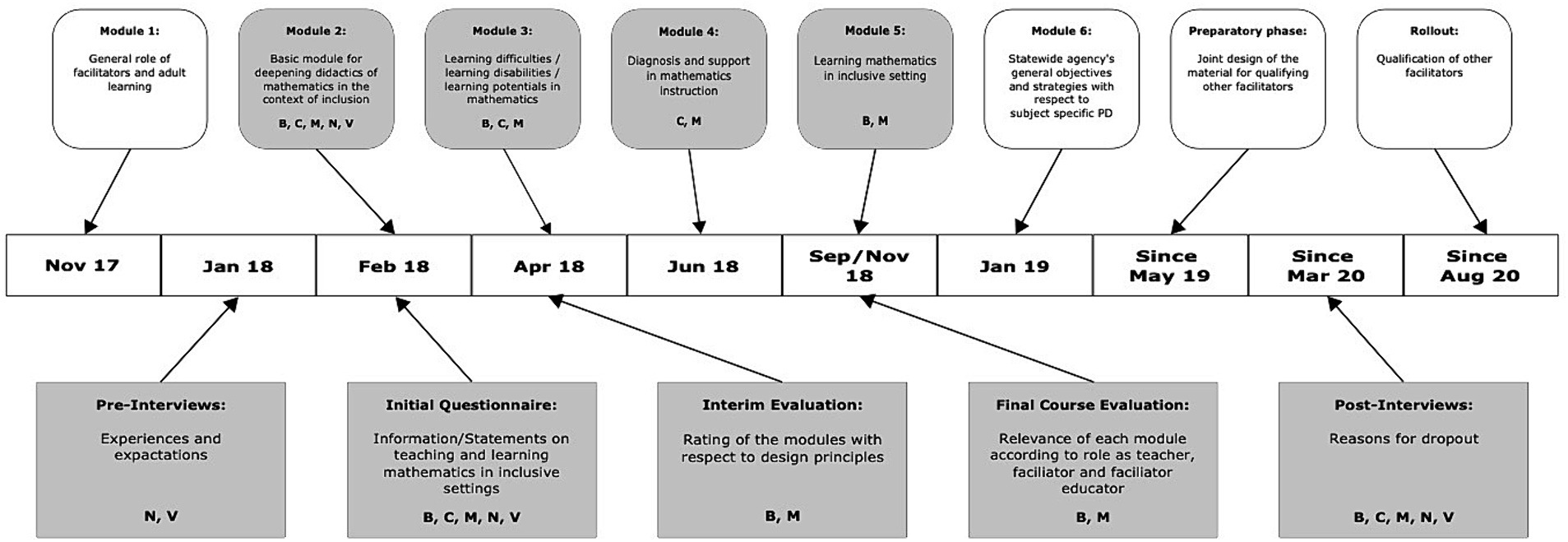
Figure 2. Time schedule including facilitators’ participation in the modules and instruments of data collection (first letters of the names refer to the respective person; gray boxes indicate the mathematics specific modules with corresponding instruments).
The design of the four mathematics modules was based on the five principles for high-quality mathematics teaching, “stemming from combining normative, epistemological, empirical, and pragmatic perspectives” (Prediger et al., 2022, p. 1): Conceptual Focus, Cognitive Demand, Student Focus and Adaptivity, Longitudinal Coherence, and Enhanced Communication. These modules included the basic module 2 as well as three thematic modules for inclusive mathematics, each module lasting 2.5 days. In particular:
Within this module, the term “inclusion” with different perspectives and empirical findings was discussed. Moreover, characteristics for “good” mathematics instruction in general and “good” inclusive mathematics instruction were discussed, emphasizing the idea that inclusive mathematics instruction does not require completely different didactics but rather deals with central questions of teaching and learning mathematics as such (e.g., how to teach mathematics according to the principle of Longitudinal Coherence or the principle of Student Focus and Adaptivity; Prediger et al., 2022 and see above). Moreover, central design principles for PD courses (see section 2.2) were dealt with and concretized for topics like heterogeneity, individualization and diagnostics in mathematics instruction.
This module concentrated on the different terms and concepts, categories of special needs and requirements in special education with respect to mathematics. For example, different students’ learning profiles were analyzed and embedded in didactical contexts.
This module presented central forms of assessment to illustrate the spectrum of standardized versus informal methods. Concrete instruments for different grades and different topics were discussed with their potentials and limitations.
This final mathematical module illustrated different approaches for inclusive settings, like forms of differentiation or universal design for learning. In particular, the challenges of considering learners’ individual needs, and – at the same time – looking for common learning situations were reflected. Concrete examples for suitable learning offers (e.g., open problems) or the realization of natural differentiation (see Scherer et al., 2019) were presented. For the discussion of different approaches, didactical as well as special education perspectives were considered.
The facilitators had to attend the course days for the different modules. Moreover, they had to work on preparatory or deepening activities through self-study. Altogether, important design principles that represent the national and international state-of-the-art research findings and that can be regarded as quality factors for effective PD were considered (see section 2.2 for a theoretical foundation, and also section 5.3 for the evaluation by the facilitators).
Beyond the meaningful content selection and consideration of the central design principles, the course concept put the main stress on addressing the role as facilitator educator, for example by integrating reflections and simulations and connecting the facilitator PD level and the teacher PD level (Prediger et al., 2019; see also section 2.1, especially Figure 1).
Connecting these different levels was also realized with different forms and instruments for evaluating the course quality and acceptance. In particular, specific elements were used that were completed individually including personal information:
• Pre-interview: these interviews collected various individual data. Apart from some background information like age, pre-service teacher education, or length of teaching experience, the interview focused on the experiences and expectations with respect to the PD course topic “inclusive mathematics”. The questions addressed participants’ roles as facilitators and teachers and the corresponding levels (classroom, teacher PD, facilitator PD; see section 2.1).
• Initial questionnaire: the questionnaire started with an open item asking for participants’ view on mathematics followed by further items with respect to the view on mathematics as well as items concerning attitudes and beliefs with respect to teaching and learning mathematics in inclusive versus regular settings or with respect to the design of inclusive mathematics settings (items taken or adapted from Felbrich et al., 2008, Meyer, 2011, and Laschke and Felbrich, 2014).
• Evaluation with respect to design principles: moreover, a standardized evaluation sheet for the design principles had to be completed within module 3, evaluating as participants the consideration of the different principles. On the one hand, this instrument had to be completed by the facilitators addressing their role as a learner. On the other hand, this instrument (as well as other forms) was made a subject of discussion and reflection with respect to future in-service courses given by them addressing their role as facilitators (see also section 4.3).
• Final course evaluation: at the end of the mathematics modules (module 2 to 5), the participants had to rate the relevance of each module, differentiated according to their role as teacher, facilitator, and facilitator educator (see also section 3.2.3).
In general, a great heterogeneity of the participants’ group had been expected, so that the collection of relevant data might provide meaningful information for the accompanying research. It should be mentioned that a heterogeneous constitution of participants is desirable for this specific topic of “inclusive mathematics” as different competencies, backgrounds, or experiences with a fruitful exchange can promote PD.
Concerning the evaluation results, in some cases created in an informal way, not all data will be in the focus of this paper but the evaluation with respect to design principles as well as the final course evaluation will be used for interpreting or supporting analyses for selected dropout reasons in the further sections.
Based on the theoretical background outlined in section 2, the focus of this article is on understanding more deeply the complex field of facilitators’ tasks, functions, and constraints with respect to their PD. Consequently, a wide range of challenges can become relevant which can finally lead to dropout. Within the context of the PD course described in section 3.1, there was a rather high dropout rate, and in particular, the reasons for dropping out are of specific interest. More precisely, the following research question will be examined:
What are facilitators’ reasons for dropping out during the process of qualification or implementation within the context of a program on inclusive mathematics education, and which of them turned out to be dominant?
Whereas 15 facilitators started to participate in the program, for a detailed analysis in this study, we use the data from five participants who did not finish the program. However, in order to allow sufficient understanding of the whole group, we also insert selected information about the other 10 facilitators, and illustrate the group’s remarkable heterogeneity: Seven of the 15 participants were teaching in primary schools, five in secondary schools, and three were special education teachers. Whereas all participants differed largely in their experiences regarding teaching mathematics in inclusive classes and providing PD courses themselves, the three special education teachers also showed great differences regarding the setting they were working in. One of them was teaching in a special school with an emphasis on language difficulties, one was teaching in an inclusive primary school, and the other in an inclusive secondary school.
With respect to the participants’ tasks as facilitators, a great diversity could also be observed. Besides providing PD courses, two participants, for example, worked as discipline leaders who trained prospective teachers, covering the entire spectrum of questions on teaching and learning mathematics. Another participant was a coach for other teachers, specialized in the field of diagnosis and support in mathematics instruction.
In the following the five participants who did not finish the program are presented in more detail.
Bob is about 60 years old. He is a special education teacher in a special school, specialist in language. He is a very experienced facilitator, especially in the field of inclusive education and mathematics for students with special needs.
Caroline is about 50 years old. She is a special education teacher in secondary school. She has been teaching inclusive mathematics classes for many years, including students with various difficulties in learning mathematics. Besides, she has been offering numerous teacher PD courses in the field of inclusive mathematics for many years.
Miranda is about 40 years old with about 15 years of teaching experience in primary school, especially in inclusive mathematics classes. She is involved in teacher PD as facilitator for several years. Besides, she provides courses at university for prospective mathematics teachers.
Naomi is about 30 years old and has been a mathematics and science teacher in secondary school for about eight years. She had only a few students with special educational needs in her classes, more with a focus on difficulties in language or behavior than difficulties in learning mathematics. At the time of the interview, right before the beginning of the program, she is taking a break from her work in school in order to develop materials for central exams at the statewide agency for teacher education responsible for the entire PD program. So far, she has little experience with teacher PD.
Victoria is about 30 years old and studied mathematics and biology to become a teacher for primary and lower secondary. However, she has never taught at school, but, instead, remained at university in order to write her PhD thesis. She is involved in the conception of teacher PD courses but not in concrete implementations.
As indicated for the whole group, in various respects, these five facilitators are also very heterogeneous. Nevertheless, the initial questionnaire showed a more or less homogeneous picture and positive attitudes of all five facilitators toward designing inclusive mathematics settings. Moreover, when comparing inclusive with regular settings, all of them mostly did not see any or just minimal differences for teaching and learning in inclusive mathematics settings compared to regular mathematics settings.
With regard to the timing of dropout, also differences are apparent: Whereas Naomi and Victoria dropped out immediately after module 2, Caroline tried to participate as long as possible, but dropped out after module 4. Bob and Miranda not only attended all mathematics modules, but have also entered the phase of planning and designing the materials together with the other participants. However, during this phase, both decided to drop out and not to offer PD courses themselves (see also Figure 2 for an overview of the time schedule).
As this high rate of dropouts (five out of 15) and different moments were unexpected and surprising to us, problem-centered interviews (Witzel, 2000) were planned to clarify underlying reasons. These interviews were carried out after the PD course between March 2020 and February 2021. In order to gain deeper insights into the participants’ situation and corresponding challenges, especially into their perception of the program and their reasons for dropping out, we used semi-structured interviews in this study. In advance, an interview guide was prepared, containing questions to the individual background as well as expectations with respect to the program, reasons for dropout and possible alternatives that they would have stayed in the program. All interviews were audiotaped and subsequently transcribed. The interviewer was one of the course participants who functioned as a coordinator for the whole group since the preparatory phase (see Figure 2).
Besides, within the PD course, we used different forms and instruments in order to evaluate the course quality and investigate participants’ satisfaction and acceptance of the PD course as mentioned in section 3.1 (see also Figure 2). Although these instruments are not in the focus of this paper, we use them for supporting some of our interview findings that will be presented in section 4. For example, an interim evaluation had to be completed in module 3 focusing on design principles for PD. Within this written evaluation, there was one item on the overall satisfaction with the PD course (five-point likert scale; 1 indicated total dissatisfaction and 5 total satisfaction), whereas the other 25 items addressed the consideration of the six design principles within the course design (four-point likert scale; 1 indicated total disagreement and 4 total agreement). The following item exemplifies the design principle “Stimulating cooperation” (see section 2.2): “I had enough opportunities to work on problems and tasks together with other participants”.
In the final course evaluation, the participants were asked to rate the relevance of each module according to their role as teacher, as facilitator, and as facilitator educator. For each of the four modules, the participants had to rate the relevance of the module with respect to their different roles: “Module no. x was for me as teacher/facilitator/facilitator educator …”. The participants were asked to answer on a six-point likert scale (1 indicated total irrelevance and 6 total relevance). Moreover, they should comment their ratings.
As these evaluations took place at different times, and as the participants dropped out at different moments (see section 3.2.2), some of these evaluations are not available for all participants (see Figure 2 for an overview).
In accordance with Thomas (2011) understanding that a “case inquirer looks at the complex interaction of many factors in few cases” (p. 512), we approached our data by a case study in order to get deep insights into facilitators’ reasons for dropout and underlying relations. The case study as such allows different methods for analysis (Stake, 2005), and for the concrete analysis, we refer to Kuckartz (2019) who suggests to consider a “cases x categories” matrix where the cases are represented in lines and the categories in columns (see Table 1 in section 4.1 and the complete Table in the Supplementary Material). In this study, the cases are the five participants who dropped out, and the categories consist of the four aspects elaborated on in section 2 (deductive categories). In addition, further inductive categories out of the material can be developed (see section 4.1).
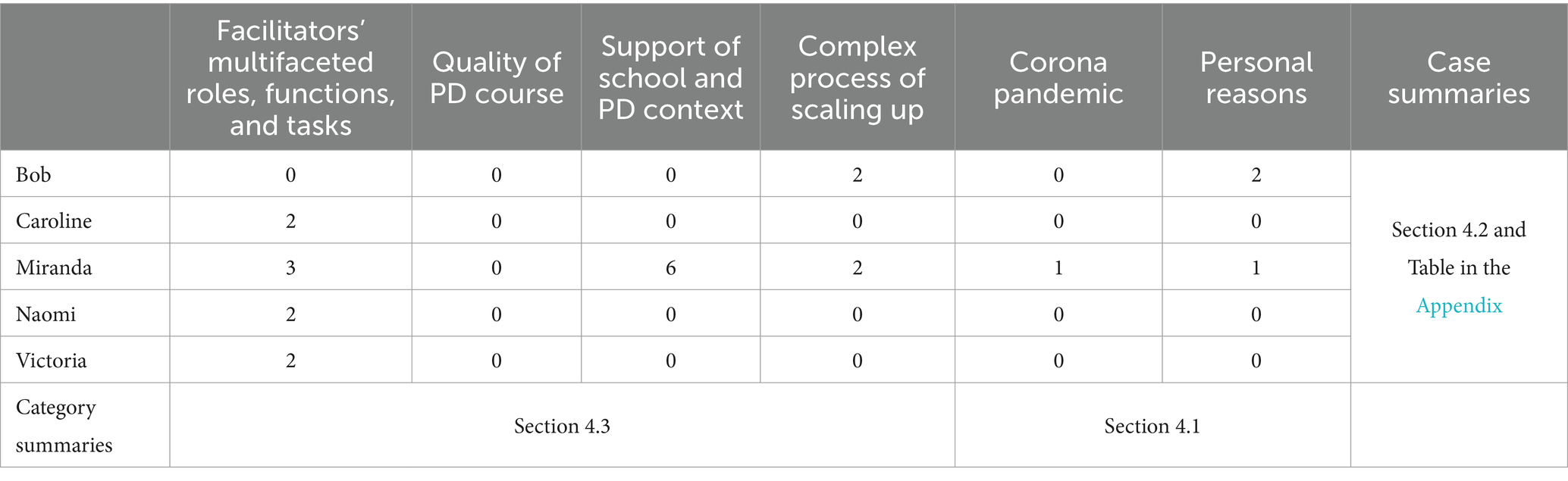
Table 1. Overview of number of coded text passages for each person and each category (four deductive categories in the columns 2–5, two inductive categories in the columns 6, 7).
For the analysis, in a first step, all text passages assigned to a specific category were inserted in the cells. Afterwards, all text passages belonging to a specific category were summarized for each case. Especially, this means that “a case-related thematic summary of all text passages available for that person on a specific topic” (Kuckartz, 2019, p. 7) is produced. Secondly, in addition to this, the material is analyzed in a case-oriented way as well as in a category-oriented way (Kuckartz, 2019, p. 7). The case-oriented analysis leads to case summaries which aggregate all reasons that were mentioned by one person, and the category-oriented analysis leads to category summaries which aggregate all facets to a specific category. Hence, the “cases x categories” matrix includes case summaries as well as category summaries. In combination with this qualitative analysis also quantitative aspects might be integrated (Kuckartz, 2019, p. 9).
In this section, we first give an overview of the findings, including some general remarks (section 4.1). After that, we focus facilitator’s challenges and concrete reasons leading to dropout illustrated by one central case, the case of Miranda (section 4.2). Finally, we elaborate on the reasons respective categories analyzing the category summaries (section 4.3).
With regard to our research question, we were interested in participants’ challenges leading to dropout. As described in section 3.2.4, we organized the data in a “cases x categories” matrix. The case-related thematic summaries for the inner cells were created on the basis of all text passages assigned to a specific category (see Table in the Supplementary Material). For a quantitative overview, Table 1 illustrates the “cases x categories” matrix where the numbers of coded text passages for each person and each category are inserted (including the inductive categories).
The following remarks are intended as a first analysis based on Table 1. As described in section 3.2.4, we used four deductive categories for the analysis, which are the four aspects identified as important in the context of facilitators’ PD (section 2).
While we used these four aspects as deductive categories, we used an open coding to identify further challenges leading to dropout that emerged from the interview data. Indeed, two inductive categories were developed out of the material. As these two inductive categories are rather not linked to the design of the PD course and cannot be directly influenced, and as they are related to some of the deductive categories, we discuss them only briefly.
The first inductive category is concerned with the Corona pandemic, and only Miranda explicitly referred to challenges due to Corona: “Right now, I am just happy not to be involved in the program anymore because at school, there is a lot of trouble due to Corona. We already have the fourth change of timetable and it is such a back and forth” (l. 71–73). Interestingly, Miranda mentioned this right before her remarks on how unsatisfactory it is for her to be torn between the immense demands at school and the requirements inherent in the PD course. Hence, a connection can be established with the category Facilitators’ multifaceted roles, functions, and tasks (see section 4.3).
The second inductive category is concerned with Personal reasons which could be observed in the cases of Bob and Miranda. At some point in the interview, Miranda rather shortly brought up health problems which could not be related to any of the other deductive categories. The other person that mentioned Personal reasons for dropping out is Bob, and his case is somewhat different because his retirement was coming up soon, and he did not see any perspective for him to take part in the implementation process. Although this reason is located on the personal level, it is closely related to the category Complex process of scaling up (see section 4.3). As illustrated in section 3, the process of scaling up was originally planned as an overlapping model. However, the first courses given by the facilitator educators started in September 2020, almost two years after the end of the PD course given by the authors.
All in all, four persons referred to just one or two categories, and only Miranda addressed five out of six categories. Miranda’s interview showed a complex and multifaceted picture representing a more or less “complete case” where the data of the other four facilitators can be located. For this reason, we will concentrate on her case in section 4.2. Considering the categories, there is only one category that is addressed by more than two facilitators: Facilitators’ multifaceted roles, functions, and tasks. Moreover, looking at the number of different reasons respective categories that were mentioned by the facilitators, no remarks at all related to the category Quality of PD course could be identified. These categories as well as the other two deductive categories will be discussed in more detail in section 4.3.
The case-oriented analysis took into consideration each facilitator’s challenges leading to dropout, based on all case-related thematic summaries of each person line by line (see Table in the Supplementary Material and the respective categories and numbers of corresponding text passages in Table 1). In the following we present the case of Miranda in detail as she shows with 14 text passages and five out of six categories a multifaceted case, and represents in the overall view the richest case:
Being explicitly asked about reasons for her dropout, Miranda stressed several aspects. The inductive categories Corona pandemic and Personal reasons are mentioned in section 4.1 and will not be included in this summary any more. At various points in her interview, she emphasized the difficulties and challenges resulting from her different roles and functions, which was coded as Facilitators’ unclear roles, functions, and tasks. At the beginning of the interview, she explained vehemently: “There was one reason that had been omnipresent all the time: it was difficult to reconcile [the PD course] with school. It was always a total drama when I said, yes, I am going to S. [the location of the PD course],” and went on imitating her colleagues at school: “Yes (sighing), what do you get out of this? […]. There will be no benefit of it” (l. 53–56). Her efforts to “arrange” her participation in the PD course, namely the attendance of the 2.5 course days for each of the four modules, and her work in school turned out to be very challenging and stressing for her. Later in the interview, Miranda expressed this even more clearly: “I cannot plan properly at all, and this is also stupid being involved in two stories, this means in school and in the PD course, and not being able to do anything in a reasonable way” (l. 73–75). This statement clearly shows that Miranda is torn between her tasks as a teacher at her school and the requirements for her own qualification as facilitator educator in the PD course. She was exposed to immense demands at school and explicated that this situation was not satisfying for her, neither with regard to school nor the qualification program. As the interview progressed, she also addressed possibilities of reducing her teaching activities at school as solution, that means that participating in the PD course should result in teaching less at school.
Another line of argumentation with regard to her dropout reasons is related to Support of school and PD context which is the category with her most text passages. The arguments mentioned in this context turned out to be strongly connected with the category Facilitators’ multifaceted roles, functions, and tasks. As mentioned above, Miranda could not reconcile her activities in school with her attendance in the PD course. Moreover, she felt a lot of resistance at her school. Whenever trying to provide her colleagues with input from the program, she experienced defensive reactions, citing her colleagues: “If I tried to hand over ideas to my math colleagues, it was often like ‘Nonsense, we cannot implement this at all!’” (l. 57–59). Besides, she would have appreciated if she could have attended the program together with another colleague from her school: “That you do not have to defend your project alone at school […]. I believe that would have given the whole thing more framework” (l. 91–94). Whereas Miranda focused here on personal support from her school for attending the program, later in the interview, at two different points, she also took into consideration a form of support from the district: “Perhaps one would have needed another person from the district” (l. 103–104) and “If I would have noticed that there were at least one, two companions in the district who give support or bring it a good step further, but being the sole prophet [is frustrating]” (l. 146–148). However, in the group of 15 facilitators were three other facilitators from her district who would have been available for cooperating and giving support. Yet, it should be mentioned that Miranda did not attend module 1 and expressed that it was a bit difficult for her “to get into it and to size up the people because they had already become so close” (l. 33–34). Interestingly, at two different points in the interview, Miranda herself reflected on further possible solutions: “That perhaps the organizers [statewide agency and authors] would have backed me more […], that they would have come to my school in order to report what we were doing, that it would get back to the schools, accompanied in a more scientific manner”. She wished that the agency or authors would have emphasized to the school management that it “is important that your teacher attends the program” (l. 85–89) and “I believe if they had written a letter to the school twice […] that would have made it a little easier” (l. 476–478). However, it is important to mention that Miranda did not express this during the PD course, and stated in the interview that she “did not have the idea at that time” (l. 477).
A further line of argumentation in Miranda’s interview concerns the Complex process of scaling up. She mentioned that the program took longer than originally expected, or rather that possible changes concerning the process of scaling up were not clearly communicated in advance: “After all, it takes three years and not just one” (l. 79–80). Indeed, the process of scaling up changed in between (see section 3.1). Later on in the interview, Miranda highlighted another aspect, relevant in the context of the complex scaling up process: On the one hand, as mentioned above, time went by, and there was no clear perspective for the facilitators regarding the PD courses to be given by them. On the other hand, at one point, they were urged to finish the materials for their future courses: “This time pressure, later, was very negative for me. The materials just have to be completed now. I certainly understand this, after such a long time” (l. 236–238).
Given the rich data, Miranda revealed to be a “key case” (Thomas, 2011, p. 514), and her case summary is as follows:
Miranda participated in the PD course while teaching at school and was constantly torn between these two fields and her different roles. This was strengthened by the lack of support of school and PD context as well as the fact that the process of scaling up took longer than originally planned.
For the category-oriented analysis, all case-related thematic summaries to the categories will be considered column by column (see Table in the Supplementary Material), and all facets mentioned will be aggregated to the corresponding category summaries. The numbers of text passages of all cases that were assigned to a certain category can be found in Table 1.
A total of nine text passages from four of the five participants were assigned to the category Facilitators’ multifaceted roles, functions, and tasks. Caroline’s, Miranda’s and Naomi’s arguments point in a similar direction. However, while all three highlighted the incompatible demands related to another role or task and their participation in the PD course, the exact circumstances differ a lot (for Caroline it is a job offer as a teacher educator in the second phase of pre-service teacher education, for Miranda her work at school, for Naomi her tasks at the statewide agency). In contrast, Victoria explicitly referred to a role conflict and stated that she could not identify herself with a facilitator. The various examples from these four facilitators show that the category Facilitators’ multifaceted roles, functions, and tasks is quite complex, and comprises diverse and manifold facets. These four persons represent a heterogeneous group, performing numerous professional roles and functions – generally, each of them occupying more than one role and function. This combination of different roles and functions turns out to be a source of tensions and conflicts. Moreover, this category seems to be central for another reason: The two categories Support of school and PD context and Complex process of scaling up are more or less related to it. The text passages and the case-related thematic summaries (see Table in the Supplementary Material) led to the following category summary:
Reasons for dropout are grounded in an unclear role as facilitator that differs from the teacher’s role. Moreover, an enormous source of tensions and conflicts within PD programs arises from the different contexts facilitators are working in, and the various functions and tasks they have to fulfill.
None of the facilitators mentioned as reasons for dropout aspects related to the quality of the PD course. One might think that this is not surprising since for the facilitators it was clear that the interviews were conducted on the designers’/authors’ request. However, the interviewed dropouts emphasized the relevance of the content and the way it was presented. Miranda, for example, expressed in her interview: “I could really use a lot for myself […], I realize this until now, for example, yesterday, the parents’ evening, I was able to draw on some things, really profound knowledge has emerged of it” (l. 36–40). Likewise, Caroline underlined the relevance of the program: “I already had prior knowledge on all topics, but I always had the possibility to find something that was a new input to me […], that was extremely valuable for me […], on the one hand, it was my own professionalization in the sense that I became more familiar with content knowledge, new literature, and on the other hand, I could share my knowledge with others and this allowed me to reflect on myself again and again” (l. 42–54). Finally, Bob, while reflecting on the relevance of the course, used notions like “deepening” (l. 142) or “broadening the basis” (l. 142–143).
Besides these positive remarks in the interviews, we additionally draw on other data illustrated in section 3.2.3 in order to support the argument that the quality of the PD course and the related content on “inclusive mathematics” was not a reason for dropping out. Indeed, there are various indications that the dropout was not due to dissatisfaction or lacking acceptance of the course which is illustrated with recourse to the different evaluation instruments in the following.
The evaluation with respect to design principles (see section 2.2 and 3.2.3) is available for Bob and Miranda (see Figure 2). With respect to the item on the overall satisfaction with the PD course (five-point likert scale; 1 indicated total dissatisfaction and 5 indicated total satisfaction), Bob rated 4 and Miranda 5. The other 25 items on the consideration of the six design principles (four-point likert scale; 1 indicated total disagreement and 4 total agreement) reveal a rather positive picture (24 times 4 which indicated total agreement, 10 times by Bob and 14 times by Miranda). Bob and Miranda rated 16 items 3 (agreement), only one item was rated 2 (disagreement) by Bob. In eight cases, Bob and Miranda chose “no information”. Interestingly, they both put this cross for some items that might be interpreted with respect to their future job as facilitator educators (exemplary item: “Within the PD course, I could try out something new and got feedback”). Overall, the PD course and especially the design principles were positively rated by these two facilitators.
Likewise, the final course evaluation is available for Bob and Miranda (Figure 2) and shows a rather positive picture, rating all statements regarding the four modules (six-point likert scale; 1 indicated total irrelevance and 6 indicated total relevance). In each of the three different roles, Bob and Miranda, rated at least 4 (see Table 2).
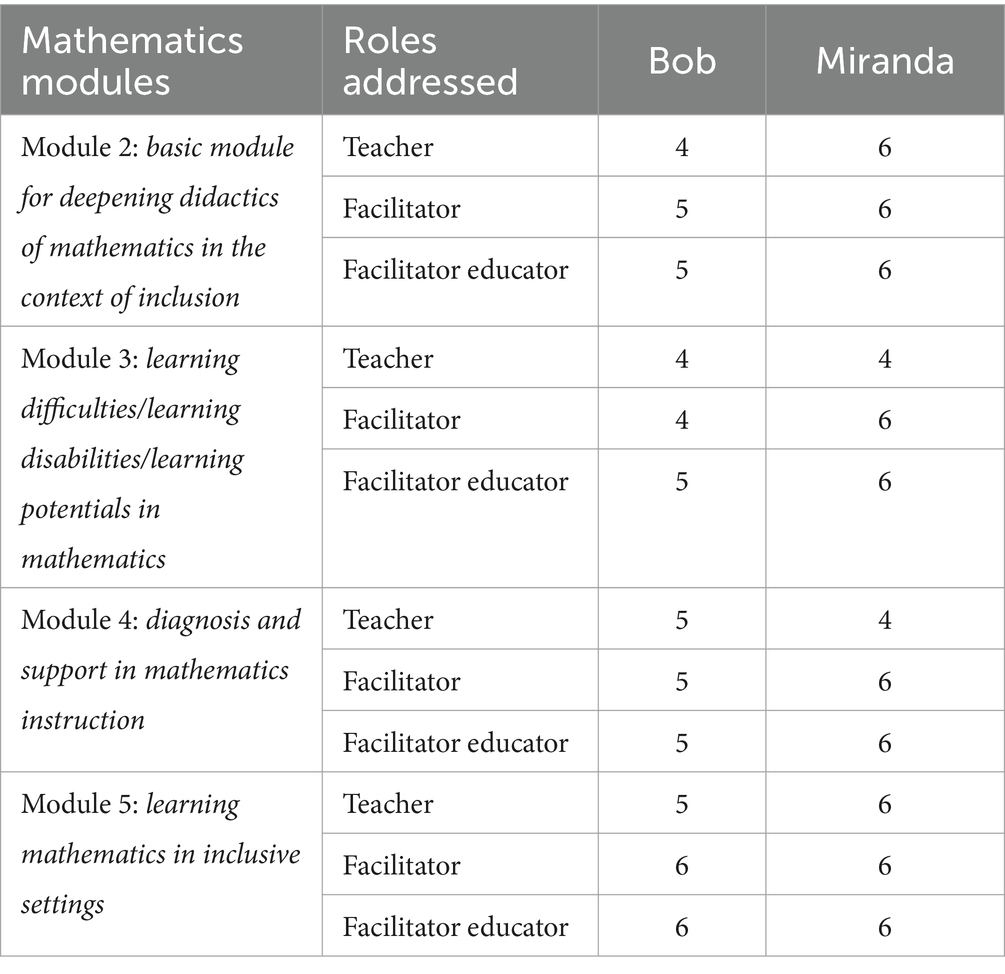
Table 2. Final course evaluation for the different mathematics modules with regard to addressing different roles.
Taking a more differentiated view on Table 2, it becomes obvious that the rating is extremely positive concerning their role as facilitator educator, and the picture is similar concerning their role as facilitator. Concerning their role as teacher, the picture is more diverse. Accordingly, from Bob’s and Miranda’s point of view, the PD course met their various needs with respect to their PD, and indeed, one main goal was to qualify and address them as facilitator educators (see section 3.1). In addition, Miranda explicated in this final course evaluation that her expertise on the classroom level allowed her to focus on her role as facilitator and facilitator educator: “I could use my knowledge and experiences as a teacher as basis for dealing with the question how to cope with it as facilitator or facilitator educator”. Accordingly, reasons for dropout were not primarily related to the relevance of the content and quality of the course.
To complete the picture, it should be added that this positive picture is true for the whole group (12 facilitators): The overall evaluation showed that all mathematics modules mainly were assessed as very relevant or relevant for the various roles (teacher, facilitator, facilitator educator), and that the three levels (classroom, teacher PD, facilitator PD) were thus addressed (cf. Scherer and Rolka, 2022). Although this category was not addressed as dropout reason, the quality of PD courses is of great importance, and a category summary is given here:
A thoughtful research-based design of PD courses, considering central design principle on the facilitators’ level, is of great importance. Moreover, addressing their roles as facilitator educator, facilitator and teacher within PD courses, entails the quality and increases the acceptance by the participants.
Miranda is the only facilitator mentioning reasons that were assigned to the category Support of school and PD context. However, she kept coming back to these ideas at various points during the interview, and we identified six different text passages in which she addressed this category (see Table 1 and section 4.2). Miranda’s participation in the PD course was not supported by school administrators. Moreover, she reported resistance among colleagues when trying to share ideas from the PD course. Especially, this category turns out to be strongly connected with Facilitators’ multifaceted roles, functions, and tasks as the former mentioned aspects came into play due to Miranda’s involvement in different tasks and functions (school vs. PD course). The missing support of school made it impossible for Miranda to bring together her different tasks and functions. Moreover, she also addressed the PD context where she did not feel supported either. Based on these text passages and the case-related thematic summary (see Table in the Supplementary Material), the category summary is as follows:
For facilitators, support from the relevant contexts – school as well as facilitator context – is essential. Inconsistent objectives regarding the different contexts represent reasons for dropout.
Reasons related to the Complex process of scaling up were mentioned by two facilitators. The process of scaling up that initially was planned as an overlapping model changed in between to a successive model, involving a great delay in time and revealing to be rather complex. Whereas for Bob, this delay in time was problematic due to his upcoming retirement, Miranda could not withstand this pressure of being involved in different working contexts for such a long time. Hence, this category is also related to Facilitators’ multifaceted roles, functions, and tasks. These text passages and the case-related thematic summaries (see Table in the Supplementary Material) resulted in the following category summary:
The process of scaling up is complex, and time factors or unexpected changes of programs represent reasons for dropout.
The study presented in this paper focused a PD course concentrating on qualifying facilitators to be facilitator educators for the topic “inclusive mathematics”. In the end, five out of 15 facilitators did not finish the program. To gain insights in the specific challenges related to facilitators’ PD and the resulting reasons for dropout, problem-centered interviews were carried out, added by further data collected during the PD process.
The rather high rate of dropout was not expected as there might be a higher commitment for program participation for facilitators in comparison to teachers. Nevertheless, several challenges for facilitators’ PD are discussed in research and literature, and four central aspects were elaborated in section 2. Against this background, we investigated the facilitators’ reasons for dropout in detail by using these four aspects as deductive categories for the interview analysis. Besides, we identified two inductive categories (Corona pandemic and Personal reasons, see section 4.1), mentioned in specific cases and only discussed briefly. Yet, with regard to the Corona pandemic, one can notice that the education system was affected in different ways (Schleicher, 2020), which concerns the school level as well as pre-service and in-service teacher education. However, in the interviews, this was not the main focus when it came to facilitators’ reasons for dropping out. Nonetheless, like under a burning glass, the Corona pandemic revealed the crucial point concerning Facilitators’ multifaceted roles, functions, and tasks (see below).
With regard to the deductive categories, Quality of PD course stands out as this was not at all explicitly mentioned as reasons for dropout. In contrast, the facilitators’ assessments based on an interim evaluation with respect to design principles, the final course evaluation, as well as the post-interview data can serve as indicator for the quality of this PD course, and showed their satisfaction and acceptance of the course (see section 4.3). What became particularly clear in our study is that a substantial and thoughtful PD design, in line with theoretical considerations on design principles, might not be sufficient in order to prevent dropout (see also Tirosh et al., 2015).
Based on our results, various measures can be considered concerning the organization of PD programs in general. The category Facilitators’ multifaceted roles, functions, and tasks turned out to be central for the participants in this PD course. These facilitators represented a heterogeneous group, and the fact that, in Germany, there do not exist standards for the professionalization of this group (see section 2.1) might foster this heterogeneity. Especially, three facilitators who addressed this category were working in other professional contexts (school, teacher education in the second phase, statewide agency) while participating in the PD course. This, in turn, was a source of tensions and conflicts (Dengerink et al., 2015). Binding agreements and sufficient time, for example by reduction of teaching activities at school, are of high importance, so that facilitators do not constantly need to balance between different tasks and commitments. However, in Germany there is an extreme shortage of teachers and it does not seem realistic to release the facilitators from teaching at school during their own qualification (which, in our case, took about ten months). However, with regard to setting up PD programs, a shorter period of time for facilitators’ own qualification seems promising which needs to be coordinated with the respective institutions that are involved in program organization.
Moreover, it is advisable to establish standards in order to clarify the facilitator’s role. Having a clear job profile, the recruitment could be much more targeted, in the sense that transparency and a detailed information about facilitator educators’ future tasks and functions help in the decision-making process for attending a program or not. Indeed, this also was mentioned as reason for dropout. In order to clarify this role, a deeper cooperation with the responsible institutions who organize the program could be aimed at. Another issue that could be a point for more cooperation between the responsible institutions and the authors/designers of a PD course concerns the category Support of school and PD context. Although, in our case, ‘inclusive mathematics’ certainly is an important and current topic, Miranda did not experience this at her school, and it remains an open question whether this PD course, mainly located on the facilitator PD level, at her school could not unfold its effects on the classroom level or if the topic of inclusive mathematics is of minor importance. However, positive influences are assumed when the PD course’s objectives are in accordance with school-related reform processes (Lipowsky and Rzejak, 2015; Tirosh et al., 2015), which was not the case for Miranda.
The Complex process of scaling up turned out to be challenging in two ways: on the one hand, the overlapping model changed in between to a successive model. On the other hand, when the scaling up was delayed more and more, the facilitators were urged to finish the materials which was, in particular, difficult for Miranda. Challenges related to the Complex process of scaling up are also reported in the literature (Krainer, 2015). It remains an open question if the overlapping model would have reduced the dropout, at least for Bob and Miranda, this seems quite plausible. Also for Victoria who did not have a clear picture about her role, functions, and tasks as a facilitator and could not identify herself with a facilitator, an overlapping model could have been a chance. However, an overlapping model might require extremely high resources with respect to time and personal engagement. Especially, for novices on the facilitator PD level, these requirements might be incompatible. With regard to the PD course at hand, it may be of interest to consider more closely the different models for scaling up (e.g., Karsenty, 2021). For the PD program presented here, the statewide agency decided to qualify the facilitators first, and the concrete preparation and adaptation of materials was planned as a working process of the whole facilitators’ group, in the sense of adaptation and reproduction (Karsenty, 2021).
To sum up, for the design of concrete PD courses and scaling up programs on the facilitator PD level, one should strengthen the systemic perspective: Although for concrete PD courses, the participants’ development with meeting their individual needs, here facilitators, is in the focus, the development of the system should also be considered in all phases. For the program reported here that would have meant to integrate, from the very beginning, the systemic conditions in a stronger way and ask for clarifications and binding decisions. As Roesken-Winter et al. (2021) brought out, for implementation strategies more research is needed on the systemic level and the interplay between personal, material, and systemic strategies.
With regard to future research, the categories analyzed in this paper can serve as a basis for further investigating the challenges facilitators are facing during their own PD in order to prevent dropout if possible. When focusing on the case of Miranda (see section 4.2), she turned out to be a “key case” (Thomas, 2011, p. 514). Considering Miranda as the only “complete case,” it becomes obvious that not all reasons need to come into play for each facilitator, and further research is needed in order to better understand possible relations between different reasons. As Tirosh et al. (2015) pointed out for measuring a programs’ impact, additional interviews could be carried out to reveal further interactions between factors and get more indications for improvement of PD programs. Moreover, as mentioned above, for the PD program at hand, the scaling up followed the ideas of adaptation and reproduction, set by the statewide agency. It remains an open question whether the co-design of the materials in joint responsibility of organizers respective researchers/authors and facilitators could have guaranteed a greater involvement and prevented dropout. Especially, future research focusing on later program phases (participants act as facilitator educators providing PD courses for other facilitators and possibly for teachers) would gain more insight in further challenges and requirements within the whole scaling up process (see Jackson et al., 2015). This remains as another open question if dropping out happens more likely within an early phase as reported here. Moreover, it would be interesting to focus on those participants who stayed in the program to gain more insight in relevant factors and successful ways for their PD.
The original contributions presented in this study are included in the article, further inquiries can be directed to the corresponding author.
Ethical approval was not required for the studies involving humans because of an agreement of the statewide agency for teacher education. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their consent to participate in this study.
PS: Writing – original draft. KR: Writing – original draft.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The project was carried out within the DZLM (Deutsches Zentrum für Lehrkräftebildung Mathematik; German Center for Mathematics Teacher Education), which was financially supported by the German Telekom Foundation.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1325083/full#supplementary-material
1. ^In Germany, pre-service teacher education encompasses two central phases: bachelor/master programs at university (first phase, 5 years), followed by education programs at school (second phase, 1.5 years).
Barzel, B., Scherer, P., and Rolka, K. (in preparation). Qualifizierung von Multiplikatorinnen und Multiplikatoren – Zur besonderen Bedeutung des Gestaltungsprinzips der Ebenen-Verknüpfung.
Barzel, B., and Selter, C. (2015). Die DZLM-Gestaltungsprinzipien für Fortbildungen. J. Math.-Didakt. 36, 259–284. doi: 10.1007/s13138-015-0076-y
Bertram, J., and Rolka, K. (2022). Teachers’ content-related learning processes: professional development content on inclusive mathematics teaching used by teachers. Math. Teach. Educ. Dev. 24, 39–57.
Borko, H., Koellner, K., and Jacobs, J. (2014). Examining novice teacher leaders’ facilitation of mathematics professional development. J. Math. Behav. 33, 149–167. doi: 10.1016/j.jmathb.2013.11.003
Darling-Hammond, L., Hyler, M. E., and Gardner, M. (2017). Effective teacher professional development. Palo Alto, CA: Learning Policy Institute.
Dengerink, J., Lunenberg, M., and Korthagen, F. (2015). The professional teacher educator: six roles. Beiträge zur Lehrerinnen- und Lehrerbildung 33, 334–344. doi: 10.36950/bzl.33.3.2015.9556
Even, R. (2014). Challenges associated with the professional development of didacticians. ZDM Math. Educ. 46, 329–333. doi: 10.1007/s11858-014-0573-3
Felbrich, A., Müller, C., and Blömeke, S. (2008). Epistemological beliefs concerning the nature of mathematics among teacher educators and teacher education students in mathematics. ZDM Math. Educ. 40, 763–776. doi: 10.1007/s11858-008-0153-5
Jackson, K., Cobb, P., Wilson, J., Webster, M., Dunlap, C., and Applegate, M. (2015). Investigating the development of mathematics leaders’ capacity to support teachers’ learning on a large scale. ZDM Math. Educ. 47, 93–104. doi: 10.1007/s11858-014-0652-5
Karsenty, R. (2021). Implementing professional development programs for mathematics teachers at scale: what counts as success? ZDM Math. Educ. 53, 1021–1033. doi: 10.1007/s11858-021-01250-5
Kennedy, A. (2005). Models of continuing professional development: a framework for analysis. J. Serv. Educ. 31, 235–250. doi: 10.1080/13674580500200277
Koster, B., and Dengerink, J. (2001). Towards a professional standard for Dutch teacher educators. Eur. J. Teach. Educ. 24, 343–354. doi: 10.1080/02619760220128897
Krainer, K. (2015). “Scaling up professional development: changes and challenges.” In Conference Proceedings: educating the educators: international approaches to scaling-up professional development in mathematics and science education. eds. K. Maaß, B. Barzel, G. Törner, D. Wernisch, E. Schäfer, and K. Reitz-Koncebovski. (Münster: WTM). 96–110.
Krainer, K., and Zehetmeier, S. (2013). Inquiry-based learning for students, teachers, researchers, and representatives of educational administration and policy: reflections on a nation-wide initiative fostering educational innovations. ZDM Math. Educ. 45, 875–886. doi: 10.1007/s11858-013-0537-z
Kuckartz, U. (2019). Qualitative content analysis: from Kracauer's beginnings to Today's challenges. Forum Qual. Soc. Res. 20:12. doi: 10.17169/fqs-20.3.3370
Laschke, C., and Felbrich, A. (2014). “Erfassung der Überzeugungen.” In Teacher Education and Development Study. (TEDS-M 2008). Dokumentation der Erhebungsinstrumente. eds. C. Laschke and S. Blömeke. (Münster: Waxmann), 109–129.
Lipowsky, F., and Rzejak, D. (2015). Key features of effective professional development programmes for teachers. Ricercazione 7, 27–51.
Meyer, N. (2011). Einstellungen von Lehrerinnen und Lehrern an Berliner Grundschulen zur Inklusion. Eine empirische Studie. Masterarbeit. Berlin: Humboldt Universität Berlin.
Peters-Dasdemir, J., Holzäpfel, L., Barzel, B., and Leuders, T. (2020). “Professionalization for facilitators in mathematics education: a competency framework.” In Proceedings of the 44th conference of the International Group for the Psychology of mathematics education, interim. eds. M. Inprasitha, N. Changsri, and N. Boonsena. (Khon Kaen, Thailand: PME). 457–465.
Prediger, S., Götze, D., Holzäpfel, L., Rösken-Winter, B., and Selter, C. (2022). Five principles for high-quality mathematics teaching: combining normative, epistemological, empirical, and pragmatic perspectives for specifying the content of professional development. Front. Educ. 7:969212. doi: 10.3389/feduc.2022.969212
Prediger, S., Roesken-Winter, B., and Leuders, T. (2019). Which research can support PD facilitators? Strategies for content-related PD research in the three-tetrahedron model. J. Math. Teach. Educ. 22, 407–425. doi: 10.1007/s10857-019-09434-3
Prediger, S., Rösken-Winter, B., Stahnke, R., and Pöhler, B. (2022). Conceptualizing content-related PD facilitator expertise. J. Math. Teach. Educ. 25, 403–428. doi: 10.1007/s10857-021-09497-1
Roesken-Winter, B., Hoyles, C., and Blömeke, S. (2015b). Evidence-based CPD: scaling up sustainable interventions. ZDM Math. Educ. 47, 1–12. doi: 10.1007/s11858-015-0682-7
Roesken-Winter, B., Schüler, S., Stahnke, R., and Blömeke, S. (2015a). Effective CPD on a large scale: examining the development of multipliers. ZDM Math. Educ. 47, 13–25. doi: 10.1007/s11858-014-0644-5
Roesken-Winter, B., Stahnke, R., Prediger, S., and Gasteiger, H. (2021). Towards a research base for implementation strategies addressing mathematics teachers and facilitators. ZDM Math. Educ. 53, 1007–1019. doi: 10.1007/s11858-021-01220-x
Scherer, P., Nührenbörger, M., and Ratte, L. (2019). “Inclusive mathematics – in-service training for out-of-field teachers.” In SEMT 2019. International symposium elementary maths teaching. August 18–23, 2019. Proceedings: Opportunities in learning and teaching elementary mathematics. eds. J. Novotná and H. Moraova. (Prague: Charles University, Faculty of Education) 382–391.
Scherer, P., and Rolka, K. (2022). “Facilitators’ professional development for inclusive mathematics – addressing their different roles. Poster.” In CERME12. Proceedings of the Twelfth Congress of the European Society for Research in Mathematics Education. eds. J. Hodgen, E. Geraniou, G. Bolondi, and F. Ferretti. (Bozen: Free University of Bozen-Bolzano) 4525–4526.
Schleicher, A. (2020). The impact of COVID-19 on education – Insights from Education at a Glance 2020. Retrieved May, 5, 2021, Available at: https://www.oecd.org/education/the-impact-of-covid-19-on-education-insights-education-at-a-glance-2020.pdf.
Schoenfeld, A. H. (2015). Thoughts on scale. ZDM Math. Educ. 47, 161–169. doi: 10.1007/s11858-014-0662-3
Shulman, L. S. (1987). Knowledge and teaching: foundations of the new reform. Harv. Educ. Rev. 57, 1–23. doi: 10.17763/haer.57.1.j463w79r56455411
Smith, K. (2020). Expansive learning for teacher educators – the story of the Norwegian National Research School in teacher education (NAFOL). Front. Educ. 5:43. doi: 10.3389/feduc.2020.00043
Stake, R. E. (2005). “Qualitative case studies” in The SAGE handbook of qualitative research. eds. N. K. Denzin and Y. S. Lincoln. 3rd ed (Thousand Oaks, CA: SAGE), 443–466.
Thomas, G. (2004). A typology of approaches to facilitator education. J. Exp. Educ. 27, 123–140. doi: 10.1177/105382590402700202
Thomas, G. (2011). A typology for the case study in Social science following a review of definition, discourse, and structure. Qual. Inq. 17, 511–521. doi: 10.1177/1077800411409884
Timperley, H., Wilson, A., Barrar, H., and Fung, I. (2007). Teacher professional learning and development. Best evidence synthesis iteration. Wellington, New Zealand: Ministry of Education.
Tirosh, D., Tsamir, P., and Levenson, E. (2015). Fundamental issues concerning the sustainment and scaling up of professional development programs. ZDM Math. Educ. 47, 153–159. doi: 10.1007/s11858-015-0665-8
Witzel, A. (2000). The problem-Centered interview. Forum Qual. Soc. Res. 1:22. doi: 10.17169/fqs-1.1.1132
Keywords: facilitators, professional development, scaling up, inclusive mathematics, reasons for dropout
Citation: Scherer P and Rolka K (2024) Challenges in facilitators’ professional development – complexities within a scaling up process as reasons for dropout. Front. Educ. 9:1325083. doi: 10.3389/feduc.2024.1325083
Received: 20 October 2023; Accepted: 09 April 2024;
Published: 09 May 2024.
Edited by:
Cheryl J. Craig, Texas A and M University, United StatesReviewed by:
Dan O’Sullivan, University of Limerick, IrelandCopyright © 2024 Scherer and Rolka. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Katrin Rolka, a2F0cmluLnJvbGthQHJ1Yi5kZQ==
†These authors have contributed equally to this work and share first authorship
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.